Mapping Hebbian Learning Rules to Coupling Resistances for Oscillatory Neural Networks

Oscillatory Neural Network (ONN) is an emerging neuromorphic architecture with oscillators representing neurons and information encoded in oscillator's phase relations. In an ONN, oscillators are coupled with electrical elements to define the network's weights and achieve massive parallel computation. As the weights preserve the network functionality, mapping weights to coupling elements plays a crucial role in ONN performance. In this work, we investigate relaxation oscillators based on VO₂ material, and we propose a methodology to map Hebbian coefficients to ONN coupling resistances, allowing a large-scale ONN design. We develop an analytical framework to map weight coefficients into coupling resistor values to analyze ONN architecture performance. We report on an ONN with 60 fully-connected oscillators that perform pattern recognition as a Hopfield Neural Network.

1. Introduction

Coupled oscillators have been studied for decades by scientists to describe natural phenomena (Winfree, 1967) such as the synchronization of pacemaker cells responsible for the heart beating, the synchronous behavior of insect populations, or to model neuronal activity. For instance, oscillator interactions have been shown to describe memory mechanisms and other cognitive processes in the brain (Fell and Axmacher, 2011). To characterize this variety of natural oscillations, several mathematical models (Acebrón et al., 2005; Izhikevich and Kuramoto, 2006) have been developed to explain the synchronization and phase relations in groups of coupled oscillators. Meanwhile, their massive parallel computing capability has been proved by Hoppensteadt and Izhikevich (2000), Vassilieva et al. (2011), and Parihar et al. (2017) and has raised interest in designing ONN as hardware accelerators for Artificial Neural Networks (ANN) by encoding neurons' activation in the phase between oscillators. Different types of ONN have since been developed using PLLs (Hoppensteadt and Izhikevich, 2000) or oscillators in CMOS technology (Maffezzoni et al., 2015a, 2016; Jackson et al., 2018), demonstrating pattern recognition or resolution of some optimization problems like the Traveling-Salesman-Problem (Endo and Takeyama, 1992). However, to design a competitive ONN at a large scale, a design framework is needed to establish a formalism on how to perform computations with ONN and also compare its energy efficiency with ANNs running on digital processors.

Researchers have developed oscillators by using non-linear devices such as spin-torque-oscillators (Raychowdhury et al., 2019) or with materials presenting a hysteresis resistive state to induce electrical oscillations when properly biased (Sharma et al., 2015; Wang et al., 2017). A compact device that transitions from metallic to insulating state (MIT) can be manufactured with vanadium dioxide (VO₂) (Corti et al., 2018), and has recently become an interesting candidate to design energy-efficient relaxation oscillators. Moreover, coupled-VO₂-based oscillators have been experimentally validated for various applications such as image saliency detection (Shukla et al., 2014), graph coloring (Parihar et al., 2017), filters in Convolutional Neural Networks (Corti et al., 2021) and implementing Hopfield Neural Networks (HNN) for pattern recognition (Corti et al., 2020).

In an HNN defined by Hopfield (1982), every neuron is connected to all the others, and synaptic weights are computed with the Hebbian rule (Hoppensteadt and Izhikevich, 2000). However, setting the right coupling element between oscillators in ONNs remains a challenge (Todri-Sanial et al., 2021). Given N fully-coupled VO₂-oscillators, it is yet unknown how to transform the coefficients obtained analytically via the Hebbian learning rule to coupling resistor values among oscillators. Further, how can one interpret the coefficient signs W_ij such as positive or negative values?

For weakly coupled oscillators with sinusoidal waveform, one can use the models that exist in literature (Izhikevich and Kuramoto, 2006; Maffezzoni et al., 2016) for synaptic design. However, it is more difficult for non-linear relaxation oscillators as there is no direct mapping between models and hardware. Two VO₂-oscillators coupled by a capacitance or a resistance have been studied (Maffezzoni et al., 2015b; Parihar et al., 2015), but to the best of our knowledge, there is not yet a formalism to map weights to coupling elements in a larger network. This formalism is a crucial step to allow large-scale ONN design exploration. A greedy approach would be to tune the coupling elements corresponding to the most negative and most positive weights and linearly interpolate all the other weight values. However, this would be impractical. It would require repeated simulations and re-tuning coupling resistances when changing any oscillator parameter; hence, it is not suitable for large-scale ONN design. Parihar et al. (2015) proposed to use capacitors or resistors to implement a negative or a positive weight, respectively. However, it would imply using twice as many components to emulate a complete signed synaptic range.

In this work, we propose a mathematical framework to map both negative and positive Hebbian coefficient values to ONN coupling resistances, as illustrated on Figure 1. We first present a single VO₂-oscillator followed by the dynamics of two coupled oscillators. Then, we show that adding switches between oscillators and coupling elements enhances the ONN dynamics control. Based on this simple architecture, we present the ONN computation style and how coupling resistances set the ONN memory expressed in different phase states. Next, by merging oscillators' dynamics with HNN formalism, we introduce the ONN mapping function that maps Hebbian coefficient values to coupling resistance values. Finally, we report on the architecture and mapping results by simulating 60 coupled VO₂-oscillators for pattern recognition.

FIGURE 1

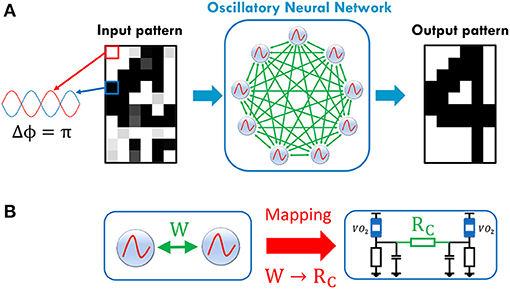
Figure 1. (A) Illustration of ONN as a Hopfield Neural Network (HNN). HNN binary activations are translated in the phase relation between oscillators and a reference (here the first oscillator). ONN stores patterns via weights between the oscillators. Patterns can be retrieved if the input pattern is sufficiently close to the stored pattern. (B) The proposed mapping function to map any weight to a coupling resistance, facilitating large scale ONN design.

2. Materials and Methods

2.1. Description of the ONN Building Blocks

2.1.1. General Properties

Unlike most ANNs where signals of interest are amplitudes, ONN consists of N VO₂-oscillators coupled by resistances where the final result is given by N-1 phase relations to a reference oscillator (Corti et al., 2018). Despite this difference, there are several aspects common to any ANN that motivate our ONN study:

• The network is composed of neurons (oscillators) having input and output nodes.

• The activation function between the oscillator input and output is non-linear. For more than two oscillators, the activation function is unknown but bounded as the output phase difference of neuron i $\text{Δ}{\varphi }_i^{out}$ is in the range [0;180°].

• ONN has a memory (coupling resistances) and can therefore be trained to achieve specific functionality.

We use these properties to implement an HNN (Hopfield, 1982) by encoding its binary outputs in the ONN phase as shown in Figure 1A. Conveniently, we can represent each oscillator's output as a black pixel if $\Delta {\varphi }_i^{out}=180^{°}$ or as a white pixel if $\Delta {\varphi }_i^{out}=0^{°}$.

2.1.2. VO₂ Device

Vanadium dioxide is a material which presents temperature-driven phase change transitions. At room temperature, it remains semiconductor (insulating state) with a monoclinic crystal structure and transitions to a rutile metallic state when the temperature reaches a threshold (Corti et al., 2021). VO₂ presents an hysteresis behavior as it needs to reach a lower temperature threshold to transition back to the insulating state (Figure 2A).

FIGURE 2

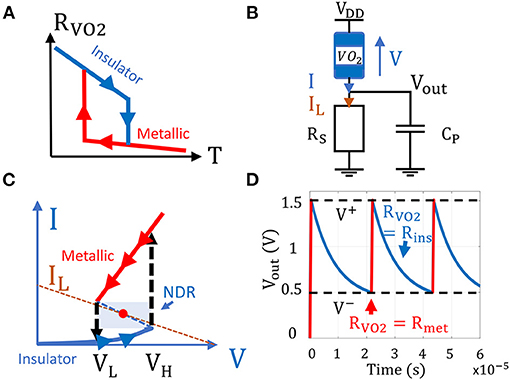
Figure 2. (A) VO₂ resistance vs. temperature. R_VO2 axis is in logarithmic scale. (B) VO₂ oscillator circuit (C) VO₂ I-V curve showing the device hysteresis behavior. When its voltage reaches a threshold V_H, it transitions from insulating to the metallic state. To transition from a metallic to insulating state, V must be lower than the threshold V_L. (D) If the device is biased in its Negative Differential Resistance region (NDR), its state alternates between the metallic and insulating state, producing electrical oscillations.

When a VO₂ device is in series with a biasing load (Figure 2B), the voltage drop V across the device induces Joule heating which can trigger the insulating to metallic transition (IMT). To obtain the VO₂ IV characteristic, we sweep the supply voltage which triggers IMT and MIT when V ≥ V_H and V ≤ V_L, respectively. The VO₂ hysteresis behavior appears in the IV characteristic with a typical Negative Differential Region (NDR) suitable to bias the device and produce oscillations (Figure 2C).

In this work, we use the VO₂ compact model from Maffezzoni et al. (2015b) which reproduces the VO₂ hysteresis along with continuous and abrupt transitions between the two states. The VO₂ hysteresis behavior is conceptually emulated by an amplifier with positive feedback that charges or discharges a RC circuit when the VO₂ is in metallic or insulating state, respectively. The voltage V_c across the capacitor commands the VO₂ conductance G_VO2 as:

$\begin{array}{ll}{G}_{V{O}_2}(t)=\frac{1-V_c(t)}{R_{ins}}+\frac{V_c(t)}{R_{met}}& (1)\end{array}$

Where R_ins and R_met are the VO₂ resistances in insulating and metallic state, respectively. The dynamics of the VO₂ conductance is given by the RC circuit where τ₀ is its time constant modeling the transition time of the VO₂:

$\begin{array}{ll}{\tau }_0\frac{d{V}_c(t)}{dt}+V_c(t)=1-V_0(t)& (2)\end{array}$

V₀(t) is the output of the positive feedback amplifier (gain α) and is expressed as:

$\begin{array}{ll}{V}_0(t)=\frac{1}{2}[1+\tanh (2\alpha ((V_H-V_L)V_0(t)+V_L-V(t))\left)\right]& (3)\end{array}$

2.1.3. VO₂ Oscillator Circuit and Dynamics

We bias the VO₂ device with a series resistor R_S to obtain a compact relaxation oscillator. To produce oscillations, the load line I_L set by V_DD and R_S must intercept the VO₂ I-V curve in its NDR to obtain an unstable fixed point (Figure 2C). The VO₂ device state hence alternates between the metallic and insulating state. When the VO₂ device is in the insulating state, the parallel capacitance C_P at the output node discharges through R_S until the VO₂ voltage reaches V_H and transitions to the metallic state. Then, C_P charges through the VO₂ device until its voltage reaches V_L and a new cycle begins (Figure 2D).

We use circuit parameters depicted in Table 1. In this case, the load resistance R_S is 20 times larger than the VO₂ metallic resistance R_met; thus, the capacitance charge time is much faster than its discharge (Figure 2D).

TABLE 1

Table 1. List of parameters used for simulations in this work.

Oscillator's dynamics can be described by Kirchoff's law as:

$\begin{array}{ll}{C}_P\frac{d{V}_{out}(t)}{dt}=(V_{DD}(t)-V_{out}(t))G_{V{O}_2}(t)-\frac{V_{out}(t)}{R_S}& (4)\end{array}$

Note that despite the first order differential equation, oscillations can occur as Equations (1–3) describe the hysteresis behavior of G_VO2(t). To solve the oscillator dynamics, we start from an initial insulating VO₂ state and solve numerically on Matlab the system of Equations (1–4) by using Euler's method and Newton-Raphson's algorithm for non-linear Equation (3). Figure 2D shows an example where V_out(t = 0) = 0V, G_VO2(t = 0) = 1/R_ins, and V_DD(t = 0) = 2.5V.

2.1.4. Initialization of Two Coupled Oscillators

Two coupled oscillators represent the smallest ONN and serve as the building block for large-scale ONN. To provide input to the ONN, we delay the second oscillator V_DD starting time with respect to the first oscillator (reference oscillator) to set an initial phase relation between them. Assuming oscillators have the same period T_osc, we can translate the input delay Δt_init as an initial phase relation as:

$\begin{array}{ll}\Delta {\varphi }_{init}=\frac{\Delta t_{init}}{T_{osc}}2\pi & (5)\end{array}$

However, if the two oscillators are always connected, they might have different oscillation periods during initialization. Therefore, their initial phase relation cannot be represented as a proportion of T_osc (5). For example, as shown in Figure 3A, the second oscillator starts Δt_init = 0.5T_osc after the first one to set an initial phase relation Δϕ_init = π. For t < Δt_init, the second oscillator is off, and its output node is floating. Therefore, during this time, the equivalent load resistance of the first oscillator is R_S//R_C, which induces a shorter period of oscillation $T_{osc}^{\prime }<T_{osc}$ and hence no control on the initial phase.

FIGURE 3

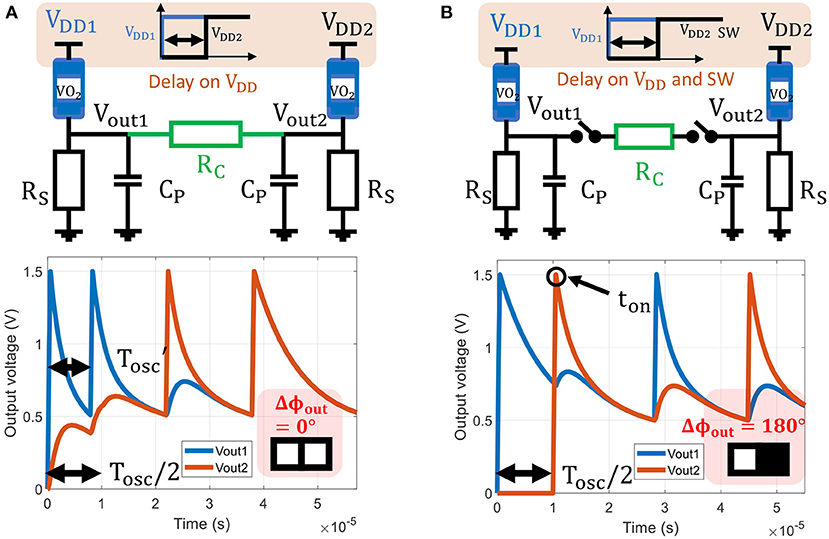
Figure 3. (A) Two oscillators are coupled by a resistance R_C=10 kΩ without coupling switches in between. V_DD2 is turned-on 0.5T_osc after V_DD1 to set an initial phase of 180°. However, for t < 0.5T_osc the first oscillator period is decreased due to the shunt R_C at its output node, and we cannot control the initial phase difference. The two oscillators are in-phase after convergence. (B) Two oscillators coupled with resistance R_C=10 kΩ and coupling switches between isolate the oscillators during initialization. This time, the 0.5T_osc input delay sets desired 180° initial phase state. Here, the switches are closed at t_on = 0.5T_osc + t_c such that $V_{out2}(t_{on})=V^{+}$. The two oscillators converge to an 180° phase state relation.

We introduce switches between each oscillator and coupling elements as in Figure 3B to tackle this lack of control. We let each oscillator switch freely with a known oscillation period T_osc before coupling them at t_on. Their dynamics can be expressed by Equation (4) and the initial conditions will be known at t_on. ONN initialization is improved at the cost of one additional switch per oscillator, which can be achieved with a transfer gate.

2.1.5. Dynamics of Two Coupled Oscillators

To predict the output phases and demonstrate ONN ability to store information, we express the dynamics of the two coupled oscillators using Kirchhoff's laws:

$\begin{array}{ll}\{\begin{array}{c}{C}_P\frac{d{V}_{out1}(t)}{dt}=(V_{DD1}(t)-V_{out1}(t))G_{V{O}_2}^1(t)-\frac{V_{out1}(t)}{R_S}+I_{c1}\\ C_P\frac{d{V}_{out2}(t)}{dt}=(V_{DD2}(t)-V_{out2}(t))G_{V{O}_2}^2(t)-\frac{V_{out2}(t)}{R_S}+I_{c2}\end{array}& (6)\end{array}$

Currents are I_c1 = −I_c2 representing the coupling element's current flow. As for the single oscillator case, we numerically solve (Equation 6) along with VO₂ (Equations 1–3). Figure 4 shows a simulation where V_DD2 is turned on 0.1T_osc after V_DD1 which initializes a light-gray pixel for oscillator 2 input image. For a small coupling resistance, R_C=10 kΩ, ONN converges to a stable state with both oscillators in-phase (0°,0°). Whereas, for R_C=100 kΩ, ONN converges to out-of-phase (0°,180°). In the next subsection, we study the role of R_C on ONN memory and investigate how to retrieve a stored pattern by applying an input delay Δt_init. This formulation is the core of our proposed mapping function to translate Hebbian coefficients to ONN coupling resistances.

FIGURE 4

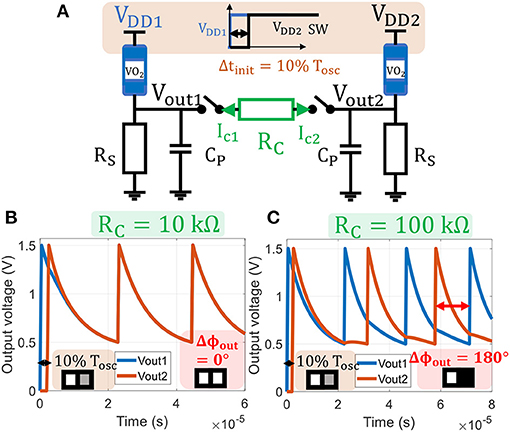
Figure 4. (A) Two identical VO₂ oscillators are coupled with a resistance R_C and switches. V_DD2 starting time and coupling time t_on are delayed by 0.1T_osc with respect to the first oscillator, representing a light-gray second pixel as ONN input. (B) Output voltages for R_C = 10kΩ: the oscillators converge to an in phase state (0°, 0°) and the corresponding output pattern corresponds to two white pixels. (C) Output voltages for R_C = 100kΩ: the oscillators are out-of-phase (0°, 180°) and the output pattern corresponds to a white and a black pixels.

2.1.6. Memory of Two Coupled Oscillators

We solve numerically (6) and extract the output phase relation between oscillators. Figure 5A shows the simulation results. As already observed by Corti et al. (2018), a large coupling resistance R_C > 40 kΩ induces oscillators in out-of-phase relation (0°, 180°) for any input delay, whereas a small coupling resistance R_C < 10kΩ aligns oscillators in-phase (0°, 0°) for any input delay.

FIGURE 5

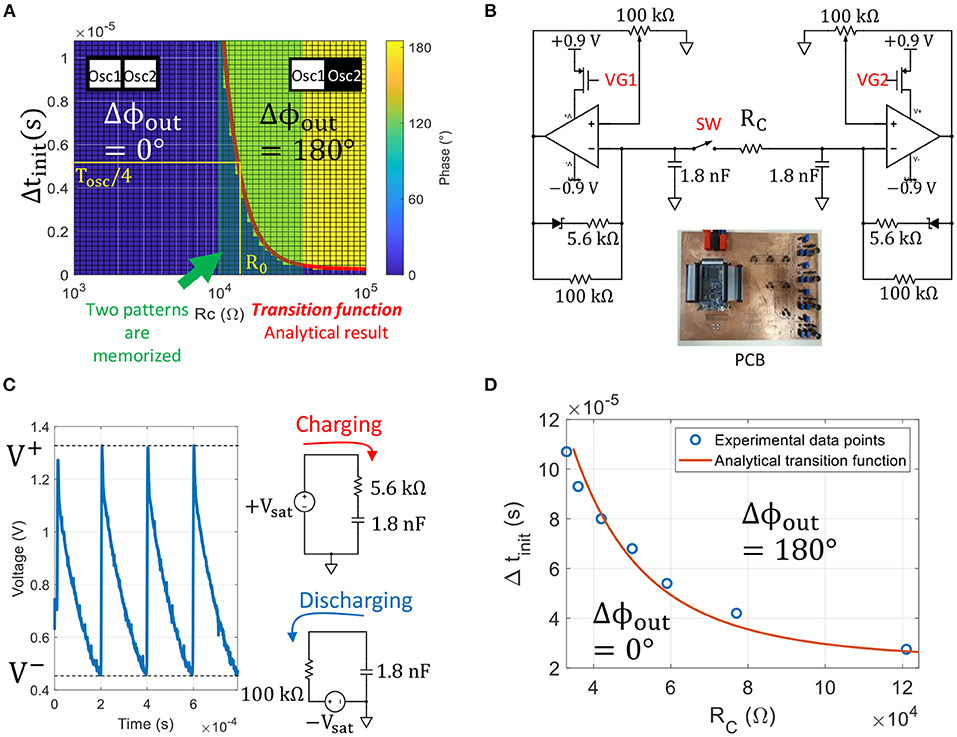
Figure 5. (A) Plot showing the phase relation between two oscillators for every set of parameters (R_C, Δt_init). As expected, small coupling resistances tend to pull the oscillator phase together, whereas large coupling resistances push the phase away. The green region shows the coupling resistance range 10kΩ < R_C < 40kΩ in which two patterns (0° and 0°) and (0° and 180°) are memorized and can be retrieved by adjusting the input delay. The red curve is our analytical model describing the transition between the two phase states in the plan (R_C, Δt_init), and plays a major role in the ONN ability to memorize patterns. (B) Experimental set-up of two coupled relaxation oscillators based on MCP6001 OPAs. We delay VG2 with respect to VG1 by Δt_init to set the initial phase, and we close SW after initialization. (C) Experimental oscillating waveform and equivalent circuits during charge and discharge of the output capacitor. (D) Experimental phase transition curve and analytical model in plain line.

In contrast, we examine the region between these two ranges, highlighted in the center of Figure 5A. We observe that for 10kΩ ≤ R_C ≤ 40kΩ both states co-exist and oscillators store two patterns (0°, 0°) and (0°, 180°) that can be retrieved by adjusting the input delay. The line transition function between in-phase and out-of-phase regions represents our analytical function for ONN memory with respect to coupling resistance and initialization. It is defined as:

$\begin{array}{ll}\begin{array}{c}\hfill \zeta :R_C\to \Delta t_{transit}\end{array}& (7)\end{array}$

With Δt_transit the initial delay such that:

$\begin{array}{ll}\Delta t_{transit}=\zeta (R_C)|\{\begin{array}{l}\Delta t_{init}<\Delta t_{transit}\Rightarrow \Delta {\varphi }_{out}=0^{°}\\ \Delta t_{init}\ge \Delta t_{transit}\Rightarrow \Delta {\varphi }_{out}=180^{°}\end{array}& (8)\end{array}$

To confirm the existence of ζ(R_C), we emulate VO₂ oscillators with off-the-shelf components on a Printed Circuit Board (PCB) and we reproduce the experiment of two coupled oscillators. The relaxation oscillator circuit consists of an inverting Schmitt trigger (Schmitt, 1938) Operational Amplifier (OPA) that implements the VO₂ hysteresis behavior (Figure 5B). The OPA saturates to +V_sat and −V_sat while the 1.8 nF output capacitor charges and discharges, respectively. Figure 5C shows the voltage across the output capacitor for a decoupled oscillator. Similarly to a VO₂ oscillator, the OPA transitions to another state when the voltage across the output capacitor reaches V⁺ or V⁻. The 5.6 kΩ resistor implements the metallic VO₂ resistance, whereas the 100 kΩ resistor corresponds to the load R_S. For a fixed oscillating period of T_osc=200 μs, we vary R_C and we measure Δt_transit values that define the experimental transition function ζ(R_C) (Figure 5D). There is a good match between experimental ζ(R_C) data points and the analytical transition function derived in next subsection. Such formulation ζ(R_C) is of interest as it represents a closed-form representation of ONN memory instead of repeating numerical simulations for different oscillator parameters.

2.1.7. Phase Transition Function for Two Coupled Oscillators

The phase transition function has already been observed (Nez et al., 2021) but to the best of our knowledge, no closed-form expression has ever been reported. To obtain the transition function, we solve node voltage equations analytically for two coupled oscillators during initialization (see Supplementary Material). We derive oscillator outputs as:

$\begin{array}{ll}\Delta V=V_{out2}-V_{out1}=(V_{out2}^0-V_{out1}^0)exp(-\frac{t}{{\tau }^{\prime }})& (9)\end{array}$

$V_{out1}^0$ and $V_{out2}^0$ are the initial voltages when oscillators are coupled and τ′ is defined in Supplementary Material Equation (S18). Equation (9) describes both oscillator output voltages attracted via the coupling resistance R_C. If the coupling is strong enough (small R_C), both oscillators are rapidly pulled together with a speed determined by τ′. If ΔV < ϵ (ϵ defined in Supplementary Material Equation S22) before reaching the VO₂ threshold V⁻, then both oscillators will transition to low resistive states, and the exponential term in Equation (9) will keep the two voltages locked. This concept is illustrated in Figure 6A when both oscillators are in-phase. However, if V_out1 reaches V⁻ before V_out2 such that ΔV > ϵ as in Figure 6B, the first oscillator transitions to a low resistance state (metallic state) while the other oscillator is still in high resistance state (insulating state). The two oscillators are then in opposite states, and this leads to out-of-phase relation.

FIGURE 6

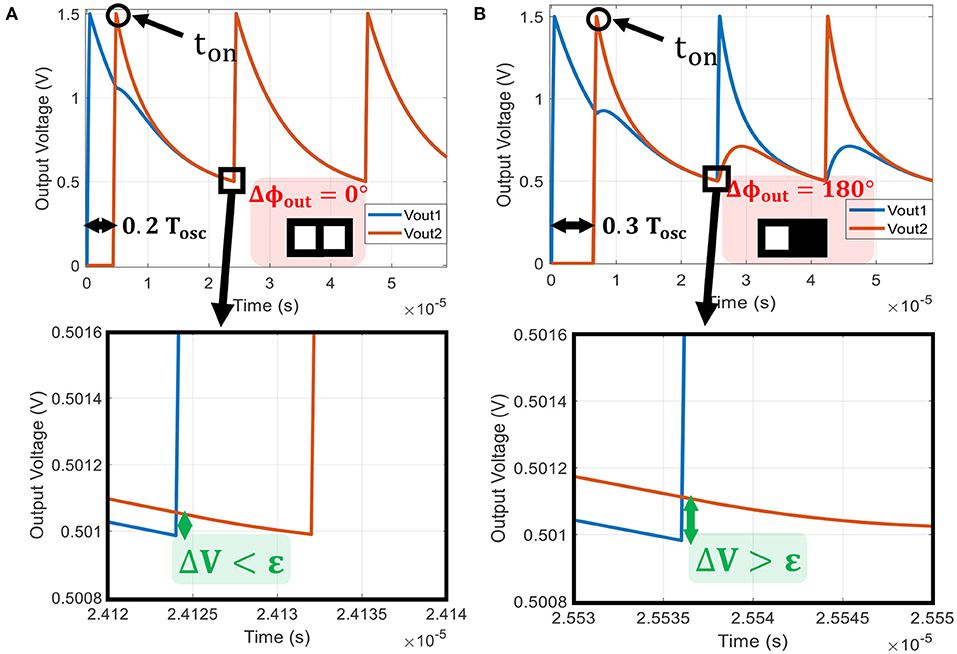
Figure 6. Two identical oscillators coupled by R_C = 12kΩ. (A) The second oscillator is turned on at 0.2 T_osc after the first one. By zooming on the waveform when the first oscillator reaches V⁻, we observe a voltage difference ΔV < ϵ. Therefore, the oscillators converge to an in-phase state. (B) The second oscillator is turned-on 0.3 T_osc after the first one. In this case, we observe a voltage difference ΔV > ϵ and the oscillators converge to an out-of-phase state.

Thus, to obtain the transition function ζ (Equation 7), we study the case when both ΔV = ϵ and $V_{out1}=V^{-}$ conditions are fulfilled (see Supplementary Material for details). By combining (Equations S17, S24, and S25 in Supplementary Material) we derive coupling resistance as:

$\begin{array}{ll}{R}_C=2\frac{R_S{R}_{ins}}{R_S+R_{ins}}\frac{log\left(\frac{V^{-}-V_{std}^{ins}}{V_{out1}^0/2+V_{out2}^0/2-V_{std}^{ins}}\right)}{log\left(\frac{ϵ(R_C)}{V_{out2}^0-V_{out1}^0}\right)-log\left(\frac{V^{-}-V_{std}^{ins}}{V_{out1}^0/2+V_{out2}^0/2-V_{std}^{ins}}\right)}& (10)\end{array}$

where $V_{std}^{ins}$ is defined in Supplementary Material Equation (S5). Finally, we introduce (Equation S9 in Supplementary Material) into Equation (10), and obtain a relation between R_C and Δt_transit. Note that ϵ is a function of R_C, thus we cannot solve (10) analytically. Instead, we numerically solve (Equation 10) using Newton-Raphson's algorithm for Δt_transit values. We finally obtain R_C values that describe the inverse of the transition function as:

$\begin{array}{ll}\begin{array}{c}\hfill {\zeta }^{-1}:\Delta t_{transit}\to R_C\end{array}& (11)\end{array}$

Transition function ζ is plotted as the curve line (red line) in Figure 5A, and there is an excellent fit between our analytical model, simulations (transition region between dark and light green in (R_C, Δt_init) plan) and the transition curve obtained experimentally with off-the-shelf relaxation oscillators (Figure 5D). In addition, we can now extract the coupling resistor R₀ that corresponds to a neutral synaptic connection W = 0. As by definition, both output phase states can equally occur for W = 0, we extract R₀ as:

$\begin{array}{ll}{R}_0={\zeta }^{-1}(\Delta t_{init}=T_{osc}/4)& (12)\end{array}$

Finally, based on the transition function, we predict the final phase relation as:

$\begin{array}{ll}\Delta {\varphi }_{out}=180^{°}\left(sign\right(R_C-{\zeta }^{-1}(\Delta t_{init}))+1)/2& (13)\end{array}$

Analogous to ANNs, Equation (13) can be thought of as oscillator's activation function. Because, it provides the oscillator's output phase based on its input phase (set by Δt_init; Equation 5) and the weight implemented by R_C.

2.1.8. Impact of VO₂ Parameters Variations on the Phase Transition Function

Fabricating reliable VO₂ devices is challenging (Corti et al., 2019) and ONN experiments with VO₂ are currently limited to few devices because of device variability (Shukla et al., 2016). Here, we study the impact of VO₂ variability on the ability to phase-lock and on the synaptic range. The transition function ζ(R_C) defines the boundary between two phase regions, and allows direct identification of the neutral coupling resistor R₀ corresponding to the weight W = 0 (Equation 12). Thus, we use ζ and R₀ as metrics to assess the impact of VO₂ parameters' variations. We apply relative variations on VO₂ parameters one at a time from –20% up to +20%, as shown in Figure 7A. Note that we vary V_H from –4% up to +4% only, as for larger positive variations oscillations do not occur (load line crosses the insulating branch and forms a fixed point). For all cases, we discretize the whole input space (R_C, Δt_init) and perform multiples transient simulations to extract the new phase regions. Then, we numerically solve (Equation 10) with the new sets of parameters and we verify that the transition function ζ matches the phases boundary obtained via transient simulations, as in Figure 5A.

FIGURE 7

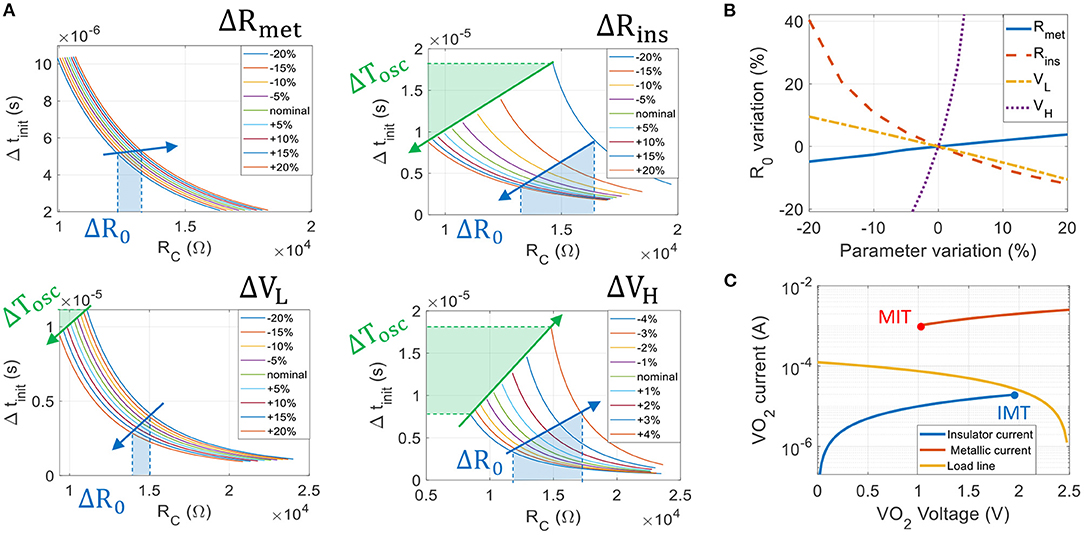
Figure 7. (A) Phase transition curves ζ(R_C) when varying VO₂ parameters R_met, R_ins, V_L from –20 to +20%, and V_H from –4 to +4% for circuit parameters listed in Table 1. Left hand side of the transition curve corresponds to inputs (Δt_init, R_C) inducing $\Delta {\varphi }_{out}=0^{°}$ whereas right hand side corresponds to $\Delta {\varphi }_{out}=180^{°}$ phase region. V_H and R_ins variations correspond to IMT point variations and have the most detrimental impact on the transition function variations. The oscillating period almost doubles due to IMT variations. (B) Variations of the neutral synaptic resistance R₀ with respect to VO₂ parameters' variations. R₀ is very sensitive to V_H as –4 and +4% V_H variations induce –20 and +40% R₀ variations, respectively. (C) The ONN sensitivity to IMT point is mainly due to the load line I_L = (V_DD−V)/R_S placed close to IMT point. Any IMT variation greatly impacts the oscillators' dynamics defined by C_PdV/dt = I_L−I.

Figure 7A shows the set of phase transition curves obtained when varying R_met, R_ins, V_L and V_H. Note that our current formalism assumes matched oscillators and hence, variations are applied to both coupled oscillators. For all curves, the maximum Δt_init value corresponds to an input delay of T_osc/2 and shows the oscillation period variation (highlighted in green in Figure 7A). Finally, we extract R₀ for each configuration (Figure 7B). We observe that variations on the IMT point (defined by R_ins and V_H) induce the largest T_osc and R₀ variations. With our biasing set by R_S and V_DD (Table 1), the most sensitive VO₂ parameter is V_H as +4 and –4% V_H variations induces +40 and –20% R₀ variations, respectively. As the dynamic of the voltage V across the VO₂ device is given by C_PdV/dt = I_L−I, we believe this sensitivity is mainly due to the load line that passes very close to the IMT point on the VO₂ IV characteristic (Figure 7C). In this case near IMT, I_L(V_H)−I(V_H) is small and the voltage “slows down” and is very sensitive to any IMT variation. When applying –4% up to +4% V_H variations, the oscillating period T_osc almost doubles (same remark with –20 and +20% R_ins variations). Ideally, we would then place the load line at equal distances between MIT and IMT points (I(V_L) − I_L(V_L) ≈ I_L(V_H) − I(V_H)) to homogenize the impact of VO₂ variations. However, we show in the next subsection that such biasing would prevent binary phase locking and that resistively coupled oscillators need a very asymmetric waveform to phase-lock to 180°.

2.1.9. Impact of Oscillators' Waveform Shape on ONN Phase-Locking

Oscillators' circuit parameters listed in Table 1 influence the oscillating frequency, amplitude and waveform shape. The oscillating waveform shape has a major influence on ONN phase-locking capability and has been studied for PLL-based ONNs by Hoppensteadt and Izhikevich (2000). Here, we study the impact of the oscillating waveform shape on the capability for pairs of oscillators to lock to the 180° phase state. We characterize the oscillating waveform shape with the ratio τ_d/τ_c, where τ_d and τ_c are the discharging and charging time constant, respectively (defined in Supplementary Material Equations S6, S7). Our transition function ζ links ONN phase-locking properties to the metric τ_d/τ_c, as ζ only depends on oscillators' internal parameters.

We reproduce the previous simulation with two coupled oscillators to extract the output phase regions for different load resistances R_S that set τ_d/τ_c (Figure 8A). Note that we also could have varied VO₂ parameters such as R_met, but instead we consider the same device. For τ_d/τ_c = 3.7 (R_S = 3 kΩ), we observe that the two oscillators cannot lock to $\Delta {\varphi }_{out}=180^{°}$ for small Δt_init values. In other words, the phase state $\Delta {\varphi }_{out}=180^{°}$ stored by a large R_C cannot be fully recovered. This can be an issue for some pairs of oscillators that need an out-of-phase relationship for any input delay.

FIGURE 8

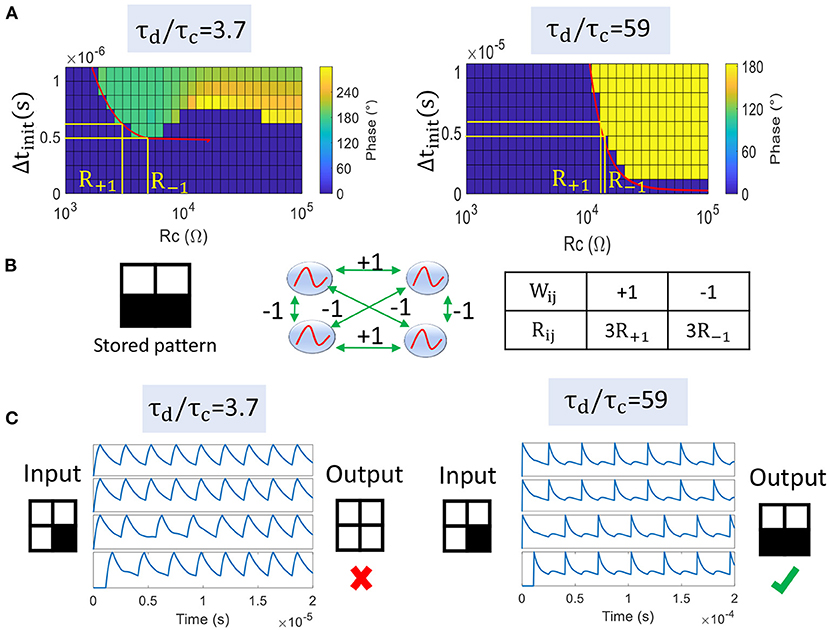
Figure 8. (A) Phase plots showing Δϕ_out with respect to Δt_init and coupling resistance R_C between two oscillators. For τ_d/τ_c = 3.7, 180° phase state is not reachable for low Δt_init values. In contrast for τ_d/τ_c = 59, 180° phase-locking can occur for any Δt_init value for large R_C. The red line is our analytical model ζ(R_C) and captures well the boundary between phase regions. (B) Four coupled oscillators store a pattern composed of 2 white and 2 black pixels. Positive and negative weights are mapped to 3xR₊₁ and 3xR₋₁, respectively. (C) ONN inference for τ_d/τ_c = 3.7 and τ_d/τ_c = 59. The first configuration leads to a wrong in-phase relationship for all oscillators. In the latter case, ONN retrieves the correct stored pattern.

If τ_d/τ_c = 59 (R_S = 20 kΩ), the charging time is much smaller than the discharging time and the oscillating waveform becomes very asymmetrical. Interestingly, this configuration enlarges the 180° phase region and $\Delta {\varphi }_{out}=180^{°}$ is reachable for any Δt_init value for large R_C. Our analytical model ζ(R_C) predicts the correct boundary between the two phase regions (red plain lines in Figure 8A).

We study a simple case where 4 VO₂-oscillators are coupled by resistances to store a single pattern (Figure 8B). Based on transition functions obtained for 2 coupled oscillators, we compute coupling resistances R₊₁ and R₋₁ that correspond to synaptic coefficients +1 and –1, respectively. We set R₊₁ and R₋₁ around R₀ as $R_{+1}={\zeta }^{-1}(T_{osc}/4+T_{osc}/8)$ and $R_{-1}={\zeta }^{-1}(T_{osc}/4-T_{osc}/8)$, respectively. Then, we scale coupling resistances as 3xR₊₁ and 3xR₋₁ as every oscillator is connected to 3 others (Figure 8B). We notice that ONN with τ_d/τ_c = 59 retrieves the correct stored pattern whereas ONN with τ_d/τ_c = 3.7 produces a wrong output (Figure 8C). In the latter case, we observe that all oscillators converge to an in-phase relationship. We believe this wrong behavior is mainly due to the small τ_d/τ_c value for which it is less likely ONN converges to $\Delta {\varphi }_{out}=180^{°}$, as described by the transition function ζ.

Figure 9 shows results of the same experiment for τ_d/τ_c varied from 1.8 up to 59 (obtained for 2 kΩ ≤ R_S ≤ 20 kΩ). We observe that τ_d/τ_c > 20 is required to retrieve the correct pattern. Interestingly for τ_d/τ_c ≤ 20, there are cases where the fourth oscillator locks to a phase state around 270°. 270° phase value is also obtained in the phase plot between two coupled oscillators, such as on the left-hand side of Figure 8A. This phenomenon would allow more than two phase values but is not captured by our current formalism. In contrast, we set τ_d/τ_c to high values (59 in this work) to ensure binary 0° and 180° phase locking.

FIGURE 9

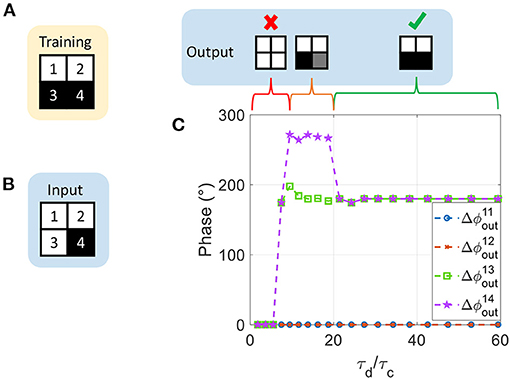
Figure 9. (A) Training pattern stored by the ONN. (B) ONN input pattern. (C) Output phase with respect to τ_d/τ_c. For τ_d/τ_c < 7, all oscillators converge to a wrong in-phase relationship. For 7 ≤ τ_d/τ_c < 20, the fourth oscillator locks to a 270° phase state. A very asymmetrical waveform such that τ_d/τ_c ≥ 20 leads to a correct binary phase-locking.

To implement a large-scale neural network such as HNN with an ONN, we need a systematic approach to map the weights to ONN coupling resistances. In the next section, we exploit some HNN features and our knowledge of two coupled oscillators to propose a mapping function.

2.2. ONN Weight Mapping

2.2.1. Applying HNN Formalism to ONN

We exploit HNN formalism to build an analogous representation in ONN. For equivalence, we treat HNN neurons similar to ONN oscillators. Such as, we consider a neuron i with two possible states S_i that can be thought of as equivalent to ONN oscillators with 0° or 180° phase relations as:

$\begin{array}{ll}{S}_i=\{\begin{array}{c}+1\\ -1\end{array}\iff \Delta {\varphi }_i=\{\begin{array}{l}{0}^{°}\\ 180^{°}\end{array}& (14)\end{array}$

In HNN, each neuron output state is dynamically determined by a sigmoid activation function g(x) = (tanh(βx) + 1)/2 (with β a positive parameter) (Gerstner et al., 2014) and shown in Figure 10. For a neuron i, g gives the probability to reach one of the two states at t + Δt for a given input weighted sum h_i(t) as

$\begin{array}{ll}P(S_i(t+\Delta t)=+1|h_i(t))=g\left(h_i(t)\right)& (15)\end{array}$

with

$\begin{array}{ll}{h}_i(t)={\displaystyle \sum _{j=1}^N}{W}_{ij}{S}_j(t)& (16)\end{array}$

In ONNs, Equation (15) would represent the probability of oscillator i to be in-phase with the reference at time-step Δt. For two oscillators case, the weighted input sum of the second oscillator is given by:

$\begin{array}{ll}{h}_2(t)=W_{21}{S}_1(t)=W_{21}& (17)\end{array}$

Then, the probability of the second oscillator to be in-phase with the reference can be derived by Equations (15) and (17), as:

$\begin{array}{ll}P(S_2(t+\Delta t)=+1|h_2(t))=P_{inphase}=g(W_{21})& (18)\end{array}$

FIGURE 10

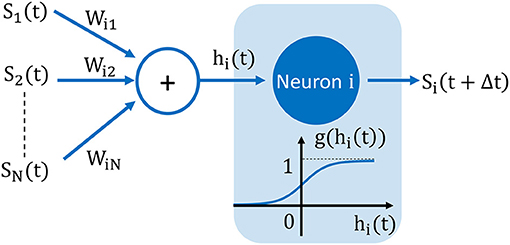
Figure 10. Model of artificial neuron used to construct our mapping function μ_N. The neuron's output state S_i(t) is either +1 or –1 and is dynamically updated at each time-step Δt according to the sigmoid activation function g. Here, g gives the probability to have one of the two states at t + Δt for a given input weighted sum h_i(t).

2.2.2. Mapping Function

Here, we apply the above definitions to derive a mapping function using the HNN formalism, as:

$\begin{array}{ll}{\mu }_N:W_{ij}\to R_{ij}& (19)\end{array}$

where, normalized weights are −1 ≤ W_ij ≤ 1 and N is ONN size. Before scaling to N oscillators, we derive a mapping function μ₂ for two coupled oscillators. The unifying step between HNN and ONN is the recasting of the phase transition curve, ζ as the probability P_inphase for a given coupling resistance R_C. In ONNs, the input delay Δt_init can be considered as a uniform random variable taking values between 0 and T_osc/2 and the transition function ζ would give the probability P_inphase (for example for R_C > 10kΩ):

$\begin{array}{ll}{P}_{inphase}=\zeta (R_C)\frac{2}{T_{osc}}& (20)\end{array}$

and by Equations (18) and (20), we finally obtain

$\begin{array}{ll}{\mu }_2(W_{21})=R_C={\zeta }^{-1}\left(\frac{T_{osc}}{2}g(W_{21})\right)& (21)\end{array}$

This mapping function is represented in Figure 11 for three different values of the sigmoid parameter, β. We see that this parameter sets the range of R_C and could be adapted for different ONN sizes. Interestingly, we notice that |ΔW₂₁/ΔR_C| is quite large for a positive weight, whereas it is much smaller for a negative one. For example, we see in Figure 11B that the function ζ⁻¹ is a logarithmic function; thus, any small variation in ΔR_C around 10kΩ is likely to change the final phase state outcome. Whereas, for large R_C, the two oscillators are almost always out-of-phase. This asymmetry in ζ⁻¹ comes from the oscillator waveform type, as ζ⁻¹ is derived from Equation (10), which is specific for relaxation oscillator waveform type. Hence, we expect some change for other types of waveforms, such as linear sawtooth, but the formulation of mapping (21) is general enough to be applied to any relaxation oscillators.

FIGURE 11

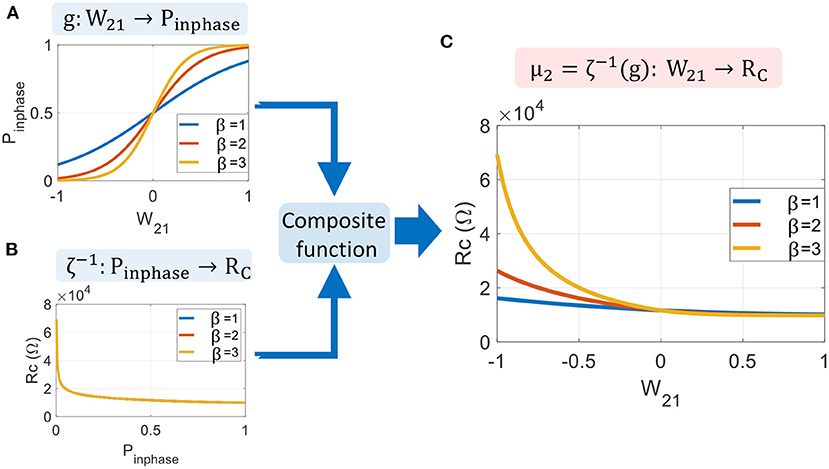
Figure 11. Mapping function for two coupled oscillators. (A) Sigmoid activation function presents the probability P_inphase for the two oscillators to be in phase. (B) Inverse of the transition function ζ⁻¹ determines the coupling resistance R_C for a given probability P_inphase. (C) The mapping function μ₂ is obtained by the composite function ζ⁻¹(g).

For large-scale ONN with N oscillators, we scale μ₂ (21) by a factor N−1 to ensure the conservation of the current flow in coupling resistances. We finally obtain:

$\begin{array}{ll}{\mu }_N(W_{ij})=R_{ij}=(N-1){\zeta }^{-1}\left(\frac{T_{osc}}{2}g(W_{ij})\right)& (22)\end{array}$

In next section, we demonstrate the effectiveness of the proposed mapping function (22) to design a 60-ONN architecture for pattern recognition as in HNN.

3. Results

3.1. ONN Design for Pattern Recognition

3.1.1. ONN Training and Mapping

In the previous section, we presented the memory capability of two coupled oscillators. Here, we apply the analytical formulas to a larger ONN size. We develop a design flow as shown in Figure 12A for pattern recognition with ONNs where we have implemented the proposed mapping function. We first compute the weights associated with the M stored patterns using the Hebbian Rule (Hoppensteadt and Izhikevich, 2000), as:

$\begin{array}{ll}{W}_{ij}=\frac{1}{N}{\displaystyle \sum _{k=1}^M}{\xi }_i^k{\xi }_j^k& (23)\end{array}$

We store M = 6 images representing digits “0”, “1” to “5” as shown in Figure 12B. Next, we use our mapping function to compute the coupling resistances associated with the Hebbian coefficients. The mapping is represented in Figure 12C for different values of parameter β which sets the slope of μ_N(W_ij). Increasing β induces a larger coupling resistance range. Because the Hebbian rule normalizes the weights by the network's size N (23), we scale β with N to keep a relative standard deviation of R_ij approximately constant when increasing the ONN size. By simulations, we found that the best accuracy is obtained for β = N/32, and we report the results in subsection 3.1.3.

FIGURE 12

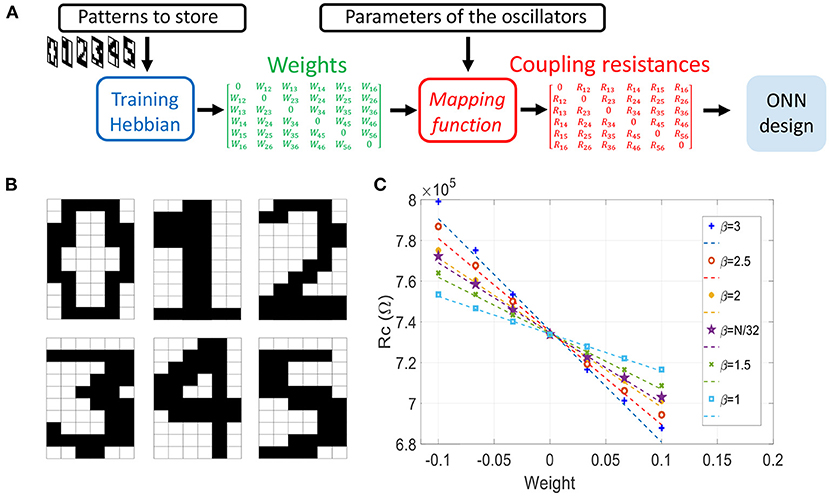
Figure 12. (A) Illustration of the ONN design flow for the associative memory application. Patterns to store can be represented as black and white images from which we compute weights with the Hebbian rule during the training process. Then, we use the mapping function μ_N to get the coupling resistances, allowing a systematic ONN design. (B) Stored patterns. (C) Coupling resistances as a function of Hebbian weights, computed with the mapping function μ_N for different values of parameter β.

3.1.2. ONN Inference

For every input, we set up the 60 ONN with black and white pixels encoded by –1 and +1, respectively. For pixels with black input, the corresponding oscillator is initialized with a delay Δt_init = T_osc/2 to set an initial out-of-phase relation (5) whereas, for a white pixel, no delay is introduced. A noisy gray pixel corresponds to an input delay between 0 and T_osc/2. After few oscillations, the ONN settles, retrieves the noiseless pattern and phase relations are measured. An example of ONN voltage dynamics is presented in Figure 13A, showing the initialization and the settling time before the ONN stabilizes. Figures 13B,C show two examples of input images where 15 pixels have been randomly altered by a uniform distribution taking values between –1 and +1. When the number of noisy input pixels is too large such as in Figure 13D (20 noisy pixels), ONN converges toward a wrong spurious state that is different from the stored patterns. The results are in accordance with original observations from Hopfield (1982), proving that our mapping can implement HNN with ONN.

FIGURE 13

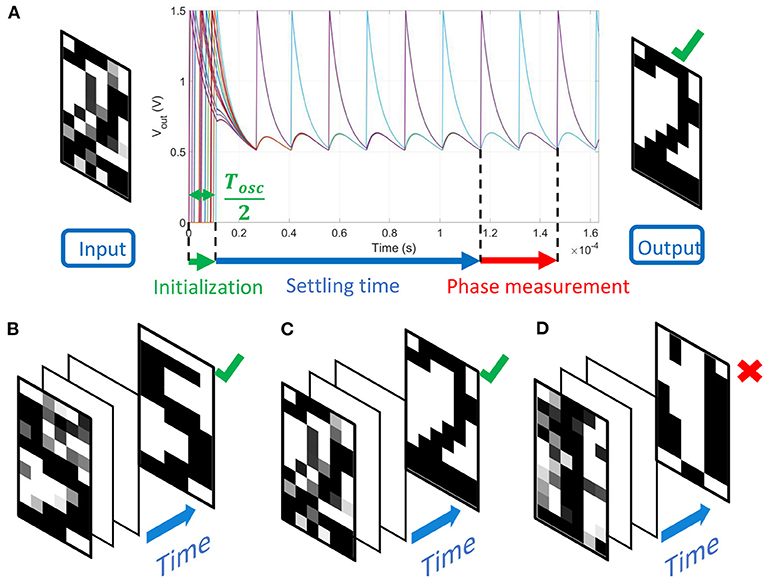
Figure 13. (A) Noisy input image “2” with 15 random altered pixels and voltage waveforms of 60 oscillators. ONN is initialized during T_osc/2 with the noisy input image. After few oscillation cycles, ONN settles, and phases are measured. ONN retrieves the correct output image that corresponds to the stored pattern “2.” (B) The input image “5” has been altered at 15 random pixel locations by a uniform distribution. ONN retrieves the corresponding stored pattern. (C) Similarly, 15 random pixels of the input image “2” are altered, and ONN retrieves the correct corresponding pattern. (D) In this example, 20 noisy input pixels are introduced to digit “1,” and ONN converges toward a spurious state.

3.1.3. ONN Recognition Accuracy

Here, we perform simulations to compute the pattern recognition accuracy of the 60-ONN. We randomly apply noise to training patterns to generate a test set. It consists of 20 different subsets S_k, kϵ{1, 2, .., 20} in which 60 different test patterns have k randomly located fuzzy input pixels. We vary the mapping function parameter β to assess its influence on ONN accuracy. We notice from Figure 14C that ONN achieves the best accuracy for an optimum value β = N/32 = 1.875. In this case, ONN recognizes more than 80% of test images with up to 20% of noise. As seen in Figure 12C, the slope parameter β sets the coupling resistance range, which in turn affects ONN accuracy. For instance, we observe that the set of coupling resistances obtained for β = 2 is similar to the case β = 2.5, but the accuracy is much lower in the latter case. In the next section, we quantify the coupling resistance accuracy that is required for synaptic design.

FIGURE 14

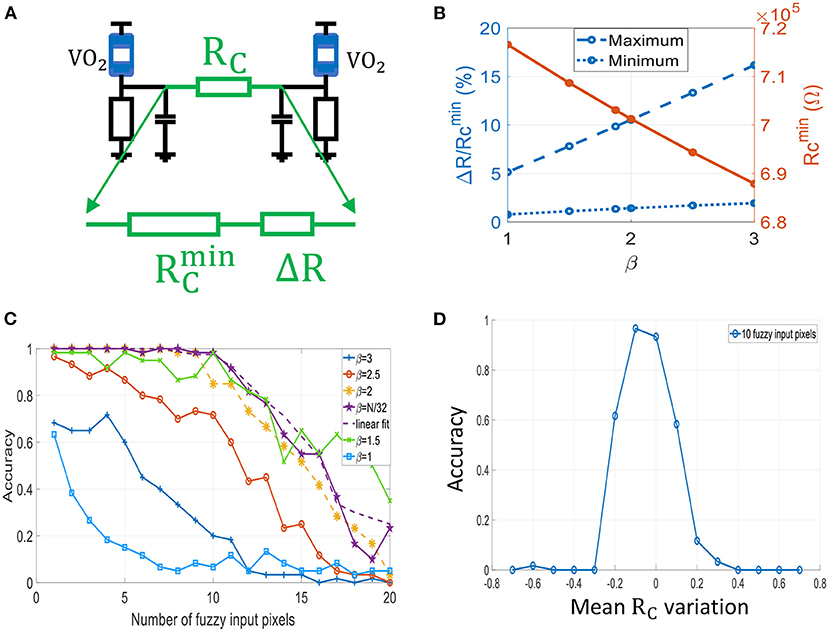
Figure 14. (A) Two oscillators coupled by R_C, which can be decomposed in two series resistances: $R_C=R_C^{min}+\Delta R$. (B) Evolution of ΔR, $R_C^{min}$ with respect to β. $\Delta R^{max}\approx 10\%R_C^{min}$ gives the best accuracy results. Note that $\Delta R^{min}=1.7\%R_C^{min}$. (C) ONN recognition accuracy for different values of β. The dashed line is obtained for a linear fit of the mapping μ_N, i.e., with coupling resistances that are linearly spaced. (D) Impact of R_C's mean variation on recognition accuracy.

3.1.4. ONN Coupling Resistance Range

We study the impact of R_C's relative variations and R_C's mean value. $R_C^{min}$ is the minimum resistance common to all coupling resistances, and ΔR is the additional series resistance to distinguish between weights (Figure 14A). Using the Hebbian rule, weights are located near “0” coefficient as in Figure 12C and our mapping function can be fitted linearly (dashed lines). Therefore, every coupling resistances can be approximated by $R_C\approx R_C^{min}+n\Delta R^{min}$ with nϵ{0, 1, 2, .., M}. Using this linear approximation, we can verify ONN accuracy is similar to the nominal case of mapping function with β = N/32, as shown in Figure 14C with the magenta dashed line.

As observed in previous sections, ONN accuracy is quite sensitive to the coupling resistances. We obtain $\Delta R^{max}\approx 15\%R_C^{min}$ for β = 3, and $\Delta R^{max}\approx 5\%R_C^{min}$ for β = 1 (Figure 14B). For these two cases as shown in Figure 14C, ONN shows poor accuracy. It is rather for β = N/32 = 1.875 with $\Delta R^{max}\approx 10\%R_C^{min}$ that ONN accuracy is above 90%.

To achieve the best ONN accuracy, a very good resistor matching is required, as we need a precision of $\Delta R^{min}=1.7\%R_C^{min}$ between two consecutive weights. To study the influence of the R_C's mean value only, we apply the same variation to all coupling resistances for β = N/32 and for 10 fuzzy input pixels (Figure 14D). We notice that the mean value of coupling resistances can vary from –10% up to +5% from its nominal value to achieve a similar accuracy.

4. Discussion

Oscillatory neural networks are triggering great interest for parallel processing applications, but a remaining challenge is how to compute with ONNs. To do so, we build analogies with ANN to determine the mapping between Hebbian learning coefficients (weights) to coupling resistors, knowing that they are essential elements for the network functionality. In this work, we proposed a mapping function that translates Hebbian signed weights to coupling resistances in a VO₂-based ONN for systematic ONN analysis. Our simulations on 60-oscillators test case study highlighted a strong dependency between the ONN recognition accuracy and its coupling resistance range, set by mapping parameter β. Although we identified a suitable value β = N/32 to achieve good ONN accuracy, our mapping formulation provides coupling resistances that differ only with few percent. This would lead to significant hardware design constraints, as resistor mismatches smaller than 1.7% would be required to emulate two consecutive weights. In our mapping formalism, we used the phase transition function ζ, which provides the coupling resistance range holding the ONN memory. As we only derived ζ from oscillator dynamics, we believe the oscillator design could be optimized to expand the coupling resistance range and relax synaptic design constraints. For example, oscillator biasing current and supply voltage are the knobs that could be adjusted to maximize the synaptic range.

Here, we reported on a mapping function to compute coupling resistances from signed Hebbian coefficients in a VO₂-based ONN. We first enhanced the ONN initialization control based on a simple architecture where every oscillator can be decoupled from the network via a switch. We were able to derive the phase transition function from the ONN dynamics, which is crucial for ONN memory. We then merged this analytical formulation with a sigmoid activation function from ANN formalism to build a mapping function. To demonstrate the ONN architecture's applicability with the proposed mapping function, we presented a test case of pattern recognition with 60 fully coupled oscillators. Finally, we showed that ONN recognition accuracy is very sensitive to relative variations between coupling resistances.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

CD and AT-S developed the analytical formulation of ONN mapping and wrote the article. CD implemented the ONN circuit-solver framework on Matlab and performed simulations. Both authors contributed to the article and approved the submitted version.

Funding

This work is supported by the European Union's Horizon 2020 research and innovation program, EU H2020 NEURONN (www.neuronn.eu) project under Grant No. 871501.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnins.2021.694549/full#supplementary-material

References

Acebrón, J. A., Bonilla, L. L., Pérez Vicente, C. J., Ritort, F., and Spigler, R. (2005). The kuramoto model: a simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77, 137–185. doi: 10.1103/RevModPhys.77.137

CrossRef Full Text | Google Scholar

Corti, E., Cornejo Jimenez, J. A., Niang, K. M., Robertson, J., Moselund, K. E., Gotsmann, B., et al. (2021). Coupled vo2 oscillators circuit as analog first layer filter in convolutional neural networks. Front. Neurosci. 15:19. doi: 10.3389/fnins.2021.628254

PubMed Abstract | CrossRef Full Text | Google Scholar

Corti, E., Gotsmann, B., Moselund, K., Stolichnov, I., Ionescu, A., and Karg, S. (2018). “Resistive coupled vo2 oscillators for image recognition,” in 2018 IEEE International Conference on Rebooting Computing (ICRC) (McLean, VA: IEEE), 1–7.

Google Scholar

Corti, E., Gotsmann, B., Moselund, K., Stolichnov, I., Ionescu, A., Zhong, G., et al. (2019). “Vo2 oscillators coupling for neuromorphic computation,” in 2019 Joint International EUROSOI Workshop and International Conference on Ultimate Integration on Silicon (EUROSOI-ULIS) (Grenoble: IEEE), 1–4.

Google Scholar

Corti, E., Khanna, A., Niang, K., Robertson, J., Moselund, K. E., Gotsmann, B., et al. (2020). Time-delay encoded image recognition in a network of resistively coupled vo on si oscillators. IEEE Electron. Device Lett. 41, 629–632. doi: 10.1109/LED.2020.2972006

CrossRef Full Text | Google Scholar

Endo, T., and Takeyama, K. (1992). Neural network using oscillators. Electron. Commun. Jpn. 75, 51–59. doi: 10.1002/ecjc.4430750505

CrossRef Full Text | Google Scholar

Fell, J., and Axmacher, N. (2011). The role of phase synchronization in memory processes. Nat. Rev. Neurosci. 12, 105–118. doi: 10.1038/nrn2979

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerstner, W., Kistler, W. M., Naud, R., and Paninski, L. (2014). Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition, Chapter 17.2. New York, NY; Cambdrige University Press.

Google Scholar

Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U.S.A. 79, 2554–2558. doi: 10.1073/pnas.79.8.2554

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoppensteadt, F. C., and Izhikevich, E. M. (2000). Pattern recognition via synchronization in phase-locked loop neural networks. IEEE Trans. Neural Netw. 11, 734–738. doi: 10.1109/72.846744

PubMed Abstract | CrossRef Full Text | Google Scholar

Izhikevich, E., and Kuramoto, Y. (2006). Weakly coupled oscillators. Encyclopedia Math. Phys. 448–53. doi: 10.1016/B0-12-512666-2/00106-1

CrossRef Full Text | Google Scholar

Jackson, T., Pagliarini, S., and Pileggi, L. (2018). “An oscillatory neural network with programmable resistive synapses in 28 nm CMOS,” in 2018 IEEE International Conference on Rebooting Computing (ICRC) (McLean, VA: IEEE), 1–7.

Google Scholar

Maffezzoni, P., Bahr, B., Zhang, Z., and Daniel, L. (2015a). Oscillator array models for associative memory and pattern recognition. IEEE Trans. Circ. Syst. I Regul. Pap. 62, 1591–1598. doi: 10.1109/TCSI.2015.2418851

CrossRef Full Text | Google Scholar

Maffezzoni, P., Bahr, B., Zhang, Z., and Daniel, L. (2016). Analysis and design of boolean associative memories made of resonant oscillator arrays. IEEE Trans. Circ. Syst. I Regul. Pap. 63, 1964–1973. doi: 10.1109/TCSI.2016.2596300

CrossRef Full Text | Google Scholar

Maffezzoni, P., Daniel, L., Shukla, N., Datta, S., and Raychowdhury, A. (2015b). Modeling and simulation of vanadium dioxide relaxation oscillators. IEEE Trans. Circ. Syst. I Regul. Pap. 62, 2207–2215. doi: 10.1109/TCSI.2015.2452332

CrossRef Full Text | Google Scholar

Nez, J., Avedillo, M. J., Jimnez, M., Quintana, J. M., Todri-Sanial, A., Corti, E., et al. (2021). Oscillatory neural networks using vo2 based phase encoded logic. Front. Neurosci. 15:442. doi: 10.3389/fnins.2021.655823

PubMed Abstract | CrossRef Full Text | Google Scholar

Parihar, A., Shukla, N., Datta, S., and Raychowdhury, A. (2015). Synchronization of pairwise-coupled, identical, relaxation oscillators based on metal-insulator phase transition devices: a model study. J. Appl. Phys. 117, 054902. doi: 10.1063/1.4906783

CrossRef Full Text | Google Scholar

Parihar, A., Shukla, N., Jerry, M., Datta, S., and Raychowdhury, A. (2017). Vertex coloring of graphs via phase dynamics of coupled oscillatory networks. Sci. Rep. 7, 911. doi: 10.1038/s41598-017-00825-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Raychowdhury, A., Parihar, A., Smith, G. H., Narayanan, V., Csaba, G., Jerry, M., et al. (2019). Computing with networks of oscillatory dynamical systems. Proc. IEEE 107, 73–89. doi: 10.1109/JPROC.2018.2878854

CrossRef Full Text | Google Scholar

Schmitt, O. H. (1938). A thermionic trigger. J. Sci. Instrum. 15, 24–26. doi: 10.1088/0950-7671/15/1/305

CrossRef Full Text | Google Scholar

Sharma, A. A., Bain, J. A., and Weldon, J. A. (2015). Phase coupling and control of oxide-based oscillators for neuromorphic computing. IEEE J. Exploratory Solid State Comput. Devices Circ. 1, 58–66. doi: 10.1109/JXCDC.2015.2448417

CrossRef Full Text | Google Scholar

Shukla, N., Parihar, A., Cotter, M., Barth, M., Li, X., Chandramoorthy, N., et al. (2014). “Pairwise coupled hybrid vanadium dioxide-mosfet (hvfet) oscillators for non-boolean associative computing,” in 2014 IEEE International Electron Devices Meeting (San Francisco, CA: IEEE), 28.7.1–28.7.4.

Google Scholar

Shukla, N., Tsai, W.-Y., Jerry, M., Barth, M., Narayanan, V., and Datta, S. (2016). “Ultra low power coupled oscillator arrays for computer vision applications,” in 2016 IEEE Symposium on VLSI Technology (Honolulu, HI: IEEE), 1–2.

Google Scholar

Todri-Sanial, A., Carapezzi, S., Delacour, C., Abernot, M., Gil, T., Corti, E., et al (2021). How Frequency Injection Locking Can Train Oscillatory Neural Networks to Compute in Phase. Available online at: https://hal-lirmm.ccsd.cnrs.fr/lirmm-03164135 (accessed April 12, 2021).

PubMed Abstract | Google Scholar

Vassilieva, E., Pinto, G., de Barros, J., and Suppes, P. (2011). Learning pattern recognition through quasi-synchronization of phase oscillators. IEEE Trans. Neural Netw. 22, 84–95. doi: 10.1109/TNN.2010.2086476

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Qi, M., and Wang, B. (2017). Ppv modeling of memristor-based oscillators and application to onn pattern recognition. IEEE Trans. Circ. Syst. II Express Briefs 64, 610–614. doi: 10.1109/TCSII.2016.2591961

CrossRef Full Text | Google Scholar

Winfree, A. T. (1967). Biological rhythms and the behavior of populations of coupled oscillators. J. Theor. Biol. 16, 15–42. doi: 10.1016/0022-5193(67)90051-3

PubMed Abstract | CrossRef Full Text | Google Scholar