- 1Institut für Didaktik der Physik, WWU Münster, Münster, Germany
- 2Physikalisches Institut, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany
Learning quantum physics is essential for understanding the physical world. However, learning about quantum phenomena and principles poses a challenge as many of the phenomena that are observed at the quantum level cannot be directly observed or intuitively understood in terms of classical physics or thinking. Models play an important role in learning quantum physics by providing conceptual frameworks and visual representations that allow reasoning about and predicting the behavior of quantum systems. Therefore, understanding models is an essential part of learning quantum physics. In this article, we report the results of an exploratory survey study (N = 116) investigating the relationship between secondary school students’ conceptual understanding and model thinking in quantum optics with a particular focus on photons. The findings suggest a strong positive correlation between students’ functional understanding of the photon model and their conceptual understanding of quantum optics. This study contributes to our understanding of how students learn and make sense of quantum concepts through the use of models and may inform the development of instructional strategies for quantum physics education and outreach.
1 Introduction
Learning processes in the field of quantum physics are of significant interest in physics education (Michelini et al., 2022; Chiofalo and Michelini, 2023; Michelini and Stefanel, 2023), particularly in light of the increasing popularity of quantum technologies (Aiello et al., 2021; Gerke et al., 2022; Greinert et al., 2022; Kaur and Venegas-Gomez, 2022). Physics education research has identified various research-based educational paths that can help students in formal education develop a deeper understanding of the physical world and the underlying principles of quantum mechanics and its applications (Pospiech, 1999; 2000; 2021; Michelini et al., 2000; Bitzenbauer and Meyn, 2020; Aehle et al., 2022; Malgieri and Onorato, 2022; Weissman et al., 2022). Moreover, quantum science and technologies have the potential to inspire a wider audience and cultivate the next-generation of innovators and problem solvers through outreach projects, even beyond formal educational settings. For example, the paper by Bondani et al. (2022) presents an extracurricular course on quantum physics and quantum technologies for high school students, which was attended by 250 students from all over Italy, and reports on the effectiveness of the course in improving students’ knowledge about fundamental aspects of quantum mechanics and familiarizing them with quantum technology applications. Furthermore, the use of games for teaching and learning quantum physics [for an overview see Seskir et al. (2022)] in a competition-like setting has been shown to (a) be able to enhance students’ conceptual understanding and to (b) foster engagement and interest in quantum technologies (Chiofalo et al., 2022). Also, lab interventions at universities have been offered in order to influence students’ perception of the importance of quantum physics and technology (e.g., see Moraga-Calderón et al., 2020). A different approach is taken by Goorney et al. (2022) who argue for the importance of outreach in developing a modern scientific mindset, with a focus on a culturo-scientific approach that utilizes storytelling.
Whether in formal or informal settings, it is essential for students learning quantum physics to work with and understand models: One of the key challenges in learning quantum physics is that many of the phenomena that are observed at the quantum level cannot be directly observed or intuitively understood in terms of classical physics or thinking. Hence, models are needed to bridge this gap by providing conceptual frameworks and visual representations that allow to reason about and predict the behavior of quantum systems and are thus tools for describing and understanding quantum phenomena and principles (Ubben, 2020). Therefore, learning about quantum physics, at its core, is about learning about models as has been pointed out by Stefani and Tsaparlis (2009). How students’ understanding of models and their conceptual understanding of quantum concepts are connected is explored in the study presented in this paper for the context of quantum optics which is “highly relevant for almost all applications of quantum technologies, either as a core component of the application […] or as an enabling technology” (Bitzenbauer et al., 2022, p. 1181).
2 Theoretical background
2.1 Learning difficulties in quantum physics
Learning quantum physics poses a big challenge to learners (Bouchée et al., 2022)—for a comprehensive overview see Krijtenburg-Lewerissa et al. (2017). Many of these problems stem from learners not understanding how to interpret images and models related to quantum physics topics and phenomena, leading to various inadequate concepts that limit or hinder learning processes, making professionalization more difficult (Dachraoui et al., 2022). For example, learners often visualize atoms as small planetary systems and have difficulty abandoning this view due to its apparent realism (Bethge, 1988). Similarly, when it comes to the concept of electron spin, it has been reported that learners often use a classical image of a spinning ball to understand spin (Taber, 2005). An even more problematic issue is the common classical (i.e., space-time) description of quantum objects and their properties, particularly regarding photons in quantum optics, which are, amongst others, often described as being permanently localized (Fischler and Lichtfeldt, 1992). These problematic views are most often accompanied by an overly realistic interpretation of the models, objects, and principles of quantum physics, which (a) lead to inconsistent, context-specific mental models (Körhasan and Miller, 2020) and which (b) can be attributed to an inadequate understanding of models in general (Kalkanis et al., 2003). Therefore, a differentiated and professionalized understanding of models might be an important step in gaining a better understanding of quantum physics. However, how exactly model understanding in general plays a part in developing more refined ideas of quantum physics has–to our knowledge–not yet explicitly been researched, though some previous works have touched upon this connection as laid out in the following Section 2.2.
2.2 Students’ model understanding and its relevance for learning quantum physics
A study by Ubben and Heusler (2021) on model understanding in the context of the atomic shell investigated how learners understand models in terms of realism in more detail. An exploratory factor analysis showed that the atomic shell model understanding can be described using a two-factor model that explains 36% of the variance in the data. An analysis of the two factors revealed that the participants’ model understanding in the atomic hull context can be characterized via two cognitive dimensions, namely, Fidelity of Gestalt and Functional Fidelity, which have found to be uncorrelated. The two factors have been described by Ubben and Heusler (2021) as follows.
1. Fidelity of Gestalt: This dimension encodes how far models in (quantum) physics are perceived as visually adequate depictions of something real. A high value on this scale means that the person believes models to be exact visual representations of a real phenomenon.
2. Functional Fidelity: This dimension encodes how far models in (quantum) physics are perceived as functionally accurate. This means that people with a high value see mental models as functional representations.
The learners’ conceptions underlying the study mainly referred to the difference between the more intuitive Bohr or Rutherford atomic model and the more abstract, functionally adequate orbital model. Hence, this thematic restriction raised the question as to whether the two-factor structure of learners’ model understanding including the dimensions Fidelity of Gestalt and Functional Fidelity could also be transferred to more modern areas of quantum physics, such as quantum optics representing the physics of photons. Ubben and Bitzenbauer (2022) showed this two-factor structure to also be suitable as a viable framework of learners’ model understanding in this area, with the two factors explaining 44% of the total variance in the data.
Since model understanding in terms of realism is a central factor in the learning process of quantum physics topics, the question arises as to whether, and to what extent, the expression of the two factors has an influence on concept understanding. Ubben (2020) provides evidence that a high level of professionalization in quantum physics brings about a low expression of Fidelity of Gestalt and a high expression of Functional Fidelity in quantum physics model understanding. Other studies also support this hypothesis. For example, Grosslight et al. (1991) found that the deepest understanding of a model is the understanding that models are useful tools. This framing is consistent with studies by, for example, Stefani and Tsaparlis (2009), who identified this understanding of models among their professionalized participants. Therefore, it is a research desideratum to shed light on the relationships between model understanding and the degree of professionalization measured by the depth of conceptual understanding. This will be done in this investigation in the context of quantum optics, since (a) instruments for measuring Functional Fidelity and Fidelity of Gestalt as well as instruments for measuring conceptual understanding are already available there, and (b) the topic of quantum optics as a subfield of quantum physics is of particular interest, both from the perspective of physics education (e.g., see Montagnani et al., 2023; Galvez, 2019; Pearson and Jackson, 2010) and with regards to understanding aspects of modern quantum technologies (e.g., see Moody et al., 2022).
3 Research questions
In this paper, we address the research desideratum identified above for the context of photons in quantum optics since students’ conceptions of photons have comprehensively been examined in earlier research as sketched in Section 2. Hence, we pose the following research questions.
1. How is the students’ conceptual understanding of photons in quantum optics correlated with the degree of Functional Fidelity and Fidelity of Gestalt in students’ thinking of the photon model?
2. How may the degree of Functional Fidelity and Fidelity of Gestalt in students’ thinking of the photon model be used as predictors of students’ conceptual understanding of photons in quantum optics?
4 Methods
4.1 Study design and sample
To approach a clarification of our research question we conducted a survey study. We assessed N = 116 (49 female, 67 male) grade 12 secondary school students’ conceptual understanding of quantum optics and their model understanding of photons after all students had participated in introductory lessons on the quantum physics of photons during their regular physics lessons following the mandatory German high-school curriculum. No intervention provided by us was part of this study.
4.2 Instruments
4.2.1 Assessment of students’ conceptual understanding of quantum optics
To assess students’ conceptual understanding of quantum optics, we used the Quantum Optics Concept Inventory (Bitzenbauer et al., 2022) in a version suitable for the secondary school level. This instrument consists of 13 single-choice items and has been shown to (a) be psychometrically sound (e.g., Cronbach’s Alpha α = 0.78) and (b) allow for a valid test score interpretation (Bitzenbauer, 2021). For each correct answer, the respondents are assigned one point, and hence, a total score ranging from 0 to 13 points can be achieved where a higher score indicates further developed conceptual understanding of the quantum optics aspects under investigation. For the items see Bitzenbauer et al. (2022). In the following, we will use the abbreviation QOCI to refer to students’ scores in the Quantum Optics Concept Inventory.
4.2.2 Assessment of students’ model understanding of the photon
In order to evaluate students’ understanding of models with regard to photons, we employed a questionnaire that has already been utilized in our prior study concerning students’ understanding of models (Ubben and Bitzenbauer, 2022). This questionnaire originates from Ireson (1999, 2000) and has been developed further by Müller and Wiesner (2002) based on quantum mechanics’ ensemble interpretation (e.g., see Ballentine, 1970). The questionnaire is comprised of ten items, each presenting a statement related to the photon model. Students are required to indicate their level of agreement with the statements on a scale ranging from 1 (disagree) to 5 (agree).
From the ten items, six items comprise a scale to measure the degree of Functional Fidelity in students’ model understanding of photons. Cronbach’s Alpha as an estimator for the scale’s internal consistency was found to be α = 0.73. In the following, this scale will be referred to as the so-called FF scale. The remaining four items comprise a scale to measure the degree of gestalt fidelity in students’ model understanding of photons. Cronbach’s Alpha as an estimator of the scale’s internal consistency was found to be α = 0.61. This value–though indicating rather low internal consistency–can be considered acceptable due to the low length of the scale consisting of only four items (for example, see Bauer, 2015). In the following, this scale will be referred to as the so-called FG scale. For both, the FF and FG scales, a mean score ranging from 1 to 5 can be calculated from the students’ ratings: A higher mean score indicates a higher degree of Functional Fidelity or Fidelity of Gestalt in students’ thinking of photons. For the items see Table 1.

TABLE 1. Items of the FF and FG scales to assess the degree of (a) Functional Fidelity (FF) and (b) Fidelity of Gestalt (FG) in students’ model understanding of photons taken from Ubben and Bitzenbauer (2022). Items marked with a (−) were inverted in the course of data analysis since here a low student rating would indicate a low degree of gestalt or functional thinking, respectively, as described by Ubben and Bitzenbauer (2022).
4.3 Data analysis
First, we report descriptive statistics (mean value m, standard deviation σ, minimum score min, maximum score max) for the instruments used in this study based on the data gathered.
4.3.1 Analysis carried out to answer research question 1
To investigate the relationship between students’ conceptual understanding of photons in quantum optics and the degree of Functional Fidelity and gestalt fidelity in the students’ thinking of the photon model, a correlation analysis was performed, including the students’ QOCI, FF scale and FG scale scores. Since the data were measured on a metric scale, we calculated Pearson’s correlation coefficient r. Following Hemphill (2003), the correlations were considered weak if |r| < 0.20, medium if 0.20 < |r| < 0.30, and strong if |r| > 0.30.
4.3.2 Analysis carried out to answer research question 2
To explore as to how the degree of Functional Fidelity and Fidelity of Gestalt in students’ model understanding of the photon may be used to predict students’ conceptual understanding of photons in quantum optics, we used multiple linear regression analysis. Therefore, the students’ test scores in the QOCI served as the dependent variable. The model under investigation included the students’ score in the FG and FF scales (see Table 1), respectively. To verify the assumptions required for linear regression analysis, we adopted the approach followed by Veith et al. (2022b).
5 Results
5.1 Descriptives
Descriptive statistics describing the data collected in this study are given in Table 2.
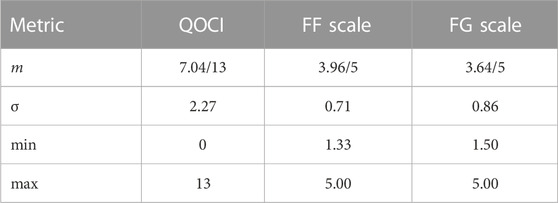
TABLE 2. Descriptive statistics for the students’ scores in the QOCI as well as the FF and FG scales, respectively (see Table 1).
5.2 Correlation analysis
The correlations between the variables under investigation are provided in Table 3. We observe a statistically significant positive correlation between students’ conceptual understanding of quantum optics and the degree of Functional Fidelity in students’ thinking of photons (r = 0.29, p < 0.01). In contrast, the degree of Fidelity of Gestalt in students’ thinking is negatively correlated with students’ conceptual understanding (r = −0.41, p < 0.001). Strikingly, the degrees of Functional Fidelity and Fidelity of Gestalt in students’ thinking of photons seem to be uncorrelated based on the data gathered in this study. This observation aligns with earlier findings for both, electron (Ubben and Heusler, 2021) and photon contexts (Bitzenbauer and Meyn, 2021a), and we will elaborate on this in the discussion section.
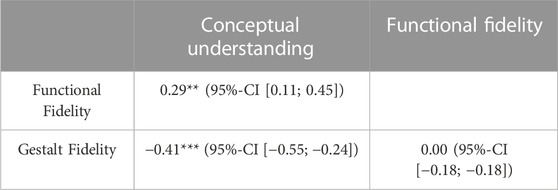
TABLE 3. Pearson’s correlation coefficient r between the students’ scores in the QOCI (conceptual understanding) as well as the FF (Functional Fidelity) and FG (Fidelity of Gestalt) scales, respectively. Statistical significance of the correlations is denoted by an asterisk: *p <.05, **p <.01, ***p <.001. For all correlations, we report 95% confidence intervals (95%-CI).
5.3 Regression analysis
Table 4 provides a summary of the multiple linear regression model under investigation. The statistical significance of the model is confirmed through an F-test which indicates that taken together, the degree of Functional Fidelity and Fidelity of Gestalt in students’ thinking of photons, were able to statistically significant predict students’ conceptual understanding (F (2, 110) = 18.46, p < 0.001). With R2 = 0.25 (adjusted R2 = 0.24) the model explains a medium degree of variance in students’ conceptual understanding according to Cohen (1988). The multiple linear regression analysis reveals that both the degree of Functional Fidelity (β = 0.29; t (110) = 3.55, p < 0.001) and Fidelity of Gestalt (β = −0.41; t (110) = −4.98, p < 0.001) in students’ thinking of photons are statistically significant predictors of students’ conceptual understanding of quantum optics.
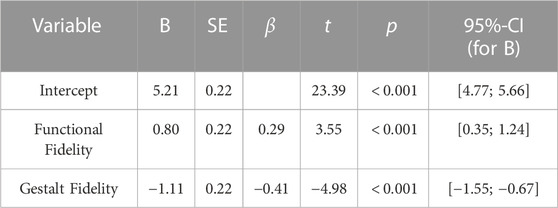
TABLE 4. Multiple linear regression model with regression coefficients B (alongside regression coefficient stand errors SE and 95% confidence intervals) and standardized regression coefficients β.
6 Discussion
6.1 Discussion of research question 1
The results of the data analysis show that significant correlations exist between the general level of professionalisation as measured by the conceptual understanding of the participants and both their Fidelity of Gestalt and their Functional Fidelity scores. The significant positive correlation of 0.29 (p < 0.01) between Functional Fidelity and conceptual understanding indicates that there is a positive connection between the two as people with a deeper and more sophisticated understanding of photons in quantum optics appear to likely also have a greater awareness of models being tools and fulfilling a functional role in describing the world. This is consistent with previous findings where experts showed to have a more functional type of thinking than novices (Stefani and Tsaparlis, 2009; Ubben and Heusler, 2021). Conversely, the correlation between conceptual understanding and Fidelity of Gestalt was negative with −0.41 (p < 0.001), though this indicates a connection as well: Experts appear to have more likely let go of the notion that appearance-wise models correspond to reality and likely have a more abstract understanding of models.
These findings are in line with previous analyses into experts’ understanding of photons (Bitzenbauer and Meyn, 2021a) and electrons in the atomic hull (Ubben and Heusler, 2021). In a broader sense, other studies though they have not explicitly measured model understanding as described by Functional Fidelity and Fidelity of Gestalt, implicitly appear to have touched on these constructs in similar science contexts such as electromagnetism (Guisasola et al., 2004; Sağlam and Millar, 2006) geometrical optics (Goldberg and McDermott, 1986; Heywood, 2005) or even in abstract algebra (Veith et al., 2022a) and gave similar characterisations for expert thinking (Stefani and Tsaparlis, 2009)—however, this type of thinking most often is only desired but not achieved.
Another striking observation is that the two factors Functional Fidelity and Fidelity of Gestalt are not correlated. This finding is consistent with previous studies in the fields of (a) electrons in the atomic hull Ubben and Heusler (2021) and (b) photons Bitzenbauer and Meyn (2021b). A possible explanation previously given for this observation (Ubben, 2020; Ubben and Bitzenbauer, 2022) is indicated by neurological research, where hemispheric specialisations regarding function (left hemisphere) and appearance (right hemisphere) were found to work independently of each other (Levy and Trevarthen, 1976). For a more extensive review of this field of research, see Gazzaniga (2005). These results are thus consistent with the finding of the two factors being uncorrelated as well. To gain a more profound understanding of the relationship between the two cognitive dimensions of Functional Fidelity and Fidelity of Gestalt, it seems necessary in future research to operationalize these two factors in specific test items.
6.2 Discussion of research question 2
Taking the results from the regression analysis, we find that both aspects of model understanding can be used to predict the level of conceptual understanding a person has about photons in quantum optics. More specifically, our findings indicate that reducing the degree of Fidelity of Gestalt (β = −0.41; t (110) = −4.98, p < 0.001) while increasing the degree of Functional Fidelity (β = 0.29; t (110) = 3.55, p < 0.001) in learners can facilitate a deeper conceptual understanding and thus increase students’ professionalisation in the field of quantum optics. These findings underpin earlier research: For example, while Greca and Moreira (2000) suggest that the development of Fidelity of Gestalt would be required for learning processes to be initiated, in her research into student learning about evolution, Evans (2000) observed a modification from Fidelity of Gestalt to Functional Fidelity among learners in later stages that lead towards a more elaborate conceptual understanding.
However, based on previous research, we consider plausible that there are two directions of effect here: That is, we believe that not only a higher degree of Functional Fidelity in learners’ model understanding is predictive for the students’ conceptual understanding in quantum optics, but that also the reverse is true: Higher conceptual understanding could also contribute to a further expression of functional ways of thinking. For example, in the context of atoms, deeper abstraction in learning, i.e., linking multiple “islands of knowledge” through underlying functionality, which enables a transfer of knowledge to new contexts, has been found to occur primarily in older learners and experts with higher conceptual understanding, but much less frequently in novices (Zarkadis et al., 2017; Ubben and Heusler, 2021).
7 Conclusion
The presented study shows results in line of previous works studying the connection between model understanding and quantum physics. In the following subsections we lay out the conclusions we draw for future educational research as well as suggestions for formal and informal educational environments that present quantum physical content.
7.1 Conclusion for educational practice
Our findings may inform teaching practice of quantum sciences in general and quantum optics in particular: As high-achieving students tended to have a low score in Fidelity of Gestalt, designing educational content with the goal of reducing the Gestalt-oriented thinking among students is likely to improve the understanding of learners (Dutt, 2011). However, as pointed out in Ubben (2020) as well, this step in cognitive development is the step of abstraction, namely, of letting go of the context and making knowledge transferable to other contexts. This step is often described as being the last step in conceptual development by various theoretical frameworks (see Section 7.2). Achieving abstraction might still be facilitated by using teaching methods designed to reduce Fidelity of Gestalt, such as.
• Using multiple representations for the same concept to enable learners to understand that there is not “the” correct gestalt but rather that many gestalts may represent the concept that is being taught. By focusing on functional similarities the concepts might then be easier understood and abstracted.
• Using obviously unrealistic gestalts to make it easier to understand that the gestalt is in fact not the central point of a model but rather how it works.
Both these ideas, however, will have to be tested to see if or how they work in educational practice. Also, one has to be careful to not dispose of a gestalt too easily: Research on very young children or very new learners heavily indicates that a first step in learning is imagining a gestalt of a model to make it concrete and give learners a foothold (e.g., see Aebli, 1973; Bethge, 1988). It is thus recommended to use images and other representations (for examples from quantum physics education, e.g., see Oss and Rosi, 2015; Dür and Heusler, 2014; Heusler and Ubben, 2019; Zaman Ahmed et al., 2021; Chhabra and Das, 2016). However, this requires teachers’ guidance, e.g., through discussing shortcomings and limitations of visualizations in the quantum realm in order to foster learners’ “acceptance that quantum systems do not admit any visualization […] by means of familiar images such as an image representing the atom’s planetary model” (Levrini and Fantini, 2013, p. 1898). Similar recommendations have already been given based on earlier research (Ke et al., 2005).
7.2 Conclusion for educational research
The present study points out new alleys for educational science to discover. The results from this study are about conceptual understanding of quantum optics, so it has to be explored whether they hold similarly true in other educational contexts from science education. Future work should try to better measure the constructs Functional Fidelity and Fidelity of Gestalt an see whether more variance can be explained with more general instruments. Previously, a general process of model understanding development based on the research presented as the basis of this study was proposed in Ubben (2020), incorporating the factors Fidelity of Gestalt and Functional Fidelity into a model of conceptual development in the area of model understanding (see Figure 1): The proposed process is that learners in quantum physics generally start with low Fidelity of Gestalt and low Functional Fidelity (non-developed type of model understanding). By increasing Fidelity of Gestalt, ideas and concepts are made accessible (architectural type of model understanding). By then increasing Functional Fidelity through (mental) interaction with the gestalt, the concept is explored, though still bound to the specific Gestalt and the specific context it is imagined in (dual type of model understanding). By decreasing Fidelity of Gestalt, i.e., mainly by abstracting the concept, the concept becomes transferable and connectable with other contexts (functional type of model understanding).
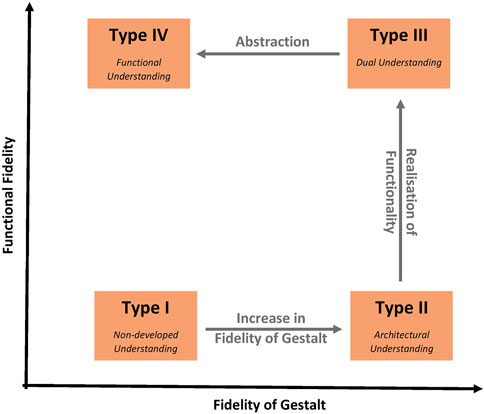
FIGURE 1. Model of development of model understanding in the quantum realm adapted from Ubben (2020) and supported through this study’s findings.
This general process has already (in parts) been repeatedly observed and has been included into theoretical frameworks of conceptual development earlier: For example, DiSessa (2018) proposed his famous framework of knowledge in pieces that addresses the same problems with abstractions previously discussed: A concept that is understood with both high Fidelity of Gestalt and Functional Fidelity is similar to a knowledge isle. In Aebli (1973), an emphasis on the necessity of images for rooting conceptual development in examples is similarly made, as was in Haeusler and Donovan (2020); Greca and Moreira (2000). We advise that further research explores whether this model of the process of conceptual development of models gives a suitable description for cases in all of science education, not only in quantum optics and physics. In addition, the relationship of this proposal to further frameworks describing the classical-to-quantum transition (e.g., see Zuccarini and Malgieri, 2022) is to be investigated.
Data availability statement
The raw data that support the findings of this study are available on request from the authors.
Author contributions
MU, conceptualization, methodology, investigation, formal analysis, data curation, writing–original draft and writing–review and editing. PB, conceptualization, methodology, investigation, formal analysis, data curation, writing–original draft and writing–review and editing. All authors contributed to the article and approved the submitted version. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aebli, H. (1973). Psychologische didaktik: Didaktische Auswertung der Psychologie von jean piaget (klett).
Aehle, S., Scheiger, P., and Cartarius, H. (2022). An approach to quantum physics teaching through analog experiments. Physics 4, 1241–1252. doi:10.3390/physics4040080
Aiello, C. D., Awschalom, D. D., Bernien, H., Brower, T., Brown, K. R., Brun, T. A., et al. (2021). Achieving a quantum smart workforce. Quantum Sci. Technol. 6, 030501. doi:10.1088/2058-9565/abfa64
Ballentine, L. (1970). The statistical interpretation of quantum mechanics. Rev. Mod. Phys. 42, 358–381. doi:10.1103/revmodphys.42.358
Bauer, A. (2015). Cronbach’s α im Kontext des Grundmodells der Klassischen Testtheorie und darüber hinaus. Master’s Thesis. Munich, Germany: Ludwig-Maximilian-University.
Bethge, T. (1988). Empirische Untersuchungen über Schülervorstellungen zur Quantenphysik. Vorträge Physikertagung, Deutsche Physikalische Gesellschaft. Fachausschuss Didaktik der Physik.
Bitzenbauer, P. (2021). Development of a test instrument to investigate secondary school students’ declarative knowledge of quantum optics. Eur. J. Sci. Math. Educ. 9, 57–79. doi:10.30935/scimath/10946
Bitzenbauer, P., and Meyn, J.-P. (2020). A new teaching concept on quantum physics in secondary schools. Phys. Educ. 55, 055031. doi:10.1088/1361-6552/aba208
Bitzenbauer, P., and Meyn, J.-P. (2021a). Förderung eines funktionalen Modellverständnisses Lernender in der Quantenphysik. Naturwissenschaftlicher Unterr. Lehrerbildung im Umbruch 41, 270–273.
Bitzenbauer, P., and Meyn, J.-P. (2021b). Fostering students’ conceptions about the quantum world–results of an interview study. Prog. Sci. Educ. (PriSE) 4, 40–51.
Bitzenbauer, P., Veith, J. M., Girnat, B., and Meyn, J.-P. (2022). Assessing engineering students’ conceptual understanding of introductory quantum optics. Physics 4, 1180–1201. doi:10.3390/physics4040077
Bondani, M., Chiofalo, M. L., Ercolessi, E., Macchiavello, C., Malgieri, M., Michelini, M., et al. (2022). Introducing quantum technologies at secondary school level: Challenges and potential impact of an online extracurricular course. Physics 4, 1150–1167. doi:10.3390/physics4040075
Bouchée, T., de Putter-Smits, L., Thurlings, M., and Pepin, B. (2022). Towards a better understanding of conceptual difficulties in introductory quantum physics courses. Stud. Sci. Educ. 58, 183–202. doi:10.1080/03057267.2021.1963579
Chhabra, M., and Das, R. (2016). Quantum mechanical wavefunction: Visualization at undergraduate level. Eur. J. Phys. 38, 015404. doi:10.1088/0143-0807/38/1/015404
Chiofalo, M. L., Foti, C., Michelini, M., Santi, L., and Stefanel, A. (2022). Games for teaching/learning quantum mechanics: A pilot study with high-school students. Educ. Sci. 12, 446. doi:10.3390/educsci12070446
Chiofalo, M. L. M., and Michelini, M. (2023). An interview with marisa Michelini: IUPAP-ICPE medal, professor of physics-education research at udine university, GIREP president. Eurasia J. Math. Sci. Technol. Educ. 19, em2243. doi:10.29333/ejmste/13031
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. 2 edn. New York: Lawrence Erlbaum Associates.
Dachraoui, S., Hassouni, T., Chakir, E., Belboukhari, A., and Belboukhari, A. (2022). Development of a survey to assess conceptual understanding of quantum mechanics among moroccan undergraduates. Eur. J. Educ. Res. 11, 2219–2243. doi:10.12973/eu-jer.11.4.2219
DiSessa, A. A. (2018). “A friendly introduction to “knowledge in pieces”: Modeling types of knowledge and their roles in learning,” in Invited lectures from the 13th international congress on mathematical education (Berlin, Germany: Springer), 65–84.
Dür, W., and Heusler, S. (2014). Visualization of the invisible: The qubit as key to quantum physics. Phys. Teach. 52, 489–492. doi:10.1119/1.4897588
Evans, E. M. (2000). The emergence of beliefs about the origins of species in school-age children. Merrill-Palmer Q. 1982, 221–254.
Fischler, H., and Lichtfeldt, M. (1992). Modern physics and students’ conceptions. Int. J. Sci. Educ. 14, 181–190. doi:10.1080/0950069920140206
Galvez, E. (2019). “Quantum optics laboratories for teaching quantum physics,” in Fifteenth Conference on Education and Training in Optics and Photonics, Quebec City, Quebec, Canada, 2 July 2019. doi:10.1117/12.2523843
Gazzaniga, M. S. (2005). Forty-five years of split-brain research and still going strong. Nat. Rev. Neurosci. 6, 653–659. doi:10.1038/nrn1723
Gerke, F., Müller, R., Bitzenbauer, P., Ubben, M., and Weber, K. (2022). Requirements for future quantum workforce–a delphi study. J. Phys. Conf. Ser. 2297, 012017.
Goldberg, F. M., and McDermott, L. C. (1986). Student difficulties in understanding image formation by a plane mirror. Phys. Teach. 24, 472–481. doi:10.1119/1.2342096
Goorney, S., Foti, C., Santi, L., Sherson, J., Yago Malo, J., and Chiofalo, M. L. (2022). Culturo-scientific storytelling. Educ. Sci. 12, 474. doi:10.3390/educsci12070474
Greca, I. M., and Moreira, M. A. (2000). Mental models, conceptual models, and modelling. Int. J. Sci. Educ. 22, 1–11. doi:10.1080/095006900289976
Greinert, F., Müller, R., Bitzenbauer, P., Ubben, M. S., and Weber, K.-A. (2022). The future quantum workforce: Competences, requirements and forecasts. arXiv preprint arXiv:2208.08249.
Grosslight, L., Unger, C., Jay, E., and Smith, C. L. (1991). Understanding models and their use in science: Conceptions of middle and high school students and experts. J. Res. Sci. Teach. 28, 799–822. doi:10.1002/tea.3660280907
Guisasola, J., Almudi, J. M., and Zubimendi, J. L. (2004). Difficulties in learning the introductory magnetic field theory in the first years of University. Sci. Educ. 88, 443–464. doi:10.1002/sce.10119
Haeusler, C., and Donovan, J. (2020). Challenging the science curriculum paradigm: Teaching primary children atomic-molecular theory. Res. Sci. Educ. 50, 23–52. doi:10.1007/s11165-017-9679-2
Hemphill, J. (2003). Interpreting the magnitudes of correlation coefficients. Am. Psychol. 58, 78–79. doi:10.1037/0003-066x.58.1.78
Heusler, S., and Ubben, M. (2019). A haptic model of entanglement, gauge symmetries and minimal interaction based on knot theory. Symmetry 11, 1399. doi:10.3390/sym11111399
Heywood, D. S. (2005). Primary trainee teachers’ learning and teaching about light: Some pedagogic implications for initial teacher training. Int. J. Sci. Educ. 27, 1447–1475. doi:10.1080/09500690500153741
Ireson, G. (1999). A multivariate analysis of undergraduate physics students’ conceptions of quantum phenomena. Eur. J. Phys. 20, 193–199. doi:10.1088/0143-0807/20/3/309
Ireson, G. (2000). The quantum understanding of pre-University physics students. Phys. Educ. 35, 15–21. doi:10.1088/0031-9120/35/1/302
Kalkanis, G., Hadzidaki, P., and Stavrou, D. (2003). An instructional model for a radical conceptual change towards quantum mechanics concepts. Sci. Educ. 87, 257–280. doi:10.1002/sce.10033
Kaur, M., and Venegas-Gomez, A. (2022). Defining the quantum workforce landscape: A review of global quantum education initiatives. Opt. Eng. 61, 081806. doi:10.1117/1.oe.61.8.081806
Ke, J.-L., Monk, M., and Duschl, R. (2005). Learning introductory quantum physics: Sensori-motor experiences and mental models. Int. J. Sci. Educ. 27, 1571–1594. doi:10.1080/09500690500186485
Körhasan, N. D., and Miller, K. (2020). Students’ mental models of wave–particle duality. Can. J. Phys. 98, 266–273. doi:10.1139/cjp-2019-0019
Krijtenburg-Lewerissa, K., Pol, H., Brinkman, A., and van Joolingen, W. (2017). Insights into teaching quantum mechanics in secondary and lower undergraduate education. Phys. Rev. Phys. Educ. Res. 13, 010109. doi:10.1103/PhysRevPhysEducRes.13.010109
Levrini, O., and Fantini, P. (2013). Encountering productive forms of complexity in learning modern physics. Sci. Educ. 22, 1895–1910. doi:10.1007/s11191-013-9587-4
Levy, J., and Trevarthen, C. (1976). Metacontrol of hemispheric function in human split-brain patients. J. Exp. Psychol. Hum. Percept. Perform. 2, 299–312. doi:10.1037/0096-1523.2.3.299
Malgieri, M., and Onorato, P. (2022). Recent progress on the sum over paths approach in quantum mechanics education. Physics 4, 1012–1025. doi:10.3390/physics4030067
Michelini, M., Faletic, S., and Pospiech, G. (2022). Work group 3 position paper: Teacher education and teaching/learning quantum physics. J. Phys. Conf. Ser. 2297, 012015.
Michelini, M., Ragazzon, R., Santi, L., and Stefanel, A. (2000). Proposal for quantum physics in secondary school. Phys. Educ. 35, 406–410. doi:10.1088/0031-9120/35/6/305
Michelini, M., and Stefanel, A. (2023). “Research studies on learning quantum physics,” in The international handbook of physics education research: Learning physics (New York: AIP Publishing LLC Melville), 8–1.
Montagnani, S., Stefanel, A., Chiofalo, M. L. M., Santi, L., and Michelini, M. (2023). An experiential program on the foundations of quantum mechanics for final-year high-school students. Phys. Educ. 58, 035003. doi:10.1088/1361-6552/acb5da
Moody, G., Sorger, V. J., Blumenthal, D. J., Juodawlkis, P. W., Loh, W., Sorace-Agaskar, C., et al. (2022). 2022 Roadmap on integrated quantum photonics. J. Phys. Photonics 4, 012501. doi:10.1088/2515-7647/ac1ef4
Moraga-Calderón, T. S., Buisman, H., and Cramer, J. (2020). The relevance of learning quantum physics from the perspective of the secondary school student: A case study. Eur. J. Sci. Math. Educ. 8, 32–50. doi:10.30935/scimath/9545
Müller, R., and Wiesner, H. (2002). Teaching quantum mechanics on an introductory level. Am. J. Phys. 70, 200–209. doi:10.1119/1.1435346
Oss, S., and Rosi, T. (2015). A bit of quantum mechanics. Phys. Teach. 53, 230–233. doi:10.1119/1.4914565
Pearson, B., and Jackson, D. (2010). A hands-on introduction to single photons and quantum mechanics for undergraduates. Am. J. Phys. 78, 471–484. doi:10.1119/1.3354986
Pospiech, G. (2021). Quantum cryptography as an approach for teaching quantum physics. Teaching-Learning Contemp. Phys. Res. Pract. 2021, 19–31.
Pospiech, G. (1999). Teaching the epr paradox at high school? Phys. Educ. 34, 311–316. doi:10.1088/0031-9120/34/5/307
Pospiech, G. (2000). Uncertainty and complementarity: The heart of quantum physics. Phys. Educ. 35, 393–399. doi:10.1088/0031-9120/35/6/303
Sağlam, M., and Millar, R. (2006). Upper high school students’ understanding of electromagnetism. Int. J. Sci. Educ. 28, 543–566. doi:10.1080/09500690500339613
Seskir, Z. C., Migdał, P., Weidner, C., Anupam, A., Case, N., Davis, N., et al. (2022). Quantum games and interactive tools for quantum technologies outreach and education. Opt. Eng. 61, 081809. doi:10.1117/1.oe.61.8.081809
Stefani, C., and Tsaparlis, G. (2009). Students’ levels of explanations, models, and misconceptions in basic quantum chemistry: A phenomenographic study. J. Res. Sci. Teach. 46, 520–536. doi:10.1002/tea.20279
Taber, K. S. (2005). Learning quanta: Barriers to stimulating transitions in student understanding of orbital ideas. Sci. Educ. 89, 94–116. doi:10.1002/sce.20038
Ubben, M. S., and Bitzenbauer, P. (2022). Two cognitive dimensions of students’ mental models in science: Fidelity of gestalt and functional fidelity. Educ. Sci. 12, 163. doi:10.3390/educsci12030163
Ubben, M. S., and Heusler, S. (2021). Gestalt and functionality as independent dimensions of mental models in science. Res. Sci. Educ. 51, 1349–1363. doi:10.1007/s11165-019-09892-y
Ubben, M. (2020). Typisierung des Verständnisses mentaler Modelle mittels empirischer Datenerhebung am Beispiel der Quantenphysik (Volume 304). Berlin, Germany: Logos Verlag Berlin.
Veith, J. M., Bitzenbauer, P., and Girnat, B. (2022a). Exploring learning difficulties in abstract algebra: The case of group theory. Educ. Sci. 12, 516. doi:10.3390/educsci12080516
Veith, J. M., Girnat, B., and Bitzenbauer, P. (2022b). The role of affective learner characteristics for learning about abstract algebra: A multiple linear regression analysis. EURASIA J. Math. Sci. Technol. Educ. 18, em2157. doi:10.29333/ejmste/12417
Weissman, E. Y., Merzel, A., Katz, N., and Galili, I. (2022). Phenomena and principles: Presenting quantum physics in a high school curriculum. Physics 4, 1299–1317. doi:10.3390/physics4040083
Zaman Ahmed, S., Jensen, J. H. M., Weidner, C. A., Sørensen, J. J., Mudrich, M., and Sherson, J. F. (2021). Quantum composer: A programmable quantum visualization and simulation tool for education and research. Am. J. Phys. 89, 307–316. doi:10.1119/10.0003396
Zarkadis, N., Papageorgiou, G., and Stamovlasis, D. (2017). Studying the consistency between and within the student mental models for atomic structure. Chem. Educ. Res. Pract. 18, 893–902. doi:10.1039/c7rp00135e
Keywords: quantum physics, conceptual understanding, model understanding, empirical investigation, correlation analysis
Citation: Ubben M and Bitzenbauer P (2023) Exploring the relationship between students’ conceptual understanding and model thinking in quantum optics. Front. Quantum Sci. Technol. 2:1207619. doi: 10.3389/frqst.2023.1207619
Received: 17 April 2023; Accepted: 04 May 2023;
Published: 12 May 2023.
Edited by:
Marisa Michelini, University of Udine, ItalyReviewed by:
Dean Zollman, Kansas State University, United StatesGesche Pospiech, Technical University Dresden, Germany
Copyright © 2023 Ubben and Bitzenbauer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Philipp Bitzenbauer, cGhpbGlwcC5iaXR6ZW5iYXVlckBmYXUuZGU=
 Malte Ubben1
Malte Ubben1 Philipp Bitzenbauer
Philipp Bitzenbauer