Abstract
Electromagnetic radiation at telecommunication frequencies has been reported to have biological effects, particularly affecting the production of reactive oxygen species, raising the question of potential mechanisms. In this study, we explored whether the radical pair mechanism (RPM) could account for these effects. Given that telecommunication frequencies are much higher than those associated with typical hyperfine interactions in biological systems, any effects would necessarily be non-resonant. Our computational simulations confirm that the RPM cannot explain these effects under experimental conditions due to the negligible influence of low-amplitude oscillating fields. We find that observable effects on radical pairs at telecommunication frequencies would require hyperfine coupling constants that are precisely fine-tuned to values far exceeding those naturally occurring in biological systems. We conclude that another mechanism must be responsible for the effects of telecommunication frequency fields in biological systems.
1 Introduction
Reactive oxygen species (ROS) are crucial signaling molecules within cells, playing vital roles in various physiological processes Terzi and Suter (2020); Sies and Jones (2020); Sies et al. (2017); Gurhan and Barnes (2023). However, excessive accumulation of ROS can trigger oxidative stress, causing substantial damage to lipids, proteins, and DNA Imlay (2013). This damage compromises cell function and is associated with the onset of various pathologies, including cancer, cardiovascular diseases, and neurodegenerative conditions Jackson and Bartek (2009); Handy and Loscalzo (2017); Incalza et al. (2018); Münzel et al. (2017); Tarafdar and Pula (2018); Sbodio et al. (2019). Thus, the regulation of ROS levels is essential for maintaining cellular integrity and preventing the progression of these pathologies Sies and Jones (2020).
Experimental evidence, detailed in Table 1, shows that electromagnetic radiation at telecommunication frequencies, particularly within the ultra-high frequency (UHF) range, can influence ROS levels even at low amplitudes. Studies utilizing exposure to UHF electromagnetic fields have observed changes in ROS production within various cell types. For instance, Luukkonen et al. reported that exposure to 872 MHz radiation at a specific absorption rate (SAR) of 5 W/kg induced ROS production and DNA damage in human SH-SY5Y neuroblastoma cells Luukkonen et al. (2009). Similarly, other investigations have shown increased ROS levels in human peripheral blood mononuclear cells Kazemi et al. (2015), human HEK293 cells Pooam et al. (2022), and astrocytes Campisi et al. (2010) following exposure at frequencies relevant to mobile communication technologies. Moreover, the effects extend beyond cellular responses to affect whole organisms. Research has shown that Drosophila exposed to DECT (Digital Enhanced Cordless Telephone) base radiation 1.88–1.90 GHz exhibited elevated ROS levels in both bodies and ovaries Manta et al. (2014). In addition, studies on human spermatozoa exposed to 2.45 GHz Wi-Fi radiation revealed significant oxidative stress damage, including increased ROS levels, DNA fragmentation, and decreased sperm motility and vitality Ding et al. (2018).
TABLE 1
| EMF exposure | Bioeffect | Ref |
|---|---|---|
| 872 MHz with SAR of 5 W/kg | Increased ROS level in human SH-SY5Y cells | Luukkonen et al. (2009) |
| 900 MHz with power of 2 W (GSM modulated, 217 Hz) | Increased ROS level in human peripheral blood mononuclear cells | Kazemi et al. (2015) |
| 1.8 GHz with signal amplitude of −8.5 dBm to −67 dBm | Increased ROS level in human HEK293 cells | Pooam et al. (2022) |
| 900 MHz with electric field of 10 V/m and power density of 0.26 | Increased ROS level and DNA fragmentation in astrocytes | Campisi et al. (2010) |
| 1.88–1.90 GHz with SAR of 0.009 W/kg | Increased ROS level in Drosophila | Manta et al. (2014) |
| 2.45 GHz with SAR of 1.0–2.5 W/kg | Increased ROS level in human semen | Ding et al. (2018) |
| 850 MHz with SAR of 1.46 W/kg | Increased ROS level in human ejaculated semen | Agarwal et al. (2009) |
| 1.8 GHz with SAR of 0.4–27.5 W/kg | Increased ROS level and DNA damage in human spermatozoa | De Iuliis et al. (2009) |
| 940 MHz with SAR of 0.09 W/kg | Increased ROS level in HEK cells | Sefidbakht et al. (2014) |
Summary of ultra-high frequency effects on ROS.
Weak magnetic fields (MFs) have been known to influence chemical reactions. Numerous studies have documented the effects of static magnetic fields (SMFs) on ROS production in various systems, highlighting their biological significance. For instance, Calabrò et al. reported that exposure to a static magnetic field of 2.2 mT significantly increased ROS production in human SH-SY5Y neuroblastoma cells Calabrò et al. (2013). Bekhite et al. found that static magnetic fields ranging from 0.2 mT to 5 mT elevated ROS levels in mouse embryoid bodies, indicating the role of ROS in SMF-induced differentiation processes Bekhite et al. (2013). Additionally, Martino and Castello demonstrated that low-level magnetic fields (45 T to 60 T) modulated hydrogen peroxide production in various cell types, including cancer cells and endothelial cells, suggesting a broader impact of magnetic fields on cellular redox states Martino and Castello (2011).
The radical pair mechanism (RPM) can explain static magnetic field effects on chemical reactions, originating from spin chemistry, with magnetoreception in avian species being a notable example Hayashi (2004); Hochstoeger et al. (2020); Huelga and Plenio (2013); Johnsen and Lohmann (2005); Wiltschko and Wiltschko (2023); Ritz et al. (2000), Ritz et al. (2004); Zadeh-Haghighi and Simon (2022a); Maeda et al. (2008); Kerpal et al. (2019); Mouritsen (2022); Xu et al. (2021). This model is based on the creation of radical pairs—molecules with unpaired electron spins in the presence of nearby nuclear spins—that are exquisitely sensitive to weak MFs Timmel and Hore (1996); Hore (2012); Hore et al. (2020). Recent studies have illustrated how RPM can influence ROS production in live cells. Usselman et al. demonstrated that coherent electron spin dynamics in radical pairs formed at flavoenzyme centers can modulate ROS levels through singlet-triplet interconversion, impacted by both static and oscillating magnetic fields Usselman et al. (2016). Superoxide radicals , as primary forms of ROS, are generated through two main pathways: mitochondrial electron transport and the action of NADPH oxidase enzymes Bedard and Krause (2007); Liu et al. (2002); Terzi and Suter (2020); Moghadam et al. (2021); Murphy (2009); Hernansanz-Agustín and Enríquez (2021). This electron transfer process—and thus ROS generation—can be modulated by magnetic fields through RPM Usselman et al. (2014). Usselman et al. further showed that these fields can alter the cellular balance of and , indicating a broader spectrum of mechanisms at play Usselman et al. (2016). This is further supported by the observation that both the mitochondrial electron transport chain and Nox enzymes can generate magnetically sensitive flavin and superoxide-based radical pairs, implicating them as potential contributors to the magnetic field effects on ROS levels Rishabh et al. (2022); Usselman et al. (2016).
Given the established effects of static magnetic fields on ROS through the RPM, it is pertinent to investigate whether the observed effects of telecommunication frequency radiation on ROS could be due to oscillating magnetic fields (OMFs) in the context of the RPM. While the RPM generally requires a resonance between the magnetic field frequency and the energy level differences in the radical pairs to have a pronounced effect, our study investigates whether telecommunication frequencies might still produce subtle non-resonant effects Timmel and Hore (1996); Rodgers et al. (2005); Hiscock et al. (2017); Woodward et al. (1997), Woodward et al. (2001); Henbest et al. (2004); Leberecht et al. (2022), Leberecht et al. (2023). Our investigation confirms that the RPM cannot account for the observed effects of radio frequencies typically found within telecommunication devices on ROS levels. This shows the need to look for alternative mechanisms, possibly involving the electric component of the UHF fields.
2 Results
2.1 Radical pair mechanism
Radical pairs, formed during processes involving molecular bond breakage or electron transfer events, exhibit behavior dictated by their intrinsic angular momentum, represented by the spin quantum number and the spin projection quantum number Zadeh-Haghighi and Simon (2022a). This intrinsic angular momentum facilitates interactions with external magnetic fields and adjacent spins. Importantly, the conservation of angular momentum during these interactions means that the electron spins within radical pairs tend to align according to the spin state of their precursor molecules Zadeh-Haghighi and Simon (2022a); Gerson and Huber (2003); Efimova and Hore (2008). Consequently, the interaction of two unpaired electron spins can yield either a singlet state (, ) or triplet states (, ). The initial state of a radical pair, whether in a singlet or triplet configuration, is influenced by the surrounding nuclear spins, which are in a maximally mixed state due to thermalization Luo (2022).
Hyperfine and Zeeman interactions. Radical pair dynamics are greatly influenced by Zeeman and hyperfine interactions. The Zeeman interaction aligns electron spins with an external magnetic field, altering energy states and influencing reaction pathways Improta and Barone (2004). This interaction is described by the following (Equation 1):where represents the electron gyromagnetic ratio, the electron spin operator, and is the external magnetic field Improta and Barone (2004). The hyperfine interaction couples electron spins with nuclear spins, consisting of isotropic (Fermi contact) and anisotropic components. The anisotropic part is often assumed to be averaged out to zero due to molecular motion. This assumption is based on the possibility of randomized orientation of the molecules Atkins and Friedman (2005); Player (2021); Hogben (2011); Rishabh et al. (2022). The isotropic Fermi contact interaction, however, plays a significant role in singlet-triplet transitions of radical pairs Atkins and Friedman (2005); Player (2021); Hogben (2011). This interaction is described as the following (Equation 2):where represents the nuclear spin of the -th nucleus and the isotropic hyperfine coupling constant (HFCC). Additionally, the exchange and dipolar interactions also influence radical pair dynamics. The exchange interaction, which accounts for electron indistinguishability, is assumed to weaken exponentially as the radical pair separates Zadeh-Haghighi and Simon (2022a). The dipolar interaction arises from the magnetic moments in radical pairs and along with exchange interaction, they can inhibit singlet-triplet interconversion Efimova and Hore (2008); Kattnig and Hore (2017); Nohr et al. (2017); Babcock and Kattnig (2021). However, in cases when radical pairs in biological contexts are well-separated, the effects of both exchange and dipolar interactions are usually minimal Kattnig and Hore (2017); Nohr et al. (2017).
Spin dynamics and radical pair interconversion. The oscillation between the singlet and triplet states of radical pairs plays a crucial role in this dynamic Anisimov et al. (1983). These oscillations become pronounced when radicals are spatially separated enough to allow for coherent interconversion Hore (2021); Hore and Mouritsen (2016). The coherence in spin dynamics and the interconversion between singlet and triplet states can be mathematically described by the Liouville master equation, which governs the time evolution of the spin density matrix, , accounting for coherent superpositions, spin relaxation, and spin-selective chemical reactions Player (2021); Timmel et al. (1998). This is given by Equation 3:
where the Liouvillian superoperator is defined as , with representing the Hamiltonian superoperator, denoting the chemical reaction superoperator, and representing the spin relaxation superoperator Player (2021). The chemical reaction superoperator is given by Equation 4:where and are the rate constants for the singlet and triplet reactions, respectively, represents the identity matrix, is the nuclear spin multiplicity, defined as , with being the spin angular momentum quantum number of the -th nucleus, and = and = are the projection operators for the singlet and triplet states Luo (2022).
Spin relaxation superoperator is modelled by random time-dependent local fields, and is given by Equation 5:where and are the spin relaxation rate constants of radicals A and B, respectively, and and are the spin operators for electrons A and B Player (2021). The solution for Liouville master equation was obtained using QuTiP, a Python library for quantum simulations that enables direct modelling of the time dependent behaviour introduced by the oscillating magnetic field.
Following insights from Timmel et al., the chemical fate of the radical pair is elucidated by considering separate spin-selective reactions for singlet and triplet pairs. These reactions are modelled with identical first-order rate constants, Timmel et al. (1998). The yield of the singlet state, denoted as is characterized by the following expression (Equation 6):
and since , knowledge of one yield allows for the calculation of the other Zadeh-Haghighi and Simon (2022a).
2.2 Specific absorption rate
The specific absorption rate is a key metric in assessing how electromagnetic fields affect biological tissues, particularly under radio frequency (RF) exposures. SAR measures the energy absorbed per unit mass of tissue, given in watts per kilogram (W/kg), and is vital for understanding the potential health impacts of RF radiation Poljak (2018). SAR provides a standardized way to compare exposure levels across different RF sources, making it important in regulatory settings. Experiments that investigate radio frequency effects on biological systems often report SAR values to quantify the intensity of exposure. For example, SAR data helps correlate RF exposure levels with biological outcomes like increased ROS production or DNA damage. To estimate the magnetic fields involved in these experiments, we use a conversion formula that relates SAR to magnetic field strengths, which assumes plane wave conditions. This estimation is crucial for aligning theoretical models with experimental conditions. The formula is as follows (Equation 7):where is the electrical conductivity of the tissue in S/m, is the electric field in medium in V/m, and is the mass density of the tissue in Poljak (2018).
Given the experiment involving SH-SY5Y cells, where the SAR, dielectric constant , effective electric conductivity , and sample density are specified, we seek to estimate the magnetic field strength in Tesla within the biological medium Buttiglione et al. (2007). These values have been applied as representative approximations for other studies lacking such detailed data, allowing for a consistent approach to estimating magnetic field strengths across various experimental setups. Assuming that the magnetic permeability of biological tissues approximates that of free space , and considering the relative permittivity , conductivity ( = 1.9 S/m), and density , we can calculate the magnetic field from the electric field in the medium by recognizing that the magnetic field and magnetic field intensity are related by Equation 8:where is the magnetic permeability of free space . Next, considering the impedance of the medium, the magnetic field intensity is related to the electric field by Equation 9:where , the impedance of the medium, incorporates the medium’s conductivity and is given by Equation 10:
in which is the permittivity of free space , is the imaginary unit, and is the angular frequency of the RF field Wolski (2014). This method enables the estimation of the magnetic from known values of , , , and , factoring in the medium’s electrical properties Poljak (2018); Buttiglione et al. (2007); Wolski (2014). Using this method, we estimated range of magnetic field amplitudes used in experimental conditions extends from approximately 95 nT to 5 T. For instance, in the study by Manta et al. Manta et al. (2014), the calculated SAR value of 0.009 W/kg corresponds to an estimated magnetic field amplitude of approximately 95 nT. Conversely, in the study by De Iuliis et al. De Iuliis et al. (2009), the SAR values ranging from 0.4 W/kg to 27.5 W/kg correspond to an estimated upper magnetic field amplitude of approximately 5 T. To align our analysis more closely with practical experimental scenarios, we selected a conservative OMF amplitude of T for comparative analysis. This chosen amplitude represents the higher end of magnetic fields estimated from SAR values in experimental settings, ensuring that our conclusions are applicable to all considered exposure scenarios.
2.3 Magnetic field effects on radical pair dynamics
By applying the principles discussed, we investigate how these fields influence the quantum states and reaction yields of radical pairs. The spin Hamiltonian for a typical radical pair system in the presence of a static magnetic field is expressed as Equation 11:where is the Larmor precession frequency for the electrons , and represent the nuclear spin operators for nuclei interacting with electrons A and B respectively, and the coefficients and are the isotropic HFCCs Improta and Barone (2004).
Focusing on ROS, we model a radical pair system comprising and to explore the magnetic field effects on radical pair dynamics. The correlated spins are represented as …], where the reaction produces either from the singlet state or maintains from the triplet state, without considering any conversion from to Rishabh et al. (2022); Usselman et al. (2016). The unpaired electron on is assumed to interact only with its H5 nucleus Rishabh et al. (2022); Lee et al. (2014). This choice to consider only the H5 nucleus is justified by the work of Hiscock et al., which highlights the significant impact of hyperfine interactions on radical pair dynamics and resonance effects. Hiscock’s studies show that the presence of multiple nuclei can lead to a variety of energy-level spacings, affecting the resonance conditions and the magnetic sensitivity of the radical pair system Hiscock et al. (2017). H5 nucleus in has a higher magnitude hyperfine coupling constant (T) compared to other nuclei, making it the most relevant for our analysis. Including additional nuclei with lower hyperfine coupling constants would complicate the model without substantially altering the primary effects we are investigating. Note that this choice would likely overestimate the magnetic field effect Rishabh et al. (2022); Lee et al. (2014); Hiscock et al. (2017).
Oscillating Magnetic Field. Oscillating magnetic fields introduce time-dependent dynamics that can alter radical pair processes, affecting the reactivity and yields of singlet and triplet products. We focus on the effects of radio frequency OMFs to assess whether the RPM can explain the observed ROS production under these conditions. The effect of an OMF on the system is incorporated into the Hamiltonian as follows (Equation 12):where represents the isotropic HFCC between the -th electron spin operator and the -th nuclear spin operator . The term accounts for the static component of the magnetic field with indicating the angle between the two magnetic fields, while introduces the oscillating magnetic field where is the amplitude of the oscillating field, and is its angular frequency Rodgers et al. (2005).
For our calculations, we set the angle as 90, the reaction rate constant , and the relaxation rate constant . Previous studies have suggested that free exhibits a spin relaxation lifetime on the order of 1 nanosecond due to fast molecular rotation and strong spin-orbit coupling Player and Hore (2019); Hogben et al. (2009). However, our chosen relaxation rate constant reflects the scenario where this fast relaxation is significantly slowed by a reduction in molecular symmetry and the quenching of orbital angular momentum, which can occur in a more constrained biological environment Player and Hore (2019); Hogben et al. (2009); Rishabh et al. (2022). For this to happen, must be bound, allowing for longer coherence times, such as those modelled by our relaxation rate constant Rishabh et al. (2022).
In our model, the radical pair …] is initially assumed to be in the singlet state, despite the oxygen molecule’s ground state typically favouring a triplet configuration. This assumption is based on the possibility of spin-orbit coupling facilitating a transition from triplet to singlet or the formation of an excited singlet state, both of which are biologically relevant in certain contexts Zadeh-Haghighi and Simon (2022b); Rishabh et al. (2022). Note that this assumption overestimates the effects of the oscillating magnetic field, as our calculations show a reduction of around 80% in the OMF effect when assuming an initial triplet state compared to a singlet state.
Figure 1 illustrates how the triplet yield of our radical pair system responds to varying static magnetic field strengths and oscillating magnetic field frequencies, with an isotropic HFCC of T. The amplitude of the radio frequency field applied here is T, a value chosen to explore the influence of radio frequencies at a relatively low amplitude on radical pair dynamics compared to the range of varying static magnetic field. We observe resonant peaks where the combination of static field strength and radio frequency increases the triplet yield. These conditions, where specific frequencies of the oscillating magnetic field combined with particular static magnetic field strengths, induce noticeable enhancements in triplet yields, demonstrating the potential of an oscillating field to modify the standard dynamics of the radical pair system. At these resonant points, the applied radio frequency enhances the conversion of radical pairs to the triplet state, resulting in altered yields of the reaction products compared to those observed in the absence of an OMF Rishabh et al. (2022); Rodgers et al. (2005). These resonances arise due to the interplay between the Zeeman effect and hyperfine interactions within the radical pair system. Specifically, the static magnetic field causes energy level splitting (Zeeman splitting) of the electron spins, while hyperfine interactions introduce additional splitting due to the coupling between the electron and nuclear spins. The normalized eigenstates of our system, corresponding to these energy levels without the oscillating field term, are given by Equation 13:
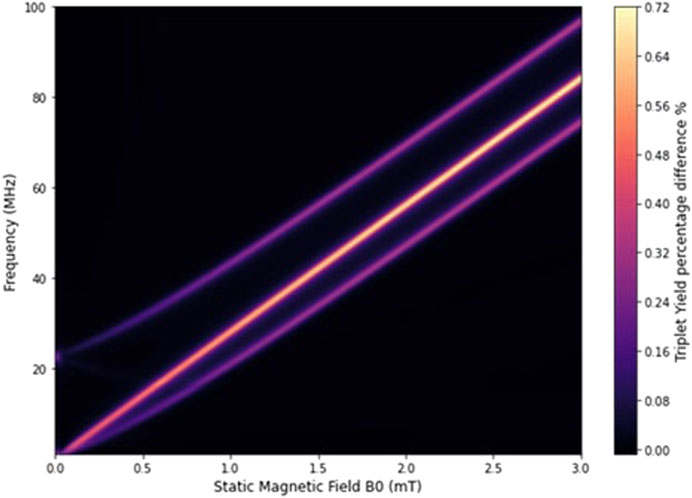
FIGURE 1
Variation in triplet yield with static magnetic field strength and radio frequency for a constant isotropic HFCC , OMF amplitude T, reaction rate constant , relaxation rate constant , and spin multiplicity . Resonant lines indicate enhanced triplet yields at specific field-frequency combinations.
where , , and .
One of these resonant peaks corresponds to the electron Larmor frequency, which is associated with transitions between specific energy levels of the radical pair system. For example, the transition from energy state , as well as the transition from , occur at this frequency. This resonant effect is particularly prominent when the static and oscillating magnetic fields are perpendicular, consistent with theoretical predictions Hore (2024). Additionally, we detected another resonant effect at a higher frequency of approximately 22.5 MHz. This resonance corresponds to transitions between the highest and lowest energy levels of the hyperfine spin Hamiltonian, such as the transition from . This aligns with the expectation that the maximum radiofrequency having a resonant effect on a radical pair at weak static fields is determined by this energy level separation Hore (2024). It is important to note that this maximum frequency is significantly lower than the telecommunication frequencies, which are typically above 800 MHz. This difference means that any observed effect must be non-resonant. Finally, we observe another resonance at an even lower frequency, which is associated with additional hyperfine splitting and transitions such as the one between states .
To investigate effects in higher-frequency fields, particularly those above 800 MHz, we studied the influence of the initial hyperfine coupling constant (T) and amplitude T under geomagnetic-strength static field of T. Our observations at 872 MHz, a frequency choice based on the study by Luukonen et al., reveal that the effects observed when an oscillating magnetic field is applied alongside a static magnetic field are very small compared to when only the static magnetic field is present Luukkonen et al. (2009). As shown in Figure 2, the presence of an OMF at 872 MHz produces effects similar to those observed without it. When comparing these scenarios in the presence of a static magnetic field at geomagnetic field strength, the effect size is extremely small, with only an approximate % difference between applying and not applying an OMF at 872 MHz. This observation suggests that, for the given initial HFCC, the impact of UHF fields on the dynamics of the radical pair may not be significant. Such findings prompt further exploration into additional factors that might contribute to the interactions observed at such frequencies.
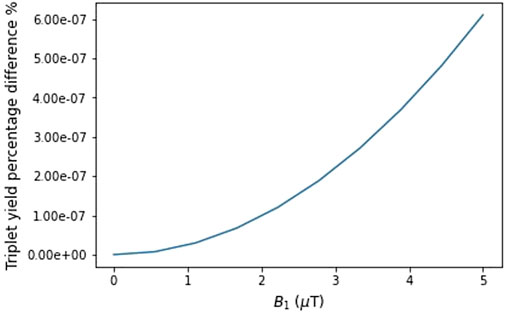
FIGURE 2
Effect of varying OMF amplitudes at 872 MHz from 0 to 5 T on the triplet yield for a system at a static magnetic field of 50 T. The analysis was conducted with a hyperfine coupling constant T, reaction rate constant , relaxation rate constant , and spin multiplicity . The results indicate a minimal influence, with approximately a 6.11 % difference at a 5 T OMF amplitude.
The hyperfine coupling constant is a critical factor that modulates the response of radical pair systems to magnetic fields. It indicates a possible mechanism through which higher frequency fields can exert biological effects even when the static magnetic field aligns with Earth’s geomagnetic field strengths. Figure 3 addresses how varying the HFCC impact the triplet yield of a radical pair under a static magnetic field typical of the geomagnetic range.
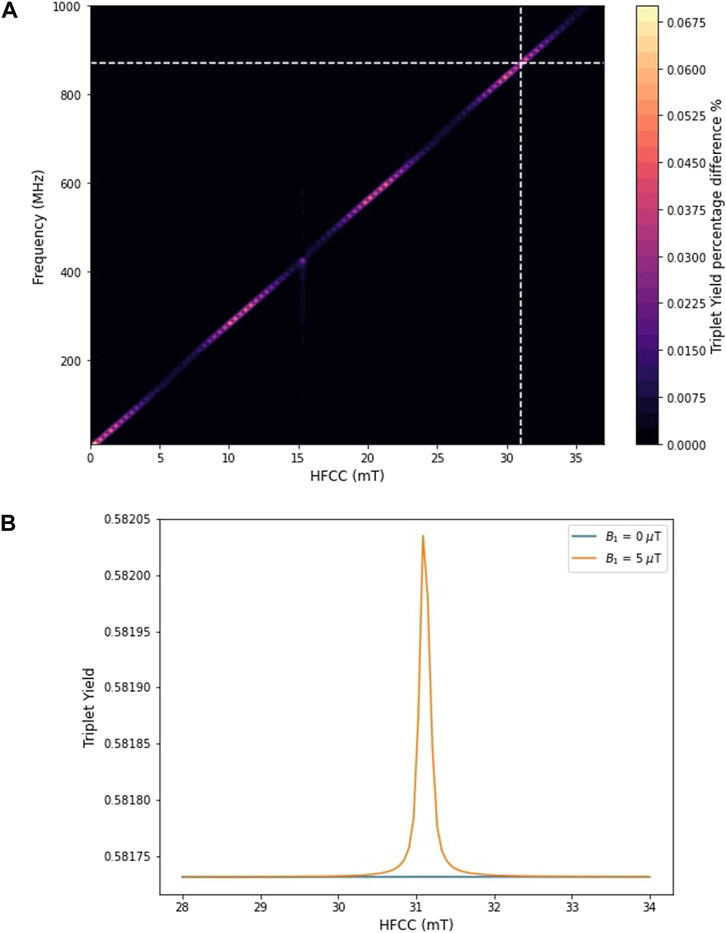
FIGURE 3
(A) Variation in triplet yield difference with and without OMF (T) as a function of hyperfine coupling constant (HFCC) and frequency at geomagnetic static field strength (T). The dashed white line at 872 MHz indicates the HFCC (31.14 mT) needed for a measurable OMF effect. (B) Triplet yield as a function of the HFCC at a geomagnetic-strength static field (T) and a radio frequency of 872 MHz. The blue line indicates the triplet yield in the absence of an OMF, whereas the orange line depicts the yield when subjected to an OMF of strength T. The graph highlights a narrow HFCC range where the OMF effect is maximized, around an HFCC value of 31.14 mT with approximately 0.05% difference in the triplet yield. The analysis in all cases was conducted with reaction rate constant , relaxation rate constant , and spin multiplicity .
Our analysis reveals a direct correlation between the magnitude of the HFCC and the effect of an oscillating magnetic field on the triplet yield at higher frequencies. Notably, an HFCC of approximately 31.14 mT is required to observe an effect at a radio frequency of 872 MHz, shown as dashed white line on Figure 3A. Figure 3B further illustrates that the triplet yield varies significantly with HFCC, showing a narrow range around 31.14 mT where the effect of the oscillating magnetic field is maximized, which corresponds to a percentage difference of approximately 0.05% when comparing the triplet yield with and without the application of a 5 T OMF. This suggests that not only would the HFCC need to be exceptionally large but also finely tuned to account for effects at such high frequencies. This seems highly improbable, casting doubt on the likelihood that large HFCC values are the correct explanation for the observed phenomena, as typical HFCC values in biological systems are much lower, generally in the range of microtesla to a few millitesla. For instance, studies on radicals derived from amino acids and other biological molecules show that the HFCCs typically range up to 5 mT Ban et al. (2013).
Nevertheless, given the minimal impact observed with the initial HFCC, we adjusted the HFCC to 31.14 mT to explore the influence of radio frequency on the triplet yield within a geomagnetic field range. We investigated the effects of varying reaction and relaxation rate constants while keeping the OMF amplitude fixed at 5 T and the static magnetic field constant at 50 T. Figure 4 shows that, even for this very large and finely tuned value of the HFCC, the influence of the magnetic component of the electromagnetic radiation at telecommunication frequencies remains less than 0.09%, underscoring the limited impact of low amplitude OMF on the radical pair system.
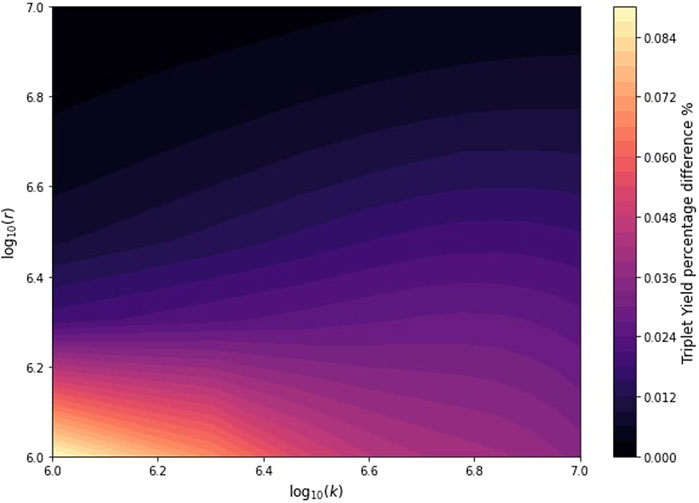
FIGURE 4
Analysis showing the percentage difference in triplet yield with and without an OMF at an amplitude of T, frequency of 872 MHz, HFCC mT, and spin multiplicity across various relaxation and reaction rate constants at a presence of geomagnetic field (T).
3 Discussion
Consistent with simple resonance arguments, our study highlights the limitations of the radical pair mechanism in explaining the observed effects of radio frequency fields, particularly in the telecommunications range, such as 872 MHz. A critical finding of our analysis is the requirement for hyperfine coupling constants values, which are finely tuned and significantly higher than those observed in biological systems, to detect effects at these high frequencies under geomagnetic conditions Lee et al. (2014); Ban et al. (2013). Additionally, when we varied the OMF from 0 to 5 T, the relevant range for the experiments under consideration, we found that the impact of ultra-high radio frequencies on radical pair systems remains negligible even at the estimated upper range amplitude.
Therefore, while the RPM can well explain static magnetic field effects on ROS, it cannot account for the effects of telecommunication-frequency radiation on reactive oxygen species. Note that our modelling assumptions, such as utilizing a single nucleus H5, assuming an initial singlet state, and disregarding dipole-dipole and exchange interactions, have very likely led to an overestimation of the effects observed Efimova and Hore (2008); Kattnig and Hore (2017); Nohr et al. (2017); Babcock and Kattnig (2021); Luo (2023). Additionally, our choice of the spin relaxation rate constant is associated with the maximum observed effect. Since the effect diminishes with increasing relaxation rate constant, as shown in Figure 4, this suggests that the chosen relaxation rate constant may overestimate the effect of the OMF. This potential overestimation suggests that the actual impact of ultra-high radio frequencies on the radical pair system could be even lower, further emphasizing the significant limitation of the radical pair mechanism in explaining observed effects within biological systems.
We also chose to focus on a radical pair system that directly involves , which lacks nuclear spins and therefore experiences relatively larger magnetic effects. This configuration likely represents an upper bound on the expected effects of the RPM under telecommunication frequencies. Other radical pairs that do not involve superoxide directly are expected to show even smaller responses due to the additional nuclear spin interactions that further suppress magnetic sensitivity. Thus, our findings suggest that if the RPM cannot account for the observed effects in a superoxide-containing system, it is even less likely to do so in systems involving alternative radical pairs.
Several studies have described amplification routes that might enhance otherwise subtle RPM-based effects. For instance, a study demonstrated that an enzyme kinetic cycle could amplify small magnetic effects on radical pair recombination and Walleczek described magnetokinetic effects feeding into larger biochemical processes, including or redox signaling Eichwald and Walleczek (1996); Walleczek (1995). Additionally, Kattnig et al. (2016), Player et al. (2021), Rishabh et al. (2023), and Zandieh et al. (2025) each proposed different scenarios in which small spin-state changes might be magnified. These studies suggest that under favorable biochemical conditions, amplification factors could range from several-fold to up to 100-fold, depending on enzymatic, oscillatory, or kinetic constraints. Even with this degree of amplification, the predicted effect remains exceedingly small. In the absence of resonance, our simulations estimate the RPM effect to be %, and even when applying the largest plausible amplification factor, the effect would still only reach %. This suggests that RPM-based amplifiers alone cannot account for the observed effects at telecommunication frequencies, as the fundamental resonance mismatch remains unaddressed.
Given these limitations, it seems plausible that these effects may be more attributable to the electrical component of the electromagnetic field in the context of telecommunication devices. Electric fields directly interact with charged cellular structures, particularly voltage-gated ion channels and membrane-bound enzymes, providing a non-magnetic route to ROS modulation Panagopoulos et al. (2021); Bertagna et al. (2021); Liu et al. (2024). Friedman et al. (2007) demonstrated that 875 MHz RF exposure activates NADH oxidase, leading to ROS generation, matrix metalloproteinase (MMP) activation, and epidermal growth factor receptor (EGFR) signaling, ultimately stimulating the extracellular signal-regulated kinase (ERK) cascade. Subsequently, Georgiou and Margaritis (2021) proposed that exposure to 875 MHz RF (0.240 ) increased NADPH oxidase (NOX) activity threefold in HeLa cells, though this increase was observed relative to its inhibition by diphenyleneiodonium (DPI), a NOX inhibitor that also blocks certain cation channels, which suggests that the effect was likely mediated by voltage-gated ion channels rather than direct RF interaction with NOX. Since NOX-driven ROS production depends on voltage-gated proton (Hv1) and cation (, , ) channels, RF-induced ion channel perturbations may disrupt redox balance and amplify oxidative stress Georgiou and Margaritis (2021). The dual inhibition of NOX and ion channels by DPI further supports ion transport as a key mediator of RF-induced ROS production, although other contributing mechanisms cannot be ruled out.
Our work highlights the need for a broader investigation to account for the observed effects. In general, electromagnetic field effects, including those related to ROS modulation, may intersect with signaling pathways fundamental to cellular processes. Future studies could explore the role of such interactions in more complex systems, including potential implications for electromagnetic influences on neuronal communication.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
OT: Conceptualization, Investigation, Methodology, Formal analysis, Software, Validation, Writing – original draft, Writing – review and editing. HZ-H: Conceptualization, Methodology, Validation, Supervision, Writing – review and editing. CS: Conceptualization, Funding acquisition, Methodology, Supervision, Writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Natural Sciences and Engineering Research Council through its Discovery Grant program and the Alliance Quantum Consortia grant ‘Quantum Enhanced Sensing and Imaging (QuEnSI)’, as well as the National Research Council of Canada through its Quantum Sensing Challenge Program.
Acknowledgments
The authors would like to thank Rishabh for his valuable comments and insights.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
Agarwal A. Desai N. R. Makker K. Varghese A. Mouradi R. Sabanegh E. et al (2009). Effects of radiofrequency electromagnetic waves (RF-EMW) from cellular phones on human ejaculated semen: an in vitro pilot study. Fertil. Steril.92, 1318–1325. 10.1016/j.fertnstert.2008.08.022
2
Anisimov O. A. Bizyaev V. L. Lukzen N. N. Grigoryants V. M. Molin Y. N. (1983). The induction of quantum beats by hyperfine interactions in radical-ion pair recombination. Chem. Phys. Lett.101, 131–135. 10.1016/0009-2614(83)87356-4
3
Atkins P. W. Friedman R. (2005). Molecular quantum mechanics. New York: Oxford University Press.
4
Babcock N. S. Kattnig D. R. (2021). Radical scavenging could answer the Challenge posed by electron–electron dipolar interactions in the cryptochrome compass model. JACS Au1, 2033–2046. 10.1021/jacsau.1c00332
5
Ban F. Gauld J. W. Wetmore S. D. Boyd R. J. (2013). The calculation of the hyperfine coupling tensors of biological radicals. Dordrecht: Springer Netherlands, 285–322.
6
Bedard K. Krause K.-H. (2007). The NOX family of ROS-generating NADPH oxidases: physiology and pathophysiology. Physiol. Rev.87, 245–313. 10.1152/physrev.00044.2005
7
Bekhite M. M. Figulla H.-R. Sauer H. Wartenberg M. (2013). Static magnetic fields increase cardiomyocyte differentiation of Flk-1+ cells derived from mouse embryonic stem cells via Ca2+ influx and ROS production. Int. J. Cardiol.167, 798–808. 10.1016/j.ijcard.2012.02.020
8
Bertagna F. Lewis R. Silva S. R. P. McFadden J. Jeevaratnam K. (2021). Effects of electromagnetic fields on neuronal ion channels: a systematic review. Ann. N. Y. Acad. Sci.1499, 82–103. 10.1111/nyas.14597
9
Buttiglione M. Roca L. Montemurno E. Vitiello F. Capozzi V. Cibelli G. (2007). Radiofrequency radiation (900 MHz) induces Egr-1 gene expression and affects cell-cycle control in human neuroblastoma cells. J. Cell. Physiology213, 759–767. 10.1002/jcp.21146
10
Calabrò E. Condello S. Currò M. Ferlazzo N. Caccamo D. Magazù S. et al (2013). Effects of low intensity static magnetic field on FTIR spectra and ROS production in SH-SY5Y neuronal-like cells. Bioelectromagnetics34, 618–629. 10.1002/bem.21815
11
Campisi A. Gulino M. Acquaviva R. Bellia P. Raciti G. Grasso R. et al (2010). Reactive oxygen species levels and DNA fragmentation on astrocytes in primary culture after acute exposure to low intensity microwave electromagnetic field. Neurosci. Lett.473, 52–55. 10.1016/j.neulet.2010.02.018
12
De Iuliis G. N. Newey R. J. King B. V. Aitken R. J. (2009). Mobile phone radiation induces reactive oxygen species production and DNA damage in human spermatozoa in vitro. PLoS ONE4, e6446. 10.1371/journal.pone.0006446
13
Ding S.-S. Sun P. Zhang Z. Liu X. Tian H. Huo Y. W. et al (2018). Moderate dose of trolox preventing the deleterious effects of wi-fi radiation on spermatozoa in vitro through reduction of oxidative stress damage. Chin. Med. J. Engl.131, 402–412. 10.4103/0366-6999.225045
14
Efimova O. Hore P. J. (2008). Role of exchange and dipolar interactions in the radical pair model of the avian magnetic compass. Biophysical J.94, 1565–1574. 10.1529/biophysj.107.119362
15
Eichwald C. Walleczek J. (1996). Model for magnetic field effects on radical pair recombination in enzyme kinetics. Biophysical J.71, 623–631. 10.1016/S0006-3495(96)79263-9
16
Friedman J. Kraus S. Hauptman Y. Schiff Y. Seger R. (2007). Mechanism of short-term erk activation by electromagnetic fields at mobile phone frequencies. Biochem. J.405, 559–568. 10.1042/BJ20061653
17
Georgiou C. D. Margaritis L. H. (2021). Oxidative stress and nadph oxidase: connecting electromagnetic fields, cation channels and biological effects. Int. J. Mol. Sci.22, 10041. 10.3390/ijms221810041
18
Gerson F. Huber W. (2003). Electron spin resonance spectroscopy of organic radicals. Weinheim: Wiley VCH.
19
Gurhan H. Barnes F. (2023). Impact of weak radiofrequency and static magnetic fields on key signaling molecules, intracellular ph, membrane potential, and cell growth in HT-1080 fibrosarcoma cells. Sci. Rep.13, 14223. 10.1038/s41598-023-41167-5
20
Handy D. E. Loscalzo J. (2017). Responses to reductive stress in the cardiovascular system. Free Radic. Biol. Med.109, 114–124. 10.1016/j.freeradbiomed.2016.12.006
21
Hayashi H. (2004). Introduction to dynamic spin chemistry: magnetic field effects on chemical and biochemical reactions, vol. 8 (World Scientific)
22
Henbest K. B. Kukura P. Rodgers C. T. Hore P. J. Timmel C. R. (2004). Radio frequency magnetic field effects on a radical recombination reaction: a diagnostic test for the radical pair mechanism. J. Am. Chem. Soc.126, 8102–8103. 10.1021/ja048220q
23
Hernansanz-Agustín P. Enríquez J. A. (2021). Generation of reactive oxygen species by mitochondria. Antioxidants10, 415. 10.3390/antiox10030415
24
Hiscock H. G. Mouritsen H. Manolopoulos D. E. Hore P. J. (2017). Disruption of magnetic compass orientation in migratory birds by radiofrequency electromagnetic fields. Biophysical J.113, 1475–1484. 10.1016/j.bpj.2017.07.031
25
Hochstoeger T. Al Said T. Maestre D. Walter F. Vilceanu A. Pedron M. et al (2020). The biophysical, molecular, and anatomical landscape of pigeon cry4: a candidate light-based quantal magnetosensor. Sci. Adv.6, eabb9110. 10.1126/sciadv.abb9110
26
Hogben H. (2011). Coherent spin dynamics of radical pairs in weak magnetic fields. Oxford, United Kingdom: University of Oxford. Ph.D. thesis.
27
Hogben H. J. Efimova O. Wagner-Rundell N. Timmel C. R. Hore P. (2009). Possible involvement of superoxide and dioxygen with cryptochrome in avian magnetoreception: origin of Zeeman resonances observed by in vivo EPR spectroscopy. Chem. Phys. Lett.480, 118–122. 10.1016/j.cplett.2009.08.051
28
Hore P. J. (2012). Are biochemical reactions affected by weak magnetic fields?Proc. Natl. Acad. Sci. U.S.A.109, 1357–1358. 10.1073/pnas.1120531109
29
Hore P. J. (2021). Radical quantum oscillations. Science374, 1447–1448. 10.1126/science.abm9261
30
Hore P. J. (2024). Spin chemistry in living systems. Natl. Sci. Rev.11, nwae126. 10.1093/nsr/nwae126
31
Hore P. J. Ivanov K. L. Wasielewski M. R. (2020). Spin chemistry. J. Chem. Phys.152, 120401. 10.1063/5.0006547
32
Hore P. J. Mouritsen H. (2016). The radical-pair mechanism of magnetoreception. Annu. Rev. Biophysics45, 299–344. 10.1146/annurev-biophys-032116-094545
33
Huelga S. F. Plenio M. B. (2013). Vibrations, quanta and biology. Contemp. Phys.54, 181–207. 10.1080/00405000.2013.829687
34
Imlay J. A. (2013). The molecular mechanisms and physiological consequences of oxidative stress: lessons from a model bacterium. Nat. Rev. Microbiol.11, 443–454. 10.1038/nrmicro3032
35
Improta R. Barone V. (2004). Interplay of electronic, environmental, and vibrational effects in determining the hyperfine coupling constants of organic free radicals. Chem. Rev.104, 1231–1254. 10.1021/cr960085f
36
Incalza M. A. D'Oria R. Natalicchio A. Perrini S. Laviola L. Giorgino F. (2018). Oxidative stress and reactive oxygen species in endothelial dysfunction associated with cardiovascular and metabolic diseases. Vasc. Pharmacol.100, 1–19. 10.1016/j.vph.2017.05.005
37
Jackson S. P. Bartek J. (2009). The DNA-damage response in human biology and disease. Nature461, 1071–1078. 10.1038/nature08467
38
Johnsen S. Lohmann K. J. (2005). The physics and neurobiology of magnetoreception. Nat. Rev. Neurosci.6, 703–712. 10.1038/nrn1745
39
Kattnig D. R. Evans E. W. Déjean V. Dodson C. A. Wallace M. I. Mackenzie S. R. et al (2016). Chemical amplification of magnetic field effects relevant to avian magnetoreception. Nat. Chem.8, 384–391. 10.1038/nchem.2447
40
Kattnig D. R. Hore P. J. (2017). The sensitivity of a radical pair compass magnetoreceptor can Be significantly amplified by radical scavengers. Sci. Rep.7, 11640. 10.1038/s41598-017-09914-7
41
Kazemi E. Mortazavi S. M. J. Ali-Ghanbari A. Sharifzadeh S. Ranjbaran R. Mostafavi-Pour Z. et al (2015). Effect of 900 MHz electromagnetic radiation on the induction of ROS in human peripheral blood mononuclear cells. J. Biomed. Phys. Eng.5, 105–114.
42
Kerpal C. Richert S. Storey J. G. Pillai S. Liddell P. A. Gust D. et al (2019). Chemical compass behaviour at microtesla magnetic fields strengthens the radical pair hypothesis of avian magnetoreception. Nat. Commun.10, 3707. 10.1038/s41467-019-11655-2
43
Leberecht B. Kobylkov D. Karwinkel T. Döge S. Burnus L. Wong S. Y. et al (2022). Broadband 75–85 MHz radiofrequency fields disrupt magnetic compass orientation in night-migratory songbirds consistent with a flavin-based radical pair magnetoreceptor. J. Comp. Physiology A208, 97–106. 10.1007/s00359-021-01537-8
44
Leberecht B. Wong S. Y. Satish B. Döge S. Hindman J. Venkatraman L. et al (2023). Upper bound for broadband radiofrequency field disruption of magnetic compass orientation in night-migratory songbirds. Proc. Natl. Acad. Sci. U.S.A.120, e2301153120. 10.1073/pnas.2301153120
45
Lee A. A. Lau J. C. S. Hogben H. J. Biskup T. Kattnig D. R. Hore P. J. (2014). Alternative radical pairs for cryptochrome-based magnetoreception. J. R. Soc. Interface11, 20131063. 10.1098/rsif.2013.1063
46
Liu L. Huang B. Lu Y. Zhao Y. Tang X. Shi Y. (2024). Interactions between electromagnetic radiation and biological systems. iScience27, 109201. 10.1016/j.isci.2024.109201
47
Liu Y. Fiskum G. Schubert D. (2002). Generation of reactive oxygen species by the mitochondrial electron transport chain. J. Neurochem.80, 780–787. 10.1046/j.0022-3042.2002.00744.x
48
Luo J. (2022). Spin dynamics of radical pairs in magnetic fields. Oxford, United Kingdom: University of Oxford. Ph.D. thesis.
49
Luo J.-L. (2023). On the anisotropic weak magnetic field effect in radical-pair reactions. J. Chem. Phys.158, 234302. 10.1063/5.0149644
50
Luukkonen J. Hakulinen P. Mäki-Paakkanen J. Juutilainen J. Naarala J. (2009). Enhancement of chemically induced reactive oxygen species production and DNA damage in human SH-SY5Y neuroblastoma cells by 872 MHz radiofrequency radiation. Mutat. Research/Fundamental Mol. Mech. Mutagen.662, 54–58. 10.1016/j.mrfmmm.2008.12.005
51
Maeda K. Henbest K. B. Cintolesi F. Kuprov I. Rodgers C. T. Liddell P. A. et al (2008). Chemical compass model of avian magnetoreception. Nature453, 387–390. 10.1038/nature06834
52
Manta A. K. Stravopodis D. J. Papassideri I. S. Margaritis L. H. (2014). Reactive oxygen species elevation and recovery in Drosophila bodies and ovaries following short-term and long-term exposure to DECT base EMF. Electromagn. Biol. Med.33, 118–131. 10.3109/15368378.2013.791991
53
Martino C. F. Castello P. R. (2011). Modulation of hydrogen peroxide production in cellular systems by low level magnetic fields. PLoS ONE6, e22753. 10.1371/journal.pone.0022753
54
Moghadam Z. M. Henneke P. Kolter J. (2021). From flies to men: ROS and the NADPH oxidase in phagocytes. Front. Cell. Dev. Biol.9, 628991. 10.3389/fcell.2021.628991
55
Mouritsen H. (2022). “Magnetoreception in birds and its use for long-distance migration,” in Sturkie’s avian physiology. Editors ScanesC. G.DridiS., Seventh Edition (San Diego: Academic Press), 233–256.
56
Münzel T. Camici G. G. Maack C. Bonetti N. R. Fuster V. Kovacic J. C. (2017). Impact of oxidative stress on the heart and vasculature: Part 2 of a 3-Part Series. J. Am. Coll. Cardiol.70, 212–229. 10.1016/j.jacc.2017.05.035
57
Murphy M. P. (2009). How mitochondria produce reactive oxygen species. Biochem. J.417, 1–13. 10.1042/bj20081386
58
Nohr D. Paulus B. Rodriguez R. Okafuji A. Bittl R. Schleicher E. et al (2017). Determination of radical–radical distances in light-active proteins and their implication for biological magnetoreception. Angew. Chem. Int. Ed.56, 8550–8554. 10.1002/anie.201700389
59
Panagopoulos D. J. Karabarbounis A. Yakymenko I. Chrousos G. P. (2021). Human-made electromagnetic fields: ion forced-oscillation and voltage-gated ion channel dysfunction, oxidative stress and dna damage (review). Int. J. Oncol.59, 92. Epub 2021 Oct 7. 10.3892/ijo.2021.5272
60
Player T. (2021). Spin dynamics calculations applied to systems of potential biological significance. Oxford, United Kingdom: University of Oxford. Ph.D. thesis.
61
Player T. C. Baxter E. D. A. Allatt S. Hore P. J. (2021). Amplification of weak magnetic field effects on oscillating reactions. Sci. Rep.11, 9615. 10.1038/s41598-021-88871-8
62
Player T. C. Hore P. J. (2019). Viability of superoxide-containing radical pairs as magnetoreceptors. J. Chem. Phys.151, 225101. 10.1063/1.5129608
63
Poljak D. (2018). “Chapter 7 - on the use of boundary integral methods in bioelectromagnetics,” in Numerical methods and advanced simulation in biomechanics and biological processes. Editors CerrolazaM.ShefelbineS. J.Garzón-AlvaradoD. (Academic Press), 119–143.
64
Pooam M. Jourdan N. Aguida B. Dahon C. Baouz S. Terry C. et al (2022). Exposure to 1.8 ghz radiofrequency field modulates ros in human HEK293 cells as a function of signal amplitude. Commun. and Integr. Biol.15, 54–66. 10.1080/19420889.2022.2027698
65
Rishabh R. Zadeh-Haghighi H. Salahub D. Simon C. (2022). Radical pairs may explain reactive oxygen species-mediated effects of hypomagnetic field on neurogenesis. PLoS Comput. Biol.18, e1010198. 10.1371/journal.pcbi.1010198
66
Rishabh R. Zadeh-Haghighi H. Simon C. (2023). Radical pairs and superoxide amplification can explain magnetic field effects on planarian regeneration. bioRxiv. 10.1101/2023.12.11.571125
67
Ritz T. Adem S. Schulten K. (2000). A model for photoreceptor-based magnetoreception in birds. Biophys. J.78, 707–718. 10.1016/s0006-3495(00)76629-x
68
Ritz T. Thalau P. Phillips J. B. Wiltschko R. Wiltschko W. (2004). Resonance effects indicate a radical-pair mechanism for avian magnetic compass. Nature429, 177–180. 10.1038/nature02534
69
Rodgers C. T. Henbest K. B. Kukura P. Timmel C. R. Hore P. J. (2005). Low-field optically detected EPR spectroscopy of transient photoinduced radical pairs. J. Phys. Chem. A109, 5035–5041. 10.1021/jp050765z
70
Sbodio J. I. Snyder S. H. Paul B. D. (2019). Redox mechanisms in neurodegeneration: from disease outcomes to therapeutic opportunities. Antioxid. Redox Signal.30, 1450–1499. 10.1089/ars.2017.7321
71
Sefidbakht Y. Moosavi-Movahedi A. A. Hosseinkhani S. Khodagholi F. Torkzadeh-Mahani M. Foolad F. et al (2014). Effects of 940 MHz EMF on bioluminescence and oxidative response of stable luciferase producing HEK cells. Photochem Photobiol. Sci.13, 1082–1092. 10.1039/c3pp50451d
72
Sies H. Berndt C. Jones D. P. (2017). Oxidative stress. Annu. Rev. Biochem.86, 715–748. 10.1146/annurev-biochem-061516-045037
73
Sies H. Jones D. P. (2020). Reactive oxygen species (ROS) as pleiotropic physiological signalling agents. Nat. Rev. Mol. Cell. Biol.21, 363–383. 10.1038/s41580-020-0230-3
74
Tarafdar A. Pula G. (2018). The role of NADPH oxidases and oxidative stress in neurodegenerative disorders. Int. J. Mol. Sci.19, 3824. 10.3390/ijms19123824
75
Terzi A. Suter D. M. (2020). The role of NADPH oxidases in neuronal development. Free Radic. Biol. Med.154, 33–47. 10.1016/j.freeradbiomed.2020.04.027
76
Timmel C. R. Hore P. J. (1996). Oscillating magnetic field effects on the yields of radical pair reactions. Chem. Phys. Lett.257, 401–408. 10.1016/0009-2614(96)00466-6
77
Timmel C. R. Till U. Brocklehurst B. Mclauchlan K. A. Hore P. J. (1998). Effects of weak magnetic fields on free radical recombination reactions. Mol. Phys.95, 71–89. 10.1080/002689798167395
78
Usselman R. J. Chavarriaga C. Castello P. R. Procopio M. Ritz T. Dratz E. A. et al (2016). The quantum biology of reactive oxygen species partitioning impacts cellular bioenergetics. Sci. Rep.6, 38543. 10.1038/srep38543
79
Usselman R. J. Hill I. Singel D. J. Martino C. F. (2014). Spin biochemistry modulates reactive oxygen species (ROS) production by radio frequency magnetic fields. PLOS ONE9, e93065. 10.1371/journal.pone.0093065
80
Walleczek J. (1995). Magnetokinetic effects on radical pairs: a paradigm for magnetic field interactions with biological systems at lower than thermal energy, 395, 420. 10.1021/ba-1995-0250.ch022
81
Wiltschko R. Wiltschko W. (2023). Animal navigation: how animals use environmental factors to find their way. Eur. Phys. J. Spec. Top.232, 237–252. 10.1140/epjs/s11734-022-00610-w
82
Wolski A. (2014). Theory of electromagnetic fields.
83
Woodward J. Jackson R. Timmel C. Hore P. McLauchlan K. (1997). Resonant radiofrequency magnetic field effects on a chemical reaction. Chem. Phys. Lett.272, 376–382. 10.1016/s0009-2614(97)00542-3
84
Woodward J. R. Timmel C. R. McLauchlan K. A. Hore P. J. (2001). Radio frequency magnetic field effects on electron-hole recombination. Phys. Rev. Lett.87, 077602. 10.1103/physrevlett.87.077602
85
Xu J. Jarocha L. E. Zollitsch T. Konowalczyk M. Henbest K. B. Richert S. et al (2021). Magnetic sensitivity of cryptochrome 4 from a migratory songbird. Nature594, 535–540. 10.1038/s41586-021-03618-9
86
Zadeh-Haghighi H. Simon C. (2022a). Magnetic field effects in biology from the perspective of the radical pair mechanism. J. R. Soc. Interface19, 20220325. 10.1098/rsif.2022.0325
87
Zadeh-Haghighi H. Simon C. (2022b). Radical pairs can explain magnetic field and lithium effects on the circadian clock. Sci. Rep.12, 269. 10.1038/s41598-021-04334-0
88
Zandieh A. Shariatpanahi S. P. Ravassipour A. A. Azadipour J. Nezamtaheri M. S. Habibi-Kelishomi Z. et al (2025). An amplification mechanism for weak elf magnetic fields quantum-bio effects in cancer cells. Sci. Rep.15, 2964. 10.1038/s41598-025-87235-w
Summary
Keywords
radical pair mechanism (RPM), reactive oxygen species (ROS), electromagnetic fields, telecommunication frequency, oscillating magnetic field (OMF)
Citation
Talbi O, Zadeh-Haghighi H and Simon C (2025) The radical pair mechanism cannot explain telecommunication frequency effects on reactive oxygen species. Front. Quantum Sci. Technol. 4:1544473. doi: 10.3389/frqst.2025.1544473
Received
13 December 2024
Accepted
25 March 2025
Published
09 April 2025
Volume
4 - 2025
Edited by
Marco Cavaglià, Polytechnic University of Turin, Italy
Reviewed by
Abdulbast A. Abushgra, Ashland University, United States
Richard H. W. Funk, Technical University Dresden, Germany
Updates
Copyright
© 2025 Talbi, Zadeh-Haghighi and Simon.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Owaiss Talbi, owaiss.talbi@ucalgary.ca; Christoph Simon, csimo@ucalgary.ca
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.