Joint observables induced by indirect measurements in cavity QED

Raikisto, Kalle; Luoma, Kimmo

doi:10.3389/frqst.2025.1601795

BRIEF RESEARCH REPORT article

Front. Quantum Sci. Technol., 17 October 2025

Sec. Quantum Information Theory

Volume 4 - 2025 | https://doi.org/10.3389/frqst.2025.1601795

This article is part of the Research TopicOpen Quantum Systems in Quantum TechnologiesView all 4 articles

Joint observables induced by indirect measurements in cavity QED

Kalle Raikisto

Kimmo Luoma*

Department of Physics and Astronomy, University of Turku, Turku, Finland

A fundamental feature of quantum mechanics is that there are observable pairs that cannot be measured jointly, such as observables corresponding to position and momentum or spin direction measurements. However, unsharp versions of non-jointly measurable observables may become jointly measurable. In this study, we investigate the joint measurability of time-continuous observables emerging from indirect time-continuous measurements. In particular, we study a paradigmatic situation where a qubit is interacting with a mode of light in a cavity, and the light escaping the cavity is continuously monitored. We find that the properties of the observables can be tuned by changing the type of the monitoring scheme or by tuning the initial state of the cavity. In particular, we demonstrate that heterodyne measurements are a joint measurement of a noisy homodyne measurement of a pair of canonical quadratures. Moreover, we investigate the purity of the induced qubit observables as a function of the noise.

1 Introduction

One of the most important differences between classical and quantum physics is how measurements are defined. Indeterminacy in classical mechanics is captured by classical probability theory, and in particular, arbitrarily precise simultaneous measurements of multiple degrees of freedom are possible (Busch et al., 2016). In quantum theory, however, different degrees of freedom, such as position and momentum, for example, do not commute (Born and Jordan, 1925). This leads to fundamental differences between quantum and classical theory, such as various uncertainty relations (Busch et al., 2007). A general description of a quantum measurement is given by a positive operator-valued measure (POVM), which provides the measurement outcome probabilities predicted by quantum mechanics (Heinosaari and Ziman, 2011). POVMs, in contrast to sharp or projective measurements, are more general. For example, they discriminate quantum states better (Oszmaniec and Biswas, 2019; Uola et al., 2019) and are a more realistic model for measurement implementation (Busch et al., 2016; Wiseman, 1996; Guryanova et al., 2020).

Another advantage of POVMs arises from measurement uncertainty. Projective measurements can only be measured accurately together if they commute; otherwise the measurements will have uncertainty, following Heisenberg’s and Robertson’s famous uncertainty relations (Heisenberg, 1927; Robertson, 1929; Robertson, 1934). However, due to the larger number of possible measurements, we can have POVMs that are non-commuting but can still be measured accurately. For this reason, the notion of the joint measurability of POVMs was introduced (Busch, 1985; Busch, 1986). A set of measurements is said to be compatible or jointly measurable if a single measurement exists from which it is possible to postprocess, using classical probability theory, the measurement outcomes of all of the measurements in the set (Heinosaari and Ziman, 2011; Stano et al., 2008; Uola et al., 2016).

Research on joint measurability has often focused on finding criteria for joint measurability (Busch, 1986; Stano et al., 2008; Jae et al., 2019; Uola et al., 2014; Busch and Schmidt, 2010; Yu et al., 2010; Beneduci, 2014; Pellonpää et al., 2023), quantifying incompatibility (Heinosaari et al., 2015; Designolle et al., 2019; Pusey, 2015; Haapasalo, 2015; Uola et al., 2015; Cavalcanti et al., 2016), its relation to other similar concepts such as coexistence (Lahti, 2003; Haapasalo et al., 2015; Reeb et al., 2013), and its applications in quantum information processing such as quantum steering (Karthik et al., 2015; Uola et al., 2020; Kiukas et al., 2017; Quintino et al., 2014; Nguyen et al., 2019; Cavalcanti and Skrzypczyk, 2016; Chen et al., 2016.; Chen et al., 2017; Uola et al., 2021; Uola et al., 2018), Bell nonlocality (Fine, 1982; Wolf et al., 2009; Andersson et al., 2005; Son et al., 2005; Bene and Vértesi, 2018; Quintino et al., 2016; Hirsch et al., 2018), quantum contextuality (Budroni et al., 2022; Xu and Cabello, 2019; Spekkens, 2005; Tavakoli and Uola, 2020; Selby et al., 2023), self-testing (Tavakoli et al., 2020), tests on Heisenberg uncertainty relations (Mao et al., 2022), and estimating the parameters of quantum Hamiltonians (McNulty et al., 2023). More information can be found in a recent review by Gühne et al. (2023).

Joint measurements can be constructed, for example, by mixing POVMs adaptively (Uola et al., 2016), using an ansatz that produces desired marginals (Jae et al., 2019), or by Naimark dilation (Haapasalo and Pellonpää, 2017). In this study, we focus on the indirect construction of joint measurements by time-continuous quantum measurements using the paradigmatic heterodyne and homodyne measurement schemes well known from quantum optics and cavity QED.

Continuous measurements themselves are a well-established concept. Pioneering research on them goes as far back as the 1980s (Srinivas and Davies, 1981; Barchielli et al., 1982; Gisin, 1984; Barchielli and Lupieri, 1985; Diósi, , 1986; Diósi, 1988; B and elavkin, 1989). They have been applied in quantum optics (Wiseman, 1996; Carmichael et al., 1989; Wiseman, 1993; Wiseman and Milburn, 1993; Garraway and Knight, 1994; Wiseman, 1995; Plenio and Knight, 1998; Doherty and Jacobs, 1999). Some early derivations of continuous measurement driven by Gaussian noise, similar to what will be used later here, have been derived in Carmichael et al. (1989), Wiseman and Milburn (1993), and Doherty and Jacobs (1999). For a comprehensive treatise on continuous measurements, see, for example, Jacobs and Steck (2006). Time-continuous joint measurements have seen some use in entanglement generation, theoretically (Duan et al., 2000; Clark et al., 2003; Motzoi et al., 2015) and experimentally (Roch et al., 2014). Simultaneous continuous weak measurements have also been used to measure non-commuting observables (Jordan and Büttiker, 2005; Wei and Nazarov, 2008; Ruskov et al., 2010; Chantasri et al., 2018) with even an experimental demonstration of a measurement on a superconducting qubit (Hacohe et al., 2016).

It has been established in the case of an empty cavity mode that such a scenario implements a POVM that depends on the continuously measured photon stream and is measured on the initial state prepared in the cavity (Wiseman, 1996; Goetsch and Graham, 1994). We here extend this concept to a situation where a two-level system (a qubit), such as an atom, is placed into the cavity, and we ask how sharp the measurements implemented on the qubit are. In particular, we focus on two situations: the heterodyne and the homodyne measurement schemes.

Previous research has focused on the concept of compatibility and the applications of joint measurements in quantum information processing. Measurement construction, however, has been a less popular topic in research, particularly constructions of time-continuous joint measurements. We study here the construction of time-continuous measurements. We will indirectly construct a noisy joint measurement using the paradigmatic heterodyne and homodyne measurement schemes well-known from quantum optics and cavity QED. We also study squeezing of the initial state of the cavity as a potential tuning parameter. We compare the sharpness of the marginal observables in the heterodyne and homodyne case. We find that homodyning produces sharper observables than heterodyning and that the sharpness of the measured quadrature can be improved by squeezing the initial state of the cavity in the same quadrature being continuously measured.

This approach may open up new ways of constructing joint observables that can be tuned using techniques known from quantum optics. Our theoretical results have applications beyond cavity QED setups and could also be experimentally used in superconducting qubits in microwave resonators or ultracold atomic gases.

The outline of this article is as follows. In Section 2, we discuss the concept of joint measurability and introduce a quantifier for the sharpness of qubit observables. Section 3 presents the model system we study and the different time-continuous measurements investigated. Then, in Section 4, we numerically compute the qubit observables induced by the time-continuous measurement of the light escaping from the cavity, and present our findings. Lastly, Section 5 discusses the implications of our findings.

2 Joint measurability

A “positive operator valued measure” (POVM) is a collection of positive operators which is complete. The POVMs we consider in this work have a continuous sample space $Ω_{F}$ which is the set of possible measurement outcomes. In the examples we consider, this will be a space of functions which are interpreted as the observed photocurrents (Loubenets, 2001; Krönke and Strunz, 2012; Megier et al., 2020). A probability measure $ν (z)$ on sample space $Ω_{F}$ and positive operators $F_{z}$ (effects) define a POVM if

\int_{Ω_{F}} d ν (z) F_{z} = I .

If a system is prepared into a state $ρ$ , then the probability of obtaining a measurement outcome $z \in Z$ when $F$ is measured is computed using the Born rule

P (z \in Z) = \int_{Z} d ν (z) t r \{ρ F_{z}\} .

Effects $A_{x}, B_{y}$ are said to be jointly measurable if a probability measure $ν_{A B} (x, y)$ and a positive operator $C (x, y)$ exist, such that

\begin{array}{l} P_{A} (x \in X) & = \int_{X} \int_{Ω_{B}} d ν (x, y) t r \{ρ C_{x, y}\}, \\ P_{B} (y \in Y) & = \int_{Ω_{A}} \int_{Y} d ν (x, y) t r \{ρ C_{x, y}\}, \end{array}

for any state $ρ$ . Joint measurability is a correct notion for describing simultaneous measurement properties of observables. For example, all sharp observables that commute are jointly measurable, but there may be non-commuting POVMs for which joint measurability exists (Gühne et al., 2023). Joint measurability is important in experimental work since it is a way to measure multiple quantities (Designolle et al., 2021; Zhou et al., 2016; Anwer et al., 2020; Smirne et al., 2022). A well-known example of a joint observable for unsharp position and momentum is provided by the Husimi $Q$ -function (Husimi, 1940)

Q (z) = \frac{⟨ z | ρ | z ⟩}{π},

where $| z 〉$ is a coherent state and $z = \frac{1}{\sqrt{2}} (q + i p)$ , $q, p \in R$ . In particular, $Q (z) > 0$ for any quantum state. $Q (z)$ corresponds to a joint measurement of noisy position and momentum observables (Appleby, 2000; Leonhardt, 1997; Wódkiewicz, 1984; Arthurs and Kelly, 1965; Raymer, 1994; Leonhardt and Paul, 1993a; Leonhardt and Paul, 1993b). The effects for these measurements are given by the projection operators which are convoluted with a Gaussian probability distribution,

\begin{array}{l} 〈 ψ | E_{Q} (X) | ψ 〉 & = \frac{1}{\sqrt{π}} \int_{X} d q \int_{R} d q^{'} | ψ (q) |^{2} e^{- {(q - q^{'})}^{2}}, \\ 〈 ψ | E_{P} (Y) | ψ 〉 & = \frac{1}{\sqrt{π}} \int_{Y} d p \int_{R} d p^{'} | \tilde{ψ} (p) |^{2} e^{- {(p - p^{'})}^{2}}, \end{array}

where $ψ (q), \tilde{ψ} (p)$ are, respectively, the position and momentum representations of the state $| ψ 〉$ . The $Q$ -function strongly contrasts with the Wigner distribution, which can be negative but provides the correct marginal distributions for sharp position and momentum observables (Hillery et al., 1984). We illustrate this in Figure 1 in the case of the Fock state $| 4 〉$ .

Figure 1

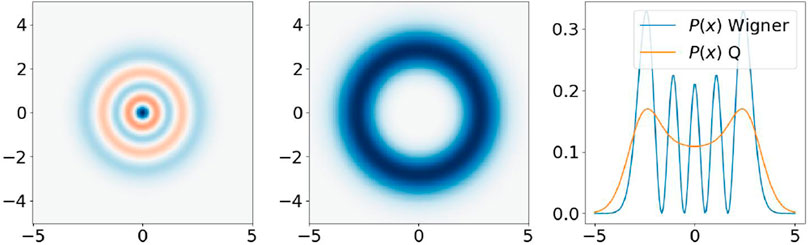
Three-panel image showing visualizations of quantum states. The left panel depicts concentric colored circles, indicating a quantum state, with red and blue hues. The center panel displays a larger, darker blue ring, illustrating another quantum state. The right panel features a graph comparing two plots labeled P(x) Wigner and P(x) Q, highlighting differences between these quantum representations using blue and orange lines.

Figure 1. Wigner function (left), Husimi Q-function (middle) and their marginal position distribution (right) for a number state $| 4 〉$ of a quantum harmonic oscillator. The Wigner function has sharp position and momentum marginals but may be negative. The Husimi Q-function is always positive but provides unsharp position and momentum distributions as marginals. Heterodyne measurement of a cavity mode corresponds to measuring the Husimi Q function, thus providing an example of a joint measurement of the position and momentum.

Importantly, heterodyne measurement provides an implementation of the measurement of the Husimi $Q$ -function (Wiseman, 1996).

Measurements on two-level systems or qubits are very well understood. In particular, joint measurability for qubits is well established (Busch, 1986; Stano et al., 2008; Busch and Schmidt, 2010; Yu et al., 2010). A positive operator (effect) acting on a two-dimensional Hilbert space can be written in terms of a bias $μ$ and a Bloch vector $a$ as

F = \frac{1}{2} (μ I + a \cdot σ), | | a | | \leq μ \leq 2 - | | a | |,

where the latter inequalities are conditions for positivity. We collect the parameters of the effect into a four-vector.

v = (μ, a) .

The effect $I - F$ has the four-vector $v^{⊥} = (2 - μ, - a)$ . We define the Minkowski scalar product between the two four-vectors $v, v^{'}$ as

(v | v^{'}) = μ μ^{'} - a \cdot a^{'} .

This also defines a scalar product between the effects. The positivity condition is compactly written as $v, v^{⊥} \in F_{+}$ where $F_{+} = \{r | (r | r) \geq 0, μ \geq 0\}$ (Busch and Schmidt, 2010). The sharpness of the effect is (Stano et al., 2008)

G (v) = \frac{1}{2} ((v | v^{⊥}) - \sqrt{(v | v) (v^{⊥} | v^{⊥})}) .

$G (v) = 1$ if the measurement is projective, and $G (v) = 0$ if the effect is proportional to the identity operator.

3 Joint time-continuous measurement

In this study, we focus on the Markov regime and on heterodyne and homodyne measurements of a qubit in a leaky cavity (Figure 2). The qubit, the cavity mode, and their interaction are described by the following Hamiltonian in the rotating wave approximation:

H = \frac{ω_{A}}{2} σ_{z} + ω_{C} a^{†} a + g (σ_{-} a + σ_{+} a^{†}) .

Figure 2

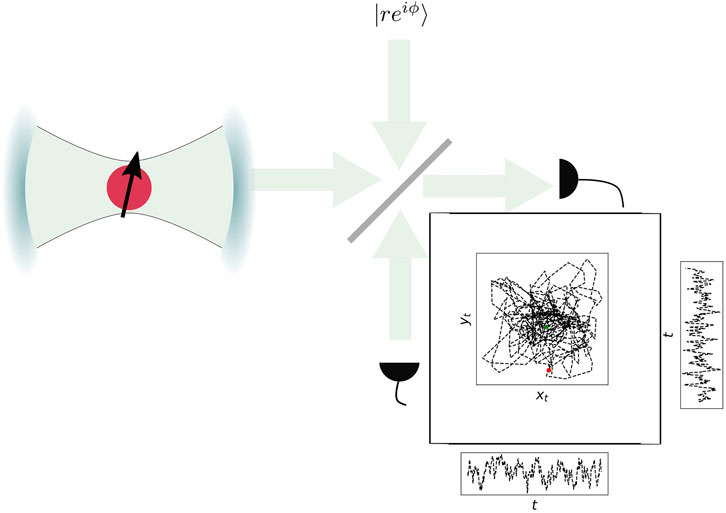
Diagram showing quantum measurement feedback loop. A cavity with a red circle and black arrow on the left transmits a signal. The signal splits at a beam splitter, indicated by a gray diagonal line, with arrows denoting paths. A detector analyses one path, linking to a feedback system represented by a box. Inside, a plot displays zigzag lines on an x-y graph, flanked by additional time series plots illustrating fluctuations over time. Mathematical notation \$|re^{i\\phi}\$| is present near the beam splitter.

Figure 2. Measurement scheme. A qubit is interacting with a leaky cavity mode, and the light escaping from the cavity is measured. Measurement outcomes $x_{t}$ and $y_{t}$ are recorded. If a joint measurement exists, then these currents could be post-processed from a complex measurement record $ξ_{t} = x_{t} + i y_{t}$ . This occurs, for example, in the heterodyne case. We show that the separately measured currents $x_{t}, y_{t}$ using homodyne measurement are compatible with an optimal joint qubit observable.

This is the famous Jaynes–Cummings Hamiltonian (Jaynes and Cummings, 1963). The cavity mode is leaky (with rate $κ \geq 0$ ) and leads to decoherence and dissipation. Such mixed state dynamics of the average state ${\bar{ρ}}_{t}$ are described by the following Gorini–Kossakowski–Sudarshan–Lindblad (GKSL) master equation (Gorini et al., 1976; Lindblad, 1976):

\partial_{t} {\bar{ρ}}_{t} = - i [H, {\bar{ρ}}_{t}] + κ (a {\bar{ρ}}_{t} a^{†} - \frac{1}{2} \{a^{†} a, {\bar{ρ}}_{t}\}) = L {\bar{ρ}}_{t} .

The dynamics above can be unraveled in various ways into stochastic trajectories driven by white noise processes such that the ensemble average dynamics coincide with the average state dynamics. The linear quantum state diffusion (QSD) equation (Gisin and Percival, 1992) that unravels the GKSL equation is

\partial_{t} ρ_{t} = - i [H, ρ_{t}] - \frac{κ}{2} \{a^{†} a, ρ_{t}\} + ξ_{t}^{} a ρ_{t} + ξ_{t} ρ_{t} a^{†}, (1)

where $ξ_{t}^{}$ is a complex-valued Gaussian white noise process with zero mean and correlations $M [ξ_{t} ξ_{s}^{}] = κ δ (t - s)$ , where $M [\cdot]$ is taken with respect to the Gaussian measure $ν (ξ_{t})$ of the white noise. We here use the Stratonovich convention consistently. This equation describes time-continuous heterodyne measurement of the cavity mode.

The ensemble average over different realizations of $ξ_{t}$ is denoted by ${\bar{ρ}}_{t} = M [ρ_{t}]$ . The ensemble average over the trace $M [t r \{ρ_{t}\}] = 1$ is a manifestation of the trace preservation condition. When we denote by $G_{t} (ρ)$ , the propagator of the linear QSD equation and move to the Heisenberg picture, and we can write the trace of the state as $t r \{ρ_{t}\} = t r \{ρ G_{t}^{†} (I)\}$ , where $G_{t}^{†} (I)$ is the dual map of the propagator acting on the identity. $G_{t}^{†} (I)$ is a positive operator. The trace preservation condition $1 = M [ρ G_{t}^{†} (I)]$ holds for any initial state $ρ$ . Thus, $G_{t}^{†} (I)$ can be also interpreted as a POVM element corresponding to a particular measurement outcome process $ξ_{t}$ which has a Gaussian measure. Moving back to the Schrödinger picture, we can see that measurement outcome probabilities are proportional to the norm of the state $t r \{ρ_{t}\}$ . The physical probability (density) for a particular $ξ_{t}$ to occur is

d ν (ξ_{t}) t r \{ρ_{t}\},

which is the product of the probability (density) for the stochastic process and the norm of the state. From the linear QSD equation, we deduce

t r \{{\dot{ρ}}_{t}\} = t r \{ρ_{t} (ξ_{t}^{} a + ξ_{t} a^{†} - κ a^{†} a)\} .

We can express the noise $ξ_{t}$ in terms of its real and imaginary parts

ξ_{t} = x_{t} + i y_{t},

where $x_{t}$ and $y_{t}$ are mutually uncorrelated real-valued Gaussian processes with zero mean and

M_{x} [x_{t} x_{s}] = \frac{1}{2} κ δ (t - s), M_{y} [y_{t} y_{s}] = \frac{1}{2} κ δ (t - s),

are averages with respect to different marginals of the joint measure for the process $ξ_{t}$ . We can average over $x_{t}$ and $y_{t}$ separately in Equation 1. When we average over the imaginary part, we obtain $ρ_{t}^{X} = M_{y} [ρ_{t}]$ and similarly $ρ_{t}^{Y} = M_{x} [ρ_{t}]$ . The equations of motion for $ρ_{t}^{X}$ are

\begin{align} {\dot{ρ}}_{t}^{X} & = - i [H, ρ_{t}^{X}] - \frac{κ}{2} \{a^{†} a, ρ_{t}^{X}\} + \frac{κ}{2} a ρ_{t}^{X} a^{†} \\ - \frac{κ}{4} (a^{2} ρ_{t}^{X} + ρ_{t}^{X} a^{† 2}) + x_{t} (a ρ_{t}^{X} + ρ_{t}^{X} a^{†}), \end{align}

where we used $M_{y_{t}} [y_{t} a ρ_{t}] = \frac{i κ}{4} a ρ_{t}^{X} a^{†} - \frac{i κ}{4} a^{2} ρ_{t}^{X}$ . Similarly, we obtain

\begin{align} {\dot{ρ}}_{t}^{Y} & = - i [H, ρ_{t}^{Y}] - \frac{κ}{2} \{a^{†} a, ρ_{t}^{Y}\} + \frac{κ}{2} a ρ_{t}^{Y} a^{†} \\ + \frac{κ}{4} (a^{2} ρ_{t}^{Y} + ρ_{t}^{Y} a^{† 2}) - i y_{t} (a ρ_{t}^{Y} - ρ_{t}^{Y} a^{†}), \end{align}

when averaging over the real part of the noise. We see that the partial averaging produces a sandwich term and terms containing $a^{2}$ and $a^{† 2}$ . We also see that when we average over the remaining noise, we recover the desired average dynamics in both cases. The norm of the state is a solution to

t r \{{\dot{ρ}}_{t}^{X}\} = t r \{ρ_{t}^{X} (x_{t} (a + a^{†}) - \frac{κ}{4} (a^{2} + a^{† 2}) - \frac{κ}{2} a^{†} a)\}

for the $X$ quadrature and

t r \{{\dot{ρ}}_{t}^{Y}\} = t r \{ρ_{t}^{Y} (i y_{t} (a^{†} - a) + \frac{κ}{4} (a^{2} + a^{† 2}) - \frac{κ}{2} a^{†} a)\},

for the $Y$ quadrature.

These equations are to be contrasted with an equation where we directly measure either $x_{t}$ or $y_{t}$ (Wiseman, 1996; Wiseman, 1993; Jacobs and Steck, 2006; Wiseman and Milburn, 2009; Barchielli and Gregoratti, 2009). To achieve this, we propose a noisy version of the $X$ and $Y$ quadrature homodyning equations where we scale the noise term by $\sqrt{λ}$ and the noise-free terms with $λ$ and add the average evolution with weight $(1 - λ)$ . For the $X$ quadrature, this results in

\begin{align} {\dot{ϱ}}_{t}^{λ X} & = λ (- i [H, ϱ_{t}^{λ X}] - \frac{κ}{2} \{a^{†} a, ϱ_{t}^{λ X}\} - \frac{κ}{2} (a^{2} ϱ_{t}^{λ X} + ϱ_{t}^{λ X} a^{† 2})) \\ + \sqrt{2 λ} (x_{t} (a ϱ_{t}^{λ X} + ϱ_{t}^{λ X} a^{†})) \\ + (1 - λ) L ϱ_{t}^{λ X} . \end{align}

A similar equation also holds for the $Y$ quadrature:

\begin{align} {\dot{ϱ}}_{t}^{λ Y} & = λ (- i [H, ϱ_{t}^{λ Y}] - \frac{κ}{2} \{a^{†} a, ϱ_{t}^{λ Y}\} + \frac{κ}{2} (a^{2} ϱ_{t}^{λ Y} + ϱ_{t}^{λ Y} a^{† 2})) \\ - i \sqrt{2 λ} (y_{t} (a ϱ_{t}^{λ Y} - ϱ_{t}^{λ Y} a^{†})) \\ + (1 - λ) L ϱ_{t}^{λ Y} . \end{align}

The average evolution for noisy $X$ and $Y$ quadratures again coincides with the desired average dynamics. The parameter $0 \leq λ \leq 1$ interpolates between not measuring $(λ = 0)$ or making a perfect $X$ or $Y$ quadrature homodyning measurement $(λ = 1)$ . The norm of the state evolves according to

\begin{align} t r \{{\dot{ϱ}}_{t}^{λ X}\} & = t r \{ϱ_{t}^{λ X} (\sqrt{2 λ} x_{t} (a + a^{†}))\} \\ - t r \{ϱ_{t}^{λ X} (λ κ a^{†} a + λ \frac{κ}{2} (a^{† 2} + a^{2}))\}, \end{align}

and

\begin{align} t r \{{\dot{ϱ}}_{t}^{λ Y}\} & = t r \{ϱ_{t}^{λ Y} (\sqrt{2 λ} i y_{t} (a^{†} - a))\} \\ - t r \{ϱ_{t}^{λ Y} (λ κ a^{†} a - λ \frac{κ}{2} (a^{† 2} + a^{2}))\}, \end{align}

for the $X$ and $Y$ quadratures, respectively. It is easy to see for the choice $λ = \frac{1}{2}$ that the time evolution of the states $ϱ_{t}^{X / 2}$ and $ϱ_{t}^{Y / 2}$ matches the evolution of the states $ρ_{t}^{X}$ and $ρ_{t}^{Y}$ , respectively, where the latter are obtained from the QSD equation through partial averaging.

We have thus determined that the noisy $X$ and $Y$ POVMs become compatible when $λ = 1 / 2$ and the joint observable is given by the heterodyning unraveling—that is, the linear QSD equation.

The same noise bound holds for the induced qubit observable because the trace of the marginal state is the same as that of the joint state

{t r}_{A} \{ρ_{A}\} = {t r}_{A} \{{t r}_{C} \{ρ_{A C}\}\} = t r \{ρ_{A C}\},

where $ρ_{A C}$ is the joint state and ${t r}_{A} \{\cdot\}, {t r}_{C} \{\cdot\}$ are partial traces over the qubit and the cavity degrees of freedom, respectively. This is intuitively also clear since whenever there is a joint observable for the qubit and the cavity mode, the qubit observables may be constructed simply by tracing over the cavity.

4 Numerical examples

It is well known that the heterodyne detection corresponds to measuring the Husimi $Q$ distribution and the homodyning corresponds to measuring a quadrature of the cavity mode. The Husimi $Q$ distribution is a joint distribution for unsharp position and momentum observables, whereas the quadrature measurement corresponds to a measurement of sharp, and thus incompatible, quadratures. In this section, we numerically investigate the noisy time-continuous version of this relation in terms of the purity of the induced observables on the qubit.

We consider that the system and the cavity are in a product state before the measurement process begins. We also assume that the state of the cavity is pure. We consider two cases: the vacuum state $| 0 〉$ and the squeezed vacuum state $| s 〉 = e^{\frac{1}{2} s (a^{2} - a^{† 2})} | 0 〉$ . We use the following values in the numerical examples: $ℏ = 1$ , $g / ω_{A} = 1.0$ , $κ / ω_{A} = 2.0$ , and $ω_{C} / ω_{A} = 1.0$ . The noise $ξ_{t} = x_{t} + i y_{t}$ used for the numerical examples is an approximation of a white noise process with the statistics

M [x_{t}] = M [y_{t}] = M [x_{t} y_{s}] = 0,

and

M [x_{t} x_{s}] = M [y_{t} y_{s}] = \frac{κ Γ}{2} e^{- Γ | t - s |}

This is illustrated in Figure 2, with the inverse of the correlation time being $Γ / ω_{A} = 15$ . On this timescale, this Ornstein–Uhlenbeck process is a good approximation of a white noise process. We can solve the resulting differential equations as they were ordinary differential equations, and in the white noise limit they converge to Stratonovich equations (Wong and Zakai, 1965).

The linear stochastic equations analyzed in this work are all solved by a propagator

ρ_{t} = G_{t} ρ_{0}, G_{0} ρ_{0} = ρ_{0} .

Depending on the particular scenario, this propagator is a functional of $x_{t}$ , $y_{t}$ , or $x_{t} + i y_{t}$ . As the processes $x_{t}$ and $y_{t}$ are Gaussians, their probability measure is readily constructed either in the white noise limit or as an Ornstein–Uhlenbeck process. Suppose that we observe the process $x_{τ}$ with $0 \leq τ \leq t$ with probability $μ_{t} (x)$ , then as with process $y_{t}$ we have a probability $μ_{t} (y)$ . The POVM element $F_{t} [x_{t}]$ or $F_{t} [y_{t}]$ acting on the qubit is obtained from the formula

p (x_{t}) = t r \{G_{t} [x_{t}] ρ_{0}\} = t r \{F_{t} [x_{t}] ρ_{A}\},

with a similar formula for $F_{t} [y_{t}]$ . The initial state is $ρ_{0} = ρ_{A} \otimes | ψ_{C} 〉 〈 ψ_{C} |$ . Using the properties of the Pauli matrices, we can reconstruct $F_{t} [x_{t}] = \frac{1}{2} (μ_{t} [x_{t}] I + a_{t} [x_{t}] \cdot σ)$ by propagating initial states $ρ_{0} = \frac{1}{2} I$ and $ρ_{i} = \frac{1}{2} (I + σ_{i})$ , where $σ_{i}$ corresponds to Pauli matrices in the $x, y$ , and $z$ directions. We set $p_{t}^{i} [x_{t}] = t r \{F_{t} [x_{t}] ρ_{i}\}$ and determine that

μ_{t} [x_{t}] = 2 p_{t}^{0} [x_{t}], a_{t}^{i} [x_{t}] = 2 p_{t}^{i} [x_{t}] - μ_{t} [x_{t}],

with similar formulas for $F_{t} [y_{t}]$ . Operator $F_{t}$ constructed this way is positive but does not yet normalize to unity. Proper normalization is achieved when integrated against the Gaussian probability measure (Wiseman, 1996; Barchielli and Gregoratti, 2009). In the following, we analyze the sharpness of the unnormalized operators.

The continuous measurement yields more information about the initial state the longer the system is measured. This means that for measurements of negligible duration, the POVM element is the identity. This is independent of the initial state of the system (Figure 3).

Figure 3

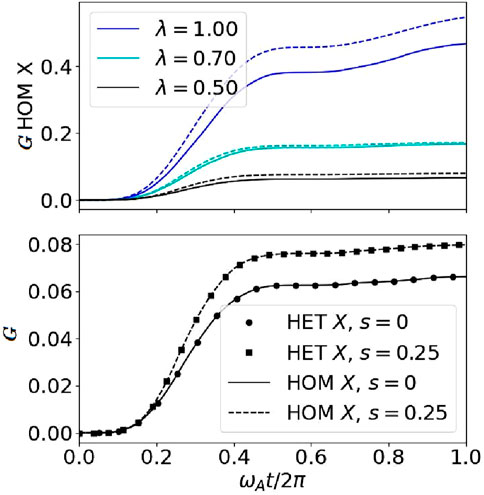
Two line graphs depict scientific data. The top graph shows \$ G_{HOM} X \$ versus \$ \\frac{\\omega_A t}{2\\pi} \$ with three lines for different \$ \\lambda \$ values: 1.00 (blue), 0.70 (cyan), and 0.50 (black). The bottom graph shows \$ G \$ versus \$ \\frac{\\omega_A t}{2\\pi} \$ with four lines representing different \$ HET \$ and \$ HOM \$ configurations, featuring solid and dashed lines with dot markers. Both graphs exhibit an increasing trend, with the legends indicating line styles and parameters.

Figure 3. Top: Sharpness of the homodyne measured $X$ quadrature for different values of the parameter $λ$ . Dashed lines correspond to the case where the squeezing parameter for the initial cavity state is $s = 0.25$ and solid lines correspond to the vacuum initial state $s = 0$ . Bottom: Sharpness of the heterodyned $X$ (squares and circles) and homodyne $X$ (solid and dashed line) quadratures when $λ = 0.5$ . Solid line and square symbols correspond to the squeezed initial state and dashed line and circles to the vacuum initial state.

In the top panel of Figure 3, we see that the sharpness $G$ for the homodyne measurement is increased by the squeezing. This occurs because we squeeze the same quadrature that we measure. Moreover, for values $0.5 < λ \leq 1$ , homodyne measurement is sharper than the heterodyne measurement (top panel). In the lower panel, we compare the case $λ = 1 / 2$ and we see that the noisy homodyne measurement coincides with the heterodyne measurement. We also observe that the squeezing also increases the sharpness of the observable in the heterodyne case.

5 Discussion

Since joint measurements have become the standard for describing the measurement of multiple POVMs, their properties have been significantly researched. It is of interest to find the least noisy joint observables whose properties can be tailored. The focus of previous research has been on the concept of compatibility and the applications of joint measurements in quantum information processing, while constructing actual joint measurements has been a less popular topic of research. Specifically, there are very few studies that construct time-continuous joint measurements.

In this study, we have ventured on this less traversed avenue. We explicitly constructed the noisy time-continuous quadratures that are jointly implemented in the heterodyning measurement. In particular, we found an explicit threshold for mixing the homodyne measurement with the average dynamics, leading to the noisy quadrature measurements implemented in the heterodyning scenario. This approach may open up new ways to construct joint observables that can be tuned using techniques known from quantum optics. A simple tuning parameter we investigated here was the squeezing of the initial state of the cavity.

We investigated the sharpness of the marginal observables induced for the qubit subsystem in the heterodyne case and compared those with the homodyne case. We found that homodyning produces sharper observables than heterodyning and the sharpness of the measured quadrature can be improved by squeezing the initial state of the cavity in the same quadrature being continuously measured.

This research may open up new ways to implement joint measurements. Our results are applicable beyond cavity QED setups and would work for any system where general dyne measurements can be carried out, such as superconducting qubits in microwave resonators or ultra cold atomic gases. These new implementations for joint measurements could also be applied in quantum network settings, since joint measurement are necessary for zero-error quantum communication (Gyongyosi et al., 2018).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

KR: Writing – review and editing. KL: Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Funding from the Quantum QDOC doctoral pilot program and Turku Collegium for Science Medicine and Technology (TCSMT) is greatly acknowledged.

Acknowledgments

KL would like to thank Roope Uola, Erkka Haapasalo, Juha-Pekka Pellonpää, Pauli Jokinen, Andrea Smirne, and Konstantin Beyer for helpful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andersson, E., Barnett, S. M., and Aspect, A. (2005). Joint measurements of spin, operational locality, and uncertainty. Phys. Rev. A 72, 042104. doi:10.1103/physreva.72.042104