Certified random number generation using quantum computers

We investigate how current noisy quantum computers can be leveraged for generating secure random numbers certified by Quantum Mechanics. While random numbers can be generated and certified in a device-independent manner through the violation of Bell’s inequality, this method requires significant spatial separation to satisfy the no-signaling condition, making it impractical for implementation on a single quantum computer. Instead, we employ temporal correlations to generate randomness by violating the Leggett-Garg inequality, which relies on the No-Signaling in Time condition to certify randomness, thus overcoming spatial constraints. By applying this protocol to different IBMQ platforms, we demonstrate the feasibility of secure, semi-device-independent random number generation using low-depth circuits with single-qubit gates. We show how error mitigation techniques lead to LGI violation compatible with theoretical predictions on the existing IBMQ machines.

1 Introduction

Randomness generation (Marsaglia et al., 1990; Marsaglia and Zaman, 1991; Marsaglia, 2003; L’Ecuyer, 2012; Hull and Dobell, 1962; Jennewein et al., 2000; Stipčević and Koç, 2014; Hellekalek, 1998) plays a crucial role in various domains, including Cryptography, Statistics, and Biology, with applications ranging from encryption key generation to simulating complex systems and even in gaming. Conventionally, computers generate random numbers using mathematical algorithms that rely on an initial random seed. These deterministic processes, known as Pseudo Random Number Generators (PRNG) (Blum et al., 1986; Vazirani and Vazirani, 1984), are limited by their predictability, as their randomness is entirely dependent on the initial seed. Consequently, PRNGs are unsuitable for applications requiring high-security standards.

In contrast, True Random Number Generators (TRNGs) (Stipčević and Koç, 2014; Yu et al., 2019; Fischer and Drutarovskỳ, 2002; Bagini and Bucci, 1999; Sunar et al., 2006) utilize physical processes which are inherently non-deterministic. This approach provides a high degree of entropy, essential for generating cryptographic keys that are resistant to guessing or brute-force attacks. Cryptographic algorithms heavily depend on the secrecy of distributing cryptographic keys, necessitating the use of random numbers as seeds that cannot be predicted by potential eavesdroppers. In addition to conventional cryptographic primitives, random numbers are also indispensable in advanced optical cryptography, such as image encryption Li et al. (2025) and dual-color image watermarking schemes Gong and Luo (2023).

However, trusting the manufacturer of a TRNG is paramount to ensuring the integrity of the generated random numbers. A potential security threat is the memory stick attack (Acín and Masanes, 2016), where high-quality random numbers are stored in a memory stick within the TRNG device, posing a risk to security. While statistical tests (Rukhin et al., 2001; Bassham et al., 2010; Bassham et al., 2010) can assess the uniformity of generated bits, certifying the randomness of the source remains a challenging problem. Moreover, characterizing the quality of the random bits or the entropy of the source based on the generated outputs is a complex task. Another challenge with a TRNG is that it is a physical device and, like all hardware, it degrades over time.

Quantum processes due to their inherent randomness are excellent sources for generating random numbers (Herrero-Collantes and Garcia-Escartin, 2017; Ma et al., 2016). Quantum correlations violate certain inequalities which cannot be violated by classical correlations. A class of these constraints known as Bell inequalities (Bell, 1964; Brunner et al., 2014; Cirel’son 1980; Franson, 1989; Peres, 1999; Aspect, 1999) can be used to certify the quantum nature of the random bits generated (Acín and Masanes, 2016) in a device independent way from just the statistics of the measurement outcomes without any assumptions on the device used. This novel idea of generating device-independent randomness certified by quantum mechanics was first demonstrated by violating the CHSH inequality (Pironio et al., 2010), which was followed by loophole-free demonstrations of the Bell inequality violation experiment (Shalm et al., 2021; Bierhorst et al., 2018; Liu et al., 2018b; Zhang et al., 2020; Liu et al., 2018a; Shen et al., 2018; Abellán et al., 2015; Storz et al., 2023).

The temporal analogue of the Bell Inequalities, viz. the Leggett-Garg Inequalities (Emary et al., 2013; Leggett and Garg, 1985), can be used for certifying quantum randomness in a table-top experiment (Joarder et al., 2022). This was demonstrated in a photonic setup (Nath et al., 2024) where random numbers were generated in a loophole free experiment for LGI violation. Overcoming the distance barrier seen in Bell experiments, this approach presents a promising avenue for practical implementation. A significant step forward would be to use the developed methodology on commercially available devices that need not be custom-made for the purpose. This brings us to a question: Can we use for instance a NISQ quantum computer to generate such random numbers by violating LGI? Not only will this be a fantastic practical use case for the current quantum computers, but it will in fact be a very unique platform that brings forth the use of a quantum computer in a niche quantum security application.

In this paper, we go on to do just that successfully! We adopt this protocol, to generate random numbers on available IBM superconducting quantum computers (Javadi-Abhari et al., 2024). Although cloud-based quantum computers were used previously to generate random numbers (Li et al., 2021; Jacak et al., 2021; Orts et al., 2023; Kumar et al., 2022; Sinha et al., 2023), their quantum nature cannot be certified device-independently, making them less secure. In contrast, our implementation leverages Leggett-Garg Inequality (LGI) violation to certify the randomness coming from a quantum source, thus offering a practical use case for NISQ devices.

In summary, our aim is to demonstrate that certified randomness generation can be achieved with robust protocols implemented through simple circuits on currently available quantum computers. This eliminates the need for elaborate experimental setups, making the approach convenient for end-users. At the same time, it establishes that even within the NISQ era, quantum devices can already be harnessed for practical advantages such as certified randomness.

2 Protocol for randomness generation

The Leggett Garg Inequality (LGI) characterizes a single-time evolving system where measurements of a dichotomic variable $Q$ with eigenvalues $+1$ and $-1$ are taken at different times. The inequality is expressed in Equation 1:

$⟨Q_1{Q}_2⟩+⟨Q_2{Q}_3⟩-⟨Q_1{Q}_3⟩\le 1.(1)$

Here, $Q_i=Q(t_i)$ represents the measurement outcome at time $t_i$ in a time sequence $t_1<t_2<t_3$. The correlation functions are defined in Equation 2:

$⟨Q_i{Q}_j⟩={\displaystyle \sum _{a_i,a_j=\pm 1}}{a}_i{a}_{j}P\left(a_i,a_j|Q_i,Q_j\right),(2)$

where $P(a_i,a_j|Q_i,Q_j)$ denotes the probability of obtaining outcomes $a_i$ and $a_j$ for $Q_i$ and $Q_j$ respectively. The quantum mechanical violation of this inequality, capped at 1.5, is associated with the breach of assumptions defining macrorealism (Emary et al., 2013; Leggett and Garg, 1985; Mal et al., 2016; Nath et al., 2024).

LGI can be derived from Predictability and No Signaling in Time (NSIT) (Kofler and Brukner, 2008; Clemente and Kofler, 2015; Kofler and Brukner, 2013), similar to the derivation of Bell-CHSH inequality from Predictability and No Signaling across spatial separation (Mal et al., 2016; Cavalcanti and Wiseman, 2012; Halliwell, 2016). In the Bell Scenario, if the measurement outcomes of an entangled state at two well-separated measurement stations violate the Bell Inequality, they are confirmed to be random (Pironio et al., 2010; Pironio, 2018; Acín and Masanes, 2016; Cavalcanti and Wiseman, 2012). Similarly, if an experiment’s measurements adhere to the constraints of the NSIT condition while violating LGI, the measurement outcomes are random according to the predictability condition. This unpredictability is valuable in security applications, such as cryptographic protocols that require a source of secure randomness. A test can be formulated to confirm the quantum nature of these random numbers, utilizing the protocol to design an experiment satisfying NSIT and violating LGI, certifying random outputs according to Quantum Mechanics.

For the three-time LGI, the No Signaling in Time conditions are defined in Equation 3:

$\begin{array}{ll}\hfill & P\left(+|Q_2\right)=P\left(++|Q_1,Q_2\right)+P\left(-+|Q_1,Q_2\right)\hfill \\ \hfill & P\left(+|Q_3\right)=P\left(++|Q_1,Q_3\right)+P\left(-+|Q_1,Q_3\right)\hfill \\ \hfill & P\left(+|Q_3\right)=P\left(++|Q_2,Q_3\right)+P\left(-+|Q_2,Q_3\right)\hfill \end{array}(3)$

Our setup consists of a system with two degrees of freedom in the form of a qubit, subjected to projective measurements at times $t_1$, $t_2$, and $t_3$. The detailed construction of this setup will be presented in Section 3, where we build the corresponding circuit. For this scenario, we use the bound derived by Nath et al. (2024) to certify randomness, given by Equation 4

$-{\log }_2\left(\frac{1+\alpha +\sqrt{1-2\alpha }}{2}\right).(4)$

Here, $I=1+\alpha$ denotes the observed LGI violation, and the bound holds provided that all NSIT conditions three are satisfied.

Algorithm 1

Algorithm 1.

3 IBMQ results

We utilized IBM Quantum Hardware for the generation of random numbers through the violation of the Leggett-Garg Inequality (see Figure 1 and Algorithm 1). The unitaries in the circuits can easily be decomposed into a sequence of Z-rotation$(R_Z)$ and $SX$ gates, facilitating implementation in the hardware with minimal error rates. The circuits computing the correlations $⟨Q_1{Q}_2⟩$, $⟨Q_1{Q}_3⟩$, and $⟨Q_2{Q}_3⟩$ after transpilation in the IBM backends can be decomposed into $SX$ Gates and $R_Z$ Gates as shown in Figure 2. Quantum Circuit We employ a simplified circuit to generate random numbers by concurrently violating LGI and adhering to the NSIT constraints. The most general one qubit state, characterized by the parameters $n_x$, $n_y$, and $n_z$, is expressed in Equation 5:

$\rho =\frac{1}{2}\left(\mathbb{1}+\vec{n}\cdot \vec{\sigma }\right),\vec{n}=\left(n_x,n_y,n_z\right)\in {\mathbb{R}}^3(5)$

such that $n_x^2+n_y^2+n_z^2⩽1$. To keep things simple we set the parameters as $n_x=0$, $n_y=1$, and $n_z=0$, which corresponds to the state, $(|0\rangle -i|1\rangle )/\sqrt{2}$. For the time evolution, we opt for the basic rotation gates $U_1$ and $U_2$ parameterized by angle $\theta$ in Equation 6,

$U_i=\left(\begin{array}{cc}\hfill \cos \left[{\theta }_i\right]\hfill & \hfill \sin \left[{\theta }_i\right]\hfill \\ \hfill -\sin \left[{\theta }_i\right]\hfill & \hfill \cos \left[{\theta }_i\right]\hfill \end{array}\right)\text{\hspace{0.17em}for\hspace{0.17em}}i=\mathrm{1,2},{\theta }_i\in \mathbb{R}(6)$

Figure 1

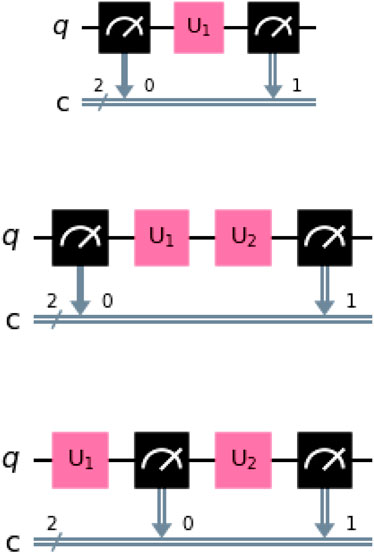
Figure 1. The circuits for different measurement settings $t_1{t}_2$, $t_1{t}_3$ and $t_2{t}_3$. $U_1$ and $U_2$ denotes the rotation operators with angles ${\theta }_1$ and ${\theta }_2$.

Figure 2

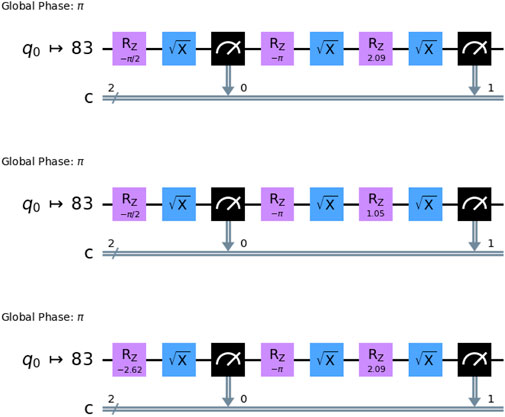
Figure 2. Circuits for correlation measurements of $t_1{t}_2$, $t_2{t}_3$ and $t_1{t}_3$ transpiled in the IBMQ Brussels backend. The Unitaries for rotation operators involving the angles ${\theta }_1$ and ${\theta }_2$ are decomposed in terms of the $R_Z$ and $SX$ gates available in the backend. The qubit 12 was selected after analyzing the best possible layout for our circuit using the mapomatic algorithm.

We perform projective measurements at time instances $t_1$, $t_2$, and $t_3$ in the computational basis. The projectors for this basis are defined in Equation 7:

$P_{+}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right),P_{-}=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right).(7)$

Notably, adopting a different measurement basis would necessitate additional gates, introducing potential sources of errors.

Using the specified initial state along with the chosen unitaries and measurement settings, we compute the expressions for the LGI and the NSIT conditions. The parameters ${\theta }_1$ and ${\theta }_2$ are then determined through numerical optimization, ensuring that all three NSIT conditions are satisfied. The resulting values corresponding to different levels of LGI violation are summarized in Table 1.

Table 1

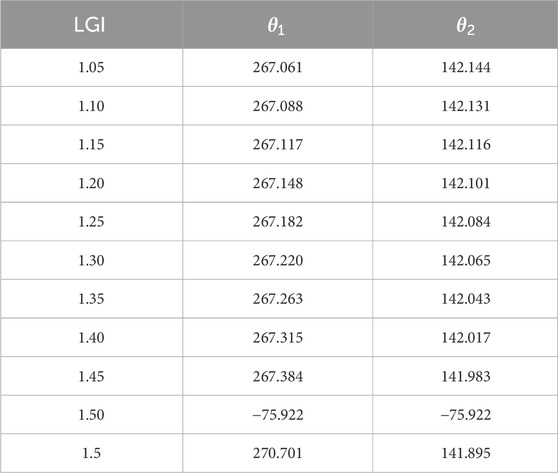
Table 1. The parameters ${\theta }_1$ and ${\theta }_2$ correspond to the rotation gates for time translations $t_1\to t_2$ and $t_2\to t_3$, based on the specified initial state and projective measurements. The circuits utilizing these $\theta$ values exhibit a violation of the LGI at a specific point while also satisfying all NSIT conditions, enabling secure randomness generation.

In principle we can start with a different initial state, and choose more general measurements, which will lead to different parameters for the Unitaries. For example, as shown in Supplementary Table S1 of Section 6 of the Supplementary Material, we have demonstrated that starting with a mixed state allows for the design of an appropriate circuit. We emphasize that this choice of circuit for our algorithm might not be the most optimized choice and further research is warranted to solve the equations and identify the most efficient circuit for the algorithm. Regardless, the RNG does not depend on the choice of the circuit, only the complexity of implementing the algorithm will differ.

It is important to note that the certification protocol here is semi-device independent because while deriving the bound for genuine randomness (Supplementary Equation 2) it was assumed that the state of the system used is two-dimensional and the measurements at time $t_1$ and $t_2$ are projective measurements Nath et al. (2024). The circuit we used above is one of the possible choices of the family of circuits given these constraints.

To verify the No-Signaling In Time (NSIT) conditions, two additional circuits perform measurements solely at $t_2$ and $t_3$ (Figure 3) without prior measurements. The outcomes from these circuits, coupled with the results from correlation calculations, are employed to validate Equation 3. The concurrent violation of LGI and the satisfaction of NSIT conditions collectively ensure the unpredictability of the outputs generated in the correlation measurements.

Figure 3

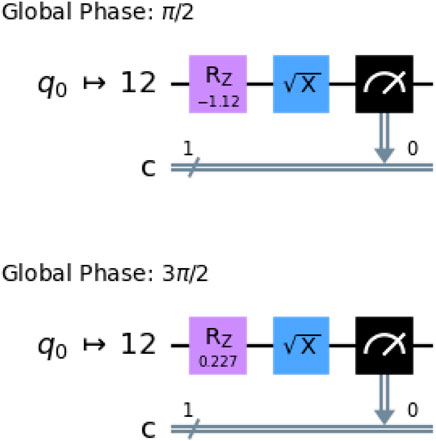
Figure 3. Circuit for computing the one time probabilities at $t_2$ and $t_3$. These circuits are utilized in the verification of the NSIT conditions and are not used in generating random bits. These circuits also can be decomposed in terms of the $SX$ and $R_Z$ gates followed by a single measurement.

In each experiment, we employ the five circuits for $N=\mathrm{50,000}$ shots each and compute the expected LGI and NSIT values. We repeat the experiment for each LGI violation value 10 times and see that the spread of LGI violation is around the range of the expected LGI value (Figure 4) and the NSIT conditions are satisfied up to an order $10^{-2}$. In each run of the experiment, we generate $2N$ bits from each of the first three sub-runs of the experiment for calculating the correlations. In order to protect the random bits from the attacks involved in state preparation, we discard the first bit and employ conditional probabilities to compute the Genuine Randomness as shown in (Nath et al., 2024). The Genuine Randomness computed in this manner follows the bound derived in (Nath et al., 2024) (Supplementary Material: Equation 2) and is shown in Figure 5. Thus, for $N=\mathrm{50,000}$ with the experiment repeated 10 times, we generate $\mathrm{50,000}\times 3\times 10$ random bits.

Figure 4

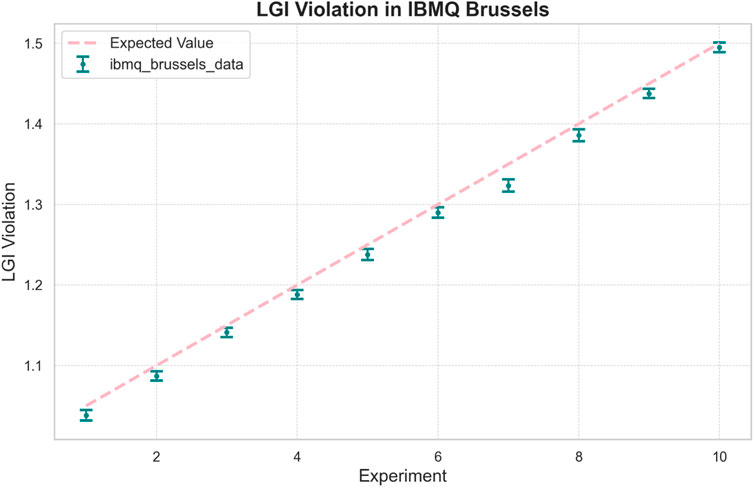
Figure 4. LGI violation experiment in IBMQ Brussels. We repeated the experiment for each value 10 times, each of the experiments was run for 50,000 shots. We observe that for all cases the experimental results are slightly lower than the expected values, which is due to the noise factors in the backend as demonstrated later.

Figure 5

Figure 5. Genuine Randomness vs. LGI violation plotted alongside the theoretical analytical bound for the experiment in IBMQ Brussels. The genuine randomness spread is a bit lower than the expected lower bound because the results of the LGI values in the experiment were lower than the expected values.

To compare with the certified randomness bound in Equation 4, we note that the randomness observed in our experiments is close to the theoretical bound derived for this scenario. The values appear slightly lower, which is consistent with the fact that the experimentally measured LGI violations are themselves smaller than the expected ideal values.

Noise Mitigation: In order to mitigate the noise in the quantum hardware we employed multiple techniques. We transpiled the original circuit against our backend to decompose it in terms of the available gates in the backend. We used mapomatic library (Nation and Treinish, 2023) to select the layouts/qubits in which our circuit fits. Then we used the mapomatic algorithm to score the best possible layout for our circuit in terms of the mapomatic score, which is calculated by combining the noise rates of each of the operations in the circuit for the noise parameters of the layout. Details of the noise analysis are included in Section 7. Apart from the major experiment conducted in the IBMQ Brussels backend, we also generated secure random numbers using some deprecated IBM backends: IBM Perth, IBM Lagos, and IBM Kyoto. Certification was achieved through the successful violation of the Leggett-Garg Inequality and the satisfaction of the No Signaling in Time Conditions. The results of these experiments are given in Section 5 of the Supplementary Material.

4 Advantages over the Bell based certified randomness scheme

We demonstrate that it is possible to violate Bell’s inequality using a quantum computer. This can be achieved by creating a maximally entangled state and selecting specific measurement bases for each qubit. In our example, we chose the measurement angles for Alice as ${\theta }_a=0$ and ${\theta }_a^{\prime }=\pi /4$, and for Bob as ${\theta }_b=\pi /8$ and ${\theta }_b^{\prime }=3\pi /8$, resulting in a Bell violation of $2\sqrt{2}$. For each iteration, a random seed was used to select the measurement settings for Alice and Bob, and then the results were used to compute the correlations. The corresponding quantum circuit for this experiment is shown in Figure 6.

Figure 6

Figure 6. Circuit for violating the Bell inequality. A maximally entangled state is created and distributed between Alice and Bob. The measurement settings ${\theta }_A$ and ${\theta }_B$ are randomly selected from the possible choices.

However, the bits generated from the measurement outcomes of Alice and Bob in the above experiment cannot be certified, as generating certified randomness from Bell inequality violations requires the additional constraint of satisfying the No-Signaling condition. To meet this requirement, the two measurement stations (Alice and Bob) must be sufficiently separated so that Alice is unaware of Bob’s random seed and vice versa. Currently, this level of separation cannot be achieved, as communication between quantum computers is not feasible. Nevertheless, our protocol satisfies the necessary conditions for certified randomness, as the circuits are designed to violate the Leggett-Garg inequality (LGI) while also fulfilling the No-Signaling-in-Time condition.

4.1 Loopholes

We briefly discuss the potential loopholes in our experiment and how we have addressed the same. For the clumsiness loophole, Huffman and Mizel (2017); Wilde and Mizel (2012) our experiment was designed so that a measurement made at an earlier time cannot be compared to a measurement made later. This was ensured by setting the parameters for the unitaries in such a way that they satisfy the No Signaling in Time condition, which is a necessary condition for the measurements to be non-invasive Emary (2017). The results of our experiment, satisfy the NSIT condition up to a tolerance of $10^{-2}$. The detection efficiency loophole, coincidence loophole and the multi-photon emission loophole are irrelevant for LGI violation on superconducting quantum computers. The preparation state loophole is automatically closed by the state preparation procedures of the IBM quantum chips, as they consistently produce the same initial state.

5 Noise Mitigation using mthree

We used IBM error mitigation techniques (Nation et al., 2021) to further reduce readout errors in our experiment. The primary motivation for this approach was to strengthen the NSIT condition by eliminating classical sources of errors, particularly readout errors. Among the various sources of errors, measurement errors were the most dominant as in Figure 7, and their careful mitigation is crucial to obtain more accurate values for Leggett-Garg inequality (LGI) violations.

Figure 7

Figure 7. $T1$(Thermal relaxation time), $T2$(dephasing time), $SX$-error rates, $R_z$-error rates and readout error rates for randomnly selected qubits in the ibmq brussels backend.

We utilized the Mthree command.

M3Mitigation.cals_from_system() to compute the calibration matrix for the qubits used in the experiment. Furthermore, we applied M3Mitigation.apply_correction() to obtain the corrected probabilities. The experiment was repeated and Mthree error mitigation techniques were applied to generate the readout error-mitigated results, as illustrated in Figure 8. As shown in Section 2 of the Supplementary Material, readout errors systematically reduce the LGI violation values below the expected levels. The application of readout error mitigation significantly improved these values, bringing them closer to the theoretically expected results. This importantly proves that we can trust the random numbers generated this way, as the errors are systematic in nature and can thus be effectively mitigated. The Root Mean Square Error (RMSE), calculated by squaring the difference between the experimental results and expected values, then averaging over all experiments, is 0.00073 without error mitigation. This improves to 0.000183 after applying error mitigation.

Figure 8

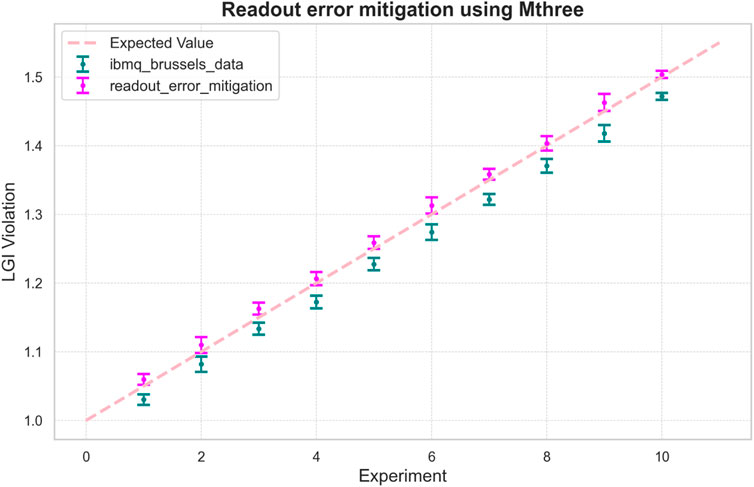
Figure 8. Comparison of raw and readout error-mitigated values of LGI violations, performed in IBM Brussels. For each LGI violation, the experiment was repeated 10 times, with $50,000$ shots per experiment. The readout error-mitigated values, obtained using Mthree’s correction techniques, are elevated and align more closely with the expected theoretical values, demonstrating the effectiveness of the mitigation process.

Currently, the Sampler does not have the capability to mitigate gate errors, which were a minor source of error in our experiment. However, this can be addressed in the future as such methods are adopted to enhance result precision.

6 Qiskit: Advanced functions and challenges

During the final stages of our experiment, we utilized advanced functionalities of the latest version of Qiskit, such as the Sampler and Batch features. These tools proved to be highly effective in implementing error mitigation strategies, significantly enhancing the reliability of our results. Although most of our outcomes aligned well with theoretical expectations, we occasionally observed results that were inconsistent or uncorrelated with the expected behavior. These anomalies, though infrequent, highlight the inherent challenges and variability associated with current quantum computing hardware. Despite these occasional discrepancies, the advanced capabilities of Qiskit provided a robust framework for achieving meaningful and reproducible results in our study.

7 Noise analysis

In all of the above experiments we saw that the LGI value of the experiment is lower than the expected LGI value. To analyze the noise, we started with some sanity checks on the results. We ran the experiment in the qiskit Aer simulator and verified that it matches the exact result. We then imported the noise parameters from the device at the time of running the experiment and created a noise model from these noise parameters. Using this noise model on the Aer Simulator we ran the experiment and the results of this noisy simulation match with those of the original experiment as shown in Figure 9. For better visibility of the actual results with the noise simulation, we displaced them slightly on the horizontal axis.

Figure 9

Figure 9. Noise simulation of the experiment using the noise parameters from the IBMQ Brussels backend, compared with the results of the actual experiment. Each experiment is conducted with 50,000 shots and repeated 10 times. We displaced the noisy simulation slightly from the actual one for better visibility. The close but not complete agreement between the simulation and experimental results demonstrates the impact of noise on the system.

Although the experimental results are very close to the expected values, we want to address the potential sources of errors. The circuits used consist of $R_z$ and $SX$ gates. The $R_z$ gates are implemented flawlessly without any noise because they are diagonal gates, which can be implemented virtually in hardware through frame changes, resulting in zero error and no time duration. On the other hand, the $SX$ gates have an error rate of approximately $10^{-4}$. Although this error rate is very low compared to two-qubit gates such as CNOT and ECR(Echoed Cross Resonance), it could still be a possible source of error.

The readout errors are significant, compared to the gate error rates. The readout error rates and gate error rates for selected qubits in the IBMQ Brussels backend are shown in Figure 10.

Figure 10

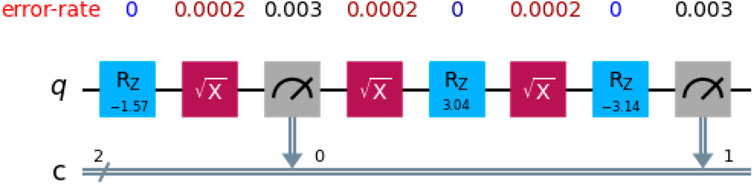
Figure 10. Error rates of the gates in the one-qubit circuit used to compute two-time correlations. The error analysis includes the gate error rates for $R_z$ and $SX$, as well as measurement errors. The $R_z$ gates are implemented flawlessly, with no detectable error. The $SX$ gates exhibit minimal errors, contributing only slightly to the overall noise. Despite the generally high readout errors, qubits with the lowest readout error rates were carefully selected to ensure the most accurate measurements possible.

Regarding decoherence errors, we computed the total time required to run the circuit by calculating the implementation time for each element, as shown in Figure 11. The $R_z$ gates are implemented instantly, while the $SX$ gates require time on the order of nanoseconds. The measurements take more time, on the order of microseconds. Consequently, the entire circuit is executed in a few microseconds. Given that the decoherence times for the qubits in our backend are on the order of $10^{-4}$ seconds, the circuit is safely implemented within the decoherence time.

Figure 11

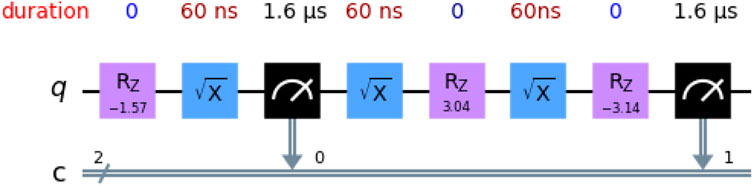
Figure 11. Duration of the elements in the one-qubit circuit to compute the two time correlations. The $R_z$ gates are implemented instantaneously with no measurable duration. The $SX$ gates operate on the scale of nanoseconds, while the measurement process occurs on the scale of microseconds.

We selected a subset of qubits at random from the 127 qubits available on the IBM Brussels backend, and their corresponding $T_1$ (thermal relaxation time) and $T_2$ (dephasing time) values are shown in Figure 7. This analysis demonstrates that our algorithm is well suited for implementation on the best available qubits in the back-end without suffering from decoherence.

8 Conclusion

In the NISQ era, algorithm design departs from the ideal of universal, fault-tolerant quantum computing and instead embraces hardware limitations such as shallow circuits, noise, and device-specific constraints (Bharti et al., 2022; Lau et al., 2022; Chen et al., 2023). Central to this effort are variational quantum algorithms (VQAs) like VQE (Tilly et al., 2022; Kandala et al., 2017) and QAOA, which combine quantum state preparation with classical optimization, often using hardware-efficient ansätze adapted to qubit topology. These hybrid methods are complemented by error mitigation strategies (e.g., zero-noise extrapolation, probabilistic error cancellation), mid-circuit measurements, and qubit reuse, extending algorithmic depth without full error correction. Despite challenges such as barren plateaus (McClean et al., 2018; Larocca et al., 2025) and the data-loading bottleneck, NISQ devices have enabled demonstrations of quantum advantage, from Google’s 2019 random circuit sampling (Arute et al., 2019) to boson sampling with (Zhong et al., 2020) and more recent utility-driven experiments (Rosenberg et al., 2024). While early supremacy claims often involved contrived benchmarks, the field now emphasizes “quantum advantage” and “quantum utility” as measures of tangible progress, with applications extending beyond speedup to tasks uniquely enabled by quantum physics, such as certified randomness generation. In this spirit, our proposed randomness-generation protocol adopts a NISQ philosophy—shallow, hardware-efficient, and noise-resilient—illustrating how present-day devices can already realize practical, qualitatively new capabilities.

We generate secure random numbers certified by the principles of quantum mechanics, using IBMQ backends, specifically Brussels, Perth, Lagos, and Kyoto. Certification of these random numbers was achieved through the successful violation of the Leggett-Garg Inequality and compliance with the No Signaling in Time conditions. The implemented protocol is notably simple, requiring minimal circuits composed of gates that can be executed with high accuracy and minimal errors. In addition, we conducted a thorough noise analysis to demonstrate and understand the impact of noise on our experimental results.

One shortcoming of the current implementation is that the process is conducted in the cloud, and thus, sub-runs are performed one after another without specifying a seed. Thus, incorporating a random seed and implementing an extraction procedure can further secure the generated bits. Random numbers were generated using a random seed in the Qiskit simulator as shown in Section 4 of the Supplementary Material. This step is computationally expensive on a quantum computer because it requires running a different circuit each time, so we used the Qiskit simulator for these experiments to demonstrate a first proof-of-principle.

This work also serves as a fundamental validation of quantum mechanics on a quantum computer. In addition to contributing to a growing body of quantum mechanical tests (Sadana et al., 2022; 2023; Santini and Vitale, 2022) conducted on quantum computers, it also has practical applications for benchmarking quantum devices. Given that our test requires only a single qubit, it provides a straightforward method for benchmarking individual qubits as well.

Quantum random number generation on quantum computers has been explored through diverse approaches: some employ source-independent protocols (Li et al., 2021; Jacak et al., 2021), others rely on statistical tests of output randomness to assess qubit stability (Tamura and Shikano, 2021; Kumar et al., 2022), and still others propose optimized, fault-tolerant circuits with resource-efficient comparators for generating numbers within user-defined intervals (Orts et al., 2023). More recently, it has also been shown that quantum computers can be programmed to realize flexible TRNGs capable of sampling from user-defined probability mass functions (PMFs), producing multiple random bits per execution while mitigating device imperfections through extractor functions Sinha et al. (2023). Despite these advances, most approaches lack formal certification, which is essential for guaranteeing unpredictability and cryptographic security. A notable certified scheme Liu et al. (2025) uses random circuit sampling, where a client generates challenge circuits from a small seed, sends them to an untrusted quantum server, and verifies the outcomes classically. While powerful, this method demands significant computational resources. By contrast, our protocol achieves certification using only two stringent conditions—the violation of the Leggett–Garg inequality (LGI) and the satisfaction of no-signaling in time (NSIT)—both implemented efficiently on a single qubit.

In summary, we demonstrate an efficient and resource-light protocol for certified quantum randomness generation on current NISQ-era devices. Unlike most certified schemes, it is directly implementable on quantum hardware, relying only on shallow circuits composed of high-fidelity single-qubit gates. This simplicity makes it well suited to today’s platforms, while also pointing toward future deployment on commercial quantum processors, where it could provide secure and accessible randomness for a wide range of applications.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

PN: Methodology, Validation, Writing – review and editing, Data curation, Formal Analysis, Conceptualization, Software, Writing – original draft, Investigation. AS: Validation, Methodology, Conceptualization, Writing – original draft, Supervision, Project administration, Investigation, Formal Analysis, Writing – review and editing. US: Investigation, Funding acquisition, Supervision, Conceptualization, Writing – review and editing, Formal Analysis, Project administration, Writing – original draft, Validation, Methodology.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. MEITY: Provided partial support for the fundamental architecture for the whole research enterprise by the Quantum Information and Computing lab. NQM: Partial support for the core research. CERC, QHA: Partial support for research personnel time. SERB core grant: Partial support for the core research IBM: IBM Quantum Credits were being used for our work.

Acknowledgments

We especially thank Dipankar Home for useful discussions. We extend our sincere gratitude to Sean Wagner(IBM) for his invaluable assistance in utilizing the advanced functionalities of Qiskit. His expertise significantly contributed to improving the quality and accuracy of our results. We are also deeply grateful to Jagan Natarajan (IBM) for his guidance and support in migrating our code to the newer version of Qiskit. We thank Subhadip Dutta for running the NIST tests for the random bits generated in the experiments. US acknowledges partial support provided by the Ministry of Electronics and Information Technology (MeitY), Government of India under a grant for Centre for Excellence in Quantum Technologies with Ref. No. 4(7)/2020-ITEA, the National Quantum Mission of the DST for partial support as well as from a Canada Excellence Research Chair professorship. AS acknowledges support from the SERB core grant CRG/2021/000873 and a Quantum Horizons Alberta chair professorship. We acknowledge the use of IBM Quantum Credits for this work. The views expressed are those of the authors, and do not reflect the official policy or position of IBM or the IBM Quantum team.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frqst.2025.1661544/full#supplementary-material

References

Abellán, C., Amaya, W., Mitrani, D., Pruneri, V., and Mitchell, M. W. (2015). Generation of fresh and pure random numbers for loophole-free bell tests. Phys. Rev. Lett. 115, 250403. doi:10.1103/physrevlett.115.250403

PubMed Abstract | CrossRef Full Text | Google Scholar

Acín, A., and Masanes, L. (2016). Certified randomness in quantum physics. Nature 540, 213–219. doi:10.1038/nature20119

PubMed Abstract | CrossRef Full Text | Google Scholar

Arute, F., Arya, K., Babbush, R., Bacon, D., Bardin, J. C., Barends, R., et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510. doi:10.1038/s41586-019-1666-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Aspect, A. (1999). Bell’s inequality test: more ideal than ever. Nature 398, 189–190. doi:10.1038/18296

CrossRef Full Text | Google Scholar

Bagini, V., and Bucci, M. (1999). “A design of reliable true random number generator for cryptographic applications,” in Cryptographic hardware and embedded systems: first InternationalWorkshop, CHES’99 Worcester, MA, USA, August 12–13, 1999 proceedings 1 (Springer), 204–218.

Google Scholar

Bassham, L. E., Rukhin, A. L., Soto, J., Nechvatal, J. R., Smid, M. E., Leigh, S. D., et al. (2010). A statistical test suite for random and pseudorandom number generators for cryptographic applications

Google Scholar

Bell, J. S. (1964). On the einstein podolsky rosen paradox. Phys. Phys. Fiz. 1, 195–200. doi:10.1103/physicsphysiquefizika.1.195

CrossRef Full Text | Google Scholar

Bharti, K., Cervera-Lierta, A., Kyaw, T. H., Haug, T., Alperin-Lea, S., Anand, A., et al. (2022). Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 94, 015004. doi:10.1103/RevModPhys.94.015004

CrossRef Full Text | Google Scholar

Bierhorst, P., Knill, E., Glancy, S., Zhang, Y., Mink, A., Jordan, S., et al. (2018). Experimentally generated randomness certified by the impossibility of superluminal signals. Nature 556, 223–226. doi:10.1038/s41586-018-0019-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Blum, L., Blum, M., and Shub, M. (1986). A simple unpredictable pseudo-random number generator. SIAM J. Comput. 15, 364–383. doi:10.1137/0215025

CrossRef Full Text | Google Scholar

Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V., and Wehner, S. (2014). Bell nonlocality. Rev. Mod. Phys. 86, 419–478. doi:10.1103/revmodphys.86.419

CrossRef Full Text | Google Scholar

Cavalcanti, E. G., and Wiseman, H. M. (2012). Bell nonlocality, signal locality and unpredictability or what bohr could have told einstein at solvay had he known about bell experiments. Found. Phys. 42, 1329–1338. doi:10.1007/s10701-012-9669-1

CrossRef Full Text | Google Scholar

Chen, S., Cotler, J., Huang, H.-Y., and Li, J. (2023). The complexity of nisq. Nat. Commun. 14, 6001. doi:10.1038/s41467-023-41217-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Cirel’son, B. S. (1980). Quantum generalizations of bell’s inequality. Lett. Math. Phys. 4, 93–100. doi:10.1007/bf00417500

CrossRef Full Text | Google Scholar

Clemente, L., and Kofler, J. (2015). Necessary and sufficient conditions for macroscopic realism from quantum mechanics. Phys. Rev. A 91, 062103. doi:10.1103/physreva.91.062103

CrossRef Full Text | Google Scholar

Emary, C. (2017). Ambiguous measurements, signaling, and violations of leggett-garg inequalities. Phys. Rev. A 96, 042102. doi:10.1103/physreva.96.042102

CrossRef Full Text | Google Scholar

Emary, C., Lambert, N., and Nori, F. (2013). Leggett–garg inequalities. Rep. Prog. Phys. 77, 016001. doi:10.1088/0034-4885/77/1/016001

CrossRef Full Text | Google Scholar

Fischer, V., and Drutarovskỳ, M. (2002). “True random number generator embedded in reconfigurable hardware,” in International workshop on cryptographic hardware and embedded systems (Springer), 415–430.

Google Scholar

Franson, J. D. (1989). Bell inequality for position and time. Phys. Rev. Lett. 62, 2205–2208. doi:10.1103/physrevlett.62.2205

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, L.-H., and Luo, H.-X. (2023). Dual color images watermarking scheme with geometric correction based on quaternion froofmms and ls-svr. Opt. and Laser Technol. 167, 109665. doi:10.1016/j.optlastec.2023.109665

CrossRef Full Text | Google Scholar

Halliwell, J. (2016). Leggett-garg inequalities and no-signaling in time: a quasiprobability approach. Phys. Rev. A 93, 022123. doi:10.1103/physreva.93.022123

CrossRef Full Text | Google Scholar

Hellekalek, P. (1998). Good random number generators are (not so) easy to find. Math. Comput. Simul. 46, 485–505. doi:10.1016/s0378-4754(98)00078-0

CrossRef Full Text | Google Scholar

Herrero-Collantes, M., and Garcia-Escartin, J. C. (2017). Quantum random number generators. Rev. Mod. Phys. 89, 015004. doi:10.1103/revmodphys.89.015004

CrossRef Full Text | Google Scholar

Huffman, E., and Mizel, A. (2017). Violation of noninvasive macrorealism by a superconducting qubit: implementation of a leggett-garg test that addresses the clumsiness loophole. Phys. Rev. A 95, 032131. doi:10.1103/physreva.95.032131

CrossRef Full Text | Google Scholar

Hull, T. E., and Dobell, A. R. (1962). Random number generators. SIAM Rev. 4, 230–254. doi:10.1137/1004061

CrossRef Full Text | Google Scholar

Jacak, M. M., Jóźwiak, P., Niemczuk, J., and Jacak, J. E. (2021). Quantum generators of random numbers. Sci. Rep. 11, 16108. doi:10.1038/s41598-021-95388-7

PubMed Abstract | CrossRef Full Text | Google Scholar

[Dataset] Javadi-Abhari, A., Treinish, M., Krsulich, K., Wood, C. J., Lishman, J., Gacon, J., et al. (2024). Quantum computing with Qiskit.

Google Scholar

Jennewein, T., Achleitner, U., Weihs, G., Weinfurter, H., and Zeilinger, A. (2000). A fast and compact quantum random number generator. Rev. Sci. Instrum. 71, 1675–1680. doi:10.1063/1.1150518

CrossRef Full Text | Google Scholar

Joarder, K., Saha, D., Home, D., and Sinha, U. (2022). Loophole-free interferometric test of macrorealism using heralded single photons. PRX Quantum 3, 010307. doi:10.1103/prxquantum.3.010307

CrossRef Full Text | Google Scholar

Kandala, A., Mezzacapo, A., Temme, K., Takita, M., Brink, M., Chow, J. M., et al. (2017). Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. nature 549, 242–246. doi:10.1038/nature23879

PubMed Abstract | CrossRef Full Text | Google Scholar

Kofler, J., and Brukner, Č. (2008). Conditions for quantum violation of macroscopic realism. Phys. Rev. Lett. 101, 090403. doi:10.1103/physrevlett.101.090403

PubMed Abstract | CrossRef Full Text | Google Scholar

Kofler, J., and Brukner, Č. (2013). Condition for macroscopic realism beyond the leggett-garg inequalities. Phys. Rev. A 87, 052115. doi:10.1103/physreva.87.052115

CrossRef Full Text | Google Scholar

Kumar, V., Rayappan, J. B. B., Amirtharajan, R., and Praveenkumar, P. (2022). Quantum true random number generation on ibm’s cloud platform. J. King Saud University-Computer Inf. Sci. 34, 6453–6465. doi:10.1016/j.jksuci.2022.01.015

CrossRef Full Text | Google Scholar

Larocca, M., Thanasilp, S., Wang, S., Sharma, K., Biamonte, J., Coles, P. J., et al. (2025). Barren plateaus in variational quantum computing. Nat. Rev. Phys. 7, 174–189. doi:10.1038/s42254-025-00813-9

CrossRef Full Text | Google Scholar

Lau, J. W. Z., Lim, K. H., Shrotriya, H., and Kwek, L. C. (2022). Nisq computing: where are we and where do we go? AAPPS Bull. 32, 27. doi:10.1007/s43673-022-00058-z

CrossRef Full Text | Google Scholar

Leggett, A. J., and Garg, A. (1985). Quantum mechanics versus macroscopic realism: is the flux there when nobody looks? Phys. Rev. Lett. 54, 857–860. doi:10.1103/physrevlett.54.857

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Fei, Y., Wang, W., Meng, X., Wang, H., Duan, Q., et al. (2021). Quantum random number generator using a cloud superconducting quantum computer based on source-independent protocol. Sci. Rep. 11, 23873. doi:10.1038/s41598-021-03286-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Chen, L., Mao, H., and Qu, Q. (2025). The image encryption system based on optical orbital angular momentum holography and nonlinear authentication. J. Opt. 27, 045606. doi:10.1088/2040-8986/adbcc2

CrossRef Full Text | Google Scholar

Liu, Y., Yuan, X., Li, M.-H., Zhang, W., Zhao, Q., Zhong, J., et al. (2018a). High-speed device-independent quantum random number generation without a detection loophole. Phys. Rev. Lett. 120, 010503. doi:10.1103/physrevlett.120.010503

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Zhao, Q., Li, M.-H., Guan, J.-Y., Zhang, Y., Bai, B., et al. (2018b). Device-independent quantum random-number generation. Nature 562, 548–551. doi:10.1038/s41586-018-0559-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, M., Shaydulin, R., Niroula, P., DeCross, M., Hung, S.-H., Kon, W. Y., et al. (2025). Certified randomness using a trapped-ion quantum processor. Nature 640, 343–348. doi:10.1038/s41586-025-08737-1

PubMed Abstract | CrossRef Full Text | Google Scholar

L’Ecuyer, P. (2012). Random number generation. Springer.

Google Scholar

Ma, X., Yuan, X., Cao, Z., Qi, B., and Zhang, Z. (2016). Quantum random number generation. Quantum Inf. 2, 16021–16029. doi:10.1038/npjqi.2016.21

CrossRef Full Text | Google Scholar

Mal, S., Banik, M., and Choudhary, S. K. (2016). Temporal correlations and device-independent randomness. Quantum Inf. Process. 15, 2993–3004. doi:10.1007/s11128-016-1321-0

CrossRef Full Text | Google Scholar

Marsaglia, G. (2003). Random number generators. J. Mod. Appl. Stat. Methods 2, 2–13. doi:10.22237/jmasm/1051747320

CrossRef Full Text | Google Scholar

Marsaglia, G., and Zaman, A. (1991). A new class of random number generators. Ann. Appl. Probab. 1, 462–480. doi:10.1214/aoap/1177005878

CrossRef Full Text | Google Scholar

Marsaglia, G., Zaman, A., and Tsang, W. W. (1990). Toward a universal random number generator. Statistics and Probab. Lett. 9, 35–39. doi:10.1016/0167-7152(90)90092-l

CrossRef Full Text | Google Scholar

McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush, R., and Neven, H. (2018). Barren plateaus in quantum neural network training landscapes. Nat. Commun. 9, 4812. doi:10.1038/s41467-018-07090-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Nath, P. P., Saha, D., Home, D., and Sinha, U. (2024). Single-system-based generation of certified randomness using leggett-garg inequality. Phys. Rev. Lett. 133, 020802. doi:10.1103/physrevlett.133.020802

PubMed Abstract | CrossRef Full Text | Google Scholar

Nation, P. D., and Treinish, M. (2023). Suppressing quantum circuit errors due to system variability. PRX Quantum 4, 010327. doi:10.1103/prxquantum.4.010327

CrossRef Full Text | Google Scholar

Nation, P. D., Kang, H., Sundaresan, N., and Gambetta, J. M. (2021). Scalable mitigation of measurement errors on quantum computers. PRX Quantum 2, 040326. doi:10.1103/prxquantum.2.040326

CrossRef Full Text | Google Scholar

Orts, F., Filatovas, E., Garzón, E. M., and Ortega, G. (2023). A quantum circuit to generate random numbers within a specific interval. EPJ Quantum Technol. 10, 17. doi:10.1140/epjqt/s40507-023-00174-1

CrossRef Full Text | Google Scholar

Peres, A. (1999). All the bell inequalities. Found. Phys. 29, 589–614. doi:10.1023/a:1018816310000

CrossRef Full Text | Google Scholar

[Dataset] Pironio, S. (2018). The certainty of quantum randomness. Nature 556, 176–177. doi:10.1038/d41586-018-04105-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Pironio, S., Acín, A., Massar, S., de La Giroday, A. B., Matsukevich, D. N., Maunz, P., et al. (2010). Random numbers certified by bell’s theorem. Nature 464, 1021–1024. doi:10.1038/nature09008

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenberg, E., Andersen, T., Samajdar, R., Petukhov, A., Hoke, J., Abanin, D., et al. (2024). Dynamics of magnetization at infinite temperature in a heisenberg spin chain. Science 384, 48–53. doi:10.1126/science.adi7877

PubMed Abstract | CrossRef Full Text | Google Scholar

Rukhin, A., Soto, J., Nechvatal, J., Smid, M., Barker, E., Leigh, S., et al. (2001). A statistical test suite for random and pseudorandom number generators for cryptographic applications, 22. US Department of Commerce, Technology Administration, USA.: National Institute of. Standards and Technology.

Google Scholar

Sadana, S., Maccone, L., and Sinha, U. (2022). Testing quantum foundations with quantum computers. Phys. Rev. Res. 4, L022001. doi:10.1103/physrevresearch.4.l022001

CrossRef Full Text | Google Scholar

Sadana, S., Maccone, L., and Sinha, U. (2023). Noise analysis for the sorkin and peres tests performed on a quantum computer. Quantum Inf. Process. 22, 317. doi:10.1007/s11128-023-04072-4

CrossRef Full Text | Google Scholar

Santini, A., and Vitale, V. (2022). Experimental violations of leggett-garg inequalities on a quantum computer. Phys. Rev. A 105, 032610. doi:10.1103/physreva.105.032610

CrossRef Full Text | Google Scholar

Shalm, L. K., Zhang, Y., Bienfang, J. C., Schlager, C., Stevens, M. J., Mazurek, M. D., et al. (2021). Device-independent randomness expansion with entangled photons. Nat. Phys. 17, 452–456. doi:10.1038/s41567-020-01153-4

CrossRef Full Text | Google Scholar

Shen, L., Lee, J., Bancal, J.-D., Cerè, A., Lamas-Linares, A., Lita, A., et al. (2018). Randomness extraction from bell violation with continuous parametric down-conversion. Phys. Rev. Lett. 121, 150402. doi:10.1103/physrevlett.121.150402

PubMed Abstract | CrossRef Full Text | Google Scholar

Sinha, A., Henderson, E. R., Henderson, J. M., Larson, E. C., and Thornton, M. A. (2023). A programmable true random number generator using commercial quantum computers. Quantum Inf. Sci. Sens. Comput. XV (SPIE) 12517, 35–49. doi:10.1117/12.2663497

CrossRef Full Text | Google Scholar

Stipčević, M., and Koç, Ç. K. (2014). “True random number generators,” in Open problems in mathematics and computational science (Springer), 275–315.

Google Scholar

Storz, S., Schär, J., Kulikov, A., Magnard, P., Kurpiers, P., Lütolf, J., et al. (2023). Loophole-free bell inequality violation with superconducting circuits. Nature 617, 265–270. doi:10.1038/s41586-023-05885-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Sunar, B., Martin, W. J., and Stinson, D. R. (2006). A provably secure true random number generator with built-in tolerance to active attacks. IEEE Trans. Comput. 56, 109–119. doi:10.1109/tc.2007.250627

CrossRef Full Text | Google Scholar

Tamura, K., and Shikano, Y. (2021). “Quantum random numbers generated by a cloud superconducting quantum computer,” in International symposium on mathematics, quantum theory, and cryptography: proceedings of MQC 2019 (Springer Singapore), 17–37.

CrossRef Full Text | Google Scholar

Tilly, J., Chen, H., Cao, S., Picozzi, D., Setia, K., Li, Y., et al. (2022). The variational quantum eigensolver: a review of methods and best practices. Phys. Rep. 986, 1–128. doi:10.1016/j.physrep.2022.08.003

CrossRef Full Text | Google Scholar

Vazirani, U. V., and Vazirani, V. V. (1984). “Efficient and secure pseudo-random number generation,” in Workshop on the theory and application of cryptographic techniques (Springer), 193–202.

Google Scholar

Wilde, M. M., and Mizel, A. (2012). Addressing the clumsiness loophole in a leggett-garg test of macrorealism. Found. Phys. 42, 256–265. doi:10.1007/s10701-011-9598-4

CrossRef Full Text | Google Scholar

Yu, F., Li, L., Tang, Q., Cai, S., Song, Y., and Xu, Q. (2019). A survey on true random number generators based on chaos. Discrete Dyn. Nat. Soc. 2019, 1–10. doi:10.1155/2019/2545123

CrossRef Full Text | Google Scholar

Zhang, Y., Shalm, L. K., Bienfang, J. C., Stevens, M. J., Mazurek, M. D., Nam, S. W., et al. (2020). Experimental low-latency device-independent quantum randomness. Phys. Rev. Lett. 124, 010505. doi:10.1103/physrevlett.124.010505

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhong, H.-S., Wang, H., Deng, Y.-H., Chen, M.-C., Peng, L.-C., Luo, Y.-H., et al. (2020). Quantum computational advantage using photons. Science 370, 1460–1463. doi:10.1126/science.abe8770

PubMed Abstract | CrossRef Full Text | Google Scholar