Abstract
Artificial intelligence (AI) is increasingly proposed as a solution to environmental sustainability challenges, with applications aimed at optimizing resource utilization and energy consumption. However, AI technologies also have significant negative environmental impacts. This duality underscores the need to critically evaluate AI's role in sustainable practices. One example of AI's application in sustainability is the Occupant Controlled Smart Thermostat (OCST). These systems optimize indoor temperature management by responding to dynamic signals, such as energy price fluctuations, which reflect power grid stress. Accordingly, regulatory frameworks have mandated performance standards for such technologies to ensure effective demand responsiveness. While OCSTs are effective in managing energy demand through predefined norms like price signals, their current designs often fail to accommodate the complex interplay of conflicting priorities, such as user comfort and grid optimization, particularly in uncertain climatic conditions. For instance, extreme weather events can amplify energy demands and user needs, necessitating a more context sensitive approach. This adaptability requires OCSTs to dynamically shift between multiple normative constraints (i.e., norms), such as prioritizing userdefined temperature settings over price-based energy restrictions when contextually appropriate. In this paper, we propose an innovative approach that combines the theory of active inference from theoretical neuroscience and robotics with a rulebook formalism to enhance the decision-making capabilities of autonomous AI agents. Using simulation studies, we demonstrate how these AI agents can resolve conflicts among norms under environmental uncertainty. A minimal use case is presented, where an OCST must decide whether to warm a room based on two conflicting rules: a “price” rule that restricts energy use above a cost threshold and a “need” rule that prioritizes maintaining the user's desired temperature. Our findings illustrate the potential for advanced AI-driven OCST systems to navigate conflicting norms, enabling more resilient and user-centered solutions to sustainable energy challenges.
1 Introduction
Artificial intelligence (AI) has been offered as a solution to issues of environmental sustainability (Addimulam, 2024; Albarracin et al., 2024a,b; Challoumis, 2024). AI, particularly that involving generative models and large-scale machine learning applications, exert significant environmental pressures. These include high electricity consumption during training and inference phases, reliance on energy-intensive data centers that contribute up to 1.3% of global electricity demand, and the resultant greenhouse gas emissions—often exceeding 7.84 kg CO2 equivalent for a single instance of complex inference (Berthelot et al., 2024; Luccioni et al., 2024). The production and operation of the necessary hardware exacerbate resource depletion, particularly rare metals, and increase abiotic depletion potential (Kristian et al., 2024; Luccioni et al., 2024). Despite AI having a significant negative impact on the environment (Berthelot et al., 2024; Kristian et al., 2024; Luccioni et al., 2024), AI technologies promise to help us tackle environmental challenges by optimizing resource utilization and energy consumption (Kristian et al., 2024). One example of a sustainable use of AI technology is Occupant Controlled Smart Thermostat (OCST). OCSTs allow for intelligently adjusting the temperature in an indoor environment by considering a variety of real-time signals; including price signals, which may be indicative of a higher energy demand and pressure on power grids. By lowering demand locally—when global demand is too high—OCSTs, such as smart thermostats, smart lighting, smart plugs, smart security systems, or electric vehicle charges are capable of optimizing utilization of the power grid. For that reason, regulations have been developed to ensure that thermostats systems sold as OCST meet certain requirements in responding to relevant variables, such as price signals tracking energy demands (e.g., the appendix JA5 for Technical Specifications for Demand Responsive Thermostats of the California Energy Commission).
In an ideal world, OCSTs should be capable of making decisions by balancing responses to multiple norms in context that may conflict with one another, and not just those related to price signals. For instance, if a homeowner has a preference that conflicts with responses to a price signal, given the context at hand, the OCST should be capable of shifting norms, from the homeowner defined norm to the price signal-based norm, or to any number of norms. Such an ability to shift among norms—in a context sensitive fashion—is particularly relevant in uncertain climates. In normal weather, price and energy demands may be well balanced with energy needs, such that a single price rule may allow to optimize comfort and energy demand. In turn, in case of extreme temperature shifts, both population demands, and individual needs are exacerbated. A single rule about price or comfort may put too much stress on the power grid or disregard the needs of OCST owners, which may cause undue stress or discomfort for occupants, and damage to their property.
In this paper, we show through simulation studies how active inference (Da Costa et al., 2022; Lanillos et al., 2021) can be combined with a rulebook formalism (Anne et al., 2021; Censi et al., 2019) to develop autonomous AI agents capable of shifting between levels of conflicting norms under environmental uncertainty. Traditional approaches to OCST decision making, such as the Nest Learning Thermostat, use pure Machine Learning approaches, which limits the ability of OCSTs to adapt to novel scenarios or noisy data. In turn, active inference approaches, which are based on Bayesian techniques, allow models to respond confidently to novel scenarios. This is so because they are built out of cause-and-effect relationships and factor into inference the quantification of uncertainty about outcomes and decision. This allows for probabilistic recommendations or decision making that can adapt to novel environments and allows for learning even when there is minimal data, missing data or noisy data.
Although there may be several advantages to using active inference instead of reinforcement learning for OCST agents, the goal of this paper is not to demonstrate such advantages. The aim of this paper is to show how active inference can be used to address some of difficulties an OCST agent may face when presented with conflicts of norms defined by a user. We apply our proposed approach to a minimal use case of OCST behavior that must decide whether or not to warm a room under conflicting norms that occasionally conflict. The first norm is a “price” rule (r1) that states that the OCST shall not use energy to warm up or cool down the house when the price of energy is above a predefined threshold. The second norm is a “need” rule (r2) that states that the OCST shall ensure that the temperature of the house always meets the desired temperature preset by the owner, or temperature threshold. There are few methods of behavioral specification—for autonomous AI systems—that address conflicting norms (Censi et al., 2019). Conflicting norms may include legal norms (Arkin, 2008) (e.g., rules of a traffic code in the case of an autonomous vehicle), as well as implementation limitations (e.g., rules regarding energy consumption and computation limits), preference based, local cultural norms of conduct (e.g., courtesy norms between users of the road) (Thornton et al., 2017), or moral or ethical norms (Bjørgen et al., 2018). The “rulebook” is one of the few formalisms that has been developed to incorporate a diversity of conflicting rules to enable adaptive conduct in autonomous agents (Anne et al., 2021; Censi et al., 2019). The rulebook formalism was initially developed to model normative reasoning in autonomous vehicles. However, nothing prevents applying the rulebook formalism to other sorts of autonomous systems. The rulebook provides formalism for representing the priority among rules and the extent to which a given behavioral outcome will jointly satisfy the different rules encoded in the rulebook. The rulebook determines whether a given outcome should be entertained, given the order of priority over the various rules to be satisfied; an outcome being allowed, for instance, if it satisfies higher level norms despite failing to satisfy lower level norms. We show how active inference can enhance the rulebook formalism by equipping it with context sensitivity.
2 Method
2.1 The simulation scenario
In cold climates, assuming a dynamic pricing scheme, rules r1 (the price rule) and r2 (the need rule) described in the introduction are naturally in conflict depending on the time of the day, or energetic “context”. In the morning, the temperature of the house is lower, and the price of energy is higher, as the population demand on the power grid is higher (Figure 1, context 1). In the afternoon, as the sun warms the house and the environment—and as people leave the house to go to work and demand on appliances reduces—the demand on the power grid falls and prices reduce (Figure 1, context 2). This is so, despite the need for cooling down houses as the afternoon temperature rises. In the afternoon, r1 and r2 are not in conflict. Then, in the evening, as the demand for energy and the need to warm up the house kick back in, r1 and r2 enter in conflict again, as homeowners may want to respect their price threshold while meeting their needs (e.g., warming up the house). This pattern is described in Figure 1.
Figure 1
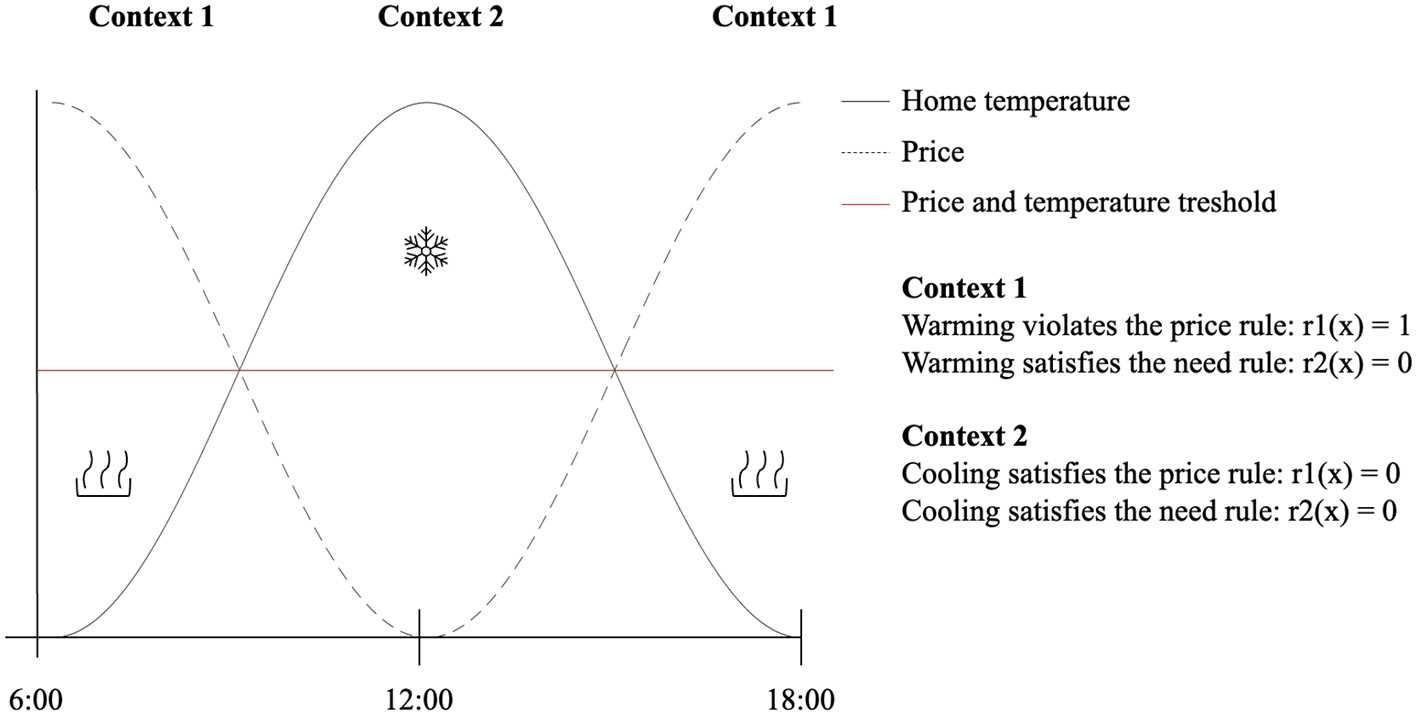
Scenario for the simulation studies. Home temperature and price are anti-correlated, and fluctuate throughout the day. For simplicity, the price and temperature thresholds that underwrite the rules are the same (red line). In context 1, expending energy (e.g., to warm up or cool down) violates the price rule, but satisfies the need rule. In context 2, expending energy satisfies both the need and price rule. Note that this depiction serves as a heuristic to illustrate situations wherein rules may conflict (e.g., context 1), and situations wherein rule may be complementary (e.g., context 2). This simplified depiction does not consider additional patterns, such as space context and occupation. For instance, office buildings tend to be unoccupied in the evening but are busier in the morning. Including such factors would require adjusting the demand curve accordingly. Additionally, here we are only displaying a 12-hour window to illustrate typical peaks in demand that occur during wake time.
Alternatively, occupants may temporarily or permanently bypass these rules, disregarding the established priority order. This approach would prioritize comfort over energy efficiency. In turn, if a user wishes to join a demand response program, they are required to relinquish control of the thermostat setpoint, refrigerator compressor cycles, and other settings, which will be directly adjusted by the power company using Power Line Communication signals during peak demand times. For example, if there are 100 homes in the neighborhood, these will be randomly organized into four groups based on total usage, with 25 homes cycled through every 15 mins during peak demand hour. This method effectively reduces the load on the grid. Automation in this industry operates under a strict “if this, then that” framework, leaving no room for fuzzy logic or ambiguity. The challenge faced by an ideal OCST would be to act as an intermediary solution between relinquishing decisional power and abandoning participation to demand response programs altogether. The job of the OCST in this case is to decide, based on the user's needs and budget, whether to expend energy given where the price and temperature threshold are and where the price and temperature curves are at the time of decision.
At first glance, rulebooks appear to be a good solution to meet such a challenge. An OCST implementing a rulebook could have one of two possible orders of priority: r2 over r1, meaning that the price rule (r1) would be prioritized over the need rule. The consequence of this order would be that in an energy context such as that of the morning or the evening (e.g., contexts 1, Figure 1), when the house temperature is below the temperature threshold set by the owner, and the price of energy above the price threshold set by the owner, the OCST would not be allowed to warm up the house. In turn, in a context such as that of the afternoon (i.e., context 2, Figure 1), the OCST would be allowed to expend energy to bring down the temperature to the threshold as the price of energy is low. An OCST implementing the opposite order of priority r1 over r2 would have the opposite behavior in contexts 1, warming up in the morning and the evening.
Unless a rulebook is restructured, its order of priority will always be respected. This is fine as long as the OCST knows for sure that respecting the order of priority imposed by the rulebook will yield the right decision given the energetic context and associated true environmental temperature (e.g., not warming up in the morning, cooling down in the afternoon, and warming up in the evening). However, sometimes, due to the uncertain nature of the weather, we may want the OCST to override the base case for the order of priority. For instance, when the climate is relatively predictable, adhering to a rulebook might suffice—such as following set thermostat cycles like WAKE (ramp up), AWAY, HOME, and SLEEP (ramp down). However, in cases of extreme climate conditions or homes with specific thermal loads, such as those with many windows causing significant heat gain during the day, it may be desirable to override the base order of operations. For example, warming up in the morning or cooling earlier in the afternoon could help prevent thermal stress on the house infrastructure. While the rulebook formalism allows for predefined solutions—such as adjusting priorities, collapsing rules with similar importance, or introducing new rules—it lacks a mechanism to autonomously and dynamically adapt or “navigate” these rules in real-time; the only solution being the restructuring of the rulebook, which is also a problem since restructuring or learning a new rulebook creates a lag period during which temperature control will be suboptimal. In other words, rulebooks preclude adaptability or context sensitivity.
This reflects the fact that rulebooks are not adaptable and flexible enough to handle uncertainty in novel scenarios. Addressing such dynamic scenarios effectively requires integrating causal factors into a generative model that learns over time. For instance, instead of relying on static sensing (e.g., using an Ecobee thermostat in areas of high thermal load), a Bayesian approach could adapt to varying conditions, optimizing heating and cooling cycles across the entire home to reduce inefficiencies and waste. Accordingly, the alternative that we propose in this paper is to consider OCST as solving an inference problem; namely, inferring the context and deploying the most likely policy that satisfies prior preferences or constraints implicit in multiple rules. Specifically, we use the Bayesian approach of active inference to trigger an override of the base order of priority, when the environmental or climatic context becomes uncertain, to ensure operation within sustainable bounds given known regulations. Our approach allows the OCST to respect the base order of priority in times of certainty, and to autonomously shift to the override of that order of priority in time of uncertainty. Our simulation study shows how this approach remains robust despite fluctuations in energetic contexts.
2.2 The rulebook formalism
The rulebook 〈R, ≤ 〉 is a tuple, or set of hierarchically organized “rules” r that each define the extent to which a certain outcome violates or satisfies a rule. A rulebook can also be a set of rules with a (partial) order, where “partial” means that not all the rules are necessarily comparable to each other. In this case, the rulebook is not a tuple. R is a finite set of rules, and ≤ is a priority order for the rules. The rulebook allows one to formally express the relation between conflicting or equivalent rules related in order of priorities (e.g., prefer satisfying rule 1 over rule 2). Outcomes “o” are realized in the environment or world. The rulebook defines a set of preference relations between outcomes called “realization”, where each outcome “o” corresponds to an element on the realization set. Realization could also be modeled as combined states of the world; for instance, o = (P,T,s) where p could be the current price, T the temperature and s the current time stamp. It could also be a world trajectory {i.e. a function o → [P(o), T(o)]} tracking temperature and price over time. For the simple OCST agent considered in this paper, an element oi of the realization may be “use energy to increase or decrease the temperature”. Rules “r” constitute scoring functions over the elements of the realization set, such that for each element of o, there will be a rule r(o). The output r(o) = 0 means that the outcome “o” on the realization set respects the rule r, and the output r(o) > 0 means that the outcome violates the rule. This means the rules effectively encode cost functions of outcomes. Of course, one can use any domain in which an ordering exists, and is not limited to 0 and 1, that may allow for more fine-grained evaluations of the extent to which a rule is violated. In our simple use case, the function r(o) for discrete outcomes is expressed as:
The cost function r(o) computes the degree of violation of its argument (e.g., 0 or 1 in Equation 1), which is the outcome of the realization set o. This means that if r(o1) < r(o2), the outcome o2 on the realization set violates r more than o1. Rules in a rulebook can be expressed as a directed graph that reflects the hierarchy of rules, or preordering ≤ . In such a graph, nodes represent the rules, and the edges represent the ordering, such that r1 > r2 means that r2 is ranked higher than r1. If r2 has priority over r1. If an outcome x satisfies r2 but not r1, then the outcome “o” will be allowed. If the outcome violates r2 [i.e., r2(o) = 1], despite satisfying r1 [e.g., r1(o) = 0], then the outcome “o” will be disallowed. If one wants to interchange those orders of priority (e.g., flipping the edge), then one has to restructure the rulebook, which could be computationally expensive and likely to introduce lags and bugs.
2.3 Active inference for rulebooks
The active inference approach proposed in this paper leverages the rulebook formalism to represent the order of priority between rules, but adds to the rulebook the computational capacity to navigate, or move through the rule book, by overriding not only norms, such as allowed by the order of priority of the rulebook (e.g., the override of r1 by r2), but by overriding the base case of priorities itself (e.g., acting according to r2 > r1 instead of r1 > r2). Active inference, understood broadly, is a Bayesian decision-making scheme that, upon receipt of an input, (1) infers the cause of the input using information about the likelihood of that input under each possible cause, and (2) predicts what the future input will be if the system acts in such a way to change the input generating cause. Active inference enables decision-making under uncertainty by considering “preferences” that a system may have for certain outcomes, while acting to disclose the causal structure of the world—learning this structure along the way. The upshot of this is a rich decision-making scheme with information seeking (epistemic) and constraint satisfying (utilitarian) aspects. These dual aspects are formally equivalent to Bayes optimality under Bayesian decision theory (minimizing expected cost) and optimal design (maximizing expected information gain), respectively (Berger, 2011; Lindley, 1956; Parr et al., 2022).
We use a discrete state space generative model based on active inference (Parr et al., 2022). This model implements a Partially Observable Markov Decision Process (POMDP), such as commonly used in the active inference literature (for a detailed description of the generative model and update equations, see Friston et al., 2017; Parr et al., 2019). Active inference models are typically used to model agentic behavior: e.g., navigation and planning (Kaplan and Friston, 2018), but can be used to model any sequence of events of a controlled process (e.g., series of human decisions). Agents in active inference are generative models represented as a joint probability of (latent or hidden) states denoted as st = (s1,s2, … sT), observations denoted as ot = (o1,o2, … oT), and policies that determine the transition among states. Update equations are then applied to these models to infer the current state of affairs, given the observations at hand, and to forecast or predict the next states and observations given the possible actions available to the: the action selected being that which is most likely to generate the most preferred observation. Technically, action or policy selection minimizes expected free energy, which can be decomposed into expected information gain and expected cost, where expected cost corresponds to the rule-based violations above. For a detailed description of the update equations, see (Smith et al., 2022).
For an illustration of the basic approach, we use the T-maze paradigm, which is a specific implementation of active inference used to simulate decision making under uncertainty for multi-armed bandit tasks (Pezzulo et al., 2015). The T-maze paradigm illustrates the unique capabilities of active inference by implementing—in the process of decision making—an adjudication component based on the resolution of an explore-exploit trade-off based upon the relative precision of expected information gain and expected cost, respectively. The implicit adjudication resolves as the agent learns the structure of the T-maze environment. After resolving uncertainty about the environment, the expected information gain receipts, leaving expected cost has the principal determinant of choice behavior (for the complete MATLAB specification of the T-maze used in this paper, see Smith et al., 2022).
We use the A,B,C,D notation characteristic of active inference, where A denotes a likelihood mapping between the states of the environment and observable consequences. The remaining variables B,C,D parameterize prior beliefs about environmental dynamics and preferred outcomes (Da Costa et al., 2020). In the T-maze, the agent makes a decision that minimizes expected cost (specified as prior constraints over the possible outcomes of its decision and implemented in the C parameters of the generative model (Co = -ln P(o)). Note that when the prior constraints are very precise, the preferred outcome o* renders the cost = 0, as in the case of r(o*) = 0.
Depending on the context of the trial (encoded by the parameters Ds = P(s0) of the generative model, the preferred outcome will be on either the left arm of the T-maze or the right arm of the T-maze (i.e., left arm is better: D = [1 0]; right arm is better: D = [0 1]). This corresponds to the (unknown) position of the rewarding outcome, under the generative process, or true environmental structure.
If the agent makes the right decision right away, it receives a reward. Alternatively, the agent can search for information; i.e., explore by seeking information that indicates the context. However, if the agent makes the decision to go to the informative cue—at the bottom arm of the maze—and only then makes the right decision, its reward is halved, because it is only allowed two moves and has to commit to the upper arm it chooses. This is the explore-exploit trade-off: go right away and find your reward 50% of the time, or use the first move to resolve uncertainty about where the reward is and then secure it on the second trial. Active inference dissolves the explore-exploit dilemma by minimizing expected free energy, which includes expected information gain. This means the Bayes optimal policy is to seek out information that resolves uncertainty about the context and then exploit the information gained by securing preferred outcomes.
The agent has parametric beliefs “d” over the context of the trial. The agent also has beliefs “a” about the likelihood of where the desired outcome may be, and which track the true probability A = (P(o | s)) of where the outcome is situated. The (Dirichlet) parameters a and d can be learned over time, which allows the agent to make the right decision even when starting with uncertainty about context and outcome contingencies. Finally, the agent has beliefs about the ways it can navigate the T-maze, or about the probability of transitioning between states when engaging an action u. The transition probabilities are encoded in B = P(st|st − 1,u), a prior on dynamics under the generative model.
The behavioral manifestation of the explore-exploit trade-off, if the agent is allowed to learn the structure of the environment, is that at the beginning of a series of trials, the agent will tend to acquire information about the context, before retrieving its reward. If the context is predictable (i.e., the reward is always on the right), the agent will learn that the context is invariant. At some point, the expected information gain will fall below the expected cost, and the agent will switch from exploration (i.e., responding to epistemic affordance) to exploitation (i.e., responding to pragmatic constraints). The point at which this occurs depends upon the precision of prior constraints, relative to expected information gain. In other words, if there are certain outcomes that must be avoided at all costs, these outcomes will be avoided, even if they could be informative. Note that prior constraints (like rules) are specified over all possible outcome modalities (i.e., the different kinds of things the agent can measure or observe). Some kinds of outcomes may have imprecise or forgiving constraints, while others may be specified very precisely and will therefore be prioritized over the remaining constraints.
Note that the agent could also be allowed to learn its own priors C with respect to preferred outcomes (Sajid et al., 2022), thereby updating the agent's predisposition toward constraint satisfaction. Here, we do not allow for constraint learning. It is the expression of the explore-exploit tradeoff that we leverage in our simulation, the context of the T-maze being energetic context for the decision of the OCST, the arms of the T-maze being the decision of expending—or not—energy to warm up or cool down the house, and the prior constraints on outcomes specified by the rules at hand (see Figure 2). In the following simulations, the option two visit the lower arm—to sample the “cue” and resolve uncertainty about the energetic context—entails a suspension of overt action (i.e., expending energy) to gather information about the current context.
Figure 2
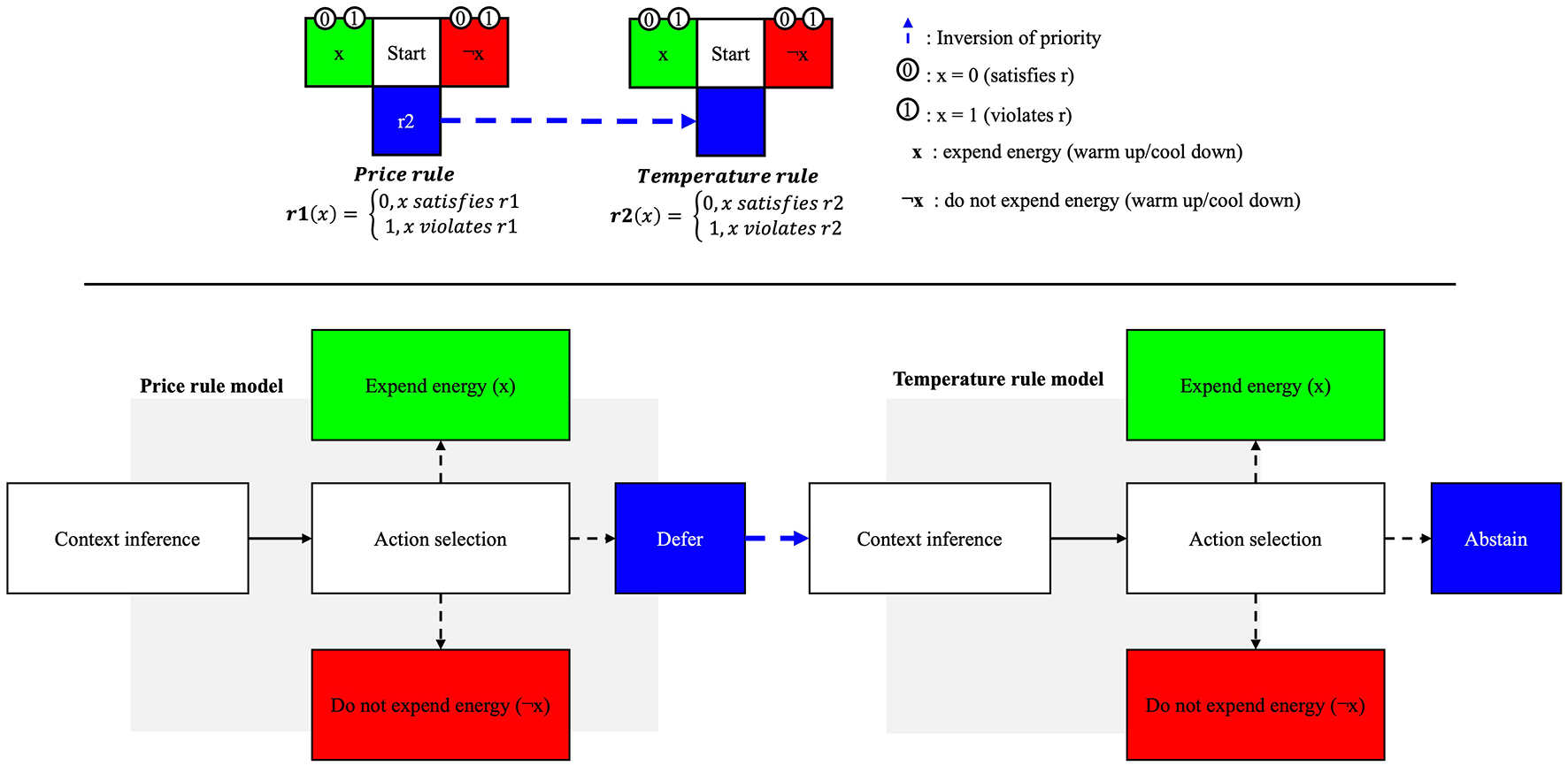
Top row: Relation between the two T-mazes. The bottom T-maze implements r1 (price rule) by being parameterized to avoid expending energy in context 1. The top T-maze implements r2 (need rule) by being parameterized to expend energy in context 1. Bottom row: Flowchart of the interaction between the two T-mazes. From left to right, the first T-maze implementing the price infers the energetic context and decides (action selection) whether it should expend energy or not, or whether it should defer the decision to the next T-maze implementing the temperature rule. The second T-maze decides to either expend energy, refrain from expending energy, or to abstain from deciding altogether.
2.4 Simulation setup
Our simulations implement the rulebook formalism using the T-maze paradigm by allowing the agent to reverse the base priority when unsure about action selection. This involves using two T-maze agents (or one agent with two states of mind), each parameterized to comply with the two rules r1 (price rule) or r2 (temperature rule). Crucially, one of the T-mazes “defers” to the other when opting for the “cue” option (lower arm) instead of deciding to expend energy (left arm) or not (right arm). In our simulation, we assume that the first rule of the rulebook, r1, has priority over the second rule, r2. The rule r1 is the “price” rule which states that o can satisfy (0) or violate (1) r1 depending on whether the current price of energy is above or below a price threshold set by the homeowner. The second rule, r2, is the temperature rule, which states that o can satisfy (0) or violate (1) r2 depending on whether the temperature of the house is above or below a temperature threshold set by the homeowner (cf. Figure 1).
In more detail, we implemented the rulebook formalism under the T-maze paradigm by adapting the semantics of the rulebook to the semantic of the T-maze. Instead of representing the “left” and “right” positions, the arms of the T-mazes represent states sanctioned under r1 and r2, namely, expending energy (left arm) or not (right arm). The outcomes associated with these states are the elements on the domain of the rulebook, which here correspond to “0” or “1”. The likelihoods that the energy expenditure states afford outcomes scoring “1” or “0” are inverted within each T-maze, reflecting the constraints due to price and temperature. As we will see below, depending on the conditions of our simulation, there may be no uncertainty in the likelihoods of observing 1 or 0 in each state or they can be some ambiguity or uncertainty.
Because the agents prefer “0” (i.e., to satisfy r) over “1” (i.e., to violate r), the agent in each T-maze will have an incentive to select the action “u” that will bring it to the state that satisfies the rule implemented by the agent. Now, because the two agents implement rules that contradict one another, the “satisfying” state in each T-maze relative to context must be inverted. This is the novelty of our approach. For the agent implementing r1 (price rule), not to expend energy is better under context 1, whereas for the agent implementing r2, to expend energy is better under context 1. In context 2, expending energy is satisfying for both agents. The context under which decisions should be made is encoded in prior beliefs about initial states D, which are updated on the basis of previous trials. As the context changes, with the fluctuations in the weather, the agent learns the probability of each context through accumulating Dirichlet parameters in d.
Depending on the order of priority in the rulebook, this setup allows deferring to a lower priority rule, when uncertain about what to do concerning the high priority rule (see Figure 3). In other words, by inducing this setup in endows the implementation of a rulebook with a context sensitivity that accommodates the uncertainty about context. In the particular example considered in this paper, context sensitivity is operationalized through a conditional statement (if, then) that triggers inference by the r2 T-maze if the final decision in the r1 T-maze is to abstain from moving from the initial state.1 This reflects the ability of the OCST to defer to other rules in the rulebook when uncertain about the lawfulness of a satisfying course of action under the rule that has priority. The corollary of this is that the OCST (i) will act according to its order of priority only when certain about its decision, which in our simulation is a mixture of certainty about context and outcome probability, and (ii) will reverse the priority order when uncertain about the overall situation by deferring to the T-maze implementing r2.
Figure 3
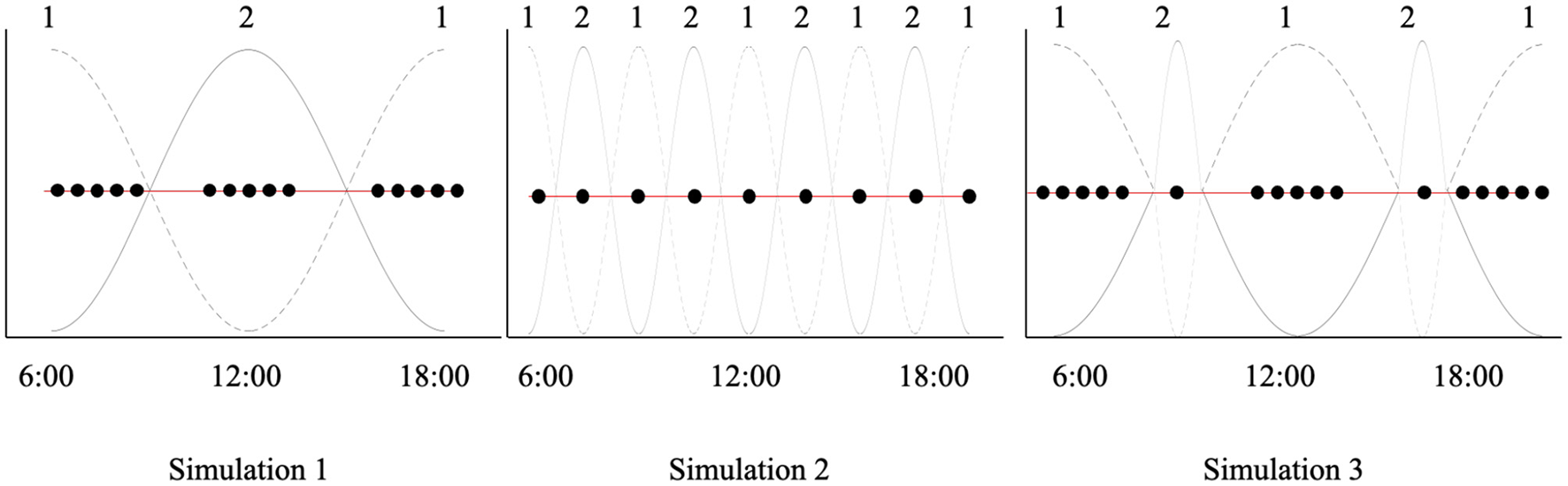
Context fluctuation in simulations 1, 2 and 3.
The consequence of this—as shown in the result section—is that, when there is no uncertainty about the probability of outcomes (i.e., A), and only uncertainty about the energetic context—which fluctuates over trials—the OCST will learn the context and rarely defer to r2. In turn, when there is uncertainty about the likelihood of outcomes, as well as uncertainty in beliefs about the energetic context, the agent will learn the probability of outcomes and the energetic context, and defer to r2, thereby inverting the priority order. Narratively, this means “respecting the price rule, as per the order of priority when the climate makes the OCST confident about its decisions and inverting the order of priority to respect the temperature rule when the climate renders the OCST uncertain of its decision”.
We ran three simulations under two different conditions (6 simulations in total). Each simulation was over 50 trials. In each trial, the OCST was presented with one of the two energetic contexts detailed in Figure 1. Under each condition, each of the three simulations takes one of the 3 possible patterns of contextual volatility (see Table 1, Figure 4). The first pattern alternates over the 50 trials between context 1, which presents 5 times, and context 2, which presents 5 times. The second pattern alternates between context 1 and 2 on each trial. The third pattern presents context 1 five times and context 1 one time, and context 1 five times and context 1 one time repeatedly, over 50 trials. The goal of such fluctuations in context was to challenge the model, which has to learn the fluctuation in context to settle on the right decisions given the context at hand. Learning was implemented by passing the Dirichlet parameters of the likelihood a and initial states d from the previous trial to the next trial, enabling the agents to accumulate evidence for the relative probability of each context in the different experimental conditions.
Table 1
| Simulation 1 | Simulation 2 | Simulation 3 | |
|---|---|---|---|
| Condition 1 | Pattern: 1 1 1 1 1 2 2 2 2 2 … | Pattern: 1 2 … | Pattern: 1 1 1 1 1 2 … |
| GP certainty: 100% | GP certainty: 100% | GP certainty: 100% | |
| Condition 2 | Pattern: 1 1 1 1 1 2 2 2 2 2 … | Pattern: 1 2 … | Pattern: 1 1 1 1 1 2 … |
| GP certainty: 91.5% | GP certainty: 91.5% | GP certainty: 91.5% |
Conditions.
Figure 4
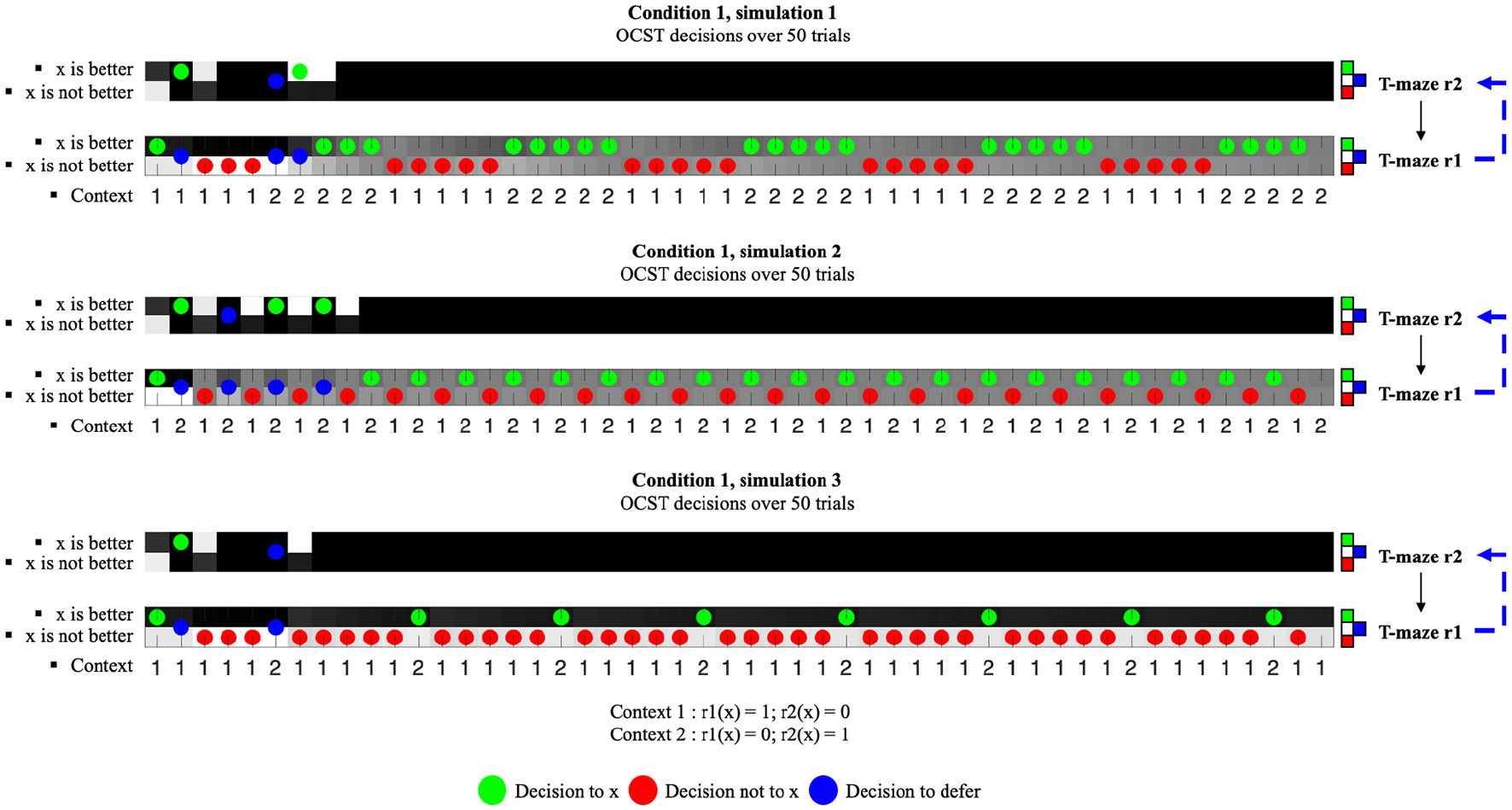
OCST robustness in the absence of environmental uncertainty.
Narratively, the simulations amount to a situation where, in the same 12 h span, from 6am to 6pm, the energetic context relative reflecting the temperature and price conditions would fluctuate with regularity (simulation 1), fluctuate with regularity, but more quickly (simulation 2), and finally would fluctuate with less regularity with varied pace. Conditions 1 and 2 correspond to levels of certainty in the generative process producing the outcomes used by the OCST to infer the right action.
The outcomes of interest in our simulation—over which there can be uncertainty—are whether an arm of the T-maze representing performing the behavior (u) or not performing the behavior (¬u) will satisfy (0) or violate (1) the rules at hand (r1 and r2).
While our study does not include a sensitivity analysis—to test how active inference handles spikes in energy and price, extreme weather, or user overrides based on real world data—it does include simulation scenarios; wherein the price and weather fluctuate in ways that makes self-correction increasingly difficult. This is reflected in Figure 5, in the scenario that is the hardest to predict (scenario 3). When allowing for uncertainty in environmental inputs, the OCST defers to the priority rule, thereby defaulting to a “better safe than sorry” strategy when conditions change unexpectedly.
Figure 5
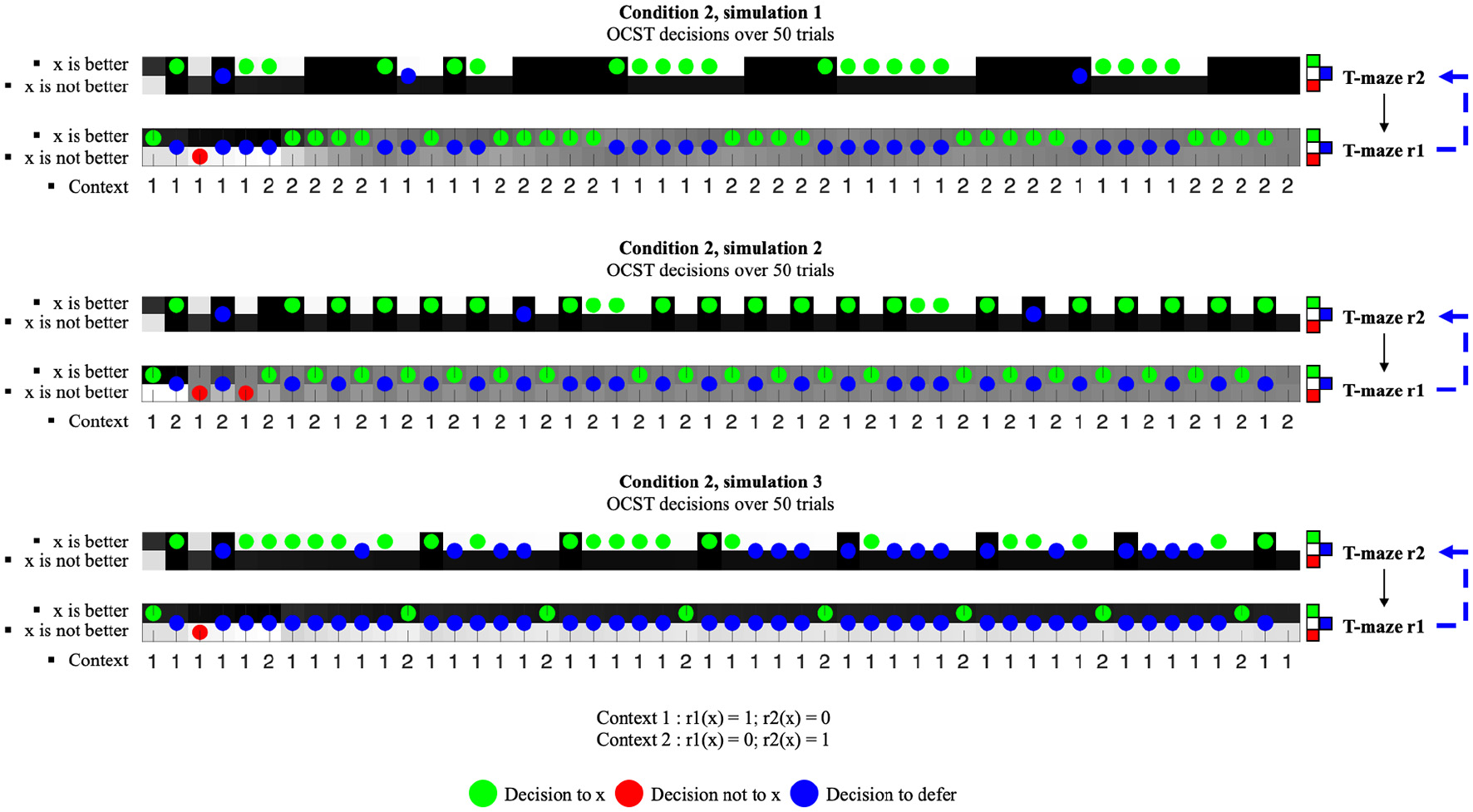
OCST robustness under environmental uncertainty.
In condition 1, there is no additional uncertainty over which of the true outcomes will be generated by the generative process. This facilitates learning. Under condition 2, we allow some uncertainty in the generative process of the true outcomes. In our scenario, this represents an environment with uncertain weather conditions. This means that our simulated OCST faces a dual challenge. First, it must learn the pattern of energetic context to generate the right behavior. Second, it must learn whether its action (i.e., expending energy, u, or not expending to warming or cooling, ¬u) will violate or satisfy the rule, which is made more difficult under condition 2 where the OCST is faced with a volatile and unpredictable scenario (i.e., uncertainty in the generative process). Note that active inference, in the context of this study, could have been used to learn and adjust the OCST's behavior to the user's preferences regarding the conflicting rules. This could be achieved (e.g., through user control) by learning the prior preferences of the model to reflect the user preference over the base order of priorities (e.g., between r1 and r2).
3 Results
The 3 simulations under condition 1 show how our model for OCST remains robust despite irregularities, or fluctuations in context (Table 2). Under condition 1 (Figure 4), our OCST is supposed to function just like a normal rulebook-based OCST, giving priority to the price rule (r1). Under context 1, the OCST learns to refuse to warm up, and learns to cool down in context 2, irrespective of the patterns of context fluctuation. Figures 4, 5 show the decisions over the 50 trials, under each condition and simulation. In each figure, the green dots represent a decision to expend energy, which is allowed when r(o) = 0. The red dots represent the opposite decision. This depends on the context, which is represented as “1” or “2” at the bottom of the plot for each simulation. The top series in each plot represents the decision of the T-maze complying to the temperature rule (r2). The bottom series represents the decision of the T-maze complying to the price rule (r1). Blue dots indicate that the decision was to defer to the r2 T-maze when the blue dot is on the bottom series. Blue dots indicate that the trial ends on an “abstention” to act when the blue dot is on the top series and the bottom series. Each series is separated into 50 columns and 2 rows. The top row represents the beliefs about the context (i.e., o is better, or o is not better), which—depending on the T-maze at hand—will match the true context “1” or the true context “2”.
Table 2
| Simulation 1 | Simulation 2 | Simulation 3 | ||||
|---|---|---|---|---|---|---|
| Condition 1 | Condition 2 | Condition 1 | Condition 2 | Condition 1 | Condition 2 | |
| Hit | 47 (94%) | 44(88%) | 47 (94%) | 45 (90%) | 47 (94%) | 30 (60%) |
| r1(x) = 0 | 45 | 23 | 43 | 22 | 46 | 8 |
| r2(x) = 0 | 2 | 21 | 3 | 23 | 1 | 22 |
| Miss r2(x) = 1 | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) |
| Miss r1(x) = 1 | 1 (2%) | 2 (4%) | 1 (2%) | 1 (2%) | 1 (2%) | 1 (2%) |
| Deferring (a blue dot at the bottom) | 3 (6%) | 24 (48%) | 4 (8%) | 26 (52%) | 2 (4%) | 40 (80%) |
| Abstention (two blue dots) | 1 (2%) | 3 (6%) | 1 (2%) | 3 (6%) | 1 (2%) | 18 (16%) |
Results under conditions 1 and 2 showing the number of decision outcomes that were lawful given the true context at hand (Hit), the number of unlawful decisions given the true context at hand (Miss), the number of times the model implementing rule 1 deferred to the model implementing rule 2 (deferring), and the number of times the rule 1 model deferred and the rule 2 model did not make a decision to either use energy or not (abstentions).
For instance, for the bottom T-maze representing the price rule (r1), it is better not to warm up when in context 1, whereas for the top T-maze representing the temperature rule (r2), it is better to warm up in context 1. Note that the background at each column presents a black-white gradient (white = 1, black = 0). This gradient corresponds to the beliefs of the OCST concerning the context [P(s0)]. The numbers 1 and 2 at the bottom of the plot correspond to the true context. The OCST's beliefs about the context update to track the pattern of true fluctuations in the energetic context. For instance, in condition 1 simulation 1, we can see that with a regular pattern of change in energetic context that gives the agent the time to adjust, the model gradually adjust its beliefs about the current context; the gradient starting with a sharp black and white distinction, and smoothly transitioning to alternating shades of gray tracking the true change in energetic context.
The 3 simulations under condition 2 show how our model also allows for robust OCST response, though, by overriding the order of priority of the price rule (r1) over the need rule (r2), without having to change the order of priority itself. This represents the fact that under uncertain climatic conditions, in condition 2, our OCST prefers to maintain the house temperature at the desired level, over respecting the price rule.
To foreground the inversion of priority order—that emerges under active inference—we measured the number of correct decisions, or “hits” (i.e., when o returned 0, given the true context at hand), the number of incorrect decisions, or “miss” (i.e., when o returned 1, given the true context at hand), the number of time the T-maze representing r1 deferred to the T-maze representing r2, and the number of abstentions, or number of times both T-mazes went to the “cue” position. The noticeable results—when comparing conditions 1 and 2—are the hit results and the deferring results. The percentages of hits slightly decreased under condition 2, with a significant decrease only under simulation 3, yet remaining well above chance. This means that the behavior of the OCST remained robust even under environmental uncertainty. The main difference is at the level of the number of times the OCST deferred to r2, or inverted the order of priority. As expected, when facing environmental uncertainty, the OCST defers to prioritize the temperature rule (r2).
4 Discussion
We have shown that active inference facilitates intelligent energy management, optimizing resource expenditure, while considering various norms reflecting personal, social and economic factors. The holistic nature of this approach makes sustainability not just a byproduct but a core consideration of OCST decisions. Although the approach presented in this paper focused on the issue of AI and sustainability, with the case of Occupant Control Smart Thermostat, our approach could easily generalize to any complex case of “normative” autonomous decision making. Normative decision making is complex when having to make decisions based on norms that conflict, and whose conflict is dependent on the environmental context. More generally, our approach could be viewed as an approach to rule-following allowing us to embed the capability for flexible adaptive normative compliance into AI systems.
Our proposed approach to rule-following introduces a novel way to embed the capability for adaptive legal compliance into AI systems, balancing adherence to laws with necessary context sensitivity and flexibility. We used active inference to extend the Rule-book approach, such that AI can dynamically navigate competing norms in real time, much like we do. This capacity for norm-shifting is essential because the world is not static, nor is it simple; especially under volatile or uncertain conditions, AI agents need to make contextually relevant decisions. A context sensitive approach contrasts with more rigid rule-based systems that lack adaptability, aligning instead with human-like decision-making, where trade-offs and situational awareness underwrite our appraisal of appropriate choices. This ensures that AI agents are rule-compliant but can also reason about the context and implications of their choices, making them versatile partners in legal and ethical domains.
One could argue that incorporating active inference into AI design paves the way for a robust governance framework suited to future AI advancements. Current AI governance strategies often focus on ex-ante obligations that regulate AI development and deployment before it reaches the market. However, integrating active inference introduces an ongoing, self-regulatory mechanism that complements ex-post controls and fosters continuous compliance with ethical and legal norms. This shift moves toward “agent governance,” where AI systems autonomously manage their decision-making processes, while ensuring that these processes remain explainable and transparent. The generative models underpinning these systems can elucidate how decisions are made and adjusted over time, enhancing trust and facilitating collaborative legal justifications. This transparency may in time foster a cooperative relationship between human decision-makers and AI, supporting a shared understanding and alignment.
Active inference inherently supports explainability. It plays a crucial role in AI deployment within regulated spaces. Because we model decision-making through Bayesian belief updating, the systems are transparently—and can report how they navigate and comply with various regulatory requirements, and most importantly why (in terms of the epistemic and utilitarian motivations). This feature means that AI agents reason through legal frameworks and norms explicitly. We thus offer a clear audit trail for their choices. Consequently, in principle, such systems adhere to established rules and can justify their behavior in a manner that aligns with human expectations for accountability. This capacity to operate with embedded legal justifications opens pathways for more seamless human-AI collaboration, where AI is an active, explainable agent in the decision-making processes.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
AC: Writing – original draft, Writing – review & editing. MA: Writing – original draft, Writing – review & editing. MP: Writing – original draft, Writing – review & editing. HT: Writing – original draft, Writing – review & editing. KF: Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by a European Research Council Grant (XSCAPE) ERC-2020-SyG 951631. KF was supported by funding from the Wellcome Trust (Ref: 226793/Z/22/Z).
Conflict of interest
MA, MP, HT are employees of the company VERSES AI Inc., KF is an independent contractor providing services to VERSES AI Inc., and AC is the president of the company Axel Constant Inc. providing services to the company VERSES AI Inc.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1.^ Note that because we allowed decisions over 2-time steps, and because we considered the abstention as resulting from the decision over the end state, some of the abstentions result from deciding on the first decision step but deciding not to decide on the second timestep by returning to the starting location. This ensures all the decisions are made by the T-mazes in full confidence.
References
1
Addimulam S. (2024). Digitalization and AI for sustainable development: expectations from the Sustainable Action Conference 2024 (SAC 2.0). Digital. Sustainab. Rev.4, 1–15.
2
Albarracin M. Hipolito I. Raffa M. Kinghorn P. (2024a). Modeling sustainable resource management using active inference. arXiv [preprint] arXiv:2406.07593. 10.1007/978-3-031-77138-5_16
3
Albarracin M. Ramstead M. Pitliya R. J. Hipolito I. Da Costa L. Raffa M. et al . (2024b). Sustainability under active inference. Systems12:163. 10.3390/systems12050163
4
Anne C. Artur B. Scott P. Tebbens R. D. (2021). “Safety of the intended driving behavior using Rulebooks,” in arXiv [preprint] arXiv:2105.04472. 10.1109/IV47402.2020.9304588
5
Arkin R. C. (2008). “Governing lethal behavior,” in Proceedings of the 3rd ACM/IEEE International Conference on Human Robot Interaction. HRI '08: International Conference on Human Robot Interaction (Amsterdam: IEEE).
6
Berger J. O. (2011). Statistical Decision Theory and Bayesian Analysis. New York: Springer.
7
Berthelot A. Caron E. Jay M. Lefèvre L. (2024). Estimating the environmental impact of Generative-AI services using an LCA-based methodology. Procedia CIRP, 122, 707–712. 10.1016/j.procir.2024.01.098
8
Bjørgen E. P. Madsen S. Bjørknes T. S. Heimsæter F. V. Håvik R. Linderud M. et al . (2018). “Cake, Death, and Trolleys: Dilemmas as benchmarks of ethical decision-making,” in Proceedings of the 2018 AAAI/ACM Conference on AI, Ethics, and Society. AIES '18: AAAI/ACM Conference on AI, Ethics, and Society (New Orleans LA: ACM).
9
Censi A. Slutsky K. Wongpiromsarn T. Yershov D. Pendleton S. Fu J. et al . (2019). “Liability, ethics, and culture-aware behavior specification using rulebooks,” in 2019 International Conference on Robotics and Automation (ICRA) (Montreal, QC: ICAR).
10
Challoumis C. (2024). “Building a sustainable economy-how AI can optimize resource allocation,” in XVI International Scientific Conference (Philadelphia, PA), 190–224.
11
Da Costa L. Lanillos P. Sajid N. Friston K. Khan S. (2022). How active inference could help revolutionise robotics. Entropy24:e2403036110.3390/e24030361
12
Da Costa L. Parr T. Sajid N. Veselic S. Neacsu V. Friston K. (2020). Active inference on discrete state-spaces: a synthesis. J. Mathem. Psychol.99:102447. 10.1016/j.jmp.2020.102447
13
Friston K. J. Parr T. de Vries B. (2017). The graphical brain: belief propagation and active inference. Netw. Neurosci.1, 381–414. 10.1162/NETN_a_00018
14
Kaplan R. Friston K. J. (2018). Planning and navigation as active inference. Biol. Cybernet. 112, 323–343. 10.1007/s00422-018-0753-2
15
Kristian A. Sumarsan Goh T. Ramadan A. Erica A. Visiana Sihotang S. (2024). Application of AI in optimizing energy and resource management: effectiveness of Deep Learning models. Int. Trans. Artif. Intellig.2, 99–105. 10.33050/italic.v2i2.530
16
Lanillos P. Meo C. Pezzato C. Meera A. A. Baioumy M. Ohata W. et al . (2021). Active inference in robotics and artificial agents: survey and challenges. arXiv [preprint] arXiv:2112.01871. 10.48550/arXiv.2112.01871
17
Lindley D.V. (1956). On a measure of the information provided by an experiment. Ann. Mathem. Statist.27, 986–1005. 10.1214/aoms/1177728069
18
Luccioni S. Jernite Y. Strubell E. (2024). “Power hungry processing: Watts driving the cost of AI deployment,” in The 2024 ACM Conference on Fairness, Accountability, and Transparency (Rio de Janeiro: IEEE).
19
Parr T. Markovic D. Kiebel S. J. Friston K. J. (2019). Neuronal message passing using Mean-field, Bethe, and Marginal approximations. Scientific Rep.9:1889. 10.1038/s41598-018-38246-3
20
Parr T. Pezzulo G. Friston K. J. (2022). Active Inference: The Free Energy Principle in Mind, Brain, and Behavior. Cambridge, MA: MIT Press.
21
Pezzulo G. Rigoli F. Friston K. (2015). Active Inference, homeostatic regulation and adaptive behavioural control. Prog. Neurobiol.134, 17–35. 10.1016/j.pneurobio.2015.09.001
22
Sajid N. Tigas P. Friston K. (2022). Active inference, preference learning and adaptive behaviour. IOP Conf. Series. Mater. Sci. Eng. 1261(1), 012020. 10.1088/1757-899X/1261/1/012020
23
Smith R. Friston K. J. Whyte C. J. (2022). A step-by-step tutorial on active inference and its application to empirical data. J. Mathem. Psychol. 107:102632. 10.1016/j.jmp.2021.102632
24
Thornton S. M. Pan S. Erlien S. M. Gerdes J. C. (2017). Incorporating ethical considerations into automated vehicle control. IEEE Trans. Intellig. Transport. Syst.18, 1429–1439. 10.1109/TITS.2016.2609339
Summary
Keywords
artificial intelligence, environmental sustainability, active inference, Occupant Controlled Smart Thermostat, internet of things
Citation
Constant A, Albarracin M, Perin M, Thiruvengada H and Friston KJ (2025) Agentic rulebooks using active inference: an artificial intelligence application for environmental sustainability. Front. Sustain. Cities 7:1571613. doi: 10.3389/frsc.2025.1571613
Received
05 February 2025
Accepted
14 April 2025
Published
09 May 2025
Volume
7 - 2025
Edited by
Abuelnuor Abuelnuor, Al Baha University, Saudi Arabia
Reviewed by
Najeem Olawale Adelakun, Federal College of Education Iwo, Nigeria
Ahmed M. Hanafi, October 6 University, Egypt
Updates
Copyright
© 2025 Constant, Albarracin, Perin, Thiruvengada and Friston.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Axel Constant axel.constant.pruvost@gmail.comKarl J. Friston k.friston@ucl.ac.uk
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.