On macrohedging problem in semimartingale markets

1. Introduction

Traditional hedging requires that one hedges individual assets comprising the portfolio. On the other hand, macrohedging is about reducing several underlying risk factors, such as, volatility of interest rate, volatility of exchange rates and variability of a portfolio of assets as a whole. In a macrohedge one must carry on an investment policy to maximize returns, and a hedge policy that reduces the risk of the entire portfolio, a balance sheet or a financial entity with hedge instruments, such as, futures and option contracts.

Examples of macrohedge strategies are plenty in practice, we will mention a few here. Consider an index fund manager who wants to reduce the risk of a probable future down turn in the price of an index fund. The fund manager can take a short position in index futures to lock in the value of the index fund and hedge the potential risk of any downfall [1]. Interest rate portfolio managers invest in fixed income assets that follow rates of credible global debt, for example, US treasury bills, European goverment bonds, developed or emerging nation government bonds. Fixed income securities are traded over-the-counter or in derivatives' markets dominated by banks and institutional funds. A fixed income macrohedge strategies include, an outright directional trades of government debt or relative value trading, in which one trades one debt instrument relative to another [2]. Global investment funds are wider in scope than indices. They focuses on investing in instruments whose price variation are based on changes in economic policies and flow of capital around the globe. Global funds macrohedge strategies accounts primarily for market risks, e.g., credit risk and liquidity risks, to drive trading decisions [2] and ignore other local and minor risk factors. Global funds hedge against currency prices fluctuations, interest rates changes and global events, such as, a possible break down of the Euro a collapse of the Chinese banking system, escalation of the conflict in Ukraine, hurricanes etc. Moreover, global funds focus on indices based hedge instruments to hedge their positions. Each scenario involves different co-movements of asset classes and must be dealt with in the context of macrohedging [3].

Another common examples of macrohedges are from the commodities markets. Suppose an airline company wants to avoid the variation in the price of jet fuel for which futures or option contracts may not exist or with enough liquidity and time horizons. By buying futures in another correlated assets such as oil and natural gas the company can offset the risk of the price of jet fuel fluctuations [4]. But note that, even though jet fuel prices are correlated with oil and gas, the different properties of the underlying and a possible maturity dates mismatches makes it impossible to hedge all the risk associated with jet fuel price variability. Another example of hedging in the commodities market, specially for commodities such as oil and gas, is that of commodities exporters. Global commodities exporters can insure against the risk in exported income by accumulating foreign assets in stabilization funds, or by hedging with derivatives [5].

In insurance market, insurance companies are considering more of a macro view to hedge their risks [6]. There are many risks inherent to the portfolio of an insurer, not all of it are market risks. Some of these risk factors offset one another. To hedge each instrument independently is redundant and costly. Therefore, a macrohedge strategy is used to hedge leftover risk. The fact that some risk factors in an insurer portfolio offset each other is not just true for insurance portfolios, it is true for all diversified financial portfolios. Hence, macrohedging is in principle the best option for hedging the risks in large financial portfolios.

From the examples above one realizes the benefits macrohedging. First, the risk factors of the entire portfolio is less than the absolute sum of risk factors of assets comprising the portfolio if they were to be taken independently. This stems from the fact that anticorrelated assets in a portfolio offset each other. Furthermore, hedging of the entire portfolio can be less costly than hedging the assets comprising it individually. Moreover, macrohedging is better suited for hedging global economic risks such as interest rate fluctuations, currency price changes, wars, changes in weather and changes in economic policies. Additionally, In certain cases, some assets don't have tradable or liquid hedge instruments and can only be hedged by other instruments of correlated underlying assets. In addition to the benefits of macrohedge we have listed, Casano [7] pointed out that macrostrategies have outperformed other investment strategies for three fundamental reasons: one, macrohedges benefits from a sustained increase in volatility of currencies, interest rates, and commodities. Two, macrohedges have a low correlation to equities. Three, they are driven by macroeconomic themes and not by individual bottom-up fundamental analysis.

With all its benefits, macrohedging is hard to implement in practice. Because, it is not usually possible to find a fewer set of hedging instruments that can offset most of the risk factors of the broader aspects of a portfolio. Also, buying the necessary set of hedge instruments to eliminate all risks of a portfolio may not be possible due to costs and availability. Furthermore, macrohedging requires that we assess risk exposures on a continuous basis at the portfolio level where as time passes new exposures are being added to the portfolio and others removed [8]. This is a difficult problem known as the open dynamic portfolio hedging problem. Macrohedge instruments have a finite time horizon with which portfolio exposures are hedged. As a result of these changes, multiple finite time horizons and the addition and removal of risk exposure, one can address them by treating the macrohedged portfolio as a series of closed portfolios with short lives. However, this introduces complexities in accounting of hedges as regards to tracking, amortization of hedge, and adjustments and classification of gains and losses. So, one must examine the impact of each hedging strategy in terms of the trade offs between risk and return IAS14.

Furthermore, we like to point out that having a macroportfolio and then applying a hedge policy on it can be suboptimal. The best method is to find the optimal portfolio is to include the hedge instruments and assets together in a single portfolio and use utility maximization given some constraints algorithm to find the optimal allocation of assets and hedge instruments. However, this may not be possible in practice for a variety of reasons such as cost, liquidity and computational complexity of the optimization problem for a large number of financial instruments. To address these problems one uses hierarchical optimization techniques [9]. Hierarchical optimization partitions the optimization problem in a way, such that, a subset of variables (assets) are constrained to a solution of an optimization problem (e.g., to maximize returns) and the remaining variables (hedge instruments) are optimized by another objective function (e.g., to minimize risk exposure).

One can state that macrohedging entails solving several related problems: (1) Selecting the set of assets that make up the portfolio. (2) Find the optimal portfolio to achieve, for example, optimal expected returns. (3) Assessing the risk exposures of the portfolio. (4) Selecting the appropriate hedge instruments based on some sort of a selection criteria keeping in mind time horizons and costs. (5) Finding the hedge policy—the allocation of hedge instruments by which one can hedge most of the of the investment portfolio risks. The problems we will examine in this work are (5) and (4); That is in a general Cadlag semimartingale market under the usual conditions, given a portfolio of assets and a number of hedging instruments we will show how one can find a hedge portfolio to remove part of the portfolio risks using different methods. We will also show that given a set of hedge instruments how can we select a smaller subset that is perhaps less costly and hedges most of the portfolio exposures. We will illustrate the workings of our methods in a Black-Scholes market.

The paper is organized as follows: In Section 2, we formulate the macrohedging problem in a general semimartingale market. In Section 3, we describe two different methods to derive the macrohedge. In Section 4, we present an example of a macrohedge in a Black-Scholes financial market.

2. Market Model

Let (Ω, , F = (_t)_{t ≥ 0}, P) be the standard stochastic basis and that the financial market evolves on this basis over a time horizon [0, T]. In this world, the market is composed of two baskets of assets: the portfolio basket of assets and a set of hedging instruments. An example of such a world is, a portfolio basket could be a bond and a stock while the hedging instrument is a European put option on the stock. Another example is of a portfolio of a stock and a put option on another stock “closely related” to the portfolio stock.

Let X = (X¹, X², …, Xⁿ) be a vector of n assets determining the value V of the portfolio π. The portfolio basket (or space) of assets is X and X ∈ X. Let Y be the space of hedging instruments and Y = (Y¹, Y², …, Y^m) is the vector of instruments in Y. We associate with X the filtration F^X = (^X_t)_{t ≥ 0} which we assume complete and right continuous. With Y we associate the filtration F^Y = (^Y_t)_{t ≥ 0}, which we also assume to be complete and right continuous. Together σ (^X_t ∪ ^Y_t) ⊆ _t for all t. The space of all possible self financing portfolios is Π and the vector π = (π₁, π₂, …, π_n) ∈ Π. All securities and hedge instruments in this market are Cadlag semimartingales.

Note that in general [Xⁱ, Y^k] ≠ 0 and ^X ∩ ^Y ≠ ∅ for all t and (i, k). In other words, the spaces X and Y overlap in most practical cases and that we will assume this true in our model of the market. This overlap is needed for the hedging instruments to be useful.

The value V of portfolio π is given by

$V={\displaystyle {\sum }_{i=1}^n{\pi }_i}{X}_t^i={\pi }^{\prime }X.$

The portfolio π is self financing and a predictable process that depends on X, hence it is an ^X-measurable process. Therefore, the value process V is also ^X measurable. We let F^V = (^V_t)_{t ≥ 0} be the filtration associated with the value process V and assume that, it is right continuous and complete and F^V ⊆ F^X.

Now, let us consider the hedging portfolio λ over the set of the hedge instruments Y having the value,

$U={\lambda }^{\prime }Y.$

Similarly, we require that λ be self-financing. Let Λ be the set of all self-financing portfolios over Y for which λ ∈ Λ. We let F^U = (^U_t)_{t ≥ 0} be the filtration associated with the value process U and assume that, it is right continuous and complete and F^U ⊆ F^Y.

The macroportfolio is ϕ = (π, λ) is composed of both the assets and hedge instruments and has a value

$Z={\pi }^{\prime }X+{\lambda }^{\prime }Y.$

Therefore, one can define macrohedging as all those methods by which one can select a hedge portfolio λ given the investment portfolio π. Since π is usually the optimal portfolio for some objective function J_X that maximizes wealth, one can understand macrohedging as a hierarchical optimization problem; First, one optimizes the objective function J_X, for example, to maximize returns. Then, followed by a risk minimization problem in which one minimized the risk of the entire portfolio. Risk minimization can be achieved by minimizing some sort of a risk measure say ρ_Z such as variance of Z or Value-at-Risk of Z. Below we will consider two different but simple methodologies of finding λ.

3. Macrohedging

Here we describe several methods for macrohedging under the assumptions we have described above.

3.1. Quadratic projection

Here we describe macrohedging in semimartingales market using “quadratic projection.” The projection of macroportfolio Z on the space Y where the projection here is computed in the sense of the quadratic variation.

THEOREM 3.1. Given the portfolio and its associated value (π, V) and hedge instruments Y such that, E[V, V]_t < ∞, E[Y, Y′]_t < ∞ and the matrix [Y, Y′]_t is not singular for all t ≥ 0 then one can write the value as

$V={\lambda }^{\prime }Y+\xi$

where $\lambda =\frac{d\left[V,Y^{\prime }\right]}{d\left[Y,Y^{\prime }\right]}$ and [ξ, Y′] = 0.

Proof: Consider the process V − λ′Y where λ is a predictable process. Then λ that renders the quadratic variation [V − λ′Y, Y′] = 0 is

$\begin{array}{l}0=\left[V-{\lambda }^{\prime }Y,Y^{\prime }\right]=\left[V,Y^{\prime }\right]-{\lambda }^{\prime }·\left[Y,Y^{\prime }\right]\Rightarrow \\ \lambda =\frac{d\left[V,Y^{\prime }\right]}{d\left[Y,Y^{\prime }\right]}.\end{array}$

So, one sets ξ = V − λ′Y and the theorem is proven.

REMARK 3.2. Note that the process $\widehat{V}$ = λ′Y with $\lambda =\frac{d\left[V,Y^{\prime }\right]}{d\left[Y,Y^{\prime }\right]}$ is F^Y-measurable defined over the space of hedge instruments Y, and we will refer to it as the projection of V on Y. Furthermore, the quadratic variation of the unhedged part ξ = V − $\widehat{V}$ of V is [ξ, ξ] = [ξ, V − $\widehat{V}$] = [ξ, V]; since [ξ, $\widehat{V}$] = 0. So

$\left[\xi ,\xi \right]=[V,V]-\left[V,Y^{\prime }\right]{\left[Y,Y^{\prime }\right]}^{-1}\left[Y,V\right].$

Now we layout simple consequences as relates to the projection process $\widehat{V}$.

PROPOSITION 3.3. In general, the quadratic correlation of the portfolio V and $\widehat{V}$, defined as

$\lfloor V,\widehat{V}\rfloor =\frac{\left[V,\widehat{V}\right]}{\sqrt{\left[V,V\right]}\sqrt{\left[\widehat{V},\widehat{V}\right]}}$

is either zero, less that or equal to 1 or larger than or equal to −1.

Proof: Simply by using Kunita-Watanabe inequality $\left|\left[V,\widehat{V}\right]\right|\le {\left[V,V\right]}^{1/2}{\left[\widehat{V},\widehat{V}\right]}^{1/2}$, the fact that V ≥ 0, the fact that Y_k ≥ 0 for each component k in Y, and that the components of the hedge portfolio λ could either be positive or negative depending on the position with respect to the hedge instrument we arrives at

$-1\le \lfloor V,\widehat{V}\rfloor \le 1,$

which proves the result.

REMARK 3.4. This simple result is an interesting one. It allows us to take a portfolio and hedge instruments and hedge the projection of the portfolio on the instruments by going short or long according to its quadratic correlation of the hedge instrument with the portfolio. Moreover, one notices that it is possible for $\lfloor V,\widehat{V}\rfloor =0$ meaning that we can form a 0 variance portfolio in the projection space Y. A similar result was presented by Denev [3] in the context of two period model using standard correlation as a measure of risk.

The next result will help us determine a hedge portfolio for which the projection of the macroportfolio value Z on Y is zero.

THEOREM 3.5. Given the macroportfolio Z there is a hedge portfolio $\lambda =-\pi \frac{d\left[X,Y^{\prime }\right]}{d\left[Y,Y^{\prime }\right]}$ such that [Z, Y′] = 0 and for which the maximally hedged macroportfolio $\stackrel{\circ }{Z}$ is given by

$\stackrel{°}{Z}=\pi \left[X-\frac{d\left[X,Y^{\prime }\right]}{d\left[Y,Y^{\prime }\right]}Y\right].$

Proof: Let us compute the projection of Z = V + U on Y;

$\begin{array}{l}\left[Z,Y^{\prime }\right]=\left[V,Y^{\prime }\right]+\left[U,Y^{\prime }\right]\\ =\left[V,Y^{\prime }\right]+{\lambda }^{\prime }·\left[Y,Y^{\prime }\right],\end{array}$

since λ is self-financing and predictable i.e., [U, Y′] = λ′ · [Y, Y′]. Set [Z, Y′] = 0 one finds λ,

$\stackrel{\circ }{{\lambda }^{\prime }}=-\frac{d\left[V,Y^{\prime }\right]}{d\left[Y,Y^{\prime }\right]}=-{\pi }^{\prime }\frac{d\left[X,Y^{\prime }\right]}{d\left[Y,Y^{\prime }\right]}.$

Similarly, since π is self-financing and predictable then d[V, Y′] = π′d[X, Y′]. Substituting $\stackrel{\circ }{\lambda }$ in Z one finds the maximally hedged portfolio $\stackrel{\circ }{Z}$,

$\begin{array}{l}\stackrel{°}{Z}={\pi }^{\prime }X-{\pi }^{\prime }\frac{d\left[X,Y^{\prime }\right]}{d\left[Y,Y^{\prime }\right]}Y\\ ={\pi }^{\prime }\left[X-\frac{d\left[X,Y^{\prime }\right]}{d\left[Y,Y^{\prime }\right]}Y\right].\end{array}$

REMARK 3.6. The choice of the hedge portfolio λ provided by the above theorem will affect the average returns of the portfolio π in the case of non-0 price instruments.

A different approach and perhaps a more general one is to consider macrohedge in the context of a portfolio optimization problem where one finds the hedge portfolio to minimize some sort of a risk measure under constraints. Next we will consider this approach to macrohedging.

3.1.1. Quadratic-Variation Minimization Problem

There are several macrohedge risk minimization problems that are possible. Here we outline a procedure for determining a hedge portfolio that minimizes the quadratic variation of the macroportfolio as a whole. Few authors have investigate the macrohedge risk minimization problem. Denev [3] considered macrohedging in a two period financing model. Borensztein et al. [5] considered macrohedging for commodity exporters. They used a dynamic optimization in discrete time to estimate welfare gains of hedging against commodities' price risk for commodities exporting countries by using futures and options to reduce the volatility of exported income.

Macrohedging can be thought of as a general risk minimization problem under constraints. Constraint risk minimization problems have been addressed in the mathematical finance literature. We mention a few here. For example, in Becherer and Ward [10] the problem of finding a minimum variance hedge of a portfolio of derivatives through other derivatives (i.e., partial hedging) was investigated. In incomplete markets a contingent claim cannot be perfectly replicated but it is possible to eliminate risk by superhedging [11]. Another method of hedging is quantile hedging first developed by Follmer [12].

Here we will consider local minimization of macroportfolio quadratic variation. The optimization problem can be stated as follows,

$\begin{array}{cc}{\stackrel{°}{\lambda }}_t=\arg \underset{\lambda \in \Lambda }{\min }{[Z,Z]}_t.& (1)\end{array}$

The solution of this problem is contained in the following simple theorem.

THEOREM 3.7. The solution of 1 is

$\stackrel{°}{\lambda }=-\frac{d[X,Y^{\prime }]}{d\left[Y,Y^{\prime }\right]}\pi .$

Proof: Let's write the quadratic variation of Z;

$\begin{array}{l}{[Z,Z]}_t={[U+V,U+V]}_t\\ ={[U,U]}_t+2{[U,V]}_t+{[V,V]}_t\\ ={\left[\pi \prime X,X^{\prime }\pi \right]}_t+2{[{\pi }^{\prime }X,Y^{\prime }\lambda ]}_t+{\left[{\lambda }^{\prime }Y,Y^{\prime }\lambda \right]}_t\\ ={\displaystyle {\int }_0^t{{\pi }^{\prime }}_s}d{\left[X,X^{\prime }\right]}_s{\pi }_s+2{{\pi }^{\prime }}_{s}d{[X,Y^{\prime }]}_s{\lambda }_s+{{\lambda }^{\prime }}_{s}d{\left[Y,Y^{\prime }\right]}_s{\lambda }_s.\end{array}$

Given π, X, and Y are constraint, one must vary λ to minimize the integral above. We can approach this problem by computing the derivative of [Z, Z] with respect to λ,

$\begin{array}{cc}\frac{\partial [Z,Z]}{\partial \lambda }=2{\pi }^{\prime }d[X,Y^{\prime }]+2{\lambda }^{\prime }d\left[Y,Y^{\prime }\right]=0.& (2)\end{array}$

Solving for λ_t,

$\begin{array}{cc}\stackrel{°}{\lambda }{}_t{}^{\prime }=-{\pi }_t^{\prime }\frac{d{[X,Y^{\prime }]}_t}{d{\left[Y,Y^{\prime }\right]}_t}.& (3)\end{array}$

REMARK 3.8. Equation (2) can be justified by Embedding λ_t(ω) in the space $\left\{\left(\omega ,t,\lambda \right)\right\}$. One can think of λ_t(ω) as a curve on a surface in this space. A curve on a surface in {(ω, t, λ)} can be defined as a function (ω, t, λ) = λ_t(ω). Then, we can write

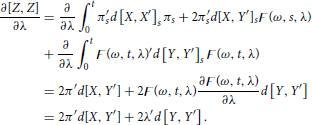
Further details, are out of scope of the current paper.

REMARK 3.9. The optimal solution of the local optimization problem inf_{λ ∈ Λ}[Z, Z]_t is the same solution as the one we have obtained by solving the projection problem in theorem 5 were we have set the projection [Z, Y] = 0. By substituting for $\stackrel{\circ }{\lambda }$ in the macroportfolio one finds the minimum risk portfolio value,

$\begin{array}{l}\stackrel{\circ }{Z}=V+{\stackrel{\circ }{\lambda }}^{\prime }Y=V-{\pi }_t^{\prime }\frac{d{[X,Y^{\prime }]}_t}{d{\left[Y,Y^{\prime }\right]}_t}Y\\ ={\pi }_t^{\prime }\left[X-\frac{d\left[X,Y^{\prime }\right]}{d\left[Y,Y^{\prime }\right]}Y\right].\end{array}$

The two views are equivalent.

REMARK 3.10. The term $X-\frac{d\left[X,Y^{\prime }\right]}{d\left[Y,Y^{\prime }\right]}Y$ are the basket of assets hedged by instruments Y. This term tells us that one can first think about hedging the basket of assets without knowing the portfolio π. Then with this new basket of hedged instrument we can go ahead and compute the optimal portfolio. This provides us with an alternative way of looking at macrohedging.

The usefulness of the optimization problem stems from the fact that we can add constraints to the optimization problem and solve the problem using Lagrangian method. Consider for example, minimizing the quadratic variation but subject to the initial cost of the hedge being less than some positive constant value u,

$\begin{array}{l}{\stackrel{\circ }{\lambda }}_t=\arg \underset{{}_{\lambda \in \Lambda }}{\min }{[Z,Z]}_t,\\ s.t.U_0\le u.\end{array}$

This is an important problem that we will consider in future work.

Next we consider macrohedging in markets were assets and hedge instruments are described by stochastic exponential.

3.1.2. Stochastic-Exponential Markets and Macrohedging

Suppose that the securities and hedge instruments in this market follow the stochastic exponential equations,

$\begin{array}{ll}{X}_t^i=X_0^iℰ(x_t^i),x_t^i=a_t^i+M_t^i\hfill & (4)\hfill \end{array}$

and

$\begin{array}{ll}{Y}_t^k=Y_0^kℰ(y_t^k),y_t^k=b_t^k+N_t^k\hfill & (5)\hfill \end{array}$

where ℰ(·) is the Dolean-Dade exponential. X₀ and Y₀ are ₀-measurable random variables. y^k = (y^k_t)_{t ≥ 0} and xⁱ = (xⁱ_t)_{t ≤ 0} are semimartingales admitting the representation shown above where aⁱ = (aⁱ_t)_{t ≥ 0} and b^k = (b^k_t)_{t ≥ 0} are locally bounded variation processes (aⁱ, b^k ∈ ), Mⁱ = (Mⁱ_t)_{t ≥ 0} and N^k = (N^k_t)_{t ≥ 0} are local martingales in _loc with respect to P.

In this market the optimal hedging portfolio Equation (3) can be written as follows,

$\begin{array}{ll}\begin{array}{l}{\stackrel{\circ }{\lambda }}_t^{\prime }=-{\pi }_t^{\prime }\frac{d{[X,Y^{\prime }]}_t}{d{\left[Y,Y^{\prime }\right]}_t}=-{\pi }_t^{\prime }\frac{diag\left(X_{t-}\right)d{[M,N^{\prime }]}_{t}diag\left(Y_{t-}\right)}{diag\left(Y_{t-}\right)d{\left[N,N^{\prime }\right]}_{t}diag\left(Y_{t-}\right)}\\ =-{\pi }_t^{\prime }\frac{diag\left(X_{t-}\right)d{[M,N^{\prime }]}_t}{diag\left(Y_{t-}\right)d{\left[N,N^{\prime }\right]}_t}.\end{array}\hfill & (6)\hfill \end{array}$

A fundamental issue in macrohedging, is how do we find the best subset of instruments of the many available ones to hedge our portfolio with. Below we provide a recipe that will address this problem.

3.1.3. Essential hedge instruments

With macrohedging one might not want to hedge with all given hedge instruments. This could be as a result of, the price of the total hedge and transaction costs. In this case one must search for the best possible subset of hedge instrument that can offset much of the risk. Here we propose the following method.

First, we compute the total square of quadratic covariation of V and all hedge instruments Y over the duration of the hedge [0, T];

$\begin{array}{ll}{(V,Y^i)}_T={\displaystyle {\int }_{\text{0}}^T{[V,Y^i]}_s^{2}ds.}\hfill & (7)\hfill \end{array}$

Then, one simply select k < m largest values in the set $\left\{{\left(V,Y^i\right)}_T\right\}$ as our new subset of hedge instruments. The largest values represent the hedge instrument that are most correlated with the assets X and therefore would offset most of the risk.

REMARK 3.11. One might wonder how do we calculate the integral in Equation (7). One possibility is by simulation. Knowing the volatilities and drifts of the processes X and Y from historical data one can predict the matrix (V, Y′)_T.

Next we consider macrohedging from a different point view, describe hedging by optional projection on the filtration generated by hedge instruments.

3.2. Information projection

An alternative approach to “quadratic projection” is to find the hedging portfolio by optional projection on the filtration generated by the hedge instruments ^Y_t,

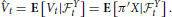
$\widehat{V}$ is the value process of the hedgable part of the portfolio π. Since ^Y represents the total accumulated information up to time t of the hedging instruments the E[V_t|^Y_t] is a projection of the investment portfolio on the hedging instrument space Y. It is essentially that part where it is possible to eliminate the risk. Therefore, the process ξ = V − $\widehat{V}$ represent the value process associate with the unhedgable part of the portfolio π.

For E[V_t|^Y_t] to have a computational value one usually seeks to find an integral representation of $\widehat{V}$ in terms of Y. However, Y is a semimartingale under the measure P. That brings us to a related problem of finding a decomposition of V in terms of Y. We will not be able to consider this problem in its entirety but we would like to allude to the theorem of optional decomposition due to Kramkov [13] as a possible way to solving this problem. Here is the gist of our approach.

Let 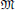(Y) be the family of all equivalent local martingale measures Q for Y where we assume in this case to be a locally bounded hedge instruments, and V our portfolio be a positive process, which is reasonable to assume. Then the portfolio value V is a supermartingale for every Q ∈ 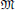(Y) if and only if V admits the decomposition:

$\begin{array}{ll}{V}_t=V_0+{\displaystyle {\int }_0^t{\lambda }_s^{\prime }}d{Y}_s-{\xi }_t\text{ a}\text{.s}\text{. }Q.\hfill & (8)\hfill \end{array}$

where ξ is an optional adapted increasing process. By the above decomposition one can identify the representation of $\widehat{V}$,

$\begin{array}{ll}\widehat{V}={\widehat{V}}_0+{\displaystyle {\int }_0^t{\lambda }_s^{\prime }}d{Y}_s\text{ a}\text{.s}\text{. }Q.\hfill & (9)\hfill \end{array}$

and ξ = V − $\widehat{V}$.

From Equation (9) we write the hedge portfolio λ as,

$\stackrel{\circ }{\lambda }=\frac{d\widehat{V}}{dY}\text{ a}\text{.s}\text{. }Q.$

We conclude this work by an example of macrohedge on a Black-Scholes market.

4. Example

Consider a Black-Scholes market of n assets and m hedge instruments m ≤ n. We assume either that the interest rate on the money market account is zero or that all assets are hedge instruments are discounted by the rate of growth of the money market account. Let the basket of assets be described by

$X_t^i=X_0^i\exp \left({\mu }^{i}t+{\displaystyle {\sum }_{i=1}^n{\sigma }_j^i}{B}_t^j\right).$

The portfolio π is to hold the following allocation π = (π₁, π₂, …, π_n) for a market duration [0, T]. The value of the portfolio is $V_t={\displaystyle {\sum }_{i=1}^n{\pi }_i{X}_t^i}$.

Let ^Y = σ (B¹, …, B^m) be the filtration generated by hedge instruments, which is a subset of sources of risks in the assets i.e., B¹ to Bⁿ, as risk factors. The hedge instruments are specified by the following equations,

$Y^k(t,T)=Y^k(0,T)\exp \left({\rho }^k(T-t)+{\displaystyle {\sum }_{l=1}^m{\gamma }_j^l}{B}_t^j\right).$

REMARK 4.1. Without loss of generality we have assumed a particular ordering of the risk factors (B¹, …, Bⁿ) where the first m risk factors are to be hedged by the available hedge instruments.

Let us compute the 〈Y, Y′〉 and 〈X, Y′〉; since all processes are continuos we can use the sharp brackets instead of square ones. Because both hedge and assets are of stochastic exponential form (see Equation 6) we only have to compute the following two matrices

$\begin{array}{l}\sigma {\left[{\left(B^1,\mathrm{...},B^n\right)}^{\prime },\left(B^1,\mathrm{...},B^m\right)\right]}_t\gamma =\left[\sigma 1_n^{\prime }{1}_m{\gamma }^{\prime }\right]t,\\ \gamma {\left[{\left(B^1,\mathrm{...},B^m\right)}^{\prime },\left(B^1,\mathrm{...},B^m\right)\right]}_t\gamma =\left[\gamma 1_{m\times m}{\gamma }^{\prime }\right]t\end{array}$

where 1_n and 1_m are vectors of 1s of length n and m, respectively. 1_{m × m} is identity matrix of size $m^2.\gamma =\left({\gamma }_i^j\right)$ and $\sigma =\left({\sigma }_i^j\right)$ are matrices of instruments and assets volatilities, respectively. Therefore, the hedge portfolio will be

$\begin{array}{l}\stackrel{\circ }{\lambda }=-{\pi }_t^{\prime }\exp \left(\mu t+\sigma B_t^n\right)\left[\sigma 1_n^{\prime }{1}_m{\gamma }^{\prime }\right]{\left[\gamma 1_{m\times m}{\gamma }^{\prime }\right]}^{-1}\\ \exp \left(-\rho (T-t)-\gamma B_t^m\right).\end{array}$

where μ = diag(μⁱ), ρ = diag(ρⁱ), Bⁿ = (B¹, …, Bⁿ) and B^m = (B¹, …, B^m).

Let us consider computing the hedge in terms of a numerical example. We choose

$\begin{array}{l}\sigma =\left[\begin{array}{cccc}4& 3& 1& 0\\ 0& -2.9& 1& 1\\ 0& 0& -3& 1\\ 0& 0& 0& -1\end{array}\right],\mu =\left[\begin{array}{c}5\\ 4\\ 3\\ 1\end{array}\right],\\ \gamma =\left[\begin{array}{ccc}1& 0& 1\\ 0& -1& 1\\ 0& 0& -1\end{array}\right],\rho =\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right].\end{array}$

where ^X = σ (B¹, B², B³, B⁴) and ^Y = σ (B¹, B², B³). Calculating quadratic variations we find

$\begin{array}{l}\sigma {\left[{\left(B^1,B^2,B^3,B^4\right)}^{\prime },\left(B^1,B^2,B^3\right)\right]}_t\gamma =t\sigma \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right]{\gamma }^{\prime }\\ =\left[\begin{array}{ccc}5& -2& -1\\ 1& 3.9& -1\\ -3& -3& 3\\ 0& 0& 0\end{array}\right]t\end{array}$

and

$\gamma {\left[{\left(B^1,B^2,B^3\right)}^{\prime },\left(B^1,B^2,B^3\right)\right]}_t{\gamma }^{\prime }=\left[\begin{array}{ccc}2& 1& -1\\ 1& 2& -1\\ -1& -1& 1\end{array}\right]t.$

Therefore, the hedge is

$\begin{array}{l}{\stackrel{\circ }{\lambda }}_t=-{\pi }_t^{\prime }\exp \left(\mu t+\sigma B_{t-}^n\right)\left[\begin{array}{ccc}4& -3& 0\\ 0& 2.9& 1.9\\ 0& 0& 3\\ 0& 0& 0\end{array}\right]\\ \exp \left(-\rho (T-t)-\gamma B_{t-}^m\right).\end{array}$

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The research is supported by the NSERC discovery grant #5901.

References

1. Loader, D. Exchange Traded Derivatives. Chartered Institute for Securities & Investment (2013). Available online at: http://www.cisi.org/bookmark/bitmark/Uploads/Publications/86743898/Exchange-Traded%20Derivatives%20Ed19.pdf

2. Hedge, B. Macro Hedge Fund Strategy (2014). Available online at: http://www.barclayhedge.com/research/educational-articles/hedge-fund-strategy-definition/hedge-fund-macro.html

3. Denev, A. Macro-hedging of Portfolios of Assets (2014). Available online at: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2405181

4. Carter, D, Rogers, D, and Simkins, B. Fuel Hedging in the Airline Industry: The case of Southwest Airlines (2004). Available online at: http://papers.ssrn.com/sol3/papers.cfm

5. Borensztein, F, Jeanne, O, and Sandri, D. Macro-hedging for commodity exporters. J Dev Econ. (2009) 101:105–16. doi: 10.1016/j.jdeveco.2012.08.005

CrossRef Full Text | Google Scholar

6. Evans-Pritchard, B. Taking the Macro View. Insurance Risk (2012). Available online at: http://www.risk.net/insurance-risk/feature/2202418/taking-the-macro-view

7. Casano, J. Global Macro Hedge Fund Investing An Overview of the Strategy (2010). NEPC, Cambridge, MA. Available online at: https://www.efficient.com/pdfs/Global_Macro_Hedge_Fund_Investing_An_Overview_of_the_Strategy.pdf

8. IASplus. Financial Instruments: Macro Hedge Accounting. Finance Stochast. (2014). Available online at: http://www.iasplus.com/en/projects/major/macro-hedge-accounting

9. Stoilova, K, and Stoilov, T. Hierarchical optimization for fast resource allocation. Time Manag. (2012) 2:31–46. doi: 10.5772/36693. Available online at: http://www.intechopen.com/books/time-management/hierarchical-optimization-for-fast-resource-allocation

CrossRef Full Text

10. Becherer, D, and Ward, I. Optimal weak static hedging of equity and credit risk using derivatives. Appl Math Finance. (2010) 17:1–28. doi: 10.1080/13504860903075522

CrossRef Full Text | Google Scholar

11. Rudloff, B. Convex hedging in incomplete markets. Appl Math Finance. (2007) 14:437–52. doi: 10.1080/13504860701352206

CrossRef Full Text | Google Scholar

12. Follmer, H, and Leukert, P. Quantile hedging. Finance Stochast. (2013) 3:251–73. doi: 10.1007/s007800050062

CrossRef Full Text

13. Kramkov, DO. Optional decomposition of supermartingales and hedging contingent claims in incomplete security markets. Probab Theory Relat Fields. (1996) 105:459–79. doi: 10.1007/BF01191909

CrossRef Full Text | Google Scholar