- 1Faculty of Mathematics, Technische Universität Chemnitz, Chemnitz, Germany
- 2Institute of Mathematics, University of Rostock, Rostock, Germany
In spectral estimation, one has to determine all parameters of an exponential sum for finitely many (noisy) sampled data of this exponential sum. Frequently used methods for spectral estimation are MUSIC (MUltiple SIgnal Classification) and ESPRIT (Estimation of Signal Parameters via Rotational Invariance Technique). For a trigonometric polynomial of large sparsity, we present a new sparse fast Fourier transform by shifted sampling and using MUSIC resp. ESPRIT, where the ESPRIT based method has lower computational cost. Later this technique is extended to a new reconstruction of a multivariate trigonometric polynomial of large sparsity for given (noisy) values sampled on a reconstructing rank-1 lattice. Numerical experiments illustrate the high performance of these procedures.
1. Introduction
The problem of spectral estimation resp. frequency analysis arises quite often in signal processing, electrical engineering, and mathematical physics (see e.g., the books [1, 2] or the survey [3]) and reads as follows:
(P1) Recover the positive integer M, the distinct frequencies , and the complex coefficients cj ≠ 0 (j = 1, …, M) in the exponential sum of sparsity M
if noisy sampled data (k = 0, …, N − 1) with N ≥ 2M are given, where ek ∈ ℂ are small error terms with .
Introducing so-called left/right signal spaces and noise spaces in Section 2, we explain the numerical solution of the problem (P1) by the MUSIC method (created by Schmidt [4], see also Manolakis et al. [1, Section 9.6.3] and the references therein) and the ESPRIT method (created by Roy and Kailath [5], see also Manolakis et al. [1, Section 9.6.5], Stoica and Moses [2, Chapter 4] and the references therein). In a new unified approach to MUSIC and ESPRIT, we show that both methods are based on singular value decomposition (SVD) of a rectangular Hankel matrix of given sampled data. For the MUSIC and ESPRIT method, it is important to choose the window length L (number of rows) of the rectangular Hankel matrix in an optimal way. Based on Theorem 2.5, where we estimate the singular values and the spectral norm condition number of the rectangular Hankel matrix of noiseless data, one can see that is a good choice. By the right choice of L, one can detect the correct sparsity M of (1.1) and avoid the computation of spurious frequencies.
The main disadvantages of MUSIC and ESPRIT are the relatively high computational cost in the case of large sparsity M, caused mainly by the SVD. The known algorithms for MUSIC and ESPRIT have moderate computational cost only for small sparsity M. Thus, following question arises: How can one improve the MUSIC and ESPRIT methods for spectral estimation of exponential sums with large sparsity M? In this paper, we show that this is possible by a special divide-and-conquer technique. In the numerical examples of Section 5, the cases M = 256 and M = 1024 are handled.
The computational cost of an algorithm is measured in the number of arithmetical operations, where all operations are counted equally. Often the computational cost of an algorithm is reduced to the leading term, i.e., all lower order terms are omitted. For a unified approach to Prony–like methods for the parameter estimation of (1.1), namely the classical Prony method, the matrix pencil method [6, 7], and the ESPRIT method [5, 8], we refer also to Potts and Tasche [9] and the references therein. For a survey of the most successful methods for the data fitting problem with linear combinations of complex exponentials, we refer to Pereyra and Scherer [10].
Section 3 is the core of this paper. Here we present a new efficient spectral estimation with low computational cost for large sparsity M and a moderate number of given samples, if one has to recover a trigonometric polynomial of large sparsity M. This means we specialize the problem (P1). Let S > 0 be a large even integer. Assume that , where . Replacing the variable x by Sx in (1.1), we consider the 1-periodic trigonometric polynomial of sparsity M
with integer frequencies . Consequently we investigate the following spectral estimation problem:
(P2) Recover the sparsity M ∈ ℕ, all integer frequencies as well as all non-zero coefficients cj ∈ ℂ of the trigonometric polynomial (1.2) for noisy sampled values (k = 0, …, N − 1) with N ≥ 2M, where ek ∈ ℂ are small error terms with . Often one considers the modified problem (P2*), where the sparsity M is known.
A numerical solution of problem (P2) or (P2*) with low computational cost is called sparse fast Fourier transform (sparse FFT). Using divide-and-conquer technique, the trigonometric polynomial (1.2) of large sparsity M is split into some trigonometric polynomials of lower sparsity and corresponding samples are determined by fast Fourier transform (FFT). Here we borrow an idea from sparse FFT in Lawlor et al. [11] and Christlieb et al. [12] and use shifted sampling of (1.2), i.e., equidistant sampling with few equidistant shifts. Then the trigonometric polynomials of lower sparsity can be recovered by MUSIC resp. ESPRIT. The computational cost of the new sparse FFT is analyzed too.
A similar splitting technique is suggested in Lawlor et al. [11] and Christlieb et al. [12], but with a different method to detect frequencies, when aliasing between two or more frequencies occurs. The method in Lawlor et al. [11] and Christlieb et al. [12] follows an idea of Iwen [13], which is based on the Chinese Remainder Theorem, see also Ben-Or and Tiwari [14]. A different method for the sparse FFT, based on efficient filters is suggested in Hassanieh et al. [15] and Gilbert et al. [16]. We remark that there are two types of methods, deterministic (see [13]) and randomized (see [15, 11, 16]). Further related randomized methods based on compressed sensing can be found in the papers [17, 18, 19] and in the monograph [20]. Please note that the sparse FFT methods mentioned before solve the problem (P2*), i.e., one assumes that the sparsity (or an upper bound) is known, whereas our new deterministic sparse FFT also detects the sparsity M. We remark that preliminary tests of the implementation [21, 22] of the sfft version 3 algorithm [15] suggest that this method also works if the sparsity input parameter is chosen larger than the actual sparsity of the signal. For further references on sparse FFTs, we refer to Remark 3.1.
In Section 4, we extend our method to a new reconstruction of multivariate trigonometric polynomials of large sparsity, where sampled data on a convenient rank-1 lattice are given. In Section 5, several numerical experiments with noiseless resp. noisy sampled data illustrate the high performance of the sparse FFT as proposed in Section 3. Note that in the case of successful recovery of the sparse trigonometric polynomial (1.2) all frequencies are correctly detected. For the modified sparse FFT of Section 4, numerical examples for the reconstruction of six-variate trigonometric polynomials of sparsity 256 are given too. Moreover, we compare our results with preliminary tests of the implementation [21, 22] of the sfft version 3 algorithm [15].
In summary we present a splitting method, in between the well-known methods ESPRIT, MUSIC, and FFT for the problem (P2) with the parameters in Table 1. For the results, see the Tables 3, 4 in Section 3. Furthermore, we use a reconstructing rank-1 lattice in order to reconstruct multivariate trigonometric polynomials, see Section 4. Here in the case of successful recovery of a sparse multivariate trigonometric polynomial, all frequency vectors are detected without errors.

Table 1. Numbers of required samples and computational costs for ESPRIT, MUSIC, and FFT, where M denotes the sparsity of (1.1) and S is a large even integer so that all frequencies φj are of the form with .
2. Reconstruction of Exponential Sums
The main difficulty is the recovery of the frequency set Φ: = {φ1, …, φM} in (1.1).
We introduce the rectangular Fourier–type matrix Note that FN, M coincides with the rectangular Vandermonde matrix with , where (j = 1, …, M) are distinct nodes on the unit circle. Then the spectral estimation problem can be formulated in following matrix-vector form
where is the vector of noisy sampled data and the vector of complex coefficients of (1.1).
Under the natural assumption that the nodes zj (j = 1, …, M) are well-separated on the unit circle, it can be shown that FP, M has a uniformly bounded spectral norm condition number for sufficiently large integer P > M.
Theorem 2.1 (see [23, Theorem 2]) Assume that the frequencies (j = 1, …, M) are well-separated by the separation distance
and that .
Then the discrete Ingham inequalities related to FP, M indicate that for all x ∈ ℂM
with and
Furthermore, the rectangular Fourier–type matrix FP, M has a uniformly bounded spectral norm condition number
Proof. The assumption is sufficient for the gap condition
to hold. The gap condition (2.3) ensures that α1(P) > 0. For a proof of the discrete Ingham inequalities (2.2) under the gap condition (2.3) see Liao and Fannjiang [23, Theorem 2]. Let λ1 ≥ … ≥ λM > 0 be the ordered eigenvalues of . Using the Raleigh–Ritz Theorem and (2.2), we obtain that for all x ∈ ℂM
and hence
Thus, is positive definite and
This completes the proof. □
Corollary 2.2 Assume that the frequencies (j = 1, …, M) are well-separated by the separation distance q > 0 and that .
Then the discrete Ingham inequalities related to indicate that for all y ∈ ℂP
Proof. The matrices FP, M and possess the same singular values λj (j = 1, …, M). By the Rayleigh–Ritz Theorem we obtain that
for all y ∈ ℂP. Applying (2.4), we obtain the discrete Ingham inequalities (2.5). □
Remark 2.3 The Riesz stability of the exponentials (j = 1, …, M) in the Hilbert space follows immediately from the discrete Ingham inequalities (2.2), where ℤN : = {0, …, N − 1} denotes the sampling grid. If the assumptions of Theorem 2.1 are fulfilled for P = N, then the exponentials (j = 1, …, M) are Riesz stable with respect to the discrete norm of , i.e.,
for all exponential sums (1.1) with arbitrary coefficient vectors . Note that the Riesz stability of these exponentials related to continuous norms was formerly discussed and applied in spectral estimation in Peter et al. [24] and Potts and Tasche [25]. □
In practice, the sparsity M of the exponential sum (1.1) is often unknown. Assume that L ∈ ℕ is a convenient upper bound of M with M ≤ L ≤ N − M + 1. In applications, such an upper bound L is mostly known a priori. If this is not the case, then one can choose . As mentioned in Remark 2.6, the choice is optimal in some sense. Often the sequence of sampled data is called a time series of length N. Then we form the L-trajectory matrix of this time series
with the window length L ∈ {M, …, N − M + 1}. Analogously, we define the L-trajectory matrix of noiseless data
Obviously, (2.6) and (2.7) are L×(N − L+1) Hankel matrices. For simplicity, we consider mainly the noiseless case, i.e. (k = 0, …, N − 1).
The main step in the solution of the frequency analysis problem (P1) is the determination of the sparsity M and the computation of the frequencies φj or alternatively of the nodes (j = 1, …, M). Afterwards one can calculate the coefficient vector c ∈ ℂM as least squares solution of the overdetermined linear system (2.1), i.e., the coefficient vector c is the solution of the least squares problem
We denote square matrices with only one index and refer to the well known fact that the square Vandermonde matrix VM(z) is invertible and the matrix VN, L(z) with L ∈ {M, …, N − M + 1} has full column rank. Additionally we introduce the rectangular Hankel matrices
In the case of noiseless data (k = 0, …, N − 1), the related Hankel matrices (2.8) are denoted by HL, N − L(s) (s = 0, 1).
Remark 2.4 The Hankel matrix HL, N − L + 1 of noiseless data has the rank M for each window length L ∈ {M, …, N − M + 1} and the related Hankel matrices HL, N − L(s) (s = 0, 1) possess the same rank M for each window length L ∈ {M, …, N − M} (see [9, Lemma 2.1]). Consequently, the sparsity M of the exponential sum (1.1) coincides with the rank of these Hankel matrices. □
By the Vandermonde decomposition of the Hankel matrix HL, N − L + 1 we obtain that
Under mild conditions, the Hankel matrix HL, N − L + 1 of noiseless data has a bounded spectral norm condition number too.
Theorem 2.5 Let L, N ∈ ℕ with M ≤ L ≤ N − M + 1 and be given. Assume that the frequencies (j = 1, …, M) are well-separated by the separation distance q > 0 and that the non-zero coefficients cj (j = 1, …, M) of the exponential sum (1.1) fulfill the condition
Then for all y ∈ ℂN − L + 1
Further, the lowest resp. largest positive singular value of HL, N − L + 1 can be estimated by
The spectral norm condition number of HL, N − L + 1 is bounded by
Proof. By the Vandermonde decomposition (2.9) of the Hankel matrix HL, N − L + 1, we obtain that for all y ∈ ℂN − L + 1
By the discrete Ingham inequalities (2.2) and the assumption (2.10), it follows that
Using the discrete Ingham inequalities (2.5), we obtain the estimates (2.11). Finally, the estimates of the lowest resp. largest positive singular value and the spectral norm condition number of HL, N − L + 1 arise from (2.11) and the Rayleigh–Ritz Theorem.
Remark 2.6 For fixed N, the positive singular values as well as the spectral norm condition number of the Hankel matrix HL, N − L + 1 depend strongly on L ∈ {M, …, N − M + 1}. A good criterion for the choice of optimal window length L is to maximize the lowest positive singular value σM of HL, N − L + 1. It was shown in Potts and Tasche [submitted, Lemma 3.1 and Remark 3.3] that the squared singular values increase almost monotonously for and decrease almost monotonously for . Note that the lower bound (2.12) of the lowest positive singular value σM is maximal for . Further the upper bound (2.13) of the spectral norm condition number of (2.7) is minimal for . Therefore, we prefer to choose as optimal window length. Thus, we can ensure that σM > 0 is not too small. This property is decisively for the correct detection of the sparsity M in the first step of the MUSIC resp. ESPRIT Algorithm 2.8 resp. 2.9. □
The ranges of HL, N − L + 1 and VL, M(z) coincide in the noiseless case with M ≤ L ≤ N − M + 1 by (2.9). If L > M, then the range of VL, M(z) is a proper subspace of ℂL. This subspace is called left signal space L. The left signal space L is of dimension M and is generated by the M columns eL(φj) (j = 1, …, M), where
Note that for each . The left noise space L is defined as the orthogonal complement of L in ℂL. The dimension of L is equal to L − M.
Remark 2.7 Let M ≤ L < N − M + 1 be given. If we use instead of HL, N − L + 1, then we can define the right signal space as the range of , where denotes the complex conjugate of z. The right signal space is an M-dimensional subspace of ℂN − L + 1 and is generated by the M linearly independent vectors eN − L + 1 (− φj) (j = 1, …, M). Then the corresponding right noise space is the orthogonal complement of the right signal space in ℂN − L + 1. □
By QL we denote the orthogonal projection onto the left noise space L. Since eL(φj) ∈ L (j = 1, …, M) and L ⊥ L, we obtain that
If the number , then the vectors are linearly independent, since the square Vandermonde matrix
is invertible for each L ≥ M + 1. Hence eL(φ) ∉ L = span{eL(φ1), …, eL(φM)}, i.e. QLeL(φ) ≠ 0. Thus, the frequency set Φ can be determined via the zeros of the left noise-space correlation function
since NL(φj) = 0 for each j = 1, …, M and 0 < NL(φ) ≤ 1 for all , where QLeL(φ) can be computed on an equispaced fine grid. Alternatively, one can seek the peaks of the left imaging function
In this approach, we prefer the zeros resp. the lowest local minima of the left noise-space correlation function NL(φ).
In the next step we determine the orthogonal projection QL onto the left noise space L. Here we can use the SVD or the QR decomposition of the L-trajectory matrix HL, N − L + 1. For an application of QR decomposition see Potts and Tasche [9]. Applying SVD, we obtain that
where and are unitary matrices and where is a rectangular diagonal matrix. The diagonal entries of DL, N − L+1 are the singular values σj of the L-trajectory matrix arranged in non-increasing order σ1 ≥ … ≥ σM > σM + 1 = … = σmin{L, N − L + 1} = 0. Thus, we can determine the sparsity M of the exponential sum (1.1) by the number of positive singular values σj.
Introducing the matrices
with orthonormal columns, we see that the columns of form an orthonormal basis of L and that the columns of are an orthonormal basis of L. Hence the orthogonal projection onto the left noise space L has the form
Consequently, we obtain that
Hence the left noise-space correlation function can be represented by
In MUSIC, one determines the lowest local minima of the left noise-space correlation function, see e.g., [1, 4, 26, 27].
Algorithm 2.8 (MUSIC via SVD)
Input: N ∈ ℕ (N ≥ 2M) number of samples, window length, (k = 0, …, N − 1) noisy sampled values of (1.1), 0 < ε ≪ 1 tolerance.
1. Compute the SVD of the rectangular Hankel matrix from (2.6), where the singular values (ℓ = 1, …, min{L, N − L + 1}) are arranged in non-increasing order. Determine the numerical rank M of (2.6) such that and . Form the matrix .
2. Calculate the left noise-space correlation function on an equispaced grid for sufficiently large S.
3. The M lowest local minima of (k = 1, …, S) form the frequency set . Set (j = 1, …, M).
4. Compute the coefficient vector as solution of the least squares problem
where denotes the vector of computed nodes.
Output: M ∈ ℕ sparsity, frequencies, coefficients (j = 1, …, M).
Let L, N ∈ ℕ with M < L ≤ N − M + 1 be given. For noisy sampled data (k = 0, …, N − 1), the MUSIC Algorithm 2.8 is relatively insensitive to small perturbations on the data (see [23, Theorem 3]).
In opposite to the MUSIC Algorithm 2.8, the following ESPRIT Algorithm is based on orthogonal projection onto a right signal space. For details see [5, 9, submitted].
Algorithm 2.9 (ESPRIT via SVD)
Input: N ∈ ℕ (N ≥ 2M) number of samples, window length, (k = 0, …, N − 1) noisy sampled values of (1.1), 0 < ε≪1 tolerance.
1. Compute the SVD of the rectangular Hankel matrix from (2.6), where the singular values (ℓ = 1, …, min{L, N − L + 1}) are arranged in non-increasing order. Determine the numerical rank M of (2.6) such that and . Form the submatrices
2. Calculate the matrix
where denotes the Moore–Penrose pseudoinverse.
3. Determine all eigenvalues (j = 1, …, M) of . Set
where Argz ∈ (−π, π] means the principal value of the argument of z ∈ ℂ\{0}.
4. Compute the coefficient vector as solution of the least squares problem
where denotes the vector of computed nodes .
Output: M ∈ ℕ sparsity, frequencies, coefficients (j = 1, …, M).
Note that in Algorithms 2.8 and 2.9 the tolerance can be theoretically chosen as . Then by Theorem 2.5, the tolerance ε is not too small for . A simple procedure for the practical choice of ε is described in the Example 5.1. By the right choice of the window length , we can recover the correct sparsity M of (1.1) and avoid the determination of spurious frequencies.
The numbers of required samples and the computational costs of the Algorithms 2.8 and 2.9 are listed in Table 2. Thus, the main disadvantages of these algorithms are the high computational costs for large sparsity M, caused mainly by the SVD. Therefore, in Potts and Tasche [28], we have suggested to use a partial SVD (based on partial Lanczos bidiagonalization) instead of a complete SVD. For both Algorithms 2.8 and 2.9, one needs too many operations in the case of large sparsity M, see Table 2.

Table 2. Computational costs for the Algorithms 2.8 and 2.9 in the case of N given samples, where S is a large even integer so that all frequencies φj are of the form with .
3. Sparse Fast Fourier Transform
In this section, we apply Algorithm 2.8 (MUSIC) resp. Algorithm 2.9 (ESPRIT) to the reconstruction of sparse trigonometric polynomials. Clearly, one can approximate the unknown frequencies φj of the exponential sum (1.1) by fractions. Therefore, we assume that the unknown frequencies φj of (1.1) are fractions with , where S is a large even integer. Replacing the variable x by Sx in (1.1), we obtain the new exponential sum (1.2). Then (1.2) is a 1-periodic trigonometric polynomial with sparsity M. Consequently we consider the spectral estimation problem (P2) as mentioned in Section 1. A fast algorithm, which solves the problem (P2) or (P2*), is called sparse fast Fourier transform (sparse FFT). In recent years many sublinear algorithms for sparse FFTs were proposed, see Section 1 and Remark 3.1.
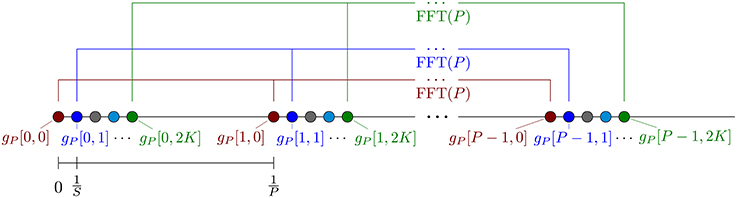
In the following, we propose a new deterministic sparse FFT for solving the problem (P2) of a trigonometric polynomial (1.2) with large sparsity M. Using divide–and–conquer technique, we split the trigonometric polynomial (1.2) of large sparsity M into some trigonometric polynomials of lower sparsity and determine corresponding samples. Here we borrow an idea from sparse FFT in Christlieb et al. [12] and use shifted sampling of (1.2). For a positive integer P ≤ S and a parameter K ∈ ℕ, K ≥ 2, we construct a discrete array of samples of size P×(2K + 1) via
For each k = 0, …, 2K we form the discrete Fourier transform (DFT) of length P and obtain
The fast Fourier transform (FFT) allows the rapid computation of this DFT of length P in (P log P) operations. In Figure 1, the sampling scheme and the applied DFTs are visualized. Next, for each ℓ = 0, …, P − 1, it follows that
Now we define the index sets
Such that
Consequently, for each ℓ = 0, …, P − 1, we may interpret ĝP[ℓ, k] (k = 0, …, 2K) as samples of a trigonometric polynomial with frequencies supported only on the index set ⊂ {ω1, …, ωM}, where the samples are taken at the nodes k∕S (k = 0, …, 2K). In simplified terms, the trigonometric polynomial (1.2) is partitioned into P many trigonometric polynomials of smaller sparsity.
Next, we use K ∈ ℕ, K ≥ 2, as sparsity cut-off parameter. This means for each ℓ = 0, …, P − 1, we apply Algorithm 2.8 resp. 2.9 to the “samples” (k = 0, …, 2K) and we check if we can uniquely identify all frequencies ωj, j ∈ IP(ℓ), i.e., if the determined sparsity Mℓ: = M from Algorithm 2.8 resp. 2.9 fulfills Mℓ < K. In this case, we use the obtained local fractions to compute the frequencies by rounding to nearest integer and we use the corresponding coefficients cj.
When the condition |IP(ℓ)| < K is fulfilled for all ℓ = 0, …, P − 1, this approach requires (2K + 1)P samples of g and 2K + 1 FFTs of length P. The computational costs for the corresponding algorithms are listed in Table 3.

Table 3. Computational cost of one iteration step of Algorithm 3.2 in the case of (2K + 1)P given samples (3.1).
If we cannot uniquely identify all frequencies, i.e., if |IP(ℓ)| ≥ K for some ℓ, then we form iteratively the new trigonometric polynomial
where I is the union of all IP(ℓ) with the property |IP(ℓ)| < K. In the next iteration step, we choose a positive integer P1 ≤ S different from P and repeat the method on the trigonometric polynomial g1. In doing so, we can compute the values
by the non-equispaced fast Fourier transform (NFFT) [29] in (P1(K logK + |I|)) arithmetic operations.
We perform additional iterations until all frequencies can be identified, i.e., if |IP1(ℓ)| < K for all ℓ = 0, …, P1 − 1. Note that our algorithm is related to the sparse FFT proposed in Christlieb et al. [12]. But here we use the methods of Section 2, if aliasing with respect to modulo P occurs.
Remark 3.1 (Relations to other sparse FFTs) In Hassanieh et al. [15], an algorithm for the problem (P2*) is presented, which allows to determine the (unknown) support I and the Fourier coefficients cj from (M log S) samples with computational cost of (M log S) operations, as well as a second algorithm, which allows the M-sparse ℓ2 best approximation of the Fourier coefficients of g from (M log(S) log(S∕M)) samples with computational cost of (M log(S) log(S∕M)) operations. As mentioned in the introduction, preliminary tests of the implementation [21] suggest that this method may also work for the problem (P2), if an upper bound for the sparsity of the signal is used as sparsity input parameter. In Indyk et al. [30], another variant was discussed, where the number of samples is (M logS)(log logS)(1) and the computational cost is (M log2S)(log logS)(1).
Recently in Indyk and Kapralov [31], a result was presented for the multivariate case where the number of required samples is (M log S) for constant dimensions d and the computational cost is (Sd log (1)S). In general the exact constants, especially the dependence on d, are unknown due to missing implementations. For instance the number of samples (M log S) of the last mentioned algorithm contains a factor of d(d), see Section [31, Section 4].
Moreover, a deterministic sparse FFT, using the Chinese Remainder Theorem, was presented in [13] for the univariate case and in Iwen [32] for the multivariate case, which takes (d4M2 log4(dS)) samples and arithmetic operations. This means there is neither a exponential/super-exponential dependency on the dimension d ∈ ℕ nor a dependency on a failure probability in the asymptotics of the number of samples and arithmetic operations for this method. Besides this deterministic algorithm, there also exists a randomized version which only requires (d4M log4(dS)) samples and arithmetic operations.
Recently, another sparse FFT, which is based on a multiscale approach, was presented in Christlieb et al. [12] as an extension of the method [11]. Their algorithm is able to handle (additive) noise and requires (M log(S∕M)) on average.
For further references on the sparse FFT we refer to the nice webpage http://groups.csail.mit.edu/netmit/sFFT/. Despite the fact that the computational cost of the sparse FFT is lower, it is not clear which algorithm is indeed faster and more stable for the practical problems mentioned in the Section 5.
We stress again that it is already well known that one can use Prony-type methods for the sparse FFT, see e.g., Heider et al. [33]. Using the proposed splitting approach, one can significantly decrease the high computational cost of MUSIC and ESPRIT, but keep the numerical stable evaluation. Clearly one can combine the suggested method with a reconstruction of the non-zero Fourier coefficients in a dimension incremental way [34]. □
All of the methods described in Section 2 apply an SVD and use the tolerance ε as a relative threshold parameter to determine the local sparsity Mℓ of the signal. A good choice of this parameter may depend without limitation on noise in the sampling values of the trigonometric polynomial g and on the smallest distance between two frequencies, where this distance may change for each ℓ ∈ {0, …, P − 1} in each iteration. We propose to use a (small) list of possible relative threshold parameters ε, which are tested for each ℓ ∈ {0, …, P − 1} in each iteration.
Our sparse FFT for recovery of a trigonometric polynomial (1.2) with large sparsity M reads as follows:
Algorithm 3.2 (Sparse FFT via MUSIC resp. ESPRIT, see Algorithm 6.1 for detailed listing with extended parameter list).
Input: S ∈ 2ℕ frequency grid parameter, K ∈ ℕ (K ≥ 2) Hankel matrix size parameter, P ∈ ℕ (P ≤ S) initial FFT length, 1-periodic sparse trigonometric polynomial (1.2) of unknown sparsity M ∈ ℕ with frequencies in perturbed by noise.
1. For each k = 0, …, 2K, sample , s = 0, …, P − 1, and compute by FFT of .
2. for ℓ = 0, …, P − 1
2.1. Apply Algorithm 2.8 resp. 2.9 with L: = K and N: = 2K + 1 on the values to obtain the local sparsity Mℓ: = M and the local fractions for m = 1, …, Mℓ. If Mℓ ≥ K, then go to step 2 and continue with next ℓ. Otherwise, compute the local frequencies by rounding to nearest integer.
2.2. Compute the local coefficients cℓ, m as least squares solution of the overdetermined Vandermonde system
2.3. If the residual of (3.4) is small (see step 3.3.6 of Algorithm 6.1), then append the frequencies ωℓ, m (m = 1, …, Mℓ) to the frequency set Ω.
3. If the (global) residual
is small, then exit the algorithm. Otherwise, form the new trigonometric polynomial (3.3). In the next iteration step choose a positive integer P1 ≤ S different from P, sample (3.3) on for s = 0, …, P1 − 1 and k = 0, …, 2K, and repeat the above method.
Output: set of recovered frequencies ωj (j = 1, …, M), M: = |Ω| detected sparsity, cj ∈ ℂ coefficient related to ωj (j = 1, …, M).
For (2K + 1)P given samples (3.1), the computational cost for one iteration of Algorithm 3.2 is shown in Table 3.
If we take (2K + 1)P = (M) samples, then we obtain minimal computational cost for the parameters K = (M1∕3) and P = (M2∕3). For this case, we compare the numbers of required samples and computational costs for different methods of spectral estimation in Table 4 such as sparse FFT via MUSIC, sparse FFT via ESPRIT, MUSIC, ESPRIT, and classical FFT. As we can see, the sparse FFT via ESPRIT is very useful for the spectral estimation by a relatively low number of samples and low computational cost.
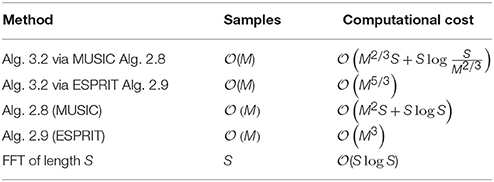
Table 4. Numbers of required samples and computational costs using the splitting approach for one iteration of Algorithm 3.2 as well as for Algorithms 2.8 and 2.9 in the case K = (M1∕3), P = (M2∕3) and M ≈ L∕2 ≈ N∕4.
4. Reconstruction of Multivariate Trigonometric Polynomials
Let d, M ∈ ℕ with d > 1 be given. We consider the d-variate exponential sum of sparsity M
for with non-zero coefficients cj ∈ ℂ and distinct frequency vectors . Here the dot in the exponent denotes the usual scalar product in ℝd. Note that the function (4.1) is a d-variate trigonometric polynomial of sparsity M which is 1-periodical with respect to each variable. Let Ω: = {ω1, …, ωM} be the set of the frequency vectors.
Assume that it is known a priori that ωj are contained in a frequency set Γ ⊂ ℤd. Then the cardinality of Γ satisfies |Γ| ≥ M. Examples of possible frequency sets Γ are the cube and the symmetric hyperbolic cross
For given z ∈ ℤd and S ∈ ℕ, the set
is called rank–1 lattice, where 1: = (1, …, 1)T. Note that xk = xk+nS for k = 0, …, S − 1 and n ∈ ℤ. For given Γ ⊂ ℤd, there exists a reconstructing rank-1 lattice Λ(z, S) such that the matrix
fulfills the condition (see [35] and [36, Section 3.2])
Then we consider the following spectral estimation problem:
(P3) Assume that ωj ∈ Γ (j = 1, …, M) and that Λ(z, S) is a reconstructing rank–1 lattice with respect to Γ. Recover the sparsity M ∈ ℕ, all frequencies ωj ∈ Γ as well as all non-zero coefficients cj ∈ ℂ of the d-variate exponential sum (4.1), if noisy sampled data
for all k = 0, …, 2L − 2 are given, where xk ∈ Λ(z, S), S ≥ L > M and ek ∈ ℂ are small error terms.
For simplicity we discuss only noiseless data. Let be the response matrix of the given data. Then HL is a Hankel matrix. Further we introduce the rectangular Fourier-type matrix
From (4.2) it follows in the case L = S that and hence for all x ∈ ℂM
Consequently, all positive singular values of FS, M are equal to and cond2FS, M = 1.
The matrix HL can be represented in the form
The ranges of HL and FL, M coincide in the noiseless case by (4.3). The range of FL, M is a proper subspace of ℂL. This subspace is called left signal space L. The left signal space L is of dimension M and is generated by the M columns eL(ωj) (j = 1, …, M), where
Note that for each ω ∈ Γ. The left noise space L is defined as the orthogonal complement of L in ℂL. The dimension of L is equal to L − M > 0.
By QL we denote the orthogonal projection onto the left noise space L. Since eL(ωj) ∈ L (j = 1, …, M) and L⊥L, we obtain that
If ω ∈ Γ \ Ω, then the vectors are linearly independent for S ≥ L > M. This can be seen as follows: For distinct ω, ω′ ∈ Γ, it follows by [36, Lemma 3.1] that
Consequently the vectors
and eL(ω) with ω ∈ Γ \ Ω are linearly independent for S ≥ L > M, since the square Vandermonde matrix
is invertible for each L ≥ M + 1. Hence
i.e. QLeL(ω) ≠ 0.
Thus, the frequency vectors can be determined via the M zeros resp. lowest local minima of the left noise-space correlation function
or via the M peaks of the left imaging function
Similar to Section 2, one can determine the left noise-space correlation function resp. the left imaging function on Γ by using SVD of the response matrix HL.
Now, we proceed analogously to Section 3. For a positive integer P ≤ S and a parameter K ∈ ℕ, K ≥ 2, we construct the sampling array of (4.1) of size P × (2K + 1) via
As in the univariate case, for each k = 0, …, 2K we form the DFT of length P
For each ℓ = 0, …, P − 1, we obtain that
Introducing the index sets
it follows that
This means for each ℓ = 0, …, P − 1, we may interpret ĝP[ℓ, k] (k = 0, …, 2K) as samples of a multivariate trigonometric polynomial with frequencies supported on the index set {ωj}j ∈ IP(ℓ) ⊂ {ω1, …, ωM}, where the samples are taken at the nodes (k = 0, …, 2K). In Figure 2, a two-dimensional example is shown which visualizes the partitioning by the index sets IP(ℓ).
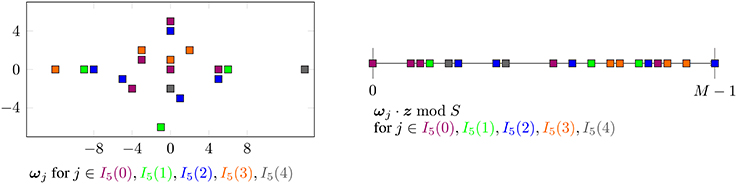
Figure 2. Illustration of an example frequency index set and corresponding one-dimensional frequencies ωj · z mod S partitioned by IP(ℓ) with parameters P: = 5, z: = (1, 33)T, S: = 37.
Next, we apply Algorithm 2.8 resp. 2.9 with L: = K and N: = 2K + 1 on the values (k = 0, …, 2K) for each ℓ = 0, …, P − 1 to obtain the local sparsity Mℓ = M and the local fractions for m = 1, …, Mℓ. Afterwards, we compute the one-dimensional frequencies by rounding to nearest integer. We transform these one-dimensional frequencies ωℓ, m into their d-dimensional counterparts ωℓ, m ∈ Γ using the relation ωℓ, m · z ≡ ωℓ, m (mod S) given by the reconstructing rank-1 lattice Λ(z, S). Then we compute coefficients cℓ, m from the samples ĝP[ℓ, k] (k = 0, …, 2K) by solving the corresponding overdetermined Vandermonde system. If we cannot identify all the frequencies, i.e., if |IP(ℓ)| ≥ K for some indices ℓ, we consider the new trigonometric polynomial
in an additional iteration, where the index set I contains all index sets IP(ℓ) with |IP(ℓ)| < K. In the next iteration, we choose a positive integer P1 ≤ S different from P and repeat the method for the trigonometric polynomial g1. In doing so, we compute the values
of the second sum in (4.4) evaluated at the nodes with the univariate NFFT [29] in (P1(K log K + |I|)) arithmetic operations. We perform additional iterations until all frequencies can be identified, i.e. |IP1(ℓ)| < K for all ℓ = 0, …, P1 − 1.
We modify Algorithm 3.2 from Section 3 as described above and additionally in the following way. Here, we describe the changes in the detailed listing (see Algorithm 6.1) of Algorithm 3.2. In step 1, we sample the multivariate trigonometric polynomial at the nodes . In step 3.3.3, we compute the local frequencies for m = 1, …, Mℓ. Next, we compute the d-dimensional counterparts ωℓ, m of the one-dimensional frequencies ωℓ, m using the relation ωℓ, m · z ≡ ωℓ, m (mod S). In step 3.3.4, we filter the frequencies ωℓ, m by removing non-unique ones and by keeping only those with ωℓ, m · z ≡ ℓ(mod P). We remark that we have to modify step 3.3.4 and that we have to perform the conversion of one-dimensional frequencies ωℓ, m to their d-dimensional counterparts ωℓ, m before the filtering, since the conditions ωℓ, m · z ≡ ℓ(mod P) and ωℓ, m ≡ ℓ(mod P) are not equivalent in general if P is not a divisor of S.
5. Numerical Experiments
In this section, we present some numerical results for Algorithm 3.2. The related software is available from the authors' homepage. All computations are performed in MATLAB with IEEE double–precision arithmetic. First we consider noiseless sampled data and later the case, where the sampled data are perturbed by additive (white) Gaussian noise. Finally we present some numerical results for the modified Algorithm 3.2 of Section 4.
5.1. Noiseless Sampled Data
Example 5.1 From noiseless sampled values, we reconstruct 100 trigonometric polynomials (1.2) of sparsity M = 256 with random frequencies and random coefficients cj on the unit circle. We set the array of relative SVD threshold values epsilon_svd_list: = [10−3, 10−4, …, 10−8], the parameter , the absolute value of minimal non-zero coefficients and the maximal number of iterations R: = 10, see Algorithm 6.1 for the extended parameter list. Applying the sparse FFT Algorithm 3.2 with MUSIC in the case S = 216 with parameters K ∈ {6, 12, 16} and P ∈ {16, 32, 64, 128}, we can successfully detect all integer frequencies ωj. In Table 5, the column “iterations” depicts the maximal number of iterations actually used by the Algorithm 3.2 (computed over 100 trigonometric polynomials). The column “samples” contains the maximal number of sampled values used by the Algorithm 3.2. The column “ℓ2–errors” shows the maximal relative ℓ2–error of the coefficients, which are locally computed in step 2.2 of Algorithm 3.2. The column “updated ℓ2–errors” shows the maximal relative ℓ2–error of the coefficients, which are determined by additionally solving one large Vandermonde system at the end of Algorithm 3.2 with all frequencies as well as all samples of (1.2). For comparison, the classical FFT of length 216 requires 216 samples and the resulting ℓ2–error is 2.6e-16. The minimal number of samples for the cases K ∈ {6, 12, 16} and P ∈ {16, 32, 64, 128} is reached for K = P = 16 with 1716 samples, the next smallest number of samples is 1725 for K = 12 and P = 32. If we do not use the splitting approach (P = 1 and R = 1), we observe that the detection of some frequencies fails for exactly 1 of the 100 signals for K = 750 and the detection of all frequencies of all 100 signals succeeds for K = 850 requiring 1701 samples. This number of samples is very close to the minimum of 1716 samples from above. However, a direct application of MUSIC method (entry K = 850) has distinctly more computational cost than using the sparse FFT Algorithm 3.2. Note that R denotes the maximal number of iterations in Algorithm 6.1, the detailed description of Algorithm 3.2. □
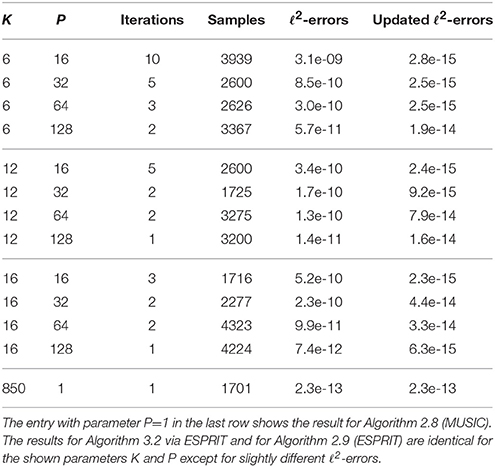
Table 5. Results for Algorithm 3.2 via MUSIC for frequency grid parameter S = 216 and sparsity M = 256 with random coefficients on the unit circle.
Example 5.2 Now we apply Algorithm 3.2 via ESPRIT with the same parameters as in Example 5.1. Then we obtain identical results for the number of iterations and samples as well as almost identical ℓ2-errors, but Algorithm 3.2 via ESPRIT has lower computational cost. If we do not use the splitting approach (P = 1 and R = 1), we observe that the detection of some frequencies fails for exactly 2 of the 100 signals for K = 750 and the detection of all frequencies of all 100 signals again succeeds for K = 850 requiring 1701 samples.
Additionally, we apply the implementation [21] of the sfft version 3 algorithm. The number of used samples is 7669, which is about two to four times the number of samples for the MUSIC and ESPRIT algorithm in Table 5, and the maximal relative ℓ2-error of the coefficients is 3.6e-04, which is about five orders of magnitude larger. □
Example 5.3 We generate 100 random trigonometric polynomials (1.2), where the coefficients cj are drawn uniformly at random from [−1, 1] + [−1, 1]i with . We set the absolute value of minimal non-zero coefficients . For the cases K ∈ {6, 12, 16} and P ∈ {16, 32, 64, 128}, we apply Algorithm 3.2 via ESPRIT. We obtain results almost identical to the ones from Example 5.2. This means, all frequencies of all 100 signals are correctly detected and the maximal relative ℓ2-errors differ slightly from those in Table 5. The maximal numbers of iterations and samples are identical.
Additionally, we apply the implementation [21] of the sfft version 3 algorithm. For each signal, the number of taken samples is 7669. Only for 16 of the 100 signals, all frequencies are detected correctly, whereas between 1 and 7 frequencies are not correctly detected for 84 signals. □
Example 5.4 Next we apply Algorithm 3.2 via ESPRIT for signals with higher sparsity. From noiseless sampled values, we reconstruct 100 trigonometric polynomials (1.2) of sparsity M = 1024 with random frequencies and random coefficients cj on the unit circle. The results for the frequency grid parameter S: = 222 are shown in Table 6. The minimal number of samples is about six times higher compared to the results in Table 5.
In general, we observe that the maximal number of used iterations decreases for increasing initial FFT length P ∈ {64, 128, 256, 512} as well as for increasing values K ∈ {8, 10, 12}. In the cases, where all frequencies of all the 100 trigonometric polynomials are correctly detected, the number of required samples first decreases and later increases again for increasing initial FFT length P and fixed values K. The reason for this is that the number of samples per iteration increases for growing FFT length, while the number of used iterations decreases until its minimum one is reached.
Again, we apply the implementation [21] of the sfft version 3 algorithm. Here, the number of used samples is 31718, which is up to three times the number of samples of Algorithm 3.2 via ESPRIT in Table 6, and the maximal relative ℓ2-error of the coefficients is 3.6e-04, which is about five orders of magnitude larger than in Table 6. □
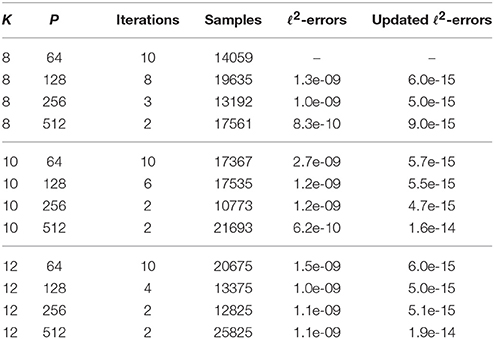
Table 6. Results for Algorithm 3.2 via ESPRIT for frequency grid parameter S = 222 and sparsity M = 1024 with random coefficients on the unit circle.
5.2. Noisy Case
In this subsection, we test the robustness to noise of Algorithm 3.2. For this, we perturb the samples of the trigonometric polynomials g from (1.2) by additive complex white Gaussian noise with zero mean and standard deviation σ, i.e., we have measurements , where ηk, s ∈ ℂ are independent and identically distributed complex Gaussian noise values. Then, we may approximately compute the signal-to-noise ratio (SNR) in our case by
Correspondingly, we choose for a targeted SNR value. For the numerical computations in MATLAB, we generate the noise by *(randn + 1i*randn). Moreover, we choose the parameter εspatial: = 5σ and this means that the absolute value of the noise |ηk, s| ≤ εspatial for more than 99.9998% of the noise values ηk, s. Since we assume that the absolute value of the noise throughout this paper, we should choose the SNR such that , which yields .
Example 5.5 As in Example 5.1, we generate 100 trigonometric polynomials (1.2) of sparsity M = 256 with random frequencies and random coefficients cj from the unit circle. We set the frequency grid parameter S = 216, the signal sparsity M = 256, the array of relative SVD threshold values epsilon_svd_list: = [10−3, 10−4, …, 10−8] and the maximal number of iterations R: = 10. Here, we set the absolute value of minimal non-zero coefficients and we use the parameters P ∈ {32, 64, 128} and K ∈ {12, 24}. For possible SNR values, we have and we consider the SNR values 1010, 108, and 106 in our numerical tests. The results of Algorithm 3.2 via ESPRIT are presented in Table 7. Additionally, we test the sparsity cut-off parameter K2 ∈ ℕ differently from the Hankel matrix size parameter K, see Algorithm 6.1. Here, we use the parameter combinations (K, K2) ∈ {(12, 6), (12, 12), (24, 12)}. In general, we observe that we require more samples for SNR = 106 than for SNR = 108 and again more for SNR = 108 than for SNR = 1010. The relative errors are about one order of magnitude larger for SNR = 106 than for SNR = 108 as well as for SNR = 108 than for SNR = 1010, since the maximal noise values ηk, s are larger by about one order of magnitude with high probability each time. Moreover, the maximal number of samples in the noisy case is higher than in the noiseless case, cf. Table 5. For some parameter combinations at SNR = 108, exactly one of the 100 signals is not correctly detected and this is indicated by the entry “–” in the column “ℓ2-errors” resp. “updated ℓ2-errors.” For SNR = 106 with K = 12, K2 = 6, and P = 64 exactly one frequency at three of the 100 signals is not correctly detected, whereas all frequencies of all 100 signals for SNR = 106 are correctly detected in the other cases shown in Table 7. All parameters of (1.2) are correctly detected in the case SNR = 1010 for the parameter combinations (K, K2) ∈ {(12, 6), (12, 12), (24, 12)} and P = 32. For the considered test parameters, the choices (K, K2) ∈ {(12, 6), (24, 12)}, which yield a higher oversampling within the ESPRIT algorithm, give slightly better results compared to the choice K = K2 = 12.
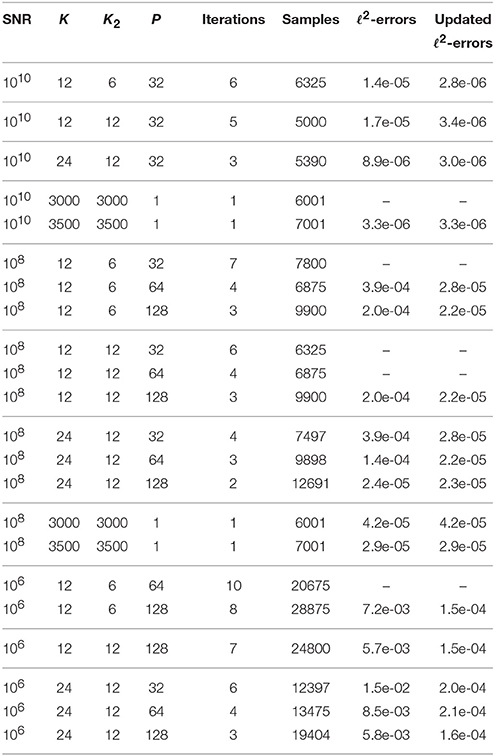
Table 7. Results for Algorithm 3.2 via ESPRIT for frequency grid parameter S = 216 and sparsity M = 256 with noisy data.
Additionally, we apply the implementation [21] of the sfft version 3 algorithm. We remark that this particular algorithm is not suited for noisy samples. The number of taken samples is 7669 for all signals, which is about 50 percent higher than for Algorithm 3.2 at SNR = 1010 and similar at SNR = 108. In the cases SNR = 1010 and SNR = 108, all frequencies of all 100 signals are correctly detected and the maximal relative ℓ2-errors of the Fourier coefficients are about 3.6e-04. For SNR = 106, all frequencies of 94 of the 100 signals are correctly detected and up to four frequencies at four of the 100 signals are not correctly detected. □
Example 5.6 Additionally, we generate 100 random trigonometric polynomials (1.2), where the coefficients cj are drawn uniformly at random from [−1, 1] + [−1, 1]i with . We set the absolute value of minimal non-zero coefficients . In the case SNR = 108, we observe in each considered parameter combination that the correct detection of one or two frequencies fails for several of the 100 trigonometric polynomials. The most likely reason is the fact that the smallest coefficient can be very close to the noise level. If we decrease the noise by one order of magnitude, i.e. SNR = 1010, the frequency detection succeeds for all considered parameter combinations.
Furthermore, we generate 100 random trigonometric polynomials (1.2), where the coefficients cj are drawn uniformly at random from [−1, 1] + [−1, 1]i with . Then we set the absolute value of minimal non-zero coefficients . This means that the smallest possible coefficient as well as the parameter εfc_min are by one order of magnitude larger than before. Now in both of the cases SNR = 1010 and SNR = 108, we observe for each parameter combination (K, K2) ∈ {(12, 6), (12, 12), (24, 12)} and P ∈ {32, 64, 128} that all frequencies of all trigonometric polynomials are correctly detected.
For results of the implementation [21] of the sfft version 3 algorithm, we refer to Example 5.3. □
5.3. Reconstruction of 6-variate Trigonometric Polynomials
Finally we test the modified Algorithm 3.2 of Section 4 for the reconstruction of six-variate trigonometric polynomials with the sparsity M = 256.
Example 5.7 We choose the index set Γ of possible frequency vectors as the six-dimensional hyperbolic cross of cardinality 169209. Further we use the reconstructing rank-1 lattice Λ(z, S) with generating vector z = (1, 33, 579, 3628, 21944, 169230)T and rank-1 lattice size S = 1105193, see Kämmerer et al. [37, Table 6.2]. We generate 100 random trigonometric polynomials (4.1) with sparsity M = 256, where the frequency vectors ωj (j = 1, …, M) are chosen uniformly at random from Γ (without repetition) and the corresponding coefficients cj are randomly chosen on the unit circle. We set the array of relative SVD threshold values epsilon_svd_list: = [10−3, 10−4, …, 10−8], the absolute value of minimal non-zero coefficients , and the maximal number of iterations R: = 10. In the noiseless case, we set the parameter , and in the noisy case as described in Section 5.2. The results of the modified Algorithm 3.2 via ESPRIT are presented in Table 8.
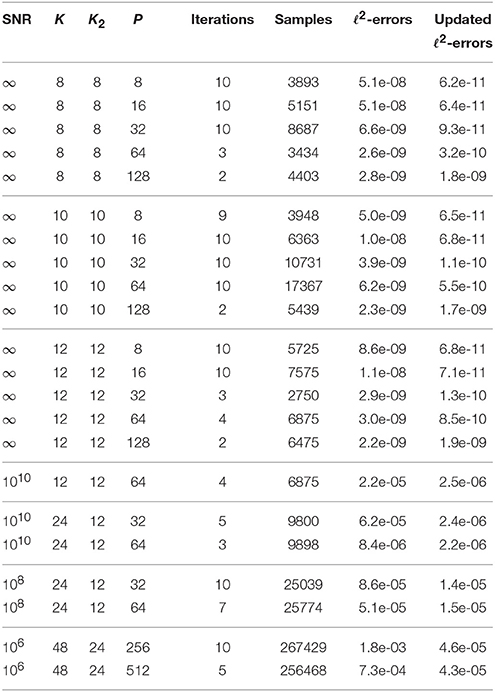
Table 8. Results of the modified Algorithm 3.2 via ESPRIT with sparsity M = 256, frequency vectors within six-dimensional hyperbolic cross index set , and reconstructing rank-1 lattice Λ(z, S) with z = (1, 33, 579, 3628, 21944, 169230)T and S = 1105193.
The columns of Table 8 have the same meaning as in Section 5.2. For the noiseless case, i.e., “SNR = ∞,” we observe the same behavior as in the one-dimensional case in Section 5.1. The detection of all frequency vectors of all 100 trigonometric polynomials (4.1) succeeds for K = K2 ∈ {8, 10, 12} and P ∈ {8, 16, 32, 64, 128}. For the noisy case, the results are worse than in Table 7 of the one-dimensional case. The reason for this is that we have a bijective mapping between six-dimensional ωj and one-dimensional frequencies ωj by means of the reconstructing rank-1 lattice, ωj · z ≡ ωj(modS), and the rank-1 lattice size S influences how close two distinct one-dimensional fractional frequencies and may get in the ESPRIT algorithm, see also Figure 2.
We tried to apply the implementation [21] of the sfft version 3 algorithm in this test setting. However, the implementation failed with an internal error caused by the used problem size n = S = 1105193 and sparsity M = 256. Another test run with rank-1 lattice size S = 221 = 2097152 yielded 7938 samples and a maximal relative ℓ2-error of 6.8e-04, where the latter is about 4 orders of magnitude larger than the results in Table 8. Moreover, we consider the noisy case. Again, we remark that the implementation [21] is not suited for noisy samples. For SNR = 1010, the detection of one frequency fails for one of the 100 signals. If we increase the SNR to 108, then between one and 9 frequencies are not correctly detected for 81 of the 100 signals. □
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The first and last named author gratefully acknowledge the funding by the European Union and the Free State of Saxony (EFRE/ESF NBest-SF). The results of this paper were first presented during the Dagstuhl Seminar 15251 on “Sparse modeling and multi-exponential analysis” (June 14 – 19, 2015). Moreover, the authors would like to thank the referees for their valuable suggestions.
References
1. Manolakis DG, Ingle VK, Kogon SM. Statistical and Adaptive Signal Processing. Boston, MA: McGraw-Hill (2005).
3. Plonka G, Tasche M. Prony methods for recovery of structured functions. GAMM–Mitt. (2014) 37:239–58. doi: 10.1002/gamm.201410011
4. Schmidt RO. Multiple emitter location and signal parameter estimation. IEEE Trans Antennas Propag. (1986) 34:276–80.
5. Roy R, Kailath T. ESPRIT—estimation of signal parameters via rotational invariance techniques. IEEE Trans Acoustic Speech Signal Process. (1989) 37:984–94.
6. Hua Y, Sarkar TK. Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise. IEEE Trans Acoust Speech Signal Process. (1990) 38:814–24.
7. Golub GH, Milanfar P, Varah J. A stable numerical method for inverting shape from moments. SIAM J Sci Comput. (1999) 21:1222–43.
8. Roy R, Kailath T. ESPRIT—estimation of signal parameters via rotational invariance techniques. In: Auslander L, Grünbaum FA, Helton JW, Kailath T, Khargoneka P, Mitter S, editors. Signal Processing, Part II. Vol. 23 of IMA Volumes in Mathematics and its Applications. New York, NY: Springer (1990). pp. 369–411.
9. Potts D, Tasche M. Parameter estimation for nonincreasing exponential sums by Prony-like methods. Linear Algebra Appl. (2013) 439:1024–39. doi: 10.1016/j.laa.2012.10.036
10. Pereyra V, Scherer G. Exponential data fitting. In: Pereyra V, Scherer G, editors. Exponential Data Fitting and its Applications. Sharjah: Bentham Science Publishers; IEEE Computer Society (2010). pp. 1–26.
11. Lawlor D, Wang Y, Christlieb A. Adaptive sub-linear time Fourier algorithms. Adv Adapt Data Anal. (2013) 5:25. doi: 10.1142/S1793536913500039
12. Christlieb A, Lawlor D, Wang. A multiscale sub-linear time Fourier algorithm for noisy data. Appl Comput Harmon Anal. (in press). doi: 10.1016/j.acha.2015.04.002
13. Iwen MA. Combinatorial sublinear-time Fourier algorithms. Found Comput Math. (2010) 10:303–38. doi: 10.1007/s10208-009-9057-1
14. Ben-Or M, Tiwari P. A deterministic algorithm for sparse multivariate polynomial interpolation. In: Twentieth Annual ACM Symposium on the Theory of Computing. New York, NY: ACM Press (1988). pp. 301–9.
15. Hassanieh H, Indyk P, Katabi D, Price E. Nearly optimal sparse Fourier transform. In: Proceedings of the Forty-fourth Annual ACM Symposium on Theory of Computing. New York, NY: ACM (2012). pp. 563–78.
16. Gilbert AC, Indyk P, Iwen M, Schmidt L. Recent developments in the sparse Fourier transform: a compressed Fourier transform for big data. IEEE Signal Proc Mag. (2014) 31:91–100. doi: 10.1109/MSP.2014.2329131
17. Rauhut H. Random sampling of sparse trigonometric polynomials. Appl Comput Harmon Anal. (2007) 22:16–42. doi: 10.1016/j.acha.2006.05.002
18. Kunis S, Rauhut H. Random sampling of sparse trigonometric polynomials II, orthogonal matching pursuit versus basis pursuit. Found Comput Math. (2008) 8:737–63. doi: 10.1007/s10208-007-9005-x
19. Gröchenig K, Pötscher BM, Rauhut H. Learning trigonometric polynomials from random samples and exponential inequalities for eigenvalues of random matrices. arXiv:math/0701781v2. (2010).
20. Foucart S, Rauhut H. A mathematical introduction to compressive sensing. In: Applied and Numerical Harmonic Analysis. New York, NY: Birkhäuser;Springer (2013).
21. Schumacher J. sFFT 0.1.0 (2013). Available online at: http://spiral.net/software/sfft.html.
22. Schumacher J, Püschel M. High-performance sparse fast Fourier transforms. In: Proceedings of IEEE Workshop on Signal Processing Systems (SIPS). Belfast, UK: IEEE (2014). pp. 1–6.
23. Liao W, Fannjiang A. MUSIC for single-snapshot spectral estimation: stability and super-resolution. Appl Comput Harmon Anal. (2016) 40:33–67. doi: 10.1016/j.acha.2014.12.003
24. Peter T, Potts D, Tasche M. Nonlinear approximation by sums of exponentials and translates. SIAM J Sci Comput. (2011) 33:314–34. doi: 10.1137/100790094
25. Potts D, Tasche M. Parameter estimation for multivariate exponential sums. Electron Trans Numer Anal. (2013) 40:204–224.
26. Fannjiang AC. The MUSIC algorithm for sparse objects: a compressed sensing analysis. Inverse Problems (2011) 27:32. doi: 10.1088/0266-5611/27/3/035013
27. Kirsch A. The MUSIC algorithm and the factorization method in inverse scattering theory for inhomogeneous media. Inverse Problems (2002) 18:1025–1040. doi: 10.1088/0266-5611/18/4/306
28. Potts D, Tasche M. Fast ESPRIT algorithms based on partial singular value decompositions. Appl Numer Math. (2015) 88:31–45. doi: 10.1016/j.apnum.2014.10.003
29. Keiner J, Kunis S, Potts D. Using NFFT3 - a software library for various nonequispaced Fast Fourier Transforms. ACM Trans Math Softw. (2009) 36: 1–30. doi: 10.1145/1555386.1555388
30. Indyk P, Kapralov M, Price E. (Nearly) sample-optimal sparse Fourier transform. In: Proceedings of the Forty-fourth Annual ACM Symposium on Theory of Computing. Portland: ACM (2014). pp. 563–78.
31. Indyk P, Kapralov M. Sample-optimal Fourier sampling in any constant dimension. In: Foundations of Computer Science (FOCS), 2014 IEEE 55th Annual Symposium on. Philadelphia, PA (2014). pp. 514–23.
32. Iwen MA. Improved approximation guarantees for sublinear-time Fourier algorithms. Appl Comput Harmon Anal. (2013) 34:57–82. doi: 10.1016/j.acha.2012.03.007
33. Heider S, Kunis S, Potts D, Veit M. A sparse prony FFT. In: 10th International Conference on Sampling Theory and Applications. Bremen (2013).
34. Potts D, Volkmer T. Sparse high-dimensional FFT based on rank-1 lattice sampling. Appl Comput Harmon Anal. (in press). doi: 10.1016/j.acha.2015.05.002
35. Kämmerer L. Reconstructing multivariate trigonometric polynomials from samples along rank-1 lattices. In: Fasshauer GE, Schumaker LL, editors. Approximation Theory XIV: San Antonio 2013. Cham: Springer International Publishing (2014). pp. 255–71.
36. Kämmerer L. High Dimensional Fast Fourier Transform Based on Rank-1 Lattice Sampling. Dissertation. Universitätsverlag Chemnitz (2014). Available online at: http://nbn-resolving.de/urn:nbn:de:bsz:ch1-qucosa-157673
37. Kämmerer L, Potts D, Volkmer T. Approximation of multivariate periodic functions by trigonometric polynomials based on rank-1 lattice sampling. J Complex. (2015) 31:543–76. doi: 10.1016/j.jco.2015.02.004
Appendix
Detailed Sparse FFT Algorithm
Algorithm 6.1 (Detailed listing of Algorithm 3.2 with extended parameter list)
Input: S ∈ 2ℕ frequency grid parameter, K ∈ ℕ Hankel matrix size parameter, K2 ∈ ℕ sparsity cut-off parameter (default value K), P ∈ ℕ initial FFT length, g 1-periodic sparse trigonometric polynomial of unknown sparsity M ∈ ℕ with frequencies in , epsilon_svd_list array of relative SVD threshold values 0 < εSVD < 1 in descending order, εspatial > 0 estimate for maximal noise value, εfc_min > 0 lower bound of absolute values of non-zero coefficients, R ∈ ℕ maximal number of iterations.
Create empty index set array Ω and coefficient array C.
for iteration r: = 1, …, R
1. Construct the discrete array of samples of g of length P×(2K + 1) via
2. Compute for each k = 0, …, 2K an FFT of length P and obtain array ĝP of length P×(2K + 1), for ℓ = 0, …, P − 1, if P > 1. Otherwise if P = 1, then set ĝP[ℓ, k]: = gP[ℓ, k] for ℓ = 0, …, P − 1.
3. for ℓ: = 0, …, P − 1
3.1. If ∥ĝP[ℓ, 0:2K]∥∞∕P < εspatial, then go to 3. and continue with next ℓ.
3.2. Set variable found_svd: = 0.
3.3. for εSVD in epsilon_svd_list
3.3.1. Apply Algorithm 2.8 resp. 2.9 with L: = K, N: = 2K + 1 and ε: = εSVD on the values to obtain the (local) sparsity Mℓ: = M and fractions for j = m, …, Mℓ.
3.3.2. If Mℓ ≥ K2 then go to 3.3. and continue with next (smaller) εSVD.
3.3.3. Compute local frequencies for m = 1, …, Mℓ.
3.3.4. Filter frequencies ωℓ, m by removing non-unique ones and by keeping only those where ωℓ,m ≡ ℓ (modP). Set Mℓ to number of resulting frequencies ωℓ, m.
3.3.5. Compute (local) Fourier coefficients cℓ, m as least squares solution from the overdetermined Vandermonde system .
3.3.6. If the residual , then set variable found_svd: = 1, leave for εSVD loop and go to 3.5. Otherwise, go to 3.3. and continue with next (smaller) εSVD.
3.3. end for εSVD
3.4. If found_svd ≠ 1, then go to 3. and continue with next ℓ.
3.5. If a frequency has already been found, i.e., for any m = 1, …, Mℓ, then update the corresponding coefficient C[j′] by computing .
3.6. Append new frequencies of ωℓ, m, m = 1, …, Mℓ, to array Ω and append corresponding coefficients to array C.
3. end for ℓ
4. Remove small coefficients from array C and remove corresponding frequencies from array Ω for any j′.
5. If the residual
then set Rused: = r and exit r-loop.
Otherwise, determine next prime number larger than current FFT length P and use this larger prime as P in the next iteration.
end for iteration r
Output: Detected sparsity M: = |Ω| ∈ ℕ, array of detected frequencies, array C ∈ ℂM of corresponding coefficients.
Keywords: Spectral estimation, ESPRIT, MUSIC, parameter identification, exponential sum, sparse trigonometric polynomial, sparse FFT
AMS Subject Classifications: 65T50, 42A16, 94A12.
Citation: Potts D, Tasche M and Volkmer T (2016) Efficient Spectral Estimation by MUSIC and ESPRIT with Application to Sparse FFT. Front. Appl. Math. Stat. 2:1. doi: 10.3389/fams.2016.00001
Received: 04 December 2015; Accepted: 05 February 2016;
Published: 29 February 2016.
Edited by:
Charles K. Chui, Stanford University and Hong Kong Baptist University, USAReviewed by:
Ronny Bergmann, University Kaiserslautern, GermanyHyenkyun Woo, Korea University of Technology and Education, South Korea
Copyright © 2016 Potts, Tasche and Volkmer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daniel Potts, cG90dHNAbWF0aGVtYXRpay50dS1jaGVtbml0ei5kZQ==
 Daniel Potts
Daniel Potts Manfred Tasche2
Manfred Tasche2 Toni Volkmer
Toni Volkmer