Construction of Scaling Partitions of Unity

1. Introduction

A function g : ℝ^d → ℂ is said to have the (scaling) partition of unity property with respect to a real invertible d × d matrix ${A}$ if

$\begin{array}{ll}{\displaystyle \sum _{j=-\infty }^{\infty }g}({{A}}^j\gamma )=1,\forall \gamma \in {ℝ}^d\setminus \left\{0\right\}.& (1.1)\end{array}$

Partitions of unity of this form appear in several parts of analysis, e.g., wavelet analysis and the theory for Triebel-Lizorkin spaces, and the question of how to construct them has attracted some attention. In particular, this issue comes up in connection with the analysis of tight wavelet frames in L²(ℝ^d) [1] and the more general case of dual wavelet frame pairs [2, 3].

In this paper we will give a surprisingly simple characterization of the scaling partition of unity property. In the special case where ${A}$ is an expanding matrix, i.e., a real matrix with all its eigenvalues having absolute value strictly greater than one, the characterization leads to easy ways of constructing appropriate functions g with attractive properties like high regularity and small support. Under certain conditions, nonnegativity of the function g can be guaranteed. We also discuss a class of integral transforms that can be used to generate functions with the partition of unity property. The one-dimensional version of the transform leads in a natural fashion to a definition of a recursively given family of nonuniform splines. These splines have some similarities with the classical B-splines: their regularity and support grow with the order, and they satisfy the de Boor recursion formula [4, 5]. However, there are also differences: all the splines have support within [−1, 1], and they satisfy a scaling partition of unity condition instead of the translation partition of unity condition. Finally, the key results are applied to the construction of dual pairs of wavelet frames.

The paper is organized as follows. In section 2, we characterize the scaling partition of unity condition and provide explicit and easily verifiable sufficient conditions in the case where ${A}$ is an expanding matrix. Section 3 deals with the above mentioned one-dimensional integral transform and its lifting to higher dimensions. Finally, section 4 applies the results to obtain easy constructions of wavelet frames in L²(ℝ^d) and their associated dual frames.

2. Characterization of the Partition of Unity Property

We first establish a characterization of the scaling partition of unity property. Despite its simplicity we have not been able to find it stated in the literature.

Theorem 2.1. Consider a function g : ℝ^d → ℂ and any real invertible d × d matrix ${A}$. Then the following hold:

(i) Assume that the infinite series $\sum _{j=-\infty }^{\infty }g({{A}}^j\gamma )$ is convergent for all γ ∈ ℝ^d \ {0}. Then there is a function φ : ℝ^d → ℂ such that

$\begin{array}{ll}g(\gamma )=\phi (\gamma )-\phi ({A}\gamma ),\forall \gamma \in {ℝ}^d\setminus \left\{0\right\}.& (2.1)\end{array}$

(ii) On the other hand, take any function φ : ℝ^d → ℂ such that (2.1) holds. Then, fixing any γ ∈ ℝ^d \ {0}, the series $\sum _{j=-\infty }^{\infty }g({{A}}^j\gamma )$ is convergent if and only if the two limits ${lim}_{N\to \pm \infty }\phi ({{A}}^N\gamma )$ exist.

(iii) Take again any function φ : ℝ^d → ℂ such that (2.1) holds. Then the partition of unity condition (1.1) holds if and only if the two limits ${lim}_{N\to \pm \infty }\phi ({{A}}^N\gamma )$ exist and

$\begin{array}{l}\underset{N\to -\infty }{\lim }\phi ({{A}}^N\gamma )-\underset{N\to \infty }{\lim }\phi ({{A}}^N\gamma )=1\end{array}$

for all γ ∈ ℝ^d \ {0}.

Proof. For the proof of (i), assume that the infinite series $\sum _{j=-\infty }^{\infty }g({{A}}^j\gamma )$ is convergent for all γ ∈ ℝ^d \ {0}. Then

$\begin{array}{l}g(\gamma )={\displaystyle \sum _{j=0}^{\infty }g}({{A}}^j\gamma )-{\displaystyle \sum _{j=1}^{\infty }g}({{A}}^j\gamma )={\displaystyle \sum _{j=0}^{\infty }g}({{A}}^j\gamma )-{\displaystyle \sum _{j=0}^{\infty }g}({{A}}^j{A}\gamma ).\end{array}$

Taking now $\phi (\gamma ):=\sum _{j=0}^{\infty }g({{A}}^j\gamma ),\gamma \in {ℝ}^d\backslash \left\{0\right\},$ yields the result. For the proof of (ii), by direct calculation and for any M, N ∈ ℕ,

$\begin{array}{l}{\displaystyle \sum _{j=-M}^{N}g}({{A}}^j\gamma )=\left[\phi ({{A}}^{-M}\gamma )-\phi ({{A}}^{-M+1}\gamma )\right]+[\phi ({{A}}^{-M+1}\gamma )\\ -\phi ({{A}}^{-M+2}\gamma )]+\cdots +[\phi ({{A}}^N\gamma )\\ -\phi ({{A}}^{N+1}\gamma )]\\ =\phi ({{A}}^{-M}\gamma )-\phi ({{A}}^{N+1}\gamma ).\end{array}$

Then (ii) follows immediately; and (iii) is a consequence of (ii).□

Note that the function φ satisfying (2.1) for a given function g is not unique. In the sequel φ will denote any such function, not necessarily the one constructed in the proof of Theorem 2.1.

Via Theorem 2.1, we can now show that any expanding matrix ${A}$ leads to the partition of unity property for a large class of functions g. The following result and its proof hold whenever ||·|| denotes an arbitrary norm on ℝ^d.

Proposition 2.2 Let ${A}$ be any expanding d × d matrix, and consider any function φ : ℝ^d → ℂ which is continuous at γ = 0 and satisfies the conditions that φ(0) = 1 and ${lim}_{\left|\right|\gamma \left|\right|\to \infty }\phi (\gamma )=0.$ Then the function $g(\gamma ):=\phi (\gamma )-\phi ({A}\gamma )$ satisfies the partition of unity condition (1.1).

Proof. By Lemma 5.2 in Hernandez et al. [6], a matrix ${A}$ is expanding if and only if there exist constants C ∈ (0, 1] and α > 1 such that

$\begin{array}{ll}\left|\right|{{A}}^N\gamma \left|\right|\ge C{\alpha }^N\left|\right|\gamma \left|\right|& (2.2)\end{array}$

for all γ ∈ ℝ^d and N ∈ ℕ ∪ {0}. Thus, the assumption ${lim}_{\left|\right|\gamma \left|\right|\to \infty }\phi (\gamma )=0$ immediately implies that ${lim}_{N\to \infty }\phi ({{A}}^N\gamma )=0$ for all γ ∈ ℝ^d \ {0}. Replacing γ by ${{A}}^{-N}\gamma$ in the inequality (2.2) shows that $\left|\right|{{A}}^{-N}\gamma \left|\right|\le C^{-1}{\alpha }^{-N}\left|\right|\gamma \left|\right|$ for all γ ∈ ℝ^d and N ∈ ℕ ∪ {0}; thus the assumptions imply that ${lim}_{N\to -\infty }\phi ({{A}}^N\gamma )=1.$ The result now follows from Theorem 2.1.□

Example 2.3 We first give an example of a partition of unity based on a diagonal matrix, and then a construction that works for arbitrary expanding matrices.

(i) Consider an even, continuous and nonnegative function k : ℝ → ℝ such that ${\int }_0^{\infty }k(t)dt=1.$ Then the function

$\begin{array}{l}\phi (\gamma ):={\displaystyle {\int }_{\gamma }^{\infty }k}(t)dt,\gamma \in ℝ,\end{array}$

satisfies the conditions in Proposition 2.2. Thus, for any a > 1, the function

$\begin{array}{l}g(\gamma )=\phi (\gamma )-\phi (a\gamma )={\displaystyle {\int }_{\gamma }^{a\gamma }k}(t)dt\end{array}$

satisfies the partition of unity condition ${\sum }_{j\in \mathbb{Z}}g(a^j\gamma )=1,\gamma \in ℝ\backslash \left\{0\right\}.$ Clearly, g ∈ C¹(ℝ). Note that for any choice of a norm ||·|| on ℝ^d, the function g can be lifted to a radial function $\tilde{g}:{ℝ}^d\to ℝ,$ by defining $\tilde{g}(\gamma ):=g(\left|\right|\gamma \left|\right|),\gamma \in {ℝ}^d;$ the function $\tilde{g}$ satisfies the partition of unity condition with respect to the d × d diagonal matrix ${A}=aI.$

(ii) Let ||·|| be the Euclidean norm on ℝ^d. The function φ(γ) : = e^−||γ||2, γ ∈ ℝ^d, satisfies the conditions in Proposition 2.2. Thus, for any expanding d × d matrix ${A},$ the function

$\begin{array}{l}g(\gamma )=\phi (\gamma )-\phi ({A}\gamma )=e^{-\left|\right|\gamma |{|}^2}-e^{-\left|\right|{A}\gamma |{|}^2}\end{array}$

satisfies the partition of unity condition (1.1). Clearly, g ∈ C^∞(ℝ^d).□

Proposition 2.2 makes it easy to construct partitions of unity for arbitrary expanding matrices ${A}.$ Furthermore, several properties of the generating function g can be controlled directly in terms of the function φ, e.g., regularity and support. We now prove that nonnegativity of g can also be guaranteed by choosing φ to be a radial function with respect to a given norm ||·|| on ℝ^d:

Proposition 2.4. Let ||·|| be an arbitrary norm on ℝ^d and consider an expanding d × d matrix ${A}$ such that $\left|\right|\gamma \left|\right|\le \left|\right|{A}\gamma \left|\right|$ for all γ ∈ ℝ^d. Let r :[0, ∞) → ℝ denote a continuous decreasing function such that r(0) = 1 and r(s) → 0 as s → ∞. Letting φ(γ) : = r(||γ||), γ ∈ ℝ^d, the function $g(\gamma )=\phi (\gamma )-\phi ({A}\gamma )$ has the following properties:

(i) g ≥ 0.

(ii) ${\sum }_{j\in \mathbb{Z}}g({{A}}^j\gamma )=1,\forall \gamma \in {ℝ}^d\backslash \left\{0\right\}.$

(iii) There exists a constant C > 0 such that

$\begin{array}{ll}C\le {\displaystyle \sum _{j\in \mathbb{Z}}|}g({{A}}^j\gamma ){|}^2\le 1,\forall \gamma \in {ℝ}^d\setminus \left\{0\right\}.& (2.3)\end{array}$

Proof. Since the function r is decreasing, (i) follows immediately from the assumption that $\left|\right|\gamma \left|\right|\le \left|\right|{A}\gamma \left|\right|$ for all γ ∈ ℝ^d. The partition of unity (ii) follows from Proposition 2.2, so we only need to prove (iii). In order to do so, the nonnegativity of g and (ii) imply that $0\le g({{A}}^j\gamma )\le 1$ for every j ∈ ℤ and all γ ∈ ℝ^d \ {0}; thus, ${\sum }_{j\in \mathbb{Z}}|g({{A}}^j\gamma ){|}^2\le {\sum }_{j\in \mathbb{Z}}g({{A}}^j\gamma )=1.$

In order to prove the lower bound in (2.3), let η ∈ ℝ^d \ {0}. Then by (ii), there exists j_η ∈ ℤ such that ${ϵ}_{\eta }:=g({{A}}^{j_{\eta }}\eta )>0.$ Thus, we can choose an open set I_η containing η such that $g({{A}}^{j_{\eta }}\gamma )\ge {ϵ}_{\eta }/2$ for all γ ∈ I_η. Letting B(0, 1) denote the closed unit ball in ℝ^d with respect to the norm ||·||, the open sets I_η, η ∈ B(0, 1), form a cover of B(0, 1); thus, we can select a finite subcover, i.e., B(0, 1) ⊂ I_η1 ∪ I_η2 ∪ ⋯ ∪ I_ηn for some η₁, …, η_n ∈ B(0, 1). It follows that for any γ ∈ ℝ^d with ||γ|| ≤ 1, γ must lie in I_ηℓ for some ℓ ∈ {1, …, n}; thus,

$\begin{array}{l}{\displaystyle \sum _{j\in \mathbb{Z}}|}g({{A}}^j\gamma ){|}^2\ge |g({{A}}^{j_{{\eta }_{\ell }}}\gamma ){|}^2\ge \frac{1}{4}{ϵ}_{{\eta }_{\ell }}^2\ge \frac{1}{4}\min \{{ϵ}_{{\eta }_1}^2,\dots ,{ϵ}_{{\eta }_n}^2\}.\end{array}$

This proves the lower bound in (2.3) for γ belonging to the closed unit ball in ℝ^d. Taking now an arbitrary γ ∈ ℝ^d \ {0}, the argument in the proof of Proposition 2.2 shows that there exists N ∈ ℕ such that $\left|\right|{{A}}^{-N}\gamma \left|\right|\le 1;$ thus, by a change of variable,

$\begin{array}{l}{\displaystyle \sum _{j\in \mathbb{Z}}|}g({{A}}^j\gamma ){|}^2={\displaystyle \sum _{j\in \mathbb{Z}}|}g({{A}}^{j+N}({{A}}^{-N}\gamma )){|}^2={\displaystyle \sum _{j\in \mathbb{Z}}|}g({{A}}^j({{A}}^{-N}\gamma )){|}^2\\ \ge \frac{1}{4}\min \{{ϵ}_{{\eta }_1}^2,\dots ,{ϵ}_{{\eta }_n}^2\}.\end{array}$

This completes the proof.□

The condition $\left|\right|\gamma \left|\right|\le \left|\right|{A}\gamma \left|\right|,\gamma \in {ℝ}^d,$ is clearly necessary for the nonnegativity of $g(\gamma )=\phi (\gamma )-\phi ({A}\gamma )$ whenever φ is a function of the type considered in Proposition 2.4. Note that the condition does not follow from ${A}$ being expanding, as we shall see in the example below.

Example 2.5 Take ||·|| to be the Euclidean norm on ℝ² and let ${A}=\left(\begin{array}{cc}0& 2\\ 3/4& 0\end{array}\right).$ The eigenvalues are $\pm \sqrt{3/2},$ so ${A}$ is indeed expanding. However ${A}\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 3/4\end{array}\right),$ so the condition $\left|\right|\gamma \left|\right|\le \left|\right|{A}\gamma \left|\right|$ is clearly violated.□

3. An Integral Transform Preserving Partitions of Unity

In this section, we consider certain integral transforms that map a function g having the scaling partition of unity property to another function with the same property. We first discuss the transform on ℝ^d and then specialize to the one-dimensional case, where explicit calculations are much easier. It turns out that the one-dimensional case leads to a definition of a class of splines in a natural way.

3.1. The Integral Transform on ℝ^d

Fix a measurable function g : ℝ^d → ℂ and consider formally the integral operator K_g that maps a function f : ℝ^d → ℂ to

$\begin{array}{ll}h(\gamma )=(K_{g}f)(\gamma ):={\displaystyle {\int }_{{ℝ}^d}f(t)g(\frac{\gamma }{||t||})dt,\gamma \in {ℝ}^d,}& (3.1)\end{array}$

where ||·|| is an arbitrary norm on ℝ^d. The set of functions f for which the transform is well-defined clearly depends on the choice of the function g. Typically, we assume that g is supported on an annulus

$\begin{array}{l}a(R_1,R_2):=\{t\in {ℝ}^d|R_1\le ||t||\le R_2\}\end{array}$

for some R₂ > R₁ > 0. For example, if a function f ∈ L¹(ℝ) has support in an annulus a(R₁, R₂) and g is a bounded function with support in an annulus a(R₃, R₄), then h is well-defined and supported on the annulus a(R₃R₁, R₄R₂).

The following proposition describes a case where the integral transform is well-defined for all f ∈ L¹(ℝ) and generates a family of partitions of unity.

Proposition 3.1 Let g : ℝ^d → ℂ, and consider a real invertible d × d matrix ${A}$ such that

$\begin{array}{l}{\displaystyle \sum _{j\in \mathbb{Z}}g}({{A}}^j\gamma )=1,\forall \gamma \in {ℝ}^d\setminus \left\{0\right\},\end{array}$

and there exists a constant C > 0 for which

$\begin{array}{l}{\displaystyle \sum _{j\in \mathbb{Z}}|}g({{A}}^j\gamma )|\le C,\forall \gamma \in {ℝ}^d\setminus \{0\}.\end{array}$

Then the integral transform K_g in (3.1) is well-defined for every f ∈ L¹(ℝ^d), and

$\begin{array}{l}{\displaystyle \sum _{j\in \mathbb{Z}}h}({{A}}^j\gamma )={\displaystyle {\int }_{{ℝ}^d}f}(t)dt,\forall \gamma \in {ℝ}^d\setminus \left\{0\right\}.\end{array}$

In particular, if f ∈ L¹(ℝ^d) is chosen such that ${\int }_{{ℝ}^d}f(t)dt=1,$ then the function h has the scaling partition of unity property with respect to the matrix ${A}.$ If the function g is nonnegative, then the transform K_g maps nonnegative functions f to nonnegative functions h = K_gf.

Proof. The assumptions imply that g is bounded, so it is clear that the integral in (3.1) is well-defined for every γ ∈ ℝ^d whenever f ∈ L¹(ℝ^d). Fixing any γ ∈ ℝ^d \ {0},

$\begin{array}{l}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum _{j\in \mathbb{Z}}|}f(t)g(\frac{{{A}}^j\gamma }{||t||})|dt}={\displaystyle {\int }_{{ℝ}^d}|f(t)|{\displaystyle \sum _{j\in \mathbb{Z}}|}g({{A}}^j(\gamma ||t|{|}^{-1}))|dt}\\ \le C{\displaystyle {\int }_{{ℝ}^d}|f(t)|dt<\infty ;}\end{array}$

thus, by Lebesgue's dominated convergence theorem,

${\displaystyle \sum _{j\in \mathbb{Z}}h}({{A}}^j\gamma )={\displaystyle {\int }_{{ℝ}^d}f(t){\displaystyle \sum _{j\in \mathbb{Z}}g}({{A}}^j(\gamma ||t|{|}^{-1}))dt}={\displaystyle {\int }_{{ℝ}^d}f(t)dt.}$

The rest of the proof is clear.    □

A similar but more general result can be obtained by replacing the expression $g(\frac{\gamma }{\left|\right|t\left|\right|})$ in (3.1) by a function g(t, γ) that yields a partition of unity in the second variable. We leave the exact formulation to the interested reader.

3.2. An Example of the Integral Transform on ℝ and A Class of Splines

In this subsection, we will study the one-dimensional version of the integral transform in (3.1). We will fix a constant c ∈ (0, 1), and consider the set

$S:=[-1,-c)\cup (c,1].$

Furthermore, we will fix g: = χ_S. Then the integral transform K_g in (3.1), which we denote simply as K here, takes the form

$\begin{array}{ll}h(\gamma )=Kf(\gamma ):={\displaystyle {\int }_{-\infty }^{\infty }f(t)}{\chi }_S\left(\frac{\gamma }{\left|t\right|}\right)dt,\gamma \in ℝ.& (3.2)\end{array}$

Note that for any fixed γ ∈ ℝ,

${\chi }_S(\frac{\gamma }{|t|})=1\iff c|t|<|\gamma |\le |t|\iff |\gamma |\le |t|<|\gamma |/c;$

thus,

$\begin{array}{ll}h(\gamma )={\displaystyle {\int }_{-\left|\gamma \right|/c}^{-\left|\gamma \right|}f}(t)dt+{\displaystyle {\int }_{\left|\gamma \right|}^{\left|\gamma \right|/c}f(t)dt.}& (3.3)\end{array}$

In particular, the integral in (3.3) is well-defined for all γ ∈ ℝ whenever $f\in L_{\mathrm{\text{loc}}}^1(ℝ).$ We leave the short proof of the following result to the reader.

Lemma 3.2 For any $f\in L_{\mathrm{\text{loc}}}^1(ℝ),$ the function h = Kf is even; and if f is an even function, then for γ > 0,

$h(\gamma )=2{\displaystyle {\int }_{\gamma }^{\gamma /c}f}(t)dt.$

The main merits of the transform K are that it increases the regularity of f and that the resulting function h = Kf satisfies the scaling partition of unity property under some weak conditions on f:

Proposition 3.3 Let $f\in L_{\mathrm{\text{loc}}}^1(ℝ)$ and consider the integral transform h = Kf in (3.2). Then the following hold:

(i) If f ∈ L¹(ℝ), then

${\displaystyle \sum _{j\in \mathbb{Z}}h}(c^j\gamma )={\displaystyle {\int }_{-\infty }^{\infty }f(t)dt,\forall \gamma \in ℝ\setminus \left\{0\right\}.}$

(ii) If f ∈ C^k(ℝ) for some k ∈ ℕ ∪ {0} and f is supported away from the origin, then h ∈ C^{k + 1}(ℝ).

Proof. As (i) clearly follows from Proposition 3.1, we only have to prove (ii). Letting $F(\gamma ):={\int }_0^{\gamma }f(t)dt,\gamma \in ℝ,$ it follows from (3.3) that

$\begin{array}{l}h(\gamma )=F(|\gamma |/c)-F(|\gamma |)+F(-|\gamma |)-F(-|\gamma |/c)\\ =\{\begin{array}{ll}F(\gamma /c)-F(\gamma )+F(-\gamma )-F(-\gamma /c),\hfill & \text{if }\gamma \ge 0,\hfill \\ -[F(\gamma /c)-F(\gamma )+F(-\gamma )-F(-\gamma /c)],\hfill & \text{if }\gamma \le 0.\hfill \end{array}\end{array}$

For γ > 0, the function h is obviously differentiable, and

$h^{\prime }(\gamma )=\frac{1}{c}f(\gamma /c)-f(\gamma )-f(-\gamma )+\frac{1}{c}f(-\gamma /c);$

thus under the stated assumptions h is (k+1) times continuously differentiable for γ > 0. Similarly, h is (k+1) times continuously differentiable for γ < 0; and since the function h vanishes on a neighborhood of zero, h is even infinitely differentiable at γ = 0. □

Example 3.4 Let f(t) = e^{− |t|}, t ∈ ℝ. Then for γ ∈ ℝ,

$\begin{array}{l}h(\gamma )={\displaystyle {\int }_{-\infty }^{\infty }{e}^{-|t|}{\chi }_S\left(\frac{\gamma }{|t|}\right)dt}\\ =2{\displaystyle {\int }_{|\gamma |}^{|\gamma |/c}{e}^{-|t|}}dt=2(e^{-|\gamma |}-e^{-|\gamma |/c}).\end{array}$

Observe that Proposition 3.3(i) implies that h ∈ C(ℝ) and ${\sum }_{j\in \mathbb{Z}}h(c^j\gamma )=2$ for γ ∈ ℝ \ {0}. We could of course obtain this construction via Proposition 2.2 as well. □

We will now use the integral transform K to give a direct definition of a class of splines with attractive properties.

Definition 3.5 Let h₁ : = χ_S, and define the functions h_n, n ≥ 2, inductively by

$\begin{array}{ll}{h}_n(\gamma ):=K{h}_{n-1}(\gamma )={\displaystyle {\int }_{-\infty }^{\infty }{h}_{n-1}}(t){\chi }_S\left(\frac{\gamma }{|t|}\right)dt,\gamma \in ℝ.& (3.4)\end{array}$

Example 3.6 Direct calculation based on (3.4) shows that

$h_2(\gamma )=\{\begin{array}{ll}0,\hfill & \text{if }\left|\gamma \right|\le c^2,\hfill \\ 2c^{-1}\left|\gamma \right|-2c,\hfill & \text{if }{c}^2\le \left|\gamma \right|\le c,\hfill \\ 2-2\left|\gamma \right|,\hfill & \text{if }c\le \left|\gamma \right|\le 1,\hfill \\ 0,\hfill & \text{if }1\le \left|\gamma \right|,\hfill \end{array}$

and

$h_3(\gamma )=\{\begin{array}{ll}0,\hfill & \text{if }\left|\gamma \right|\le c^3,\hfill \\ 2c^{-3}|\gamma {|}^2-4|\gamma |+2c^3,\hfill & \text{if }{c}^3\le \left|\gamma \right|\le c^2,\hfill \\ -2(c^{-1}+c^{-2})|\gamma {|}^2+4(c+c^{-1})\hfill & \text{if }{c}^2\le \left|\gamma \right|\le c,\hfill \\ \left|\gamma \right|-2(c+c^2),\hfill & \hfill \\ 2{(1-|\gamma |)}^2,\hfill & \text{if }c\le \left|\gamma \right|\le 1,\hfill \\ 0,\hfill & \text{if }1\le \left|\gamma \right|.\hfill \end{array}$

□

Let us collect some of the key properties of the spline functions h_n:

Proposition 3.7. The functions h_n, n ∈ ℕ, have the following properties:

(i) h_n is a spline, with knots at the points ±cⁿ, ±cⁿ⁻¹, …, ±1.

(ii) h_n is even.

(iii) For n ≥ 2, $h_n\in C^{n-2}(ℝ).$

(iv) $\mathrm{\text{supp }}{h}_n=\left[-1,-c^n\right]\cup \left[c^n,1\right]$ and h_n > 0 on (−1, − cⁿ) ∪ (cⁿ, 1).

(v) $Q_n:={\int }_{-\infty }^{\infty }{h}_n(\gamma )d\gamma >0$ for all n∈ℕ, and Q₁ = 2(1−c).

(vi) $\frac{1}{Q_{n-1}}{h}_n$ satisfies the partition of unity condition

$\frac{1}{Q_{n-1}}{\displaystyle \sum _{j\in \mathbb{Z}}{h}_n}(c^j\gamma )=1,\forall \gamma \in ℝ\setminus \left\{0\right\}.$

(vii) There exists a constant C > 0 such that

$C\le \frac{1}{Q_{n-1}^2}{\displaystyle \sum _{j\in \mathbb{Z}}|}{h}_n(c^j\gamma ){|}^2\le 1,\forall \gamma \in ℝ\setminus \left\{0\right\}.$

(viii) For n ≥ 2, the functions h_n satisfy the recursion formula

$\begin{array}{l}{h}_n(\gamma )=\frac{2}{n-1}[(1-\left|\gamma \right|)h_{n-1}(\gamma )\\ +(c^{-1}|\gamma |-c^{n-1})h_{n-1}(c^{-1}\gamma )],\gamma \in ℝ.& (3.5)\end{array}$

Proof. Most of the results are immediate consequences of results that are already proved. Indeed, (i) follows from (viii), which will be proved below; (ii) follows from the definition and Lemma 3.2; and (iii) and (vi) are obtained from Proposition 3.3 and Example 3.6. In addition, (iv) is proved by a straightforward induction, (v) is a consequence of (iv) plus a direct calculation of Q₁; and (vii) follows from the partition of unity exactly as in the proof of Proposition 2.4(iii).

We will now prove the only item that remains, namely (viii). Since h_n is even for all n ∈ ℕ, we will assume that γ ≥ 0. To get started, direct calculations based on the expressions in Example 3.6 show that the recursion formula holds for n = 2 and n = 3. Thus, we will now consider n ≥ 4. Define the function H_n by

$\begin{array}{ll}{H}_n(\gamma ):={\displaystyle {\int }_0^{\gamma }{h}_n}(t)dt,\gamma \ge 0.& (3.6)\end{array}$

We will perform an inductive proof of the recursion formula for h_n, assuming that it holds for h_k for all k = 2, …, n − 1. Now, using Lemma 3.2 and the induction hypothesis,

$\begin{array}{l}{h}_n(\gamma )=\frac{4}{n-2}{\displaystyle {\int }_{\gamma }^{\gamma /c}[(1-t)}{h}_{n-2}(t)\\ +(c^{-1}t-c^{n-2})h_{n-2}(c^{-1}t)]dt.\end{array}$

Then a direct calculation using integration by parts yields that

$\begin{array}{l}{h}_n(\gamma )=\frac{4}{n-2}{\displaystyle [-{\displaystyle {\int }_{\gamma }^{\gamma /c}(H_{n-2}(}t/c)-H_{n-2}(t))dt}\\ +(1-\gamma )(H_{n-2}(\gamma /c)-H_{n-2}(\gamma ))\\ {\displaystyle +(c^{-1}\gamma -c^{n-1})(H_{n-2}(\gamma /c^2)-H_{n-2}(\gamma /c))]}.& (3.7)\end{array}$

Now, it follows from (3.6) and Lemma 3.2 that

${\displaystyle {\int }_{\gamma }^{\gamma /c}(H_{n-2}(t/c)-H_{n-2}(t))}dt=\frac{1}{2}{\displaystyle {\int }_{\gamma }^{\gamma /c}{h}_{n-1}}(t)dt=\frac{1}{4}{h}_n(\gamma ).$

Also,

$H_{n-2}(\gamma /c)-H_{n-2}(\gamma )={\displaystyle {\int }_{\gamma }^{\gamma /c}{h}_{n-2}}(t)dt=\frac{1}{2}{h}_{n-1}(\gamma ).$

Hence, based on (3.7), after solving for h_n(γ), we obtain (3.5).□

The splines in Definition 3.5 are indeed well-known: as noted from the recursion formula (3.5), they are the symmetrized version of the nonuniform B-splines with knots at cⁿ, cⁿ⁻¹,…, 1, see [4, 5]. Here, we have provided another perspective in obtaining them. Their properties also serve as a concrete illustration of the general properties we derived in Propositions 3.1 and 3.3. Other related papers on polynomial splines with geometric knots include [7–9].

As a further comment on the one-dimensional transform K in (3.2), we observe that it can be lifted to a transform acting on functions on ℝ^d:

Example 3.8 In this example, we describe a way of lifting the transform K to generate radial functions on ℝ^d.

(i) We can easily lift the integral transform to an operator that yields a radial function $\tilde{h}:{ℝ}^d\to ℂ$ as output. Indeed, taking an arbitrary norm ||·|| on ℝ^d, define the integral transform $\tilde{K},$ acting on functions $f\in L_{\mathrm{\text{loc}}}^1(ℝ)$, by

$\tilde{h}(\gamma )=\tilde{K}f(\gamma ):={\displaystyle {\int }_{-\infty }^{\infty }f}(t){\chi }_S(\frac{\left|\right|\gamma \left|\right|}{\left|t\right|})dt,\gamma \in {ℝ}^d.$

Clearly, in terms of the transform K in (3.2), we have $\tilde{h}(\gamma )=Kf(\left|\right|\gamma \left|\right|)=h(\left|\right|\gamma \left|\right|).$ Furthermore, if f ∈ L¹(ℝ), then

${\displaystyle \sum _{j\in \mathbb{Z}}\tilde{h}}(c^j\gamma )={\displaystyle {\int }_{-\infty }^{\infty }f(t)}dt,\forall \gamma \in {ℝ}^d\setminus \{0\}.$

(ii) As a special case of (i) and based on the nonuniform B-splines h_n in (3.4), we can define a family of radial functions $\widetilde{h_n}$ on ℝ^d by

$\widetilde{h_n}(\gamma ):=h_n(|\left|\gamma \right||),\gamma \in {ℝ}^d.$

Each of these radial functions is supported on an annulus, and they can be easily calculated using the recursion formula in Proposition 3.7. Also, $\widetilde{h_n}$ satisfies the partition of unity condition

${\displaystyle \sum _{j\in \mathbb{Z}}\widetilde{h_n}}(c^j\gamma )={\displaystyle {\int }_{-\infty }^{\infty }{h}_{n-1}}(t)dt,\forall \gamma \in {ℝ}^d\setminus \{0\}.$

□

4. Wavelet Frames in L²(ℝ^d) and Dual Frames

In this section, we apply the results on the scaling partition of unity to construct dual pairs of matrix-based wavelet frames in L²(ℝ^d). Since wavelet frames is a well-studied area by itself (see, e.g., [10–12]), we will not make any attempt to motivate them or highlight their applications but just state the definitions and results that are strictly necessary for our discussion.

Given an invertible d × d matrix ${A}$ with real entries, we define the scaling operator $D_{{A}}:L^2({ℝ}^d)\to L^2({ℝ}^d)$ by $(D_{{A}}f)(x)$ := $|det{A}{|}^{1/2}f({A}x);$ and, for ν ∈ ℝ^d, the translation operator $T_{\nu }:L^2({ℝ}^d)\to L^2({ℝ}^d)$ by T_νf(x) := f(x − ν). Fixing a function ψ ∈ L²(ℝ^d), a d × d matrix ${A}$ and a translation parameter b > 0, the associated wavelet system is given by ${\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}.$ Denoting the canonical norm on L²(ℝ^d) by || · ||₂, the wavelet system ${\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ is said to form a frame for L²(ℝ^d) if there exist constants A, B > 0 such that

$\begin{array}{ll}A\left|\right|f|{|}_2^2\le {\displaystyle \sum _{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}|}\langle f,D_{{{A}}^j}{T}_{bk}\psi \rangle {|}^2\le B|\left|f\right|{|}_2^2,\forall f\in L^2({\text{R}}^d);& (4.1)\end{array}$

if at least the upper condition in (4.1) is satisfied, it is called a Bessel sequence. Two Bessel sequences ${\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ and ${\left\{D_{{{A}}^j}{T}_{bk}\tilde{\psi }\right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d},$ where $\psi ,\tilde{\psi }\in L^2({ℝ}^d),$ are said to form dual frames if

$f={\displaystyle \sum _{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}\langle f,D_{{{A}}^j}{T}_{bk}\tilde{\psi }\rangle }{D}_{{{A}}^j}{T}_{bk}\psi ,\forall f\in L^2{\text{(R}}^d).$

We will need the following result, which gives sufficient conditions for wavelet systems to form Bessel sequences, frames, and dual frames. It exists in several variants in the literature: (i) was first stated explicitly in Lemvig [3], while versions of (ii) can be found, e.g., in [6, 13]; see also [14]. We define the Fourier transform on L¹(ℝ^d) by ${F}f(\gamma )=\hat{f}(\gamma ):={\int }_{{ℝ}^d}f(x)e^{-2\pi ix·\gamma }dx,\gamma \in {ℝ}^d,$ with the usual extension to L²(ℝ^d).

Lemma 4.1. Let ${A}$ denote an invertible d × d matrix with real entries, and let b > 0. Then the following hold:

(i) If ψ ∈ L²(ℝ^d) and

$\begin{array}{l}B:=\frac{1}{b^d}\underset{\gamma \in {ℝ}^d}{\text{ess sup}}{\displaystyle \sum _{j\in \mathbb{Z}}{\displaystyle \sum _{k\in {\mathbb{Z}}^d}|}}\widehat{\psi }\left({\left({{A}}^T\right)}^j\gamma \right)\widehat{\psi }\left({\left({{A}}^T\right)}^j\gamma -k/b\right)\\ |<\infty ,\text{then}{\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}\end{array}$

is a Bessel sequence. If furthermore

$\begin{array}{l}{A}:=\frac{1}{b^d}\underset{\gamma \in {ℝ}^d}{\text{ess inf}}({\displaystyle \sum _{j\in \mathbb{Z}}|}\widehat{\psi }({({{A}}^T)}^j\gamma ){|}^2\\ -{\displaystyle \sum _{j\in \mathbb{Z}}{\displaystyle \sum _{k\ne 0}|}}\widehat{\psi }({({{A}}^T)}^j\gamma )\widehat{\psi }({({{A}}^T)}^j\gamma -k/b)|)>0,\end{array}$

then ${\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ is a frame for L²(ℝ^d) with bounds A, B.

(ii) Assume that the matrix ${A}$ is expanding and suppose that for some $\psi ,\tilde{\psi }\in L^2({ℝ}^d),$ ${\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d},$ ${\left\{D_{{{A}}^j}{T}_{bk}\tilde{\psi }\right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ are Bessel sequences. Then ${\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d},$ ${\left\{D_{{{A}}^j}{T}_{bk}\tilde{\psi }\right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ are dual frames for L²(ℝ^d) if and only if for all m ∈ ℤ^d,

$\begin{array}{l}{\displaystyle \sum _{\{j\in \mathbb{Z}|{(A^T)}^{-j}m\in {\mathbb{Z}}^d\}}\overline{\widehat{\psi }{(({{A}}^T)}^{-j}\gamma )}}\widehat{\tilde{\psi }}{(({{A}}^T)}^{-j}\gamma +{({{A}}^T)}^{-j}m/b)\\ =b^d{\delta }_{m,0},{A}.e.\gamma \in {ℝ}^d.& (4.2)\end{array}$

Remark 4.2. It follows from Lemma 4.1 that if $\hat{\psi }$ is supported on the closed ball B(0, R) of radius R in ℝ^d and b ≤ (2R)⁻¹, then ${\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ is a Bessel sequence when ${\text{ess sup}}_{\gamma \in {ℝ}^d}{\sum }_{j\in \mathbb{Z}}|\hat{\psi }({({{A}}^T)}^j\gamma ){|}^2<\infty ;$ and it is a frame when

$0<\underset{\gamma \in {ℝ}^d}{\text{ess inf}}{\displaystyle \sum _{j\in \mathbb{Z}}|}\widehat{\psi }({({{A}}^T)}^j\gamma ){|}^2\le \underset{\gamma \in {ℝ}^d}{\text{ess sup}}{\displaystyle \sum _{j\in \mathbb{Z}}|}\widehat{\psi }({({{A}}^T)}^j\gamma ){|}^2<\infty .$

If both $\hat{\psi }$ and $\hat{\tilde{\psi }}$ are supported on B(0, R), then (4.2) is satisfied for m ∈ ℤ^d\{0} when b ≤ (2R)⁻¹; in this case the condition (4.2) consists of the single equation

${\displaystyle \sum _{j\in \mathbb{Z}}\overline{\widehat{\psi }({({{A}}^T)}^{-j}\gamma )}}\widehat{\tilde{\psi }}({({{A}}^T)}^{-j}\gamma )=b^d,\text{ a.e. }\gamma \in {ℝ}^d.$

Up to the factor b^d, this essentially means that the function $\overline{\hat{\psi }}\hat{\tilde{\psi }}$ satisfies the scaling partition of unity property with respect to the matrix ${{A}}^T$.

Proposition 3.7 and Lemma 4.1 lead to the following frame result on L²(ℝ) for the splines h_n in (3.4):

Theorem 4.3 Given any n ∈ ℕ and c ∈ (0, 1), consider the spline h_n in (3.4). Fix b ∈ (0, cⁿ⁻¹/2] and define the functions $\psi ,\tilde{\psi }\in L^2(ℝ)$ by $\hat{\psi }$ := h_n and

$\begin{array}{ll}\widehat{\tilde{\psi }}(\gamma ):=\frac{b}{Q_{n-1}^2}{\displaystyle \sum _{j=-n+1}^{n-1}{h}_n}(c^j\gamma ),\gamma \in ℝ.& (4.3)\end{array}$

Then ${\left\{D_{c^j}{T}_{kb}\psi \right\}}_{j,k\in \mathbb{Z}}$ and ${\left\{D_{c^j}{T}_{kb}\tilde{\psi }\right\}}_{j,k\in \mathbb{Z}}$ are dual wavelet frames for L²(ℝ).

Proof. Since $\mathrm{\text{supp }}\hat{\psi }\subset \left[-1,1\right]\subseteq \left[-c^{-n+1},c^{-n+1}\right],$ the frame property of ${\left\{D_{c^j}{T}_{kb}\psi \right\}}_{j,k\in \mathbb{Z}}$ follows directly from Proposition 3.7(vii) and Remark 4.2. Now, by the partition of unity condition in Proposition 3.7(vi), we have

$\begin{array}{ll}\frac{1}{Q_{n-1}}{\displaystyle \sum _{j\in \mathbb{Z}}\widehat{\psi }}(c^j\gamma )=1,\forall \gamma \in ℝ\setminus \left\{0\right\}.& (4.4)\end{array}$

The expression on the right-hand side of (4.3) clearly defines a bounded function, with compact support [−c⁻ⁿ⁺¹, −cⁿ⁻¹] ∪ [cⁿ⁻¹, c⁻ⁿ⁺¹] which is bounded away from the origin. Thus the function $\tilde{\psi }$ is well-defined and ${\left\{D_{c^j}{T}_{kb}\tilde{\psi }\right\}}_{j,k\in \mathbb{Z}}$ is a Bessel sequence by Lemma 4.1(i) and Remark 4.2.

If $\gamma \in \mathrm{\text{supp }}\hat{\psi }$, then $\hat{\psi }(c^j\gamma )$ can only be nonzero for j = −n + 1, −n + 2, …, n− 1; thus (4.4) implies that $\hat{\tilde{\psi }}(\gamma )=\frac{b}{Q_{n-1}}$ for $\gamma \in \mathrm{\text{supp }}\hat{\psi }$. It follows that $\overline{\hat{\psi }(\gamma )}\hat{\tilde{\psi }}(\gamma )=\frac{b}{Q_{n-1}}\overline{\hat{\psi }(\gamma )}$ for all γ ∈ ℝ; using again (4.4) now shows that

$\begin{array}{l}{\displaystyle \sum _{j\in \mathbb{Z}}\overline{\widehat{\psi }(c^j\gamma )}}\widehat{\tilde{\psi }}(c^j\gamma )=b,\forall \gamma \in ℝ\setminus \left\{0\right\}.\end{array}$

Hence we conclude from Lemma 4.1(ii) and Remark 4.2 that ${\left\{D_{c^j}{T}_{kb}\psi \right\}}_{j,k\in \mathbb{Z}},$ ${\left\{D_{c^j}{T}_{kb}\tilde{\psi }\right\}}_{j,k\in \mathbb{Z}}$ are indeed dual frames.□

Note that a different dual frame ${\left\{D_{c^j}{T}_{kb}\tilde{\psi }\right\}}_{j,k\in \mathbb{Z}}$ associated with ${\left\{D_{c^j}{T}_{kb}\psi \right\}}_{j,k\in \mathbb{Z}}$ could have been obtained via the results in Lemvig [2]. Also, by combining the result with the lifting transform in Example 3.8, it is easy to construct radial dual wavelet frames ${\left\{D_{c^{j}I}{T}_{kb}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ and ${\left\{D_{c^{j}I}{T}_{kb}\tilde{\psi }\right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ for L²(ℝ^d), where $\psi ,\tilde{\psi }\in L^2({ℝ}^d);$ we leave the details to the reader.

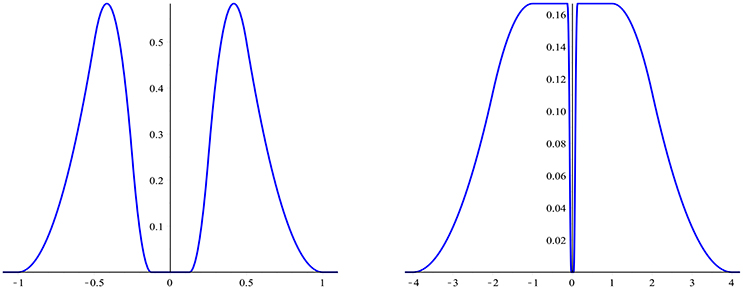
We also note that the unitary extension principle and its many variants is a classical tool to construct wavelet frames based on splines, see, e.g., [10−12]. However, in this case the frame generators themselves are splines, while in our construction the splines occur in the Fourier domain. Figure 1 shows the graphs of the splines $\hat{\psi }$ and $\hat{\tilde{\psi }}$ in Theorem 4.3 when c = 1/2, n = 3 and b = cⁿ⁻¹/2.

FIGURE 1

Figure 1. Plots of the splines $\hat{\psi }$ and $\hat{\tilde{\psi }}$ in Theorem 4.3 when c = 1/2, n = 3 and b = cⁿ⁻¹/2.

We will now establish a result about the construction of wavelet frames in L²(ℝ^d), based on Proposition 2.4:

Theorem 4.4 Let || · || denote any norm on ℝ^d, and consider an expanding d × d matrix ${A}$ such that $\left|\right|\gamma \left|\right|\le \left|\right|{{A}}^T\gamma \left|\right|$ for all γ ∈ ℝ^d. Let r:[0, ∞) → ℝ be a continuous decreasing function supported on [0, R] for some R > 0 such that r(0) = 1. Consider the function ψ : ℝ^d → ℝ defined via $\hat{\psi }(\gamma ):=r(\left|\right|\gamma \left|\right|)-r(\left|\right|{{A}}^T\gamma \left|\right|),\gamma \in {ℝ}^d.$ Then the following hold:

(i) Whenever b ≤ (2R)⁻¹, ${\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ is a wavelet frame for L²(ℝ^d).

(ii) If r(γ) = 1 for γ ∈ [0, R₁] for some R₁ > 0, there exists a finite index set J containing 0, which depends on the matrix ${A}$ and the numbers R, R₁, such that

$\begin{array}{l}{\displaystyle \sum _{j\in J}\widehat{\psi }}({({{A}}^T)}^j\gamma )=1,\forall \gamma \in \text{ supp }\widehat{\psi }.\end{array}$

(iii) If r(γ) = 1 for γ ∈ [0, R₁] for some R₁ > 0, choose an index set J as in (ii) and for b > 0, define the function $\tilde{\psi }:{ℝ}^d\to ℝ$ via

$\begin{array}{ll}\widehat{\tilde{\psi }}(\gamma ):=b^d{\displaystyle \sum _{j\in J}\widehat{\psi }}({({{A}}^T)}^j\gamma ),\gamma \in {ℝ}^d.& (4.5)\end{array}$

Then for sufficiently small values of b, ${\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ and ${\left\{D_{{{A}}^j}{T}_{bk}\tilde{\psi }\right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ are dual frames for L²(ℝ^d).

Proof. The matrix ${{A}}^T$ is expanding, so Proposition 2.4(iii) implies that there exists a constant C > 0 such that $C\le {\sum }_{j\in \mathbb{Z}}|\hat{\psi }({({{A}}^T)}^j\gamma ){|}^2\le 1$ for all γ ∈ ℝ^d \ {0}. The result in (i) now follows from Remark 4.2.

In order to prove (ii), we will first show that the function $\hat{\psi }$ is supported on the annulus $a(R_1\left|\right|{{A}}^T|{|}^{-1},R).$ (This annulus is well-defined as $\left|\right|\gamma \left|\right|\le \left|\right|{{A}}^T\gamma \left|\right|\le \left|\right|{{A}}^T\left|\right|\left|\right|\gamma \left|\right|$ implies that $\left|\right|{{A}}^T\left|\right|\ge 1.$) If ||γ|| ≥ R, we also have that $\left|\right|{{A}}^T\gamma \left|\right|\ge R,$ so indeed $\hat{\psi }(\gamma )=0.$ Now, assume that $\left|\right|\gamma \left|\right|\le R_1\left|\right|{{A}}^T|{|}^{-1}.$ Then ||γ|| ≤ R₁ and

$\begin{array}{l}\left|{{A}}^T\gamma \right||\le |\left|{{A}}^T\right|\left|\right|\left|\gamma \right||\le |\left|{{A}}^T\right|\left|R_1\right|\left|{{A}}^T\right|{|}^{-1}=R_1;\end{array}$

thus $\hat{\psi }(\gamma )=r(\left|\right|\gamma \left|\right|)-r(\left|\right|{{A}}^T\gamma \left|\right|)=1-1=0$ as claimed.

Now, applying Proposition 2.4(ii) to the expanding matrix ${{A}}^T,$ we have

$\begin{array}{ll}{\displaystyle \sum _{j\in \mathbb{Z}}\widehat{\psi }}({({{A}}^T)}^j\gamma )=1,\forall \gamma \in {ℝ}^d\setminus \left\{0\right\}.& (4.6)\end{array}$

Since ${{A}}^T$ is expanding, there exist constants C′ ∈ (0, 1] and α > 1 such that $\left|\right|{({{A}}^T)}^j\gamma \left|\right|\ge C^{\prime }{\alpha }^j\left|\right|\gamma \left|\right|$ for all γ ∈ ℝ^d and j ∈ ℕ ∪ {0}. Thus, for j ∈ ℕ ∪ {0} and any $\gamma \in \mathrm{\text{ supp }}\hat{\psi },$

$\begin{array}{l}\left|{({{A}}^T)}^j\gamma \right||\ge C^{\prime }{\alpha }^j|\left|\gamma \right||\ge C^{\prime }{\alpha }^j{R}_1|\left|{{A}}^T\right|{|}^{-1}.\end{array}$

It follows that for $\gamma \in \mathrm{\text{supp}}\hat{\psi },$ we have $\hat{\psi }({({{A}}^T)}^j\gamma )=0$ whenever $C^{\prime }{\alpha }^j{R}_1\left|\right|{{A}}^T|{|}^{-1}\ge R,$ i.e., for j sufficiently large. On the other hand, since $\left|\right|{({{A}}^T)}^{-j}\gamma \left|\right|\le {(C^{\prime })}^{-1}{\alpha }^{-j}\left|\right|\gamma \left|\right|$ for all γ ∈ ℝ^d and j ∈ ℕ ∪ {0}, it also follows that for $\gamma \in \mathrm{\text{supp}}\hat{\psi },$

$\begin{array}{l}\left|{({{A}}^T)}^{-j}\gamma \right||\le {(C\prime )}^{-1}{\alpha }^{-j}R;\end{array}$

thus $\hat{\psi }({({{A}}^T)}^{-j}\gamma )=0$ whenever ${(C^{\prime })}^{-1}{\alpha }^{-j}R\le R_1\left|\right|{{A}}^T|{|}^{-1},$ i.e., for j sufficiently large. This completes the proof of (ii).

Finally, to establish (iii), we first note that for every j ∈ ℤ, there exist constants λ_j, μ_j > 0 such that

$\begin{array}{ll}{\lambda }_j\left|\right|\gamma \left|\right|\le \left|\right|{({{A}}^T)}^j\gamma \left|\right|\le {\mu }_j\left|\right|\gamma \left|\right|,\forall \gamma \in {ℝ}^d.& (4.7)\end{array}$

Indeed, for j = 0, we simply take λ₀ = μ₀ = 1. If j ∈ ℕ, then $C^{\prime }{\alpha }^j\left|\right|\gamma \left|\right|\le \left|\right|{({{A}}^T)}^j\gamma \left|\right|\le \left|\right|{({{A}}^T)}^j\left|\right|\left|\right|\gamma \left|\right|$ for all γ ∈ ℝ^d. On the other hand, $\left|\right|{({{A}}^T)}^{-j}\gamma \left|\right|\le {(C^{\prime })}^{-1}{\alpha }^{-j}\left|\right|\gamma \left|\right|$ and $\left|\right|\gamma \left|\right|=\left|\right|{({{A}}^T)}^j{({{A}}^T)}^{-j}\gamma \left|\right|\le \left|\right|{({{A}}^T)}^j\left|\right|\left|\right|{({{A}}^T)}^{-j}\gamma \left|\right|$ for all γ ∈ ℝ^d. Next, using the fact that $\mathrm{\text{supp}}\hat{\psi }\subset a(R_1\left|\right|{{A}}^T|{|}^{-1},R),$ it follows from (4.7) that $\mathrm{\text{supp }}\hat{\psi }({({{A}}^T)}^j·)\subset a(R_1\left|\right|{{A}}^T|{|}^{-1}{\mu }_j^{-1},R{\lambda }_j^{-1})$ for every j ∈ ℤ. Thus the definition of $\hat{\tilde{\psi }}$ in (4.5) shows that $\hat{\tilde{\psi }}$ is a bounded function, with

$\begin{array}{l}\text{supp }\widehat{\tilde{\psi }}\subset {\displaystyle \underset{j\in J}{\cup }\text{ supp }}\tilde{\widehat{\psi }}({({{A}}^T)}^j·)\subset a(R_1|\left|{{A}}^T\right|{|}^{-1}\underset{j\in J}{\text{ min }}{\mu }_j^{-1},R\underset{j\in J}{\text{ max }}{\lambda }_j^{-1}).\end{array}$

Since J is a finite set containing 0, ${max}_{j\in J}{\lambda }_j^{-1}\ge {\lambda }_0^{-1}=1$ and so $R{max}_{j\in J}{\lambda }_j^{-1}\ge R.$ Consequently, both $\hat{\psi }$ and $\hat{\tilde{\psi }}$ are supported on the closed ball $B(0,R{max}_{j\in J}{\lambda }_j^{-1}).$ The rest of the proof of (iii) is similar to the proof of Theorem 4.3, where Lemma 4.1 and Remark 4.2 are applied. Specifically, we see that whenever $b\le {(2R{max}_{j\in J}{\lambda }_j^{-1})}^{-1}$, ${\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ and ${\left\{D_{{{A}}^j}{T}_{bk}\tilde{\psi }\right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ are Bessel sequences. Also, the partition of unity condition (4.6) together with (ii) shows that

$\begin{array}{l}{\displaystyle \sum _{j\in \mathbb{Z}}\overline{\widehat{\psi }({({{A}}^T)}^j\gamma )}}\widehat{\tilde{\psi }}({({{A}}^T)}^j\gamma )=b^d,\forall \gamma \in {ℝ}^d\setminus \left\{0\right\};\end{array}$

and hence, ${\left\{D_{{{A}}^j}{T}_{bk}\psi \right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ and ${\left\{D_{{{A}}^j}{T}_{bk}\tilde{\psi }\right\}}_{j\in \mathbb{Z},k\in {\mathbb{Z}}^d}$ are dual frames for L²(ℝ^d).□

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

OC would like to thank the National University of Singapore for its warm hospitality during one-month stays in 2016 and 2017.

References

1. Dai X, Diao Y, Gu Q, Han D. Frame wavelet sets in ℝ^d. J Comput Appl Math. (2003) 155:69–82.

Google Scholar

2. Lemvig J. Constructing pairs of dual bandlimited framelets with desired time localization. Adv Comput Math. (2009) 30:231–47. doi: 10.1007/s10444-008-9066-7

CrossRef Full Text | Google Scholar

3. Lemvig J. Constructing pairs of dual bandlimited frame wavelets in L²(ℝⁿ). Appl Comput Harmon Anal. (2012) 32:313–28.

Google Scholar

4. de Boor C. On calculating with B-splines. J Approx Theory (1972) 6:50–62.

Google Scholar

5. de Boor C. A Practical Guide to Splines. New York, NY: Springer (2001).

Google Scholar

6. Hernandez E, Labate D, Weiss G. A unified characterization of reproducing systems generated by a finite family II. J Geom Anal. (2002) 12:615–62. doi: 10.1007/BF02930656

CrossRef Full Text | Google Scholar

7. Goodman TNT, Lee SL. Homogeneous polynomial splines. Proc R Soc Edinburgh Sec A (1991) 117:89–102.

Google Scholar

8. Lee SL. The use of homogeneous coordinates in spline functions and polynomial interpolation, In: Haußmann W, Jetter K, editors. Multivariate Approximation and Interpolation. Basel: Birkhäuser (1990). p. 167–78.

9. Micchelli CA. Cardinal ${L}$-splines, In: Karlin S, Micchelli CA, Pinkus A, Schoenberg IJ, editors. Studies in Spline Functions and Approximation Theory. New York, NY: Academic Press (1976). p. 203–50.

10. Chui CK, He W, Stöckler J. Compactly supported tight and sibling frames with maximum vanishing moments. Appl Comput Harmon Anal. (2002) 13:224–62.

Google Scholar

11. Daubechies I, Han B, Ron A, Shen Z. Framelets: MRA-based constructions of wavelet frames. Appl Comput Harmon Anal. (2003) 14:1–46. doi: 10.1016/S1063-5203(02)00511-0

CrossRef Full Text | Google Scholar

12. Ron A, Shen Z. Affine systems in $L_2({ℝ}^d)$: the analysis of the analysis operator. J Funct Anal. (1997) 148:408–47.

Google Scholar

13. Chui CK, Czaja C, Maggioni M, Weiss G. Characterization of general tight wavelet frames with matrix dilations and tightness preserving oversampling. J Fourier Anal Appl. (2002) 8:173–200. doi: 10.1007/s00041-002-0007-4

CrossRef Full Text | Google Scholar

14. Christensen O. An Introduction to Frames and Riesz Bases. Second Expanded Edition. Boston: Birkhäuser (2016).