- MATH, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland
This paper deals with fast simulations of the hemodynamics in large arteries by considering a reduced model of the associated fluid-structure interaction problem, which in turn allows an additional reduction in terms of the numerical discretisation. The resulting method is both accurate and computationally cheap. This goal is achieved by means of two levels of reduction: first, we describe the model equations with a reduced mathematical formulation which allows to write the fluid-structure interaction problem as a Navier-Stokes system with non-standard boundary conditions; second, we employ numerical reduction techniques to further and drastically lower the computational costs. The non standard boundary condition is of a generalized Robin type, with a boundary mass and boundary stiffness terms accounting for the arterial wall compliance. The numerical reduction is obtained coupling two well-known techniques: the proper orthogonal decomposition and the reduced basis method, in particular the greedy algorithm. We start by reducing the numerical dimension of the problem at hand with a proper orthogonal decomposition and we measure the system energy with specific norms; this allows to take into account the different orders of magnitude of the state variables, the velocity and the pressure. Then, we introduce a strategy based on a greedy procedure which aims at enriching the reduced discretization space with low offline computational costs. As application, we consider a realistic hemodynamics problem with a perturbation in the boundary conditions and we show the good performances of the reduction techniques presented in the paper. The results obtained with the numerical reduction algorithm are compared with the one obtained by a standard finite element method. The gains obtained in term of CPU time are of three orders of magnitude.
1. Introduction
When modeling hemodynamics phenomena in big arteries, the resulting model is a complex unsteady fluid-dynamics system, usually coupled with a structural model for the vessel wall. In specific cases, suitable assumptions can be made to reduce the complexity of the model equations. In particular, when the displacement is small, the moving domain can be linearized around a reference steady configuration and the dynamics of the vessel motion can be embedded in the equations for the blood flow. In such way we obtain a Reduced Fluid-Structure Interaction (RFSI) formulation where a Navier-Stokes system in a fixed fluid domain is supplemented by a Robin boundary condition that represents a surrogate of the structure model.
Although the RFSI model is faster with respect to fully three-dimensional (3D) models where the structure is solved separately, the numerical computation of one heartbeat is still expensive: the resolution of an entire heartbeat, that typically lasts one physical second, takes orders of hours of computational time on a supercomputer. A big challenge in realistic applications is to achieve a real time resolution of fluid-structure interaction problems. In particular, in hemodynamics applications, this would grant the possibility to perform real time diagnosis. Nevertheless, the great variability of patient-specific data requires the parametrization of the model with respect to many physical and geometrical quantities. Moreover, as we have recalled above, the complexity of the hemodynamics phenomena requires a mathematical description with complex unsteady models that are difficult to be solved in real time. The RFSI model is already a simpler version of the fully 3D FSI system; a further reduction of the physical model would result in an inaccurate estimation of specific outputs, like e.g., the wall shear stress when using a rigid wall model [1, 2]. Thus, to further reduce numerical costs, in this work, we focus on the reduction of the discretization space. In realistic applications, the finite element space has order of 106 degrees of freedom. The aim is to construct a discretization space such that the number of degrees of freedom is reduced to less than 100 and then to be able to solve one heartbeat in 1 s.
In the past few years, due to their relevance in realistic applications, a lot of interest has been devoted to discretization reduction techniques for parametrized Partial Differential Equation (PDE) problems (e.g., [3–6]). These techniques aim to define a suitable reduced order model which can be solved with marginal computational costs for different values of the model parameters. Reduced order models are then important in the many query context, when a parametrized model has to be solved for different values of the parameter, and in the real time problems, when the solution has to be computed with marginal computational costs. To obtain a suitable reduced order model, we typically start from a problem written in a high-fidelity approximation framework, e.g., using the finite element method. The dimension of the discretized system is then drastically reduced through suitable projection operators. The construction of these projection operators is the core of the reduced order technique. Another key concept in the reduction framework is the subdivision of the computational costs into two stages: an offline stage, expensive but performed once, and an online stage, real time and performed each time new values of the model parameters are considered. During the offline stage the projection space is generated by a reduced basis of functions of the high-fidelity approximation space.
Reduced order models applied to the Burgers equation parametrized with respect to the Péclet number is considered in Yano et al. [7] and Nguyen et al. [8]. Other applications of reduced basis techniques applied to fluid problems can be found (e.g., in [9–18] and in the recent volume [6]).
The aim of this work is indeed to propose a suitable discretization reduction algorithm that can be applied to a RFSI problem. The work is organized as follows. In section 2 we present the partial differential equations that we are interested in solving. We propose a possible parametrization of the unsteady equations with respect to temporal varying data and with respect to a perturbation of the boundary data. In section 3 we then present how the standard proper orthogonal decomposition algorithm can be applied to the problem at hand in order to generate a suitable reduced space. Moreover, we propose a way to improve the quality of the reduced approximation based on a greedy procedure. Finally, in section 4 we apply the reduction algorithms presented to a realistic hemodynamic problem. Conclusions follow.
2. Model Equation
Blood is in large vessels can be modeled as an incompressible viscous fluid the well-known Navier-Stokes equations (e.g., [19, 20]). Being [0, T] the temporal interval of interest the Navier-Stokes system reads as follows:
where u and p are the velocity and pressure of the blood, respectively, and ρf is its density. We denote by the Cauchy stress tensor
with I being the identity tensor and μf the blood dynamic viscosity. Ω denote the domain of interest, in our case, the lumen of the vessels where we are interested in computing the dynamics of blood. Due to the compliant vessel wall, Ω should be time dependent. Considering that the wall displacement is relatively small with respect to the arterial diameter, we assume Ω as fixed which allows us to reduce the computational complexity otherwise generated from a moving domain. Nevertheless, to retrieve the physical effect of the wall compliance we introduce a non-rigid boundary condition on the lateral surface of the lumen. The condition is derived by a three dimensional linear isotropic elastic model condensed as a two dimensional membrane [1, 21]. Denoting Γ the lateral surface (i.e., the fluid-structure interface), ΠΓ(ds), the stress-strain relation of this membrane, can be written as:
where ∇Γds is the tangential gradient of ds, Es is the structural Young modulus, νs is the Poisson's ratio and hs is the material thickness. All the physical parameters of the structure are assumed homogeneous in space.
Let us now suppose that the boundary ∂Ω is divided into three non intersecting parts such that ∂Ω = Γ ∪ ΓD ∪ ΓN. ΓD is the Dirichlet boundary, typically the inflow of a vessel, ΓN is the Neumann boundary, typically the outflows. We introduce the Hilbert space and the correspondent vectorial spaces V = [V]3 and V = [V]3. Moreover, we introduce a suitable couple standard finite element spaces Vh and Qh such that Vh ⊂ V and and they represent a stable coupled of finite element spaces for the Navier-Stokes equations. We set Xh: = Vh × Qh. We define [t0 T] a time interval of interest and we divide it into subintervals [tn tn+1] for n = 0, .., NT − 1 such that t0 < t1 < t2 < … < tNT = T and tn+1 − tn = Δt; let us define the collections of all the temporal indexes n. For a generic function ϕ(t) we use . Finally, we define the operators D(·) and DΓ(·) as follows:
where ∇(·) is the standard gradient operator and ∇Γ(·) is the tangential component of the gradient with respect to the surface Γ.
The RFSI model as presented in Colciago et al. [1] is an unsteady Navier-Stokes model set on a fixed domain with generalized Robin boundary conditions (For similar models see e.g., [21–24]). Let us introduce the velocity and pressure unknowns [uh, ph] and the corresponding test functions [vh, qh]. Although the RFSI model lives in a fixed domain, it is necessary to define an auxiliary variable which stands for the displacement of the arterial wall ds, h. Using a backward Euler finite difference method for the time derivatives, the fully discrete weak formulation of the RFSI problem is written as follows:
for each n = 0, .., NT − 1, find such that on ΓD and
where
with and ρs represents the density of the solid. The functions gN(x, t) and gD(x, t) are sufficiently regular functions that stand for the Dirichlet and Neumann boundary data, respectively. Finally the problem should be equipped with suitable initial condition that, without any loss of generality, we suppose to be equal to zero.
As said before, the RFSI problem (1) is indeed a linearized Navier-Stokes on a fixed domain with a non standard boundary condition on the interface Γ. In particular is a generalized Robin boundary condition that contains both a mass and a stiffness boundary term to mimic the presence of a compliant arterial wall surrounding the fluid domain (see [25] for more detailed on the analysis of partial differential equations with generalized Robin boundary condition). We remark that does not represents a problem unknown since it is indeed reconstructed as a weighted sum of the velocities at different time instants
2.1. Boundary Condition
Problem (1) is endowed with Dirichlet velocity boundary condition on the inlet surface ΓD. Given the inlet velocity data gD(x, t), at the time instant tn+1 we impose:
The Neumann boundary condition is imposed weakly on ΓN. The solution of problems (1)–(3) depends on the time variable t through the inlet and outlet data: gN(x, t) and gD(x, t). We suppose that
that is we separate the contribution of the space and temporal variables in the inlet and outlet data. In realistic applications, the separation of variables (4) often derives directly from modeling choices. If at the outlet we prescribe an average normal stress, no spatial variability is involved in the boundary condition data gN. At the inlet, the Dirichlet data is imposed by means of a velocity profile; typically Poiseuille or Womersley profiles are chosen in hemodynamics applications [20]. The separation of variables in gD(x, t) in this case is straightforward.
Assumption (4) allows to write an affine decomposition of the operators in problem (2) with respect to σ1(t) and σ2(t). With respect to the latter we have:
The non homogeneous Dirichlet boundary condition (3) is not directly included in the variational form (1). In order to write the affine decomposition with respect to the parameter σ1(t), a suitable choice to embed condition (3) into the variational formulation has to be made. In the literature two possible approaches are proposed: a strong imposition, using a lifting function or suitable Lagrange multipliers [17], and a weak imposition adding suitable penalty variational terms [2, 26]. Due to the fact that the Dirichlet data can be written in the form (4), a single time independent lifting function can be constructed and properly weighted by a scalar in order to represent the lifting at each temporal instant.
We explain how problem (1) is modified when a lifting function for the Dirichlet condition (3) is introduced. Let us directly consider the fully discretized formulation (1). We define the time independent lifting function such that and
At the time level tn+1, the lifting function of the data reads . Then, for each tn+1, we introduce the following change of variable:
We define the space Xh,ΓD as and we observe that on Γ.
2.1.1. Affine Decomposition
Using the definitions of the functionals as in (2), we are now ready to write the affine decomposition of problem (1) with respect to the temporal parameters σ1(t) and σ2(t). We remark that the lifting function does not depend on the time variable, thus the problem parameter at a fixed time level can be gathered in the following vector:
One single time step of finite element approximation of the RFSI problem can be written under the form:
for each n = 0, .., NT − 1, find such that
where
Due to the fact that we use a semi-implicit treatment of the convective term the formulation of the RFSI problem at one single time instant tn+1 can be interpreted as a linear steady problem parametrized with respect to and .
Furthermore, we can introduce a parameter in the inlet flow rate function representing a small perturbation with respect to a reference value: the inlet flow rate function (4) is then modified as
where , being the set of the admissible value of α. The same affine decomposition 8, with the following modification: the parameter becomes and in (8) we substitute μ0 with μ3μ0 and μ2 with μ2μ3.
3. Numerical Reduction
In this section we briefly introduce some of the basic concepts of the reduced basis method that are useful to our purpose. For more details on the reduced basis theory we address the interested reader to e.g., Rozza et al. [5], Hesthaven et al. [27], and Quarteroni et al. [28]. We already introduced that, at each time instant is the a high-fidelity approximation of the exact solution and is computed as a finite element solution with a sufficiently fine mesh. The solutions of problem (7) are, in general, expensive to obtain from the computational point of view, since in realistic applications the finite element spaces has order of 106 degrees of freedom and the complexity of the geometrical domain does not always allow for the generation of structured meshes. We conclude that due to the magnitude of the finite element problem a real time computation would be impossible to achieve.
As in the standard reduced basis theory, we state the following assumption: the family of solutions obtained for different realizations of the parameters belongs to a low dimensional manifold . The aim of the reduction techniques is to find a suitable approximation of the manifold through the construction of a low dimensional space XN ⊂ Xh,ΓD. The dimension of the reduced space N needs to be orders of magnitude lower that the dimension of the finite element space. The reduced approximation of RFSI problem reads:
given , for each n = 0, .., NT − 1, find such that
where a(·, ·) and F(·) are defined as in (8).
3.1. Proper Orthogonal Decomposition
We apply a discretization reduction to the RFSI problem (7) and the Proper Orthogonal Decomposition (POD) method. In the context of this work we only detail the specific choices performed in relation to the problem at hand, for more details about POD applied to fluid problems we address the reader to e.g., Rowley [29] and Willcox and Peraire [30].
We define a subset of temporal indexes with cardinality NS and consider the solutions of problem (1) at the time instants for . The solutions , called snapshots, represent our starting point for the POD analysis. Since the RFSI problem (7) is a saddle point problem in two variables (velocity and pressure) with different characteristic order of magnitude, we split the POD into two eigenvalue decompositions: one for the velocity variable and another for the pressure one [31]. We measure the energy associated to the snapshots using the following scalar products: for the velocity, we set
and for the pressure,
Then, we compute the two Gramian matrices
and we perform the eigenvalue decomposition of Gu and the one of Gp, obtaining the pairs and where and are the k − th eigenvalues and eigenvectors of the velocity and pressure Gramian matrices, respectively, for . Fixing the same tolerance for both the velocity and pressure decompositions, we select the first Nu and Np eigenpairs such that:
respectively. The j−th velocity eigenfunction is reconstructed using the linear combination:
Similarly for for j = 1, .., Np. We remark that, since the velocity basis are linear combinations of solutions of problem (7), they all verify , ∀qh ∈ Qh for j = 1, .., Nu. Thus, the linear system induced by the bilinear form a(·, ·) as in (2) would be singular if we consider the functional spaces generated from the velocity functions and the pressure modes . One of the possibilities often employed in the context of Navier-Stokes equations is to restrict the system and to solve the problem only for the velocity unknown (see e.g., [32]). Unfortunately, this is not possible when considering problem (2). The generalized boundary condition applied on Γ derives from a structural model which solution is driven by the pressure condition set on the external boundary in the structural model (see [1, 22]). If we solve the reduced system not taking into account the pressure variable, we cannot recover the velocity on the boundary Γ and the output functionals that depends on these values (e.g., wall shear stress). For these reasons, following Rozza and Veroy [33], for each selected pressure mode , we define the corresponding supremizer function σj ∈ Vh as the solution of the following problem:
We then add them to the POD basis. The POD reduced space associated to the RFSI model is composed by the basis functions , ξj ∈ Xh defined as follows:
where for j = 1, .., Np represent the orthonormalization of the supremizer functions σj, obtained with a Gram-Schmidt algorithm with respect to the scalar product (·, ·)V.
3.2. Greedy Enrichment
The bottleneck of the POD procedure is the computation of the high-fidelity solutions necessary to build the correlation matrix: we have to solve a finite element problem NT times. Moreover if we choose , the Gramian matrix becomes too large and its eigenvalue decomposition gets too much expensive. We can envision two situations where we would like to improve the quality of the approximation obtained with the POD reduced space without changing the snapshots sample. For example, if NS is five times smaller than NT, the information carried by the snapshots sample refers to only the 25% of the entire set of the truth solutions. Is it possible to improve the quality of the reduced approximation, without increasing the number of snapshots selected? In another scenario, suppose that a perturbation parameter α is introduced in the unsteady problem (7), as proposed in (9), and that the snapshots are computed for a specific value of α = α1. We would like to generate a reduced space that suitably approximates also the truth solutions for other values of α without recomputing all the high-fidelity snapshots.
With these two scenarios in mind, we propose a strategy to improve the quality of the reduced approximation based on a greedy algorithm. For references to standard greedy algorithms applied to parametrized PDEs see e.g., Hesthaven et al. [27] and Quarteroni et al. [28].
We introduce another solution that belongs to an intermediate problem between (7) and (10): find such that
We notice that problem (17) is set in the high-fidelity approximation framework but the right hand side and the advection field are defined by (10). In fact, in (7), these terms are evaluated using the truth solution , while in (17) it is evaluated using the reduced solution , as in problem (10). Considering the error between and in a generic norm ||·||*, the following triangular inequality holds:
The greedy procedure that we propose focuses on the first contribution . Subtracting problem (10) from (17) allows to state a result of Galerkin orthogonality:
We assume that the dual norm of the residual can be used as an indicator of the error . In particular, at each time level tn+1, we consider
and its associated dual norm .
We now have defined all the necessary quantities, we can proceed presenting the steps to be performed when we want to enrich the POD basis with a greedy algorithm. First, perform a POD on the snapshots , for and we construct the reduced space . Then, we start the greedy enrichment setting :
1. Generate the reduced basis solutions , , by solving the reduced order problem (10).
2. Compute the dual norms of the residuals , , which are used as error indicators.
3. Select n* such that
4. Compute the by solving the reduced order problem (17).
5. Split into its velocity and pressure components, and , respectively. Compute the supremizer associated with the pressure component.
6. Compute ϕu representing the orthonormalization of the velocity function with respect to the reduced space XN, obtained with a Gram-Schmidt algorithm considering the scalar product (·, ·)V; similarly for ϕp and .
7. Build defined as is (16).
8. Compute ϕσ representing the orthonormalization of the velocity function with respect to the reduced space XN+2, obtained with a Gram-Schmidt algorithm considering the scalar product (·, ·)V.
9. Build defined as is (16).
10. Update the structures for the online computation of the reduced solutions and the dual norms of the residuals.
11. Set N = N + 3 and XN = XN+3. Repeat until a predefined stopping criterion is satisfied.
Remark. We remark that the functions that are added to the space XN in step 5 are derived from and not the truth solution . We have no guarantee that is close to or that it belongs to the low dimensional manifold of the truth solutions. We would like also to remark that even if we are trying to reduce the error , to date we have no proof that the algorithm converges. In fact, we cannot theoretically prove that
For this lack of theoretical convergence results, to stop the greedy enrichment procedure, we rather opt for a fixed number of solutions Nmax chosen a priori, instead of using a certain tolerance on the a posteriori error estimator. Nevertheless, in the next section we will show some numerical evidence that the greedy enrichment is able to improve the quality of the approximation space.
4. Application to a Femoropopliteal Bypass
4.1. Application and Motivation
Atherosclerotic plaques often occur in the femoral arteries. The obstruction of the blood flow results in a lower perfusion of the lower limbs and the most common symptom of this disease is an intermittent claudication, which affects the 4% of people over the age of 55 years [34]. In order to restore the physiological blood circulation, different medical treatments are possible. In critical cases, the stenosis is treated with surgical intervention that bypasses the obstruction using a graft and providing an alternative way where blood can flow. The bypass creates a side-to-end anastomosis between the graft and the upstream artery (before the occlusion) and an end-to-side anastomosis with the distal downstream part. In particular, the design of end-to-side anastomosis affects the flow downstream the bypass and provokes remodeling phenomena inside the arterial wall. The arteries adapt their size in order to maintain a certain level of shear stress, which results in a thickening of the intima layer and in an increasing risk of thrombi formation. The arterial wall remodeling is in fact linked with hemodynamic factors such as the wall shear stress magnitude and direction. Moreover, velocity profiles and separation of flows have been investigated when studying the bypass end-to-side anastomosis [35, 36]. Studies with idealized geometrical models have been proposed in order to define an optimal design for the anastomosis [37]. Nevertheless, the geometry of the vessel is one of the most important factors that affect the pattern of the wall shear stress. Further, patient specific data would be required in order to analyse each particular case.
We focus our attention on the patient-specific femoropopliteal bypass performed with a venous graft bridging the circulation from the femoral artery to the popliteal one. As a domain of interest we select the end-to-side anastomosis (see Figure 1). The geometry was reconstructed by CT-scan images as it is detailed in Marchandise et al. [38] and inlet and outlet flow rates are provided from the experimental data in Marchandise et al. [38]. We compute the Reynolds number as , being ρf the blood density, Qin the inlet flow rate, D the vessel diameter and μ the blood viscosity. The average Reynolds number ranges from 144 and 380 (at the systolic peak), in agreement with the values provided in Loth et al. [36].
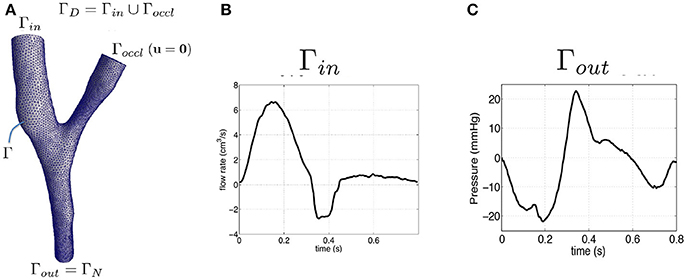
Figure 1. Realistic geometry of the end-to-side anastomosis. Graph of the inlet and outlet boundary conditions. (A) End-to-side geometry. (B) Inlet flow rate. (C) Outlet pressure.
4.2. Test Case
4.2.1. Application of the POD Algorithm
In this section we investigate the behavior of the POD and the greedy enriched POD algorithms on a case representing the femoropopliteal bypass application where the finite element resolution is performed on a coarse mesh. The usage of a coarse grid allows us to lower the offline computational costs and, thus, to test and compare several reduced basis approximations. Since we are interested in the realistic application of the femoropopliteal bypass, the physical parameters and boundary data are patient-specific. The coarse mesh is composed by 5,823 tetrahedra and 1.309 vertices. To obtain the high fidelity solutions of the RFSI model we use standard ℙ1+Bubble-ℙ1 finite elements for a total of 22,702 degrees of freedom. The boundary conditions are periodic with period of 0.8 s (one heartbeat). We set the solutions at time t = 0 equal to zero. To get rid of the dependence of these initial condition we perform the simulation of an entire heartbeat and we focus on the solutions obtained for the subsequent heartbeat. Thus, to test the POD reduction algorithm, we compute the high fidelity numerical solutions for a time lapse corresponding to the second heartbeat, from t0 = 0.8 s to tNT = 1.6 s with a time step Δt = 0.001 for a number of time intervals NT = 800. We denote with the superscript varying from 0 to NT the sequence of computed solutions:
We save the finite element solutions every five time steps and we use the apex , nS = 5k, with k = 0, .., NS (NS = 160) to address the stored functions, that represent the snapshot sample:
Indeed, we compute the POD starting from the 160 snapshots , , which represent the 25% of the finite element solutions computed for the second heartbeat. To check the quality of the reduced space approximations, we monitor the following errors:
• relative error of the velocity at time tnS and correspondent space-time error:
• relative error of the pressure at time tnS and correspondent space-time error:
• space-time dual norm of the residual scaled with respect to the space-time norm of the global solution
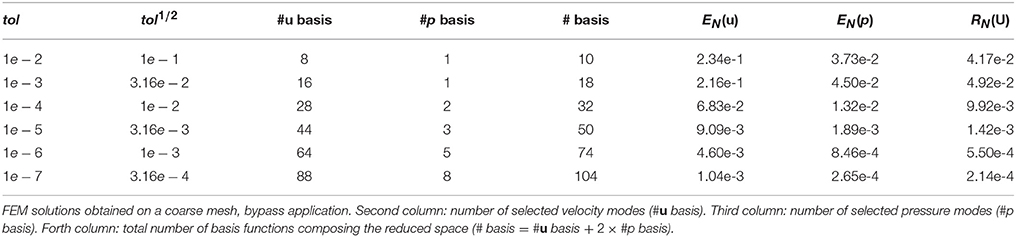
We build a sequence of POD reduced spaces with decreasing values of the tolerance tol and we compute the aforementioned indicators for each one of the reduced spaces generated. The space-time errors are reported in Table 1. In particular, we show: the number of selected velocity modes (#u basis); the number of selected pressure modes (#p basis); the total number of basis functions composing the reduced space (# basis = #u basis + 2 × #p basis); the space-time errors and residuals as defined above. Since the problem at hand is unsteady and the solution at a time instant tn depends on the solutions at the previous instants, the POD model errors EN(u) and EN(p) are bounded from above by the fixed tolerance but they are however of the same order of magnitude (see Table 1). We notice that, even if does not represent an upper bound for the error, nevertheless, from experimental results, we can use it as an indicator of (see Figure 2). The apparent strong correlation between the dual norm of the residual and the global error norm is probably due to the strong contribution of the mass term in the unsteady formulation. Indeed, if we choose a time step of 0.001, the mass matrix is multiplied for a factor of 103. We remark that the magnitudes of the absolute errors for the velocity span from 10−1 to 102 and the associated velocity solutions norms are of order of 102 − 103. For the pressure, we have absolute errors of order 100 − 103, while their solutions norms are of order 103−5. Indeed, in absolute terms the global error is mostly related with the pressure one.
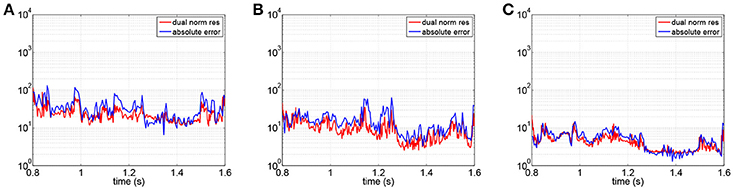
Figure 2. Dual norms of the residuals and norms of the global errors with respect to time for different choices of the POD tolerance tol. (A) tol = 1e-5. (B) tol = 1e-6. (C) tol = 1e-7.
4.2.2. Application of the Greedy Enriched POD Algorithm
The POD algorithm provided satisfactory results and we were able to reduce the approximation space dimension from 105 to 10 − 100. In this section we aim at comparing the greedy enrichment algorithm with the POD one, in order to understand if using different basis functions than POD modes provides the same quality of reduced approximations. Thus, we compare the magnitude of the reduced approximation errors obtained using a reduced space generated through a standard POD algorithm with the ones obtained using the POD coupled with the greedy enrichment as introduced in section 3.2. We recall that the snapshots sample represents a subset of the time instants we solve in the unsteady simulation: indeed we store only the 25% of the time instants solutions computed. As there is no error bound available, we use the dual norm of the residual as surrogate. This is a rough approximation, also because the real error includes time integration, while the dual norm of the residual can only represent a space error. Of course we do not expect the greedy enriched POD to perform better, on the contrary it can have (and actually has) limitations.
Remark We are interested to simulate a fluid-dynamics phenomena with cyclic inputs. Typically in hemodynamics applications, we are interested in several heartbeats. Thus, instead of performing the greedy research only on one single heartbeat, we exploit as much as we can the information on the truth solutions coming from the snapshots. For each single snapshot , we perform a simulation that starts from the initial time tns and ends at tns+NT = tns+0.8. We define a vector index n = (nT, nS) with nT = nS+n such that being the approximate solution at time obtained starting from the initial condition . We define the set of indexes . The generalization of the greedy enrichment presented in Section 3.2 is straightforwards substituting n with n. In particular, the selection of the worst approximated index n* in the greedy enrichment can be generalized as follows:
In order to initialize the greedy enrichment algorithm we compute a POD basis fixing the tolerance tol = 1e − 5 (50 velocity modes, 3 pressure modes, 3 supremizers). To compare the POD approximation with the greedy enriched one, we augment the initial reduced space with two strategies. On one side, we apply the greedy enrichment and, at each iteration, we add the triplet of functions selected by the largest dual norm of the residual in space. On the other side, we augment the basis by adding, at each algorithm iteration, one POD mode for the velocity and one POD mode for the pressure with its associated supremizer. In both cases, at each iteration, we increase the reduced space dimensions of three units. The results obtained using only POD modes are displayed in black and addressed with the label POD, while the results obtained with the greedy enrichment are shown in red and addressed with the label Greedy enriched POD (see Figure 3).
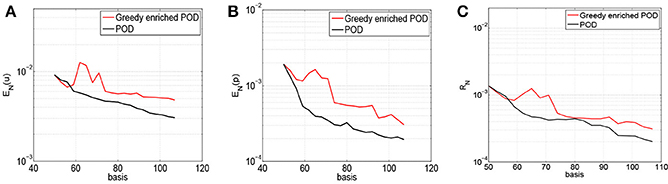
Figure 3. Space-time errors vs. the number of basis, comparison between the standard POD and the greedy enriched POD, starting from 50 POD basis functions. FEM solutions obtained on a coarse mesh, bypass application. (A) Space-time velocity error. (B) Space-time pressure error. (C) Space-time dual norm of the residuals.
From Figure 3, we note that the decrements of the errors in the greedy enrichment algorithm are slower than when adding POD modes. Nevertheless, we notice that both the space-time pressure error and residuals are comparable when adding POD modes or greedy basis functions (see Figures 3B,C). On the contrary the decrements of the velocity is much slower when we use the greedy enrichment with respect to adding POD modes. We recall, however, than the residual is mostly related to the pressure error component.
4.3. Realistic Case
4.3.1. Application of the POD Algorithm
In this section we perform a discretization reduction of the RFSI model applied to the femoropopliteal bypass case, where the high fidelity approximations are computed using a fine mesh. As before, a parabolic velocity profile is imposed at the inlet section and a mean pressure condition at the outlet. The ℙ1+Bubble-ℙ1 discretization yields 1,410,475 degrees of freedom on the fine mesh. We first test the discretization reduction using a standard POD procedure: we compute the high fidelity numerical solutions for two heartbeats with a time step Δt = 0.001 and we store the ones related to the second heartbeat every five time steps. Thus, and . We compute the Gramian matrices associated to the 160 snapshots , separating the velocity and pressure components. We denote and for k = 1, ..NS the eigenvalues associated to the decomposition of the correlation matrices of the velocity and pressure, respectively (see section 3.1). In both cases they decrease exponentially fast. The eigenvalues associated to the pressure snapshots (Figure 4B) decrease faster than the ones associated to the velocity (Figure 4A). Thus, by fixing the same tolerance, we expect that a fewer number of pressure modes will be selected with respect to the velocity ones.
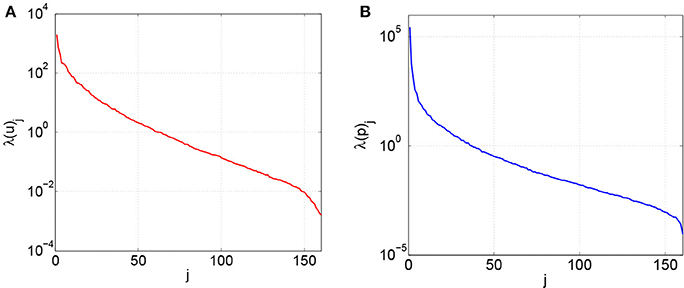
Figure 4. Velocity and pressure eigenvalues computed with 160 snapshots sampled every 0.005 s. (A) Velocity eigenvalues, . (B) Pressure eigenvalues, .
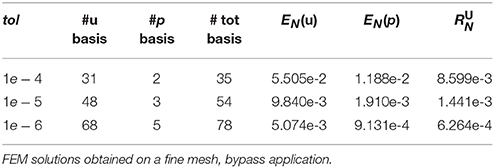
We compute the POD reduced spaces using three different values for the tolerance: tol ∈ {1e − 4, 1e − 5, 1e − 6}. As it was done in section 4.2, in Table 2, we record the selected number of modes and we compute the space-time errors EN(u) and EN(p) of the velocity and pressure, respectively. By taking advantage of the generated reduced space, at each time iteration we solve the reduced system and we compute a linear functional of the approximate solution that evaluates the outlet flow rate. We record the computational time associated with the offline and online computations in Table 3. We can appreciate that the resolution of the reduced problem combined with the evaluation of a linear output functional is performed in almost real time: using 35 basis functions we solve 1.6 physical seconds in 0.8 computational seconds, while a ten heartbeats simulation (8 physical seconds) selecting the POD space with 54 basis functions takes 12.6 s on a notebook. Performing the same simulation with the high fidelity model would have taken around 40 h on 256 processors of a supercomputer. The offline costs of the POD reduction (without the snapshots generation) are reported in the third column of Table 3. We remark that most of this time is spent in the generation of the structures for the residual evaluation.
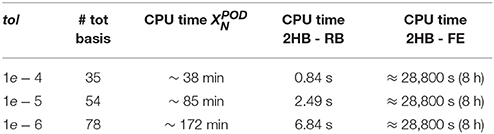
Table 3. CPU time : offline computations costs for the generation of the POD reduced spaces (without the finite element computations) on 512 processors; CPU time 2HB - RB: online computational time corresponding to the simulation of 2 heartbeats (2HB) on a personal laptop; CPU time 2HB - FE: finite element computational time corresponding to the simulation of 2 heartbeats (2HB) on 256 processes on a supercomputer.
Note that the POD model errors EN(u) and EN(p) decrease significantly when increasing the number of basis functions, as it is reported from both the values of Table 2. Once again, we notice that the dual norm of the residual is a good indicator of the approximation error (see Figure 5).
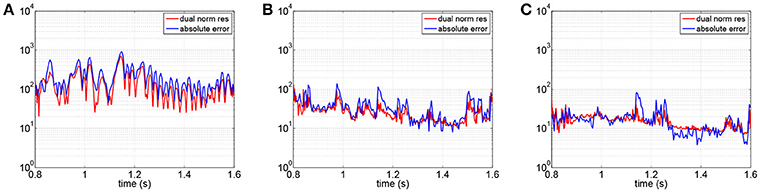
Figure 5. Dual norm of the residuals and X-norm of the errors with respect to the time instant for different choices of the POD tolerance tol. FEM solutions obtained on a fine mesh, bypass application. (A) tol = 1e-4. (B) tol = 1e-5. (C) tol = 1e-6.
In the femoropopliteal bypass application, we are interested in measuring also the errors on the output of interests. Being the stress tensor and n the normal vector to the surface Γ, we compute the wall shear stress as and we also consider the averaged wall shear stresses on a generic area A: . We remark that to properly estimate the selected output of interest we need accurate high fidelity solutions with a mesh refined at the wall, as shown by Marchandise et al. [38]; the fine mesh used in this work is similar to the fine one used in that paper. Reducing the dimension of the finite element space does not lead to the same results that we obtain reducing the degrees of freedom using the POD decomposition. In fact, the wall shear stress values computed using a coarse finite element space underestimate considerably the values obtained with the fine grid (see Figure 6), while the results obtained with the POD reduced approximation mostly overlapped with the ones computed with the finite element discretization.
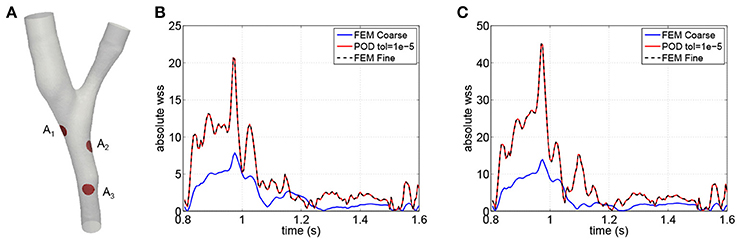
Figure 6. Averaged wall shear stress (in [g/cm s]) computed in different location of the interface. Comparisons between the values obtained with the finite element discretization on the fine mesh (FEM Fine), the coarse one (FEM Coarse) and the reduced basis approximation (POD tol = 1e-5). (A) Areas location. (B) Wss absolute values - Area 1. (C) Wss absolute values - Area 2.
4.3.2. Percentage of Flow Coming From the Occluded Artery
In many cases, the artery is not completely occluded but a residual flow is still provided by the original vessel. Studying the distribution of fluid-dynamic quantities could be important to identify, for example, whether it would be better or not to surgically close the original artery. Our approach allows to study the variation of the flow and wall shear stress for different values of flow percentage coming from the occluded artery with low computational costs.
Here the percentage of flow coming from the occluded artery is an additional parameter. We solve the high fidelity model for two extreme cases: μ1 = 0% (full occlusion) and μ2 = 50% of flow. Using a POD algorithm with tol = 10−5, we construct the reduced space of dimension N1, associated with the snapshots computed with μ1. We obtain N1 = 54, where 48 basis functions are velocity modes, 3 pressure modes and 3 supremizers. Then, we consider the snapshots associated with μ2, we build a second POD reduced space of dimension N2, also fixing tol = 10−5. We obtain N2 = 55 where 47 basis functions are velocity modes, 4 pressure ones and 4 supremizers. Finally, we check that the basis functions are linear independent and orthonormalize the basis of with respect to . Indeed, none of the basis functions obtained for μ2 = 0.5 is as a linear combination of the basis related to μ1 = 0 and the final reduced space XN has dimension N = N1 + N2 = 109.
We then choose a parameter μ3 = 25% of flow coming from the occluded artery. We focus on the velocity profiles near the systolic peak and in the early diastole (see Figure 7) and the averaged wall shear stress (see Figure 8). We compare the target outputs obtained using the finite element approximation (label: FEM 25%) and the reduced ones (label: POD 25%). Moreover, we display the selected quantities also for the high fidelity solutions obtained with μ1 = 0 (label: FEM 0%), μ2 = 0.5 (label: FEM 50%) in order to clarify how the system dynamics changes when different values of the percentage are considered.
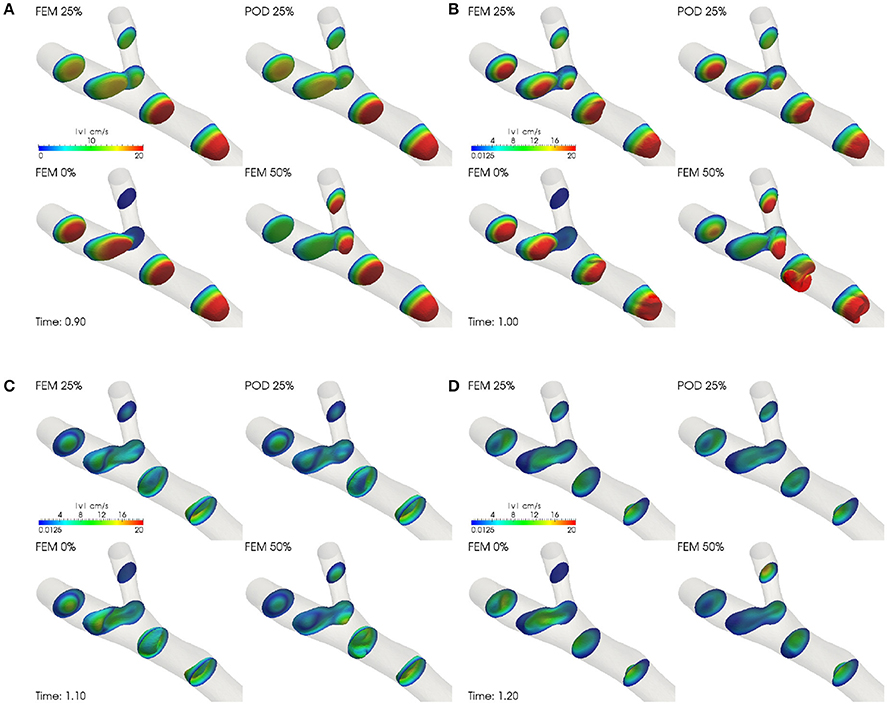
Figure 7. Velocity profiles for two time instants of the diastolic phase. Comparisons between finite element and reduced approximations. Femoropopliteal bypass application in which the high fidelity solutions are obtained using a finite element approximation on a fine mesh. (A) Systole, 0.9 s. (B) Peak systole, 1 s. (C) Diastole, 1.1 s. (D) Diastole, 1.2 s.
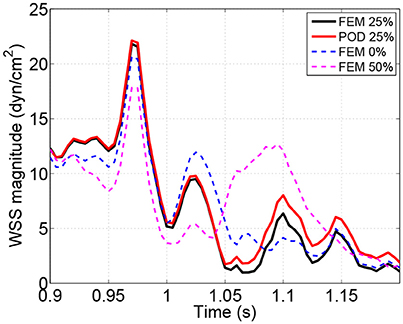
Figure 8. Averaged wall shear stress computed in the location A1, cf. Figure 6. Comparisons between finite element (corse and fine meshe) and reduced approximations.
During the systolic phase the reduced solutions well reproduce the high fidelity ones, while during the diastole, the differences are more visible, in particular in some locations as, for example, near the anastomosis between the arterial vessel and the bypass graft (see Figure 7). We remark that the velocity profiles for different values of the parameter are significantly different between themselves. Our reduced solution approximates well the value of the wall shear stress associated to μ3 (see Figure 8). We can appreciate the good agreement between the reduced and the high fidelity results, even when the values of wall shear stress associated to μ3 are not berween those associated to μ1 and μ2 (see Figure 8B). Moreover, the approximation of the wall shear stress using a finite element approximation with a coarse grid leads to a consistent underestimation of their values (see Figure 8C).
4.3.3. Application of the Greedy Enriched Algorithm With Perturbed Data
In this section we apply the greedy enrichment in the case of perturbed boundary data. In particular, as in (9), we introduce a parameter in the inlet flow rate function representing a small perturbation with respect to a reference value. The perturbation function θ(α, t) is define as follows:
where α is supposed to vary between 0 and 0.2. Thus, the maximum relative difference with the original flow rate is equal to the 20%. We denote with with * = {h}, {N} or {N, h} the numerical solutions at the time instant tn that depend on the parameter α and with the residuals. In the perturbed case, the algorithm steps in section 3.2 are modified as follows. First we perform a POD algorithm fixing α = α1 = 0.0; the resulting reduced space is addressed with , where the apex α1 denotes the choice of the α parameter. Then, we set α2 = 0.2:
1. Generate the reduced basis solutions , by solving the reduced order problem (10).
2. Compute the dual norms of the residuals , , which are used as error indicators.
3. Select n* such that .
4. Compute the by solving the reduced order problem (17).
5. Split into its velocity and pressure components, and , respectively. Compute the supremizer associated with the pressure component.
6. Compute ϕu representing the orthonormalization of the velocity function with respect to the reduced space XN, obtained with a Gram-Schmidt algorithm considering the scalar product (·, ·)V; similarly for ϕp and .
7. Build built as is (16).
8. Compute ϕσ representing the orthonormalization of the velocity function with respect to the reduced space XN+2, obtained with a Gram-Schmidt algorithm considering the scalar product (·, ·)V.
9. Build built as is (16).
10. Update the structures for the online computation of the reduced solutions and the dual norms of the residuals.
11. Set N = N + 3 and XN = XN+3. Repeat until a predefined stopping criterion is satisfied.
The real modification is indeed related to the fact that the initial POD is computed for α = α1 = 0, while the greedy enrichment is performed fixing α = α2 = 0.2. The resulting reduced space XN aims to represent a suitable space of approximation for both values of α. In the parametrized case, by using greedy enrichment we aim at saving a part of the offline computational costs: indeed, in a standard POD-Greedy procedure (see [39]), each new evaluation of the parameter α requires the computation of the associated finite element solutions for each time instant . In our application, this would require about 8 h on 256 processors. Instead, during the greedy enrichment, we perform only one finite element resolution for a single time step, while the remaining computations are dedicated to reduced basis structures.
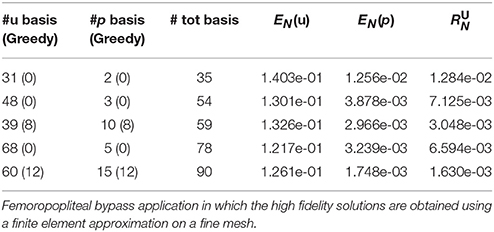
We test the greedy enrichment algorithm by initializing it with two different starting POD reduced spaces: in one case we consider the modes selected with tol = 1e − 4 (35 POD basis functions) and in the other one we consider the POD modes corresponding to tol = 1e − 5 (54 POD basis functions). In the first case, we enrich the space by adding 8 triplets selected by the greedy algorithm; we obtain the reduced space X59. In the second case, starting from , we enrich the space adding 12 triplets, obtaining X90. All the errors and residuals computed and shown below are referred to the solutions obtained with α2 = 0.2. In particular, in Table 4 we report the velocity and pressure errors generated by the greedy enriched reduced spaces as well as the ones obtained with the standard POD ones. Moreover, we compute the space-time dual norm of the residual, scaled by the solution norm (sixth column of Table 4).
We note that the space-time velocity error does not decrease significantly neither when adding greedy basis functions nor when augmenting the number of selected POD modes. If we look at the pressure, using the greedy enrichment we manage to decrease its error more than if we use POD modes. Also the space-time dual norm of the residual is smaller when considering the greedy enriched space than the POD ones.
Regarding the offline costs, to generate the space X59 starting form the , we perform 8 iterations of the greedy enrichment algorithm: this takes 82 min on 512 processors where the most of the time is devoted to the generation of the reduced structures for the residual evaluation. We remark that computing a standard POD reduced space for the parameter evaluation corresponding to α = 0.2 would require about 8 h on 256 processors for the finite element computation of two periods, plus about 1 h on 512 processors for the generation of the reduced space itself.
To explain why we obtain better results for the pressure than for the velocity, we investigate the absolute values of velocity, pressure and global solutions errors and we compare them to the dual norms of the residuals (see Figure 9). Since the velocity and pressure norms have two different magnitudes (10 − 102 for the velocity and 103 − 105 for the pressure), the corresponding absolute values of the pressure errors are bigger than the velocity ones, even if the relative errors are lower. The greedy procedure selects the worst approximated time instant based on the dual norms of the residuals and these quantities are indicators of the global absolute errors. Since the latter is mostly due to the pressure error, this can explain why the greedy enrichment provides better results for the pressure than for the velocity.
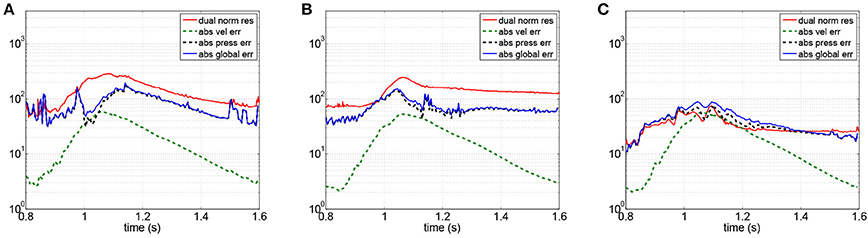
Figure 9. Dual norms of the residuals and norms of the global errors with respect to time for different choices of the POD tolerance tol. Femoropopliteal bypass application in which the high fidelity solutions are obtained using a finite element approximation on a fine mesh. (A) 54 Basis - POD. (B) 78 Basis - POD. (C) 90 Basis - Greedy enriched POD.
5. Conclusions
In this work we presented an application of reduced order modeling to a RFSI problem that is indeed an unsteady Navier-Stokes problem with generalized Robin boundary conditions. We detailed how an affine decomposition with respect to boundary data varying in time can be obtained under suitable hypothesis. Moreover, we presented and detailed how the POD can be applied to the RFSI problem in order to take into account the different order of magnitudes of the variables. We discussed the introduction of the supremizer functions inside the reduced basis, necessary to include the pressure in the reduced system. Afterwards, we proposed an enrichment of the POD reduced basis based on a greedy algorithm. All the algorithms presented were then numerically tested on a realistic hemodynamics problem. We tested the POD and greedy enrichment algorithm on two cases: a test case, where the finite element solution is obtained with a coarse grid, and a fine case, where the finite element space has order of 106 degrees of freedom. The results showed the good performances of the POD reduction algorithm on the RFSI problem, also with respect to the evaluation of specific hemodynamics target output (wall shear stress). Moreover we provided numerical evidence of how the reduced approximation can be improved using the greedy enrichment algorithm, in particular regarding the pressure error. The different behavior of the velocity and pressure errors is due to the use of the dual norm of the residual as an indicator of the global solution error. Indeed, since we do not have suitable a-posteriori error estimators, one for the velocity and one for the pressure variables, we measure the dual norm of the residual as a surrogate estimator. Being the pressure variable and the correspondent error two order of magnitudes grater that the velocity ones, the residual is indeed an indicator of the pressure errors. Nevertheless, even in lack of theoretical results, numerical experiments showed that the greedy enrichment is able to improve the quality of the reduced approximation allowing us to save computational time. The development of suitable a-posteriori error estimators for the pressure and velocity in the case of RFSI problem would be required to improve the performances of the greedy enrichment.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer, JC, and handling Editor declared their shared affiliation.
Acknowledgments
The authors acknowledge support of the European Research Council under the Advanced Grant ERC-2008-AdG 227058, Mathcard, Mathematical Modeling and Simulation of the Cardiovascular System, and of the FNS project 200021E-168311, Domain-Decomposition-Based Fluid Structure Interaction Algorithms for Highly Nonlinear and Anisotropic Elastic Arterial Wall Models in 3D. Moreover, we thank Prof. Bernard Haasdonk and Prof. Alfio Quarteroni for the insightful discussion. We gratefully acknowledge the Swiss National Supercomputing Center (CSCS) for providing the CPU resources for the numerical simulations under the projects IDs s475 and s796.
References
1. Colciago CM, Deparis S, Quarteroni A. Comparisons between reduced order models and full 3D models for fluid-structure interaction problems in haemodynamics. J Comput Appl Math. (2014) 265:120–38. doi: 10.1016/j.cam.2013.09.049
2. Bazilevs Y, Michler C, Calo VM, Hughes TJR. Weak Dirichlet boundary conditions for wall-bounded turbulent flows. Comput Methods Appl Mech Eng. (2007) 196:4853–62. doi: 10.1016/j.cma.2007.06.026
3. Manzoni A, Negri F. Rigorous and Heuristic Strategies for the Approximation of Stability Factors in Nonlinear Parametrized PDEs. Preprint available as Mathicse Report Nr. 08.2014 (2014).
4. Lassila T, Manzoni A, Quarteroni A, Rozza G. Model order reduction in fluid dynamics: challenges and perspectives. In: Quarteroni A, Rozza G, editors. Reduced Order Methods for Modeling and Computational Reduction. Vol. 9 of MS&A Series. Milano: Springer (2014).
5. Rozza G, Huynh DBP, Patera AT. Reduced basis approximation and a posteriori error estimation for affinely parametrized elliptic coercive partial differential equations. Arch Comput Methods Eng. (2008) 15:229–75. doi: 10.1007/s11831-008-9019-9
6. Quarteroni A, Rozza G, editors. Reduced Order Methods for Modeling and Computational Reduction. MS&A, Modeling, Simulation and Applications. Milano: Springer (2013). Available online at: http://www.springer.com/mathematics/computational+science+
7. Yano M, Patera AT, Urban K. A space-time hp-interpolation-based certified reduced basis method for Burgers' equation. Math Models Methods Appl Sci. (2014) 24:1903–35. doi: 10.1142/S0218202514500110
8. Nguyen NC, Rozza G, Patera AT. Reduced basis approximation and a posteriori error estimation for the time-dependent viscous Burgers equation. Calcolo (2009) 46:157–85. doi: 10.1007/s10092-009-0005-x
9. Wirtz D, Sorensen DC, Haasdonk B. A posteriori error estimation for DEIM reduced nonlinear dynamical systems. SIAM J Sci Comput. (2014) 36:A311–38. doi: 10.1137/120899042
10. Deparis S, Lovgren AE. Stabilized reduced basis approximation of incompressible three-dimensional Navier-Stokes equations in parametrized deformed domains. J Sci Comput. (2012) 50:198–212. doi: 10.1007/s10915-011-9478-2
11. Iapichino L, Quarteroni A, Rozza G. A reduced basis hybrid method for the coupling of parametrized domains represented by fluidic networks. Comput Methods Appl Mech Eng. (2012) 221–222:63–82. doi: 10.1016/j.cma.2012.02.005
12. Amsallem D, Farhat C. An online method for interpolating linear parametric reduced-order models. SIAM J Sci Comput. (2011) 33:2169–98. doi: 10.1137/100813051
13. Gerner AL, Veroy K. Reduced basis a posteriori error bounds for the Stokes equations in parametrized domains: a penalty approach. Math Models Methods Appl Sci. (2011) 21:2103–34. doi: 10.1142/S0218202511005672
14. Deparis S, Rozza G. Reduced basis method for multi-parameter-dependent steady NavierStokes equations: applications to natural convection in a cavity. J Comput Phys. (2009) 228:4359–78. doi: 10.1016/j.jcp.2009.03.008
15. Grinberg L, Yakhot A, Karniadakis G. Analyzing transient turbulence in a stenosed carotid artery by proper orthogonal decomposition. Ann Biomed Eng. (2009) 37:2200–17. doi: 10.1007/s10439-009-9769-z
16. Deparis S. Reduced basis error bound computation of parameter-dependent Navier-Stokes equations by the natural norm approach. SIAM J Numer Anal. (2008) 46:2039–67. doi: 10.1137/060674181
17. Gunzburger MD, Peterson JS, Shadid JN. Reduced-order modeling of time-dependent {PDEs} with multiple parameters in the boundary data. Comput Methods Appl Mech Eng. (2007) 196:1030–47. doi: 10.1016/j.cma.2006.08.004
18. Sen S, Veroy K, Huynh DBP, Deparis S, Nguyen NC, Patera AT. Natural norm a posteriori error estimators for reduced basis approximations. J Comput Phys. (2006) 217:37–62. doi: 10.1016/j.jcp.2006.02.012
19. Nichols WW, O'Rourke MF. McDonald's Blood Flow in Arteries - Theoretical, Experimental and Clinical Principles. London: Arnold (1998).
20. Formaggia L, Quarteroni A, Veneziani A. Cardiovascular Mathematics. Heidelberg: Springer (2009).
21. Figueroa CA, Vignon-Clementel IE, Jansen KE, Hughes TJR, Taylor CA. A coupled momentum method for modeling blood flow in three-dimensional deformable arteries. Comput Methods Appl Mech Eng. (2006) 195:5685–706. doi: 10.1016/j.cma.2005.11.011
22. Moireau P, Xiao N, Astorino M, Figueroa CA, Chapelle D, Taylor CA, et al. External tissue support and fluid-structure simulation in blood flows. Biomech Model Mechanobiol. (2012) 11:1–18. doi: 10.1007/s10237-011-0289-z
23. Figueroa CA, Baek S, Taylor CA, Humphrey JD. A computational framework for fluid-solid-growth modeling in cardiovascular simulations. Comput Methods Appl Mech Eng. (2009) 198:3583–601. doi: 10.1016/j.cma.2008.09.013
24. Nobile F, Vergara C. An effective fluid-structure interaction formulation for vascular dynamics by generalized robin conditions. SIAM J Sci Comput. (2008) 30:731–63. doi: 10.1137/060678439
25. Kashiwabara T, Colciago CM, Dedé L, Quarteroni A. Well-posedness, regularity, and convergence analysis of the finite element approximation of a generalized Robin boundary value problem. SIAM J Numer Anal. (2015) 53:105–26. doi: 10.1137/140954477
26. Sirisup S, Karniadakis GE. Stability and accuracy of periodic flow solutions obtained by a POD-penalty method. Physica D (2005) 202:218–37. doi: 10.1016/j.physd.2005.02.006
27. Hesthaven JS, Rozza G, Stamm B. Certified Reduced Basis Methods for Parametrized Partial Differential Equations. Cham: Springer (2016).
28. Quarteroni A, Manzoni A, Negri F. Reduced Basis Methods for Partial Differential Equations: An Introduction, Vol. 92. Heildelberg: Springer (2015).
29. Rowley CW. Model reduction for fluids, using balanced proper orthogonal decomposition. Int J Bifurcat Chaos. (2005) 15:997–1013. doi: 10.1142/S0218127405012429
30. Willcox K, Peraire J. Balanced model reduction via the proper orthogonal decomposition. AIAA J. (2002) 40:2323–30. doi: 10.2514/2.1570
31. Gerner AL, Reusken A, Veroy K. Reduced Basis a Posteriori Error Bounds for the Instationary Stokes Equations. Singapore: World Scientific (2012).
32. Burkardt J, Gunzburger M, Lee HC. {POD} and CVT-based reduced-order modeling of NavierStokes flows. Comput Methods Appl Mech Eng. (2006) 196:337–55. doi: 10.1016/j.cma.2006.04.004
33. Rozza G, Veroy K. On the stability of the reduced basis method for Stokes equations in parametrized domains. Comput Methods Appl Mech Eng. (2007) 196:1244–60. doi: 10.1016/j.cma.2006.09.005
34. Giordana S, Sherwin SJ, Peir J, Doorly DJ, Crane JS, Lee KE, et al. Local and global geometric influence on steady flow in distal anastomoses of peripheral bypass grafts. J Biomech Eng. (2005) 127:1087–98. doi: 10.1115/1.2073507
35. Loth F, Jones SA, Zarins CK, Giddens DP, Nassar RF, Glagov S, et al. Relative contribution of wall shear stress and injury in experimental intimal thickening at PTFE end-to-side arterial anastomoses. J Biomech Eng. (2002) 124:44–51. doi: 10.1115/1.1428554
36. Loth F, Fischer PF, Bassiouny HS. Blood flow in end-to-side anastomoses. Annu Rev Fluid Mech. (2008) 40:367–93. doi: 10.1146/annurev.fluid.40.111406.102119
37. Lassila T, Manzoni A, Quarteroni A, Rozza G. Boundary control and shape optimization for the robust design of bypass anastomoses under uncertainty. ESAIM Math Model Numer Anal. (2013) 47:1107–31. doi: 10.1051/m2an/2012059
38. Marchandise E, Crosetto P, Geuzaine C, Remacle JF, Sauvage E. Quality open source mesh generation for cardiovascula flow simulation. In: Ambrosi D, Quarteroni A, Rozza G, editors. Modeling of Physiological Flows. Milano: Springer (2011) 395–414.
Keywords: fluid-structure interaction, Navier-Stokes equations, reduced order modeling, proper orthogonal decomposition, reduced basis method, hemodynamics
Citation: Colciago CM and Deparis S (2018) Reduced Numerical Approximation of Reduced Fluid-Structure Interaction Problems With Applications in Hemodynamics. Front. Appl. Math. Stat. 4:18. doi: 10.3389/fams.2018.00018
Received: 15 January 2018; Accepted: 16 May 2018;
Published: 29 June 2018.
Edited by:
Mariano Vázquez, Barcelona Supercomputing Center, SpainReviewed by:
Alexey Goltsov, Abertay University, United KingdomJuan Carlos Cajas García, Barcelona Supercomputing Center, Spain
Copyright © 2018 Colciago and Deparis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Simone Deparis, c2ltb25lLmRlcGFyaXNAZXBmbC5jaA==
 Claudia M. Colciago
Claudia M. Colciago Simone Deparis
Simone Deparis