- 1Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto, Universidade de São Paulo, Ribeirão Preto, Brazil
- 2Instituto Nacional de Ciência e Tecnologia em Sistema Complexos, Rio de Janeiro, Brazil
A large number of studies have demonstrated that intertemporal decision making process usually results in preferences that reverse over time, or choices that are inconsistent over time. Inconsistency can be explained by different discount models by the effect of reward value perception at different moments. Otherwise, one can also understand inconsistency as the result of the time perception effect. Here, we address inconsistency as the result of a subjective time dilation perception effect. We use arguments inspired by the special theory of relativity and focused our study on a generalized model that encompasses psychophysical effects on time perception, where we look for a transformation of the time interval between the pay times of two rewards. Additionally, we present a generalized two-argument hyperbolic utility function for the Bernoulli (logarithmic) one, associating their difference to subjective time intervals.
1. Introduction
Individuals subjected to intertemporal decision making have to choose between two rewards: a smaller and more immediate and a greater and later one. In intertemporal decision making, the time interval between the present instant and the delivery time of the reward is called delay. Studies have led to a strong consensus that later rewards are discounted (or devalued) relative to more immediate ones [1]. The value of a reward, V, decreases as the delay increases. The undiscounted (real) value of a given reward is called objective value, V0. The reward value to be received with a given delay, V(t), is called subjective value and is equal to the subjective value V0 discounted. Experiments with humans and animals have been carried out to determine the indifference points [2–8]. Discount functions model the behavior of a reward subjective value as a function of the delay, being monotonic decreasing and vanishing functions. Despite the difficulty of measuring V(t) (by the indifference point determination), several phenomenological models have been addressed to establish discount functions that adequately describe the discount process as a function of the experimentally observed delay. At the outset, the exponential and hyperbolic functions are the main models, which can be retrieved as particular cases of more general ones [8–10].
Discount models can be elaborated taking into account time perception/distortion effects. In Physics, according to the special theory of relativity, time dilation is an effect characterized by the difference in the elapsed time measured by two observers. That difference may be due to the fact that observers are in different inertial systems moving uniformly and rectilinearly with respect to each other or because they are under the action of gravitational fields of different intensities [11]. In cases involving two inertial reference systems, an observer measures a shorter time interval (“proper time”) between two co-local events (that happen at the same place in her/his system) than another observer, who measures the time interval between these same events from her/his system (for her/him, the events happen at different places). The expression for time dilation is Δt = γΔt0, where Δt0 is the time interval between two co-local events for an observer in some inertial reference system (proper time), Δt is the time interval between those same events, but measured by an observer in a reference system moving with velocity v with respect to the first one. Here, is the Lorentz factor, where v is the relative velocity of the inertial systems and c is the speed light.
Returning to intertemporal decision making, a dynamically inconsistent individual prefers smaller and more immediate rewards, but opts for greater and later ones in distant futures, as if the increase in the delay in receiving the rewards distorts her/his perception of Δτ—the time interval between the pay times of two rewards. Here, we propose to deal with the dynamic inconsistency as the result of a subjective time dilation effect of the interval Δτ perceived by the decision maker. We obtain a generalized transformation equation for the effect of Δτ distortion, similar to that from the special theory of relativity. Our proposal is an important contribution to the characterization of subjective time in an individual basis, which is provided by the parameter. According to a study conducted in 2017 by Agostino et al. [12], characterizing subjective time in an individual basis is indispensable to study the deviations from average. Additionally, we present a generalized two-argument hyperbolic utility function for the Bernoulli (logarithmic) one, associating their difference to subjective time intervals. This issue relates two distinct subjetive perceptions: time and value.
2. Models
Here, we present the exponential and hyperbolic discount models and their first and second derivatives with respect to time as the impulsivity and degree of inconsistency, respectively. Takahashi et al. and Cajueiro discount models are similar and allow us to understand impulsivity and inconsistency as subjective time perception. This is suitably described mathematically using the generalized logarithm and exponential functions.
In standard economic theory, the present value of a future reward decreases with a fixed ratio per unit of delay, in the same way that a bank balance increases with a fixed interest rate over time. In this case, the discount of the real (objective) value of a reward is characterized by an exponential decay model [13]:
where the parameter k is the rate at which an individual discounts late rewards. High k values correspond to discount curves with more pronounced decay. In this model, the preference between two intertemporal rewards does not depend on how much the two rewards options are moved into the future with the same amount of time.
However, experimental results [14–19] show that the reward value discount as a function of the delay is best described by a hyperbolic function [5]:
In intertemporal choices, impulsivity is defined as the preference for smaller and immediate rewards to greater and later ones [7]. Let the individual “A” chose the smaller and more immediate reward V1(t), and if individual “B” chooses the greater and later reward V2(t + τ), we say “A” is more impulsive than “B.” The relative variation of the discount function is used as a measure of impulsivity in the context of intertemporal decision making. The discount rate is the relative variation of the discount function [7]:
The anti-impulsive behavior is defined as self-control.
Returning to the example, where the “A” is more impulsive than “B,” if “A” changes her/his choice after a certain delay t (if she/he happens to prefer the greater and later reward), her/his intertemporal choice is said to be dynamically inconsistent. Experiments involving humans and animals [2, 20–25] have shown that individuals tend to prefer smaller and more immediate rewards, but opt for greater and later ones in distant futures. In decision making studies, this preference reversal over time is called dynamic inconsistency in intertemporal choices [7, 25]. The degree of inconsistency was defined by Prelec in 2004 [26] and interpreted by Takahashi in 2010 as the time variation of I:
where I is given by Equation (3). Defining the quantity that measures the degree of inconsistency as the temporal variation of the so-called impulsivity (the preference for smaller and immediate rewards to greater and later rewards [7, 26]), several models attribute this behavior to the effects of psychophysical perception of delay [1, 8, 9, 27–31]. For the exponential discount model, which describes the behavior of the rational decision-makers from neoclassical economic theory, the discount rate I(e)(t) = k is constant and, therefore, the degree of inconsistency vanishes (𝕀(e) = 0). Thus, the exponential model can not describe the inconsistency observed experimentally in intertemporal decision making. For the hyperbolic discount model, the discount rate is a decreasing function of t. In this case, the value of a reward is strongly discounted on relatively small delays, but it is more moderately discounted as the delay increases. For this model, the degree of inconsistency does not vanish and is: 𝕀(h)(t) = −[I(h)(t)]2.
Recent studies [28–31] analyze the discount process from the perspective the time perception. Takahashi et al. [8] proposed to include the logarithmic perception of delay, according the second law of psychophysics (or Weber-Fechner's law), on the temporal exponential discount, calling
the subjective time interval, where a and b are psychophysical parameters with g = ka, one has [28]: . For this model, I(T)(t) = g2/(1+bt) and I(T)(t) = −bI(T)(t)/(1+bt). It is interesting to point out that as g → 0, this model retrieves the exponential behavior and when g = 1, the hyperbolic one.
Using the -logarithm and -exponential functions allows one the retrieve known models without taking limits, since these limits are implicit [10, 32–39]. The -logarithm function is defined as the value under the curve in the interval w ∈ [1, x] [40]:
For any value of , the area is negative for 0 < x < 1, null for x = 1 () and positive for x > 1. This function is not the logarithm function in base (), but the generalization for the definition of natural logarithm with a parameter. For , ln0(x) = ln(x), the natural logarithm function. The point x = 1 is special because . The -exponential function is defined as the value w, in such a way that the area under the curve , in the interval , is x. In other words, it is the inverse of the -logarithm function and reads:
where is not real valued if . This is a nonnegative function and x = 0 is a special point because , independently of the value of . For , exp0(x) = exp(x), the exponential function.
Let us point out two properties that make the algebraic manipulations easier with these functions. Consider the following properties [40]:
with the sum and subtraction operators defined as:
Generalized operator can be defined for multiplication and division, but this is out of the scope of this paper. Note that the result of the -minus operation is a hyperbole on the b variable.
In 2006, Cajueiro [9] proposed a -generalized discount function, given by:
where V0 is the objective value of the reward and is an impulsivity parameter. For , Equation (14) retrieves the exponential discount function (Equation 1). For , it retrieves the hyperbolic discount function (Equation 2). In Equation (14), using and , this model is mathematically equivalent to the Weber-Fechner's exponential with psychophysical effects on time perception model. In this way, models the subjectivity of one individual. It is expected that different individuals have different values, as in Anteneodo et al. [32].
3. Results
In this section, we define a proper time (reference time) and analytically calculate a subjective time perception transformation. Let us consider an intertemporal choice process involving two rewards, “1” and “2.” The objective value of the reward “2” is greater than that of the reward “1,” V1(0) < V2(0). These rewards must be paid with different delays, t = 0 and t = Δτ, respectively (see Figure 1A). One compares the values of these two rewards and prefers/chooses the one “perceived” as greater. Since individuals tend to prefer smaller and more immediate rewards, let us suppose V1(0) > V2(Δτ), which leads to the choice of the smaller and immediate reward V1(0) (the objective value of the reward “1”) to the greater and later one V2(Δτ) (the subjective value of the reward “2” in the delay Δτ) (see Figure 1B). If these same two options are presented repeatedly, but gradually decreasing the value of Δτ each time, there is a delay (Δτ0) where V1(0) = V2(Δτ0). For this delay, where the individual changes his choice and starts choosing V2(Δτ) to V1(0) (see Figure 1C).
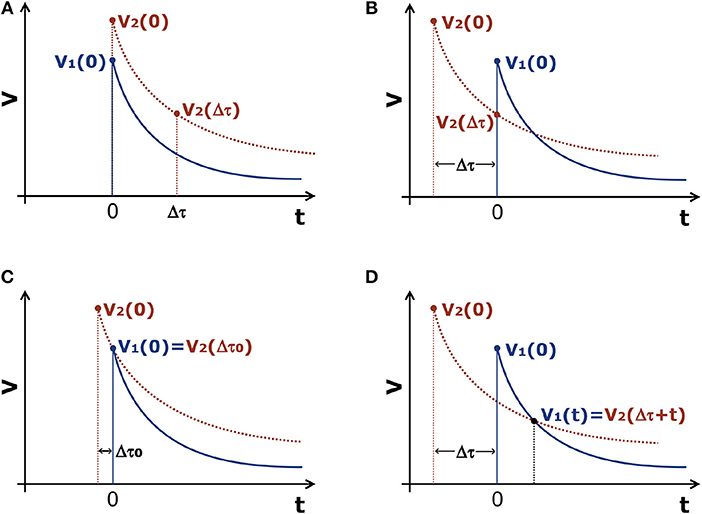
Figure 1. Intertemporal choice process involving two rewards, “1” and “2,” where V1(0) < V2(0). The curves are from discount models that predict the dynamic inconsistency. The continuous curve refers to V1 and the dashed one to V2. (A) One should choose between these two rewards, to be paid with different delays: V1(0) (the objective value of the reward “1”) or V2(Δτ) (the subjective value of the reward “2” in the delay Δτ). (B) To facilitate the comparison of these values, the curve of reward “2” was translated to the left to a “distance” of Δτ, so that V1(0) and V2(Δτ) were vertically aligned; one sees that V1(0) > V2(Δτ), which leads to the choice of reward “1.” (C) Decreasing gradually the value of Δτ, shifting the curve of reward “2” to the right, one finds a delay (Δτ0) where V1(0) = V2(Δτ0). In this case, Δτ0 is analogous to the “proper time” of the special theory of relativity and it is defined as the maximum delay from which individuals prefer the greater and later reward to the smaller and immediate one. (D) There is a specify value of t where V1(t) = V2(Δτ+t). Here, There is an intertemporal preference reversal, because from this point individuals prefer the greater and later reward, V2(Δτ+t), to the smaller and more immediate one, V1(t).
In this context, for models that predict the dynamic inconsistency, Δτ0 is analogous to the “proper time” from the special theory of relativity and it is defined as the maximum delay from which the individual prefers the greater and later reward, V2(Δτ0), to the smaller and immediate one, V1(0). For the Cajueiro's generalized model (Equation 14), , leading to (see derivation process in the Supplementary Material):
where V01 = V1(0) and V02 = V2(0) are the objective values of the rewards “1” and “2,” respectively, and the superscript (C) is a reference to the generalized model.
For , the exponential model, , which is the difference of the Bernoulli's (logarithmic) utility functions [41] u(0)(V) = ln V for the reference values in monetary unities. One can write a generalized utility function based on this analogy. Since from Equation (9), with -minus operator given by Equation (13), one can build a two-argument hyperbolic subjective utility function
This leads to and (see derivation process in the Supplementary Material)
which shows that the time interval can be written as the difference of two utility functions.
Analogously, for models that predict the dynamic inconsistency, like the hyperbolic one (Equation 1) 1, we can present repeatedly the same previous two options, V1(0) and V2(Δτ), but with equal and gradual increases in the delays for receiving the rewards. Thus, one expects that the choice also changes (intertemporal preference reversal), i.e., V1(t) = V2(Δτ + t) and one prefers the greater and later reward, V2(Δτ + t), to the smaller and more immediate one, V1(t), from a certain time t (see Figure 1D). In the same way that the special theory of relativity presents a relation between the time intervals Δt and Δt0, we propose expressions that relates Δτ and Δτ0. For the Cajueiro's generalized model (Equation 14) (see derivation process in the Supplementary Material):
where is analogous to the Lorentz factor γ from the special theory of relativity. As expected for the exponential model, where , , but subjective time dilation is expected for any .
If t = 0, one must choose between a smaller and immediate reward (an objective value) and a greater and later one (a subjective value). In this case, she/he agrees to wait a maximum time Δτ0 to choose the greater and later reward. But, as t increases, one starts to choose between a smaller and more immediate reward and a greater and later one (two subjective values). Here, she/he agrees to wait a maximum time Δτ [Equation (18)]—the temporal interval between the pay times of the rewards – to choose the greater and later reward, where Δτ > Δτ0. In this paper, we assume that a gradual increase of t leads one to experience an increasing kind of subjective time dilation. Thus, the time t can make one feel the same “sensation” when she/he subjectively evaluates the “duration” of Δτ0 and Δτ.
4. Discussion
In this paper, we use arguments inspired by the special theory of relativity to deal with the dynamic inconsistency in intertemporal choices as the result of a subjective time dilation effect. We define the maximum time delay for which individuals prefer a greater and later reward to a smaller and immediate one, Δτ0, and relate it to the “proper time” from the special theory of relativity. In the same way, we define the maximum time delay for which individuals prefer a greater and later reward to a smaller and more immediate in a future time t, Δτ. Focusing the study on a generalized model, which encompasses other ones that predict the dynamic inconsistence (for instance, the hyperbolic one), we find a factor, analogous to the Lorentz factor γ from the special theory of relativity, which relates Δτ and Δτ0: , where the superscript (C) is a reference to the generalized model.
We assume that the gradual increase of t leads one to experience an increasing kind of subjective time dilation, in a similar way to that performed by the increase of velocity in the special theory of relativity. Thus, the increase of time t makes the individual that subjectively evaluates the “duration” of Δτ feel the same time sensation caused by the “duration” of Δτ0, even Δτ > Δτ0. It is important to point out that we assume individuals have the same value of k (discount rate) for the two rewards – the greater and later one an the smaller and more immediate one.
We stress that the time dilation effect of the special theory of relativity is a consequence of two hypothesis [11]: (1) The Principle of Relativity—there are an infinite number of inertial systems of reference in which all physical laws assume their simplest form; (2) The Principle of the Constancy of Light—in inertial system, the velocity of light has the same value when measured with length-measures and clocks of the same kind. Here, the subjective time dilation effect proposed in this paper is not the description of a physical effect, but a new interpretation for the dynamic inconsistency, and the consequent preference reversal over time in intertemporal choices. This interpretation is derived from models that predict the dynamic inconsistency, which are covered here by a generalized model, and permit a new way of facing this anomaly.
The use of generalized models provides a simple and practical way to include different psychophysical effects on time perception on the temporal discount functions. For instance, the logarithmic based Weber-Fechner and the power-law based Stevens' law [42] (third law of psychophysics) can be written in a unified way using the presented generalization of the logarithm function. Based on Equation (5), one writes the subjetive time as:
where the second law of phychophysics is retrieved for s = 0. In 2011, Destefano and Martinez [33] proposed a very general and unified model for the discount process taking into account:
In Destefano and Martinez [33], a complete study of possible values of and s has been performed. Also, the authors have shown that it is possible to dissociate the degree of inconsistency in two distinct parts of perception: one for value and other for time. The authors demonstrated that the direct analysis of the degree of inconsistency is the natural measure that favors the interpretation of the discount process. For the model of Equation 20,
and
This equation does not simply connect Δτ(D)(t) with as in Eq. (18). This non-linear behavior may lead to some effect that will be studied in detail in a near future.
A study conducted in 2017 by Agostino et al. [12] have shown the importance of the individual differences to the average and individual psychophysical functions of long-range time representation. It suggests that the study of the deviations from exponential discount models in intertemporal choices to other ones that predict dynamic inconsistency must involve “…the characterization of subjective time in an individual-participant basis.” That is exactly what our model provides, fitting individual data and account for the differences in discount rate, as the parameter can be individually adjusted an generate different discount functions. Our characterization of the subjective time in intertemporal choices procedures also covers cases where dynamic inconsistency is not involved, since the generalized discount model that we adopt encompasses other ones, like the exponential model, which do not deal with this anomaly.
To conclude, we have shown that dynamic inconsistency in intertemporal decision making can be seen as the result of a subjective time dilation perception effect. Based on a well-established theoretical framework, we have found a simple transformation equation for the time interval between the pay times of two rewards, showing that this subjective perception effect can be modeled by generalized models that encompasses particular cases that predict dynamic inconsistency. We also have found a broader transformation equation, derived from a very general and unified discount model, which will be further studied. Since the Bernoulli utility function is logarithmic, one can face it as a special case of a generalized hyperbolic one . In this way, our “proper time” can be written as , which associate a time interval with the difference of two utility functions. Our proposals of a two-value utility function and a time interval transformation unveils the subtle connection between the subjectivity on value and time perceptions. Anomalies in intertemporal decision making can be translated and quantified in terms of value perceptions and shall be further explored.
Author Contributions
Both authors contributed equally on the discussion of the ideas, development of the study and writing the manuscript.
Funding
AM holds grant from Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) (127151/2012-5).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank the fruitful discussions with Natália Destefano, Fabiano Simões Corrêa and Guilherme Leme and acknowledge the Brazilian agencies and the Núcleo de Apoio à Pesquisa em Física Médica da USP for support.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2018.00054/full#supplementary-material
Footnotes
1. ^and exponential with psychophysical effects on time perception (Equation 2) one
References
1. Green L, Myerson J. A discounting framework for choice with delayed and probabilistic rewards. Psychol Bull. (2004) 130:769–92. doi: 10.1037/0033-2909.130.5.769
2. Ainslie G. Impulse control in pigeons. J Exp Anal Behav. (1974) 21:485–9. doi: 10.1901/jeab.1974.21-485
3. Bickel WK, Odum AL, Madden GJ. Impulsivity and cigarette smoking: delay discounting in current, never, and ex-smokers. Psychopharmacology (1999) 146:447–54. doi: 10.1007/PL00005490
4. Green L, Fry AF, Myerson J. Discounting of delayed rewards: a life-span comparison. Psychol Sci. (1994) 5:33–6. doi: 10.1111/j.1467-9280.1994.tb00610.x
5. Mazur JE, Biondi DR Delay-amount tradeoffs in choices by pigeons and rats: hyperbolic versus exponential discounting. J Exp Anal Behav. (2009) 91:197–211. doi: 10.1901/jeab.2009.91-197
6. Reynolds B, de Wit H, Richards JB. Delay of gratification and delay discounting in rats. Behav Process. (2002) 59:157–68. doi: 10.1016/S0376-6357(02)00088-8
7. Takahashi T, Oono H, Radford MHB. Empirical estimation of consistency parameter in intertemporal choicebased on Tsallis' statistics. Physica A (2007) 381:338–42. doi: 10.1016/j.physa.2007.03.038
8. Takahashi T, Oono H, Radford MHB. Psychophysics of time perception and intertemporal choice models. Physica A (2008) 387:2066–74. doi: 10.1016/j.physa.2007.11.047
9. Cajueiro DO. A note on the relevance of the q-exponential function in the contextof intertemporal choices. Physica A (2006) 364:385–8. doi: 10.1016/j.physa.2005.08.056
10. Martinez AS, González RS, Espíndola AL. Generalized exponential function and discrete growth models. Physica A (2009) 388:2922–30. doi: 10.1016/j.physa.2009.03.035
12. Agostino CS, Caetano MS, Balci F, Claessens PME, Zana Y. Individual differences in long-range time representation. Attent Percept Psychophys. (2017) 79:833–40. doi: 10.3758/s13414-017-1286-9
13. Samuelson PA. A note on measurement of utility. Rev Econ Stud. (1937) 4:155–61. doi: 10.2307/2967612
14. Kirby KN. Bidding on the future: evidence against normative discounting of delayed rewards. J Exp Psychol (1997) 126:54–70. doi: 10.1037/0096-3445.126.1.54
15. Madden GJ, Begotka AM, Raiff BR, Kastern LL. Delay discounting of real and hypothetical rewards. Exp Clin Psychopharmacol. (2003) 11:139–45. doi: 10.1037/1064-1297.11.2.139
16. McKerchar TL, Green L, Myerson J, Pickford TS, Hill JC, Stout SC. A comparison of four models of delay discounting in humans. Behav Process. (2009) 81:256–9. doi: 10.1016/j.beproc.2008.12.017
17. Rachlin H, Raineri A, Cross D. Subjective probability and delay. J Exp Anal Behav. (1991) 55:233–44. doi: 10.1901/jeab.1991.55-233
18. Reynolds B, Schiffbauer R. Measuring state changes in human delay discounting: an experiential discounting task. Behav Process. (2004) 67:343–56. doi: 10.1016/S0376-6357(04)00140-8
19. Rodriguez ML, Logue AW. Adjusting delay to reinforcement: comparing choice in pigeons and humans. J Exp Psychol. (1988) 14:105–17.
20. Baron J. Can we use human judgments to determine the discount rate? Risk Anal. (2000) 20:861–8. doi: 10.1111/0272-4332.206079
21. Green L, Estle SJ. Preference reversals with food and water reinforcers in rats. J Exp Anal Behav. (2003) 79:233–42. doi: 10.1901/jeab.2003.79-233
22. Green L, Fisher EB, Perlow S, Sherman L. Preference reversal and self control: choice as a function of reward amount and delay. Behav Anal Lett. (1981) 1:43–51.
23. Green L, Fristoe N, Myerson J. Temporal discounting and preference reversals in choice between delayed outcomes. Psychon Bull Rev. (1994) 1:383–9. doi: 10.3758/BF03213979
24. Kirby KN, Herrnstein RJ. Preference reversals due to myopic discounting of delayed reward. Psychol Sci. (1995) 6:83–9. doi: 10.1111/j.1467-9280.1995.tb00311.x
25. Thaler RH. Some empirical evidence on dynamic inconsistency. Econ Lett. (1981) 8:201–7. doi: 10.1016/0165-1765(81)90067-7
26. Prelec D. Decreasing impatience: a criterion for non-stationary time preference and “hyperbolic” discounting. Scand J Econ. (2004) 106:511–32. doi: 10.1111/j.0347-0520.2004.00375.x
27. Norwich KH, Wong W. Unification of psychophysical phenomena: the complete form of Fechner's law. Percept Psychophys. (1997) 59:929–40. doi: 10.3758/BF03205509
28. Takahashi T. Loss of self-control in intertemporal choice may be attributable to logarithmic time-perception. Med Hypotheses (2005) 65:691–3. doi: 10.1016/j.mehy.2005.04.040
29. Takahashi T. Time-estimation error following Weber Fechner law may explain subadditive time-discounting. Med Hypotheses (2006) 67:1372–4. doi: 10.1016/j.mehy.2006.05.056
30. West BJ, Grigolini P. A psychophysical model of decision making. Physica A (2010) 389:3580–7. doi: 10.1016/j.physa.2010.03.039
31. Zauberman G, Kim BK, Malkoc SA, Bettman JR. Discounting time and time discounting: subjective time perception and intertemporal preferences. J Market Res. (2009) XLVI:543–56. doi: 10.1509/jmkr.46.4.543
32. Anteneodo C, Tsallis C, Martinez AS. Risk aversion in economic transactions. Europhys Lett. (2002) 59:635–41. doi: 10.1209/epl/i2002-00172-5
33. Destefano N, Martinez AS. The additive property of the inconsistency degree in intertemporal decision making through the generalization of psychophysical laws. Physica A (2011) 390:1763–72. doi: 10.1016/j.physa.2011.01.016
34. dos Santos LS, Cabella BCT, Martinez AS. Generalized Allee effect model. Theory Biosci. (2014) 133:117–24. doi: 10.1007/s12064-014-0199-6
35. dos Santos LS, Destefano N, Martinez AS. Decision making generalized by a cumulative probability weighting function. Physica A (2018) 490:250–9. doi: 10.1016/j.physa.2017.08.022
36. Martinez AS, González RS, Terçariol CAS. Continuous growth models in terms of generalized logarithm and exponential functions. Physica A (2008) 387:5679–87. doi: 10.1016/j.physa.2008.06.015
37. Takahashi T. A comparison of intertemporal choices for oneself versus someone else based on Tsallis statistics. Physica A (2007) 385:637–44. doi: 10.1016/j.physa.2007.07.020
38. Takahashi T. A probabilistic choice model based on Tsallis' statistics. Physica A (2007) 386:335–8. doi: 10.1016/j.physa.2007.07.005
39. Takahashi T. A comparison between Tsallis's statistics-based and generalized quasi-hyperbolic discount models in humans. Physica A (2008) 387:551–6. doi: 10.1016/j.physa.2007.09.007
40. Arruda TJ, González RS, Terçariol CAS, Martinez AS. Arithmetical and geometrical means of generalized logarithmic and exponential functions: generalized sum and product operators. Phys Lett A (2008) 372:2578–82. doi: 10.1016/j.physleta.2007.12.020
41. Bernoulli D. Specimen theoriae novae de mensura sortis. Commentarii Academiae Scientiarum Imperialis Petropolitanae (1738) 5:175–92. English version: Exposition of a new theory on the measurement of risk. Econometrica (1954) 22:23–36. doi: 10.2307/1909829
Keywords: econophysics, psychophysics, intertemporal decision making, inconsistency, time perception, generalized models, utility functions
Citation: dos Santos LS and Martinez AS (2018) Inconsistency and Subjective Time Dilation Perception in Intertemporal Decision Making. Front. Appl. Math. Stat. 4:54. doi: 10.3389/fams.2018.00054
Received: 20 April 2018; Accepted: 02 November 2018;
Published: 21 November 2018.
Edited by:
Taiki Takahashi, Hokkaido University, JapanReviewed by:
Saori C. Tanaka, Advanced Telecommunications Research Institute International (ATR), JapanMarcelo S. Caetano, Universidade Federal do ABC, Brazil
Copyright © 2018 dos Santos and Martinez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lindomar Soares dos Santos, bHNvYXJlc3NhbnRvc0BnbWFpbC5jb20=
 Lindomar Soares dos Santos
Lindomar Soares dos Santos Alexandre Souto Martinez
Alexandre Souto Martinez