- 1Institut für Theoretische Physik, Technische Universität Berlin, Berlin, Germany
- 2Complex Systems Lab, Discipline of Physics, Indian Institute of Technology Indore, Indore, India
Time delay in complex networks with multiple interacting layers gives rise to special dynamics. We study the scenarios of time delay induced patterns in a three-layer network of FitzHugh-Nagumo oscillators. The topology of each layer is given by a nonlocally coupled ring. For appropriate values of the time delay in the couplings between the nodes, we find chimera states, i.e., hybrid spatio-temporal patterns characterized by coexisting domains with incoherent and coherent dynamics. In particular, we focus on the interplay of time delay in the intra-layer and inter-layer coupling term. In the parameter plane of the two delay times we find regions where chimera states are observed alternating with coherent dynamics. Moreover, in the presence of time delay we detect full and relay inter-layer synchronization.
1. Introduction
During the early eighteenth century, Leonhard Euler published a paper on The Seven Bridges of Königsberg providing a mathematical background on vertices and edges [1]. Later on, it became the cornerstone of the field of network science. Network science presents a unique platform to study various complex real-world systems by analyzing the interactions between its constituent entities and collectively investigating its behaviors [2–4]. A recent addition to the network science is the multiplex framework which incorporates multiple types of interactions among nodes by representing them in different layers [5, 6]. For example, the neurons in the brain form different groups consisting of the same neurons but interacting in different ways (chemical interaction or electrical synapses) to perform different tasks [7, 8]. Multiplex framework divides these neuronal groups into different layers based on their functionalities [9]. Similarly, transportation networks, communication networks, social networks and a lot of other real-world networks can be represented in a multiplex framework to understand their structural and dynamical features in a better fashion [10].
Recently, various synchronization scenarios have been investigated in multilayer structures, including remote and relay synchronization [11–14]. Moreover, it has been shown that multiplexing can be used to control spatio-temporal patterns in networks [15–18]. The advantage of control schemes based on multiplexing is that they allow to achieve the desired state in a certain layer without manipulating its parameters, and they can work for weak inter-layer coupling. For example, it has been found that weak multiplexing can induce coherence resonance [19] as well as chimera states [18] in neural networks.
Chimera state is a peculiar partial synchronization pattern that refers to a hybrid dynamics where coherence and incoherence emerge simultaneously in a network of identical oscillators [20–22]. Since its inception [23, 24], chimera state has attracted massive interest from the nonlinear community for both its significance in understanding complex spatiotemporal patterns and its probable applicabilities in various fields, especially in neuroscience [25]. Here we study the role of the interplay of intra- and inter-layer time delays for the emergence of chimera states in a multi(tri)plex network. Time delays represent an essential factor in real-world networks due to the finite speed of information propagating through channels connecting the nodes. They play a crucial role in determining the dynamical behavior of a complex system [26–32]. Time delays have been shown to heavily influence the parameter range for which chimera states appear for both single and multiplex networks [14, 15, 33–35]. Moreover, recently a scheme has been proposed for engineering chimera states using suitably placed heterogeneous delays [36]. In the present work we demonstrate that just the variation of delay values in the intra- and inter-layer edges can lead to various dynamical states and allows for control of spatio-temporal patterns.
2. The Model
We study a multiplex network with three layers (triplex) as shown in Figure 1. Every single layer represents a ring of N identical FitzHugh-Nagumo (FHN) oscillators with non-local (intra-layer) topology. The outer layers i = 1 and i = 3 are coupled with the middle layer i = 2, so that it acts as a relay layer. There is no direct connection between layers 1 and 3 (so-called ordinal coupling). Our system is described by the following equations:
where , k ∈ {1, …, N}, i ∈ {1, …, 3} with all indices modulo N, describe the set of activator (u) and inhibitor (v) variables. The intra-layer delay time is τi and the inter-layer delay time is τij. The coupling radius in layer i is given by Ri. The local dynamics of each oscillator is given by
where ε = 0.05 is the parameter characterizing the time scale separation. The FHN oscillator exhibits either oscillatory (|a| < 1) or excitable (|a| > 1) behavior depending on the threshold parameter a. In this work we focus on the oscillatory regime (a = 0.5). The parameter σi stands for the coupling strength inside the layer (intra-layer coupling), and σij is the inter-layer coupling. For an ordinal inter-layer coupling with constant row sum we set σ12 = σ23, which yields the inter-layer coupling matrix
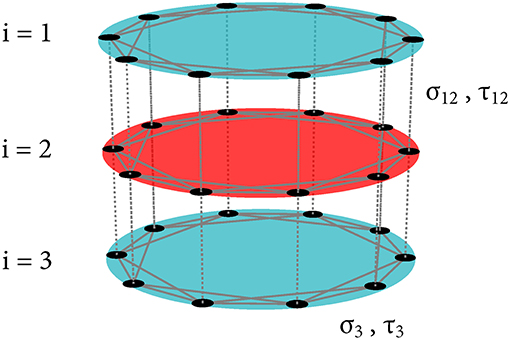
Figure 1. Triplex network with ordinal coupling: The middle layer i = 2 (red) acts as relay layer between the two outer layers i = 1, 3 (blue). Black dots indicate the nodes, solid lines represent the intra-layer connections, and dashed lines denote the inter-layer links. The intra-layer coupling is characterized by the strength σi and time delay τi, and the inter-layer coupling is characterized by the strength σij and time delay τij. For example, in layer 3 the intra-layer coupling strength is given by σ3 and the intra-layer time delay is τ3. Similarly, for the layers 1 and 2 the inter-layer coupling strength is given by σ12 and the inter-layer time delay is τ12.
The connections between the nodes are given by the diffusive coupling with the following coupling matrix
and coupling phase [37]. This coupling configuration (i.e., predominantly activator-inhibitor cross-coupling) is similar to a phase-lag of approximately π/2 in the Kuramoto model that ensures the occurrence of chimera states [37].
3. Interplay of Time Delays
Chimera states are spatio-temporal patterns where incoherent and coherent domains coexist in space. For certain values of coupling strength σi and coupling radius Ri one can detect them in the ith layer [37]. Recently, the phenomenon of relay synchronization of chimera states has been studied in a three-layer network of FHN oscillators [38]. In more detail, for varying the coupling delay and strength in the inter-layer connections relay synchronization of chimera states in the outer network layers has been reported. For appropriate parameters the so-called “double” chimeras are possible where the coherent parts of the chimera states are synchronized, whereas the incoherent parts remain desynchronized. Additionally, the transitions between different synchronization scenarios have been studied. Moreover, time delay in the inter-layer coupling has been shown to be a powerful tool for controlling various partial synchronization patterns in the three-layer network [14]. Therefore, by multiplexing and introducing inter-layer time delays it is possible to destroy or induce chimera states. Here we study the interplay of inter- and intra-layer time delay.
To provide an overview of the patterns observed in the network, we calculate the map of regimes in the parameter plane of intra-layer delay time τi and inter-layer delay time τij (Figure 2). The dominating region is the one corresponding to coherent states (blue region in Figure 2). On the one hand, we detect the in-phase synchronization regime (see Figure 3C), on the other hand, we also observe a region of coherent traveling waves (see Figure 4C). By varying the delay times we can not only switch between these states, but also adjust the speed of traveling waves. In addition, we can observe salt and pepper states (green region in Figure 2), where all nodes oscillate with the same phase velocity but they are distributed between states with phase lag π incoherently [40] (see Figures 3B, 4B). The reason for this are strong variations on very short length scales, so that the dynamical patterns have arbitrarily short wavelengths. Besides these two patterns characterized by the same mean phase velocity for all the nodes in the network, we also observe chimera states (red region in Figure 2), where the oscillators within each layer show a characteristic arc-shaped mean phase velocity profile. The mean phase velocities of the oscillators are given by ωk = 2πSk/ΔT, k = 1, …, N, where Sk denotes the number of complete rotations performed by the kth oscillator during the time ΔT. The value ΔT = 10, 000 is fixed throughout the paper. Because of the delay, the system often exhibits traveling structures. Therefore, the classical arc-shaped profile is transformed into a wider, conical one [41] (see Figures 3A, 4A (right column)). We distinguish between the different regions on the one hand, by analyzing the mean phase velocity and a snapshot of variables uk, on the other hand, by means of the Laplacian distance measure [39]. The latter identifies strong local curvature in an otherwise smooth spatial profile of by calculating the discrete Laplacian for each k. In case of coherent dynamics we obtain low values (≈ 0) for all k, in case of salt and pepper states we get high values (> 2). Chimera states show low and high values for the coherent and incoherent domains, respectively. By taking the mean over all k, we can distinguish between coherent, chimera and “salt & pepper” states. For the numerical integration an Euler integration method is used with a step size Δt = 0.0025 and a transient time ttrans = 2, 000. All simulations are evaluated then after ΔT = 10, 000 as mentioned above.
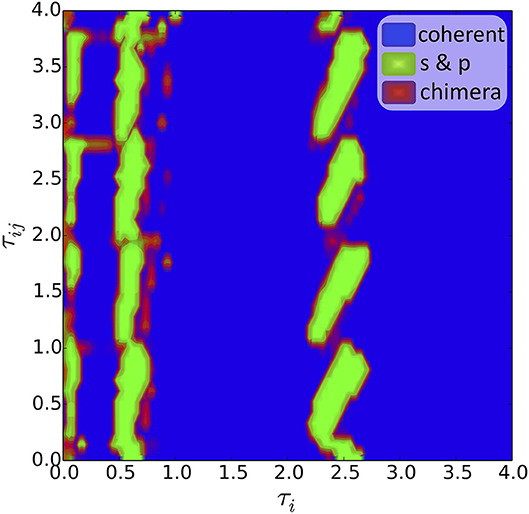
Figure 2. Dynamical regimes in the parameter plane of intra-layer coupling delay τi ≡ τ1 = τ2 = τ3 and inter-layer coupling delay τij ≡ τ12 = τ23: “salt & pepper” states (green islands) occur in the region of coherent states (blue region) as traveling waves, cluster or synchronized states. At the border between these two regimes chimera states can be found (red color). We distinguish between the different regions on the one hand, by analyzing the mean phase velocity and a snapshot of variables uk, on the other hand, by means of the Laplacian distance measure [39]. The boundaries of these regions are fitted linearly after the (τi, τij) plane has been sampled in steps Δτi = 0.05 and Δτij = 0.1. For all simulations of Equation (1) random initial conditions are taken. Parameters are chosen as ε = 0.05, a = 0.5, σi = 0.2, σij = 0.05, N = 500, Ri = 170, , and i,j = 1, 2, 3.
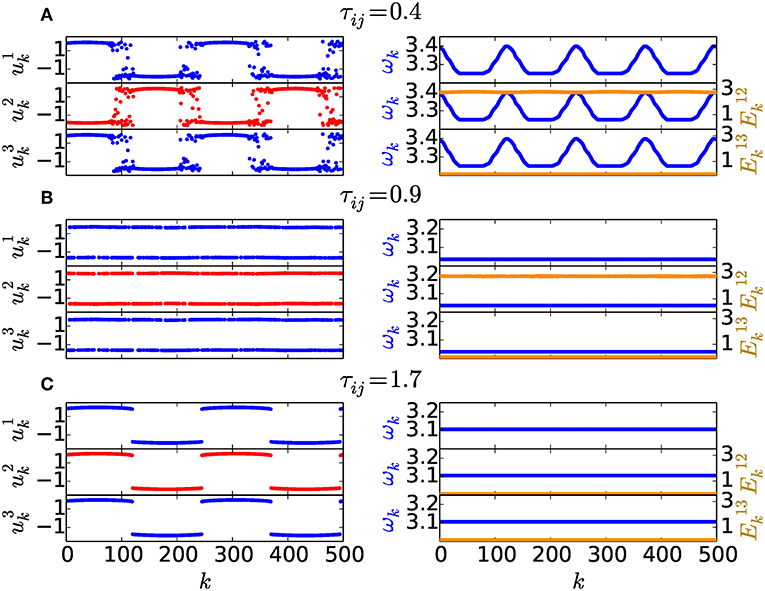
Figure 3. Dynamics in all three layers for different values of the inter-layer delay time τij: (A) Chimera state for τij = 0.4, (B) “salt & pepper” state for τij = 0.9, (C) coherent state (cluster state) for τij = 1.7. The intra-layer delay time is fixed at τi = 0.8. The left column displays snapshots of variables for the layers i = 1, 2, 3, while the right column illustrates the mean phase velocity profile ωk (dark blue) for the individual layers and the local inter-layer synchronization error (light yellow). Other parameters as in Figure 2.
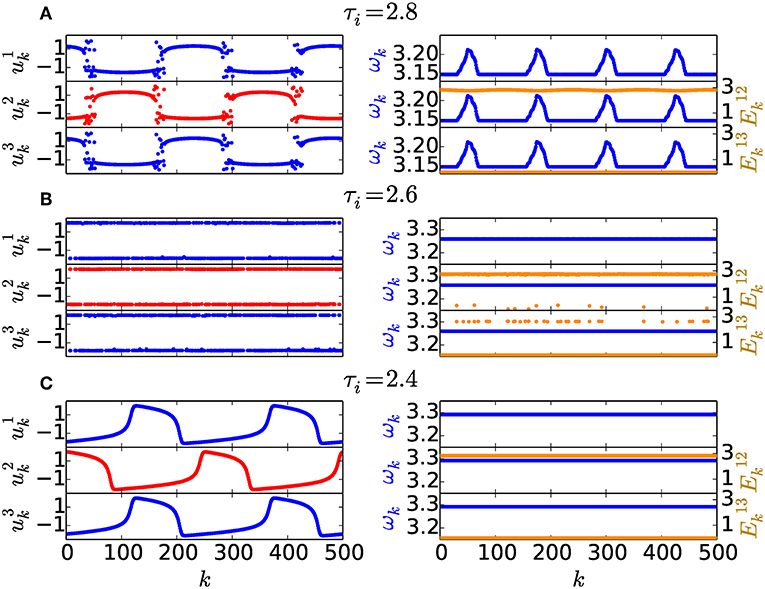
Figure 4. Dynamics in all three layers for different values of the intra-layer delay time τi: (A) Chimera state for τi = 2.8, (B) “salt & pepper” state for τi = 2.6, (C) coherent state (traveling wave) for τi = 2.4. The inter-layer delay time is fixed at τij = 2.6. The left column displays snapshots of variables for the layers i = 1, 2, 3, while the right column illustrates the mean phase velocity profile ωk (dark blue) for the individual layers and the local inter-layer synchronization error (light yellow). Other parameters as in Figure 2.
In many systems with time delays resonance effects can be expected if the delay time is an integer or half-integer multiple of the period in the uncoupled system [42–44]. Regarding the inter-layer delay time τij we can observe this effect for half-integer multiples of the period T = 2.3 of a uncoupled FHN oscillator (see Figure 2 for τi ≈ 2.5). Concerning the intra-layer delay time τi we find a resonance effect in the case of integer multiple of the delay. For greater values of the delay times τi and τij the dynamical regions are becoming curved (see green islands in Figure 2 at τi ≈ 2.5). This can be explained by the fact that branches of periodic solutions, which are reappearing for integer multiples of the intrinsic period, are becoming stretched with increasing delay time [41]. In comparison to the almost vertical shape at τi ≈ 0.5, the green islands at τi ≈ 2.5 are rotated clockwise by approximate π/8. The consequence is an overlapping of the delay islands for small intra-layer delay time τi, whereas for larger delays the islands become separated.
4. Relay Synchronization
Networks with multiple layers demonstrate remote synchronization of distant layers via a relay layer. Regarding the inter-layer synchronization, two synchronization mechanisms are conceivable in a triplex network:
• full inter-layer synchronization when synchronization is observed between all the layers and
• relay inter-layer synchronization when synchronization occurs exclusively between the two outer layers.
A useful measure for synchronization between two layers i, j is given by the global inter-layer synchronization error Eij [14, 45]:
where ∥·∥ denotes the Euclidean norm. One can distinguish between the two synchronization mechanisms by measuring the global inter-layer synchronization error between the first and second layer E12 and between the first and third layer E13: In the case of full inter-layer synchronization E12 = 0 as well as E13 = 0, while in the case of relay inter-layer synchronization E12 ≠ 0 and E13 = 0.
To provide more insight into the synchronizability of patterns between two layers i, j, the local inter-layer synchronization error in dependence of every single node k can be used [14]:
The local inter-layer synchronization error is convenient for detecting the synchronized nodes between two layers. In Figures 3, 4 (right column) is plotted (light yellow) together with the mean phase velocity (blue): Depending on the delay times τi and τij we can find full inter-layer synchronization (see Figure 3C) as well as relay inter-layer synchronization (see Figures 3A,B, 4A,C). These synchronization scenarios can be found for both coherent and incoherent dynamics. An additional effect is the partial relay synchronization scenario in Figure 4B: In all three layers “salt & pepper” dynamics can be observed. The nodes in the outer layers are almost all synchronized, but a small part of them destroys the relay synchronization. On the other hand a few oscillators in the relay layer are synchronized with the outer layers.
5. Conclusion
In conclusion, we have studied chimera states in a three-layer network of FitzHugh-Nagumo oscillators, where each layer has a nonlocal coupling topology. Focusing on the role of time delays in the coupling terms and their influence on chimera states, we have performed a numerical study of complex spatio-temporal patterns in the network. In the parameter plane of the intra-layer τi and the inter-layer τij time delay, we have determined the regions where chimera patterns occur, alternating with regimes of coherent states. A proper choice of time delay allows to achieve the desired state of the network: chimera state or coherent pattern, full or relay inter-layer synchronization.
Combining the delayed interactions with the multiplex framework considered in this work can provide additional insight into the formation of the complex spatio-temporal patterns in real-world systems. Specifically, in brain networks where EEG patterns are recently reported to display chimera-like behavior at the onset of a seizure [46–48]. Inducing the chimera states by tuning the inter- and intra-layer delay values provides us with a powerful tool to control chimera states.
Author Contributions
JS did the numerical simulations and the theoretical analysis. AZ supervised the study. All authors designed the study and contributed to the preparation of the manuscript. All the authors have read and approved the final manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Projektnummer—163436311—SFB 910 and by the German Academic Exchange Service (DAAD) and the Department of Science and Technology of India (DST) within the PPP project (INT/FRG/DAAD/P-06/2018).
References
1. Euler L. Solutio problematis ad geometriam situs pertinentis. Comment Acad Sci Petropol. (1741) 8:128–40.
2. Albert R, Barabási AL. Statistical mechanics of complex networks. Rev Mod Phys. (2002) 74:47–97. doi: 10.1103/revmodphys.74.47
3. Havlin S, Kenett DY, Ben-Jacob E, Bunde A, Cohen R, Hermann H, et al. Challenges in network science: applications to infrastructures, climate, social systems and economics. Eur Phys J Spec Top. (2012) 214:273–93. doi: 10.1140/epjst/e2012-01695-x
4. Jalan S, Sarkar C, Madhusudanan A, Dwivedi SK. Uncovering randomness and success in society. PLoS ONE. (2014) 9:1–8. doi: 10.1371/journal.pone.0088249
5. Boccaletti S, Bianconi G, Criado R, del Genio CI, Gómez-Gardeñes J, Romance M, et al. The structure and dynamics of multilayer networks. Phys Rep. (2014) 544:1–122. doi: 10.1016/j.physrep.2014.07.001
6. Sarkar C, Yadav A, Jalan S. Multilayer network decoding versatility and trust. Europhys Lett. (2016) 113:18007. doi: 10.1209/0295-5075/113/18007
7. Majhi S, Perc M, Ghosh D. Chimera states in a multilayer network of coupled and uncoupled neurons. Chaos. (2017) 27:073109. doi: 10.1063/1.4993836
8. Buldú JM, Porter MA. Frequency-based brain networks: from a multiplex framework to a full multilayer description. Netw Neurosci. (2018) 2:418–41. doi: 10.1162/netn_a_00033
9. De Domenico M. Multilayer modeling and analysis of human brain networks. Gigascience. (2017) 6:1–8. doi: 10.1093/gigascience/gix004
10. Kivelä M, Arenas A, Barthélemy M, Gleeson JP, Moreno Y, Porter MA. Multilayer networks. J Complex Netw. (2014) 2:203–71. doi: 10.1093/comnet/cnu016
11. Nicosia V, Valencia M, Chavez M, Díaz-Guilera A, Latora V. Remote synchronization reveals network symmetries and functional modules. Phys Rev Lett. (2013) 110:174102. doi: 10.1103/physrevlett.110.174102
12. Ghosh S, Jalan S. Emergence of chimera in multiplex network. Int J Bifurc Chaos. (2016) 26:1650120. doi: 10.1142/s0218127416501200
13. Zhang L, Motter AE, Nishikawa T. Incoherence-mediated remote synchronization. Phys Rev Lett. (2017) 118:174102. doi: 10.1103/physrevlett.118.174102
14. Sawicki J, Omelchenko I, Zakharova A, Schöll E. Delay controls chimera relay synchronization in multiplex networks. Phys Rev E. (2018a) 98:062224. doi: 10.1103/PhysRevE.98.062224
15. Ghosh S, Kumar A, Zakharova A, Jalan S. Birth and death of chimera: interplay of delay and multiplexing. Europhys Lett. (2016) 115:60005. doi: 10.1209/0295-5075/115/60005
16. Ghosh S, Zakharova A, Jalan S. Non-identical multiplexing promotes chimera states. Chaos Sol Fract. (2018) 106:56–60. doi: 10.1016/j.chaos.2017.11.010
17. Jalan S, Singh A. Cluster synchronization in multiplex networks. Europhys Lett. (2016) 113:30002. doi: 10.1209/0295-5075/113/30002
18. Mikhaylenko M, Ramlow L, Jalan S, Zakharova A. Weak multiplexing in neural networks: switching between chimera and solitary states. Chaos. (2019) 29:023122. doi: 10.1063/1.5057418
19. Semenova N, Zakharova A. Weak multiplexing induces coherence resonance. Chaos. (2018) 28:051104. doi: 10.1063/1.5037584
20. Panaggio MJ, Abrams DM. Chimera states: coexistence of coherence and incoherence in networks of coupled oscillators. Nonlinearity. (2015) 28:R67. doi: 10.1088/0951-7715/28/3/r67
21. Schöll E. Synchronization patterns and chimera states in complex networks: interplay of topology and dynamics. Eur Phys J Spec Top. (2016) 225:891–919. doi: 10.1140/epjst/e2016-02646-3
22. Omel'chenko OE. The mathematics behind chimera states. Nonlinearity (2018) 31:R121. doi: 10.1088/1261-6544/aaaa07
23. Kuramoto Y, Battogtokh D. Coexistence of coherence and incoherence in nonlocally coupled phase oscillators. Nonlin Phen Complex Syst. (2002) 5:380–5.
24. Abrams DM, Strogatz SH. Chimera states for coupled oscillators. Phys Rev Lett. (2004) 93:174102. doi: 10.1103/physrevlett.93.174102
25. Majhi S, Bera BK, Ghosh D, Perc M. Chimera states in neuronal networks: a review. Phys Life Rev. (2018). doi: 10.1016/j.plrev.2018.09.003. [Epub ahead of print].
26. Ashwin P, Timme M. Unstable attractors: existence and robustness in networks of oscillators with delayed pulse coupling. Nonlinearity. (2005) 18:2035. doi: 10.1088/0951-7715/18/5/009
27. Ahlborn A, Parlitz U. Controlling spatiotemporal chaos using multiple delays. Phys Rev E. (2007) 75:65202. doi: 10.1103/PhysRevE.75.065202
28. Atay FM (ed.). Complex Time-Delay Systems. Understanding Complex Systems. Berlin Heidelberg: Springer (2010).
29. Singh A, Jalan S, Kurths J. Role of delay in the mechanism of cluster formation. Phys Rev E. (2013) 87:030902(R). doi: 10.1103/PhysRevE.87.030902
30. Singh A, Ghosh S, Jalan S, Kurths J. Synchronization in delayed multiplex networks. Europhys Lett. (2015) 111:30010. doi: 10.1209/0295-5075/111/30010
31. Semenov V, Feoktistov A, Vadivasova T, Schöll E, Zakharova A. Time-delayed feedback control of coherence resonance near subcritical Hopf bifurcation: theory versus experiment. Chaos. (2015) 25:033111. doi: 10.1063/1.4915066
32. Masoliver M, Malik N, Schöll E, Zakharova A. Coherence resonance in a network of FitzHugh-Nagumo systems: interplay of noise, time-delay and topology. Chaos. (2017) 27:101102. doi: 10.1063/1.5003237
33. Semenov V, Zakharova A, Maistrenko Y, Schöll E. Delayed-feedback chimera states: forced multiclusters and stochastic resonance. Europhys Lett. (2016) 115:10005. doi: 10.1209/0295-5075/115/10005
34. Gjurchinovski A, Schöll E, Zakharova A. Control of amplitude chimeras by time delay in dynamical networks. Phys Rev E. (2017) 95:042218. doi: 10.1103/physreve.95.042218
35. Zakharova A, Semenova N, Anishchenko VS, Schöll E. Time-delayed feedback control of coherence resonance chimeras. Chaos. (2017) 27:114320. doi: 10.1063/1.5008385
36. Ghosh S, Jalan S. Engineering chimera patterns in networks using heterogeneous delays. Chaos. (2018) 28:071103. doi: 10.1063/1.5042133
37. Omelchenko I, Omel'chenko OE, Hövel P, Schöll E. When nonlocal coupling between oscillators becomes stronger: patched synchrony or multichimera states. Phys Rev Lett. (2013) 110:224101. doi: 10.1103/physrevlett.110.224101
38. Sawicki J, Omelchenko I, Zakharova A, Schöll E. Synchronization scenarios of chimeras in multiplex networks. Eur Phys J Spec Top. (2018b) 227:1161. doi: 10.1140/epjst/e2018-800039-y
39. Kemeth FP, Haugland SW, Schmidt L, Kevrekidis YG, Krischer K. A classification scheme for chimera states. Chaos. (2016) 26:094815. doi: 10.1063/1.4959804
40. Bachmair CA, Schöll E. Nonlocal control of pulse propagation in excitable media. Eur Phys J B. (2014) 87:276. doi: 10.1140/epjb/e2014-50339-2
41. Sawicki J, Omelchenko I, Zakharova A, Schöll E. Delay-induced chimeras in neural networks with fractal topology. Eur Phys J B. (2019) 92:54. doi: 10.1140/epjb/e2019-90309-6
42. Hövel P, Schöll E. Control of unstable steady states by time-delayed feedback methods. Phys Rev E. (2005) 72:046203. doi: 10.1103/PhysRevE.72.046203
43. Yanchuk S, Wolfrum M, Hövel P, Schöll E. Control of unstable steady states by long delay feedback. Phys Rev E. (2006) 74:026201. doi: 10.1103/PhysRevE.74.026201
44. Geffert PM, Zakharova A, Vüllings A, Just W, Schöll E. Modulating coherence resonance in non-excitable systems by time-delayed feedback. Eur Phys J B. (2014) 87:291. doi: 10.1140/epjb/e2014-50541-2
45. Leyva I, Sendiña-Nadal I, Sevilla-Escoboza R, Vera-Avila VP, Chholak P, Boccaletti S. Relay synchronization in multiplex networks. Sci Rep. (2018) 8:8629. doi: 10.1038/s41598-018-26945-w
46. Rothkegel A, Lehnertz K. Irregular macroscopic dynamics due to chimera states in small-world networks of pulse-coupled oscillators. New J Phys. (2014) 16:055006. doi: 10.1088/1367-2630/16/5/055006
47. Andrzejak RG, Rummel C, Mormann F, Schindler K. All together now: analogies between chimera state collapses and epileptic seizures. Sci Rep. (2016) 6:23000. doi: 10.1038/srep23000
Keywords: chimera states, multiplex networks, FitzHugh-Nagumo oscillator, time delay, relay synchronization
Citation: Sawicki J, Ghosh S, Jalan S and Zakharova A (2019) Chimeras in Multiplex Networks: Interplay of Inter- and Intra-Layer Delays. Front. Appl. Math. Stat. 5:19. doi: 10.3389/fams.2019.00019
Received: 10 January 2019; Accepted: 28 March 2019;
Published: 24 April 2019.
Edited by:
Jun Ma, Lanzhou University of Technology, ChinaReviewed by:
Tanmoy Banerjee, University of Burdwan, IndiaCarlo Laing, College of Sciences, Massey University, New Zealand
V. K. Chandrasekar, SASTRA University, India
Copyright © 2019 Sawicki, Ghosh, Jalan and Zakharova. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jakub Sawicki, emVyZ29uQGdteC5uZXQ=
 Jakub Sawicki
Jakub Sawicki Saptarshi Ghosh2
Saptarshi Ghosh2 Anna Zakharova
Anna Zakharova