- 1Department of Mathematics, Hong Kong Baptist University, Kowloon, Hong Kong
- 2Department of Statistics, Stanford University, Stanford, CA, United States
- 3Department of Mathematics, Wenzhou University, Wenzhou, China
- 4Department of Mathematics, School of Data Science, City University of Hong Kong, Kowloon, Hong Kong
Deep learning has been successfully used in various applications including image classification, natural language processing and game theory. The heart of deep learning is to adopt deep neural networks (deep nets for short) with certain structures to build up the estimator. Depth and structure of deep nets are two crucial factors in promoting the development of deep learning. In this paper, we propose a novel tree structure to equip deep nets to compensate the capacity drawback of deep fully connected neural networks (DFCN) and enhance the approximation ability of deep convolutional neural networks (DCNN). Based on an empirical risk minimization algorithm, we derive fast learning rates for deep nets.
1. Introduction
Deep learning [1], a learning strategy based on deep neural networks (deep nets), has recently made significant breakthrough on bottlenecks of classical learning schemes, such as support vector machines, random forests and boosting algorithms, by demonstrating its remarkable success in such research areas as computer vision [2], speech recognition [3], and game theory [4]. Understanding the theory of deep learning has recently triggered enormous research activities in communities of statistics, optimization, approximation theory, and learning theory. Continually rapid developments on the deep learning methodology as well as its rationality verifications gradually uncover its mysterious veils.
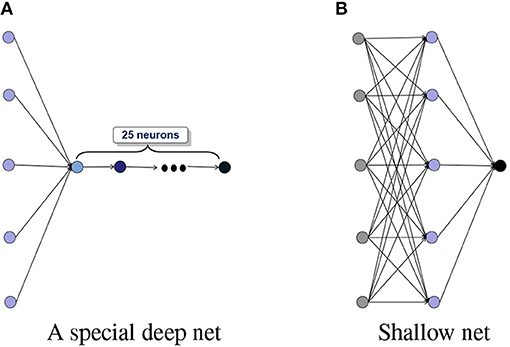
Depth and structure of deep nets are two crucial factors in promoting the development of deep learning [5]. The necessity of depth has been rigorously verified from the viewpoints of approximation theory and representation theory, via showing the advantages of deep nets in localized approximation [6], sparse approximation in the frequency domain [7, 8], sparse approximation in the spatial domain [9], manifold learning [10, 11], hierarchical structures grasping [12, 13], piecewise smoothness realization [14], universality with bounded number of parameters [15, 16] and rotation invariance protection [17]. We refer the readers to Pinkus [18] and Poggio et al. [19] for details on the theoretical advantages of deep nets over shallow neural networks (shallow nets). The gain in approximation and feature extraction inevitable leads to large capacity of deep nets, making the derived estimators sensitive to noise accumulated from significant increase amount of computation. In particular, under some capacity measurements like the number of linear regions [20], Betti numbers [21], and number of monomials [22], it is well-known that while the capacity of deep nets increases exponentially with respect to depth and polynomially with respect to width, the increase in depth of the network brings additional risk in stability, additional difficulty in designing learning algorithms, and may result in large variance. In this regard, we would like to point out that although there are the same number of free parameters in neural networks presented in Figure 1, the capacity of the network in Figure 1A is much larger than that in Figure 1B.
Fortunately, the structure, reflected by the layer-to-layer conjunction rule, compensates for the capacity drawback of deep nets and allows deep learning feasible and even practical. Two dominant structures of deep nets, as shown in Figure 2, are the deep fully connected neural networks (DFCN) and deep convolutional neural networks (DCNN). While the pros of DFCN is its excellent approximation ability, since all the conjunctions are considered in this structure, its cons, however, lies in the extremely large capacity, leading to scalable difficulty and large variance from the learning theory viewpoint [23]. On the other hand, the advantage of DCNN is its small number of free parameters as a result of sparse connectivity and weight-sharing mechanisms. For example, there are 2 free parameters in each layers for a DCNN with filter length 2 (see Figure 2B). Such a parameter reduction certainly brings the benefit in stability and consequently small variance. However, it is questionable if DCNN could maintain the attractive approximation ability of DFCN. Indeed, with the exception of the universal approximation property and approximation rate estimates [24, 25], there is insufficient theoretical study in the assessment of the approximation capability of DCNN. Thus, equipping deep nets with an appropriate structure to reduce the number of parameters of DFCN while enhancing the approximation ability of DCNN requires some desirable balance of the bias and variance in the learning process.
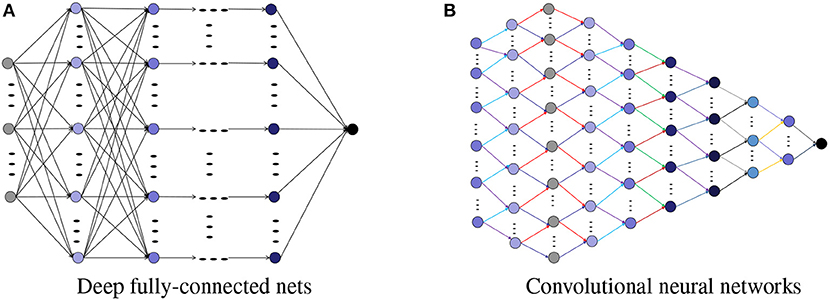
Figure 2. Structures for deep nets. (A) Deep fully-connected nets. (B) Convolutional neural networks.
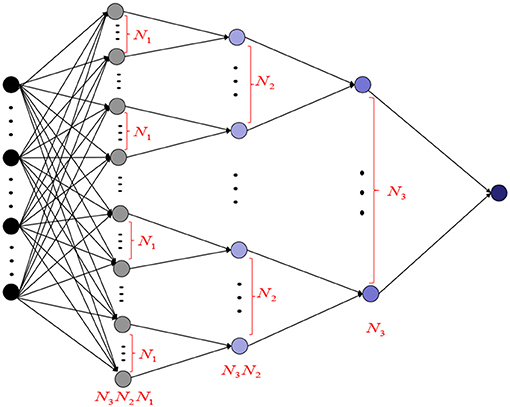
In this paper, we propose an appropriate structure to equip deep nets with a combination of some smaller variance provided by DCNN and a corresponding less bias advantage of DFCN. Two important ingredients of our approach are feature grouping via dimensionality-leveraging and tree-type feature extraction. Our construction is motivated by the structures of deep nets presented in Chui et al. [6] and Lin [9] for the realization of locality and sparsity features. As shown in Figure 3A, to capture the position information for x ∈ ℝd among 4 candidates, a dimensionality-leveraging, from d to 8d, is used to group each position information via 2d neurons. With the help of the neural networks in dimensionality-leveraging, features are coupled in a group of neurons, and then the tree structure, instead of the convolutional structure, is sufficient to capture such features. Thus, we will use the first hidden layer to group the features via dimensionality-leveraging, and will then utilize the tree structure to extract the features, as exhibited in Figure 3B.
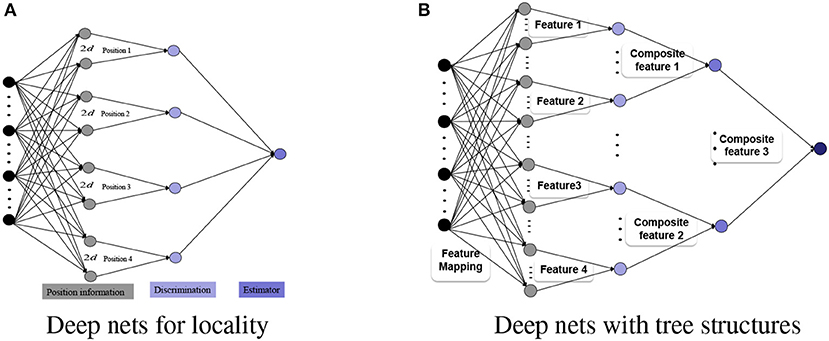
Figure 3. Deep nets with tree structures. (A) Deep nets for locality. (B) Deep nets with tree structures.
It is important to emphasize that the aim of the present paper is not to pursue the advantages of deep nets with tree structures in approximation, since this has been the subject of investigation in a vast amount of literature (see for example [6, 9, 10, 13, 15, 17, 26]), but to show the benefit of tree structures in deriving small variance. In particular, using the tree structures, we are able to decouple deep nets, layer by layer, and derive a tight covering number [27] estimate by using the Lipschitz property of the activation function. Since there are much fewer free parameters in deep nets with tree structures than those in DFCN, with the same number of neurons, the covering number of the former is smaller than that of the latter, resulting in smaller variance of deep nets with tree structures. We will then derive fast learning rates for “generalization error” for implementing the empirical risk minimization on deep nets. Deep nets with tree structures, revealed by our study, possess three theoretical advantages, namely: the capacity, as measured by the covering number, is much smaller than that of DFCN; based on tree structures, the approximation capability is comparable with that of DFCN; and fast learning rate is achieved, by applying an empirical risk minimization algorithm.
2. Deep Nets With Tree Structures
In image processing, a standard approach is to leverage a low-dimensional image to a high-dimensional pixel-scale image. While leveraging is a brutal approach that loses such image features as sparsity, locality and symmetry, and makes the variables highly inter-related, one method to capture the structure information by means of grouping the adjacent variables is machine learning. In particular, DCNN with numerous hidden layers, as exhibited in Figure 4, has been utilized, with the underlying intuition that the convolutional structure can extract missing features by deepening the network. The problem is, however, that with the exception of being able to extract transition-invariance features [28], there is no theoretical verification that DCNN could out-perform other neural network structures in feature extraction. Motivated by the application of DCNN in image processing, we propose a novel structure to equip deep nets for feature extraction and learning. Our basic idea is to group different features via several neurons in the first hidden layer rather than brutal leveraging. In this way, each group is independent and thus a tree structure feature extraction is sufficient to extract the grouped feature, just as Figure 3B purports to show.
In the following, we present the detailed definition of deep nets with tree structures. Let 𝕀: = [−1, 1], x = (x(1), …, x(d)) ∈ 𝕀d = [−1, 1]d, and L ∈ ℕ denote the number of hidden layers. Also let ϕk : ℝ → ℝ, k = 0, 1, …, L, be univariate activation functions. Let N0 = d and for each j = 1, …, L, denote by Nj ≥ 2, the size of tree in the j-th hidden layer. Set
Then a deep net with the tree structure of L layers can be formulated recursively by
where for each j ∈ {1, 2, …, Nk}, k ∈ {0, 1, …, L}, and . Let denote the set of output functions for at the L-th layer. For 0 ≤ k ≤ L − 1 and , denote by the set of functions defined in (2).
By setting ϕ0(t) = t and , it is easy to see that reduces to the classical shallow net. In view of the tree structure, it follows from (1), (2) and Figure 5 that there are a total of
free parameters for . For , we introduce the notation
With the restrictions imposed by (4) on deep nets, the parameters are bounded. This is indeed a necessity condition, since it can be found in Guo et al. [29] and Maiorov and Pinkus [15] that there exists some with finitely many neurons but infinite capacity (covering number).
3. Advantages of Deep Nets With Tree Structures
The study of the advantages of deep nets over shallow nets in approximation is a classical topic and several theoretical benefits of deep nets are revealed in a large literature. We refer the readers to a fruitful review paper [18] for more details. Due to the concise mathematical formulation, deep nets with tree structures are one of the most popular structures in approximation theory. It dates back to Mhaskar [26], where it was proved that deep nets with tree structures can be constructed to overcome the saturation phenomenon of shallow nets in the sense that the approximation rate cannot go beyond a certain level when the regularity of the target function increases. In Chui et al. [6], deep nets with two hidden layers and tree structures were constructed to provide localized approximation, which is beyond the performance of shallow nets. In Maiorov and Pinkus [15], a deep net with tree structures, two hidden layers and finitely many neurons, was demonstrated to possess the universal approximation property. Furthermore, in our recent papers Chui et al. [10, 17], deep nets with tree structures were proved to be capable of extracting the manifold structure feature and rotation-invariance feature, respectively.
Most importantly, it is clear from the above-mentioned results that deep nets with tree structures do not degrade the approximation performance of DFCN, while sparse connections between neurons significantly reduces the number of free parameters. In the following, we will show that deep nets with tree structures have an overall advantage over DFCN by deriving tight covering number estimates. Let 𝔹 be a Banach space and V be a subset of 𝔹. Denote by the ε-covering number of V under the metric of 𝔹 [27], defined by the minimal number of elements in an ε-net of V. For , we set for brevity. The objective of this consideration is to establish the following theorem, that exhibits a tight bound for covering numbers of .
Theorem 1. Assume that
Then for any 0 < ε ≤ 1,
where and is defined by (3).
The proof of Theorem 1 is delayed to section 5. We remark that the assumption (5) is mild. Indeed, almost all widely used activation functions including the logistic function , hyperbolic tangent sigmoidal function with tanh(t) = (e2t − 1)/(e2t + 1), arctan sigmoidal function Gompertz function ϕ(t) = e−ae−bt with a, b > 0 and Gaussian function σ(t) = e−t2 satisfy this assumption. We also remark that numerous quantities such as the number of linear regions [20], Betti numbers [21], VC-dimension [30], and number of monomials [22] have been employed to measuring the capacity of deep nets. To compare these measurements, it is noted that covering numbers possess three advantages. Firstly, the covering number is close to the coding length in information theory according to the encode-decode theory proposed by Donoho [31]. Thus, it is a powerful capacity measurement to show the expressivity of deep nets. Secondly, covering numbers determine the limitations of approximation ability of deep nets [17, 29]. Therefore, studying covering numbers of deep nets facilitates the verification of the optimality of the existing approximation results in Chui et al. [6, 10, 17] and Mhaskar [26]. Finally, covering numbers usually correspond to some oracle inequalities [23] and can reflect the stability of learning algorithms. All these features suggest the rationality of adopting the covering number to measure the capacity of deep nets.
Under the Lipchitz assumption (5) for the activation function, a bound of the covering number for the set
with ‖ · ‖* denoting some norm including the uniform norm was derived in Kůrková and Sanguineti [32]. Based on this, Maiorov [33] presented a tight estimate for shallow nets as
where
and Γn > 0 depending on n.
Estimates of covering number for deep nets were first studied in Kohler and Krzyżak [34], where a tight bound for covering numbers of deep nets with tree structures and two hidden layers is derived. Using a similar approach, it was presented in Kohler and Krzyżak [34] and Lin [9] an upper bound estimate for deep nets with tree structures, five hidden layers and without the Liptchitz assumption (5) of the activation function. Recently, Kohler and Krzyzak [13] provided an estimate for covering numbers of deep nets with L-hidden layers with L ∈ ℕ. Furthermore, covering numbers for deep nets with arbitrary structures and bounded parameters were deduced in Guo et al. [29]. Our result, exhibited in Theorem 1, establishes a covering number estimate for deep nets with arbitrarily many hidden layers and tree structures. This result improves the estimate in Guo et al. [29] by reducing the exponent of from L2 to (L + 1), since is usually very large. The main tool in our analysis is to use the Liptchitz property of the activation function and boundedness of the free parameters to decouple the depth layer by layer due to tree structures. It should be mentioned that Theorem 1 also removes the monotonic increasing assumption on the activation function while exhibits a similar covering number estimate as Anthony and Bartlett [35, Theorem 14.5]. Due to the boundedness assumption (5), our result excludes the covering number estimate for deep nets with the widely used rectifier linear unit (ReLU). Using the technique in Guo et al. [29, Lemma 1], we can derive upper bound estimates of deep nets in different layers. But it leads to an additional power L on in (6), i.e., . Thus, it requires a novel technique to derive the same covering number estimate for deep ReLU nets as Theorem 1. We leave it as a future work.
4. Generalization Error Estimates for Deep Nets
In this section, we present the generalization error estimates for empirical risk minimization on deep nets in the framework of learning theory [23]. In this framework, samples are assumed to be drawn independently according to the Borel probability measure ρ on with and for some M > 0. The primary objective is to apply the regression function:
which minimizes the generalization error
where ρ(y|x) denotes the conditional distribution at x induced by ρ. Let ρX be the marginal distribution of ρ on and be the Hilbert space of ρX square-integrable functions on . For , we have [23]
Denote by the empirical risk for the estimator f. Before presenting the generalization error for deep nets with tree structures, we derive an oracle inequality based on covering numbers for the empirical risk minimization (ERM) algorithm, i.e.,
where is a set of continuous functions on and is in our study. Since |y| ≤ M almost everywhere, we have |fρ(x)| ≤ M. It is natural to project an output function onto the interval [−M, M] by the projection operator
Thus, the estimator we study in this paper is . The following theorem presents the oracle inequality for ERM based on covering numbers.
Theorem 2. Suppose there exist , such that
Then for any and ϵ > 0,
The proof of Theorem 2 will be given in the next section. Theorem 2 shows that the covering number plays an important role in deducing the generalization error. As a result of this theorem and Theorem 1, we can derive tight generalization error bounds for ERM on deep nets with tree structures. Suppose that there exist some β > 0, , and α > 0, such that
Define
We then derive the following generalization error estimate for (12).
Theorem 3. Let 0 < δ < 1. Suppose that there exist some such that (11) holds. If (5) holds and , then with confidence at least 1 − δ, we have
where C, C′, C″ are constants independent of , L, N1, …, NL, m, or δ.
The proof of Theorem 3 will be given in the next section. Assumption (11) describes the expressivity of . For some constants , the exponent β in (11) implies the regularity for the regression function fρ. In particular, it can be found in Chui et al. [17] and Guo et al. [29] that the Liptchitz continuity and radial property of fρ corresponds to β = 1/d and β = 1, respectively. It was shown in (13) that there is an additional L2β in our estimate, which is different from generalization errors of shallow nets [36] and deep nets with fixed depth [10]. The main reason is that there is an additional L in the exponent for the covering numbers of in (6). With the same number of parameters, large depth of deep nets with tree structures usually leads to large variance, as shown in (13). However, it was also shown in Chui et al. [6, 10, 17], Guo et al. [29], Lin [9, 37], Mhaskar and Poggio [12], and Pinkus [18] that the depth is necessary in improving the performance of deep nets. It would be of some interest to study the smallest depth of deep nets with tree structures in extracting specific features. This study is left in a future work.
5. Proofs of Main Results
To facilitate our proof of Theorem 1, let us first establish the following lemma:
Lemma 1. Let ι ∈ ℕ, 𝔸 ⊆ ℝι, B be a Banach space of functions on 𝔸 and . For , set and . Then it follows that for any ε, ν > 0,
In addition, if , for all and , and , then
Proof. Let {f1, …, fN} and be an ε-cover and a ν-cover of and with
Then, for every and , there exist k ∈ {1, …, N} and ℓ ∈ {1, …, N′}, such that
By the triangle inequality, we have
Thus, is an (ε + ν)-cover of . Therefore, (16) implies
This establishes (14).
To prove (15), let {f1, …, fN*} and be an -cover and a -cover of and , respectively, with
Then, for every and , there exist k ∈ {1, …, N*} and that satisfy and such that
It then follows from the triangle inequality that
which implies that is an (ε + ν)-cover of . This together with (17) imply
This completes the proof of Lemma 1.
We are now ready to prove Theorem 1 as follows.
Proof of Theorem 1: Define, for k ∈ {0, 1, …, L} and ,
Then, (14) implies that for ε > 0,
where for 1 ≤ j ≤ Nk,
For each j ∈ {1, …, Nk}, since and ‖ϕk‖L∞(ℝ) ≤ 1, we obtain, from (15) with ι = 1, B = L∞(ℝ), and , that
where
Since ϕk satisfies (5), it follows from the definition of the covering number that
and
where
Using (14) again, we have
Combing (19), (20), (21), (22), and (23), we get
Using (24), we have
which implies by induction
For arbitrary ν > 0, using the same arguments as those in proving (24), we get
For j ∈ {1, …, N0} and , noting that is in a two dimensional linear space whose elements are bounded by , we get
This implies
Inserting this estimate into (25), we have
Recalling (3), Nk ≥ 2 for arbitrary k ∈ {0, 1, …, N}, we have
and
Thus, yields
This completes the proof of Theorem 1.
The proof of Theorem 2 depends on the following two concentration inequalities, which can be found in Cucker and Zhou [23], Wu and Zhou [38], and Zhou and Jetter [39], respectively.
Lemma 2 (B-Inequality). Let ξ be a random variable in a probability space with mean E(ξ) and variance σ2(ξ) = σ2. If |ξ(z) − E(ξ)| ≤ Mξ for almost all , then for any ε > 0,
Lemma 3 (C-Inequality). Let be a set of continuous functions on such that, for some , |f* − E(f*)| ≤ B′ almost surely and for all . Then for every ε > 0,
We now turn to the proof of Theorem 2.
Proof of Theorem 2: For , from (9) we have , which together with , implies
In the following we set, for convenience,
and
Then we have
To apply the B-Inequality in Lemma 2, let the random variable ξ on be defined by
Then since |y| ≤ M and |fρ(x)| ≤ M almost surely, we have
almost surely. It then follows from B-Inequality with , that
holds with confidence at least
On the other hand, for
and any (fixed) there exists an such that . Therefore, it follows from (8) that
and
Since |y| ≤ M and |fρ(x)| ≤ M almost surely, we have
which implies
Hence, we may apply C-Inequality to , with , to conclude that
holds with confidence at least
For any , we have
Thus, an -covering of provides an ε-covering of for any ε > 0. This implies that
This together with (10) implies
Hence, (29) implies that
holds with confidence at least
Inserting (27), (28), (30), and (31) into (26), we conclude that
holds with confidence at least
This completes the proof of Theorem 2 by re-scaling 4ε to ε.
To complete the discussion in this paper, we now prove Theorem 3 by applying Theorem 1 and Theorem 2, as follows.
Proof of Theorem 3: Due to (11), there exists some such that
Since (5) holds, Theorem 1 implies
Applying Theorem 2 with , to and setting with giving below, we have that for
so that
where is a constant independent of or L. Setting to be a constant independent of L or such that , and , we have
Then setting
we obtain
Thus, it follows from (33) that with confidence of at least 1 − δ, we have
where . This completes the proof of Theorem 3.
6. Conclusion
In this paper, we provided a novel tree structure to equip deep nets and studied its theoretical advantages. Our studied showed that deep nets with tree structure succeeded in reducing the free parameters of deep fully-connected nets without sacrificing their excellent approximation ability. Under this circumstance, implementing the well known empirical risk minimization on deep nets with tree structures yields fast learning rates.
Data Availability
All datasets generated and analyzed for this study are included in the manuscript and the supplementary files.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
The research of CC was partially supported by Hong Kong Research Council [Grant Nos. 12300917 and 12303218] and Hong Kong Baptist University [Grant No. HKBU-RC-ICRS/16-17/03]. The research of S-BL was supported by the National Natural Science Foundation of China [Grant No. 61876133], and the research of D-XZ was partially supported by the Research Grant Council of Hong Kong [Project No. CityU 11306617].
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Hinton GE, Osindero S, Teh YW. A fast learning algorithm for deep belief netws. Neural Comput. (2006) 18:1527–54. doi: 10.1162/neco.2006.18.7.1527
2. Krizhevsky A, Sutskever I, Hinton GE. Imagenet Classification With Deep Convolutional Neural Networks. Lake Tahoe (2012). 1097–105.
3. Lee H, Pham P, Largman Y, Ng AY. Unsupervised feature learning for audio classification using convolutional deep belief networks. In: Neural Information Processing Systems. Vancouver, BC (2010). p. 469–77.
4. Silver D, Huang A, Maddison CJ, Guez A, Sifre L, van den Driessche G, et al. Mastering the game of Go with deep neural networks and tree search. Nature. (2016) 529:484–9. doi: 10.1038/nature16961
6. Chui CK, Li X, Mhaskar HN. Neural networks for localized approximation. Math Comput. (1994) 63:607–23. doi: 10.2307/2153285
7. Lin HW, Tegmark M, Rolnick D. Why does deep and cheap learning works so well? J Stat Phys. (2017) 168:1223–47. doi: 10.1007/s10955-017-1836-5
8. Schwab C, Zech J. Deep learning in high dimension: neural network expression rates for generalized polynomial chaos expansions in UQ. Anal Appl. (2018). doi: 10.1142/S0219530518500203
9. Lin SB. Generalization and expressivity for deep nets. IEEE Trans Neural Netw Learn Syst. (2019) 30:1392–406. doi: 10.1109/TNNLS.2018.2868980
10. Chui CK, Lin SB, Zhou DX. Construction of neural networks for realization of localized deep learning. Front Appl Math Stat. (2018) 4:14. doi: 10.3389/fams.2018.00014
11. Shaham U, Cloninger A, Coifman RR. Provable approximation properties for deep neural networks. Appl Comput Harmon Anal. (2018) 44:537–57. doi: 10.1016/j.acha.2016.04.003
12. Mhaskar H, Poggio T. Deep vs shallow networks: an approximation theory perspective. Anal Appl. (2006) 14:829–48. doi: 10.1142/S0219530516400042
13. Kohler M, Krzyzak A. Nonparametric regression based on hierarchical interaction models. IEEE Trans Inform Theory. (2017) 63:1620–30. doi: 10.1109/TIT.2016.2634401
14. Petersen P, Voigtlaender F. Optimal aproximation of piecewise smooth functions using deep ReLU neural networks. Neural Netw. (2018) 108:296–330. doi: 10.1016/j.neunet.2018.08.019
15. Maiorov V, Pinkus A. Lower bounds for approximation by MLP neural networks. Neurocomputing. (1999) 25:81–91. doi: 10.1016/S0925-2312(98)00111-8
16. Ismailov VE. On the approximation by neural networks with bounded number of neurons in hidden layers. J Math Anal Appl. (2014) 417:963–9. doi: 10.1016/j.jmaa.2014.03.092
17. Chui CK, Lin SB, Zhou DX. Deep neural networks for rotation-invariance approximation and learning. Anal Appl. arXiv:1904.01814.
18. Pinkus A. Approximation theory of the MLP model in neural networks. Acta Numer. (1999) 8:143–95. doi: 10.1017/S0962492900002919
19. Poggio T, Mhaskar H, Rosasco L, Miranda B, Liao Q. Why and when can deep-but not shallow-networks avoid the curse of dimensionality: a review. Int J Auto Comput. (2017). 14: 503–19. doi: 10.1007/s11633-017-1054-2
20. Montúfar G, Pascanu R, Cho K, Bengio Y. On the number of linear regions of deep neural networks. In: Neural Information Processing Systems. Montréal, QC (2014). p. 2924–32.
21. Bianchini M, Scarselli F. On the complexity of neural network classifiers: a comparison between shallow and deep architectures, IEEE Trans Neural Netw Learn Syst. (2014) 25:1553–65. doi: 10.1109/TNNLS.2013.2293637
22. Delalleau O, Bengio Y. Shallow vs. deep sum-product networks. In: Advances in Neural Information Processing Systems. Granada (2011). p. 666–74.
23. Cucker F, Zhou DX. Learning Theory: An Approximation Theory Viewpoint. Cambridge: Cambridge University Press (2007).
24. Zhou DX. Deep distributed convolutional neural networks: universality. Anal Appl. (2018) 16:895–919. doi: 10.1142/S0219530518500124
25. Zhou DX. Universality of deep convolutional neural networks. Appl Comput Harmonic Anal. arXiv:1805.10769.
26. Mhaskar H. Approximation properties of a multilayered feedforward artificial neural network. Adv Comput Math. (1993) 1:61–80. doi: 10.1007/BF02070821
27. Zhou DX. Capacity of reproducing kernel spaces in learning theory. IEEE Trans Inform Theory. (2003) 49:1743–52. doi: 10.1109/TIT.2003.813564
28. Bruna J, Mallat S. Invariant scattering convolution networks. IEEE Trans Patt Anal Mach Intel. (2013) 35:1872–86. doi: 10.1109/TPAMI.2012.230
30. Harvey N, Liaw C, Mehrabian A. Nearly-tight VC-dimension bounds for piecewise linear neural networks. Conference on Learning Theory. Amsterdam (2017). p. 1064–8.
31. Donoho DL. Unconditional bases are optimal bases for data compression and for statistical estimation. Appl Comput Harmonic Anal. (1993) 1:100–15. doi: 10.1006/acha.1993.1008
32. Kůrková V, Sanguineti M. Estimates of covering numbers of convex sets with slowly decaying orthogonal subsets. Discrete Appl Math. (2007) 155:1930–42. doi: 10.1016/j.dam.2007.04.007
33. Maiorov V. Pseudo-dimension and entropy of manifolds formed by affine-invariant dictionary. Adv Comput Math. (2006) 25:435–50. doi: 10.1007/s10444-004-7645-9
34. Kohler M, Krzyżak A. Adaptive regression estimation with multilayer feedforward neural networks. J Nonparametric Stat. (2005) 17:891–913. doi: 10.1080/10485250500309608
35. Anthony M, Bartlett PL. Neural Network Learning: Theoretical Foundations. Cambridge: Cambridge University Press (2009).
36. Maiorov V. Approximation by neural networks and learning theory. J Complex. (2006) 22:102–17. doi: 10.1016/j.jco.2005.09.001
37. Lin SB. Limitations of shallow nets approximation. Neural Netw. (2017) 94:96–102. doi: 10.1016/j.neunet.2017.06.016
38. Wu Q, Zhou DX. SVM soft margin classifiers: linear programming versus quadratic programming. Neural Comput. (2015) 17:1160–87. doi: 10.1162/0899766053491896
Keywords: deep nets, learning theory, deep learning, tree structure, empirical risk minimization
Citation: Chui CK, Lin S-B and Zhou D-X (2019) Deep Net Tree Structure for Balance of Capacity and Approximation Ability. Front. Appl. Math. Stat. 5:46. doi: 10.3389/fams.2019.00046
Received: 20 June 2019; Accepted: 27 August 2019;
Published: 11 September 2019.
Edited by:
Lucia Tabacu, Old Dominion University, United StatesReviewed by:
Jianjun Wang, Southwest University, ChinaJinshan Zeng, Jiangxi Normal University, China
Copyright © 2019 Chui, Lin and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shao-Bo Lin, c2JsaW4xOTgzQGdtYWlsLmNvbQ==
†These authors have contributed equally to this work
 Charles K. Chui
Charles K. Chui Shao-Bo Lin
Shao-Bo Lin Ding-Xuan Zhou
Ding-Xuan Zhou