Finite-Time Synchronization Between Two Different Chaotic Systems by Adaptive Sliding Mode Control

1 Introduction

Chaotic systems are very complex nonlinear systems that are highly sensitive to initial conditions and the system’s parameters. Recently, the synchronization of chaotic systems has attracted several researchers. A basic concept of synchronization is to design a suitable controller to control the slave system such that the states of the slave system have the same amplitude as the master states. There have been many control methods for synchronization of chaotic systems such as adaptive control [1], observer-based control [2], backstepping control [3], active control [4], and sliding mode control [5]. In general, the parameters of the chaotic system are inevitably perturbed by external disturbance. To handle this problem, the sliding mode control which is one of the most effective methods was proposed in [6] for chaos synchronization with uncertainties and disturbances. Generally, the traditional sliding mode control (SMC) has some important problems such as discontinuous control, which often causes the chattering phenomenon. To cope with the mentioned problem, some new SMC has been developed. Moreover, SMC cannot ensure the system states will converge to the equilibrium point in finite time. As a result, a new control method which is called a terminal sliding mode (TSM) control was proposed in [7]. It was developed by introducing fractional power into the sliding mode, which guarantees chaos synchronization is achieved in finite time and it gives a fast convergence and good tracking precision. In [8], the authors have investigated a chattering-free by introducing a new and improved robust predefined-time sliding mode control (CFRPSMC) scheme to eliminate the chattering phenomenon and solved the trajectory tracking problem of a remotely operated vehicle with matching uncertainties in predefined-time. However, when the system states are far away from the equilibrium point, TSMC may not present a good convergent efficiency. The fast terminal sliding mode (FTSM) control in [9] was developed for second-order uncertain systems to ensure the system states have a faster convergence speed when they are far away from the equilibrium point in finite time. In the last case, there is a singularity problem because the terms with negative fraction power may exist. To overcome this problem, a new type of sliding mode control method called nonsingular terminal sliding mode (NTSM) control was presented in [10].

In any case, these methods still require a knowledge of the upper bound of the disturbances or uncertainties. Therefore, an adaptive technique was applied for the type of sliding mode control to adjust the control gain of the controllers. In [11] the authors studied the synchronization of two different uncertain chaotic systems with unknown parameters using a robust adaptive sliding mode controller. The synchronization of the second-order chaotic systems which was controlled by an adaptive terminal sliding mode controller with input nonlinearity was studied in [12]. Two novel controllers NTSMC and ANTSMC methods were designed in [13] for synchronization of smart grid chaotic systems which eliminate the undesirable chattering phenomenon in finite time. In [14], the authors have designed two novel controllers by using AFSMC methods to solve the chattering problem for a class of single-input multiple-out (SIMO) nonlinear systems with unknown mismatched uncertainties in finite time.

Motivated by the above discussions, in this paper, the adaptive control technique is applied to design a new and improved nonsingular fast terminal sliding mode (NFTSM) control to solve the synchronization problem between two different chaotic systems with unknown parameters and disturbances. The finite-time stability is achieved by using some finite-time lemma and the Lyapunov stability theory. Furthermore, numerical results are given to confirm the effectiveness of our proposed controllers. The main contributions are listed as following.

• An improved ANFTSM controller is designed to succeed the finite-time synchronization of two different chaotic systems with external and disturbance.

• The fast nonsingular terminal sliding mode is used to eliminate the singularity problem and to provide a fast rate of when the system states are far away from the origin.

• An ANFTSM controller does not require the knowledge of the upper bound of the disturbances or uncertainties.

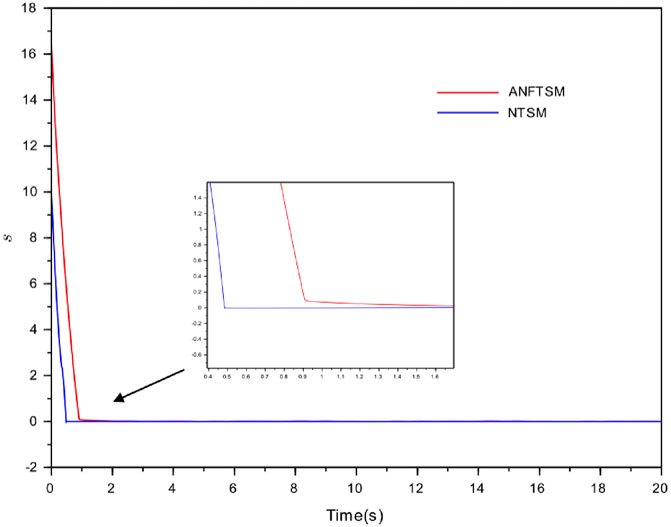
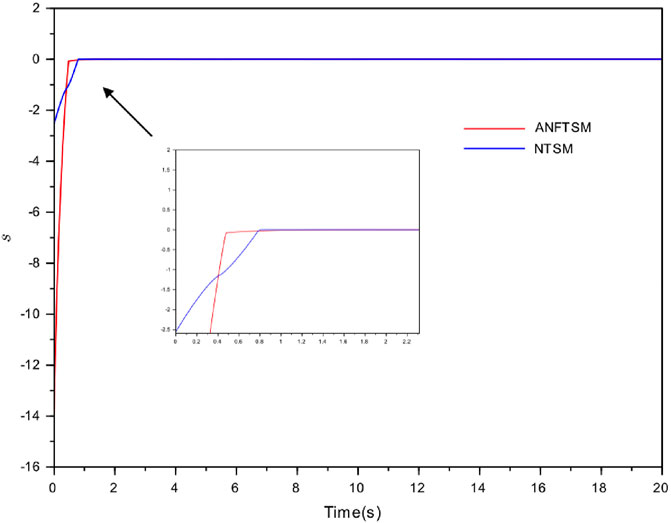
• A comparison between the effectiveness of ANFTSM and NTSM controllers is given which shows that ANFTSM controller gives a faster convergence rate to zero for the synchronization error in finite time.

The rest of this paper is organized as follows. In Section 2, the synchronization problem is addressed and necessary preliminary results are given. The main result is given in Section 3. In Section 4, numerical examples and discussions are presented. Finally, the conclusion is given in Section 5.

2 Problem Description

In this section, the definition of the finite-time synchronization concept and some necessary lemmas are given.

Consider the second-order chaotic system with unknown parameters [15] which is of the following forms:

The master system:

$\begin{array}{l}{\dot{y}}_1\left(t\right)=y_2\left(t\right),\\ {\dot{y}}_2\left(t\right)=g\left(y,t\right)+\text{Δ}g\left(y,t\right),\end{array}(1)$

where $y_1\left(t\right)$ and $y_2\left(t\right)\in R$ are the states of the master system, $g\left(y,t\right)\in R$ is the nonlinear function of the master system, $\text{Δ}g\left(y,t\right)\in R$ is the uncertain parameter of the master system and $t\in R$ with R being the set of real numbers.

The slave system:

$\begin{array}{l}{\dot{x}}_1\left(t\right)=x_2\left(t\right),\\ {\dot{x}}_2\left(t\right)=f\left(x,t\right)+\text{Δ}f\left(x,t\right)+v\left(t\right)+u\left(t\right),\end{array}(2)$

where $x_1\left(t\right)$ and $x_2\left(t\right)\in R$ are the state vectors of the slave system, $f\left(x,t\right)\in R$ is the nonlinear function of the slave system, $\text{Δ}f\left(x,t\right)\in R$ is the uncertain parameter of the slave system, $v\left(t\right)$ is the disturbance input of the slave system and $u\left(t\right)\in R$ is the control input. The synchronization error is defined as $e\left(t\right)=x\left(t\right)-y\left(t\right).$

Let $e_1\left(t\right)=e\left(t\right)$ and $e_2\left(t\right)=\dot{e}\left(t\right)$. Using Eqs. 1, 2, one obtains

$\begin{array}{l}{\dot{e}}_1\left(t\right)=e_2\left(t\right),\\ {\dot{e}}_2\left(t\right)=f\left(x,t\right)-g\left(y,t\right)+d\left(x,y,t\right)+u\left(t\right),\end{array}(3)$

where $d\left(x,y,t\right)=\text{Δ}f\left(x,t\right)-\text{Δ}g\left(y,t\right)+v\left(t\right)$ is the perturbation term.

ASSUMPTION 2.1. The perturbation term is bounded, namely,

$\left|d\left(x,y,t\right)\right|\le D,(4)$

where D is a known positive constant.

DEFINITION 2.2. The master system 1) and slave systems 2) are said to be synchronized in finite time if there exists a constant $T=T\left(e\left(0\right)\right)>0$ such that $\underset{t\to T}{\text{lim}}\left|\left|e\left(t\right)\right|\right|$ = $\underset{t\to T}{\text{lim}}\left|\left|x\left(t\right)-y\left(t\right)\right|\right|=0$ and $\Vert e\left(t\right)\Vert =0$ for $t\ge T$. In this case, T is called the settling time of synchronization.

LEMMA 2.3 [16]. Consider the system

$\dot{x}=f\left(x\right),f\left(0\right)=0,x\in R^n(5)$

where $f:D\to R^n$ is continuous in an open set $D\subset R^n$. Assume that there is a continuous differential positive-definite function $V:D\to R$, and real numbers $\text{Γ}>0$ and $0<\varsigma <1$, such that

$\dot{V}\left(x\right)+\text{Γ}{V}^{\varsigma }\left(x\right)\le 0,\forall x\in D,$

then the equilibrium$x=0$of (Eq. 5) is locally finite-time stable. The settling time, depending on the initial state$x\left(0\right)=x_0$, satisfies

$T\left(x_0\right)\le \frac{V^{1-\varsigma }\left(x_0\right)}{\text{Γ}\left(1-\varsigma \right)}.$

In addition, if$D=R^n$and$V\left(x\right)$is radially unbounded, then the equilibrium$x=0$of (Eq. 5) is globally finite-time stable.

The following lemma is required for the design of fast terminal sliding mode control.

Lemma 2.4 [17]. Assume that there is a continuous differentiable positive-definite function $V:D\to R$ satisfying

$\dot{V}\left(x\right)+{\lambda }_{1}V\left(x\right)+{\lambda }_2{V}^{\varpi }\left(x\right)\le 0,$

where ${\lambda }_1>0,{\lambda }_2>0$ and, $0<\varpi <1$. Then, the settling time $T=T\left(x_0\right)$ , depending on the initial state $x\left(0\right)=x_0$, satisfies

$T\left(x_0\right)\le \frac{1}{{\lambda }_1\left(1-\varpi \right)}\text{ln}\frac{{\lambda }_1{V}^{1-\varpi }\left(x_0\right)+{\lambda }_2}{{\lambda }_2}.$

3 Design of Finite-Time Sliding Mode Controller

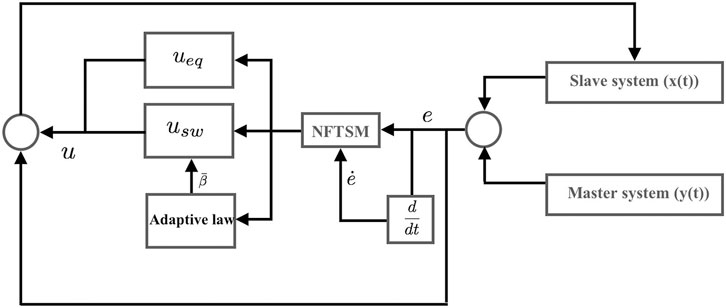
In this section, a new adaptive nonsingular fast terminal sliding mode (ANFTSM) controller is designed to achieve the synchronization between two different chaotic systems with unknown parameters and disturbances. There are two steps to design the controller. In the first step, a suitable nonsingular terminal sliding surface for the desired sliding motion is selected. That is the trajectory of the system along this surface approaches zero in a finite time. In the second step, an adaptive finite-time controller is designed to force the system motion from any initial condition to the sliding surface in a given finite time.

To design the ANFTSM controller, the nonsingular fast terminal sliding surface is introduced as:

$s\left(t\right)=e_2\left(t\right)+k_1{e}_1\left(t\right)+k_2{\left|e_1\right|}^{\gamma }sign\left(e_1\left(t\right)\right)(6)$

where $k_1$ , $k_2$ and $0.5<\gamma <1$ are positive constants.

For the system motion on the terminal sliding surface $s\left(t\right)=0$, the dynamic of the presented nonsingular fast terminal sliding mode can be obtained as:

${\dot{e}}_1\left(t\right)=-k_1{e}_1\left(t\right)-k_2|e_1\left(t\right){|}^{\gamma }sign\left(e_1\left(t\right)\right).(7)$

The designed controller $u\left(t\right)$ is as follows:

$u\left(t\right)=-f\left(x,t\right)+g\left(y,t\right)-k_1{e}_2\left(t\right)-k_2\gamma |e_1\left(t\right){|}^{\gamma -1}{\dot{e}}_1\left(t\right)-\beta sign\left(s\left(t\right)\right),(8)$

where β is the control parameter satisfying the adaptive law $\dot{\beta }=\overline{\beta }\left|s\left(t\right)\right|$ with $\overline{\beta }>0$ and there exists a positive constant ${\beta }^{\text{*}}$ so that. $\beta \le {\beta }^{\text{*}}.$

The block diagram for synchronization between the master system 1) and the slave system 2) using ANFTSM controller is shown in Figure 1.

FIGURE 1

FIGURE 1. The block diagram of chaos synchronization using ANFTSM controller.

Remark 3.1: In [18], the authors have investigated a new recurrent neural network (RNN) fractional-order sliding mode control to compensate harmonic current of active power filter (APF). In the proposed method, the controller gives a high approximation accuracy and quickly tracks the detected harmonic compensation. Moreover, the unknown function of the system is approximated by the recurrent neural network (RNN). In (Juntao et al., 2020a), the authors have proposed an adaptive terminal sliding mode control by applying fuzzy double hidden layer neural network (FDHLRNN) for single-phase active power filter (APE). The designed controller made the tracking error of the system converges to zero in a finite time. In [19], the authors have designed the super-twisting sliding mode controller based on the fractional-order nonsingular terminal sliding mode control for a micro gyroscope with unknown uncertainty by using a double-loop fuzzy neural network (DLFNN) to estimate the unknown uncertainty of the micro gyroscope system. There are several advantages by using such a designed controller, namely, the tracking error converges to zero in a finite time, the singular problem has been handled, and the unwanted chattering phenomena has been alleviated. In [20], the authors have introduced an adaptive $H_{\infty }$ tracking control technique for the nonlinear z-axis micro gyroscope system. The controller gives an accurate tracking trajectory of convergence to zero, and also a robust performance to uncertainties and disturbances. Furthermore, the unknown system parameters are estimated by using an adaptive law. The difference between our studies and [18, 19, 21], and [20] is that we apply the nonsingular fast terminal sliding mode control with an adaptive law technique to achieve finite-time synchronization between two different chaotic systems with unknown parameters and disturbances.

In the following result, by using the proposed controller (8), it is shown that the synchronization errors $e_1$ and $e_2$ converge to sliding surface $s\left(t\right)=0$ in finite time.

Theorem 3.1. For the system (3) and the controller (8), the error trajectory converges to sliding surface $s\left(t\right)=0$ in finite time.

Proof. Let us consider the Lyapunov function as

$V_1=\frac{1}{2}{s}^2+\frac{1}{2\rho }{\left(\beta -{\beta }^{\text{*}}\right)}^2(9)$

where ρ is a constant which satisfies$0<\rho <\overline{\beta }$. and$s\left(t\right)$is defined in (Eq. 6)

Taking the derivative of $V_1\left(t\right)$ in (Eq. 9) for sliding surface, we have

$\begin{array}{c}\dot{V_1}=s\dot{s}+\frac{1}{\rho }\left(\beta -{\beta }^{\text{*}}\right)\dot{\beta }\\ =s[{\dot{e}}_2+k_1{\dot{e}}_1+k_2\gamma |e_1{|}^{\gamma -1}{\dot{e}}_1]+\frac{\overline{\beta }}{\rho }\left(\beta -{\beta }^{\text{*}}\right)\left|s\right|.\end{array}(10)$

Substituting (Eq.3) and the controller (Eq. 8) in (Eq. 10), we get

$\begin{array}{c}\dot{V_1}\le -\beta \left|s\right|+D\left|s\right|+\frac{\overline{\beta }}{\rho }\left|\beta -{\beta }^{\text{*}}\right|\left|s\right|\\ =\left(D-{\beta }^{\text{*}}\right)\left|s\right|-|\beta -{\beta }^{\text{*}}|\left|s\right|+\frac{\overline{\beta }}{\rho }|\beta -{\beta }^{\text{*}}|\left|s\right|\\ =-\left({\beta }^{\text{*}}-D\right)\left|s\right|+\left(-\left|s\right|+\frac{\overline{\beta }}{\rho }\left|s\right|\right)\left|\beta -{\beta }^{\text{*}}\right|\\ \le -\sigma \left|s\right|-\xi \left|\beta -{\beta }^{\text{*}}\right|\\ =-\sigma \frac{\sqrt{2}}{\sqrt{2}}\left|s\right|-\xi \frac{\sqrt{2\rho }}{\sqrt{2\rho }}\left|\beta -{\beta }^{\text{*}}\right|\\ \le -min\left\{\sigma \sqrt{2},\xi \sqrt{2\rho }\right\}\left(\frac{\left|s\right|}{\sqrt{2}}+\frac{\left|\beta -{\beta }^{\text{*}}\right|}{\sqrt{2\rho }}\right)\\ =-\eta V_1^{\frac{1}{2}}\end{array}(11)$

where $\eta =\sqrt{2}min\left\{\sigma ,\sqrt{\rho }\xi \right\}$, $\sigma =\left({\beta }^{\text{*}}-D\right)>0$ and $\xi =\frac{\overline{\beta }}{\rho }\left|s\right|-\left|s\right|>0$. Thus, it follows from (Eq. 11) that

$\dot{V_1}\left(t\right)+\eta V_1{\left(t\right)}^{\frac{1}{2}}\le 0.$

By Lemma 2.3, the error trajectory $e\left(t\right)$ converges to sliding surface $s\left(t\right)=0$ in finite time $T_r\le \frac{2V_1^{\frac{1}{2}}\left(t_0\right)}{\eta }$.

As is shown above that the errors trajectory converges to sliding surface $s\left(t\right)=0$ in a finite time, it is required to show that the synchronization error $e_1$ and $e_2$ in (3) converge to zero in a finite time.

Theorem 3.3. Consider the nonsingular terminal sliding mode dynamics (7). This system is finite-time stable and it approaches zero in a finite time $T_s$. Namely, the system (1) and the system (2) are synchronized with a settling time $T_s$ which is determined by

$T_s\le \frac{1}{k_1\left(1-\gamma \right)}\ell n\left(\frac{2k_1{V}_2^{\frac{1-\gamma }{2}}\left(t_0\right)+{\left(\sqrt{2}\right)}^{\gamma +1}{k}_2}{{\left(\sqrt{2}\right)}^{\gamma +1}{k}_2}\right).$

Proof. Consider the Lyapunov function:

$V_2\left(t\right)=\frac{1}{2}{e}_1^2\left(t\right).(12)$

Substituting (Eq. 7) into the derivative of $V_2$ in (Eq. 12), yields

$\begin{array}{c}{\dot{V}}_2\left(t\right)=e_1\left(t\right){\dot{e}}_1\left(t\right)\\ =e_1\left(t\right)\left(-k_1{e}_1\left(t\right)-k_2|e_1\left(t\right){|}^{\gamma }sign\left(e_1\left(t\right)\right)\right)\\ =-k_1{e}_1^2\left(t\right)-k_2|e_1\left(t\right){|}^{\gamma +1}\end{array}$

Using (Eq. 12), we know that $e_1^2\left(t\right)=2V_2\left(t\right)$ and $\left|e_1\left(t\right)\right|=\sqrt{2}{V}_2^{\frac{1}{2}}\left(t\right)$. Then, ${\dot{V}}_2\left(t\right)$ becomes

${\dot{V}}_2\left(t\right)=-2k_1{V}_2-{\left(\sqrt{2}\right)}^{\gamma +1}{k}_2{V}_2^{\frac{\gamma +1}{2}}\le 0.$

By Lemma 2.4, the settling time $T_s$ is determined by:

$T_s\le \frac{1}{k_1\left(1-\gamma \right)}\ell n\left(\frac{2k_1{V}_2^{\frac{1-\gamma }{2}}\left(t_0\right)+{\left(\sqrt{2}\right)}^{\gamma +1}{k}_2}{{\left(\sqrt{2}\right)}^{\gamma +1}{k}_2}\right).$

Therefore, the error $e_1\left(t\right)$ converges to zero in a finite time $T_s$. After that, the error $e_2\left(t\right)$ also tends to zero in finite time $T_s$. In other words, the synchronization between the system (1) and the system (2) is achieved in a finite time $T_s$.

4 Numerical Examples

In this section, the effectiveness of the designed ANFTSM controller is presented. Moreover, the comparison between the performances of ANFTSM and the NTSM is given. First, we introduce some chaotic systems which will be applied to demonstrate the synchronization problems under the designed ANFTSM controller.

4.1 The Chaotic Systems

4.1.1 The Duffing-Holmes System

The Duffing-Holmes system [22] is a nonlinear dynamical system exhibiting complex and chaotic behavior given by

$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=-p_1{x}_1-p_2{x}_2-x_1^3+h\cos \left(\omega t\right),\end{array}(13)$

where $x_1$ and $x_2$ are the state variables, $p_1$ and $p_2$ are the coefficients exhibiting the friction, ω is the angular frequency of the external driving force, and h is the amplitude of the external force.

4.1.2 The Gyroscope System

The gyroscope system [23] is an important dynamical system which has several applications such as navigation system, space engineering, and aircraft system. The gyroscope system is given by

$\begin{array}{l}\dot{x_1}=x_2\\ \dot{x_2}=-c_1{x}_2-c_2{x}_2^3-{\alpha }^2\frac{{\left(1-\text{cos}\left(x_1\right)\right)}^2}{{\text{sin}}^3\left(x_1\right)}+\left({\beta }_0+{\beta }_1\sin \left(\theta t\right)\right)\text{sin}\left(x_1\right),\end{array}(14)$

where $x_1$ and $x_2$ are the state variables, $c_1$ and $c_2$ are the damping coefficients, ${\beta }_0$ and ${\beta }_1$ are normalized amplitudes of the external harmonic excitation, and θ is the frequency of the external harmonic excitation.

4.1.3 The Power System

The power system [24] is a nonlinear dynamical system given by

$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=-a\sin \left(x_1\right)-b{x}_2+c+F\cos \left(\lambda t\right),\end{array}(15)$

where $x_1$ and $x_2$ are the state variables of the system, F and λ represent amplitude and frequency of load disturbance, and a and b are generator inertia and damping coefficient, respectively.

4.2 Examples of Synchronization Between Two Different Chaotic Systems

In this subsection, two numerical examples for synchronization between two different chaotic systems which were introduced in Subsection 4.1 are presented to demonstrate the effectiveness of the designed ANFTSM controller. In Example 1, synchronization between the gyroscope system and the Duffing-Holmes system is considered. In Example 2, synchronization between the Duffing-Holmes system and the power system is studied.

Example 1

In this example, the effectiveness of the proposed ANFTSM to succeed finite-time synchronization between the gyroscope (14) system and the Duffing-Holmes (13) system is presented. For this propose, the system(14) is taken as the master system and the system (13) as the slave system. For simulation purpose, the nonlinear functions $f\left(x,t\right)$ and $g\left(y,t\right)$ are chosen as

$g\left(y,t\right)=-c_1{y}_2-c_2{y}_2^3-{\alpha }^2\frac{{\left(1-\text{cos}\left(y_1\right)\right)}^2}{{\text{sin}}^3\left(y_1\right)}+\left({\beta }_0+{\beta }_1\text{sin}\left(\theta t\right)\right)\text{sin}\left(y_1\right),$

$f\left(x,t\right)=-p_1{x}_1-p_2{x}_2-x_1^3+h\text{cos}\left(\omega t\right).$

The uncertain parameters for both systems are chosen as follows: $\text{Δ}g\left(y,t\right)=0.6\text{sin}\left(y_1\right)$, $\text{Δ}f\left(x,t\right)=-0.1\text{sin}\left(x_2\right)$. The disturbance term is chosen as $v\left(t\right)=0.4\text{sin}\left(t\right)$. The system parameters are selected as $p_1=1,p_2=0.25,h=0.3,\omega =1$, ${\beta }_0=1,{\beta }_1=35.5,{\alpha }^2=100,c_1=0.5,c_2=0.05$ and. $\theta =2.$

To achieve the finite-time synchronization, the parameters of the nonsingular fast terminal sliding surface (6) are chosen as $k_1=2,k_2=6$ and $\gamma =0.8$. The adaptive law β is chosen to satisfy $\dot{\beta }=\overline{\beta }\left|s\left(t\right)\right|$ with $\overline{\beta }=2$ and the initial condition $\beta \left(0\right)=2$; in which the upper bound ${\beta }^{\text{*}}$ satisfies ${\beta }^{\text{*}}\le 15$. The initial conditions for the Duffing-Holmes are chosen as $\left[x_1\left(0\right),x_2\left(0\right)]=[\mathrm{1,3}\right]$ and $\left[y_1\left(0\right),y_2\left(0\right)]=[-\mathrm{1,1}\right]$, respectively. From which, it follows from Theorem 3.2 that yields the synchronization errors $e_1\left(t\right)$ and $e_2\left(t\right)$ converge to zero in finite time $T_s\le 0.8105$.

For comparison purpose, we consider the NTSM controller which was considered in ([10]) with sliding surface given by $s=e_1+\kappa |e_2{|}^{\alpha }sign\left(e_2\right)$ with $\kappa =3$ and $\alpha =1.4$. The comparisons of the performance between ANFTSM and NTSM controllers are presented in Figures 2–6. Figure 2 and Figure 3 show that the master and slave systems are finite-time synchronized with a settling-time at about three and seven by using the ANFTSM controller and the NTSM controller, respectively. Figure 4 shows the synchronization errors $e_1\left(t\right)$ and $e_2\left(t\right)$ converge to zero in finite time. It can seen from Figure 4 that the ANFTSM controller gives a better synchronization performance and faster response in comparison with the NTSM controller method. Figure 5 demonstrates that the sliding surface approaches zero in finite time. The time responses of the ANFTSM and NTSM controllers are shown in Figure 6.

FIGURE 2

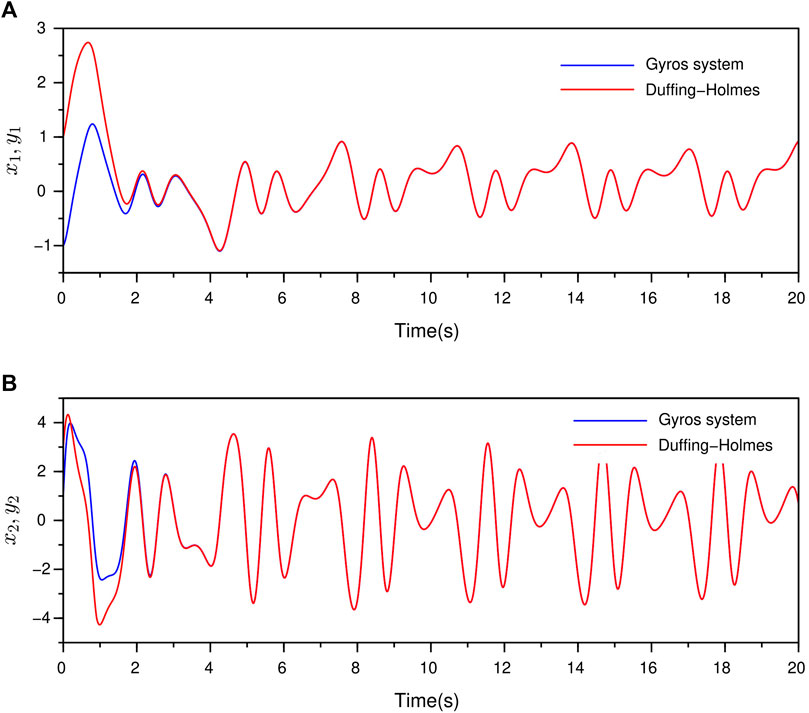
FIGURE 2. Synchronization between the Gyros and the Duffing-Holmes systems in Example 1 by ANFTSM controller (A) the synchronization between $x_1$ and $y_1$(B) the synchronization between $x_2$ and $y_2$.

FIGURE 3

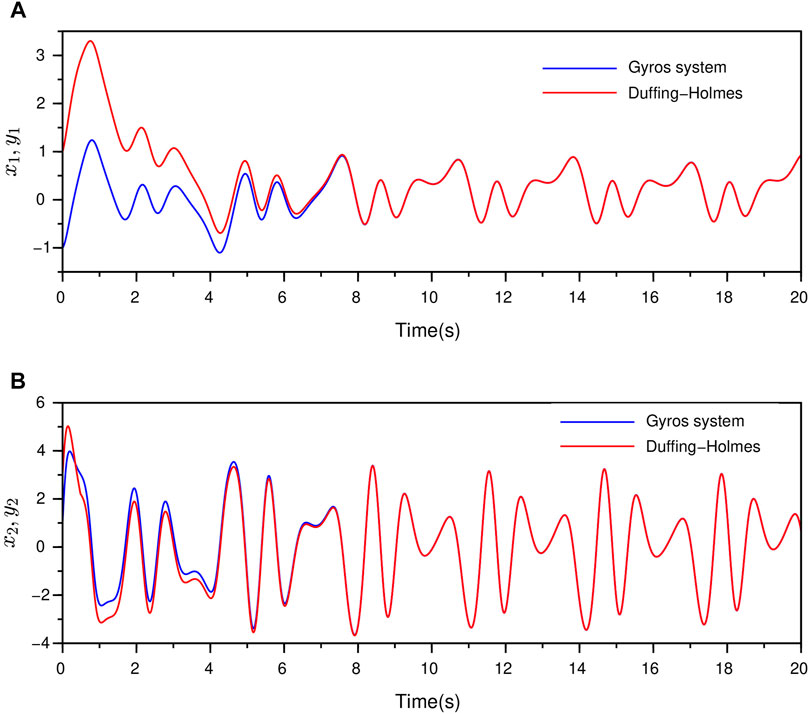
FIGURE 3. Synchronization between the Gyros and the Duffing-Holmes systems in Example 1 by NTSM controller (A) the synchronization between $x_1$ and $y_1$(B) the synchronization between $x_2$ and $y_2$.

FIGURE 4

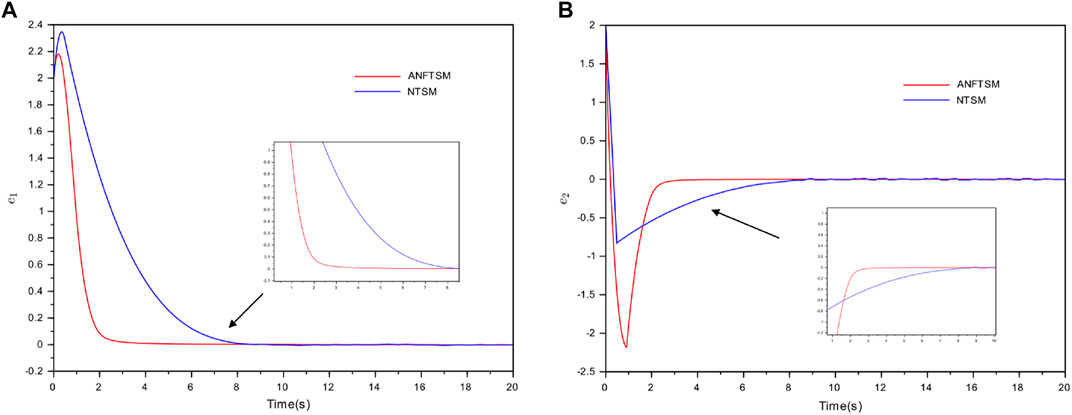
FIGURE 4. The comparison of synchronization errors between ANFTSM and NTSM of Example 1 (A) the synchronization error $e_1$(B) the synchronization error $e_2$.

FIGURE 5

FIGURE 5. Sliding surface for Example 1.

FIGURE 6

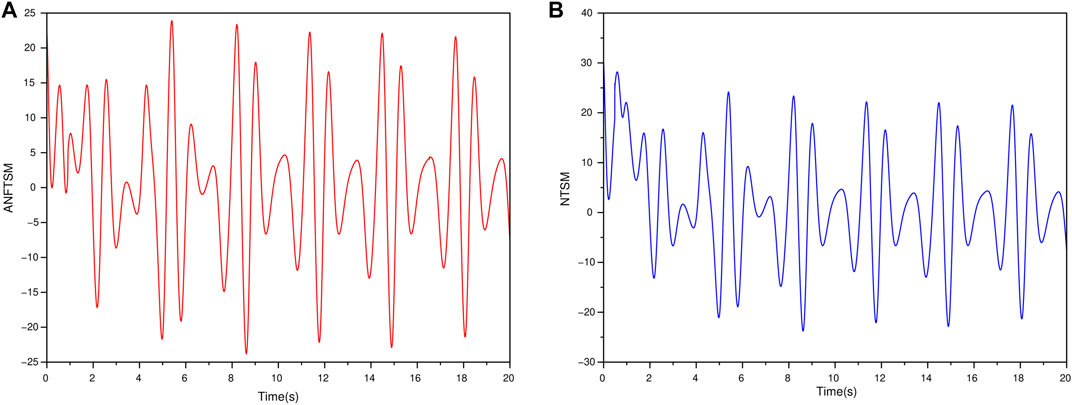
FIGURE 6. The time response of the design controller $u\left(t\right)$ in Example 1 (A) the ANFTSM controller (B) the NTSM controller.

Furthermore, the upper bound of the settling time of finite-time synchronization seems to get smaller by adjusting the parameters of the ANFTSM controller as shown in Table 1. Note that, to get a smaller value of settling-time, the parameters $k_1$and $k_2$ should be increased and γ should be sufficiently small. Nonetheless, adjusting parameters $k_1,k_2$ and γ may cause an undesired chattering phenomenon.

Example 2

TABLE 1

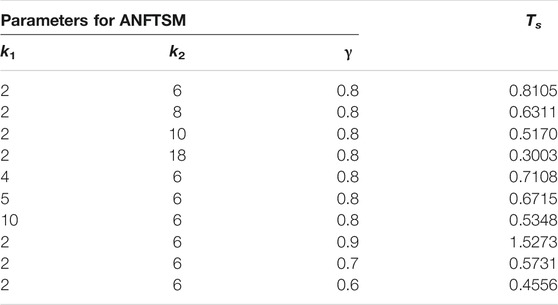
TABLE 1. Upper bounds of settling-time for ANFTSM controller with various parameter values for Example 1.

In this example, synchronization problem between the Duffing-Holmes system and the power system by using ANFTSM controller are considered. For this propose, we take the system (13) as the master system and the system (15) as the slave system. For simulation purpose, the nonlinear function is chosen as

$\begin{array}{l}g\left(y,t\right)=-p_1{y}_1-p_2{y}_2-y_1^3+h\cos \left(\omega t\right),\\ f\left(x,t\right)=a\sin \left(x_1\right)-b{x}_2+c.\end{array}$

The uncertain function of the system is chosen as $\text{Δ}f=-0.1\text{sin}\left(x_2\right)$ and the external disturbance is chosen as $v=F\text{cos}\left(\lambda t\right)$. The system parameters are chosen as $p_1=1,p_2=0.25,h=0.3,q=0.95,\omega =1,\text{Δ}f\left(x,t\right)=-0.1\text{sin}\left(x_2\right)$ and $d\left(t\right)=0.3\text{cos}\left(5t\right)$, $a=1,b=0.02,c=0.2,F=0.2593$ and. $\lambda =\mathrm{0.0174.}$

To achieve the finite-time synchronization, the parameters of the nonsingular fast terminal sliding surface (6) are chosen as $k_1=2$ and $k_2=8$ and $\gamma =0.8$. The adaptive law β is chosen to satisfy $\dot{\beta }=\overline{\beta }\left|s\left(t\right)\right|$ with $\overline{\beta }=2$ and the initial condition $\beta \left(0\right)=1.994$. It may be shown that the upper bound ${\beta }^{\text{*}}$ satisfies ${\beta }^{\text{*}}\le 11$. From which, it follows from Theorem 3.2 that the synchronization errors $e_1\left(t\right)$ and $e_2\left(t\right)$ in sliding mode converge to zero in finite time $T_s\le 0.5041$.

The parameters of NTSM are selected as $\kappa =0.5$ and $\alpha =1.25$. The initial conditions of the Duffing-Holmes and the Power systems are chosen as $\left[y_1\left(0\right),y_2\left(0\right)\right]=\left[\mathrm{1,3}\right]$ and $\left[x_1\left(0\right),x_2\left(0\right)\right]=\left[0.43,0.003\right]$, respectively.

For comparison purpose, we consider the NTSM controller which was considered in ([10]) with sliding surface given by $s=e_1+\kappa |e_2{|}^{\alpha }sign\left(e_2\right)$ with $\kappa =3$ and $\alpha =1.4$. The comparisons of the performance between ANFTSM and NTSM controllers are demonstrated in Figures 7–11. Figures 7, 8 show that the Duffing-Holmes system and the power system are finite-time synchronized by using the ANFTSM and the NTSM controllers, respectively. From Figure 9, it can be seen that by using the ANFTSM, the synchronization errors converge to zero faster than using the NTSM controller. Figure 10 shows the time response for the sliding surface which can be seen that by using the proposed ANFTSM controller, the sliding surface converges to zero faster than using the NTSM controller. The time responses of the ANFTSM and NTSM controllers are shown in Figure 11. Similar to a discussion given in Example 4.1, the settling time may be reduced by adjusting the parameters of the ANFTSM controller as shown in the Table 2; namely $k_1$ and $k_2$ should be increased while γ should be sufficiently small. However, by adjusting parameter $k_1$, $k_2$, and γ may cause an undesirable chattering phenomenon.

FIGURE 7

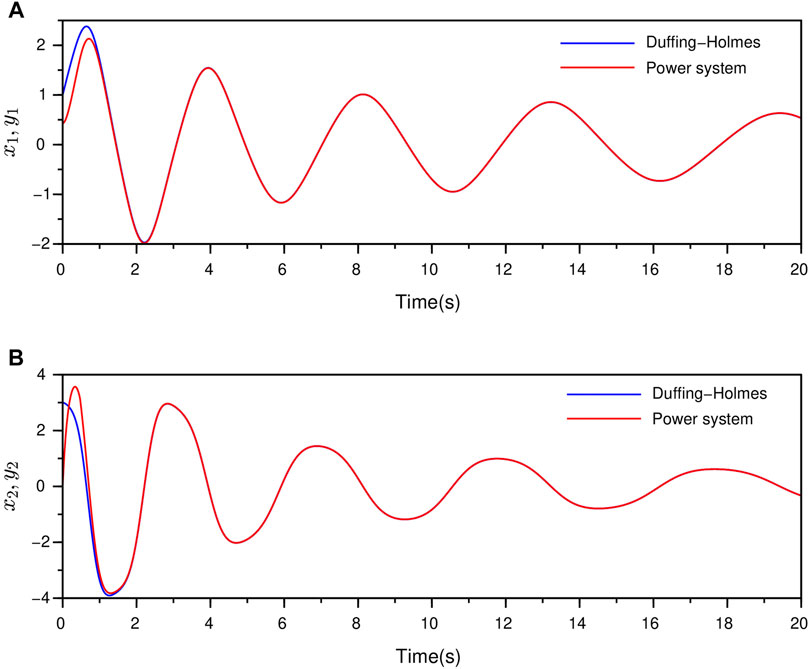
FIGURE 7. Synchronization the Duffing-Holmes and the Power systems in Example 2 by ANFTSM controller (A) the synchronization between $x_1$ and $y_1$(B) the synchronization between $x_2$ and $y_2$.

FIGURE 8

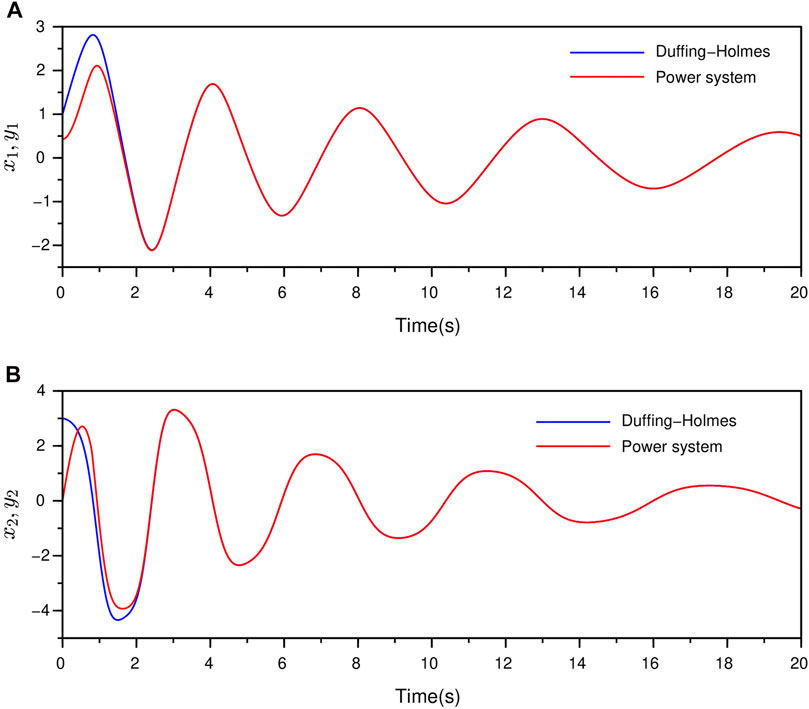
FIGURE 8. Synchronization between the Duffing-Holmes and the Power systems in Example 2 by NTSM controller (A) the synchronization of $x_1$ and $y_1$(B) the synchronization between $x_2$ and $y_2$.

FIGURE 9

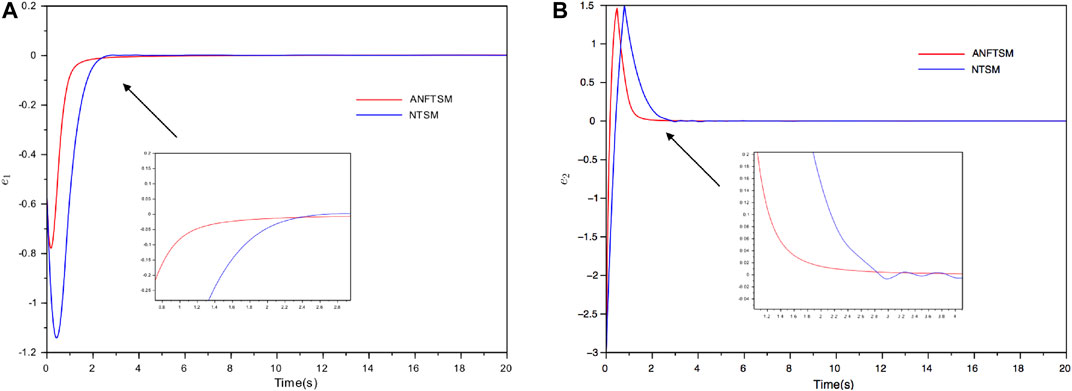
FIGURE 9. The comparison of synchronization errors between the ANFTSM and NTSM in Example 2 (A) the synchronization error $e_1$(B) the synchronization error $e_2$.

FIGURE 10

FIGURE 10. Sliding surface for Example 2.

FIGURE 11

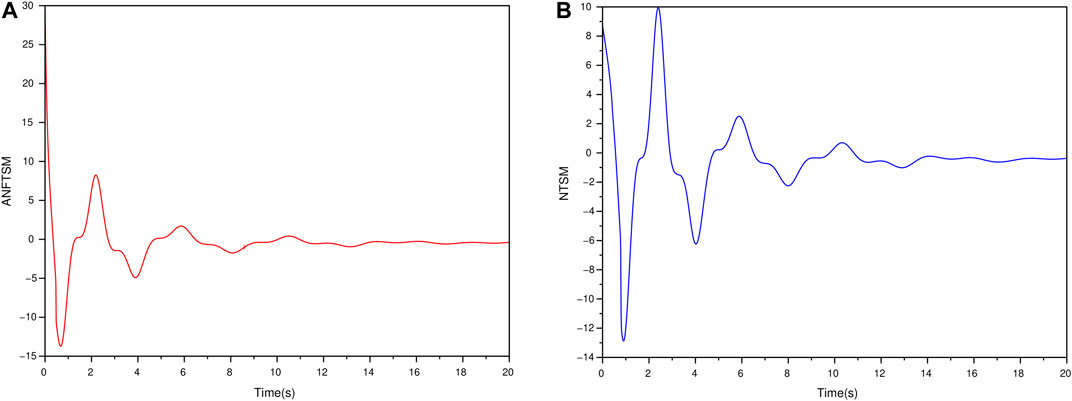
FIGURE 11. The time response of the design controller $u\left(t\right)$ in Example 2 (A) ANFTSM controller (B) NTSM controller.

TABLE 2

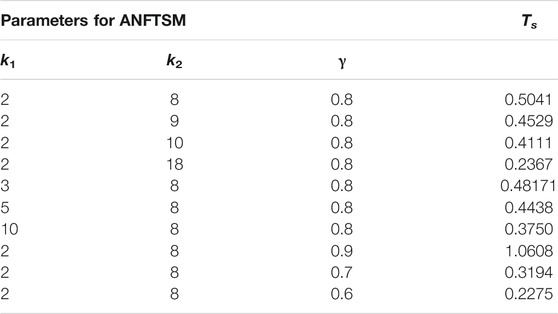
TABLE 2. Upper bounds of settling-time for ANFTSM controller with various parameter values for Example 2.

Remark 3.2: It is worth mentioning that, by using the SMC controller scheme, an unwanted chattering phenomena may occur due to discontinuity of the control law, see [8] and references cited therein. There are several studies on how to alleviate this phenomenon of undesirable chattering, see [14]. In this work, we have focused mainly on a design of ANFTSM to achieve synchronization of two different chaotic systems in which an undesirable chattering phenomenon might still occur as can be seen from Figure 6. It is a very interesting and challenging problem for handling the undesirable chattering phenomenon which is the main focus for our future investigation.

5 Conclusion

In this studied, an adaptive nonsingular fast terminal sliding mode (ANFTSM) control is developed to achieve the finite-time synchronization between two different chaotic systems with uncertain parameters and disturbances. Numerical results are given to demonstrate the effectiveness of the designed ANFTSM controller. Moreover, comparison of the performances between ANFTSM and NTSM controllers have been given which shows that ANFTSM controller gives a better performance than NTSM controller. Nonetheless, the proposed ANFTSM controller may cause an unwanted chattering phenomenon which is a main focus for our future investigation.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research is supported by Chiang Mai University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The first author thanks the Science Achievement Scholarship of Thailand (SAST) for financial support for her Ph.D. study. The authors express their sincere gratitude to the associate editor and reviewers for their valuable comments and suggestions which help to improve the quality of the paper.

References

1. Lin, J-S, and Yan, J-J. Adaptive Synchronization for Two Identical Generalized Lorenz Chaotic Systems via a Single Controller. Nonlinear Anal Real World Appl (2009) 10:1151–9. doi:10.1016/j.nonrwa.2007.12.005

CrossRef Full Text | Google Scholar

2. Chen, M, Zhou, D, and Shang, Y. A New Observer-Based Synchronization Scheme for Private Communication. Chaos, Solitons & Fractals (2005) 24:1025–30. doi:10.1016/j.chaos.2004.09.096

CrossRef Full Text | Google Scholar

3. Peng, C-C, Hsue, AW-J, and Chen, C-L. Variable Structure Based Robust Backstepping Controller Design for Nonlinear Systems. Nonlinear Dyn (2011) 63:253–62. doi:10.1007/s11071-010-9801-8

CrossRef Full Text | Google Scholar

4. Njah, AN. Synchronization via active control of parametrically and externally excited Φ6 Van der Pol and Duffing oscillators and application to secure communications. J Vibration Control (2011) 17:493–504. doi:10.1177/1077546309357024

CrossRef Full Text | Google Scholar

5. Zribi, M, Smaoui, N, and Salim, H. Synchronization of the Unified Chaotic Systems Using Sliding Mode Controller. Chaos, Solitons, and Fractals (2010) 42:3197–209. doi:10.1016/j.chaos.2009.04.051

Google Scholar

6. Bo, W, and Guanjun, W. On the Synchronization of Uncertain Master-Slave Chaotic System with Disturbance. Chaos, Solitons, and Fractals (2009) 41:145–51. doi:10.1016/j.chaos.20.7.11.019

Google Scholar

7. Zhao, Z-S, Zhang, J, and Sun, L-K. Sliding Mode Control in Finite Time Stabilization for Synchronization of Chaotic Systems. ISRN Appl Mathematics (2013) 2013:1–6. doi:10.1155/2013/320180

CrossRef Full Text | Google Scholar

8. Pooyan, AH, Ali, SSA, Saad, M, and Hemanshu, RP. Chattering-free Trajectory Tracking Robust Predefined-Time Sliding Mode Control for a Remotely Operated Vehicle. Automation Electr Syst (2020) 1–19. doi:10.1007/s40313-020-00599-4

Google Scholar

9. Xin, L, Wang, Q, and Li, Y. A New Fast Nonsingular Terminal Sliding Mode Control for a Class of Second-Order Uncertain Systems. Math Probl Eng (2016) 2016:1–12. doi:10.1155/2016/1743861

CrossRef Full Text | Google Scholar

10. Feng, Y, Yu, X, and Man, Z. Non-singular Terminal Sliding Mode Control of Rigid Manipulators. Automatica (2002) 38:2159–67. doi:10.1016/s0005-1098(02)00147-4

CrossRef Full Text | Google Scholar

11. Mohammad, P, Soharb, K, and Ghassem, A. Synchronization of Two Different Uncertain Chaotic Systems with Unknown Parameters Using a Robust Adaptive Sliding Mode Controller. J Common Nonlinear Sci Numer Simulation (2011) 16:2853–68. doi:10.1016/j.cnsns.2010.09.038

Google Scholar

12. Chang, C. Synchronization of Second-Order Chaotic Systems via Adaptive Terminal Sliding Mode Control with Input Nonlinearity. J Franklin Inst (2012) 349:2019–32. doi:10.1016/j.jfranklin.2012.03.01

Google Scholar

13. Ali, SA, Pooyan, AH, and Saad, M. Two Novel Approaches of NTSMC and ANTSMC Synchronization for Smart Gritd Chaotic Systems. Tech Econ smart grids Sustain Energ (2018), 3–14. doi:10.1007/s40866-018-0050-0

Google Scholar

14. Pooyan, AH, Ali, SA, Saad, M, and Hemanshu, RP. Two Novel Approaches of Adaptive Finite-Time Sliding Mode Control for a Class of Single-Input Multiple-Output Uncertain Nonlinear System. IET Cyber-systems and Robotics (2021) 1–11. doi:10.1049/csy2.12012

Google Scholar

15. Wang, H, Han, Z-Z, Xie, Q-Y, and Zhang, W. Finite-time Chaos Control via Nonsingular Terminal Sliding Mode Control. Commun Nonlinear Sci Numer Simulation (2009) 14:2728–33. doi:10.1016/j.cnsns.2008.08.013

CrossRef Full Text | Google Scholar

16. Mohammad, PA, Sohrab, K, and Ghassem, A. Finite-time Synchronization of Two Different Chaotic Systems with Unknown Parameters via Sliding Mode Technique. Appl Math Model (2011) 35:3080–91. doi:10.1016/j.apm.2010.12.020

Google Scholar

17. Yu, S, Yu, X, Shirinzadeh, B, and Man, Z. Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Mode. Automatica (2005) 41:1957–64. doi:10.1016/j.automatica.2005.07.001

CrossRef Full Text | Google Scholar

18. Juntao, F, and Huan, W. Experiment Investigation of Recurrent Nural Network Fractional-Order Sliding Mode Control of Active Power Filter. IEEE Trans Circuits Syst Express Briefs (2019) 1–5. doi:10.1109/tcsii.2019.2953223

Google Scholar

19. Juntao, F, and Zhilin, F. Fractional-order Finite-Time Super-twisting Sliding Mode Control of Micro Gyroscope Based on Double-Loop Fuzzy Neural Network. IEEE Trans Syst Man, Cybernetics: Syst (2020) 2168–216. doi:10.1109/tfuzz.2020.3012760

Google Scholar

20. Yunmei, F, Cuicui, A, Wanru, J, and Juntao, F. Adaptive H-Infinity Tracking Control for the Micro Gyroscope. Adv Mech Eng (2020) 12(6):1–9. doi:10.1109/tsmc.2020.2979979

Google Scholar

21. Junao, F, and Yun, C. Fuzzy Double Hidden Layer Recurrent Neural Terminal Sliding Mode Control of Single-phase Active Power Filter. IEEE Trans Fuzzy Syst (2020) 1–33. doi:10.1177/1687814020927832

Google Scholar

22. Li, L, Fang, T, Li, Z, and Li, R. Adaptive Terminal Sliding Mode Control for Anti-synchronization of Uncertain Chaotic Systems. Nonlinear Dyn (2013) 74(4):991–1002. doi:10.1007/s11071-013-1017-2

CrossRef Full Text | Google Scholar

23. Behjameh, MR, Delavari, H, and Vali, A. Global Finite-Time Synchronization of Two Nonlinear Chaotic Gyros Using High Order Sliding Mode Control. J Appl Comput Mech (2014) 1(1):26–34. doi:10.22055/jacm.2014.10549

Google Scholar

24. Wang, HO, Abed, EH, and Hamdan, AMA. Bifurcations, Chaos, and Crises in Voltage Collapse of a Model Power System. IEEE Trans Circuits Syst (1994) 41:294–302. doi:10.1109/81.285684

CrossRef Full Text | Google Scholar