- Department of Statistics, Florida State University, Tallahassee, FL, Unites States
This article develops an agent-level stochastic simulation model, termed RAW-ALPS, for simulating the spread of an epidemic in a community. The mechanism of transmission is agent-to-agent contact, using parameters reported for the COVID-19 pandemic. When unconstrained, the agents follow independent random walks and catch infections due to physical proximity with infected agents. Under lockdown, an infected agent can only infect a coinhabitant, leading to a reduction in the spread. The main goal of the RAW-ALPS simulation is to help quantify the effects of preventive measures—timing and durations of lockdowns—on infections, fatalities, and recoveries. The model helps measure changes in infection rates and casualties due to the imposition and maintenance of restrictive measures. It considers three types of lockdowns: 1) whole population (except the essential workers), 2) only the infected agents, and 3) only the symptomatic agents. The results show that the most effective use of lockdown measures is when all infected agents, including both symptomatic and asymptomatic, are quarantined, while the uninfected agents are allowed to move freely. This result calls for regular and extensive testing of a population to isolate and restrict all infected agents.
1 Introduction
There is a great interest in stochastic modeling and analysis of medical, economical, and epidemiological data resulting from the ongoing COVID-19 pandemic [1]. Until a large amount of infection, treatment, vaccination, containment, and recovery data from this pandemic become available, the community will have to rely primarily on simulation models to help assess situations and to evaluate countermeasures [2]. Naturally, simulation systems that follow precise mathematical and statistical models will play an important role in understanding this dynamic and complex situation [3]. There have been a large number of models proposed in the past literature, relating to the spread of epidemics through human contact or otherwise. They can be broadly categorized in two main classes (a more detailed taxonomy of simulation models can be found in [4]):
1. Population-Level, Deterministic, Dynamic Models: A large number of epidemiological models have focused on coarse, population-level summaries, that is, counts of infected (I), susceptible (S), removed or recovered (R), etc., whose evolutions are governed by deterministic differential equations. The original model of this type is the Susceptible-Infected-Removed (SIR) model [5], proposed by Kermack and McKendrick in 1927, that uses ordinary differential equations to model a constrained growth of the counts in those three categories. Since then, researchers have developed several advancements and variations of this model, including the SIRD model [6] given by
The scalar parameters β, γ, and µ together control the dynamics of infections, recovery, and mortality. The zero-sum condition
While they provide useful population-level summaries, these models do not generally focus on capturing spatial dynamics. Specifically, they do not explicitly model agent dynamics as residents move around in a community or across communities. Also, these models often provide deterministic outcomes, with no mechanism to incorporate randomness in the model. Several recent simulation models, focusing directly on the COVID-19 illness, also rely on such coarser community-level models [9].
2. Agent-Level Modeling: While dynamical evolutions of population variables are simple and effective, especially for the overall assessment, they do not take into account any social dynamics, human behavior, societal restrictions, and complexities of human interactions explicitly. The models that study these human-level factors and variables, while tracking disease at an individual level, are called agent-level models [10]. Here one models the mobility, health status, and interactions of individual subjects (agents) to construct an overall population-level picture in a bottom-up way. The advantages of agent-based models are that they are more detailed and one can vary the parameters of lockdown measures, such as social distancing, at a granular level to infer overall outcomes. Furthermore, these models have built-in stochastic components for agent motions, interactions, infections, and recoveries, thus enabling a more realistic simulation environment. Agent-based models have been discussed in several articles, including [4, 11–13] and so on. The importance of simulation-based analysis of epidemic spread is emphasized in Ref. [14] but with a focus on infection models within a host. Ref. [12] constructed a detailed agent-based model for spread of infectious diseases, taking into account population demographics and other social conditions, but they did not consider countermeasures such as lockdowns in their simulations. A broad organization of different agent-based simulation methods has been presented in Ref. [4]. A recent article [15] studies the socioeconomic impact of social distancing using agent-based models. Although there are numerous other articles on the topic of agent-based simulations for simulating the spread of infections, we have only listed the most relevant ones.
In this article, we develop a mathematical simulation model, named RAW-ALPS, to simulate the spread of an infectious disease, such as COVID-19, in a confined community and to study the influence of some external interventions on outcomes. Since RAW-ALPS is purely a simulation model, the underlying assumptions and choices of statistical distributions for random quantities become critical in its success. On the one hand, it is important to capture the intricacies of the observed phenomena as closely as possible, using sophisticated modeling tools. On the other hand, it is desirable to keep the model efficient and tractable (for individual laptops) by using simplifying assumptions. One can, of course, relax these assumptions and obtain more and more realistic models as desired, albeit with increased computational complexity.
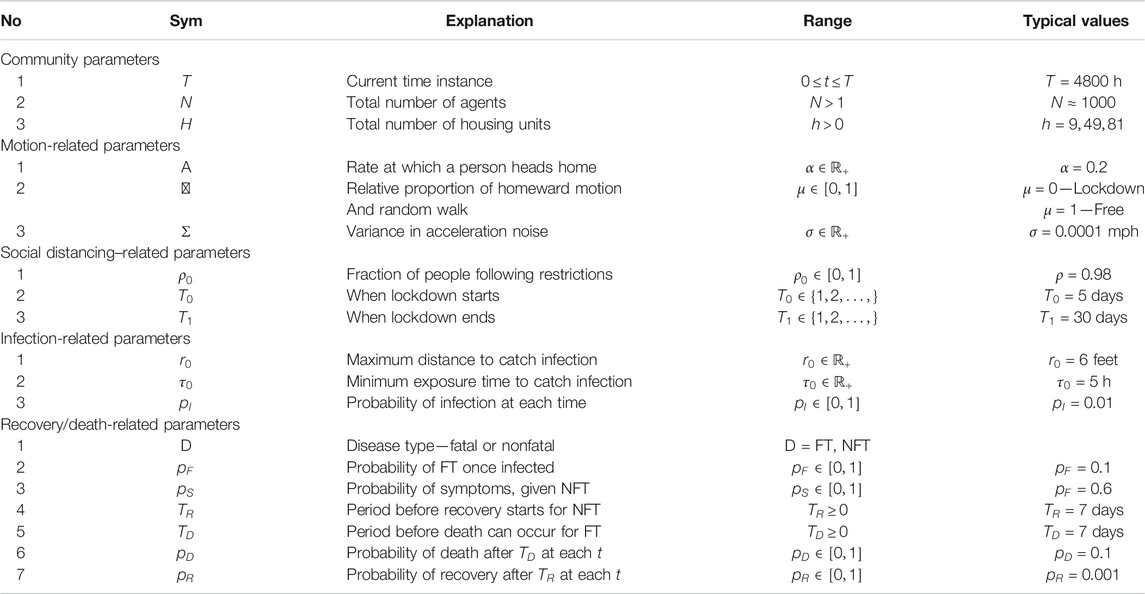
Simulation Setup: We assume a closed community with infection initiated by a single infected agent at the beginning. The infections are transmitted through physical exposure (proximity) of mobile susceptible agents to mobile infected agents, as shown in the middle panel of Figure 1. When unconstrained, the agents follow a smooth random-walk motion, independent of other agents (see the left panel of Figure 1). When instructed to enter lockdown, an agent moves toward his/her allocated household unit and stays put until the restrictions are imposed. The households are arranged, so that they are equally spaced at the grid points of a square domain (see the right panel of Figure 1).
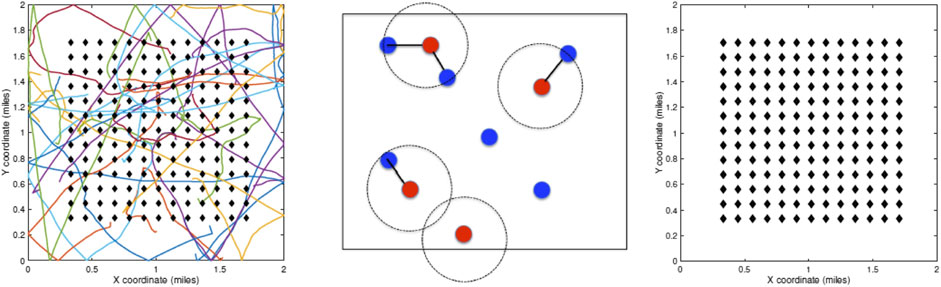
FIGURE 1. Left: random walk model for agent motions. Middle: proximity-based spread of infections from infected to susceptible agents. Right: layout of households on a square grid in the center of the domain.
An agent’s health situation follows the chart shown on the left side of Figure 2. Susceptible agents become infected when exposed to infected agents, with a certain probability. The infected agents go through a period of sickness, with two eventual outcomes—full recovery for most and death for a small fraction. That is, one starts as noninfected or susceptible, potentially gets infected with a certain probability, and later recovers or dies according to their event probabilities. Those with nonfatal infections are further labeled as symptomatic or asymptomatic agents. Naturally, agents with fatal outcomes are labeled as symptomatic. This labeling allows for the selective imposition of lockdown measures on a subset of the population. Once recovered, we assume that the agents can no longer be infected, as suggested by the CDC FAQ [16]. The social dynamical model used here is based on a fixed domicile, that is, each agent has a fixed housing unit. Under unrestricted conditions, that is, no lockdown, the agents are free to move over the full domain using a simple motion model. These motions are independent across agents and encourage smooth paths. Under lockdown conditions, the required agents head directly to their housing units and generally stay there during that period. The remaining agents, including a small fraction of agents, termed essential workers, are allowed to move freely under the restrictions. The infected agents under lockdown can only infect other susceptible agents living in the same household and not the general public, as shown on the right side of Figure 2. Similarly, mobile infected agents can only infect other mobile agents but not those under the lockdown. Three types of lockdowns are considered: 1) lockdown of the full population or LD1, 2) lockdown of infected agents or LD2, and 3) lockdown of symptomatic agents or LD3.
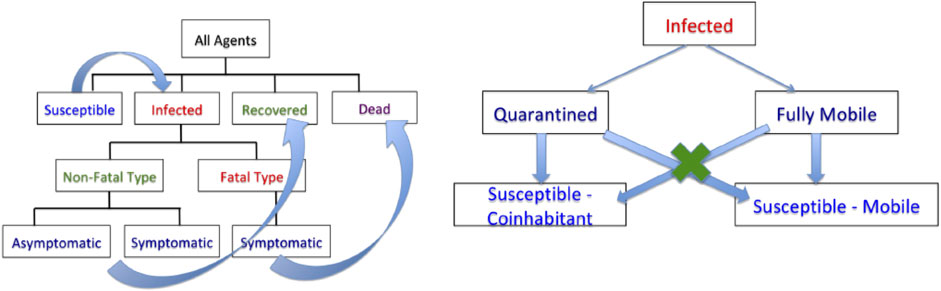
FIGURE 2. Left: flow chart for evolution of infection dynamics for the population. Right: scheme for infection of susceptible agents from infected agents.
The main highlights and contributions of this article are as follows: 1) agent-level transmission of infections and thus, a more granular analysis than (population-level) deterministic dynamical models, 2) random-walk motions of agents when unconstrained and restricted to households when under lockdowns, 3) different classifications of infections: fatal and nonfatal, with the latter being either symptomatic or asymptomatic, 4) selective lockdowns for different strata of the population, and 5) statistical quantifications of gains resulting from lockdown restrictions and their timings on infection rates.
The rest of this article is as follows. Random-Walk, Agent-Level Pandemic Simulation (RAW-ALPS) develops the proposed RAW-ALPS model, specifying the underlying assumptions and motivating model choices. It also discusses choices of model parameters and provides comparisons with the SIRD model. Exemplar Outcomes and Computational Cost presents some illustrative examples and discusses the computational complexity of RAW-ALPS, while Analyzing Effects of Lockdown Measures develops the use of RAW-ALPS in understanding the influences of countermeasures. The article ends by discussing model limitations and suggesting some future directions.
2 Random-Walk, Agent-Level Pandemic Simulation (RAW-ALPS)
In this section, we develop our simulation model for agent-level interactions and the spread of the infections. For this, we consider a population in a predetermined geographical domain. In terms of the model design, there are competing requirements for such a simulation to be useful. On the one hand, we want to capture detailed properties of agents and their pertinent environments, to render a realistic scenario for pandemic evolution. On the other hand, we want to keep model complexity reasonably low, to utilize it for analyzing variable conditions and countermeasures. Also, to obtain statistical summaries of pandemic conditions under different scenarios, we want to run a large number of simulations and compute averages. This process also requires keeping the overall model simple, from a computational perspective, to allow for multiple runs of RAW-ALPS.
2.1 Simplifying Assumptions
The overall setting of the simulation model is as follows. We assume that the community is located in a square geographical region D with h household units arranged centrally on a uniformly spaced square grid in D (see the right panel of Figure 1). We assume that there is a fixed number, say N, of total agents in the community (including all classifications—uninfected, infected, dead, etc.) and their health status updates every unit interval (e.g., 1 h), indexed by variable t. The unconstrained agents can traverse freely through all parts of D but are largely restricted to their home units under restrictions. Next, we specify some simplifying assumptions:
• Independent Agents: An agent’s movements and infection status are independent of those of other agents. The actual infection event is, of course, dependent on one being in close proximity to an infected carrier (within a certain distance, say ≈ 6 feet) for a certain exposure time. But the probability of an agent being infected is independent of such events for other agents.
• Full Mobility in Absence of Restrictive Measures: As mentioned above, we assume that each agent is fully mobile and moves across the domain freely when no restrictive measures have been imposed. In other words, there is no effect of an agent’s age, gender, or health on his/her mobility. Also, we do not impose any day/night schedules on the motions. Some articles, including [17], provide two- or three-state models where the agents transition between some stable states (home, workplace, shopping, etc.) in a predetermined manner. To implement such detailed models requires careful considerations about the daily movement patterns of agents, and that increases model complexity.
• Homestay During Restrictive Measures: We assume that most agents comply with instructions and stay at home at all times during the lockdown conditions. Only a small percentage (set as a parameter
• Sealed Region Boundaries: In order to avoid complications resulting from a transportation model in the system, we assume that there is no transfer of agents into and out of the region D. The region is modeled to have reflecting boundaries to ensure that all citizens stay within the region. The only way the population of D can be changed is through death.
• Fixed Domicile: The whole community is divided into a certain number of living units (households or buildings). These units are placed in square blocks with uniform spacing. Each agent has a fixed domicile at one of the units. During a lockdown period, the agents proceed to and stay at home with a high compliance level. We assume that all agents within a domicile unit are exposed to each other, that is, they are in close proximity and can potentially infect others.
• No Reinfection: We assume that once a person has recovered from the disease, he/she cannot be infected again for the remaining observation period. While this is an important unresolved issue for the current COVID-19 infections, it has been a valid assumption for the past coronavirus infections and it remains the current CDC guideline [16].
• Single Patient Ground Zero: The infection is introduced in the population using a single carrier, termed patient ground zero at time t = 0. This patient is selected randomly from the population and the time t is measured relative to this initial event.
• Constant Immunity Level: The probability of infection of agents, under the exposure conditions, remains the same over time. We do not assume any increase or decrease in an agent’s immunity level over time. Also, we do not assign any age or ethnicity to the agents and all agents are assumed to have equal immunity levels.
2.2 Model Specifications
There are several parts of the model that require individual specifications. These parts include modeling the movements of each agent (with or without restrictions in place), the mechanisms of transmitting infections from agent to agent, and the processes of recovery and fatality for infected agents. A full listing of the model parameters and some typical values are given in Table A1 in the Appendix.
• Motion Model: The movement of an agent follows a simple random-walk model where the instantaneous velocity
Using mathematical notation, the model for instantaneous position
Here
Reflecting Boundaries: When a subject reaches the boundary of the domain D, the motion is reflected, and the motion continues in the opposite direction.
Figure 3 shows examples of random agent motions under different simulation conditions. The leftmost panel shows a situation with no lockdown and the agents are moving freely according to Eq. 2. The middle panel shows the case where the restrictions are imposed on Day 10 and stay in place after that. The last panel shows the case where a lockdown is imposed on Day 10 and then lifted on Day 20. The blue curves represent free motion before a lockdown, the red denotes motion toward home during a lockdown, and the green represents free motion again after the lockdown is lifted.
• Lockdown Model: Once the lockdown starts, at time say
where
• Exposure–Infection Model: Infection of a susceptible agent depends on the level of exposure to an infected agent, irrespective of the infected agent being symptomatic or not. Recall that mobile infected agents can only infect other mobile agents, while agents in a lockdown can only infect agents in the same household. To create the conditions for the spread of infection:
• The physical distance between the susceptible agent and the infected agent during exposure should be less than
• The exposure time in terms of the time units is at least
• Under these conditions, the probability of being infected at each time t is an independent Bernoulli random variable with probability
• Recovery–Death Model: Once a subject is infected, we randomly assign a label or infection type immediately. Either an infected agent is going to recover (nonfatal type, or NFT) or the person is eventually going to die (fatal type, or FT). The probability of having a fatal type, given that a person is infected, is
• Recovery: An agent with a nonfatal type (NFT) is sick for a period of
• Fatality: An agent with a fatal type (FT) is sick for a period of
FIGURE 3. Sample agent motions under different conditions. Blue curves denote unrestricted movements, red curves denote movement toward home units during a lockdown, and green curves denote movement after lockdown.
2.3 Chosen Parameter Values
A complete listing of the ALPS model parameters is provided in Appendix Table A1. In this section, we motivate the values chosen for those parameters in these simulations. We justify these choices from the current reports of the COVID-19 pandemic. As argued in [18], a realistic choice of parameters is very important in establishing the validity of simulation models.
• Population Density: We use a square domain D of size
The time unit for updating configurations is 1 h and the occurrence of major events is specified in days. For example, the lockdown can start on Day 1 and end on Day 30.
• Agent Speeds: The standard deviation for accelerations, denoted by σ, in agent mobility are approximately 1–5 feet/h (fph). Through integration over time, this results in agent speeds up to 1,000 fph. We assume that
• Infection Rates: The physical distance between agents to catch infection should be at most
• Fatality Rate: Once infected, the probability of having a fatal outcome is set at 5–10%, according to the mortality rate listed by the CDC [21]. The period of recovery for agents with nonfatal outcomes starts at 7 days. The probability of reaching full recovery for those agents is
• Asymptomatic Infected Agents: The percentage of infected agents who remain asymptomatic is set to be in the range of 15–40% [22, 23]).
Figure 1 provides a pseudocode for the RAW-ALPS algorithm.
2.4. Model Validation
Although RAW-ALPS is perhaps too simple model to capture the intricate dynamics of an actual active society, it does provide an efficient tool for analyzing effects of countermeasures during the spread of a pandemic. Before it can be used in practice, there is an important need to validate it in some way.
As described in Ref. [4], there are several ways to validate a simulation model. One is to use real data (an observed census of infections over time) in a community to estimate model parameters, followed by a statistical model testing. While such data may emerge for COVID-19 in the future (especially with the deployment of tracking apps in many countries), there are currently no such agent-level data available for COVID-19. The other approach for validation is to consider coarse population-level variables and their dynamics and compare them against established models such as SIR and its variations. We will perform validation of RAW-ALPS in two ways.
2.4.1. Qualitative Comparisons with SIR Model
As the first comparison, we study shapes of infection curves resulting from the RAW-ALPS model and compare them qualitatively to the shapes resulting from the SIR model. Figure 4 shows plots of the evolutions of global infection counts (susceptible, infected, and recovered) in a community under the well-known SIR model (on the left) and the proposed ALPS model (on the right). In the ALPS model, the counts for recovered and fatalities are kept separate, while in the SIR model, these two categories are combined. One can see a remarkable similarity in the shapes of the corresponding curves, and this provides a certain validation to the RAW-ALPS model. In fact, given the dynamical models of agent-level mobility and infections, one can derive the parameters of the population-level differential equations used in the SIRD model. We pursue this topic in the next section.
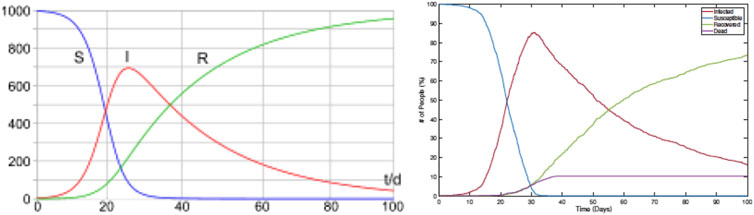
FIGURE 4. Evolution of population-level infection measurements under a typical SIR model (left) (source: Wikipedia) and the RAW-ALPS model (right). Visually, the RAW-ALPS model can generate infection curves with shapes similar to those of the SIR model.
2.4.2 Estimation of SIRD Parameters
In this section, we use data simulated from RAW-ALPS to fit the SIRD model given in Eq. 1 and use estimated SIRD model parameters to provide interpretations. Rearranging equations in the SIRD model (Eq. 1), we get the instantaneous values of the parameters:
Let
Since in our simulations we have a small population size (N), the number of dead agents becomes a constant soon after any changes are complete, making
Figure 5 shows an example of this estimation using data simulated from RAW-ALPS for an unrestricted situation. The left plot shows the evolution of
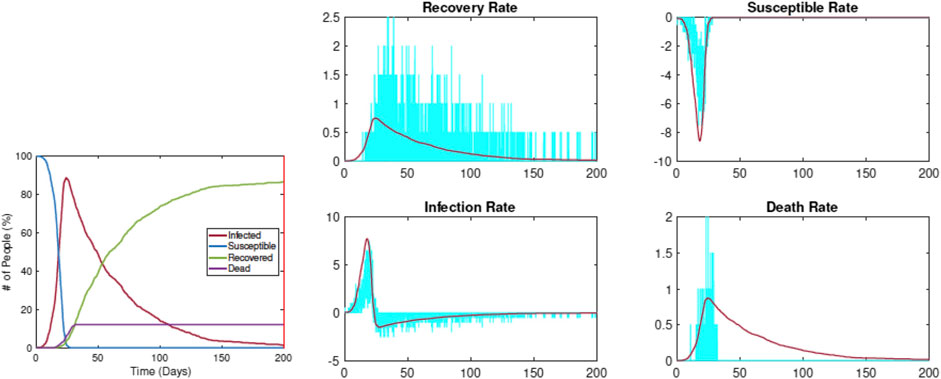
FIGURE 5. Estimation of SIRD parameters from data simulated by RAW-ALPS for an unconstrained spread. The pandemic curves generated by the SIRD model with estimated parameters match the RAW-ALPS output.
Figure 6 shows when the restrictions are imposed on Day 5. The left plot shows the evolution of
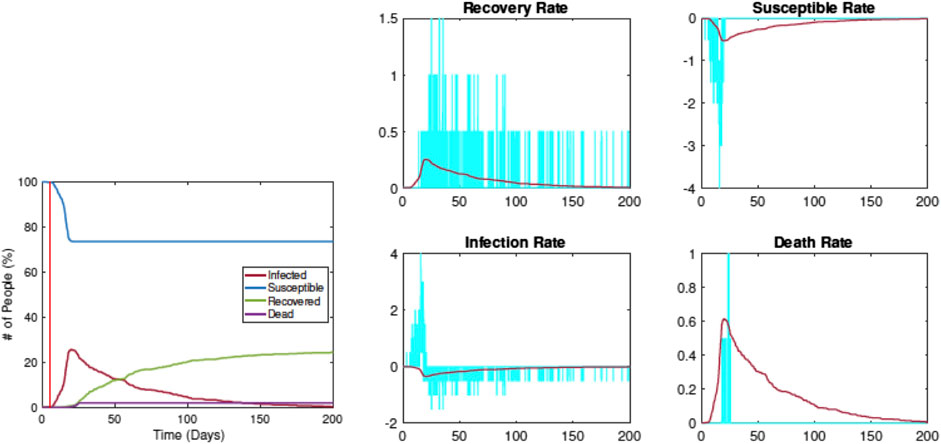
FIGURE 6. Estimation of SIRD parameters from data simulated by RAW-ALPS for the case when the restrictions are imposed on Day 5. Once again, the pandemic curves generated by the SIRD model with estimated parameters match the RAW-ALPS output.
Compared with the previous example, we see that the infection rate comes down significantly, from
3 Exemplar Outcomes and Computational Cost
We illustrate the use of the RAW-ALPS model by presenting some sample outcomes under some typical scenarios. Furthermore, we discuss the computational cost of running RAW-ALPS on a laptop computer.
3.1 Examples From RAW-ALPS
We start by showing sample outputs of RAW-ALPS under some interesting settings. In these examples, we use a relatively small number of agents (
1. Example 1—No Restrictive Measures: Figure 7 shows a sequence of temporal snapshots representing the community at different times over the observation period. In this example, the population is fully mobile over the observation period and no social distancing restrictions are imposed. The snapshots show the situations on Day 8, 17, 33, and 42. The corresponding time evolutions of global count measures
2. Example 2—Early Restrictions: In the second example, a lockdown of all the infected agents is introduced on Day 5 and these measures stay in place after that. The results are shown in Figure 8. Once again we show snapshots for situations on Day 8, 17, 33, and 42. The corresponding time evolutions of global count measures are shown in the bottom right panel. As the summary shows, an early restriction of lockdown is very effective in controlling the spread of the infection and the peak infection rate is minuscule at 3%.
3. Example 3—Early Restrictions but Removed Later: In the next example, a full lockdown or LD1 is introduced on Day 2 but removed on Day 30. The results are shown in Figure 9. In early snapshots, the population is under a lockdown and the spread is minimal. By Day 33, the lockdown is released, and the population is fully mobile. Consequently, the infection begins to spread again, and by Day 42, the infection reaches its peak value.
4. Example 4—Delay in Imposing Restrictions: In the last example, with results shown in Figure 10, a full lockdown (LD1) is introduced very late (on Day 10). In this simulation run, the infection rate reaches a peak value of 80% despite a lockdown. This is because the infection had already spread extensively in the population by the time the lockdown starts.
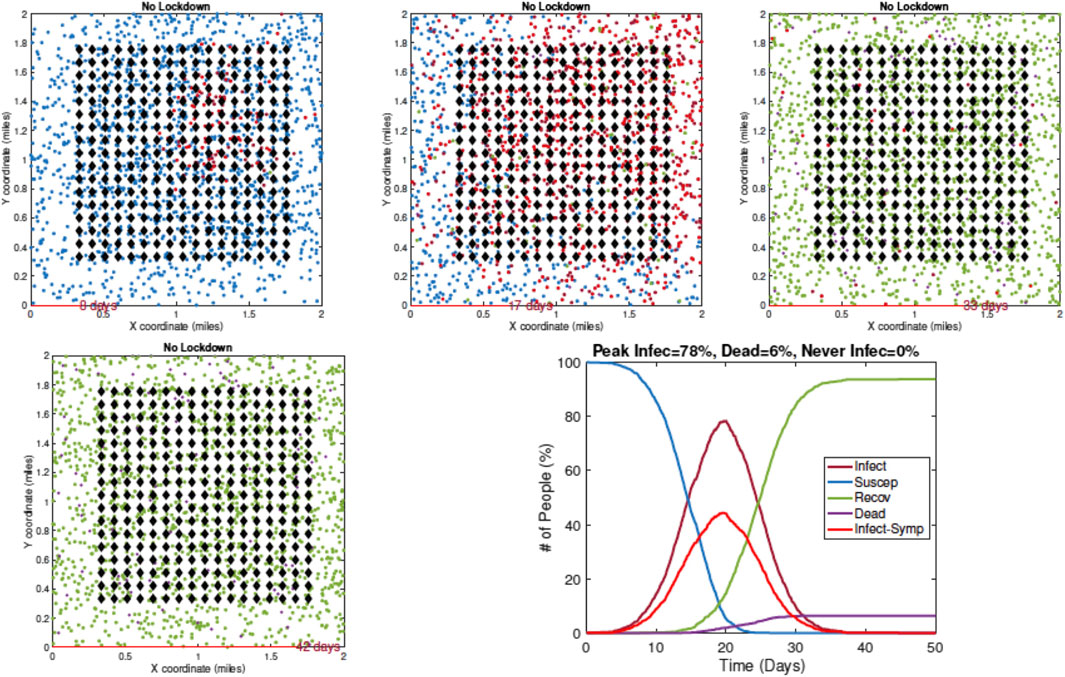
FIGURE 7. Example 1: model outputs at different times under no restrictive measures. Blue dots are susceptible agents, red dots are infected agents, green dots are recovered agents, and purple circles denote fatalities. The pandemic curves in the bottom right exhibit typical behavior of the RAW-ALPS model at the population level.
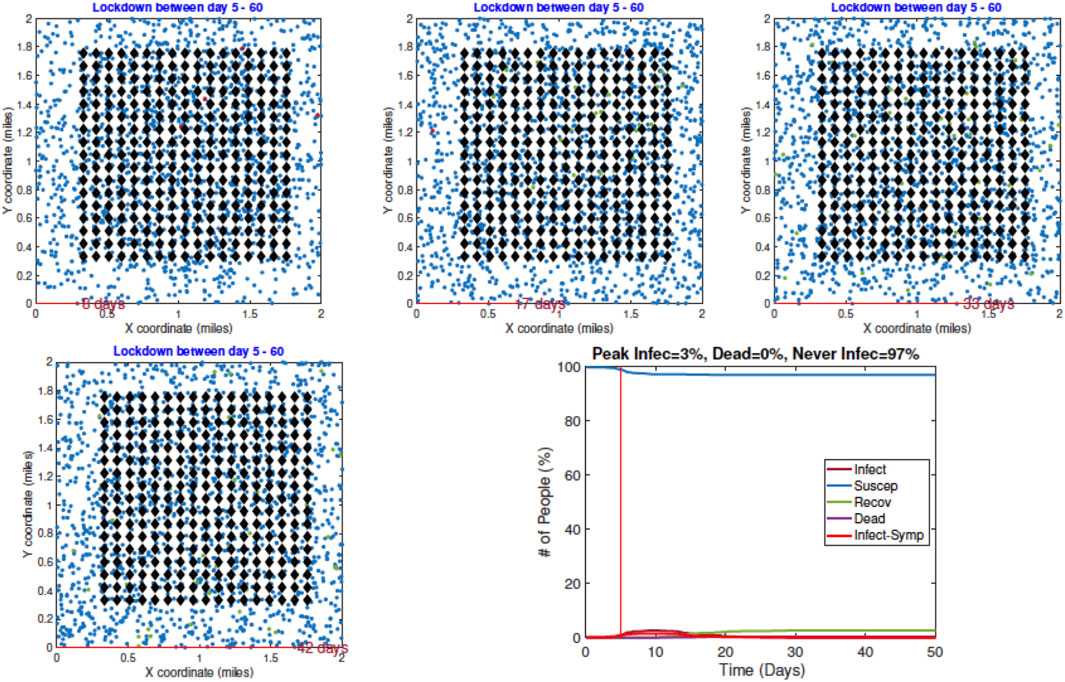
FIGURE 8. Example 2: displays of model outputs when a lockdown of infected people (LD2) is imposed on Day 5. The pandemic curves in the bottom right show a drastic reduction in infection due to the lockdown.
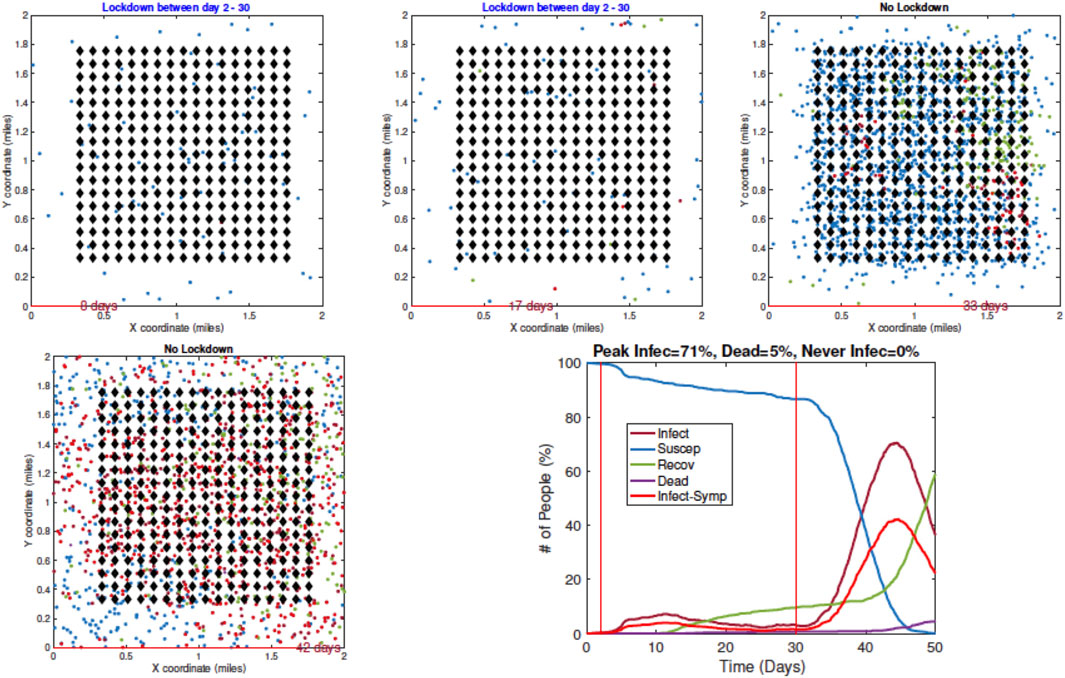
FIGURE 9. Example 3: model outputs when a full lockdown or LD1 is imposed on Day 2 and removed on Day 30. As seen in the plot of the resulting pandemic curves, the infection is controlled at first by the lockdown, but it spreads fast after the lockdown is lifted.
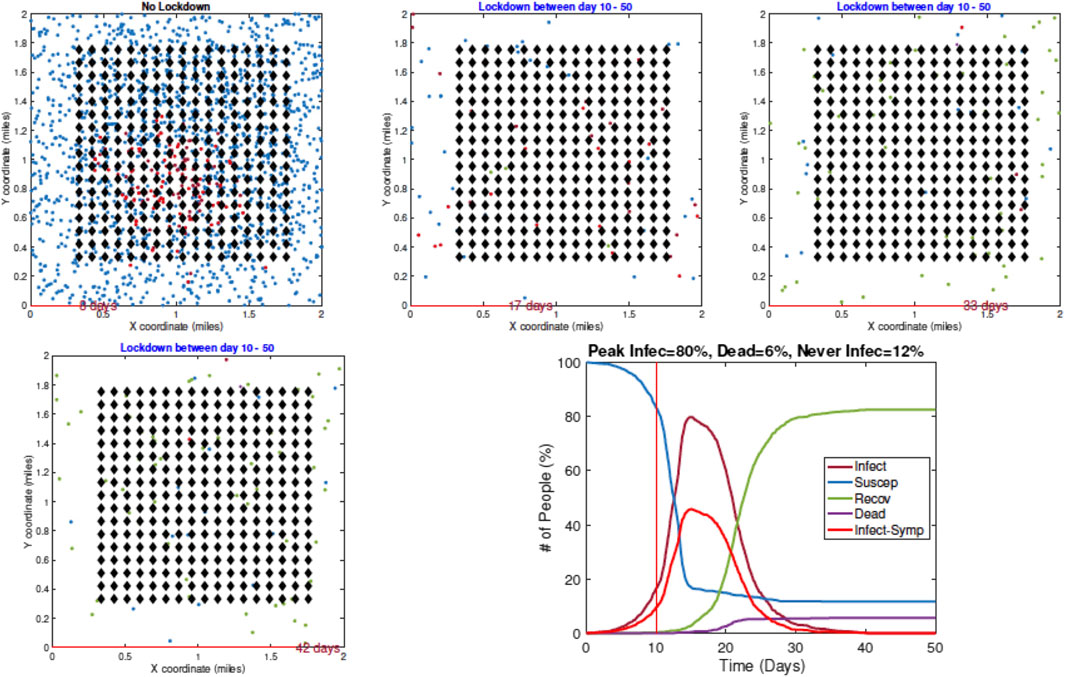
FIGURE 10. Example 4: model outputs when a full lockdown is imposed on Day 10. The pandemic curves show that the infection has spread widely in the community by the time a lockdown is imposed.
3.2. Computational Complexity
The main computational cost in the simulation comes from the need to update the following variables at each time t:
• locations of all agent according to their independent motion model;
• pairwise distance matrix between Susceptible agents and Infected agents; and
• infection status of each agent according to the infection dynamics.
In general, we obtain some efficiency by performing matrix operations, rather than using “for loops” for these updates across agents. Additionally, we increase speed by maintaining a list of neighborhoods for each agent and checking interactions only between the neighbors at each t.
Since the computational efficiency of the simulator is of vital importance, we study the computational cost of running RAW-ALPS for different variable sizes. In these experiments, we note the time taken by RAW-ALPS code on a MacBook Pro laptop with an Intel 2.8 GHz Core i7 processor and 16 GB memory. In Figure 11 we plot average run times (using five runs in a setting) of the code for different values of N, h, and T. Recall that h is the number of household units, N is the number of agents, and T is the period length. From these results, we see that the computational cost is linear in T, which makes sense. The computational cost is superlinear in N, keeping other variables fixed. This is because an increase in N represents a higher density and increased infection rates, thus requiring additional computations for tracking infected agents. Interestingly, for the range of parameter values studied here, the computational cost does not grow with an increase in h. As an aside, we note that for
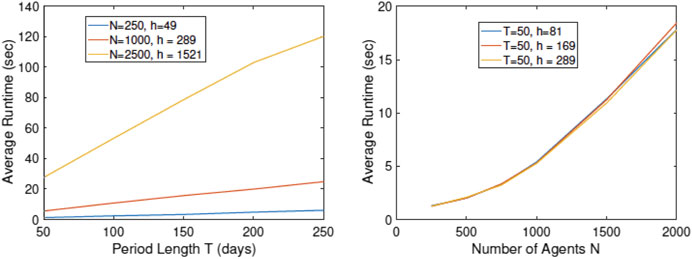
FIGURE 11. Plots of run times vs. simulation parameters T, N, and h. The algorithmic cost is linear in T but superlinear in N.
4 Analyzing Effects of Lockdown Measures
There are several ways to utilize this model for prediction, planning, and decision-making. We illustrate some of these ideas using examples.
4.1 Timing of Imposition of Full Lockdown
First, we study the effect of time of a full lockdown on the epidemic infections. In the following simulations, we have used
Figure 12 shows examples of RAW-ALPS outputs when we impose a full lockdown on the community but at different times. From top to bottom, the plots show lockdowns starting on Day 2, Day 10, and Day 30, respectively, with the last row showing results for no lockdown. Once the restrictions are imposed, they are not removed in these examples. As expected, the best results are obtained for the earliest imposition of restrictions. In the case of no lockdown, the peak infection rate in the population ranges from 60 to 80%, which is very high for a community. The fraction of fatalities ranges from 6 to 8%, and the fraction of community that is never infected is zero in all runs. In case the restrictions are imposed on Day 2, with all other parameters held the same, there is a remarkable improvement in the situation. The peak infection goes down to 2–3%, the fatalities decrease to 0.1–0.2%, and the fraction of uninfected goes up to 98–99%. Thus, an early imposition of full lockdown measures helps significantly reduce infection in the community.
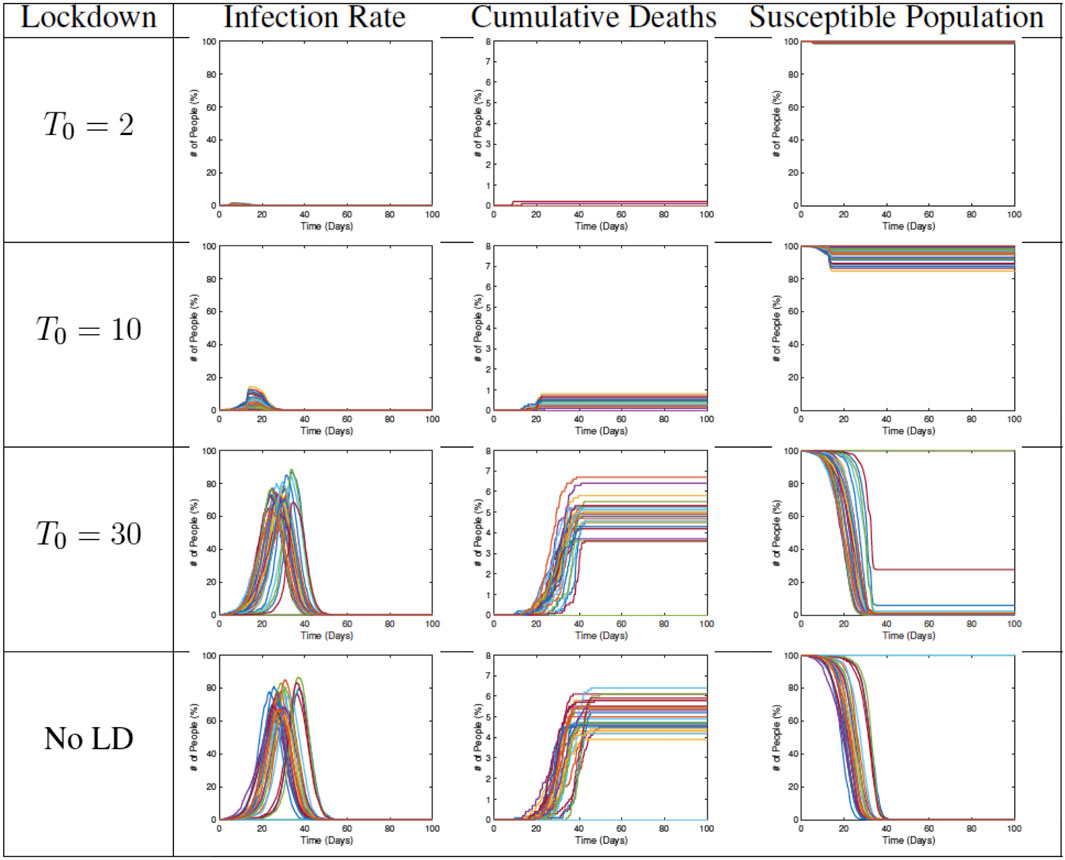
FIGURE 12. Results from RAW-ALPS runs for a full lockdown (LD1) starting at different times. Going from top to bottom, we impose lockdowns later and later. The effect of a lockdown diminishes significantly if the start of the lockdown is delayed.
4.2 Timing of Removal of Restrictions
In the next set of simulations, we study the effects of lifting restrictions and thus re-allowing full mobility in the community. Some sample results are shown in Figure 13. Each plot shows the evolution for a different end time
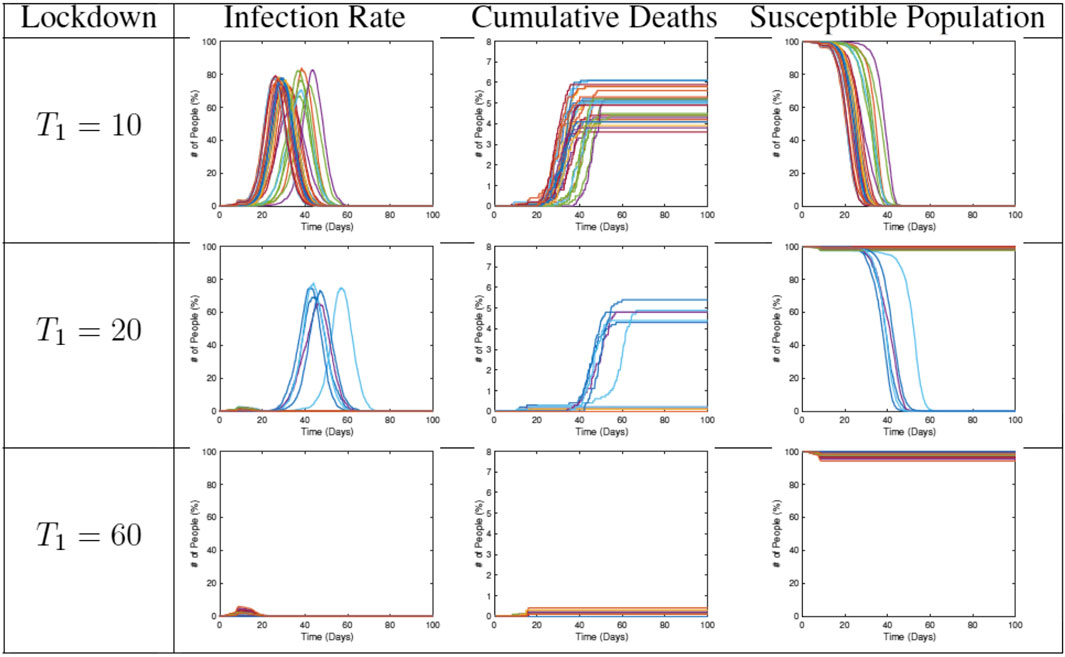
FIGURE 13. Results from RAW-ALPS runs for a full lockdown (LD1) ending at different times. Going from top to bottom, we keep the lockdowns for longer periods. A longer imposition of lockdown helps in reducing the spread of the epidemic.
4.3 Statistical Summaries
In the next set of experiments, we compute average values of some variables of interest using 30 runs of RAW-ALPS. In the first result, we study three variables—number of deaths, number of agents remaining uninfected, and the peak infection rate—using
Figure 14 shows box plots of these three variables against
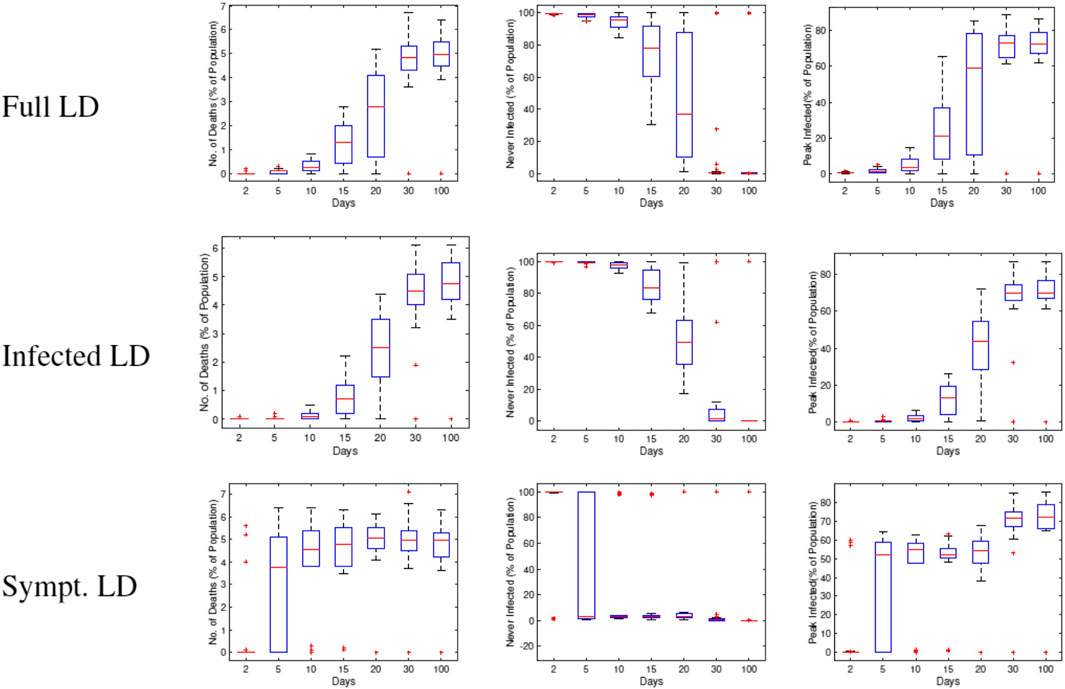
FIGURE 14. Statistical summaries of infection variables obtained using 30 runs of RAW-ALPS, plotted against the starting day of the lockdown. In all three lockdown types, a delay in imposing lockdown causes an increase in infections and casualties.
In Figure 15, we study the impact of changing
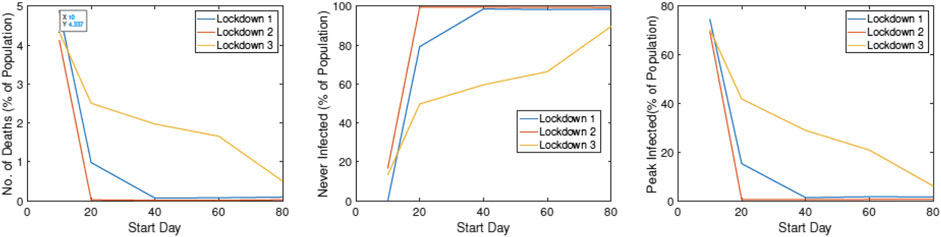
FIGURE 15. Statistical summaries of infection variables obtained using 30 runs of ALPS, plotted against
5 Discussion and Conclusion
This article develops an agent-based simulation model, called RAW-ALPS, for modeling the spread of an infectious disease in a closed community. Several simplifying yet reasonable assumptions make RAW-ALPS efficient and effective for statistical analysis. The model is validated at a population level by comparing it with the popular SIR model in epidemiology.
The results from RAW-ALPS show that a lockdown of only the infected agents (LD2) is the most effective kind. However, this includes both symptomatic and asymptomatic agents, with the latter ones not being easy to detect. This calls for regular and extensive testing of the population to isolate and restrict all infected agents while allowing for free movements of all uninfected agents. Furthermore, these results indicate that 1) early imposition of lockdown measures (right after the first infection) significantly reduces infection rates and fatalities; 2) lifting of lockdown measures recommences the spread of the disease, and the infections eventually reach the same level as that of the unrestricted community; and 3) in the absence of any extraneous solutions (a medical treatment/cure, a weakening mutation of the virus, or natural development of agent immunity), the only viable option for preventing large infections is the judicious use of lockdown measures.
The strengths and limitations of the RAW-ALPS model are the following. It provides efficient yet comprehensive modeling of the spread of infections in a self-contained community, using simple model assumptions. The model can prove very useful in evaluating costs and effects of imposing different types of social lockdown measures in a society. In the current version, the initial placement of agents is set to be normally distributed with means given by their home units and fixed variance. This variance is kept large to allow for near arbitrary placements of agents in the community. In practice, however, agents typically follow semirigid daily schedules of being at work, performing chores, or being at home. Thus, at the time of imposition of a lockdown, the agents can be better placed in the scenes according to their regular schedules, rather than being placed arbitrarily.
In terms of future directions, there are many ways to develop this simulation model to capture more realistic scenarios. 1) It is possible to model multiple, interactive communities instead of a single isolated community. 2) One can include typical daily schedules for agents in the simulations. A typical agent may leave home in the morning, spend time at work during the day, and return home in the evening. 3) It is possible to provide age demographics to the community and assign immunity to agents according to their demographic labels [24]. 4) As more data becomes available in the future, one can change immunity levels of agents over time according to the spread and seasons. 5) In practice, when an agent is infected, he/she goes through different stages of the disease, associated with varying degrees of mobility [13]. One can introduce an additional variable to track these stages of infections in the model and change agent mobility accordingly. 6) One can incorporate super spreader events in the model to help capture these mechanisms of transmission. 7) Finally, one can use the output of RAW-ALPS, in conjunction with techniques for the analysis of epidemic curves [25–27], to further adapt simulation parameters to a given community or region.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research was supported in part by the grants NSF DMS-1621787 and NSF DMS-1953087.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix: listing of alps parameters
Table A1 provides a listing of all the parameters one can adjust in ALPS to achieve different scenarios. It also provides some typical values used in the experiments presented in the article.
References
1. Bertozzi, AL, Franco, E, Mohler, G, Short, MB, and Sledge, D. The challenges of modeling and forecasting the spread of COVID-19. Proc Natl Acad Sci (2020). 117:16732–16738. doi:10.1073/pnas.2006520117
2. Adam, D. Special report: the simulations driving the world’s response to COVID-19. Nature (2020). 580 (7803):316–8. doi:10.1038/d41586-020-01003-6
3. Chao, DL, Halloran, ME, Obenchain, VJ, and Longini, JIM. FluTE, a publicly available stochastic influenza epidemic simulation model. Plos Comput Biol (2010). 6:e1000656. doi:10.1371/journal.pcbi.1000656
4. Hunter, E, Mac Namee, B, and Kelleher, JD. A taxonomy for agent-based models in human infectious disease epidemiology. J Artif Societies Soc Simulation (2017). 20. doi:10.18564/jasss.3414
5. Kermack, WO, and McKendrick, AG. A contribution to the mathematical theory of epidemics. Proc R Soc A (1927). 115:700–721. doi:10.1098/rspa.1927.0118
6. Osemwinyen, AC, and Diakhaby, A. Mathematical modelling of the transmission dynamics of ebola virus. Appl Comput Math (2015). 4:313–320. doi:10.11648/j.acm.20150404.19
7. Timpka, T, Eriksson, H, Gursky, EA, Nyce, JM, Morin, M, and Jenvald, J. Population-based simulations of influenza pandemics: validity and significance for public health policy. Bull World Health Organ (2009). 87:305–311. doi:10.2471/BLT.07.050203
8. Hao, X, Cheng, S, Wu, D, Wu, T, Lin, X, and Wang, C. Reconstruction of the full transmission dynamics of COVID-19 in wuhan. Nature (2020). 584:420–424. doi:10.1038/s41586-020-2554-8
9. Verity, R, and Okell, LC, Dorigatti, I, Winskill, P, Whittaker, C, and Imai, N. Estimates of the severity of coronavirus disease 2019: a model-based analysis. Lancet Infect Dis (2020). 20:P669–P677. doi:10.1016/S1473-3099(20)30243-7
11. Epstein, JM, and Axtell, RL. Growing artificial societies Social science from the bottom up. Cambridge, MA: MIT Press (1996).
12. Hunter, E, Namee, BM, and Kelleher, J. An open-data-driven agent-based model to simulate infectious disease outbreaks. PLoS ONE (2018). 13:e0208775. doi:10.1371/journal.pone.0208775
13. Perez, L, and Dragicevic, S. An agent-based approach for modeling dynamics of contagious disease spread. Int J Health Geographics (2009). 08:50. doi:10.1186/1476-072X-8-50
14. Nguyen, V, Mikolajczyk, R, and Hernandez-Vargas, E. High-resolution epidemic simulation using within-host infection and contact data. BMC Public Health (2018). 18. doi:10.1101/133421
15. Silva, PC, Batista, PV, Lima, HS, Alves, MA, Guimaraes, FG, and Silva, RC. COVID-ABS: an agent-based model of COVID-19 epidemic to simulate health and economic effects of social distancing interventions. Chaos Solitons Fractals (2020). 139:110088. doi:10.1016/j.chaos.2020.110088
16.Center for Disease Control. Clinical questions about COVID-19: questions and answers (2020). Available at:https://www.cdc.gov/coronavirus/2019-ncov/hcp/faq.html
17. Dunham, JB. An agent-based spatially explicit epidemiological model in MASON. J Artif Soc Soc Simul (2005). 9:1–3.
18. Gurdasani, D, and Ziauddeen, H. On fallability of smulations models in informing pandemic responses. Lancet Glob Health (2020). 8:E776–E777. doi:10.1016/S2214-109X(20)30219-9
19.Center for Disease Control. Contact tracing resources: resources for conducting contact tracing to stop the spread of COVID-19 (2020). Available at:https://www.cdc.gov/coronavirus/2019-ncov/php/open-america/contact-tracing-resources.html
20.Covid Volunteer Team. The COVID tracking project (2020). Available at: https://covidtracking.com/
21.Center for Disease Control. Coronavirus disease 2019 (COVID-19) (2020c). Available at: https://www.cdc.gov/coronavirus/2019-ncov/covid-data/covidview/index.html
22. Byambasuren, O, Cardona, M, Bell, K, Clark, J, McLaws, M-L, and Glasziou, P. Estimating the extent of asymptomatic COVID-19 and its potential for community transmission: systematic review and meta-analysis. medRxiv (2020). 10.1101/2020.05.10.20097543
23.Science News. Whole-town study reveals more than 40% of COVID-19 infections had no symptoms (2020). Available from: https://www.sciencedaily.com/releases/2020/06/200630103557.htm (Accessed September 2020).
24. Chang, SL, Harding, N, Zachreson, C, Cliff, OM, and Prokopenko, M. Modelling transmission and control of the COVID-19 pandemic in Australia. arXiv (2020).
25. Srivastava, A, and Chowell, G. Understanding spatial heterogeneity of COVID-19 pandemic using shape analysis qof growth rate curves. medRxiv (2020). doi:10.1101/2020.05.25.20112433
26. Srivastava, A, and Klassen, E. Functional and shape data analysis. New York, US: Springer (2016).
Keywords: COVID-19 simulations, random-walk models, lockdown measures, agent-level models, SIR model
Citation: Srivastava A (2021) Random-Walk, Agent-Level Pandemic Simulation (RAW-ALPS) for Analyzing Effects of Different Lockdown Measures. Front. Appl. Math. Stat. 7:638996. doi: 10.3389/fams.2021.638996
Received: 08 December 2020; Accepted: 16 February 2021;
Published: 28 April 2021.
Edited by:
Waleed Isa Al Mannai, New York Institute of Technology Bahrain, BahrainReviewed by:
Shuo Chen, University of Maryland, Baltimore, United StatesHalim Zeghdoudi, University of Annaba, Algeria
Copyright © 2021 Srivastava. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anuj Srivastava, YW51akBzdGF0LmZzdS5lZHU=
 Anuj Srivastava
Anuj Srivastava