Sequential Decision-Making in Ants and Implications to the Evidence Accumulation Decision Model

Cooperative transport of large food loads by Paratrechina longicornis ants demands repeated decision-making. Inspired by the Evidence Accumulation (EA) model classically used to describe decision-making in the brain, we conducted a binary choice experiment where carrying ants rely on social information to choose between two paths. We found that the carried load performs a biased random walk that continuously alternates between the two options. We show that this motion constitutes a physical realization of the abstract EA model and exhibits an emergent version of the psychophysical Weber’s law. In contrast to the EA model, we found that the load’s random step size is not fixed but, rather, varies with both evidence and circumstances. Using theoretical modeling we show that variable step size expands the scope of the EA model from isolated to sequential decisions. We hypothesize that this phenomenon may also be relevant in neuronal circuits that perform sequential decisions.

1 Introduction

The capacity to decide between multiple options is key to the survival of any organism. Typically, decision-making was studied in an isolated, “single-shot” context where the process ends once a first choice has been taken [1]. Under natural conditions, however, animals often diverge from this static description and exhibit dynamic behaviors where decisions change from time to time according to external conditions and internal states [2–7]. Sequential decision-making is particularly relevant to foraging behavior: Foragers in a patchy environment engage in an ongoing process wherein they continuously update their decision of whether to continue exploiting a dwindling patch or, rather, move on in search for more profitable locations [8–10]. Such decisions are often reflected in sharp transitions between local motions during exploitation and long-range displacements during exploration [11]. The strong links between foraging and decision-making suggest that models originally developed to describe isolated decisions may be extended to capture dynamic decisions in natural foraging contexts [4, 11, 12].

The “evidence accumulation” (EA) model [13] constitutes a central neuroscientific paradigm and is supported by empirical evidence on both the mechanistic and the behavioral levels [1, 14]. The model describes a single binary decision which relies on incoming evidence and priors. It aims to capture electrophysiological measurements that indicate that the moment of decision is proceeded by a rise in neuronal firing rates up to some fixed threshold. In the model, these firing rates are represented by an abstract “decision variable”, which integrates over the gathered evidence. As the evidence is typically noisy, the dynamics of this variable are approximated by a random walk. Asymmetric evidence which favors one decision over the other is modeled as a bias in this random walk and effectively makes the EA a drift-diffusion model. A decision is reached once the decision variable surpasses a given threshold [15, 16].

The EA model was originally developed to describe isolated, single-shot decisions. However, there is no apparent reason that the networks and firing patterns discovered in these studies do not play a part in more dynamic scenarios. Indeed, rising firing rates and decision thresholds that are compatible with this model show up in recordings from monkey brains confronted with dynamic, foraging-inspired tasks [4, 12]. Moreover, the EA model has been shown to provide a good approximation to C. elegans sequential decisions as it forages within a patchy environment [11]. The EA model is therefore found to be relevant in a broader set of scenarios than those it was originally aimed to describe. This motivates further empirical and theoretical work, aimed at the expansion and refinement of this basic conceptual model [17].

The capacity to make decisions is not unique to individual animals but, rather, carries over to group-living animals, which exhibit consensus choices that preserve group cohesion [18, 19]. Even more, by integrating over collectively available information, groups can reach decisions that are improved over those of its individual members [20–23]. Interestingly, there are many analogies between the decision-making mechanisms in animal groups and in the neuronal ensembles within the relevant decision-making areas in a single brain [24–27]. Among these analogies, the EA model has been shown to apply to consensus single-shot decisions taken by ants [28]. Here, we follow the decisions that ants take during a collective foraging task as an empirical means of revisiting the basic assumptions of the EA model in dynamic sequential scenarios and testing different modifications to this model [17].

We studied the decisions [29] taken by a group of ants engaged in cooperative transport of food to the nest [30, 31]. To do this, we confronted the ants with a binary choice within an environment that constitutes a physical realization of the abstract EA model. This was achieved by placing the load within a one-dimensional track with two decoy exits, one at each end. The decoy exits’ dimensions assure that while they serve as exits for individual ants they are too narrow to allow passage of the carried loads. Hence, in contrast to classical binary decision making protocols where a correct decision leads to immediate reward, in our case the decoy exits imply the withholding of reward. This induces a dynamic decision making process in which the cargo continuously alternates between the two possible choices. In the language of foraging theory, lingering near a decoy exit corresponds to exploitation while traveling the long distance between the two exits corresponds to an exploratory phase.

The ant behavior within the one-dimensional setup displays similarities to decision making processes by an individual animal. First, we demonstrate the emergence of a psychophysical Weber-like law [32] in this collective system. Second, we show that the motion of the carried cargo within the one-dimensional setup is highly reminiscent of dynamics of the EA model’s decision variable. Importantly, we identify a critical deviation between the ants’ behavior and classical EA dynamics that extends the scope of the evidence accumulation from isolated to sequential decisions. Namely, we find that incoming evidence controls not only the bias of the random motion but also its step size or persistence length. We further show how this correction emerges from an established microscopic model of the decisions taken by individual ants while engaged in cooperative transport [33] and hypothesize that similar corrections may be apparent in neuronal circuits involved in sequential decision making. Finally, we show how the ants’ behavior can occupy different regimes of decision-making space and theoretically argue that these correspond to differences in risk management.

2 Results

A Experimental Setup

We tracked Paratrechina longicornis ants as they collectively transport a large load toward their nest. Experiments included four load sizes with radii ranging from 0.2 cm and carried by a few individuals to 1.1 cm, carried by a few tens of ants (Supplementary Figure S1). To pare down the binary decision-making facet of this motion we confined the load to a long, rectangular cross section, channel (Supplementary Section S1) that has either one small exit at one of its ends or two identical exits, one at each end (Figure 1). The exits were designed to be narrow enough to deny passage of anything larger than an ant.

FIGURE 1

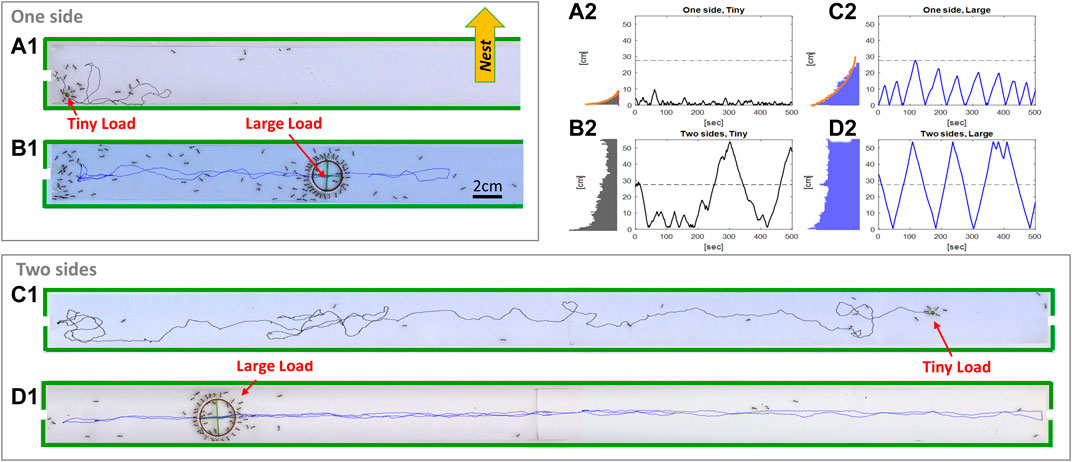
FIGURE 1. Experimental arena and sample trajectories. (A1–D1). Sample snapshots of the left half of a one exit experimental setup (A1,B1) and the two exit experimental setup (C1,D1), with loads of radii 1.1 [cm] (B1,D1) and 0.1 [cm] (A1,C1). Full lines indicate recent load trajectories. The direction to the nest is for all panels is indicated by the yellow arrow). (A2–D2). Sample time lines of loads position along the main channel axis. Numbering as above. A histogram of loads position is plotted to the left of each time line. Exponential fits (orange) are provided for the single-exit experiments.

We placed the channel near the entrance to the ants’ nest such that its long dimension was orientated perpendicular to the direction to the ants’ nest. In the two exit case, the channel was placed such that its two entrances were roughly at equal distances from the nest entrance. Experiments were initiated after a short recruitment stage in which we made sure that ants reach the load through all (i.e. either one or two) available exits. The ants’ immediate goal at this stage is to cooperatively transport the load and deliver it through one of the exits to the nest [33]. Since neither of the two exits allows the load to pass, the ants are, in practice, denied of achieving this goal.

We video taped the transport process for about 1 h at a rate of 25 frames per second. The resulting movies (see sample clip in Supplementary Video S1) were then analyzed to extract load location as a function of time (Figure 1), the occupation of the cargo by carrying ants (Supplementary Figures S2, S9, S11) and the net inward fluxes of ants through each of the two exits (Supplementary Figures S2, S3). For more details see Supplementary Section S2.

B General Motion Characteristics

We find that when only one entrance was open, the load spent most of the time in its near vicinity (Figures 1A1,B1). When the load did venture away from the entrance it traveled a random distance away, but once it changed its direction back toward the exit, it would usually travel all the way back (Figures 1A2,B2). This behavior is evident in the spatial distribution of the load location which is an exponential that decays with the distance from the exit (see histograms in Figures 1A2,B2). We find that the decay constant of this distribution grows with load size (Figure 2A), but is largely independent of the flux of ants through the single exit (see Supplementary Figure S6).

FIGURE 2

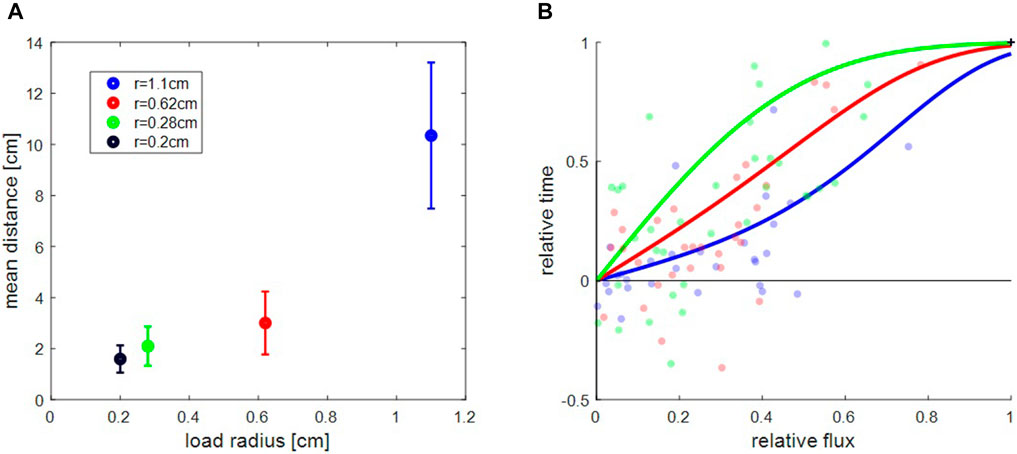
FIGURE 2. Global properties of collective motions. (A). Mean distance traveled toward closed side in one exit experiments as a function of load size. Presented values correspond to the length-scale of the exponential decay in the spatial distribution of the load away from the exit (Figures 1A1,B1). Error-bars represent standard error of the mean over, from largest object to the smallest one, $N=\mathrm{21,20,12}$ and six 15 min time windows. (B). In two exit experiments, the relative time, $T_{rel}=\left(T_H-T_L\right)/\left(T_H+T_L\right)$, i.e. the normalized difference between the time spent at the exit with the higher ant influx and that with lower influx, rises with the relative flux advantage of the majority entrance, $f_{rel}=\left(f_H-f_L\right)/\left(f_H+f_L\right)$. Curves are calculated theoretically for a run-and-tumble model (Supplementary Equations S56–S59), and rely on the exponential fits for the dependence of the turning probabilities (λ) on $f^{rel}$ (Figure 3A). Each experimental data point represents a 15 min window slice, where the filled circles represent two side experiments and the + symbols represent one side experiments. Color code as in panel (A).

In the experiments where both entrances were open to ants, when the load ventured away from one exit it would traverse longer distances, which often spanned the entire channel, to reach the opposite side (Figures 1C,D). Load motion, in these experiments, was more irregular for smaller loads which exhibited more frequent direction changes when compared to the larger loads (compare Figures 1C2,D2).

The influx of ants through the available exits ($f_H$ from the side with higher influx and $f_L$ from the side with lower influx) can be viewed as a proxy for the “evidence” in favor of approaching either one of the available exit routes. It is therefore interesting to check how the characteristics of the ants’ collective motion depend on these influxes. To do this we used the natural fluctuations that occur in the influx of ants within an experiment and in between experiments (Supplementary Figure S3). While these fluctuations average out over long time-scales, fluxes remain relatively stable over periods of $\sim 15$ min (Supplementary Figure S3, Supplementary Section S3). Therefore, throughout this work, we quantify the effect of ant flux on the characteristics of the collective motion by analyzing consecutive, non-overlapping 15 min time windows.

We found that, for all load sizes, the load tended to spend longer times near the exit with the higher ant influx (Figure 2B). We defined $T_H$ to be the fraction of time that the load spent near (i.e. within 10 cm) the exit through which there is higher ant influx, and $T_L$ the fraction of time near the exit with lower influx. The curves in Figure 2B are not fits to the measured data points, but are calculated theoretically using a run-and-tumble model (Supplementary Equations S56–S59), and rely on the exponential fits to the turning probabilities (λ) as function of $f^{rel}$ (Figure 3A).

FIGURE 3

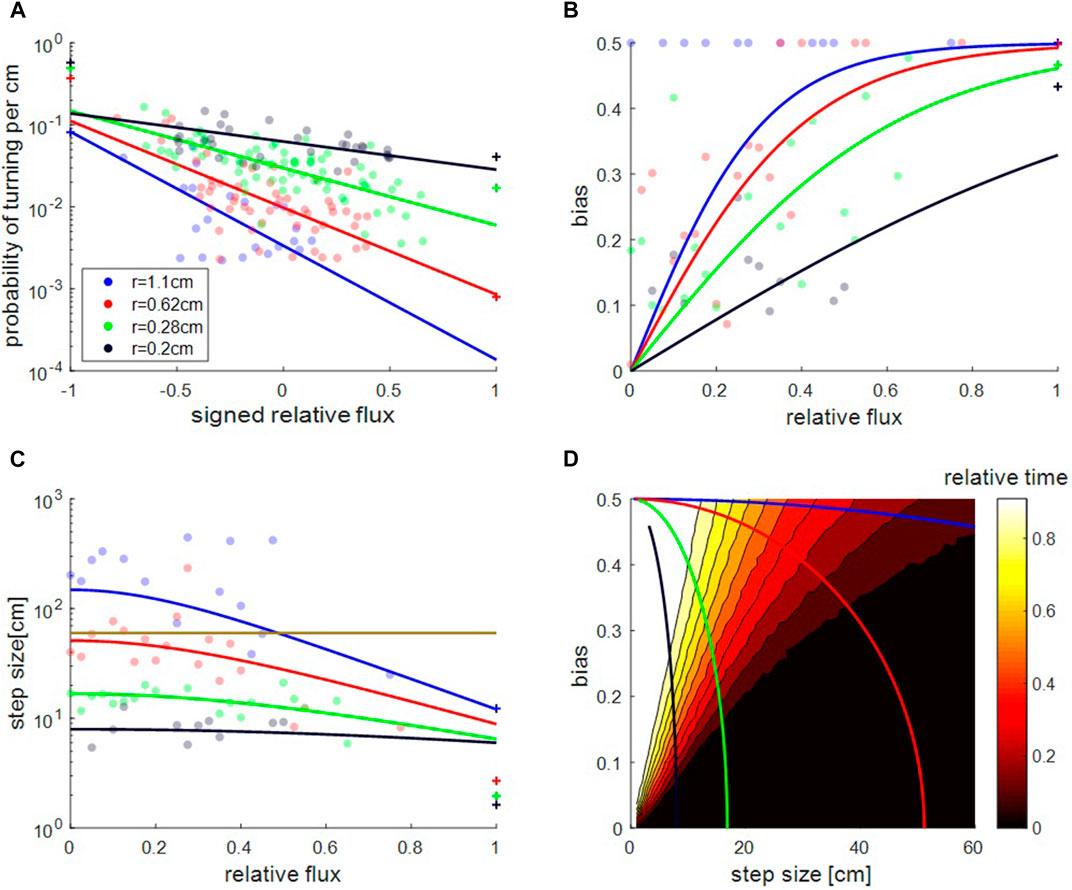
FIGURE 3. Collective load motion as a random walk. (A). Turning probability per cm, λ, as a function of the signed relative flux, ${\overline{f}}^{rel}$. Full lines are exponential fits (Supplementary Equation S58) and display larger slopes for larger loads. Data points at the two extremes ($+$ symbols in panels a–c) represent data from one exit experiments. (B). Bias of the random motion as a function of $f^{rel}$. The Bias is calculated using the turning probabilities found in panel (A), and Eq. 1. The bias, b, decreases when the fluxes from both sides become similar. The full lines are the theoretical curves calculated with the use of the λ dependencies as found in (A) and assuming a run-and-tumble model (see Supplementary Equation S61). (C). Mean step size, s, as a function of $f^{rel}$. Step size is calculated using the turning probabilities found in panel (A), and Eq. 1. The step size increases when the fluxes through both exits are similar. The brown horizontal line denotes the size of the system. Full lines are the theoretical curves calculated by using of the λ dependencies found in panel a. and assuming a run-and-tumble model (see Supplementary Equation S60). (D). Relative time advantage in favor of the dominant exit (color coded) as a function of both bias and step size. These were calculated by simulating a 1D biased random walk, with a exponentially distributed step size (whose mean value is denoted on the x-axis) and constant bias (y-axis), that is bound within a 55 cm domain. Overlaid on the graph are lines which indicate the relation between bias and step size for the different load sizes (as deduced from panels b and c). Color code in all panels as specified in panel (A).

We find that the relative time ($T_{rel}=\frac{T_H-T_L}{T_H+T_L}$ monotonously increases with the relative flux of ants, $f^{rel}=\frac{f_H-f_L}{f_H+f_L}$, (Figure 2B). While this increase was near-linear for the load of radius 0.62 [cm], we observe a sub-linear increase for the larger load (1.1 [cm]) and super-linear increase for the smaller load one of radius 0.28 [cm] (Figure 2B).

Figure 2B does not include the experimental data for the smallest object ($r=0.2$cm). This is since objects of this size were observed to spend extended time periods moving up and down the closed end of the channel. Such motion along a barrier with an opening was observed in previous studies [33, 34], and emphasizes that near the ends of the channel the motion of the smallest object was distinctly non-one-dimensional (with respect to the channel’s long axis). The time spent by this object near the ends was therefore much longer, and incomparable to the time spent at the ends by the larger objects (which moved in a quasi-one-dimensional manner along the channel length, and near the ends) nor to the our one-dimensional models as presented below.

C Collective Motion as a Decision Process

We interpret the cargo’s motion as a binary choice between the two alternative exit routes. This interpretation allows us to approach the collective motion through the prism of well-established neuronal decision-making models. In this section we present the relations between the assumptions of the EA model and the properties of our experimental system. We then point to similarities and differences between EA model predictions and the ants’ empirical motion.

A first assumption of the EA model is that information is integrated by accumulating fragments of evidence, each of which supports one or the other decision. These evidence fragments are analogous to the small quanta of information that individual ant attachments provide the carrying group [33]. Further, since most newly attached ants are “informed” [33], and tend to guide (pull) the group toward the direction from which they approached [29], differences in ant fluxes through the two exits translate to asymmetric evidence in the EA model.

A second EA model assumption is that the evidence is additively accumulated by an abstract one-dimensional decision variable that performs a random walk, which is biased in the presence of asymmetric evidence. A main advantage of the ant system is that, unlike brains, the analog of the abstract decision variable is readily and directly measurable as the location of the load. The dynamics of this decision variable are manifested as the load’s motion.

The last major assumption of the EA model is that a decision occurs once the decision variable reaches a threshold value. Viewing the load motion as a decision-making process we define a decision as the presence of the load in the vicinity of one of the two exits. We note that since in our experimental system both decisions lead to impassable routes, no reward is ever provided and decisions are ongoing rather than restricted to a single shot.

Since dynamic sequential decisions need not be qualitatively different from single-shot, isolated decisions, it is not a far-fetched assumption that they share the same underlying principles [6]. It is therefore of interest to explore the possibility of extending the EA model to include ongoing, sequential decisions.

Our experimental system therefore complies with many of the model’s assumptions. While this fact may not be surprising per se, it does allow for a comparison between the ants’ collective transport dynamics to the EA model’s predictions. An extreme scenario is one where only one of the exits is open. In this case, ant fluxes arrive only from the available direction such that the evidence for this side is overwhelming. Therefore, the EA model would predict a strongly biased random walk. This prediction is indeed compatible with the exponential distribution of the load location in the single alternative case (Figures 1A–B).

The ant collective motion deviates from the predictions of the EA model when both exits are open. In this case, some evidence supports motion toward the right exit while, other, toward the left. Consider, for example, the case where the ant flux through one exit is much larger than the flux through the other. Since this is a small deviation from the single exit case, the EA model would predict a small change to the bias. We would therefore expect that the spatial distributions, while slightly wider, should still be localized near the dominant exit. Another way of looking at this is the following: for the three smaller loads the step size, as measured in the single sided experiments, is under 3 cm (Figure 2A) which is very small in comparison to the length of the entire system. In these cases, if there is a bias toward one of the openings then traversing the corridor would require a large number of steps against the bias and this is highly improbable. Nevertheless, our empirical observations are not compatible with these descriptions. Indeed, even when ant fluxes are highly imbalanced the load often crosses the entire channel to reach the minority exit. This is even more pronounced for large objects where the sub-linear increase in relative time with respect to the relative flux, $f^{rel}$ (Figure 2B), implies that the minority option attracts the load for a disproportionately large fraction of the time. This constitutes a clear deviation between the predictions of the basic EA model and the ants’ collective motion. In the following sections, we discuss the reasons for this deviation as well as the central role that it plays in facilitating sequential decision making in natural contexts.

D Relative-Flux Affects Both Bias and Step Size

Next, we generalize the simple biased-random-walk version of the EA model, as to make it compatible with our empirical observations. To do this we take a more detailed view on the actual dynamics of the load’s random motion.

The random motion of the load can be described by a run-and-tumble process (see Supplementary Section S4 and Supplementary Equation S54), in which the load either continues (runs) in its current direction or, with probability ${\lambda }_{R,L}$ per unit length, tumbles and switches direction (turns to the right/left). The inverse of the tumbling probabilities is the persistence length (the average step-size between consecutive tumbles) in each direction.

The run-and-tumble model provides a good description of the one-side experiments. In this case, the probability to turn away from the exit is essentially zero, so only one value of λ is finite. Hence, the decay constant of the exponential distributions in Figures 1A1,B1 is simply the persistence length for the motion away from the exit, or ${\lambda }^{-1}$ (Figure 2A).

When both exits are open, we find that the turning probabilities ${\lambda }_{R,L}$ vary not only with object size but also with the signed relative flux of ants, ${\overline{f}}^{rel}$, (Figure 3A). The signed relative flux is defined as ${\overline{f}}^{rel}=\frac{f_T-f_A}{f_T+f_A}$ where $f_T$ is the ant influx through the exit toward which the load is heading and $f_A$ is the influx through the exit it is heading away from. The relative flux, as defined above, is simply the absolute value of the signed relative flux. The clear dependence of turning probabilities on ${\overline{f}}^{rel}$ is consistent with the fact that the ants’ decision making depends on this variable. Indeed, turning rate data shows that turning rates are more informatively described by relative flux (Figure 2B) than by flux differences (Supplementary Figures S7A,B), and that this holds for all load sizes. This finding implies that, similar to previous observations [35, 36], here too the ants as a group follow a form of Weber-like psychophysical rule and are sensitive to the relative differences in the relevant stimuli.

Notably, the probability to turn away from the exit with the larger signed relative flux (positive ${\overline{f}}^{rel}$) is significantly (exponentially) smaller than the probability to turn toward it (negative ${\overline{f}}^{rel}$). We quantified the dependence of the measured turning rates on ${\overline{f}}^{rel}$ using exponential fits (Figure 3A, Supplementary Equation S58). We then used these fits to assess the effect of these probabilities on the global decision-making parameters. We find that the relative time spent near each side as a function of $f^{rel}$, as calculated using the run-and-tumble model (Supplementary Equations S57, S59), stands in agreement with the experimental data for any load size (Figure 2B).

To connect these findings to the language of biased random walks, typically employed in EA models, we derive the following mapping (Supplementary Section S4):

$s=\frac{1}{{\lambda }_R+{\lambda }_L};b=\frac{1}{2}\frac{{\lambda }_R-{\lambda }_L}{{\lambda }_R+{\lambda }_L}\text{.}(1)$

We find that the bias b (Figure 3B), and the average step size s (Figure 3C), depend on $f^{rel}$ and on load size. Note that for the largest object (blue data points in Figure 3B) we have not observed any instances where the direction of motion switches against the bias in the influx of ants (Correspondingly, there are also no data points with positive ${\overline{f}}^{rel}$ in Figure 3A). This means that one of the lambda’s that we extract from this data is zero, and when substituted in Eq. 1 gives a bias of 0.5 (Figure 3B). The lines in Figure 3B show the bias as calculated from the exponential fits to the experimental data in Figure 3A, they are not fitted to the data in Figure 3B. For the largest objects the step-size is larger than the length of the channel (Figure 3C), which makes it difficult to obtain the intrinsic run-and-tumble parameters of the motion from the experimental data.

The variations in the step size allow the ants to tune their behavior and, depending on the bias, either repeatably visit both sides of the channel or remain confined to an area near the exit with the higher flux (Figure 3D). By comparison, a simulated random walker which has control over bias alone is limited: if its step size is small compared to the tube length (say 10 cm, compared to the tube of length 55 cm, which applies to all load sizes in the case of a single open exit (Figure 2A)), then the object fully commits to the majority exit even if the bias is merely $\sim 0.2$. In other words, a modest bias prevents the ants from exploring the other exit (white area on the top-left side of Figure 3D). On the other extreme, if the step size is large (say 50 cm), the ants continue to explore both exits when the bias is intermediate (black area on the right side of Figure 3D), which may be useful if both exits are open but wasteful, if one exit is completely closed.

Compared to this hypothetical random walker, the ants exhibit a more flexible behavior that depends on the cargo size (see colored lines in Figure 3D). For small cargoes (black curve in Figure 3D), the small step size means that a modest bias commits the ants to the majority exit. This may be useful, as for a small cargo its less crucial to find the correct (optimal) path, since it is highly likely that due to its size it can eventually pass through both routes. However, for larger cargoes (see, for example, red curve in Figure 3D) the ants use a large step-size even for intermediate biases and this allows them to thoroughly explore both exits. In this way, the large cargo, which is difficult to transport, fully explores the available paths to find a traversable route. Only when the bias is very large, the ants reduce the step-size of the large cargo and this allows them to commit to the probable exit and avoid wasting time at the closed side. In subsection F (below) we present an abstract quantitative model to study the optimal balance between the time invested at each exit under different circumstances.

Hence, decision making and time balancing are direct consequences of the effect of the relative flux on step size. Specifically, a larger step size when the fluxes from both exits are similar allow the ants to collectively explore both options (Figure 3C). The condition that gives rise to a monotonous increase in step size, s, as $f^{rel}$ decreases from a value of 1 (the single side case) to 0 (the two-option cases) is that λ is a convex function in $f^{rel}$. In other words, the condition that $ds/d{f}^{rel}<0$, translates into (using Eq. 1):$\lambda \text{′}\left(f^{rel}\right)>\lambda \text{′}\left(-f^{rel}\right)$, which indeed holds for the measured exponential dependencies shown in Figure 3A.

In the next section we present a microscopic, mechanical model of individual ant forces and decisions [33] and tune it to fit the experimental results. We then use this model to explain two central aspects of the ant decision making process: the emergence of Weber’s law and the exponential dependence of the turning rate on $f^{rel}$.

E Microscopic Theory

We turn to investigate the emergent collective behavior observed in the experiments described above, using an established microscopic model [33]. In accordance with the quasi-one-dimensional nature of our experimental setup we employed a one-dimensional version of the two-dimensional model as used in previous studies [33, 34, 37]. The one dimensional model employs a simplified object with just a front and a back which moves on a line. The adjustments made to reduce the two dimensional system into a 1D model are explained in detail in SI section S5.

The model is based on the experimental observation that ants attached to the object either pull or lift it. In calculating the net force we ignore the lifters’ contribution whose effect is a reduction in friction that is usually saturated, and assume that each puller applies a force whose magnitude is constant - $f_0$. The total number of binding sites on each side of the one-dimensional objects is denoted by N, which is proportional to the object size. We further assume that ants can only pull toward the side to which they are attached [37]. The net force is then simply $F=f_0\left(n_R-n_L\right)$ with $n_{R/L}$ being the number of pullers on the right/left. The speed of the object, v, is proportional to the net force exerted on it, F [33].

In the model, carrying ants can change their role between puller and lifter. The rate at which an individual ant switches her role depends on the size and direction of the total force, as exerted by all other ants, with respect to the body axis of the ant [33]:

$\begin{array}{l}{r}_{p\to l}^R=k\frac{1}{1+e^{\frac{F}{F_{ind}}}}=k\frac{1}{1+e^{\beta \text{Δ}n}};r_{l\to p}^R=k\frac{1}{1+e^{-\frac{F}{F_{ind}}}}=k\frac{1}{1+e^{-\beta \text{Δ}n}}\\ r_{p\to l}^L=k\frac{1}{1+e^{-\frac{F}{F_{ind}}}}=k\frac{1}{1+e^{-\beta \text{Δ}n}};r_{l\to p}^L=k\frac{1}{1+e^{\frac{F}{F_{ind}}}}=k\frac{1}{1+e^{\beta \text{Δ}n}};\end{array}(2)$

where $r_{p\to l}^R$, for example, is the rate at which a puller on the right becomes a lifter, and k is a constant with dimensions of $[1/time]$. The parameter $F_{ind}$ acts as a temperature analogue, and determines the degree to which an ant tends to align with the total force exerted by the rest of the group. We further use the notations $\beta =f_0/F_{ind}$ and $\text{Δ}n=n_R-n_L$. With this choice of rates ants are more likely to align themselves in a way that maximizes the total force, F, as they spontaneously form an ordered state below a critical value of $F_{ind}$, or above a critical total number of ants [33].

The role-changing rates specified in Eq. 2 apply only to ants which are attached to the object. However, ants come and go, and those who have only just latched onto the object have a predetermined preferred direction in which to take the object. These ants, which arrive from the scent trail, are called “informed”, and upon attachment choose their role such that they only pull in the direction from which they had arrived (or lift if they happen to attach on the opposite side of the object). Informed ants become regular carrying ants, at a constant rate $k_{forget}$ (corresponding to an average time of $\sim 10-15$sec [33]), and are then governed by Eq. 2.

We simulated the 1D model and calibrated its parameters by comparing the results to one-side-open experimental data. The model reasonably reproduces the trajectories (compare Figure 4A to Figures 1A2,B2), velocity and spatial distributions (Supplementary Figures S12, S13), albeit less successfully for smaller objects where a 1D approximation is, indeed, expected to be less accurate. The model further captures the length-scale of the spatial distribution of the cargo away from the single exit, and qualitatively reproduces the empirical dependence on cargo size (compare Figure 4C, to Figure 2A).

FIGURE 4

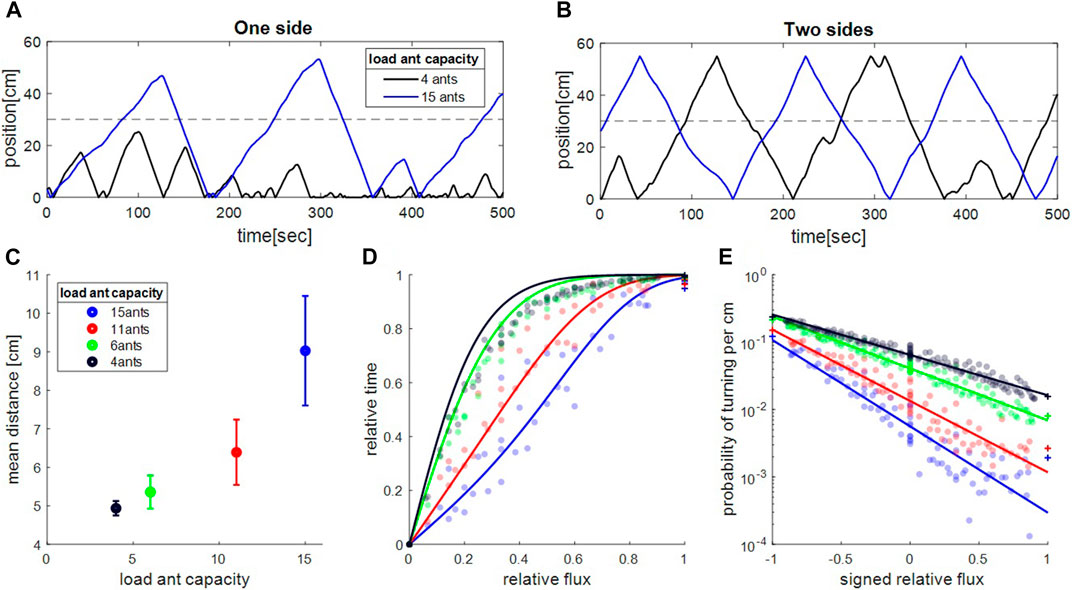
FIGURE 4. Microscopic model captures empirical properties of motion. (A–B). Simulated sample trajectories for one exit (A) and two exit (B) trajectories and two load sizes (4 and 15 ants). These are qualitatively comparable to the experimental trajectories shown in Figures 1A2–D2. (C). Mean distance traveled toward closed side in one side experiments. Data points were calculated assuming mean ant occupancy values that coincide with those measured in the one-side experiments (Supplementary Figure S11). Error-bars represent standard error of the mean over, from largest object to the smallest one, $N=\mathrm{11,5,7}$ and eight independent runs of the simulation (each on the order of hundreds of hours). These results can be compared to the experimental results shown in Figures 2A(D). Simulated relative time (see Supplementary Equation S56), with $d=10\left[cm\right]$ and $L=55\left[cm\right]$) spent near the two exits function of the relative flux, $f^{rel}$. Full lines are the theoretical curves calculated with the use of the exponential fits of the probabilities of turning (λ) as a function of ${\overline{f}}^{rel}$ (Figure 4E, Supplementary Equation S58), assuming a run-and-tumble model (see Supplementary Equation S59). Compare to the experimental results shown in Figures 2B(E). Simulated turning probability per cm, λ, as a function of the signed relative flux ${\overline{f}}^{rel}$. Full lines represent an exponential fit to the data (linear when plotted on a logarithmic scale, Supplementary Equation S58), with a larger slope for larger loads. The points at the ends (${\overline{f}}^{rel}=\pm 1$) represent averaged turning probabilities from one side experiments.

Having fixed the model parameters we then turned to simulate the more complex scenario where the exits at both sides are open and informed ants arrive from both ends. In our model the fluxes of the ants entering from each exit, appear as the rates of informed ants that attempt to attach onto the cargo, from either side. We assume that these attachment rates are proportional to the ant fluxes that enter the tube, as measured in the experiments (see Supplementary Section S5). Typical trajectories from the simulations are shown in Figure 4B, where we find that both small and large cargoes traverse the entire length of the set-up (compare to experimental trajectories in Figures 1C2,D2). The simulated trajectories were used to calculate the durations in which the object stayed near each exit. Similar to the experiments, we find a transition from super-linear to sub-linear dependence of the relative time difference on the relative flux, $f^{rel}$, as the cargo size increases (compare Figure 4D with Figure 2B).

A key ingredient of the motion is the dependence of turning rates on the ant fluxes from both sides. Similar to the experimental measurements (Figures 2B, 3A–C), the simulated data show that, when calculating turning rates (Supplementary Figure S14), signed relative flux is a more informative variable than flux difference (see Supplementary Figure S7C,D). This result provides us with further evidence regarding the applicability of Weber’s law to this decision making system. Furthermore, the simulations reproduce the approximate exponential dependence of the turning rate on the $f^{rel}$ compare Figure 4E to Figure 3A, and on cargo size. Next, we show how the exponential dependence and the emergence of Weber's law arise from the microscopic model.

In Supplementary Section S6, we present a simplified version of our model which is analytically solvable. In this simplified version the cargo is fully occupied by the ants, with fixed occupation, and the informed ants are treated as an external force [34, 37]. We use this simplified model to calculate the turning rates, by analyzing an escape process in velocity-space [38] described by Kramers theory [39]. This approximation should be valid at low temperatures, in the phase where the ants are coordinated. We obtain the following approximate analytic expression for the turning rate when the ant fluxes from both sides are equal, $f^{rel}=0$ (Supplementary Equation S88)

$r_{Kramer}(f^{rel}=0)\sim \frac{k}{\pi }{e}^{-2N}\frac{\beta N}{2}{e}^{-\frac{\beta N}{2}}(3)$

This equation describes the dependence of the turning rates on the size of the object (number of ants N) and the inverse temperature (ß) and stands in reasonable agreement with the simulated turning rates (Supplementary Figure S15).

Next, we calculated the effect of non-zero values of $f^{rel}$ on the turning rate, where the fluxes from each exit determine the average occupation by both uninformed and informed ants on each side. When the flux through a particular exit is large, both of these effects bias the motion in the same direction. The difference in uninformed ants induces a shift in the total number of ants on one side when compared to the other: N and $N-{\delta }_N$, respectively. The effect of a difference in the number of informed ants induces a net external force that is proportional to: $\delta =n_R-n_L$. From our analytic approximation of the turning rate (Eq. 3) we find that each of these effects modifies the turning rate in a simple exponential manner (see details in the Supplementary Section S6)

$r_{Kramer}(\delta ,{\delta }_N)=r_{Kramer}(f^{rel}=0)e^{-\left(\delta +{\delta }_N\right)\left(\frac{\beta }{2}+2\right)}(4)$

where the sign in the exponential changes if the turning is toward or against the bias. Using the full one-dimensional simulation model, we calculated the average occupation of informed and uninformed ants as a function of the fluxes of ants that enter from the two exits (Supplementary Section S7, Supplementary Equation S110), and use it to write δ and ${\delta }_N$ as functions of the incoming fluxes (Supplementary Equations S117, S118). These turn out to be (in the limit of an object saturated by attached ants, as in the experiments)

$\delta ,{\delta }_N\propto \frac{f_R-f_L}{f_R+f_L}=f^{rel}(5)$

where $f_{R/L}$ are the fluxes of ants $\left[\frac{ant}{sec}\right]$ coming from the right/left opening. Substituting Eq. 5 in Eq. 4 brings us to the conclusion that the turning rates depend on ant fluxes through $f^{rel}$ (Eqs 4, 5). This suggests an explanation for Weber’s law found in the simulations (Figures 4D,E) and, specifically, for the fact that the turning rates exhibit an exponential dependence on the $f^{rel}$ (Figure 4E).

An intuitive explanation for the result given in Eq. 5 relates the extent of the bias in the cargo motion to the signed relative flux. The bias in the motion depends on an imbalance of pulling ants on each end of the object (see Supplementary Section S7). The number of pulling ants on each side is naturally proportional to the flux of informed ants arriving from the exit that faces this side. However, any resulting bias is diminished by uninformed ants attaching evenly on both sides, and informed ants “leaking” from the opposite side (which act as pullers). These latter processes increase with the total flux from both sides, and diminish the bias of pulling ants toward the exit with the larger flux. The average number of pullers on each side is therefore given by the flux entering from that side, divided by an additive combination of both fluxes (Supplementary Equation S110). The difference between the average number of pullers on both sides, in the limit of an object that is saturated with ants, is therefore found to be proportional to $f^{rel}$ (Eq. 5), and directly enters the turning rates due to Kramers theorem (Eq. 4).

Note that the dependence of the response on the signed relative flux ${\overline{f}}^{rel}$ is another form of Fold-Change Detection (FCD), which is observed in biology on different scales, from bacteria to humans [40]. This property provides a beneficial increase in the dynamic range over which the system is sensitive to changes in the environment. It requires different mechanisms for its realization in different biological contexts, and is never exact. In our system, it emerges only in the limit in which the load is saturated by ants (Supplementary Equations S117, S118).

The microscopic model used here was originally developed to describe the free transport of cargo along a single scent trail [33]. The fact that this model also captures the collective motion of the ants in the presence of two opposing scent trails is therefore a non-trivial result. Rather, this supports the idea that individual ants are not aware of the conflict nor of the fact that they are part of a collective decision making process. The ants follow simple behavioral rules as if they were transporting the food item along a single, well-defined path toward the nest. The collective decision making dynamics evident on the scale of the entire group is an emergent phenomenon.

F Algorithmic Considerations in Sequential Decisions

We now explore optimal strategies for an agent faced with a dilemma that is similar to that of the ants. We will do this by considering an abstract dilemma, and compare the optimal strategies to the observed behavior of the ants. This will allow us to assess the efficiency of the ants’ behavior.

The basic EA model assumes exclusive investment in the exit with more evidence [15]. This is clearly the optimal course of action for a single-shot decision. In our experimental set-up the ants act differently: they repeatedly sample both sides of the arena, where the relative fraction of time invested in each side depends both on evidence (fluxes) and on load size (Figure 2B). In general, back-and-forth motion of the kind exhibited by the ants is common in dynamic scenarios in which every decision is followed by an immediate reward or feedback. One example includes foraging on a replenishing food source where the animal revisits depleted food patches after they have replenished [10]. In other cases, animals may repeatedly visit food sources to gather information regarding the probability of reward [41, 42], and update their visitations accordingly. Such feedback-based strategies are thoroughly studied theoretically under the framework of multi-armed bandit problems [43]. The ant behavior studied here is different as it includes no rewards. In fact, the only feedback that the ants get upon trying an exit is a negative one, indicated by the fact that they do not manage to cross the obstacle. In this sense, the ant scenario is similar to cases where animals search for sparse targets [44] and no positive feedback is available before finding the target.

To study dynamic decisions without reward we start by considering a toy model (Supplementary Section S8). This model is not meant to capture actual ant behavior; Rather, it aims to demonstrate how an optimal dynamic decision strategies may naturally lead to some of the key features evident in the ants’ behavior. Namely, we will use the toy model to show that in the lack of reward, optimal strategies are expected to employ back-and-forth sampling. We will further show that the relative weight attributed to the minority evidence in the optimal sampling strategy varies with circumstances. Specifically, we wish to explain why in some cases we expect that the time spent near the minority opinion would be larger than its share of the evidence, while in other cases it would be smaller (as in Figure 2B).

We first consider a simple scenario which would correspond to an extreme case of the model. Consider a person that has lost her key somewhere in an apartment. Reminiscing her past actions she reaches the conclusion that with probability $q_K=q$ the key is in the kitchen and with probability $q_L=1-q$ it is in the living room. During every minute of search in the “correct room”, i.e., the room where the key is, she has some small constant chance, p, of recovering the lost key. The question is how should this person divide the time between the two rooms in order to find the key as quickly as possible.

Simplifying the setting, we assume that traveling between the kitchen and the living room incurs no time cost. We further restrict attention to “memoryless strategies” where in each minute, the kitchen is searched with probability α and the living room with probability $1-\alpha$, for some $0\le \alpha \le 1$ that completely specifies the strategy. The expected time, $T\left(\alpha \right)$, until the key is found is then:

$\begin{array}{c}T\left(\alpha \right)=\mathcal{E}\left(Time|keyisinkitchen\right)\cdot q_K+\mathcal{E}\left(Time|keyisinlivingroom\right)\cdot q_L\\ =\frac{q_K}{\alpha \cdot p}+\frac{q_L}{\left(1-\alpha \right)\cdot p}\\ =\frac{1}{p}\left(\frac{q}{\alpha }+\frac{1-q}{1-\alpha }\right).\end{array}$

where $\mathcal{E}\left(Time|X\right)$ is the expected search time given the key is in room X. It is easy to see that, in contrast to the case of a single isolated decision, investing all the time exclusively in one of the rooms is far from optimal and actually leads to infinitely long expected search times, $T\left(0\right)=T\left(1\right)=\infty$. Therefore minimizing search time requires that the search effort be partitioned between the two rooms. The value of α that minimizes the expected search time is independent of p, the probability to find the key per unit time, and is given by:

$\alpha =\frac{1}{\sqrt{\frac{1-q}{q}}+1}.(6)$

To facilitate comparisons to the ant behavior we perform the following parameter transformation. We view $q_K$ and $q_L$ as the evidence for the key being in each of the rooms assuming, without loss of generality, that $q_K=q>0.5$. The relative evidence (analogous to the $f^{rel}$ as defined above) is therefore: $\left(q_K-q_L\right)/\left(q_K+q_L\right)=2q-1$. Similarly, the relative time difference in favor of the majority option is: $T_{rel}=\frac{T_K-T_L}{T_K+T_L}=\frac{\alpha -\left(1-\alpha \right)}{\alpha +\left(1-\alpha \right)}=2\alpha -1$.

The relation between these two relative variables is depicted by the blue curve in Figure 5B. A first conclusion is that the relative time spent near the majority option is a monotone increasing function of the relative evidence. This property of repeated decision-making deviates from the results of the classic EA model which provides exclusive investment at the option suggested by the majority of evidence. More interestingly, Eq. 6 shows that the time invested searching a room is sub-linear in the probability that the key is there. In other words, the optimal strategy dictates that if there is a small probability of finding the key in a certain room, one should invest a dis-proportionally larger time searching there (blue curve in Figure 5B). For example, if the probability that the key is in the living room is 0.05 ($f^{rel}=0.9$) then the fraction of time spent searching the living room is 0.19 ($T_{rel}=0.62$).

FIGURE 5

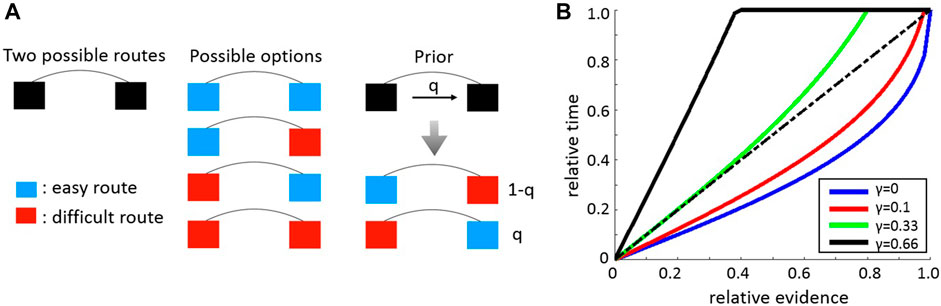
FIGURE 5. Abstract obstacle circumvention model. (A). The model describes an obstacle which can be circumvented using two separate routes (black squares on left hand column) each of which can offer either easy (blue) or difficult (red) traversal. There are therefore exactly four distinct obstacle combinations (central column). Circumvention time for symmetric obstacles is independent of strategy. However, for asymmetric obstacles (right hand column) an optimal circumvention strategy depends on external information encoded by the parameter q which specifies the probability that the easily traversable path is on the right. (B). Optimal time balancing strategies. The relative difference in the time invested in one of the routes as a function of the relative evidence indicating it to be the easy route. Different colors signify different values of the parameter $\gamma =p_{\text{diff}}/p_{\text{easy}}$, the ratio between the traversal efficiency for the two routes. $\gamma =0$ corresponds to the case where only one route is traversable (equivalent to the key search example, see text) and displays sub-linear behavior: even very small evidence toward one route dictates large search times in that direction. Increasing the value of γ leads to super-linear behavior where low evidence towards a route dictates little to no search time invested there.

Next, we generalize the aforementioned key-search scenario into a model which is more comparable with obstacle circumvention. The model describes an obstacle which can be bypassed via two routes (Figure 5A, left column). We assume a simplified environment wherein each of these routes can be either “easy” or “difficult”. An “easy” (respectively, “difficult”) route means that it can be passed with probability $p_{\text{easy}}$ (respectively, $p_{\text{diff}}$) on each attempt, where $p_{\text{easy}}>p_{\text{diff}}$. The values of $p_{\text{easy}}$ and $p_{\text{diff}}$ depend on the context, but are assumed to be fixed and known. We define the parameter $\gamma =p_{\text{diff}}/p_{\text{easy}}$ to describe the relative success rates. Note that the “lost key” example presented above is equivalent to choosing $p_{\text{diff}}=0$ (or, equivalently, $\gamma =0$). In this simplified problem there are exactly four options for an obstacle which include the possible permutations of easy and difficult routes (Figure 5A, central column). In cases where both passages are of equal difficulty, circumvention efficiency is independent of how time is partitioned between the two options and are thus not interesting. We therefore focus on the two asymmetric cases (Figure 5A, central column, two central options) where one route is easy and the other is difficult.

What are the search strategies that minimize the circumvention time around asymmetric obstacles? If it is known which of the two asymmetric options one currently faces, the optimal decision would become trivial—simply invest all the time at the easy route. Similarly to the “lost key” example, when information is not perfect, the optimal strategy could benefit from external evidence which we model by the parameter q. This parameter signifies the probability that the route on the right hand side is the easy one (Figure 5A, right column). Based on the parameters γ and q we seek the optimal way to partition time between the two routes. As in the aforementioned “lost key” example, we consider memoryless strategies where the right-hand route is approached with probability α, and the left-hand route is approached with probability $1-\alpha$.

We find (see Figure 5B and Supplementary Section S8) that the relative time invested in an option (say, the left route) rises with the evidence q pointing at this option. More interesting, we find that depending on the value of γ, the optimal relative time invested in this route can be either sub-linear or super-linear in the relative evidence (see Figure 5B). For instance, when $\gamma =0$, which is simply the “lost key” example, it is sub-linear, whereas for e.g., $\gamma =1/3$ it is super-linear.

These results are qualitatively reminiscent of the empirical results presented in Figure 2B. Indeed, note first that in our experimental setting, when evidence arrives at a load from some direction, then necessarily this implies that at least individual ants can pass through the corresponding route. Since the small load is not much larger than a single ant the probability that it passes through almost any passage with supporting evidence is large. This suggests that for small loads we expect that $p_{\text{diff}}$ is not far from 1, which implies that $\gamma \approx 1$. In this case the model predicts super-linear behavior which is in line with the observation that ants that carry small loads tend to spend most of their time near the passage with the larger flux. Conversely, large loads are more similar in their dynamics to the model predictions when γ is small. This is consistent with the fact that the chances that a large load traverses a ragged route can be very small, i.e. $p_{\text{diff}}$ is near zero. Accordingly, and similarly to the predictions of the abstract model for the case of small γ, large loads tend to spend relatively long times near the minority opinion.

More intuitively, information about which of the two escape routes is favorable can often be uncertain. For small loads, the optimal course of action in this case is to spend long times at the direction with higher evidence. Even if the evidence is misleading the price to pay in terms of escape time is not large. In the case of large loads, attempting to escape through the inferior route may be highly costly in terms of time. In this case, it is algorithmically favorable to put less emphasis on the differences in information, and to alternate between the two options. It is notable that the ants emergent behavior at the level of the collective is in qualitative agreement with these optimal strategy considerations, although individual ants can not comprehend such considerations.

3 Discussion

In this paper, we study ant collective decisions between binary choices with evidence pointing at either option. The study of collective decision-making in the context of ant groups confers several advantages. First, the compact arena size and the large number of individuals allow for the collection of large amounts of comprehensive and quantitative experimental data. Second, the existence of a reliable, quantitative model [33] for ant interactions during cooperative transport allows us to raise hypotheses and strengthen assumptions regarding the collective decision-making process. Finally, cooperative transport also imposes strong interactions between the carrying ants which, in turn, all move together as a single cohesive body. This stands in contrast to the more studied case where collective decisions are taken by migrating animal groups, which are less cohesive (more spatially distributed) and display sparser interaction networks [22, 23, 28]. The ant system may therefore constitute a stronger analogy to the “super-organism” concept, whereby an animal collective displays behavioral characteristics which are shared with a single-brain [36].

In this vein, our setup may be viewed as a physical analogue of the abstract evidence accumulation (EA) model developed to study decision-making by single animals. However, in contrast to the isolated decisions to which this model is typically applied, here we tracked the ants for extended time periods which allow for a more dynamic behavior in which decisions are continuously updated. Rather than exclusively converging on the majority choice, we find that the ants continuously explore both alternatives in a manner that depends both on group size and on the relative flux of incoming information [45]. It is particularly interesting that the weight given to the majority opinion may drastically change according to circumstances. For example, ants that carry a large load tend to extensively explore both options, even when significantly more evidence point at one of the exits. Conversely, ants that carry a small load tend to spend longer times at the option with more evidence, even if the extent of this majority is rather weak.

To understand the ants’ behavior, we investigated three complementary models, describing the abstract, macro, and the micro scales, respectively:

On the abstract level, to qualitatively explain the range of observed behaviors, we developed an idealized theoretical model that describes general considerations in dynamic decision-making. This model is aimed at identifying the optimal fraction of time invested in the two options of a binary choice setting. Note that in single shot decisions, the answer to this question is trivial, and the optimal action is to follow the majority opinion. In contrast, for the dynamic setting studied here, we found that depending on the parameters of the problem, optimal strategies weigh the majority opinion in either a super-linear or a sub-linear manner. Because of its non-trivial predictions, it would be interesting to study applications of this simple decision-making model in other biological systems, including human behavior.

The abstract model suggests that the time allocated to each of the choices depends on the environmental statistics as well as the currently available information. One way in which the ants can achieve the desired flexibility is by applying a random walk in which both the bias and the step size are variable and depend on the evidence. This deviates from the basic formulation of the EA model where asymmetries in evidence are reflected in changes to the bias only. In accordance with this prediction, we found that, on this macro scale, ant behavior in different experimental regimes can indeed be described by a biased random walk where the bias and step-size both covary. In particular, we found that when the fluxes of incoming ants from both directions are nearly equal, such that the identity of the best route is uncertain, the step-size is maximal. This allows the group to explore both options more often, and may be beneficial in allowing for efficient solutions.

Finally, we showed how a random walk with varying bias and step size arises from an established microscopic model of cooperative transport. This model correctly predicts how the characteristics of the random walk vary with group size and with the relative evidence. We used this model to demonstrate that while the relative evidence for both sides, is not available to any individual, it is still perceived by the group as a whole, which processes this global information toward a collective decision [34]. This strengthens the case for a truly emergent decision-making process in this distributed ant system [46].

Our experimental observations and microscopic model further demonstrate the emergence of a psychophysical law, Weber’s law [35]. Specifically, the group’s collective motion is controlled by the relative flux of ants arriving from the two alternative paths. While Weber’s law has previously been demonstrated in other group contexts, it is often difficult to infer whether it is not a simple consequence of relative perception on the scale of individual sensory systems [47–49]. In the ant collective choice system, Weber’s law is a truly emergent property, as an individual ant most probably cannot assess the fluxes nor their relative difference [50, 51].

Finally, we wish to reflect on possible implications of the current work on the EA model. The EA model was originally proposed to describe isolated, single-shot, decisions, whereas the ants’ in our study engage in a dynamic scenario, in which consecutive decisions must be taken. However, it is reasonable to assume that in practice, the decision-making process in a single-shot scenario would not be fundamentally different than the one used in more dynamic cases. Since tuning of the step size and the bias is useful in dynamic scenarios, we hypothesize that other systems functioning in dynamic conditions also employ such decision-making processes. In particular, we hypothesize that relative evidence can affect the dynamics of the abstract decision-making variable, as encoded in neuronal firing rates, by altering not only the bias of its random dynamics but also, concurrently, its step size. We further wish to stress, that in the context of neuroscience, varying step size may equivalently be achieved by modifying decision thresholds which have previously been suggested to be a tuning parameter important for speed/accuracy trade-offs [52].

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreements No. 648032 and 770964). NSG thanks the support of the Minerva Grant Nos. 712601. OF is the incumbent of the H. J. Leir Professorial chair. EF is the incumbent of the Tom Beck Research Fellow Chair. NSG. is the incumbent of the Lee and William Abramowitz Professorial Chair of Biophysics. This work is made possible through the historic generosity of the Perlman family.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Jacobo Levy-Abitbol for running the initial experiments, Jonathan E. Ron for initial simulations and Guy Han for technical help.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2021.672773/full#supplementary-material

References

1. Gold, JI, and Shadlen, MN. The Neural Basis of Decision Making. Annu Rev Neurosci (2007). 30:535–74. doi:10.1146/annurev.neuro.29.051605.113038

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Calhoun, AJ, and Benjamin, YH. The Foraging Brain. Curr Opin Behav Sci (2015). 5:24–31.

CrossRef Full Text | Google Scholar

3. Stephens, DW, and Krebs, JR. Foraging Theory, 1. Princeton University Press (1986).

4. Kolling, N, Behrens, TE, Mars, RB, and Rushworth, MF. Neural Mechanisms of Foraging. Science (2012). 336:95–8. doi:10.1126/science.1216930

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Fehr, E, and Fischbacher, U. The Nature of Human Altruism. Nature (2003). 425(6960):785–91. doi:10.1038/nature02043

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Pearson, JM, Watson, KK, and Platt, ML. Decision Making: the Neuroethological Turn. Neuron (2014). 82(5):950–65. doi:10.1016/j.neuron.2014.04.037

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Stephens, DW. Decision Ecology: Foraging and the Ecology of Animal Decision Making. Cogn Affective, Behav Neurosci (2008). 8(4):475–84. doi:10.3758/cabn.8.4.475

CrossRef Full Text | Google Scholar

8. Charnov, EL Optimal Foraging, the Marginal Value Theorem (1976). 9.2:129–136

9. Ohashi, K, and Thomson, JD. Efficient Harvesting of Renewing Resources. Behav Ecol (2005). 16(3):592–605. doi:10.1093/beheco/ari031

CrossRef Full Text | Google Scholar

10. Goldshtein, A, Handel, M, Eitan, O, Bonstein, A, Shaler, T, Collet, S, et al. Reinforcement Learning Enables Resource Partitioning in Foraging Bats. Curr Biol (2020). 30(20): 4096–102.

Google Scholar

11. Calhoun, AJ, Chalasani, SH, and Sharpee, TO. Maximally Informative Foraging by caenorhabditis Elegans. Elife (2014). 3:e04220. doi:10.7554/eLife.04220

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Hayden, BY, Pearson, JM, and Platt, ML. Neuronal Basis of Sequential Foraging Decisions in a Patchy Environment. Nat Neurosci (2011). 14(7):933–9. doi:10.1038/nn.2856

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ratcliff, R, Smith, PL, Brown, SD, and McKoon, G. Diffusion Decision Model: Current Issues and History. Trends Cognitive Sciences (2016). 20(4):260–81. doi:10.1016/j.tics.2016.01.007

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Usher, M, and McClelland, JL. The Time Course of Perceptual Choice: the Leaky, Competing Accumulator Model. Psychol Rev (2001). 108(3):550–92. doi:10.1037/0033-295x.108.3.550

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Shadlen, MN, and Newsome, WT. Neural Basis of a Perceptual Decision in the Parietal Cortex (Area Lip) of the Rhesus Monkey. J Neurophysiol (2001). 86(4):1916–36. doi:10.1152/jn.2001.86.4.1916

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Schall, JD. Neural Basis of Deciding, Choosing and Acting. Nat Rev Neurosci (2001). 2(1):33–42. doi:10.1038/35049054

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Davidson, JD, and El Hady, A. Foraging as an Evidence Accumulation Process. Plos Comput Biol (2019). 15(7):e1007060. doi:10.1371/journal.pcbi.1007060

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Miller, N, Garnier, S, Hartnett, AT, and Couzin, ID. Both information and Social Cohesion Determine Collective Decisions in Animal Groups. Proc Natl Acad Sci (2013). 110(13):5263–8. doi:10.1073/pnas.1217513110

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sumpter, DJT, and Pratt, SC. Quorum responses and Consensus Decision Making. Phil Trans R Soc B (2009). 364(1518):743–53. doi:10.1098/rstb.2008.0204

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Simons, A. Many Wrongs: the Advantage of Group Navigation. Trends Ecol Evol (2004). 19(9):453–5. doi:10.1016/j.tree.2004.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Arganda, S, Pérez-Escudero, A, and de Polavieja, GG. A Common Rule for Decision Making in Animal Collectives across Species. Proc Natl Acad Sci U S A (2012). 109(50): 20508–13. doi:10.1073/pnas.1210664109

CrossRef Full Text | Google Scholar

22. Biro, D, Sumpter, DJT, Meade, J, and Guilford, T. From Compromise to Leadership in pigeon Homing. Curr Biol (2006). 16(21):2123–8. doi:10.1016/j.cub.2006.08.087

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Strandburg-Peshkin, A, Farine, DR, Couzin, ID, and Crofoot, MC. Shared Decision-Making Drives Collective Movement in Wild Baboons. Science (2015). 348(6241):1358–61. doi:10.1126/science.aaa5099

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Couzin, ID. Collective Cognition in Animal Groups. Trends Cogn Sci (2009). 13(1):36–43. doi:10.1016/j.tics.2008.10.002

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Passino, KM, Seeley, TD, and Visscher, PK. Swarm Cognition in Honey Bees. Behav Ecol Sociobiol (2008). 62(3):401–14. doi:10.1007/s00265-007-0468-1

CrossRef Full Text | Google Scholar

26. Seeley, TD, Visscher, PK, Schlegel, T, Hogan, PM, Franks, NR, and Marshall, JA. Stop Signals Provide Cross Inhibition in Collective Decision-Making by Honeybee Swarms. Science (2012). 335(6064):108–11. doi:10.1126/science.1210361

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Pagliara, R, Gordon, DM, and Leonard, NE. Regulation of Harvester Ant Foraging as a Closed-Loop Excitable System. Plos Comput Biol (2018). 14(12):e1006200. doi:10.1371/journal.pcbi.1006200

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Marshall, JA, Bogacz, R, Dornhaus, A, Planqué, R, Kovacs, T, and Franks, NR. On Optimal Decision-Making in Brains and Social Insect Colonies. J R Soc Interf (2009). 6(40):1065–74. doi:10.1098/rsif.2008.0511

CrossRef Full Text | Google Scholar

29. Fonio, E, Heyman, Y, Boczkowski, L, Gelblum, A, Kosowski, A, Korman, A, et al. A Locally-Blazed Ant Trail Achieves Efficient Collective Navigation Despite Limited Information. Elife (2016). 5:e20185. doi:10.7554/eLife.20185

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Czaczkes, TJ, and Ratnieks, FLW. Cooperative Transport in Ants (Hymenoptera: Formicidae) and Elsewhere. Myrmecol News (2013). 18(1–11).

Google Scholar

31. Feinerman, O, Pinkoviezky, I, Gelblum, A, Fonio, E, and Gov, NS. The Physics of Cooperative Transport in Groups of Ants. Nat Phys (2018). 14(7):683–93. doi:10.1038/s41567-018-0107-y

CrossRef Full Text | Google Scholar

32. Thurstone, LL. Three Psychophysical Laws. Psychol Rev (1927). 34(6):424–32. doi:10.1037/h0073028

CrossRef Full Text | Google Scholar

33. Gelblum, A, Pinkoviezky, I, Fonio, E, Ghosh, A, Gov, N, and Feinerman, O. Ant Groups Optimally Amplify the Effect of Transiently Informed Individuals. Nat Commun (2015). 6:7729. doi:10.1038/ncomms8729

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Ron, JE, Pinkoviezky, I, Fonio, E, Feinerman, O, and Gov, NS. Bi-stability in Cooperative Transport by Ants in the Presence of Obstacles. Plos Comput Biol (2018). 14(5):e1006068. doi:10.1371/journal.pcbi.1006068

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Reina, A, Bose, T, Trianni, V, and Marshall, JAR. Psychophysical Laws and the Superorganism. Sci Rep (2018). 8(1):4387–8. doi:10.1038/s41598-018-22616-y

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Sasaki, T, and Pratt, SC. The Psychology of Superorganisms: Collective Decision Making by Insect Societies. Annu Rev Entomol (2018). 63:259–75. doi:10.1146/annurev-ento-020117-043249

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Gelblum, A, Pinkoviezky, I, Fonio, E, Gov, NS, and Feinerman, O. Emergent Oscillations Assist Obstacle Negotiation during Ant Cooperative Transport. Proc Natl Acad Sci USA (2016). 113(51):14615–20. doi:10.1073/pnas.1611509113

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Pinkoviezky, I, Couzin, ID, and Gov, NS. Collective Conflict Resolution in Groups on the Move. Phys Rev E (2018). 97(3):032304. doi:10.1103/PhysRevE.97.032304

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Risken, H. Fokker-planck Equation. Springer (1996).

40. Adler, M, and Alon, U. Fold-change Detection in Biological Systems. Curr Opin Syst Biol (2018). 8:81–9. doi:10.1016/j.coisb.2017.12.005

CrossRef Full Text | Google Scholar

41. Ilan, T, Katsnelson, E, Motro, U, Feldman, MW, and Lotem, A. The Role of Beginner's luck in Learning to Prefer Risky Patches by Socially Foraging House Sparrows. Behav Ecol (2013). 24(6):1398–406. doi:10.1093/beheco/art079

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Reid, CR, MacDonald, H, Mann, RP, Marshall, JAR, Latty, T, and Garnier, S. Decision-making without a Brain: How an Amoeboid Organism Solves the Two-Armed Bandit. J R Soc Interf (2016). 13(119):20160030. doi:10.1098/rsif.2016.0030

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Srivastava, V, Paul, R, and Leonard, NE. On Optimal Foraging and Multi-Armed Bandits. 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton): IEEE (2013). p. 494–9.

Google Scholar

44. Feinerman, O, and Korman, A. The Ants Problem. Distrib Comput (2017). 30(3):149–68. doi:10.1007/s00446-016-0285-8

CrossRef Full Text | Google Scholar

45. Couzin, ID, Ioannou, CC, Demirel, G, Gross, T, Torney, CJ, Hartnett, A, et al. Uninformed Individuals Promote Democratic Consensus in Animal Groups. science (2011). 334(6062):1578–80. doi:10.1126/science.1210280

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Feinerman, O, and Korman, A. Individual versus Collective Cognition in Social Insects. J Exp Biol (2017). 220(1):73–82. doi:10.1242/jeb.143891

PubMed Abstract | CrossRef Full Text | Google Scholar

47. von Thienen, W, Metzler, D, Choe, D-H, and Witte, V. Pheromone Communication in Ants: a Detailed Analysis of Concentration-dependent Decisions in Three Species. Behav Ecol Sociobiol (2014). 68(10):1611–27. doi:10.1007/s00265-014-1770-3

CrossRef Full Text | Google Scholar

48. Perna, A, Granovskiy, B, Garnier, S, Nicolis, SC, Labédan, M, Theraulaz, G, et al. Individual Rules for Trail Pattern Formation in Argentine Ants (Linepithema Humile). Plos Comput Biol (2012). 8(7):e1002592. doi:10.1371/journal.pcbi.1002592

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Cronin, AL. Ratio-dependent Quantity Discrimination in Quorum Sensing Ants. Anim Cogn (2014). 17(6):1261–8. doi:10.1007/s10071-014-0758-8

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Reina, A, Marshall, JAR, Trianni, V, and Bose, T. Model of the Best-Of-N Nest-Site Selection Process in Honeybees. Phys Rev E (2017). 95(5):052411. doi:10.1103/PhysRevE.95.052411

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Pais, D, Hogan, PM, Schlegel, T, Franks, NR, Leonard, NE, and Marshall, JAR. A Mechanism for Value-Sensitive Decision-Making. PloS one (2013). 8(9):e73216. doi:10.1371/journal.pone.0073216

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Heitz, RP, and Schall, JD. Neural Mechanisms of Speed-Accuracy Tradeoff. Neuron (2012). 76(3):616–28. doi:10.1016/j.neuron.2012.08.030

PubMed Abstract | CrossRef Full Text | Google Scholar