- 1Team MIMESIS, INRIA Nancy Grand Est, Strasbourg, France
- 2ILCB and INT UMR 7289, Aix Marseille Université, Marseille, France
- 3R&D Department, Hyland Switzerland Sarl, Geneva, Switzerland
- 4Krembil Research Institute, University Health Network, Toronto, ON, Canada
Additive noise is known to tune the stability of nonlinear systems. Using a network of two randomly connected interacting excitatory and inhibitory neural populations driven by additive noise, we derive a closed mean-field representation that captures the global network dynamics. Building on the spectral properties of Erdös-Rényi networks, mean-field dynamics are obtained via a projection of the network dynamics onto the random network’s principal eigenmode. We consider Gaussian zero-mean and Poisson-like noise stimuli to excitatory neurons and show that these noise types induce coherence resonance. Specifically, the stochastic stimulation induces coherent stochastic oscillations in the γ-frequency range at intermediate noise intensity. We further show that this is valid for both global stimulation and partial stimulation, i.e. whenever a subset of excitatory neurons is stimulated only. The mean-field dynamics exposes the coherence resonance dynamics in the γ-range by a transition from a stable non-oscillatory equilibrium to an oscillatory equilibrium via a saddle-node bifurcation. We evaluate the transition between non-coherent and coherent state by various power spectra, Spike Field Coherence and information-theoretic measures.
1 Introduction
Synchronization is a well characterized phenomenon in natural systems [1]. A confluence of experimental studies indicate that synchronization may be a hallmark pattern of self-organization [2–4]. While various mechanisms are possible, synchronization may emerge notably through an enhancement of internal interactions or via changes in external stimuli statistics. A specific type of synchronization can occur due to random external perturbations, leading to a noise-induced coherent activity. Such a phenomenon is called coherence resonance (CR) and has been found experimentally in solid states [5], nanotubes [6] and in neural systems [7, 8]. Theoretical descriptions of CR have been developed for single excitable elements [9, 9, 10], for excitable populations [11] and for clustered networks [12].
In general, stimulus-induced synchronization is well-known in neural systems [2]. Synchronization has been observed intracranially in the presence of noise between single neurons in specific brain areas [13, 14] and between brain areas [15–17]. The source of these random perturbations is still under debate. In this context, it is interesting to mention that [18] have found that the ascending reticular arousal system (ARAS) affects synchronization in the visual cortex. The ARAS provides dynamic inputs to many brain areas [19–21]. It has thus been hypothesized that synchronization in the visual system represents a CR effect triggered by ARAS-mediated drive. This hypothesis has been supported recently by [22] showing in numerical simulations that an intermediate intensity of noise maximizes the interaction in a neural network of Hodgkin-Huxley neurons. Furthermore, recent theoretical work [21] has provided key insights on how human occipital electrocorticographic γ-activity (40–120 Hz) commonly observed with open eyes [21] is closely linked to CR. Coherence resonance has further been associated with states of elevated information processing and transfer [22], which are difficult to assess in the absence of mean-field descriptions. For illustration, Figure 1 (upper panel) shows average network activity for increasing noise intensities
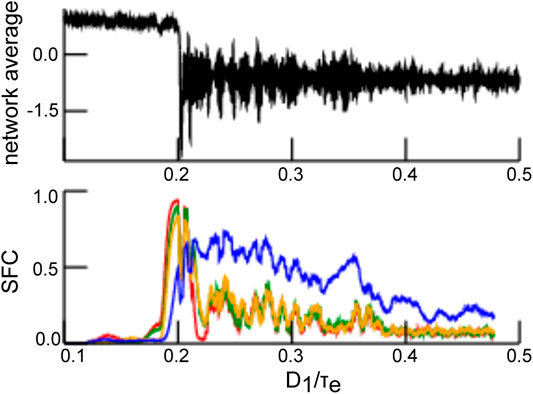
FIGURE 1. Synchronization dependent on noise intensity as a marker of coherence resonance. The top panel shows the network average of
To better understand the mechanisms underlying CR and its impact on information processing, we consider a simple two-population Erdös-Rényi network of interconnected McCullogh-Pitts neurons. Our goal is to use this model to provide some insight into the emergence of stimulus-induced synchronization in neural systems and its influence on the neural network’s information content. The neural network under study has random connections, a simplification inspired from the lack structure neural circuits possess at microscopic scales. Previous studies [23] have shown that such systems are capable of noise-induced CR. Building on these results, we here provide a rigorous derivation of a mean-field equation based on an appropriate eigenmode decomposition to highlight the role of the network’s connectivity–Erdös-Rényi more specifically eigenspectrum in supporting accurate mean-field representations. We extend previous results by further considering both global (all neurons are stimulated) and partial (some neurons are stimulated) stochastic stimulation and its impact on CR similar to some previous studies [24–26]. This partial stimulation is both more general and realistic than global stimulation as considered in most previous studies [11, 23, 27]. We apply our results to both zero-mean Gaussian and Poisson-like stochastic stimuli, and derive the resulting mean-field description. It is demonstrated rigorously that partial stochastic stimulation shifts the system’s dynamic topology and promotes CR, compared to global stimulation. We confirm and explore the presence of CR using various statistical measures.
2 Materials and Methods
We first introduce the network model under study, motivate the mean-field description, mentions the nonlinear analysis employed and provides details on the statistical evaluation.
2.1 The Network Model
Generically, biological neuronal networks are composed of randomly connected excitatory and inhibitory neurons, which interact through synapses with opposite influence on post-synaptic cells. We assume neural populations of excitatory
This formulation is reminiscent of many rate-based models discussed previously [28], where it is assumed that neuronal activity is asynchronous and synaptic response functions are of first order. The state variables
The present work considers directed Erdös-Rényi networks (ERN) with connection probability density
with the corresponding Bernoulli distribution variance
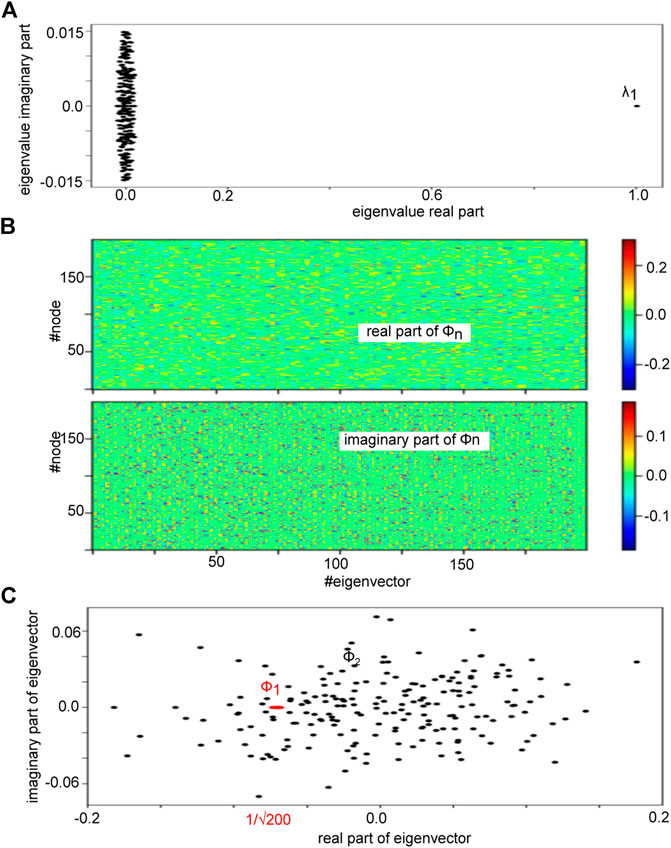
FIGURE 2. Eigenvalue spectrum of an Erdös-Rényi adjency matrix A under study and its eigenbasis. (A) The plot shows the eigenvalues in the complex plane demonstrating a clear spectral gap between the first eigenvalue
Moreover, we assume that each noise process at inhibitory neurons
Conversely each noise process at excitatory neurons
In the following, we assume two classes
In biological neural systems, the input to a neural population is well-described by incoming spike trains that induce dendritic currents at synaptic receptors. According to renewal theory, neurons emit spike trains whose interspike interval obeys a Poisson distribution [35]. Then incoming spike trains at mean spike rate r induce random responses at excitatory synapses with time constant
2.2 Conventional Mean-Field Analysis
To compare mesoscopic neural population dynamics to macroscopic experimental findings, it is commonplace to describe the network activity by the mean population response, i.e. the mean-field dynamics [37–39]. A naive mean-field approach was performed in early neuroscience studies [40–42], in which one blindly computes the mean network activity to obtain
with the network average
Combined, these assumptions lead to mean-field equations.
In this approximate description, additive noise does not affect the system dynamics. The assumption (Eq. 4) is very strong and typically not valid. In a more reasonable ansatz.
with
Motivated by previous studies on stochastic bifurcations [44–53], in which additive noise may tune the stability close to the bifurcation point, the present work shows how additive noise strongly impacts the nonlinear dynamics of the system for arbitrary noise intensity and away from the bifurcation. Previous ad-hoc studies have already used mean-field approaches [23, 54, 55] which circumvents the closure problem (Eq. 6) through a different mean-field ansatz. These motivational studies left open a more rigorous derivation. This derivation will be given in the present work: presenting in more detail its power and its limits of validity.
2.3 Equilibria, Stability and Quasi-Cycles
The dynamic topology of a model differential equation system may be described partially by the number and characteristics of its equilibria. In general, for the non-autonomous differential equation system
with state variable
The stability of an equilibrium
where
2.4 Numerical Simulations
The Langevin Eq. 1 have been integrated over time utilizing the Euler-Maruyama scheme [58]. Table 1 presents the parameters used. In certain cases, the noise variance has been changed over time t according to
with the maximum integration time T and the maximum and minimum noise variance values
2.5 Numerical Spectral Data Analysis
Since prominent oscillations of the network mean activity indicates synchronized activity in the population, we have computed the power spectrum of the network mean activity
In addition to the power spectrum, the synchronization between single neuron spike activity and the dendritic current reflects the degree of coherence in the system. To this end, we have computed the Spike Field Coherence (SFC) [59]. To estimate the SFC, we have chosen a time window of 5s for zero-mean Gaussian stimulation and 8s for Poisson stimulation and computed the spike-triggered average and power spectra in these time windows to compute the SFC for each frequency. Then we have averaged the SFC in the
2.6 Information Measures
Coherence quantifies the degree of mutual behavior of different elements. Interestingly, recent studies of biological neural systems have shown that synchronization and information content are related [60, 61]. For instance, under general anesthesia asynchronous cortical activity in conscious patients is accompanied by less stored information and much available information whereas synchronous cortical activity in unconscious patients exhibits more stored information and less available information [19, 20, 62–64]. We are curious how much information is stored and available in coherence resonance described in the present work. The result may indicate a strong link between coherence and information content. To this end, we compute the amount of stored information in the excitatory population as the predictable information and the amount of available information as the population’s entropy, cf [64].
The predictable information in the excitatory population is computed as the Active Information Storage
where
with
Moreover, we compute the available information in the excitatory cortex of the dendritic current
and entropy differences at different noise intensities are evaluated statistically by an unpaired Welch t-test with
In subsequent sections, we have computed
3 Results
The subsequent section shows the derivation of the mean-field equations, before they are applied to describe network dynamics for two types of partial stimulation.
3.1 Mean-Field Description
To derive the final equations, we first introduce the idea of a mode projection before deriving the mean-field equations as a projection on the principal mode. The extension to partial stimuli extends the description.
Mode Decomposition
In the model (1), the system activity
with complex mode amplitude
Here,
with the complex mode amplitude
Projecting
Now let us assume that
and
Then
cf. section 2.1, where we have utilized the bi-orthogonality of the basis. Equivalently,
We observe that
due to (Eq. 9) and equivalently
with some coefficients
with
The Mean-Field Equations
Equations 12, 13 describe an Ornstein-Uhlenbeck process with solution
for
Inserting expressions in Eq. 14 into these expressions leads to
By virtue of the completeness of the basis, it is
with the unity matrix
We define
with
and the mean-field equations can the be written as
By virtue of the finite-size fluctuations over time
Equation 14 describe an Ornstein-Uhlenbeck process of mode k and thus
where the approximation is good for large N. Specifically, for Gaussian zero-mean uncorrelated noise
Similarly,
Moreover, if the mean input is
obeys deterministic dynamics. However, the above formulation depends implicitly on the additive noise through the convolution of the transfer function.
Partial Stimuli
Each noise baseline stimulus at inhibitory neurons
Using Eq. 18 and Eq. 19 and assuming
whose probability density function
with
Then, utilizing Eqs 22, 23 and specifying S to a step function (cf. section 2.1), the mean-field transfer functions in Eq. 24 read
Here,
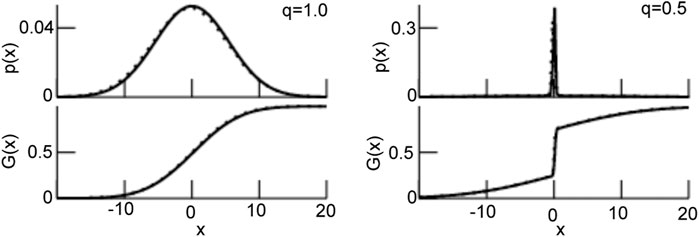
FIGURE 3. The probability density function p (Eq. 26) and the resulting transfer function G (Eq. 27). For
Essentially, the mean-field obeys
utilizing (Eq. 27).
3.2 Zero-Mean Gaussian Partial Stimulation
At first, we consider the case of a partial noise stimulation with zero network mean, i.e.
FIGURE 4. Enhanced zero-mean Gaussian noise induces phase transitions in spatiotemporal dynamics. The panels show the network activity
Figure 5 shows the respective power spectra of the network mean
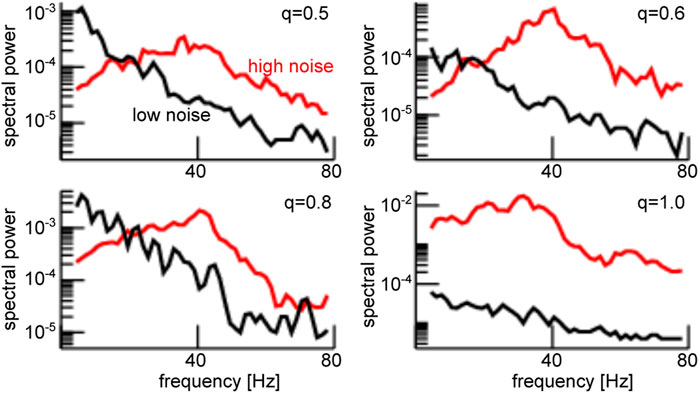
FIGURE 5. Enhanced noise yields strong power of the global mode
Stronger power spectral density at a given frequency is the signature of a coherent network, as seen in Figure 5. Since the neurons in our network model emit spikes and exhibit synaptic input currents, noise-induced coherence may be visible in the coherence between spiking and synaptic activity as well. In fact, in Figure 6A one observes a significant strongly enhanced Spike Field Coherence at high noise intensities for both global and partial stimulation. Hence, in sum the system exhibits coherence resonance in the sense that strong noise induces coherent oscillations that are not present at low noise intensities.
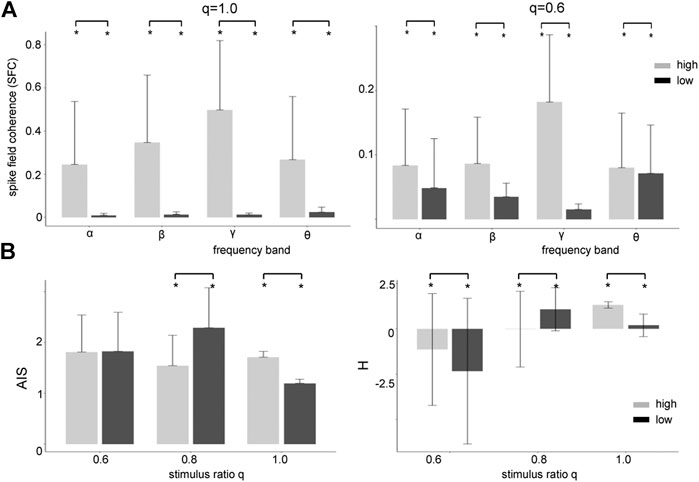
FIGURE 6. High zero-mean Gaussian noise enhances the Spike Field Coherence in all frequency bands and affects heterogeneously Active Information Storage (AIS) and differential entropy (H). (A) The differences between high noise intensity (grey-colored) and low noise intensity (black-colored) is significant
Coherence resonance is supposed to be linked to information processing in neural systems. Thus we investigate the relationship between stimulus noise intensity and information in the system across frequency bands. Figure 6B shows how much information is stored in the networks (AIS) and how much information is available (H). We observe that significantly more information is stored (AIS) and available (H) at high noise intensities for global stimulation
To understand this noise-induced coherence, we take a closer look at the dynamic topology of the mean-field Eq. 28. Their equilibria (cf. section 2.3) for negligible finite-size fluctuations
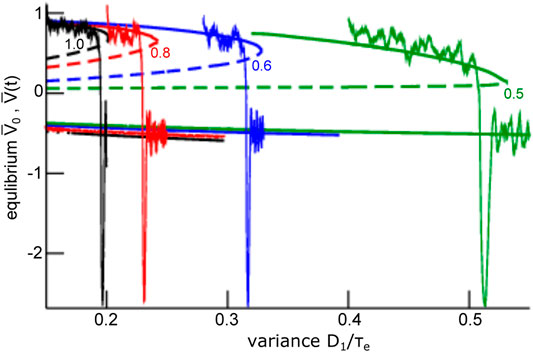
FIGURE 7. Equilibria and representative time series of the global mode
The mean-field solution involves finite-size fluctuations that affect the solutions principal oscillation frequency and magnitude. By construction, these mean-field solutions converge to the network average for increasing network size N. Figure 8 compares the time series of mean-field solutions and network averages for increasing network sizes and affirms the convergence and thus the validity of the mean-field description. It is interesting to note that, besides the mean-field dynamics, the network’s dynamical properties change with increasing N as well. Figure 8 provides the principal oscillation frequencies for both solutions for the given network size: the network speeds up with increasing size and its frequency converges to the mean-field principal frequency that remains about the same value. However, we point out that the mean-field solution remains still slightly different even for very large N since it implies the approximation of negligible connectivity matrix bulk spectra. Figure 9 affirms this finding by comparing simulation trials of the transitions from the non-oscillatory to the oscillatory coherent state. We observe that the transition values of
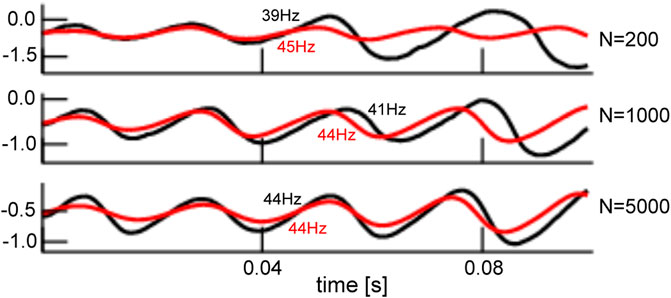
FIGURE 8. Comparison of network average and mean-field solution for different network sizes. The network average (black) and mean-field solutions (red) resembles more and more the larger the network of size N. This holds for the magnitude and frequency (provided in panels) of both solutions. The initial value of the mean-field activity has been chosen to the initial value of the network average. Simulations consider zero-mean Gaussian simulations with
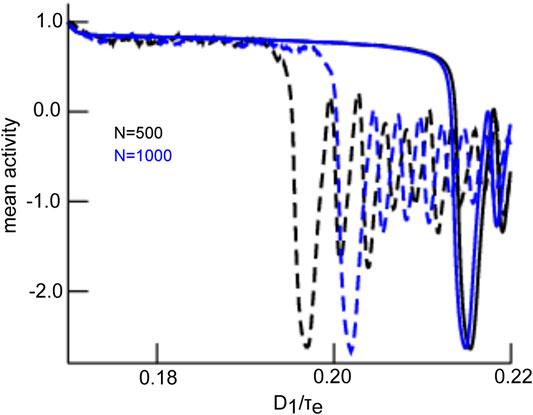
FIGURE 9. Comparison of transitions in network and mean-field for different network sizes. The network average (dashed line) and mean-field solutions (solid line) resemble more for larger network size N. This is explained by reduced finite-size fluctuations for larger networks. The initial value of the mean-field activity has been chosen to the initial value of the network average. Simulations consider zero-mean Gaussian simulations with
The frequency range of oscillations observed for steady states located within the lower branch (see Figure 7) is a consequence of both network connectivity and neuronal properties and is further tuned by additive noise. Figure 10 shows the maximum eigenvalue real part for the upper (A) and the lower branch (B, top opanel) and the eigenfrequency (cf. section 2.3) of the equilibrium at the lower branch (B, lowel panel). We observe that increasing noise intensity decreases slightly the eigenfrequency in the
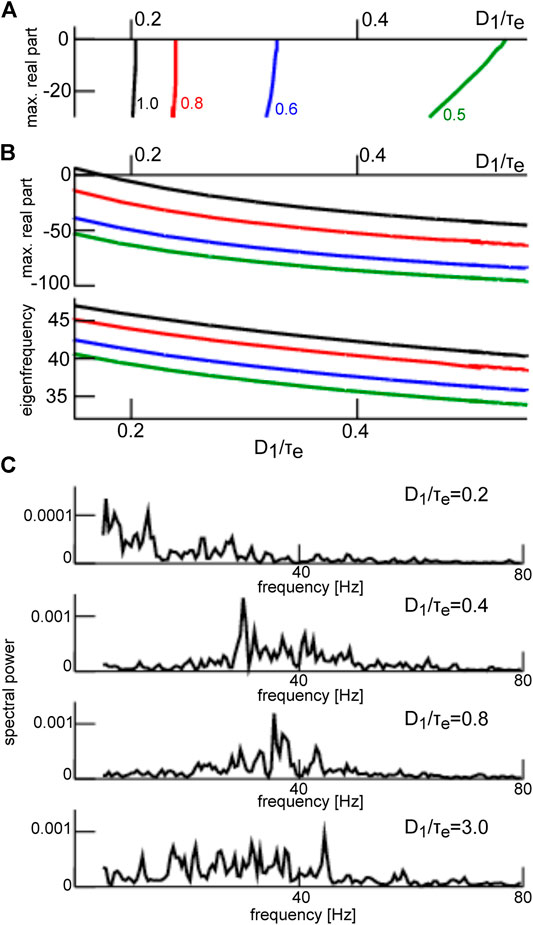
FIGURE 10. Eigenvalues at the top and bottom branch in Figure 7 and corresponding power spectra. (A) maximum eigenvalue of equilibria on the top branch in Figure 7. (B) maximum real part r of the eigenvalue
3.3 Poisson Partial Stimulation
Synaptic receptors respond to afferent Poisson-distributed input spike trains, whose properties differ substantially from the Gaussian noise processes we considered so far. To generalize our results to more physiological stimuli statistics, we considered a partial Poisson noise stimulation with dependent mean and variance. Specifically, afferent spike trains at spike rate
and finite-size fluctuations
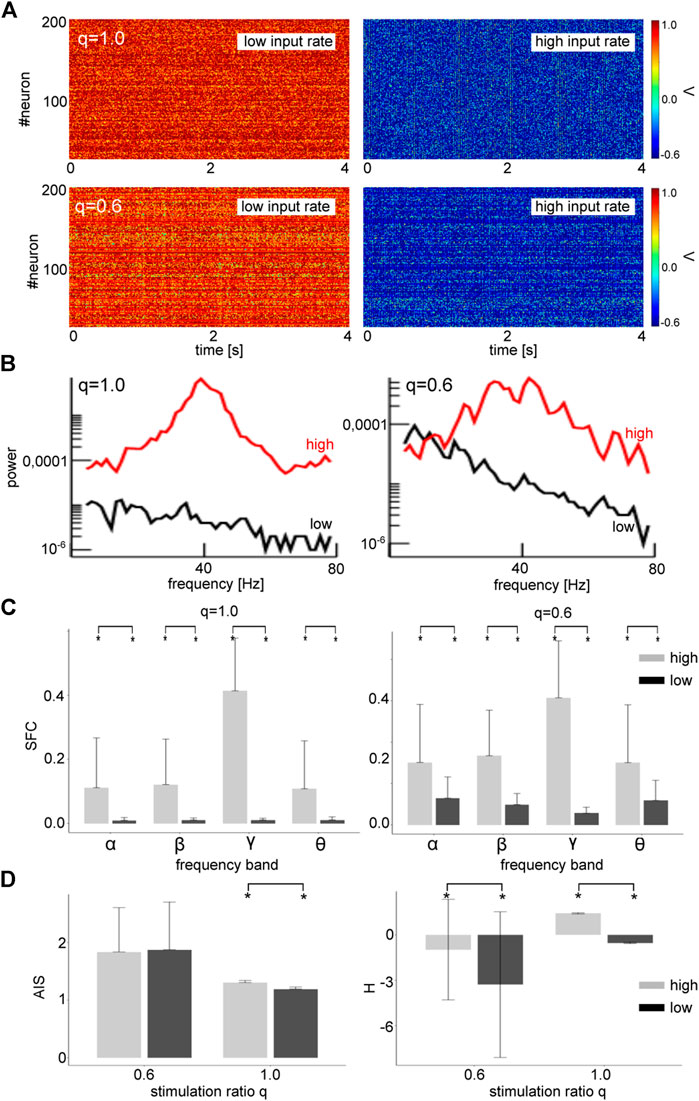
FIGURE 11. Poisson noise induces transitions from a non-oscillatory to an oscillatory state for both global and partial stimulation. (A) Network activity
These results can be understood by taking a closer look at the dynamic topology of the system. Figure 12 reveals that, for global stimulation
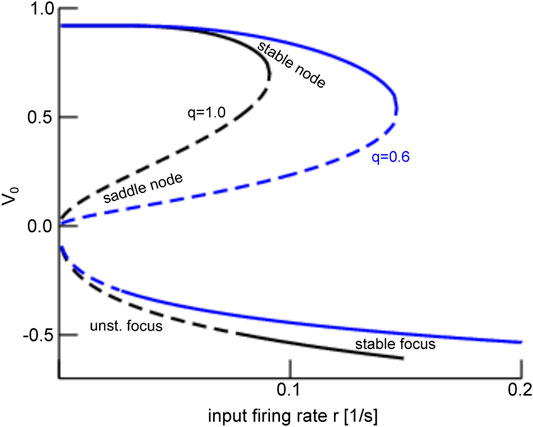
FIGURE 12. Equilibria of the mean-field
4 Discussion
This study presents a rigorous derivation of mean-field equations for two nonlinearly coupled non-sparse Erdös-Rényi networks (ERN) that are stimulated by additive noise. This mean field representation is made possible through spectral separation: the eigenspectrum of ERN networks exhibits a large spectral gap between the eigenvalue with largest real part and the rest of the spectrum. We show that the projection of the network dynamics onto the leading eigenmode represents the mean-field. Its dynamics are shaped by eigenmodes located in the complement subspace spanned by non-leading eigenmodes. In our model, the subspace dynamics are governed and influenced by additive noise statistics and they obey an Ornstein-Uhlenbeck process.
We extended the mean-field derivation to various types of additive noise, such as global and partial noise stimuli (i.e. when only a fraction of the excitatory neurons are stimulated) and for both zero-mean Gaussian and Poisson-like noise. Collectively, our analysis shows that additive noise induces a phase transition from a non-oscillatory state to an oscillatory coherent state. Such noise-induced coherence is known as coherence resonance (CR). This phase transition has been shown to occur not only for Gaussian zero-mean noise but also for Poisson-like noise. To the best of our knowledge, CR has not been found yet for such Poisson-like noise. The general underlying mechanism is a noise-induced multiplicative impact of additive stimulation via the nonlinear coupling of different modes. This multiplicative effect modifies the net transfer function of the network and thus enlarges its dynamical repertoire. This resembles the impact of additive noise in stochastic bifurcations [51, 52, 70, 71].
Embedding into Literature
Our results build on previous studies from the authors [23, 54, 55] to provide a rigorous derivation of the mean-field description, whereas previous work have motivated heuristically the mean-field reduction and, e.g., failed to show in detail whether the mean-field equation is the only solution for any given additive stimuli. Several other previous studies have presented mean-field descriptions in stochastically driven systems. For instance, Bressloff et al. [28] have derived rigorously mean-field equations for stochastic neural fields considering, inter alia, finite-element fluctuations by utilizing a Master equation and van Kampen’s volume expansion approach. We note here that we also took into account finite-size fluctuations resulting from a non-negligible variance of statistical mean values. Moreover [28], do not specify the network type and results in a rather opaque description, whereas we assume an ERN and thus exploit its unique eigenspectrum structure. This yields directly to a mean-field description, whose dependence of stochastic forces is obvious and avoids its implicit closure problem known from mean-field theories [43]. This is possible since the ERN considered share many properties with Izing models, that are known to permit an analytically treatable solution of the closure problem, see e.g. [72].
Moreover, several technical analysis steps in the present work have been applied in previous studies in a similar context. In a work on stochastic neural mean-field theory, Faugeras and others [27] have assumed that the system activity fluctuations obey a normal probability distribution and have derived an effective nonlinear interaction in their Proposition 2.1 similar to our Eq. 22. Further, the authors have shown how the fluctuation correlation function, i.e. the system activity’s second moment, determine the mean-field dynamics. This is in line with our result (Eq. 22) showing how the mean and variance of the additive noise tunes the system’s stability. However, the authors have not considered in detail the random nature of the system connectivity, whereas we have worked out the interaction of external stimulation and the ERN. This interaction yields directly the mean-field and its dependence of the external stimulus that is not present in [27]. Moreover, the present work also shows how the mean-field fluctuations affect the mean-field dynamics by deriving the fluctuation’s probability density function that describes all higher moments.
Noise-induced synchronization has been found recently in a system of stochastically driven linearly coupled FitzHugh-Nagumo neurons by Touboul and others [73]. The authors have found a minimum ratio of activated neurons that are necessary to induce global oscillatory synchronization, i.e. CR in the sense presented in our work. This question has been considered in the present work as well by asking how the mean-field dynamics, and thus how noise-induced synchronization, changes when modifying the ratio of stimulated excitatory neurons q while retaining the stimulation of inhibitory neurons. We find that global stimulation, i.e. stimulation of all excitatory neurons, yields a finite critical noise intensity below which the system is bistable and exhibits CR. Partial stimulation shifts this critical noise intensity to larger values and enlarges the bistability parameter space and thus promotes CR.
Several previous studies of mean-field dynamics in neural systems have applied the master equation formalism [74–76]. This works nicely in completely irregular networks and the asynchronous activity regime and has been applied successfully to neural populations considering biological neuron models [77–80]. However, the analysis of more regular networks will be very difficult to develop with the Master equation since the implicit integration over system states would be more complex. Conversely, our presented approach may consider regular structures by a corresponding matrix eigenvalue decomposition.
At last, we mention the relation to the Master stability function [81, 82]. This function describes the stability of identical synchronization of complex networks in a synchronization manifold and this manifold corresponds to the mean-field in our study. Although the Master stability function has been proven to be powerful, to the best of our knowledge it does not allow to reveal coherence resonance as the current work.
Limits and Outlook
The present work proposes to describe mean-field dynamics in a topological network by projection onto the networks eigenmodes. This works well for non-sparse random ERN with large connectivity probability. This network does not exhibit a spatial structure. However, less connected ERN networks show different dynamics, cf. the Supplementary Appendix. Moreover, biological networks are not purely random but may exhibit distance-dependent synaptic weights [83] or spatial clusters [84]. Our specific analysis applies for networks with a large spectral gap in their eigenspectra and it might fail for biological networks with smaller spectral gaps (as shown in the Supplementary Appendix). Future work will attempt to utilize the presented approach to derive mean-field dynamics for heterogeneous networks that exhibit a smaller spectral gap, such as scale-free networks [84].
Moreover, the single neuron model in the present work assumes a simple static threshold firing dynamics (McCullough-Pitts neuron) while neglecting somatic dynamics as described by Hodgkin-Huxley type models or the widely used FitzHugh-Nagumo model [11, 73]. Future work will aim at reinforcing the biological relevance of neurons coupled through ERN. This will be possible by extending the trivial transfer function from a step function to sigmoidal shapes for type I or type II neurons [76, 85, 86].
Our results show that noise-induced CR emerges in the
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
AH conceived the work structure motivated by intensive discussions with JL; AH, TW, NV, and JH contributed different work parts and all authors have written the work.
Conflict of Interest
JH was employed by Hyland Switzerland Sarl.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2021.697904/full#supplementary-material
References
1. Pikovsky, A, Rosenblum, M, and Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge University Press (2001).
2. Singer, W. The Brain as a Self-Organizing System. Eur Arch Psychiatr Neurol Sci (1986) 236:4–9. doi:10.1007/bf00641050
3. Witthaut, D, Wimberger, S, Burioni, R, and Timme, M. Classical Synchronization Indicates Persistent Entanglement in Isolated Quantum Systems. Nat Commun (2017) 8:14829. doi:10.1038/ncomms14829
5. Mompo, E, Ruiz-Garcia, M, Carretero, M, Grahn, HT, Zhang, Y, and Bonilla, LL. Coherence Resonance and Stochastic Resonance in an Excitable Semiconductor Superlattice. Phys Rev Lett (2018) 121:086805. doi:10.1103/PhysRevLett.121.086805
6. Lee, CY, Choi, W, Han, J-H, and Strano, MS. Coherence Resonance in a Single-Walled Carbon Nanotube Ion Channel. Science (2010) 329:1320–4. doi:10.1126/science.1193383
7. Gu, H, Yang, M, Li, L, Liu, Z, and Ren, W. Experimental Observation of the Stochastic Bursting Caused by Coherence Resonance in a Neural Pacemaker. Neuroreport (2002) 13:1657–60. doi:10.1097/00001756-200209160-00018
8. Ratas, I, and Pyragas, K. Noise-induced Macroscopic Oscillations in a Network of Synaptically Coupled Quadratic Integrate-And-Fire Neurons. Phys Rev E (2019) 100:052211. doi:10.1103/PhysRevE.100.052211
9. Pikovsky, AS, and Kurths, J. Coherence Resonance in a Noise-Driven Excitable System. Phys Rev Lett (1997) 78:775–8. doi:10.1103/physrevlett.78.775
10. Gang, H, Ditzinger, T, Ning, CZ, and Haken, H. Stochastic Resonance without External Periodic Force. Phys Rev Lett (1993) 71:807–10. doi:10.1103/physrevlett.71.807
11. Baspinar, E, Schüler, L, Olmi, S, and Zakharova, A. Coherence Resonance in Neuronal Populations: Mean-Field versus Network Model. Submitted (2020).
12. Tönjes, R, Fiore, CE, and Pereira, T. Coherence Resonance in Influencer Networks. Nat Commun (2021) 12:72. doi:10.1038/s41467-020-20441-4
13. Singer, W, and Gray, CM. Visual Feature Integration and the Temporal Correlation Hypothesis. Annu Rev Neurosci (1995) 18:555–86. doi:10.1146/annurev.ne.18.030195.003011
14. Eckhorn, R, Bauer, R, Jordan, W, Brosch, M, Kruse, W, Munk, M, et al. Coherent Oscillations: A Mechanism of Feature Linking in the Visual Cortex? Biol Cybern (1988) 60:121–30. doi:10.1007/bf00202899
15. Castelo-Branco, M, Neuenschwander, S, and Singer, W. Synchronization of Visual Responses between the Cortex, Lateral Geniculate Nucleus, and Retina in the Anesthetized Cat. J Neurosci (1998) 18:6395–410. doi:10.1523/jneurosci.18-16-06395.1998
16. Nelson, JI, Salin, PA, Munk, MH-J, Arzi, M, and Bullier, J. Spatial and Temporal Coherence in Cortico-Cortical Connections: a Cross-Correlation Study in Areas 17 and 18 in the Cat. Vis Neurosci (1992) 9:21–37. doi:10.1017/s0952523800006349
17. Bressler, SL. Interareal Synchronization in the Visual Cortex. Behav Brain Res (1996) 76:37–49. doi:10.1016/0166-4328(95)00187-5
18. Munk, MHJ, Roelfsema, PR, Konig, P, Engel, AK, and Singer, W. Role of Reticular Activation in the Modulation of Intracortical Synchronization. Science (1996) 272:271–4. doi:10.1126/science.272.5259.271
19. Hutt, A, Lefebvre, J, Hight, D, and Sleigh, J. Suppression of Underlying Neuronal Fluctuations Mediates EEG Slowing during General Anaesthesia. Neuroimage (2018) 179:414–28. doi:10.1016/j.neuroimage.2018.06.043
20. Hutt, A. Cortico-thalamic Circuit Model for Bottom-Up and Top-Down Mechanisms in General Anesthesia Involving the Reticular Activating System. Arch Neurosci (2019) 6:e95498. doi:10.5812/ans.95498
21. Hutt, A, and Lefebvre, J. Arousal Fluctuations Govern Oscillatory Transitions between Dominant γ- and α Occipital Activity during Eyes Open/Closed Conditions. Brain Topography (2021), in press.
22. Pisarchik, AN, Maksimenko, VA, Andreev, AV, Frolov, NS, Makarov, VV, Zhuravlev, MO, et al. Coherent Resonance in the Distributed Cortical Network during Sensory Information Processing. Sci Rep (2019) 9:18325. doi:10.1038/s41598-019-54577-1
23. Hutt, A, Lefebvre, J, Hight, D, and Kaiser, HA. Phase Coherence Induced by Additive Gaussian and Non-gaussian Noise in Excitable Networks with Application to Burst Suppression-like Brain Signals. Front Appl Math Stat (2020) 5:69. doi:10.3389/fams.2019.00069
24. Chacron, MJ, Longtin, A, and Maler, L. The Effects of Spontaneous Activity, Background Noise, and the Stimulus Ensemble on Information Transfer in Neurons. Netw Comput Neural Syst (2003) 14:803–24. doi:10.1088/0954-898x_14_4_010
25. Chacron, MJ, Lindner, B, and Longtin, A. Noise Shaping by Interval Correlations Increases Information Transfer. Phys.Rev.Lett. (2004) 93:059904. doi:10.1103/physrevlett.93.059904
26. Chacron, MJ, doiron, B, Maler, L, Longtin, A, and Bastian, J. Non-classical Receptive Field Mediates Switch in a Sensory Neuron's Frequency Tuning. Nature (2003) 423:77–81. doi:10.1038/nature01590
27. Faugeras, OD, Touboul, JD, and Cessac, B. A Constructive Mean-Field Analysis of Multi Population Neural Networks with Random Synaptic Weights and Stochastic Inputs. Front Comput Neurosci (2008) 3:1. doi:10.3389/neuro.10.001.2009
28. Bressloff, PC. Stochastic Neural Field Theory and the System Size Expansion. SIAM J Appl Math (2009) 70:1488–521.
29. Terney, D, Chaieb, L, Moliadze, V, Antal, A, and Paulus, W. Increasing Human Brain Excitability by Transcranial High-Frequency Random Noise Stimulation. J Neurosci (2008) 28:14147–55. doi:10.1523/jneurosci.4248-08.2008
30. Erdős, L, Knowles, A, Yau, H-T, and Yin, J. Spectral Statistics of Erdős-Rényi Graphs I: Local Semicircle Law. Ann Probab (2013) 41:2279–375. doi:10.1214/11-AOP734
31. Ding, X, and Jiang, T. Spectral Distributions of Adjacency and Laplacian Matrices of Random Graphs. Ann Appl Prob (2010) 20:2086–117. doi:10.1214/10-aap677
32. Kadavankandy, A. Spectral Analysis of Random Graphs with Application to Clustering and Sampling. In: Ph.D. Thesis, Université Cote d’Azur. Nice, France: NNT: 2017AZUR4059 (2017).
33. Füredi, Z, and Komlós, J. The Eigenvalues of Random Symmetric Matrices. Combinatorica (1981) 1:233–41. doi:10.1007/bf02579329
34. O'Rourke, S, Vu, V, and Wang, K. Eigenvectors of Random Matrices: A Survey. J Comb Theor Ser A (2016) 144:361–442. doi:10.1016/j.jcta.2016.06.008
37. Wright, JJ, and Kydd, RR. The Electroencephalogram and Cortical Neural Networks. Netw Comput Neural Syst (1992) 3:341–62. doi:10.1088/0954-898x_3_3_006
38. Nunez, PL. Toward a Quantitative Description of Large-Scale Neocortical Dynamic Function and EEG. Behav Brain Sci (2000) 23:371–98. doi:10.1017/s0140525x00003253
39. Nunez, P, and Srinivasan, R. Electric Fields of the Brain: The Neurophysics of EEG. New York - Oxford: Oxford University Press (2006).
40. Wilson, HR, and Cowan, JD. Excitatory and Inhibitory Interactions in Localized Populations of Model Neurons. Biophysical J (1972) 12:1–24. doi:10.1016/s0006-3495(72)86068-5
41. Gerstner, W, and Kistler, W. Spiking Neuron Models. Cambridge: Cambridge University Press (2002).
42. Bressloff, PC, and Coombes, S. Physics of the Extended Neuron. Int J Mod Phys B (1997) 11:2343–92. doi:10.1142/s0217979297001209
43. Kuehn, C. Moment Closure-A Brief Review. In: Schöll E, Klapp S, and Hövel P, editors. Control of Self-Organizing Nonlinear Systems. Heidelberg: Springer (2016). p. 253–71. doi:10.1007/978-3-319-28028-8_13
44. Sri Namachchivaya, N. Stochastic Bifurcation. Appl Math Comput (1990) 39:37s–95s. doi:10.1016/0096-3003(90)90003-L
45. Berglund, N, and Gentz, B. Geometric Singular Perturbation Theory for Stochastic Differential Equations. J Differential Equations (2003) 191:1–54. doi:10.1016/s0022-0396(03)00020-2
46. Bloemker, D, Hairer, M, and Pavliotis, GA. Modulation Equations: Stochastic Bifurcation in Large Domains. Commun Math Phys (2005) 258:479–512. doi:10.1007/s00220-005-1368-8
47. Boxler, P. A Stochastic Version of center Manifold Theory. Probab Th Rel Fields (1989) 83:509–45. doi:10.1007/bf01845701
48. Hutt, A, and Lefebvre, J. Stochastic center Manifold Analysis in Scalar Nonlinear Systems Involving Distributed Delays and Additive Noise. Markov Proc Rel Fields (2016) 22:555–72.
49. Lefebvre, J, Hutt, A, LeBlanc, VG, and Longtin, A. Reduced Dynamics for Delayed Systems with Harmonic or Stochastic Forcing. Chaos (2012) 22:043121. doi:10.1063/1.4760250
50. Hutt, A. Additive Noise May Change the Stability of Nonlinear Systems. Europhys Lett (2008) 84:34003. doi:10.1209/0295-5075/84/34003
51. Hutt, A, Longtin, A, and Schimansky-Geier, L. Additive Noise-Induced Turing Transitions in Spatial Systems with Application to Neural fields and the Swift-Hohenberg Equation. Physica D: Nonlinear Phenomena (2008) 237:755–73. doi:10.1016/j.physd.2007.10.013
52. Hutt, A, Longtin, A, and Schimansky-Geier, L. Additive Global Noise Delays Turing Bifurcations. Phys Rev Lett (2007) 98:230601. doi:10.1103/physrevlett.98.230601
53. Hutt, A, and Lefebvre, J. Additive Noise Tunes the Self-Organization in Complex Systems. In: Hutt A, and Haken H, editors. Synergetics, Encyclopedia of Complexity and Systems Science Series. New York: Springer (2020). p. 183–95. doi:10.1007/978-1-0716-0421-2_696
54. Lefebvre, J, Hutt, A, Knebel, J-F, Whittingstall, K, and Murray, MM. Stimulus Statistics Shape Oscillations in Nonlinear Recurrent Neural Networks. J Neurosci (2015) 35:2895–903. doi:10.1523/jneurosci.3609-14.2015
55. Hutt, A, Mierau, A, and Lefebvre, J. Dynamic Control of Synchronous Activity in Networks of Spiking Neurons. PLoS One (2016) 11:e0161488. doi:10.1371/journal.pone.0161488
56. Hutt, A, Sutherland, C, and Longtin, A. Driving Neural Oscillations with Correlated Spatial Input and Topographic Feedback. Phys.Rev.E (2008) 78:021911. doi:10.1103/physreve.78.021911
57. Hashemi, M, Hutt, A, and Sleigh, J. How the Cortico-Thalamic Feedback Affects the EEG Power Spectrum over Frontal and Occipital Regions during Propofol-Induced Sedation. J Comput Neurosci (2015) 39:155–79. doi:10.1007/s10827-015-0569-1
58. Klöden, PE, and Platen, E. Numerical Solution of Stochastic Differential Equations. Heidelberg: Springer-Verlag (1992).
59. Fries, P, Reynolds, J, Rorie, A, and Desimone, R. Modulation of Oscillatory Neuronal Synchronization by Selective Visual Attention. Science (2001) 291:1560–3. doi:10.1126/science.1055465
60. Tononi, G. An Information Integration Theory of Consciousness. BMC Neurosci (2004) 5:42. doi:10.1186/1471-2202-5-42
61. Alkire, MT, Hudetz, AG, and Tononi, G. Consciousness and Anesthesia. Science (2008) 322:876–80. doi:10.1126/science.1149213
62. Lee, M, Sanders, RD, Yeom, S-K, Won, D-O, Seo, K-S, Kim, HJ, et al. Network Properties in Transitions of Consciousness during Propofol-Induced Sedation. Sci Rep (2017) 7:16791. doi:10.1038/s41598-017-15082-5
63. Massimini, M, Ferrarelli, F, Huber, R, Esser, SK, Singh, H, and Tononi, G. Breakdown of Cortical Effective Connectivity during Sleep. Science (2005) 309:2228–32. doi:10.1126/science.1117256
64. Wollstadt, P, Sellers, KK, Rudelt, L, Priesemann, V, Hutt, A, Fröhlich, F, et al. Breakdown of Local Information Processing May Underlie Isoflurane Anesthesia Effects. Plos Comput Biol (2017) 13:e1005511. doi:10.1371/journal.pcbi.1005511
65. Lizier, JT, Prokopenko, M, and Zomaya, AY. Local Measures of Information Storage in Complex Distributed Computation. Inf Sci (2012) 208:39–54. doi:10.1016/j.ins.2012.04.016
66. Wibral, M, Lizier, JT, Vögler, S, Priesemann, V, and Galuske, R. Local Active Information Storage as a Tool to Understand Distributed Neural Information Processing. Front Neuroinform (2014) 8:1. doi:10.3389/fninf.2014.00001
67. Ince, RAA, Giordano, BL, Kayser, C, Rousselet, GA, Gross, J, and Schyns, PG. A Statistical Framework for Neuroimaging Data Analysis Based on Mutual Information Estimated via a Gaussian Copula. Hum Brain Mapp (2017) 38:1541–73. doi:10.1002/hbm.23471
68. Wibral, M, Pampu, N, Priesemann, V, Siebenhühner, F, Seiwert, H, Lindner, RV, et al. Measuring Information-Transfer Delays. PLoS One (2013) 8:e55809. doi:10.1371/journal.pone.0055809
69. Risken, H. The Fokker-Planck Equation — Methods of Solution and Applications. Berlin: Springer (1989).
71. Xu, C, and Roberts, AJ. On the Low-Dimensional Modelling of Stratonovich Stochastic Differential Equations. Physica A: Stat Mech its Appl (1996) 225:62–80. doi:10.1016/0378-4371(95)00387-8
72. Derrida, B, Gardner, E, and Zippelius, A. An Exactly Solvable Asymmetric Neural Network Model. Europhys Lett (1987) 4:187. doi:10.1209/0295-5075/4/2/007
73. Touboul, JD, Piette, C, Venance, L, and Ermentrout, GB. Noise-Induced Synchronization and Antiresonance in Interacting Excitable Systems: Applications to Deep Brain Stimulation in Parkinson's Disease. Phys Rev X (2019) 10:011073. doi:10.1103/PhysRevX.10.011073
74. El Boustani, S, and Destexhe, A. A Master Equation Formalism for Macroscopic Modeling of Asynchronous Irregular Activity States. Neural Comput (2009) 21:46–100. doi:10.1162/neco.2009.02-08-710
75. Soula, H, and Chow, CC. Stochastic Dynamics of a Finite-Size Spiking Neural Network. Neural Comput (2007) 19:3262–92. doi:10.1162/neco.2007.19.12.3262
76. Montbrio, E, Pazo, D, and Roxin, A. Macroscopic Description for Networks of Spiking Neurons. Phys Rev X (2015) 5:021028. doi:10.1103/physrevx.5.021028
77. Brunel, N, and Hakim, V. Fast Global Oscillations in Networks of Integrate-And-Fire Neurons with Low Firing Rates. Neural Comput (1999) 11:1621–71. doi:10.1162/089976699300016179
78. Roxin, A, Brunel, N, and Hansel, D. Rate Models with Delays and the Dynamics of Large Networks of Spiking Neurons. Prog Theor Phys Suppl (2006) 161:68–85. doi:10.1143/ptps.161.68
79. Fourcaud, N, and Brunel, N. Dynamics of the Firing Probability of Noisy Integrate-And-Fire Neurons. Neural Comput (2002) 14:2057–110. doi:10.1162/089976602320264015
80. di Volo, M, and Torcini, A. Transition from Asynchronous to Oscillatory Dynamics in Balanced Spiking Networks with Instantaneous Synapses. Phys Rev Lett (2018) 121:128301. doi:10.1103/physrevlett.121.128301
81. Arenas, A, Díaz-Guilera, A, Kurths, J, Moreno, Y, and Zhou, C. Synchronization in Complex Networks. Phys Rep (2008) 469:93–153. doi:10.1016/j.physrep.2008.09.002
82. Della Rossa, F, and DeLellis, P. Stochastic Master Stability Function for Noisy Complex Networks. Phys Rev E (2020) 101:052211. doi:10.1103/PhysRevE.101.052211
83. Hellwig, B. A Quantitative Analysis of the Local Connectivity between Pyramidal Neurons in Layers 2/3 of the Rat Visual Cortex. Biol Cybern (2000) 82:111–21. doi:10.1007/pl00007964
84. Yan, G, Martinez, ND, and Liu, Y-Y. Degree Heterogeneity and Stability of Ecological Networks. J R Soc Interf (2017) 14:20170189. doi:10.1098/rsif.2017.0189
85. Hutt, A, and Buhry, L. Study of GABAergic Extra-synaptic Tonic Inhibition in Single Neurons and Neural Populations by Traversing Neural Scales: Application to Propofol-Induced Anaesthesia. J Comput Neurosci (2014) 37:417–37. doi:10.1007/s10827-014-0512-x
86. Brunel, N. Dynamics of Sparsely Connected Networks of Excitatory and Inhibitory Spiking Neurons. J Comput Neurosci (2000) 8:183–208. doi:10.1023/a:1008925309027
87. Steinmetz, PN, Roy, A, Fitzgerald, PJ, Hsiao, SS, Johnson, KO, and Niebur, E. Attention Modulates Synchronized Neuronal Firing in Primate Somatosensory Cortex. Nature (2000) 404:187–90. doi:10.1038/35004588
88. Coull, J. Neural Correlates of Attention and Arousal: Insights from Electrophysiology, Functional Neuroimaging and Psychopharmacology. Prog Neurobiol (2019) 55:343–61. doi:10.1016/s0301-0082(98)00011-2
89. Lakatos, P, Szilágyi, N, Pincze, Z, Rajkai, C, Ulbert, I, and Karmos, G. Attention and Arousal Related Modulation of Spontaneous Gamma-Activity in the Auditory Cortex of the Cat. Cogn Brain Res (2004) 19:1–9. doi:10.1016/j.cogbrainres.2003.10.023
90. Kinomura, S, Larsson, J, Guly s, Bz., and Roland, PE. Activation by Attention of the Human Reticular Formation and Thalamic Intralaminar Nuclei. Science (1996) 271:512–5. doi:10.1126/science.271.5248.512
91. Galbraith, GC, Olfman, DM, and Huffman, TM. Selective Attention Affects Human Brain Stem Frequency-Following Response. Neuroreport (2003) 14:735–8. doi:10.1097/00001756-200304150-00015
92. Koval’zon, V. Ascending Reticular Activating System of the Brain. Transl Neurosci Clin (2016) 2:275–85. doi:10.18679/CN11-6030/R.2016.034
Keywords: coherence resonance, phase transition, stochastic process, excitable system, mean-field, random networks
Citation: Hutt A, Wahl T, Voges N, Hausmann J and Lefebvre J (2021) Coherence Resonance in Random Erdös-Rényi Neural Networks: Mean-Field Theory. Front. Appl. Math. Stat. 7:697904. doi: 10.3389/fams.2021.697904
Received: 20 April 2021; Accepted: 17 June 2021;
Published: 15 July 2021.
Edited by:
Alessandro Torcini, Université de Cergy-Pontoise, FranceReviewed by:
Matteo Di Volo, Université de Cergy-Pontoise, FranceMiguel Pineda, University College London, United Kingdom
Copyright © 2021 Hutt, Wahl, Voges, Hausmann and Lefebvre. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A. Hutt, YXhlbC5odXR0QGlucmlhLmZy
 A. Hutt
A. Hutt T. Wahl1
T. Wahl1 N. Voges
N. Voges Jo Hausmann
Jo Hausmann