Synchronization in Networks With Heterogeneous Adaptation Rules and Applications to Distance-Dependent Synaptic Plasticity

1 Introduction

In nature and technology, complex networks serve as a ubiquitous paradigm with a broad range of applications from physics, chemistry, biology, neuroscience, socioeconomic, and other systems [1]. Dynamical networks consist of interacting dynamical units, such as neurons or lasers. Collective behavior in dynamical networks has attracted much attention in recent decades. Depending on the network and the specific dynamical system, various synchronization patterns with increasing complexity were explored [2–5]. Even in simple models of coupled oscillators, patterns such as complete synchronization [6, 7], cluster synchronization [8–11], and various forms of partial synchronization have been found, such as frequency clusters [12], solitary [13–15], or chimera states [16–20]. In particular, synchronization is believed to play a crucial role in brain networks, for example, under normal conditions in the context of cognition and learning [21, 22], and under pathological conditions, such as Parkinson’s disease [23–25], epilepsy [26–29], tinnitus [30, 31], schizophrenia, to name a few [32].

The powerful methodology of master stability function [33] has been a milestone for the analysis of synchronization phenomena. This method allows for the separation of dynamic and structural features in dynamical networks. It greatly simplifies the problem by reducing the dimension and unifying the synchronization study for different networks. Since its introduction, the master stability approach has been extended and refined for various complex systems [34–42], and methods beyond the local stability analysis have been developed [43–47]. More recently, the master stability approach has been extended to another class of oscillator networks with high application potential, namely adaptive networks [48].

Adaptive networks are commonly used models for various systems from nature and technology [49–57]. A prominent example are neuronal networks with spike-timing dependent plasticity, in which the synaptic coupling between neurons changes depending on their relative spiking times [58–61]. There are a large number of studies investigating the dynamic properties induced by this form of synaptic plasticity [62]. However, analysis is usually limited to only one or two forms of spike timing-dependent plasticity within a neuronal population. On the other hand, experimental studies indicate that different forms of spike timing-dependent plasticity may be present within a neuronal population, where the form depends on the connection structure between the axons and dendrites [63]. Among all structural aspects, an important factor for the specific form of the plasticity rule is the distance between neurons [64–66]. More specifically, it has been found that the plasticity rule between proximal or distal neurons, respectively, can change from Hebbian-like to anti-Hebbian-like [67, 68].

This work introduces a methodology to study synchronization in adaptive networks with heterogeneous plasticity (adaptation) rules. As a paradigmatic system, we consider an adaptively coupled phase oscillator network [69–75], which is proven to be useful for predicting and describing phenomena occurring in more realistic and detailed models [76–79]. More specifically, in the spirit of the master stability function approach, we consider the synchronization problem as the interplay between network structure and a heterogeneous adaptation rule arising from distance- (or location-)dependent synaptic plasticity. For a given heterogeneous adaptation rule, our master stability function provides synchronization criteria for any coupling configuration. As illustrative examples, we consider a nonlocally coupled ring with biologically motivated plasticity rule, and a network with a Gaussian distance-dependent coupling weights. We explained such intriguing effects as synchronization or desynchronization by enhancement of long-distance links.

We introduce the model in Section 2. Building on findings from [48], we develop a master stability approach in Section 3 that takes a heterogeneous adaptation rule in account. In Section 4.1, we provide an approximation of the structural eigenvalues that determine the stability of the synchronous state. We then consider two different setups: a nonlocally coupled ring in Section 4.2 and a weighted network with Gaussian distance distribution of coupling weights in Section 4.3. Both systems are equipped with a biologically motivated plasticity rule. In Section 5, we summarize the results.

2 Model

In this work, we study the synchronization on networks with adaptive coupling weights, where the adaptation (plasticity) rule depends on the distance between oscillators (neurons). We consider the model of adaptively coupled phase oscillators, which has proven to be useful for understanding dynamics in neuronal systems with spike timing-dependent plasticity [77, 79, 48]. The model reads as follows:

$\frac{\text{d}}{\text{d}t}{\varphi }_i=\omega +\stackrel{N}{{\displaystyle \sum }_{j=1}}{a}_{ij}{\kappa }_{ij}g\left({\varphi }_i-{\varphi }_j\right),(1)$

$\frac{\text{d}}{\text{d}t}{\kappa }_{ij}=-\mathit{ϵ}\left({\kappa }_{ij}+h_{ij}\left({\varphi }_i-{\varphi }_j\right)\right),(2)$

where ${\varphi }_i\in S^1=\mathrm{ℝ}/2\pi \mathrm{\mathbb{Z}}$ ($i=1,\dots ,N$) is the phase of the ith oscillator, ${\kappa }_{ij}$ ($i,j=1,\dots ,N$) is the dynamical coupling weight from oscillator j to i, ω denotes the natural frequency of each oscillator, and $a_{ij}\in \left[\mathrm{0,1}\right]$ are the entries of the weighted adjacency matrix A describing the network connectivity. The time scales of the “fast” phase oscillators and “slow” coupling weights are separated by the parameter ϵ, which we assume to be small $0<\mathit{ϵ}\ll 1$. The functions g and $h_{ij}$ denote the coupling and the $N^2$ plasticity functions, respectively. For illustrative purposes, the coupling function is set throughout the paper to $g\left(\varphi \right)=-\text{sin}\left(\varphi +\alpha \right)/N$ with the phase lag parameter α [80]. Such a phase lag can account for a small synaptic propagation delay [81, 48]. For formal derivations, however, a generic coupling function is used. Note that the system Eqs. 1, 2 is shift-symmetric, i.e., invariant under the transformation ${\varphi }_i\mapsto {\varphi }_i+\psi$ for any $\psi \in S^1$. This allows us to restrict our consideration to the case $\omega =0$ by introducing a new “co-rotating” coordinate system ${\varphi }_{i,\text{new}}={\psi }_i-\omega t$.

The main difference of system Eqs. 1, 2 from the models considered previously in the literature [40, 70, 71, 74, 82], is that the plasticity functions $h_{ij}$ can be different for each network connection $j\to i$.

A solution to Eqs. 1, 2 is called phase-locked if, for all $i=1,\dots ,N$, the phases evolve as ${\varphi }_i=\text{Ω}t+{\vartheta }_i$ with some collective frequency$\text{Ω}\in \mathrm{ℝ}$ and ${\vartheta }_i\in S^1$. If ${\vartheta }_i=\vartheta$ for all $i=1,\dots ,N$, the phase-locked state is called in-phase synchronous or, short, synchronous state.

In the case of in-phase synchronous state, we can set ${\vartheta }_i=0$ for each oscillator due to the shift symmetry of Eqs. 1, 2. The in-phase synchronous state is given as

${\varphi }^s\left(t\right)=-wg\left(0\right)t,(3)$

${\kappa }_{ij}^s=-h_{ij}\left(0\right),(4)$

where we assume that the weighted row sum $w={\displaystyle {\sum }_{j=1}^N{a}_{ij}{h}_{ij}\left(0\right)}$ is constant for all. Such an assumption of constant row sum is necessary for the existence of the synchronous state. Moreover, it is satisfied for commonly considered cases of global or nonlocal shift-invariant coupling.

In the following section, we show how the stability of the synchronous state is determined in a master-stability-like approach.

3 Master Stability Approach

In Section 2, we have introduced a general class of models and the synchronous state, that are considered throughout this paper. In this section, we derive a framework for the local stability analysis of the synchronous states. We note that the master stability approach for homogeneous adaptations $h_{ij}=h$ was introduced in [48, 83]. Here we extend the methodology to heterogeneous adaptation rules.

To describe the local stability, we introduce the variations ${\xi }_i={\varphi }_i-{\varphi }^s$ and ${\chi }_{ij}={\kappa }_{ij}-{\kappa }_{ij}^s$. The linearized equations for these variations can be written in the following matrix form

$\frac{\text{d}}{\text{d}t}\left(\begin{array}{c}\mathit{\xi }\\ \mathit{\chi }\end{array}\right)=J\left(\begin{array}{c}\mathit{\xi }\\ \mathit{\chi }\end{array}\right)=\left(\begin{array}{cc}\text{D}g\left(0\right)L^h& g\left(0\right)B\\ -\mathit{ϵ}C& -\mathit{ϵ}{\mathbb{I}}_{N^2}\end{array}\right)\left(\begin{array}{c}\mathit{\xi }\\ \mathit{\chi }\end{array}\right),(5)$

where $\mathit{\xi }={\left({\xi }_1,\dots ,{\xi }_N\right)}^T$ is N-dimensional vector containing the perturbations ${\xi }_i=\delta {\varphi }_i$ of the phases and $\mathit{\chi }={\left({\chi }_{11},{\chi }_{12},\dots ,{\chi }_{NN}\right)}^T$ are $N^2$- dimensional vectorized perturbations of coupling weights $\mathit{\chi }=\mathbf{vec}\left[\delta {\kappa }_{ij}\right]$, respectively. The $N\times N$ weighted Laplacian matrix $L^h$ has the following elements

$l_{ij}^h=\{\begin{array}{cc}-{\displaystyle {\sum }_{m=1,m\ne i}^N{a}_{im}{h}_{im}\left(0\right)},& i=j,\\ a_{ij}{h}_{ij}\left(0\right),& i\ne j.\end{array}(6)$

The time-independent matrices B and C are

$B=\left(\begin{array}{ccc}{\mathit{a}}_1& & \\ & \ddots & \\ & & {\mathit{a}}_N\end{array}\right),C=\left(\begin{array}{ccc}{\left(\text{D}h\right)}_1^T& & \\ & \ddots & \\ & & {\left(\text{D}h\right)}_N^T\end{array}\right)-\left(\begin{array}{c}\text{diag}{\left(\text{D}h\right)}_1\\ ⋮\\ \text{diag}{\left(\text{D}h\right)}_N\end{array}\right),$

where ${\mathit{a}}_i=\left(a_{i1},\dots ,a_{iN}\right)$, ${\left(\text{D}h\right)}_i=\left(\text{D}{h}_{i1}\left(0\right),\dots ,\text{D}{h}_{iN}\left(0\right)\right)$, and

$\text{diag}{\left(\text{D}h\left(0\right)\right)}_i=\left(\begin{array}{ccc}\text{D}{h}_{i1}\left(0\right)& & \\ & \ddots & \\ & & \text{D}{h}_{iN}\left(0\right)\end{array}\right).$

Note that due to the shift symmetry of Eqs. 1, 2, the Jacobian J in Eq. 5 is time independent. Therefore, the real parts of the $N\left(N+1\right)$ eigenvalues λ of J are the Lyapunov exponents of the synchronous state and hence determine its local stability. In the following proposition, we exploit the fact that J contains a large diagonal block $-\mathit{ϵ}{\mathbb{I}}_{N^2}$ to reduce the dimension of the eigenvalue problem for J.

Proposition 1. Suppose${\varphi }_i=\text{Ω}t$is an in-phase synchronous state of Eqs. 1, 2. Then its linear stability is determined by the $2N$-dimensional linear system

$\frac{\text{d}}{\text{d}t}\mathit{v}=\left(\begin{array}{cc}\text{D}g\left(0\right)L^h& g\left(0\right){\mathbb{I}}_N\\ \mathit{ϵ}{L}^{\text{D}h}& -\mathit{ϵ}{\mathbb{I}}_N\end{array}\right)\mathit{v},(7)$

where $\text{D}g\left(0\right)$ and $L^h$are as in Eq. 5and the$N\times N$ weighted Laplacian matrix $L^{\text{D}h}$possesses the following elements

$l_{ij}^{\text{D}h}=\{\begin{array}{ll}-{\displaystyle {\sum }_{m=1,m\ne i}^N{a}_{im}\text{D}{h}_{im}\left(0\right)},\hfill & i=j,\hfill \\ a_{ij}\text{D}{h}_{ij}\left(0\right),\hfill & i\ne j.\hfill \end{array}(8)$

Proof. We remind that system Eq. 5 determines the spectrum (Lyapunov exponents) of the synchronous state. The Jacobian matrix in Eq. 5 is sparse with a large $N^2\times N^2$ block given by the simple diagonal matrix $-\mathit{ϵ}{\mathbb{I}}_{N^2}$. This implies that Eq. 5 possess $N^2-N$ stable directions with Lyapunov exponents $-\mathit{ϵ}$. To find these directions, we substitute $\left(\mathit{\xi },\mathit{\chi }\right)=e^{-\mathit{ϵ}t}\left({\mathit{\xi }}_0,{\mathit{\chi }}_0\right)$ into Eq. 5 and obtain the linear system

$\left(\begin{array}{cc}\text{D}g\left(0\right)L^h+\mathit{ϵ}{\mathbb{I}}_N& g\left(0\right)B\\ -\mathit{ϵ}C& 0\end{array}\right)\left(\begin{array}{c}{\mathit{\xi }}_0\\ {\mathit{\chi }}_0\end{array}\right)=0.(9)$

This system has at least $N^2-N$ linearly independent solutions, since the matrix in Eq. 9 is degenerate due to the large $N^2\times N^2$ zero block. The structure of the invariant subspaces in system Eq. 5 allows for introducing new coordinates, which separate the $N^2-N$ stable directions (corresponding to the eigenvalues $-\mathit{ϵ}$) from the remaining $2N$ directions. Explicitly, this transformation is given by

$\left(\begin{array}{c}\mathit{\xi }\\ \mathit{\chi }\end{array}\right)=R\left(\begin{array}{c}\mathit{\xi }\\ \widehat{\mathit{\chi }}\end{array}\right),R=\left(\begin{array}{ccc}{\mathbb{I}}_N& 0& 0\\ 0& \left(1/r\right)B^T& K\end{array}\right)$

with $\left(N^2+N\right)\times \left(N^2+N\right)$ matrix R. Here K is an $\left(N^2-N\right)\times \left(N^2-N\right)$ orthogonal matrix with $BK=0$. Applying this transformation, we obtain the following system

$\frac{\text{d}}{\text{d}t}\left(\begin{array}{c}\mathit{\xi }\\ {\mathit{\chi }}_N\\ {\mathit{\chi }}_{N^2-N}\end{array}\right)=\left(\begin{array}{ccc}\text{D}g\left(0\right)L^h& g\left(0\right){\mathbb{I}}_N& 0\\ \mathit{ϵ}{L}^{\text{D}h}& -\mathit{ϵ}{\mathbb{I}}_N& 0\\ -\mathit{ϵ}{K}^{T}C& 0& -\mathit{ϵ}{\mathbb{I}}_{N^2-N}\end{array}\right)\left(\begin{array}{c}\mathit{\xi }\\ {\mathit{\chi }}_N\\ {\mathit{\chi }}_{N^2-N}\end{array}\right),(10)$

where ${\left(\mathit{\xi },{\mathit{\chi }}_N,{\mathit{\chi }}_{N^2-N}\right)}^T={\left(\mathit{\xi },\widehat{\mathit{\chi }}\right)}^T,$ with ${\mathit{\chi }}_N$ and ${\mathit{\chi }}_{N^2-N}$ are an N and $N^2-N$-dimensional vectors, respectively, and the $N\times N$ weighted Laplacian matrix $L^{\text{D}h}$ as given in Eq. 8. For more details on the transformation, we refer the reader to [48, 83]. We observe that the variables $\left(\mathit{\xi },{\mathit{\chi }}_N\right)$ are independent on ${\mathit{\chi }}_{N^2-N}$. Hence, separating the master from the slave system, the resulting coupled differential equations that determine the stability of the synchronous state are given by system Eq. 7. This concludes the proof. Proposition 1 reduces the problem’s dimension significantly from $N\left(N+1\right)$ to $2N$. In the spirit of the master stability approach [33], we aim for further decomposition of the $2N$- dimensional coupled system Eq. 7 into dynamically independent blocks of dimension 2. For this, we restrict our consideration to the case when $L^h$ can be diagonalized $S^h=Q^{-1}{L}^{h}Q$ by a nonsingular complex-valued matrix Q. Note that the eigenvalues ${\mu }_i$ of $L^h$ lie on the diagonal of $S^h$. In general, the matrices $L^h$ and $L^{\text{D}h}$ do not commute. Therefore, $Q^{-1}{L}^{\text{D}h}Q$ is not necessarily of upper triangular shape. Regardless of this fact, the following proposition provides an explicit form for the eigenvalues of J in Eq. 5 in the limit of slow adaptation, i.e., $\mathit{ϵ}\ll 1$.

Proposition 2. Assume that$L^h$is diagonalizable, with$S^h=Q^{-1}{L}^{h}Q$being the associated diagonal matrix and Q the corresponding transformation. Let${\varphi }_i=\text{Ω}t$be an in-phase synchronous state ofEqs. 1, 2Then, the local stability of this state is determined by the solutions of N quadratic equations, which are given up to the first order in ϵ as

${\lambda }^2+\left(\mathit{ϵ}-\text{D}g\left(0\right){\mu }_i\right)\lambda -\mathit{ϵ}\left(\text{D}g\left(0\right){\mu }_i+g\left(0\right){\nu }_i\right)=0,i=1,\dots ,N,(11)$

where${\mu }_i$are the eigenvalues of$L^h$located on the diagonal of$S^h$and${\nu }_i$are the corresponding diagonal elements of$Q^{-1}{L}^{\text{D}h}Q$. If$L^h$and$L^{\text{D}h}$commute, thenEq. 11is exact, and${\nu }_i$are the eigenvalues of$L^{\text{D}h}$.Proof. Due to Proposition 1, the eigenvalues of the Jacobian in Eq. 5 are given by

$\text{det}\left(\begin{array}{cc}\text{D}g\left(0\right)L^h-\lambda {\mathbb{I}}_N& g\left(0\right){\mathbb{I}}_N\\ \mathit{ϵ}{L}^{\text{D}h}& -\left(\mathit{ϵ}+\lambda \right){\mathbb{I}}_N\end{array}\right)=\text{det}\left(\begin{array}{cc}\text{D}g\left(0\right)S^h-\lambda {\mathbb{I}}_N& g\left(0\right){\mathbb{I}}_N\\ \mathit{ϵ}{Q}^{-1}{L}^{\text{D}h}Q& -\left(\mathit{ϵ}+\lambda \right){\mathbb{I}}_N\end{array}\right)=0,$

where we have used the transformation Q that brings $L^h$ to the diagonal form $S^h=Q^{-1}{L}^{h}Q$. Making further use of the Schur complement [84], we obtain

$\text{det}\left(\begin{array}{cc}\text{D}g\left(0\right)S^h-\lambda {\mathbb{I}}_N& g\left(0\right){\mathbb{I}}_N\\ \mathit{ϵ}{Q}^{-1}{L}^{\text{D}h}Q& -\left(\mathit{ϵ}+\lambda \right){\mathbb{I}}_N\end{array}\right)=\text{det}\left(\begin{array}{c}\left(\lambda +\mathit{ϵ}\right)\left(\lambda {\mathbb{I}}_N-\text{D}g\left(0\right)S^h\right)-\mathit{ϵ}g\left(0\right)Q^{-1}{L}^{\text{D}h}Q\end{array}\right)=0.(12)$

The latter equation is almost diagonal. The only off-diagonal components remain from $Q^{-1}{L}^{\text{D}h}Q$ and scale with ϵ. Let us consider the Leibniz formula for the determinant of an $N\times N$ matrix F with entries $f_{ij}$, that reads $\text{det}\left(F\right)={\displaystyle {\sum }_{\sigma \in \text{Perm}\left(N\right)}\text{sgn}\left(\sigma \right)}{\displaystyle {\prod }_{i=1}^N{f}_{i\sigma \left(i\right)}}$. In the latter expression $\text{Perm}\left(N\right)$ denotes the set of all permutations σ of the integer numbers $1,\dots ,N$ and $\text{sgn}\left(\sigma \right)\in \left\{-\mathrm{1,1}\right\}$ is the sign of the permutation. Since all off-diagonal terms of the matrix considered in Eq. 12 scale with ϵ, for any but the identical permutation each term ${\displaystyle {\prod }_{i=1}^N{f}_{i\sigma \left(i\right)}}$ scales with ${\mathit{ϵ}}^2$ or higher. Hence, we are left with $\text{det}\left(F\right)={\displaystyle {\prod }_{i=1}^N{f}_{ii}+\mathrm{\prod }\left({\mathit{ϵ}}^2\right)}$ and find

$\text{det}\left(\begin{array}{c}\left(\lambda +\mathit{ϵ}\right)\left(\lambda {\mathbb{I}}_N-\text{D}g\left(0\right)S^h\right)-\mathit{ϵ}g\left(0\right)Q^{-1}{L}^{\text{D}h}Q\end{array}\right)={\displaystyle \prod _{i=1}\left({\lambda }^2+\left(\mathit{ϵ}-\text{D}g\left(0\right){\mu }_i\right)\lambda -\mathit{ϵ}\left(\text{D}g\left(0\right){\mu }_i+g\left(0\right){\nu }_i\right)\right)}+\mathrm{\prod }\left({\mathit{ϵ}}^2\right)=0,(13)$

where ${\mu }_i$ are the eigenvalues of $L^h$, ${\nu }_i$ are the diagonal elements of $Q^{-1}{L}^{\text{D}h}Q$ and $\mathrm{\prod }\left({\mathit{ϵ}}^2\right)$ denotes higher order terms (${\mathit{ϵ}}^m,m>1$). If $L^h$ and $L^{\text{D}h}$ commute, both matrices share the same set of eigenvectors and hence they can be brought to the diagonal form with the same transformation Q. In this case, the diagonal elements ${\nu }_i$ are the eigenvalues of $L^{\text{D}h}$ and the higher order terms $\mathrm{\prod }\left({\mathit{ϵ}}^2\right)$ in Eq. 13 vanish.The $2N$ solutions ${\lambda }_i$ of the NEq. 11 determine the stability of the synchronous state. More precisely, the real parts of theses solutions determine the Lyapunov exponents. If $\text{Λ}={\text{max}}_i\text{Re}\left({\lambda }_i\right)<0$, then the synchronous state is locally stable, while for $\text{Λ}>0$ it is locally unstable. The case $\text{Λ}=0$ provides the stability boundary.Note that for a fixed time scale parameter $\mathit{ϵ}\ll 1$, the Eq. 11 and hence its solutions depend on the coupling function g, the connectivity, and the adaptation structure. This dependence, however, is only encoded in the two complex parameters $\text{D}g\left(0\right)\mu$ and $g\left(0\right)\nu$. Therefore, we define the master stability function $\text{Λ}:{\mathrm{ℂ}}^2\to \mathrm{ℝ}$ with $\text{Λ}\left(\text{D}g\left(0\right)\mu ,g\left(0\right)\nu \right)={\text{max}}_i\text{Re}\left({\lambda }_i\left(\text{D}g\left(0\right)\mu ,g\left(0\right)\nu \right)\right)$ that maps each pair of parameters $\left(\text{D}g\left(0\right)\mu ,g\left(0\right)\nu \right)$ to the corresponding Lyapunov exponent.For an illustration, we consider a cross-section of $\left(\text{D}g\left(0\right)\mu ,g\left(0\right)\nu \right)$- space by setting $\text{Im}\left(\mu \right)=0$ and $\text{Im}\left(\nu \right)=0$. This cross-section is of particular interest in cases of symmetric matrices $L^h$ and $L^{\text{D}h}$ since their eigenvalues are real. In Figure 1, we present the master stability function for the coupling function $g\left(\varphi \right)=-\text{sin}\left(\varphi +\alpha \right)/N$ and different values of the parameter α. In case of real μ and ν, we obtain two explicit stability conditions from Eq. 11: The synchronous state is locally stable ($\text{Λ}<0$) if

$c_1\left(\alpha ,\mu \right)=\text{cos}\left(\alpha \right)\mu >-\mathit{ϵ},(14)$

$c_2\left(\alpha ,\mu ,\nu \right)=\text{cos}\left(\alpha \right)\mu +\text{sin}\left(\alpha \right)\nu >0.(15)$

These conditions agree with the black dashed lines in Figure 1 and are used subsequently to describe stability for certain network models.

FIGURE 1

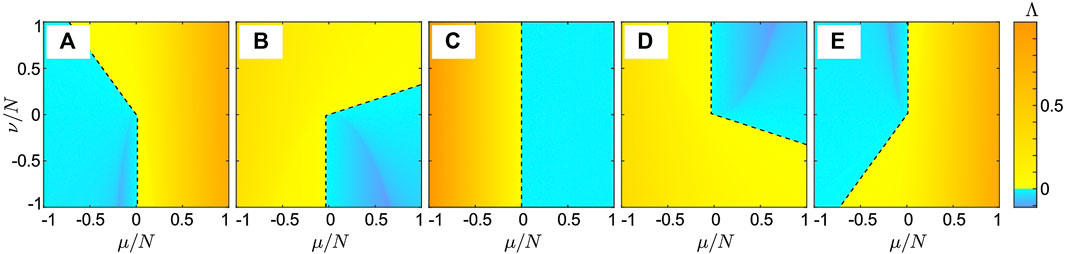
FIGURE 1. The master stability function $\text{Λ}\left(\text{D}g\left(0\right)\mu ,g\left(0\right)\nu \right)$ for the coupling function $g\left(\varphi \right)=-\text{sin}\left(\varphi +\alpha \right)/N$ and real μ and ν ($\text{Im}\left(\mu \right)=0$, $\text{Im}\left(\nu \right)=0$). The values of the master stability function are color-coded in all panels (A–E). The dashed black line describes the border between regions corresponding to local stability and instability, respectively. Parameters: $\mathit{ϵ}=0.01$, (A)$\alpha =-0.8\pi$, (B)$\alpha =-0.4\pi$, (C)$\alpha =0$, (D)$\alpha =0.4\pi$, and (E)$\alpha =0.8\pi$.

4 Synchronization on Networks With Distance-Dependent Plasticity

In the previous section, we established a generic analytic tool for studying stability of synchronous states. In this section, we focus on the application of the tool to certain network models. For the rest of the work, we restrict our attention to the following generalization of the Kuramoto-Sakaguchi system with distance-dependent synaptic plasticity

$\frac{\text{d}}{\text{d}t}{\varphi }_i=\omega -\frac{1}{N}\stackrel{N}{{\displaystyle \sum }_{j=1}}{a}_{ij}{\kappa }_{ij}\text{sin}\left({\varphi }_i-{\varphi }_j+\alpha \right),(16)$

$\frac{\text{d}}{\text{d}t}{\kappa }_{ij}=-\mathit{ϵ}\left({\kappa }_{ij}+h\left({\varphi }_i-{\varphi }_j,d_{ij}\right)\right).(17)$

The plasticity function h depends on the phase difference ${\varphi }_i-{\varphi }_j$ and on the distance $d_{ij}$. In this work, we associate the distance to the difference of indices by $d_{ij}=\left|j-i\right|$. For the plasticity function, we consider

$h_{ij}\left(\varphi \right)=h\left(\varphi ,\frac{d_{ij}}{N}\right)=\{\begin{array}{cc}\widehat{h}\left(\varphi ,\frac{d_{ij}}{N}\right)& d_{ij}\le N/2,\\ \widehat{h}\left(\varphi ,1-\frac{d_{ij}}{N}\right)& d_{ij}>N/2.\end{array}(18)$

With this form of the adaptation function, we have a symmetric $h_{ij}\left(\varphi \right)=h_{ji}\left(\varphi \right)$ and a circulant $h_{i+l,j+l}\left(\varphi \right)=h_{ij}\left(\varphi \right)$ structure of the corresponding matrix with entries $h_{ij}$. Particularly, for the numerical analysis, we use

$\widehat{h}\left(\varphi ,d_{ij}/N\right)=\text{sin}\left(\varphi +\beta \left(d_{ij}/N\right)\right),(19)$

where the distance dependence is encoded in the phase shift function

$\beta \left(\frac{d_{ij}}{N}\right)=\{\begin{array}{cc}\left(\frac{2}{N}{d}_{ij}-1\right)\pi ,& N\text{ even},\\ \left(\frac{2}{\left(N+1\right)}{d}_{ij}-1\right)\pi ,& N\text{ odd}.\end{array}(20)$

In Figure 2A, we illustrate the distance-dependent plasticity function Eqs. 18–20 for a network of $N=12$ nodes. The illustration shows the different plasticity functions depending on the distance between the nodes $d_{ij}$. The plasticity function changes from a Hebbian to anti-Hebbian rule for proximal and distal node, respectively. This change, particularly in the proximity of $\varphi =0$, is in qualitative agreement with the experimental findings in [67]. Note the symmetry of the plasticity function that renders the matrix with elements $h_{ij}$ circulant.

FIGURE 2

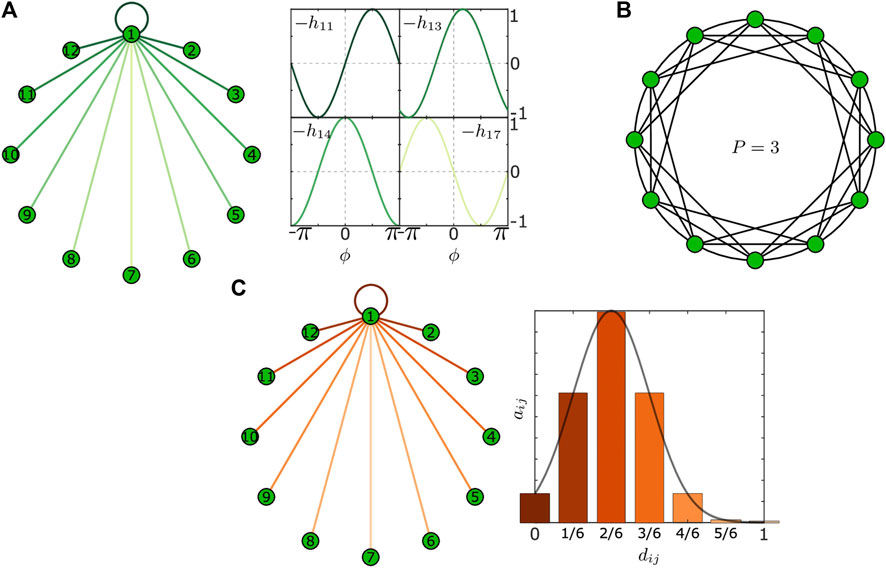
FIGURE 2. Panel (A) shows the plasticity function $h_{1j}$ given in Eqs. 18–20 depending on the distance $d_{1j}$ exemplified for node $i=1$ in a network with $N=12$ nodes. Note that the colors of the links in the network (left) correspond to the colors of the depicted plasticity function (right). Panel (B) displays the connectivity structure of a nonlocally coupled ring network with $N=12$ nodes and a coupling range $P=3$. Panel (C) displays the weighted connectivity structure of a network with $N=12$ nodes (left) with distance-dependent Gaussian weight distribution (right). Note that the colors of the links in the network (left) correspond to the colors of the bars in the weight distribution (right).

If not indicated differently, we consider the coupling structure given by

$a_{ij}=a\left(d_{ij}/N\right),(21)$

where $a:\left[\mathrm{0,1}\right]\to \left[\mathrm{0,1}\right]$ is a bounded and piece-wise continuous function. This corresponds to a distant-dependent coupling, and it results to a dihedral symmetry in the coupling structure (ring-like).

In the following section, we provide an approximation for the eigenvalues of $L^h$ and $L^{\text{Dh}}$ for large networks with circulant connectivity and plasticity structure. Using this approximation, we subsequently analyze the stability of the synchronous state on nonlocally coupled networks and on isotropic networks with Gaussian weight distribution.

4.1 Approximation of the Eigenvalues for Large Systems With Circulant Structure

In the previous part, we have defined the plasticity functions $h_{ij}$ in such a way that the structures of $L^h$ and $L^{\text{D}h}$ inherit important properties from the underlying network structure $a\left(d_{ij}/N\right)$. In particular, assuming that the adjacency matrix is circulant, renders $L^h$ and $L^{\text{D}h}$ to be circulant, as well.

In this section, we briefly recall how one can derive the eigenvalues ${\mu }_k$ and ${\nu }_k$ ($k=0,\dots ,N-1$) in case of a circulant structure. It is well-known that for a circulant matrix the eigenvalues are determined by applying a discrete Fourier approach [85]. More precisely, suppose L is a circulant $N\times N$ matrix where the elements of the first row are given by the entries $l_j$ with $j=1,\dots ,N$. Then the kth eigenvalue is explicitly given by

${\mu }_k=l_1+\stackrel{N}{{\displaystyle \sum }_{j=2}}{l}_j\exp \left(\text{i}\frac{2\pi }{N}\left(j-1\right)k\right).$

For the case of $L^h$ as in Eq. 6, $a_{ij}$ and $h_{ij}$ as in Eqs. 18 and 21, we obtain

$\text{Re}\left({\mu }_k\right)=\text{Re}\left(l_{11}^h\right)+\frac{1}{N}\stackrel{N}{{\displaystyle \sum }_{j=2}}a\left(x_j\right)h\left(0,x_j\right)\text{cos}\left(2\pi x_{j}k\right),(22)$

with $x_j=d_{1j}/N$ and $\text{Re}\left(l_{11}^h\right)=-\frac{1}{N}{\displaystyle {\sum }_{j=2}^{N}a\left(x_j\right)h\left(0,x_j\right)}$. Since the adjacency matrix A is assumed to be symmetric, the eigenvalues of $L^h$ are real. Therefore, we omit considering the imaginary part of ${\mu }_k$. Eq. 22 provides exact expressions for the eigenvalues. However, the values depend on the total number of oscillators N that makes it harder to study the influence of other system properties, such as the coupling structure or the plasticity function. To remove this N-dependence, we consider the continuum limit $N\to \infty$ (compare with [86]) and obtain

$\text{Re}\left({\mu }_k\right)=\text{Re}\left(l_{11}^h\right)+{\displaystyle {\int }_0^{1}a\left(x\right)h\left(0,x\right)\text{cos}\left(2\pi xk\right)\text{d}x},$

Due to the definition of h and the symmetry of $a\left(x\right)$, we find

$\text{Re}\left({\mu }_k\right)=2{\displaystyle {\int }_0^{1/2}a\left(x\right)h\left(0,x\right)\left(\text{cos}\left(2\pi xk\right)-1\right)\text{d}x}(23)$

for any k. This explicit expression allows studying the distribution of the eigenvalues ${\mu }_k$ for a given plasticity function h and coupling structure a. Note that a similar expression as (23) can be analogously derived for the eigenvalues of $L^{\text{D}h}$ and reads

$\text{Re}\left({\nu }_k\right)=2{\displaystyle {\int }_0^{1/2}a\left(x\right)\text{D}h\left(0,x\right)\left(\text{cos}\left(2\pi xk\right)-1\right)\text{d}x}.(24)$

We note that ${\mu }_0={\nu }_0=0$ due to the Laplacian structure of $L^h$ and $L^{\text{D}h}$.

The results from Eqs. 23 and 24 are applied in the next sections to analyze different networks.

4.2 Synchronization on Nonlocally Coupled Ring Networks

In this section, we analyze the effect of long distance connections on the stability of synchronous states in nonlocally coupled ring networks. We consider the coupling structure given by

$a_{ij}=a\left(d_{ij}/N\right)=\{\begin{array}{ll}1\text{for}0<d_{ij}\le P,\hfill & \hfill \\ 1\text{for}0<N-d_{ij}\le P,\hfill & \hfill \\ 0\text{otherwise}.\hfill & \hfill \end{array}(25)$

This means that any two oscillators are coupled if they are separated at most by the coupling range P. The coupling Eq. 25 defines a nonlocal ring structure with coupling range p to each side and two special limiting cases: local ring for $P=1$ and globally coupled network for $P=N/2$ (if N is even, else $P=\left(N+1\right)/2$). The matrix of the form Eq. 25 is circulant [85] and has constant row sum, i.e., ${\displaystyle {\sum }_{j=1}^N{a}_{ij}}=2P$ for all $i=1,\dots ,N$. An illustration for $N=12$ adn $P=3$ is presented in Figure 2B.

In order to study the influence of the coupling range, we use the approximations for the eigenvalues ${\mu }_k$ and ${\nu }_k$ derived in Section 4.1. The nonlocally coupled ring structure is expressed by the piecewise continuous function $a\left(x\right)=0$ for $p<x<1-p$ and $a\left(x\right)=1$ otherwise with relative coupling range $p=P/N$. Thus, for a nonlocally coupled ring Eq. 25 and plasticity function Eqs. 18–20, we find

$\text{Re}\left({\mu }_k\right)=-2{\displaystyle {\int }_0^p\text{sin}\left(2\pi x\right)\left(\text{cos}\left(2\pi kx\right)-1\right)\text{d}x}=\frac{\left(1-\text{cos}\left(2\pi p\right)\right)}{\pi }+\frac{1}{\pi }\{\begin{array}{ll}\frac{1}{2}\left({\text{cos}}^2\left(2\pi p\right)-1\right)\hfill & k=1\hfill \\ \frac{1}{\left(1-k^2\right)}\left(k\text{sin}\left(2\pi p\right)\text{sin}\left(2\pi kp\right)+\text{cos}\left(2\pi p\right)\text{cos}\left(2\pi kp\right)-1\right)\hfill & k\ne 1\hfill \end{array}(26)$

for the eigenvalues ${\mu }_k$ of $L^h$. Analogously, we obtain

$\text{Re}\left({\nu }_k\right)=-2{\displaystyle {\int }_0^p\text{cos}\left(2\pi x\right)\left(\text{cos}\left(2\pi kx\right)-1\right)\text{d}x}=\frac{\text{sin}\left(2\pi p\right)}{\pi }-\frac{1}{\pi }\{\begin{array}{cc}p\pi +\frac{\text{sin}\left(4\pi p\right)}{4}& k=1\\ \frac{1}{\left(1-k^2\right)}\left(\text{sin}\left(2\pi p\right)\cos \left(2\pi kp\right)-k\cos \left(2\pi p\right)\text{sin}\left(2\pi kp\right)\right)& k\ne 1\end{array}(27)$

for ${\nu }_k$ of $L^{\text{D}h}$.

In Figure 3A, we provide an error analysis of the approximations Eqs. 26 and 27 compared to the exact eigenvalues given by Eq. 22. As expected, the errors tend to zero as the number of oscillators increases. Additionally in Figures 3B,C, we display ${\mu }_k$ and ${\nu }_k$ for several values of k depending on the relative coupling range p. We observe that ${\mu }_k\ge 0$ for all k. This is due to given plasticity function Eqs. 18–20, for which the update is positive (or equal to zero) for all distances at $\varphi =0$, i.e., $h\left(0,d_{ij}\right)\ge 0$ for all $d_{ij}$.

FIGURE 3

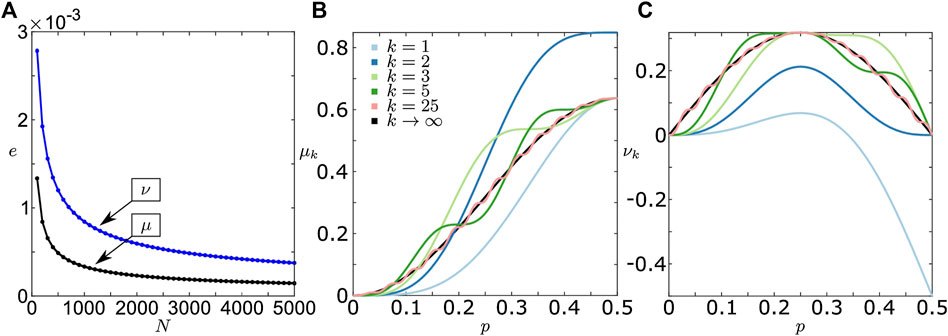
FIGURE 3. Panel (A) shows the errors $e\left(\mu \right)$ (black) and $e\left(\nu \right)$ (blue) with $e\left(\gamma \right)=\sqrt{\frac{{{{\displaystyle \sum }}^{\text{}}}_{k=0}^{N-1}{\left({\gamma }_k^{\text{exact}}-{\gamma }_k\right)}^2}{N}}$ of the approximations Eqs. 26, 27, respectively, where ${\gamma }_k^{\text{exact}}$ are the exact eigenvalues derived by a discrete Fourier transformation, see Eq. 22. The errors are displayed in dependence of the system size N (number of oscillators). The relative coupling range is set to $p=0.1$. Panel (B) and (C) show the approximated eigenvalues given by Eqs. 26, 27, respectively, depending on the relative coupling range p for different values of k.

It is important to note, that our choice of the circulant adaptation functions imply that the matrices $L^h$ and $L^{\text{D}h}$ are diagonalizable and commute. Hence, Proposition 2 holds with the master stability Eq. 11 being exact. Therefore, the stability criterium Eq. 14 is also exact.

Combining the fact ${\mu }_k\ge 0$ with the stability criterium Eq. 14, we find $\text{cos}\left(\alpha \right)>0$ as a necessary condition for the stability of the synchronous state for $\mathit{ϵ}\to 0$. This yields, that the synchronous state can be stable only for $\alpha \in \left(-\pi /2,\pi /2\right)$. In contrast to $L^h$, the $L^{\text{D}h}$ is in general neither positive nor negative definite, hence the eigenvalues ${\nu }_k$ may take positive or negative values. This is due to the fact that the plasticity function may change sign at the origin, i.e., $\text{D}{h}_{ij}$ may change signs depending on the distance $d_{ij}$. In particular, we find that only the eigenvalue ${\nu }_1$ changes the sign, see Figure 3C. This change may lead to a destabilization of the synchronous states as we show in the subsequent analysis. Finally, note that there exist ${\mu }_{\infty }=\left(1-\text{cos}\left(2\pi p\right)\right)/\pi$ and ${\nu }_{\infty }=-\text{sin}\left(2\pi p\right)/\pi$ to which the eigenvalues converge for large values of k. These limits are displayed in Figures 3B,C as black lines.

In Figure 4, we show different scenarios for the stability of the synchronous state depending on the phase lag parameter α and the coupling range p. Due to the necessary condition $\text{cos}\left(\alpha \right)>0$ as $\mathit{ϵ}\to 0$, we consider $\alpha \in \left(-\pi /2,\pi ,2\right)$ only. Figures 4A,B show that for $-\pi /2<\alpha <0$, the second stability condition Eq. 15 is only fulfilled for p larger than a critical value of the coupling range $p_c\left(\alpha \right)$. In these cases, a higher coupling range stabilizes the synchronous state. Note that $p_c\left(\alpha \right)\to 0$ as $\alpha \to 0$ with $\alpha <0$. The results seen in Figures 4A,B are in agreement with the results for a network of $N=200$ coupled phase oscillators. For this network, we calculate the Laplacian eigenvalues and plot them along with the master stability function in Figures 4E,F. The outcomes from numerical simulations are presented in Figures 4I,J.

FIGURE 4

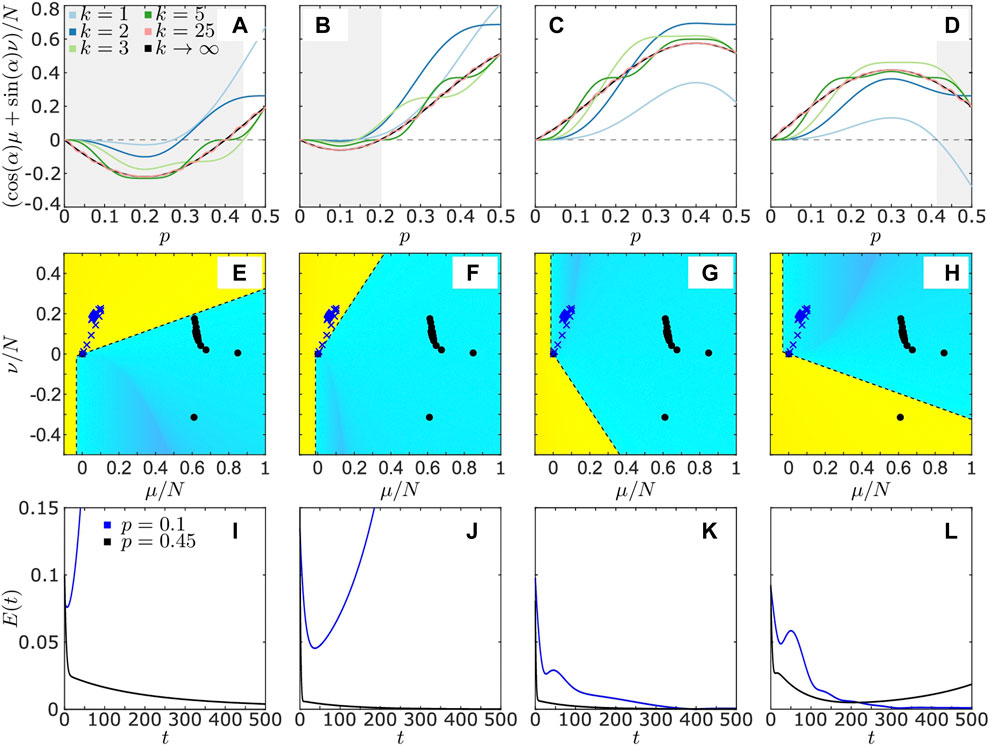
FIGURE 4. Stability analysis of the synchronous state of system Eqs. 16, 17 with plasticity rule Eqs. 18–20 and coupling structure Eq. 25. Panels (A–D) show the function $c_2\left(\alpha ,{\mu }_k\left(p\right),{\nu }_k\left(p\right)\right)$ for different α, see Eq. 15, calculated with the approximations Eqs. 26, 27 depending on the relative coupling range p. In each panel, $c_2$ is displayed for different values of k. The gray shaded regions refer to unstable synchronous states. Panels (e,f,g,h) show the master stability function $\text{Λ}\left(\text{D}g\left(0\right)\mu ,g\left(0\right)\nu \right)$ for the cross-section $\text{Im}\left(\mu \right)=0$ and $\text{Im}\left(\nu \right)=0$ for different values of α with color code as in Figure 1. The crosses and dots correspond to two sets of eigenvalue pairs $\left({\mu }_k,{\nu }_k\right)$ ($k=0,\dots ,N-1$) for relative coupling range $p=0.1$ (blue crosses) and $p=0.45$ (black points), respectively. Panels (I–L) show the synchronization error $E\left(t\right)=\sqrt{{\displaystyle {\sum }_{i=1}^N{\left({\varphi }_i\left(t\right)-{\varphi }_1\left(t\right)\right)}^2}}$ for simulations with relative coupling range $p=0.1$ (blue) and $p=0.45$ (black). Each simulation is initialized at a slightly perturbed synchronous state. Parameters: $N=200$, $\mathit{ϵ}=0.01$, (A, E, I)$\alpha =-0.4\pi$, (B, F, J)$\alpha =-0.2\pi$, (C, G, K)$\alpha =0.2\pi$, (D, H, L)$\alpha =0.4\pi$.

The situation changes for $0<\alpha <\pi /2$, as shown in Figures 4C,D. Here, for a large range of α, all nonlocally coupled networks lead to a stable synchronous state. However, closer to $\pi /2$, long distance connections destabilize the synchronous state. In particular, this destabilization can be traced back to the single negative eigenvalue ${\nu }_1$ of the Laplacian $L^{\text{D}h}$, see Figure 4H. Hence, the unstable manifold of the synchronous state is only one-dimensional. This finding is in agreement with the example of $N=200$ phase oscillators presented in Figures 4G,H,K, L. Particularly in Figure 4L, the low dimension of the unstable manifold manifests itself as follows: The black trajectory first tends to the synchronous state along the $N\left(N+1\right)-1$ stable directions before it is repelled along the direction corresponding to ${\nu }_1$.

We have shown that long distance interactions may stabilize or destabilize the synchronous state depending on the phase lag parameter α. In this section, all links have the same weight independent of the corresponding distance. In the next section, we analyze a network with a more realistic structure with a distance-dependent distribution of weights.

4.3 Synchronization on Isotropic and Homogeneous Network With Gaussian Distance Distribution

In the previous section, we used the prototypical example of a nonlocally coupled rings to study the effects of long-range interaction on synchronization. In this setup, however, all links are equally weighted. In realistic systems, in contrast, the number of links with a certain distance are distributed, see [67] for details. To incorporate this into our network model, we weight the links with respect to a distance distribution. Measurements suggest that the distance distribution can be estimated by a mean and a distribution width [67]. The Gaussian distributions is a paradigmatic distribution that allows for studying effects emanating from the mean and the distribution width. For the remainder of the section, we consider the link distance distribution given by a Gaussian distribution, and weight the links of the network connectivity structure A accordingly, i.e.

$a_{ij}\left(d_{ij}/N\right)=\{\begin{array}{cc}{e}^{-\frac{{\left(d_{ij}/N-\xi \right)}^2}{2{\sigma }^2}}& d_{ij}\le N/2,\\ e^{-\frac{{\left(1-d_{ij}/N-\xi \right)}^2}{2{\sigma }^2}}& d_{ij}>N/2.\end{array}(28)$

where ξ and σ are the mean value and the standard deviation, respectively. Note that the standard deviation characterizes the width of the distribution. For the numerical simulations, we normalize each row of A by ${\displaystyle {\sum }_{j=1}^N{a}_{ij}}$. Here, we further make the assumption that the network is homogeneous and isotropic. This means that in any direction from a node and at each node the network looks the same. Hence, we obtain a circulant connectivity structure. An illustration of the weight distribution for $N=12$ is presented in Figure 2C.

As we know from Eqs. 14 and 15, for $\mathit{ϵ}\ll 1$, the values of $c_2\left(\alpha ,{\mu }_k,{\nu }_k\right)$ determine the stability of the synchronous state. In particular, the synchronous state is stable if $c_{\text{min}}={\text{min}}_{k\in 1,N-1}{c}_2\left(\alpha ,{\mu }_k,{\nu }_k\right)>0$ for a given N and unstable otherwise. In Figure 5A, we display $c_{\text{min}}$ for $\alpha =-0.4\pi$ and different mean values ξ and standard deviations σ of the weight distribution. In agreement with the finding in Section 4.2, the synchronized state stabilizes due to an increase of long distance interaction expressed by an increase of σ. Complementing the finding in Section 4.2, here, we note that the stability can be also achieved by distributions with peaks at long distance links alone. In this case, the width of the distribution is not important. Figure 5B shows how the boundary between regions corresponding to stable and unstable synchronization change for different values of α. As in the case of nonlocally coupled ring networks, with $\alpha \to 0$ (with $\alpha <0$) the boundary tends to the limiting point $\left(\sigma ,\xi \right)=\left(\mathrm{0,0}\right)$. On the contrary, if $\alpha \to -\pi /2$ (with $\alpha >-\pi /2$), the width of the distribution has to increase to have stable synchronization for small values of the mean ξ.

FIGURE 5

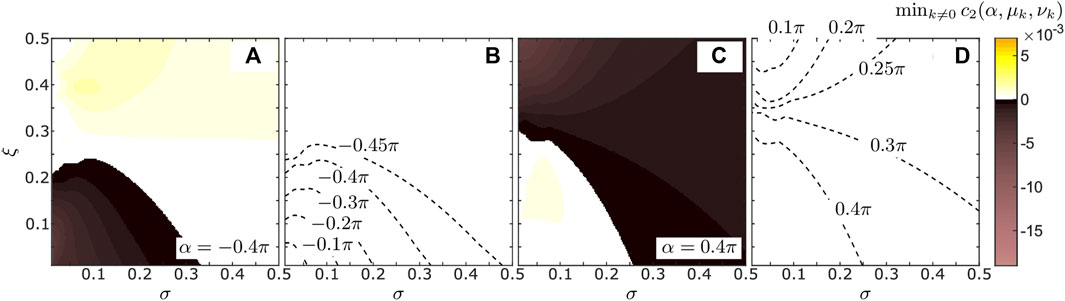
FIGURE 5. Stability analysis of the synchronous state of system Eqs. 16, 17 with plasticity rule Eqs. 18–20 and coupling structure Eq. 28. Panels (A, C) show the minimum over all $k\ne 0<N$ of $c_2$, se Eq. 15, for two different values of α depending on the mean value ξ and the standard deviation σ of the weight distribution. The minima are displayed in color code. Panels (B, D) show the boundaries between stable and unstable regions in $\left(\sigma ,\xi \right)$- plane for different values of α as given in the figure. Parameters: (A)$N=400$, $\alpha =-0.4\pi$, (C)$N=400$, $\alpha =0.4\pi$, (B, C)$N=200$.

An opposite scenario is shown in Figure 5C for $\alpha =0.4\pi$. Here, an increase of the weights for long distance links destabilizes the synchronous state, as in Figures 4D,H,L. We also note that for small values α, the synchronous state is stable for almost all values of σ and ξ, see Figure 5D. Only in cases of distribution sharply peaked at long distances, i.e., ξ close to $1/2$ and σ close to 0, the synchronous state is unstable. This effect could not be found in networks with nonlocally coupled rings, see Section 4.2.

5 Conclusion

In summary, we have investigated the phenomenon of synchronization on adaptive networks with heterogeneous plasticity rules. In particular, we have modeled systems with distance-dependent plasticity as they have been found in neuronal networks experimentally [64–67] as well as computational models [68]. For the realization, we have used a ring-like network architecture and associated the distance of two nodes with the distance of their placement on the ring.

In Section 3, we have developed a generalized master stability approach for phase oscillator models that are adaptively coupled and where each link has its own adaptation rule (plasticity). By using an explicit splitting of the time scales between fast dynamics of the phase oscillators and slow dynamics of the link weights, we have established an explicit stability condition for the synchronous state. More precisely, we found that the stability is governed by the coupling function and the eigenvalues of two structure matrices. These structure matrices $L^h$ and $L^{\text{D}h}$ are determined by the connectivity of the network and the plasticity rules of the link weights. Note that for the structural matrices, the plasticity rule needs only to be known in the vicinity of 0, which greatly facilitates the application of the approach to realistic forms of synaptic plasticity. Thus, we have extended previous work on the master stability function of adaptive networks [48, 83] and broaden the scope of potential future applications for this methodology.

In Section 4, we applied the novel technique to a system of adaptively coupled oscillators with distance-dependent plasticity. Here, we have used a ring-like network structure to study the impact of long- and short-distance connections on the stability of synchronization. For this purpose we introduced an approximation of the eigenvalues for the structure matrices in Section 4.1. This approximation allows for a comprehensive analysis of the stability as a function of various system parameters. Moreover, it enables us to identify critical eigenvalues that govern the stability of the synchronous state. In Sections 4.2 and 4.3, we have brought together all methodological findings and applied them to systems with a nonlocally coupled ring structure and with a Gaussian distribution of link weights. The latter structure accounts for the fact that in realistic neuronal populations the number of links with different distances are not uniformly distributed [67]. We found that long-distance connections can stabilize or destabilize the synchronous state, depending on the coupling function between the oscillators. A remarkable fact with respect to neuronal applications relates to the destabilization scenario. Here we observed that the destabilization can be attributed to the pronounced change of the plasticity rule from Hebbian to anti-Hebbian. For more realistic connectivity structures, we found that weight distributions of the connectivity structure with sharp peaks at long distances lead to destabilization for a wide range of the coupling function.

All in all, in this article, we have provided a general framework to study the emergence of synchronization in neuronal system with a heterogeneous plasticity rule. The developed methodology is not limited to distance-dependent types of plasticity and can also be used for non-symmetric setups. For the latter case, we have provided the necessary analytical result. In this work, we have restricted our attention to the case of phase oscillators, but the methods can be extended to more realistic neuron models by using techniques established, for example, in [48]. Moreover, techniques are available that allow for further generalization toward systems with slightly different local dynamics at each node [87]. On the one hand, the master stability approach offers a great tool to study the stability of the synchronous state depending on the networks structure. On the other hand, this approach allows for characterizing the network structures that are, in some sense, optimal for synchronization [88, 89]. In this regard, it remains an open question as to how plasticity optimizes the synchronizability of the network in a self-organized way. In addition, recent studies have shown that there is a great interest in synchronization phenomena to understand diseases such as Parkinson’s disease [90–92] or epilepsy [29, 93] for the development of proper therapeutic treatments. We believe that our work provides an important step toward understanding synchronization under realistic conditions.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

RB designed the study and did the numerical simulations. RB and SY developed the analytical results. Both authors contributed to the preparation of the manuscript. Both authors read and approved the final manuscript.

Funding

This work was supported by the German Research Foundation DFG, Project Nos. 411803875 and 440145547, and the Open Access Publication Fund of TU Berlin.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Newman, MEJ. The Structure and Function of Complex Networks. SIAM Rev (2003) 45:167–256. doi:10.1137/s003614450342480

CrossRef Full Text | Google Scholar

2. Pikovsky, A, Rosenblum, M, and Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences. 1st ed. Cambridge: Cambridge University Press (2001).

3. Strogatz, SH. Exploring Complex Networks. Nature (2001) 410:268–76. doi:10.1038/35065725

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Arenas, A, Díaz-Guilera, A, Kurths, J, Moreno, Y, and Zhou, C. Synchronization in Complex Networks. Phys Rep (2008) 469:93–153. doi:10.1016/j.physrep.2008.09.002

CrossRef Full Text | Google Scholar

5. Boccaletti, S, Pisarchik, AN, del Genio, CI, and Amann, A. Synchronization: From Coupled Systems to Complex Networks. Cambridge: Cambridge University Press (2018).

6. Kuramoto, Y. Chemical Oscillations, Waves and Turbulence. Berlin: Springer-Verlag (1984).

7. Pecora, LM, Carroll, TL, Johnson, GA, Mar, DJ, and Heagy, JF. Fundamentals of Synchronization in Chaotic Systems, Concepts, and Applications. Chaos (1997) 7:520–43. doi:10.1063/1.166278 https://doi.org/10.1063/1.166278

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yanchuk, S, Maistrenko, Y, and Mosekilde, E. Partial Synchronization and Clustering in a System of Diffusively Coupled Chaotic Oscillators. Mathematics Comput Simulation (2001) 54:491–508. doi:10.1016/S0378-4754(00)00276-7

CrossRef Full Text | Google Scholar

9. Choe, C-U, Dahms, T, Hövel, P, and Schöll, E. Controlling Synchrony by Delay Coupling in Networks: from In-phase to Splay and Cluster States. Phys Rev E (2010) 81:025205. doi:10.1103/physreve.81.025205

CrossRef Full Text | Google Scholar

10. Belykh, I, and Hasler, M. Mesoscale and Clusters of Synchrony in Networks of Bursting Neurons. Chaos (2011) 21:016106. doi:10.1063/1.3563581

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zhang, Y, and Motter, AE. Symmetry-independent Stability Analysis of Synchronization Patterns. SIAM Rev (2020) 62:817–36. doi:10.1137/19m127358x

CrossRef Full Text | Google Scholar

12. Berner, R, Schöll, E, and Yanchuk, S. Multiclusters in Networks of Adaptively Coupled Phase Oscillators. SIAM J Appl Dyn Syst (2019) 18:2227–66. doi:10.1137/18m1210150

CrossRef Full Text | Google Scholar

13. Jaros, P, Brezetsky, S, Levchenko, R, Dudkowski, D, Kapitaniak, T, and Maistrenko, Y. Solitary States for Coupled Oscillators with Inertia. Chaos (2018) 28:011103. doi:10.1063/1.5019792

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Teichmann, E, and Rosenblum, M. Solitary States and Partial Synchrony in Oscillatory Ensembles with Attractive and Repulsive Interactions. Chaos (2019) 29:093124. doi:10.1063/1.5118843

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Berner, R, Polanska, A, Schöll, E, and Yanchuk, S. Solitary States in Adaptive Nonlocal Oscillator Networks. Eur Phys J Spec Top (2020) 229:2183–203. doi:10.1140/epjst/e2020-900253-0

CrossRef Full Text | Google Scholar

16. Kuramoto, Y, and Battogtokh, D. Coexistence of Coherence and Incoherence in Nonlocally Coupled Phase Oscillators. Nonlin Phen Complex Sys (2002) 5(4):380–5.

Google Scholar

17. Abrams, DM, and Strogatz, SH. Chimera States for Coupled Oscillators. Phys Rev Lett (2004) 93:174102. doi:10.1103/physrevlett.93.174102

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Schöll, E. Synchronization Patterns and Chimera States in Complex Networks: Interplay of Topology and Dynamics. Eur Phys J Spec Top (2016) 225:891–919. doi:10.1140/epjst/e2016-02646-3

CrossRef Full Text | Google Scholar

19. Omel’chenko, OE. The Mathematics behind Chimera States. Nonlinearity (2018) 31:R121. doi:10.1088/1261-6544/aaaa07

CrossRef Full Text | Google Scholar

20. Omel’chenko, OE, and Knobloch, E. Chimerapedia: Coherence-Incoherence Patterns in One, Two and Three Dimensions. New J Phys (2019) 21:093034. doi:10.1088/1367-2630/ab3f6b

CrossRef Full Text | Google Scholar

21. Singer, W. Neuronal Synchrony: A Versatile Code for the Definition of Relations? Neuron (1999) 24:49–65. doi:10.1016/s0896-6273(00)80821-1

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Fell, J, and Axmacher, N. The Role of Phase Synchronization in Memory Processes. Nat Rev Neurosci (2011) 12:105–18. doi:10.1038/nrn2979

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Hammond, C, Bergman, H, and Brown, P. Pathological Synchronization in Parkinson's Disease: Networks, Models and Treatments. Trends Neurosciences (2007) 30:357–64. doi:10.1016/j.tins.2007.05.004

CrossRef Full Text | Google Scholar

24. Goriely, A, Kuhl, E, and Bick, C. Neuronal Oscillations on Evolving Networks: Dynamics, Damage, Degradation, Decline, Dementia, and Death. Phys Rev Lett (2020) 125:128102. doi:10.1103/physrevlett.125.128102

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Pfeifer, KJ, Kromer, JA, Cook, AJ, Hornbeck, T, Lim, EA, Mortimer, BJP, et al. Coordinated Reset Vibrotactile Stimulation Induces Sustained Cumulative Benefits in Parkinson's Disease. Front Physiol (2021) 12:624317. doi:10.3389/fphys.2021.624317

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Jiruska, P, de Curtis, M, Jefferys, JGR, Schevon, CA, Schiff, SJ, and Schindler, K. Synchronization and Desynchronization in Epilepsy: Controversies and Hypotheses. J Physiol (2013) 591(4):787–97. doi:10.1113/jphysiol.2012.239590

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Jirsa, VK, Stacey, WC, Quilichini, PP, Ivanov, AI, and Bernard, C. On the Nature of Seizure Dynamics. Brain (2014) 137:2210–30. doi:10.1093/brain/awu133

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Andrzejak, RG, Rummel, C, Mormann, F, and Schindler, K. All Together Now: Analogies between Chimera State Collapses and Epileptic Seizures. Sci Rep (2016) 6:23000. doi:10.1038/srep23000

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Gerster, M, Berner, R, Sawicki, J, Zakharova, A, Škoch, A, Hlinka, J, et al. FitzHugh-Nagumo Oscillators on Complex Networks Mimic Epileptic-Seizure-Related Synchronization Phenomena. Chaos (2020) 30:123130. doi:10.1063/5.0021420

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Tass, PA, Adamchic, I, Freund, H-J, von Stackelberg, T, and Hauptmann, C. Counteracting Tinnitus by Acoustic Coordinated Reset Neuromodulation. Restor Neurol Neurosci (2012) 30:137–59. doi:10.3233/rnn-2012-110218

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Tass, PA, and Popovych, OV. Unlearning Tinnitus-Related Cerebral Synchrony with Acoustic Coordinated Reset Stimulation: Theoretical Concept and Modelling. Biol Cybern (2012) 106:27–36. doi:10.1007/s00422-012-0479-5

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Uhlhaas, P, Pipa, G, Lima, B, Melloni, L, Neuenschwander, S, Nikolic, D, et al. Neural Synchrony in Cortical Networks: History, Concept and Current Status. Front Integr Neurosci (2009) 3:17. doi:10.3389/neuro.07.017.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Pecora, LM, and Carroll, TL. Master Stability Functions for Synchronized Coupled Systems. Phys Rev Lett (1998) 80:2109–12. doi:10.1103/physrevlett.80.2109

CrossRef Full Text | Google Scholar

34. Flunkert, V, Yanchuk, S, Dahms, T, and Schöll, E. Synchronizing Distant Nodes: a Universal Classification of Networks. Phys Rev Lett (2010) 105:254101. doi:10.1103/physrevlett.105.254101

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Dahms, T, Lehnert, J, and Schöll, E. Cluster and Group Synchronization in Delay-Coupled Networks. Phys Rev E (2012) 86:016202. doi:10.1103/physreve.86.016202

CrossRef Full Text | Google Scholar

36. Keane, A, Dahms, T, Lehnert, J, Suryanarayana, SA, Hövel, P, and Schöll, E. Synchronisation in Networks of Delay-Coupled Type-I Excitable Systems. Eur Phys J B (2012) 85:407. doi:10.1140/epjb/e2012-30810-x

CrossRef Full Text | Google Scholar

37. Kyrychko, YN, Blyuss, KB, and Schöll, E. Synchronization of Networks of Oscillators with Distributed Delay Coupling. Chaos (2014) 24:043117. doi:10.1063/1.4898771

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Lehnert, J. Controlling Synchronization Patterns in Complex Networks. Springer Theses. Heidelberg: Springer (2016).

39. Tang, L, Wu, X, Lü, J, Lu, JA, and D'Souza, RM. Master Stability Functions for Complete, Intralayer, and Interlayer Synchronization in Multiplex Networks of Coupled Rössler Oscillators. Phys Rev E (2019) 99:012304. doi:10.1103/PhysRevE.99.012304

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Berner, R, Sawicki, J, and Schöll, E. Birth and Stabilization of Phase Clusters by Multiplexing of Adaptive Networks. Phys Rev Lett (2020) 124:088301. doi:10.1103/physrevlett.124.088301

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Börner, R, Schultz, P, Ünzelmann, B, Wang, D, Hellmann, F, and Kurths, J. Delay Master Stability of Inertial Oscillator Networks. Phys Rev Res (2020) 2:023409. doi:10.1103/physrevresearch.2.023409

CrossRef Full Text | Google Scholar

42. Mulas, R, Kuehn, C, and Jost, J. Coupled Dynamics on Hypergraphs: Master Stability of Steady States and Synchronization. Phys Rev E (2020) 101:062313. doi:10.1103/physreve.101.062313

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Belykh, VN, Belykh, IV, and Hasler, M. Connection Graph Stability Method for Synchronized Coupled Chaotic Systems. Physica D: Nonlinear Phenomena (2004) 195:159–87. doi:10.1016/j.physd.2004.03.012

CrossRef Full Text | Google Scholar

44. Belykh, I, de Lange, E, and Hasler, M. Synchronization of Bursting Neurons: What Matters in the Network Topology. Phys Rev Lett (2005) 94:188101. doi:10.1103/physrevlett.94.188101

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Belykh, I, Belykh, V, and Hasler, M. Generalized Connection Graph Method for Synchronization in Asymmetrical Networks. Physica D: Nonlinear Phenomena (2006) 224:42–51. doi:10.1016/j.physd.2006.09.014

CrossRef Full Text | Google Scholar

46. Belykh, I, Belykh, V, and Hasler, M. Synchronization in Asymmetrically Coupled Networks with Node Balance. Chaos (2006) 16:015102. doi:10.1063/1.2146180 https://doi.org/10.1063/1.2146180

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Daley, K, Zhao, K, and Belykh, IV. Synchronizability of Directed Networks: The Power of Non-existent Ties. Chaos (2020) 30:043102. doi:10.1063/1.5134920

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Berner, R, Vock, S, Schöll, E, and Yanchuk, S. Desynchronization Transitions in Adaptive Networks. Phys Rev Lett (2021) 126:028301. doi:10.1103/physrevlett.126.028301

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Jain, S, and Krishna, S. A Model for the Emergence of Cooperation, Interdependence, and Structure in Evolving Networks. Proc Natl Acad Sci (2001) 98:543–7. doi:10.1073/pnas.98.2.543

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Proulx, S, Promislow, D, and Phillips, P. Network Thinking in Ecology and Evolution. Trends Ecol Evol (2005) 20:345–53. doi:10.1016/j.tree.2005.04.004

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Gross, T, D’Lima, CJD, and Blasius, B. Epidemic Dynamics on an Adaptive Network. Phys Rev Lett (2006) 96:208701. doi:10.1103/physrevlett.96.208701

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Martens, EA, and Klemm, K. Transitions from Trees to Cycles in Adaptive Flow Networks. Front Phys (2017) 5:62. doi:10.3389/fphy.2017.00062

CrossRef Full Text | Google Scholar

53. Kuehn, C. Multiscale Dynamics of an Adaptive Catalytic Network. Math Model Nat Phenom (2019) 14:402. doi:10.1051/mmnp/2019015

CrossRef Full Text | Google Scholar

54. Horstmeyer, L, and Kuehn, C. Adaptive Voter Model on Simplicial Complexes. Phys Rev E (2020) 101:022305. doi:10.1103/physreve.101.022305

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Meisel, C, and Gross, T. Adaptive Self-Organization in a Realistic Neural Network Model. Phys Rev E (2009) 80:061917. doi:10.1103/physreve.80.061917

CrossRef Full Text | Google Scholar

56. Mikkelsen, K, Imparato, A, and Torcini, A. Emergence of Slow Collective Oscillations in Neural Networks with Spike-Timing Dependent Plasticity. Phys Rev Lett (2013) 110:208101. doi:10.1103/physrevlett.110.208101

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Mikkelsen, K, Imparato, A, and Torcini, A. Sisyphus Effect in Pulse-Coupled Excitatory Neural Networks with Spike-timing-dependent Plasticity. Phys Rev E (2014) 89:062701. doi:10.1103/physreve.89.062701

CrossRef Full Text | Google Scholar

58. Markram, H, Lübke, J, Frotscher, M, and Sakmann, B. Regulation of Synaptic Efficacy by Coincidence of Postsynaptic APs and EPSPs. Science (1997) 275:213–5. doi:10.1126/science.275.5297.213

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Abbott, LF, and Nelson, SB. Synaptic Plasticity: Taming the Beast. Nat Neurosci (2000) 3:1178–83. doi:10.1038/81453

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Caporale, N, and Dan, Y. Spike Timing-dependent Plasticity: A Hebbian Learning Rule. Annu Rev Neurosci (2008) 31:25–46. doi:10.1146/annurev.neuro.31.060407.125639

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Popovych, OV, Yanchuk, S, and Tass, PA. Self-organized Noise Resistance of Oscillatory Neural Networks with Spike Timing-dependent Plasticity. Sci Rep (2013) 3:2926. doi:10.1038/srep02926

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Zenke, F, Agnes, EJ, and Gerstner, W. Diverse Synaptic Plasticity Mechanisms Orchestrated to Form and Retrieve Memories in Spiking Neural Networks. Nat Commun (2015) 6:6922. doi:10.1038/ncomms7922

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Tazerart, S, Mitchell, DE, Miranda-Rottmann, S, and Araya, R. A Spike-timing-dependent Plasticity Rule for Dendritic Spines. Nat Commun (2020) 11:4276. doi:10.1038/s41467-020-17861-7

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Froemke, RC, Poo, M-m., and Dan, Y. Spike-timing-dependent Synaptic Plasticity Depends on Dendritic Location. Nature (2005) 434:221–5. doi:10.1038/nature03366

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Sjöström, PJ, and Häusser, M. A Cooperative Switch Determines the Sign of Synaptic Plasticity in Distal Dendrites of Neocortical Pyramidal Neurons. Neuron (2006) 51:227–38. doi:10.1016/j.neuron.2006.06.017

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Froemke, RC, Letzkus, JJ, Kampa, BM, Hang, GB, and Stuart, GJ. Dendritic Synapse Location and Neocortical Spike-timing-dependent Plasticity. Front.Syna.Neurosci. (2010) 2:29. doi:10.3389/fnsyn.2010.00029

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Letzkus, JJ, Kampa, BM, and Stuart, GJ. Learning Rules for Spike Timing-dependent Plasticity Depend on Dendritic Synapse Location. J Neurosci (2006) 26:10420–9. doi:10.1523/jneurosci.2650-06.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Meissner-Bernard, C, Tsai, MC, Logiaco, L, and Gerstner, W. Dendritic Voltage Recordings Explain Paradoxical Synaptic Plasticity: A Modeling Study. Front Synaptic Neurosci (2020) 12:585539. doi:10.3389/fnsyn.2020.585539

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Aoki, T, and Aoyagi, T. Co-evolution of Phases and Connection Strengths in a Network of Phase Oscillators. Phys Rev Lett (2009) 102:034101. doi:10.1103/physrevlett.102.034101

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Kasatkin, DV, Yanchuk, S, Schöll, E, and Nekorkin, VI. Self-organized Emergence of Multilayer Structure and Chimera States in Dynamical Networks with Adaptive Couplings. Phys Rev E (2017) 96:062211. doi:10.1103/physreve.96.062211

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Kasatkin, DV, and Nekorkin, VI. The Effect of Topology on Organization of Synchronous Behavior in Dynamical Networks with Adaptive Couplings. Eur Phys J Spec Top (2018) 227:1051–61. doi:10.1140/epjst/e2018-800077-7

CrossRef Full Text | Google Scholar

72. Berner, R, Fialkowski, J, Kasatkin, D, Nekorkin, V, Yanchuk, S, and Schöll, E. Hierarchical Frequency Clusters in Adaptive Networks of Phase Oscillators. Chaos (2019) 29:103134. doi:10.1063/1.5097835

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Berner, R, Yanchuk, S, and Schöll, E. What Adaptive Neuronal Networks Teach Us about Power Grids. Phys Rev E (2021) 103:042315. doi:10.1103/physreve.103.042315

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Feketa, P, Schaum, A, and Meurer, T. Synchronization and Multi-Cluster Capabilities of Oscillatory Networks with Adaptive Coupling. IEEE Trans Automat Control (2020) 66(7):3084. doi:10.1109/tac.2020.3012528

CrossRef Full Text | Google Scholar

75. Franović, I, Yanchuk, S, Eydam, S, Bačić, I, and Wolfrum, M. Dynamics of a Stochastic Excitable System with Slowly Adapting Feedback. Chaos (2020) 30:083109. doi:10.1063/1.5145176

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Popovych, OV, Xenakis, MN, and Tass, PA. The Spacing Principle for Unlearning Abnormal Neuronal Synchrony. PLoS ONE (2015) 10:e0117205. doi:10.1371/journal.pone.0117205

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Lücken, L, Popovych, OV, Tass, PA, and Yanchuk, S. Noise-enhanced Coupling between Two Oscillators with Long-Term Plasticity. Phys Rev E (2016) 93:032210. doi:10.1103/physreve.93.032210

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Chakravartula, S, Indic, P, Sundaram, B, and Killingback, T. Emergence of Local Synchronization in Neuronal Networks with Adaptive Couplings. PLoS ONE (2017) 12:e0178975. doi:10.1371/journal.pone.0178975

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Röhr, V, Berner, R, Lameu, EL, Popovych, OV, and Yanchuk, S. Frequency Cluster Formation and Slow Oscillations in Neural Populations with Plasticity. PLoS ONE (2019) 14:e0225094. doi:10.1371/journal.pone.0225094

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Sakaguchi, H, and Kuramoto, Y. A Soluble Active Rotater Model Showing Phase Transitions via Mutual Entertainment. Prog Theor Phys (1986) 76:576–81. doi:10.1143/ptp.76.576

CrossRef Full Text | Google Scholar

81. Madadi Asl, M, Valizadeh, A, and Tass, PA. Dendritic and Axonal Propagation Delays Determine Emergent Structures of Neuronal Networks with Plastic Synapses. Sci Rep (2017) 7:39682. doi:10.1038/srep39682

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Madadi Asl, M, Valizadeh, A, and Tass, PA. Dendritic and Axonal Propagation Delays May Shape Neuronal Networks with Plastic Synapses. Front Physiol (2018) 9:1849. doi:10.3389/fphys.2018.01849

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Vock, S, Berner, R, Yanchuk, S, and Schöll, E. Effect of Diluted Connectivities on Cluster Synchronization of Adaptively Coupled Oscillator Networks. Scientia Iranica D (2021) 28(3):1669.

84. Liesen, J, and Mehrmann, V. Linear Algebra. Cham: Springer (2015). doi:10.1007/978-3-319-24346-7

CrossRef Full Text

85. Gray, RM Toeplitz and Circulant Matrices: A Review. Found. Trends Commun. Inf. Theory, Hanover, MA, USA: Now Publishers Inc. (2006). p. 155–239.

86. Aoki, T, and Aoyagi, T. Self-organized Network of Phase Oscillators Coupled by Activity-dependent Interactions. Phys Rev E (2011) 84:066109. doi:10.1103/physreve.84.066109

CrossRef Full Text | Google Scholar

87. Sun, J, Bollt, EM, and Nishikawa, T. Master Stability Functions for Coupled Nearly Identical Dynamical Systems. Europhys Lett (2009) 85:60011. doi:10.1209/0295-5075/85/60011

CrossRef Full Text | Google Scholar

88. Skardal, PS, Taylor, D, and Sun, J. Optimal Synchronization of Complex Networks. Phys Rev Lett (2014) 113:144101. doi:10.1103/physrevlett.113.144101

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Acharyya, S, and Amritkar, RE. Synchronization of Nearly Identical Dynamical Systems: Size Instability. Phys Rev E (2015) 92:052902. doi:10.1103/physreve.92.052902

CrossRef Full Text | Google Scholar

90. Kromer, JA, and Tass, PA. Long-lasting Desynchronization by Decoupling Stimulation. Phys Rev Res (2020) 2:033101. doi:10.1103/physrevresearch.2.033101

CrossRef Full Text | Google Scholar

91. Kromer, JA, Khaledi-Nasab, A, and Tass, PA. Impact of Number of Stimulation Sites on Long-Lasting Desynchronization Effects of Coordinated Reset Stimulation. Chaos (2020) 30:083134. doi:10.1063/5.0015196

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Khaledi-Nasab, A, Kromer, JA, and Tass, PA. Long-Lasting Desynchronization of Plastic Neural Networks by Random Reset Stimulation. Front Physiol (2021) 11:622620. doi:10.3389/fphys.2020.622620

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Olmi, S, Petkoski, S, Guye, M, Bartolomei, F, and Jirsa, V. Controlling Seizure Propagation in Large-Scale Brain Networks. Plos Comput Biol (2019) 15:e1006805. doi:10.1371/journal.pcbi.1006805

PubMed Abstract | CrossRef Full Text | Google Scholar