Adaptive composite learning dynamic surface control for chaotic fractional-order permanent magnet synchronous motors

This paper aims to address the tracking problem of uncertain fractional-order permanent magnet synchronous motors with parametric uncertainties. To guarantee the system stability and offset the effect of parametric uncertainties, an adaptive backstepping composite learning neural control scheme based on interval excitation is presented. Moreover, dynamic surface technique is exploited to overcome the technical limitation of “explosion of complexity” caused by standard backstepping framework. In virtue of stability analysis and illustrative simulation, it is confirmed that the proposed control scheme not only attenuates the tracking error as small as possible, but also achieves satisfactory parametric convergence with high estimation precision.

1. Introduction

Fractional calculus is an important mathematical discipline with a history of several centuries. In recent decades, fractional differential equations have made great progress in engineering, mechanics, physics, chemistry, and many other fields. Compared with classical mathematical models governed by integer-order differential equations, most fractional-order models have abundant advantages in describing the memory and genetic characteristics of the process [1, 2]. In addition, owing to the particularity of fractional calculus, fractional-order systems always exhibit rich dynamic behaviors [3–8].

Permanent magnet synchronous motor (PMSM) [9] has a great deal of advantages such as low production cost, high energy consumption, strong robustness, compact structure, superior performance, high inertia torque ratio, large power capacity. The existing results show that integer-order PMSM has chaotic characteristics under some certain operating conditions. So far, several chaos control methods [10–14] have been put forward to attenuate the effect of chaotic oscillation and maintain the stable operation of integer-order PMSM. Fractional order PMSM [15–18] reflects the same complex chaotic dynamics, because fractional calculus provides a powerful tool for describing the genetic and infinite memory properties of different substances more accurately and essentially. Thus, the establishment of a chaos control scheme for fractional-order PMSM instead of the traditional one is of vast significance.

Radial basis function network (RBFNN) [19] has been widely concerned and applied due to its valuable characteristics of approximation for coping with functional uncertainty in controlled systems. The approximation ability of RBFNNs can greatly reduce the difficulty of modeling procedure in practical control problems and hence facilitates to simplify the controller design. Although a majority of the existing neural control approaches facilitates to realize error convergence, the approximation abilities of RBFNNs are generally restricted for the reason that the persistent excitation (PE) condition [20] must be met during the overal adaptation process. Actually, the PE condition for the implementation of traditional adaptive neural control is very strict and sometimes even infeasible in practical applications. In Wang and Hill [21], a neural control method based on a practical PE condition was proposed to guarantee the exponential stability of the closed-loop system as well as the exact approximation of RBFNNs. However, the parametric convergence rate via such a learning-based neural control method or its outgrowths (e.g., [22–24]) is highly dependent on the strength of PE, which may lead to very slow learning speed in general. Aiming to overcome this limitation, several scholars put forward useful composite learning control strategies [25–30]. Composite learning significantly relaxes the PE condition into the interval excitation (IE) condition. The essential idea of this method is to synthesize the online data and the historical data for the generation of a so-called prediction error and then to configure a composite adaptive law integrated with the tracking error and the prediction error for the better update of adaptive parameters.

Based on the above theoretical background, this paper studies the tracking issue of fractional-order PMSM. A neural network-based adaptive composite learning control approach is proposed, which can accurately estimate unknown functions under certain parameter design conditions. It will be proven that expected tracking performance and fast parametric convergence are realized once the proposed method is applied.

The main innovations of this work are worthy of emphasis as 2-fold: (1) Relying on fractional-order Lyapunov stability criterion, a novel fractional-order adaptive nerual-network chaos controller is constructed to achieve robust tracking performance. Compared with the existing researches [10–14] on integer-order PMSM, the tracking control problem of fractional-order PMSM dynamic model studied in the article is more challenging and significant due to the memory and genetic characteristics of fractional calculus. (2) A composite learning algorithm is proposed. Different from the conventional adaptive control methods [15–18] under the PE condition for fractional-order PMSM, the proposed composite learning adaptive control method relaxes the stringer PE condition into the IE condition which is relatively easy to be implemented. It will be proven that the designed composite learning algorithm not only updates the adaptive parameters of RBFNNs via taking advantage of the online data, but also effectively promote the estimation accuracy of all unknown functions.

The architecture of this article is organized as below. In Section 2, the fundamental background of fractional calculus, radial basis function network, persistent excitation, and interval excitation are recalled. Section 3 describes the considered problem formulation, and then, an adaptive neural-network controller based on composite learning scheme is systematically elaborated. It is verified that the proposed method facilitates to achieve satisfactory tracking performance and highly accurate parametric estimation under interval excitation condition. In Section 4, a numerical simulation is carried out to evaluate the feasibility of the proposed approach. In Section 5, the whole conclusion of the paper and the prospect of future research are summarized.

2. Preliminaries

2.1. Fractional calculus

In this overall article, ℕ (resp. ℝ, ℝⁿ, ℝ⁺, ℂ) means the family of all non-zero natural numbers (resp. real numbers, n dimensional real vectors, positive numbers, complex numbers). Given a k ∈ ℕ, C^k is the family of all differentiable functions with continuous i-order derivatives for all i = 1, 2, ⋯ , k. L_∞ denotes the space of all bounded signals. sign(·) expresses the signum function. The transpose of an x ∈ ℝⁿ is denoted by x^T. ${\Omega }_r\triangleq \left\{x\in ℝ:\left|x\right|\le r,r\in {ℝ}^{+}\right\}$.

Definition 1. Podlubny [2] The β-order Caputo fractional derivative for a given differentiable function φ(t) is formulated by

${}_{t_0}{\mathcal{D}}_t^{\beta }\phi (t)=\frac{1}{\Gamma (k-\beta )}{\displaystyle {\int }_{t_0}^t\frac{{\phi }^{(k)}(s)}{{(t-s)}^{\gamma +1-k}}ds}$

with k − 1 ≤ β < k in which k ∈ ℕ. When t₀ = 0, we write ${{D}}^{\beta }\phi (t)$ simply instead of ${}_{t_0}{{D}}_t^{\beta }\phi (t)$.

Definition 2. Podlubny [2] A mapping E_β,γ :ℂ → ℂ with double parameters β, γ ∈ ℝ⁺ is called the Mittag-Leffler function, defined as

$\begin{array}{l}{E}_{\beta ,\gamma }(z)={\displaystyle \sum _{k=0}^{\infty }}\frac{z^k}{\Gamma (\beta k+\gamma )},\forall z\in ℂ.\end{array}$

Particularly, $E_{1,1}(z)=e^z$. Let E_β(z) ≜ E_β,1(z) whenever γ = 1.

Lemma 1. Podlubny [2] Given β ∈ (0, 2), γ ∈ ℝ. For an arbitrary z ∈ ℂ, if the argument arg(z) satisfies

$\begin{array}{l}\theta \le |arg(z)|\le \pi \end{array}$

with βπ/2 < θ ≤ min{π, βπ}, then the value of E_β,γ(z) is limited within the estimation range:

$\begin{array}{l}\left|E_{\beta ,\gamma }(z)\right|\le \frac{C}{1+\left|z\right|},\end{array}$

where C ∈ ℝ⁺ is a constant.

Lemma 2. Gong [4] Let V(t) be a continuous nonnegative function. Suppose that

$\begin{array}{l}{{D}}^{\beta }V(t)\le -\lambda V(t)+\rho ,\end{array}$

where λ > 0, ρ ≥ 0. Then

$\begin{array}{l}V(t)\le V(0)E_{\beta }(-\lambda t^{\beta })+\frac{M\rho }{\lambda },\end{array}$

where M = max{1, C}, C ∈ ℝ⁺ is defined as in Lemma 1.

Lemma 3. Podlubny [2] Let x(t) and y(t) be differentiable functions, C ∈ ℝ, β ∈ (0, 1). Then (1) ${{D}}^{\beta }C=0.$ (2) ${{D}}^{\beta }(mx(t)+ny(t))=m{{D}}^{\beta }x(t)+n{{D}}^{\beta }y(t)$, where m, n ∈ ℝ are constants.

Lemma 4. Aguila-Camacho et al. [3] Let x(t) be a differentiable function, β ∈ (0, 1). Then

$\begin{array}{l}\frac{1}{2}{{D}}^{\beta }{x}^2(t)\le x(t){{D}}^{\beta }x(t).\end{array}$

2.2. Radial basis function network

Recall the notion of radial basis function network (RBFNN) [19]. An RBFNN is represented by

$\begin{array}{ll}\widehat{f}(x(t))={\Theta }^T(t)\text{Ψ}(x(t)),& (1)\end{array}$

where $\widehat{f}(x(t))\in ℝ$ is referred to as the output of RBFNN, x(t) ∈ ℝⁿ is referred to as the input of RBFNN, $\Theta (t)={\left[{\theta }_1(t),\cdots ,{\theta }_m(t)\right]}^T\in {ℝ}^m$ is a weight vector with m being the number of neural nodes, and Ψ(x(t)) ∈ ℝ^m is a vector of radial basis functions, the jth coordinate ψ_j(x(t)) of Ψ(x(t)) is usually defined to be the Gaussian function, that is

$\begin{array}{l}{\psi }_j(x(t))=exp\left[-\frac{1}{w_j^2}{(x(t)-{\varsigma }_j)}^T(x(t)-{\varsigma }_j)\right],\end{array}$

where ${\varsigma }_j\in {ℝ}^n$ describes the center of the receptive field, $w_j\in {ℝ}^{+}$ means the width of ψ_j(x(t)).

Lemma 5. Sanner and Slotine [19] For any continuous function f(x(t)) defined over a compact set Ω_r and any small positive scalar $\bar{\epsilon }$, one can find an RBFNN, denoted by Θ^*TΨ(x(t)), such that

$\begin{array}{l}{\displaystyle \underset{x(t)\in {\Omega }_r}{sup}}|f(x(t))-{\Theta }^T\text{Ψ}(x(t))|\le \bar{\epsilon },\end{array}$

in which Θ^* is the optimal RBFNN parameter, described by

$\begin{array}{l}{\Theta }^{}=\arg \underset{\Theta (t)\in {ℝ}^m}{\min }\left\{\underset{x(t)\in {\Omega }_r}{\sup }\left|f(x(t))-{\Theta }^T(t)\Psi (x(t))\right|\right\}.\hfill \end{array}$

Lemma 6. Kurdila et al. [20] Given an x(t) ∈ ℝⁿ. Then, there exists a positive scalar ψ irrelevant with x(t) such that the regressor Ψ(x(t)) defined in Equation (1) satisfies max{||Ψ(x(t))||, ||Ψ(ẋ(t))||} ≤ ψ.

Definition 3. Pan et al. [25] Let μ > 0 be an excitation strength and τ₀ > 0 be a time duration. A time-varying vector Ψ(t) is said to be of persistent excitation (PE), provided that ${\int }_{t-{\tau }_0}^t{\text{Ψ}}^T(\tau )\text{Ψ}(\tau )d\tau \ge \mu I_{m\times m}$ for all t > τ₀, where I_m×m is an m × m unit matrix.

Definition 4. Pan et al. [25] Let μ > 0 be an excitation strength and τ₀ > 0 be a time duration. A time-varying vector Ψ(t) is said to be of interval excitation (IE) over the interval [T_e − τ₀, T_e] with T_e > τ₀, if ${\int }_{T_e-{\tau }_0}^{T_e}{\text{Ψ}}^T(\tau )\text{Ψ}(\tau )d\tau \ge \mu I_{m\times m}$.

3. Main results

3.1. Problem formulation

Permanent magnet synchronous motor (PMSM) is a sort of special mechanical device whose dynamic behaviors manifest exclusive chaotic attractor. An integer-order PMSM dynamic system [10] can be modeled by

$\begin{array}{ll}\{\begin{array}{l}\frac{d\omega }{dt}=\sigma (i_q-\omega ),\\ \frac{d{i}_q}{dt}=\gamma \omega -\omega i_d-i_q,\\ \frac{d{i}_d}{dt}=u_d+\omega i_q-i_d,\end{array}& (2)\end{array}$

where ω, i_d, and i_q symbolize the angular velocity, the d-axis current, and the q-axis current, respectively. σ and γ are two positive coefficients.

Put ω = x₁, i_q = x₂ and i_d = x₃ in Equation (2), respectively. By substituting the β-order derivative operator ${{D}}^{\beta }(·)$ with 0 < β < 1 for $\frac{d(·)}{dt}$, we generalize the aforesaid formulation into an uncertain fractional-order PMSM dynamic system in the state-space form as follows:

$\begin{array}{ll}\{\begin{array}{l}{{D}}^{\beta }{x}_1(t)=f_1({\overline{x}}_1)+\sigma (x_2(t)-x_1(t)),\\ {{D}}^{\beta }{x}_2(t)=f_2({\overline{x}}_2)+\gamma x_1(t)-x_1(t)x_3(t)-x_2(t),\\ {{D}}^{\beta }{x}_3(t)=f_3({\overline{x}}_3)+u_d(t)+x_1(t)x_2(t)-x_3(t),\\ y\left(t\right)=x_1\left(t\right),\end{array}& (3)\end{array}$

where ${\bar{x}}_i={\left[x_1,\cdots ,x_i\right]}^T\in {ℝ}^i$ (i = 1, 2, 3) is a measurable state vector, $f_i:{ℝ}^i\to ℝ$ (i = 1, 2, 3) is an unknown bounded continuous nonlinear function, y(t) ∈ ℝ is the system output, and u_d(t) ∈ ℝ is the control input.

Let the initial values be x₁(0) = x₂(0) = x₃(0) = 0.8. When β = 0.98, σ = 3, and γ = 30, the chaotic attractor appears in the dynamic behaviors of fractional-order PMSM, see Figure 1.

FIGURE 1

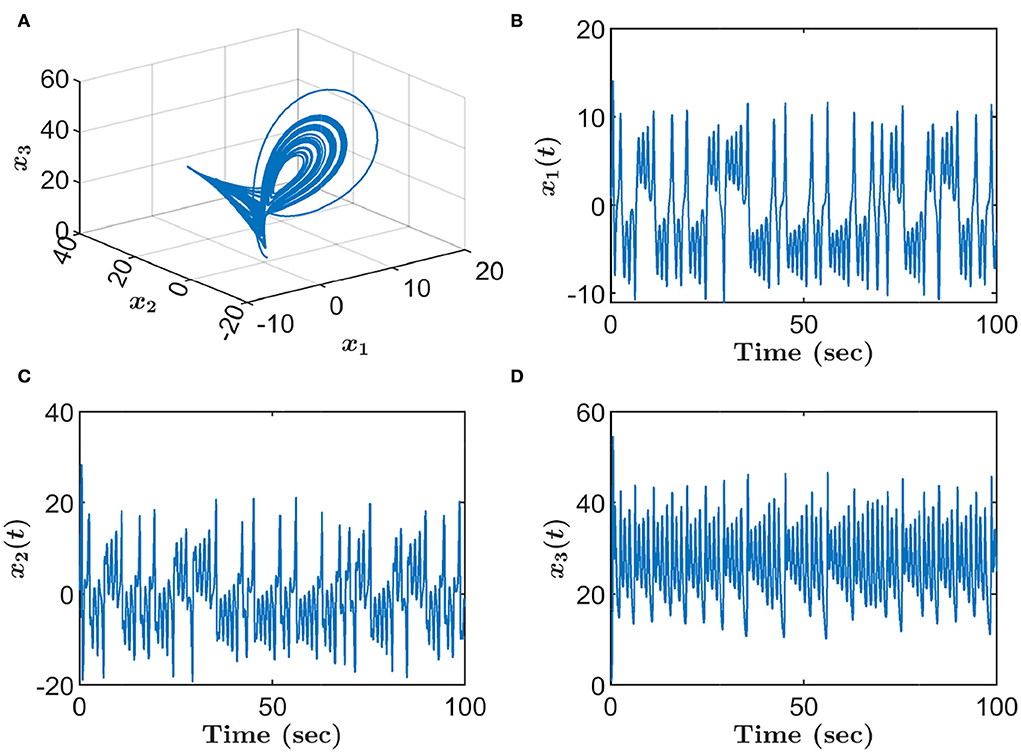
Figure 1. Chaotic attractor of fractional-order PMSM with β = 0.98, σ = 3, and γ = 30. (A) 3D phase portrait. (B) Time evolution of x₁. (C) Time evolution of x₂. (D) Time evolution of x₃.

The system controller will be designed in the next subsection such that the output signal y(t) is driven to track the desired signal y_d(t). To accomplish this tracking task, one needs to invoke the following assumption.

Assumption 1. Both of the signals y_d(t) and ${{D}}^{\beta }{y}_d(t)$ are known, bounded and smooth.

3.2. Control design

Next, let us expound the backstepping control design process for fractional-order PMSM.

Denote the virtual inputs by α₁(t) and α₂(t) for the first subsystem and the second subsystem, respectively. Let α₁(t) and α₂(t) pass the following fractional-order dynamic surfaces

$\begin{array}{ll}{{D}}^{\beta }{\alpha }_{i,c}(t)=-{\phi }_i({\alpha }_{i,c}(t)-{\alpha }_i(t)),i=1,2& (4)\end{array}$

respectively, where ${\phi }_i\in {ℝ}^{+}$ are given constants, and the filter outputs α_i,c(t) satisfy the initial conditions α_i,c(0) = α_i(0). Suppose that the parameters φ_i are selected suitably large. According to Liu et al. [27, Lemma 3], there are constants ${\zeta }_i\in {ℝ}^{+}$ such that |α_i,c(t) − α_i(t)| ≤ ζ_i for all t ≥ 0.

Consider the following coordinate translation:

$\begin{array}{ll}{e}_1(t)=x_1(t)-y_d(t),& (5)\end{array}$

$\begin{array}{ll}{e}_{i+1}(t)=x_{i+1}(t)-{\alpha }_{i,c}(t)\text{for}i=1,2.& (6)\end{array}$

In light of Lemma 5, the existence of optimal RBFNN parameters ${\Theta }_{f_i}^{ }$ for i = 1, 2, 3 is guaranteed so that

$\begin{array}{ll}{f}_i({\bar{x}}_i)={\Theta }_{f_i}^T{\text{Ψ}}_{f_i}({\bar{x}}_i)+{\epsilon }_{f_i}(t),i=1,2,3& (7)\end{array}$

respectively, in which ε_fi(t) represents the approximation error variable, which satisfies $\left|{\epsilon }_{f_i}(t)\right|\le {\bar{\epsilon }}_i$ for some given scalar ${\bar{\epsilon }}_i\in {ℝ}^{+}$. The parametric estimation error is taken as ${\tilde{\Theta }}_{f_i}(t)={\widehat{\Theta }}_{f_i}(t)-{\Theta }_{f_i}^{ }$.

Step 1. From Equations (3) and (7), it holds

$\begin{array}{ll}{{D}}^{\beta }{x}_1(t)={\Theta }_{f_i}^T{\text{Ψ}}_{f_i}({\bar{x}}_i)+{\epsilon }_{f_i}(t)+\sigma {)x}_2(t)-x_1(t)).& (8)\end{array}$

Hence, owing to Equations (5), (6), and (8), computing the fractional time derivative of e₁(t) yields

$\begin{array}{l}{{D}}^{\beta }{e}_1(t)={{D}}^{\beta }{x}_1(t)-{{D}}^{\beta }{y}_d(t)\\ =f_1({\overline{x}}_1)+\sigma (x_2(t)-x_1(t))-{{D}}^{\beta }{y}_d(t)\\ =f_1({\overline{x}}_1)+(\sigma -1)(x_2(t)-x_1(t))+(x_2(t)-{\alpha }_{1,c}(t))\\ +({\alpha }_{1,c}(t)-{\alpha }_1(t))+({\alpha }_1(t)-x_1(t))-{{D}}^{\beta }{y}_d(t)\\ ={\widehat{\Theta }}_{f_1}^T(t){\Psi }_{f_1}({\overline{x}}_1)-{\tilde{\Theta }}_{f_1}^T(t){\Psi }_{f_1}({\overline{x}}_1)\\ +{\epsilon }_{f_1}(t)+(\sigma -1)(x_2(t)-x_1(t))+e_2(t)+z_1(t)\\ +{\alpha }_1(t)-x_1(t)-{{D}}^{\beta }{y}_d(t),& (9)\end{array}$

where z₁(t) = α_1,c(t) − α₁(t) is the filter error.

The virtual control function for the first subsystem is defined by

$\begin{array}{l}{\alpha }_1(t)=-k_1{e}_1(t)-{\widehat{\Theta }}_{f_1}^T(t){\Psi }_{f_1}({\overline{x}}_1)-(\sigma -1)(x_2(t)-x_1(t))\\ +x_1(t)-e_1(t)+{{D}}^{\beta }{y}_d(t),& (10)\end{array}$

where k₁ is a positive known constant.

Incorporating Equation (10) into Equation (9) infers

$\begin{array}{l}{{D}}^{\beta }{e}_1(t)=-{\tilde{\Theta }}_{f_1}^T(t){\text{Ψ}}_{f_1}({\bar{x}}_1)+{\epsilon }_{f_1}(t)-k_1{e}_1(t)\\ +e_2(t)-e_1(t)+z_1(t).& (11)\end{array}$

It is worth noting that |z₁(t)| ≤ ζ₁. By Young inequality, multiplying both sides of Equation (11) by e₁(t) induces

$\begin{array}{l}{e}_1(t){{D}}^{\beta }{e}_1(t)=-e_1(t){\tilde{\Theta }}_{f_1}^T(t){\Psi }_{f_1}({\overline{x}}_1)+e_1(t){\epsilon }_{f_1}(t)\\ -k_1{e}_1^2(t)+e_1(t)e_2(t)-e_1^2(t)+e_1(t)z_1(t)\\ \le -e_1(t){\tilde{\Theta }}_{f_1}^T(t){\Psi }_{f_1}({\overline{x}}_1)+\frac{1}{2}{e}_1^2(t)+\frac{1}{2}{\epsilon }_{f_1}^2(t)\\ -k_1{e}_1^2(t)+e_1(t)e_2(t)-e_1^2(t)+\frac{1}{2}{e}_1^2(t)+\frac{1}{2}{\zeta }_1^2\\ =-e_1(t){\tilde{\Theta }}_{f_1}^T(t){\Psi }_{f_1}({\overline{x}}_1)-k_1{e}_1^2(t)+e_1(t)e_2(t)\\ +\frac{1}{2}{\overline{\epsilon }}_1^2+\frac{1}{2}{\zeta }_1^2.& (12)\end{array}$

In general, the traditional adaptation law can only make sure that the parametric estimation error ${\tilde{\Theta }}_{f_1}(t)$ is bounded under the PE condition. However, the PE condition is sometimes too stringent to be fulfilled, and thus, satisfactory parametric convergence cannot be ensured. Motivated by this reason, a composite learning approach will be studied in the sequel to achieve higher precision of ${\widehat{\Theta }}_{f_1}(t)$ with the removal of the rigorous PE condition.

Define a mapping $m_1:[0,+\infty )\to {ℝ}^{m\times m}$ by

$\begin{array}{l}{m}_1(t)={\displaystyle {\int }_{t-{\tau }_1}^t}{\text{Ψ}}_{f_1}({\bar{x}}_1(\tau )){\text{Ψ}}_{f_1}^T({\bar{x}}_1(\tau ))d\tau ,\end{array}$

where τ₁ > 0 is a certain integration duration.

Suppose that m₁(t) ≥ μ₁I with μ₁ > 0 standing for the exciting strength, whenever ${\text{Ψ}}_{f_1}({\bar{x}}_1(t))$ is of IE on t ∈ [T_e1 − τ₁, T_e1] for a time instant T_e1 > τ₁. Take into account the next prediction error defined by

$\begin{array}{ll}{\widehat{\epsilon }}_1(t)=\{\begin{array}{l}\begin{array}{cc}{m}_1(t){\tilde{\Theta }}_{f_1}(t)-{\tilde{\epsilon }}_{f_1}(t),& t<T_{e_1}\end{array}\\ \begin{array}{cc}{m}_1(t){\tilde{\Theta }}_{f_1}(T_{e_1})-{\tilde{\epsilon }}_{f_1}(T_{e_1}),& t\ge T_{e_1}\end{array}\end{array}& (13)\end{array}$

where ${\tilde{\epsilon }}_{f_1}:[0,+\infty )\to {ℝ}^{m\times 1}$ is expressed as

$\begin{array}{l}{\tilde{\epsilon }}_{f_1}(t)={\displaystyle {\int }_{t-{\tau }_1}^t}{\text{Ψ}}_{f_1}({\bar{x}}_1(\tau )){\epsilon }_{f_1}(\tau )d\tau .\end{array}$

The fractional-order composite learning adaptation law is designed as

$\begin{array}{ll}{{D}}^{\beta }{\widehat{\Theta }}_{f_1}(t)={\varrho }_1{e}_1(t){\text{Ψ}}_{f_1}({\bar{x}}_1(t))-{\eta }_1{\widehat{\Theta }}_{f_1}(t)-{\varrho }_1{\varpi }_1{\widehat{\epsilon }}_1(t),& (14)\end{array}$

where ϱ₁, η₁, and ${\varpi }_1\in {ℝ}^{+}$ are known constants.

Construct an auxiliary variable H₁(t) by

$\begin{array}{ll}{H}_1(t)=m_1(t){\Theta }_{f_1}^{}+{\tilde{\epsilon }}_{f_1}(t).& (15)\end{array}$

Apparently, it is observed from Equation (8) that

$\begin{array}{ll}{\Theta }_{f_1}^T{\text{Ψ}}_{f_1}({\bar{x}}_1)+{\epsilon }_{f_1}(t)={{D}}^{\beta }{x}_1(t)-\sigma {(x}_2(t)-x_1(t)).& (16)\end{array}$

Multiply both sides of Equation (16) by ${\text{Ψ}}_{f_1}({\bar{x}}_1)$. Then, it is inferred that

$\begin{array}{l}{\text{Ψ}}_{f_1}({\bar{x}}_1)\left[{\text{Ψ}}_{f_1}^T({\bar{x}}_1){\Theta }_{f_1}^{}+{\epsilon }_{f_1}(t)\right]\\ ={\text{Ψ}}_{f_1}({\bar{x}}_1)\left[{{D}}^{\beta }{x}_1(t)-\sigma {(x}_2(t)-x_1(t))\right].& (17)\end{array}$

Invoking Equations (15) and (17), we can gain access to the precise value of H₁(t) as

$\begin{array}{l}{H}_1(t)={\displaystyle {\int }_{t-{\tau }_1}^t}{\text{Ψ}}_{f_1}({\bar{x}}_1(\tau ))\left[{{D}}^{\beta }{x}_1(\tau )-\sigma {(x}_2(\tau )-x_1(\tau ))\right]d\tau .\end{array}$

Consequently, the value of ${\widehat{\epsilon }}_1(t)$ can be acquired precisely as

$\begin{array}{l}{\widehat{\epsilon }}_1(t)=m_1(t){\widehat{\Theta }}_{f_1}(t)-m_1(t){\Theta }_{f_1}^{}(t)-{\tilde{\epsilon }}_{f_1}(t)\\ =m_1(t){\widehat{\Theta }}_{f_1}(t)-H_1(t).& (18)\end{array}$

Substituting Equation (18) into Equation (14), one arrives at

$\begin{array}{l}{{D}}^{\beta }{\widehat{\Theta }}_{f_1}(t)={\varrho }_1{e}_1(t){\text{Ψ}}_{f_1}({\bar{x}}_1(t))-{\eta }_1{\widehat{\Theta }}_{f_1}(t)\\ +{\varrho }_1{\varpi }_1(H_1(t)-m_1(t){\widehat{\Theta }}_{f_1}(t)).& (19)\end{array}$

Consider the next quadratic Lyapunov function:

$\begin{array}{ll}{V}_1(t)=\frac{1}{2}{e}_1^2(t)+\frac{1}{2{\varrho }_1}{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t).& (20)\end{array}$

Invoking Lemmas 3 and 4, simple manipulation on the fractional differentiation of Equation (20) renders

$\begin{array}{l}{{D}}^{\beta }{V}_1(t)=\frac{1}{2}{{D}}^{\beta }{e}_1^2(t)+\frac{1}{2{\varrho }_1}{{D}}^{\beta }({\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t))\\ \le e_1(t){{D}}^{\beta }{e}_1(t)+\frac{1}{{\varrho }_1}{\tilde{\Theta }}_{f_1}^T(t){{D}}^{\beta }{\tilde{\Theta }}_{f_1}(t)\\ =e_1(t){{D}}^{\beta }{e}_1(t)+\frac{1}{{\varrho }_1}{\tilde{\Theta }}_{f_1}^T(t){{D}}^{\beta }{\widehat{\Theta }}_{f_1}(t).& (21)\end{array}$

Application of Young's inequality gives

$\begin{array}{l}-{\tilde{\Theta }}_{f_1}^T(t){\widehat{\Theta }}_{f_1}(t)=-{\tilde{\Theta }}_{f_1}^T(t){\Theta }_{f_1}^{}-{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t)\\ \le \frac{1}{2}{\Theta }_{f_1}^T{\Theta }_{f_1}^{}+\frac{1}{2}{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t)-{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t)\\ =\frac{1}{2}{\Theta }_{f_1}^T{\Theta }_{f_1}^{}-\frac{1}{2}{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t).& (22)\end{array}$

Moreover, by using Young's inequality and Lemma 6, it is shown that

$\begin{array}{l}{\varpi }_1{\tilde{\Theta }}_{f_1}^T(t){\tilde{\epsilon }}_{f_1}(t)\le \frac{1}{2}{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t)+\frac{1}{2}{\varpi }_1^2{\tilde{\epsilon }}_{f_1}^T(t){\tilde{\epsilon }}_{f_1}(t)\\ \le \frac{1}{2}{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t)+\frac{1}{2}{\varpi }_1^2{\tilde{\epsilon }}_1^2\\ \underset{\tau \in [t-{\tau }_1,t]}{\max }\left|\right|{\Psi }_{f_1}({\overline{x}}_1(\tau ))|{|}^2{\left({\displaystyle {\int }_{t-{\tau }_1}^{t}d\tau }\right)}^2\\ \le \frac{1}{2}{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t)+\frac{1}{2}{\left({\varpi }_1{\tilde{\epsilon }}_1{\psi }_1{\tau }_1\right)}^2& (23)\end{array}$

with ψ₁ > 0 being a constant which is independent of ${\bar{x}}_1(t)$ and the number of neural nodes.

Considering Equations (12)–(14) and Equation (19)–(23), we conclude

$\begin{array}{l}{{D}}^{\beta }{V}_1(t)\\ \le -e_1(t){\tilde{\Theta }}_{f_1}^T(t){\text{Ψ}}_{f_1}({\bar{x}}_1)-k_1{e}_1^2(t)+e_1(t)e_2(t)+\frac{1}{2}{\zeta }_1^2+\frac{1}{2}{\bar{\epsilon }}_1^2\\ +\frac{1}{{\varrho }_1}{\tilde{\Theta }}_{f_1}^T(t)\left[{\varrho }_1{e}_1(t){\text{Ψ}}_{f_1}({\bar{x}}_1)-{\eta }_1{\widehat{\Theta }}_{f_1}(t)-{\varrho }_1{\varpi }_1{\widehat{\epsilon }}_1(t)\right]\\ =-k_1{e}_1^2(t)+e_1(t)e_2(t)-\frac{{\eta }_1}{{\varrho }_1}{\tilde{\Theta }}_{f_1}^T(t){\widehat{\Theta }}_{f_1}(t)\\ -{\varpi }_1{\tilde{\Theta }}_{f_1}^T(t){\widehat{\epsilon }}_1(t)+\frac{1}{2}{\zeta }_1^2+\frac{1}{2}{\bar{\epsilon }}_1^2\\ \le -k_1{e}_1^2(t)+e_1(t)e_2(t)-\frac{{\eta }_1}{2{\varrho }_1}{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t)\\ +\frac{{\eta }_1}{2{\varrho }_1}{\Theta }_{f_1}^T{\Theta }_{f_1}^{}+\frac{1}{2}{\zeta }_1^2+\frac{1}{2}{\bar{\epsilon }}_1^2\\ -{\varpi }_1{\tilde{\Theta }}_{f_1}^T(t)(m_1(t){\tilde{\Theta }}_{f_1}(t)-{\tilde{\epsilon }}_{f_1}(t))\\ =-k_1{e}_1^2(t)+e_1(t)e_2(t)-\frac{{\eta }_1}{2{\varrho }_1}{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t)+\frac{{\eta }_1}{2{\varrho }_1}{\Theta }_{f_1}^T{\Theta }_{f_1}^{}\\ -{\varpi }_1{\mu }_1{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t)+{\varpi }_1{\tilde{\Theta }}_{f_1}^T(t){\tilde{\epsilon }}_{f_1}(t)+\frac{1}{2}{\zeta }_1^2+\frac{1}{2}{\bar{\epsilon }}_1^2\\ \le -k_1{e}_1^2(t)+e_1(t)e_2(t)-\frac{{\eta }_1+{\varrho }_1(2{\varpi }_1{\mu }_1-1)}{2{\varrho }_1}{\tilde{\Theta }}_{f_1}^T(t){\tilde{\Theta }}_{f_1}(t)\\ +\frac{{\eta }_1}{2{\varrho }_1}{\Theta }_{f_1}^T{\Theta }_{f_1}^{}+\frac{1}{2}{({\varpi }_1{\bar{\epsilon }}_1{\psi }_1{\tau }_1)}^2+\frac{1}{2}{\zeta }_1^2+\frac{1}{2}{\bar{\epsilon }}_1^2\\ \le -a_1{V}_1(t)+e_1(t)e_2(t)+b_1,& (24)\end{array}$

where a₁ = min{2k₁, η₁ + ϱ₁(2ϖ₁μ₁ − 1)}, $b_1=0.5{\varrho }_1^{-1}{\eta }_1\left|\right|{\Theta }_{f_1}^{ }|{|}^2+0.5{\varpi }_1^2{\bar{\epsilon }}_1^2{\psi }_1^2{\tau }_1^2+0.5{\zeta }_1^2+0.5{\bar{\epsilon }}_1^2$.

Step 2. According to Equations (3) and (7), we have

$\begin{array}{ll}{{D}}^{\beta }{x}_2(t)={\Theta }_{f_2}^T{\text{Ψ}}_{f_2}({\bar{x}}_2)+{\epsilon }_{f_2}(t)+\gamma x_1(t)-x_1(t)x_3(t)-x_2(t).& (25)\end{array}$

With the aid of Equations (6) and (25), we can derive

$\begin{array}{l}{{D}}^{\beta }{e}_2(t)={{D}}^{\beta }{x}_2(t)-{{D}}^{\beta }{\alpha }_{1,c}(t)\\ =f_2({\bar{x}}_2)-x_2(t)-x_1(t)x_3(t)+\gamma x_1(t)-{{D}}^{\beta }{\alpha }_{1,c}(t)\\ ={\widehat{\Theta }}_{f_2}^T(t){\text{Ψ}}_{f_2}({\bar{x}}_2)-{\tilde{\Theta }}_{f_2}^T(t){\text{Ψ}}_{f_2}({\bar{x}}_2)+{\epsilon }_{f_2}(t)\\ -x_2(t)-x_1(t)e_3(t)-x_1(t)z_2(t)-x_1(t){\alpha }_2(t)\\ +\gamma x_1(t)-{{D}}^{\beta }{\alpha }_{1,c}(t),& (26)\end{array}$

where z₂(t) = α_2,c(t) − α₂(t) is the filter error.

The virtual controller is provided as

$\begin{array}{l}{\alpha }_2(t)=\frac{1}{x_1(t)}[k_2{e}_2(t)+\frac{1}{2}(x_1^2(t)+1)e_2(t)+{\widehat{\Theta }}_{f_2}^T(t){\Psi }_{f_2}({\overline{x}}_2)\\ -x_2(t)+\gamma x_1(t)+e_1(t)-{{D}}^{\beta }{\alpha }_{1,c}(t)]& (27)\end{array}$

with k₂ > 0 being a design parameter.

Substituting Equation (27) into Equation (26) induces

$\begin{array}{l}{{D}}^{\beta }{e}_2(t)=-k_2{e}_2(t)-\frac{1}{2}(x_1^2(t)+1)e_2(t)-{\tilde{\Theta }}_{f_2}^T(t){\text{Ψ}}_{f_2}({\bar{x}}_2)\\ +{\epsilon }_{f_2}(t)-e_1(t)-x_1(t)z_2(t)-x_1(t)e_3(t).& (28)\end{array}$

Multiply both sides of Equation (28) by e₂(t). Employing Lemma 4 and Young inequality, we argue

$\begin{array}{l}{e}_2(t){{D}}^{\beta }{e}_2(t)=-k_2{e}_2^2(t)-\frac{1}{2}(x_1^2(t)+1)e_2^2(t)\\ -e_2(t){\tilde{\Theta }}_{f_2}^T(t){\text{Ψ}}_{f_2}({\bar{x}}_2)+e_2(t){\epsilon }_{f_2}(t)\\ -x_1(t)e_2(t)e_3(t)-x_1(t)e_2(t)z_2(t)-e_1(t)e_2(t)\\ \le -k_2{e}_2^2(t)-\frac{1}{2}(x_1^2(t)+1)e_2^2(t)-e_2(t){\tilde{\Theta }}_{f_2}^T(t)\\ {\text{Ψ}}_{f_2}({\bar{x}}_2)+\frac{1}{2}{e}_2^2(t)+\frac{1}{2}{\bar{\epsilon }}_2^2-x_1(t)e_2(t)e_3(t)\\ +\frac{1}{2}{x}_1^2(t)e_2^2(t)+\frac{1}{2}{\zeta }_2^2-e_1(t)e_2(t)\\ \le -k_2{e}_2^2(t)-e_2(t){\tilde{\Theta }}_{f_2}^T(t){\text{Ψ}}_{f_2}({\bar{x}}_2)-x_1(t)e_2(t)e_3(t)\\ -e_1(t)e_2(t)+\frac{1}{2}{\zeta }_2^2+\frac{1}{2}{\bar{\epsilon }}_2^2.& (29)\end{array}$

Let ${\text{Ψ}}_{f_2}({\bar{x}}_2(t))$ be of IE over the interval [T_e2 − τ₂, T_e2] for some τ₂ > 0 and T_e2 > τ₂.

Define the following prediction error

$\begin{array}{ll}{\widehat{\epsilon }}_2(t)=\{\begin{array}{l}\begin{array}{cc}{m}_2(t){\tilde{\Theta }}_{f_2}(t)-{\tilde{\epsilon }}_{f_2}(t),& t<T_{e_2}\end{array}\\ \begin{array}{cc}{m}_2(t){\tilde{\Theta }}_{f_2}(T_{e_2})-{\tilde{\epsilon }}_{f_2}(T_{e_2}),& t\ge T_{e_2}\end{array}\end{array}& (30)\end{array}$

where $m_2:[0,+\infty )\to {ℝ}^{m\times m}$ and ${\tilde{\epsilon }}_{f_2}:[0,+\infty )\to {ℝ}^{m\times 1}$ are formulated by

$\begin{array}{l}{m}_2(t)={\displaystyle {\int }_{t-{\tau }_0}^t}{\text{Ψ}}_{f_2}({\bar{x}}_2(\tau )){\text{Ψ}}_{f_2}^T({\bar{x}}_2(\tau ))d\tau ,\end{array}$

and

$\begin{array}{l}{\tilde{\epsilon }}_{f_2}(t)={\displaystyle {\int }_{t-{\tau }_2}^t}{\text{Ψ}}_{f_2}({\bar{x}}_2(\tau )){\epsilon }_{f_2}(\tau )d\tau ,\end{array}$

respectively. Presume that m₂(t) ≥ μ₂I, where μ₂ is the exciting strength.

Choose the composite learning-based adaptation law as below:

$\begin{array}{ll}{{D}}^{\beta }{\widehat{\Theta }}_{f_2}(t)={\varrho }_2{e}_2(t){\text{Ψ}}_{f_2}({\bar{x}}_2(t))-{\eta }_2{\widehat{\Theta }}_{f_2}(t)-{\varrho }_2{\varpi }_2{\widehat{\epsilon }}_2(t),& (31)\end{array}$

where ϱ₂, η₂, and ϖ₂ are given positive scalars.

Define the following auxiliary term:

$\begin{array}{ll}{H}_2(t)=m_2(t){\Theta }_{f_2}^{}+{\tilde{\epsilon }}_{f_2}(t).& (32)\end{array}$

On account of Equation (25), it is trivially seen that

$\begin{array}{ll}{\Theta }_{f_2}^T{\text{Ψ}}_{f_2}({\bar{x}}_2)+{\epsilon }_{f_2}(t)={{D}}^{\beta }{x}_2(t)-\gamma x_1(t)+x_1(t)x_3(t)+x_2(t).& (33)\end{array}$

Multiply both sides of Equation (33) by ${\text{Ψ}}_{f_2}({\bar{x}}_2)$. Then, it is inferred that

$\begin{array}{l}{\text{Ψ}}_{f_2}({\bar{x}}_2)\left[{\text{Ψ}}_{f_2}^T({\bar{x}}_2){\Theta }_{f_2}^{}+{\epsilon }_{f_2}(t)\right]\\ ={\text{Ψ}}_{f_2}({\bar{x}}_2)\left[{{D}}^{\beta }{x}_2(t)-\gamma x_1(t)+x_1(t)x_3(t)+x_2(t)\right].& (34)\end{array}$

Due to Equations (32) and (34), the computational result of H₂(t) is attainable, that is

$\begin{array}{l}{H}_2(t)={\displaystyle {\int }_{t-{\tau }_2}^t}{\text{Ψ}}_{f_2}({\bar{x}}_2)\left[{{D}}^{\beta }{x}_2(\tau )-\gamma x_1(\tau )+x_1(\tau )x_3(\tau )+x_2(\tau )\right].\end{array}$

Accordingly, the precise value of ${\widehat{\epsilon }}_2(t)$ is determined by

$\begin{array}{l}{\widehat{\epsilon }}_2(t)=m_2(t){\widehat{\Theta }}_{f_2}(t)-H_2(t).\end{array}$

Define the Lyapunov function by

$\begin{array}{ll}{V}_2(t)=V_1(t)+\frac{1}{2}{e}_2^2(t)+\frac{1}{2{\varrho }_2}{\tilde{\Theta }}_{f_2}^T(t){\tilde{\Theta }}_{f_2}(t).& (35)\end{array}$

By Lemmas 3 and 4, taking the fractional derivative of Equation (35) leads to

$\begin{array}{l}{{D}}^{\beta }{V}_2(t)={{D}}^{\beta }{V}_1(t)+\frac{1}{2}{{D}}^{\beta }{e}_2^2(t)+\frac{1}{2{\varrho }_1}{{D}}^{\beta }{\tilde{\Theta }}_{f_2}^T(t){\tilde{\Theta }}_{f_2}(t)\\ \le {{D}}^{\beta }{V}_1(t)+e_2(t){{D}}^{\beta }{e}_2(t)+\frac{1}{{\varrho }_2}{\tilde{\Theta }}_{f_2}^T(t){{D}}^{\beta }{\tilde{\Theta }}_{f_2}(t)\\ ={{D}}^{\beta }{V}_1(t)+e_2(t){{D}}^{\beta }{e}_2(t)+\frac{1}{{\varrho }_2}{\tilde{\Theta }}_{f_2}^T(t){{D}}^{\beta }{\widehat{\Theta }}_{f_2}(t).& (36)\end{array}$

Analogs to Equations (22) and (23), it is easily verified that

$\begin{array}{ll}-{\tilde{\Theta }}_{f_2}^T(t){\widehat{\Theta }}_{f_2}(t)\le -\frac{1}{2}{\tilde{\Theta }}_{f_2}^T(t){\tilde{\Theta }}_{f_2}(t)+\frac{1}{2}{\Theta }_{f_2}^T{\Theta }_{f_2}^{},& (37)\end{array}$

$\begin{array}{ll}{\varpi }_2{\tilde{\Theta }}_{f_2}^T(t){\tilde{\epsilon }}_{f_2}(t)\le \frac{1}{2}{\tilde{\Theta }}_{f_2}^T(t){\tilde{\Theta }}_{f_2}(t)+\frac{1}{2}{({\varpi }_2{\bar{\epsilon }}_2{\psi }_2{\tau }_2)}^2,& (38)\end{array}$

in which ${\psi }_2\ge \left|\right|{\text{Ψ}}_{f_2}({\bar{x}}_2(t))\left|\right|$ is a positive constant irrelevant with ${\bar{x}}_2(t)$ and the number of neural nodes.

By means of Equations (29), (31), and (36)–(38), we get

$\begin{array}{l}{{D}}^{\beta }{V}_2(t)\\ \le {{D}}^{\beta }{V}_1(t)+e_2(t){{D}}^{\beta }{e}_2(t)+\frac{1}{2}{\zeta }_2^2+\frac{1}{2}{\bar{\epsilon }}_2^2\\ +\frac{1}{{\varrho }_2}{\tilde{\Theta }}_{f_2}^T(t){\varrho }_2{e}_2(t){\text{Ψ}}_{f_2}({\bar{x}}_2)-{\eta }_2{\widehat{\Theta }}_{f_2}(t)-{\varrho }_2{\varpi }_2{\widehat{\epsilon }}_2(t)\\ \le {{D}}^{\beta }{V}_1(t)-k_2{e}_2^2(t)-e_1(t)e_2(t)-x_1(t)e_2(t)e_3(t)\\ -\frac{{\eta }_2}{2{\varrho }_2}{\tilde{\Theta }}_{f_2}^T(t){\tilde{\Theta }}_{f_2}(t)\\ +\frac{{\eta }_2}{2{\varrho }_2}{\Theta }_{f_2}^T{\Theta }_{f_2}^{}-{\varpi }_2{\mu }_2{\tilde{\Theta }}_{f_2}^T(t){\tilde{\Theta }}_{f_2}(t)+{\varpi }_2{\tilde{\Theta }}_{f_2}^T(t){\tilde{\epsilon }}_{f_2}(t)\\ +\frac{1}{2}{\zeta }_2^2+\frac{1}{2}{\bar{\epsilon }}_2^2\\ \le -a_1{V}_1(t)+e_1(t)e_2(t)+b_1-k_2{e}_2^2(t)-x_1(t)e_2(t)e_3(t)-\\ e_1(t)e_2(t)+\frac{{\eta }_2}{2{\varrho }_2}{\Theta }_{f_2}^T{\Theta }_{f_2}^{}\\ -\frac{{\eta }_2+{\varrho }_2(2{\varpi }_2{\mu }_2-1)}{2{\varrho }_2}{\tilde{\Theta }}_{f_2}^T(t){\tilde{\Theta }}_{f_2}(t)+\frac{1}{2}{({\varpi }_2{\bar{\epsilon }}_2{\psi }_2{\tau }_2)}^2\\ +\frac{1}{2}{\zeta }_2^2+\frac{1}{2}{\bar{\epsilon }}_2^2\\ \le -a_2{V}_2(t)-x_1(t)e_2(t)e_3(t)+b_2,& (39)\end{array}$

where a₂ = min{a₁, 2k₂, η₂ + ϱ₂(2ϖ₂μ₂ − 1)}, $b_2=b_1+0.5{\varrho }_2^{-1}{\eta }_2\left|\right|{\Theta }_{f_2}^{ }|{|}^2+0.5{\varpi }_2^2{\bar{\epsilon }}_2^2{\psi }_2^2{\tau }_2^2+0.5{\zeta }_2^2+0.5{\bar{\epsilon }}_2^2$.

Step 3. In virtue of Equations (3) and (7), we know

$\begin{array}{ll}{{D}}^{\beta }{x}_3(t)={\Theta }_{f_3}^T{\text{Ψ}}_{f_3}({\bar{x}}_3)+{\epsilon }_{f_3}(t)+u_d(t)+x_1(t)x_2(t)-x_3(t).& (40)\end{array}$

On the basis of Equations (3) and (6), it is not difficult to check

$\begin{array}{l}{{D}}^{\beta }{e}_3(t)={{D}}^{\beta }{x}_3(t)-{{D}}^{\beta }{\alpha }_{2,c}(t)\\ ={\widehat{\Theta }}_{f_3}^T(t){\text{Ψ}}_{f_3}({\bar{x}}_3)-{\tilde{\Theta }}_{f_3}^T(t){\text{Ψ}}_{f_3}({\bar{x}}_3)+{\epsilon }_{f_3}(t)+u_d(t)\\ +x_1(t)x_2(t)-x_3(t)-{{D}}^{\beta }{\alpha }_{2,c}(t).& (41)\end{array}$

Configure the actual control law as

$\begin{array}{l}{u}_d(t)=-k_3{e}_3(t)+x_1(t)e_2(t)-{\widehat{\Theta }}_{f_3}^T(t){\text{Ψ}}_{f_3}({\bar{x}}_3)+x_3(t)\\ -x_1(t)x_2(t)+{{D}}^{\beta }{\alpha }_{2,c}(t),& (42)\end{array}$

where k₃ is a given positive scalar.

By substituting Equation (42) into Equation (41), it is directly implied that

$\begin{array}{ll}{{D}}^{\beta }{e}_3(t)=-k_3{e}_3(t)+x_1(t)e_2(t)-{\tilde{\Theta }}_{f_3}^T(t){\text{Ψ}}_{f_3}({\bar{x}}_3)+{\epsilon }_{f_3}(t).& (43)\end{array}$

Multiply both sides of Equation (43) by e₃(t). Then according to Lemma 4, it follows that

$\begin{array}{l}{e}_3(t){{D}}^{\beta }{e}_3(t)\\ \le -k_3{e}_3^2(t)+x_1(t)e_2(t)e_3(t)-e_3(t){\tilde{\Theta }}_{f_3}^T(t){\text{Ψ}}_{f_3}({\bar{x}}_3)+e_3(t){\epsilon }_{f_3}(t)\\ \le -k_3{e}_3^2(t)+x_1(t)e_2(t)e_3(t)-e_3(t){\tilde{\Theta }}_{f_3}^T(t){\text{Ψ}}_{f_3}({\bar{x}}_3)\\ \le -k_3{e}_3^2(t)+x_1(t)e_2(t)e_3(t)-e_3(t){\tilde{\Theta }}_{f_3}^T(t){\text{Ψ}}_{f_3}({\bar{x}}_3).& (44)\end{array}$

Define a mapping $m_3:[0,+\infty )\to {ℝ}^{m\times m}$ by

$\begin{array}{l}{m}_3(t)={\displaystyle {\int }_{t-{\tau }_3}^t}{\text{Ψ}}_{f_3}({\bar{x}}_3(\tau )){\text{Ψ}}_{f_3}^T({\bar{x}}_3(\tau ))d\tau \end{array}$

with τ₃ > 0 being the length of an integral interval.

Inspired by the similar argument in Step 2, we construct the prediction error by

${\widehat{\epsilon }}_3(t)=\{\begin{array}{l}\begin{array}{cc}{m}_3(t){\tilde{\Theta }}_{f_3}(t)-{\tilde{\epsilon }}_{f_3}(t),& t<T_{e_3}\end{array}\\ \begin{array}{cc}{m}_3(t){\tilde{\Theta }}_{f_2}(T_{e_3})-{\tilde{\epsilon }}_{f_3}(T_{e_3}),& t\ge T_{e_3}\end{array}\end{array}$

where ${\tilde{\epsilon }}_{f_2}:[0,+\infty )\to {ℝ}^{m\times 1}$ is described as

$\begin{array}{l}{\tilde{\epsilon }}_{f_3}(t)={\displaystyle {\int }_{t-{\tau }_3}^t}{\text{Ψ}}_{f_3}({\bar{x}}_3(\tau )){\epsilon }_{f_3}(\tau )d\tau ,\end{array}$

respectively. Let the IE condition be fulfilled, that is, m₃(t) ≥ μ₃I with a positive scalar μ₃ being the exciting strength, which implies ${\text{Ψ}}_{f_3}({\bar{x}}_3(t))$ is of IE on t ∈ [T_e3 − τ₃, T_e3] for some T_e3 > τ₃.

Introduce the adaptation law from composite learning as follows:

$\begin{array}{ll}{{D}}^{\beta }{\widehat{\Theta }}_{f_3}(t)={\varrho }_3{e}_3(t){\text{Ψ}}_{f_3}({\bar{x}}_3(t))-{\eta }_3{\widehat{\Theta }}_{f_3}(t)-{\varrho }_3{\varpi }_3{\widehat{\epsilon }}_3(t)& (45)\end{array}$

with ϱ₃, η₃, and ϖ₃ being positive design parameters.

To figure out the value of ${\widehat{\epsilon }}_3(t)$, let us define an auxiliary variable H₃(t) by

$\begin{array}{ll}{H}_3(t)=m_3(t){\Theta }_{f_3}^{}+{\tilde{\epsilon }}_{f_3}(t).& (46)\end{array}$

Equivalently, Equation (40) can be rewritten as

$\begin{array}{ll}{\Theta }_{f_3}^T{\text{Ψ}}_{f_3}({\bar{x}}_3)+{\epsilon }_{f_3}(t)={{D}}^{\beta }{x}_3(t)-u_d(t)-x_1(t)x_2(t)+x_3(t).& (47)\end{array}$

Multiplying both sides of Equation (47) by ${\text{Ψ}}_{f_3}({\bar{x}}_3(t))$, we can see

$\begin{array}{l}{\text{Ψ}}_{f_3}({\bar{x}}_3(t))\left[{\text{Ψ}}_{f_3}^T({\bar{x}}_3(t)){\Theta }_{f_3}^{}+{\epsilon }_{f_3}(t)\right]\\ ={\text{Ψ}}_{f_3}({\bar{x}}_3(t))\left[{{D}}^{\beta }{x}_3(t)-u_d(t)-x_1(t)x_2(t)+x_3(t)\right].& (48)\end{array}$

From Equations (46) and (48), it is deduced that

$\begin{array}{l}{H}_3(t)={\displaystyle {\int }_{t-{\tau }_0}^t{\Psi }_{f_3}({\overline{x}}_3(\tau ))}[{{D}}^{\beta }{x}_3(\tau )-u_d(\tau )\\ -x_1(\tau )x_2(\tau )+x_3(\tau )]d\tau .& (49)\end{array}$

Thereby, calculating the accurate value of ${\widehat{\epsilon }}_3(t)$ leads to

$\begin{array}{l}{\widehat{\epsilon }}_3(t)=m_3(t){\widehat{\Theta }}_{f_3}(t)-H_3(t).\end{array}$

Select the candidate of Lyapunov function V₃ as the following formula:

$\begin{array}{ll}{V}_3(t)=V_2(t)+\frac{1}{2}{e}_3^2(t)+\frac{1}{2{\varrho }_3}{\tilde{\Theta }}_{f_3}^T(t){\tilde{\Theta }}_{f_3}(t).& (50)\end{array}$

In virtue of Lemma 4, taking the fractional derivative of Equation (50) implies

$\begin{array}{l}{{D}}^{\beta }{V}_3(t)={{D}}^{\beta }{V}_2(t)+\frac{1}{2}{{D}}^{\beta }{e}_3^2(t)+\frac{1}{2{\varrho }_3}{{D}}^{\beta }{\tilde{\Theta }}_{f_3}^T(t){\tilde{\Theta }}_{f_3}(t)\\ \le {{D}}^{\beta }{V}_2(t)+e_3(t){{D}}^{\beta }{e}_3(t)+\frac{1}{{\varrho }_3}{\tilde{\Theta }}_{f_3}^T(t){{D}}^{\beta }{\tilde{\Theta }}_{f_3}(t)\\ ={{D}}^{\beta }{V}_2(t)+e_3(t){{D}}^{\beta }{e}_3(t)+\frac{1}{{\varrho }_3}{\tilde{\Theta }}_{f_3}^T(t){{D}}^{\beta }{\widehat{\Theta }}_{f_3}(t).& (51)\end{array}$

Analogs to Equations (37) and (38), it is easily verified that

$\begin{array}{ll}-{\tilde{\Theta }}_{f_3}^T(t){\widehat{\Theta }}_{f_3}(t)\le -\frac{1}{2}{\tilde{\Theta }}_{f_3}^T(t){\tilde{\Theta }}_{f_3}(t)+\frac{1}{2}{\Theta }_{f_3}^T{\Theta }_{f_3}^{},& (52)\end{array}$

$\begin{array}{ll}{\varpi }_3{\tilde{\Theta }}_{f_3}^T(t){\tilde{\epsilon }}_{f_3}(t)\le \frac{1}{2}{\tilde{\Theta }}_{f_3}^T(t){\tilde{\Theta }}_{f_3}(t)+\frac{1}{2}{({\varpi }_3{\bar{\epsilon }}_3{\psi }_3{\tau }_3)}^2,& (53)\end{array}$

in which ${\psi }_3\ge \left|\right|{\text{Ψ}}_{f_3}({\bar{x}}_3(t))\left|\right|$ is a positive constant irrelevant with ${\bar{x}}_3(t)$ and the number of neural nodes.

Synthesizing Equations (39), (44), (45), and (51)–(53) with Lemma 6, we arrive at

$\begin{array}{l}{{D}}^{\beta }{V}_3(t)\\ \le {{D}}^{\beta }{V}_2(t)+e_3(t){{D}}^{\beta }{e}_3(t)\\ +\frac{1}{{\varrho }_3}{\tilde{\Theta }}_{f_3}^T(t)\left[{\varrho }_3{e}_3(t){\text{Ψ}}_{f_3}({\bar{x}}_3)-{\eta }_3{\widehat{\Theta }}_{f_3}(t)-{\varrho }_3{\varpi }_3{\widehat{\epsilon }}_3(t)\right]\\ \le {{D}}^{\beta }{V}_2(t)-k_3{e}_3^2(t)+x_1(t)e_2(t)e_3(t)-\frac{{\eta }_3}{2{\varrho }_3}{\tilde{\Theta }}_{f_3}^T(t){\tilde{\Theta }}_{f_3}(t)\\ +\frac{{\eta }_3}{2{\varrho }_3}{\Theta }_{f_3}^T{\Theta }_{f_3}^{}-{\varpi }_3{\mu }_3{\tilde{\Theta }}_{f_3}^T(t){\tilde{\Theta }}_{f_3}(t)+{\varpi }_3{\tilde{\Theta }}_{f_3}^T(t){\tilde{\epsilon }}_{f_3}(t)\\ \le -a_2{V}_2(t)-x_1(t)e_2(t)e_3(t)+b_2-k_3{e}_3^2(t)+x_1(t)e_2(t)e_3(t)\\ -\frac{{\eta }_3+{\varrho }_3(2{\varpi }_3{\mu }_3-1)}{2{\varrho }_3}{\tilde{\Theta }}_{f_3}^T(t){\tilde{\Theta }}_{f_3}(t)\\ +\frac{{\eta }_3}{2{\varrho }_3}{\Theta }_{f_3}^T{\Theta }_{f_3}^{}+\frac{1}{2}{({\varpi }_3{\bar{\epsilon }}_3{\psi }_3{\tau }_3)}^2\\ \le -a_3{V}_3(t)+b_3,& (54)\end{array}$

where a₃ = min{a₂, 2k₃, η₃ + ϱ₃(2ϖ₃μ₃ − 1)}, $b_3=b_2+0.5{\varrho }_3^{-1}{\eta }_3\left|\right|{\Theta }_{f_3}^{ }|{|}^2+0.5{\varpi }_3^2{\bar{\epsilon }}_3^2{\psi }_3^2{\tau }_3^2$.

By virtue of Equation (54) and Lemma 2, it is straightly examined that

$\begin{array}{l}{V}_3(t)\le V_3(0)E_{\beta }(-a_3{t}^{\beta })+\frac{M{b}_3}{a_3}\\ \le V_3(0)\frac{C}{1+|-a_3{t}^{\beta }|}+\frac{M{b}_3}{a_3}\\ \le V_3(0)C+\frac{M{b}_3}{a_3},& (55)\end{array}$

for all t ≥ 0, where C ∈ ℝ⁺ is a certain constant, M = max{1, C}. Therefore, $\left|e_i\right|\le \sqrt{2(V_3(0)C+M{b}_3/a_3)}$ and $\left|\right|{\tilde{\Theta }}_i\left|\right|\le \sqrt{2{\varrho }_i(V_3(0)C+M{b}_3/a_3)}$ for i = 1, 2, 3, which indicates $e_i,\left|\right|{\tilde{\Theta }}_i\left|\right|\in L_{\infty }$. This demonstrates the boundedness of the whole signals in the closed-loop system.

Given a sufficient small positive scalar ϵ = ϵ₁ + ϵ₂ where ${ϵ}_1\ge \frac{M{b}_3}{a_3}$ and ϵ₂ > 0. By Equation (55), as t → ∞, we have

$\begin{array}{ll}0<E_{\beta }(-a_3{t}^{\beta })\le \frac{C}{1+a_3{t}^{\beta }}\to 0.& (56)\end{array}$

Based on Equations (55) and (56), if all design parameters are selected adequately, then there exists a certain T > 0 such that $E_{\beta }(-a_3{t}^{\beta })\le {ϵ}_2$ whenever t ≥ T and hence V₃(t) ≤ ϵ. Consequently, the dynamic errors e_i and ${\tilde{\Theta }}_i$ converge toward a compact region of the origin, and the radius of the bounded region can be adjusted as small as possible.

Summarizing the above arguments, we obtain the following main result with respect to the system stability.

Theorem 1. Take into account the system Equation (3) with Assumption 1. Suppose that the control scheme comprises the virtual control functions Equations (10) and (27), the actual control law Equation (42), together with the composite learning laws (Equations 14, 45). Then, all the closed-loop signals are bounded, and the error variables e_i, ${\tilde{\Theta }}_i$ (i = 1, 2, 3) converge toward a small enough compact region of the origin.

Remark 1. In Xue et al. [8], a class of second-order command filter was extended into fractional form:

$\begin{array}{ll}\{\begin{array}{l}{{D}}^{\beta }{\upsilon }_1(t)=\phi {\upsilon }_2(t),\\ {{D}}^{\beta }{\upsilon }_2(t)=-2\lambda \phi {\upsilon }_2(t)-\phi ({\upsilon }_1(t)-\alpha (t)),\end{array}& (57)\end{array}$

where α(t) is the filter input, φ ∈ ℝ⁺, λ ∈ [0, 1]. The main advantage of Equation (57) is that its approximation accuracy for the input α(t) is much better than that of fractional-order dynamic surface (Equation 4) used in this paper. However, in contrast with Equation (57 which needs to satisfy that both ${{D}}^{\beta }\alpha (t)$ and ${{D}}^{\beta }{{D}}^{\beta }\alpha (t)$ are bounded, Equation (4) only requires the boundedness of ${{D}}^{\beta }\alpha (t)$ and shows less conservation.

4. Simulation research

In this part, let us validate the efficiency of the proposed control scheme.

Pay attention to the practical model of fractional-order PMSM as follows:

$\begin{array}{ll}\{\begin{array}{l}{{D}}^{\beta }{x}_1(t)=f_1({\overline{x}}_1)+\sigma (x_2(t)-x_1(t)),\\ {{D}}^{\beta }{x}_2(t)=f_2({\overline{x}}_2)+\gamma x_1(t)-x_1(t)x_3(t)-x_2(t),\\ {{D}}^{\beta }{x}_3(t)=u_d(t)+x_1(t)x_2(t)-x_3(t),\end{array}& (58)\end{array}$

where β = 0.98, σ = 3, γ = 30, $f_1({\bar{x}}_1)=sin{x}_1$, and $f_2({\bar{x}}_2)=x_1-x_2^2$ are unknown functions. The initial value of the full-state vector ${\bar{x}}_3$ is considered as ${\bar{x}}_3(0)={\left[3,3,3\right]}^T$. Let the target signal be y_d(t) = 2 + 0.5sin(0.5t) + 0.5sin(t).

Due to the uncertainty of f₁ and f₂, we take advantage of three RBFNNs ${\widehat{f}}_1$ and ${\widehat{f}}_2$ in the simulation to approximate f₁ and f₂, respectively. The single input of the first RBFNN ${\widehat{f}}_1$ is x₁, and the radial basis function is composed of twenty-one Gaussian functions which are uniformly distributed over the interval [−2, 2]. With respect to the second RBFNN ${\widehat{f}}_2$, we regard its input variables as x₁ and x₂, and eight Gaussian functions evenly distributed on the interval [−2, 2] are given for each input to induce the corresponding radial basis function. Thus, the number of all neural-network nodes related to ${\widehat{f}}_2$ is selected as 8 × 8 = 64.

The design parameters are now selected as follows. First, let the input gain parameters are k₁ = k₂ = k₃ = 15. Second, the gain parameters of the dynamic surfaces are considered as φ₁ = φ₂ = 80. Third, set the integration duration to be τ_d = 15 and the finalization time instants for IE to be T_e1 = T_e2 = T_e3 = 20. At last, choose ϱ_i = 30 and η_i = ϖ_i = 0.001 with i = 1, 2, 3 for the composite learning adaptive control.

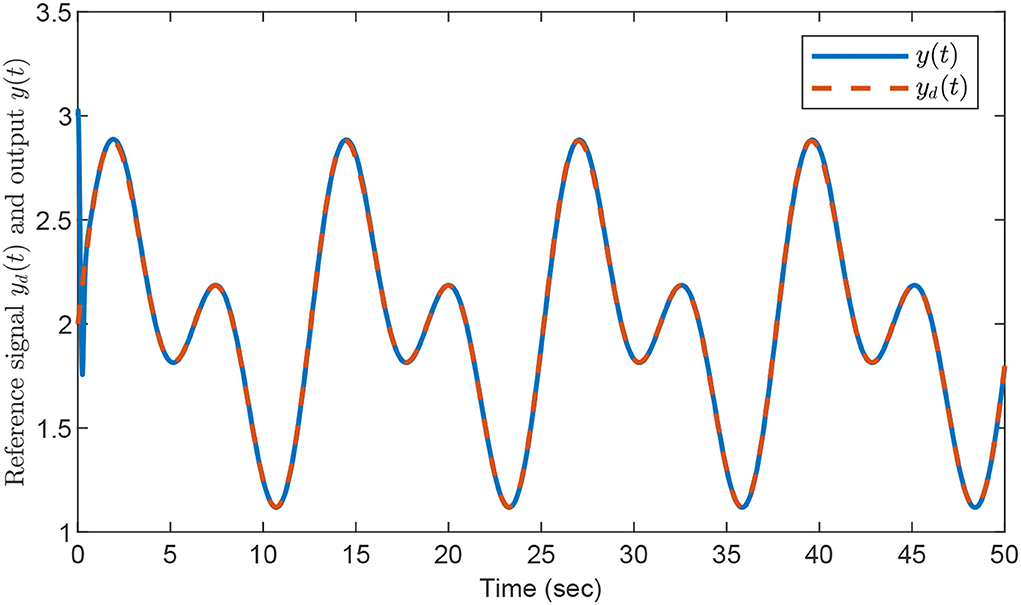
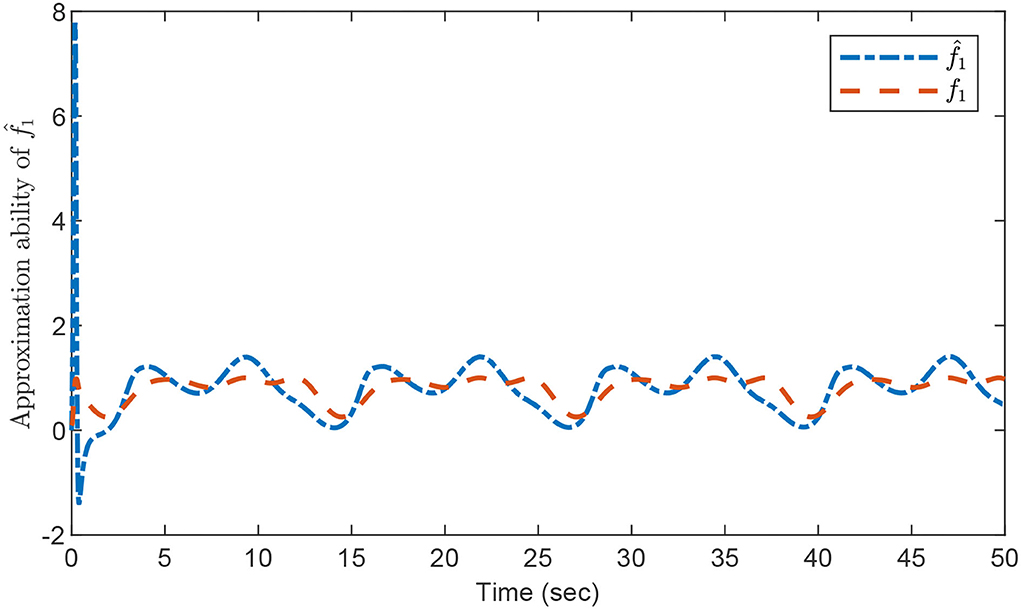
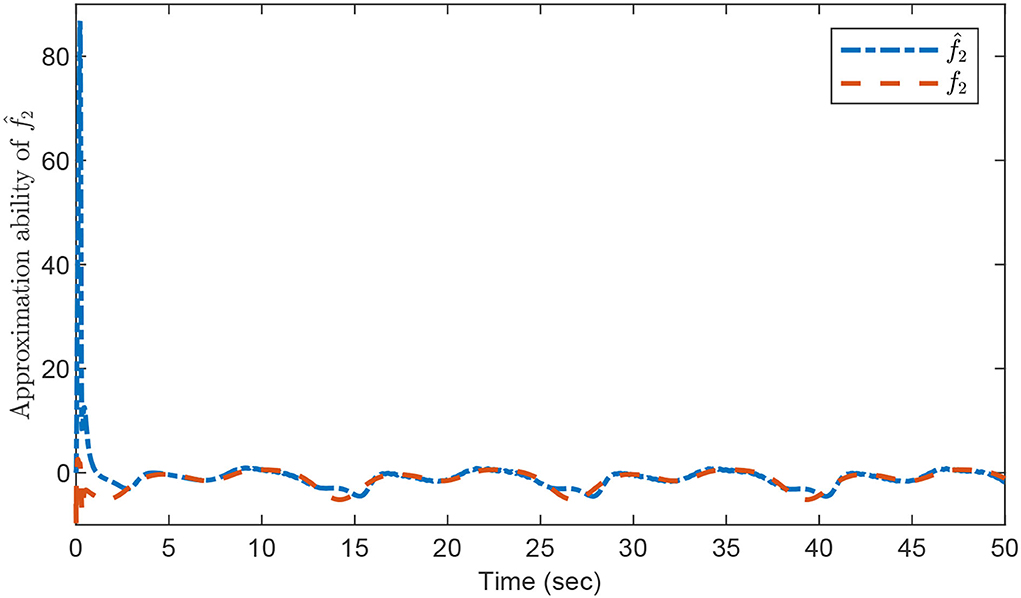
The relevant performance results are illustrated in Figures 2–4. Figure 2 shows that fast system response is achieved and the output signal y(t) can track the target trajectory y_d(t) closely as desired. The approximation abilities of the estimations ${\widehat{f}}_i$ for f_i with i = 1, 2 via the designed composite learning algorithm are displayed in Figures 3, 4, respectively. By using the introduced composite learning adaptive control method under the IE condition, one can observe that excellent estimation preciseness is obtained, which confirms the robustness of the introduced composite learning neural control approach as well as its powerful capability of chaos suppression.

FIGURE 2

Figure 2. Tracking performance of the output y with respect to the reference signal y_d.

FIGURE 3

Figure 3. Approximation ability of ${\widehat{f}}_1$ by using composite learning adaptive control.

FIGURE 4

Figure 4. Approximation ability of ${\widehat{f}}_2$ by using composite learning adaptive control.

5. Conclusion

In the article, the tracking control of fractional-order PMSMs is studied by establishing an adaptive backstepping composite learning neural control scheme. Neural networks are applied to serve as functional approximations, and a composite learning adaptive control algorithm is constructed to guarantee the high estimation accuracy of adaptation parameters. Employing the extended Lyapunov stability criterion, it is proven that the proposed control method achieves robust control performance and plays a vital role in tackling the tracking control problem of uncertainty fractional-order PMSMs. The simulation example reveals that the provided control method can improve the tracking efficiency. In future, we will focus on the study of fractional permanent magnet motor system with complicated characteristics of control input, such as input saturation, input dead-zone, and input delay.

Author contributions

CW: conceptualization, methodology, formal analysis, investigation, validation, software, data curation, and writing.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 11302184), the Fujian Provincial Natural Science Foundation (Grant No. 2021J011194), and Research Climbing Program of Xiamen University of Technology (Grant No. XPDKQ20020).

Acknowledgments

The author would like to convey his acknowledgments to the editors and the reviewers for their helpful comments and recommendations.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Miller KS, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations. New York, NY: Wiley-Interscience Publication (1993).

2. Podlubny I. Fractional Differential Equations. New York, NY: Academic Press (1999).

Google Scholar

3. Aguila-Camacho N, Duarte-Mermoud MA, Gallegos JA. Lyapunov functions for fractional order systems. Commun Nonlinear Sci Num Simulat. (2014) 19:2951–7. doi: 10.1016/j.cnsns.2014.01.022

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Gong P. Distributed tracking of heterogeneous nonlinear fractional-order multi-agent systems with an unknown leader. J Franklin Inst. (2017) 354:2226–44. doi: 10.1016/j.jfranklin.2017.01.001

CrossRef Full Text | Google Scholar

5. Han SI. Fractional-Order command filtered backstepping sliding mode control with fractional-order nonlinear disturbance observer for nonlinear systems. J Franklin Inst. (2020) 357:6760–76. doi: 10.1016/j.jfranklin.2020.04.055

CrossRef Full Text | Google Scholar

6. Liu H, Pan Y, Cao J, Zhou Y, Wang H. Positivity and stability analysis for fractional-order delayed systems: a T-S fuzzy model approach. IEEE Trans Fuzzy Syst. (2021) 29:927–39. doi: 10.1109/TFUZZ.2020.2966420

CrossRef Full Text | Google Scholar

7. Song S, Park JH, Zhang B, Song X. Observer-based adaptive hybrid fuzzy resilient control for fractional-order nonlinear systems with time-varying delays and actuator failures. IEEE Trans Fuzzy Syst. (2021) 29:471–85. doi: 10.1109/TFUZZ.2019.2955051

CrossRef Full Text | Google Scholar

8. Xue G, Lin F, Li S, Liu H. Adaptive fuzzy finite-time backstepping control of fractional-order nonlinear systems with actuator faults via command-filtering and sliding mode technique. Inf Sci. (2022) 600:189–208. doi: 10.1016/j.ins.2022.03.084

CrossRef Full Text | Google Scholar

9. Li Z, Park JB, Joo YH, Zhang B, Chen G. Bifurcations and chaos in a permanent-magnet synchronous motor. IEEE Trans Circ Syst I Fundament Theory Appl. (2002) 49:383–7. doi: 10.1109/81.989176

CrossRef Full Text | Google Scholar

10. Yu J, Chen B, Yu H, Gao J. Adaptive fuzzy tracking control for the chaotic permanent magnet synchronous motor drive system via backstepping. Nonlinear Anal. (2011) 12:671–81. doi: 10.1016/j.nonrwa.2010.07.009

CrossRef Full Text | Google Scholar

11. Yang X, Yu J, Wang QG, Zhao L, Yu H, Lin C. Adaptive fuzzy finite-time command filtered tracking control for permanent magnet synchronous motors. Neurocomputing. (2019) 337:110–9. doi: 10.1016/j.neucom.2019.01.057

CrossRef Full Text | Google Scholar

12. Zhou S, Sui S, Tong S. Adaptive neural networks optimal control of permanent magnet synchronous motor system with state constraints. Neurocomputing. (2022) 504:132–40. doi: 10.1016/j.neucom.2022.06.114

CrossRef Full Text | Google Scholar

13. Basin M, Rodriguez-Ramirez P, Ramos-Lopez V. Continuous fixed-time convergent controller for permanent-magnet synchronous motor with unbounded perturbations. J Franklin Inst. (2020) 357:11900–13. doi: 10.1016/j.jfranklin.2019.11.059

CrossRef Full Text | Google Scholar

14. Gil J, You S, Lee Y, Kim W. Nonlinear sliding mode controller using disturbance observer for permanent magnet synchronous motors under disturbance. Expert Syst Appl. (2023) 214:119085. doi: 10.1016/j.eswa.2022.119085

CrossRef Full Text | Google Scholar

15. Li C, Yu S, Luo X. Fractional-order permanent magnet synchronous motor and its adaptive chaotic control. Chin Phys B. (2012) 21:168–73. doi: 10.1088/1674-1056/21/10/100506

CrossRef Full Text | Google Scholar

16. Xue W, Li Y, Cang S, Jia H, Wang Z. Chaotic behavior and circuit implementation of a fractional-order permanent magnet synchronous motor model. J Franklin Inst. (2015) 352:2887–98. doi: 10.1016/j.jfranklin.2015.05.025

CrossRef Full Text | Google Scholar

17. Lu S, Wang X, Li Y. Adaptive neural network finite-time command filtered tracking control of fractional-order permanent magnet synchronous motor with input saturation. J Franklin Inst. (2020) 357:13707–33. doi: 10.1016/j.jfranklin.2020.10.021

CrossRef Full Text | Google Scholar

18. Zhang S, Wang C, Zhang H, Ma P, Li X. Dynamic analysis and bursting oscillation control of fractional-order permanent magnet synchronous motor system. Chaos Solit Fractals. (2022) 156:111809. doi: 10.1016/j.chaos.2022.111809

CrossRef Full Text | Google Scholar

19. Sanner RM, Slotine JJE. Gaussian networks for direct adaptive control. IEEE Trans Neural Netw. (1992) 3:837–63. doi: 10.1109/72.165588

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kurdila AJ, Narcowich FJ, Ward JD. Persistency of excitation in identification using radial basis function approximants. SIAM J Control Optim. (2006) 33:625–42. doi: 10.1137/S0363012992232555

CrossRef Full Text | Google Scholar

21. Wang C, Hill DJ. Learning from neural control. IEEE Trans Neural Netw. (2006) 17:130–46. doi: 10.1109/TNN.2005.860843

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Wang C, Wang M, Liu T, Hill DJ. Learning from ISS-modular adaptive NN control of nonlinear strict-feedback systems. IEEE Trans Neural Netw Learn Syst. (2012) 23:1539–50. doi: 10.1109/TNNLS.2012.2205702

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Wang M, Wang C, Liu X. Dynamic learning from adaptive neural control with predefined performance for a class of nonlinear systems. Inf Sci. (2014) 279:874–88. doi: 10.1016/j.ins.2014.04.038

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Pan Y, Yu H. Biomimetic hybrid feedback feedforward neural-network learning control. IEEE Trans Neural Netw Learn Syst. (2017) 28:1481–7. doi: 10.1109/TNNLS.2016.2527501

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Pan Y, Sun T, Liu Y, Yu H. Composite learning from adaptive backstepping neural network control. Neural Network. (2017) 95:134–42. doi: 10.1016/j.neunet.2017.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Xu B, Sun F, Pan Y, Chen B. Disturbance observer based composite learning fuzzy control of nonlinear systems with unknown dead zone. IEEE Trans Syst Man Cybern Syst. (2017) 47:1854–62. doi: 10.1109/TSMC.2016.2562502

CrossRef Full Text | Google Scholar

27. Liu H, Pan Y, Cao J. Composite learning adaptive dynamic surface control of fractional-order nonlinear systems. IEEE Trans Cybern. (2020) 50:2557–67. doi: 10.1109/TCYB.2019.2938754

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Guo Y, Qin H, Xu B, Han Y, Fan QY, Zhang P. Composite learning adaptive sliding mode control for AUV target tracking. Neurocomputing. (2019) 351:180–6. doi: 10.1016/j.neucom.2019.03.033

CrossRef Full Text | Google Scholar

29. Guo K, Pan Y, Zheng D, Yu H. Composite learning control of robotic systems: a least squares modulated approach. Automatica. (2020) 111:108612. doi: 10.1016/j.automatica.2019.108612

CrossRef Full Text | Google Scholar

30. Xue G, Lin F, Li S, Liu H. Composite learning control of uncertain fractional-order nonlinear systems with actuator faults based on command filtering and fuzzy approximation. Int J Fuzzy Syst. (2022) 24:1839–58. doi: 10.1007/s40815-021-01242-3

CrossRef Full Text | Google Scholar