- 1Department of Mathematics, Padjadjaran University, Bandung, Indonesia
- 2Department of Computer Science, Padjadjaran University, Bandung, Indonesia
- 3Department of Computer Engineering and Science, Albaha University, Al Bahah, Saudi Arabia
In the last two decades, the number of model developments in the field of Geostatistics increased rapidly, especially in the Spatio-temporal models. Almost of these models are based on Euclidean distance, only a few which based on non-Euclidean distance. The purpose of this study is to analyze and visualize the types of literatures on stationary Spatio-temporal models that utilize General Product-sum and Hydrological distance through bibliometric analysis methods, by considering a set of bibliometric metrics, including productive and impact measures, methods analysis, and co-authorships analysis. Scientific research works related to Spatio-temporal models using the product-sum field that consider hydrological aspects, published between 2002 and 2022 are reviewed. Some of the most relevant research works in this field and some of the newest trends are collected during September 2022 from Google Scholar, Scopus and Dimensions databases. The literature search method is carried out in two steps. Firstly, literature sources were obtained from Google Scholar, Scopus and Dimensions. Secondly, meta-analysis is performed using Harzing's Publish or Perish and VOSviewer software program. Total of 488 articles related to Spatio-temporal product-sum, and 8 articles related to Spatio-temporal product-sum based on hydrologic distance are selected. The analysis result shows that the proposed topic “Spatio-temporal model using product-sum based on hydrologic distance” has a different significant attribute from the existing research works, i.e., the hydrologic distance. Therefore, the proposed topic can be considered has a novelty.
1. Introduction
The processes of Spatio-modeling development are very important in many fields of geostatistics, meteorology, reservoir engineering and environmental science. In addition of hydrologic studies, the variogram is significant correlation measure and a convenient tool for Spatio-temporal modeling. Even though many variogram or space-time covariance models are presented, Product-sum and General Product-sum model coined by De Iaco et al. [1] are commonly used from its simplified function of two parameters into one parameter.
However, studies that focused on Spatio-temporal Product-sum based on hydrologic distance yet quite uncommon. Literature review conducted in this study aims to gain insights from existing research works and find a novelty in studies related to Spatio-Temporal using General Product-Sum based on hydrologic distance.
Literature review is a piece of academic writing demonstrating knowledge and understanding of the academic literature on a specific topic placed in context. A literature review also includes a critical evaluation of the material. Thus, the research questions of this work are as follows:
1. How the Spatio-temporal model using product-sum or general product-sum studies are developed during 2002–2022;
2. What known methods were applied for the spatio-temporal general product-sum based on the river distance or hydrologic distance during 2002–2022.
While the aims of this study are as follows:
1. Conducting bibliometric analysis to gain insights about Spatio-temporal model using product-sum or general product-sum publications developed during 2002–2022;
2. To identify known methods applied on Spatio-temporal model using product-sum based on river distance or hydrologic distance during 2002–2022.
The rest of the paper is structured as follows: Section Literature review describes briefly the Spatio-temporal models and concept, literature review process and literature review method. Section Analysis results presents the analysis results. Lastly, Section Discussions presents discussion along with the strengths and limitations of this study.
2. Literature review
2.1. Spatio-temporal model concept
An auto-covariance or a covariance function is a basic concept in the Spatio-temporal model, especially in the field of Geostatistics, either the spatial model or the Spatio-temporal model because it is related to a concept of a semivariogram function and Kriging method. In general, there are several types of Spatio-temporal covariance models, i.e.,(1) Sum model [2], (2) Combined metric-sum model, (3) Product model [3, 4], (4) Product-sum model, [1, 5–7], (5) General product-sum [8], (6) Mixture-based models [9], (7) Integrated product and product-sum models [8], and (8) Metric models [10].
Several contributions to the development of Spatio-temporal models over the past two decades, particularly non-separable models have been carried out [1, 5–8].
Rationale for developing a Spatio-temporal model using the general product-sum auto-covariance function based on hydrological distance comes from the article of De Iaco et al. [1, 8] and Ver Hoef et al. [11–13]. Cressie et al. [9] developed a spatial auto-covariance function based on hydrological distance with a moving average function approach for stream networks, while De Iaco et al. [1, 8] developed a Spatio-temporal with the product-sum model [5] based on Euclid's distance, which is more general (general product-sum model) and has a simpler function of two parameters into one parameter.
Developed Spatio-temporal function is based on the main theoretical of spatial model for stream networks based on a hydrologic distance or a river distance [11–13], and also the Spatio-temporal model using the general product-sum based on Euclidean Distance [1]. Combining these theoretical provides the developed Spatio-temporal model. Thus, this section outlines the conceptual theory of Spatio-temporal model.
Spatial auto-covariance functions generally use Euclidean distance [14]. However, there is no guarantee that the auto-covariant function is valid, such as in case of conditionally negative definite or positive-definite, for stream networks or a non-Euclidean distance [15]. The non-Euclidean distance for stream network is often called as the hydrological distance, or stream distance [11–13] or the river distance [14]. Applying moving average approach in the field of Geostatistics can be found in [11–13, 16].
Hydrological distance is an important keyword in this research. Ver Hoef et al. [11–13] proposed a moving average construction method that incorporates both hydrologic distance and flow direction. Incorporating flow direction can be achieved by choosing moving average functions whose tails go along with or against the flow direction and named as tail-down and tail-up models, respectively. The tail-up model is valid only for flow-connected. This investigation will be focused on the tail-up model. The application of this hydrological distance-based spatial model is generally applied to the prediction of river water quality, for example in [17–22].
Function of moving average in the field of spatial models was introduced by [11–13, 16] and those formulated by [17] as a large class of auto-covariance functions with the formulation in (1) and (2)
where W(x) is white noise process and g(x − s|θ) is moving average function and is defined at ℜ1 and covariance between random variables Z(sk) dan Z(sl) for tail-up model is expressed as (3) and (4)
and
and
where, h is the hydrological distance, ρ(.) represents the correlation function, and is a vector, the elements of which are nugget, sill, and range, respectively. To ensure a stationary in Equation (3), ωk+ωl = 1must be satisfied. Spatial auto-covariance function based on hydrologic distance in Equation (3) [23], can also be represented by (5)
where, Cu(h) is the unweighted tail-up auto-covariance model between the two sites and ωijis the spatial weight between the two sites sidan sj, which is determined by the structure branching process.
There are two questions addressed in the modeling of Spatio-temporal in product-sum: (1) how to ensure one has a valid model, and (2) how to fit data to the model [24]. The product model was used in De Cesare et al. [4] which was extended to a product-sum model [5, 6]. De Iaco et al. [1] was subsequently developed the product-sum which is less in the number of parameters to become a general product-sum model. The general product-sum model serves a large class of models that is not attainable by Cressie and Huang [14] and which are easily modeled using techniques similar to those used for modeling spatial variogram [1]. In a decade, the Spatio-temporal model has accrued fast in a different approach. A Covariance model is a basic concept in the Spatio-temporal model, especially in the field of Geostatistics because it is related to the concept of semivariogram functions and a Kriging method.
In general, there are several types of Spatio-temporal covariance models [26], i.e., (1) Sum model [2], (2) Combined metric-sum model, (3) Product model [3, 4], (4) Product-sum model [1, 5, 6], (5) General product-sum [1, 7, 8], (6) Mixture-based models [9], and (7) Integrated product and product-sum models [8], Metric models [10], Ma mixture [27, 28], Ma linear combination [29, 30], Stein [31], and Gregori [32]. All of these covariances, in addition to the separable and product-sum covariance rely on an assumption of full-symmetry. A Spatio-temporal covariance is fully symmetric if the covariance between two Spatio-temporal locations does not depend on the specific pairing of the two spatial locations and two time points [26]. There has been a great deal of research in constructing covariance that are not fully symmetric [24, 31, 33–36], are not stationary [9, 18, 19], or are not isotropic [9, 21, 23], but we do not focus on this paper.
Although there are many Spatio-temporal models, in this study, the Spatio-temporal with the general product-sum model was used [1]. This model has several advantages over other models, including:
1) the model is more flexible and practical in its use [9];
2) the model serves a large class of models that is not attainable by Cressie and Huang [14] and which are easily modeled using techniques similar to those used for modeling spatial variogram [1]; and
3) Xu and Shu [25] claim the product-sum covariance is the most widely used Spatio-temporal covariance in practical applications.
Space-time data is assumed to be the realization of a stochastic process:
with the domain D ⊆ ℜd, d ≤ 3, and T = (1, 2, …)is viewed as a time series data of spatial processes, each process occurs at points that have the same interval.
Stationary Spatio-temporal product-sum model based on Euclid's distance was first developed by De Cesare et al. [1] as (6).
and semivariogram is stated as in (7)
where, h = si − sj and u = ti − tj denote the spatial distance between two locations and the distance between two times, respectively. Equations (7) that Cs and Ct spatial and temporal covariance models are positive-definite, respectively. The covariance model of Equation (6) is declared a positive-definite if k1 > 0, k2 ≥ 0, and k3 ≥ 0, while Equation (7) is said to be valid if it meets a conditionally negative-definite requirements [26]. The product-sum model has something to do with a marginal Spatio-temporal (8) and (9).
and
It follows that (k2 + k1Ct(0)) = ks and (k3 + k1Ct(0)) = kt, and γ (h, 0) and γ (0, u) are respectively proportionality of γ(h, 0) and γ s(h), as well as γ(0, u) and γ t(u). Assuming both of the relationships are in (10)—(12).
and,
Therefore, γ(h, 0) and γ(0, u) can be estimated by γs(h) and γt(u), and also estimation of k1, k2 and k3.
The restricted in Equation (10), (11), and (12) are not necessary [1] because examining the asymptotic behavior of γ(h, 0), γ(0, u), and γs, t(h, u) that their theorem shows that these variograms do not reach the same sill value. De Iaco et al. [1] mention that Equations (13) and (14) remain maintained without making the restriction, and De Iaco et al. [1] extended to the general product-sum.
General product-sum model in the form of covariant function and semivariogram is given as in (13) and (14)
and
where Cs(h), Ct(u), and Cs, t(h, u) are respectively a covariant function of space, time, and space and time.
The Equation (14) is said to be a valid if k meets the below inequality as follows:
where
If Cs, t is expressed as product-sum of purely spatial and temporal with coefficients, namelyk1 > 0, k2 ≥ 0, and k3 ≥ 0, and the constant k in Equation (16), then it results that k > 0. Conversely, if k satisfies in Equation (15), then Equation (14) will be a valid variogram. In the process of estimating and modeling γs(h, 0) and γt(0, u) one will have already obtained the sill valuesksCs(0) and ktCt(0).
There was a publication on the general product-sum that has potentially a negative definite theoretically by Gregori et al. [32], but De Iaco et al. [37] disputed his publication through mathematical analysis and concluded that there was no potentially negative-definite.
2.2. Bibiliometric literature review
Many bibliometric literatures analysis in different fields have been carried out [38–41]. We discuss here, three of hot bibliometric researches. Yu et al. [42] conduct bibliometric literatures analysis on development in the field of Fuzzy theory in China. The authors collected samples of 12,936 publications authored by Chinese scholars on the field researches during the past 3 decades and explore the patterns and dynamics by analyzing the geographic distribution of publications, international collaboration, research hot spot, subject categories and journals, and publication contributors. The results indicate that the scientific publications are highly unbalanced at regional levels in China, and the USA is China's most important partner in Fuzzy theory cooperative researches. The analysis results indicate that the scientific publications are highly unbalanced at regional levels in China, and the USA is China's most important partner in Fuzzy theory cooperative researches. The emerging trends of Fuzzy theory researches from Chinese scholars have shifted away from basic Fuzzy theory researches to the applications, such as the areas of decision making, optimization, modeling and design.
He et al. [43] performed bibliometric literature analysis on Ordered weighted averaging (OWA) operator on Web of Science (WOS). The authors anlyze the publications on OWA operator between 1988 and 2015, and it is based on 1213 bibliographic records obtained by using topic search from WOS. The disciplinary distribution, most cited papers, influential journals, as well as influential authors are analyzed through citation and cocitation analysis. The emerging trends in OWA operator research are explored by keywords and references burst detection analysis. The research methods and results in this paper are meaningful for researchers associated with OWA operator field to understand the knowledge domain and establish their own future research direction.
Yu et al. [44] study on an analysis of collaboration evolution in analytic hierarchy process (AHP) research in the period of 1982–2018. As an important developed approach of AHP, analytic network process (ANP) is also considered in the review. 9,859 publications are harvested from Web of Science to conduct the bibliometric analysis. Country and institution are the two primary objectives to investigate the collaboration pattern of the 9,859 publications. The most prolific countries and institutions are identified based on bibliometric indicators, and the collaboration relationships between connected countries or institutions are explored based on science mapping techniques. The study assists in developing the collaboration evolution analysis in the AHP field.
2.3. The proposed literature review method
Literature review is a piece of academic writing demonstrating knowledge and understanding of the academic literature on a specific topic placed in context. A literature review also includes a critical evaluation of the material; this is why it is called a literature review rather than a literature report. There are three types of literature reviews: (1) bibliometric analysis, (2) meta-analysis, and (3) systematic literature review [45]. This study is focused on bibliometric analysis and systematic literature review.
Bibliometric analysis has acquired immense fame for conducting the literature review in recent years. Applying for this kind gives results: (1) handling a large volume of scientific data, and (2) producing a high research impact. The bibliometric analysis can be analyzed in quantitative ways [46]. Conversely, the systematic literature review is a classic method that applies to a narrow scope of the study and is used for a number of papers for review relatively small in number (e.g., between tens) and low hundreds [47]. The systematic review is generally analyzed in a qualitative way, therefore, it can be an adverse effect because of the different interpretations among scholars that give biased outcome.
Bibliometric analysis of this study provides an overview in spatio-temporal models that use the product-sum or General product-sum studies, and systematic literature review examine hydrological distance studies specifically.
This literature review adheres the most recent Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) tools and guide [48]. In general, four inclusion criteria were used on this study: (1) publications with article, journal or proceeding document types; (2) publications with published date between January 2002–July 2022; (3) publications with English language; and (4) publications with at least 1 citation. While for exclusion criteria, we consider: (1) publications with book, e-magazine, blog etc.; (2) publications beyond the time range; (3) publications with non-English languages; (4) publications with zero citation.
Two-step screening is used in this study. First step is using keywords for bibliometric analysis to find relevant publication in the title or abstract of the articles as follows.
1. (“Spatio-temporal” OR “space-time”)
2. (“product-sum” OR “general product-sum”)
3. 1 AND 2.
In the second stept, keywords are used in systematic literature review to find relevant publication in the title or abstract of the articles.
1. (“Spatio-temporal” OR “space-time”)
2. (“product-sum” OR “general product-sum”)
3. (“hydrologic distance” OR “river distance” OR “stream networks”)
4. 1 AND 2 AND 3.
Articles obtained from applying the above keywords are sorted automatically and manually. Dataset were obtained during September 2022 from Google Scholar, Scopus and Dimensions databases. These databases were used from its simplicity of use and open-source. Moreover, mentioned databases have comprehensive search methods for detailed results. Furthermore, hand-searching methods are conducted to search articles that deemed fit in this study but did not include in mentioned databases due to lack details in titles and abstracts. After automatic filter process, data were manually reviewed to ensure relevancy of this study. Papers reviewing are performed manually for checking title, abstract and keywords, then followed by full paper analysis whenever the full papers are available. Harzing's Publish or Perish Version 8 software program is used in this study to retrieve raw citation from databases and analyze the academic citations [49]. The input for the software is bibliographic records. Having done filtering process, the publications data were processed with VOSViewer to construct and visualize articles data [50]. Since we focus on spatio-temporal general product-sum model as the main keywords, potential articles that should fit in this study could be excluded as it is automatic filtered by databases and not found in hand-searching method.
Bibliometric analysis is conducted to exhibit the development of spatio-temporal product-sum model studies over time. Moreover, systematic literature review is also conducted to gain specific insights by adding inclusion criteria of hydrologic distance studies related. Specific keywords also used in publication search to narrow down articles that have broad subject other than the focus of the literature review.
3. Analysis results
Searching of Spatio-temporal product sum related studies resulted 2,582 publications, with 2,580 publications identified from databases and two publications identified through hand-searching. As many as 1,600 duplicate publications found, leaving 980 publications to screen for eligibility. Applying step-one screening, 492 publications excluded from the review, leaving 488 publications included for bibliometric data extraction. Then for the step-two screening, we found 5 publications included for systematic literature review. Flow diagram in Figure 1 represents the steps to retrieve publications in this study.
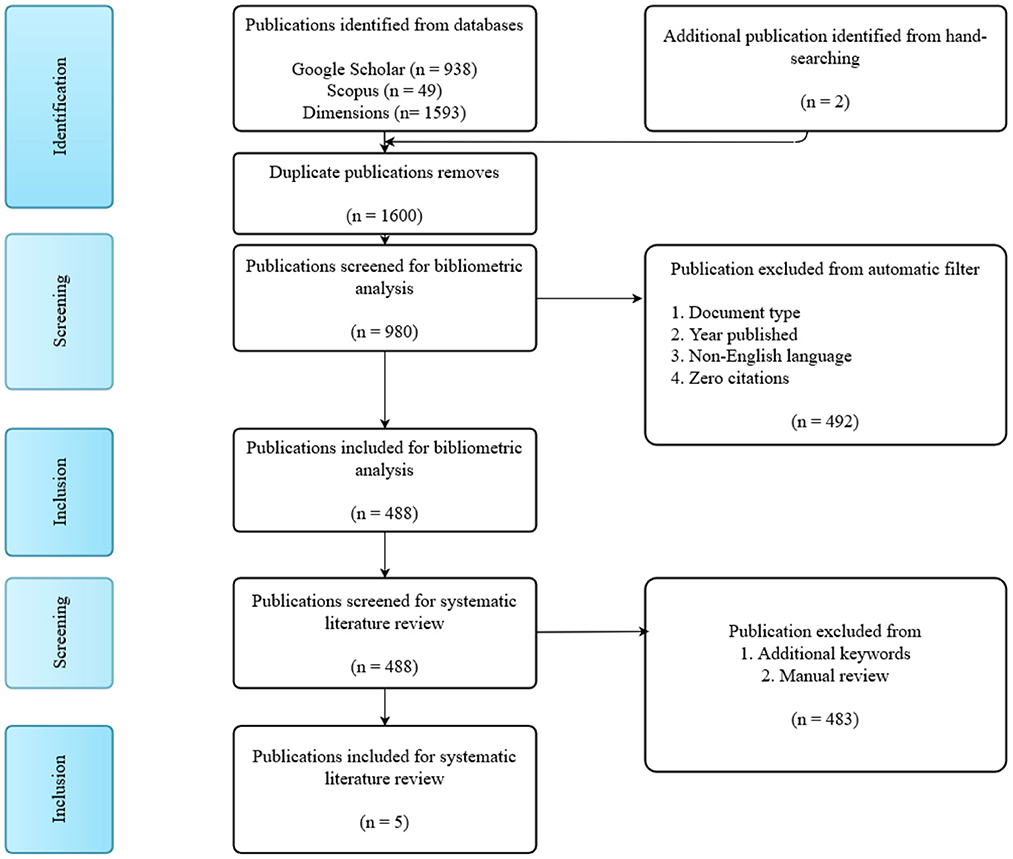
Figure 1. Flow diagram of identification and inclusion of spatio-temporal general product-sum research works.
3.1. Bibliometric analysis
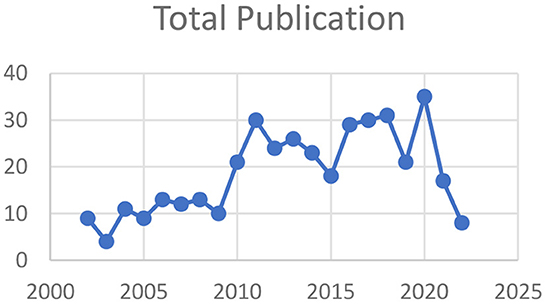
From 488 extracted data, we conduct bibliometric analysis to gain insights of Spatio-temporal product-sum studies. After product-sum model terms coined by De Iaco [1], publication related to spatio-temporal product-sum model has become much more active in recent years globally. Figure 2 points out annual publication starting from Year 2002 with nine publications. Number of research works increase and decrease over time, with notable increase in Year 2011 with 30 publications, peaked at 2020 with 35 publications, before declining in 2021 with only 17 publications and 2022 with eight publications, with a note that the publication may increase toward year-end of 2022.
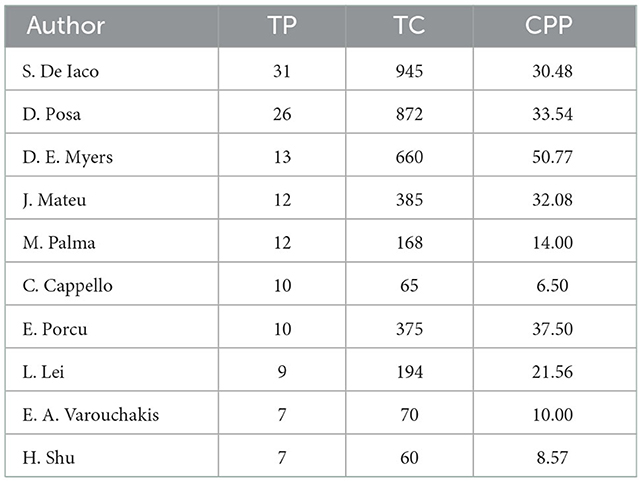
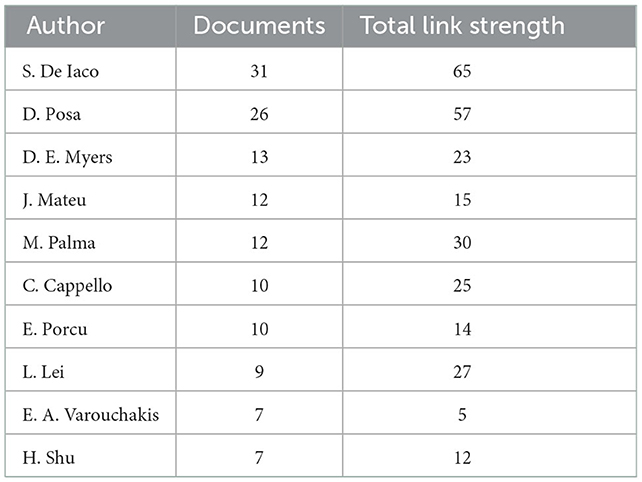
From the extracted data, we identify the most productive authors shown in Table 1. De Iaco is the most productive author with 31 total publications (TP), accumulated 945 total citations (TC) and average of 30.44 citations per paper (CPP) score. Posa in the second place with 26 TP, accumulated 872 TC, and average 33.54 score of CPP. In the third place of publication productivity is Myers that has published 13 TP, accumulated 660 TC and average of 50.77 CPP score.
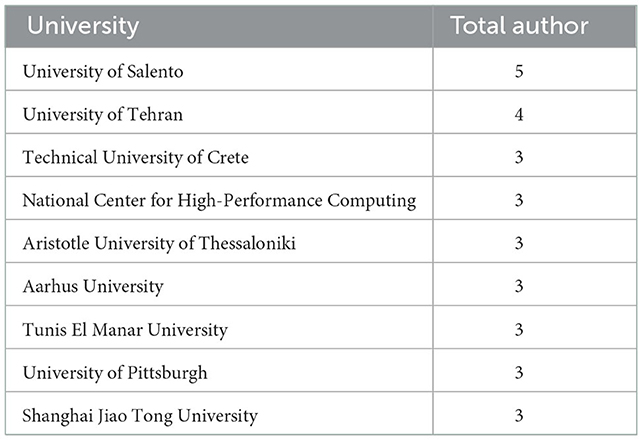
We also identify institute with highest productivity presented in Table 2. University of Salento have the highest contributor with five authors publishing spatio-temporal product-sum studies, while University of Tehran have four authors publishing related studies, and Technical University of Crete, National Center for High-Performance Computing, Aristotle University of Thessaloniki, Aarhus University, Tunis El Manar University, University of Pittsburgh, and Shanghai Jiao Tong University have three authors each publishing spatio-temporal product-sum studies.
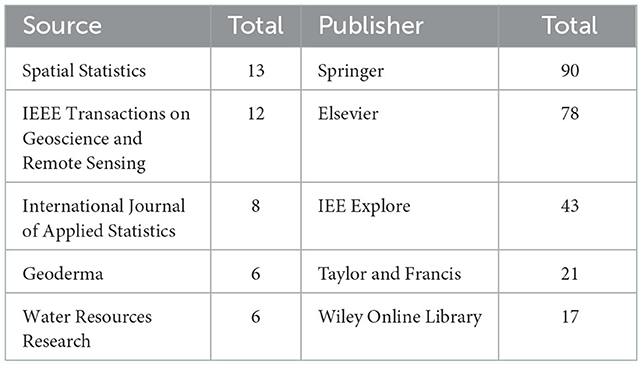
Other than the most productive institute mentioned above, we identify top five sources or journals that publish articles related to spatio-temporal product-sum, as well as top five publisher containing spatio-temporal product-sum studies. Table 3 presents the top sources or journals and publishers, with the first source is Journal of Spatial Statistics with 13 publications, and IEEE Transaction on Geoscience and Remote Sensing Journal in second place with 12 publications, and International Journal of Applied Statistics with eight total publications. Top publisher that containing spatio-temporal product-sum studies is Springer publisher with 90 total publications, while Elsevier publisher in the second most top publisher with 78 publications, followed by IIEE Explore publisher in the third place with 43 publications related to spatio-temporal product-sum studies.
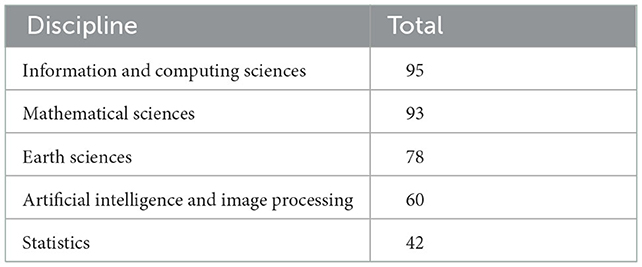
We conduct manual filtering to determine which disciplines category uses spatio-temporal product-sum studies the most. Table 4 shows top five disciplines, with Information and Computing Sciences in the first place with 96 publications on product-sum methods, while Mathematical Sciences in the second spot with 93 publications, and Earth Science in the third spot with 78 publications related to spatio-temporal product-sum studies.
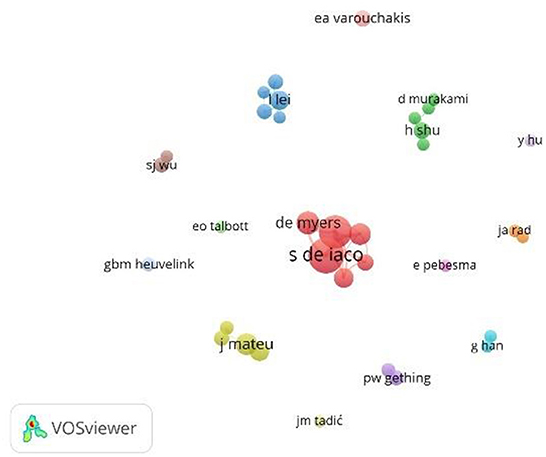
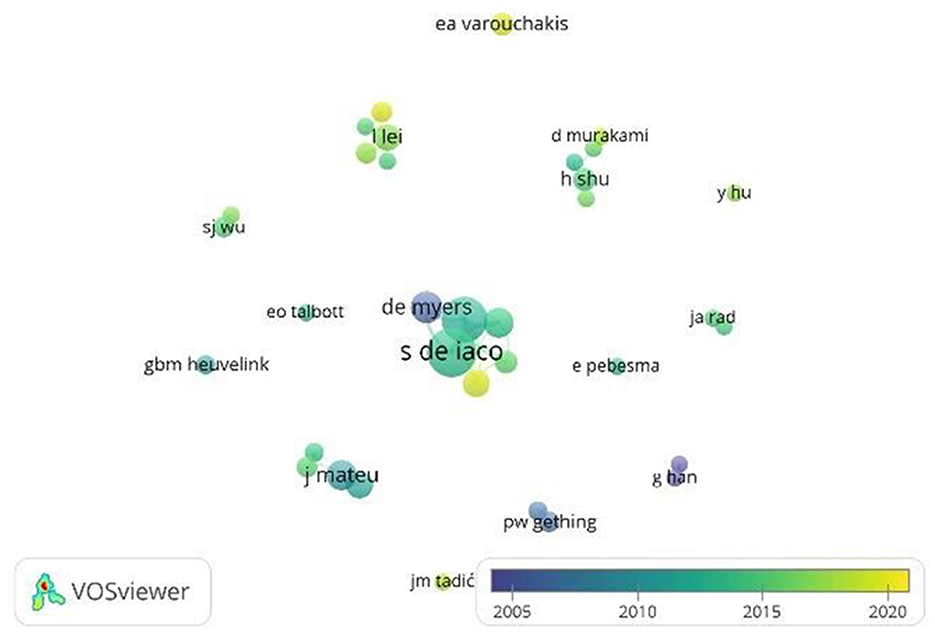
To gain insights about co-citation, dependence of the authors in spatio-temporal product-sum studies, we use VOSViewer to visualize the cooperation between researchers. With five minimal publications as the threshold, Table 5 represent the top 10 total link strength of co-citation analysis and Figure 3 presents the network visualization of co-citation analysis of spatio-temporal product-sum studies. According to VOSviewer manual, strength of each link can be explained by representing by a positive numerical value. Stronger the link will increase the total link strength value. Total link strength shows the number of publications in which two author or more occur together. With 31 documents published and 65 total link strength, S De Iaco is the most influential author on spatio-temporal product-sum studies, follows by D Posa with 26 documents with 57 total link strength and DE Myers with 13 documents and 23 total link strength. Overall, there are 14 clusters that separated from each other, with six clusters only have one dot, meaning there are no other author collaborating with researcher with minimal five documents threshold related to spatio-temporal product-sum related studies. For cluster 1 (red color), there are six authors collaboration, namely S De Iaco, D Posa, C Capello, DE Myers, M Palma, and S. Maggio. While cluster 2 (green color) there are five authors collaboration, i.e., D Murakami, DA Griffith, H Shu, J Xu, and S Li. In cluster 3 (dark blue color) there are 5 authors collaboration, i.e., L Guo, L Lei, L Li, Z Zeng, and ZC Zeng. In cluster 4 (yellowish green color) there are four authors collaboration, i.e., E Porcu, G Fernandez-Avilles, J Mateu and JM Montero. In Cluster 5 (purple color) there are two collaborators, i.e., AM Noor and PW Gething. In cluster 6 (cyan color) there are two collaborators, i.e., G Han and J Rosenthal. In cluster 7 (orange color) there are two collaborators, i.e.: JA Rad and K Parand. Lastly in cluster 8 (brown color) there are two collaborators, i.e., CT Hsu and SJ Wu. For single author without collaboration, there are E Pebesma, EA Varouchakis, EO Talbott, GBM Heuvelink, JM Tadic and Y Hu. Figure 4 presents the time overlay visualization of co-citation analysis. The darker the dot indicated the longer average publication year since author published spatio-temporal product-sum related studies. For example, DE Myers with average publication of Year 2006, we can see that the dot is the darkest in, while EA Varouchakis that average publication of Year 2019, the dot is the lightest among other dots.
3.2. Systematic literature review
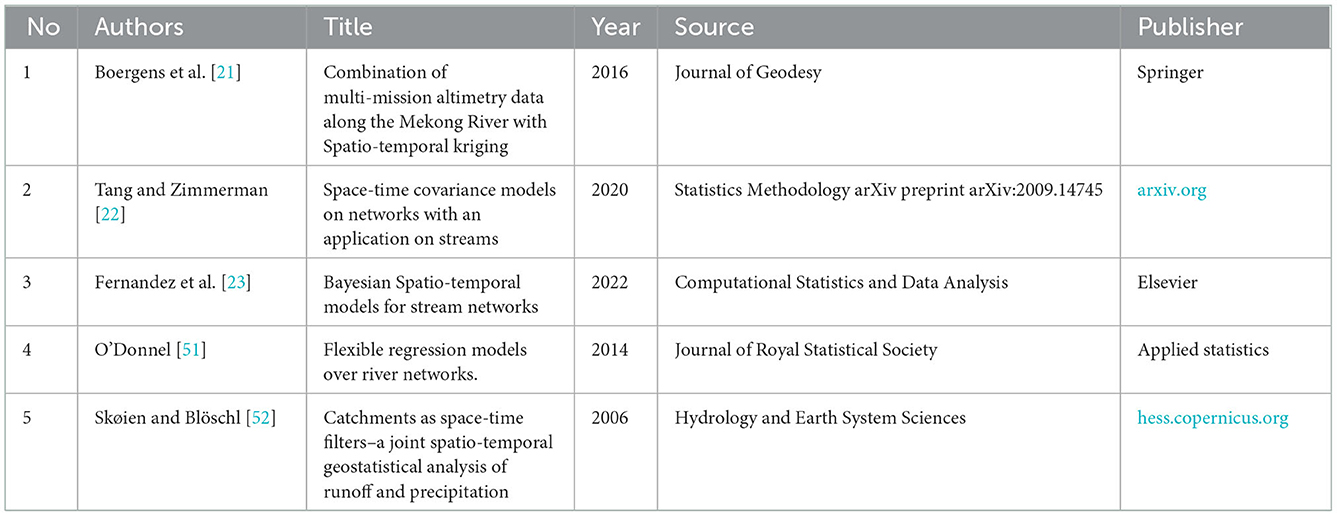
Five publications are included for systematic literature review. Table 6 describes the publications used for systematic literature review. Publication from JO Skøien and G Blöschl [52] with the title “Catchments as space-time filters–a joint spatio-temporal geostatistical analysis of runoff and precipitation” is the oldest publication that mentioning hydrologic distance in their study, while publication from Fernandez et al. [23] with the title “Bayesian Spatio-temporal models for stream networks” is the most recent publication that uses hydrologic distance in their study. From five publications, three publications are sourced from statistics journal discipline, while publication from Boergens et al. [21] titled “Combination of multi-mission altimetry data along the Mekong River with Spatio-temporal kriging” sourced from Geodesy discipline and publication from Skøien and Blöschl [52] with the title “Catchments as space-time filters–a joint spatio-temporal geostatistical analysis of runoff and precipitation” is sourced from hydrology journal discipline and earth science journal discipline.
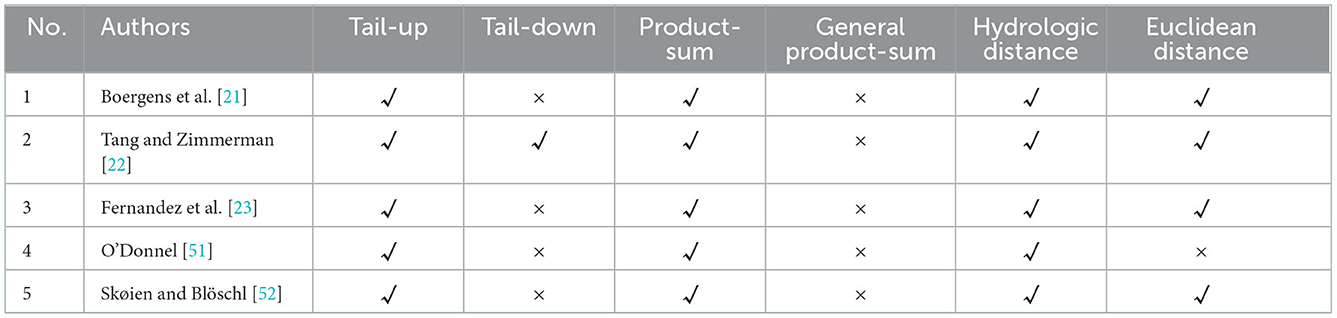
Methods used in each publication listed on Table 7. All publications focused on tail up method to compute the hydrologic distance in each study, but no publications focused on modeling product-sum. Boergens et al. [21] used the Spatio-temporal product-sum model with the two parameters set fixed, k2 = k3 = 0, and the application of the spatial model based on hydrological distance was used for non-stationarity. The spatial model theoretically can be applied to non-stationarity with weights as in Equation (3), when water flows into its two branches. It does not require the constraint of weight, namely ωk+ωl = 1. Furthermore, Tang and Zimmerman [22] developed a mixture model based on hydrological distance, with the Tail-up autocovariance function as in Equation (3) and Ver Hoef et al. [12] and Ver Hoef, and Peterso [13] introduced Tail-down autocovariance function in Equation (4). Meanwhile, when Euclid's distance is used, then the model is a product-sum [1]. O'Donnel [51] also developed a Spatio-temporal model for hydrological distance based on a river network with a non-parametric approach, namely penalized splines. The hydrological distance-based autocovariance function in the tail-up model is used in Equation (5). Fernandez et al. [23] used a Spatio-temporal model for a river network with a Bayesian framework. This proposed model was carried out using a sum model whose components of the covariance function with distance are: Euclidean, as well as hydrological in the tail-up and tail-down models. By comparing all the attributes of the topic, certain similarities and dissimilarities were found. For example, there was a difference in the proposed topic with four publications, which all used the product-sum model. Therefore, it can be concluded that the proposed topic of Spatio-temporal Model using Product-Sum Based on Hydrologic Distance is a novelty.
4. Discussions
Spatio-temporal product-sum model first developed by De Cesare et al. [6] two decades ago, and De Iaco et al. [1] coined the general product-sum model. Bibliometric analysis was conducted to gain insights about spatio-temporal product-sum or general product-sum model. Product-sum model have upward trend but in latest year it declining with only 17 publications in 2021 and eight publications in 2022, meaning that two models were not widely applied by researchers as shown in Figure 2.
One of the possible reasons for this decline is that it has started to become saturated and applied by collaborations only between researchers. University of Salento as the leading institute have a solid team of five authors publishing spatio-temporal product-sum studies, namely De Iaco, Posa, Myers, Capello and Porcu in University of Salento as seen in Table 2 and Figure 3.
Journal of Spatial Statistics are considered the top source while Springer considered as the top publisher that covers spatio-temporal product-sum studies. Disciplines that use the most the spatio-temporal product sum model is Information and Computing Sciences, Mathematical Sciences and Earth Sciences. The overview of co-citation analysis was presented to observe the dynamic between researchers.
One of the benefits of this study is to assist researchers in developing a spatio-temporal model using a general product-sum based on stream, river, or hydrologic distances. Systematic literature review was conducted to seek similarities and difference from each publication so a novelty of the method can be concluded through literature review on research works by Boergens et al. [21], Tang and Zimmerman [22], Fernandez et al. [23], O'Donnel [51] and Skøien and Blöschl [52]. There still few publications of the spatio-temporal models based on the stream distance and both models are applied based on Euclidean or linear distance. Thus, the model that will be developed following this study can dilute the saturation of the two models so that this study could attract other researchers, either in theoretical as well as practical aspects. Other works on spatial temporal covariance models have been carried out in [33–36]. The developed model also considers stationary covariance models [53–58].
To the best of our knowledge, this is the first comprehensive bibliometric literature review that focuses on Spatio-Temporal Model using a General Product-Sum Based on a Hydrological Distance.
Some limitations of this study are noteworthy for future research. Future studies have to consider using publications with zero citation for broader result. While our study focused on hydrologic distance that included in the earth science disciplines, diversify of broader studies.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research was funded by Universitas Padjadjaran with the Doctoral Dissertation Grant (RDDU) contract number 1427/UN6.3.1/LT/2020.
Acknowledgments
Authors would like to thank the Rector of Universitas Padjadjaran that provided funds for this research. Authors also grateful to the editor, referee, and reviewers for valuable suggestions that greatly improved the paper manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2022.994287/full#supplementary-material
References
1. De Iaco S, Myers DE, Posa D. Space-time analysis using a general product-sum model. Stat Probab Lett. (2001) 52:21–8. doi: 10.1016/S0167-7152(00)00200-5
2. Rouhani S, Hall TJ. Space-time kriging of groundwater data. In:Geostatistics, Armstrong M. (, , ed.). (1989) p. 639–51. doi: 10.1007/978-94-015-6844-9_50
3. Mejia J, Rodriguez M. On the Synthesis of the random field sampling from spectrum: An application to the generation of hydrologic spatial processes. Water Res Res. (1974) 10:705–11 doi: 10.1029/WR010i004p00705
4. De Cesare L, Myers D, Posa D. Spasial-temporal modelling of SO2 in Milan district. Kluwer Academic Publisher. (1997) 2:1031–42. doi: 10.1007/978-94-011-5726-1_34
5. De Cesare L, Myers D. Space-time analysis using a general product -sum model. Stat Probab Lett. (2001) 51:9–14.
6. De Cesare L, Myers DE, Posa D. Product-sum covariance for space-time modeling: an environmental application. Environmetrics. (2001) 12:11–23. doi: 10.1002/1099-095X(200102)12:1<11::AID-ENV426>3.0.CO;2-P
7. De Iaco S, Myers DE, Posa D. Space-time variogram and a functional from for total air pollution measurements. Comput Stat Data Anal. (2002) 41:311–28. doi: 10.1016/S0167-9473(02)00081-6
8. De laco S, Myers DE, Posa D. (2002) Nonseparable space-time covariance models: some parametric families. Math Geol. 34:23–42 doi: 10.1023/A:1014075310344
9. Porcu E, Mateu J. Mixture-based modeling for space-time data. Environmetrics. (2007) 18:285–302. doi: 10.1002/env.832
10. Dimitrakopoulos R, Luo X. Spatiotemporal modeling: covariances and ordinary kriging system. In:Dimitrakopoulos R. (, , ed.), Geostatistics for the Next Century. (1994) p. 88–93 (Dordrecht: Kluwer Academic Publishers). doi: 10.1007/978-94-011-0824-9_11
11. Ver Hoef JM, Barry RP. Constructing and fitting models for cokriging and multivariate spatial prediction. J Stat Plan Inference. (1998) 69:275–94 doi: 10.1016/S0378-3758(97)00162-6
12. Ver Hoef JM, Peterson EE, Theobald D. Spatial statistical models that use flow and stream distance. Environ Ecol Stat. (2006) 13:449–64. doi: 10.1007/s10651-006-0022-8
13. Ver Hoef JM, Peterson EE. A moving average approach for spasial statistical models of stream networks. J Am Stat Assoc. (2010) 105:6–18. doi: 10.1198/jasa.2009.ap08248
14. Cressie N, Huang C. Classes of nonseparable, spatiotemporal stationary covariance functions. J Am Stat Assoc. (1999) 94:1330–40. doi: 10.1080/01621459.1999.10473885
15. Curriero FC. On the use of Non-Euclidean Isotropy in Geostatistics. Berkeley, CA: The Berkeley Electronic Press. Johns Hopkins University, Dept. of Biostatistics Working Papers. (2005).
16. Barry RP, Ver Hoef JM. Blackbox kriging: spatial prediction without specifying variogram models. J Agric Biol Environ Stat. (1996) 1:297–322. doi: 10.2307/1400521
17. Baretta V, Monestiez P, Ver Hoef JM. Spatial modelling and prediction networks: up model, down model or hybrid? New York, NY: John Wiley & Sons Ltd. (2009).
18. Peterson EE, Theobald DM, Ver Hoef JM. Geostatistical modelling on stream networks: developing valid covariance matrices based on hydrologic distance and stream flow. Freshwater Biol. (2010) 32:267–9. doi: 10.1111/j.1365-2427.2006.01686.x
19. Peterson EE, Ver Hoef JM. A mix ed model moving average approach to geostatistical modeling in stream network. Ecology. (2010) 91:644–55. doi: 10.1890/08-1668.1
21. Boergens E, Buhl S, Dettmering D, Klüppelberg C, Seitz F. Combination of Multi-Mission Altimetry Data Along the Mekong River With Spatio-Temporal Kriging. (2016). Available online at: www.springerlink.com
22. Tang J, Zimmerman D. Space-Time Covariance Models on Networks with An Application on Streams. Iowa City, IA: Department of Statistics and Actuarial Science, University of Iowa. (2022).
23. Fernandez ES, Ver Hoef JM, Peterson EE, McGree J, Issak DJ, Mengersen K. Bayesian Spatio-temporal models for stream networks. Comput Stat Data Anal. (2022) 170. doi: 10.1016/j.csda.2022.107446
24. Christakos G. On the Problem of permissible covariance and Variogram models. Water Resources Res. (1984) 2:251–65. doi: 10.1029/WR020i002p00251
25. Xu J, Shu H. Spatio-temporal kriging based on the product-sum model: some computational aspects. Earth Sci Inform. (2015) 8:639–48. doi: 10.1007/s12145-014-0195-x
26. Montero JM, Aviles. GF, and Matheu J. Spatial and Spatio-temporal Geostatistical Modelling and Kriging. The First Ed. United Kingdom: John Wiley and Sons Ltd. (2015).
27. Ma C. Spatio-temporal covariance function generated by mixtures. Math Geol. (2002) 34:965–75. doi: 10.1023/A:1021368723926
28. Ma C. Families of Spatio-temporal stationary covariance models. J Stat Plan Inference. (2003) 116:489–501. doi: 10.1016/S0378-3758(02)00353-1
29. Ma C. Linear combinations of space-time covariance function and variograms. IEEE Signal Process Lett. (2005) 53:857–64. doi: 10.1109/TSP.2004.842186
30. Ma C. Semiparametric Spatio-temporal covariance models with the ARMA temporal margin. Ann Inst Stat Math. (2005) 57:221–33. doi: 10.1007/BF02507023
31. Stein ML. Space-time covariance functions. J Am Stat Assoc. (2005) 100:310–21. doi: 10.1198/016214504000000854
32. Gregori P, Porcu E, Montero J, Sasvari Z. On potentially negative space–time covariances obtained as sum of products of marginal ones. Ann Inst Stat Math. (2008) 60:865–82. doi: 10.1007/s10463-007-0122-8
33. Jones RH, Zhang Y. Models for continuous stationary space-time processes. In: Modelling Longitudinal and Spatially Correlated Data. (1997) p. 289-98. New Yor.: Springer-Verlag. doi: 10.1007/978-1-4612-0699-6_25
34. Brown PE, Karesen KF, Roberts GO, Tonellato S. Blur-generated non-separable space-time models. J R Stat Soc Series B Stat Methodol. (2000) 62:847–60. doi: 10.1111/1467-9868.00269
35. Gneiting T. Stationary covariance function for space-time data. J Am Stat Assoc. (2002) 97:590–600. doi: 10.1198/016214502760047113
36. Kolovos A, Chirstakos G, Hristopulos DT, Serre ML. methods for generating non-separable spatiotemporal covariance models with potential environmental applications. Adv Water Resour. (2004) 27:815–30. doi: 10.1016/j.advwatres.2004.04.002
37. De Iaco S, Myers DE, Posa D. On strict positive definiteness of product and product-sum covariance model. J Stat Plan Infer. (2011) 141:1132–40. doi: 10.1016/j.jspi.2010.09.01
38. Fetscherin M, Heinrich D. Consumer brand relationships research: a bibliometric citation meta-analysis. J Bus Res. (2015) 68:380–90. doi: 10.1016/j.jbusres.2014.06.010
39. Muhuri PK, Shukla AK, Abraham A. Industry 4.0: A bibliometric analysis and detailed overview. Eng. Appl. Artif. Intell. (2019) 78:218–35. doi: 10.1016/j.engappai.2018.11.007
40. Soliman M, Lyulyov O, Shvindina H, Figueiredo R, Pimonenko T. Scientific output of the european journal of tourism research: a bibliometric overview and visualization. Eur J Tour Res. (2021) 28:2801. doi: 10.54055/ejtr.v28i.2069
41. Fahimnia B, Sarkis J, Davarzani H. Green supply chain management: a review and bibliometric analysis. Int J Product Econ. (2015) 162:101–14. doi: 10.1016/j.ijpe.2015.01.003
42. Yu D, Xu Z, Wang W. Bibliometric analysis of fuzzy theory research in China: a 30-year perspective. Knowl Based Syst. (2018) 141:188–99. doi: 10.1016/j.knosys.2017.11.018
43. He X, Wu Y, Yu D, Merigó JM. Exploring the ordered weighted averaging operator knowledge domain: a bibliometric analysis. Int J Int Syst. (2017) 32:1151–66. doi: 10.1002/int.21894
44. Yu D, Kou G, Xu Z, Shi S. Analysis of Collaboration Evolution in AHP Research: 1982–2018, Int J Inf Tech Decision Making (IJITDM). (2021) 20:7–36. doi: 10.1142/S0219622020500406
45. Donthu N, Kumar S, Mukherjee D, Pandey N, Lim WM. How to conduct a bibliometric analysis: An overview and guidelines. J Busi Res. (2021) 133:285–96. doi: 10.1016/j.jbusres.2021.04.070
46. Michael Hall C. Publish and perish? Bibliometric analysis, journal ranking and the assessment of research quality in tourism. Tourism Manag. (2011) 32:16–27. doi: 10.1016/j.tourman.2010.07.001
47. Snyder H. Literature review as a research methodology: An overview and guidelines. J Busi Res. (2019) 104:333–39, doi: 10.1016/j.jbusres.2019.07.039
48. Page MJ, McKenzie JE, Bossuyt PM, Boutron I, Hoffmann TC, Mulrow CD, et al. The PRISMA 2020 statement: an updated guideline for reporting systematic reviews. BMJ. (2021) 372:n71 doi: 10.1136/bmj.n71
49. Harzing AW. The Publish or Perish Book: Your Guide to Effective and Responsible Citation Analysis. First Edition. Melbourne, Australia: Tarma Sofware Research. (2011).
50. VOSviewer. The Centre for Science and Technology Studies (CWTS). Leiden: Universiteit Leiden. (2018).
51. O'Donnell D, Rushworth A, Bowman AW, Marian Scott E, Hallard M. Flexible regression models over river networks. J R Stat Soc C: Appl Stat. (2013) 63:47–63. doi: 10.1111/rssc.12024
52. Skøien JO, Blöschl G. Catchments as space-time filters – a joint spatio-temporal geostatistical analysis of runoff and precipitation. Hydrol Earth Syst Sci. (2016) 10:645–62. doi: 10.5194/hess-10-645-2006
53. Ma C. Nonstationary covariance function that model space-time interactions. Stat Probab Lett. (2003) 61:411–9. doi: 10.1016/S0167-7152(02)00401-7
54. Ma C. Spatio-temporal variograms and covariance models. Adv Appl Probab. (2005) 37:706–25. doi: 10.1017/S0001867800000434
55. Taglom A. An Introduction to the Theory of Stationary Random Functions. Mineola, New York: Dover Pub., Inc. (1962).
56. De Cesare L, Myers DE, Posa D. FORTRAN programs for space-time modeling. Computational Geosci. (2002) 28:205–12. doi: 10.1016/S0098-3004(01)00040-1
57. Ma C. Spatio-temporal stationary covariance models. J Multivar Anal. (2003) 86:97–107. doi: 10.1016/S0047-259X(02)00014-3
Keywords: bibliometric analysis, spatio-temporal model, general product-sum, hydrologic distance, spatio-temporal covariance function, spatio-temporal semivariogram
Citation: Bachrudin A, Ruchjana BN, Abdullah AS and Budiarto R (2022) Bibliometric analysis of spatio-temporal model using a general product-sum based on a hydrological distance. Front. Appl. Math. Stat. 8:994287. doi: 10.3389/fams.2022.994287
Received: 14 July 2022; Accepted: 30 November 2022;
Published: 19 December 2022.
Edited by:
Jacques Demongeot, Université Grenoble Alpes, FranceReviewed by:
Dejian Yu, Nanjing Audit University, ChinaPradeep Isawasan, MARA University of Technology, Malaysia
Copyright © 2022 Bachrudin, Ruchjana, Abdullah and Budiarto. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Achmad Bachrudin,  YWNobWFkLmJhY2hydWRpbkB1bnBhZC5hYy5pZA==
YWNobWFkLmJhY2hydWRpbkB1bnBhZC5hYy5pZA==
 Achmad Bachrudin
Achmad Bachrudin Budi Nurani Ruchjana1
Budi Nurani Ruchjana1