- 1LaPS Laboratory, Badji-Mokhtar University, Annaba, Algeria
- 2Department of Quality Measurement and Evaluation, Deanship of Quality and Academic Accreditation, Imam Abdulrahman Bin Faisal University, Dammam, Saudi Arabia
The composite length-biased exponential-Pareto (CLBEP) distribution is a new composite distribution that is introduced in this article. This model's probability density function, moments, and quantiles, among other statistical characteristics, are determined mathematically. The parameters' maximum-likelihood estimation and stochastic ordering are discussed. A comparison study with other new composite and conventional distributions is also included. Specifically, using two actual fire insurance data sets, the goodness of fit of this new model is contrasted with the composite exponential-Pareto, composite lognormal-Pareto, and composite Rayleigh-Pareto distributions (Algerian and Danish fire insurance losses).
2010 AMS subject classifications: 62E10; 60E05.
1. Introduction
Currently, digital methods are being used in the fields of biology, economics, physical sciences, statistical sciences, and other fields. In the applications of other fields as well as in daily life, the statistical sciences are essential. Probability distributions are frequently the foundation of statistical science because many problems in these fields frequently do not follow one of the fundamental probability distributions. Actuarial science and finance generally use common distributions to express their data on payments, quantity and number of claims, and premium computation. Examples of these distributions are exponential, Poisson, length-biased exponential, and Pareto.
The length-biased exponential distribution, on the other hand, offers a wide range of practical applications in several industries (reliability, actuarial science, survival analysis, and mathematical financiers). The lifetime of a phenomenon with no memory, no aging, no wear and tear, or the profits of an insurance company, or various models of surpluses and financial assets, are frequently modeled using the length-biased exponential distribution.
The modeling of unimodal insurance loss data with a long tail appeals to actuaries. Distributions that may replicate the heavy tail of insurance loss data are necessary to provide a sufficiently precise estimate of the degree of connected business risk, including gamma, Pareto, length-biased exponential, Rayleigh lognormal, and Weibull.
For example, if there are both modest and significant losses, insurance companies may experience losses. When modeling very large losses, practitioners seem to favor the Pareto distribution for size distribution. Length-biased exponential, lognormal, Rayleigh, or Weibull models are preferred when the losses are composed of smaller values with high frequencies and larger losses with low frequencies [1]. Nevertheless, no conventional size model can simultaneously account for losses that are both minor and significant. Unlike length-biased, lognormal, Rayleigh, or Weibull exponential models, which have a positive general fit but fit the tail poorly, Pareto models actually fit the tail well.
When modeling data that have heavy tails, the composite distributions appear appropriate. For instance, the one-parameter exponential-Pareto (exp-Pareto) model and the one-parameter inverse gamma-Pareto (IG-Pareto) model have both been proposed as potential models for the modeling of insurance data. When they are fitted to well-known insurance data sets, such as the Danish fire insurance data set, they still are unable to perform satisfactorily. So, the model needs to be improved. By exponentiation of the random variable linked to the probability density function (pdf) of an inverse gamma-Pareto distribution, Liu and Ananda [2] suggested an improved version of the one-parameter IG-Pareto model. Their suggested model outperformed the original model significantly across several data sets. Furthermore, there are other composite models such as the composite lognormal-Pareto (cLP) model (see Scollnik [3] and composite Rayleigh-Pareto (cRP) model (see Benatmane et al. [4]). For more details see [5–12].
As a result, we suggest, in this study, a novel composite distribution that blends length-biased and Pareto exponential distributions. This effort aims to introduce a new composite distribution. As a result, the CLBEP distribution has a single parameter. It is simple to determine mathematical qualities in an explicit form. Due to its composition (two types of distributions that can be simulated for survival analysis and actuarial purposes), this new distribution offers advantages. Many real-life data sets can be analyzed using the CLBEP model, which provides suitable fits to these data sets.
The current article is structured as follows: The composite length-biased exponential-Pareto distribution and some of its statistical characteristics are discussed in Section 2. The estimation of parameters is addressed in Section 3. A numerical example with a comparison of various classical and composite models using two real data sets is provided in Section 4.
2. Formulation of the CLBEP distribution
For many theoretical issues, the length-biased exponential and Pareto distributions might not be adequate. We created the composite length-biased exponential-Pareto (CLBEP) distribution, based on the composite transformation, to have a flexible model. Let T be an arbitrary random variable with density function
where f1 is a length-biased exponential density, f2 is a two-parameter Pareto density, and c is the normalizing constant. Hence,
where λ, α, and θ are unknown non-negative parameters. To obtain a composite smooth density function, we use the continuity and differentiability conditions at the threshold point θ, i.e.,
These two restrictions give
After some calculation, we get
Using the numerical methods, we find
To find the normalizing constant, we use the density condition which has
Since f(t; θ) can be expressed as
2.1. Statistical properties of the CLBEP distribution
In this subsection, many statistical properties are presented, such as the behavior of PDF and quantile function, as well as the moments and stochastic ordering.
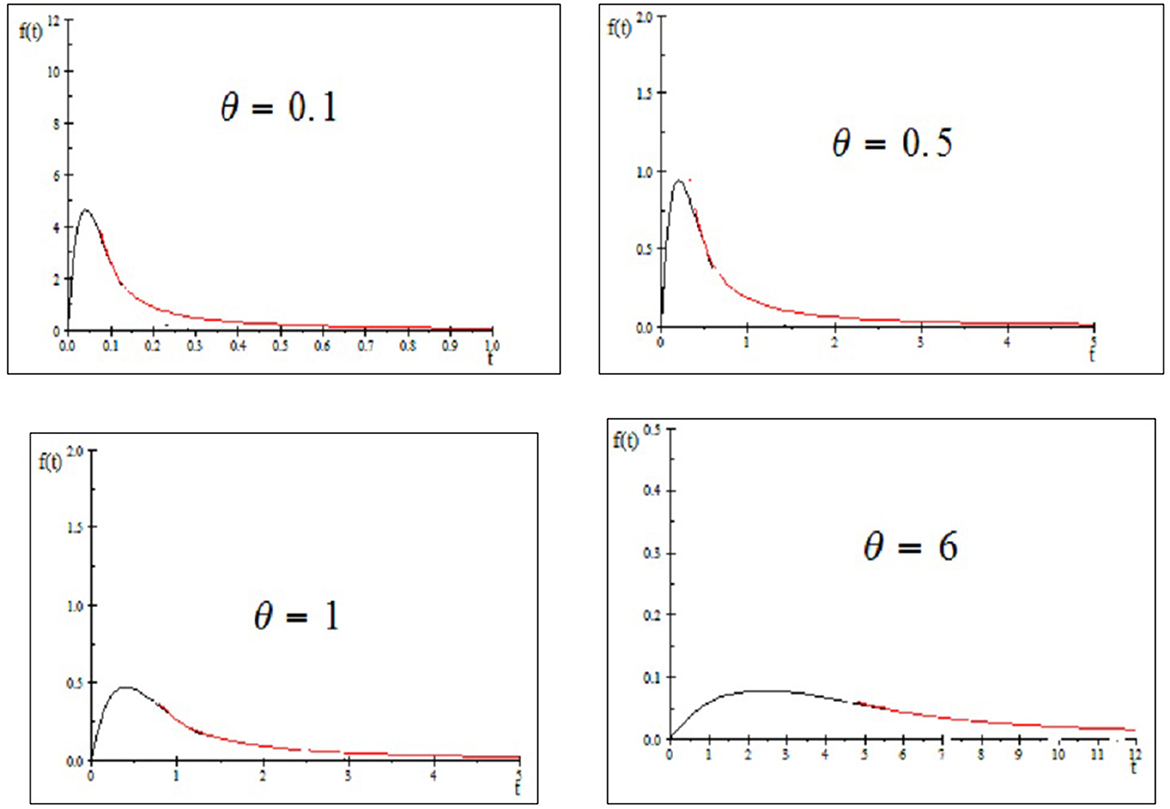
The following proposition states that there is one shape for the PDF of the CLBEP distribution. Furthermore, the plots of PDF for some parameter value of the proposed model are presented in Figure 1.
Proposition 1. The PDF f(t; θ) in Equation (1) of the CLBEP distribution is unimodal for θ > 0.
Proof. The first derivative of f(t; θ) is
The CLBEP distribution is unimodal with maximum value at the point where the unique mode is tmod = 0.39814θ.
2.2. Cumulative distribution function and moments of the CLBEP distribution
The cumulative distribution function (c.d.f.) of this composite model is
The kth moment about the origin of the CLBEP distribution can be obtained as:
which E(Tk) = ∞ (infinite), for k ≥ 2.
The mean of the CLBEP distribution is given by
2.3. The quantile function of the CLBEP distribution
The quantile function of the CLBEP distribution is given in the following theorem.
Theorem 1. The quantile function of the CLBEP distribution is
where u0 = 0.43768.
Proof. For u ∈ ]0;u0[, we have to solve the equation F(t) = u with respect to t, t > 0
Multiplying by e−1 both sides, we find
We see that is the Lambert W function of the real argument Then, we have
Moreover, for any θ, t > 0, it is immediate that and it can also be checked that
since u ∈ ]0;u0[
Therefore, by taking into account the properties of the negative branch of the Lambert W function, Equation (3) becomes
Finally, ∀θ > 0,
Now, for u ∈ ]u0; 1[, we have to solve the equation F(t) = u with respect to t, t > 0
it is easy to find
2.4. Stochastic ordering
Consider two random variables Z1 and Z2. Then, Z1 is said to be smaller than Z2 in the following cases:
1. Stochastic order (Z1 <S Z2 ), if FZ1(t) < FZ2(t), ∀t.
2. Convex order (Z1 ≤cx X2), if for all convex functions Ψ and provided expectation exists, E[Ψ(Z1)] ≤ E[Ψ(Z2)].
3. Hazard rate order (Z1 ≤hr Z2), if hZ1(t) ≥ hZ2(t), ∀t.
4. Likelihood ratio order (Z1 <lr Z2), if is decreasing in t.
Remark 1. Likelihood ratio order ⇒ hazard rate order ⇒ stochastic order, If E[Z1] = E[Z2], then convex order ⇔ stochastic order.
Theorem 2. Let Zi ∽ CLBEP distribution (θi); i = 1, 2 be two random variables. If θ1 ≤ θ2, then Z1 <lr Z2, Z1 <hr Z2; Z1 <S Z2 and Z1 ≤cx Z2.
Proof.
Case I: 0 < t ≤ θ
We have
Using the for simplification, we can find
To this end, if θ1 ≤ θ2, we have . This means that Z1 <lr Z2.
Case II: θ ≤ t < ∞
We have
We can see, if θ1 ≤ θ2, then fZ2(t; θ2) ≤ fZ2(t; θ2). Furthermore, according to Remark 1, the theorem is proved.
3. Generating random values from the CLBEP distribution
3.1. Parameter estimation
In this section, we will introduce two methods of estimating the unknown parameter θ.
3.1.1. An ad hoc procedure based on percentiles
The following ad hoc procedure provides a closed form for the parameter θ, estimated using percentiles. Let t1, t2, …, tn be a random sample from the CLBEP model. Assume that t1 ≤ t2 ≤… ≤ tn and tm ≤ θ ≤ tm+1. Based on percentiles, the parameter θ can be estimated, as the pth percentile, where p = F(θ)
According to Klugman et al. [1], we have a smooth empirical estimate of the pth percentile given by
with
The Pareto distribution or the length-biased exponential distribution will be a more superior model than the composite length-biased exponential-Pareto distribution according as is closer to t1 or tn.
3.1.2. Maximum-likelihood estimation
Assume again that t1 ≤ t2 ≤… ≤ tn and tm ≤ θ ≤ tm+1. Then, the likelihood function is
with
Define .
Differentiating ln L with respect to θ gives
Hence, the solution of the likelihood equation is
Since this estimator requires the value of m, we recommend the following algorithm (see Teodorescu and Vernic [13]):
4. Numerical and application examples
In this section, the estimation procedure described in Section 3 has been explained using two data samples generated from the CLBEP model. The generating algorithm used is based on the inversion of the c.d.f. (Equation 2).
4.1. Example
The data set given in this subsection, consisting of 108 values, was sampled from a length-biased exponential-Pareto population with parameter θ = 5 (see Table 1 in the Appendix).
The estimated values of the parameter are:
- By Algorithm 1, m = 39:
- By Algorithm 2, MLE Step 1:
- By Algorithm 2, MLE Step 2 :
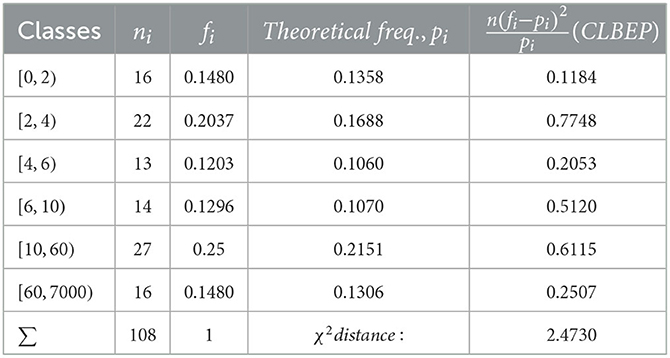
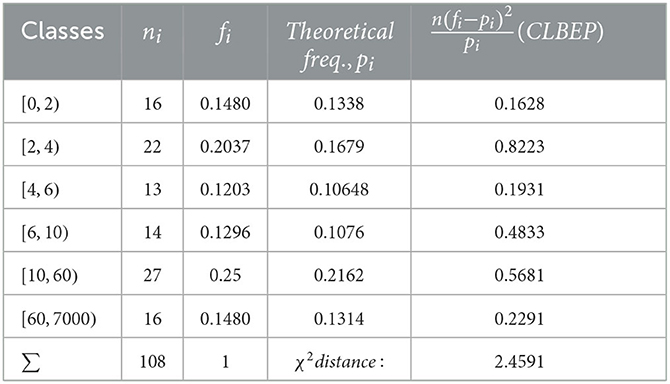
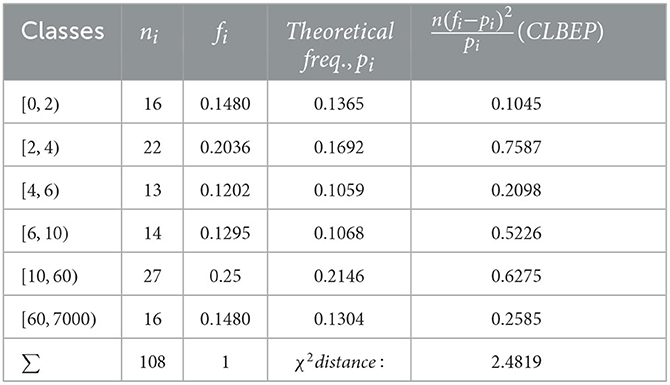
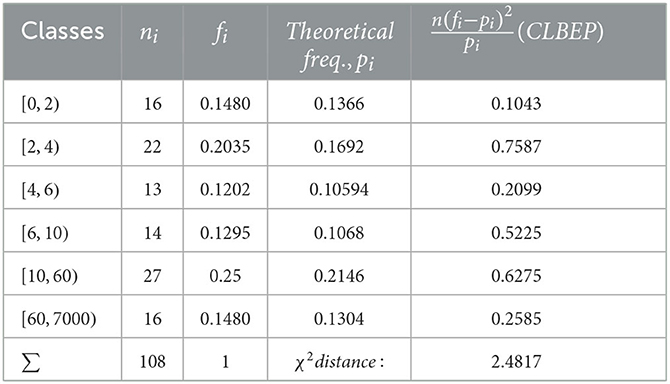
We notice that Algorithm 2 in Step 1 gives a more accurate value. We also applied the χ2 test to check the distribution fitting, and the results for are given in Tables 1–4.
The χ2 distances calculated for all the estimated values of the parameters are
The χ2 test accepts the length-biased exponential Pareto model for all values of the parameter as expected, which is a minimum.
4.2. Goodness of fit
In this subsection, we apply the composite length-biased exponential-Pareto model to two real insurance data sets.
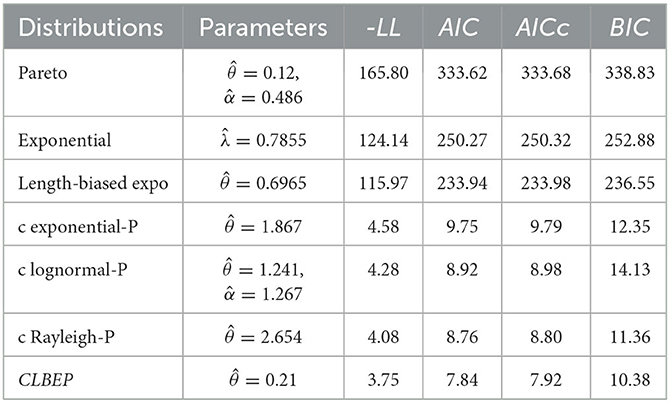
Data set I: is 100 Algerian (SAA company) fire insurance losses (see Appendix).
We provide in Table 5 the estimated value of fitted models and the values of the −LL, AIC, AICc, and BIC evaluated at the maximum-likelihood estimators.
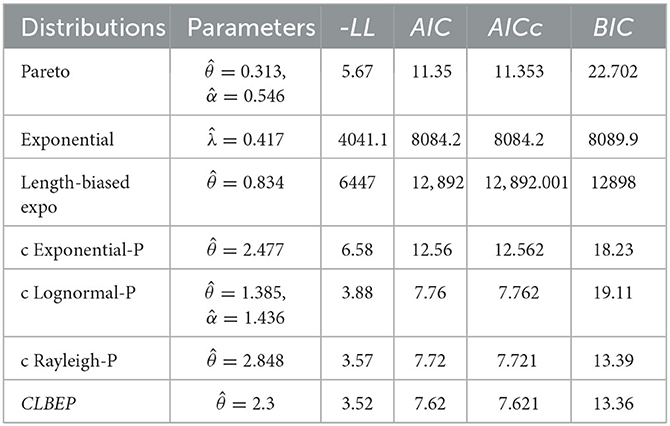
Data set II: is 2, 156 Danish fire insurance losses.
We use the same analysis, we find
Tables 5, 6 indicate that the CLBEP model outperforms classical distributions, composite Rayleigh-Pareto, composite exponential-Pareto, and composite lognormal-Pareto models in terms of −LL, AIC, AICc, and BIC for data sets I and II. In addition, in data set II, the Pareto model outperforms the conventional model since it covers a larger loss (n = 2, 156).
5. Conclusion
A unique distribution known as the composite length-biased exponential Pareto generated is suggested for application. Some of the mathematical features of this distribution include the quantile function, stochastic ordering, moments of the CLBEP, and maximum-likelihood estimation. In contrast to other conventional and new composite distributions, the distribution proposed in this work gives very satisfactory results. The goodness of fit of this novel model is compared to different conventional and new composite models, such as composite exponential-Pareto, composite lognormal-Pareto, and composite Rayleigh-Pareto distributions, using two real fire insurance data sets (Algerian and Danish fire insurance losses). Compared to the standard models, the composite models provided a far better fit to the data. The composite exponential-Pareto, composite lognormal-Pareto, and composite Rayleigh-Pareto distributions do not fit as well as the CLBEP model provides. We predict that researchers interested in statistical sciences and their applications, such as dependability and actuarial sciences, will be drawn to the CLBEP model. A future research may examine the Bayesian estimation of the CLBEP parameter, introducing the truncated version of the CLBEP distribution. In addition, it is interesting to use similar composite distributions to model the epidemic problem.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Acknowledgments
The authors acknowledge the Editor, FM and the referees of this journal for their constant encouragement to finalize the paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2023.1137036/full#supplementary-material
References
1. Klugman SA, Panjer HH, Willmot G. Loss Models: From Data to Decisions. New York, NY: Wiley (2008).
2. Liu B, Ananda MMA. Analyzing insurance data with an exponentiated composite Inverse-Gamma Pareto Model. Commun Stat Theory Methods. (2022) 2022:399. doi: 10.1080/03610926.2022.2050399
3. Scollnik DPM. On composite Lognormal-Pareto models. Scand Actuarial J. (2007) 2007:20–33. doi: 10.1080/03461230601110447
4. Benatmane, C, Zeghdoudi H, Shanker R, Lazri, N. Composite Rayleigh-Pareto distribution: application to real fire insurance losses data set. J Stat Manag Syst. (2021) 24:545–57. doi: 10.1080/09720510.2020.1759253
5. Elbatal I, Aryal G. A new generalization of the exponential Pareto distribution. J Inf Optim Sci. (2017) 38:675–97. doi: 10.1080/02522667.2016.1220079
6. EL-Sagheer RM, Mahmoud MAW, Abdallah SHM. Statistical inferences for new Weibull-Pareto distribution under an adaptive type-ii progressive censored data. J Stat Manag Syst. (2018) 21:1021–57. doi: 10.1080/09720510.2018.1467628
7. Aminzadeh MS, Deng, M. Bayesian predictive modeling for Inverse Gamma-Pareto composite distribution. Commun Stat Theory Methods. (2019) 48:1938–54. doi: 10.1080/03610926.2018.1440595
8. Cebrian A, Denuit M, Lambert PH. Generalized Pareto fit to the society of Actuaries' large claims database. North Am Actuarial J. (2003) 7:18–36. doi: 10.1080/10920277.2003.10596098
9. Preda V, Ciumara R. On composite models: Weibull-Pareto lognormal-Pareto. A comparative study. Rom J Econ Forecast. (2006) 3:32–46.
10. Cooray K, Ananda MA. Modeling actuarial data with a composite Lognormal-Pareto model. Scand Actuarial J. (2005) 5:321–34. doi: 10.1080/03461230510009763
11. Teodorescu S, Vernic R. Some composite exponential-Pareto models for actuarial prediction. Rom J Econ Forecast. (2009) 12:82–100.
Keywords: composite distribution, Pareto distribution, length-biased exponential, maximum-likelihood estimation, quantile function
Citation: Benchettah MH, Zeghdoudi H and Raman V (2023) On composite length-biased exponential-Pareto distribution: Properties, simulation, and application in actuarial science. Front. Appl. Math. Stat. 9:1137036. doi: 10.3389/fams.2023.1137036
Received: 03 January 2023; Accepted: 23 February 2023;
Published: 20 March 2023.
Edited by:
Fabrizio Maturo, Universitas Mercatorum, ItalyReviewed by:
Fuxia Cheng, Illinois State University, United StatesAbdelfateh Beghriche, Université Frères Mentouri Constantine 1, Algeria
Seghier Fatma Zohra, University of Skikda, Algeria
Copyright © 2023 Benchettah, Zeghdoudi and Raman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Halim Zeghdoudi, aGFsaW16ZWdoZG91ZGk3N0BnbWFpbC5jb20=
 Moulouk Halima Benchettah1
Moulouk Halima Benchettah1 Halim Zeghdoudi
Halim Zeghdoudi Vinoth Raman
Vinoth Raman