From energy to ecology: decarbonization pathways for sustainable high-performance computing through global carbon-energy nexus analysis

Introduction: High-performance computing (HPC) has been a pivotal driving force of technological development.

Methods: This study evaluates the environmental impact of HPC by analyzing energy consumption and carbon emissions across major global centers. We analyzed data from the top 500 HPC centers, using linear regression to fill in missing values for max power due to a high Pearson correlation. The representativeness of the TOP500 dataset was validated via distribution fitting and Monte Carlo simulations, confirming that it captures over 99.8% of high-end global HPC power consumption.

Results: (1) Applying a logistic model to relate the average utilization rate of the four major countries to the ratio of HPC market size to the number of centers (R² = 0.775). Global annual energy consumption ranges from 2.3–4.2 billion kW·h at average utilization, with the US accounting for 1.68 billion kW·h. (2) Carbon footprint calculations using energy mix data (2016–2022) incorporated an Environmental Impact Index (EII) to weigh ecological sensitivity, linking CO₂ emissions to a 0.5% GDP loss per trillion tons, totaling $2.18 million in economic losses. (3) Forecasting models projected 2030 emissions at 1.071 × 10²⁰ kg under average utilization with sobol analysis demonstrating marginal energy consumption fluctuations due to uncertainty. (4) Renewable energy adoption analysis showed strong inverse correlations between clean energy use and emissions in the US (R² = 0.904), China (R² = 0.99), and Germany (R² = 0.779), while quantifying air pollutants like SO₂, NOx and PM10. (5) The combined differential equation and regression models captured the dynamic evolution of energy efficiency and its impact on energy consumption, revealing through 2025 projections that policy incentives can substantially enhance energy efficiency (from 21.22 to 30.90) while reducing energy consumption (from 0.3449 to 0.3278).

Discussion: This study underscores the urgency of balancing HPC growth with sustainability through renewable integration and operational efficiency.

1 Introduction

The rapid advancement of computer technologies has propelled high-performance computing (HPC) to the forefront of technological innovation. HPC systems have driven breakthroughs in scientific research, machine learning, and simulation modeling by processing massive datasets at unprecedented speeds (1). However, these computational capabilities incur significant environmental costs, particularly through energy-intensive operations.

The escalating emissions of greenhouse gases have emerged as a crucial challenge in contemporary world, where climate change mitigation dominates global discourse (2). The generation of electricity often correlates with greenhouse gas emission, especially when relying on fossil fuels. This certainly leads to vast amount of CO₂ production. The demanding nature of HPC capabilities often imposes extra burden on the local power grids, resulting in a less environmentally friendly reliance on non-renewable energy sources. Furthermore, the environmental concern brought by HPC is far more than carbon emission. HPC poses various environmental challenges beyond energy consumption (3), including significant water usage for cooling, electronic waste generation, habitat destruction from rare earth material extraction, land use concerns, air pollution from fossil fuel power plants, risks from cooling system chemicals, and socioeconomic disparities in energy access due to large data centers and resource mining.

As HPC emerges as a cornerstone of global technological advancement, reconciling its indispensable role with environmental stewardship becomes imperative. Indeed, we ought to explore sustainable solutions to mitigate the impact of high-powered computing on the planet. Researchers and policymakers are increasingly focusing on understanding and quantifying the environmental footprint of HPC, as well as developing strategies to promote energy efficiency, renewable energy adoption, and responsible waste management practices within the industry.

In this study, we aim to achieve the following goals: (1) Qualify global HPC energy demand by analyzing annual consumption under both average and peak utilization scenarios. (2) Develop a carbon emission model that evaluates HPC’s carbon footprint to reflect real-world operational variability. (3) Project future impacts by integrating HPC growth trajectories, sectoral energy demands, and evolving energy mixes, establishing 2030 emission scenarios. (4) Develop a renewable energy adoption model to assess emission reduction potential and challenges in transitioning to 100% renewables, while exploring synergies with other environmental factors like energy efficiency. (5) Provide a series of feasible solutions, including both technical and policy solutions that can solve alleviate HPC’s impact on the environment.

2 Preliminaries

2.1 Assumptions

2.1.1 Assumption 1

The TOP500 list comprehensively represents global HPC infrastructure.

2.1.1.1 Approach: distribution fitting and representativeness estimation of TOP500 power data

To evaluate this Assumption, power consumption data from the 2016 HPC TOP500 list were processed. Missing values were imputed using least squares fitting. Subsequently, the Kolmogorov–Smirnov (K-S) test was employed to assess whether the sample data followed a specific theoretical distribution. Four candidate distributions were considered: lognormal, gamma, Weibull-min, and normal. The optimal distribution was selected based on the smallest K-S statistic and the largest p-value.

To further assess the goodness of fit, quantile–quantile (Q-Q) plots were generated by comparing the sample quantiles to those of the candidate distributions. The closer the plotted points lay along the reference line, the better the fit. Once the best-fitting distribution was identified, its parameters were used to define a probability density function (F(P)), with the corresponding cumulative distribution function given by:

$\begin{array}{ll}F\left(P\right)=\mathbb{P}(P_i\le P)& (1)\end{array}$

Where F(P) represented the probability that the power consumption P_i of a system was less than or equal to a given value P. Let P_min denoted the minimum power consumption observed in the TOP500 dataset. The TOP500 list then corresponded to those systems with power consumption greater than or equal to P_min, and the proportion r was defined as:

$\begin{array}{ll}log\left(x\right)~\mathcal{N}(\mu ,{\sigma }^2)& (2)\end{array}$

Where N was the total number of HPC systems worldwide. By analyzing the value of r, one can determine whether the TOP500 dataset was representative of the broader global HPC power consumption landscape.

2.1.1.2 Findings: results of distribution testing and parameter estimation

This study calculated the K-S statistics and p-values for each of the four candidate distributions. Among them, the lognormal distribution yielded the smallest K-S statistic (0.0575), indicating the closest match to the empirical data. Its p-value was 0.087, which exceeds the conventional significance threshold of 0.05, suggesting insufficient evidence to reject the null hypothesis that the data follow a lognormal distribution. Therefore, this distribution curve was selected for fitting.

Meanwhile, this conclusion was further supported by the Q-Q plots shown in Figure 1A and the distribution curve in Figure 1B, which visually confirm the appropriateness of the lognormal fit.

Figure 1

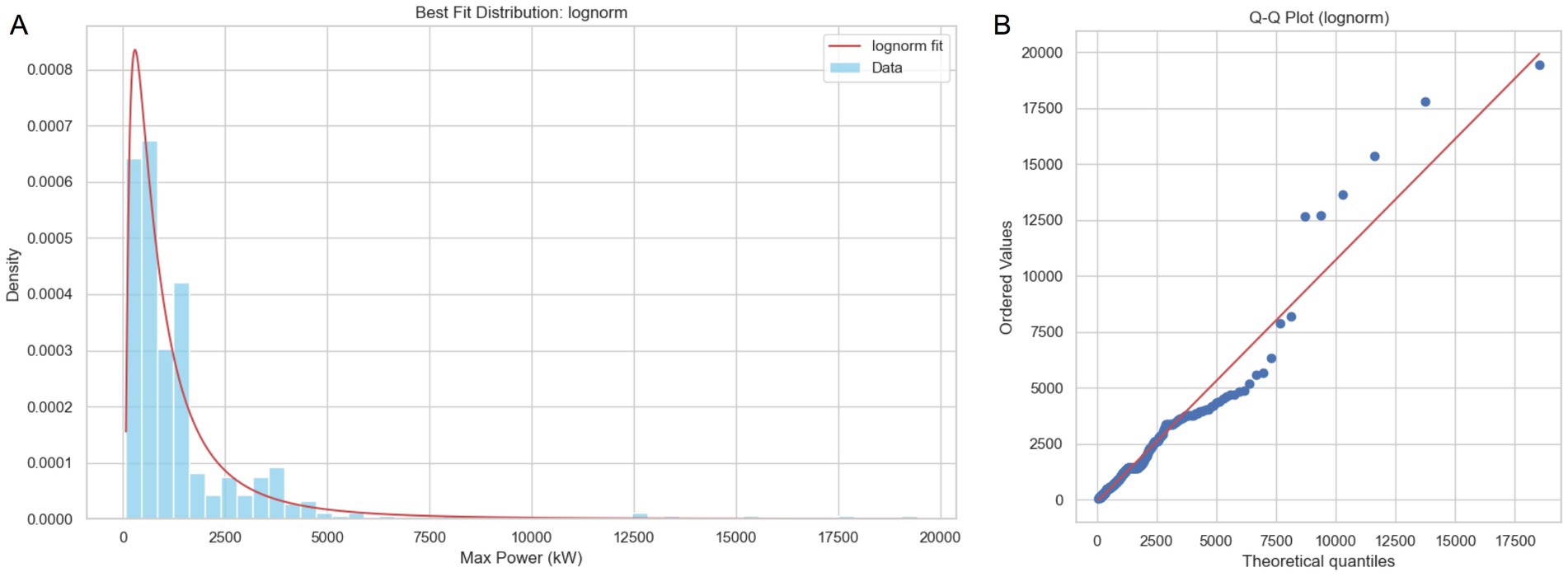
Figure 1. The Q–Q plot and the lognormal distribution curve. (A) Displays he lognormal distribution curve. (B) Displays the Q–Q plot.

The fitted parameters of the lognormal distribution were: μ = 53.7102, σ = 1.1294, s = 723.6495. Here, μ₀ denoted the location (shift) parameter, σ was the shape parameter (standard deviation in the logarithmic space), and s was the scale parameter, typically represented as s = e^mu.

According to the original dataset, the minimum power consumption in the TOP500 list was 77 kW. Based on the fitted cumulative distribution function, the corresponding value of r = 0.0012, indicating that the TOP500 represents approximately the top 0.12% in terms of energy consumption. This implies that the TOP500 dataset effectively captures the power consumption characteristics of the most energy-intensive HPC systems worldwide.

2.1.1.3 Justification: distributional characteristics and modeling implications

The findings suggested that the lognormal distribution was a statistically and conceptually appropriate model for characterizing HPC power consumption. From a physical standpoint, the power consumption of HPC systems is mainly shaped by several key factors, including hardware configuration (such as the number of CPUs or GPUs and the size of memory), architectural efficiency, system utilization, and cooling technology. These factors collectively result in a distribution of energy consumption that displays several distinct features. First, the distribution is clearly right-skewed: the majority of HPC systems operate in the low to moderate power range, while a small number of machines, consume exceptionally high levels of energy. Second, energy consumption is inherently non-negative, as it cannot fall below zero. Third, the power values span a broad range, from several tens of kilowatts to multiple megawatts, indicating a significant degree of variation across systems. Given these characteristics, it is appropriate to consider statistical models that can capture long-tailed, positively skewed distributions. The lognormal distribution is a natural choice in this context, as it commonly arises in multiplicative processes and has been widely used to describe phenomena such as energy consumption, wealth distribution, and city population sizes. In contrast, gamma and Weibull distributions offer flexible alternatives, while power-law distributions, though relevant in extreme-value theory, may overstate the dominance of outlier systems.

From a modeling perspective, the method of estimating global representativeness through cumulative distribution analysis is both parsimonious and informative. By comparing the empirical minimum of the TOP500 to the fitted cumulative distribution function, the resulting value of r serves as a proxy for the proportion of systems that the dataset effectively represents. The result of r = 0.0012 indicates that the TOP500 comprises the top 0.12% of energy-consuming HPC systems, reinforcing the assumption that the sample is representative of high-end global trends. However, caution is warranted in extending this representativeness to mid- and low-range HPC systems, which may follow different structural and operational dynamics. Future studies could benefit from additional data sources beyond the TOP500 list, including regional or industrial computing facilities, to further validate the distributional assumptions and improve global energy modeling accuracy.

2.1.2 Assumption 2

The energy consumption structure of HPC centers in each country follows the overall energy structure of that country.

2.1.2.1 Justification

This assumption was supported by Li et al., their result conducted a comprehensive empirical analysis of HPC system carbon footprints across multiple geographical regions (4). Their findings indicate that the operational carbon emissions of HPC systems were strongly correlated with the carbon intensity of the regional power grid, rather than with any independent or customized energy sourcing. Specifically, they analyzed HPC facilities in countries such as Japan, the United Kingdom, and the United States, and demonstrated that the same system—when powered by different national grids—results in significantly different carbon footprints. This implies that HPC centers typically rely on standard national electricity supply infrastructures, and thus their energy sourcing reflects the composition of the broader grid, including proportions of coal, natural gas, nuclear, and renewable energy. The study concludes that the regional grid’s carbon intensity is the dominant factor in determining the operational sustainability of HPC. Therefore, it is both methodologically valid and empirically grounded to assume that an HPC center’s energy structure follows that of its host country.

2.1.3 Assumption 3

HPC facilities consist primarily of CPU, memory and storage.

2.1.3.1 Justification

These three components consume the most of an HPC facility’s power, so in the calculation of HPC energy consumption, the influence of other minor components is negligible.

2.1.4 Assumption 4

There will not be a sudden decrease in the demand for HPC caused by unpredictable factors, such as economic downturns.

2.1.4.1 Justification

Based on projections from Fortune Business Insights (5), the global HPC market is expected to grow steadily from 2019 to 2032, driven by the integration of AI and the increasing computational demands of complex algorithms. The report emphasizes HPC’s central role in enabling major advances across industries such as data analytics, predictive modeling, and enhanced simulations.

This steady growth projection, even in the face of economic uncertainties in recent years, provides strong support for the assumption that demand for HPC is unlikely to experience a sudden decline due to unpredictable factors such as economic downturns.

2.2 Data and variables

We collected data on worldwide HPC centers’ P_max, N_c, and R_max from the TOP500 HPC list for 2014 to 2024, which enabled the calculation of average power consumption (6, 7). We assessed utilization rates in China, France, Germany, and the United States, using data from 19 countries to establish benchmarks from 2016 to 2024. To estimate energy consumption, we identified emission factors for oil, natural gas, coal, nuclear, and renewable sources, quantifying CO₂ emissions per unit of energy. We analyzed carbon emissions for 2016, 2019, and 2022 across 20 countries to evaluate the contribution of each energy type (8).

Our environmental impact assessment included emissions of sulfur dioxide (SO₂), nitrogen dioxide (NO₂), carbon monoxide (CO), and particulate matter (PM10). We considered the fuel proportions—natural gas, oil, and coal—used in each country, calculating total emissions by evaluating fuel consumption and applying corresponding emission factors. We also collected impact factor data for each fuel type.

Additionally, we incorporated global GDP data and assessed costs related to carbon emission reduction, developing an environmental impact index based on various energy sources. We utilized R_peak data for HPC development with global GDP data to evaluate energy demand in other sectors, optimizing our energy consumption model. Energy efficiency data for each HPC from 2014 to 2023 was also collected to calculate average efficiency.

Detailed variables are found in Supplementary Table 1.

3 Mathematical modeling and results

3.1 Problem 1: understanding the scope

To calculate and predict energy consumption of different countries while considering full capacity and average utilization rates, we construct the following formula (see Figure 2):

$\begin{array}{ll}E{C}_{\max }=P_{\max }·T& (3)\end{array}$

$\begin{array}{ll}E{C}_{\mathrm{avg}}=P_{\max }·{\eta }_{\mathrm{avg}}·T& (4)\end{array}$

Figure 2

Figure 2. Logical flow of Problem 1.

Here, T represented the annual time basis (8,760 h).

3.1.1 The use of linear regression to fill in missing data

This paper collected data on worldwide HPC centers’ P_max, N_c, and R_max from the TOP500 HPC list from 2014 to 2024, enabling the calculation of average power consumption (6, 7).

After arranging the HPCs in ascending order based on N_c, this study identified missing P_max values of some HPC centers. To address this issue, linear regression was implemented to model the relationship between the existing N_c and P_max values. Missing P_max values were estimated by substituting N_c into the derived function.

To address this issue, we implemented linear regression to estimate these values due to the strong linear relationships indicated by the Pearson correlation coefficients, as shown in Figure 3A.

Figure 3

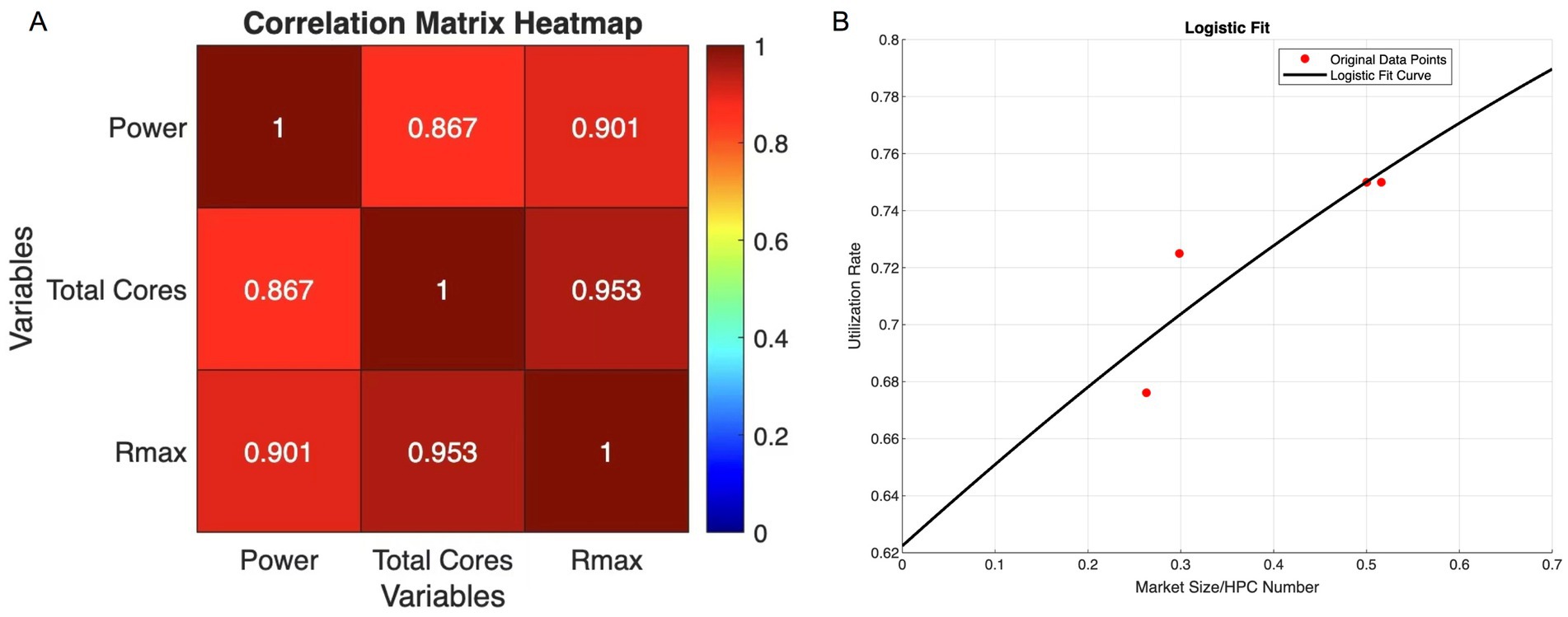
Figure 3. Understanding the scope. (A) Displays Pearson matrix of P_max, R_max, and N_c. (B) Displays logistic fit for utilization rate.

The resulting regression function is as follows:

$\begin{array}{l}{P}_{\max }=5.282\times {10}^2+6.027\times {10}^{-4}·N_{\mathrm{c}}\\ +4.723\times {10}^{-4}·R_{\max },R^2=0.813\end{array}\text{ (5)}$

The R² of this regression function is as high as 0.813, which means that by using this function, we can fill in all missing P_max effectively.

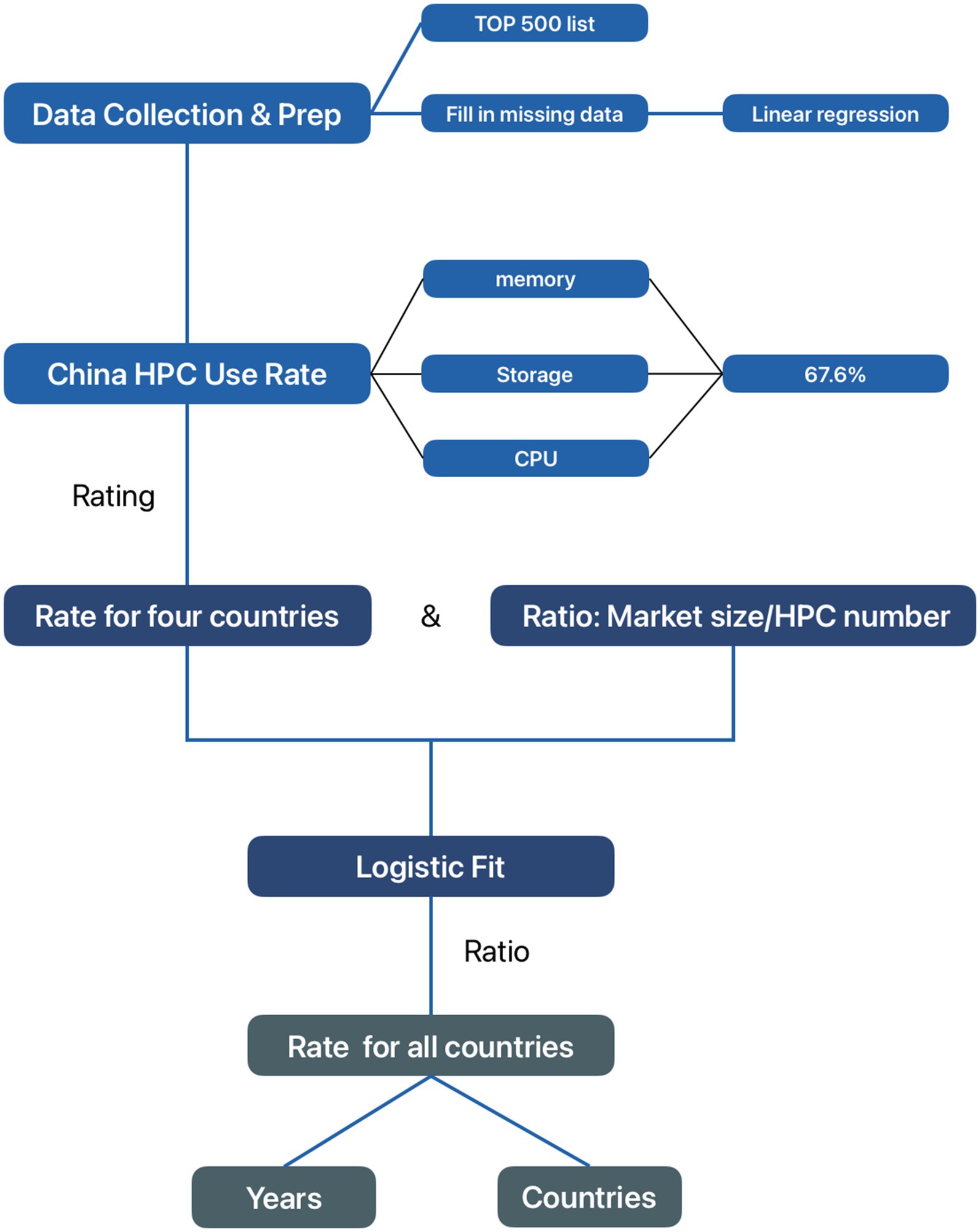
3.1.2 Calculation of average utilization rate

To calculate the average utilization, our team refers to a formal essay that records the η_cpu, η_mem, η_stg of 50 HPCs in China in 2016 (9). The relevant equations, adopted from another research, apply to our calculation of η_avg. The calculations of P_cpu and P_mem were based on the models of another study (10).

$\begin{array}{ll}{P}_{\max }=P_{\mathrm{cpu}}+P_{\mathrm{mem}}+P_{\mathrm{stg}}& (6)\end{array}$

$\begin{array}{ll}{P}_{\mathrm{avg}}=P_{\max }·{\eta }_{\mathrm{avg}}& (7)\end{array}$

The final equation utilized was:

$\begin{array}{ll}{P}_{\max }·{\eta }_{\mathrm{avg}}=P_{\mathrm{cpu}}·{\eta }_{\mathrm{cpu}}+P_{\mathrm{mem}}·{\eta }_{\mathrm{mem}}+P_{\mathrm{stg}}·{\eta }_{\mathrm{stg}}& (8)\end{array}$

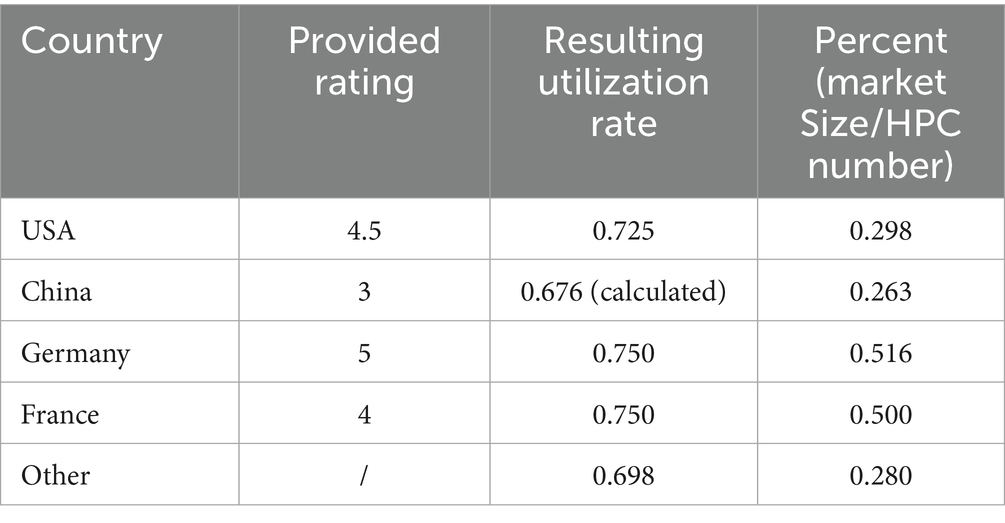
The calculated η_avg for 50 Chinese HPCs in 2016 was 67.6%.

3.1.3 Logistic fits

This study used a rating provided by a previous study to calculate the average utilization rate of the United States, Germany, and France in 2016 based on the utilization of China HPCs (11). To estimate the average utilization rate for HPCs in various countries other than these four countries, and in other years other than 2016, we use these four countries’ ratio of market size to the number of HPCs and the average utilization rate to plot a scatter graph (shown in Figure 3B) (12, 13).

We observed the relationship between the ratio and the rate. Because there was an upper and a lower limit of the utilization rate of HPCs, we use logistic fit instead of linear regression:

$\begin{array}{ll}{\eta }_{\mathrm{avg}}=\frac{0.95}{1+e^{-1.360·(E+0.472)}},R^2=0.775& (9)\end{array}$

The logistic model helps us estimate the average use rate of different countries at any year using the ratio of Market size to HPC number. France, Germany, America, and China have distinct utilization rates because of available market size data. The market size of the rest of the countries was recorded as a whole, so we categorized them as “other” and calculated their market size per HPC by subtracting the HPCs in the four major countries from 500. The use rate of other was then calculated. Table 1 displays the rating and ratio used and the resulting utilization rate.

Table 1

Table 1. Utilization rates and market size ratios by country.

3.1.4 Change of energy consumption across time and countries

For each country group, energy consumption at the average utilization rate and at full capacity was computed. This study calculated and compared an HPC’s energy consumption at the average utilization rate by multiplying the EC_max of that facility by the average utilization rate in the country where that HPC facility was located. Global totals were derived by summing values for all TOP500 HPCs. Thus, 19 representative countries that possess HPC had been selected. This paper calculated the annual energy consumption of HPC facilities in each country in the last decade.

The changes of energy consumption of HPC facilities in each country during the last decade were shown in the following graphs, with separate graphs for the USA, Japan, and China (Figures 4A–F).

Figure 4

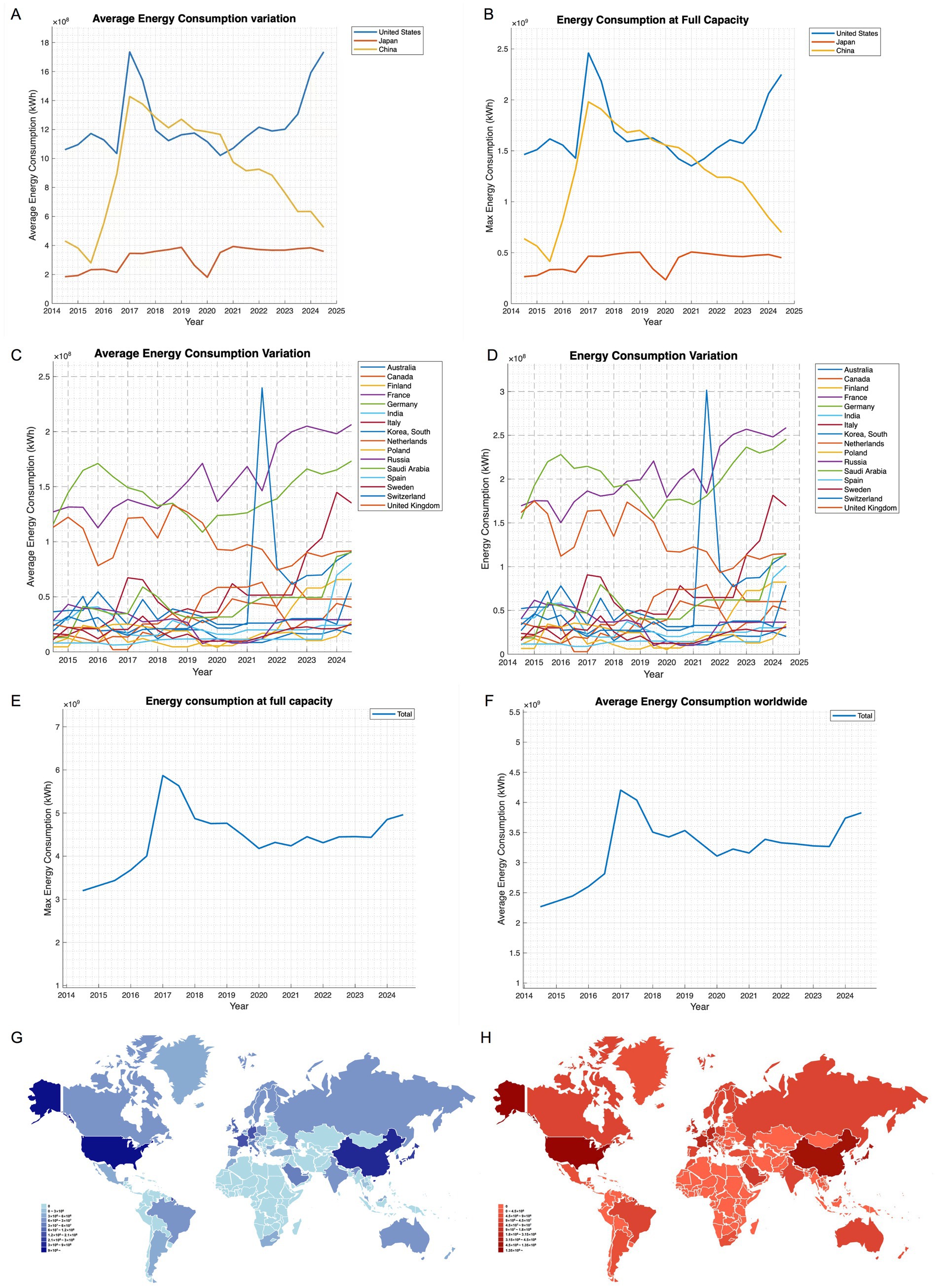
Figure 4. Change of energy consumption. (A) Displays average energy consumption of America, Japan, and China. (B) Displays max energy consumption of America, Japan, and China. (C) Displays average energy consumption of different countries. (D) Displays max energy consumption of different countries. (E) Displays max energy consumption of the whole world. (F) Displays average energy consumption of the whole world. (G) Displays average energy consumption distribution heatmap. (H) Displays max energy consumption distribution heatmap.

Global annual energy consumption ranges were:

$3,198,786,630\le E{C}_{\max }\le 5,869,681,840$

$2,267,243,623\le E{C}_{\mathrm{avg}}\le 4,203,676,800$

Both EC_max and EC_avg were highest in 2017 and lowest in 2014.

Country-specific distributions (Figures 4G,H) showed:

$20,686,068\le E{C}_{\max }\le 1,676,768,241$

$15,674,290\le E{C}_{\mathrm{avg}}\le 1,239,115,648$

When divided by countries, both EC_max and EC_avg were the highest in America and the lowest in Poland.

3.2 Problem 2: HPC carbon emissions model

3.2.1 Carbon footprint calculation

Our analysis employed EC_avg as the primary metric for representing the real-world energy usage patterns. Drawing upon energy structure data from 20 representative HPC-intensive countries (12, 13). This study categorized national energy portfolios into 5 distinct types: coal, natural gas, petroleum, nuclear energy, and renewable energy (14).

$\begin{array}{ll}{C}_{\text{total}}=(\sum _{i\in \{c,g,p,n,r\}}{\alpha }_i·k_i)·\mathit{EC}& (10)\end{array}$

The calculation framework utilized the following notation:

α_i represented the proportion of the i-th energy type within the national energy mix

k_i denotes CO₂ emissions (kg per kWh) for each energy type.

Subscripts indicated energy sources: c (coal), g (gas), p (petroleum), n (nuclear), r (renewable).

Notably, α_r carried an emission factor of zero as renewable energy generation produces no direct carbon emissions. Thus, the studies’ calculations focused on the four non-renewable energy categories.

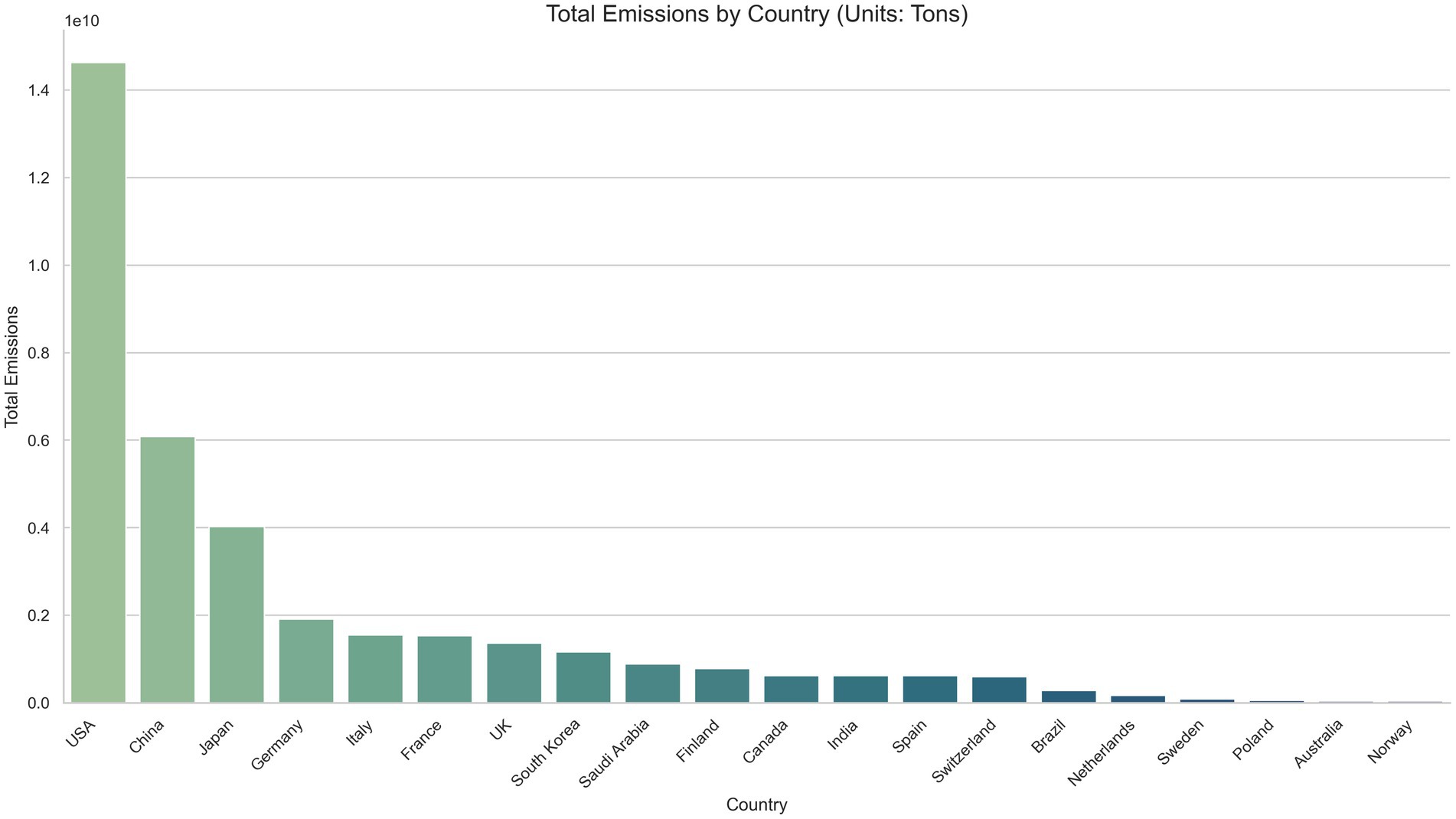
The total carbon emissions from HPC countries in 2016, 2019, and 2022 were as shown in Figure 5A. China and the United States exhibited carbon emissions significantly higher than those of other countries (China: 0.7681 billion tons in 2016, 0.651 billion tons in 2019, 0.4647 billion tons in 2022; United States: 0.8256 billion tons in 2016, 0.4884 billion tons in 2019, 0.4938 billion tons in 2022), while Japan’s carbon emissions were of the same order of magnitude (174.5 million tons in 2016, 93.55 million tons in 2019, 184.1 million tons in 2022). Generally, the total carbon emissions from HPC decreased in countries with larger economic scales and increased in countries with lower economic scales (e.g., Brazil: 0.626 million tons in 2016, 3.212 million tons in 2019, 11.61 million tons in 2022).

Figure 5

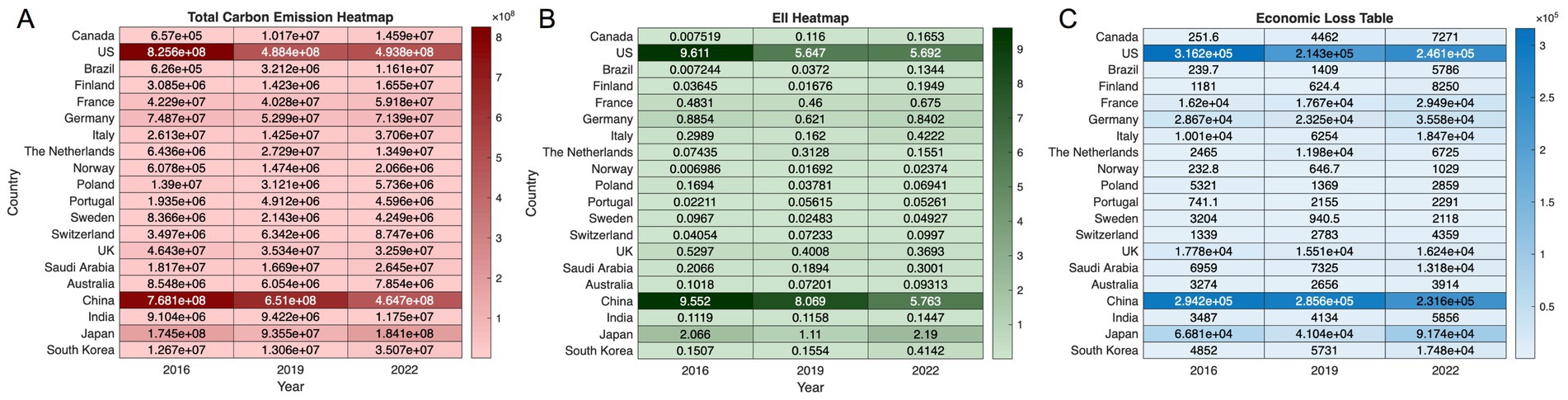
Figure 5. HPC carbon emissions model. (A) Displays carbon emission of HPC countries. (B) Displays EII graph of HPC countries. (C) Displays economic loss of HPC in the main HPC countries.

3.2.2 Environmental impact index (EII) calculation

The Environmental Impact Index (EII) incorporated energy-specific sensitivity coefficients (Sensitivity _i ) that quantified the relative environmental impact of each energy type. This study derived the EII through a weighted summation of carbon emissions multiplied by their respective sensitivity coefficients, normalized by total emissions. This index provided a standardized measure of HPC’s environmental impact across different national contexts.

$\begin{array}{ll}\mathit{EII}=\frac{{\sum }^{i\in \{c,g,p,n\}}{\alpha }_i\times E_i\left(t\right)\times {\text{Sensitivity}}_i}{\overline{C_{\text{total}}}}& (11)\end{array}$

Figure 5B displayed the results of the EII calculation, which quantified the environmental impact of HPC in these countries for the three selected years. As the figure indicated, the EII of the United States and China was far higher than that of other countries, while Japan, Germany, France, and the United Kingdom followed closely.

3.2.3 Economic loss measurement

This study quantified the economic consequences of HPC-related emissions using established climate-economy relationships. The model applied a conversion factor whereby each trillion tons of CO₂ emissions corresponded to 0.5% reduction in global GDP (15).

$\begin{array}{ll}\mathit{EL}=\frac{C_{\text{total}}}{1\times {10}^{15}\mathit{kg}}·0.5\%·\mathit{GDP}& (12)\end{array}$

The total world GDP in 2016, 2019, and 2022 was 76.59 trillion dollars, 87.752 trillion dollars, and 99.67 trillion dollars, respectively. The economic loss caused by HPC in each HPC country is then calculated and shown in Figure 5C. The total economic loss due to carbon emission from HPC in 2016, 2019, and 2022 reached as high as 2,183,499 dollars.

3.3 Problem 3: future HPC and energy trends projection

To analyze the impact of HPC development and rising energy demands from other sectors, as well as the effects of different energy structures on carbon emissions, a regression model was first established to link the development of HPC computing and the growth of energy demand in other sectors to overall energy consumption. Based on the model developed in the second question, carbon emissions were derived from energy consumption.

3.3.1 Factor in terms of HPC development

To quantify the impact of the evolution of HPC over time on energy consumption, the peak theoretical performance of supercomputers (R_peak) was used as a key metric for HPC development. Data for R_peak from the TOP500 list during the years 2014–2023 were collected.

A quadratic regression model was adopted due to its strong fit and better alignment with recent trends. The general form of the fitted model was:

$\begin{array}{ll}{R}_{\text{peak}}=a·{\text{Year}}^2+b·\text{Year}+c& (13)\end{array}$

Subsequently, the predicted R_peak values were obtained for the years 2014 to 2030 using the fitted model. These values were used as input to the energy consumption projection model established in Section 3.2.3.

The regression analysis yielded the following quadratic equation for HPC performance:

$\begin{array}{ll}{R}_{\text{peak}}=8.0\times {10}^8·{\text{Year}}^2+3.0724\times {10}^9·\text{Year}+2.8082\times {10}^9& (14)\end{array}$

This model achieved a coefficient of determination of R² = 0.9519, indicating a strong fit with the observed data and reflecting the decelerated growth of computing power in recent years.

3.3.2 Factor in terms of increasing demand of the other sector

In qualifying the extent to which increasing energy demand in other sectors would impact future energy consumption of HPC, the energy price was considered (14). In this respect, data of the global energy commodity price index, which was expressed as PI, from 2014 to 2023 were correlated and analyzed for their correlation with energy consumption EC_other in other sectors, which was derived via subtracting EC of HPC from the global energy consumption (16–19). Since energy price was highly interrelated with various social factors such as current affairs, data points with large fluctuations were intentionally removed. Based on the remaining data, a logistic fitting model was constructed to examine how PI would change with increasing EC_other.

To evaluate the relationship between energy demand in other sectors and global energy prices, a logistic regression model was applied. The resulting equation was:

$\begin{array}{ll}\mathit{PI}=\frac{334.2864}{1+exp(-0.0000045632\times (E{C}_{\text{other}}-1,674,700\left)\right)}& (15)\end{array}$

With an R² of 0.7868, this model was capable of explaining about 79% of the increase in energy prices due to the growth of energy demand in other sectors. Assuming that there were no other variables playing roles in the system, a reasonable prediction of the future energy prices could be made.

3.3.3 Energy structure model after optimization by two above factors

Building upon the previous analysis regarding HPC development and rising energy demand in other sectors, these two factors were integrated into the energy structure model to improve its representational accuracy. A multivariate polynomial regression was used to fit the relationship between average energy consumption EC_avg2 and the two variables: peak computing power R_peak and energy price index PI. The specific degrees of two independent variables and interaction terms were determined based on the R-squared value and consistency with reality. The regression model was in the following form:

$\begin{array}{ll}E{C}_{\mathrm{avg}2}=\mathrm{f}(\mathit{PI},{\mathrm{R}}_{\text{peak}})& (16)\end{array}$

A similar model was constructed for estimating the maximum energy consumption EC_max2, using the same independent variables and polynomial form.

Subsequently, the regression functions were brought back into the carbon emission function from Section 3.2:

$\begin{array}{ll}{C}_{\text{total}}=(\sum _{i\in \{c,g,p,n,r\}}{\alpha }_i·k_i)·\mathit{EC}& (17)\end{array}$

Where

$\begin{array}{ll}\sum _{i\in \{c,g,p,n,r\}}{\alpha }_i=1& (18)\end{array}$

By altering the percentage of various energy sources, this approach could provide insights into the change in carbon emissions.

Indeed, building upon these inputs, the following polynomial regression equations were established for average and maximum energy consumption:

$\begin{array}{c}E{C}_{\mathrm{avg}2}=0.2881-0.0047\mathrm{PI}-0.0496R_{\text{peak}}\\ +0.0600\mathrm{PI}·R_{\text{peak}}-0.0096{R_{\text{peak}}}^2\end{array}\text{ (19)}$

With R² = 0.8425. In this model, the variable PI represented the normalized energy price index, where the original price values were standardized using a mean of 75.09 and a standard deviation of 18.6. The variable R_peak represented the normalized peak computing power of HPC systems, standardized using a mean of 3.528 × 10⁹ and a standard deviation of 3.341 × 10⁹. Moreover, for maximum energy consumption:

$\begin{array}{c}E{C}_{max2}=0.3748+0.0099\mathrm{PI}-0.0423R_{\text{peak}}\\ +0.0047{\mathrm{PI}}^2+0.0368\mathrm{PI}·R_{\text{peak}}+0.0076{R_{\text{peak}}}^2\end{array}\text{ (20)}$

With R² = 0.9983. In this model, the variable PI and R_peak were normalized based on the same standard above.

Here, Figures 6A–D provided visual representations of the polynomial fitting surfaces for EC_avg and EC_max, respectively. In Figures 6A,B, when energy prices were extremely low, average energy consumption decreased as R_peak increases, reflecting the energy-saving benefits of improved computational efficiency. When computing power was low, a rise in energy prices also led to reduced consumption, likely due to suppressed computational demand. However, at higher levels of R_peak, the opposite trend emerged—higher prices coincided with increased energy use. This may be explained by the behavior of large-scale HPC centers, where organizations concentrated intensive workloads under rising energy costs to optimize budget efficiency, resulting in greater total consumption. Figures 6C,D revealed similar patterns for EC_max, though the trends appeared more pronounced. In particular, maximum energy consumption increased rapidly when both computing power and energy price were high. Overall, despite potential uncertainties, both models demonstrated strong predictive performance, with high goodness-of-fit and consistency with observed real-world behavior.

Figure 6

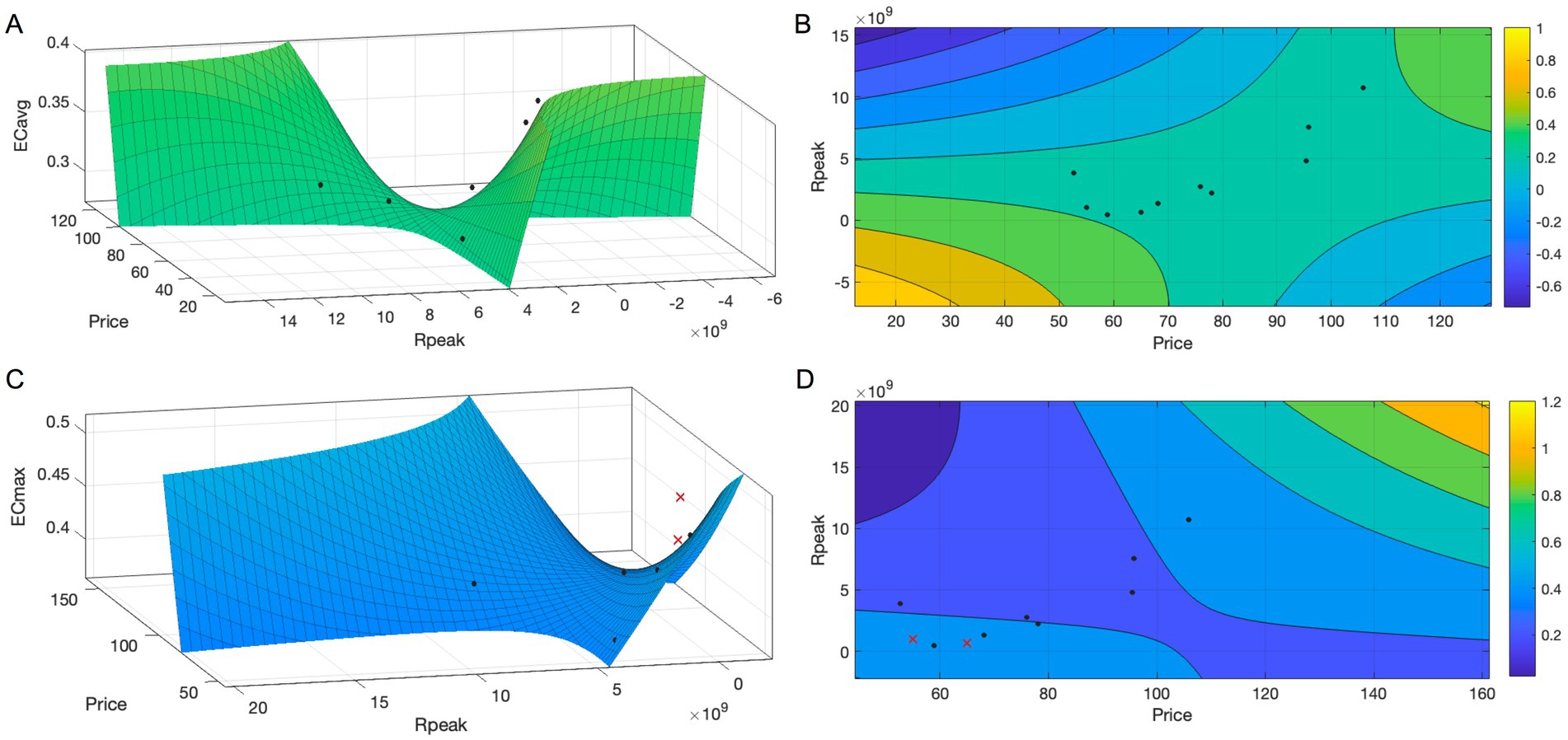
Figure 6. Energy structure model after optimization by two above factors. (A) Displays fitting curve of EC_avg. (B) Displays contour map of EC_avg. (C) Displays fitting curve of EC_max. (D) Displays contour map of EC_max.

3.3.4 Realistic bounds in 2030

To make a prediction of the future EC_avg and EC_max2, the growth models of R_peak and PI ought to be constructed. The value of R_peak in 2030 could be readily obtained, while for PI, future data of EC_other was required. A linear regression model was constructed to make this projection, which was given by:

$\begin{array}{ll}E{C}_{\text{other}}=a·\mathit{\text{Year}}-b& (21)\end{array}$

By substituting the value of EC_other into the previous function of PI, the change in PI in the following years was calculated. Then, the scope of EC in 2030 can be acquired.

To further estimate the scope of carbon emissions in the 2030s, projections of national energy structures were required. In this part of the study, the Grey Prediction Model GM(1,1) was primarily employed.

To construct the input for the GM model, data from the years 2013, 2016, 2019, and 2022 were collected for each country because of availability, detailing the share of four major energy types—nuclear, coal, oil, and natural gas—in total national energy consumption (20–23). Thus, for each energy type and country, a separate GM(1,1) model was built to project its share in 2031, representing the carbon emission scenario in the 2030s. All grey model forecasts followed the standard GM(1,1) procedure: the original data series x⁽⁰⁾ was first accumulated to generate the series x⁽¹⁾; the background values z⁽¹⁾ were then computed as the average of consecutive elements in x⁽¹⁾; finally, the parameters a and b were estimated via least squares using the equation $x^{\left(0\right)}\left(k\right)+a{z}^{\left(1\right)}\left(k\right)=b$ . The initial value $x^{\left(0\right)}\left(1\right)$ , corresponding to the first observation year (2013), was used as the initial condition to solve the model analytically:

$\widehat{x^{\left(1\right)}}\left(k\right)=\left(x^{\left(0\right)}\right(1)-\frac{b}{a})e^{-a(k-1)}+\frac{b}{a},$

$\begin{array}{ll}\widehat{x^{\left(0\right)}}\left(k\right)=\widehat{x^{\left(1\right)}}\left(k\right)-\widehat{x^{\left(1\right)}}(k-1)& (22)\end{array}$

Although the original years were 2013, 2016, 2019, 2022, for modeling convenience, the time series was set as k = 1, 2, 3, 4, assuming uniform step intervals.

The validity and accuracy of these models were assessed through level ratio tests and relative error evaluations, which provided guidance on both the applicability of the GM model and the reliability of its forecasts.

In cases where the GM model failed the diagnostic tests or yielded low-accuracy results, alternative curve-fitting methods were employed. These included linear regression, logarithmic regression, inverse regression, and S-curve (logistic) fitting. For each problematic data series, multiple models were tested and the one with the highest R² value and best visual fit to empirical patterns was selected.

Data limitations were also addressed appropriately. For China, India, Japan, and South Korea, where nuclear energy data for 2019 were unavailable, the missing value was replaced by the average of the 2016 and 2022 figures. Negative values produced by any forecasting method were adjusted to zero, and the share of renewable energy was subsequently calculated as the residual from unity (i.e., 1—sum of other shares). If this residual yielded a negative value, it was likewise adjusted to zero.

Subsequently, using the energy consumption predictions and the carbon emission function introduced in Problem 2, the final estimates of national and global carbon emissions in 2030 were calculated. To obtain the energy consumption in 2031 in each country, GM(1,1) was again utilized, with data collected from the HPC TOP500 List in 2013, 2016, 2019, and 2022. After classification and summation, the researcher calculated the power ratio R_P by dividing the total average power P_{avg, i} of each country by the total average power of the world P_avg. All the data was in original percentage shares without normalization. Due to some data deficiency, missing values were filled up using average values, and abnormal values were processed as well. Then, the projected power ratio in 2031 was calculated through GM(1,1), with level ratio tests and relative error evaluations determining whether the model was suitable. Again, for cases where the GM model did not fit, linear regression, logarithm regression, or inverse regression were incorporated as alternatives.

Since

$\begin{array}{ll}{R}_P=\frac{P_{\mathrm{avg},i}}{P_{\mathrm{avg}}}=\frac{(P_{\mathrm{avg},i}\times 360\times 24)}{(P_{\mathrm{avg}}\times 360\times 24)}=\frac{E_{\mathrm{avg},i}}{E_{\mathrm{avg}}}& (23)\end{array}$

Where E_{avg, i} refers to the average energy consumption of each country, and E_avg2 refers to the average energy consumption in the world, which could be obtained through the equation in Section 3.3.3. Therefore, the energy consumption EC_i in each country was given by:

$\begin{array}{ll}{\mathit{EC}}_p=R_p\times E_{\mathrm{avg}2}& (24)\end{array}$

Through Equation 13, the final carbon emission value could be obtained.

In order to estimate the energy price index P in 2030, the following linear regression was used to forecast EC_other:

$\begin{array}{ll}y=1.8887e+04\times \text{year}-3.6714e+07& (25)\end{array}$

With an R² value of 0.9092, indicating a strong linear growth trend. Substituting the projected value of EC_other into Equation 12, future values of PI were obtained. These, together with the extrapolated value of R_peak, enabled the calculation of both EC_avg and EC_max for 2030, which were 1.127180873 and 1.623270845, respectively. In 2031, EC_avg and EC_max were 1.35256363 and 1.967819606.

To further quantify the resulting carbon emissions, national energy structures were forecasted for each country. In evaluating the accuracy of the national energy mix projections, the level ratio test and relative error evaluation demonstrated that the majority of the GM(1,1) models achieved acceptable predictive accuracy and fit. In cases where the GM model showed instability or failed the tests, alternative modeling approaches were adopted. Notably, Sweden’s nuclear energy share was forecasted using linear regression due to the instability of GM results, while France’s natural gas data required the removal of outliers and subsequent linear fitting. Germany, Norway, Poland, and Sweden also employed logarithmic regression for natural gas projections after outlier removal. For Switzerland, the natural gas share was forecasted using an S-curve (logistic) model, which captured the gradual growth pattern more effectively than alternatives. The average power share for each country was calculated using consistent methods; detailed procedures were not included here due to the extensive volume of data. Missing values were imputed by taking the arithmetic mean of adjacent years, while abnormal entries—caused by limitations in the original data source—were corrected using linear interpolation. This approach was justified by the fact that HPC systems were large-scale infrastructure that were rarely dismantled or abruptly shut down, and thus their energy consumption rates were expected to remain relatively stable over time. The results were shown in the table below. Through calculation, the total carbon emission generated by maximal power operation was 1.071 × 10²⁰ kg.

Detailed information is found in Supplementary Table 2.

Finally, a visual representation of the resulting emission bounds under different structural assumptions was provided in Figure 7, which illustrated the potential variability in national and global carbon emissions based on the projected changes in energy consumption and structure.

Figure 7

Figure 7. Carbon emission prediction histogram by country.

3.3.5 Sensitivity analysis

To quantify the impact of input uncertainties on the model output, a global sensitivity analysis was conducted using the Sobol method, a variance-based technique capable of decomposing the output variance into contributions attributable to individual input variables and their interactions. The objective was to identify the relative influence of the energy price index and peak computing power on the predicted average energy consumption per unit of computing power in 2030.

The Sobol method was grounded in the functional ANOVA decomposition of a model function $f\left(X\right)$ , where $f\left(x\right)=(X_1,X_2)$represents the input parameter vector. The total variance of the model output $Y=f\left(X\right)$ was decomposed as:

$\mathit{Var}\left(Y\right)=\sum _{i=1}^k{V}_i+\sum _{i<j}{V}_{\mathit{ij}}+\dots +V_{1,2,\dots ,k,}$

$\begin{array}{ll}{S}_{\mathit{Ti}}=1-\frac{V_{~i}}{\mathit{Var}\left(Y\right)}& (26)\end{array}$

Where $V_i={\mathit{\text{VarX}}}_i\left(\mathbb{E}\right[Y\mid X_i\left]\right)$ denoted the variance contribution of input X_i, V_ij represented the second-order interaction between X_i and X_j, and the final term accounts for higher-order interactions. From this decomposition, three key sensitivity indices were defined: the first-order index $S_i=\frac{V_i}{\mathit{Var}\left(Y\right)}$the total-order index $S_{\mathit{Ti}}=1-\frac{V_{~i}}{\mathit{Var}\left(Y\right)}$ (where $V_{~i}$ denoted the variance excluding X_i), and the second-order index $S_{\mathit{ij}}=\frac{V_{\mathit{ij}}}{\mathit{Var}\left(Y\right)}$ , which quantified pairwise interactions.

In this study, the model inputs included the original energy price index $P{I}_{\text{original}}$ and the original peak computing power R_{peak original}), both defined within the range (10⁻⁶, 10¹⁰). To ensure adequate coverage of the input space and accurate estimation of sensitivity indices, input samples were generated using the Saltelli sampling scheme, which was a quasi-Monte Carlo method designed specifically for Sobol analysis. A base sample size of 1,024 was used, resulting in a total of 6,144 evaluations, consistent with the sampling requirement of N(k + 2), where N was the base sample size and k the number of input variables.

Each sampled input pair was evaluated through a standardized model function. The original variables were first standardized to improve numerical stability and interpretability. The standardized variables were then substituted into the following predictive equation:

$\begin{array}{c}E{C}_{\mathrm{avg}}=0.2881-0.0047·\mathit{PI}-0.0496·R_{\text{peak}}\\ +0.0600·\mathit{PI}·R_{\text{peak}}-0.0096·R_{\text{peak}}^2\end{array}\text{ (27)}$

Where $\mathit{PI}=\frac{P{I}_{\text{original}}–75.09}{18.6}$ and $R_{\text{peak}}=\frac{R_{\text{peak original}}-3.528\times {10}^9}{3.341\times {10}^9}$

The Sobol sensitivity analysis was then performed using the SALib Python library. The output variance was decomposed to compute the first-order sensitivity indices (S₁), representing the direct contribution of each variable to output variance, and the total-order indices (S_T), accounting for both direct and interaction effects. Additionally, second-order indices (S₂) were calculated to evaluate the joint interaction effect between the two inputs.

This approach provided a comprehensive assessment of how variability in the input space propagates through the model and affects predictions of future energy efficiency. The results were visualized through bar plots for S₁ and S_T, and a heatmap for S₂, enabling a detailed interpretation of individual and interactive parameter influences.

For the first-order Sobol sensitivity indices, the parameter R_{peak original} showed a high first-order index of 0.7214, indicating it contributed the most to the output variance when considered individually. In contrast, PI_original had a much lower first-order index of 0.0459, suggesting a relatively minor direct effect. The corresponding confidence intervals were ±0.0878 for R_{peak original} and ±0.0459 for PI_original.

Regarding the total-order Sobol indices, R_{peak original} again exhibited a dominant influence with a total-order index of 0.9578, compared to 0.2815 for PI_original. This indicates that R_{peak original} not only has a strong direct effect but also plays a substantial role through interactions with other parameters. The confidence intervals were ±0.0862 and ±0.0372 for R_{peak original} and PI_original, respectively.

As for the second-order interaction effects, the interaction between PI_original and R_{peak original} yielded a Sobol index of 0.2363, with a confidence interval of ±0.0810. This suggested that there was a notable synergistic effect between the two parameters that contributes appreciably to the overall model uncertainty.

The results indicated that R_{peak original} was the dominant influencing factor, contributing the mostly to both the first order and total variance. A strong interaction effect was also observed between the two input variables.

3.4 Problem 4: renewable energy impact expansion

3.4.1 Investigation on renewable energy

3.4.1.1 The impact of increasing proportion of renewable energy

This study selected three representative countries with high HPC deployment and substantial carbon emissions: the United States, China, and Germany (24). In the analysis, the proportion of renewable energy was used as the independent variable (x), while carbon emissions served as the dependent variable (y). Our study plotted data points of carbon emissions against renewable energy share, including the theoretical endpoint (100%, 0), which represents a fully renewable scenario with zero emissions (25). After testing several regression functions, this study founded that an inverse function provided the best fits for the data points (26, 27), capturing the non-linear relationship between increasing renewable energy usage and corresponding carbon emissions reduction. The regression for these three countries was shown in Figure 8.

Figure 8

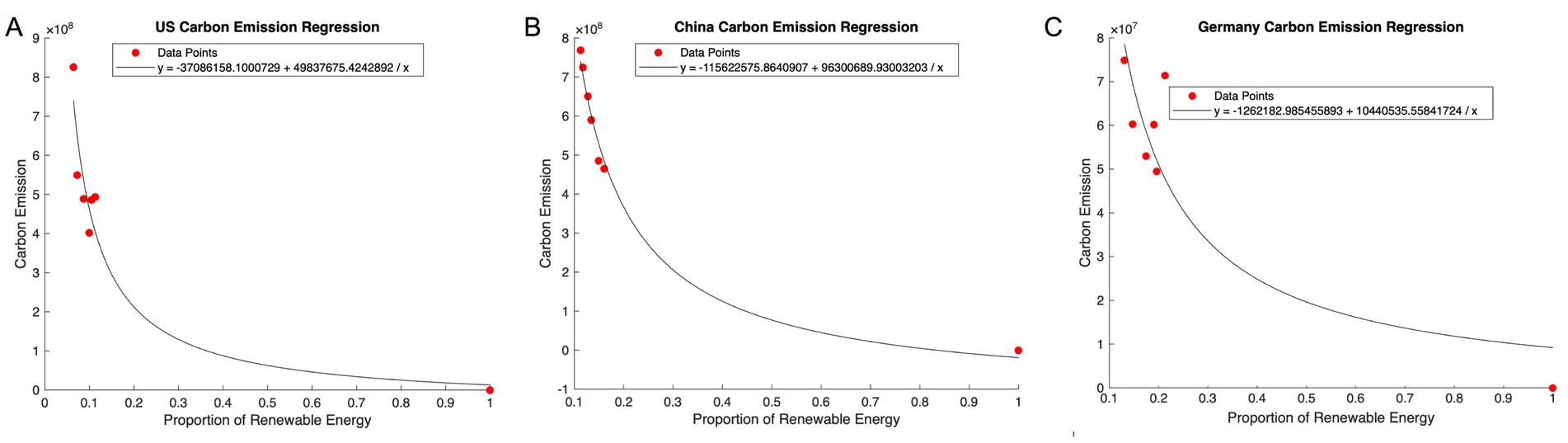
Figure 8. Regression graph of carbon emission of three typical countries. (A) Displays regression graph of carbon emission of US. (B) Displays regression graph of carbon emission of China. (C) Displays regression graph of carbon emission of Germany.

Regression function for US carbon emission:

$\begin{array}{ll}\widehat{y}=-3.709\times {10}^7+\frac{4.984\times {10}^7}{x},R^2=0.904& (28)\end{array}$

Regression function for China carbon emission:

$\begin{array}{ll}\widehat{y}=-1.156\times {10}^8+\frac{9.630\times {10}^7}{x},R^2=0.99& (29)\end{array}$

Regression function for Germany carbon emission:

$\begin{array}{ll}\widehat{y}=-1.262\times {10}^6+\frac{1.044\times {10}^7}{x},R^2=0.779& (30)\end{array}$

Anchored in the fact that renewable energy still generates carbon emission in the production, transportation, and instillation process, we utilized the model which has horizontal asymptote, thereby more realistic and reasonable assessing carbon emissions changes (28).

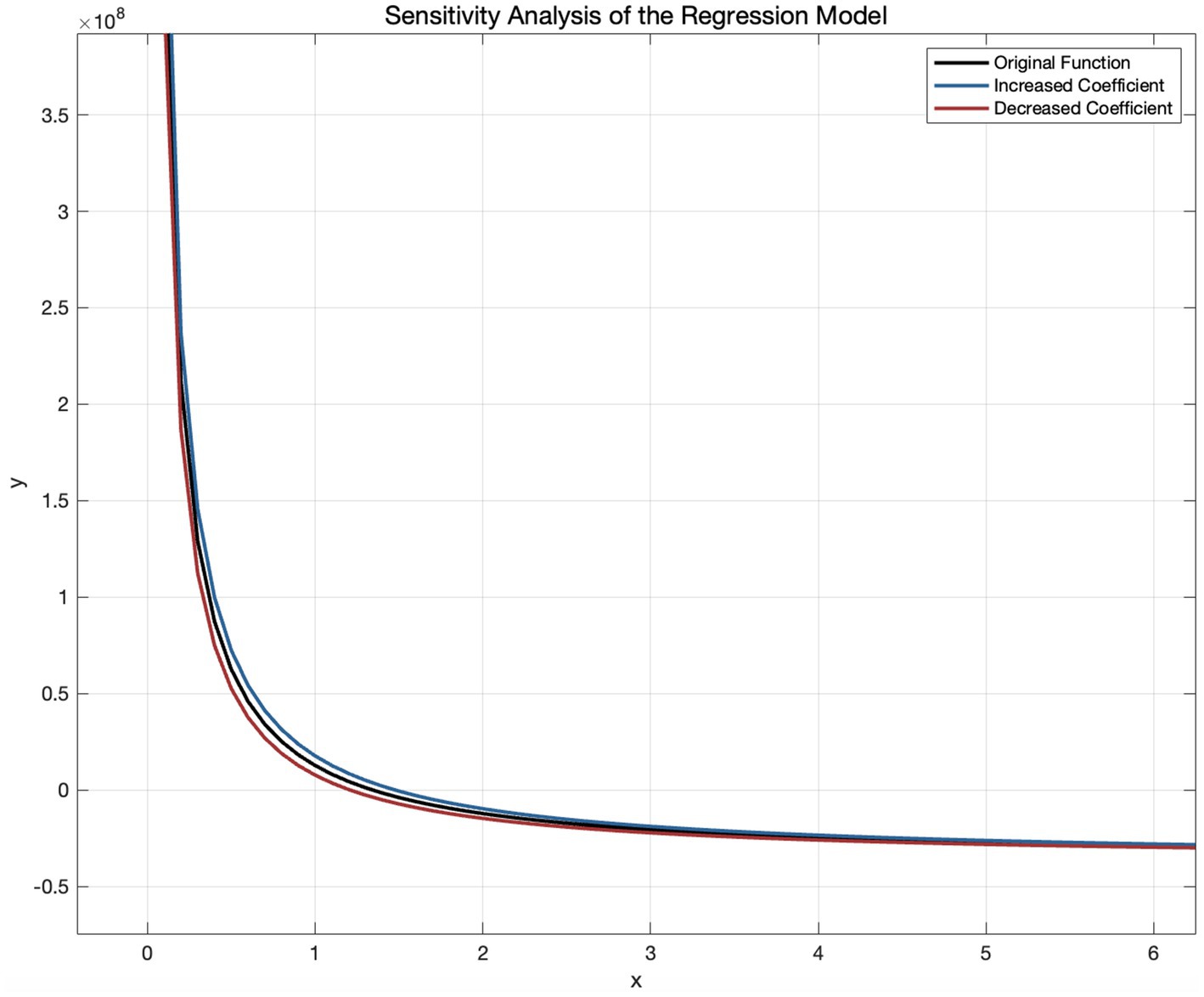
3.4.1.2 Sensitivity analysis

This study conducted a sensitivity analysis of the inverse regression models (see Figure 9). Using the U.S. model as an example, this study varied the coefficient by ±10%, resulting in a = 4.984 × 10⁷ ± 4.984 × 10⁶. Setting x = 0.2, the baseline result was 2.1211 × 10⁸. After changing a₀ or a₁ by 10%, the result was 2.3703 × 10⁸ or 1.8719 × 10⁸, which only changed by 11.75%, this means that our model was relatively stable and insensitive to abnormal data.

Figure 9

Figure 9. Sensitivity analysis.

3.4.2 The impact of HPC on the other major field

3.4.2.1 Further study about HPC gas emission

Beyond carbon emissions, HPC systems contributed to environmental degradation through the release of other pollutants. This model incorporated key pollutants such as sulfur dioxide (SO₂), nitrogen oxides (NO^x), carbon monoxide (CO), and particulate matter (PM₁₀), based on established emission guidelines.

This study considered three primary fuel types—coal, oil, and natural gas—in our calculations. The energy derived from each fuel type (E_fuel,i) was computed as:

$\begin{array}{ll}{E}_{\text{fuel},i}=p_i·E{C}_{\text{total}}& (31)\end{array}$

Then, the corresponding mass or volume was calculated as:

$\begin{array}{ll}{M}_{\text{fuel},i}=\frac{E_{\text{fuel},i}}{{\text{HeatingValue}}_i}& (32)\end{array}$

$\begin{array}{ll}{V}_{\text{fuel},i}=\frac{M_{\text{fuel},i}}{{\text{Density}}_i}& (33)\end{array}$

Pollutant emissions were then computed using:

$\begin{array}{ll}{m}_{\text{pollutant},i}=M_{\text{fuel},i}\times f_{\text{pollutant},i}& (34)\end{array}$

Or

$\begin{array}{ll}{m}_{\text{pollutant},i}=V_{\text{fuel},i}\times f_{\text{pollutant},i}& (35)\end{array}$

Thus, the comprehensive formulas for emissions become:

$\begin{array}{ll}{m}_{\text{pollutant},i}=\left(\frac{E_{\text{fuel},i}}{{\text{Heating Value}}_i}\right)\times f_{\text{pollutant},i}\left(\text{for mass}\right)& (36)\end{array}$

Or

$\begin{array}{ll}{m}_{\text{pollutant},i}=\left(\frac{E_{\text{fuel},i}}{{\text{Heating Value}}_i·{\text{Density}}_i}\right)\times f_{\text{pollutant},i}\left(\text{for volume}\right)& (37)\end{array}$

This process allowed for the accurate calculation of emissions based on the characteristics of each fuel type utilized in HPC. The following was the diagram that reveal the harmful gases emission data (see Figure 10A):

Figure 10

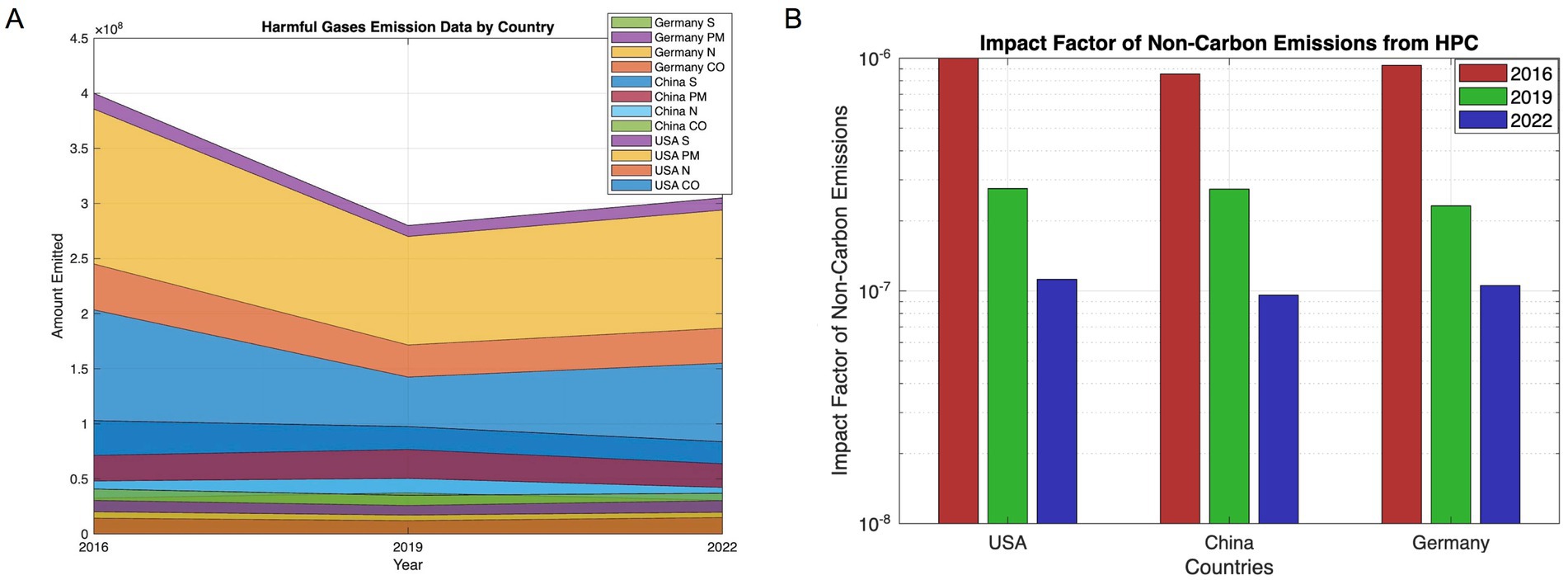
Figure 10. Harmful gases by country. (A) Displays harmful gases emission data by country. (B) Displays harmful gases impact index by country varied from years.

In addition, to directly calculate the environmental impact of emissions from different fuels used in HPC, this study multiplied the emissions of each pollutant by its unit impact index on human health and then sum these values to obtain the total HPC impact index. This could be expressed mathematically as:

$\begin{array}{ll}{I}_{\mathrm{HPC}}=\left(\sum ^{j\in \mathit{PM}10,\mathit{CO},S{O}_2,N{O}_2}\frac{m_{\text{pollutant},j}}{C_{max,j}}\right)·\frac{1}{4.68\times {10}^{20}{\mathrm{m}}^3}& (38)\end{array}$

Here, c_max was the maximum concentration of that gas that people could survive, and 4.68 × 10²⁰ m³ was the total volume of the atmosphere.

The graphs showed each impact index of different countries in each year (see Figure 10B):

3.5 Problem 5: solutions and advocacy

Fuzzy evaluation was employed to assess multiple factors, including feasibility, cost, environmental impact, policy support, sustainability, and risk, based on a comprehensive membership vector S (29, 30). Recommendations were categorized into technological and policy options. The fuzzy evaluation method was applied to four solution categories—energy efficiency optimization, renewable energy integration, waste heat recovery systems, and environmental monitoring and reporting—to identify the optimal approach through multi-criteria scoring (14, 31, 32).

3.5.1 Fuzzy decision

The followings were the basic model of Fuzzy Decision, the detailed model was in Supplementary Table 3.

3.5.1.1 Fuzzy decision matrices

1. Energy Efficiency Optimization

2. $\left[\begin{array}{cccc}{\tilde{a}}_{11}& {\tilde{a}}_{12}& \cdots & {\tilde{a}}_{1n}\\ {\tilde{a}}_{21}& {\tilde{a}}_{22}& \cdots & {\tilde{a}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{a}}_{m1}& {\tilde{a}}_{m2}& \cdots & {\tilde{a}}_{\mathit{mn}}\end{array}\right]$

3. Renewable Energy Integration

4. $\left[\begin{array}{cccc}{\tilde{b}}_{11}& {\tilde{b}}_{12}& \cdots & {\tilde{b}}_{1n}\\ {\tilde{b}}_{21}& {\tilde{b}}_{22}& \cdots & {\tilde{b}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{b}}_{m1}& {\tilde{b}}_{m2}& \cdots & {\tilde{b}}_{\mathit{mn}}\end{array}\right]$

5. Waste Heat Recovery System

6. $\left[\begin{array}{cccc}{\tilde{c}}_{11}& {\tilde{c}}_{12}& \cdots & {\tilde{c}}_{1n}\\ {\tilde{c}}_{21}& {\tilde{c}}_{22}& \cdots & {\tilde{c}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{c}}_{m1}& {\tilde{c}}_{m2}& \cdots & {\tilde{c}}_{\mathit{mn}}\end{array}\right]$

7. Environmental Monitoring and Reporting

8. $\left[\begin{array}{cccc}{\tilde{d}}_{11}& {\tilde{d}}_{12}& \cdots & {\tilde{d}}_{1n}\\ {\tilde{d}}_{21}& {\tilde{d}}_{22}& \cdots & {\tilde{d}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{d}}_{m1}& {\tilde{d}}_{m2}& \cdots & {\tilde{d}}_{\mathit{mn}}\end{array}\right]$

Equations below were collectively followed to evaluate both technology and government factors and calculate the score:

$\begin{array}{ll}{S}_1=\sum _{k=1}^m\left(\sum _{i=1}^n{\omega }_i{\mu }_{\mathit{ik}}\right){\nu }_k& (39)\end{array}$

Shown equation above, the total score S was computed by calculating the integrated membership vector for each score level k as follows:

$\begin{array}{ll}{M}_k=\sum {\omega }_i·{\mu }_{\mathit{ik}}& (40)\end{array}$

Where w_i was the factor weights and μ_ik was the corresponding membership degrees. The total score was then obtained by summing the products of these integrated membership vectors and their associated scores v_k. The weight μ_ik was determined using the Analytic Hierarchy Process (AHP) to conduct a comprehensive evaluation from multiple perspectives (the specific AHP procedure was presented in a later section).

$\begin{array}{ll}S=\sum M_k·{\upsilon }_k& (41)\end{array}$

The following was the dual weight method equation:

$\begin{array}{ll}{S}_2=\sum _{k=1}^m\left(\sum _{i=1}^n{\omega }_i{\mu }_{\mathit{ik}}\right)\frac{{\upsilon }_k}{{\sum }_{j=1}^m{\upsilon }_j}& (42)\end{array}$

The dual weight method above normalized each score v_k by the total sum $\sum _{j=1}^m{\upsilon }_j$ . The integrated membership vector for each level k was computed similarly, leading to the final score S:

$\begin{array}{ll}S=\sum M_k·\frac{{\nu }_k}{{\sum }_{j=1}^m{\upsilon }_j}& (43)\end{array}$

3.5.2 Analytic hierarchy process for weight calculation

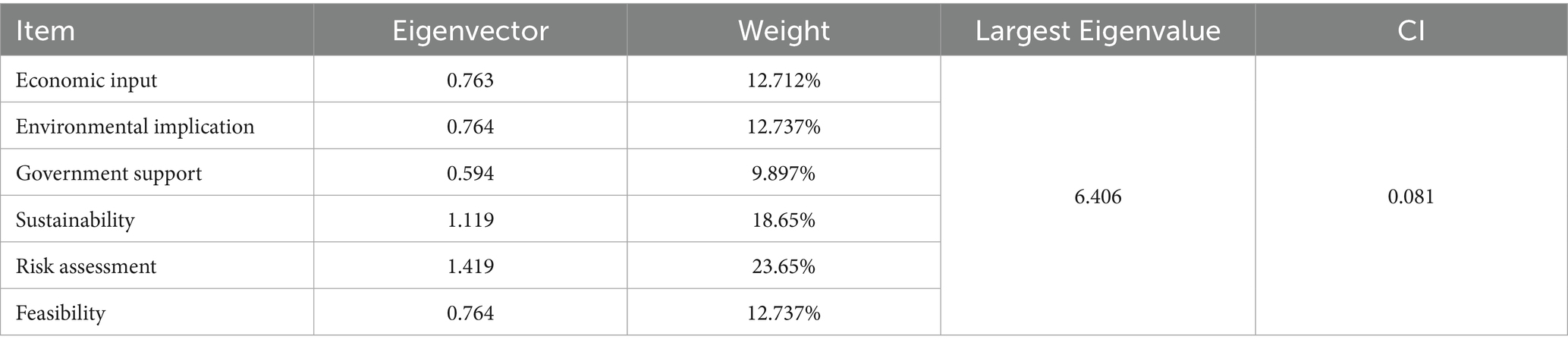
Subsequently, the AHP was utilized to determine the weight of each evaluation criterion. The consistency index was calculated to ensure that the results met the required threshold (see Table 2).

Table 2

Table 2. AHP results.

The table presented the AHP results, which systematically derived the relative weights of evaluation criteria through pairwise comparisons. The weight distribution demonstrated that risk assessment carried the highest priority (23.65%), followed by environmental impact (22.355%) and sustainability (18.65%), while feasibility (12.737%), economic investment (12.712%), and policy support (9.897%) constituted relatively lower weights in the decision framework.

The procedure began with the construction of a judgment matrix A, where each element a_ij represented the relative importance of factor a_i compared to a_j, thus forming a subjective evaluation matrix.

$A=\left[\begin{array}{cccc}{\tilde{a}}_{11}& {\tilde{a}}_{12}& \cdots & {\tilde{a}}_{1n}\\ {\tilde{a}}_{21}& {\tilde{a}}_{22}& \cdots & {\tilde{a}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{a}}_{m1}& {\tilde{a}}_{m2}& \cdots & {\tilde{a}}_{\mathit{mn}}\end{array}\right]$

Then, when determining the weights of each indicator, this study adopted the square root method to calculate the eigenvector.

The specific steps were as follows: First, this paper computed the geometric mean of each row in the judgment matrix to derive the initial weights. Next, these values were normalized to obtain the relative weights (eigenvector), followed by a consistency check to ensure the reliability of the results.

This approach ensured an objective and systematic determination of the weights for each factor in the AHP model.

$\begin{array}{ll}{w}_i^{\ast }=\sqrt[n]{\prod _{j=1}^n{a}_{\mathit{ij}}},i=1,2,\dots ,n& (44)\end{array}$

Then, normalized the weight vector.

$\begin{array}{ll}{w}_i=\frac{w_i^{\ast }}{{\sum }_{k=1}^n{w}_k^{\ast }},i=1,2,\dots ,n& (45)\end{array}$

The final weight vector:

$\begin{array}{ll}W={[w_1,w_2,\dots ,w_n]}^T& (46)\end{array}$

Next, a consistency check was conducted. The first step involved calculating the maximum eigenvalue (λ_max) of the judgment matrix.

$\begin{array}{ll}{\lambda }_{\max }=\frac{1}{n}\sum _{i=1}^n\frac{{\left(\mathit{AW}\right)}_i}{w_i}& (47)\end{array}$

Among them, (AW) _i was the i-th element of the product of the matrix A and the weight vector W.

Then the consistency index CI and the consistency ratio CR were calculated.

$\begin{array}{ll}\mathit{CI}=\frac{{\lambda }_{\max }-n}{n-1}& (48)\end{array}$

$\begin{array}{ll}\mathit{CR}=\frac{\mathit{CI}}{\mathit{RI}}& (49)\end{array}$

Here, RI was the random consistency index, obtained by looking up the table. If CR < 0.1, the matrix passed the consistency test; otherwise, the judgment matrix needed to be adjusted.

The consistency validation confirmed the reliability of these judgments, with the maximum eigenvalue (λ_max) calculated as 6.406. Using the standard random consistency index (RI) of 1.25 for the matrix dimension, the consistency ratio (CR = CI/RI = 0.065) satisfied the acceptable threshold (CR < 0.1), thereby validating the consistency of the pairwise comparison matrix. This mathematical verification ensured the logical coherence of the expert judgments in the AHP implementation.

3.5.3 Final score calculation

Finally, weights for the scores of t technologies and policy were evaluated to obtain the final total plan score. The formula for the final total scores, considering the political and technology policy score, was:

$\begin{array}{ll}{S}_k=\alpha S_1+\beta S_2& (50)\end{array}$

Since this study considered both policies to be equally important, we simply added their scores together and divided by two.

Finally, we calculated both Double-Weight Method Scores and Total Score Method Scores for each policy and method. First, the Double-Weight Method Scores for the eight policies—including the use of low-power processors and GPUs, establishment of energy efficiency standards for HPC centers, installation of solar panels or wind turbines, encouragement of HPC centers to invest in renewable energy infrastructure, design of waste heat recovery systems, regulated recovery and utilization of waste heat, and establishment of an environmental monitoring system to track energy consumption and emissions in real time—were 0.172, 0.172, 0.162, 0.164, 0.161, 0.173, 0.162, and 0.159, respectively. The corresponding Total Score Method Scores were 58.553, 58.512, 54.973, 55.829, 54.659, 58.819, 55.122, and 54.079.

The final Double-Weight Method Scores for the methods—including Energy Efficiency Optimization, Renewable Energy Integration, Waste Heat Recovery System, and Environmental Monitoring and Reporting—after incorporating both political and technological policies were 0.1722, 0.1630, 0.1670, and 0.1606, respectively. The final Total Score Method Scores for these methods were 58.5329, 55.4015, 56.7392, and 54.6009.

In conclusion, based on both the data and the graph, the Energy Efficiency Optimization scheme achieved higher scores in both evaluation systems. Therefore, Energy Efficiency Optimization was highly recommended.

3.5.4 Incorporation of recommended scheme in the model

To incorporate energy efficiency schemes into our model and optimize its performance, this study first collected energy efficiency data from 2016 to 2023 based on the Top500 HPC rankings (6, 7). It was assumed that the energy efficiency (EE) of HPC systems improved over time at a natural rate, influenced by the current state of efficiency and technological constraints. To evaluate the effectiveness of incentive mechanisms in improving energy efficiency and reducing energy consumption, this study first constructed a dynamic model based on differential equations to describe the temporal evolution of energy efficiency (EE). A logistic growth model was employed to represent the natural progression of technology:

$\begin{array}{ll}\frac{\mathit{dE}{E}_{\mathrm{old}}}{\mathit{dt}}=b·E{E}_{\mathrm{old}}(1-\frac{E{E}_{\mathrm{old}}}{a})& (51)\end{array}$

Here, EE_old denoted the energy efficiency (i.e., computing power per unit of energy) at a given time t in the baseline model. The parameter b represented the intrinsic growth rate, reflecting the pace of technological advancement, while a denoted the theoretical upper bound of energy efficiency. The initial condition was set as EE(0) = EE₀. This model captured the typical logistic growth behavior: rapid initial improvement, gradually slowing progress due to increasing technological difficulty, and eventual saturation as the efficiency approaches the upper limit.

Building on the policy incentive mechanism for high-efficiency HPC systems discussed in the previous section, the model was extended as follows:

$\begin{array}{ll}\frac{\mathit{dE}{E}_{\mathrm{new}}}{\mathit{dt}}=(b+\delta )·E{E}_{\mathrm{new}}(1-\frac{E{E}_{\mathrm{new}}}{a})& (52)\end{array}$

In this formulation, EE_new represents the energy efficiency under policy intervention, and $\delta$ > 0 captures the additional growth rate attributed to policy incentives. This modification allowed the efficiency to improve more rapidly and approach the upper limit an earlier.

Analytical solutions to both differential equations were derived, and the parameters were subsequently determined via least squares fitting. Based on this, a logarithmic regression model was established between EC_max and EE, in order to predict how changes in energy efficiency influence the maximum energy consumption.

Here, a denoted the maximum achievable energy efficiency, b represented the natural growth rate, and $\delta$ reflected the additional growth rate induced by policy incentives.

By solving the above differential equations analytically, this study derived the following logistic functions for EE under the two scenarios:

$\begin{array}{ll}E{E}_{\mathrm{old}}\left(t\right)=\frac{a}{1+exp(-b(t-c_{\mathrm{old}}\left)\right)}& (53)\end{array}$

$\begin{array}{ll}E{E}_{\mathrm{new}}\left(t\right)=\frac{a}{1+exp(-(b+\delta \left)\right(t-c_{\mathrm{new}}\left)\right)}& (54)\end{array}$

In these equations, c indicated the inflection point, corresponding to the time at which EE reached half of its maximum value and experienced the most rapid growth.

Based on historical data fitting, the study determined the model parameters as follows: the theoretical upper bound of energy efficiency b was 56.7134, the intrinsic growth rate b was 0.3675, and the policy-induced additional growth rate $\delta$ was 0.2325. Furthermore, the predicted saturation years for energy efficiency under the baseline and policy-intervention scenarios were c_old = 2026.4 and c_new = 2024.7, respectively. These results indicated that policy incentived accelerate the improvement of energy efficiency, leading to an earlier convergence toward the maximum achievable efficiency.

The baseline model exhibited a high goodness-of-fit with R² = 0.96286, while the incentivized model achieved a slightly lower but acceptable R² = 0.84245, still capturing the accelerated growth trend effectively. The value of $\delta =0.2325$ was selected through multiple simulations, balancing empirical fit with plausible policy impact.

Building upon the EE projection, this study further established a regression model to investigate the relationship between EE and the maximum potential energy consumption per unit time ( $E{C}_{\max }$ ). The following logarithmic regression function was obtained:

$\begin{array}{ll}E{C}_{\max }=-0.0456·log\left(\mathit{EE}\right)+0.4843& (55)\end{array}$

This model yielded a goodness-of-fit of R² = 0.7715 and presented a concave-up, decreasing trend, indicating that improvements in energy efficiency were associated with reductions in energy consumption.

To quantify the impact of the incentive mechanism, this study forecasted EE and $E{C}_{\max }$ values for the year 2025 under both baseline and incentivized scenarios. The results are presented in Table 3.

Table 3

Table 3. Projected values of energy efficiency and maximum energy consumption in 2025 (baseline vs. incentivized scenario).

As shown in Table 3, under the incentivized scenario in 2025, energy efficiency increased significantly (from 21.22 to 30.90), while the maximum energy consumption decreased (from 0.3449 to 0.3278). These findings suggested that enhancing energy efficiency through policy incentives played a critical role in mitigating energy consumption.

4 Discussion

The present study has addressed that the environmental impact of HPC and how it can be mitigated through decarbonization pathways. Our analysis of HPC centers worldwide reveals that global annual energy consumption ranges from 3.2 billion kW·h to 5.9 billion kW·h, with the United States being the largest consumer. The carbon footprint associated with HPC energy consumption was substantial, with total economic losses reaching over $2 million due to CO₂ emissions. Furthermore, our prediction models indicate that by 2030, the environmental impact of HPC was projected to grow, with total carbon emissions of approximately 1.7 billion kg at average utilization rates. Regression models for the US, China, and Germany demonstrate that as renewable energy adoption increases, carbon emissions decrease significantly. Additionally, energy efficiency optimization strategies, such as those derived from the AHP, can reduce energy consumption while maintaining sustainability.

4.1 HPC energy consumption and environmental impact

The carbon footprint calculation approach was selected based on its alignment with guidelines for sector-specific emissions accounting (8, 33). Moreover, the average energy consumption rather than peak demand was utilized to reflect real-world HPC operational conditions. In addition, the EII’s incorporation of sensitivity coefficients addressed a key limitation of conventional carbon accounting by differentiating emission sources based on their ecological harm potential. This approach was derived from established environmental risk assessment frameworks (34). The persistent high EII values for coal-dependent HPC operations underscored the importance of considering both the quantity and type of emissions in sustainability assessments.

The study of carbon emissions from HPC centers using both the EII and economic loss calculations indicated the severe environmental impacts that arise from HPC centers. Our result also emphasized the potential for reducing carbon emissions by increasing the share of renewable energy in HPC energy mixes. These cumulative $2.18 million global impact figure serves as a valuable baseline for future studies examining the economic returns of green computing initiatives.

Additionally, our model has supplemented previous research, particularly regarding energy consumption in HPC. HPC systems emitted not only carbon dioxide but also various pollutants, including sulfur compounds (e.g., sulfur dioxide), nitrogen oxides, carbon monoxide, and particulate matter (PM10). This comprehensive approach enables a thorough assessment of HPC’s environmental impact and clarifies the relationship between energy use and pollution (29, 30). Thus, accurately evaluating these emissions could provide a scientific basis for effective reduction strategies and help mitigate HPC’s carbon footprint. By examining these pollutants, we could better understand their cumulative effects on public health and the environment, guiding policymakers and industry stakeholders. As global emphasis on sustainability grows, transitioning HPC systems to cleaner, low-carbon energy sources was essential. Our model aims to support research and inform policy, promoting the sustainable development of HPC technologies while balancing technological progress with environmental protection.

4.2 Renewable energy necessity

It is important to note that an inverse regression model has quantified the relationship between renewable energy share and carbon emissions. Using 100% renewable energy to power HPC facilities might lead to significant benefits but also meet challenges. Transition to renewable sources such as solar, wind, and hydroelectric power can alleviate carbon footprint and improve energy security by reducing reliance on fossil fuels, which are significantly subject to market volatility and geopolitical tensions (35). The Verne Global data center in Iceland effectively utilizes the country’s abundant geothermal and hydroelectric resources for sustainable energy (36). However, many regions lack the necessary sunlight, wind, or geographical conditions for large-scale renewable energy utilization, which impedes global implementation of renewable energy (37, 38). Additionally, the intermittent and unpredictable nature of solar and wind energy poses challenges for the stability of power supply demanded by HPC facilities (39–41). Moreover, the transition to renewable energy can disrupt existing energy markets and economic structures, impacting jobs and industries in charge of fossil fuels. This shift requires policies to mitigate economic impacts and ensure a just transition for affected workers and communities (42).

Specifically, carbon emissions declined significantly as the renewable energy share increased, with sharper reductions observed at higher renewable levels. Therefore, the present analysis confirmed that the inverse function model maintained predictive consistency under moderate uncertainty, affirming its applicability while suggesting that further refinement through advanced sensitivity methods may enhance precision.

4.3 Policy recommendations

This investigation employed the fuzzy decision framework and AHP to evaluate the emission-reduction policies. As global attention increasingly shifted toward sustainability, transitioning HPC systems to cleaner, low-carbon energy sources has become imperative. The model in the research was designed to support ongoing research and guide policy decisions, fostering the sustainable development of HPC technologies while balancing innovation with environmental stewardship.

Furthermore, AHP enabled the decomposition of complex decision problems into hierarchical structures and leveraged expert knowledge to derive weights that were transparent and theoretically justified. While the method was not without its dependence on expert inputs—which could introduce bias—its systematized logic and interpretability rendered it particularly suited to multi-criteria decision-making contexts. This article suggests that beyond technological improvements, policy interventions also played a pivotal role in shaping emission reduction trajectories, coordinating stakeholders, and establishing long-term regulatory frameworks. Therefore, which showed that these were two key policy orientations: technology-driven and politically driven approaches. The findings suggested that both dimensions exerted critical influence on the success of emission-reduction efforts in HPC. To reflect this co-dependence, the final scoring model assigned equal weights (50%) to technological and political factors, thus emphasizing their joint importance. Compared to approaches that disproportionately emphasized a single domain, this balanced weighting scheme enhanced both the comprehensiveness and stability of the overall policy evaluation framework.

In short, we could determine that the energy efficiency optimization scheme had both higher score in two evaluation system. That is to say, we highly recommended energy efficiency optimization.

4.4 Limitations and future directions

Nonetheless, this study had several limitations. First, limited by the available data, we could not find data that described all countries’ HPC facilities’ situation. Instead, we had to use model to estimate the value, which might cause deviation compared to real situation. Second, although the logistic model was theoretically sound, it might underestimate growth potential in the presence of breakthrough innovations. Moreover, factors such as the cost of efficiency improvements and the specific types or intensities of policy instruments were not explicitly modeled, potentially constraining the realism of the scenario simulations. Despite these limitations, efforts were made to mitigate their impact through parameter sensitivity analyses and model validation. The model remained parsimonious in structure while yielding reasonable forecasts and policy-relevant insights. Thus, the adopted methodology was considered acceptable and meaningful for macro-level analysis.

We suggest that partner with HPC facilities to collect real-time energy mix data, develop region-specific impact factors and integration with macroeconomic models for HPC siting optimization should be future research priorities.

5 Conclusion

In summary, this study offered a systematic analytical framework for understanding the evolution of energy efficiency and provided theoretical and empirical support for the role of policy incentives in shaping energy consumption trajectories in HPC systems. Our results provided a solid foundation for discussing the carbon-energy nexus within global computing infrastructure. These findings highlight the urgent needed for cleaner energy sources and energy-efficient HPC practices to mitigate the sector’s ecological impact and ensure a more sustainable technological future.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

GY: Conceptualization, Investigation, Methodology, Software, Visualization, Writing – original draft. ZW: Data curation, Investigation, Methodology, Validation, Writing – original draft. YX: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Writing – original draft. ZS: Conceptualization, Data curation, Writing – original draft. SC: Project administration, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2025.1595365/full#supplementary-material

References

1. Le Piane, F, Vozza, M, Baldoni, M, and Mercuri, F. Integrating high-performance computing, machine learning, data management workflows, and infrastructures for multiscale simulations and nanomaterials technologies. Beilstein J Nanotechnol. (2024) 15:1498–521. doi: 10.3762/bjnano.15.119

PubMed Abstract | Crossref Full Text | Google Scholar

2. International Energy Agency. Global energy review: CO₂ emissions in 2021. Paris: IEA Publications (2022).

Google Scholar

3. Takahashi, KI, Tatemichi, H, Tanaka, T, Nishi, S, and Kunioka, T. Environmental impact of information and communication technologies including rebound effects. IEEE International Symposium on Electronics and the Environment, in: Electronics and the environment, pp. 13–16; (2004). doi: 10.1109/ISEE.2004.1299680

Crossref Full Text | Google Scholar

4. Li, B, Samsi, S, Gadepally, V, and Tiwari, D. Toward Sustainable HPC: Carbon Footprint Estimation and Environmental Implications of HPC Systems; (2023). doi: 10.48550/arXiv.2306.13177

Crossref Full Text | Google Scholar

5. Fortune Business Insights. High performance computing (HPC) and high performance data analytics (HPDA) market size, share & industry analysis, 2024–2032; (2024). Available online at: https://www.fortunebusinessinsights.com/industry-reports/high-performance-computing-hpc-and-high-performance-data-analytics-hpda-market-100636 (Accessed May 22, 2025).

Google Scholar

6. TOP500. TOP500 Lists (2014–2024). (2024). Available online at: https://www.top500.org/lists/ (Accessed May 22, 2025).

Google Scholar

7. Angelelli, L, Carastan-Santos, D, and Dutot, PF. Run your HPC jobs in Eco-Mode: revealing the potential of user-assisted power capping in supercomputing systems. arXiv (2024). arXiv:2404.03271. doi: 10.48550/arXiv.2404.03271

Crossref Full Text | Google Scholar

8. IPCC. AR6 Synthesis Report: Climate Change 2023 (2023). Available online at: https://www.ipcc.ch/report/sixth-assessment-report-cycle/ (Accessed May 22, 2025).

Google Scholar

9. Sha, C, Zhang, J, An, L, Zhang, Y, Wang, Z, Ilijaš, T, et al. Facilitating HPC operation and administration via cloud. Supercomput Front Innov. (2019) 6:23–35. doi: 10.14529/js190105

Crossref Full Text | Google Scholar

10. Zhang, F, and Chen, L. HPC-oriented power evaluation method. IEEE 2015 44th International Conference on Parallel Processing Workshops, 203–212; (2015). doi: 10.1109/ICPPW.2015.30

Crossref Full Text | Google Scholar

11. Borghesi, A, Bartolini, A, Lombardi, M, Milano, M, and Benini, L. Predictive modeling for job power consumption in HPC systems. High Perform Comput. (2016) 9697:181–99. doi: 10.1007/978-3-319-41321-1_10

Crossref Full Text | Google Scholar

12. International Energy Agency (IEA). World Energy Outlook 2022; (2022). Available online at: https://www.iea.org/reports/world-energy-outlook-2022 (Accessed May 22, 2025).

Google Scholar

13. Kaspar, A, and Kunsch, A. Energy transition – insights and trends. Geomech Tunn. (2022) 15:703–10. doi: 10.1002/geot.202200043

Crossref Full Text | Google Scholar

14. Al Mubarak, F, Rezaee, R, and Wood, DA. Economic, societal, and environmental impacts of available energy sources: a review. Acad J. (2024) 5:1232–65. doi: 10.3390/eng5030067

PubMed Abstract | Crossref Full Text | Google Scholar

15. Theis, TN, and Wong, HSP. The end of Moore's law: a new beginning for information technology. Comput Sci Eng. (2017) 19:41–50. doi: 10.1109/MCSE.2017.29

Crossref Full Text | Google Scholar

16. Statista. Global energy commodity price index 2013-2025 (2024a). Available online at: https://www.statista.com/statistics/252795/weighted-price-index-of-energy/ (Accessed May 22, 2025).

Google Scholar

17. Statista. Energy consumption worldwide from 2000 to 2022, with a forecast until 2050, by energy source (2024b). Available online at: https://www.statista.com/statistics/222066/projected-global-energy-consumption-by-source/ (Accessed May 22, 2025).

Google Scholar

18. Parker, M. A global database for energy consumer price indices. Energy Econ. (2024) 136:107645. doi: 10.1016/j.eneco.2024.107645

PubMed Abstract | Crossref Full Text | Google Scholar

19. Foell, WK. A two-century analysis of household energy transitions in Europe and the United States: From the Swiss Alps to Wisconsin. Energy Res Soc Sci. (2019) 54:96–112. doi: 10.1016/j.erss.2019.03.009

Crossref Full Text | Google Scholar

20. BP p.l.c, Statistical Review of World Energy; London (2013). Available online at: https://www.bp.com/de_de/germany/home/presse/energie-analysen/statistical-review.html (Accessed May 22, 2025).

Google Scholar

21. BP p.l.c. Statistical Review of World Energy; London (2016). Available online at: https://www.bp.com/de_de/germany/home/presse/energie-analysen/statistical-review.html (Accessed May 22, 2025).

Google Scholar

22. BP p.l.c. Statistical Review of World Energy; London (2019). Available online at: https://www.bp.com/de_de/germany/home/presse/energie-analysen/statistical-review.html (Accessed May 22, 2025).

Google Scholar

23. BP p.l.c. Statistical Review of World Energy; London (2022). Available online at: https://www.bp.com/de_de/germany/home/presse/energie-analysen/statistical-review.html (Accessed May 22, 2025).

Google Scholar

24. Yeom, JM, Deo, RC, Adamwoski, JF, Chae, T, Kim, DS, Han, KS, et al. Exploring solar and wind energy resources in North Korea with COMS MI geostationary satellite data coupled with numerical weather prediction reanalysis variables. Renew Sust Energ Rev. (2020) 119:109519:109570. doi: 10.1016/j.rser.2019.109570

Crossref Full Text | Google Scholar

25. Niemeijer, R, and Buijs, P. A greener last mile: Analyzing the carbon emission impact of pickup points in last-mile parcel delivery. Renew Sust Energ Rev. (2023) 10:1–11. doi: 10.1016/j.rser.2023.113630

Crossref Full Text | Google Scholar

26. Wang, LP. Research on the dynamic relationship between China’s renewable energy consumption and carbon emissions based on ARDL model. Resour Policy. (2022) 77:102764. doi: 10.1016/j.resourpol.2022.102764

Crossref Full Text | Google Scholar

27. Huang, WP, Ortiz, GGR, Kuo, YL, Maneengam, A, Nassani, AA, and Haff, M. The non-linear impact of renewable energy and trade on consumption-based carbon emissions. Energy. (2022) 324:124423. doi: 10.1016/j.fuel.2022.124423

PubMed Abstract | Crossref Full Text | Google Scholar

28. Nugent, D, and Sovacool, BK. Assessing the lifecycle greenhouse gas emissions from solar PV and wind energy: A critical meta-survey. Energy Policy. (2014) 65:229–44. doi: 10.1016/j.enpol.2013.10.048

Crossref Full Text | Google Scholar

29. de Oliveira Castro, P. Some thoughts on the environmental impact of High Performance Computing; (2022). Available online at: https://sifflez.org/publications/environment-hpc/ (Accessed May 22, 2025).

Google Scholar

30. Masciari, E, and Napolitano, EV. The environmental cost of high performance computing system simulation. 32nd Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP); (2024): 289–292. doi: 10.1109/PDP62718.2024.00048

Crossref Full Text | Google Scholar

31. Lee, S, and Makhmudov, M. Decision making for the intuitionistic fuzzy score function with the KL-divergence on multi-criteria. Intelligent and Fuzzy Systems, Infus 2024 Conference, Vol. 1; (2024) 1088: 567–574. doi: 10.1007/978-3-031-70018-7_63

Crossref Full Text | Google Scholar

32. Yang, YF, Chen, HY, Chen, YH, Ho, SP, Wang, CS, and Lin, CF. Refining environmental sustainability governance reports through fuzzy systems evaluation and scoring. Sustainability. (2024) 16:7227. doi: 10.3390/su16167227

Crossref Full Text | Google Scholar

33. IPCC. AR5 Climate Change 2014: Mitigation of Climate Change; (2014). Available online at: https://www.ipcc.ch/report/ar5/wg3/ (Accessed May 22, 2025).

Google Scholar

34. Baudrot, V, and Charles, S. Recommendations to address uncertainties in environmental risk assessment using toxicokinetic-toxicodynamic models. Sci Rep. (2019) 9:11432. doi: 10.1038/s41598-019-47698-0

PubMed Abstract | Crossref Full Text | Google Scholar

35. Silva, CA, Vilaça, R, Pereira, A, and Bessa, RJ. A review on the decarbonization of high-performance computing centers. Renew Sust Energ Rev. (2024) 189:114019. doi: 10.1016/j.rser.2023.114019

PubMed Abstract | Crossref Full Text | Google Scholar

36. Stefansson, B, Palsson, B, and Fridleifsson, GO. Iceland deep drilling project, exploration of supercritical geothermal resources. IEEE Power & Energy Society General Meeting (2008): 7. doi: 10.1109/PES.2008.4596668

Crossref Full Text | Google Scholar

37. World Bank Group. Global Photovoltaic Power Potential by Country; (2020). Available online at: https://openknowledge.worldbank.org/entities/publication/54953ca8-b949-520a-aceb-74e9e3c68833 (Accessed May 22, 2025).

Google Scholar

38. Yang, XQ, Chen, YX, Zhou, ZH, Du, YH, Wang, C, Liu, JW, et al. Enhancing photovoltaic power generation through hydrogel-based passive cooling: Theoretical model and global application potential. Appl Energy. (2024) 376:124174. doi: 10.1016/j.apenergy.2024.124174

Crossref Full Text | Google Scholar

39. International Renewable Energy Agency (IRENA). Renewable Energy and Jobs – Annual Review 2021; (2021). Available online at: https://www.irena.org/Publications/2021/Oct/Renewable-Energy-and-Jobs-Annual-Review-2021 (Accessed May 22, 2025).

Google Scholar

40. Fabra, N, Gutiérrez, E, Lacuesta, A, and Ramos, R. Do renewable energy investments create local jobs? J Public Econ. (2024) 239:105212. doi: 10.1016/j.jpubeco.2024.105212

Crossref Full Text | Google Scholar

41. Jin, GZ, and Huang, ZH. Statistical pathways to low-carbon cities: Analyzing renewable integration, energy-efficient design, and job creation. Sustain Cities Soc. (2024) 107:105429. doi: 10.1016/j.scs.2024.105429

Crossref Full Text | Google Scholar

42. Dongarra, J, Beckman, P, Moore, T, Aerts, P, Aloisio, G, Andre, JC, et al. The International Exascale Software Project Roadmap. Int J High Perform Comput Appl. (2011) 25:3–60. doi: 10.1177/1094342010391989

Crossref Full Text | Google Scholar