Discrete Anatomical Coordinates for Speech Production and Synthesis

The sounds of all languages are described by a finite set of symbols, which are extracted from the continuum of sounds produced by the vocal organ. How the discrete phonemic identity is encoded in the continuous movements producing speech remains an open question for the experimental phonology. In this work, this question is assessed by using Hall-effect transducers and magnets—mounted on the tongue, lips, and jaw—to track the kinematics of the oral tract during the vocalization of vowel-consonant-vowel structures. Using a threshold strategy, the time traces of the transducers were converted into discrete motor coordinates unambiguously associated with the vocalized phonemes. Furthermore, the signals of the transducers combined with the discretization strategy were used to drive a low-dimensional vocal model capable of synthesizing intelligible speech. The current work not only assesses a relevant inquiry of the biology of language, but also demonstrates the performance of the experimental technique to monitor the displacement of the main articulators of the vocal tract while speaking. This novel electronic device represents an economic and portable option to the standard systems used to study the vocal tract movements.

Introduction

Among all species, humans are within the very few that generate learned vocalizations and are, by far, the species producing the more advanced ones (Petkov and Jarvis, 2012). This complex process, that distinguishes us from other species, emerges as an interaction between the brain activity and the physical properties of the vocal system. This interaction implies a precise control of a set of articulators (lips, tongue, and jaw) to dynamically modify the shape of the upper vocal tract (Levelt, 1993). The output of this process is the speech wave sound, which can be discretized and represented by a finite set of symbols: the phonemes. Moreover, the phonemes across languages can be hierarchically organized in terms of articulatory features, as described by the International Phonetic Alphabet (International Phonetic Association, 1999) (IPA). On the other side of the process, at the brain level, intracranial recordings registered during speech production have showed that motor areas encode these articulatory features (Bouchard et al., 2013). Thus, an important question arises: how does the continuous vocal tract movement which generates speech encode the discrete phonemic information?

During speech, the articulators modify the vocal tract configuration allowing: (i) to filter the sound produced by the oscillations of the vocal folds at the larynx (i.e., vowels) and (ii) to produce a turbulent sound source by occluding (i.e., stop consonants) or constricting (i.e., fricatives) the tract (Stevens, 2000). Previous work developed biophysical models for this process (Maeda, 1990; Story, 2013) and tested its capabilities to synthesize realistic voice (Assaneo et al., 2016). In principle, those models could have a high dimensionality, especially due to the many degrees of freedom of the tongue (Maeda, 1990). However, their dimensions ranges between 3 and 7, suggesting that a small number of experimental measurements of the vocal tract movements should be able to successfully decode speech and to feed the synthesizers.

In this study, the oral dynamics was monitored using sets of Hall-effect transducers and magnets mounted on the tongue, lips and jaw during the utterance of a corpus of syllables (including all the Spanish vowels and voiced stop consonants). By applying a threshold strategy on the signals recorded by three sensors, it was possible to decode the uttered phonemes well above chance. Moreover, the signals were used to drive an articulatory synthesizer producing intelligible speech.

From a technical point of view, this work belongs to the broad field of silent speech interfaces (Denby et al., 2010; Schultz et al., 2017). This area of research attempts to develop a device enabling speech communication even when the acoustic speech signal is degraded or absent. Such a device would serve for multiple applications, as for example: restoring speech in paralyzed or laryngectomized patients, enhancing communication under noisy environmental conditions and providing private conversations within public spaces. Despite the large amount of effort devoted to this topic during the last years, the puzzle remains unsolved. Currently, four varieties of solutions are being pursued, the difference between them being on whether the reconstruction of the speech signal is done: (i) neurophysiological measurements (Guenther et al., 2009; Brumberg et al., 2010; Toda et al., 2012); (ii) non-audible vibrations (Tran et al., 2010); (iii) the dynamic of the main articulators involved in speech (Hueber et al., 2010; Bocquelet et al., 2016; Stone and Birkholz, 2016); and from the electrical signal produced by the muscles responsible for the articulators' movements (Meltzner et al., 2011; Deng et al., 2012). The device described in the current work represents an alternative method—portable and inexpensive—embraced within the third category of solutions.

Materials and Methods

Ethics Statements

All participants signed an informed consent to participate in the experiment. The protocol was approved by the CEPI ethics committee of Hospital Italiano de Buenos Aires, qualified by ICH (FDA-USA, European Community, Japan) IRb00003580, and all methods were performed in accordance with the relevant guidelines and regulations.

Participants

Four individuals (1 female) within an age range of 29 ± 6 years and with no motor or vocal impairments participated in the recordings of anatomical and speech sound data. They were all native Spanish speakers, graduate students working at the University of Buenos Aires. Fifteen participants (9 females, age range of 27 ± 4), also native Spanish speakers participated in the audio tests.

Experimental Device for the Anatomical Recordings

Following the procedure described by Assaneo et al. (2013) 3 Hall-effect transducers (Ratiometric Linear Hall Effect Sensor ICs for High-Temperature Operation, A1323 Allegro) and 4 small biocompatible Sm-Co magnets (1–3 g) were mounted on the subject's upper vocal tract to record the displacement of the articulators (jaw, tongue, and lips; Figure 1A). The position of the elements was chosen in a way that each transducer signal was modulated by a subset of magnets (color code in Figure 1B). The upper teeth transducer signal represented an indirect measurement of aperture of the jaw, the lips transducer signal the roundness and closure of the lips and the palate transducer gave an indirect measure of the position of the tongue within the oral cavity.

FIGURE 1

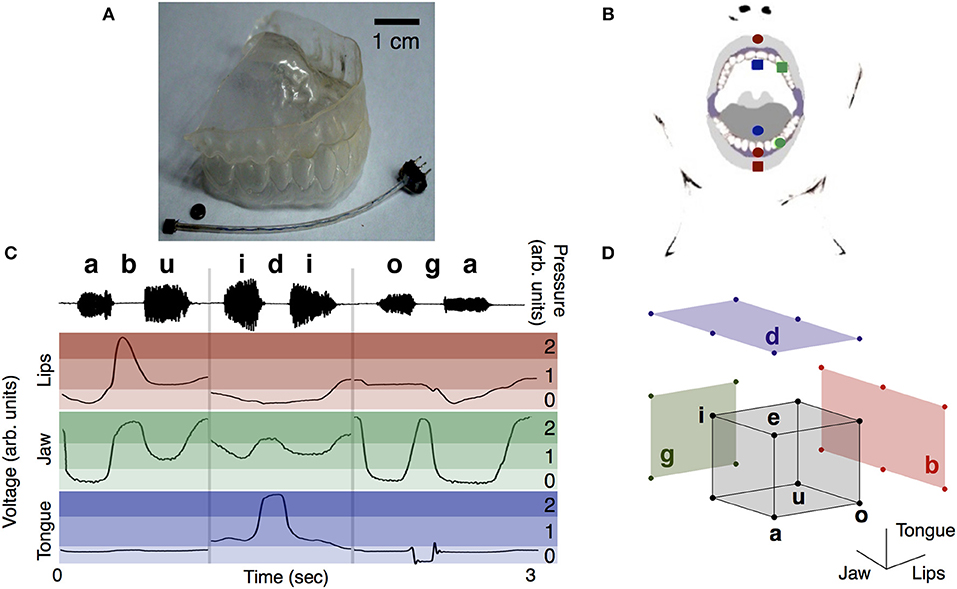
Figure 1. Discrete coordinates are extracted from the time traces of three detectors in the oral cavity. (A) The dental plastic replica with a magnet and a Hall-effect transducer. (B) Sketch of the position of the set of transducers (squares) and magnets (circles) in the oral cavity. In green the set tracking the jaw -the magnet and transducer were glued to the molds at the upper and lower left canines, respectively. In blue the set tracking the tongue -the transducer fixed to the mold at the palate and the magnet to the tip of the tongue. In red the set tracking the lips—the transducer fixed in the center of the lower lip, one magnet glued to the lower mold, between the lower central incisors, and another in the center of the upper lip. Figure adapted from Assaneo et al. (2013). (C) Discretization of the signals. Upper panel: VCV phonemes and sound wave. Lower panel: time traces of the transducers signals during the vocalizations. The intensity of the shaded regions differentiates the discrete states. (D) States of vowels and consonants in the discrete motor space. The corners of the gray cube represent the vowels and the colored walls de different consonants.

Participants wore a removable plastic dental cast of the superior and inferior dentures (1 mm thick, Figure 1A) during the experiments. Transducer and magnets were glued to the plastic molds using cyanoacrylate glue (Crazyglue, Archer, Fort Worth, TX). Denture adhesive (Fixodent Original Denture Adhesive Cream 2.4 Oz) was used to attach magnets to the tongue and medical paper tape (3M Micropore Medical Tape) to fix the transducers to the lips.

Details of the configuration of the 3 magnet-transducer sets are shown in Figure 1B.

Red, Lips

One cylindrical magnet (3.0 mm diameter and 1.5 mm height) was glued to the dental cast between the lower central incisors. Another one (5.0 mm diameter and 1.0 mm height) was fixed at the center of the upper lip. The transducer was attached at the center of the lower lip. The magnets were oriented in such a way that their magnetic field had opposite signs in the privileged axis of the transducer.

Green, Jaw

A spherical magnet (5.0 mm diameter) and the transducer were glued to the dental casts, in the space between the canine and the first premolar of the upper and lower teeth, respectively.

Blue, Tongue

A cylindrical magnet (5.0 mm diameter and 1.0 mm height) was attached at a distance of about 15 mm from the tip of the tongue. The transducer was glued to the dental plastic replica, at the hard palate, ~10 mm right over the superior teeth (sagittal plane). Transducer wire was glued to the plastic replica and routed away to allow free mouth movements.

The hall-effect transducers produce a voltage output proportional to the magnetic field along their preferred axis. Accordingly, their signals represent a combination of the distance magnet-chip and the orientation of the magnet. In the current state, this prototype operates with signals that do not represent dimensional values of the articulator's displacements. Importantly, the specifications of the selected sensors make them appropriate for the presented application (Allegro MicroSystem)¹, some of their relevant features are: (i) internal clock frequency of 150 KHz, (ii) operating ambient temperature range from −40 to 150°C, and (iii) low cost, 5 pieces cost US$ 13. It is worth noting that the particular device employed in this work is no longer available, for future experiments the A1326LUA-T could be used instead.

Recording Sessions

Four native Spanish speakers were instructed to vocalize a corpus of syllables while wearing the device. The transducer signals (h_J(t), h_T(t), and h_L(t) for the jaw, tongue, and lips, respectively) were recorded simultaneously with the produced speech. Three example of the three sensor signals and the corresponding audio signal is shown in Figure 1C. Each participant completed 3 sessions on different days during a period of 1 month. Participants, with the device mounted, sat in a silent room 20 cm away from a microphone and in front of a computer screen. They were instructed to repeat a set of vowel-consonant-vowel structures (VCVs) that were prompted on the screen starting from (and ending to) a comfortable closed mouth configuration. Each session incorporates the production of 75 VCVs strings, including the whole set of Spanish vowels (/a/, /e/, /i/, /o/, and /u/) and voiced plosive consonants (/b/, /d/, and /,g/). The VCVs strings spanned all possible combinations (i.e., for /b/ the following strings were used: /aba/, /abe/, /abi/, /abo/, /abu/, /eba/, /ebe/, /ebi/, /ebo/, /ebu/, /iba/, /ibe/, /ibi/, /ibo/, /ibu/, /oba/, /obe/, /obi/, /obo/, /obu/, /uba/, /ube/, /ubi/, /ubo/, and /ubu/).

The VCVs order was randomized for each session. The first 15 VCVs were defined as the training set. Thus, they were supervised to include the same number of each phoneme (5 /b/, 5/g/, 5 /d/, 6 samples of each vowel). The speech sounds were recorded simultaneously with the three signals of the transducers.

The consonants chosen for this study are produced by the activation of different articulators. They represent the main hierarchies used by IPA (Goldsmith et al., 2011) to categorize the consonants according to their place of articulation: /b/ labial, /d/ coronal, and dorsal /g/.

Signals' Preprocessing

Each transducer's signal was subsampled at 441 Hz and preprocessed within each session data set. The preprocessing consisted in subtracting the resting state and dividing by the maximum absolute value. The resting state value was estimated as the average of the 50 ms previous and posterior of each vocalization. This process set the signal's value between −1 and 1.

Thresholds Adjustment

A previous study showed that applying one threshold for each transducer was enough to decode the 5 Spanish vowels (Assaneo et al., 2013). Following the same strategy, an extra threshold per signal was added in order to include the stop consonants to the description. Following this rationale, fitting two thresholds allowed us to discretize the signals: a vowel threshold v, separating vowels, and a consonant threshold c, separating vowels from consonants. A visual exploration of the signals (see Figure 1C for an example) suggested the following rules to fit the thresholds:

Vowels: the lips v_L threshold divides vowels according to the roundness of the lips (above: /u/ and /o/ below: /a/ /e/ and /i/); the jaw v_J threshold differentiates close (/u/ and /i/, above) from open (/a/ /e/ and /o/, below) vowels; the tongue v_T threshold separates front vowels (/e/ and /i/, above) from back (/a/ /o/ and /u/, below) ones.

Consonants: the lips c_L threshold differentiates /b/ (above) from all other phonemes (below); the jaw c_J threshold differentiates all stop consonants from all vowels (above: /g/ /b/ and /d/, below: (/a/ /e/ /i/ /o/ and /u/); the tongue c_T threshold separates /d/ (above) from all other phonemes.

These threshold rules defined three regions as the ones shown in Figure 1C in shades of red for the lips, green for the jaw and blue for the tongue. Associating the values 0, 1, and 2 to the transducer signals falling within the light, medium, and dark value ranges; the phonemes could be represented on a discrete 3-dimensional motor space as shown in Figure 1D, were the first coordinate represented the lips state, the second the jaw and the third the tongue. Each vowel was represented by a unique vector: /a/ = (0,0,0); /e/ = (0,0,1); /i/ = (0,1,1); /o/ = (1,0,0); /u/ = (1,1,0); while the consonants had multiple representations: /b/ = (2,x,y), /d/ = (y,x,2), and /g/ = (x,2,y), where x is 0, 1, or 2, and y is 0 or 1.

The thresholds were fixed independently for each transducer signal, by choosing the value maximizing the decoding performance over the training data set, according to the rules detailed above. For example, for the tongue vocalic threshold the rule was: /e/ and /i/ above (1) and /a/ /o/ and /u/ below (0). The [-1; 1] range was discretized in 200 evenly spaced values, and each value was tested as the threshold over the tongue's signals of the complete testing data set. The value with the highest performance sorting the data according to the rule was selected as the threshold.

Mathematical Description for the Discretization Process

The transformation from continuous transducer signals to discrete values can be mathematically accomplished through saturating functions of the form: $S_m(x)=1/(1+e^{-mx})$. This function goes from zero to one in a small interval around x = 0, whose size is inversely proportional to m. Then, S_∞(h(t) − v) is zero for h(t)<v and one for h(t)>v. These are the conditions that define the binary coordinates for vowels. Using the transducer signals h_L(t), h_J(t), h_T(t), and the threshold values v_L, v_J, and v_T for the lips, jaw, and tongue, respectively, a vowel vo reads:

$\begin{array}{cc}vo=\left(\begin{array}{c}{S}_{\infty }\left(h_J\left(t\right)-{\nu }_J\right)\\ S_{\infty }\left(h_T\left(t\right)-v_T\right)\\ S_{\infty }\left(h_L\left(t\right)-v_L\right)\end{array}\right)& (1)\end{array}$

A more general approach of a sigmoid function over a step one was chosen because m-values smaller than infinity were used later in this study.

Plosive consonants represented articulatory activations reaching the dark areas of Figure 1C, assigned to the value 2. In order to include them to the description, an extra saturating function was added to each coordinate, using the consonant thresholds c_J, c_T, and c_L. Following the previous notation, phonemes p (either vowels or consonants) were represented in the discrete space directly from the transducer signals as:

$\begin{array}{cc}p=\left(\begin{array}{c}{S}_{\infty }\left(h_J\left(t\right)-v_J\right)+S_{\infty }\left(h_J\left(t\right)-c_J\right)\\ S_{\infty }\left(h_T\left(t\right)-v_T\right)+S_{\infty }\left(h_T\left(t\right)-c_T\right)\\ S_{\infty }\left(h_J\left(t\right)-v_L\right)+S_{\infty }\left(h_L\left(t\right)-c_L\right)\end{array}\right)& (2)\end{array}$

Articulatory Synthesizer

Articulatory synthesis relies on the computational simulation of the physical processes involved in the speech generation phenomenon. During the past decades, many research has focused on this topic and high quality speech signals have been achieved (Browman and Goldstein, 1990; Story and Titze, 1995; Lloyd et al., 2012; Birkholz et al., 2017). In the current study, an articulatory synthesizer was chosen because it facilitates a translation from physiological measurements to acoustic signals. The goal was to test the suitability of our electronic device to feed such a synthesizer in order to produce intelligible speech. The quality of the synthesized voice was out of the scope of this work. Thus, a simplified version of the artificial talker described by Story was implemented (Story, 2013). Specifically, the simplification consisted in replacing the realistic kinematic model of the vocal folds for a first order approximation of the glottal airflow, as proposed by Laje et al. (2001). Below, the used articulatory synthesizer is broadly described, for more detail see the previously mentioned works (Laje et al., 2001; Story, 2013).

During the production of voiced sounds, the vocal folds oscillate producing a stereotyped airflow waveform (Titze and Martin, 1998) that can be approximated by relaxation oscillations (Laje et al., 2001) such as that produced by a van der Pol system:

$\begin{array}{cc}\{\begin{array}{c}\frac{du}{dt}=55f_0\left(v-\frac{u^3}{3}+u\right)\\ \frac{dv}{dt}=11\frac{f_0}{5}\left(u-a\right)\end{array}& (3)\end{array}$

The glottal airflow is the variable u for u > 0, and u = 0 else. The fundamental frequency of the glottal flow is f ₀ (Hz) and the oscillations' onset is attained for a > −1.

The pressure perturbations produced by the injection of airflow at the entrance of the tract propagate along the vocal tract. The propagation of sound waves in a pipe of variable cross section A(x) follows a partial differential equation (Landau and Lifshitz, 1987). Approximations have been proposed to replace this equation by a series of coupled ordinary differential equations, as the wave-reflection model (Liljencrants, 1985; Story, 1995; Murphy et al., 2007) and the transmission line analog (Flanagan, 2013). Those models approximate the pipe as a concatenation of N = 44 tubes of fixed cross-section A_i and length l_i. In the transmission line analog, the sound propagation along each tube follows the same equations as the circuit shown in Figure 2, where the current plays the role of the airflow u and the voltage the role of sound pressure p. The flows u₁, u₂, and u₃ along the meshes displayed in Figure 2, follow the set of equations:

$\begin{array}{cc}\{\begin{array}{l}{\ddot{u}}_{1i}={\ddot{u}}_{3(i-1)}+\frac{G_{i-1}}{C_i}({\dot{u}}_{2i}-{\dot{u}}_{1i})\hfill \\ {\ddot{u}}_{2i}=\frac{1}{L_i+L{w}_i}[{\ddot{u}}_{3i}L{w}_i+\frac{u_{1i}-u_{1i}}{C_i}+\frac{u_{3i}-u_{2i}}{C{w}_i}+({\dot{u}}_{3i}-{\dot{u}}_{2i})R{w}_i-{\dot{u}}_{2i}{R}_i]\hfill \\ {\ddot{u}}_{3i}={\ddot{u}}_{2i}+\frac{1}{L{w}_i}[\frac{u_{2i}-u_{3i}}{C{w}_i}+({\dot{u}}_{2i}-{\dot{u}}_{3i})R{w}_i+\frac{u_{1(i+1)}-u_{3i}}{G_i}]\hfill \end{array}& (4)\end{array}$

FIGURE 2

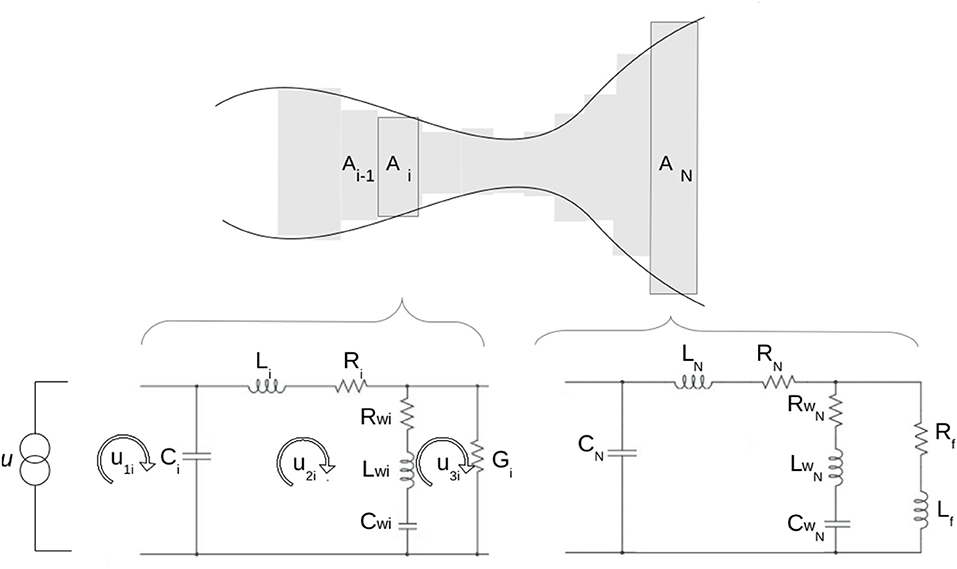
Figure 2. Articulatory synthesizer. Sketch of the model used for the vocal system. The glottal airflow (u) is obtained by solving a Van del Pol system (Laje et al., 2001). The vocal tract is approximated by a concatenation of N = 44 tubes of different cross-sectional areas A_i and lengths l_i. The lower panels show the equivalent electrical transmission line used to simulate the propagation of the sound along the ith and the last tube (N), respectively.

The components L_i, C_i, R_i, and G_i represent the acoustic inheritance, the air compressibility, the power dissipated in viscous friction and the heat conduction at the tube wall, respectively. The components marked with w account for the vibration of the walls of the tract and the mesh for the last tube (i = N) includes elements (R_f and L_f) that account for the mouth radiation. For a complete description of the model and the numerical parameters (see Flanagan, 2013).

Speech was synthesized using the glottal airflow u as input for the first circuit i = 1 (Figure 2), which represents the entrance to the tract. Then, the propagation of the sound along the vocal tract was modeled through N sets of Equation (4).

Importantly, L_i, C_i, R_i, and G_i are functions of the cross-section and length of the i-th tube. More precisely: $L_i=\frac{\rho }{A_i},C_i=\frac{A_i}{\rho c^2},R_i=\frac{S}{A^2}\sqrt{\frac{\text{ωρμ}}{2}}and{G}_i=S\frac{\eta -1}{\rho c^2}\sqrt{\frac{\text{λω}}{2c_p\rho }}$; where A and S are the cross section and the circumference of the i-th tube, respectively, ρ is the air density, c the sound velocity, μ the viscosity coefficient, λ the coefficient of heat conduction, η the adiabatic constant, c_p is the specific heat of air at constant pressure and ω is the sound frequency. Thus, the vocal tract shape is required in order to solve the set of equations defining the flow.

Discrete States to Vocal Tract Anatomies

The shape of the vocal tract can be mathematically described by its cross-sectional area A(x) at distance x from the glottal exit to the mouth. Moreover, previous works (Story, 1995; Story and Titze, 1996; Story et al., 1996) developed a representation in which the vocal tract shape A(x) for any vowel and plosive consonant can be expressed as:

$\begin{array}{cc}A\left(x\right)=\frac{\pi }{4}{\left[\text{Ω}\left(x\right)+q_1{\phi }_1(x)+q_2{\phi }_2(x)\right]}^2\left[1-w_c{e}^{-\ln (16){\left[(x-x_c)/r_c\right]}^2}\right]& (5)\end{array}$

The first factor in square brackets represents the shape of the vocal tract for vowels, the vowel substrate. The function Ω(x) is the neutral vocal tract, and the functions ϕ₁(x) and ϕ₂(x) are the first empirical modes of an orthogonal decomposition calculated over a corpus of MRI anatomical data for vowels (Story et al., 1996). The shape of the vowels is determined by fixing just two coefficients, q₁ and q₂ (Story and Titze, 1996). The second factor represents the consonant occlusion. It takes the value 1 except for an interval of width r_c around the point x = x_c, where it smoothly decreases to 1-w_c and therefore represents a local constriction in the vocal tract, active during a plosive consonant. Thus, x_c and r_c define the place and the length of the occlusion, respectively, and confer the identity to the consonant. The parameter w_c goes to one during the consonant occlusion and stays in zero in other case.

This description of the anatomy of the vocal tract fits well with our discrete representation. A previous study (Assaneo et al., 2013) showed that a simple map connects the discrete space and the morphology of the vocal tract for vowels. It is carried out by a simple affine transformation defined by:

$\begin{array}{cc}\left(\begin{array}{ccc}-2& -4& -5.5\\ -3& -1& 2\end{array}\right)\left(\begin{array}{c}{S}_{\infty }\left(h_L\left(t\right)-v_L\right)\\ S_{\infty }\left(h_J\left(t\right)-v_J\right)\\ S_{\infty }\left(h_T\left(t\right)-v_T\right)\end{array}\right)+\left(\begin{array}{c}4\\ 1\end{array}\right)=\left(\begin{array}{c}{q}_1(t)\\ q_2(t)\end{array}\right)(6)& (6)\end{array}$

The numerical values of the transformation were phenomenologically found to correctly map the discrete states to the vowel coefficients q₁ and q₂. Together, Equations (5, 6) allowed the reconstruction of the vocal tract shape of the different vowels from the transducer signals.

During plosive consonants, the vocal tract was occluded at different locations. In our description, this corresponded to have a value 2 in one or more coordinates, which means that the transducers signal crosses the consonant threshold c. The saturating functions with the consonant threshold were used to control the parameter w_c of Equation (5) that controls the constriction. More specifically, the following equations were used to generate the consonants:

$\begin{array}{cc}\begin{array}{c}{w}_c\left(t\right)=S_m\left(h_L\left(t\right)-c_L\right),x_c=44,r_c=4for/b/\\ w_c\left(t\right)=S_m\left(h_T\left(t\right)-c_T\right),x_c=39,r_c=6for/d/\\ w_c\left(t\right)=S_m\left(h_J\left(t\right)-c_J\right),x_c=29,r_c=10for/g/\end{array}& (7)\end{array}$

The parameters x_c and r_c are in units of a vocal tract segmented in 44 parts, starting from the vocal tract entrance (x_c = 1) to the mouth (x_c = 44). The values were fixed according to a previous work (Story, 2005), in which they were optimized to minimize the squared difference between the area functions generated by the model and the corresponding MRI anatomical data. More precisely, we adopted the values reported for the unvoiced version of each consonant (i.e., the values reported for /p/, /t/, /k/ were selected for /b/, /d/, /g/, respectively).

This completed the path that goes from discretized transducer signals h_J(t), h_T(t), and h_L(t) to the shape of the vocal tract A(x,t) for vowels and plosive consonants.

Vocal Tract Dynamics Driven by Transducers' Data

To produce continuous changes in a virtual vocal tract controlled by the transducers, it was necessary to replace the step functions of Equations (6, 7) by smooth transitions from 0 to 1. Therefore, the condition m = ∞ was replaced by finite steepness values m₁, m₂ and m₃. The values used to synthesize continuous speech were m₁ = 300, m₂ = 300, and m₃ = 900 for lips, tongue, and jaw, respectively. These numerical values were manually fixed with the following constrain: applying Equation (6) over the recorded signals during the stable part of the vowels, and using the obtained (q₁, q₂) to synthesize speech should produce recognizable vowels. This process is explained below.

First, the mean values of the transducer signals during the production of vowels for one participant were computed (left panel Figure 3). More precisely, just the set of corrected decoded vowels for subject 1, using the intersession threshold, were selected. Second, different exploratory sets of (m₁,m₂,m₃) were used to calculate the corresponding (q₁, q₂) , by means of Equation (6). Then, the given vocal shapes [A(x) in Equation (5)] were reconstructed and the vocalic sounds were synthetized, from which the first two formants were extracted using Praat (Boersma and Weenink, 2011). Each set of (m₁,m₂,m₃) produced a different transformation from the sensor space to the formants space (Figure 3).

FIGURE 3

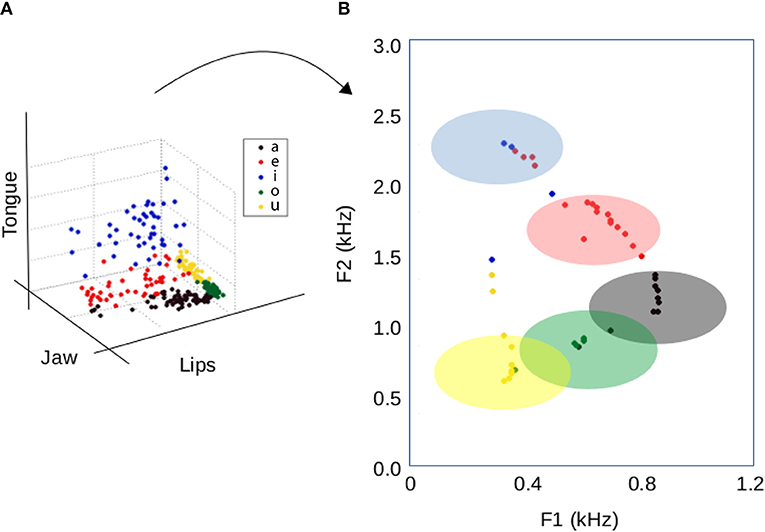
Figure 3. Mapping the transducer signals into the formants space. The left panel shows the mean values h_J, h_T and h_L of the transducer signals during the utterance of vowels by one participant. Each dot represents a vowel, colors stands for the vowel's identity (/a/ is black, /e/ red, /i/ blue, /o/ green, /u/ yellow). The right panel maps each point in the transducers space to the formants space as described above, for (m₁,m₂,m₃) = (300,300,900). The shaded regions represent the experimental variation in the formants F₁ and F₂ for Spanish vowels (Aronson et al., 2000).

The first two formants of a vocalic sound define its identity (Titze, 1994); its variability for real vocalizations of Spanish vowels is represented by the shaded areas on the right panel of Figure 3 according to previous reported results (Aronson et al., 2000). The chosen steepness values (m₁ = 300, m₂ = 300, and m₃ = 900) converted more than 90% of the transducer data—obtained during the vowel's production—into the experimental (F₁,F₂) regions, as shown in Figure 3.

Synthetic Speech

To synthesize speech it was necessary to solve the set of equations described in the Articulatory synthesizer section (Equations 3, 4). In order to simulate the glottal flow a value for the pitch (f₀) was needed; and to solve the electric analog for the discretized tube the vocal tract shape was required. The pitch value was extracted using Praat (Boersma and Weenink, 2011) from the speech recordings. The time evolution of the vocal tract shape was reconstructed from the recording signals using Equations (5–7). Videos of the vocal tract dynamics driven by the transducers are available at Supplementary Material for different VCV structures.

Audio wav files were generated using the transducers' time traces and the pitch contours produced by one of the participants while vocalizing: /oga/, /agu/, /ogu/, /oda/, /odi/, /ide/, /ibu/, /iba/, /obe/ (data available as Supplementary Material). The audio files were generated by integrating Equations (3, 4) in N = 44 tubes, using a Runge-Kutta 4 algorithm (Press et al., 2007) coded in C at a sampling rate of 44.1 kHz. The sound intensity of the files was equalized at 50 dB.

Fifteen participants using headphones (Sennheister HD202) listened to the synthetic speech trials in random order. They were instructed to write down a VCV structure after listening to each audio file. The experiment was written in Psychtoolbox (Brainard, 1997).

Results

From Continuous Dynamics to a Discrete Motor Representation

A visual inspection of the data revealed that the sensors' signals executed rapid excursions during the transitions in order to reach the following state (see Figure 1C) and that the signals were bounded to the same range of values during different vocalizations of the same phoneme. These observations invited us to hypothesize that each phoneme could be described in a three dimensional discrete space by adjusting thresholds over the signals. This hypothesis was first mathematically formalized (see section Materials and Methods) and then tested using training and test sets to extract the thresholds and compute the decoding performance, respectively.

It is worth noting that sensors provided articulatory information beyond the ones collected here for signal discretization using thresholds. For instance, the brief bumps present around /g/ in Figure 1 were not common across subjects, but rather the signature of a particular speaker or speech habit. We leave for future work a characterization of the continuous signals (for instance using machine learning techniques) to find speech patterns and/or to characterize speakers.

Decoding Performance: Intra-subject and Intra-session

To perform the decoding it was necessary to define the threshold values. In this case, one set of thresholds was adjusted for each participant and session. More precisely, the first 15 VCVs of the session were used as training set, i.e., to fix the thresholds (see Table S1 for the numerical values). The following 60 VCVs of the corresponding session were used as the test set, i.e., to calculate the decoding performance using the thresholds optimized on the training set.

Figure 4A shows the confusion matrix obtained by averaging the decoding performance across participants and sessions (see Figure S1 for each participant's confusion matrix). Every phoneme was decoded with performances well above chance levels. This result validates the discretization strategy and discloses a discrete encoding of the phonemic identity in the continuous vocal tract movements.

FIGURE 4

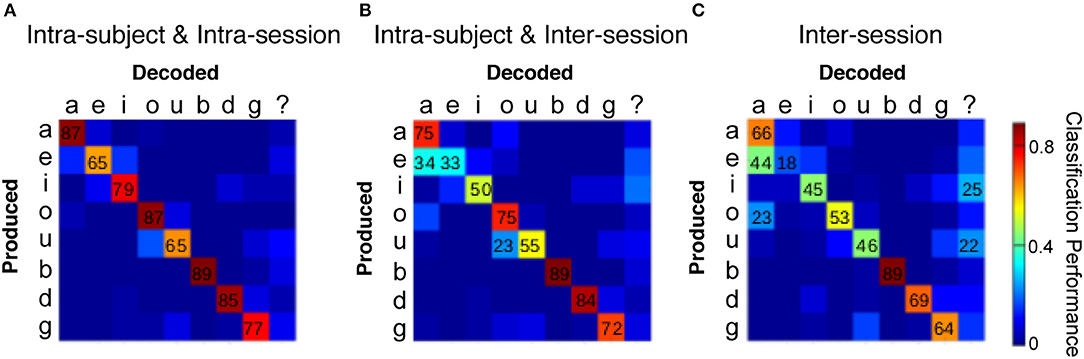
Figure 4. Decoding performance of the discrete representation. (A) Confusion matrix using one set of thresholds per session. Average across sessions and participants. (B) Confusion matrix using one set of thresholds per participant. Average across participants. (C) Confusion matrix computed using one set of thresholds for all participants. Numerical values above 20% are displayed for visualization purposes. Thresholds values and matrix means with standard deviations are shown in Tables S1, S2, respectively, at Supplementary Material.

Decoding Performance: Intra-subject and Inter-session

The previous result led to the question of whether thresholds could be defined for each participant, independently of the variations in the device mounting across sessions. To explore this, the VCV data of all sessions were pooled together for each participant. Then, the 10% of the data was used to adjust thresholds and the performance was tested on the rest. More specifically, a 50-fold cross-validation was performed over each subject's data set. The confusion matrix of Figure 2B exposes the confusion matrix obtained by averaging the decoding performance across participants (see Figure S2 for individual participant's confusion matrixes and Table S1 for the mean value and standard deviation of the 50 thresholds). The performance remained well above chance for every phoneme, with the only one exception of the vowel /e/, that was confused with /a/. As shown in Figure 1D, these two vowels were distinguished by the state of the tongue, the articulator for which the mounting of the device was more difficult to standardize.

Decoding Performance: Inter-subject and Inter-session

Next, the robustness of the configuration, regardless anatomical differences amongst subjects, was tested. Therefore, the VCV data from all sessions and participants were pooled together and the 10% of the data was used to fix thresholds (see Table S1). The confusion matrix of Figure 4C represents the average values obtained from 50-fold cross-validation. As in the previous case, the vowel /e/ was mistaken for /a/, revealing that the mounting of the magnet on the tongue needs to be treated with a more fine protocol. This result showed that the discretization strategy was robust even while dealing with different anatomies, suggesting that the encoding of the sounds of a specific language in a low-dimensional discrete motor space represents a general property of the speech production system.

Summarizing, the matrices shown in Figure 4 correspond to a calibration of the discrete decoding system per session (a), per speaker (b) and a general calibration across speakers and sessions (c). It is important to notice that only the first one (a) represents the performance of the prototype as a speech recognition system. The other two (b, c) are meant to explore the robustness of the mounting of detectors and magnets, and the generalization of the motor coordinates across anatomies and speech habits.

Occupation of the Consonant's Free States

As pointed out before, vowels and consonants had different ranks in the discrete representation: while each vowel was represented by a vertex of the cube of Figure 1D, each consonant was compatible with many states, shown as the points on the “walls” surrounding the cube, herein named free state. For example, the discrete representation for /d/ is (y,x,2), meaning that the lips and jaw are free states that can take any value—e.g., (0,1,2) represents a /d/ and (1,0,2) also does. The occupation levels of the free states were explored. The discrete state for each consonant was computed using the intra-subject and intra-session decoding, for all participants and sessions, and just the VCVs that were correctly decoding were kept for this analysis. The occupations of the different consonantal states are shown in Figure 5A.

FIGURE 5

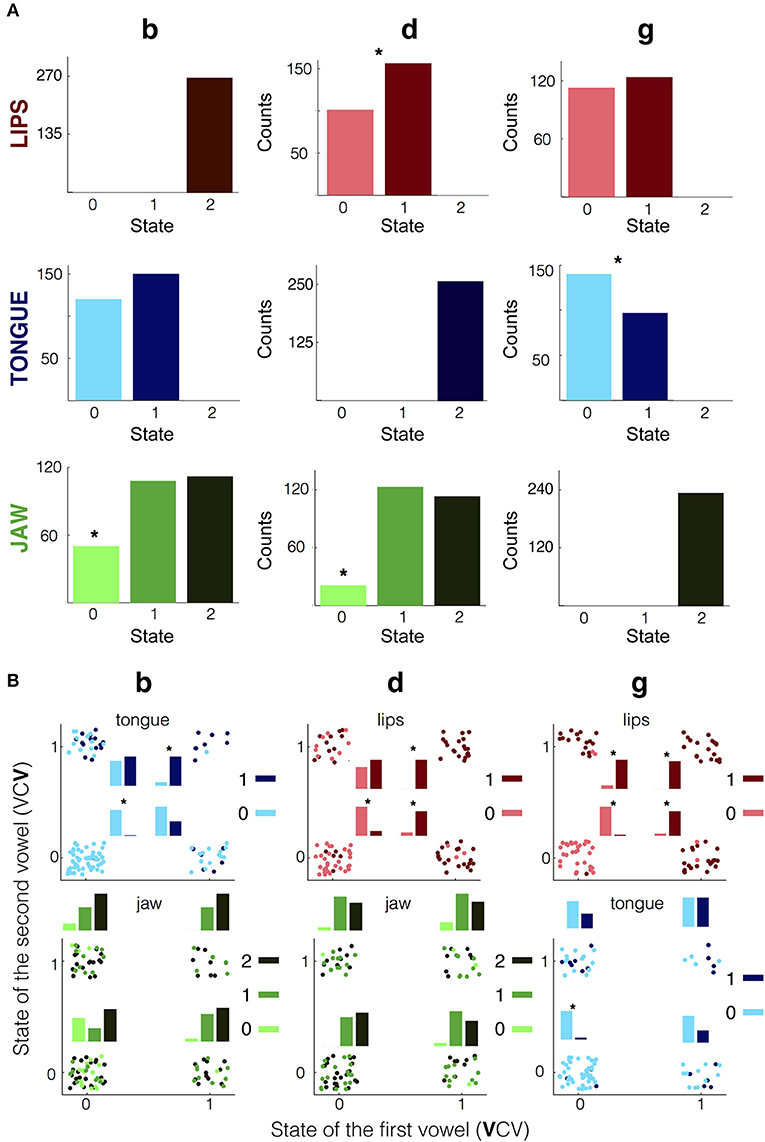
Figure 5. Occupation of the free coordinates. (A) Counts of occurrence of each state, for the complete pool of sessions and participants using the intra-subject and intra-session thresholds for the discretization. Just the correctly decoded VCVs were kept for this analysis. Columns represent the different consonants (/b/, /d/ and /g/) and rows the articulators (jaw, tongue and lips). Asterisks indicate significant difference between states (p < 0.01 binomial test). (B) Occupation levels of the free coordinates as a function of the surrounding vowels. Each column represents a consonant and the rows its corresponding free states. For each panel the y-axis defines the state of the incoming vowel and the x-axis the state of the previous one. Within each panel, each dot represents a corrected decoded consonant, the darkness of the dot its corresponding state, and its location indicates the pre and post vowel's state in the corresponding articulator. Also, histograms are displayed for each combination of states of pre and post vowel. Asterisks indicate a significant difference between states (p < 0.001).

The /b/ was defined by the lips in state 2; the tongue and the jaw were free coordinates. The state 2 was not observed in the tongue, and is presumably incompatible with the motor gesture of this consonant, however no significant differences were found between the states 0 and 1 (binomial test with equal probabilities, p = 0.1). Similarly, for the jaw coordinate the state 0 was underrepresented, with an occupation of the 18%, below the chance level of 1/3 (binomial test, p < 0.001). The /d/ was defined by the tongue in state 2; the lips and the jaw were free coordinates. The lips showed a dominance of the state 1 over the 0 (binomial test, p < 0.001), and the state 0 of the jaw was significantly less populated than the others with an occupation of the 8%, lower than the chance level of 1/3 (binomial test, p < 0.001). The /g/ had free lips and tongue coordinates. The lips showed no significant differences between the states 0 and 1 (binomial test with equal probabilities, p = 0.52), and the state 0 was preferred for the tongue (binomial test with equal probabilities, p = 0.006).

A well-known effect in the experimental phonology field is coarticulation, which refers to the modification of the articulation of the consonants by their neighboring vowels (Hardcastle and Hewlett, 2006). The occupation levels of the consonants as a function of their surrounding vowels were calculated (Figure 5B) and coarticulation effects were revealed. The results showed that, when the surrounding vowels shared some of the consonant's free states, this state was transferred to the consonant. Specifically, when the previous and following vowels shared the lip state its value was inherited by the consonants with a free lip's coordinate, being /d/ and /g/ (p < 0.001 for the four binomial tests). Additionally, /b/ inherited the state of the tongue of the surrounding vowels when both shared that state (p < 0.001 for both binomial tests), and when both vowels shared the tongue state 0, it was inherited by the /g/ (binomial test, p < 0.001). No coarticulation was presented by the jaw: for /b/ and /d/ the jaw was homogeneously occupied by states 1 and 2, regardless of the states of the surrounding vowels.

Synthesizing Intelligible Speech From the Anatomical Recordings

One of the goals of this study was to produce synthetic speech from the recordings of the upper vocal tract movements by driving an articulatory synthesizer with the signals coming from the sensors. Moreover, since the discrete representation successfully decoded the phonemes (see Figure 4), the synthesizer was driven by Equation (2), instead of by the raw signals. Since normal speech arises from continuous changes in the vocal tract, rather than instantaneous passages from one configuration to the other, it was necessary to get smooth transitions from one state to the other. Therefore, m = ∞ in Equation (2) were replaced with finite values m₁, m₂, and m₃, for the lip, jaw, and tongue coordinates, respectively (see section Materials and Methods). The smooth version of Equation (2) was used to drive the articulatory synthesizer described in the Materials and Methods section. More precisely, audio files were generated by driving the synthesizer with Equation (2) fed with the transducers' time traces and the pitch contours produced by one of the participants while uttering /oga/, /agu/, /ogu/, /oda/, /odi/, /ide/, /ibu/, /iba/, /obe/ (examples available as Supplementary Material). Details of this process can be found in the Materials and Methods section.

Finally, to test the intelligibility of the synthetic speech, the samples were presented to 15 participants, who were instructed to write down a VCV structure after listening to each audio file. The confusion matrices obtained from the transcription are shown in Figure 6 (see panel A for consonants and B for vowels). All values were above chance levels (33% for consonants and 20% for vowels).

FIGURE 6

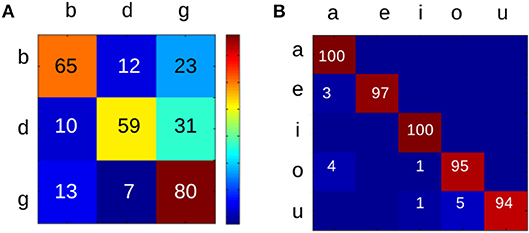
Figure 6. Confusion matrices for the intelligibility of the synthetic speech. Rows represent the produced phoneme and columns the transcribed one. (A) Consonants. (B) Vowels. The color code represents the percentage of responses for each condition.

Discussion

The current work presented two main findings: (i) a discrete representation of the vocal gestures for Spanish vowels and plosive consonants, reconstructed from the direct measurements of the continuous upper vocal tract movements; and (ii) a prototype of a speech recognition system, capable of monitoring the upper vocal tract movements during speech and to decode and synthesize VCV structures using the discretization strategy.

A Discrete Motor Space Representation

This study showed that discretizing three continuous signals given by the movements of the main articulators of the vocal tract while vocalizing VCV structures was enough to recover the phonemic information. This result represents a follow up of a previous work were the same experimental procedure was applied over isolated vowels. Here, the discrete motor vowel representation was validated during continuous speech and the Spanish stop consonants were integrated to the description.

In order to recover the vowel's identity, just one threshold per signal was needed. Thus, the vowels were represented in the discrete motor space as the corners of a cube. Curiously, the dimension of the vowel cube (eight) is in agreement with the number of Cardinal Vowels (McClure, 1972), a set of vocalic sounds used by the phoneticians to approximate the whole set of cross-language vowels. This suggests that the discrete motor states captured by this study could represent the basic motor gestures of vowels. Moreover, the state on each articulator's transducer corresponded to an extreme value along the two-dimensional coordinate system used by the International Phonetic Alphabet to describe vowels. Interestingly, the same discrete representation for vowels could be recovered from direct measurements of human brain activity during vocalizations (Tankus et al., 2012).

The consonants chosen for this study were /b d g/. They cause a complete occlusion of the vocal tract produced by the constriction gesture of one of the three independent oral articulator sets (lips for /b/, tongue tip for /d/, and tongue body for /g/). Interestingly, these consonants have been suggested as the basic units of the articulatory gestures (Browman and Goldstein, 1989). Therefore, they appear as the natural candidates to study the presence of discrete information within the continuous movements of the oral tract.

According to the International Phonetic Alphabet, two features define the consonants: the place and the manner of articulation (International Phonetic Association, 1999). This work focused in the place dimension, since the phoneme selected cover the three main groups used to describe the place of articulation of consonants: labial (/b/), coronal (/d/), and dorsal (/g/). The results revealed the plausibility of recovering the main place of articulation just by monitoring (and discretizing) the kinematics of three points in the upper vocal tract. Similarly, at the brain level, spatial patterns of activity during speech are known to show a hierarchal organization of phonemes by articulatory features, with the primary tier of organization being defined by the three major places of articulation: dorsal, labial, or coronal (Bouchard et al., 2013).

How the discrete phonemic identity is encoded in the continuous movements producing speech remains an open question for the experimental phonology. The presence of compositional motor units into the continuous articulatory movements has been widely theorized on the literature (Browman and Goldstein, 1986, 1990; Saltzman and Munhall, 1989); and some experimental evidence has supported this hypothesis (Goldrick and Blumstein, 2006; Goldstein et al., 2007a,b). In this work we recovered a discrete representation for the complete set of Spanish vowels and stop consonants from direct measurements of the upper vocal tract movements during continuous speech. This result links the discrete information at the brain level with the discrete phonemic space through the experimental evidence of discrete motor gestures of speech.

A Novel Device to Track the Vocal Tract Movements During Continuous Speech

After a short training session, the prototype presented in this work -the electronic device used with the threshold strategy to feed the articulatory synthesizer- produced intelligible speech within the corpus of Spanish vowels and plosive consonants. Although further work is needed to compare our prototype with other synthesizers (Heracleous and Hagita, 2011; Bocquelet et al., 2016), it presents two conceptual advantages: (i) it is portable; and (ii) the motor gestures involved in the control of the articulatory model are saturating signals, a shared feature with the brain activation during speech which represents a clear benefit for brain-computer interface applications.

From a more general point of view, this implementation represents an alternative to the extended strategy used in the bioprosthetic field: large amounts of non-specific physiological data processed by statistical algorithms to extract relevant features for vocal instructions (Guenther et al., 2009; Bouchard et al., 2016). Instead, in the current approach a small set of recordings from the movements of the speech articulators, in conjunction with a threshold strategy, were used to control a biophysical model of the vocal system.

Although this approach showed potential benefits for bioprothetic applications, further work is needed to optimize the system. On the one hand, the mounting protocol for the tongue should be tightened up to get stable thresholds across sessions. On the other, the protocol should be refined to increase the phonemic corpus.

Regarding the consonants, several improvements can be implemented. To distinguish voiced from unvoiced consonants, different specific sensors (Kim et al., 2011) could be added to our prototype in order to detect laryngeal vibrations, such as piezoelectric films adhered to the neck. This would provide an extra discrete state (for instance, 1 for voiced and 0 for unvoiced) that would allow to distinguish the complete set of plosives. In the same way different tools that detect nasal air flow (Chaaban and Corey, 2011) could be easily implemented to our device to recognize nasals. Further work is needed to include other phonemic groups to the present description, such as the fricatives [s, f, x], the approximant [l], and the flap [r]. Arguably, the fricatives could be integrated by including different sets of thresholds; and increasing the number of magnet-transducer sets mounted on the vocal tract could retrieve other places of articulation.

Regarding the vowels, the current vocalic space is complete for the Spanish language and has the flexibility to be extended to languages with up to 8 vowels (the dimension of the vowel's cube). However, in the current state, the device used with the threshold strategy is not appropriate for languages with a larger number of vowels. As mentioned above, a possible solution would be to add sets of thresholds and/or increasing the number of magnet-transducers.

The state of the art of the techniques used to monitor the articulatory movements during speech remained stagnant during the last decades, with some exceptions employing different technologies to measure the different articulators (Bouchard et al., 2016). The standard method used to track the articulator's displacements during speech is the EMA (Schönle et al., 1987; Uchida et al., 2014). This technique provides very accurate recordings (Goozée et al., 2000; Engwall, 2003; Steiner et al., 2013) at the expenses of being non portable and expensive. Here, a novel method is introduced and proved to be able to capture the identity of the uttered phoneme, to detect coarticulation effects and to correctly drive an articulatory speech synthesizer. This prototype presents two main advantages: it is portable and is non-expensive. The portability of the system makes it suitable for silent speech interface applications; and, crucially, because of the low cost of its components, it could significantly improve the speech research done in non-developed countries.

Data Availability

Additional data related to this paper may be requested from the authors. Correspondence and request for materials should be addressed to MA (fassaneo@gmail.com).

Ethics Statement

All participants signed an informed consent to participate in the experiments. The protocol was approved by the CEPI ethics committee of Hospital Italiano de Buenos Aires, qualified by ICH (FDA -USA, European Community, Japan) IRb00003580, and all methods were performed in accordance with the relevant guidelines and regulations.

Author Contributions

GM conceived the experiments; GM, MFA, and MT designed the experiments; MFA ran the experiments; DR, MFA, and MT coded the synthesizer; MFA and MT analyzed the data and wrote the manuscript.

Funding

This work describes research partially funded by CONICET, ANCyT, UBA.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomm.2019.00013/full#supplementary-material

Footnotes

1. ^Allegro MicroSystem. https://www.allegromicro.com/en/Products/Magnetic-Linear-And-Angular-Position-Sensor-ICs/Linear-Position-Sensor-ICs/A1321-2-3.aspx

References

Aronson, L., Furmanski, H. M., Rufiner, L., and Estienne, P. (2000). Características acústicas de las vocales del español rioplatense. Fonoaudiológica 46, 12–20.

Google Scholar

Assaneo, M. F., Sigman, M., Cohen, L., and Trevisan, M. A. (2016). Exploring the anatomical encoding of voice with a mathematical model of the vocal system. Neuroimage 141, 31–39. doi: 10.1016/j.neuroimage.2016.07.033

PubMed Abstract | CrossRef Full Text | Google Scholar

Assaneo, M. F., Trevisan, M. A., and Mindlin, G. B. (2013). Discrete motor coordinates for vowel production. PLoS ONE 8:e80373. doi: 10.1371/journal.pone.0080373

PubMed Abstract | CrossRef Full Text | Google Scholar

Birkholz, P., Martin, L., Xu, Y., Scherbaum, S., and Neuschaefer-Rube, C. (2017). Manipulation of the prosodic features of vocal tract length, nasality and articulatory precision using articulatory synthesis. Comput. Speech Lang. 41, 116–127. doi: 10.1016/j.csl.2016.06.004

CrossRef Full Text | Google Scholar

Bocquelet, F., Hueber, T., Girin, L., Savariaux, C., and Yvert, B. (2016). Real-time control of an articulatory-based speech synthesizer for brain computer interfaces. PLoS Comput. Biol. 12:e1005119. doi: 10.1371/journal.pcbi.1005119

PubMed Abstract | CrossRef Full Text | Google Scholar

Boersma, P., and Weenink, D. (2011). Praat: Doing Phonetics by Computer.

Bouchard, K. E., Conant, D. F., Anumanchipalli, G. K., Dichter, B., Chaisanguanthum, K. S., and Johnson, K. (2016). High-resolution, non-invasive imaging of upper vocal tract articulators compatible with human brain recordings. PLoS ONE 11:e0151327. doi: 10.1371/journal.pone.0151327

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouchard, K. E., Mesgarani, N., Johnson, K., and Chang, E. F. (2013). Functional organization of human sensorimotor cortex for speech articulation. Nature 495, 327–332. doi: 10.1038/nature11911

PubMed Abstract | CrossRef Full Text | Google Scholar

Brainard, D. H. (1997). The psychophysics toolbox. Spat. Vis. 10, 433–436. doi: 10.1163/156856897X00357

PubMed Abstract | CrossRef Full Text | Google Scholar

Browman, C., and Goldstein, L. M. (1986). Towards an articulatory phonology. Phonol. Yearb. 3, 219–252. doi: 10.1017/S0952675700000658

CrossRef Full Text | Google Scholar

Browman, C. P., and Goldstein, L. (1989). Articulatory gestures as phonological units. Phonology 6, 201–251. doi: 10.1017/S0952675700001019

CrossRef Full Text | Google Scholar

Browman, C. P., and Goldstein, L. (1990). “Tiers in articulatory phonology, with some implications for casual speech,” in Papers in Laboratory Phonology, eds J. Kingston and M. E. Beckman (Cambridge: Cambridge University Press), 341–376.

Google Scholar

Brumberg, J. S., Nieto-Castanon, A., Kennedy, P. R., and Guenther, F. H. (2010). Brain-computer interfaces for speech communication. Speech Commun. 52, 367–379. doi: 10.1016/j.specom.2010.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaaban, M., and Corey, J. P. (2011). Assessing nasal air flow: options and utility. Proc. Am. Thorac. Soc. 8, 70–78. doi: 10.1513/pats.201005-034RN

PubMed Abstract | CrossRef Full Text | Google Scholar

Denby, B., Schultz, T., Honda, K., Hueber, T., Gilbert, J. M., and Brumberg, J. S. (2010). Silent speech interfaces. Speech Commun. 52, 270–287. doi: 10.1016/j.specom.2009.08.002

CrossRef Full Text | Google Scholar

Deng, Y., Colby, G., Heaton, J. T., and Meltzner, G. S. (2012). “Signal processing advances for the MUTE sEMG-based silent speech recognition system,” in Proceedings - IEEE Military Communications Conference MILCOM. (Orlando, FL)

Google Scholar

Engwall, O. (2003). Combining, MRI, EMA and EPG measurements in a three-dimensional tongue model. Speech Commun. 41, 303–329. doi: 10.1016/S0167-6393(02)00132-2

CrossRef Full Text | Google Scholar

Flanagan, J. L. (2013). Speech Analysis Synthesis and Perception. Berlin; Heidelberg: Springer Science & Business Media.

Google Scholar

Goldrick, M., and Blumstein, S. E. (2006). Cascading activation from phonological planning to articulatory processes: evidence from tongue twisters. Lang. Cogn. Process. 21, 649–683. doi: 10.1080/01690960500181332

CrossRef Full Text | Google Scholar

Goldsmith, J., Riggle, J., and Yu, A. C. L. (2011). The Handbook of Phonological Theory, 2nd Edn. Hoboken, NJ: John Wiley & Sons

Google Scholar

Goldstein, L., Chitoran, I., and Selkirk, E. (2007a). Syllable structure as coupled oscillator modes: evidence from Georgian vs. Tashlhiyt Berber. Proc. XVI Int. Congr. Phon. Sci. 241–244.

Google Scholar

Goldstein, L., Pouplier, M., Chen, L., Saltzman, E., and Byrd, D. (2007b). Dynamic action units slip in speech production errors. Cognition 103, 386–412. doi: 10.1016/j.cognition.2006.05.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Goozée, J. V., Murdoch, B. E., Theodoros, D. G., and Stokes, P. D. (2000). Kinematic analysis of tongue movements in dysarthria following traumatic brain injury using electromagnetic articulography. Brain Inj. 14, 153–174. doi: 10.1080/026990500120817

PubMed Abstract | CrossRef Full Text | Google Scholar

Guenther, F. H., Brumberg, J. S., Wright, E. J., Nieto-Castanon, A., Tourville, J. A., and Panko, M. (2009). A wireless brain-machine interface for real-time speech synthesis. PLoS ONE 4:e8218. doi: 10.1371/journal.pone.0008218

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardcastle, W. J., and Hewlett, N. (2006). Coarticulation: Theory, Data and Techniques. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511486395

CrossRef Full Text | Google Scholar

Heracleous, P., and Hagita, N. (2011). “Automatic recognition of speech without any audio information,” in 2011 IEEE International Conference on Acoustics, Speech, and Signal Processing (Prague), 2392–2395.

Google Scholar

Hueber, T., Benaroya, E.-L., Chollet, G., Dreyfus, G., and Stone, M. (2010). Development of a silent speech interface driven by ultrasound and optical images of the tongue and lips. Speech Commun. 52, 288–300. doi: 10.1016/j.specom.2009.11.004

CrossRef Full Text | Google Scholar

International Phonetic Association (1999). Handbook of the International Phonetic Association. Cambridge: Cambridge University Press.

Kim, D. H., Lu, N., Ma, R., Kim, Y.S., Kim, R.H., Wang, S., et al. (2011). Epidermal electronics. Science 333, 838–843. doi: 10.1126/science.1206157

PubMed Abstract | CrossRef Full Text | Google Scholar

Laje, R., Gardner, T., and Mindlin, G. (2001). Continuous model for vocal fold oscillations to study the effect of feedback. Phys. Rev. E 64, 1–7. doi: 10.1103/PhysRevE.64.056201

PubMed Abstract | CrossRef Full Text | Google Scholar

Landau, L. D., and Lifshitz, E. M. (1987). Fluid Mechanics. Rochester, NY: Image.

Levelt, W. J. M. (1993). Speaking: From Intention to Articulation. Cambridge, MA: MIT Press.

Google Scholar

Liljencrants, J. (1985). Speech Synthesis With a Reflection-Type Line Analog. Stockholm: Royal Institute of Technology.

Google Scholar

Lloyd, J. E., Stavness, I., and Fels, S. (2012). “ArtiSynth: a fast interactive biomechanical modeling toolkit combining multibody and finite element simulation,” in Soft Tissue Biomechanical Modeling for Computer Assisted Surgery, 355–394.

Google Scholar

Maeda, S. (1990). Compensatory articulation during speech: evidence from the analysis and synthesis of vocal-tract shapes using an articulatory model. Speech Prod. Speech Model. 131–149. doi: 10.1007/978-94-009-2037-8_6

CrossRef Full Text | Google Scholar

McClure, J. D. (1972). A suggested revision for the Cardinal Vowel system. J. Int. Phon. Assoc. 2, 20–25. doi: 10.1017/S0025100300000402

CrossRef Full Text | Google Scholar

Meltzner, G. S., Colby, G., Deng, Y., and Heaton, J. T. (2011). “Signal acquisition and processing techniques for sEMG based silent speech recognition,” in Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS (Boston, MA).

Google Scholar

Murphy, D., Kelloniemi, A., Mullen, J., and Shelley, S. (2007). Acoustic modeling using the digital waveguide mesh. IEEE Signal Process. Magazine. 24, 55–66. doi: 10.1109/MSP.2007.323264

CrossRef Full Text | Google Scholar

Petkov, C. I., and Jarvis, E. D. (2012). Birds, primates, and spoken language origins: behavioral phenotypes and neurobiological substrates. Front. Evol. Neurosci. 4:12 doi: 10.3389/fnevo.2012.00012

PubMed Abstract | CrossRef Full Text | Google Scholar

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. (2007). Numerical Recipes 3rd Edition: The Art of Scientific Computing. Cambridge: Cambridge University Press.

Google Scholar

Saltzman, E. L., and Munhall, K. G. (1989). A dynamical approach to gestural patterning in speech production. Ecol. Psychol. 1, 333–382. doi: 10.1207/s15326969eco0104_2

CrossRef Full Text | Google Scholar

Schönle, P. W., Gräbe, K., Wenig, P., Höhne, J., Schrader, J., and Conrad, B. (1987). Electromagnetic articulography: use of alternating magnetic fields for tracking movements of multiple points inside and outside the vocal tract. Brain Lang. 31, 26–35. doi: 10.1016/0093-934X(87)90058-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Schultz, T., Wand, M., Hueber, T., Krusienski, D. J., Herff, C., and Brumberg, J. S. (2017). Biosignal-based spoken communication: a survey. IEEE/ACM Trans. Audio Speech Lang. Proc. 25, 2257–2271.

Google Scholar

Steiner, I., Richmond, K., and Ouni, S. (2013). Speech animation using electromagnetic articulography as motion capture data. In 12th IEEE International Conference on Acoustics, Speech, and Signal Processing (Vancouver, BC), 55–60.

Google Scholar

Stevens, K. N. (2000). Acoustic Phonetics. Cambridge, MA: MIT Press.

Google Scholar

Stone, S., and Birkholz, P. (2016). “Silent-speech command word recognition using electro-optical stomatography,” in Proceedings of the Annual Conference of the International Speech Communication Association, Interspeech (San Francisco, CA).

Google Scholar

Story, B., and Titze, I. R. (1996). Parametrization of vocal tract area functions by empirical orthogonal modes. Natl. Cent. Voice Speech Status Prog. Rep. 10, 9–23.

Google Scholar

Story, B. H. (1995). Physiologically-Based Speech Simulation Using an Enhanced Wave-Reflection Model of the Vocal Tract. Ph.D. thesis, The University of Iowa.

Story, B. H. (2005). A parametric model of the vocal tract area function for vowel and consonant simulation. J. Acoust. Soc. Am. 117:3231. doi: 10.1121/1.1869752

PubMed Abstract | CrossRef Full Text | Google Scholar

Story, B. H. (2013). Phrase-level speech simulation with an airway modulation model of speech production. Comput. Speech Lang. 27, 989–1010. doi: 10.1016/j.csl.2012.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Story, B. H., and Titze, I. R. (1995). Voice simulation with a body-cover model of the vocal folds. J. Acoust. Soc. Am. 97, 1249–1260. doi: 10.1121/1.412234

PubMed Abstract | CrossRef Full Text | Google Scholar

Story, B. H., Titze, I. R., and Hoffman, E. A. (1996). Vocal tract area functions from magnetic resonance imaging. J. Acoust. Soc. Am. 100, 537–554. doi: 10.1121/1.415960

PubMed Abstract | CrossRef Full Text | Google Scholar

Tankus, A., Fried, I., and Shoham, S. (2012). Structured neuronal encoding and decoding of human speech features. Nat. Commun. 3:1015. doi: 10.1038/ncomms1995

PubMed Abstract | CrossRef Full Text | Google Scholar

Titze, I. R. (1994). Principles of Voice Production. Englewood Cliffs, NJ: Prentice Hall.

Google Scholar

Titze, I. R., and Martin, D. W. (1998). Principles of voice production. J. Acoust. Soc. Am. 104, 1148–1148.

Google Scholar

Toda, T., Nakagiri, M., and Shikano, K. (2012). “Statistical voice conversion techniques for body-conducted unvoiced speech enhancement,” in Proceedings of the Annual Conference of the International Speech Communication Association.

Google Scholar

Tran, V. A., Bailly, G., Lœvenbruck, H., and Toda, T. (2010). Improvement to a NAM-captured whisper-to-speech system. Speech Commun. 52, 314–326. doi: 10.1016/j.specom.2009.11.005

CrossRef Full Text | Google Scholar

Uchida, H., Wakamiya, K., and Kaburagi, T. (2014). “A study on the improvement of measurement accuracy of the three-dimensional electromagnetic articulography,” in Proceedings of the Annual Conference of the International Speech Communication Association, INTERSPEECH (Singapore), 726–730.

Google Scholar