A Processing-Oriented Investigation of Inflectional Complexity

1. Introduction

Assessment of the complexity of the inflection system of a language and its comparison with a functionally-equivalent system of another language are hot topics in contemporary linguistic inquiry (Bearman et al., 2015). Their goals may vary from a typological interest in classifying different morphologies, to a search for the most compact formal description of an inflection system, to an investigation of the nature of word knowledge and its connection with processing and learning issues (Juola, 1998; Goldsmith, 2001; Moscoso del Prado Mart́ın et al., 2004; Bane, 2008; Ackerman and Malouf, 2013).

From a cross-linguistic perspective, the way morphosyntactic features are contextually realized through processes of word inflection probably represents the widest dimension of grammatical variation across languages, in a somewhat striking contrast with universal invariances along other dimensions (Evans and Levinson, 2009). This has encouraged linguists to focus on differences in morphological marking. Inflectional complexity is thus approached as a problem of feature counting, through comprehensive catalogs of the morphological markers and patterns in a given language or language type. In contrast with such “enumerative” approaches (Ackerman and Malouf, 2013), information-theoretic models have addressed the issue in terms of either algorithmic complexity (Kolmogorov, 1968), measuring the length of the most compact formal description of an inflection system, or in terms of information entropy (Shannon, 1948), which measures the amount of uncertainty in inferring a particular inflected form from another form, or, alternatively, from a set of paradigmatically related forms.

An altogether different approach, more conducive to addressing fundamental psycholinguistic and cognitive issues, is to conceive of complexity as related to the problem of learning how to process an inflection system. This step has far reaching consequences for the way we look at word knowledge, shifting our focus from what speakers know when they know inflection (mainly representations), to how speakers develop knowledge of inflection by processing input data (learning). According to this perspective, redundant patterns are predominantly statistical, and even irregularities appear to be motivated by their frequency distribution in the system and by the speaker's processing bias. All these issues are very different in character from the formal constraints on units, representations or rule systems proposed within theoretical and computational models, and make room for an empirical validation grounded in learning theory.

In this paper, we show the potential of such a learning-based, processing-oriented view of inflection complexity through a quantitative analysis of the behavior of Temporal Self-Organizing Maps (or TSOMs, Ferro et al., 2011; Marzi et al., 2012; Pirrelli et al., 2015), a recurrent variant of classical Self-Organizing Maps (Kohonen, 2002), independently trained on the inflectional systems of Standard Modern Arabic, English, German, Greek, Italian and Spanish.

The choice of TSOMs as neuro-biologically inspired computational learning models is motivated here by practical and theoretical reasons. First, their role is instrumental, as we use them to illustrate the dynamic approach to complexity we intend to advocate. Hence, some of the points made here will also hold, with some qualifications, for other existing computational models (Althaus and Mareschal, 2013; Baayen et al., 2019; Li et al., 2007; Mayor and Plunkett, 2010, among others). Secondly, TSOMs are based on discriminative principles of selective synchronization of processing nodes, supporting a Word-and-Paradigm view of the mental lexicon¹. Accordingly, words are dynamically represented as emergent, superpositional patterns of short-term node activation, reflecting gradient levels of lexical specificity: from holistic to decompositional lexical representations. Thirdly, for each input word, TSOMs make it possible to inspect levels of node activation during online processing with a fixed sampling rate. This allows us to monitor patterns of node activation changing non-linearly with time as more symbols of the input word are presented, and check how levels of uncertainty in processing correlate with structural transitions in the input word (e.g., from a stem to its inflectional ending). Finally, we can correlate the TSOM temporal patterns with multiple defining features of typologically different inflectional systems, including: (i) the number of realization patterns of formal contrast (ranging from suppletion to extensive syncretism, through a whole range of intermediate cases); (ii) the type of such formal patterns (continuous, discontinuous or mixed); (iii) the amount of formal transparency they exhibit (ranging from a more fusional to a more agglutinative pattern); (iv) the frequency distribution of inflectionally marked forms within the same paradigm, and their relative dominance; (v) the frequency distribution of markers in their inflectional classes, and (vi) the amount of interpredictability among patterns (e.g., how easy it is for a speaker to predict an unknown inflected form from an already known inflected form of the same paradigm) as a function of their transparency and systematic nature.

As we shall see, data from our simulations makes room for an insightful analysis of time-bound patterns of structural organization of the network and its processing responses, accounting for the correlation between the complexity of inflectional data and processing aspects like speed of recognition, learnability and ease of production. Variation in complexity may have multiple, and in some cases opposite effects on all these issues, depending on the factors involved. For example, while regularly inflected forms are easier to learn because they take part of larger paradigm families, irregularly inflected forms are easier to discriminate because they are more isolated and ultimately less confusable. Based on non-linear analyses of simulation data reported in this paper and other linear analyses from our previous work (Marzi et al., 2018), we suggest that inflection is better understood as a dynamic, potentially unstable system, whose complexity results from a balancing act between competing processing and communicative requirements, finely tuned during language acquisition.

2. Inflectional Complexity

Inflection lies at the intersection of two independent but interacting issues: (i) what syntactic contexts require morphosyntactic and/or morphosemantic word marking, and for what lexical and grammatical units; (ii) how morphosyntactic and morphosemantic information is overtly realized on lexical and grammatical units. In this paper, our attention will be devoted to the second issue, by simulating and evaluating the learning dynamics of differently graded morphological (ir-)regularities. To investigate the issue of how degrees of inflectional complexity affect word processing strategies, we selected 6 languages that are differently positioned in a typological continuum ranging from a more isolating type to a more fusional inflecting one:²namely English, German, Spanish, Italian, Greek, and, to broaden our typological coverage, Standard Modern Arabic.

We will focus on systemic aspects of lexical organization that are common to most (if not all) inflection systems, and in particular we will examine the possibility of discovering morphological organization in the implicative network of relations between words, in order to understand the impact of this organization on word processing and learning issues. All inflection systems share the property that they have families of related word forms exhibiting collective properties that cannot be deduced from any one of these forms individually. This is the hallmark of inflectional paradigms, i.e., clusters of fully inflected forms which are associated with an individual lexical exponent (e.g., English walk, walks, walking and walked) and mutually related through inflectional classes (i.e., classes of inflectional markers in complementary distribution).

2.1. Paradigm Complexity

Over the last decades, investigation of the formal properties of inflectional paradigms has played a prominent role in changing the research agenda in inflectional morphology, marking a tendency to move away from part-whole relations within complex words, toward descriptive relations between inflected forms (Matthews, 1991; Blevins, 2016). Accordingly, the complexity of a paradigm resides in two basic dimensions. The first dimension defines the amount of full formal contrast realized within the paradigm, i.e., how many different markers are uniquely associated with distinct combinations of morphosyntactic features (or paradigm cells, e.g., present indicative 1st singular), and how structurally different these markers are. The second dimension describes the number of interpredictability patterns between words in the same paradigm, i.e., how easy it is for a speaker to infer an unknown paradigmatic form from other familiar forms within the same paradigm.

Both dimensions of complexity are functionally relevant. Patterns of formal contrast serve to distinguish paradigmatically-related forms, and associate them with specific cells to communicate meaning or function within an inflectional system. We refer to this dimension as the level of “discriminative complexity” of the system. At the same time, variation in patterns of formal contrast is not scattered randomly across paradigm cells. Formal patterns tend to be interdependent, to the extent that knowing the inflection in one paradigm cell allows speakers to predict the inflection in another cell. This type of interdependency defines the “inferential complexity” of an inflectional system: paradigms where many forms are predicted upon exposure to one or few forms only, are less complex than paradigms where fewer forms are predicted from other forms.

From a cross-linguistic perspective, the discriminative complexity of an inflectional system is typically measured by enumerating the number of category values instantiated in the system (e.g., person, number or tense features) and the range of available markers for their realization. Accordingly, the larger the number of paradigm cells and their markers, the more difficult the resulting system (McWorther, 2001; Bickel and Nichols, 2005; Shosted, 2006). This notion of “Enumerative Complexity,” however, has been criticized on several grounds (Bane, 2008; Sagot and Walther, 2011; Ackerman and Malouf, 2013; Sagot, 2018). It soon gets difficult, if not impossible, to compare inflectional systems whose feature-value inventories differ dramatically. For instance, according to the World Atlas of Language Structures (Haspelmath et al., 2005), there are more than 10 different cases in Hungarian and none in Swahili, and more than 5 gender values in Swahili as opposed to none in Hungarian. In cases like this, we have no principled basis for arguing that either system is more or less complex than the other. In addition, even in the most favorable case of two hypothetical systems whose feature-value inventories match perfectly, simple counting can be misleading. Suppose we are comparing two systems, each with only two categories (say, singular and plural) and three different endings for each category: A, B, C for singular, and D, E, and F for plural. In the first system, paradigms are found to present three possible pairs of endings only: <A, D>, <B, E>, <C, F>, which can be described as corresponding to three different inflection classes. In the second system, any combination is attested. Clearly, the latter system would be more difficult to learn than the former, as it makes it harder to infer the plural form of a word from its singular form (or the singular from the plural for that matter). Nonetheless, both systems present the same degree of Enumerative complexity.

Recently, information theoretic approaches have been proposed as a way to circumvent the limitations of pure feature counting methods. Following Kolmogorov (Kolmogorov, 1968), the complexity of a dataset of inflected forms can be measured by the shortest possible grammar needed to describe them, or their algorithmic complexity, in line with the Minimum Description Length (MDL) principle (Rissanen, 2007). For example, following Goldsmith (2001), we can model the task of morphological induction as a data compression problem: find the collection of markers forming the shortest grammar that fits the empirical evidence best. To illustrate, English conjugation can be modeled as consisting of sets of endings in complementary distribution (somewhat reminiscent of “inflectional classes,” referred to by Goldsmith as “signatures”), and a set of stems. For example, the list <NULL, -er, -ing, -s> is a signature for the verb stems count, walk and mail, but not for love or notice, which require the stems lov- and notic-, and the signature <e, -ed, -ing, -es>. Licensing an irregular verb like drink in this grammar formalism is even more verbose, as it requires three stems, drink, drank and drunk, and two signatures: <NULL, -ing, -s> for drink, and <NULL> for both drank and drunk. Goldsmith's algorithm, however, models paradigm learning as a top-down optimization problem, boiling down to a grammar evaluation procedure. The segmentation of forms into sublexical constituents is based on heuristic criteria and makes no contact with the problem of finding the minimally redundant set of paradigms. Ultimately, we are left with no clues about how word processing (segmentation) interacts with the paradigmatic organization of the morphological lexicon.

An alternative information-theoretic approach to complexity is based on Shannon's entropy (Shannon, 1948), or informational complexity of a set of paradigms. Information complexity rests on the intuition that a more complex system of inflected forms presents fewer interpredictability patterns between existing forms than a less complex system does. Ackerman et al. (2009) and Ackerman and Malouf (2013) use Shannon's information entropy to quantify prediction of an inflected form as a paradigm-based change in the speaker's uncertainty. They conjecture that inflectional systems tend to minimize the average conditional entropy of predicting each form in a paradigm on the basis of any other form of the same paradigm (the Low Conditional Entropy Conjecture, or LCEC). This is measured by looking at the distribution of inflectional markers across inflection classes in the morphological system of a language. More recently, Bonami and Beniamine (2016) propose to generalize affix-to-affix inference to inference of intraparadigmatic form-to-form alternation patterns (Pirrelli and Yvon, 1999; Albright, 2002). This approach offers several advantages. It avoids the need for the theoretically-loaded segmentation of inflected forms into stems and affixes in the first place. Secondly, it models implicative relations between stem allomorphs (or stem-stem predictability), thereby providing a principled way to discover so-called “principal parts,” i.e., a minimal set of selected forms in a paradigm from which all other paradigm members can be deduced with certainty (Finkel and Stump, 2007). Finally, it emphasizes the role of joint prediction, i.e., the use of sets of forms to predict one missing form of the same paradigm, as a convenient strategy to reduce the speaker's uncertainty in addressing the cell filling problem.

In spite of their differences, however, both Kolmogorov's and Shannon's approaches are biased by a few a priori assumptions. Results obtained from the use of algorithmic complexity strongly depend on the formalism adopted for grammatical description (Sagot, 2018): for example, surface representations of verbs are typically segmented into stem-ending patterns. Information entropy dispenses with segmentation, but it rests crucially on the types of formal relations used to identify predictability patterns in inflectionally related forms. In either case, the algorithm does not adapt itself to the specific structural requirements of the systems it analyzes. Instead, it presupposes considerable knowledge of the morphology of the target language, in order to assess how effectively that knowledge can describe the language.

A more principled approach to measuring morphological complexity is to investigate the impact of incremental learning and online processing principles on paradigm organization, based on observation of the behavior of an unsupervised algorithm acquiring an inflection system from fully-inflected forms. The approach is central to establishing a connection between human language behavior, word distributions in input data, learning mechanisms and the taxonomy of units and combinatorial principles of linguistic theories. Careful quantitative analysis of the way a computational learning system can bootstrap structural information from typologically different training sets is not too far from what is done in experimental psycholinguistics, where the role of multiple factors on human processing is investigated by controlling factor interaction in the execution of a specific processing task. In the end, this allows us to frame the problem of inflectional (and paradigm) complexity into the larger context of word processing complexity, to which we turn in the following section.

2.2. Processing-Oriented Complexity

The discriminative and inferential dimensions of paradigm complexity illustrated in section 2.1 meet potentially competing communicative requirements. A maximally contrastive inflection system is one where inflected forms, both within and across paradigms, present the earliest possible point of recognition³, i.e., the position where they are uniquely distinguished from their paradigm companions. From this perspective, extensive suppletion (e.g., with English be/am/are/is/was/were) reflects a recognition-driven tendency for a maximally efficient contrast.

A maximally contrastive system, however, may require extensive storage of its forms, insofar as relatively few items can be inferred from its paradigm companions. Hence, any such system is not only slow to learn, but also fairly demanding and inefficient to use. Due to the Zipfian distribution of the forms in use within a speech community, almost half of the word forms of a language occur only once in a corpus, irrespective of corpus size (Blevins et al., 2017). This means that even high-frequency paradigms will tend to be partially attested, and speakers must be able to generalize available knowledge to rare events if they want to interpret or produce novel forms.

Issues of morphological regularity also have a bearing on the relationship between morphological complexity and word processing. We already noted that intra-paradigmatic suppletion, arguably the most radical break with systematic and predictable inflection, is functional in maximizing contrast, but may represent a hurdle for word learning. Conversely, syncretic realization of many paradigm cells with identical forms (as in the English present indicative sub-paradigm) and, more generally, paradigm ambiguity, can slow down acquisition of overtly marked forms (e.g., the third singular present indicative s-forms in English). Researchers from diverse theoretical perspectives observe that rich inflection in fact facilitates early morphological production. In competition-based (Bates and MacWhinney, 1987), as well as functional (Slobin, 1982, 1985) and cue-response discriminative perspectives (Baayen et al., 2011), non-syncretic morphological paradigms such as those of Italian conjugation are argued to provide better syntactic cues to sentence interpretation, as compared, for example, to the impoverished inflectional system of English verb agreement. Biunique form-meaning relationships make inflectional markers more transparent, more compositional and in the end more easily acquired than the one-to-many mappings of morphological forms to syntactic features that are found in English, Swedish and Dutch (Phillips, 1996, 2010). Some researchers (Crago and Allen, 2001; Blom, 2007; Legate and Yang, 2007; Xanthos et al., 2011) have focused on the amount of finite verbs that children receive from the adult input, to observe that the high percentage of overtly inflected forms correlates with the early production of finite forms by children. In the framework of Natural Morphology, Dressler and colleagues (Bittner et al., 2003) claimed that a richer inflectional system makes children more aware of morphological structure, so that they begin to develop intra-paradigmatic relations sooner than children who are confronted by simpler systems do (Xanthos et al., 2011).

The literature reports a number of effects that family size and the frequency of family members have on a variety of processing tasks. A large family size supports visual word recognition, with printed words with many neighbors being recognized more quickly than words with fewer neighbors (Andrews, 1997). However, when neighbors are considerably more frequent than the target word, recognition of the target is inhibited. A similar reversal from facilitation to inhibition is reported in spoken word recognition and related tasks (Luce and Pisoni, 1998; Magnuson et al., 2007), where many neighbors are found to delay recognition of the target word. The effect has recently been interpreted as due to serial (as opposed to parallel) processing (Chen and Mirman, 2012): a word supported by a dense neighborhood is produced and read faster. But when the same word is presented serially (e.g., in spoken word recognition), high-frequency neighbors engage in competition and inhibit processing. Such a modality-driven subdivision of processing strategies is however not clear cut.

Balling and Baayen (2012) provide evidence for the combined processing effects of two uniqueness points in both auditory and visual processing. The first is the word's initial Uniqueness Point (UP1), where an input word is distinguished from its morphologically-unrelated competitors (e.g., carrier and carpenter). The second is the later Complex Uniqueness Point (CUP), where an input word is distinguished from its morphologically-related competitors (e.g., writes and writing). They report that late UP1 and CUP are inhibitory in auditory and visual lexical decision, both independently and in interaction. In line with this evidence, more regular paradigms are predicted to favor entrenchment of shared stems and quicker acquisition of full forms, but they may cause larger effects of processing uncertainty at the stem-ending boundary than more irregular paradigms do, due to the larger range of possible following inflectional endings in regulars, as compared to irregulars.

The human exquisite sensitivity to word frequency distributions appears to be at the root of entropy-based processing effects. Milin et al. (2009a,b) report that speakers engaged in a lexical decision task are sensitive to the divergence between the word frequency distribution within a single paradigm, and the cumulative word frequency distribution in the inflection class to which the paradigm belongs. In particular, if an inflected form occurs in its paradigm less frequently than one would expect from the frequency of its ending, the visual recognition of that form gets more difficult. This finding has been confirmed in follow-up studies (Kuperman et al., 2010; Baayen et al., 2011; Milin et al., 2017).

Ferro et al. (2018) replicate these effects with TSOMs trained on inflectional paradigms with frequency distributions of varying entropy. The quantitative analysis of computer simulations is amenable to an interesting interpretation of entropic effects in terms of competition between family members. On average, word recognition is facilitated when words belonging to the same paradigm compete on a par, i.e., when their distribution is highly correlated with the distribution of their inflectional endings. When this is not the case, the entropy of the family decreases, increasing the risk that a low-frequency form is inhibited by a high-frequency member of the same family.

Marzi et al. (2018) add a cross-linguistic perspective on this evidence, by measuring the processing costs incurred by TSOMs trained on the inflectional systems of 6 languages. They observe that the averaged word processing costs for each language oscillate linearly within a small range (in keeping with Ackermann and Malouf's LCEC), whose upper and lower bounds are marked by Modern Greek conjugation (harder) and English conjugation (easier) respectively. All other inflectional systems present no statistically significant differences in the processing “overheads” they require, in spite of their typological diversity and their varying levels of morphological transparency. The analysis supports an interpretation of the LCEC as resulting from a balancing act between word processing and word learning. Word processing puts a premium on a system where word forms are maximally distinct and accessed early. Word learning, however, somewhat counteracts such a processing bias. Acquiring new forms is in fact necessary for speakers to communicate and discriminate in an ever changing social environment. The need to keep the system open thus increases processing uncertainty, as it inevitably increases the number of elements in the system.

Our present investigation is intended to go beyond these preliminary results. In the following sections, we investigate the competitive dynamic between word processing and word learning in more detail, focusing on the role that paradigm contrast plays in a variety of training conditions. Based on the data of Marzi et al. (2018), we model non-linear patterns of node activation in the online processing of inflected forms, in order to check how levels of processing uncertainty correlate with structural transitions in regularly and irregularly inflected forms within a single inflectional system, and across different inflectional systems. In addition, we model the impact of these effects on word learning, and we investigate the role that developing patterns of morphomic redundancy play during learning. As non-linear modeling can fit observed data patterns without a priori assumptions on the shape of the regression lines, this analysis is intended to lend further support to the dynamic view of inflectional complexity advocated here. In particular, we gain a better understanding of the basic language-invariant principles accounting for the discriminative and inferential dimensions of paradigm organization.

3. Materials and Methods

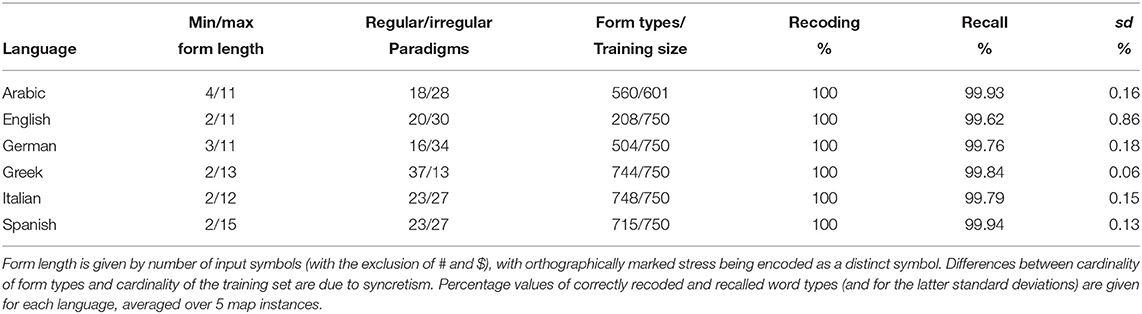
In this section and in section 4, we provide data-driven evidence of the interaction between morphological complexity and word processing in six languages. The evidence is gathered through repeated computer simulations of the acquisition of the verb inflection system in each of the input languages. For this purpose, we use Temporal Self-Organizing Maps (TSOMs), a recurrent variant of Kohonen's Self-Organizing Maps (Kohonen, 2002) that offers a neurally-inspired computational model of discriminative learning of time-series of symbolic units (Ferro et al., 2011; Marzi et al., 2014; Pirrelli et al., 2015)⁴. TSOMs can learn all training sets accurately (Table 1), while showing, at the same time, differential effects in paradigm self-organization, learning pace, and word processing. We start this section with a short description of their architecture and learning principles. A more technical, detailed description is found in the Appendix to this paper.

TABLE 1

Table 1. Statistics for the 6 datasets.

3.1. Recurrent Topological Networks for Word Learning

In TSOMs, word learning proceeds by developing maximally discriminative Markov-like chains of topologically arranged memory nodes, derived from exposure to fully inflected input forms with no morphological annotation. Nonetheless, node chains can mirror effects of gradient morphological structure and emergent paradigm organization. By developing specialized patterns of map nodes through recurrent connections, TSOMs encode input symbols auto-associatively, exploiting the formal redundancy of symbolic temporal series. Node specialization is modeled through discriminative learning equations (Ramscar and Yarlett, 2007; Baayen et al., 2011), which offer a powerful strategy for scaffolding the input stream into internalized structured representations that are efficient for word recognition and production. We provide here an informal, functional description of TSOMs. The interested reader is again referred to the Appendix for all mathematical and algorithmic details.

A lexical TSOM consists of a bank of input nodes encoding input letters, and a bank of processing nodes making up the lexical map proper (Figure 1). Each processing node is connected to the input layer through one-way input connections, and to other processing nodes (including itself) through one-time delay re-entrant temporal connections. At each time tick t, activation flows from the input layer to the map nodes through input connections. Re-entrant temporal connections update each map node with the state of activation of all nodes at the previous time tick (see the unfolded view of Figure 1). As with classical Recurrent Neural Networks (Elman, 1990), a word is input to a TSOM one symbol S at a time. Activation spreads through both input and temporal connections to yield an overall activation state, or Map Activation Pattern for S at time t: MAP_t(S). The node with the highest activation level in MAP_t(S) is called the Best Matching Unit for S at time t, or BMU_t(S). A time series of sequentially activated BMUs will be referred to as a BMU chain below. It represents the map's cumulative memory trace for an input time series.

FIGURE 1

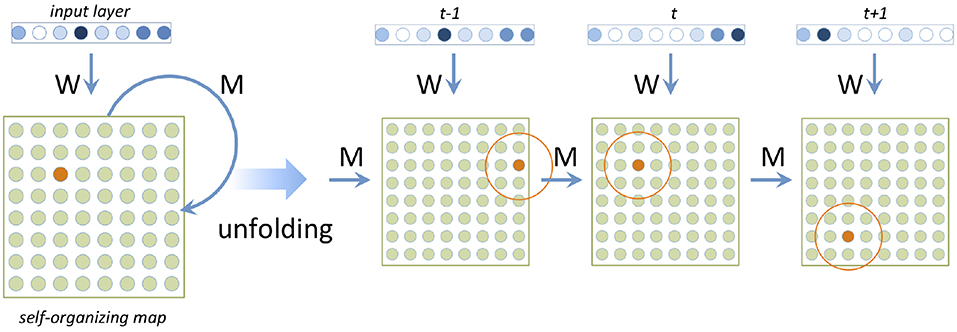
Figure 1. Architecture and unfolded view of a TSOM. Orange nodes represent Best Matching Units activated at successive time ticks.

Weights on temporal connections encode how strongly the current BMU_t is predicted by BMU_t−1, over a continuous range from 0 to 1. Temporal connection weights are trained on input data according to the following principles of discriminative learning, strongly reminiscent of Rescorla and Wagner (1972) equations (see Appendix). When the bigram ‘AX' is input, a TSOM goes through two learning steps:

1. the temporal connection between BMU_t−1(A) and BMU_t(X) is strengthened (entrenchment);

2. all other temporal connections to BMU_t(X) are weakened (competition).

Step 1. and 2. incrementally enforce node specialization. Over the course of training, the map tends to allocate maximally distinct processing nodes, as a function of the form overlap and form frequency of input strings in the training set.

To illustrate the effects of node specialization, Figure 2A sketches two possible end-states in the allocation of BMU chains responding to 9 form types of German geben ‘give': geben (infinitive, 1p and 3p, present indicative), gibst (2s, present indicative), gibt (3s, present indicative), gebe (1s, present indicative), gab (1s, 2s and 3s, preterite), gaben (1p and 3p, preterite), gabt (2p, preterite) and gebend (present participle). In the left panel, BMUs are arranged in a word tree. Any node N keeps track of all nodes that were activated in order to arrive at N. The right panel of Figure 2A, on the other hand, offers a compressed representation for the 9 form types, with shared letters activating identical BMUs. As a result, when the shared node ‘b' is activated, one loses information encoding which node was activated at the previous time tick. Let us briefly consider the implications of the two structures for word processing. In the word-tree (left), gibt, gabt, and gebt are mapped onto distinct node chains, bifurcating at the earliest branching point in the hierarchy (after the “g” node). From that point onward, the three forms activate distinct node paths. Clearly, when a node has only one outgoing connection, the TSOM has no uncertainty about what step to take next, and can anticipate the upcoming input symbol with certainty. In the word-graph on the right, on the other hand, branching paths converge to the same node as soon as input forms share an identical symbol. Having more branches that converge to a common node increases processing uncertainty. The node encapsulates information of many preceding contexts, and its possible continuation paths are multiplied accordingly.

FIGURE 2

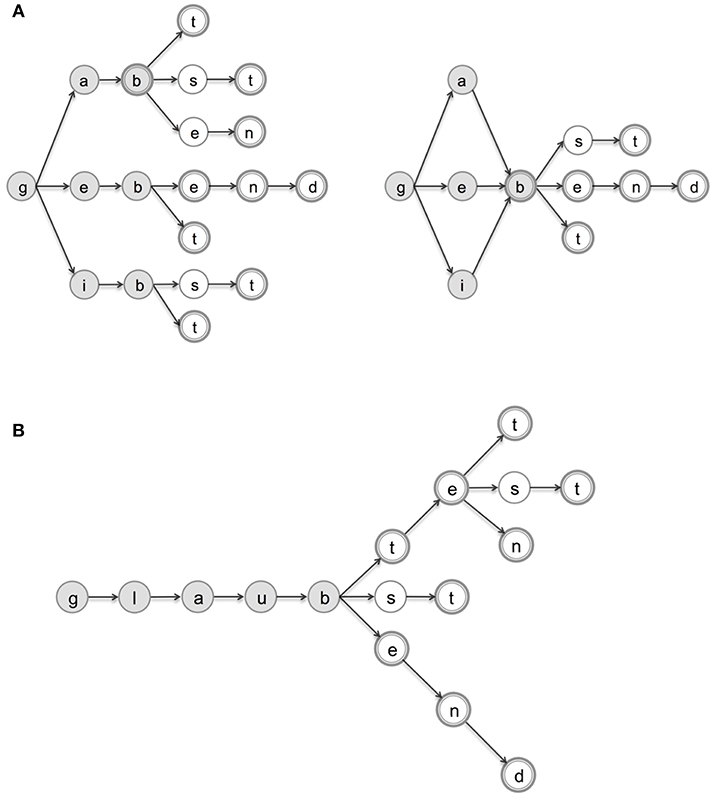
Figure 2. Graph-based representations for a few German verb forms of geben “give” (A) and glauben “believe” (B). Double-circled nodes represent word-final states, i.e., letters ending a word form; shaded nodes represent (possibly allomorphic) stems, according to the segmentation criteria of section 3.2. In (A), we provide a word-tree (left) and a word-graph (right) for the same set of 9 form types of geben.

In Figure 2B, a word tree of the German verb glauben (“believe”) is given for the 9 form types filling the same 14 paradigm cells selected for geben (Figure 1A). It is instructive to compare these structures. Of particular interest is the base stem glaub-, which is systematically shared by all its verb forms, and followed by a longer stretch of inflectional markers (conveying features of tense, person and number) than the base stems of geben (namely, geb-, gib- and gab-) are. Accordingly, the left-to-right processing of regularly inflected forms of glauben requires the traversal of more branching structures (and thus more indecision points). This marks an important structural difference between regular and irregular paradigms in all languages considered here, with a significant impact on the processing behavior of TSOMs, as we shall see later in more detail (section 5.1.1).

3.2. The Data

The TSOM architecture of Figure 1 was used to simulate the acquisition of the verb inflection system of six languages: Standard Modern Arabic, English, German, Modern Greek, Italian and Spanish. For all languages, we selected 15 forms (14 forms for Arabic) for each of the 50 top frequency paradigms sampled from a reference corpus⁵. For each language, forms were chosen from a fixed set of paradigm cells. To the greatest extent possible, the set of cells was kept comparable across languages⁶. Each input form was transliterated into an ASCII-based sequence of possibly complex symbols preceded by the start-of-word symbol (“#”), and followed by the end-of-word symbol (“$”). For Modern Standard Arabic forms we used the Buckwalter transliteration rules⁷.

Although forms are input to the map with no information about their internal structure, the dataset was annotated manually, to allow us to correlate variation in the map response after training with variation in the (morphological) structure of training forms. First, for each form, we marked up two uniqueness points: UP1 and CUP. UP1 was marked at the position in the verb form where the stem is uniquely identified, both relative to paradigmatically-unrelated onset-aligned forms in the dataset, and with respect to other possible stem allomorphs within the same paradigm. For example, the stem drunk is distinguished from the unrelated doubt at “r” in second position, but it is distinguished from drink or drank only when “u” is reached in third position⁸. The marking of CUP followed Balling and Baayen in marking the point at which the whole verb form is distinguished from other forms of the same paradigm.

In addition, we based morphological segmentation on a uniform (PREFIX) + STEM + (SUFFIX) template, where the notion of verb stem has the Aronovian, morphomic status of an unpredictable allomorph of the base stem, conveying systematic, but possibly non homogeneous clusters of morpho-lexical features (Aronoff, 1994). Accordingly, formally predictable stems derived from their base stem through a systematic process of stem formation (e.g., English past(walk) → walked) are segmented into a base and a suffix (walk-ed). Inflected forms containing unpredictable stems (e.g., English past_part(drink) → drunk, German past_1S(geben) → gab, German pres_2S(geben) → gibst) are segmented into a stem and a suffix (whenever overtly realized) (e.g., drunk-, gab-, gib-st).

Paradigms that undergo unpredictable stem formation processes are classified as irregular. Paradigms whose stems are formed transparently and systematically⁹ are annotated as regular. In Standard Modern Arabic, where verbs appear to cluster into different inflectional classes depending on the vocalic patterns intercalated with the roots, irregular (or weak) verb paradigms have stems that undergo a reduction in the number of root consonants (traditionally referred to as first, second, third weak and doubled roots, depending on the position and number of the radical consonants being dropped) (Marzi et al., 2017). Our segmentation template thus cuts across the traditional regular vs. irregular classification, yielding ya-ktub-u “he writes” and katab-a “he wrote” (as an example of a regular paradigm), together with ya-qūl-u “he says” and qāl-a “he said” (as an example of an irregular paradigm). Finally, for those languages (like Modern Greek and Italian) where regular paradigms exhibit unpredictable stem vowel selection (Ralli, 2005, 2006), stem identity/regularity was based on the form obtained by dropping the thematic vowel from the stem (Pirrelli, 2000; Pirrelli and Battista, 2000; Bompolas et al., 2017).

To annotate graded regularity in our data, we define, for each paradigm, the stem-family of a target form as the set of its formally distinct stem-sharing members. For instance, in our English training set, the forms drink, drinks and drinking are each associated with a stem-family of size 2, whereas drank and drunk have each an empty family. Likewise, the Italian verb forms veng-o “I come” and veng-ono “they come” have each a stem-family of size 1, as do vien-i “you come” (2s) and vien-e “(s)he comes.” In contrast, ven-ire “to come,” ven-iamo “we come,” ven-ite “you come” (2p), ven-isti “you came” (2s), ven-immo “we came,” and ven-iste “you came” (2p) have a stem-family of size 5. Finally, for each paradigm, we calculate its average stem-family size, and then normalize it by dividing it by the maximum number of possible stem-sharing members in the paradigm. Accordingly, the paradigm regularity for drink is $\frac{2+2+2+0+0}{5}·\frac{1}{4}=\frac{3}{10}$. The score, which we will refer to in section 4 as gradient paradigm regularity, ranges between 0 (minimum value obtained when each paradigm member is formed on a distinct stem) and 1 (maximum value, obtained when a paradigm is fully regular, i.e., when the stem-family of each paradigm member includes all other members of the same paradigm).

We used the same setting of free learning parameters for training TSOMs on all languages. However, to minimize the impact on the map topology of cross-linguistic differences in the training data (for instance, in terms of form length and number of form types: see Table 1)¹⁰, the number of nodes for each language-specific map was made to vary so as to keep constant the ratio between the map size and the number of nodes required to represent its training set with a word tree. Accordingly, a language-specific map size ranges between 35 × 35 nodes (English) and 42 × 42 nodes (Greek). Due to the combined effect of keeping this ratio constant across languages and preventing the temporal neighborhood radius (see Appendix) from decreasing to zero, maps tend to develop overlapping node chains for word forms sharing the same ending. Ultimately, these constraints on the topological organization of the map avoid data overfitting, as the map cannot possibly build up a dedicated memory traces for each form in the training set, i.e., it cannot memorize the original input data in its entirety (Marzi et al., 2014). For all languages, we stopped training at epoch 100, when all learning parameters reach minimum plasticity (see Appendix). To control for random variability in the map response, for each language we trained and tested the map 5 times on the same data, and averaged the results across all iterations.

4. Results

To analyze the results of our simulations, we focused on the way TSOMs process input words, and adjust their processing strategies while learning different inflectional systems.

Word processing describes the map's short-term response to an input word. The response consists in a distributed pattern of node activation and includes three sub-processes: input recoding, when a specific winning node (a BMU) is activated by an indvidual stimulus (a letter); prediction, i.e., the map's on-line expectation for an upcoming input letter, after a time series of input letters is presented on the input layer; and recall, which consists in retrieving a series of letters from the map's response to the series (the corresponding activation pattern). In turn, word learning consists in associating systematic, long-term patterns of node activation with input sequences of letters, so that each sequence can be discriminated from other sequences (i.e., it elicits a distinct response from the map), and letters can be retrieved from the pattern in their appropriate order for word recall. Accordingly, we can define the time of acquisition of a word as the learning epoch when the map is able to consistently recall the word correctly from its activation pattern, while making no mistakes at later epochs. It should be emphasized that, from this perspective, learning simply consists in developing long-term processing patters from repeated, short-term successful processing responses. We will return to this mutual implication between short-term processing and long-term learning in the concluding section of this paper.

Accuracy of recoding measures the ability of a TSOM to correctly map an input word form onto a chain of BMUs. When presenting a TSOM with a time-series of symbols making up an input word, the word form is recoded correctly if all BMUs are associated with the correct input symbols in the appropriate order (see Equation 1 in Appendix). Accuracy of recall measures the ability of a TSOM to correctly retrieve a word form from its memory trace (or Integrated Activation Pattern, see Appendix). This is done by iteratively spreading node activation from the start-of-word node (“#”) through the nodes making up the temporal chain of an input word. At each time step, the TSOM outputs the symbol associated with the currently most highly-activated node. The step is repeated until the node associated with the end-of-word symbol (“$”) is output (see Equations 19–21 in Appendix).

By measuring the map's prediction rate, we assess the ability of a trained map to predict an incrementally presented input word. Prediction scores across input words are calculated by symbol position. The prediction score of a correctly predicted symbol is obtained by increasing the prediction score of its immediately preceding symbol by 1-point. Wrongly predicted symbols are given a 0-point score (see Equation 18 in Appendix). For each input word, the more symbols are predicted, the higher the prediction score assigned to the word. High prediction scores thus reflect strong expectations over upcoming input symbols, and measure the relation between successful serial word processing and accurate positional encoding of symbols in a time series.

Accuracy scores for recoding and recall are given in Table 1. The performance of each language-specific map is evaluated by averaging scores across five iterations of the learning experiment for each inflection system. Performance is consistently good for all the languages in our experiments, especially when we focus on the accuracy of recall, considering the difficulty of the task. This shows that the algorithm is adaptive enough to be able to fine tune its time-sensitive representations to the orthotactic and morphotactic redundancies of each system, irrespective of the specific position a system takes along the isolating-inflecting continuum.

Some interesting differences are observed when we consider the learning pace of the maps for the different languages. Figure 3A shows the boxplot distribution of per-word learning epochs for the 6 languages. In particular, Arabic per-word learning epochs are significantly later than those of all other languages (p < 0.001), with English per-word learning epochs being significantly earlier (p < 0.01). In Figure 3B we plotted, for each language, its paradigm learning span. The span measures the number of epochs taken by a map to learn an entire paradigm after the first member of the paradigm is learned. The span thus quantifies the average inferential ability of a map learning an inflection system, and, indirectly, the learnability of the system. The ranking order of the learning span for the languages of our experiments nicely mirrors the relative complexity of the inflectional processes in the six languages, according to Bittner et al. (2003). On the one hand, the learning span for the English verb set is significantly smaller than the learning span of all other languages (p < 0.01 compared with German, and p < 0.001 compared with all other languages). On the other hand, the learning span for the Greek verb set is comparatively larger than the span of the remaining languages (p < 0.001), followed by the Italian set (which is not significantly different from the Greek one), and the Spanish one. In fact, Greek, Italian and Spanish present, unlike English and German, a verb system with more conjugation classes. The inferential process of filling empty cells from one attested form of the same paradigm thus requires preliminary identification of the appropriate conjugation class, with its set of inflectional endings¹¹. Nonetheless, the comparatively small range of variation (between 3 and 8 for median values) that these languages exhibit in their learning span lends support to Ackerman and Malouf's conjecture (Ackerman and Malouf, 2013) that the inferential complexity of inflectional system must oscillate within tight entropic bounds.

FIGURE 3

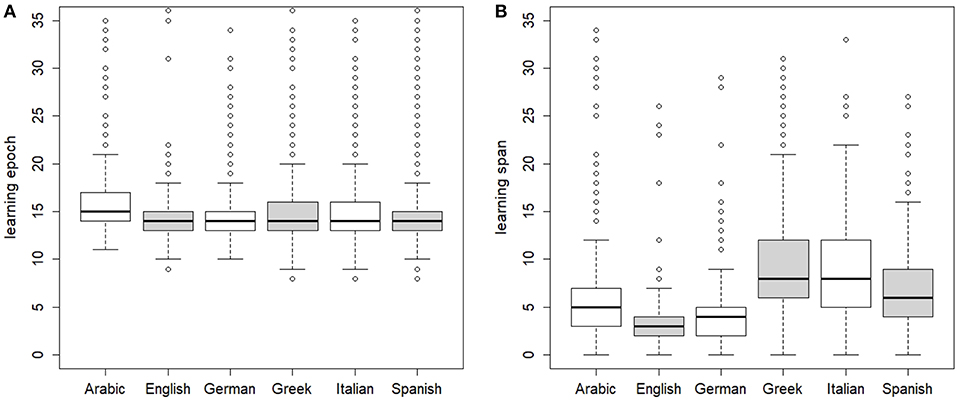
Figure 3. For each language dataset, boxplot distributions of (A) per-word learning epoch and (B) per-paradigm learning span.

Based on the results reported in this section, it appears that TSOMs are capable of learning the underlying syntagmatic structure of inflection (consisting of serialized sublexical units like prefixes, stems and suffixes), and the inferential patterns necessary for generalizing this structure. Nonetheless, this is only partially satisfactory for our present concerns. We would like to know not only that a particular inflection system can be learned, but also how it can be learned, what is actually being learned, and how hard it is for a TSOM to learn the inflection system of a language compared with that of another language. To reach this level of understanding, in the following sections we report statistical analyses of the performance of TSOMs in the prediction task and investigate their learning dynamic by using the R software (R Core Team, 2014). Our statistical models will provide a careful, quantitative interpretation of what the map does, and will enable us to suggest a non impressionistic categorization of the time-bound representations hidden in the map's topological self-organization, and match up these categories with familiar linguistic notions.

5. Data Analysis and Interpretation

The internal structure of a TSOM is not easy to examine, but there are ways to correlate the structure and distribution of the training data with the functional behavior of the map (e.g., its ability to predict what is coming next at a certain point in time in the input based on what was input until that point). In this section, we first consider categorical features of the training data: namely the language being input and its inflectional syntagmatics, by looking at the way sublexical constituents are annotated, and inflected forms are classified as regular or irregular (section 5.1). The idea is to explore the language-specific sensitivity that the map develops while being trained on a given language and its set of inflectional processes. Secondly, we move on to take a Word-and-Paradigm perspective on the same material, with a view to matching up the behavior of the map with a more graded classification of morphological regularity, and with more fundamental, cognitive effects of family size on the map's behavior (section 5.2.1). From both perspectives, we examine processing effects as well as learning effects.

5.1. Cross-Linguistic and Regularity Effects

5.1.1. Processing Effects

The leftmost panel of Figure 4 plots the linear rate of letter-by-letter prediction when a trained TSOM is processing regularly (cyan line) or irregularly inflected forms (red line), as a function of letter position (distance) to the Morpheme Boundary (MB) between stem and suffix, where MB = 0 corresponds to the first element of the suffix. The prediction rate counts how many consecutive letters are predicted by the map during word processing. The plot is a linear regression model of the letter prediction rate, using as predictors the letter position and the dichotomous regular vs. irregular classification (see section 3.2). Verb forms from the 6 languages are considered cumulatively in the model.

FIGURE 4

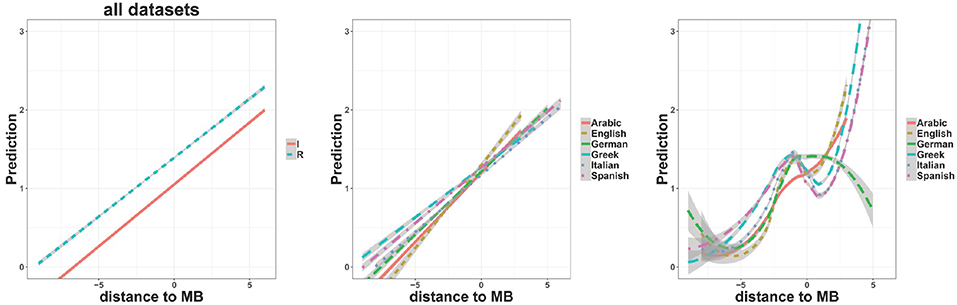
Figure 4. Regression plots of TSOM prediction rates in word recoding by letter position to the word stem-suffix boundary (distance to MB=0): (possibly prefixed) stems are associated with x-values <0, and endings with x-values ≥0. (Left panel) linear interaction with the categorical regular (cyan) vs. irregular (red) classification of verb paradigms in all languages. (Center panel) linear interaction with sample languages as categorical fixed effects. (Right panel) non-linear interaction with sample languages as categorical fixed effects. All plots are obtained by using the R ggplot2 package; related models are respectively calculated with lm function and gam function (gamm4 package). Shaded areas indicate 95% confidence intervals.

Positive slopes indicate, unsurprisingly, that the map gets more and more accurate in anticipating an upcoming symbol as more of the word input is consumed. As has already been shown (see Marzi et al., 2018 for preliminary results on the same set of the 6 languages), TSOMs appear to be significantly more accurate in predicting forms belonging to regular paradigms than to irregular ones, but no apparent interaction is observed between regularity and distance to the stem-suffix boundary. To a first approximation, the evidence seems to show that inflectional regularity consistently facilitates word processing, independently of how inflection is marked cross-linguistically. In fact, the center panel of Figure 4 shows that the 6 languages of our sample present slightly different prediction slopes. Arabic and English exhibit a steeper prediction slope compared with the slope of German, Greek, Italian, and Spanish.

A more interesting picture¹² emerges when we move from a linear regression model to a non-linear regression model of the same data. The rightmost panel of Figure 4 shows how prediction rates vary across languages when the time course of word prediction is modeled by a Generalized Additive Model (GAM). GAMs, and related plots (obtained with the ggplot function), eliminate spurious linear leveling, and allow changes over serial processing to be modeled in a fine-grained way¹³. The ascending path for increasing values of distance to MB basically confirms the linear trend observed in the center panel of Figure 4. But the non-linear interpolation highlights an important discontinuity at the stem-suffix boundary (for distance to MB=0). In English, Greek, Italian and Spanish, the stem-suffix boundary marks a sharp drop in prediction rate, supporting the intuition that when the final letter of a stem is recognized, the map has to revise its expectations for an upcoming symbol. We interpret this as an effect of structural discontinuity between the stem and the following suffix, which is deeper in regularly inflected forms than it is in irregularly inflected forms for all languages in our sample (Figure 5A).

FIGURE 5

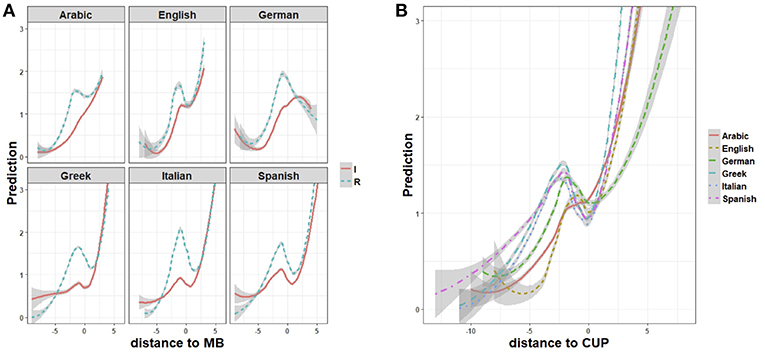
Figure 5. Regression plots (ggplot2) of interaction effects (A) between regularly (cyan lines) and irregularly (red lines) inflected forms and the distance to stem-suffix boundary (distance to MB), and (B) between sample languages and the distance to the Complex Uniqueness Point (distance to CUP=0), in non-linear models (GAMs) fitting the processing prediction rate. Shaded areas indicate 95% confidence intervals.

The same mechanism accounts for the fact that Greek, Italian and Spanish show a deeper prediction drop at the stem-suffix boundary than English does (Figure 5A). Greek, Italian and Spanish inflection markers are, in fact, more numerous and formally more contrastive than inflection markers are in English. The steeper ascending trend in the prediction of English forms has to do with the comparative simplicity of the English system, and the narrower range of possible continuations of the verb stem in regularly as well as irregularly inflected forms. The ascending prediction trend of the Arabic verb is more linear, particularly in irregular inflection (Figure 5A). In fact, the Arabic plot shows a less prominent drop at the stem-suffix boundary (for distance to MB=0), which disappears altogether in irregulars, suggesting a greater structural continuity between the stem and the suffix. This is the combined effect of two factors: stem allomorphy in the perfective forms of irregular verbs, and prefixation of person and number features in the imperfective forms, both concur to reduce processing uncertainty at the stem-suffix boundary¹⁴. Conversely, German exhibits only descending slopes after the stem-suffix boundary (for distance to MB=0). This is an effect of the full formal nesting of shorter endings within longer, onset aligned endings (for instance e-, -en, -end: see Figure 2 above), which makes it hard to predict upcoming symbols when contextual and frequency information is missing. As a result, prediction increases only at the point where the form is fully discriminated from all other forms (i.e., for distance to CUP=0), as shown by the ascending slope for CUP>0 in Figure 5B.

All in all, closer inspection of prediction curves for each language confirms that regular stems are structurally easier to process than irregular stems. Nonetheless, the processing advantage accumulated across regular stems is offset by suffix selection, which requires more effort in adjusting probabilistic expectations for regular forms than for irregular ones. This general, cross-linguistic effect can be interpreted in terms of “surprisal” as a source of processing difficulty (Levy, 2008), caused by the incremental reallocation of the map's expectation for upcoming symbols. In irregular paradigms, the initial processing disadvantage is counterbalanced by a smaller effort (i.e., a smaller decrease in certainty) in processing the transition from a stem to the following suffix. As we will see in more detail in section 5.2.1, this processing facilitation is a consequence of the fact that irregular stems exhibit a formal contrast that regularly inflected forms typically realize with suffixal material. Ultimately, this early contrast provides an early point of lexical discrimination.

5.1.2. Learning Effects

The TSOM learning algorithm has a bias to developing specialized chains of processing nodes (BMUs), which get more and more sensitive to structural discontinuity in the input data. We can monitor chain specialization by observing how prediction accuracy of online word processing evolves through learning. As training progresses, we expect prediction trends to increasingly reflect the underlying morphological structure of inflected forms. Due to chain specialization, a TSOM becomes more and more familiar with recurrent stems and endings. Its ability to predict upcoming symbols increases accordingly, and prediction rates become higher across input words as the map learns to assign maximally entrenched node chains to shared input sub-strings.

Figure 6A plots variation of word prediction rates at different learning epochs (going from epoch 5 to epoch 50 with a 5-epoch step), averaged across all languages in our sample. The prediction rate of inflectional endings starts increasing at epoch 10 (growing slope for x-values ≥0), when the TSOM is not yet able to accurately predict stems (x-values <0). This is the combined effect that input frequency and length have on memory. Endings are, on average, more frequent and shorter than stems, and are thus learned more quickly. Processing sensitivity to stems becomes more discriminative only at later epochs, as shown by the local maximum at distance to MB = −1 at epoch 15. Finally, when stems are predicted accurately (starting from learning epoch 20), the TSOM learns that some specific endings follow only some stems, and can adjust its prediction bias accordingly. This makes prediction values for endings (i.e., for x-values ≥0) increasingly higher at later epochs.

FIGURE 6

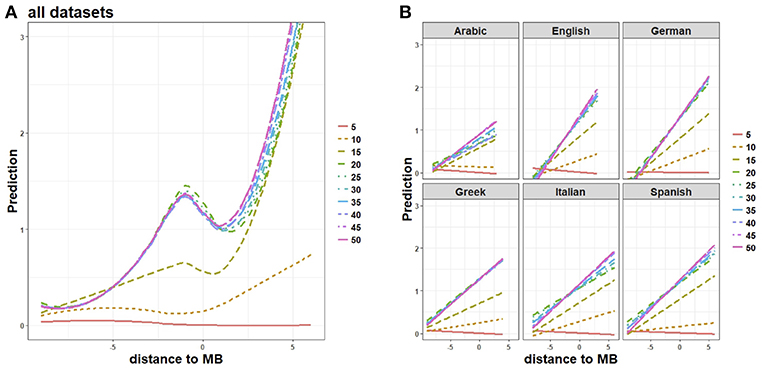
Figure 6. Word structure learning: (A) overall prediction trends and (B) their language-specific linear correlates through 5-to-50 learning epochs, for different letter positions to the stem-suffix boundary (distance to MB). Prediction scores exhibit an increasing fit to training data, weighing up the map's expectations across stems (x-values <0), and endings (x-values ≥0).

Figure 6B shows the linear growth of processing prediction for each language at different epochs (from epoch 5 to epoch 50). The trend shown by our sample of languages is consistent with the intuition that processing prediction and processing ease increase with learning as a function of memory entrenchment of word representations: the more entrenched word representations are, the more easily they are predicted during processing. This is illustrated by the word-graph in Figure 2A (right), which represents the node chains activated by a few forms of German geben “give” at an early learning epoch. At this stage, partially overlapping stem allomorphs (gib-, geb-, and gab-) activate superpositional node chains. This indicates that the Markovian order of the map cannot discriminate between b preceded by the letter a, and the same b preceded by the letter i or the letter e. During training, discriminative specialization results in the word graph being transformed into the tree-like structure of nodes on the left hand side of Figure 2A. Note that a word tree has fewer branching points than the corresponding word graph. This means that when the map arrives at a node with fewer branching paths, uncertainty about the upcoming symbol decreases, and processing prediction increases.

Learning, like prediction, is dependent on word length. However, whereas short words are comparatively more difficult to predict, they are learned more easily. Epochs of word learning as a function of word length are compared for each language in Figure 7A. Unsurprisingly, short words are learned at early epochs and longer words are learned at later epochs irrespective of language. Nonetheless, the time lag can vary depending on the specific inflection system. For example, English is shown to exhibit a steeper learning slope, i.e., a greater difficulty in learning inflected forms of increasing length, and Arabic shows both a steeper slope and a higher intercept.

FIGURE 7

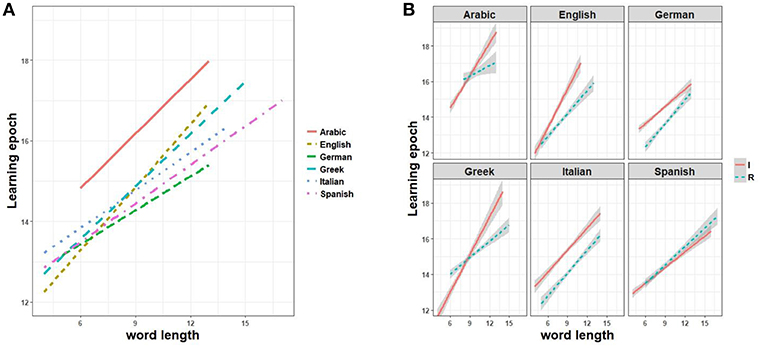
Figure 7. Regression plots of time of lexical acquisition by word length, in linear interaction with (A) sample languages and (B) regular vs. irregular classification of paradigms plotted for each language.

When we look at each language in more detail, we observe an interesting interaction between the impact of word length on learning epochs and inflectional regularity. Figure 7B plots word learning epochs as a function of word length and the regular vs. irregular dichotomous classification for each language. With the only exception of Spanish (where differences do not reach statistical significance, p > 0.1), all languages exhibit different learning paces for regulars vs. irregulars, with the former enjoying advantages over the latter. The pace of learning interacts with word length in Arabic, Greek and English, where long regulars tend to be learned progressively earlier than long irregulars. This contrasts with German, where the trend is reversed, and Italian, which shows no significantly different interaction with increasing length. Note, finally, that when Arabic and Greek irregular forms happen to be significantly shorter than regular forms, the former are learned a few epochs earlier than the latter, reversing the advantage enjoyed by regulars when length is controlled.

5.2. Stem-Family Effects

5.2.1. Processing Effects

The evidence reported in section 5.1 throws into sharp relief a theoretically interesting connection between the structural notions of morphological regularity and transparency, on the one hand, and word processing (un)certainty, on the other hand. Word-and-Paradigm approaches to inflection have questioned the primacy of sublexical constituent structure as a key to understanding speaker's word knowledge. In contrast, they support a view of inflectional competence grounded in a complex network of fully-inflected forms organized in word families of lexically-related members (paradigms) and inflectionally-related members (conjugation classes). Accordingly, morphological regularity is the expression of the formal and lexical support that each inflected form receives from its family members: regularly inflected forms tend to get the largest possible amount of formal support from their paradigmatic companions in terms of redundant stem forms (e.g., walk-s, walk-ed, walk-ing), and from their conjugation members in terms of redundant inflectional markers (e.g., walk-ing, see-ing, speak-ing). In this section, we move away from a dichotomous notion of paradigm regularity to a graded one, based on statistical patterns of lexical co-activation and competition. These patterns are better understood, in line with psycholinguistic evidence of human processing behavior, as word family effects.

In section 3.2, we introduced two ways of assessing paradigm regularity as a gradient: one is based on forms, and the other is based on paradigms. Given a target form, we can calculate the number of stem-sharing members of the form's paradigm, or stem-family size. For each verb paradigm, the (normalized) average stem-family size of the paradigm gives a graded score of paradigm regularity. The two notions are clearly correlated (in our data, r = 0.79, p < 0.001). In a fully regular paradigm, all forms have the same stem-family size. Conversely, suppletive forms in irregular paradigms tend to be isolated. Nonetheless, the two measures account for different effects on word processing. Intuitively, our paradigm regularity score is the same for all members of a paradigm, irrespective of how stem-families are distributed within the paradigm. However, a form supported by a larger stem-family has a different processing cost from a form with an empty stem-family in the same paradigm. Thus, while paradigm regularity can account for different processing costs between different paradigms, the stem-family size explains the variation, in processing costs, between paradigmatically-related forms.

In our simulations, paradigm regularity has a facilitative effect on stem processing. An identical stem, transparently shared by all paradigmatically-related forms, represents a perceptually salient, deeply entrenched formal core of the paradigm. This core is highly familiar, and is accordingly processed more easily. Conversely, degrees of alternation in stem formation for irregular paradigms tend to slow down the processing of the corresponding stems. The more stem allomorphs a paradigm presents, the larger the effort taken to process them, as more points of processing uncertainty are encountered along the way. This is again shown pictorially in Figure 2A, where the shaded nodes of the irregular verb geben, corresponding to its stem allomorphs, are arranged through branching paths, in contrast with the non-branching path associated with the regular base stem of glauben (Figure 2B).

Arabic inflection provides a somewhat exemplary illustration of this dynamic. In Arabic, all verb forms present vowel alternating stems, irrespective of their belonging to regular or irregular paradigms. Nonetheless, irregulars are predicted less easily than regulars (Figure 5), due to the greater formal diversity that irregular stem allomorphs exhibit. Compare, for example, the regular forms katab-tu/katab-ta/katab-a “I wrote”/“you (singular masculine) wrote”/“he wrote” with the second weak forms qul-tu/qul-ta/qāl-a “I said”/“you (singular masculine) said”/“he said”).

The facilitation in processing stems of regularly inflected forms is however counterbalanced by the processing uncertainty incurred at the stem-suffix boundary. In fact, the processing advantage that more regularly inflected forms enjoy across stems is offset by a deeper drop in the prediction rate for an upcoming suffix (Figure 5). This is confirmed when we partial out the interacting influence of paradigm regularity, stem-family size, word length and distance to stem-suffix boundary (MB) in a generalized additive model of prediction rates (Figure 8). Despite the strong positive correlation of paradigm regularity and stem-family size, when these predictors interact, the contributions that they make to the processing of full words go in different directions. When we model the interacting effect of each predictor for stem and ending independently, the facilitation effect of family size on stem processing (Figure 8B, second panel from the left) is reversed into a negative effect on endings (Figure 8C, second panel from the left).

FIGURE 8

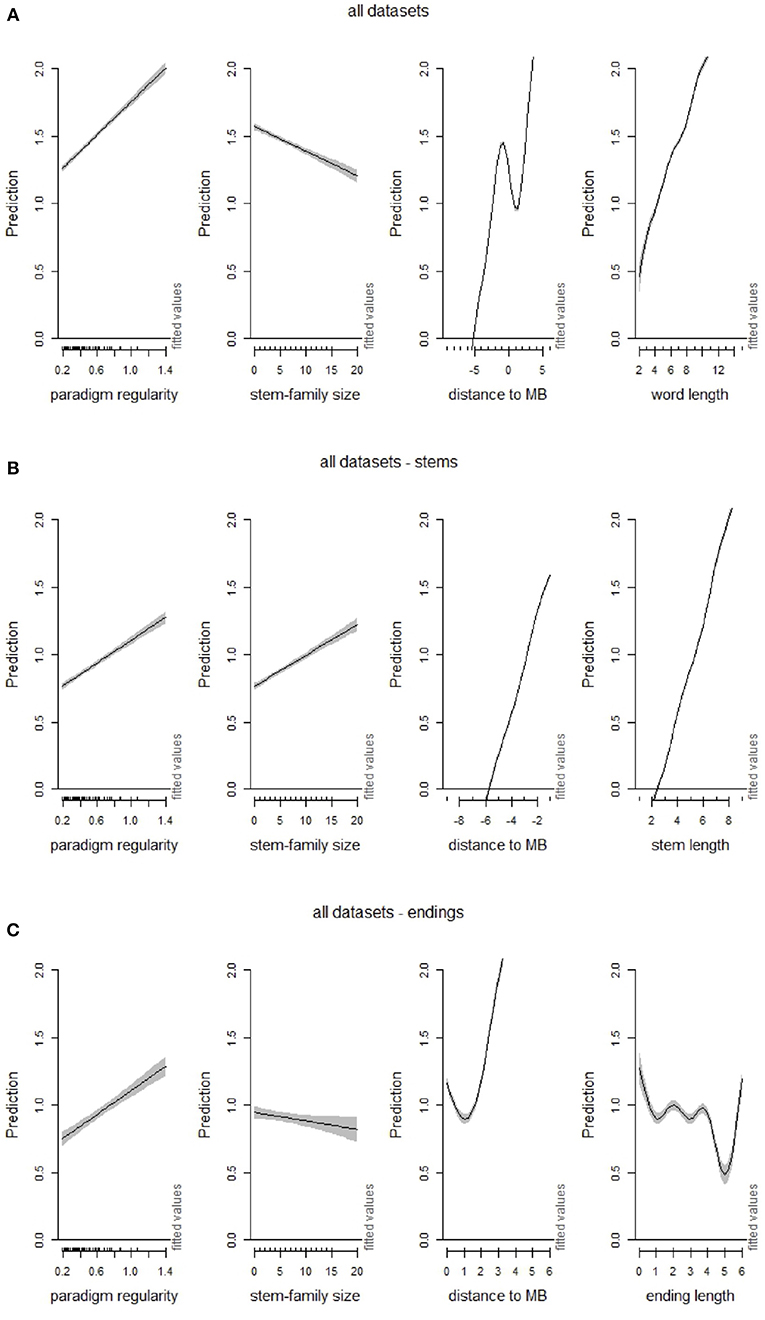
Figure 8. Effects of (graded) paradigm regularity interacting with stem-family size, distance to stem-suffix boundary (MB) and (word, stem and suffix) length in GAMs modeling TSOM prediction rates in: (A) word processing, (B) stem processing, and (C) suffix processing. The specified predictors are taken in interaction with paradigm regularity as summed effects (itsadug package, plot_smooth function).

The interaction of paradigm regularity and stem-family size on word processing is illustrated in more detail through the use of the perspective or contour plots of Figure 9, showing the additive interacting effects of paradigm regularity and stem-family size as predictors for processing prediction of full-forms, stems and suffixes. In the plots, contour lines represent prediction values: brown-yellow shades mark areas where items are processed more easily, and blue shades mark areas where items are processed less easily. Figure 9A shows that forms in more irregular paradigms are always processed with greater difficulty. However, starting from level 0.4 of paradigm regularity, forms are processed with increasing difficulty if they have large stem-families. Conversely, Figure 9B shows that stems appear to be favored by increasing stem-family size, with a mild reversal of this effect only for items in fully regular paradigms (level > 0.8 of paradigm regularity). We can explain these effects by observing that more regular stems are typically followed by a wider range of inflectional endings than highly irregular stems are, and that the number of different endings is proportional to the size of the stem-family. Hence, the larger the stem-family, the higher the processing “surprisal” for upcoming endings (Ferro et al., 2018), as shown in Figure 9C.

FIGURE 9

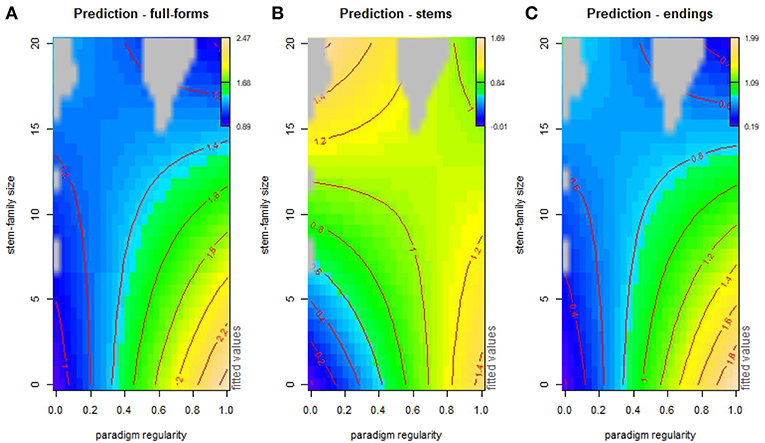
Figure 9. Contour plots of additive interaction effects of stem-family size and paradigm regularity on word (A), stem (B), and ending (C) prediction (itsadug package, fvisgam function). Grid points at a distance of ≥0.2 from the predictor variables are excluded (gray areas).

The consequences of these pervasive stem-family size effects on the perception of morphological structure during word processing are modeled in Figure 10A, where non-linear prediction rates are plotted as a function of distance to MB for classes of inflected forms with increasing stem-family size (ranging from empty to large). Here, processing curves are aligned on the structural joint between stem and suffix (distance to MB = 0), confirming that stem predictability increases with the stem-family size, together with the perception of a structural discontinuity at the stem-suffix boundary. In contrast, forms with little or no support from stem-sharing items show lower prediction rates for stems, and higher prediction rates for suffixes. Finally, smaller or no prediction drops at distance to MB = 0 suggest that an inflected form with an empty-to-small stem-family size is processed and perceived as mono-morphemic.

FIGURE 10

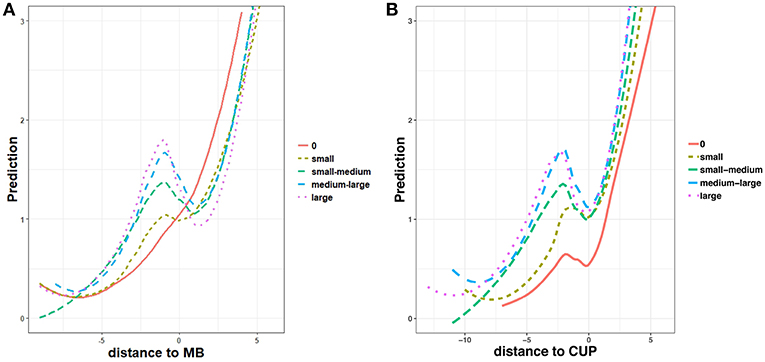
Figure 10. Regression plots of interaction effects between zero, small, small-medium, medium-large and large stem-family sizes and (A) distance to stem-suffix boundary (MB), and (B) distance to CUP, in non-linear models (GAMs) fitting processing prediction rates.

Another processing effect worth emphasizing in this connection is how easily an inflected form is discriminated from its paradigm members. Discriminability is somewhat related to the predictability of an input sequence. However, whereas predictability is related to the entrenchment of a recurrent sequence in our mental lexicon, discriminability is a function of how confusable an input sequence is with other similar sequences. In fact, full form discrimination requires identification of the form's Complex Uniqueness Point (or CUP). Intuitively, the earlier the CUP of an inflected form, the more quickly the form is singled out and accessed in serial recognition. Consider two forms like thought and walked. Unlike walked, whose paradigmatic CUP is positioned at the beginning of the inflectional ending -ed, thought is discriminated from all other forms of THINK when -o is input. Thus, thought is discriminated at an earlier point in time than walked is, because of the shorter distance between the form onset and its CUP (2 letters, vs. 4 letters for walked) and the longer tail of predicted symbols after CUP (4 letters, vs. only 1 letter predicted for walked). This tendency is confirmed by our analysis of TSOM data. Irregulars are, on average, easier to discriminate than regularly inflected items. In Figure 10B, we plot non-linear prediction rates as a function of distance to CUP, for the same five classes of stem-family size used in Figure 10A. For all forms, prediction lines are centered on CUP (i.e., for distance to CUP=0). Forms with empty stem families show a shorter time lag between their onset and their CUP. In addition, they have a longer tail of predicted symbols after CUP. As we move from isolated forms to forms with increasing stem-family size, the time interval between onset and CUP increases, and the tail of symbols after CUP shortens. Family size is a significant predictor of this trend, even when the length of inflected forms is added in interaction to the GAM.

To sum up, stem-family size appears to influence the rate at which TSOMs process verb forms, confirming that paradigm regularity facilitates processing. The stems of inflected forms with a large stem-family size are easier to predict, but this facilitation is compensated at the stem-suffix boundary, where a significant reduction in processing prediction can be interpreted as a functional correlate of structural discontinuity. Conversely, the stems of inflected items with empty-to-small stem-family size are more difficult to predict, and take more processing effort, but show a considerably smaller drop in prediction at MB, which suggests that they are processed more holistically. In addition, irregulars are discriminated more quickly from their paradigmatic companions than regularly inflected forms are. It is noteworthy that this effect is not an artifact of irregulars being, on average, shorter than regulars, but reflects a genuine morphological pattern: irregulars tend to mark, through stem allomorphy, information that regularly inflected forms mark with their suffixes. Ultimately, irregularly inflected forms are easier to discriminate because they are part of a more contrastive network of formal oppositions.

5.2.2. Learning Effects

From a learning perspective, being part of a larger stem-family is an advantage. Intuitively, the size of a stem-family defines the number of distinct affixes the stem can combine with: the larger the stem-family size, the greater the potential of the stem for filling in more paradigm cells. Hence, a stem-family defines the analogical space where a verb establishes its connections with other paradigms. Other things being equal (e.g., length, cumulative frequency, and wordlikeness), a verb form with a large stem-family is learned more easily than an isolated form, as shown in Figure 11A, where we plot a largely predominant facilitation effect of stem-family size on word learning across the entire length range. A regular paradigm is a classical example of such a stem-family, where all family members share the same stem followed by a systematic pool of inflectional endings (which are, in turn, shared by other paradigms). Being associated with a large range of differently inflected forms makes it possible for a TSOM to consolidate intra-paradigmatic formal redundancies, and infer missing forms more accurately. Conversely, more discriminated irregular forms are acquired more slowly for exactly the same reason that they are accessed more holistically and effectively: because they happen to be isolated.

FIGURE 11

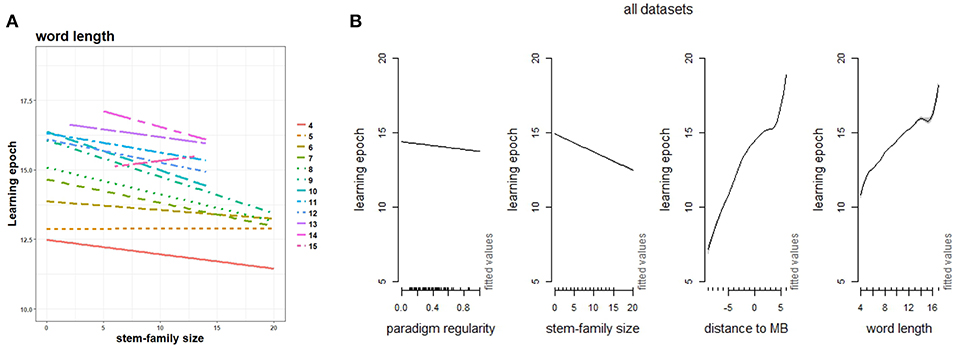
Figure 11. (A) Regression plot of time of lexical acquisition by size of stem-family in linear interaction with word length. Fixed effects are word length (as categorical predictor), and stem-family size; (B) summed effects of paradigm regularity interacting with stem-family size, distance to stem-suffix boundary (MB) and word length in a GAM modeling time of acquisition (learning epoch) for verb forms in all sample languages.

In Figure 11B, we assess the interacting influence of paradigm regularity, stem-family size, word length and distance to MB in a generalized additive model of the pace of word acquisition. In this model, acquisition is jointly facilitated by both factors, unlike what we observed for processing prediction (Figure 8A) where paradigm regularity and stem-family size have contrasting effects. The contour plots of Figure 12 show the interaction of these factors in more detail. Stem-family is shown to have a main facilitation effect on word learning, which is stronger within weakly regular paradigms. This suggests that even when a verb is associated with many unpredictable stems, the distribution of these stems in their families affects learning. Regular paradigms are facilitative too, but their influence is comparatively less prominent. It is noteworthy that this general word-level effect is differently apportioned when we focus on the pace of stem learning: stems are learned significantly more quickly within regular paradigms, whereas the size of their stem-family has only a marginal (positive) effect in the process. Finally, endings are learned more quickly in regular paradigms, but the facilitative influence of the size of the stem-family in this case is considerably more significant.

FIGURE 12

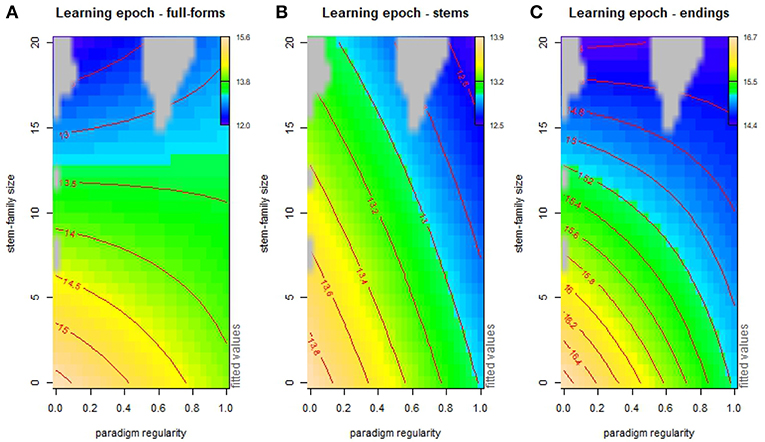
Figure 12. Contour plots of additive interaction effects of stem-family size and paradigm regularity on word (A), stem (B), and ending (C) learning. Grid points at a distance of ≥0.2 from the predictor variables are excluded (gray areas).

Finally, to assess the independent impact of stem-family size on word learning, we ran a generalized additive model including stem-family size, word length and distance to stem-suffix boundary as predictors for learning epoch (R²(adj) = 0.53), and compared it with a similar model where the paradigmatic predictor is paradigm regularity (R²(adj) = 0.28). The robustness of the stem-family model (see Table 2) provides solid support for the hypothesis that family size is the driving paradigmatic force in word learning¹⁵.

TABLE 2

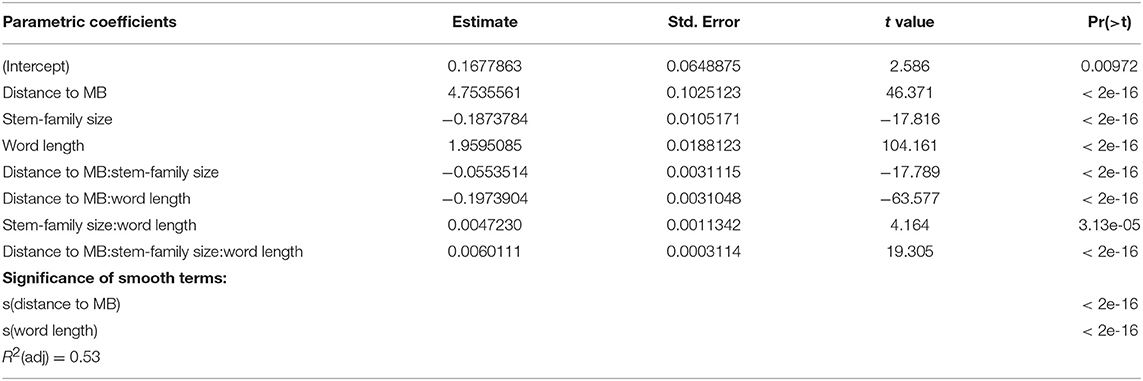
Table 2. GAM fitted to word learning epochs using stem-family size as the only paradigmatic predictor: learning epoch~ stem-family size*distance to MB*word length + s(distance to MB) + s(word length).

6. General Discussion and Concluding Remarks

Inflectional complexity is inherently multidimensional. It lends itself rather reluctantly to an assessment in terms of a single factor or measure. Traditional approaches to complexity are based on either an inventory of morphosyntactic features and their markers, or on a full grammatical description of an inflection system. Both strategies require considerable preliminary knowledge about lexical/grammatical units as well as rules/processes for their segmentation and recombination. Ultimately, they appear to place more emphasis on the descriptive adequacy of some system of formalized knowledge, than on inflectional complexity per se.

More recently, information-theoretic approaches have tried to eschew such a circular assessment of system complexity, by looking at patterns of interpredictability in the distribution of inflectional data. These patterns are not scattered randomly across inflectional paradigms. On the contrary, they are distributed in ways that reduce the amount of uncertainty in mastering inflection. Such a structured system of implicative relations addresses a few learnability issues by constraining an otherwise very large hypothesis space. This is certainly a step forward in understanding inflection and measuring its complexity. However, there are a number of important issues that it leaves unaddressed.

Form interpredictability requires preliminary identification of patterns of morphological redundancy, such as those allowing the resolution of a simple analogical proportion like <walk :: walked = talk :: ?>. However, the hypothesis space of formal mapping may vary considerably from language to language, as witnessed by proportions like <machen :: gemacht = lachen :: ?> (German) and <kataba :: yaktubu = hadama :: ?> (Arabic). For the idea of measuring the complexity of an inflectional system in terms of information entropy to be empirically verifiable, we have to be fairly specific about how speakers can acquire these patterns in the first place, and what learning principles provide the algorithmic basis for bootstrapping patterns with no a priori knowledge about them. What cues allow the identification of sublexical parts? Do these parts provide, in turn, functional cues to lexical processing? Are all morphological systems equally complex to process and learn? And if they are not, why?

To meet its communicative goals any inflection system needs to be learnable in the first place. In addition, it must also be functional from the standpoint of processing requirements, and its inner organization must address fundamental discriminative concerns about efficiency in lexical access. In particular, inflected forms should not simply be easy to generalize, but also easy to process and amenable to accurate and efficient access. Issues of learnability, processability and discriminability are not necessarily mutually contradictory, but they may pull in different directions. Examining their complex interaction requires much more than just a way to gauge inferential entropy in a static repository of inflected forms. In this paper, we suggested using basic discriminative learning principles and a type of recurrent artificial network to clarify the multidimensional nature of inflectional complexity in the light of our understanding of the interaction between learning principles and human word processing behavior.

As a general point, the evidence offered in this paper shows that the processing cost of typologically different inflectional systems oscillates within a fairly narrow range (Figure 4, center panel), and that this range is actually modulated by morphological structure (Figure 4, right panel). It is noteworthy that the steepest linear slopes of processing prediction in the center panel of Figure 4 are associated with Arabic and English, while German, Greek, Italian and Spanish present less steep word processing trends. It would be an unwarranted oversimplification, however, to conclude that Arabic and English have less complex inflection systems. In Arabic, the effect is mainly due to the discontinuous structure of verb stem allomorphs, which systematically anticipate the marking of a few morphosyntactic features in both regulars and irregulars, and make endings easier to predict. The result is a lower rate of processing uncertainty at the stem-suffix boundary, compared with other languages. A similar processing facilitation is observed in English for a different reason: the small range of endings marking inflectional contrast. Conversely, German, Greek, Italian and Spanish show higher prediction rates for stem processing, followed by a deeper drop in prediction at the stem-suffix boundary, due to a richer set of (possibly nested) inflectional suffixes. Languages typologically vary in the ways they apportion morpho-syntactic information across inflected words. This variation has a significant impact on word processing strategies, because finding information at certain points in the input word may reduce processing uncertainty at later points. Nonetheless, when the amount of morpho-syntactic information to convey through inflection is approximately constant across languages¹⁶, cross-linguistic variation in processing uncertainty can only oscillate within a narrow range.

This has also interesting repercussions on learning. Judging from the distribution of per-word learning epochs (Figure 3A), Arabic is arguably the most difficult language to learn in our sample. In TSOMs, this is caused by the strong paradigmatic competition between discontinuous roots intercalated by different vowel patterns. Nonetheless, the system appears to substantially benefit from interpredictability patterns, as shown by the distribution of learning span values in Figure 3B. This suggests that the higher cost of learning discontinuous stems in Arabic is compensated by the relatively shorter length of inflected forms (compared with the length of inflected forms in other languages), and by the fact that inflectional class information is conveyed by the stem. In other languages like Greek, Italian and Spanish, where class information is mostly conveyed after the stem, selection of the appropriate inflectional ending is considerably more uncertain (in line with Ackerman and Malouf's LCEC, Ackerman and Malouf, 2013).

From a functional perspective, the simulation evidence offered in this paper can be interpreted as the result of a balancing act between two potentially competing communicative requirements: (i) a recognition-driven tendency for a maximally contrastive system, where all inflected forms, both within and across paradigms, present the earliest possible (complex) uniqueness point of recognition; and (ii) a production-driven bias for a maximally generalizable inflection system, where most forms in a paradigm can be inferred from any other form in the same paradigm. In an efficient communication system, both requirements should be balanced. A poorly contrastive system would be dysfunctional for practical communication purposes, because the elements in the system are harder to discriminate. A communication system, however, must also be open and adaptive, because new elements must continuously be added to be able to refer to an ever changing pragmatic environment. Clearly, a maximally contrastive system of irregular forms would take the least effort to process, but would require full storage of unpredictable items, thus turning out to be slow to learn. A maximally generalizable system, on the other hand, would be comparatively easier to learn, but rather inefficient to process, especially when it comes to low-frequency items.

To conclude, there are a few implications of the present work that are worth emphasizing here because of their impact on our current understanding of word knowledge. First, from observing discriminative learning principles in action, we get a very concrete sense of the view that processing and learning issues are strongly inter-related and mutually-implied in language. Although they may pull in different directions, they are, in fact, two sides of the same coin. More precisely, they define two distinct temporal dynamics (a short-term one for processing, and a long-term one for learning) of the same unitary underlying process. Accordingly, representations of word forms in our mental lexicon are only stored patterns of their processing history: what we learn of language is basically how we process it (Marzi and Pirrelli, 2015). Secondly, temporal patterns of discontinuous redundant units in time-series are known to be more difficult to process by humans (Hahn and Bailey, 2005). Hence, it is expected that they should be more difficult to learn and organize in our mental lexicon. This point has interesting implications both for our categorization of inflectional processes into regular and irregular, and in cross-linguistic terms. Systems of formally alternating complex units are easier to discriminate, since they provide shorter CUPs and thus take, overall, a smaller processing surprisal (Balling and Baayen, 2008, 2012). However, they are more difficult to acquire, since they are more isolated from other existing forms, and thus harder to infer from familiar, redundant patterns. Less discriminative, highly syncretic systems are much easier to generalize and learn, and, for the same reason, more ambiguous (less informative) and more difficult to interpret in their context of use. Such a complex dynamic of co-existing and conflicting processing requirements has to find a balance, both within the same language (as a function of how regulars and irregular items are stored and co-organized in the mental lexicon), and cross-linguistically (as a function of typologically diverse processes of inflection marking). In the end, each language (and arguably each individual learner) is likely to strike a different balance, which nonetheless falls within a reasonably tight range of variation, bounded by a few learnability and processability requirements. This suggests that full investigation of morphological systems will likely benefit from the use of basic concepts from the toolkit of complexity theory in biological networks, such as emergence, non-linearity and self-organization.

Over the past few decades, morphological paradigms have acquired growing importance in our understanding of complex inflectional systems. While our work provides novel evidence supporting this trend, it also suggests that paradigms are functionally specialized by-products of more general principles of lexical self-organization, based on the more primitive notion of word neighborhood. The morphological correlate of this notion, namely the family of inflected types sharing the same stem, or stem-family, turned out to be key to understanding processing and learning issues. The size and distributional entropy of stem-families can ultimately account for the effects of ease of generalization, thus providing a more general, process-oriented basis for understanding patterns of interpredictability in morphology learning. This perspective lends strong support to the view that the complexity of the inflectional system of a language is a collective, emergent property that cannot be deduced from its individual forms. In addition, it suggests that a processing-oriented, discriminative view of inflection systems is not incompatible with the idea that their systemic self-organization rests on smaller “morphomic” patterns of structural redundancy.

Author Contributions

CM ran the experiments on German, English, Arabic and Spanish, conducted data analysis and statistical modeling of the results, and developed the conceptual and theoretical framework of this work. MF was responsible for computational modeling, ran the experiments on Italian and Greek, designed and extracted functional responses and structural evidence of TSOMs for quantitative data analysis. VP developed the linguistic framework and the theoretical background of the present study. Theoretical implications and concluding remarks were jointly discussed. CM and VP critically revised previous versions of the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomm.2019.00048/full#supplementary-material

Footnotes

1. ^Word-and-Paradigm Morphology (Matthews, 1991; Blevins, 2016) explicitly avoids the central problem of segmenting an inflected form like walked into meaningful sublexical parts (or “morphemes,” e.g., walk-ed), and expressing the morpho-lexical content of the whole as a function of the morpho-lexical content of its parts. Rather, inflected words are themselves parts of two parallel networks of formal and semantic relations between members of the same paradigm. Crucially, Word and Paradigm Morphology says nothing about the ways the two networks are mutually related, thus avoiding problems of morphemes with no meanings (empty morphemes), meanings with no morphemes (zero morphemes), bracketing paradoxes etc. This strikes us as the most typologically-neutral approach to an assessment of inflectional complexity, as it eschews any attempt to put a morphemic straitjacket to non agglutinative languages. As TSOMs are trained on inflected forms with no morphosemantic and morphosyntactic content, only redundant formal relations are learned.

2. ^According to Dressler and colleagues (Bittner et al., 2003), European languages can be arranged along an inflectional complexity continuum, ranging from a more inflecting/fusional type (left) to a more isolating type (right):

Lithuanian→Greek→Russian→Croatian→Italian→

Spanish→German→Dutch→French→English.

3. ^Starting from Marlsen-Wilson's classical definition of “uniqueness point” (Marslen-Wilson, 1984), we will make use of more recent refinements of this notion (Balling and Baayen, 2008, 2012).

4. ^A running version of the TSOM package can be downloaded at http://www.comphyslab.it/redirect/?id=frontiers2019.

5. ^Our data sources are: CELEX (Baayen et al., 1995), for German and English; the Italian Paisà Corpus (Lyding et al., 2014); the European Spanish Subcorpus of the Spanish TenTen Corpus (www.sketchengine.co.uk); the SUBTLEX-GR corpus (Dimitropoulou et al., 2010) for Modern Greek, and the Penn Arabic Treebank (Maamouri et al., 2004). The full set of word forms, for each language, is available at http://www.comphyslab.it/redirect/?id=lrec2018_data.

6. ^For English, German, Modern Greek, Italian and Spanish, the list includes all present and past indicative cells. English, German, Italian and Spanish also include the infinitive, past participle and gerund/present participle cells, which are replaced by the three singular cells of the simple future in Modern Greek. For Standard Modern Arabic, we selected the first, second and third masculine singular and plural cells, and the third feminine singular cell for both the imperfective and perfective.

7. ^www.qamus.org/transliteration.htm.

8. ^In fact, Ballling and Baayen's definition of UP1 is intended to index competition from morphologically unrelated words only (Balling and Baayen, 2008, 2012). However, this is justified by the fact that their database only includes regularly inflected forms, i.e., inflected forms showing no stem allomorphy: in this case, identification of the stem automatically entails identification of the entire paradigm. Our operational definition of UP1 represents a natural extension of Balling and Baayen's criteria to a dataset containing irregularly inflected forms.

9. ^In stem formation, transparency and systematicity do not necessarily correlate with predictability. Modern Greek provides a good example of transparent and systematic stem formation processes which however are not predictable, as they require a thematic vowel whose selection is based on lexical information (Ralli, 2014; Bompolas et al., 2017).

10. ^Table 1 shows that English and (to a lesser extent) German conjugations exhibit identical verb forms (morphological syncretism) in a sizable subset of the 15 paradigm cells we selected. It can be objected that we are imposing the paradigm structure of inflectionally richer languages on inflectionally more impoverished ones, with the effect of spuriously inflating the token distribution of our dataset in languages such as English, where the base form is presented to the TSOM five times as many as −s forms are. However, we contend that our training sets are indeed comparable cross-linguistically, and can mirror realistic developmental conditions. The paradigmatic space of a language is not defined by the amount of morphological contrast conveyed by its inflected forms, but by the set of morphosyntactic relations (e.g., subject-verb agreement) holding between word forms in context. Children acquire inflected forms by binding them to larger contexts (e.g., she's walking, it rains, etc., Wilson, 2003; Pine et al., 2008), and by abstracting away from recurrent combinations of number, person, gender, case, tense and aspect features in context. If a specific inflected form is seen in different such combinations (e.g., I walk, you walk, we walk, they walk), the child is repeatedly exposed to an invariant form, whose token frequency will correspondingly increase relative to other paradigmatically-related forms (e.g., walks and walking). This is confirmed by developmental evidence showing that extensive syncretism has perceivable effects on the child's intake of the amount and distribution of morphological contrast exhibited by a language inflection (Legate and Yang, 2007; Pine et al., 2008; Xanthos et al., 2011; Krajewski et al., 2012). Thus, although we are deliberately partialing out token frequency effects (which appear to show complex a interaction with word category, lexico-semantic class, modality and age of acquisition: see Bornstein et al., 2004; Goodman et al., 2008), our data enable us to focus on non trivial type-driven aspects of dynamic paradigm self-organization.

11. ^This is not needed in Standard Modern Arabic, whose learning span is smaller than in Greek, Italian and Spanish (but larger than in English and German), as Arabic class information is, in most cases, already conveyed by the verb stem.

12. ^The non-linear model is statistically more robust, as confirmed by an ANOVA Chi-squared test: p-value < 0.001.

13. ^It should be noted that all word forms are centered on the 0-value, i.e., at the stem-suffix boundary. This makes the interval representing the onset of words less confident, due the possible presence of an inflectional prefix and to differences in length between the stems.

14. ^In Arabic imperfective forms (both regular and irregular), second and third person values are conveyed by the prefixes ta- and ya- respectively, and number is marked by the suffixes -u for the singular, and -uwna for the plural. In the first person, person and number are syncretically realized by two different prefixes followed by an identical suffix (-u). Hence, the amount of residual processing uncertainty at the stem-suffix boundary is drastically reduced to a binary choice between -u and -uwna for the second person and the third person only. In perfective forms, regular verbs select one stem followed by different endings for different combinations of number, person and gender features, and irregular verbs select a specific stem allormorph for different combinations of gender and number values with the 3rd person. This further reduces processing uncertainty in the perfective forms of irregular verbs.

15. ^In Table 2, predicted, standard error and p values are detailed for each of the independent variables. The adjusted R-squared expresses the percentage of explained deviance. The intercept value is referred to our dependent variable (learning epoch) when all the independent predictors are 0.

16. ^We are not suggesting that such an invariance in the amount of inflectional information holds for all languages. For example, Basque verb agreement marks an inflected verb form with affixes for subject, direct object and indirect object case (Austin, 2010, 2012). The system is agglutinative, and the number of possible distinct affix combinations for ditransitive verbs soon gets very large (up to 102 different forms in the present indicative of the auxiliary). Thus the amount of syntactic context that must be processed for a child to check case assignment on the main verb form, is considerably larger than what is needed for languages like German, Italian or Spanish.

References

Ackerman, F., Blevins, J. P., and Malouf, R. (2009). “Parts and wholes: patterns of relatedness in complex morphological systems and why they matter,” in Analogy in Grammar: Form and Acquisition, eds J. P. Blevins and J. Blevins (Oxofrd, UK: Oxford University Press), 54–82.

Google Scholar

Ackerman, F., and Malouf, R. (2013). Morphological organization: the low conditional entropy conjecture. Language 89, 429–464. doi: 10.1353/lan.2013.0054

CrossRef Full Text | Google Scholar

Albright, A. (2002). Islands of reliability for regular morphology: evidence from italian. Language 78, 684–709. doi: 10.1353/lan.2003.0002

CrossRef Full Text | Google Scholar

Althaus, N., and Mareschal, D. (2013). Modeling cross-modal interactions in early word learning. IEEE Trans. Auton. Ment. Dev. 5, 288–297. doi: 10.1109/TAMD.2013.2264858

CrossRef Full Text | Google Scholar

Andrews, S. (1997). The effect of orthographic similarity on lexical retrieval: resolving neighborhood conflicts. Psychon. Bull. Rev. 4, 439–461. doi: 10.3758/BF03214334

CrossRef Full Text | Google Scholar

Aronoff, M. (1994). Morphology by Itself: Stems and Inflectional Classes. Number 22. Cambridge, MA: The MIT Press. doi: 10.2307/416331

CrossRef Full Text | Google Scholar

Austin, J. (2010). Rich inflection and the production of finite verbs in child language. Morphology 20, 41–69. doi: 10.1007/s11525-009-9144-7

CrossRef Full Text | Google Scholar

Austin, J. (2012). The case-agreement hierarchy in acquisition: evidence from children learning basque. Lingua 122, 289–302. doi: 10.1016/j.lingua.2011.10.013

CrossRef Full Text | Google Scholar

Baayen, H. R., Piepenbrock, P., and Gulikers, L. (1995). The CELEX Lexical Database (CD-ROM). Philadelphia, PA: Linguistic Data Consortium, University of Pennsylvania. p. 438–481.

Baayen, R. H., Chuang, Y.-Y., Shafaei-Bajestan, E., and Blevins, J. P. (2019). The discriminative lexicon: a unified computational model for the lexicon and lexical processing in comprehension and production grounded not in (de) composition but in linear discriminative learning. Complexity 2019:4895891. doi: 10.1155/2019/4895891

CrossRef Full Text | Google Scholar

Baayen, R. H., Milin, P., Ðurđević, D. F., Hendrix, P., and Marelli, M. (2011). An amorphous model for morphological processing in visual comprehension based on naive discriminative learning. Psychol. Rev. 118, 438–481. doi: 10.1037/a0023851

PubMed Abstract | CrossRef Full Text | Google Scholar

Balling, L. W., and Baayen, R. H. (2008). Morphological effects in auditory word recognition: evidence from danish. Lang. Cogn. Process. 23, 1159–1190. doi: 10.1080/01690960802201010

CrossRef Full Text | Google Scholar

Balling, L. W., and Baayen, R. H. (2012). Probability and surprisal in auditory comprehension of morphologically complex words. Cognition 125, 80–106. doi: 10.1016/j.cognition.2012.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Bane, M. (2008). “Quantifying and measuring morphological complexity,” in Proceedings of the 26th West Coast Conference on Formal Linguistics (Berkeley, CA: University of California), 69–76.

Google Scholar

Bates, E., and MacWhinney, B. (1987). “Competition, variation, and language learning,” in Mechanisms of Language Acquisition, ed B. MacWhinney (Hillsdale, NJ: Lawrence Erlbaum Associates), 157–193.

Google Scholar

Bearman, M., Brown, D., and Corbett, G. G. editors (2015). Understanding and Measuring Morphological Complexity. Oxford, UK: Oxford University Press.

Google Scholar

Bickel, B., and Nichols, J. (2005). “Inflectional synthesis of the verb,” in The World Atlas of Language Structures, eds M. Haspelmath, M. S. Dryer, D. Gil, and B. Comrie (Oxford, UK: Oxford University Press), 94–97.

Google Scholar

Bittner, D., Dressler, W. U., and Kilani-Schoch, M. editors (2003). Development of Verb Inflection in First Language Acquisition: A Cross-Linguistic Perspective. Berlin: Mouton de Gruyter.

Google Scholar

Blevins, J. P. (2016). Word and Paradigm Morphology. Oxford, UK: Oxford University Press.

Google Scholar

Blevins, J. P., Milin, P., and Ramscar, M. (2017). “The zipfian paradigm cell filling problem,” in Morphological Paradigms and Functions, eds F. Kiefer, J. P. Blevins, and H. Bartos (Leiden: Brill), 141–158.

Google Scholar

Blom, E. (2007). Modality, infinitives, and finite bare verbs in Dutch and English child language. Lang. Acquisit. 14, 75–113. doi: 10.1080/10489220701331821

CrossRef Full Text | Google Scholar

Bompolas, S., Ferro, M., Marzi, C., Cardillo, F. A., and Pirrelli, V. (2017). For a performance-oriented notion of regularity in inflection: the case of modern greek conjugation. Ital. J. Comput. Linguist. 3, 77–92. doi: 10.4000/books.aaccademia.1721

CrossRef Full Text

Bonami, O., and Beniamine, S. (2016). Joint predictiveness in inflectional paradigms. Word Struct. 9, 156–182. doi: 10.3366/word.2016.0092

CrossRef Full Text | Google Scholar

Bornstein, M. H., Cote, L. R., Maital, S., Painter, K., Park, S.-Y., Pascual, L., et al. (2004). Cross-linguistic analysis of vocabulary in young children: Spanish, dutch, french, hebrew, italian, korean, and american english. Child Dev. 75, 1115–1139. doi: 10.1111/j.1467-8624.2004.00729.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Q., and Mirman, D. (2012). Competition and cooperation among similar representations: toward a unified account of facilitative and inhibitory effects of lexical neighbors. Psychol. Rev. 119:417. doi: 10.1037/a0027175

PubMed Abstract | CrossRef Full Text | Google Scholar

Crago, M. B., and Allen, S. E. (2001). Early finiteness in inuktitut: the role of language structure and input. Lang. Acquisit. 9, 59–111. doi: 10.1207/S15327817LA0901_02

CrossRef Full Text | Google Scholar

Dimitropoulou, M., Duñabeitia, J. A., Avilés, A., Corral, J., and Carreiras, M. (2010). Subtitle-based word frequencies as the best estimate of reading behavior: the case of greek. Front. Psychol. 1:218. doi: 10.3389/fpsyg.2010.00218

PubMed Abstract | CrossRef Full Text | Google Scholar

Elman, J. L. (1990). Finding structure in time. Cogn. Sci. 14, 179–211. doi: 10.1207/s15516709cog1402_1

CrossRef Full Text | Google Scholar

Evans, N., and Levinson, S. C. (2009). The myth of language universals: language diversity and its importance for cognitive science. Behav. Brain Sci. 32, 429–492. doi: 10.1017/S0140525X0999094X

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferro, M., Marzi, C., and Pirrelli, V. (2011). A self-organizing model of word storage and processing: implications for morphology learning. Lingue e Linguaggio 10, 209–226. doi: 10.1418/35840

CrossRef Full Text | Google Scholar

Ferro, M., Marzi, C., and Pirrelli, V. (2018). Discriminative word learning is sensitive to inflectional entropy. Lingue e linguaggio 17, 307–327. doi: 10.1418/91871

CrossRef Full Text | Google Scholar

Finkel, R., and Stump, G. (2007). Principal parts and morphological typology. Morphology 17, 39–75. doi: 10.1007/s11525-007-9115-9

CrossRef Full Text | Google Scholar

Goldsmith, J. (2001). Unsupervised learning of the morphology of a natural language. Comput. Linguist. 27, 153–198. doi: 10.1162/089120101750300490

CrossRef Full Text | Google Scholar

Goodman, J. C., Dale, P. S., and Li, P. (2008). Does frequency count? Parental input and the acquisition of vocabulary. J. Child Lang. 35, 515–531. doi: 10.1017/S0305000907008641

PubMed Abstract | CrossRef Full Text | Google Scholar

Hahn, U., and Bailey, T. M. (2005). What makes words sound similar? Cognition 97, 227–267. doi: 10.1016/j.cognition.2004.09.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Haspelmath, M., Dryer, M. S., Gil, D., and Comrie, B. (eds.). (2005). The World Atlas of Language Structures, Vol. 1. Oxford, UK: Oxford University Press.

Google Scholar

Juola, P. (1998). Measuring linguistic complexity: the morphological tier. J. Quant. Linguist. 3, 206–213. doi: 10.1080/09296179808590128

CrossRef Full Text | Google Scholar

Kohonen, T. (2002). Self-Organizing Maps, volume 30 of Springer Series in Information Sciences. Berlin: Springer.

Google Scholar

Kolmogorov, A. N. (1968). Three approaches to the quantitative definition of information. Int. J. Comput. Math. 2, 157–168. doi: 10.1080/00207166808803030

CrossRef Full Text | Google Scholar

Krajewski, G., Lieven, E. V., and Theakston, A. L. (2012). Productivity of a polish child's inflectional noun morphology: a naturalistic study. Morphology 22, 9–34. doi: 10.1007/s11525-011-9199-0

CrossRef Full Text | Google Scholar

Kuperman, V., Bertram, R., and Baayen, R. H. (2010). Processing trade-offs in the reading of dutch derived words. J. Mem. Lang. 62, 83–97. doi: 10.1016/j.jml.2009.10.001

CrossRef Full Text | Google Scholar

Legate, J. A., and Yang, C. (2007). Morphosyntactic learning and the development of tense. Lang. Acquisit. 14, 315–344. doi: 10.1080/10489220701471081

CrossRef Full Text | Google Scholar

Levy, R. (2008). Expectation-based syntactic comprehension. Cognition 106, 1126–1177. doi: 10.1016/j.cognition.2007.05.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, P., Zhao, X., and Mac Whinney, B. (2007). Dynamic self-organization and early lexical development in children. Cogn. Sci. 31, 581–612. doi: 10.1080/15326900701399905

PubMed Abstract | CrossRef Full Text | Google Scholar

Luce, P. A., and Pisoni, D. B. (1998). Recognizing spoken words: the neighborhood activation model. Ear Hear. 19:1. doi: 10.1097/00003446-199802000-00001

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyding, V., Stemle, E., Borghetti, C., Brunello, M., Castagnoli, S., Dell' Orletta, F., et al. (2014). “The paisá corpus of italian web texts,” in Proceedings of the 9th Web as Corpus Workshop (WaC-9)@ EACL 2014 (Gothenburg: Association for Computational Linguistics), 36–43.

Google Scholar

Maamouri, M., Bies, A., Buckwalter, T., and Mekki, W. (2004). “The penn arabic treebank: building a large-scale annotated arabic corpus,” in NEMLAR Conference on Arabic Language Resources and Tools (Paris: ELDA), Vol. 27, 466–467.

Google Scholar

Magnuson, J. S., Dixon, J. A., Tanenhaus, M. K., and Aslin, R. N. (2007). The dynamics of lexical competition during spoken word recognition. Cogn. Sci. 31, 133–156. doi: 10.1080/03640210709336987

PubMed Abstract | CrossRef Full Text | Google Scholar

Marslen-Wilson, W. D. (1984). “Function and process in spoken word recognition: a tutorial review,” in Attention and Performance X: Control of Language Processes, eds H. Bouma and D. G. Bouwhuis (New Jersey, NJ: Lawrence Erlbaum Associates), 125–150.

Google Scholar

Marzi, C., Ferro, M., and Nahli, O. (2017). Arabic word processing and morphology induction through adaptive memory self-organisation strategies. J. King Saud Univ. Comput. Inform. Sci. 29, 179–188. doi: 10.1016/j.jksuci.2016.11.006

CrossRef Full Text | Google Scholar

Marzi, C., Ferro, M., Nahli, O., Belik, P., Bompolas, S., and Pirrelli, V. (2018). “Evaluating inflectional complexity crosslinguistically: a processing perspective,” in Proceedings of the Eleventh International Conference on Language Resources and Evaluation (LREC 2018), Miyazaki, Japan, eds N. Calzolari, K. Choukri, C. Cieri, T. Declerck, S. Goggi, K. Hasida, H. Isahara, B. Maegaard, J. Mariani, H. Mazo, A. Moreno, J. Odijk, S. Piperidis, and T. Tokunaga (Paris: European Language Resources Association (ELRA)), 3860–3866.

Google Scholar

Marzi, C., Ferro, M., and Pirrelli, V. (2012). Word alignment and paradigm induction. Lingue e Linguaggio XI, 251–274.

Google Scholar

Marzi, C., Ferro, M., and Pirrelli, V. (2014). Morphological structure through lexical parsability. Lingue e Linguaggio 13, 263–290.

Google Scholar

Marzi, C., and Pirrelli, V. (2015). A neuro-computational approach to understanding the mental lexicon. J. Cogn. Sci. 16, 493–535. doi: 10.17791/jcs.2015.16.4.492

CrossRef Full Text | Google Scholar

Matthews, P. H. (1991). Morphology. Cambridge: Cambridge University Press.

Google Scholar

Mayor, J., and Plunkett, K. (2010). A neurocomputational account of taxonomic responding and fast mapping in early word learning. Psychol. Rev. 117:1. doi: 10.1037/a0018130

PubMed Abstract | CrossRef Full Text | Google Scholar

McWorther, J. (2001). The world's simplest grammars are creole grammars. Linguist. Typol. 5, 125–166. doi: 10.1515/lity.2001.001

CrossRef Full Text | Google Scholar

Milin, P., Ðurđević, D. F., and del Prado Martín, F. M. (2009b). The simultaneous effects of inflectional paradigms and classes on lexical recognition: evidence from serbian. J. Mem. Lang. 60, 50–64. doi: 10.1016/j.jml.2008.08.007

CrossRef Full Text | Google Scholar

Milin, P., Feldman, L. B., Ramscar, M., Hendrix, P., and Baayen, R. H. (2017). Discrimination in lexical decision. PLoS ONE 12:e0171935. doi: 10.1371/journal.pone.0171935

PubMed Abstract | CrossRef Full Text | Google Scholar

Milin, P., Kuperman, V., Kostic, A., and Baayen, R. H. (2009a). “Paradigms bit by bit: an information theoretic approach to the processing of paradigmatic structure in inflection and derivation,” in Analogy in Grammar: Form and Acquisition, eds J. P. Blevins and J. Blevins (Oxford, UK: Oxford University Press), 241–252.

Google Scholar

Moscoso del Prado Martín, F., Kostić, A., and Baayen, R. H. (2004). Putting the bits together: an information theoretical perspective on morphological processing. Cognition 94, 1–18. doi: 10.1016/j.cognition.2003.10.015

CrossRef Full Text

Phillips, C. (1996). “Root infinitives are finite,” in Proceedings of the 20th Annual Boston University Conference on Language Development (Boston, MA: Cascadilla Press), 588–599.

Google Scholar

Phillips, C. (2010). Syntax at age two: cross-linguistic differences. Lang. Acquisit. 17, 70–120. doi: 10.1080/10489221003621167

CrossRef Full Text | Google Scholar

Pine, J. M., Conti-Ramsden, G., Joseph, K. L., Lieven, E. V., and Serratrice, L. (2008). Tense over time: testing the agreement/tense omission model as an account of the pattern of tense-marking provision in early child english. J. Child Lang. 35, 55–75. doi: 10.1017/S0305000907008252

PubMed Abstract | CrossRef Full Text | Google Scholar

Pirrelli, V. (2000). Paradigmi in Morfologia. Un Approccio Interdisciplinare Alla Flessione Verbale Dell'Italiano. Pisa: Istituti Editoriali e Poligrafici Internazionali.

Pirrelli, V., and Battista, M. (2000). The paradigmatic dimension of stem allomorphy in italian verb inflection. Ital. J. Linguist. 12, 307–380.

Google Scholar

Pirrelli, V., Ferro, M., and Marzi, C. (2015). “Computational complexity of abstractive morphology,” in Understanding and Measuring Morphological Complexity, eds M. Baerman, D. Brown, and G. G. Corbett (Oxford, UK: Oxford University Press), 141–166.

Pirrelli, V., and Yvon, F. (1999). The hidden dimension: a paradigmatic view of data-driven nlp. J. Exp. Theor. Artif. Intell. 11, 391–408. doi: 10.1080/095281399146472

CrossRef Full Text | Google Scholar

R Core Team (2014). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.

PubMed Abstract

Ralli, A. (2005). Morfologia [Morphology]. Athens: Patakis.

Ralli, A. (2006). On the Role of Allomorphy in Inflectional Morphology: Evidence From Dialectal Variation Monza: Polimetrica.

Google Scholar

Ralli, A. (2014). “Suppletion,” in Encyclopedia of Ancient Greek language and linguistics, ed G. K. Giannakis (Leiden: Brill), 341–344.

Ramscar, M., and Yarlett, D. (2007). Linguistic self-correction in the absence of feedback: a new approach to the logical problem of language acquisition. Cogn. Sci. 31, 927–960. doi: 10.1080/03640210701703576

PubMed Abstract | CrossRef Full Text | Google Scholar

Rescorla, R. A., and Wagner, A. R. (1972). “A theory of pavlovian conditioning: variations in the effectiveness of reinforcement and non-reinforcement,” in Classical Conditioning II: Current Research and Theory, eds A. H. Black and W. F. Prokasy (New York, NY: Appleton-Century-Crofts), 64–99.

Rissanen, J. (2007). Information and Complexity in Statistical Modeling. Berlin: Springer Science & Business Media.

Google Scholar

Sagot, B. (2018). Informatiser le lexique: Modélisation, développement et utilisation de lexiques morphologiques, syntaxiques et sémantiques. (Thèse d'Habilitation). Université Paris-Sorbonne, Paris, France.

Sagot, B., and Walther, G. (2011). “Non-canonical inflection: data, formalisation and complexity measures,” in International Workshop on Systems and Frameworks for Computational Morphology (Berlin: Springer), 23–45.

Google Scholar

Shannon, C. E. (1948). A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

Shosted, R. (2006). Correlating complexity: a typological approach. Linguist. Typol. 10, 1–40. doi: 10.1515/LINGTY.2006.001

CrossRef Full Text | Google Scholar

Slobin, D. I. (1982). “Universal and particular in the acquisition of language,” in Language Acquisition: The State of the Art, eds L. R. Gleitman and E. Wanner (Cambridge, UK: Cambridge University Press), 128–172.

Slobin, D. I. editor (1985). The Crosslinguistic Study of Language Acquisition, Vol. 1. New Jersey, NJ: Lawrence Erlbaum Associates.

Wilson, S. (2003). Lexically specific constructions in the acquisition of inflection in english. J. Child Lang. 30, 75–115. doi: 10.1017/S0305000902005512

PubMed Abstract | CrossRef Full Text | Google Scholar

Xanthos, A., Laaha, S., Gillis, S., Stephany, U., Aksu-Koç, A., Christofidou, A., et al. (2011). On the role of morphological richness in the early development of noun and verb inflection. First Lang. 31, 461–479. doi: 10.1177/0142723711409976

CrossRef Full Text | Google Scholar