- 1The European Molecular Biology Laboratory (EMBL), Heidelberg, Heidelberg, Germany
- 2The Heidelberg Collaboratory for Image Processing (HCI), University of Heidelberg, Heidelberg, Germany
- 3The Centre for Organismal Studies (COS), University of Heidelberg, Heidelberg, Germany
The throughput of electron microscopes has increased significantly in recent years, enabling detailed analysis of cell morphology and ultrastructure in fairly large tissue volumes. Analysis of neural circuits at single-synapse resolution remains the flagship target of this technique, but applications to cell and developmental biology are also starting to emerge at scale. On the light microscopy side, continuous development of light-sheet microscopes has led to a rapid increase in imaged volume dimensions, making Terabyte-scale acquisitions routine in the field. The amount of data acquired in such studies makes manual instance segmentation, a fundamental step in many analysis pipelines, impossible. While automatic segmentation approaches have improved significantly thanks to the adoption of convolutional neural networks, their accuracy still lags behind human annotations and requires additional manual proof-reading. A major hindrance to further improvements is the limited field of view of the segmentation networks preventing them from learning to exploit the expected cell morphology or other prior biological knowledge which humans use to inform their segmentation decisions. In this contribution, we show how such domain-specific information can be leveraged by expressing it as long-range interactions in a graph partitioning problem known as the lifted multicut problem. Using this formulation, we demonstrate significant improvement in segmentation accuracy for four challenging boundary-based segmentation problems from neuroscience and developmental biology.
1. Introduction
Large-scale electron microscopy (EM) imaging is becoming an increasingly important tool in different fields of biology. The technique was pioneered by the efforts to trace the neural circuitry of small animals at synaptic resolution to obtain their so-called connectome – a map of neurons and synapses between them. In the 1980's White et al. (1986) mapped the complete connectome of C. elegans in a manual tracing effort which spanned over a decade. Since then, throughput has increased by several orders of magnitude thanks to innovations in EM imaging like multi-beam serial section EM (Eberle et al., 2015) and TEM camera arrays (Bock et al., 2011) and stitching techniques, like hot-knife stitching (Hayworth et al., 2015) and gas cluster milling (Hayworth et al., 2018), which enable parallel acquisition. This allows to image much larger volumes up to the complete brain of the fruit-fly larva (Eichler et al., 2017) and even the adult fruit-fly (Zheng et al., 2018). Recently, studies based on large-scale EM have become more common in other fields of biology as well (Nixon-Abell et al., 2016; Pereira et al., 2016; Russell et al., 2017; Otsuka et al., 2018).
In light microscopy, very large image volumes became routine even earlier (Keller et al., 2008; Krzic et al., 2012; Royer et al., 2016), with Terabyte-scale acquisitions not uncommon for a single experiment. While the question of segmenting cell nuclei at such scale with high accuracy has been addressed before (Amat et al., 2014), cell segmentation based on membrane staining remains a challenge and a bottleneck in analysis pipelines.
Given the enormous amount of data generated, automated analysis of the acquired images is crucial; one of the key steps being instance segmentation of cells or cellular organelles. In recent years, the accuracy of automated segmentation algorithms has increased significantly thanks to the rise of deep learning-based tools in computer vision and the development of convolutional neural networks (CNNs) for semantic and instance segmentation (Turaga et al., 2010; Ciresan et al., 2012; Beier et al., 2017; Lee et al., 2017; Funke et al., 2018b; Januszewski et al., 2018). Still, it is not yet good enough to completely forego human proof-reading. Out of all microscopy image analysis problems, neuron segmentation in volume EM turned out to be particularly difficult (Januszewski et al., 2018) due to the small diameter and long reach of neurons and astrocytes, but other EM segmentation problems have not yet been fully automated either. Heavy metal staining used in the EM sample preparation labels all cells indiscriminately and forces segmentation algorithms to rely on membrane detection to separate the objects. The same problem arises in the analysis of light microscopy volumes with membrane staining, where methods originally developed for EM segmentation also achieve state-of-the-art results (Funke et al., 2018a).
One of the major downsides of CNN-based segmentation approaches lies in their limited field of view which makes them overly reliant on local boundary evidence. Staining artifacts, alignment issues or noise can severely weaken this evidence and often cause false merge errors where separate objects get merged into one. On the other hand, membranes of cellular organelles or objects of small diameter often cause false split errors where a single structure gets split into several segmented objects.
Human experts avoid many of these errors by exploiting additional prior knowledge on the expected object shape or constraints from higher-level biology. Following this observation, several algorithms have recently been introduced to enable detection of morphological errors in segmented objects (Rolnick et al., 2017; Zung et al., 2017; Dmitriev et al., 2018; Matejek et al., 2019). By looking at complete objects rather than a handful of pixels, these algorithms can significantly improve the accuracy of the initial segmentation. In addition to purely morphological criteria, in Krasowski et al. (2017) suggested an algorithm to exploit biological priors such as an incompatible mix of ultrastructure elements.
Building on such prior work, this contribution introduces a general approach to leverage domain-specific knowledge for the improvement of segmentation accuracy for methods based on boundary predictions. Our method can be understood as a post-processing step for CNN predictions that pulls in additional sparse and distant sources of information. It allows to incorporate a large variety of rules, explicit or learned from data, which can be expressed as the likelihood of certain areas in the image to belong to the same object in the segmentation. The areas can be sparse and/or spatially distant. In more detail, we formulate the segmentation problem with such rules as a graph partitioning problem with long-range attractive or repulsive edges.
For the problem of image segmentation, the graph in the partitioning problem corresponds to the region adjacency graph of the image pixels or superpixels. The nodes of the graph can be mapped directly to spatial locations in the image. When domain knowledge can be expressed as rules that certain locations must or must not belong to the same object, it can be distilled into lifted (long-range) edges between these locations. The weights of such lifted edges are derived from the strictness of the rules, which can colloquially range from “usually do/do not belong to the same object” to “always/never ever belong to the same object.”
In Horňáková et al. (2017) showed that this problem, which they term Lifted Multicut as it corresponds to the Multicut partitioning problem with additional edges between non-adjacent nodes, can be solved exactly in reasonable time for small problem sizes, while in Beier et al. (2016) introduced an efficient approximate solver.
In the following, we demonstrate the versatility of the Lifted Multicut based-approach by applying it to four segmentation problems, three in EM and one in LM. We incorporate starkly different kinds of prior information into this framework:
• Based on the knowledge that axons are separated from dendrites in mammalian cortex, we use indicators of axon/dendrite attribution to avoid merges between axonal and dendritic neural processes (Figure 1, left);
• Based on the knowledge of plausible neuron morphology, we correct false merge errors in the segmentation of neural processes (Figure 1, center);
• Based on the knowledge that certain biological structures form long continuous objects, we reduce the number of false splits in instance segmentation of sponge choanocytes (Figure 1, right);
• Based on the knowledge that a cell should only contain one nucleus, we improve the segmentation of growing plant lateral roots (Figure 4).
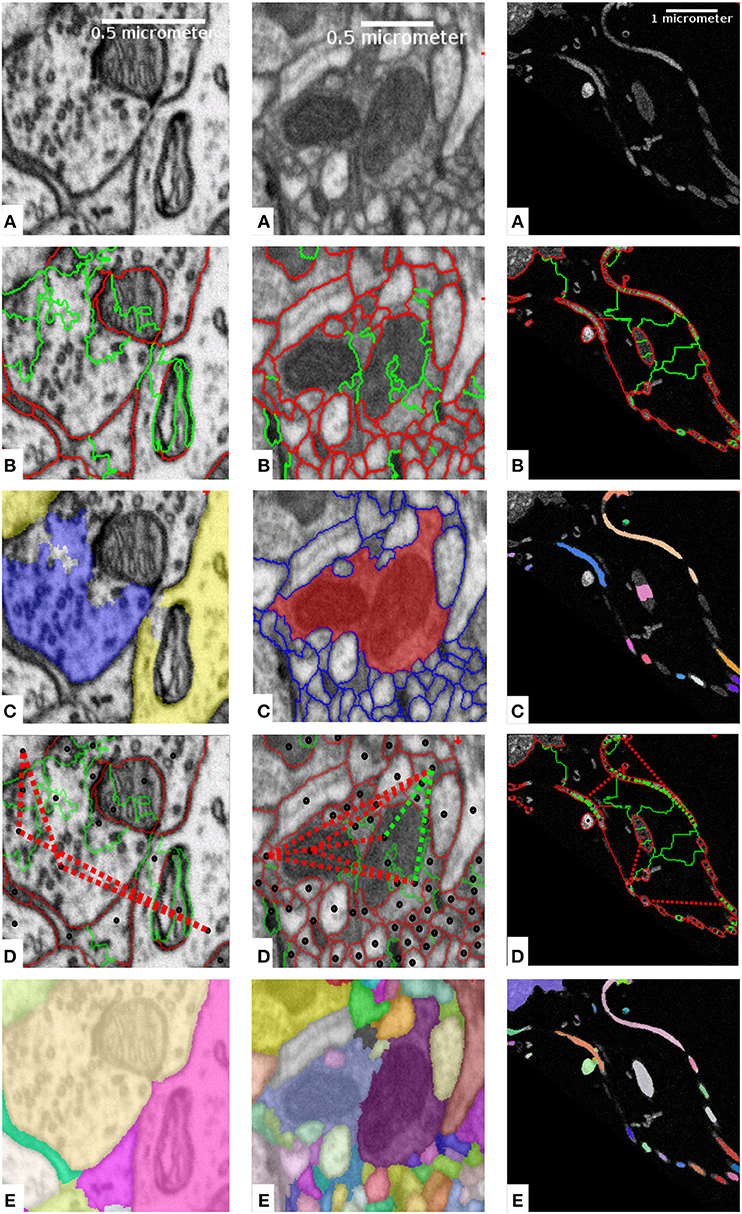
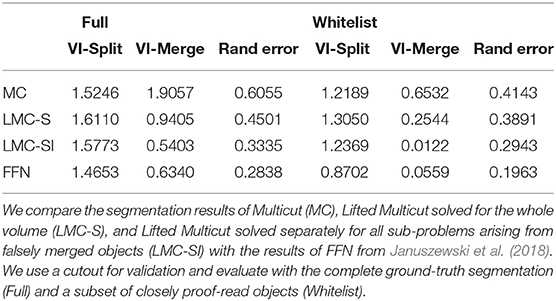
Figure 1. Mapping domain knowledge to sparse lifted edges for mammalian cortex (left), drosophila brain (middle) and sponge choanocyte chamber (right). The raw data is shown in (A). Based on local boundary evidence (not shown) predicted by a Random Forest or a CNN, we group the volume pixels into superpixels, which form a region adjacency graph. The edges of the graph correspond to boundaries between the superpixels as shown in (B). The edges are weighted, with weights derived from boundary evidence, or predicted by an additional classifier. Weights can make edges attractive (green) or repulsive (red). (C) Shows the domain knowledge mapped to superpixels: axon (blue) and dendrite (yellow) attributions (left); an object with implausible morphology (red, center); semantically different objects (one color per object, right). Superpixels with mapped domain knowledge are connected with lifted edges as shown in (D), with green for attractive and red for repulsive edges (only a subset of edges is shown to avoid clutter). (E) Displays the solution of the complete optimization problem with local and sparse lifted edges as the final segmentation.
Aiming to apply the method to data of biologically relevant size, we additionally introduce a new scalable solver for the lifted multicut problem based on our prior work from Pape et al. (2017). Our code is available at https://github.com/constantinpape/cluster_tools.
2. Related Work
Neuron segmentation for connectomics has been the main driver of the recent advances in boundary-based segmentation for microscopy. Most methods (Andres et al., 2012; Nunez-Iglesias et al., 2013; Beier et al., 2017; Lee et al., 2017; Funke et al., 2018b) follow a three step procedure: in the first step they segment boundaries, in the second compute an over-segmentation into superpixels and finally agglomerate the superpixels into objects.
The success of a CNN (Ciresan et al., 2012) in the ISBI 2012 neuron segmentation challenge (Arganda-Carreras et al., 2015) has prompted the adoption of this technique for the boundary prediction step. Most recent approaches use a U-Net (Ronneberger et al., 2015) architecture and custom loss functions (Lee et al., 2017; Funke et al., 2018b). The remaining differences between methods can be found in the superpixel merging procedure. Several approaches are based on hierarchical clustering, but differ in how they accumulate boundary weights: Lee et al. (2017) use the accumulated mean CNN boundary predictions, Funke et al. (2018b) employ quantile based accumulation and (Nunez-Iglesias et al., 2013) re-predict the weights with a random forest (Breiman, 2001) after each agglomeration step. In contrast Andres et al. (2012) and Beier et al. (2017) solve a NP-hard graph partitioning problem, the (Lifted) Multicut. Notable exception from this three step approach are the flood filling network (FFN) (Januszewski et al., 2018) and MaskExtend (Meirovitch et al., 2016) which can go directly from pixels to instances by predicting individual object masks one at a time, as well as 3C (Meirovitch et al., 2019), which can simultaneously predict multiple objects.
Krasowski et al. (2017) showed that the common three-step procedure can be modified to incorporate sparse biological priors at the superpixel agglomeration step. They use the Asymmetric Multi-Way Cut (AMWC) (Kroeger et al., 2014), a generalization of the Multicut for joint graph partition and node labeling. The method is based on exploiting the knowledge that, given the field of view of modern electron microscopes, axon- and dendrite-specific ultrastructure should not belong to the same segmented objects in mammalian cortex. While this approach can be generalized to other domain knowledge, it has two important drawbacks. First, it is not possible to encode attractive information just with node labels. Second, it is harder to express information that does not fit the node labeling category, even if it is repulsive in nature. A good example for this is the morphology-based false merge correction. In this case, defining a labeling for only a subset of nodes is not possible.
The Lifted Multicut formulation has been used for neuron segmentation before by Beier et al. (2017). However, the lifted edges were added densely and their weights and positions were not based on domain knowledge, but learned from groundtruth segmentations by the Random Forest algorithm. Only edges over a graph distance of 3 were considered. These lifted edges made the segmentation algorithm more robust against single missing boundaries, but did not counter the problem of the limited field of view of the boundary CNN and did not prevent biologically implausible objects. Note that this approach can be seen as a special case of the framework proposed here, using generic, but weak knowledge about local morphology and graph structure of segments. Besides Lifted Multicut, the recently introduced Mutex Watershed (Wolf et al., 2018, 2019) and generalized agglomerative clustering (Bailoni et al., 2019) can also exploit long-range information.
While all the listed methods demonstrate increased segmentation accuracy, they do not offer a general recipe on how to exploit domain-specific knowledge in a segmentation algorithm. We propose a versatile framework that can incorporate such information from diverse sources by mapping it to sparse lifted edges in the lifted multicut problem.
3. Methods
Our method follows the three step segmentation approach described in 2, starting from a boundary predictor and using graph partitioning to agglomerate super-pixels. First, we review the lifted multicut problem (Horňáková et al., 2017) in 3.1. We follow by proposing a general approach to incorporate domain-specific knowledge into the lifted edges (3.2). Finally, we describe four specific applications with different sources of domain knowledge and show how our previous work on lifted multicut for neuron segmentation can be positioned in terms of the proposed framework.
3.1. Lifted Multicut Graph Partition
Instance segmentation can be formulated as a graph partition problem given a graph G = {V, E} and edge weights W ∈] − ∞,∞[. In our setting, the nodes V correspond to fragments of the over-segmentation and edges E link two nodes if the two corresponding fragments share an image boundary. The weights W encode the attractive strength (positive values) or repulsive strength (negative values) of edges and are usually derived from (pseudo) probabilities P via negative log-likelihood:
The resulting partition problem is known as multicut or correlation clustering (Chopra and Rao, 1993; Demaine et al., 2006; Andres et al., 2012). Its objective is given by:
where YE are binary indicator variables linked to the edge state; 0 means that an edge connects the two adjacent nodes in the resulting partition, 1 means that it doesn't. The constraints forbid dangling edges in the partition, i.e., edges that separate two nodes (ye = 1) for which a path of connecting edges (ye = 0) exists.
The lifted multicut (Horňáková et al., 2017) is an extension of the multicut problem, which introduces a new set of edges F called lifted edges. These edges differ from regular graph edges by providing only an energy contribution, but not inducing connectivity. This is motivated by the observation that it is often helpful to derive non-local features for the connectivity of (super) pixels. The presence of an attractive non-local edge should not result in air bridges though, i.e., non-local edges that connect two pixels without a connection via local edges. In our setting, lifted edges connect nodes v and w that are not adjacent in G. With the sets of original edges E, lifted edges F, binary indicator variables Y, and weights W associated with all edges in E ∪ F the lifted multicut objective can be formulated as:
The constraints (5) correspond to Equation (2) and enforce a consistent partition without dangling edges. Constraints (6) and (7) ensure that the state of lifted edges is consistent with the connectivity, i.e., that two nodes connected by a lifted edge are also connected via a path of regular edges and two nodes separated by a lifted edge are not connected by any such path.
3.2. Sparse Lifted Edges
Our main contribution is a general recipe how to express domain-specific knowledge via sparse lifted edges that are only added between graph nodes where attribution of this knowledge is possible. The right part of Figure 2 shows a sketch of this idea: nodes with attribution are shown by shaded segments and sparse lifted edges by green dashed lines.
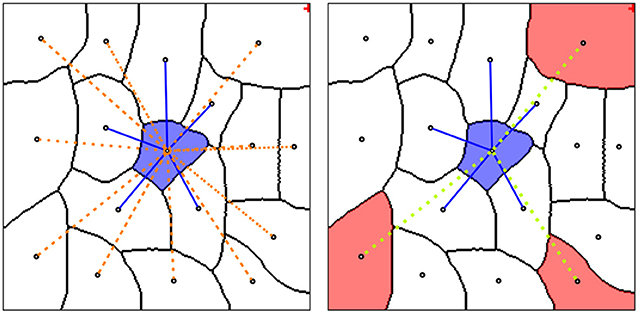
Figure 2. (Left) Graph neighborhood of a single node (blue shaded segment) with local edges (blue lines) and dense lifted edges (orange dotted edges). (Right) Neighborhood with sparse lifted edges (green dotted edges), connecting nodes with projected domain knowledge (red shaded segments).
The sparse lifted edges are constructed in several steps, see Figure 1. We compute the superpixels by running the watershed algorithm on boundary predictions and construct the corresponding region adjacency graph. Figure 1B shows regular, not lifted, edges between superpixels, green for attractive and red for repulsive weights. Then, we map the domain specific knowledge to nodes as shown in Figure 1C, and derive attractive and repulsive lifted edges, again shown as green and red lines in Figure 1D. The sign and strength of the lifted edge weights can be learned or introduced explicitly, reflecting the likelihood of incident nodes being connected. Equation (1) is used to obtain signed weights. Finally, we solve the resulting lifted multicut objective to obtain an instance segmentation, shown in Figure 1E.
3.2.1. Mouse Cortex Segmentation, EM
This application example shows how the framework described above can be used to incorporate the axon/dendrite attribution priors first introduced in Krasowski et al. (2017). We detect the axon- and dendrite-specific elements and map them to the nodes in the same way as (Krasowski et al., 2017; Figure 1C), with blue shading for axon and yellow for dendrite attribution). The difference comes in the next step: instead of introducing semantic node labels for “axon” and “dendrite” classes, we add repulsive lifted edges between nodes which got mapped differently. 4.1 includes more details on the problem set-up and results.
3.2.2. Drosophila Brain Segmentation, EM
For neurons in the insect brain, the axon/dendrite separation is not pronounced and the approach described in the previous section can not be applied directly. Instead, morphological information can be used to identify and resolve errors in segmented objects. This was first demonstrated by Rolnick et al. (2017), where a CNN was trained on downsampled segmentation masks to detect merge errors. Meirovitch et al. (2016) detect merge errors with a simple shape-based heuristic and then correct these with a MaskExtend algorithm. Zung et al. (2017) were the first to combine CNN-based error detection and flood filling network-based correction. In their formulation both false merges and false splits can be corrected. Recently, Dmitriev et al. (2018) and Matejek et al. (2019) have introduced an approach based on CNN error detection followed by a simple heuristic to correct false merges and lifted multicut graph partitioning to fix false splits.
Based on all this prior work which convincingly demonstrates that false merge errors can be detected in a post-processing step, we concentrate our efforts on error correction, emulating the detection step with an oracle. We extract skeletons for all segmented objects and have the oracle predict, for all paths connecting terminal nodes of a skeleton, if this path goes through a false merge location (passes through an unidentified boundary). Note that the oracle is not perfect and we evaluate the performance of the algorithm for different levels of oracle error.
If the oracle predicts the path to go through a false merge, we introduce a repulsive lifted edge between the terminals of the path. The weights of the edges are also predicted by the oracle. Figure 1 shows an example of this approach: the red object in the middle of Figure 1C has been detected as a false merge. The corresponding lifted edges are shown in Figure 1D.
3.2.3. Sponge Segmentation, EM
In this example, we tackle a segmentation problem in a sponge choanocyte chamber (Musser et al., 2019). These structures are built from several surrounding cells, the choanocytes, that interact with a central cell via flagella which are surrounded by a collar of microvilli. Our goal is to segment cell bodies, flagella and microvilli. This task is challenging due to the large difference in sizes of these structures. Especially the segmentation of the small flagella and microvilli is difficult. Without the use of domain specific knowledge on their continuity, the Multicut algorithm splits them up into many pieces.
In order to alleviate these false split errors, we predict which pixels in the image belong to flagella and microvilli and compute an approximate flagella and microvilli instance segmentation via thresholding and connected components. We map the component labels to nodes of the graph, see right column in Figure 1C. Then, we introduce attractive lifted edges between the nodes that were covered by the same component and repulsive lifted edges between nodes mapped to different components, see Figure 1D.
3.2.4. Lateral Root Segmentation, LM
Finally, we tackle a challenging segmentation problem in light-sheet data: segmentation of root cells in Arabidopsis thaliana. This data was imaged with two channels, showing cell membrane and nucleus markers. We use the first channel to predict cell boundaries and the second to segment individual nuclei. The nuclei then serve as bases to force each segmented cell to only contain one nucleus: we introduce repulsive lifted edges between nodes which are covered by different nuclei instances. 4.4 shows how this setup helps prevent false merge errors in cell segmentation.
3.3. Hierarchical Lifted Multicut Solver
Finding the optimal solution of the lifted multicut objective is NP-hard. Approximate solvers based on greedy algorithms (Keuper et al., 2015) and fusion moves (Beier et al., 2017) have been introduced. However, even these approximations do not scale to the large problem we need to solve in the sponge segmentation example. In order to tackle this and even larger problems, we adapt the hierarchical multicut solver of Pape et al. (2017) for lifted multicuts.
This solver extracts sub-problems from a regular tiling of the volume, solves these sub-problems in parallel and uses the solutions to contract nodes in the graph, thus reducing its size. This approach can be repeated for an increasing size of the blocks that are used to tile the volume, until the reduced problem becomes feasible with another (approximate) solver.
We extend this approach to the lifted multicut by also extracting lifted edges during the sub-problem extraction. We only extract lifted edges that connect nodes in the sub-graph defined by the block at hand. This strategy, where we ignore lifted edges crossing block boundaries, is in line with the idea that lifted edges contribute to the energy, but not to the connectivity. Note that lifted edges that are not part of any sub-problem at a given level will still be considered at a later stage. See Appendix Algorithm 1 (Supplementary Material) for pseudo-code. The comparison to other solvers in Table A2 (Supplementary Material) shows that it indeed scales better to large data. Note that this approach is conceptually similar to the fusion move based approximation of Beier et al. (2016), which extracts and solves sub-problems based on a random graph partition and accepts changes from sub-solutions if they increase the overall energy, repeating this process until convergence. Compared to this approach, we extract sub-problems from a deterministic partition of the graph. This allows us to solve only a preset number of sub-problems leading to faster convergence.
Note that our approximate solver is only applicable if the graph at hand has a spatial embedding, which allows to extract sub-problems from a tiling of space. In our case, this spatial embedding is given by the watershed fragments that correspond to nodes.
4. Results
We study the performance of the proposed method on four different problems: (i) neuron segmentation in murine cortex with priors from axon/dendrite segmentation, (ii) neuron segmentation in drosophila brain with priors from morphology-based error detection, (iii) instance segmentation in a sponge choanocyte chamber with priors from semantic classes of segmented objects, (ix) cell segmentation in Arabidopsis roots with priors from “one nucleus per cell” rule. Table A1 (Supplementary Material) summarizes the different problem set-ups. We evaluate segmentation quality using the variation of information (VI) (Meilă, 2003), which can be separated into split and merge scores, and the adapted rand score (Arganda-Carreras et al., 2015). For all error measures used here, a lower value corresponds to higher segmentation quality.
4.1. Mouse Cortex Segmentation, EM
We present results on a volume of murine somatosensory cortex that was acquired by FIBSEM at 5 × 5 × 6 nanometer resolution. The same volume has already been used in Krasowski et al. (2017) for a similar experiment. To ensure a fair comparison between the two methods for incorporating axon/dendrite priors, we obtained derived data from the authors and use it to set-up the segmentation problem.
This derived data includes probability maps for cell membrane, mitochondria, axon and dendrite attribution as well as a watershed over-segmentation derived from the cell membrane probabilities and ground-truth instance segmentation. From this data, we set up the graph partition problem as follows: we build the region adjacency graph G from the watersheds and compute weights for the regular edges with a random forest based on edge and region appearance features. See Beier et al. (2017) for a detailed description of the feature set. Next, we introduce dense lifted edges up to a graph distance of three. We use a random forest based on features derived from region appearance and clustering to predict their weights, see Beier et al. (2017) for details. In addition to the region appearance features only based on raw data, we also take into account the mitochondria attribution here. Next, we map the axon/dendrite attribution to the nodes of G and introduce sparse lifted edges between nodes mapped to different classes. We infer weights for these edges with a random forest based on features from the statistics of the axon and dendrite node mapping. We use the fusion move solver of Beier et al. (2016) for optimizing the lifted multicut objective.
We divide the volume into a 1 × 3.5 × 3.5 micron block that is used to train the random forests for edge weights and a 2.5 × 3.5 × 3.5 micron block used for evaluation. The random forest predicting pixel-wise probabilities was trained by the authors of Krasowski et al. (2017) on a separate volume, using ilastik (Sommer et al., 2011).
We compare the multicut and AMWC solutions reported in Krasowski et al. (2017) with different variants of our methods, see Table 1. As a baseline, we compute the lifted multicut only with dense lifted edges and without features from mitochondria predictions (LMC-D). We compute the full model with dense and sparse lifteds (LMC-S) with and without additional features for dense lifted edges from mitochondria predictions. In addition, we compare to an iterative approach (LMC-SI) similar to the error correction approach in 4.2, where we perform LMC-D segmentation first and introduce sparse lifted edges only for objects that contain a false merge (identified by presence of both axonic and dendritic nodes in the same object).
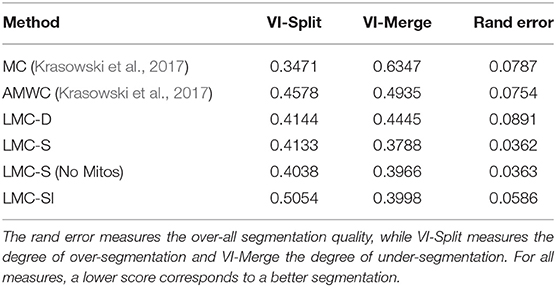
Table 1. Variants of our approach compared to the method of Krasowski et al. (2017).
The LMC-D segmentation quality is on par with the AMWC, although it does not use any input from the priors, showing the importance of dense lifted edges. Our full model with sparse lifted edges shows significantly better quality compared to LMC-D. Mitochondria-based features provide a small additional boost. The segmentation quality of the iterative approach LMC-SI is inferior to solving the full model LMC-S. This shows the importance of joint optimization of the full model with dense and sparse lifted edges.
4.2. Drosophila Brain Segmentation, EM
We test the false merge correction on parts of the Drosophila medulla using a 68 × 38 × 44 micron FIBSEM volume imaged at 8 × 8 × 8 nanometer from Takemura et al. (2015), who also provide a ground-truth segmentation for the whole volume.
First, we train a 3D U-Net for boundary prediction on a separate 2 × 2 × 2 micron cube. We use this network to predict boundaries on the whole volume, and run watershed over-segmentation based on these predictions. Then, we set up an initial Multicut with edge weights derived from mean accumulated boundary evidence. We obtain an initial segmentation by solving it with the block-wise solver of Pape et al. (2017).
In order to demonstrate segmentation improvement based on morphological features, we skeletonize all sufficiently large objects using the method of Lee et al. (1994) implemented in Van der Walt et al. (2014). We then predict false merges along all paths between skeleton terminal nodes, using the ground-truth segmentation as oracle predictor. Note that (Dmitriev et al., 2018) have shown that it is possible to train a very accurate CNN to classify false merges based on morphology information in this set-up. Given these predictions, we set up the Lifted Multicut problem by selecting all objects that have at least one path with a false merge detection. For these objects, we introduce lifted edges between all terminal nodes corresponding to paths and derive weights for these edges from the false merge probability (note that we use an imperfect oracle for some experiments, so the merge predictions are not absolutely certain). We solve two different variants of this problem, LMC-S, where we solve the whole problem using the solver introduced in 3.3 and LMC-SI, where we only solve the sub-problems arising for the individual objects. For this, we use the Fusion Moves solver of Beier et al. (2016).
Table 2 compares the results of the initial Multicut (MC) with LMC-S and LMC-SI (using a perfect oracle) as well as the current state of the art FFN based segmentation (Januszewski et al., 2018). We adopt the evaluation procedure of Januszewski et al. (2018) and use a cutout of size 23 × 19 × 23 micron for validation. We use two different versions of the ground-truth, the full segmentation and only a set of white-listed objects that were more carefully proofread. The FFN segmentation and validation ground-truth was kindly provided by the authors of Januszewski et al. (2018). The results show that our initial segmentation is inferior to FFN in terms of merge errors, but using LMC-SI we can improve the merge error to be even better than FFN. Interestingly, LMC-SI performs better than LMC-S. We suspect that this is due to the fact that we only add lifted edges inside of objects with a false merge detection, thus LMC-S does not see more information then LMC-SI, while having to solve a much bigger optimization problem.
In Figure 3 we show the initial segmentation and three corrected merges. Figure 3E evaluates LMC-S and LMC-SI on the full ground-truth when using an imperfect oracle: we tune the oracle's F-score from 0.5 to 1.0 and measure VI-split and VI-merge. The curves show that LMC-SI is fairly robust against noise in the oracle predictions; it starts with a lower VI-merge than the initial MC, even for F-Score 0.5 and its VI-split gets close to the MC value for F-Score 0.75+.
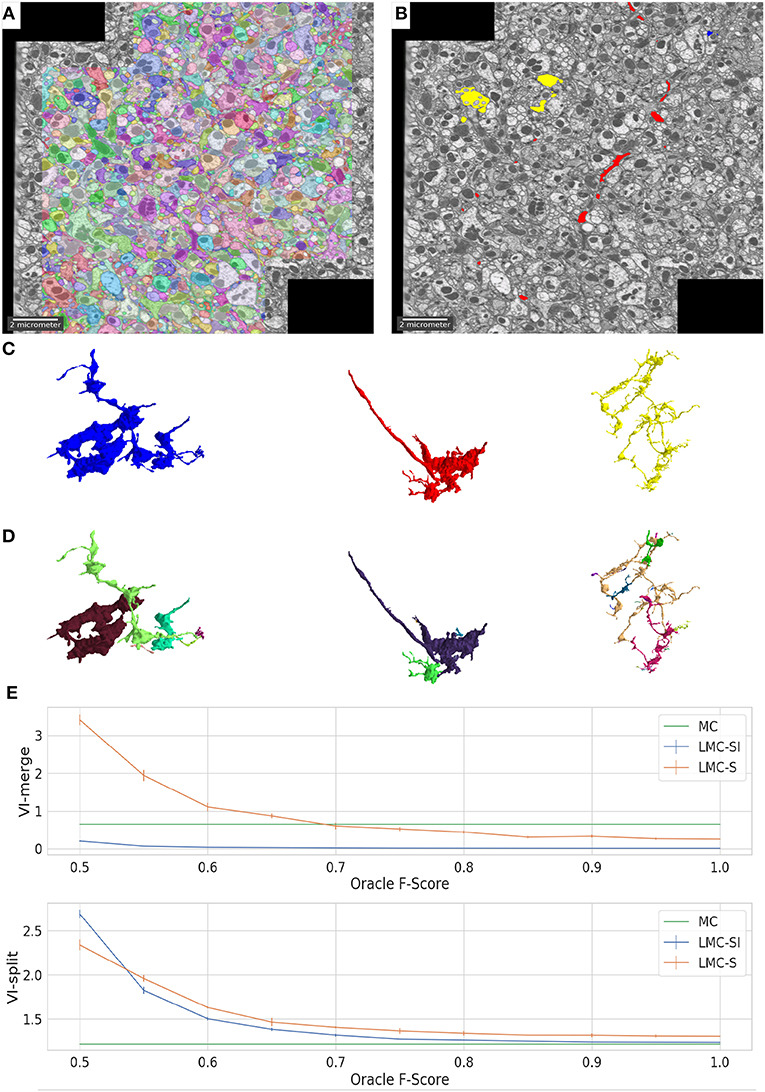
Figure 3. Overview of results on the drosophila medulla dataset. We detect merges in the initial segmentation result (A) using an oracle. The red, blue and yellow segments in (B) were flagged as false merges. (C,D) show merged / correctly resolved objects. (E) shows the performance of our approach when tuning the F-Score of our oracle predictor from 0.5 to 1.
4.3. Sponge Segmentation, EM
The two previous experiments mostly profited from repulsive information derived from ultrastructure or morphology. In order to show how attractive information can be exploited, we turn to an instance segmentation problem in a sponge choanocyte chamber. The EM volume was imaged with FIBSEM at a resolution of 15 × 15 × 15 nanometer. We aim to segment structures of three different types: cell bodies, flagella and microvilli. Flagella and microvilli have a small diameter, which make them difficult to segment with a boundary based approach. On the other hand, cell bodies have a much larger diameter and touch each other, which makes a boundary based approach appropriate.
In order to set-up the segmentation problem, we first compute probability maps for boundaries, microvilli and flagella attribution using the autocontext workflow of ilastik (Sommer et al., 2011). We set-up the lifted multicut problem by first computing watersheds based on boundary maps, extracting the region adjacency graph and computing regular edge weights from the boundary maps accumulated over the edge pixels. We do not introduce dense lifted edges. For sparse lifted edges, we compute an additional instance segmentation of flagella and microvilli by thresholding the corresponding probability maps and running connected components. Then, we map the components of this segmentation to graph nodes and connect nodes mapped to the same component via attractive lifted edges and nodes mapped to different components via repulsive lifted edges. We use the hierarchical lifted multicut solver introduced in 3.3 to solve the resulting objective, using the approximate solver of Keuper et al. (2015) to solve sub-problems. Note that the full model contained too many variables to be optimized by any other solver in a reasonable amount of time.
We run our segmentation approach on the whole volume, which covers a volume of 70 × 75 × 50 microns, corresponding to 4,600 × 5,000 × 3,300 voxels. For evaluation, we use three cutouts of size 15 × 15 × 1.5 microns with ground-truth for instance and semantic segmentation. We split the evaluation into separate scores for objects belonging to the three different structures, extracting them based on the semantic segmentation ground-truth. See Table 3 for the evaluation results, comparing the sparse lifted multicut (LMC) to the multicut baseline (MC). As expected the quality of the segmentation of cell bodies is not affected, because we don't introduce lifted edges for those. The split rate in flagella and microvilli decreases significantly leading to a better overall segmentation for these structures.
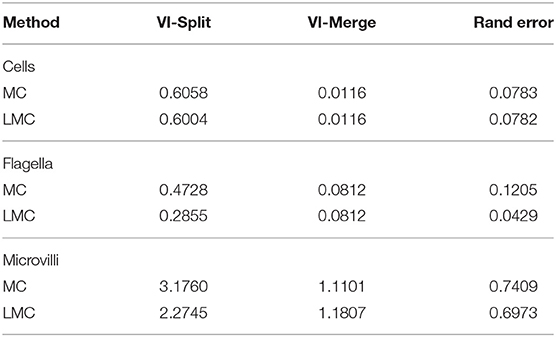
Table 3. Quality of the sponge chonanocyte segmentation for the three different types of structures.
4.4. Lateral Root Segmentation, LM
We segment cells in light-sheet image volumes of the lateral root primordia of Arabidopsis thaliana. The time-lapse video consisting of 51 time points was obtained in vivo in close-to-natural growth conditions. Each time point is a 3D volume of size 2,048 × 1,050 × 486 voxels each with resolution 0.1625 × 0.1625 × 0.25 micron. The volume has two channels, one showing membrane marker, the other nucleus marker. We work on two selected time points, namely: T45 and T49 taken from the later stages of development where the instance segmentation problem is more challenging due to growing number of cells. The time points have dense ground-truth segmentation for a 1,000 × 450 × 200 voxels cutout centered on the root primordia. Both cells and nuclei ground truth are available.
A variant of 3D U-Net (Çiçek et al., 2016) was trained in order to predict cell membranes and nuclei, respectively. The two networks were trained on dense ground-truth from time points which were not part of our evaluation. Apart from the primary task of predicting membranes and nuclei, respectively, both networks were trained on an auxiliary task of predicting long-range affinities similarly to Lee et al. (2017) which proved to improve the effectiveness of the main task.
Using these networks, we predict cell boundary probabilities and nucleus foreground probabilities. We use the nucleus predictions to obtain a nucleus instance segmentation by thresholding the probability maps at pthreshold = 0.9 and running connected components analysis.
We compute superpixels from the watershed transform on the membrane predictions and compute weights for the regular edges via mean accumulated boundary evidence. We set up lifted edges by mapping the nucleus instances to superpixels and connecting all nodes whose superpixels were mapped to different nuclei with repulsive lifted edges.
Table 4 shows the evaluation of segmentation results on the ground-truth cutouts. We can see that LMC-S clearly improves the merge errors as well the overall Rand Error while only marginally diminishing the split quality. Figure 4 shows an overview of the LMC result and two qualitative comparisons of MC and LMC results, highlighting merges that were prevented by LMC. Note that not all merges can be prevented, even if the nuclei were segmented correctly, because some merges occur already in the watersheds.
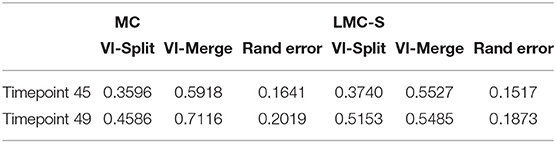
Table 4. Comparison of Multicut and Lifted Multicut segmentation results for two time points taken from the light-sheet root primordia data.
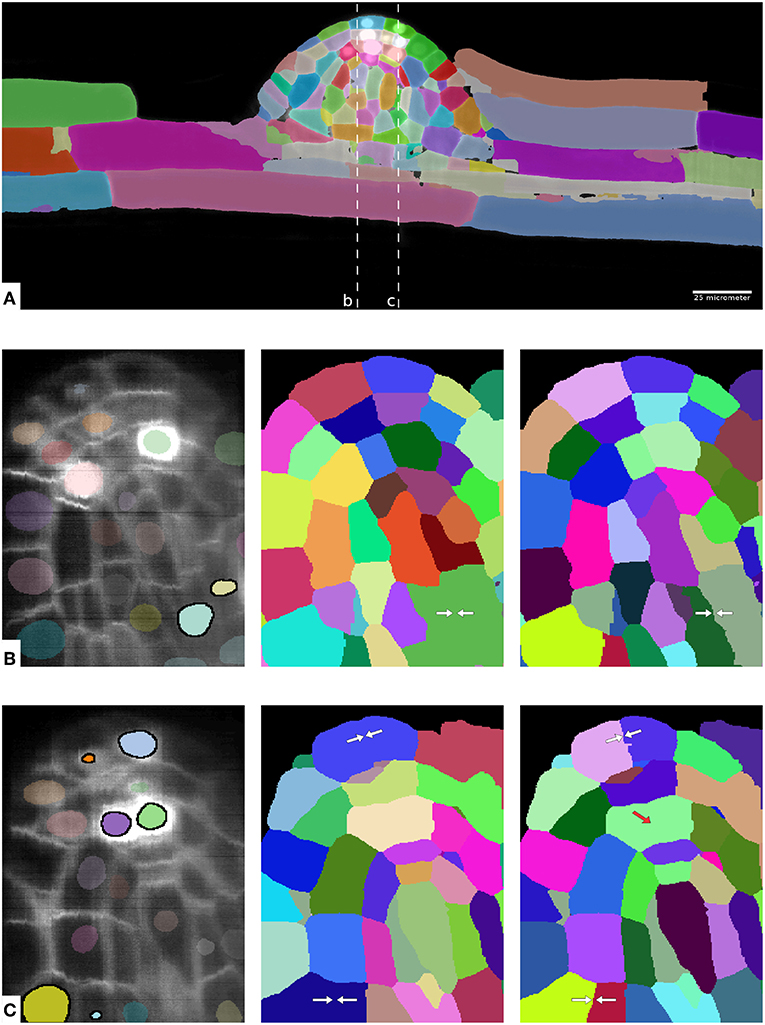
Figure 4. Overview of results on the plant root dataset. (A) Shows one complete image plane with membrane channel and overview of the LMC segmentation for timepoint 49. (B,C) Show zoom ins of the yz plane with raw data and nucleus segmentation (left), MC segmentation (middle) and LMC segmentation (right) with avoided merge errors marked by white arrows. The two dashed lines in (A) show cut planes for the zoom-ins. In (B,C) the nuclei instances inside of cells falsely merged in the MC segmentation are highlighted. Note that not all merge errors can be resolved by LMC; in some cases the watersheds are already merged, see red arrow in (C).
5. Discussion
We propose a general purpose strategy to leverage domain-specific knowledge for instance segmentation problems arising from EM image analysis. This strategy makes use of a graph partitioning problem known as lifted multicut by expressing the domain knowledge in the long-range lifted edges. Clearly, not every kind of domain knowledge can be expressed in this form, and the final accuracy improvement depends on the information content of the prior knowledge. Also, our method cannot fix merge errors in the watershed segmentation underlying the graph, even if priors indicating such an error are available, see results in 4.4.
We apply the proposed strategy to a diverse set of difficult instance segmentation problems in light and electron microscopy and consistently show an improvement in segmentation accuracy. The improvement can be demonstrated even for imperfect prior information: segmentation quality only starts to degrade at fairly high error levels in the lifted edges, see results in 4.2.
For an application with ultrastructure based priors, we also observe that the lifted multicut based formulation yields higher quality results than the AMWC formulation of Krasowski et al. (2017). We believe that this is due to joint exploitation of dense short-range and sparse long-range information. A complete joint solution, with both lifted edges and semantic labels, has recently been introduced in Levinkov et al. (2017). We look forward to exploring the potential of this objective for the neuron segmentation problem.
Similar to the findings of Kroeger et al. (2014), we demonstrated that prevention of merge errors is more efficient than their correction: the joint solution of LMC-S is more accurate than iterative LMC-SI. However, not all prior information can be incorporated directly into the original segmentation problem. For these priors we demonstrate how to construct an additional resolving step which can also significantly reduce the number of false merge errors. In the future we plan to further improve our segmentations by other sources of information: matches of the segmented objects to known cell types, manual skeletons, or correlative light microscopy imaging.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
CP developed the methods, performed the experiments, and wrote the paper. AMat contributed to method development and performed parts of the experiments for the Drosophila neural tissue dataset. AW performed parts of the experiments for the plant dataset. JH contributed to method development. GM imaged the sponge dataset and contributed to sponge dataset experiment set-up. ML and AMai contributed to plant dataset experiment set-up. JM and DA contributed to sponge dataset experiment set-up. AK developed the methods, wrote the paper, and provided funding.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We gratefully acknowledge the support of the Baden-Wuerttemberg Stiftung and partial financial support by DFG Grant HA 4364 9-1 and DFG Grant FOR2581 as well as the contributions to this work made by Klaske J. Schippers and Nicole L. Schieber in the Electron Microscopy Facility of EMBL.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2019.00006/full#supplementary-material
References
Amat, F., Lemon, W., Mossing, D. P., McDole, K., Wan, Y., Branson, K., et al. (2014). Fast, accurate reconstruction of cell lineages from large-scale fluorescence microscopy data. Nat. Methods 11:951. doi: 10.1038/nmeth.3036
Andres, B., Kroeger, T., Briggman, K. L., Denk, W., Korogod, N., Knott, G., et al. (2012). “Globally optimal closed-surface segmentation for connectomics,” in European Conference on Computer Vision (Berlin; Heidelberg: Springer), 778–791. doi: 10.1007/978-3-642-33712-3-56
Arganda-Carreras, I., Turaga, S. C., Berger, D. R., Cireşan, D., Giusti, A., Gambardella, L. M., et al. (2015). Crowdsourcing the creation of image segmentation algorithms for connectomics. Front. Neuroanatomy 9:142. doi: 10.3389/fnana.2015.00142
Bailoni, A., Pape, C., Wolf, S., Beier, T., Kreshuk, A., and Hamprecht, F. A. (2019). A generalized framework for agglomerative clustering of signed graphs applied to instance segmentation. arxiv abs/1906.11713.
Beier, T., Andres, B., Köthe, U., and Hamprecht, F. A. (2016). “An efficient fusion move algorithm for the minimum cost lifted multicut problem,” in European Conference on Computer Vision (Cham: Springer), 715–730. doi: 10.1007/978-3-319-46475-6-44
Beier, T., Pape, C., Rahaman, N., Prange, T., Berg, S., Bock, D. D., et al. (2017). Multicut brings automated neurite segmentation closer to human performance. Nat. Methods 14, 101–102. doi: 10.1038/nmeth.4151
Bock, D. D., Lee, W. C. A., Kerlin, A. M., Andermann, M. L., Hood, G., Wetzel, A. W., et al. (2011). Network anatomy and in vivo physiology of visual cortical neurons. Nature 471, 177–182. doi: 10.1038/nature09802
Çiçek, Ö., Abdulkadir, A., Lienkamp, S. S., Brox, T., and Ronneberger, O. (2016). 3d u-net: learning dense volumetric segmentation from sparse annotation. International Conference on Medical Image Computing and Computer-Assisted Intervention Medical Image Computing and Computer-Assisted Intervention - MICCAI 2016, (Cham) 424–432. doi: 10.1007/978-3-319-46723-8-49
Ciresan, D., Giusti, A., Gambardella, L. M., and Schmidhuber, J. (2012). “Deep neural networks segment neuronal membranes in electron microscopy images,” in Advances in Neural Information Processing Systems, 2843–2851.
Demaine, E. D., Emanuel, D., Fiat, A., and Immorlica, N. (2006). Correlation clustering in general weighted graphs. Theoret. Comput. Sci. 361, 172–187. doi: 10.1016/j.tcs.2006.05.008
Dmitriev, K., Parag, T., Matejek, B., Kaufman12, A. E., and Pfister, H. (2018). “Efficient correction for em connectomics with skeletal representation,” in British Machine Vision Conferemce (BMVC). Available online at: http://bmvc2018.org/
Eberle, A. L., Mikula, S., Schalek, R., Lichtman, J., Tate, M. K., and Zeidler, D. (2015). High-resolution, high-throughput imaging with a multibeam scanning electron microscope. J. Microscopy 259, 114–120. doi: 10.1111/jmi.12224
Eichler, K., Li, F., Litwin-Kumar, A., Park, Y., Andrade, I., Schneider-Mizell, C. M., et al. (2017). The complete connectome of a learning and memory centre in an insect brain. Nature 548, 175–182. doi: 10.1038/nature23455
Funke, J., Mais, L., Champion, A., Dye, N., and Kainmueller, D. (2018a). “A benchmark for epithelial cell tracking,” in The European Conference on Computer Vision (ECCV) Workshops, (Cham).
Funke, J., Tschopp, F., Grisaitis, W., Sheridan, A., Singh, C., Saalfeld, S., and Turaga, S. C. (2018b). Large scale image segmentation with structured loss based deep learning for connectome reconstruction. IEEE Trans. Pattern Anal. Mach. Intell. 41, 1669–1680. doi: 10.1109/TPAMI.2018.2835450
Hayworth, K. J., Peale, D., Lu, Z., Xu, C. S., and Hess, H. F. (2018). Serial thick section gas cluster ion beam scanning electron microscopy. Microscopy Microanal. 24, 1444–1445. doi: 10.1017/S1431927618007705
Hayworth, K. J., Xu, C. S., Lu, Z., Knott, G. W., Fetter, R. D., Tapia, J. C., et al. (2015). Ultrastructurally smooth thick partitioning and volume stitching for large-scale connectomics. Nat. Methods 12, 319–322. doi: 10.1038/nmeth.3292
Horňáková, A., Lange, J.-H., and Andres, B. (2017). “Analysis and optimization of graph decompositions by lifted multicuts,” in Proceedings of the 34th International Conference on Machine Learning-Volume 70 (JMLR. org.), 1539–1548.
Januszewski, M., Kornfeld, J., Li, P. H., Pope, A., Blakely, T., Lindsey, L., et al. (2018). High-precision automated reconstruction of neurons with flood-filling networks. Nat. Methods 15, 605–610. doi: 10.1038/s41592-018-0049-4
Keller, P. J., Schmidt, A. D., Wittbrodt, J., and Stelzer, E. H. (2008). Reconstruction of zebrafish early embryonic development by scanned light sheet microscopy. Science 322, 1065–1069. doi: 10.1126/science.1162493
Keuper, M., Levinkov, E., Bonneel, N., Lavoué, G., Brox, T., and Andres, B. (2015). “Efficient decomposition of image and mesh graphs by lifted multicuts,” in Proceedings of the IEEE International Conference on Computer Vision, (Washington, DC) 1751–1759.
Krasowski, N. E., Beier, T., Knott, G., Köthe, U., Hamprecht, F. A., and Kreshuk, A. (2017). Neuron segmentation with high-level biological priors. IEEE Trans. Med. Imaging 37, 829–839. doi: 10.1109/TMI.2017.2712360
Kroeger, T., Kappes, J. H., Beier, T., Koethe, U., and Hamprecht, F. A. (2014). “Asymmetric cuts: joint image labeling and partitioning,” in German Conference on Pattern Recognition (Cham: Springer), 199–211.
Krzic, U., Gunther, S., Saunders, T. E., Streichan, S. J., and Hufnagel, L. (2012). Multiview light-sheet microscope for rapid in toto imaging. Nat. Methods 9, 730–733. doi: 10.1038/nmeth.2064
Lee, K., Zung, J., Li, P., Jain, V., and Seung, H. S. (2017). Superhuman accuracy on the snemi3d connectomics challenge. arXiv arXiv:1706.00120.
Lee, T.-C., Kashyap, R. L., and Chu, C.-N. (1994). Building skeleton models via 3-d medial surface axis thinning algorithms. CVGIP Graph. Models Image Process. 56, 462–478. doi: 10.1006/cgip.1994.1042
Levinkov, E., Uhrig, J., Tang, S., Omran, M., Insafutdinov, E., Kirillov, A., et al. (2017). “Joint graph decomposition & node labeling: problem, algorithms, applications,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (Washington, DC) 6012–6020. doi: 10.1109/CVPR.2017.206
Matejek, B., Haehn, D., Zhu, H., Wei, D., Parag, T., and Pfister, H. (2019). “Biologically-constrained graphs for global connectomics reconstruction,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (Washington, DC) 2089–2098.
Meilă, M. (2003). “Comparing clusterings by the variation of information,” in Learning Theory and Kernel Machines (Berlin, Heidelberg: Springer), 173–187.
Meirovitch, Y., Matveev, A., Saribekyan, H., Budden, D., Rolnick, D., Odor, G., et al. (2016). A multi-pass approach to large-scale connectomics. arXiv arXiv:1612.02120.
Meirovitch, Y., Mi, L., Saribekyan, H., Matveev, A., Rolnick, D., and Shavit, N. (2019). “Cross-classification clustering: an efficient multi-object tracking technique for 3-d instance segmentation in connectomics,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (Washington, DC) 8425–8435.
Musser, J. M., Schippers, K. J., Nickel, M., Mizzon, G., Kohn, A. B., Pape, C., et al. (2019). Profiling cellular diversity in sponges informs animal cell type and nervous system evolution. bioRxiv 758276. doi: 10.1101/758276
Nixon-Abell, J., Obara, C. J., Weigel, A. V., Li, D., Legant, W. R., Xu, C. S., et al. (2016). Increased spatiotemporal resolution reveals highly dynamic dense tubular matrices in the peripheral er. Science 354:aaf3928. doi: 10.1126/science.aaf3928
Nunez-Iglesias, J., Kennedy, R., Parag, T., Shi, J., and Chklovskii, D. B. (2013). Machine learning of hierarchical clustering to segment 2d and 3d images. PLoS ONE 8:e71715. doi: 10.1371/journal.pone.0071715
Otsuka, S., Steyer, A. M., Schorb, M., Heriche, J.-K., Hossain, M. J., Sethi, S., et al. (2018). Postmitotic nuclear pore assembly proceeds by radial dilation of small membrane openings. Nat. Struct. Mol. Biol. 25, 21–28. doi: 10.1038/s41594-017-0001-9
Pape, C., Beier, T., Li, P., Jain, V., Bock, D. D., and Kreshuk, A. (2017). “Solving large multicut problems for connectomics via domain decomposition,” in Proceedings of the IEEE International Conference on Computer Vision, (Washington, DC) 1–10.
Pereira, A. F., Hageman, D. J., Garbowski, T., Riedesel, C., Knothe, U., Zeidler, D., et al. (2016). Creating high-resolution multiscale maps of human tissue using multi-beam sem. PLoS Comput. Biol. 12:e1005217. doi: 10.1371/journal.pcbi.1005217
Rolnick, D., Meirovitch, Y., Parag, T., Pfister, H., Jain, V., Lichtman, J. W., et al. (2017). Morphological error detection in 3d segmentations. arXiv arXiv:1705.10882.
Ronneberger, O., Fischer, P., and Brox, T. (2015). “U-net: convolutional networks for biomedical image segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Cham: Springer), 234–241.
Royer, L. A., Lemon, W. C., Chhetri, R. K., Wan, Y., Coleman, M., Myers, E. W., et al. (2016). Adaptive light-sheet microscopy for long-term, high-resolution imaging in living organisms. Nat. Biotechnology 34:1267. doi: 10.1038/nbt.3708
Russell, M. R., Lerner, T. R., Burden, J. J., Nkwe, D. O., Pelchen-Matthews, A., Domart, M. C., et al. (2017). 3d correlative light and electron microscopy of cultured cells using serial blockface scanning electron microscopy. J. Cell Sci. 130, 278–291. doi: 10.1242/jcs.188433
Sommer, C., Straehle, C., Koethe, U., and Hamprecht, F. A. (2011). “Ilastik: interactive learning and segmentation toolkit,” in 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro (Chicago, IL: IEEE), 230–233. doi: 10.1109/ISBI.2011.5872394
Takemura, S. Y., Xu, C. S., Lu, Z., Rivlin, P. K., Parag, T., Olbris, D. J., et al. (2015). Synaptic circuits and their variations within different columns in the visual system of drosophila. Proc. Natl. Acad. Sci. U.S.A. 112, 13711–13716. doi: 10.1073/pnas.1509820112
Turaga, S. C., Murray, J. F., Jain, V., Roth, F., Helmstaedter, M., Briggman, K., et al. (2010). Convolutional networks can learn to generate affinity graphs for image segmentation. Neural Comput. 22, 511–538. doi: 10.1162/neco.2009.10-08-881
Van der Walt, S., Schönberger, J. L., Nunez-Iglesias, J., Boulogne, F., Warner, J. D., Yager, N., et al. (2014). scikit-image: image processing in python. PeerJ 2:e453. doi: 10.7717/peerj.453
White, J. G., Southgate, E., Thomson, J. N., and Brenner, S. (1986). The structure of the nervous system of the nematode caenorhabditis elegans. Philos. Trans. R Soc. Lond. B Biol. Sci. 314, 1–340. doi: 10.1098/rstb.1986.0056
Wolf, S., Bailoni, A., Pape, C., Rahaman, N., Kreshuk, A., Köthe, U., et al. (2019). The mutex watershed and its objective: Efficient, parameter-free image partitioning. arXiv [preprint]:1904.12654. doi: 10.1007/978-3-030-01225-0-34
Wolf, S., Pape, C., Bailoni, A., Rahaman, N., Kreshuk, A., Kothe, U., et al. (2018). “The mutex watershed: efficient, parameter-free image partitioning,” in Proceedings of the European Conference on Computer Vision (ECCV), (Cham) 546–562.
Zheng, Z., Lauritzen, J. S., Perlman, E., Robinson, C. G., Nichols, M., Milkie, D., et al. (2018). A complete electron microscopy volume of the brain of adult drosophila melanogaster. Cell 174, 730–743. doi: 10.1016/j.cell.2018.06.019
Zung, J., Tartavull, I., Lee, K., and Seung, H. S. (2017). “An error detection and correction framework for connectomics,” in Advances in Neural Information Processing Systems, 6818–6829. Available online at: http://papers.nips.cc/paper/7258-an-error-detection-and-correction-framework-for-connectomics
Keywords: biomedical image analysis, instance segmentation, biological priors, EM segmentation, LM segmentation, connectomics, lifted multicut
Citation: Pape C, Matskevych A, Wolny A, Hennies J, Mizzon G, Louveaux M, Musser J, Maizel A, Arendt D and Kreshuk A (2019) Leveraging Domain Knowledge to Improve Microscopy Image Segmentation With Lifted Multicuts. Front. Comput. Sci. 1:6. doi: 10.3389/fcomp.2019.00006
Received: 05 August 2019; Accepted: 01 October 2019;
Published: 24 October 2019.
Edited by:
Ignacio Arganda-Carreras, University of the Basque Country, SpainReviewed by:
Daniel Raimund Berger, Harvard University, United StatesSuyash P. Awate, Indian Institute of Technology Bombay, India
Copyright © 2019 Pape, Matskevych, Wolny, Hennies, Mizzon, Louveaux, Musser, Maizel, Arendt and Kreshuk. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anna Kreshuk, YW5uYS5rcmVzaHVrQGVtYmwuZGU=
 Constantin Pape
Constantin Pape Alex Matskevych1
Alex Matskevych1 Adrian Wolny
Adrian Wolny Julian Hennies
Julian Hennies Marion Louveaux
Marion Louveaux Alexis Maizel
Alexis Maizel Anna Kreshuk
Anna Kreshuk