- 1Hahn-Schickard, Freiburg, Germany
- 2Intelligent Embedded Systems Lab, University of Freiburg, Freiburg, Germany
We validate the OpenSense framework for IMU-based joint angle estimation and furthermore analyze the framework's ability for sensor selection and optimal positioning during activities of daily living (ADL). Personalized musculoskeletal models were created from anthropometric data of 19 participants. Quaternion coordinates were derived from measured IMU data and served as input to the simulation framework. Six ADLs, involving upper and lower limbs were measured and a total of 26 angles analyzed. We compared the joint kinematics of IMU-based simulations with those of optical marker-based simulations for most important angles per ADL. Additionally, we analyze the influence of sensor count on estimation performance and deviations between joint angles, and derive the best sensor combinations. We report differences in functional range of motion (fRoMD) estimation performance. Results for IMU-based simulations showed MAD, RMSE, and fRoMD of 4.8°, 6.6°, 7.2° for lower limbs and for lower limbs and 9.2°, 11.4°, 13.8° for upper limbs depending on the ADL. Overall, sagittal plane movements (flexion/extension) showed lower median MAD, RMSE, and fRoMD compared to transversal and frontal plane movements (rotations, adduction/abduction). Analysis of sensor selection showed that after three sensors for the lower limbs and four sensors for the complex shoulder joint, the estimation error decreased only marginally. Global optimum (lowest RMSE) was obtained for five to eight sensors depending on the joint angle across all ADLs. The sensor combinations with the minimum count were a subset of the most frequent sensor combinations within a narrowed search space of the 5% lowest error range across all ADLs and participants. Smallest errors were on average < 2° over all joint angles. Our results showed that the open-source OpenSense framework not only serves as a valid tool for realistic representation of joint kinematics and fRoM, but also yields valid results for IMU sensor selection for a comprehensive set of ADLs involving upper and lower limbs. The results can help researchers to determine appropriate sensor positions and sensor configurations without the need for detailed biomechanical knowledge.
1 Introduction
Body-worn inertial measurement units (IMUs) are used to analyze human activity and movement performance, including the assessment of execution quality and mobility, e.g., in daily life, sports and rehabilitation (Balasubramanian et al., 2009; Spina et al., 2013; Derungs et al., 2018; Tulipani et al., 2020). Sensor recordings, even from multiple IMUs located at the human body, are a cost-effective method to acquire body movement in non-laboratory environments, where conventional marker-based video motion capture (MoCap) is impractical. Although multi-IMU systems have been used for over 40 years to estimate relative limb alignment (Picerno, 2017), determining key indicators of movement, i.e., joint angles is known to be challenging. One of the main reasons is the inherently non-linear problem to estimate sensor orientations (Saber-Sheikh et al., 2010). Commercial IMU systems exist that use proprietary movement estimation methods, where access to source code and tuning parameters is restricted. Hence, results from those commercial systems may not be reproducible or implemented with alternative solutions.
One of the key challenges in setting up IMU-based body movement monitoring is to determine sensor count and body position that balances kinematic estimation accuracy and practical aspects, including wearability concerns, computational cost, and integration complexity. In particular, determining angles of joints with multiple degrees of freedom (DoF), requires extensive experience or more than the minimum-optimal number of IMUs. For example, the 3-DoF shoulder joint has the greatest mobility in the human body (Halder et al., 2000). During movement, shoulder instability is counteracted by static (ligaments, joint capsules) and dynamic (muscle contraction) stabilization (Terry and Chopp, 2000). Hence, unlike a 1-DOF hinge joint (e.g., elbow joint), it is not straightforward to estimate its IMU count. In addition to joint angles, the functional range of motion (fROM) is of great interest to monitor individuals, as it is characterized as the necessary range of movements to sustain maximal independence and facilitate optimal conditions for ADL performance in daily life (Korp et al., 2015; Doğan et al., 2019). fRoM has been used in rehabilitation settings, where therapists could customize training plans, track progress, and ensure patients regain movement capabilities after injuries and surgeries. Furthermore, ergonomic assessments in various industries benefit from IMU-based fRoM analysis, e.g., to design employees' workstations, promote comfort, and minimize the risk of musculoskeletal problems (Nam et al., 2019; Lim and D'Souza, 2020).
In this work, we investigate IMU-based monitoring of a complementary ADL set, involving both upper and lower body activities, to establish a performance baseline for joint angle and fRoM estimation. We leverage the OpenSense framework (Al Borno et al., 2022) to evaluate sensor position selection and sensor count estimation. In particular, this paper provides the following contributions:
1. We validate the open-source framework OpenSense for ADL analysis by comparing the estimation for 26 joint angles based on IMU data against gold-standard optical motion capture (MoCap) data. Compared to previous work, we include additional ADLs, larger participant group, more joint angles, and subsequently perform a comprehensive error analysis with additional motion-specific error metrics. Researchers using our results can detect and mitigate IMU-based errors by evaluating the accuracy of their simulations, algorithms, and systems to process motion-related data.
2. We analyze the framework's ability for sensor selection. We iterate across all possible sensor combinations, participants, and ADLs to find the lowest error as function of sensor count. The results provide insight into how the sensor count affects the estimation error per joint angle and can be used to determine a minimum, close-to-optimal sensor count to estimate joint angles for a complementary set of ADLs.
3. Within a narrowed search space of the 5% lowest error range, we evaluated the most frequent sensor position combinations and sensor positions that yield the minimal sensor count across all participants and ADLs per joint angle. Results can help to prioritize sensor positions and which positions to be omitted without compromising ADL analysis accuracy, which may be transferred to other ADLs, too. Results provide a systematic and data-driven approach to sensor reduction, which will lead to efficient and practical sensor deployments.
Our validation and performance analyses can assist wearable system researchers and designers to determine realistic error ranges for joint angles and functional range of motion depending on the expected activities. In addition, sensor selection analysis inside an established open-source environment can be used to determine appropriate sensor positions without in-depth biomechanical knowledge and to selectively place sensors for full-body motion analysis according to the region of interest.
2 Related work
2.1 IMU-based joint kinematics
In the last decade, open-source IMU signal fusion algorithms have profoundly improved in kinematic estimation performance, e.g., Madgwick et al. (2011), Mahony et al. (2012), and Joukov et al. (2018), and more precise methods for sensors-to-body segment alignment were proposed (Pacher et al., 2020). Still, joint angle analysis based on IMU data is often addressing periodic lower limb movements, e.g., walking or running, over short durations (5 s –1 min) only, and was evaluated with less than ten participants (Weygers et al., 2020). Previous research utilized IMUs to assess lower limb kinematics and found a root mean square error (RMSE) of joint angles in the range of 5 − 10° (Robert-Lachaine et al., 2017; Teufl et al., 2019). Compared to MoCap-based kinematics, a greater consistency of angle measurements in the sagittal plane than in the other two planes was observed. For upper limbs Goodwin et al. (2021) investigated humeral elevation in individuals with spinal cord injury and showed that shoulder motion was highly consistent with MoCap. In a study by Wang et al. (2022), joint angles obtained from five IMUs positioned on one side of the upper body were compared with a markerless MoCap system and a standard marker-based method. The findings indicated that the RMSE for joint angles was smaller at the shoulders compared to the elbows. However, in a systematic review by Poitras et al. (2019), RMSE of the shoulder joint ranged between 0.2 and 64.5°, indicating a large heterogeneity of studies and performed movements.
The fRoM derived from joint angle estimations is of particular interest in clinical settings and assures researchers an accurate interpretation and processing of joint motion data. Doğan et al. (2019) reported smaller fRoMs (up to 40°) assessing IMU-based measurements of upper limbs and trunk joints compared to MoCap measurements and attributed the differences to measurement methods and protocols. Additionally, Rigoni et al. (2019) compared IMU-based measurements with goniometer measurements for shoulder RoM and Stołowski et al. (2023) for hip joint RoM. Yet, only intra-class correlation coefficients were analyzed with reported levels of agreement (mean difference ± standard deviation), between −4.5 − 3.2,° for the shoulder joint and < 9° for the hip joint, respectively. Moreover, Rigoni et al. (2019) defined a change >10° as clinically relevant. In summary, the previously described motions are not entirely representative for real-life behavior as ADLs are usually a combination of alternating lower and upper limb movements and might be coupled too. So far, IMU-based analyses did not adequately assess upper limb kinematics during daily activities, as mostly uniaxial movements were measured (Picerno et al., 2019). Some studies have demonstrated measures of accuracy, including waveform similarity and amplitude comparison, that were consistent with estimates of upper limb joint kinematics. In 2022, Uhlenberg et al. (2022) introduced a framework based on OpenSense to estimate joint angle accuracy in combined ADLs with three different sensor fusion algorithms. The authors considered four ADLs with 10 participants and concluded that the most accurate estimations were obtained using the Madgwick and Mahony filters. The present work expands the existing framework by considering additional ADLs, a larger participant group, more joint angles, and a comprehensive error analysis with fRoM as additional motion-specific error metrics.
Framework, sensor, and algorithm choices are closely interrelated with the error metrics described above. Previous studies have often used closed systems and algorithms to estimate joint angle, such as Xsens sensors with proprietary algorithms. The approach often involves filtering algorithms, of which many become non-transparent black boxes and can be costly or limited to specific settings and hardware (Al Borno et al., 2022). In this work, we investigate several ADLs that combine upper and lower limb movements using an open-source framework, a published sensor fusion algorithm, and raw acceleration and orientation data to validate the OpenSense framework and demonstrate the versatility of kinematic simulations for IMU sensor selection.
2.2 Simulation framework
For rigorous testing and validation of algorithms applied to IMU-based estimations, the simulation framework provides a controlled environment to assess accuracy and reliability before applying the tested methods to real-world scenarios. Within the multitude of simulation frameworks, the OpenSim (Delp et al., 2007) open-source software toolkit (Simbios, U.S. National Institutes of Health Center for Biomedical Computation at Stanford University) was used in this work for modeling and simulating movement biomechanics. In addition, software with capabilities similar to OpenSim, e.g., AnyBody (Rasmussen et al., 2005; Damsgaard et al., 2006) or Alaska/dynamicus (Hermsdorf et al., 2019) may be deployed too. However, OpenSim's free availability facilitates community modifications and enables users to examine the source code to maximize reproducibility. Related to OpenSim, OpenSense represents a novel open-source software tool tailored to the examination of motion data from IMUs. To date, the OpenSense workflow has been utilized to examine kinematic drift during 10-min walking trials and motion variability during gait (Bailey et al., 2021; Al Borno et al., 2022). In addition, in recent work from Slade et al. (2022), the IMU-based real-time solution OpenSenseRT was demonstrated to analyze Fugl-Mayer assessment tasks and trunk movements. The authors reported a RMSE for joint angle estimation of ~5°, a difference accepted as reasonable for research and many clinical applications (Del Rosario et al., 2016; Slade et al., 2022). Compared to the aforementioned literature, our work is not limited to the lower limbs and instead covers the upper limbs with selected ADLs too. Furthermore, the selected biomechanical model used in our work contains 165 DoF (see Section 3.2), whereas the model employed in the published OpenSense literature (Rajagopal et al., 2016) features 37 DoF only. The increased flexibility of the vertebrae (compared to trunk and head being one segment) captures the full human movement complexity, especially in scenarios where spinal mobility is an important factor, such as performing everyday activities.
2.3 Sensor count and selection approaches
The number of sensors in a wearable system is directly related to the amount and complexity of the available data. Sensor selection often requires prior expert knowledge concerning the type of movement. A common desire among researchers is to reduce the number of required sensors while maintaining angle estimation accuracy. However, a larger sensor count is often considered as advantageous to maximize precision and versatility (Ancillao et al., 2018), thus yielding more accurate measurements (Sy et al., 2021) for a wide range of applications. Therefore, the critical sensor count and selecting the corresponding sensor positions guide system integration, calibration, and data processing strategies to ensure optimal performance and reliability. Published literature focused on reducing the sensor count by applying kinematic chain, double-pendulum, and statistical shape models (Salarian et al., 2013; Hu et al., 2015; Marcard et al., 2017). Additionally, optimal control approaches were proposed (Dorschky et al., 2023) to investigate sparse IMU sensor sets. However, a systematic quantitative analysis of how adding or removing sensors affects performance in the context of ADLs is missing. In our work, OpenSense serves as a tool for sensor selection and as a platform for exploring, testing, and evaluating over 8,000 IMU sensor combinations. Although the kinematic chain within OpenSense should not be disrupted1 the corresponding joint angles can be analyzed as a function of sensor count and key sensor positions can be identified.
3 Methods
Figure 2 provides an overview on the simulation components and processing steps. In the following subsections, we detail the framework components and their implementation.
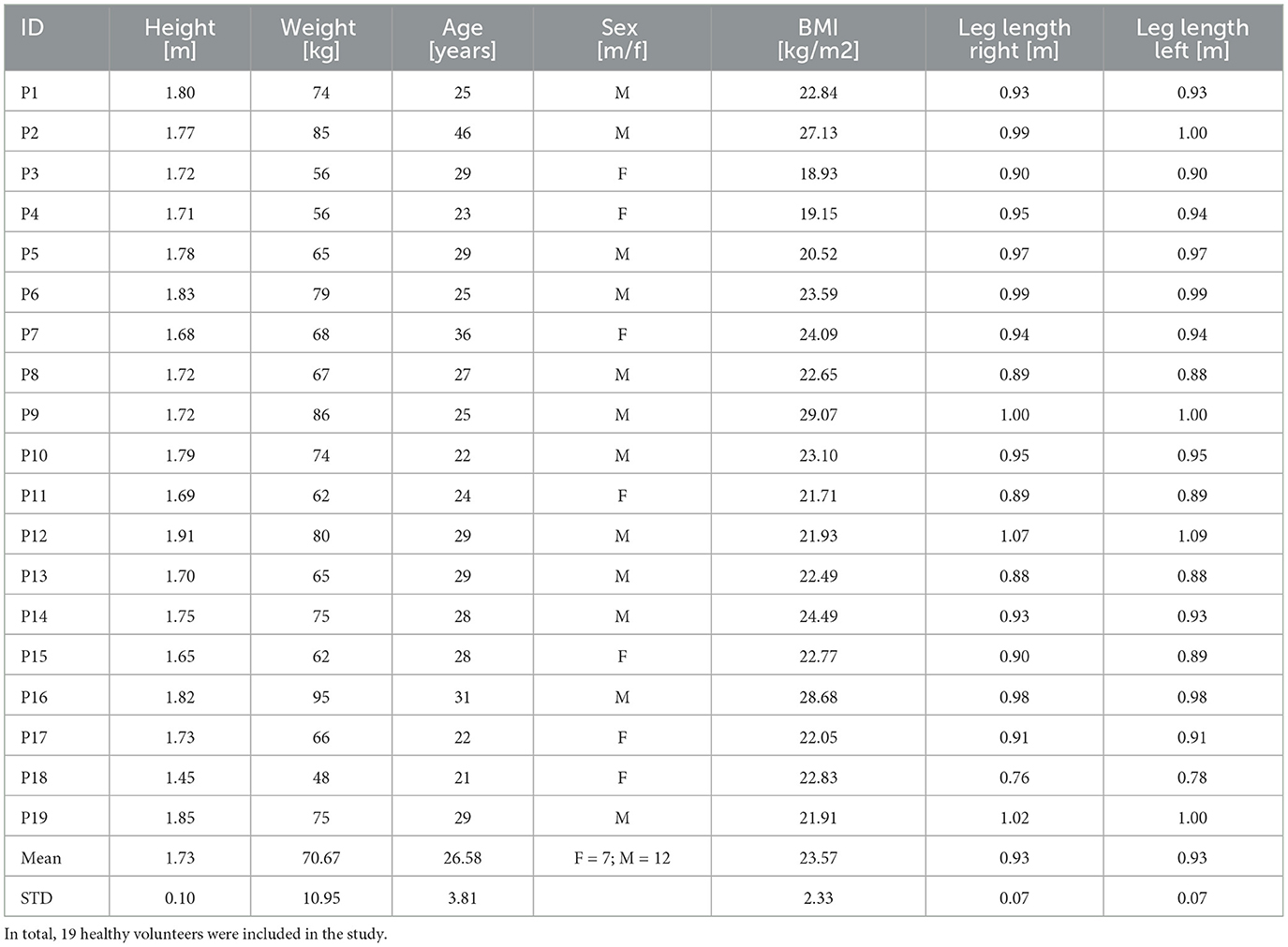
Figure 1. Illustration of all joint angles considered across all ADLs to investigate sensor position selection and sensor count estimation. Insight from the investigation can support researchers and developers in the system design and to select optimal sensor configurations. L: Left body side; R: Right body side.

Figure 2. Method overview. IMU and MoCap data were processed to create personalized biomechanical models. Orientation estimates (quaternion coordinates), derived from IMU data using the Madgwick fusion algorithm, were used in OpenSense to animate biomechanical models in ADL simulations for varying sensor combinations. Subsequently, IMU-based joint angle and functional range of motion differences (fRoMD) estimates were compared to MoCap data and a sensor selection analysis was performed.
3.1 Data acquisition and processing
We recruited 19 healthy volunteers for the evaluation study. All participants gave written consent prior to participation and ethics approval was granted by an institutional ethics board. We derived body segment masses and joint centers using Visual3D (C-Motion Inc., Germantown, USD) from the Conventional Gait model in combination with IOR trunk model (Leardini et al., 2011; C-Motion Inc., 2022). Table 1 details participant data.
We placed 54 reflective spherical MoCap markers at anatomical landmarks and attached 16 IMUs (MyoMotion, Noraxon, USD) to record each body segment (see Figure 3) using Noraxon Velcro straps with IMU pockets. A calibrated and synchronized 11-camera marker-based MoCap system (Qualisys, Gothenburg, Sweden) was used to record gold-standard MoCap data. Both systems were time-synchronized. MoCap and IMU data were recorded at a sampling rate of 100 Hz and filtered by a 6 Hz lowpass Butterworth filter. Participants performed a static reference trial, which was used to reconstruct body segments, determine body dimensions, joint centers, segment coordinate systems, and calibrate the IMU sensors. Subsequently, participants were instructed to perform each ADL three times. Data inspection was performed by two independent examiners and involved labeling and filling of MoCap marker gaps using Qualysis Track Manager, v. 2018.
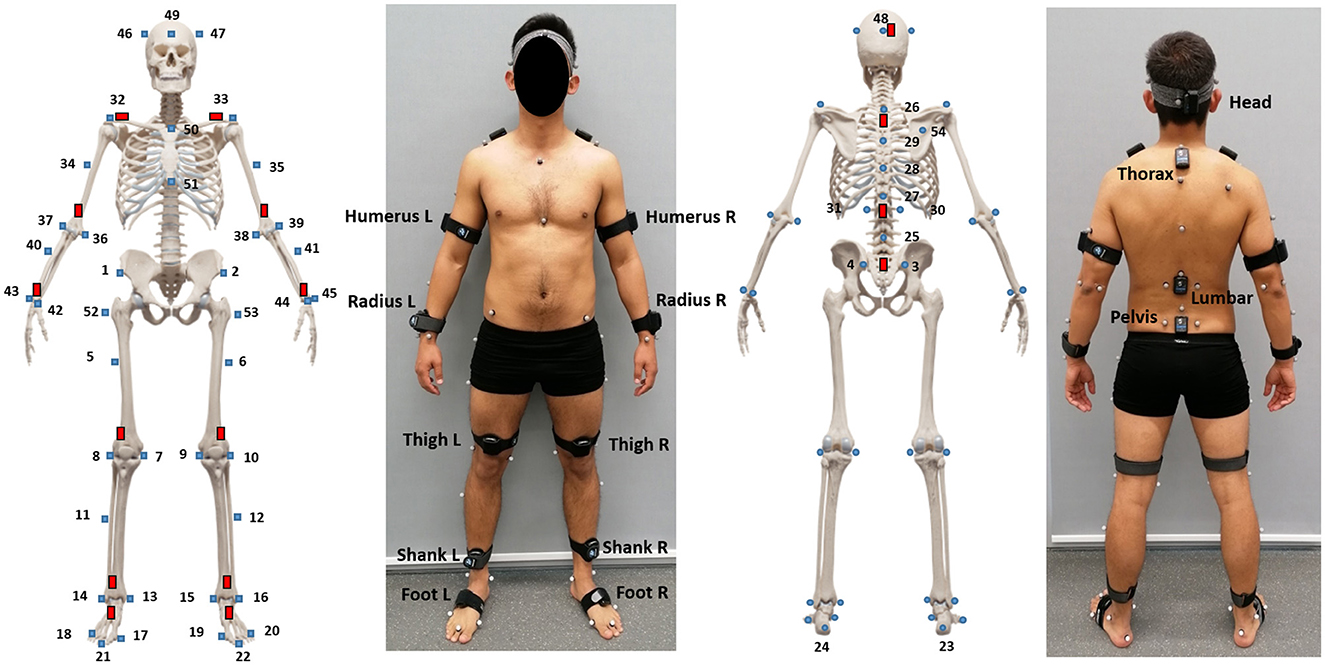
Figure 3. Marker and IMU setup for data acquisition in this work. In total 54 reflective spherical MoCap markers were placed at anatomical landmarks as well as 16 IMUs attached to body segments.
3.2 Personalized biomechanical body models
A biomechanical, personalizable body model was the basis for all simulations. We used the OpenSim full-body thoracolumbar spine model (Schmid et al., 2020), which, in contrast to previous IMU-based simulations inside OpenSense (Bailey et al., 2021; Al Borno et al., 2022; Slade et al., 2022), accounts for more DoF at upper limbs and spine area (165 vs. 37 DoF). Personalization of the biomechanical body model involved scaling, i.e., changing the body mass properties body weigth and dimensions, by comparing static distance measurements between defined model landmarks and the registration of markers (static pose weights affect to what degree a landmark-marker pair should be satisfied and were kept to the default value of 1). In summary, model personalization included body weight and measured motion capture markers.
3.3 Sensor fusion
The Madgwick sensor fusion algorithm (Madgwick et al., 2011) was used to estimate orientation in quaternion coordinates q based on the Python AHRS toolbox (Garcia, 2023). The Madgwick filter is a gradient-descent algorithm with filter gain β representing mean zero gyroscope measurement errors, expressed as , where is the estimated mean zero gyroscope measurement error of each axis.
For joint angle kinematic analysis, Leave-One-Participant-Out cross-validation (LOPOCV) was used to fit β per ADL, as described by Uhlenberg et al. (2022). Participant data that was held-out during training, was used for error analysis and results were averaged across all folds.
For sensor selection analysis, β was set to 0.1, according to published literature (Bailey et al., 2021; Al Borno et al., 2022), as well as the majority voting of LOPOCV β-fitting results across all angles, participants and ADLs. Our previous analysis on a smaller dataset showed that β = 0.1 provided lowest error and that parameter variation yielded minor error variation in a band of ±1° (Uhlenberg et al., 2022).
3.4 OpenSense
Pre-processed MoCap and IMU orientations (quaternion coordinates) as derived from the sensor fusion algorithm (see Section 3.3), were imported into OpenSim and linked to the personalized biomechanical body models. A custom sensor mapping was applied to link IMUs with corresponding rigid body parts (e.g., pelvis, thigh, etc.), represented as a “Frame” (orthogonal XYZ coordinate system). Shoulder IMUs were omitted since the underlying OpenSense shoulder angle estimation (IMU IK solver) does not consider the clavicle, but torso and humerus of the corresponding body side for joint formation (Al Borno et al., 2022). The initial IMU orientations were defined relative to the body segments at which they were placed in the static reference trial. Subsequently, the MoCap and static IMU reference data were used to define the IMU orientations relative to the body model segments as fixed rotational offsets. The modeled virtual IMU “Frames" were assigned the rotational offsets relative to the underlying rigid body, resulting in a calibrated body model.
3.5 Sensor combinations
All sensor combinations included the pelvis IMU for calibration, i.e., the smallest sensor count was two sensors. To calculate the total number of combinations, the power set P (S) was determined, where P(S) is the set including all subsets of S except the empty set (see Equation 1). Hence, 8,191 sensor combinations were simulated per participant and ADL.
OpenSense requires a closed kinematic chain to move subsequent body segments and provide meaningful error estimates. Therefore, sensor combinations that break the kinematic chain, e.g., omitting the thigh IMU for knee/ankle angle estimation or omitting the humerus IMU for elbow flexion angle, were discarded for the corresponding joint angle as limbs remained in the calibration pose. Consequently, the following number of sensor combinations were analyzed: Pelvis angles: 8,191, hip joint angles (L/R): 7,168, knee flexion (L/R): 6,144, ankle plantar flexion (L/R): 4,096, head angles: 7,168, shoulder angles and arm elevation (L/R): 7,168, elbow flexion (L/R): 6,144, and hand pronation (L/R): 6,144.
3.6 ADL simulation
For the MoCap-based reference model, the OpenSim inverse kinematics (IK) solver was used, which minimizes the difference between experimentally measured marker positions and the corresponding virtual markers in the OpenSim model. For the IMU-based model, the OpenSense IK solver was supplied with quaternion coordinates to estimate the joint angles and fRoM. The OpenSense IK solver was introduced by Al Borno et al. (2022) and minimizes the weighted squared differences between experimentally measured IMU orientations and the model's virtual IMU orientations via configurable weights (corresponding to the static pose weights used for the OpenSim modeling) as matching control per IMU. We reduced relative weights of distal IMUs (tibia: 0.5 and foot: 0.01) to minimize the influence of floor-embedded metal force plates (Al Borno et al., 2022). The force plates were used for other research questions related to the evaluation study, which are not relevant for this work.
A total of six ADLs, involving a combination of upper and lower limb movements were analyzed: shelve ordering (SO), stairs climbing (SC), walking (W), pen pickup (PP), jumping (J), and getting up from the floor (G). The ADLs were selected to cover everyday activities with alternating or combined involvement of upper and lower limbs. Apart from walking, climbing stairs, and jumping, the ADL “getting up from the floor” extends to similar daily activities, e.g., getting in and out of a bathtub, a low chair, or a car. The ability to reach and place items on shelves at different heights is used in daily life when organizing or accessing items in cupboards or shelves. Picking up a pen extends to similar activities with small objects, e.g., picking up coins or using utensils.
3.7 Evaluation
3.7.1 Error and fRoM
Joint angle estimation performance of all 26 considered angles (see Figure 1) was evaluated by deriving absolute median error (MAD) and root mean square error (RMSE) between IMU-based simulations and reference MoCap measurements for each participant and ADL according to Equations 2, 3.
with n being is the total number of samples, ŷi represents the simulation-based joint angle estimate, and yi represents the joint angle derived from MoCap measurements.
The difference of fRoM estimations between IMU-based data and MoCap reference (fRoMD) were determined by Equation 4:
where θmax and θmin represent the corresponding maximum and minimum joint angles, respectively.
As some data were not normally distributed, median and interquartile range (IQR) were computed across all participants. Outliers were defined as 1.5×IQR below or above the 25th and 75th percentile.
3.7.2 Sensor count
We determined the lowest RMSE across all sensor combinations per sensor count for all ADLs and participants to assess the error effect per joint angle. To reduce the search space for subsequent analyses, we considered all combinations within the lowest 5% RMSE range across all sensor combinations. We determined the frequencies (occurrence rate) of each sensor combination across all participants and ADLs and compared them to the sensor combination showing the lowest sensor count per joint angle.
4 Results
We summarize estimation results for joint angle and fRoMD and subsequently present results for the sensor selection analysis.
4.1 Joint angle estimation
As the evaluation of joint kinematics is one of the main research components in the investigation of motion performance, Figure 4 shows the most relevant joint angle MAD, RMSE, and fRoMD averaged across participants for each ADL. Additionally, Supplementary Table S1 summarizes all MAD, RMSE, and fRoMD per joint angle, body side, and ADL. Walking, which primarily involves lower limbs, showed lowest errors across all selected angles compared to the other five ADLs (see Figure 4A; Table 2). Between selected angles arm elevation showed the highest errors and largest IQR with MAD, RMSE and fRoMD being 15.8°, 16.8°, 9.8°, respectively. The five remaining angles ranged between 1.5°–5.2° for MAD, 1.7°–5.9° for RMSE and 2.2°–7.6° for fRoMD. Shelve ordering (Figure 4B) with predominant upper limb involvement showed larger errors and IQR for fRoMD for shoulder rotation and elevation, hand pronation and arm elevation compared to the other angles at the head and hip, except head rotation. Errors for the upper limbs ranged between 3.0°–18.1° for MAD, 4.9°–22.6° for RMSE and 10.0°–26.8° for fRoMD. For Pen pickup (Figure 4C) elbow flexion and pelvis rotation showed lowest errors within a range of 2.0°–5.4° for all three error metrics whereas arm elevation showed highest errors for all three error metrics within a range of 14.6°-34.6°. Upper limbs showed on average higher errors (MAD = 10.9°, RMSE = 15.4°, and fRoMD = 8.8°) and IQR compared to lower limbs (MAD = 4.2°, RMSE = 6.0°, and fRoMD = 6.3°) for this combined movement task. Jumping (Figure 4D) showed minimal error and IQR for hip adduction with MAD, RMSE and fRoMD being 1.5°, 2.3°, 2.8°, respectively. Again arm elevation showed highest errors and IQR for the ADL. Getting up floor (Figure 4E) showed largest IQR for fRoMD across all joint angles. Upper limbs showed on average higher errors (MAD = 10.1°, RMSE = 15.3°, and fRoMD = 14.3°) and IQR compared to lower limbs (MAD = 4.7°, RMSE = 6.6°, and fRoMD = 6.2°) and comparable ranges to Pen Pickup (see also Table 2). Comparing selected angles for stair climbing (Figure 4F), arm elevation showed the highest overall errors with MAD= 35.8°, and RMSE = 35.2°. However, fRoMD was comparably low with 16.6°, respectively. The five remaining angles ranged between 1.3°–10.1° for MAD, 1.7°–10.7° for RMSE and 1.8°–21.8° for fRoMD.
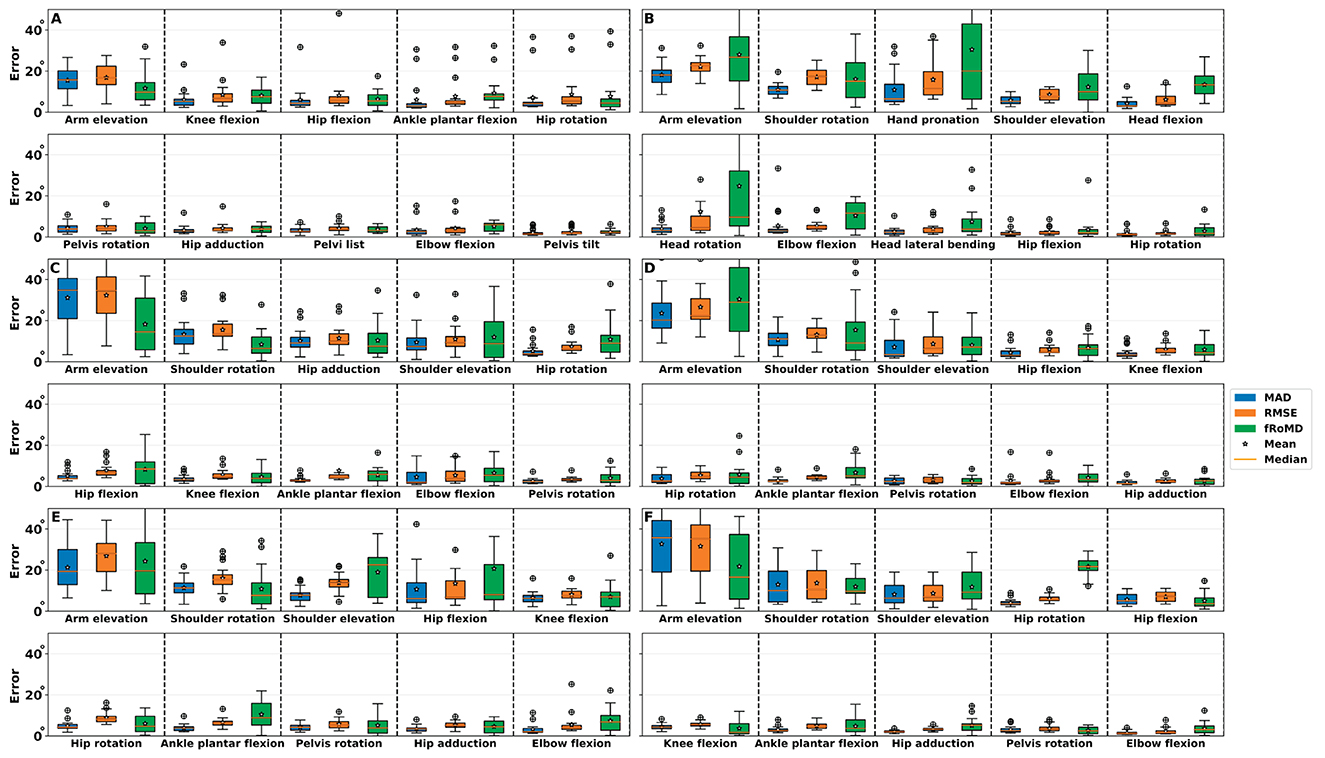
Figure 4. Errors of the most important joint angles per ADLs. (A) Walking (W). (B) Shelve ordering (SO). (C) Pen pickup (PP). (D) Jumping (J). (E) Getting up from the floor (G). (F) Stairs climbing (SC). MAD, median absolute deviation; RMSE, Root mean squared error; fRoMD, functional range of motion difference. Overall, smaller error and fRoMD were obtained for lower limb joints compared to upper limb joints. IMU-based estimation performance varies depending on ADL and joint angle, which emphasizes the importance of validated frameworks and algorithms.
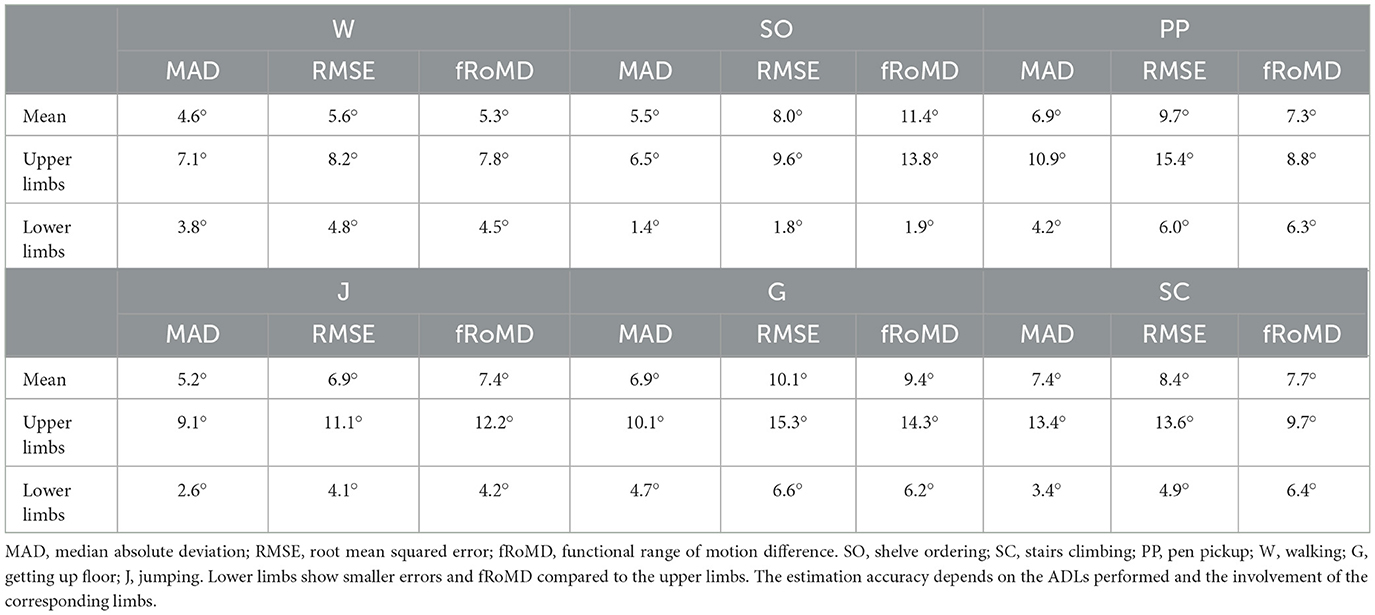
Table 2. Joint angle estimation performance for full body as well as upper and lower limbs for selected joint angles per ADL.
Overall, arm elevation showed highest MAD, RMSE, and fRoMD for the corresponding ADLs (~22.6°), followed by hand pronation (~12.7°) and shoulder rotation (~8.8°). Consequently, upper limbs showed higher error values across all error metrics compared to lower limbs across all ADLs. Moreover, sagittal plane movements, i.e., flexion/extension showed smaller errors across all metrics compared to frontal, i.e., adduction/abduction and arm elevation or axial plane movements, i.e., rotations.
4.2 Sensor count
Figure 5 shows the RMSE as function of sensor count per participant across all ADLs for head, shoulder, and hip joint angles. The joints were selected due to their comparably larger DoF, i.e., modeling complexity and proximity to the pelvis. Results for the remaining joint angles can be found in Supplementary Figure S1. For the head joint (Figures 5A, D, G) RMSE decreases for more than two sensors and slightly increases again for 10–14 sensors. The global minimum RMSE for the head joint was found for six sensors. For the shoulder joint (Figures 5B, E, H), a steep drop after two sensors can be observed, and RMSE continues to decrease up to four sensors. Subsequently, for shoulder elevation (Figure 5B) RMSE remains almost constant, while it increases again for shoulder rotation (Figure 5E) and arm elevation (Figure 5H). The minimum RMSE for shoulder joint was observed between four and six sensors, depending on the axis along which the movement occurred. For the hip joint (Figures 5C, F, I) a slight decrease in RMSE from two to three sensors was observed, after which RMSE changed only marginally. Minimum RMSE for hip joint was found at six to eight sensors, depending on the joint angle concerning all ADLs. The shoulder joint resulted in the highest average RMSE with ~ 9.0° compared to ~ 5.5° for the hip joint angles and ~ 3.6° for the head joint angles.
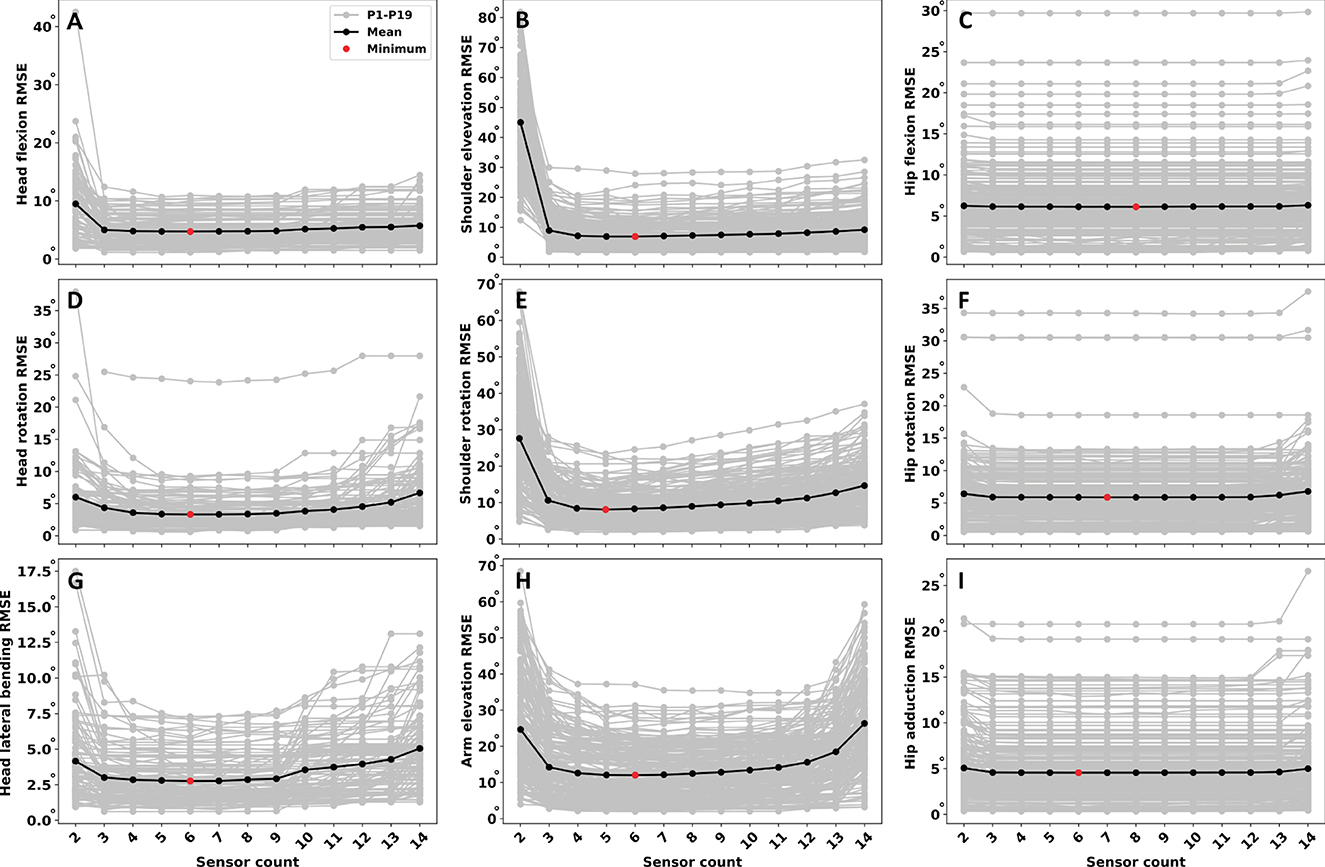
Figure 5. Error estimation as function of sensor count across all ADLs per joint angle. (A) Head flexion. (B) Shoulder elevation. (C) Hip flexion. (D) Head rotation. (E) Shoulder rotation. (F) Hip rotation. (G) Head lateral bending. (H) Arm elevation. (I) Hip abduction. Angles were selected due to the higher DoF, i.e., modeling complexity and proximity to the pelvis. Remaining joint angles can found in Supplementary Figure S1. The sensor count that leads to low error varies depending on the considered joint angle. Complex joints with comparably large DoF may benefit from additional sensors, in particular for distal body segments.
Overall, for three sensors at the lower limbs, and four sensors at the complex shoulder joint, estimation error decreases only marginally, resulting in an optimum (lowest RMSE) sensor count of five to eight, depending on the joint angle across all ADLs.
Additionally, Figure 6 shows example time series signals of shoulder and hip rotations per sensor count for Pen pickup. While the time series pattern for hip rotation matches the MoCap reference even for two sensors, patterns of shoulder rotation deviate. Agreement for the shoulder rotation increases from three sensors onward, albeit at greater overall variability compared to hip rotation.
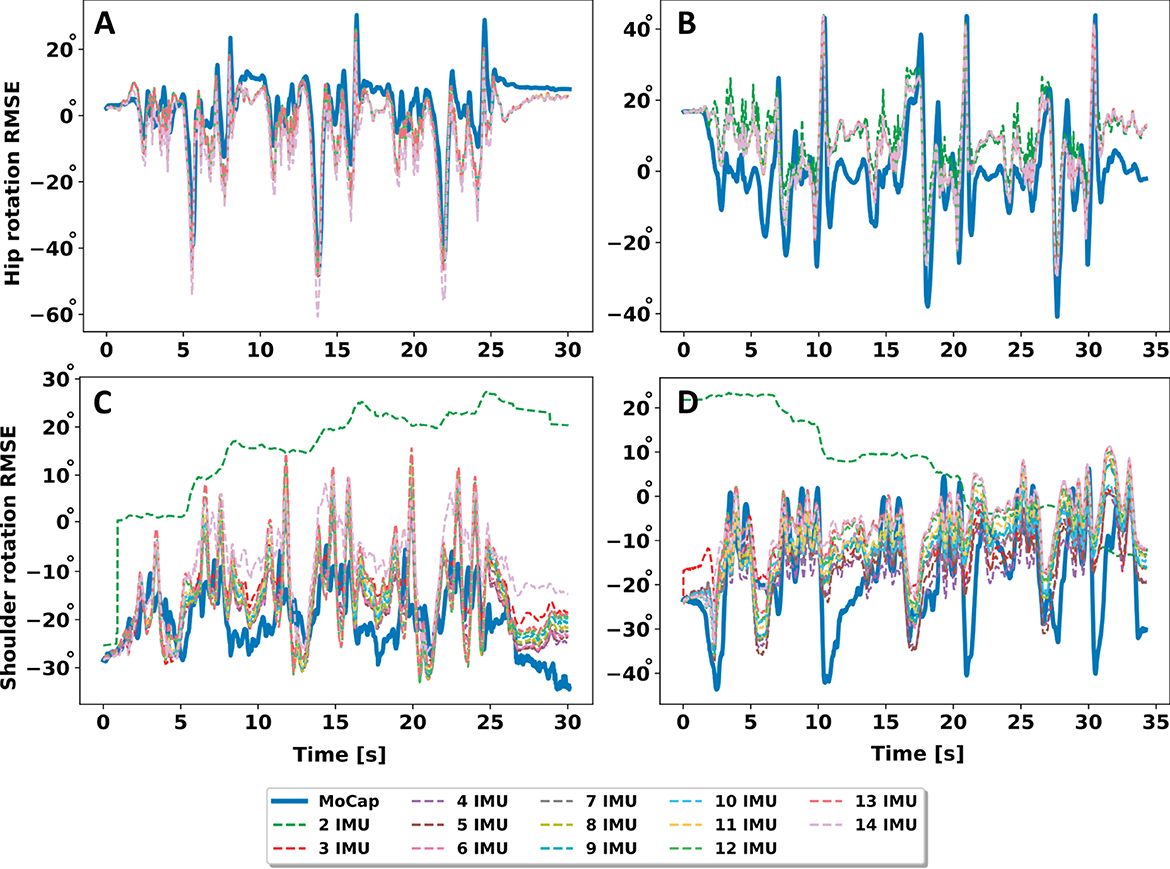
Figure 6. Example of time series comparison using increasing sensor count for pen pickup. (A) Hip rotation P11. (B) Hip rotation P14. (C) Shoulder rotation P11. (D) Shoulder rotation P14. Lower limbs match the time series pattern more closely, with less sensors and less overall variation compared to upper limbs.
Figure 7 shows the most frequent sensor combinations and the sensor combination with the minimum sensor count within the lowest 5% RMSE range across all ADLs and participants. For example, for the head joint angles, the most important IMUs are the pelvis, head and lumbar spine, after which the error decreases only slightly (see also Figures 5A, D, G). For the shoulder joint angles, the pelvis, thorax and the corresponding IMUs for the humerus and radius, depending on the body side considered, showed to be the most important IMUs (see also Figures 4B, E, H). The most frequent sensor combinations showed that sensors on the opposite side of the body or spinal sensors were included in the respective sensor sets compared to the minimal sensor combination. Results showed that the minimal sensor count combinations are a subset of the most frequent sensor combinations across all ADLs and participants. Additionally, Supplementary Tables S2–S8 show the 15 most frequent sensor combination sets.
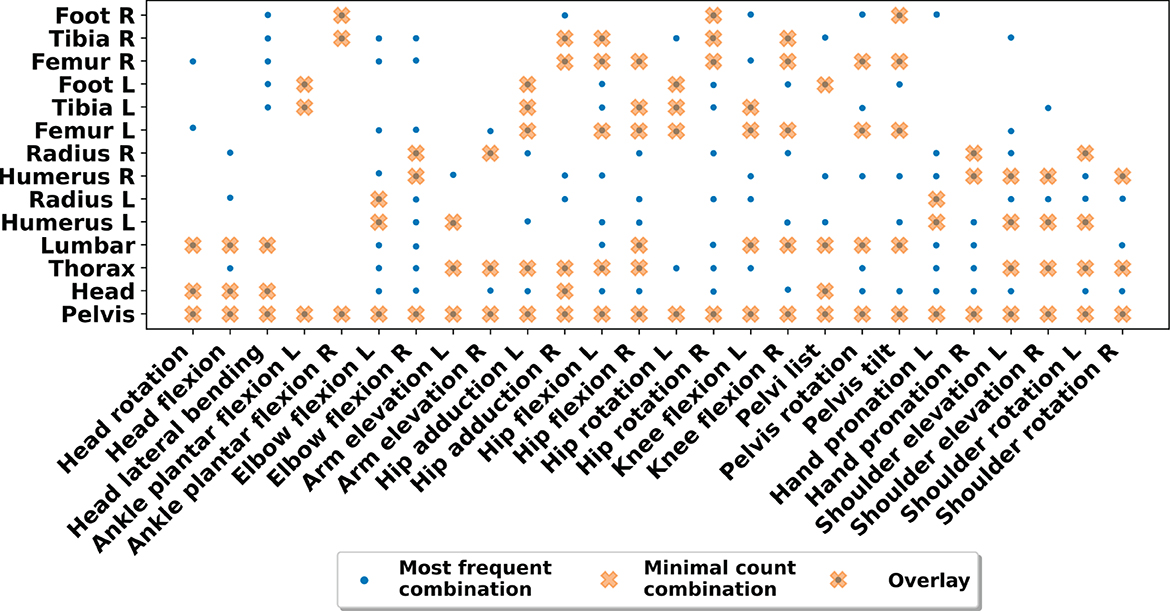
Figure 7. Matching matrix of most frequent sensor positions and positions of minimal sensor count per joint angle within the lowest 5% RMSE range. The minimal sensor count is a subset of the most frequent sensor combinations found across all ADLs and participants, affirming the potential to reduce sensors.
Figure 8 shows the MAD distribution within the 5% lowest RMSE range across all ADLs and participants. All sensor positions yielded a median MAD below 6.4°, except for shoulder rotation (7.8°), arm elevation (8.9°), and hip rotation right (9.4°). IQR for all angles was on average below 1.2°, ranging from 0.1°–5.2°. Comparing left vs. right body side, angles showed error differences that can be attributed to the ADL performance. In particular, getting up from the floor and pen pickup consisted of unilateral, partial execution. Actual pickup and lowering to the floor may occur on either body side, according to the participant's preference and with shoulder, elbow, knee, and hip involvement through flexion or extension, adduction or abduction, and rotation.
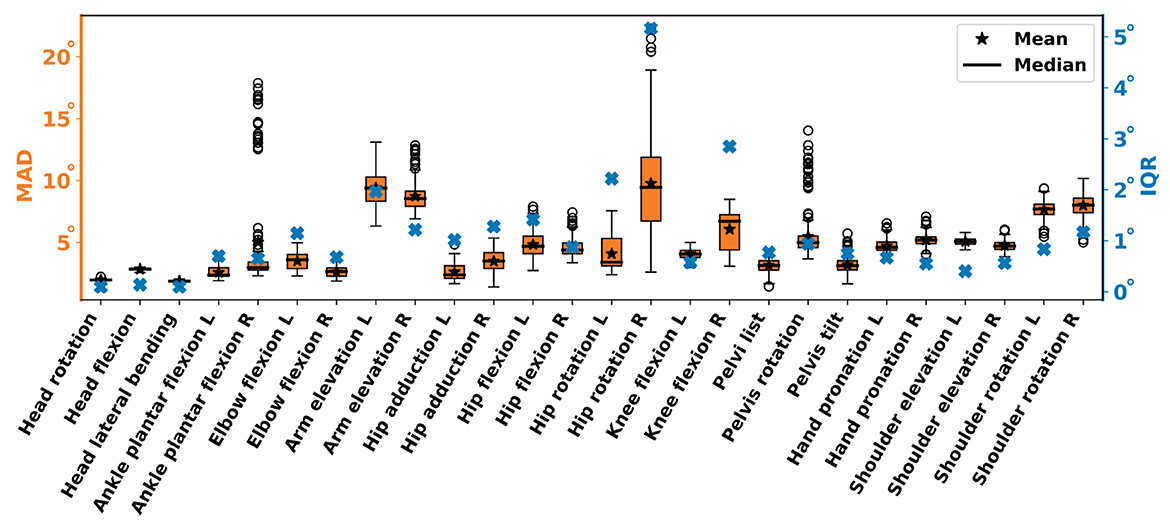
Figure 8. MAD and interquartile range (IQR) per joint angle across all participants and ADLs within the lowest 5% RMSE range. As IQRs are low, on average 1.1°, a reduction to the minimal count combination is reasonable.
5 Discussion
Joint angle estimation performances for lower limbs (see Figure 4; Table 2; Supplementary Table S1) are in agreement with literature. Overall, median MAD was 4.8 ± 2.6°, median RMSE was 6.3 ± 2.9° and median fRoMD was 7.2 ± 4.1° for lower limbs. For example, Al Borno et al. (2022) reported median RMSE between 3 − 6° for lower limb joint angles, except hip rotation (12°), during 10-min walk trials using OpenSense and Madgwick filter (same filter gain of 0.1). Furthermore, Bailey et al. (2021) reported stride-to-stride variability during treadmill gait of 4.4 − 6.7° for knee, ankle, and hip flexion, as well as hip rotation using OpenSense and Madgwick filter (same filter gain of 0.1). Compared to our previous work, adding more ADLs, participants, and joint angles, only slightly increased the median RMSE for lower limbs by 0.7° (Uhlenberg et al., 2022). In comparison to the above literature that used OpenSense, our work is not limited to the lower limbs and extends the range of upper limb movements.
For upper limbs, our median RMSE ranged between 1.9 − 16.3°, with arm elevation angles showing largest errors. However, median RMSE across all upper limb angles was 9.2 ± 7.1°, 11.5 ± 7.3°, and 13.8 ± 7.5° for MAD, RMSE, and fRoMD, respectively (see Figure 4; Table 2; Supplementary Table S1). Compared to previous work (Uhlenberg et al., 2022), and similar to the lower limbs analysis, a minor increase in median RMSE by 1.5° was observed for upper limbs. In comparison, Wang et al. (2022) reported median RMSE for their 5-IMU system ranging between 23.8 − 62.6°, with overall median RMSE below 30° across activities including grasping, lifting small/heavy objects, and reaching overhead. IMUs were mounted at one side of the upper body only and tended to overestimate shoulder rotation. Picerno et al. (2019) estimated uni-axial arm elevation in frontal, scapular, and sagittal planes with 3° and elbow flexion-extension with an error of 2° compared to an optoelectronic stereophotogrammetric system. Our results showed larger median RMSE with 4.7° for elbow flexion and shoulder rotation (14.4°), which could be explained by the multi-axial character of our selected ADLs (Robert-Lachaine et al., 2017). Compared to the aforementioned literature, our work contributes to a broader knowledge base on upper limb angle estimation with IMUs and leverages the open-source framework OpenSense with validated biomechanical models. The movements covered in the present work are more complex, considering their DoF and everyday activity character, compared to previous work.
Lower limbs showed smaller joint angle estimation errors of 4.4°, 5.2°, 6.6° for MAD, RMSE, and fRoMD, compared to upper limbs. The relatively smaller errors at lower limbs may be explained by the larger, structurally more stable body segments that tend to exhibit more consistent and predictable motion patterns during activities, compared to upper limbs. Slade et al. (2022) reported mean lower limb errors ranging from 3.9to8.4° for walking and running and 2.6 − 7.9° for upper limbs during Fugl-Meyer tasks of food cutting (participants picked up a cutting utensil, bent over a dish, and performed a cutting motion before placing the utensil back down). Authors used a constrained upper body model in OpenSense with, e.g., trunk and head represented in one segment, which explains the smaller arm and shoulder elevation/rotations errors compared to the results presented in this work. Furthermore, only five participants were analyzed, a comparably small RoM, and no overhead activities were considered. Furthermore, shoulders and arms are associated with a larger amount of soft tissue and tendon interaction during movement execution, which may introduce artifacts in IMU-based measurements. In addition, hand pronation may not have been fully reconstructed in this work as our experimental study lacked markers and IMUs at the hands. Instead, markers were attached to wrists and IMUs to the distal end of the radius bone, hence movements may have been underestimated by IMU-based simulations. Moreover, RMSE ranges of IMU-based measurements compared to MoCap were reported by Poitras et al. (2019) in a systematic review paper. Authors reported the following RMSE error ranges, which also confirm our results of larger upper limb error ranges compared to lower limb ranges: neck (1 − 9°), pronation (3 − 30°), elbow (0.2 − 30.6°), shoulder (0.2 − 64.5°), pelvis (0.4 − 8.8°), hip (0.2 − 9.2°), knee (1 − 11.5°), ankle (0.4 − 18.8°). They attributed the large variability to the nature of performed movements and used devices.
The fRoMD results of our work are also in line with ranges reported in related literature. For lower limbs we showed on average 7.2° (1.7 − 20.7° range) and 13.2° (2.1 − 40.9° range) (see Supplementary Table S1) for upper limbs across all ADLs and participants. In comparison, Doğan et al. (2019) reported fRoM differences up to 40° depending on the shoulder joint angle. The parameter fRoMD, which is derived from the accuracy of the joint angle estimation, becomes particularly sensitive if the initial estimation already deviates by up to 10° or more (see Figure 4 arm elevation angle). The described deviation could explain the considerably larger ranges in fRoMD compared to MAD or RMSE.
Generally, most of related work considered either upper or lower limbs, whereas ADLs are usually a combination of both and also coupled, e.g., picking up a pen involves lower leg flexion, torso flexion and lower arm extension. Our analysis demonstrated that combining multiple movements led to increased error ranges, which also aligns with published literature (Robert-Lachaine et al., 2017; Poitras et al., 2019). The results represent a key factor when designing rehabilitation or assistive devices that aim to support users in performing complex ADLs. IMU systems could be optimized for multi-movement ADL scenarios, to better deal with the complex ADL motion. Moreover, our work includes a comprehensive set of error metrics to estimate joint angles in both upper and lower limbs and covers a large number of participants across different ADLs and joint angles. Furthermore, our assessment of error ranges per ADLs highlights the importance of considering the context in which IMU-based motion capture is applied. ADLs showed varying error levels (see Figure 4), which may affect the suitability of IMU-based methods for specific ADLs. As a conclusion, it seems useful to tailor IMU-based solutions to the requirements of specific ADLs, thus optimizing their accuracy for real-world applications. The larger IQR for upper limb joint angles indicate greater variability among participants. The result has important clinical implications, as it suggests that upper limb mobility might require more individualized and adaptive rehabilitation strategies. Healthcare providers should consider the interpersonal variation when designing treatment plans and select assistive devices to meet the specific needs of their patients with mobility impairments.
We investigated sensor selection for IMU-based motion capture. By systematically varying sensor combinations, we demonstrated the impact of the sensor positioning on system performance, including accuracy and precision of motion capture. Our results underscore the importance of careful sensor selection in the design of IMU systems for specific applications. We determined the sensor count at which performance changes only marginally (see Figures 5, 6). The threshold for marginal performance change provides valuable insights for researchers and engineers in the field, e.g., for optimizing sensor configurations, considering both accuracy and cost-effectiveness. With the threshold for marginal performance change, resource-efficient IMU systems can be configured without compromising performance. Our results showed the relationship between sensor count, and the joint angles considered (see Figure 5). For example, the optimum sensor count for the hip/ pelvis angle was found to be six to ten sensors. However, the error changed marginally between two and ten sensors. Similar error curves were found for many other body positions. In contrast, for the complex shoulder joints, our analysis showed a steep decline in RMSE up to three to four sensors.
We analyzed the most frequent sensor combinations and the minimum sensor count among the sensor combinations that were within the lowest 5% RMSE range across all ADLs and participants, which resulted in an average of 341 combinations considered in the analysis (range 205–410 combinations depending on joint angle). However, the workflow is not limited to a particular error threshold. Alternatively, percentiles or quartiles of all sensor combinations may be used to further reduce the sensor count. Nevertheless, our analysis confirms that the approach to select sensor combinations yields meaningful results.
We showed a subset of the most frequent sensor combinations consistently performed well across various ADLs (see Figures 7, 8; Supplementary Tables S2–S8). For example, if all ADLs of the present investigation shall be covered, four sensors at, e.g., lumbar/thorax, humerus, radius, and head, would yield a performance within the lowest 5% RMSE range for all upper limb joint angles. Similarly, four sensors at, e.g., pelvis, femur, tibia, and foot, would yield a performance within the lowest 5% RMSE range for all lower limb joint angles of our investigation. However, the optimal sensor configuration depends on the considered joint angles. Since OpenSense cannot deal with missing body segment data, all 14 body segment IMUs would be needed to estimate all 26 joint angles simultaneously. Often though, not all joint angles are needed for a full body assessment and sensor count can be reduced, e.g., for pathological movement pattern analyses or to investigate the interconnection of specific movement patterns. Certainly, more selective sensor configurations can be derived when the ADL count or the number of joint angles to be monitored is reduced. To estimate optimal sensor positions, Figure 7 provides a matching matrix between sensor position and joint angles. Our results can guide the development of standardized IMU systems, thus simplifying sensor selection and body position selection for practitioners and researchers. Standardized sensor configurations can enhance interoperability and facilitate comparisons of results between studies.
For some joint angles, error increased (independent of the metric) with a larger sensor count, in particular after 9–10 IMU sensors (see Figure 5). With increasing sensor count, we expect that the estimation model becomes determined or over-determined. Hence, additional sensors do not necessarily add new, independent information. Instead, additional sensors may introduce noise and artifacts, as they will be located at increasingly irrelevant body positions. We hypothesize that increasing sensor count, and therefore potentially accumulating noise, hampers estimation performance of the OpenSense IK solver. The analysis data (Figure 5) can be interpreted accordingly: For peripheral joint angles that can be accurately estimated with 2–3 sensors, any additional, sensor position that is distant to the relevant joint may introduce irrelevant motion information. Thus, uncertainty and error, as can be seen, e.g., for arm elevation, increase profoundly with more than six sensors. In contrast, joint motion at the body core, e.g., hip flexion, almost any body position is involved in the motion. Consequently, additional sensors do not introduce artifacts, but instead, provide consistent information from further body positions and thus there is no error increase observable. Future work may proceed to analyze error sources for increased sensor count in more detail and possibly categorized by sensor combination or ADL. Moreover, filtering strategies shall be investigated to increase robustness of the OpenSense estimation. From a practical viewpoint, increasing the IMU sensor count renders calibration and synchronization more complex. Therefore, diligent consideration of sensor relevance, data fusion methodology, and overall system design is important, which is what the framework proposed in this work can support.
Sensor selection results can be used and further improved by complementing them with other existing methodologies for sensor reduction, e.g., optimal control problems defined in OpenSim using direct collocation (MOCO) (Dembia et al., 2020) or kinematic chain approaches (Salarian et al., 2013; Hu et al., 2015; Marcard et al., 2017). Further work may be directed to refine our approach and extend it to a wider methods and scenario range. For example, Sy et al. (2021) proposed a constrained Kalman filter to estimate lower limb kinematics in the sagittal plane with three sensors. The authors showed hip and knee flexion angles with RMSE of ~10° derived from three IMUs, located on the pelvis and both shanks.
The biomechanical model used in our work (Schmid et al., 2020) contains 165 DoF compared to the model used in the published literature using OpenSense (Rajagopal et al., 2016; Bailey et al., 2021; Al Borno et al., 2022) with 37 DoF only. In particular, the latter model excludes spinal mobility and treats the trunk and head as a single segment. While the 37-DoF model may be suitable for certain research objectives, it cannot capture the full complexity of human movement, especially in scenarios, where spinal mobility is an important factor, e.g., for ADLs. The DoF-difference is an important system design factor. A more complex biomechanical model requires a larger number of sensors to accurately capture and represent joint mobility and human movement. As a result, a larger sensor count at shoulders and hip area may have been estimated by our analysis, than if we had deployed the 37-DoF model. The choice of biomechanical model should be tailored to the detail level required for the analysis.
Compared to the specifications (data sheet) of proprietary IMU solutions, e.g., Noraxon Ultimum Motion and Xsense MVN Animate, our study found larger errors. The difference can be attributed to the inherent complexity of ADL movements, including natural, multi-dimensional motions, as well as the variability between participants, including differences in body morphology and movement patterns. In combination, complex ADL movements and interpersonal variability contribute to the estimation error across a heterogeneous group of study participants, including BMI and body segment lengths (see Table 1). To date, there exists no standard movement protocol to evaluate body-worn IMU systems for ADLs, nor is it a common practice to publish movement protocols with the respective system. In particular, the exact movements considered to assess performance of the above-mentioned IMU-based motion analysis systems have not been documented. Further studies may repeat the experimental protocol proposed here with other IMU-based solutions. However, the error estimation performance would most likely also differ due to the natural variance in movement execution. Furthermore, combining IMU sets from several manufacturers for simultaneous measurements may constrain participant movement. Unlike proprietary systems, however, our approach can be repurposed and implemented with various IMUs. Our results suggest that open-source IMU-based kinematic estimators can provide a transparent, reproducible, and collaborative alternative to researchers and developers, especially when customization is crucial. The ability to fine-tune and expand the approach according to specific needs and preferences opens opportunities for further investigations and developments, e.g., on algorithms and sensors, thus contributing to the continuous improvement of IMU-based systems.
6 Conclusion
We validated full-body 3D joint kinematics and fRoM estimates from body-worn IMU sensors using personalized biomechanical models. We showed that the OpenSense framework is a valid tool for sensor selection and may guide sensor reduction decisions for ADL analysis. We estimated joint angles and fRoM during dynamic motion simulations of common ADLs. Our simulations based on IMU data showed joint kinematics and fRoM estimates that correspond with MoCap reference data, thus affirming that the kinematic analyses are viable for movement monitoring in wearables.
In general, smaller MAD, RMSE, and fRoMD were observed for lower limb joint angles compared to upper limb joints, which can be attributed to the larger amount of soft tissue and tendon interaction at upper limbs as well as larger and structurally more stable body segments at lower limbs. In particular, for the shoulder, e.g., involvement of rotator cuff, the joint angle estimation is more challenging compared to lower limb joints. The iteration over all possible sensor pairs (2–14 sensors) with more than 8,000 possible combinations per joint angle, participant, and ADL showed that a near optimum estimation performance was already achieved by two sensors for the lower limb joints and four sensors for upper limb joints. Additionally, we identified the best sensor positions per sensor count. Our analysis of the most frequent sensor position combinations within the lowest 5% RMSE range revealed that the sensor positions for the minimum sensor count were a subset of the most frequent sensor combinations. Error deviations across all joint angles were on average <2° MAD. Consequently, sensors of the minimum-optimal set can be used for kinematic estimation with adequate performance, thus minimizing total sensor count.
By validating the OpenSense framework for a comprehensive set of ADLs, we improve reproducibility of IMU-based motion analysis compared to previously published modeling and simulation techniques, especially in the context of complex combined movements. Our results can help researchers to determine appropriate sensor positions without the need for detailed biomechanical knowledge. The flexible sensor selection empowers developers to tailor sensor configurations (amount of sensors and sensor positions) for specific applications. Our approach can be applied to optimize data collection and analysis for a wide range of movement monitoring wearables, from sports and fitness devices to healthcare and augmented reality solutions.
Data availability statement
The datasets presented in this article are not readily available because they are part of a larger ongoing clinical trial. The source code to run the OpenSense toolkit from Python files and Noraxon IMUs, as illustrated in our manuscript, can be accessed via the following link: https://github.com/intellembeddedsystemslab/Where-to-mount-the-IMU-. Requests to access the datasets should be directed dG9sZW5hLnVobGVuYmVyZ0BoYWhuLXNjaGlja2FyZC5kZQ==.
Ethics statement
The studies involving humans were approved by Ethics Committee of Friedrich-Alexander University Erlangen-Nuremberg. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
LU: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Validation, Visualization, Writing—original draft, Writing—review & editing. OA: Conceptualization, Methodology, Supervision, Writing—review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was partially funded by the Ministry of Economics, Labour and Tourism of Baden-Württemberg within the project WM3-4332-1 60/104/4: Dynamic Motion Simulation frameworks (DynaMoS). We acknowledge support by the Open Access Publication Fund of the University of Freiburg.
Acknowledgments
We thank Swathi Hassan Gangaraju for her support in developing the initial analysis pipeline. Moreover, we thank Juan Carlos Suarez Mora, as well as FAU LTD group and Med 3 of the University Medical Center Erlangen for their support in the study implementation and data preprocessing. Furthermore, we thank Al Borno et al. (2022) for sharing their data via OpenSimTK.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2024.1347424/full#supplementary-material
Footnotes
1. ^For breaks in the kinematic chain, OpenSense leaves the affected body segment in the calibration pose, i.e., there is no interpolation of missing limb orientation data.
References
Al Borno, M., O'Day, J., Ibarra, V., Dunne, J., Seth, A., Habib, A., et al. (2022). OpenSense: An open-source toolbox for inertial-measurement-unit-based measurement of lower extremity kinematics over long durations. J. Neuroeng. Rehabil. 19:22. doi: 10.1186/s12984-022-01001-x
Ancillao, A., Tedesco, S., Barton, J., and O'Flynn, B. (2018). Indirect measurement of ground reaction forces and moments by means of wearable inertial sensors: a systematic review. Sensors 18:2564. doi: 10.3390/s18082564
Bailey, C. A., Uchida, T. K., Nantel, J., and Graham, R. B. (2021). Validity and sensitivity of an inertial measurement unit-driven biomechanical model of motor variability for gait. Sensors. 21:7690. doi: 10.3390/s21227690
Balasubramanian, C. K., Neptune, R. R., and Kautz, S. A. (2009). Variability in spatiotemporal step characteristics and its relationship to walking performance post-stroke. Gait Post. 29, 408–414. doi: 10.1016/j.gaitpost.2008.10.061
C-Motion Inc. (2022). Tutorial: Building a Conventional Gait Model –Visual3D Wiki Documentation. Available online at: https://c-motion.com/v3dwiki/index.php?title=Tutorial:_Building_a_Conventional_Gait_Model#Summary (accessed November 4, 2023).
Damsgaard, M., Rasmussen, J., Christensen, S. T., Surma, E., and de Zee, M. (2006). Analysis of musculoskeletal systems in the anybody modeling system. Simul. Model. Pract. Theory 14, 1100–1111. doi: 10.1016/j.simpat.2006.09.001
Del Rosario, M. B. D., Lovell, N. H., and Redmond, S. J. (2016). Quaternion-based complementary filter for attitude determination of a smartphone. IEEE Sens. J. 16, 6008–6017. doi: 10.1109/JSEN.2016.2574124
Delp, S. L., Anderson, F. C., Arnold, A. S., Loan, P., Habib, A., John, C. T., et al. (2007). OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Transact. Biomed. Eng. 54, 1940–1950. doi: 10.1109/TBME.2007.901024
Dembia, C. L., Bianco, N. A., Falisse, A., Hicks, J. L., and Delp, S. L. (2020). OpenSim Moco: musculoskeletal optimal control. PLoS Comput. Biol. 16:e1008493. doi: 10.1371/journal.pcbi.1008493
Derungs, A., Soller, S., Weishäupl, A., Bleuel, J., Berschin, G., and Amft, O. (2018). “Regression-based, mistake-driven movement skill estimation in Nordic Walking using wearable inertial sensors,” in Proceedings of the 2018 IEEE International Conference on Pervasive Computing and Communications (PerCom) (Athens), 1–10.
Doğan, M., Koçcak, M., Onursal Kıılınç, Ö., Ayvat, F., Sütçü, G., Ayvat, E., et al. (2019). Functional range of motion in the upper extremity and trunk joints: nine functional everyday tasks with inertial sensors. Gait Post. 70, 141–147. doi: 10.1016/j.gaitpost.2019.02.024
Dorschky, E., Nitschke, M., Mayer, M., Weygers, I., Gassner, H., Seel, T., et al. (2023). Comparing sparse inertial sensor setups for sagittal-plane walking and running reconstructions. bioRXiv. doi: 10.1101/2023.05.25.542228
Garcia, M. (2023). AHRS: Attitude and Heading Reference Systems —AHRS 0.3.1 Documentation. Available online at: https://ahrs.readthedocs.io/en/latest/ (accessed November 15, 2023).
Goodwin, B. M., Cain, S. M., Van Straaten, M. G., Fortune, E., Jahanian, O., and Morrow, M. M. B. (2021). Humeral elevation workspace during daily life of adults with spinal cord injury who use a manual wheelchair compared to age and sex matched able-bodied controls. PLoS ONE 16:e0248978. doi: 10.1371/journal.pone.0248978
Halder, A. M., Itoi, E., and An, K.-N. (2000). Anatomy and biomechanics of the shoulder. Orthoped. Clin. N. Am. 31, 159–176. doi: 10.1016/S0030-5898(05)70138-3
Hermsdorf, H., Hofmann, N., and Keil, A. (2019). “Chapter 16 - Alaska/dynamicus –human movements in interplay with the environment,” in DHM and Posturography, eds S. Scataglini, and G. Paul (Academic Press), 187–198.
Hu, X., Yao, C., and Soh, G. S. (2015). “Performance evaluation of lower limb ambulatory measurement using reduced inertial measurement units and 3R gait model,” in 2015 IEEE International Conference on Rehabilitation Robotics (ICORR) (Singapore), 549–554.
Joukov, V., Bonnet, V., Karg, M., Venture, G., and Kulić, D. (2018). Rhythmic Extended Kalman Filter for Gait Rehabilitation Motion Estimation and Segmentation. IEEE Transact. Neural Syst. Rehabil. Eng. 26, 407–418. doi: 10.1109/TNSRE.2017.2659730
Korp, K., Richard, R., and Hawkins, D. (2015). Refining the Idiom “functional range of motion” related to burn recovery. J. of Burn Care Res. 36, e136–e145. doi: 10.1097/BCR.0000000000000149
Leardini, A., Biagi, F., Merlo, A., Belvedere, C., and Benedetti, M. G. (2011). Multi-segment trunk kinematics during locomotion and elementary exercises. Clin. Biomech. 26, 562–571. doi: 10.1016/j.clinbiomech.2011.01.015
Lim, S., and D'Souza, C. (2020). A narrative review on contemporary and emerging uses of inertial sensing in occupational ergonomics. Int. J. Ind. Ergon. 76:102937. doi: 10.1016/j.ergon.2020.102937
Madgwick, S. O. H., Harrison, A. J. L., and Vaidyanathan, A. (2011). Estimation of IMU and MARG orientation using a gradient descent algorithm,” in IEEE International Conference on Rehabilitation Robotics: [Proceedings] (Zurich), 5975346. doi: 10.1109/icorr.2011.5975346
Mahony, R., Hamel, T., Morin, P., and Malis, E. (2012). Nonlinear complementary filters on the special linear group. Int. J. Control 85, 1–17. doi: 10.1080/00207179.2012.693951
Marcard, T., Rosenhahn, B., Black, M., and Pons-Moll, G. (2017). Sparse inertial poser: automatic 3D human pose estimation from sparse IMUs. Comp. Graph. For. 36, 349–360. doi: 10.1111/cgf.13131
Nam, H. S., Lee, W. H., Seo, H. G., Kim, Y. J., Bang, M. S., and Kim, S. (2019). Inertial measurement unit based upper extremity motion characterization for action research arm test and activities of daily living. Sensors 19:1782. doi: 10.3390/s19081782
Pacher, L., Chatellier, C., Vauzelle, R., and Fradet, L. (2020). Sensor-to-segment calibration methodologies for lower-body kinematic analysis with inertial sensors: a systematic review. Sensors 20:3322. doi: 10.3390/s20113322
Picerno, P. (2017). 25 years of lower limb joint kinematics by using inertial and magnetic sensors: a review of methodological approaches. Gait Post. 51, 239–246. doi: 10.1016/j.gaitpost.2016.11.008
Picerno, P., Caliandro, P., Iacovelli, C., Simbolotti, C., Crabolu, M., Pani, D., et al. (2019). Upper limb joint kinematics using wearable magnetic and inertial measurement units: an anatomical calibration procedure based on bony landmark identification. Sci. Rep. 9:14449. doi: 10.1038/s41598-019-50759-z
Poitras, I., Dupuis, F., Bielmann, M., Campeau-Lecours, A., Mercier, C., Bouyer, L., et al. (2019). Validity and reliability of wearable sensors for joint angle estimation: a systematic review. Sensors 19:1555. doi: 10.3390/s19071555
Rajagopal, A., Dembia, C. L., DeMers, M. S., Delp, D. D., Hicks, J. L., and Delp, S. L. (2016). Full-body musculoskeletal model for muscle-driven simulation of human gait. IEEE Trans. Biomed. Eng. 63, 2068–2079. doi: 10.1109/TBME.2016.2586891
Rasmussen, J., Damsgaard, M., Tørholm, S., and de Zee, M. (2005). AnyBody—Decoding the Human Musculoskeletal System by Computational Mechanics (Trondheim: TAPIR Akademisk Forlag), 43–59.
Rigoni, M., Gill, S., Babazadeh, S., Elsewaisy, O., Gillies, H., Nguyen, N., et al. (2019). Assessment of shoulder range of motion using a wireless inertial motion capture device—a validation study. Sensors 19:1781. doi: 10.3390/s19081781
Robert-Lachaine, X., Mecheri, H., Larue, C., and Plamondon, A. (2017). Validation of inertial measurement units with an optoelectronic system for whole-body motion analysis. Med. Biol. Eng. Comp. 55, 609–619. doi: 10.1007/s11517-016-1537-2
Saber-Sheikh, K., Bryant, E. C., Glazzard, C., Hamel, A., and Lee, R. Y. W. (2010). Feasibility of using inertial sensors to assess human movement. Man. Ther. 15, 122–125. doi: 10.1016/j.math.2009.05.009
Salarian, A., Burkhard, P. R., Vingerhoets, F. J. G., Jolles, B. M., and Aminian, K. (2013). A novel approach to reducing number of sensing units for wearable gait analysis systems. IEEE Transact. Biomed. Eng. 60, 72–77. doi: 10.1109/TBME.2012.2223465
Schmid, S., Burkhart, K. A., Allaire, B. T., Grindle, D., and Anderson, D. E. (2020). Musculoskeletal full-body models including a detailed thoracolumbar spine for children and adolescents aged 6–18-years. Spine Load. Deform. 102:109305. doi: 10.1016/j.jbiomech.2019.07.049
Slade, P., Habib, A., Hicks, J. L., and Delp, S. L. (2022). An open-source and wearable system for measuring 3D human motion in real-time. IEEE Transact. Biomed. Eng. 69, 678–688. doi: 10.1109/TBME.2021.3103201
Spina, G., Huang, G., Vaes, A. W., Spruit, M. A., and Amft, O. (2013). “COPDTrainer: a smartphone-based motion rehabilitation training system with real-time acoustic feedback,” in Ubicomp 2013: Proceedings of the 2013 ACM International Joint Conference on Pervasive and Ubiquitous Computing (Zurich ACM), 597–606.
Stołowski, Ł., Niedziela, M., Lubiatowski, P., and Piontek, T. (2023). Validity and reliability of inertial measurement units in active range of motion assessment in the hip joint. Sensors. 23:8782. doi: 10.1101/2023.08.11.23293880
Sy, L., Raitor, M., Rosario, M. D., Khamis, H., Kark, L., Lovell, N. H., et al. (2021). Estimating lower limb kinematics using a reduced wearable sensor count. IEEE Transact. Biomed. Eng. 68, 1293–1304. doi: 10.1109/TBME.2020.3026464
Teufl, W., Miezal, M., Taetz, B., Fröhlich, M., and Bleser, G. (2019). Validity of inertial sensor based 3D joint kinematics of static and dynamic sport and physiotherapy specific movements. PLoS ONE 14:e0213064. doi: 10.1371/journal.pone.0213064
Tulipani, L. J., Meyer, B., Larie, D., Solomon, A. J., and McGinnis, R. S. (2020). Metrics extracted from a single wearable sensor during sit-stand transitions relate to mobility impairment and fall risk in people with multiple sclerosis. Gait Post. 80, 361–366. doi: 10.1016/j.gaitpost.2020.06.014
Uhlenberg, L., Hassan Gangaraju, S., and Amft, O. (2022). “IMUAngle: joint angle estimation with inertial sensors in daily activities,” in ISWC '22: Proceedings of the 2022 International Symposium on Wearable Computers (Cambridge: ACM).
Wang, S. L., Civillico, G., Niswander, W., and Kontson, K. L. (2022). Comparison of motion analysis systems in tracking upper body movement of myoelectric bypass prosthesis users. Sensors 22:2953. doi: 10.3390/s22082953
Keywords: framework validation, joint kinematics, multiscale modeling, sensor selection, wearable inertial sensors
Citation: Uhlenberg L and Amft O (2024) Where to mount the IMU? Validation of joint angle kinematics and sensor selection for activities of daily living. Front. Comput. Sci. 6:1347424. doi: 10.3389/fcomp.2024.1347424
Received: 30 November 2023; Accepted: 29 January 2024;
Published: 29 February 2024.
Edited by:
Bo Zhou, German Research Center for Artificial Intelligence (DFKI), GermanyReviewed by:
Nicolas Pronost, Université Claude Bernard Lyon 1, FranceSungho Suh, German Research Center for Artificial Intelligence (DFKI), Germany
Copyright © 2024 Uhlenberg and Amft. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lena Uhlenberg, bGVuYS51aGxlbmJlcmdAaGFobi1zY2hpY2thcmQuZGU=
 Lena Uhlenberg
Lena Uhlenberg Oliver Amft
Oliver Amft