Curriculum Development for Explorative Proving in Lower Secondary School Geometry: Focusing on the Levels of Planning and Constructing a Proof

Introduction

Understanding in mathematics develops through justification and discovery, with proof and proving at the center. Teaching and learning proofs is recognized internationally as a key component of mathematics curricula (Stylianides et al., 2017). For example, Mathematical Practice 3 of the Common Core State Standards for Math (CCSSM) includes “Construct[ing] viable arguments and critiqu[ing] the reasoning of others” (Standards for Mathematical Practice, 2018). However, students at the junior high school level (and beyond) still experience general difficulties learning proofs in mathematics (e.g., Healy and Hoyles, 2000; Hoyles and Healy, 2007), and Japan is no exception. Current Japanese students learn deductive proofs in Grades 8 and 9, mainly through geometry, but one of the issues, which has not been fully addressed, is how to support students who have difficulties in many activities related to proof and proving: constructing deductive proofs and why they are necessary (e.g., MEXT, 2018), understanding logical structures of deductive proofs (e.g., Miyazaki et al., 2017), and realizing explorative proving by students (Miyazaki and Fujita, 2015).

Hanna and de Villiers(2012, p. 3) explained, “a narrow view of proof [as solely a formal derivation] neither reflects mathematical practice nor offers the greatest opportunities for promoting mathematical understanding.” In school geometry, proofs are often presented in an arrangement generally referred to as the two-column format. However, as Herbst and Brach (2006) demonstrated, this approach does not necessarily support students in their construction of creative and reasoned arguments. We consider that students' difficulties in Japan might be improved if we could re-organize a curriculum from a wider view of proof and proving. For example, in contrast to this rigid view of proof, we regard proving as a flexible, dynamic, and productive activity (Komatsu, 2017). To teach this view of proving, we are currently undertaking a study based on a design experiment (Cobb et al., 2003), for developing a new explorative proving curriculum in Japanese lower secondary school (Grades 7–9, 13–15 years old). This paper reports on the findings from our experiment's first cycle, which investigated the following questions: (a) How can we make a curriculum framework based on the idea of explorative proving? (b) How can we develop a curriculum based on the framework?

Framework for Developing an Explorative Proving Curriculum

Theoretical Underpinnings: Explorative Proving

Concerning Question (a), we argue that proving activities in mathematics are not limited to writing the proof. Some previous studies specifically indicated the importance of modern axiomatic methods (van der Waerden, 1967) and relative views of truths (Fawcett, 1938), learned from the perspectives of heuristics and fallibilism (Lakatos, 1976). Thus, proving activities are flexible, dynamic, and productive in nature, and various aspects of proving activities are interrelated and resonant. We can see that proving activities involve the following: producing statements inductively/deductively/analogically, planning and constructing proofs, looking back over proving processes and overcoming global/local counter-examples or errors, and utilizing already-proved statements while working on further proofs to reflect the mathematical nature of proving (de Villiers, 1990).

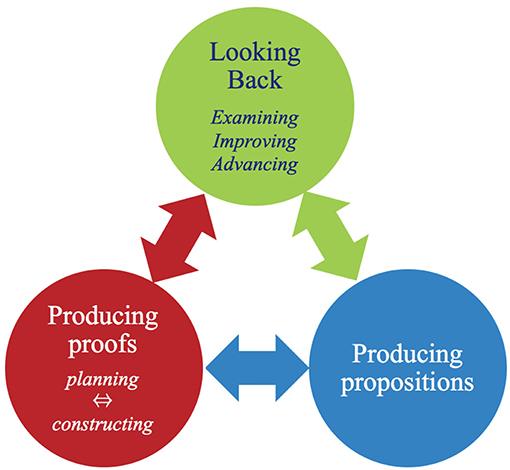
We define explorative proving based on three components and their relationships: producing propositions, producing proofs, and looking back. To produce proofs, it is necessary to plan how to prove the proposition, and construct the proof along with the plan. However, to look back at the proving process, it is necessary to examine the proving process, either by improving the process and the product (proof), or by advancing them through finding unproved propositions that are deductively based on the proof, and so on. Thus, as shown in Figure 1, producing proofs includes planning and construction, and looking back includes examining, improving, and advancing (Miyazaki and Fujita, 2015).

FIGURE 1

Figure 1. Explorative proving.

By making these aspects and their relationships more explicit in the proving curriculum, we believe that proving activities can be more productive and dynamic. This will allow students to produce mathematical statements, produce proofs, and examine/improve/advance statements and proofs independently, advancing gradually in accordance with grade level.

Levels of Planning and Constructing a Proof

In developing explorative proving curricula, it is useful to establish some theoretical learning levels as the scope of the curriculum, which enables us to follow an achievable learning progression for students. Due to the low performance in producing proofs reported among Japanese junior high students MEXT(2018, p. 121–127), we focus on how to support two aspects that enable active production of proofs: planning and constructing. The remaining aspect, looking back, is combined appropriately according to the achievement of the other two aspects (Figure 1). To succeed in our curriculum, students need to reach the elemental sub-level of the partial structural level of understanding a proof. At this level, a student begins paying attention to each component of the proof, including singular propositions (premises, conclusions, and the intermediate propositions between them), universal propositions (theorems, definitions, etc.), and the appropriate connectives between singular and universal propositions (Miyazaki et al., 2017).

Levels of Planning a Proof

Planning a proof refers to students seeking ways to connect premises and conclusions using deductive reasoning (Tsujiyama and Yui, 2018) before construction. In this activity, necessary conditions are deduced from premise to conclusion by thinking forward. In contrast, sufficient conditions are deduced in the opposite direction by thinking backward. The former proposes a network of propositions that can be deduced from premises, while the latter proposes a network of propositions that can be deduced from conclusions. In planning a proof, common propositions as joint points of the two networks need to be sought while these networks expand (Heinze et al., 2008).

For planning a proof, what can be used to connect premises and conclusions (object), and how it can be used (method), should be considered carefully. Learning to plan a proof requires differentiating the objects and methods, and then making use of them to connect premises and conclusions. This is the first learning level of planning a proof (P1).

As described above, planning a proof requires expanding the two networks of propositions, and seeking the common propositions within the two networks. Therefore, the advanced learning of planning a proof requires differentiating the method of P1 into thinking forward from premises to conclusions and thinking backward in the opposite direction, and then making use of them to connect premises and conclusions. This is the second learning level of planning a proof (P2).

We can thus hypothesize the learning levels of planning a proof as follows:

P1: Clarify what can be used and how to connect the premises and conclusion.

P2: Consider how to think backward from the conclusion and forward from the premises, as well as how to connect them.

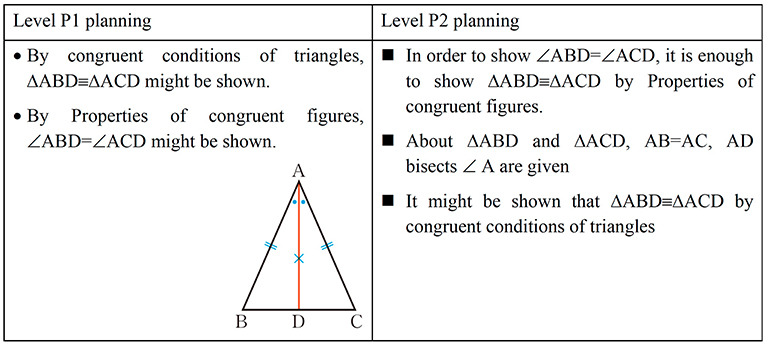
For example, as shown in Figure 2 in planning a proof of the proposition “if AB = AC in ΔABC, then ∠ABD = ∠ACD,” Level P1 only shows what and how to use the congruent condition of triangles, and the property of congruent figures. On the contrary, Level P2 shows thinking backward from the conclusion “∠B = ∠C,” thinking forward from premises related to ΔABD and ΔACD, and prospects to connect them.

FIGURE 2

Figure 2. Examples of the learning levels of planning a proof.

Levels of Constructing a Proof

Constructing a proof consists of finding common propositions in two relational networks and expressing the deductive connection between the premises and conclusion, which are suggested in the planning level. This connection can be realized using two kinds of deductive reasoning (i.e., universal instantiation and hypothetical syllogism; Miyazaki et al., 2017). Finally, constructing a proof can be achieved by expressing the realized connection with language, diagrams, etc.

In the case of a geometrical proof, premise and conclusion can be connected by hypothetical syllogism based on singular propositions particular to the diagram. Therefore, learning to construct a proof first requires students to express the connection based on hypothetical syllogism, the first learning level of constructing a proof (C1).

Furthermore, each proposition should be deduced from a universal proposition (i.e., a theorem). This deduction can be realized by universal instantiation. The student needs to differentiate universal instantiation and hypothetical syllogism from deductive reasoning, and clearly distinguish between singular propositions and universal propositions for the second level (C2).

Thus, we can hypothesize the learning levels of constructing a proof as follows:

C1: Form and express the deductive connection between the premises and conclusion.

C2: Form and express the deductive connection between the premises and conclusion by differentiating universal instantiation and hypothetical syllogism from deductive reasoning.

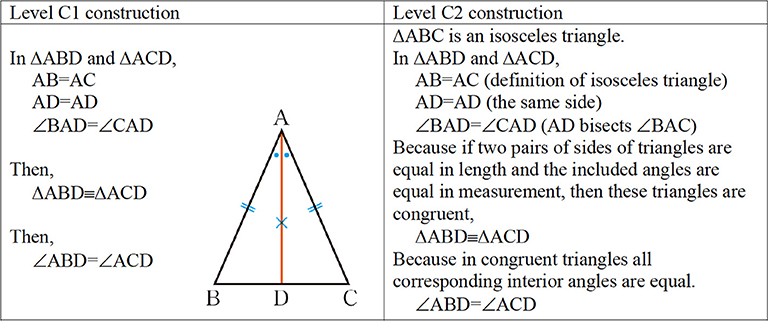
For example, for the proposition, “if AB = AC in ΔABC, then ∠ABD = ∠ACD,” which uses the angle bisector AD (see Figure 3), students at Level C2 can produce a proof that shows singular propositions (e.g., ΔABD ≡ ΔACD) deduced from a universal proposition or theorem [e.g., “if two pairs of sides of triangles are equal in length and the included angles are equal in measurement, then these triangles are congruent” (SAS)], and a chain of singular propositions by hypothetical syllogism. However, students at Level C1 can produce a simpler proof than at C2, which only shows a chain of singular propositions using hypothetical syllogism, but without any explicit identifications of which theorems are used to deduce them.

FIGURE 3

Figure 3. Examples of the learning levels of constructing a proof.

Learning Progressions in Explorative Proving

Setting the Theoretical Learning Levels for Curriculum Development

Planning and constructing are essential, interrelated aspects of mathematical explorative proving. To develop school mathematics curricula—assuming that students' development of planning and constructing are independent of each other—combining the two levels of planning a proof and the two levels of constructing a proof produces four learning levels: (P1, C1), (P2, C1), (P1, C2), and (P2, C2).

Learning level “0” is the starting point of the learning progression of explorative proving. At this level, even though there is no differentiation between planning and constructing a proof, a proof can be produced. Similarly, there are learning levels focused on either planning or constructing a proof, despite their differences. These learning levels are P1, P2, C1, and C2. Thus, we can set nine theoretical learning levels: 0, (0, P1), (0, P2), (0, C1), (0, C2), (P1, C1), (P1, C2), (P2, C1), and (P2, C2), to establish the learning levels in our proposed explorative proving curriculum.

Two Kinds of Shifts in Learning Levels and Their Processes

In lower secondary school geometry in Japan, our explorative proving curriculum should start the shift from Level 0 to Level (P2, C2) due to the correspondence with the current national curriculum, the Course of Study. The shift needs to pass through Level (P1, C1) to enhance planning and constructing a proof reciprocally. Therefore, the shift can be divided into the former [0 ⇒ (P1, C1)] and latter [(P1, C1) ⇒ (P2, C2)].

The transition process of the former shift passes through either Level C1 or P1. In the case of passing through C1, this level aims for students to connect assumptions and conclusions by a chain of singular propositions with hypothetical syllogism. Then, at the next level (P1, C1), the learning of P1, that is, clarifying what can be used and how it can be used to connect premises and conclusions, can be realized. In contrast, in the case of passing through Level P1, the learning of P1 cannot be realized because students cannot learn to clarify what can be used and how it can be used to connect the premises and conclusion (P1) without having a chance to form and express the deductive connection between them (C1).

For example, in producing the proof “if AB = AC in ΔABC, then ∠ABD = ∠ACD,” students at Level 0, where they have no differentiation between planning and constructing a proof, cannot imagine the deductive connection of the premise “AB = AC in ΔABC” and conclusion “∠ABD = ∠ACD” required to make level P1 planning. Therefore, they first understand this connection in the Level C1 proof (Figure 3), and form and express by themselves by focusing on hypothetical syllogism. At that time, they might be able to clarify what can be used and how to connect the premises and conclusion of new proof problems.

The transition process of the latter shift passes through either Level (P1, C2) or (P2, C1). In passing through (P1, C2), this level aims to form and express the connection between the premises and conclusion with differentiating universal instantiation and hypothetical syllogism from deductive reasoning. Due to carrying out deductive reasoning based on universal instantiation, at the next Level (P2, C2), thinking backward from conclusions and forward from assumptions can be differentiated and carried out together. However, in passing through Level (P2, C1), the learning of P2 is difficult to realize because students cannot learn to distinguish thinking forward from the conclusion, from thinking forward from the premises, and how to connect these processes (P2) without the chance to form and express the deductive connection based on universal instantiation and hypothetical syllogism (C2).

For example, in producing the proof “if AB = AC in ΔABC, then ∠ABD = ∠ACD,” students at Level (P1, C1) can clarify what can be used and how to connect the premises “AB = AC in ΔABC” and conclusion “∠ABD = ∠ACD” (P1), and form and express the deductive connection between them. However, they especially cannot think backward from the conclusion “∠ABD = ∠ACD,” even if they can think forward from the premise “AB = AC in ΔABC.” Therefore, passing through Level (P2, C1) is difficult for students at Level (P1, C1). To think backward from the conclusion, students first must understand the proof structure with differentiating universal instantiation and hypothetical syllogism in the Level C2 proof (Figure 3), and form and express by themselves by focusing on universal instantiation (Miyazaki et al., 2017). At that time, even to solve a new proof problem, they might be able to consider how to think backward from the conclusion and forward from the premises, as well as how to connect them.

Framework for Developing an Explorative Proving Curriculum

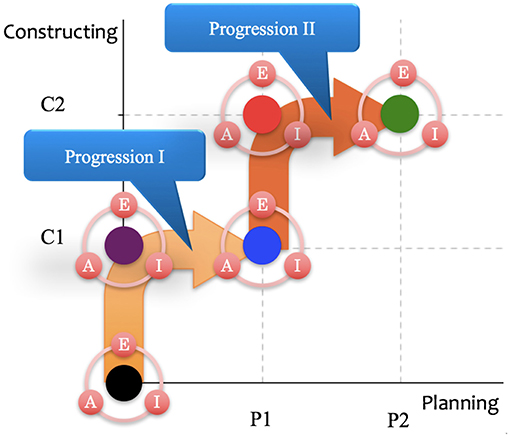
Concerning Question (a), we could specify the six learning levels and establish the two transition processes as learning progressions. The former is from Level 0 to (P1, C1) via C1, and the latter is from Level (P1, C1) to (P2, C2) via (P1, C2). For each level, the looking back component [Examining, Improving, and Advancing (EIA)] should be encouraged in explorative proving (Figure 4). Depending on the objectives, it should be decided whether looking back (EIA) is required or not. Therefore, by regarding these learning progression transitions, we can theoretically establish the following progressive model as a framework for developing an explorative proving curriculum:

FIGURE 4

Figure 4. Framework for developing an explorative proving curriculum.

Developing a Curriculum Based on the Framework

Making Correspondence Tables of Units With Learning Progressions

To answer Question (b), we first examined the existing intended curriculum and lessons in Japan's Course of Study, to show how we can make them more explorative based on our theoretical framework.

In lower high school in Japan, the Course of Study requires students to learn about the various properties of plane and three-dimensional figures mainly based on congruency and similarity, as well as the meaning of proof and how to prove formally. Although the Course of Study encourages teachers to introduce formal proofs gradually until the end of Grade 8 (14 years old), previous studies have proposed no clear method. To improve this situation, we first considered the correspondence of the intended units in the Course of Study with the two learning progressions in our theoretical framework, as illustrated in Figure 4.

For example, in Grade 8 geometry, the Course of Study requires students to study the following units: the properties of parallel lines and angles, the properties of angles of polygons, congruence and the properties of congruent triangles, proof and proving, and the properties of triangles and quadrilaterals. Assuming that Level (P1, C1) is already attained by the end of Grade 7, in Grade 8, the transition process from (P1, C1) to (P2, C2) is the key progression, which can be subdivided into the four following local progressions: (P1, C1)→(P1, C2), (P1, C2)→(P1, C2) + EIA, (P1, C2) + EIA→(P2, C2), and (P2, C2)→(P2, C2) + EIA. EIA plays important roles in supporting progressions I and II in our model.

By combining the intended teaching units in the Course of Study with the local progressions from (P1, C1) → (P2, C2)+ EIA, we can make the following correspondence table for the intended units with our local progressions (Table 1).

TABLE 1

Table 1. Correspondence of intended units with local progressions in Grade 8 geometry.

Implementing Classroom Lessons Based on the Correspondence Table

We have been designing and implementing junior high school lessons in our correspondence table derived from our theoretical examinations described above since 2009. We used the method of lesson study (Lewis et al., 2006) and a design experiment (Cobb et al., 2003) to plan, implement, and reflect on these lessons.

Localizing the Correspondence Table According to Learning Objectives

Every teaching unit in the Course of Study includes many learning objectives. To realize lessons based on the correspondence table (Table 1), it is necessary to localize each pair with the unit contents.

For example, the unit “Properties of parallel lines and angles” in Grade 8 includes seven learning objectives. Six aim to teach students about the essential geometrical properties and apply the learned properties. According to the correspondence table, this unit aims to achieve the following local progression: (P1, C1)→(P1, C2). Since achieving such progression for all learning content is neither realistic nor effective, we should aim for gradual student progress through the material as follows: Lesson 1: Vertical angles are equal (P1, C1); Lesson 2: Corresponding angles are equal ⇒ Two lines are parallel (P1, C1)→(P1, C2); Lesson 3: Alternate interior angles are equal ⇒ Two lines are parallel (P1, C1)→(P1, C2); Lesson 4: The sum of the inner angles of the same side is 180° (P1, C1)→(P1, C2); Lesson 5: The sum of the inner angles of a triangle (P1, C2); Lesson 6: The relation between the inner angles and an exterior angle in a triangle (P1, C2); Lesson 7: Angles in slanting L-shaped lines between two parallel lines (P1, C2); Lesson 8: The sum of the inner angles of n-polygon (P1, C2); Lesson 9: The sum of exterior angles of n-polygon (P1, C2); and Lesson 10: Angle of a concave quadrilateral (P1, C2). In preparing the series of lessons, we worked with expert mathematics teachers to design the local progressions. We then designed the following local progressions.

Planning and Implementing Lessons: The Unit of Properties of Parallel Lines and Angles

The lessons based on the local progressions in the unit “Properties of parallel lines and angles” were implemented in a Grade 8 class (16 boys and 19 girls) from December 10, 2014 to January 20, 2015, including winter vacation, in a public junior high in Nagano Prefecture. This school is in the city center and has six Grade 8 classes. At that time, the teacher had 15 years of experience teaching junior high mathematics.

In planning lessons, researchers explained our curriculum framework with the correspondence of intended units with local progressions in Grade 8 geometry (Table 1), and showed our plan for “Properties of parallel lines and angles” achieving the local progression (P1, C1)→(P1, C2) as above. Along with the plan, the teacher prepared lessons. After implementing each lesson, the teacher and researchers reflected on the implemented lessons, and refined the next lesson plan.

According to the local progressions in the unit, the first to fourth lessons aimed to shift the learning level from (P1, C1) to (P1, C2). Concerning P1 in every lesson, the teacher always asked students how to solve the problem from the perspective of what could be used and how. Conversely, the shift from C1 to C2 must differentiate universal instantiation and hypothetical syllogism from deductive reasoning.

Due to space limitations, we introduce the implementation of Lesson 4 corresponding to the local progression (P1, C1)→(P1, C2), that is, aiming to shift students' understanding of the proof construction from C1 to C2. Before Lesson 4, the six properties of angles in lines were found inductively, proved using simple deductive reasoning, and shared as theorems. Each of these theorems was written on a paper numbered from 1 to 6, and then listed accumulatively on the student worksheet and blackboard in every lesson: ① A straight angle is 180°, ② Vertical angles are equal, ③ Corresponding angles are equal if the two lines are parallel, ④ The two lines are parallel if the corresponding angles are equal, ⑤ Alternate interior angles are equal if the two lines are parallel, and ⑥ The two lines are parallel if the alternate interior angles are equal.

In Lesson 4, for students to explain why the sum of interior angles on the same side is 180°, a problem was proposed with the following diagram (see Figure 5, upper image).

FIGURE 5

Figure 5. Problem and students' explanations with the teacher's comments in yellow chalk.

Confirming that the six theorems can be used to solve the problem, the teacher refined the problem: “By using the learned theorems, write the reason why ∠c + ∠h = 180°.” With this instruction, the students managed to clarify what can be used and how it can be used to connect the premises and conclusion, which corresponds to planning level P1. After individual and collaborative solving, the teacher selected Student K's explanation, and K wrote it on the blackboard as follows: “Combining ∠h with ∠g makes 180°, and ∠g is equal to ∠c, then ∠c + ∠h = 180°” (Figure 5, middle image). This only showed singular propositions peculiar to the diagram and a chain of them using hypothetical syllogism. After K finished writing, the teacher asked him, “Which theorems did you use and how?” Through classroom discussion, the teacher confirmed that the theorems in the order of “① → ④” were used and wrote it on the blackboard. This suggestion encouraged students to show not only how to connect singular propositions with hypothetical syllogism in their proofs but also which universal propositions were necessary to deduce singular propositions from universal instantiations. This encouragement supported their shift from Level (P1, C1) to (P1, C2).

Next, the teacher selected two other students' explanations. After they finished writing their explanations, respectively, the teacher interacted with them as follows:

T: Both of you wrote ①, ④, and ⑤ before the calculation expressions. Why?

S1: I think the properties used are necessary to calculate angles as reasons, as we learned.

T: The same, S2?

S2: In my opinion, only by the number ①, and ⑤, it is difficult to be reminded which property is used. Then, I added the meaning of ①, and ⑤, respectively.

T: Great!

Thus, the teacher praised these students for correctly embedding the numbers of the theorems (e.g., ⑤), and drew wavy lines in yellow (Figure 5, lower image) to emphasize the importance of recognizing and writing the theorems. Through praise, the teacher again encouraged the students to indicate which universal propositions (theorems) were necessary to deduce singular propositions from universal instantiations. Finally, the teacher defined the relation of two angles “同内角” (interior angles on the same side), and wrote the theorem on a piece of paper as follows: “⑦ The sum of interior angles on the same side is 180° if two lines are parallel.”

Effects of the Implemented Curriculum

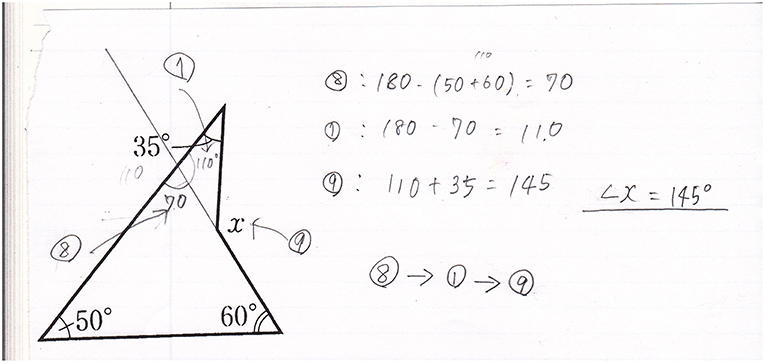
In Lesson 10, students tackled finding Angle “X” of a concave quadrilateral and explaining the reason. In this lesson, students are requested to explain why the size of Angle “X” is 145° in Level (P1, C2). This is a typical problem in the traditional curriculum. All students could easily find that the size of Angle “X” is 145°, and most could write their explanation including the number of theorems before the calculation expressions, and the order of applying theorems “⑧ → ① → ⑨” (Figure 6). The number ⑧ means the property of the sum of the inner angles of a triangle learned in Lesson 5, and ⑨ means the property of the relation between the inner angles and an exterior angle in a triangle learned in Lesson 6.

FIGURE 6

Figure 6. Typical explanation by students.

Generally, in the traditional curriculum, students do not attempt to recognize the used theorems or the order of applying theorems nor represent them, although they can also find the size of Angle “X” and write the calculation expressions without the numbers of the properties. However, in the explanation, each calculation expression is drawn by universal instantiation using a geometrical theorem, and the order of applying theorems shows the deductive connection between the premises and conclusion by hypothetical syllogism. Therefore, it is clear that most students' ability could reach Level C2 proof by the implemented curriculum.

Refining the Curriculum Through Lesson Reflection

After implementing the seven lessons, we found it possible to realize Level “(P1, C2) + EIA” in Lessons 6 and 7. For example, in Lesson 6, students focused on the relation between inner angles and an exterior angle in a triangle, and deducting reasons why based on the proof constructed in Lesson 5, “The sum of the inner angles of a triangle.” In addition, Lesson 7, in which students learn about angles in slanting L-shaped lines between two parallel lines, can advance students' proving skills by changing two parallel lines to intersect each other. This encouraged us to modify the original local progression (P1, C2) of Lessons 6 and 7 to (P1, C2)+EIA. As a result, Lesson 6 will focus more on how to discover the relation between inner angles and an exterior angle from the proof constructed in Lesson 5, and Lesson 7 will deepen students' learning at the level of (P1, C2)+EIA.

By the reflections, we refined the correspondence of intended units with local progression (Table 1). The unit “Properties of parallel lines and angles” accepts the local progression “(P1, C1)→(P1, C2)+EIA” instead of “(P1, C1)→(P1, C2),” and the unit of “Congruence and properties of congruent triangles” does not need to shift to “(P1, C2)+EIA.”

Discussion

Although gradual shifts in producing proofs in curriculum have been recognized as important, it can be realized by introducing local progressions corresponding to unit learning objectives based on the theoretical framework of explorative proving. Moreover, our curriculum will encourage students to plan, construct, and look back at their proof and proving. In particular, the learning levels of looking back provide opportunities to examine, improve, and advance their proving activities more creatively and logically. Our idea for realizing a gradual shift is rooted in hypothetical learning trajectory (Clements and Sarama, 2004) and learning progression (Empsom, 2011). Our theoretical curriculum development can be achieved by setting two levels of “Planning a proof” and “Constructing a proof,” respectively, combining them with “examining, improving, and advancing” as the characteristics of explorative proving, elucidating the two target progressions while considering the relationship of the three components of explorative proving, and then making connections between the units and the target progressions. The theoretical process of curriculum development can thus proceed as follows: identifying the key components of the learning objectives, setting their gradual levels, respectively, combining them, elucidating the target progressions, and connecting the units with the progressions.

Furthermore, with adopting the method of lesson study (Lewis et al., 2006) and a design experiment (Cobb et al., 2003), we implemented classroom lessons based on the connections between the units and one of the target progressions. By implementing and reviewing these lessons, we could find the advantages and limitations of the curriculum, and proceed with developing a more robust curriculum by refining the correspondence of intended units with local progressions. We will continue to develop and improve the curriculum by reconstructing the theoretical framework by refining the target progressions, and adjusting the corresponding unit tables, to ensure that both theoretical and realistic dimensions are considered, thereby ensuring that it is practical and valuable for teachers (Davis et al., 2014).

Concerning our research activity, we have already made the correspondence tables of units with our target progressions for Grades 7–9 geometry along with the Japanese Course of Study. Under the fruitful collaboration with expert teachers, these tables will be subdivided into local progressions according to unit learning contents, and then lesson planning and implementation will also proceed. We will conduct another cycle of our design experiment, and by reflecting on the lessons implemented in the first cycle, it is expected that by the end of the second cycle, we will be able to develop a more implementable curriculum. However, we should evaluate our curriculum from the point of learning explorative proving (e.g., How can students achieve explorative proving with our curriculum?), which remains one of the most crucial problems. For this purpose, we should develop appropriate standards and methods for evaluation.

Ethics Statement

Approval by an ethics committee was not required for this study as per applicable institutional and national guidelines and regulations. All the parents of the participating students gave written informed consent.

Author Contributions

MM and SS developed the conceptual framework of explorative proving (Figure 1), planed/implemented/analyzed the classroom lessons, and drafted the Discussion section in this article. JN, KC, and HS constructed the framework of curriculum development in geometry (Figure 4). TF and KK reviewed the related literature and revised the Discussion section.

Funding

This research was supported by the Grant-in-Aid for Scientific Research (No. 16H02068, 16H03057, 18H01021), Ministry of Education, Culture, Sports, Science, and Technology, Japan.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to express special thanks to our research colleagues: Takeshi Miyakawa (Joetsu University of Education), Koji Iwata (Fukuoka University of Education), Tomohiko Makino (Utsunomiya University), Yosuke Tsujiyama (Chiba University), Kazuhiro Aoyama (Aichi University of Education), and Hiroyuki Nakagawa (Oita University).

References

Clements, D. H., and Sarama, J. (2004). Learning trajectories in mathematics education. Math. Think. Learn. 6, 81–89. doi: 10.1207/s15327833mtl0602_1

CrossRef Full Text | Google Scholar

Cobb, P., Confrey, J., diSessa, A., Lehrer, R., and Schauble, L. (2003). Design experiments in educational research. Edu. Res. 32, 9–13. doi: 10.3102/0013189X032001009

CrossRef Full Text | Google Scholar

Davis, E. A., Palincsar, A. S., Arias, A. M., Bismack, A. S., Marulis, L. M., and Iwashyna, S. K. (2014). Designing educative curriculum materials: a theoretically and empirically driven process. Harv. Edu. Rev. 84, 24–52. doi: 10.17763/haer.84.1.g48488u230616264

CrossRef Full Text | Google Scholar

de Villiers, M. (1990). The role and function of proof on mathematics. Pythagoras 24, 17–24.

Google Scholar

Empsom, S. B. (2011). On the idea of learning trajectories: promises and pitfalls. Math. Enthus. 8, 571–596. Available at: https://scholarworks.umt.edu/tme/vol8/iss3/6

Google Scholar

Fawcett, H. P. (1938). The Nature of Proof: A Description and Evaluation of Certain Procedures Used in a Senior High School to Develop an Understanding of the Nature of Proof. New York, NY: AMS Press.

Google Scholar

Hanna, G., and de Villiers, M. (2012). “Aspects of proof in mathematics education,” in Proof and Proving in Mathematics Education: The ICMI Study, ed G. Hanna and M. de Villiers (New York, NY: Springer), 1–10.

Google Scholar

Healy, L., and Hoyles, C. (2000). A study of proof conceptions in algebra. J. Res. Math. Edu. 31, 396–428. doi: 10.2307/749651

CrossRef Full Text | Google Scholar

Heinze, A., Cheng, Y. H., Ufer, S., Lin, F. L., and Reiss, K. (2008). Strategies to foster students' competencies in constructing multi-steps geometric proofs: teaching experiments in Taiwan and Germany. ZDM 40, 443–453. doi: 10.1007/s11858-008-0092-1

CrossRef Full Text | Google Scholar

Herbst, P. G., and Brach, C. (2006). Proving and doing proofs in high school geometry classes: what is it that is going on for students? Cogn. Instruct. 24, 73–122. doi: 10.1207/s1532690xci2401_2

CrossRef Full Text | Google Scholar

Hoyles, C., and Healy, L. (2007). “Curriculum change and geometrical reasoning,” in Theorems in Schools: From History, Epistemology and Cognition to Classroom, ed P. Boero (Rotterdam: Sense Publishers), 81–115.

Google Scholar

Komatsu, K. (2017). Fostering empirical examination after proof construction in secondary school geometry. Edu. Stud. Math. 96, 129–144. doi: 10.1007/s10649-016-9731-6

CrossRef Full Text | Google Scholar

Lakatos, I. (1976). Proofs and Refutations: The Logic of Mathematical Discovery. Cambridge: Cambridge University Press.

Google Scholar

Lewis, C., Perry, R., and Murata, A. (2006). How should research contribute to instructional improvement? The case of lesson study. Edu. Res. 31, 3–14. doi: 10.3102/0013189X035003003

CrossRef Full Text | Google Scholar

MEXT. (2018). Reports of National Assessment of Academic Ability: Mathematics. Retrieved from: http://www.nier.go.jp/18chousakekkahoukoku/report/data/18mmath.pdf (accessed March 31, 2019).

Miyazaki, M., and Fujita, T. (2015). “Proving as an explorative activity in mathematics education: new trends in Japanese research into proof,” in First Sourcebook on Asian Research in Mathematics Education: China, Korea, Singapore, Japan, Malaysia and India, ed B. Sriraman (Charlotte, NC: Information Age Publishing), 1375–1407.

Google Scholar

Miyazaki, M., Fujita, T., and Jones, K. (2017). Students' understanding of the structure of deductive proof. Edu. Stud. Math. 94, 223–239. doi: 10.1007/s10649-016-9720-9

CrossRef Full Text | Google Scholar

Standards for Mathematical Practice. (2018). Construct Viable Arguments and Critique the Reasoning of Others. Retrieved from: http://www.corestandards.org/Math/Practice/MP3/ (accessed March 31, 2019).

Stylianides, G. J., Stylianides, A. J., and Weber, K. (2017). “Research on the teaching and learning of proof: taking stock and moving forward,” in Compendium for Research in Mathematics Education, ed. J. Cai (Reston, VA: National Council of Teachers of Mathematics), 237–266.

Google Scholar

Tsujiyama, Y., and Yui, K. (2018). “Using examples of unsuccessful arguments to facilitate students' reflection on their processes of proving,” in Advances in Mathematics Education Research On Proof and Proving: An International Perspective, eds A. J. Stylianides and G. H. Harel (New York, NY: Springer International Publishing), 269–281.

Google Scholar

van der Waerden, B. L. (1967). Klassische und moderne axiomatic. Elemente Math. 22, 1–4.

Google Scholar