Computational Psychometrics Approach to Holistic Learning and Assessment Systems

1. Introduction

Many of the characteristics of today's classrooms would be familiar to our great-grandparents: A teacher lecturing to students sitting in rows of organized desks; The teacher instructing from a prepared lesson plan, and the students listening attentively. This traditional education system has been in place with almost no perceptible change since the dawn of the previous century. Students are grouped into various hierarchical aggregations such as classrooms, grades, and schools. The education that students receive is then primarily tailored to these groups as a one size fits all approach rather than a personalized and adaptive experience. The fiction author William Gibson said, “The future is already here, it is just not very evenly distributed” (Rosenberg, 1992). In his quote Gibson alludes primarily to the fact that progress is simply the spread of what is niche to something that is ubiquitous and equitable. This could be said of the state of learning and assessment systems in the current era. Recent advances in computing technology have given us the tools to realize many innovative ideas previously beyond our grasp. Many of these innovative ideas are in the various fields associated with education, learning, and assessment. The new discipline computational psychometrics (von Davier, 2015, 2017) sits squarely in the intersection of these fields. Computational psychometrics describes the blend of the analytical tools from the machine learning (ML) arsenal with cutting edge work in theoretical psychometric research. Advances in ML and big data analyses have allowed psychometric researchers to incorporate these tools to form the computational psychometrics paradigm. Computational psychometrics is currently being applied to a range of learning and assessment research topics, from collaborative problem solving skills (Polyak et al., 2017) to the impact of interpersonal communications on reciprocity in economic decision making (Cipresso et al., 2015) and to learning as we describe here. Computational psychometrics explores not only novel models for new data types, such as complex process data, but also how these models can integrate and make components of teaching, learning, and assessment more holistic and connected.

In this paper we highlight the need for a framework for educational applications and practices which takes a holistic approach to assessment. Such an approach needs to not only blend together models for assessment with models for learning, as has been previously suggested (see for example Tomlinson, 2004), but also include models for navigation, which, broadly speaking, refer to the management of the educational options available to the learner at any particular point in time. We begin by describing the eXtended Learning and Assessment System (XLAS) which is our proposed framework for blending these three disciplines, assessment, learning, and navigation, in a holistic manner. Within the XLAS framework computational psychometrics provides (1) theoretical and practical foundations (e.g., learning theory, measurement rubrics, developmental trajectories, etc.) for the ongoing development of the framework and (2) computational and analytic tools for using evidence collected from the applications of the framework, to validate and improve the framework and its underlying theory, curriculum, and algorithms. Next we enumerate several concrete and ongoing projects that live in the XLAS space. Each project utilizes various aspects of computational psychometrics to bring together independent systems and blend at least two of the three components within the XLAS. We will highlight specific aspects of these projects that utilize computational psychometrics. We conclude with a brief summary along with a vision for the future of educational research.

2. Extended Learning and Assessment Systems

We are all experienced learners. From our earliest experiences grasping the concepts of movement and basic language acquisition, to our forays into arithmetic, grammar, and later, more complex constructs such as time management and teamwork, we spend a significant portion of our lives learning the skills necessary to navigate our world. The systems and frameworks that encompass and define how our learning occurs are called learning systems. Learning systems take on a variety of forms, from traditional examples such as classrooms, textbooks, and apprenticeships, to more modern adaptations such as computers and online forums.

Learning and assessment are intricately linked in a person's journey of acquiring new skills or expanding one's abilities. While learning is the process by which a person gains knowledge or skills, assessment is a way to observe the performance in a learner and produce data in such a way that inferences may be made about what the learner has learned. A particularly succinct description of the relationship between learning and assessment is that effective assessment supports learning by providing evidence (1) of learners achieving learning goals, (2) to inform teachers' decisions, and (3) that informs future instructions (Suskie, 2018). The relationship between the learning system and the assessment system may range from being completely independent to intimately related and tied together in a feedback loop in which one system provides information to the other. We call this joint system of learning and assessment the Learning and Assessment System (LAS).

In the current paper, the authors propose that there is one additional critical component in the learning and assessment loop: Navigation. Navigation is the ability to find a path from one's current state to a goal state. Navigation includes social emotional learning (SEL) skills and decision making skills, which together with the academic skills, support one's success in education and workforce in a holistic manner. In the context of the XLAS, navigation refers to the ability of the learner to utilize the affordances available from the system to make the “right” choices during the process of learning.

A model for navigation also defines what is meant by “right.” The right choices may be dependent on the purpose of the assessment or learning system, the goals of the learner, or on some other stakeholder requirements. What's right for one person at one time may not be for someone else, or the same person at another time. In educational assessment we often make assumptions about what the goals of the examinees are (e.g., to do as well as they can on the assessment) which may not hold at all. However, the framework does not prescribe one particular solution to identifying what “right” means, but rather to highlight its importance and make it clear that the goals of the system should not only be an explicit part of how assessment and learning systems are developed, but the systems should be able to accommodate a variety of goals. Whether this means allowing the learner to choose a goal, or allowing the system to try to identify a trajectory for the particular learner using learning analytics, or something else entirely is up to the particular system and designers of the system to decide on.

Examples of education and career navigation skills may include time management skills, self-knowledge of abilities and interests, knowledge about academic major and occupations, and skills related to planning and decision-making (Camara et al., 2015). Navigation components of an XLAS could include teachers as the curators of knowledge, virtual agents, or system-based affordances, such as recommendations and learning analytics. This navigation component may interact with both the learning and assessment subsystems by curating or designing learning experiences or designing and administering an assessment.

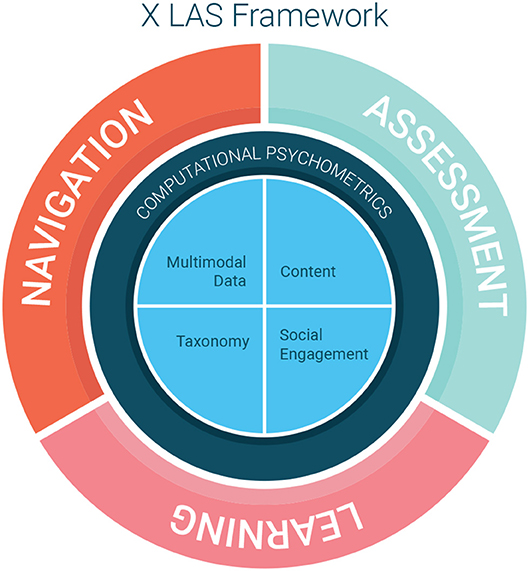
We have worked to develop models and systems that integrate these three components of the XLAS in a holistic manner. Figure 1 illustrates the interactions among the XLAS subsystems and possible components in an XLAS. Learning, assessment, and navigation all interconnect. Each subsystem interacts and informs the other two. The center of the graph portrays lower-level features and direct derivatives of these lower-level features including multimodal data, content, taxonomies, and analytics (see section 3.1). The outer ring of Figure 1 portrays the three main subsystems of the XLAS: learning, assessment, and navigation. These subsystems correspond to higher level abstract models. Examples include Item Response Theory (IRT) for assessment (van der Linden, 2018), Knowledge Space Theory (KST) for learning (Doignon and Falmagne, 1999), and Holland's Theory of Career Choice for navigation (Holland, 1958). The inner ring represents the paradigms that allow researchers to link the lower-level features and derivatives to higher level abstract models (Khan, 2017). These paradigms include computational psychometrics and machine learning.

FIGURE 1

Figure 1. Extended Learning and Assessment System (XLAS) Framework.

Not all data collection is equal or collected with intention. For example, computer based testing (CBT) nowadays collects an abundance of timing information and process data (e.g., click stream data) which is all collected indiscriminately and few consider how to design the experience so that the data collected is useful. Outside the psychometric field, say in computational social science, the big social data that have been amassed by various social media groups are analyzed post-facto. There is no design in what/how to collect the data to obtain a particular result. von Davier (2017) argues that the main feature of computational psychometrics is that the data collection is intentional and by design, hence theory-based. In this way computational psychometrics allows researchers to form links between the higher level abstract models to the concrete components at the center of the XLAS in a top-down manner. The machine learning paradigm on the other hand allows one to abstract the concrete components in a bottom-up manner by utilizing algorithms to build predictive models given all available data at hand. A note on the term “computational” in computational psychometrics: In this context, computational does not mean estimating model parameters by computer, which is what all disciplines (including psychometrics) have been doing since computers have become ubiquitous. In this context, computational means that in order to successfully analyze the multimodal big data, and to form the links from this data to higher order abstract constructs, additional analyses that utilize computational models (as opposed to statistical/psychometric models) are required. Thus, computational psychometrics represents an interdisciplinary field which fuses together theory based psychometrics with the tools developed to analyze multimodal data in order to establish how information and evidence can be derived from the multimodal data and connected to higher order constructs.

In the current paper we will illustrate each of the subsystems of the XLAS framework by using current literature and research projects as examples. In each example we highlight how we connect lower-level features to high-level abstract models. We will also further explore specific building blocks of the XLAS and summarize use cases that address these intersections among the XLAS components.

3. Building Blocks and Use Cases

3.1. Data, Taxonomies, Content, and Social Engagement

Here we delve deeper in explaining the XLAS from as portrayed in Figure 1. The subsystems of learning, assessment, and navigation in the XLAS represent high-level, complex constructs and models. In the center of the framework are lower-level features and derivatives of lower-level features, which include multimodal data and metadata. Examples of multimodal data are audio, video, and sensor-based data as well as more traditional assessment data such as response data. Metadata includes additional covariate information; for response data it may include which particular taxonomic learning standards an item has been tagged to and the demographic information for the learner. Derivatives of lower-level features include content, taxonomies, and analytics.

Lower-level features are connected to higher level complex constructs through a series of hierarchical abstractions. From the data, content, and taxonomies particular relevant features are extracted. These features are combined into mid-level representations. These mid-level representations are then used directly in the models of complex abilities such as learning or navigation. Computational psychometrics through psychometric models, machine learning, and social engagement solutions, serves as the paradigm which connects these lower-level features to higher level features. One focus of the research on the XLAS framework revolves around identifying, constructing, or obtaining useful low-level features from the multimodal data and content; another focus is on feedback and analytics. In the following sections we provide two examples of research associated with these aspect of the XLAS.

3.1.1. Theory-Based Taxonomies and Standards

The most important difference between computational psychometrics and machine learning is that the data collection in computational psychometrics is intentional and aligned with a theoretical framework (von Davier, 2017). Within a theoretical framework, a taxonomy specifies how specific knowledge, skills, abilities and other characteristics connect to broader domains of learning. Such a taxonomy is a key abstraction which allows low-level features such as response data to be connected to higher level constructs such as learning and educational success. A recent example of the development of such a taxonomy at ACT is the Holistic Model of Education and Workplace Success, also known as the Holistic Framework (HF) by Camara et al. (2015).

Policymakers and accountability systems have for a long time focused on academic measures when discussing college and career readiness. However, it is becoming increasingly clear that performance in college and in the workplace depends not only on the traditional academic measures, but also on other SEL and behavioral skills. Camara et al. (2015) identified the need for a framework which gives structure and organization to the knowledge and skills necessary to succeed. Based on a comprehensive review of relevant theory, education and work standards, empirical research, input from experts in the field, and a variety of other sources, they have developed the HF, a comprehensive framework that states what people need to know and be able to do to be successful throughout the course of their education and careers.

The framework is organized into four broad domains: core academic skills, cross-cutting capabilities, behavioral skills, and education and career navigation skills. One of the major facets of the HF is the core academic skills. This section of the HF defines the hierarchical relationship of skills that learners are expected to learn during high school in the domains of language arts, mathematics, and science. This provides a core lower-level feature in the XLAS framework, namely a taxonomy of knowledge, skills, and abilities, which allows researchers to build complex models of learning, assessment, and navigation. Another key aspect is the developmental nature of the HF. This is important because the precursors of success emerge early in life and development continues well beyond the confines of traditional education systems.

The development of the HF was fundamental to help bootstrap research in the XLAS framework. For example, developing a set of content related resources for learning that allows for best practices should rely on the HF to define the goals for learning, the knowledge structure, and scaffolds that should guide the students through the learning process. With the advent of such a taxonomy, researchers are able to connect response data from students to particular models of learning, assessment, and navigation. See Section 4.1 for an example of such research which harnesses the HF.

3.1.2. A Data Cube for Educational Data

In the previous section we saw how computational psychometrics built upon the development of a taxonomy of hierarchical standards which is a key fundamental lower-level feature that helps bootstrap model development in the XLAS framework. Further research has utilized computational psychometrics to refine the analysis of multimodal data to extend the models used in traditional psychometrics to identify lower-level features that are primed for use in the XLAS framework. This research was sparked by the fact that, in recent years, the work with educational testing data has changed due to the affordances provided by the technology, the availability of large data sets, and by the advances made in data mining and machine learning. The computational psychometrics paradigm allows researchers to create new connections between theoretical models and these new data features. However, the traditional, static, and flat representations of data (e.g., a spreadsheet) do not lend themselves well to these new real-time, data intensive computational psychometric and analytics methods. To promote the use of computational psychometric methods in order to reveal new patterns and information about students, von Davier et al. (2019) propose a new way to label, collect, and store data from large scale educational learning and assessment systems (LAS) using the concept of the “data cube” to relate and align multiple databases. The “data cube” idea has evolved over time, but the paradigm remains easy to grasp.

One of the ideas proposed by von Davier et al. (2019) is to rewrite the taxonomies and standards as mathematical vectors, and add these vectors as dimensions to the “data cube.” Similarly, they recommend vectorizing the items' metadata and align them on different dimensions of the “cube.” Psychometricians and data scientists can interactively navigate their data and visualize the results through slicing, dicing, drilling, rolling, and pivoting. A simple example of these various operations can be seen in Figure 2. The drilling-down operation illustrates that the data cube is not necessarily just a multidimensional vector. It can be seen in Figure 2 that dimensions in the data cube can also hold other metadata regarding that dimension. For example the “subject” dimension Math has associated metadata that corresponds to the hierarchical topics associated with mathematics (in the example this includes Calculus, Algebra, and Topology).

FIGURE 2

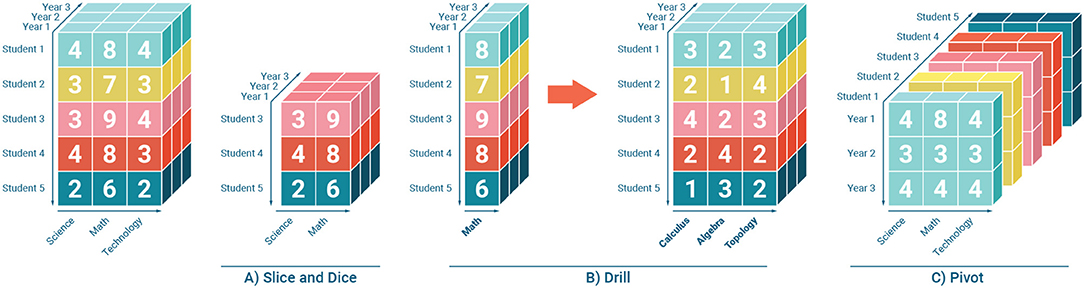
Figure 2. Data Cube for Educational Data. Adapted from von Davier et al. (2019) and used with permission under the Creative Commons Attribution (CC-BY) license.

The data cube structure works well with data exchange standards, such as the IMS Global set of standards. In principle, these standards propose data schema for various data features that the users agree upon. For example, the IMS Global Caliper standard is a template for event data collected during the process of a performance task or a learning session. Recent papers such as Rayon et al. (2014) highlight the importance of building standards and frameworks, not just for research (such as the topic of this paper) but for data itself.

The data cube and the data standards allow for real-time big data analyses, including the use of ML and computational psychometric techniques for the alignment of testing instruments, real-time updates of cognitive diagnostic models during the learning process, and real-time feedback and routing to appropriate resources for learners and test takers. The fundamental ideas behind the data cube guide many of the authors' current research projects. Specifically in sections 4, 4.1 we will see how two projects, the ACT Recommendation and Diagnostic API and the ACTNext Educational Companion App, use the various dimensions of the learning and assessment data to provide learners with deeper insights into their skills and help them navigate educational learning resources.

3.1.3. Social Engagement

Additionally, social engagement in learning, assessment and navigation refers to the degree that an individual participates in these systems within a particular community or society. Such participation can further help define and refine the links and connections between lower-level features and higher level abstract models. An example of collaborative problem solving research which utilizes social engagement to help define the links between the data and the abstract model is presented in Stoeffler et al. (2017). The data collected from the social interactions have often other features, such as the interdependence among the learners. This interdependence translates in a violation of the assumption of identically independently distributed (iid) observations, which in turn, need appropriate computational models.

3.2. Learning and Assessment

Next, we will focus on the outer ring of the XLAS framework, which consists of the three subsystems: learning, assessment, and navigation. Rather than describe in detail each subsystem we will describe the possible overlaps between these three subsystems of the framework since the framework allows research to be multifaceted. The first overlap we will discuss is the overlap between learning and assessment. Research that falls under this umbrella focuses on defining the feedback loops between systems of learning and systems of assessment. A large amount of literature is available for each of these systems on their own, but only within the past few decades have researchers started to discuss how the models in learning and the models of assessment can inform each other. Part of this work is theoretical in nature. Note that theoretical models for learning and models for assessment data have diverged and grown to leverage the salient features and distinct assumptions that embody their respective data sets. Assessment models were built to analyze cross sectional data, whereas learning models were built to analyze longitudinal data. Yet, despite the divergent development of these models there is an intimate connection between the two prominent models in these fields: Bayesian Knowledge Tracing (BKT) and Item response Theory (IRT) (Deonovic et al., 2018).

Other work on this overlapping relationship blends theory with practical need. To further explicate the overlap between systems of assessment and systems of learning we consider an extension of the well-known evidence centered design (ECD) framework for designing assessments (Mislevy et al., 1999). This extension, the extended ECD (Arieli-Attali et al., 2019), provides room for designing systems in which learning and assessment ico-exist.

3.2.1. Extended Evidence Centered Design

As mentioned before, the most important difference between computational psychometrics and machine learning is that the data collection in computational psychometrics is intentional and aligned with a theoretical framework (von Davier, 2017). Several theoretical frameworks have been developed for assessments. ECD is one such framework designed to place priority on the collection of validity evidence from the onset of the design of the assessment (Mislevy et al., 1999). The three core components of the ECD framework include the Student Model, Task Model, and Evidence Model. The Student Model specifies the latent competencies that are the target of the test, the Task Model specifies the task features that will elicit the observed data which will allow for inference about the latent competencies, and the Evidence Model makes the connection between the latent competencies specified by the Student Model and the observed data from the Task Model. This framework however does not specify how the learning component of an LAS should be designed and developed in order to properly elicit validity evidence. An extension of the ECD framework, the Extended Evidence Centered Design (e-ECD) framework broadens each of the three core components of the ECD as well as draws upon data driven techniques and computational psychometrics to power these extensions (Arieli-Attali et al., 2019).

The extended model includes a static layer, corresponding to the original components of the ECD, and a dynamic layer which addresses learning, see Figure 3. The extended components include: (1) the extended Student model, or the Knowledge-Change model, which specifies learning processes as the latent competency that the system is targeting; (2) the extended Task model, or the Task-Supports Model, which specifies principles and features of learning supports (scaffolds, feedback, hints, etc.) that guide the design of tasks; and (3) the extended Evidence model, or the Knowledge-Skills-Abilities Change model, which specifies the links between the students' responses, scaffold usage, and the target learning processes. These links allow for inference from behaviors to latent learning.

FIGURE 3

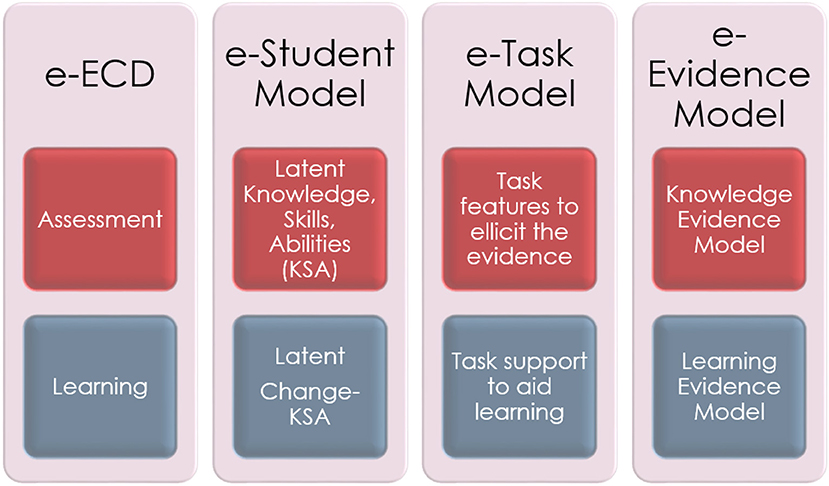
Figure 3. Extended Evidence Centered Design (e-ECD). Adapted from Arieli-Attali et al. (2019) and used with permission under the Creative Commons Attribution (CC-BY) license.

Using computational psychometrics and empirical data we can monitor the use and impact of learning supports and dynamic models of ability. This data driven approach combined with the theoretical perspective will help us to create a relevant and well-designed framework for the development of learning and assessment systems.

3.3. Navigation and Assessment

Another overlap we are considering is between navigation and assessment. If navigation can broadly be described as determining where one should go, the subsystem of assessment in this context revolves around knowing were one is at currently. Preparing individuals for the decisions they will be making throughout their educational and career journeys, along with optimizing these decisions, are important areas of study that have the potential for significant impact. We are looking at these aspects from many perspectives that reflect the computational psychometrics paradigm.

We reached out to our colleagues who worked on the navigation part of the ACT Holistic Framework to understand the role of navigation for success. Educational success depends on many factors, including what individuals know about themselves and their environments, and how they use this information to make choices, plan actions, optimize resources, and move along their education and career paths (Becky Bobek, personal communication, December 14, 2018). The literature on decision making processes related to critical navigation decision points such as educational and occupation choices is scant, and we have been working to uncover some of these processes. For example, economists (Wiswall and Zafar, 2015) refer to “unobserved tastes” as a dominant factor in the choice of major and reinforce the need to investigate these more heterogeneous aspects of major choice.

Bobek and Moore (2017) refer to the four dimensions critical to navigating education and career transitions effectively encompass

1. Self-knowledge (understanding of one's abilities, interests, skills, values, attitudes, and beliefs),

2. Environmental Factors (education/work knowledge, experiences, supports, barriers),

3. Integration (exploration, goals, congruence, education/career choice making, action plans),

4. Managing Career & Education Actions (college/job search, roles, implementation).

Research concerning the first three dimensions mentioned above is found in Paek and Bobek (2018). Separately, research has been conducted on learning analytics, recommendations, notifications, and data display (Whitmer et al., 2017) and on how to model the choices that people make (Kruis, 2018). Additional research is being conducted on the optimization of decision making process for individuals and their goals (von Davier and Arielli-Attali, unpublished).

3.4. Learning and Navigation

The final overlap on the XLAS framework we will consider is between learning and navigation. Navigation refers to knowing were one wants to go and determining how to get there. This is quite abstract as it can apply to many situations. Navigation can refer to deciding on which career to pursue and how to pursue it, deciding which college to go to and what major to enroll in, or even on a more day to day basis navigation can refer to a teacher's lesson plan, the goals they want their students to achieve and how to achieve them. Navigation with respect to learning is the process of going from where one is to where they want to go in terms of the further development of one's knowledge, skills, and abilities. Research involved in the subsystem of learning in the XLAS deals with constructing theoretical models for how learning occurs, building educational tools, and promoting learning.

There has been heavy investment into exploring the intersection between these two subfields in the last few decades in both the theoretical side and on application. On the theoretical side, the field of learning science works to understand learning and design, implement, and improve instructional methodologies. An example of research from learning theory that lives in the intersection of learning and navigation comes from mastery learning theory (Bloom, 1968). This theory states that complex skills can be broken down into parts and learning is improved if each of these parts is first mastered in turn. The main assumption is that if a student fails to learn a required prerequisite skill, then he or she will likely not be able to learn the subsequent skills. From this theoretical model of how a learner moves toward their goals researchers have built models for tracking and assessing students, such as knowledge tracing (Corbett and Anderson, 1994) which involves the overlap of assessment and learning, has been discussed in previous sections. More recent literature which analyzes mastery learning includes work by MacLaren and Koedinger (2002) in which simulation is used to study the impact of mastery learning.

On the application side of research in learning and navigation there has been an increase in interest in learning analytics. In education, Aguilar (2018) writes that learning analytics has emerged as the discipline associated with analyzing and reporting big data. Stakeholders in education utilize learning analytics as a way to make learning and learners' navigation more personalized. Aguilar (2018) points out that most learning and navigational infrastructure is primarily built to serve the “average” student, e.g., students are grouped into classrooms, grades, and schools and teachers provide instruction one class at a time. More personalized instruction has been shown to be impactful, but can be difficult to scale. Aguilar (2018) argues that learning analytics provides a solution to this problem by using computational methodology and visualizations to allow personalized learning and navigation at scale. Methods for learning analytics include:

1. Resource Analytics - resources which students use (e.g., video, quiz) and create (e.g., essay).

2. Behavior Analytics - time on task, persistence, curiosity, participation, etc.

3. Social Learning Analytics - social interaction in learning, participation in learning networks, forums, etc.

4. Predictive Analytics - within student: timely identification of at-risk behavior; and across students: identify at-risk students in terms of engagement and retention for meaningful intervention before they go off-track.

One platform which has successfully utilized learning analytics to bridge navigation and learning is the ASSISTments project. The ASSISTments project (Heffernan and Heffernan, 2014) provides a system for teachers and researchers to work together. It is a project that is perfectly situated in the learning and navigation overlap. One particular functionality which allows ASSISTments to combine learning and navigation is the ability for teachers to try out various instructional content, learning resources, and interventions on groups of children and monitor and track their learning. This allows researchers and instructors to observe the impact of the content, resources, and interventions on student learning.

However, Aguilar (2018) points out learning analytics is not a silver bullet for the problem of providing personalized learning. The data that are collected and the procedures for processing and creating visualizations needs to be thought through ahead of time. Despite the large amount of data that is collected by learning analytics systems, not every facet and dimension of a person will be captured. Thus, important decisions regarding student learning and their trajectory through the system may be ill informed. This means that at a particular point in time, the data necessary to truly provide an insightful personalized experience for a student is not available. Furthermore, many learning analytics approaches utilize machine learning techniques such as clustering or visualizations that compare particular students to other aggregates, both wash out individual characteristics and seem counter to the goals of personalized learning analytics. The insights and personalization provided by learning analytics also requires trained experts. For example, Teasley (2017) points out that providing learning analytics dashboards directly to students has not been fruitful and requires further research. Finally, Aguilar (2018) points out potential data privacy concerns, which remain to be comprehensively addressed.

4. XLAS Use Case: The ACTNext Educational Companion App

The XLAS framework successfully links learning, assessment and navigation by managing the relationship of learners' data to content (assessment and instructional), taxonomies (knowledge, skills) and analytics. The authors applied this management strategy in the development of one of our recent research-based prototypes, the ACTNext Educational Companion App. The app was designed to assist learners by providing information on their learning goal progress and to identify areas needing review by continuously processing measurement data and providing personalized instructional recommendations, all delivered in an anytime/anywhere mobile experience.

The goal of this app was to develop a prototype, designed with the XLAS in mind, which supports learning through personalized recommendations, based on the mastery theory of learning (Bloom, 1968), and through free agency given to the students, based on the theory of self-directed learning (Knowles, 1975). The app also provides students with navigational opportunities to explore their career interests. In this section, we will describe how computational psychometrics principles are used to guide the development of this app.

The app leverages multiple sources of data from ACT's portfolio of learning and assessment products. Beginning from its college readiness assessment, the ACT, the app identifies the underlying links from learners' measurement data to the taxonomic skills in English, Math, Reading and Science such as those defined by the HF (see section 3.1.1), but is general enough to be applicable to any taxonomic classification of skills. The app gathers additional academic skills evidence from a workforce skills assessment (Applied Math, Reading for Information, Locating Information) where available. Beyond the core academic skills, the app evaluates Social Emotional Learning (SEL) data from the learner's SEL assessment results, that is the results from ACT's Tessera test. Blending these data, the app generates analytics that can predict mastery of skills at multiple levels in a taxonomy such as the HF.

Through the alignment of instructional content to taxonomic structures conducted with ML methods, the app is able to identify recommended resources to drive learning activities. The app makes targeted recommendations for learners at any selected or prescribed level in a taxonomy. It uses its knowledge of the learner's predicted abilities along with the understanding of hierarchical, parent/child relationships within the content structure to produce personalized lists of content.

With additional practice activity (e.g., like that found in test preparation quiz/test sessions) the app is able to continue to update and refine its predictive analytics and adapt its recommendations to learners over time. The app uses a clearly presented, three star rating system for the top level areas of a taxonomy (e.g., subject, domains) to communicate achievement to the learner and to encourage and highlight the next areas for review.

The Companion App also features access to navigational tools that were developed by ACT researchers, e.g.,Cruce and Mattern (2018). These tools provide learners with insights about their career interests and the relationship of their personal data (e.g., assessment results, grade point average) to potential areas of study in college based on longitudinal, higher education outcome studies.

The Companion App was piloted with group of Grades 11 and 12 high school students in Clinton, South Carolina, USA between Fall 2017 and Spring 2018. The results were presented in an unpublished report (Polyak et al., unpublished).

4.1. Enabling a Personalized Learning Experience: Recommendation and Diagnostics (RAD) API

The development of the ACTNext Companion App led to the insight that the underlying capabilities could be packaged into an application programming interface (API) that can offer the diagnostic and recommendation engines as a service to other products or platforms. ACT Academy, built using a collection of free online resources from OpenEd, is one such system. ACT Academy is a free online platform designed to help students master the skills they need to improve their test scores and succeed in college and career. Students can take authentic practice quizzes and receive personalized video lessons, games, and interactive resources whenever they miss a question. ACT Academy provides a free personalized path for students to help them prepare for the ACT test. Instead of teaching to the test and going through similar questions, ACT Academy videos help students learn the actual concepts being addressed in the questions. ACTNext defined a set of API methods that:

• Accepts measurement data for a learner using a well-defined, open standard, IMS Global's Caliper for learning events¹. The Caliper AssessmentItemEvent format is used to identify who the learner is, which item they responded to and the dichotomous outcome of their interaction.

• Ingests the definition of hierarchical standard definitions using the IMS Global CASE standard. The CASE standard provides a machine-readable expression of the individual standard statements and conveys the hierarchical relationships (e.g., subject, domain, strand, sub-strands, etc.).

• Automatically caches instructional content resources from any learning object repository (LOR) using the IMS Global LTI resource search API. By caching the LOR content that has been aligned to the standards, RAD can efficiently build personalized lists dynamically with up-to-date diagnostic data.

• Continuously tracks learners' mastery of taxonomy skill/skill areas using modular, configured algorithms. As learner evidence is processed, RAD uses the algorithm that has been configured for the LAS to update new predictions of skill mastery.

• Offers diagnostic engine results for learners based on any collection level in the taxonomy. RAD method calls allow for the parameterization of requests that can indicate an area of interest with respect to the taxonomy, e.g., return current estimates of Geometry skills within Math.

• Offers recommendation engine generated, personalized lists of instructional content for any collection level in the taxonomy. RAD method calls allow for the parameterization of requests that can indicate an area of interest with respect to the taxonomy, e.g., return personalized resources for Geometry within Math.

• Allows human curators to add content rules that require selected content for specified taxonomy areas. If human curators want to promote known resources for an area, they can boost the importance of selected instructional content items at any level of the taxonomy (e.g., subject, domain, strand, etc.).

• Permits bootstrapping of diagnostic estimates using prior assessment results. This feature allows learners to present results from a prior assessment (e.g., ACT score category report ratio data) in order to estimate skill knowledge prior to taking LAS assessments.

All of these methods are delivered from the secure, highly scalable, cost-effective, manageable platform, Amazon Web Services (AWS).

The initial integration of this API was completed in September 2018 with ACT's free test preparation web-based platform, ACT Academy. ACT Academy uses a customized version of the TAO open source test delivery platform capable of generating the IMS Global Caliper events (e.g., AssessmentEvent, AssessmentItemEvent) that the RAD API uses to continuously track learner data. ACT Academy's dashboard/progress areas use RAD API's diagnostic methods to present learners with the same star-based progress report that was described above in the Companion App.

As learners navigate to the resources tab in ACT Academy, they are presented with personalized lists of instructional content that use their RAD diagnostic record to select the most relevant content based on the learner's needs. RAD effectively links assessment content and instructional content via the configured taxonomy while generating useful insights and analytics to help learners navigate their test preparation and skill practice goals.

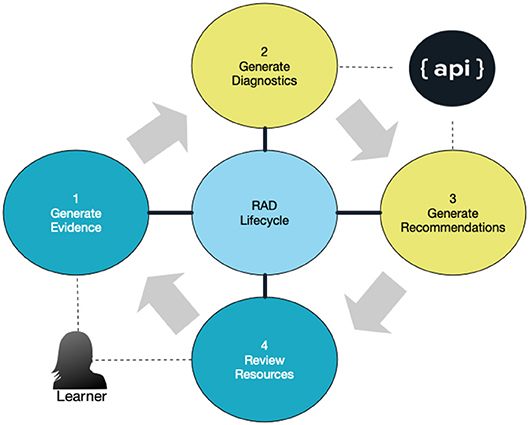
We refer to this continuous cycle of activity between the learner in an LAS and the RAD API as the RAD life-cycle as shown in Figure 4. Learners generate evidence via assessment data which RAD then uses for its analysis. The analysis itself uses techniques from computational psychometrics. Essentially, RAD connects low-level evidence data up to high-level estimates of learner abilities by applying algorithms (see section 4.1.1), coupled with an item response model, to take into account a learner's prior estimate of ability alongside the system-derived estimate of skill difficulty. Other examples of the application of computational psychometrics for this project involve the machine learning techniques used to ascertain taxonomic tagging of resources and items. Today, a semi-automatic process is used to suggest tags to human curators who can then confirm or reject proposals, helping the system to better learn the classifications in the future.

FIGURE 4

Figure 4. ACTNext Recommendation and Diagnostics (RAD) API.

The initial results of applying this computational psychometrics solution to learner diagnostic tracking has demonstrated that this is an important tool supporting our vision for unifying learning, assessment and navigation. We are currently expanding our approach to incorporate performance metrics that will:

• Report continuous classification accuracy, i.e., how well is RAD predicting that learners would get items correct/incorrect based on its diagnostic data?

• Use additional Caliper events such as MediaEvents to measure platform usage learning analytics, e.g., how many RAD recommended resources are learners reviewing?

• Evaluate the fairness of the algorithms, by investigating the population distributions of star ratings and recommendations for an LAS. We want to provide aggregate analytics that show e.g., how many 1,2,3 star ratings have been made for specified populations.

4.1.1. Diagnostic and Recommendation Models

To further detail the theoretical models, we focus next on psychometric models. Traditionally models for assessment relied on unidimensional models of latent ability. Such models are built to be able to correctly rank a set of learners from highest relative ability to lowest relative ability. However, these unidimensional models, such as models in Item Response Theory (IRT), are unsuitable for determining the source of these differences in ability. In other words they are incapable of diagnosing the underlying skills which the learners have or are lacking. Cognitive Diagnostic Models (CDMs) are built specifically for this purpose. Rather than modeling a unidimensional latent ability, CDMs equip each learner with a multidimensional latent variable where each dimension corresponds to a particular skill.

One particular project that we are working on and which utilizes concepts from CDMs is the Recommendation and Diagnostics (RAD) engine delivered through an API that was described above. The RAD API defines how a learning and assessment system can interact with the RAD engine. The RAD engine is built to be able to continuously track and update the skills in some hierarchical skill taxonomy, such as the ACT Holistic Framework. In ACT Academy a learner is able to choose a category from the Holistic Framework (HF; see section 3.1.1) to practice. The skills in the HF are organized in a hierarchical tree structure called a knowledge graph. The knowledge graph is composed of a set of nodes, where each node corresponds to a skill in the HF, along with their direct relationships represented by edges between the nodes. For each node k in the knowledge graph a learner has a proficiency value or profile value π_k, representing the probability that the learner has mastered this node. Together the knowledge graph along with a specific learner's proficiency values is called the Personal Learner Knowledge Graph (PLKG). The RAD API models the bottommost nodes (leaf nodes or nodes without any children) of each learner's PLKG. Estimates of a learner's proficiency in these bottom nodes are then percolated up the tree by averaging (see Figure 5).

FIGURE 5

Figure 5. An illustration of the Personal Learner Knowledge Graph (PLKG) along with the process of percolating information up the hierarchical tree. T₁ and T₂ represent two topics under the category of Algebra. S₁, …, S₄ are the skills that are estimated by the RAD API, where π_k represents the proficiency the learner has for skill k. The right hand side of the figure explains how information from the estimated skill or proficiencies percolate up the tree.

The learners in ACT Academy see a relatively high-level part of the HF known as the reporting category. Although the probability of node mastery is stored internally as a value between 0 and 1, it is presented to the learner in a discretized fashion as a star value (between 1 and 3 stars). Based on the learner's interests or evaluation of their HF mastery, as presented by the RAD API, the learner selects one of these categories to practice. They are then given a short set of items in the form of a quiz. The RAD API processes these responses in real-time, updates the mastery of the leaf nodes, percolates the information up the HF tree, and the whole process is repeated again when the learner selects a new topic to practice.

From the above high-level overview of the RAD API diagnostic framework we can see that the statistical model underpinning the diagnostics and the algorithm used to update the parameters in the model needs to have several key features

1. The algorithm needs to be able to process data in real-time, updating learner profiles after either every response, or after a small set of responses have been accumulated.

2. The model needs to be able to quantify a learner's mastery of every leaf node in the HF (and convert this into a value between 0 and 1).

Additionally, we require that one learner's activity should not change another learner's profile. Ideally the model would only have parameters that are updated in real-time, however we will allow some hyper-parameters that are considered fixed but allowed to be updated on a longer term schedule with a batch process of the data.

We studied several algorithms. One of the algorithms selected to power the RAD API diagnostic engine was the Elo algorithm. First, we describe the basic Elo algorithm and then we present how we adapted the Elo algorithm to fit into the RAD API. The Elo algorithm was developed to track and calibrate the rankings of players in competitive games. Its origins are from competitive chess (Elo, 1978). An example of the use of the Elo algorithm in an educational context can be found in Pelánek (2016). The model underlying the Elo system is quite simple. Every player is associated with rating θ_p. The probability that player p beats player q is modeled as follows.

$\begin{array}{ll}{E}_{pq}=\text{Pr}(p\text{ beats }q)=\frac{1}{1+e^{-({\theta }_p-{\theta }_q)}}=\sigma ({\theta }_p-{\theta }_q)& (1)\end{array}$

After every match the parameters for the players involved are updated taking into account the probability that player p wins and the actual outcome of the game.

$\begin{array}{ll}{\theta }_p^{*}={\theta }_p+K(X_{pq}-E_{pq})& (2)\end{array}$

$\begin{array}{ll}{\theta }_q^{*}={\theta }_q-K(X_{pq}-E_{pq})& (3)\end{array}$

where ${\theta }_p^{*}$ and ${\theta }_q^{*}$ are the updated values, X_pq is the result of the game (1 if p betas q and 0 otherwise), and K is a scaling factor. In practice K is usually fixed at some point depending on how the practitioner wants the algorithm to behave; small K will make the algorithm less variable but take longer to converge to the correct values while larger values of K will make the algorithm converge faster but be much more variable.

For the RAD API we adopted a similar algorithm to estimate the values in a model that is inspired by the multidimensional Rasch model and the log-linear test model (LLTM) (Pelánek, 2016; Pelánek, 2017). From the LLTM we use the idea of deconstructing the item difficulty to be linear in the difficulties of each skill. This allows us the ability to directly track skill difficulty. Let X_si be the response of student s to item i. We model the probability of a correct response as specified below,

$\begin{array}{ll}{E}_{si}=\text{Pr}(X_{si}=1)=\sigma (m_{si})& (4)\end{array}$

$\begin{array}{ll}{m}_{si}={\theta }_s+{\displaystyle \sum _k}{q}_{ik}{\theta }_{sk}-{\displaystyle \sum _k}{q}_{ik}{\beta }_k& (5)\end{array}$

where θ_s is a general measure of ability of student s, θ_sk is a skill-specific measure of ability for student s on skill k, q_ik is a vector of 1's and 0's corresponding to which skills item i is tagged to, and β_k is the difficulty of skill k.

The update formulas are adapted from the original Elo algorithm to correspond to this model as follows.

$\begin{array}{ll}{\theta }_s^{*}={\theta }_s+\frac{a_s}{1+b_s\times n_s}(X_{si}-E_{si})& (6)\end{array}$

$\begin{array}{ll}{\theta }_{sk}^{*}={\theta }_{sk}+\frac{a_{sk}}{1+b_{sk}\times n_{sk}}(X_{si}-E_{si})& (7)\end{array}$

$\begin{array}{ll}{\beta }_k^{*}={\beta }_k-\frac{a_i}{1+b_i\times n_k}(X_{si}-E_{si})& (8)\end{array}$

where ${\theta }_s^{*},{\theta }_{sk}^{*}$, and ${\beta }_k^{*}$ are the updated values, n_• are hyper-parameters controlling the sensitivity (speed) of the values' update, n_s is the number of prior items answered by student s, n_sk is the number of items on skill k that student s answered, and n_k is the number of students that have answered an item utilizing skill k. Here we have chosen the Elo scaling factor to be of the form recommended by Pelánek (2016). In this form the scaling factor gets smaller as the number of observed items on a student increases so that the algorithm quickly gets around the right neighborhood of the student ability parameters and then becomes less variable over time. In the RAD API the n parameters were chosen by cross-validation of an initial sample of students with the objective of minimizing predictive error. Initial values for all parameters θ_s, θ_sk, and β_k were set to 0. Once the parameters of the model have been updated the profile values, π_sk, of the learner's PLKG are updated as follows.

$\begin{array}{ll}{\pi }_{sk}=\sigma ({\theta }_s+{\theta }_{sk})& (9)\end{array}$

After which the rest of the learner's PLKG is updated by percolating the information up the tree. This blend of a psychometric model with an algorithmic/rating system is being described in Yudelson et al. (2019).

5. Discussion and Conclusions

In this paper we outlined a comprehensive holistic learning and assessment system and indicated how the computational psychometrics paradigm integrates all these complex pieces. This framework stems from the idea that when learning, assessment and navigation are developed together there will be an enhancement to the students' opportunities for a successful, holistic educational experience. A holistic learning and assessment system has many interdisciplinary components in which each individual component is an area for research and development: from the design, to data structures for big data, to mobile platforms, recommendation engines, the development of APIs and psychometric and ranking models for learning. Each of the areas described here include innovations, or at least extensions, of existing capabilities. Several papers are now being written simultaneously where the details of these approaches and their evaluations are being presented.

While significant progress has been made on the research and development of holistic learning and assessment systems, more work is needed to refine the methodologies, to continuously evaluate them for fairness, efficacy, and validity, and to scale them up. For example, the RAD API has been live since September 2018 and has guided over 100,000 students' choices so far; research on its efficacy and validity is in progress. The goal is to be able to provide all learners with access to quality educational resources and feedback, regardless of their background and geographic location.

Future XLAS research includes the development of new types of dynamic cognitive diagnostic models that are appropriate for learning and of artificial intelligence (AI) and multimodal analytics to enhance these psychometric models. Another area of interest is how to estimate the reliability and validity of the output from such Elo models. We also need to continue to work on more accurately aligned testing instruments and instructional resources via taxonomies.

For the authors, one of our future projects includes refining and enhancing the scalability of the Companion App. We are also developing additional micro-services to support multiple ways of personalizing and adapting the learning environment. Our goal is to integrate our research and prototypes with LAS partners and researchers, and extend the current XLAS work beyond the authors' organization with our Software as a Service (SaaS) model.

Author's Note

This paper is based on the Keynote Address given by AvD at the International Test Commission, in Montreal, Canada in July 2018.

Author Contributions

AvD, SP, and AW contributed to the conception and design of the work. BD, MY, and SP contributed to the acquisition, analysis, and interpretation of data. All authors contributed to the writing.

Conflict of Interest Statement

All authors are employed by ACT, Inc.

Acknowledgments

The work described here covers several large projects with many researchers and developers; in particular, we acknowledge the contributions of Gunter Maris to the models and recommenders presented here and of Kurt Peterschmidt to the development of the capabilities and mobile application. The authors thank Maria Bolsinova and Lu Ou for their feedback on the previous versions of the paper, to Andrew Cantine for editorial help and to Matthew Livaudais for help with the graphics.

Footnote

1. ^For the specification see IMS Global Learning Consortium, Inc. Caliper Analytics Specification, version 1.1.

References

Aguilar, S. J. (2018). Learning analytics: at the nexus of big data, digital innovation, and social justice in education. TechTrends 62, 37–45. doi: 10.1007/s11528-017-0226-9

CrossRef Full Text | Google Scholar

Arieli-Attali, M., Ward, S., Thomas, J., Deonovic, B., and von Davier, A. A. (2019). The expanded evidence-centered design (e-ecd) for learning and assessment systems: A framework for incorporating learning goals and processes within assessment design. Front. Psychol. 10:853. doi: 10.3389/fpsyg.2019.00853

PubMed Abstract | CrossRef Full Text | Google Scholar

Bloom, B. S. (1968). Learning for mastery: instruction and curriculum. Comment Eval. UCLA-CSIEP 1, 1–12.

Bobek, B. L., and Moore, R. (2017). “What can colleges do about the concerns of diverse college-bound students?” in Association for Institutional Research Forum (Washington, DC).

Camara, W., O'Connor, R., Mattern, K., and Hanson, M. A. (2015). Beyond Academics: A Holistic Framework for Enhancing Education and Workplace Success. ACT Research Report Series 4, ACT.

Google Scholar

Cipresso, P., Villani, D., Repetto, C., Bosone, L., Balgera, A., Mauri, M., et al. (2015). Computational psychometrics in communication and implications in decision making. Comput. Math. Methods Med. 2015:985032. doi: 10.1155/2015/985032

PubMed Abstract | CrossRef Full Text | Google Scholar

Corbett, A. T., and Anderson, J. R. (1994). Knowledge tracing: modeling the acquisition of procedural knowledge. User Model. User Adapt. Interact. 4, 253–278. doi: 10.1007/BF01099821

CrossRef Full Text | Google Scholar

Cruce, T., and Mattern, K. (2018). “Sticking to the plan,” in Which Factors are Related to Intended-Declared Major Consistency (Iowa City, IA: ACT).

Deonovic, B., Yudelson, M., Bolsinova, M., Attali, M., and Maris, G. (2018). Learning meets assessment. Behaviormetrika 45, 457–474. doi: 10.1007/s41237-018-0070-z

CrossRef Full Text | Google Scholar

Doignon, J.-P., and Falmagne, J.-C. (1999). Knowledge Spaces. Berlin; Heidelberg: Springer-Verlag.

Google Scholar

Elo, A. E. (1978). The Rating of Chess Players, Past and Present. New York, NY: Arco Pub.

Heffernan, N. T., and Heffernan, C. L. (2014). The assistments ecosystem: building a platform that brings scientists and teachers together for minimally invasive research on human learning and teaching. Int. J. Artif. Intell. Educ. 24, 470–497. doi: 10.1007/s40593-014-0024-x

CrossRef Full Text | Google Scholar

Holland, J. L. (1958). A personality inventory employing occupational titles. J. Appl. Psychol. 42, 336–342. doi: 10.1037/h0047330

CrossRef Full Text | Google Scholar

Khan, S. M. (2017). “Multimodal behavioral analytics in intelligent learning and assessment systems,” in Innovative Assessment of Collaboration, eds A. A. von Davier, M. Zhu, and P. C. Kyllonen (Cham: Springer International Publishing, 173–184.

Google Scholar

Knowles, M. S. (1975). Self-Directed Learning: A Guide for Learners and Teachers. New York, NY: Association Press.

Kruis, J. (2018). “A general framework for choice dynamics,” in 28th Interuniversity Graduate School of Pscyhometrics and Sociometrics Winter Conference (Arnhem).

MacLaren, B., and Koedinger, K. (2002). “When and why does mastery learning work: instructional experiments with act-r “simstudents”,” in Intelligent Tutoring Systems, eds S. A. Cerri, G. Gouardères, and F. Paraguaçu (Berlin; Heidelberg: Springer), 355–366.

Google Scholar

Mislevy, R. J., Steinberg, L. S., and Almond, R. G. (1999). On the Roles of Task Model Variables in Assessment Design. CSE Technical Report 500, University of California, National Center for Research on Evaluation, Standards, and Student Testing (CRESST).

Google Scholar

Paek, P. L., and Bobek, B. L. (2018). “Unpacking the factors contributing to summer melt and impacting college readiness,” in Symposium Conducted at the Annual Conference of the American Educational Research Association, ed M. Hailu (New York, NY).

Google Scholar

Pelánek, R. (2016). Applications of the elo rating system in adaptive educational systems. Comput. Educ. 98, 169–179. doi: 10.1016/j.compedu.2016.03.017

CrossRef Full Text | Google Scholar

Pelánek, R. (2017). Bayesian knowledge tracing, logistic models, and beyond: an overview of learner modeling techniques. User Model. User Adapt. Interact. 1–38.

Polyak, S. T., von Davier, A. A., and Peterschmidt, K. (2017). Computational psychometrics for the measurement of collaborative problem solving skills. Front. Psychol. 8:2029. doi: 10.3389/fpsyg.2017.02029

PubMed Abstract | CrossRef Full Text | Google Scholar

Rayon, A., Guenaga, M., and Nunez, A. (2014). “Ensuring the integrity and interoperability of educational usage and social data through Caliper framework to support competency-assessment,” in 2014 IEEE Frontiers in Education Conference (FIE) Proceedings (San Jose, CA), 1–9. doi: 10.1109/FIE.2014.7044448

CrossRef Full Text | Google Scholar

Rosenberg, S. (1992). Virtual reality check digital daydreams, cyberspace nightmares. San Francisco Exam. C1.

Stoeffler, K., Rosen, Y., and von Davier, A. A. (2017). “Exploring the measurement of collaborative problem solving using a human-agent educational game,” in Proceedings of the Seventh International Learning Analytics and Knowledge Conference, eds A. Wise, P. H. Winne, G. Lynch, X. Ochoa, I. Molenaar, S. Dawson, and M. Hatala (Vancouver, BC).

Google Scholar

Suskie, L. (2018). Assessing Student Learning: A Common Sense Guide. San Francisco, CA: Jossey-Bass.

Google Scholar

Teasley, S. D. (2017). Student facing dashboards: one size fits all? Technol. Knowl. Learn. 22, 377–384. doi: 10.1007/s10758-017-9314-3

CrossRef Full Text | Google Scholar

Tomlinson, M. (2004). 14-19 Curriculum and Qualifications Reform. Technical report, Department for Education and Skills (DFES).

Google Scholar

van der Linden, W. J. (2018). “Handbook of item response theory,” in Chapman and Hall/CRC Statistics in the Social and Behavioral Sciences (Boca Raton, FL: CRC Press).

Google Scholar

von Davier, A. A. (2015). “Virtual and collaborative assessments: examples, implications, and challenges for educational measurement,” in Workshop on Machine Learning for Education, International Conference on Machine Learning, eds F. Bach and D. Blei (Lille).

von Davier, A. A. (2017). Computational psychometrics in support of collaborative educational assessments. J. Educ. Meas. 54, 3–11. doi: 10.1111/jedm.12129

CrossRef Full Text | Google Scholar

von Davier, A. A., Wong, P., Polyak, S. T., and Yudelson, M. (2019). The argument for a “Data Cube” for large-scale psychometric data. Front. Educ. doi: 10.3389/feduc.2019.00071

CrossRef Full Text | Google Scholar

Whitmer, J., Nasiatka, D., and Harfield, T. (2017) “Student interest patterns in learning analytics notifications,” in Blackboard Data Science Research Brief, Blackboard Analytics (Washington, DC), 1–14.

Wiswall, M., and Zafar, B. (2015). Determinants of college major choice: identification using an information experiment. Rev. Econ. Stud. 82, 791–824. doi: 10.1093/restud/rdu044

CrossRef Full Text | Google Scholar

Yudelson, M., Deonovic, B., Chopade, P., and Polyak, S. T. (2019). “Towards dynamic adaptation and personalization in ACT Academy a free online learning platform,” in Measurement in Adaptive Learning Systems: Challenges and Solutions, Symposium Conducted at the Annual Conference of the National Council on Measurement in Education, ed M. Bolsinova (Toronto, ON).