Abstract
Multiple kinds of manipulatives, such as traditional, virtual, or technology-enhanced tangible objects, can be used in primary education to support the acquisition of mathematical concepts. They enable playful experiences and help children understand abstract concepts, but their connection with cognitive development is not totally clear. It is also not clear how virtual and physical materials influence the development of different strategies for solving instructional tasks. To shed light on these issues, we conducted a 13-day intervention with 64 children from first grade, divided into three groups: Virtual Interaction (VI), Tangible Interaction (TI), and Control Group (CO). The VI group played a fully digital version of a mathematics video game and the manipulation of the blocks took place on the tablet screen. The TI group played the same video game with digitally augmented tangible manipulatives. Finally, the CO group continued with their classroom curricular activities while we conducted the training, and only participated in the Pre and Post-Test evaluations. Our results highlighted that the use of tangible manipulatives led to a positive impact in children's mathematical abilities. Of most interest, we recorded children's actions during all the training activities, which allowed us to achieve a refined analysis of participants' operations while solving a number composition task. We explored the differences between the use of virtual and tangible manipulatives and the strategies employed. We observed that the TI group opted for a greater number of blocks in the number composition task, whereas the VI group favored solutions requiring fewer blocks. Interestingly, those children whose improvement in mathematics were greater were the ones employing a greater number of blocks. Our results suggest that tangible interactive material increases action possibilities and may also contribute to a deeper understanding of core mathematical concepts.
1. Introduction
Learning mathematics at an early age is fundamental to ensuring academic success in STEM (science, technology, engineering, and mathematics) disciplines and maximizing future integration into professional life (Wang and Goldschmidt, 2003). Research has been concerned with how to foster this core cognitive ability and enable a deep understanding of mathematical concepts. This research explores how virtual and tangible manipulatives can be used to strengthen math learning at 6 years of age.
In the current study, we used the activity of composing and decomposing sets of manipulatives representing numbers, an exercise that has been traditionally practiced with concrete material in order to foster an understanding of numerosity (Geary et al., 1992; Morin and Franks, 2009). We focused on a set of three properties (additive composition, commutativity, and associativity) and the mastery of the basic number combinations. Additive composition is the knowledge that larger sets are made up of smaller sets; the commutative property implies that changing the order of the operands doesn't affect the result; the associative property allows us to add (or multiply) numbers, no matter how the factors are grouped [(a + b) + c = a + (b + c)]; while mastering the basic number combinations leads to understanding how numbers can be composed. These properties are crucial for cardinality and number concept acquisition; and lead to the development of key strategies in arithmetical problem solving, such as addition and subtraction (Fuson, 1992; Verschaffel et al., 2007).
In mathematics curricula, teaching is frequently supported by tangible objects (three-dimensional models of geometrical shapes, etc.) that help young students to better understand abstract concepts, for instance in the acquisition of cardinality (Geary et al., 1992; Morin and Franks, 2009). The pioneer in this tradition was Maria Montessori who developed materials for geometry and mathematics specifically aimed at providing children with autonomy during the learning process (Montessori, 1917). Georges Cuisenaire, in turn, created a special set of tiles for arithmetics learning known as Cuisenaire rods (Cuisenaire, 1968). His proposal was based on the relationship between size and number and exploited the possibility of different spatial arrangements to exemplify mathematical principles like number composition. A new version of these materials can be found in Singapore Math's tiles (Wong, 2009; Wong and Lee, 2009); which is considered one of the more influential methods for teaching basic mathematics nowadays (Deng et al., 2013).
Following this vein, the acquisition of the number concept—one of the building blocks of mathematical learning—would benefit from direct interaction with objects (Dienes, 1961; Chao et al., 2000; Anstrom, 2006; McGuire et al., 2012). Interaction with objects may facilitate the passage from a concrete construal (I can see/manipulate three things in front of me) toward an abstract one (3 = * * *). This transformation begins with a process which is strongly based on perceptual, non verbal operations and turns into a symbolic one supported by an abstract association (Feigenson et al., 2004). The first stage has to do with the understanding that a given group of objects has a certain quantity of components (Gelman and Gallistel, 1978); the second with associating this quantity (of objects) to an exact number and its symbolic expression, and then understanding that any time the number is seen or heard it means that an exact quantity is being referred to (Kilpatrick et al., 2001).
The sensitivity to numerosity is improved gradually as the infant develops (Izard et al., 2009). Infants even just a few hours old are already sensitive to numerosity (e.g., Antell and Keating, 1983; Izard et al., 2009). Allegedly, this is possible due to two innate parallel number systems (see Feigenson et al., 2004; for a review see Piazza, 2010): an object file system (Feigenson and Carey, 2003) which accounts for the immediate identification of a discrete quantity of elements—subitizing (Kaufman and lord, 1949)—and is limited by the capability to attend to different objects at the same time; and an approximate number system (ANS) which accounts for a non-symbolic continuous numerical representation involving large numbers (Gallistel and Gelman, 1992; Dehaene, 2011).
Nevertheless, children are not able to explicitly identify simple quantities involving numbers from 1 to 4 until 4 years old, and up to 5 until 5 years old. To do so, different skills must be developed such as counting and conceptual subitizing; the combination of two “subitizable” numbers, for e.g., recognizing the presence of a 3 (***) and a 4 (****) and implicitly composing a set of 7 (*******) (Steffe and Cobb, 1988; Clements, 1999). Toddlers recognize that sets can be combined in different ways, but this understanding is based on nonverbal, perceptual processes (Sophian and McCorgray, 1994; Canobi et al., 2002). Commutativity is only acquired later between 4 and 5 years old, as also the understanding that commutativity of added groups leads to associativity (Gelman and Gallistel, 1978; Canobi et al., 2002). Thus, associativity reflects conceptual reasoning about how groups can be decomposed and recombined (Sarama and Clements, 2009). Further, as children learn basic number combinations, they can master a broad set of heuristics when faced with addition and subtraction problems.
To foster the conceptualization of unit items children may rely on hand actions such as pointing or grasping (Steffe and Cobb, 1988). For instance, in the case of subtraction, small children often represent the minuend with the fingers (or objects) and fold their fingers (or remove objects) for the value of the subtrahend (Groen and Resnick, 1977; Siegler, 1984). In fact, most children cannot solve complex numerical problems without the support of concrete objects until 5.5 years old (Levine et al., 1992). Later on, children acquire retrieval strategies, accessing results directly from long term memory (Rathmell, 1978; Steinberg, 1985; Kilpatrick et al., 2001). For this to be possible, children need to master basic number combinations (Baroody and Tiilikainen, 2003), but also understand associativity (Sarama and Clements, 2009). Children typically progress throughout three phases to achieve mastery on basic number combinations: (a) Counting strategies—using object counting (e.g., with blocks, fingers) or verbal counting (b) Reasoning strategies—using known information (facts and relationships) to deduce the answer of an unknown combination; (c) Mastery-efficient responses [i.e., fast and accurate (Kilpatrick et al., 2001)].
Children's addition and subtraction strategies also evolve during childhood. For instance, in order to solve 9 + 8, 4 to 5-year-old children would count from 1 to 9 for the first addend and then from 9 to 17 for the total sum (“counting all strategy”; Fuson, 1992; Verschaffel et al., 2007). Later on between 5 and 6 years old children would develop the more refined strategy of “counting on” in which the count starts from the cardinal of the larger addend (i.e., from 9 to 17; Carpenter and Moser, 1982; Siegler and Jenkins, 2014). More sophisticated part-whole strategies are developed with the achievement of associativity and the knowledge of how numbers from 1 to 10 can be composed (6–7 years old; Canobi et al., 2002). To solve 9 + 8 children would be able to retrieve that 9 + 1 is one of the forms to compose 10, and then solve the problem by the easier 10 + 7 (also retrieving that 8−1 equals 7; Carpenter and Moser, 1984; Fuson, 1992; Miura and Okamoto, 2003).
Interaction with objects may supports the development of different strategies by diminishing cognitive load and freeing up working memory, given that the perceived entities are cognitively available through the objects that represent them in space (Manches and O'Malley, 2016). Object manipulation gives rise to operations that can work as analogies of abstract operations. For example, joining 2 elements to a group of another 3 forms a new group of 5. This concrete activity would be a metaphor of act of addition: 2 + 3 = 5. These conceptual metaphors work as scaffolding that allows children to grasp abstract ideas such as commutativity or associativity (Manches and O'Malley, 2016).
With the appearance of digital technologies, researchers have been exploring how the manipulation of digital (Yerushalmy, 2005; Moyer-Packenham and Westenskow, 2013) and/or technology-enhanced concrete material (Tangible User Interfaces or TUIs; Manches, 2011) can benefit learning processes, finding promising results (see Sarama and Clements, 2016). Beyond the encouraging results obtained in several technology-based interventions, it has been claimed that the application of digital technology in the classroom posits the risk of replacing rich physical interactions with the environment by much more constrained interactions such as the use of the mouse–keyboard or multi-tactile interfaces (Bennett et al., 2008). In this vein, theories like constructivism, embodied cognition (Wilson, 2002; Anderson, 2003) and physically distributed learning (Martin and Schwartz, 2005) support the idea that physical interaction plays a key role in the learning process (Antle and Wise, 2013; for a review in this matter see Sarama and Clements, 2016).
In this study, we focus on the kinds of actions virtual and physical manipulatives offer and their impact on numerical learning. On one hand, interaction with virtual manipulatives is limited to dragging objects on the screen, but it still allows children to displace, join and isolate objects as traditional manipulatives allow (Moyer-Packenham and Westenskow, 2013). On the other hand, classic manipulatives offer interactive advantages (to grasp the object, for instance) that could have relevant consequences for educational activity (Martin and Schwartz, 2005; Manches and O'Malley, 2016). Several studies have been dedicated to this comparison, providing results which are slightly favorable to physical manipulatives (Martin and Schwartz, 2005; Schwartz et al., 2005; Klahr et al., 2008).
Technology-enhanced tangible manipulatives offer several advantages when compared with traditional or virtual manipulatives (Moyer-Packenham and Westenskow, 2013). They allow autonomous and active learning by using physical material and enable us to record a child's performance. In addition, they enable us to explore which kind of actions are relevant in specific learning activities. Importantly for the present research, our system permits analyzing and comparing the use of physical and virtual manipulatives to solve a task of additive composition. This comparison is of special theoretical interest given that it makes possible to explore the role of physicality/three-dimensionality in learning mathematics. In other words, the present research aims to investigate if it is indispensable that objects may be grasped, lifted, and explored or would it be enough to interact with virtual manipulatives? And specifically, we ask how the objects' affordances (i.e., the possibility to grasp physical objects or drag virtual ones) will shape and constrain children's composing strategies.
2. Materials and Methods
2.1. Participants
We recruited participants from one state school in Montevideo (Uruguay) with a medium-high sociocultural status consisting of 64 children (three classrooms) from first grade. All children had an informed consent form signed by their parents or legal guardians. A research protocol was approved by the Local Research Ethics Committee of the Faculty of Psychology, and is in accordance with the 2008 Helsinki Declaration. We employed a quasi-experimental design and each classroom became one of the following experimental groups: Control (CO), Virtual Interaction (VI), and Tangible Interaction (TI).
Four children (two from the VI group and another two from the TI group) failed to correctly answer 25% of the trials in our training game. Therefore, we performed subsequent analyses with the remaining 60 children (33 girls and 27 boys). Group descriptive information is shown in Table 1. We examined the effect of age and sex by conducting separated t-tests on assessment scores, but we did not find any effect.
Table 1
| TEMA-3 | |||||
|---|---|---|---|---|---|
| n |
Age
(years) |
Sex
(*girls) |
Pre | Post | |
| Passive Group (PA) | 20 | 6.6 (0.3) | 13 | 25.6 (5.7) | 28.8 (4.6) |
| Virtual Interaction Group (VI) | 20 | 6.8 (0.5) | 11 | 31.8 (9.6) | 35.1 (9.3) |
| Tangible Interaction Group (TI) | 20 | 6.8 (0.6) | 11 | 30.2 (10.3) | 34.4 (10.5) |
Mean and standard deviations at pre- and post-tests by groups.
2.2. Procedure
To evaluate the impact of both game modalities in the acquisition of mathematical abilities, we planned an intervention with three phases. A first and last phase of evaluations (Pre- and Post-Test), and a training of 13 days in between.
2.2.1. Pre-test
To evaluate children's mathematical abilities before and after training we used the third edition of the standardized Test of Early Mathematics Ability (TEMA-3, Bliss, 2006) for children between 3 and 8 years of age. The test was verbally administered and consisted of 72 items to assess: counting ability, number comparison facility, numeral literacy, mastery of number facts, basic calculation skills, and understanding of mathematical concepts. This test has high content validity (Baroody, 2003) and high reliability ranging from 0.82 to 0.97. Indeed, we found a high test–retest reliability measured by calculating TEMA-3 correlation between Pre-Test and Post-Test measures across children within each training group (TI: 0.94; VI: 0.94; CO: 0.78). We calculated scores by the sum of all the correct answers (taking into account ceiling and floor effects that are part of the test administration). Two trained evaluators conducted the evaluation and it took about 30 min per participant. This phase took one week, with 12 children evaluated per day.
2.2.2. Training/Playing
The three classes selected to participate in the study continued with their regular formal learning activities as part of the school curriculum. Apart from the fact that each class had a different teacher, teachers followed the same program and protocol, and were committed to giving the same math curricula information for the three classes. Both the TI and VI group played over 13 days (3 weeks). Sessions had a duration of 20 min each, from Monday to Friday. Two researchers were present in every session to help with any technical problems that may have arisen. In the first session, we introduced the game dynamics and made explicit the relation between size and value of each tangible and virtual block to facilitate effective use of manipulatives. The CO group continued with their regular curricular activities while the other two groups had 20 min per day of training. The CO group only participated in the Pre- and Post-Tests assessments.
2.2.3. Post-test
The same evaluators assessed the groups again with TEMA-3 and the scores were analyzed in the same manner as in the Pre-Test evaluation.
2.3. Training Game BrUNO
The video game BrUNO was developed to give the learning activity a more attractive and playful format. We took gamification theory into consideration in order to incorporate some gamification elements in BrUNO, such as: microworlds, a main-character, a tutorial, several types of prizes, and funny sounds. During the development of BrUNO, we carried out two informal user tests to inform the game design (Marichal et al., 2017a).
BrUNO is a video game designed to work on additive composition. Children played BrUNO by using five types of blocks whose length and color were associated with their value (see Figure 1). The block of 1 represents the number “1”; the block of 2 represents the number “2,” and so forth until 5. Each block has a different length which is proportional to the value that it represents).
Figure 1
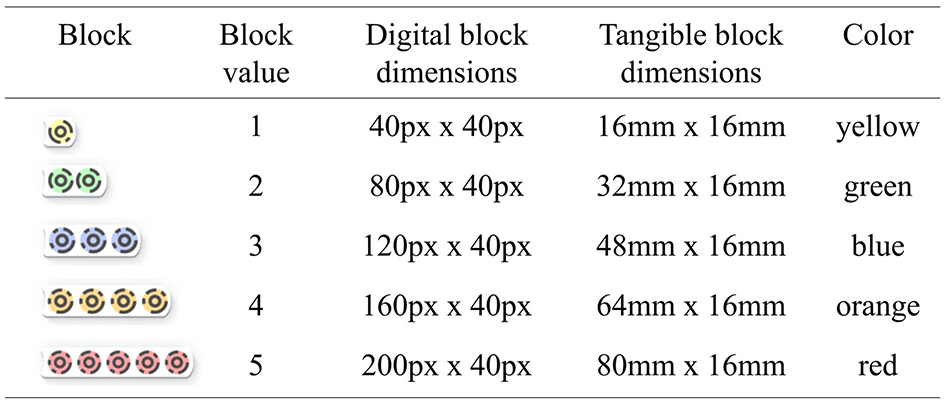
Block values, dimensions, and color.
To facilitate visual recognition of the location of the number required to build, a horizontal or vertical number line (depending on the scenario) is shown on the screen (see Figure 2). It is known that as numerosity develops, a hierarchical mental representation of how numbers should be ordered arises in the form of a number line. This line, which is based on a spatial analogy, represents the numbers from lowest to highest and locates them according to their cardinality. Thus, to reinforce this mental representation and to facilitate the additive composition task, we presented a number line to guide the players while they compose the required number. It helps to count the missing/spare units and deduce how the target number can be correctly composed. If the child has to build the number 4 and she has already put one block of 3, she can observe that the game character is 1 unit away from the prize and compose the target number by adding the block of 1. This way, the child can learn that 3 + 1 = 4. Additionally, the game helps to demonstrate that, for example, the distance between 1 and 3 is the same as between 21 and 23—a fact that is not so obvious for young children (Siegler and Booth, 2004).
Figure 2
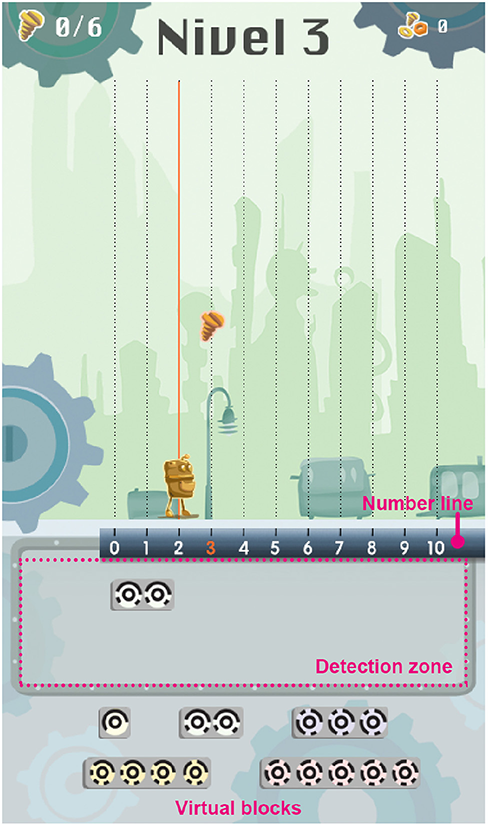
Fully virtual version of BrUNO. Prize placed in number three (as indicated by the orange color). The player has already introduced 1 block of value 2. To reach the prize, he must add one block of value 1. In this example, a horizontal number line is present to help children locating numbers and to help in adding and subtracting operations.
We developed two conditions for the evaluation of manipulatives: the Tangible Interaction Group (TI) and the Virtual Interaction Group (VI). In both cases, children played BrUNO, but the interaction with the blocks differed. In the first case, children manipulated technology-enhanced tangible blocks, and in the second case, virtual blocks.
2.3.1. Tangible Interaction Device
We designed a low cost tangible interaction device named CETA (Marichal et al., 2017a), with three main components (see Figure 3): a mirror that changes the webcam's viewing direction, allowing the system to detect objects over the table; a wooden holder that keeps the tablet vertically in portrait orientation; and a set of tangible blocks of different sizes similar to Cuisenaire Rods (representing numbers from 1 to 5; see Figure 1).
Figure 3
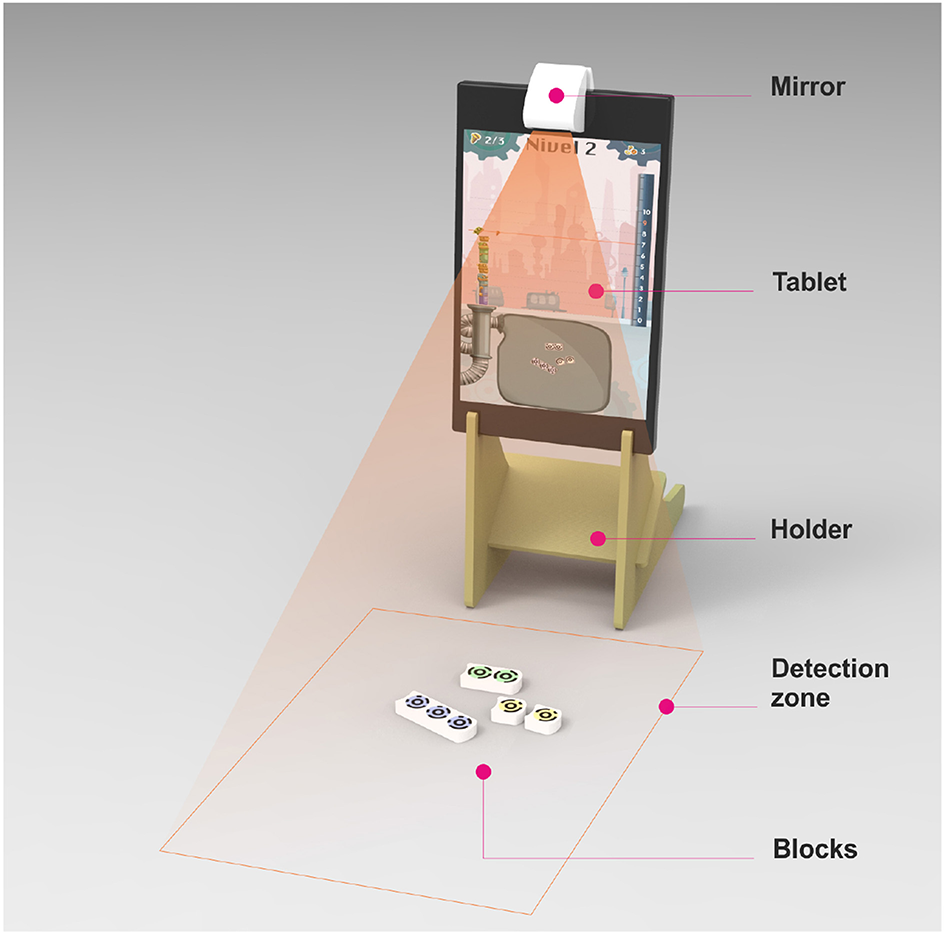
Tangible setting for BrUNO. Figure reproduced with author's permission (Marichal et al., 2017a).
We used the webcam of the tablet and a mirror to capture the image of the surface in front of the tablet holder in real-time. This image is constantly analyzed to detect blocks in the detection zone (for more details see Marichal et al., 2017b). The limits of the detection zone are determined by the webcam hardware and height of the holder. Blocks outside the detection zone are not visible to the computer vision system.
We designed a set of 25 blocks for 3D printing. The handling capabilities of the children at target age, the dimensions of the detection zone of the computer vision system, and the numeric quantities required by the different game challenges determined the dimensions of the blocks. All blocks contain magnets at their extremities, providing an affordance that increases the probability of joining blocks imitating the number line representation. Every block has a positive and a negative extremity. The concave and convex block's terminations constrain the way it can be joined. On the top face of each block we placed a set of colored markers (TopCodes; Horn, 2012) used by the computer vision system. The number of markers on each block corresponds to the block value.
2.3.2. Virtual Interaction Device
The virtual version allows to play BrUNO without CETA device. The blocks are virtual and the child has to place them in the detection zone to submit its answer to the system (Figure 2).
2.3.3. Data Collection
We recorded the children's actions to trace the quantity and the type of blocks employed in children's solutions over time. This allowed us to analyze the game strategies developed by each group and follow the performance of every single participant. After each response our system recorded the following data: (1) the number required to form, (2) the number actually formed, and (3) the blocks used to form the number.
We assumed that if the child wanted to respond with two blocks but put the first block in the detection zone while looking for the other, then we should develop a strategy to avoid considering this incomplete answer as a child's final solution. Thus, to avoid recording partial solutions we implemented what we call “action submit,” which consists of two steps. The first step is to wait for a stable solution. By stable solutions, we mean invariant responses by children for 1.5 s meaning that the blocks placed in the detection zone were not moved for 1.5 s and no blocks were added or removed. If this condition was completed, then we move to the second step in which the game character prepares itself for 1 s to execute the movement. If, during this time the child changed his or her answer, the time counter resets and “action submit” starts over again. If the answer did not change, the game character moves and the system records the blocks that composed the child's solution. To avoid duplicate responses (e.g., the child leaves the blocks in the detection zone and goes to the bathroom) we only registered the solutions that differed from the last recorded solution.
3. Results
3.1. Differences Between Groups
To test the effect of playing our training game over 13 sessions, we assessed the children's mathematics performance using TEMA-3 before and after training or without training as in the case of the CO group.
While we had a quasi-experimental design in which the groups were non-randomized at baseline, there were no significant differences between groups on Pre-Test, p = 0.84. To test for conditional differences, we used an ANCOVA with the Post-Test scores as the dependent variable, the Pre-Test as the covariate, and the Group as the independent variable. ANCOVA is advocated in this type of context because it controls for minor variations in the Pre-Test scores (Oakes and Feldman, 2001; Schneider et al., 2015). The assumptions of the ANCOVA were satisfied (as noted above, the covariate levels did not differ between conditions, and homogeneity of slopes held, as verified by running an ANOVA and customizing the model to include the interaction between the covariate and independent variable, p = 0.5). The ANCOVA identified a significant effect of Group, F(2, 54) = 20.9, p < 0.001, r = 0.44. We followed up this analysis with pairwise comparisons between Post-Test scores adjusted by the ANCOVA with the baseline Pre-Test scores. Both experimental groups obtained higher Post-Test scores than the control group (VIMean: 32.54, VISD = 0.77; TIMean: 33.27, TISD = 0.74 and COMean: 30.93, COSD = 0.86). However, only Post-Tests scores significantly differed when comparing TI vs CO (p = 0.044). We found no other significant effects between groups.
3.2. Virtual and Tangible Interaction Groups and the Minimum Blocks Coefficient (MBC)
We focused on the possible problem-solving strategies employed by the children when resolving the number composition task, and how the type of interaction could have affected their actions. To do so, we carried out exploratory analysis using participants' log files. It allowed us to observe which blocks were used to compose each number by all the participants, at every successful trial.
Firstly, we analyzed whether the number of blocks used to build the correct solution was different across groups. For example, to build the number 3, it is possible to use three blocks of 1 (“1-1-1”), one block of 1 and one block of 2 (“1-2”), or directly use one block of 3 (“3”). To evaluate how close the child was to using the minimum number of blocks that were necessary to build a number (one block in the case of numbers from 1 to 5, two blocks in case of numbers from 6 to 10, or three blocks if the number is greater than 10), we developed a score called the “Minimum Blocks Coefficient” (MBC). MBC is a metric that allows us to observe the different solutions in composing numbers while training additive composition. We aim to explore how children compose numbers using different types of manipulatives. For each correct solution it takes the minimum number of blocks necessary to build the number requested, and divides it by the number of blocks actually used. For example, in the case of number 3 the variant “1-1-1” becomes the score 1/3 = 0.33, because just one block is necessary to build the number (block of 3), and in reality, three blocks were used. The combination “1-2,” becomes 1/2 = 0.5, and “3,” becomes the score of 1.0. To calculate the MBC for one particular number and one particular group (TI or VI), we take all the correct solutions of the number formed by the participants of the group and calculate the mean value. Error rates were not analyzed because we observed that the tangible system required more time for the physical manipulation and during that time some partial solutions were recorded as errors before the child's final answer. For example, if the child wanted to respond with two blocks, but he or she put the first block in the detection zone while looking for the other and no changes occur in the detection zone for 2.5 s, the system registered the child's uncompleted solution as a response (error in this case). The algorithm is explained with more detail in the section “2.3.3.” For the aforementioned reasons we decided to only analyze the correct answers, so we were confident that we analyzed explicitly correct answers rather than random solutions.
3.2.1. Minimum Blocks Coefficient by Numbers (1–13)
We applied a two-way ANOVA considering the MBC as the dependent variable and Group and Numbers as the independent variables. Numbers is the variable that represents the number the child is asked to build. We divided all the Numbers that appear in the game (1–13) into three ranges based on the theoretical MBC that could be used for those numbers. Specifically, the theoretical MBC for numbers ranged from 1 to 5 is one block (i.e., they have the possibility to respond with a minimum of one block); for the numbers ranged 6–10 is two (i.e., they have the possibility to respond with a minimum of two blocks) and for the numbers ranged from 11 to 13 is three blocks (i.e., they have the possibility to respond with a minimum of three blocks).
The results showed that the type of manipulatives (TI or VI group) [F(1, 126) = 6.21, p = 0.014, r = 0.076] and the Number [F(2, 126) = 10.8, p < 0.001, r = 0.060] (see Figure 4) significantly influenced the MBC. We found no further interaction. The TI group used significantly more pieces (lower MBC) comparing with the VI group (TIMean = 0.65, TISD = 0.19, VIMean = 0.72, VISD = 0.15). These differences between TI and VI may be a result of the diverse composing strategies used when solving the number composition task.
Figure 4
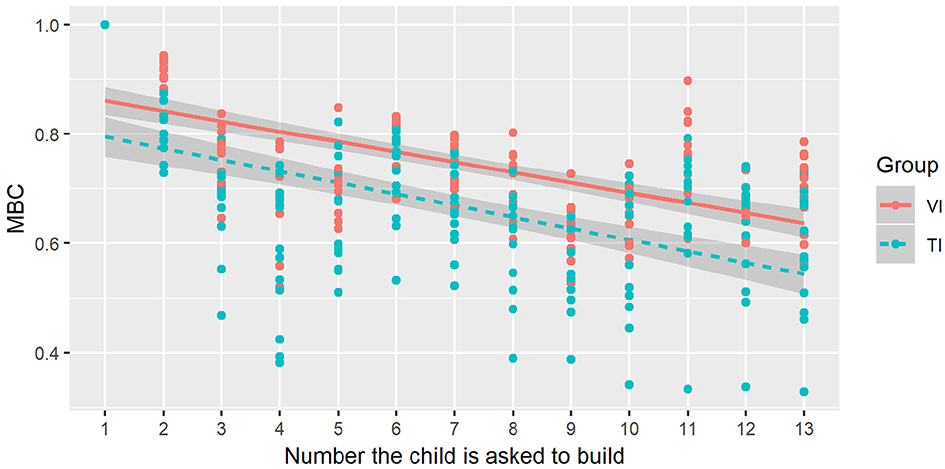
The Minimum Blocks Coefficient (MBC) for each number the child was asked to build. We applied a linear model to data points with a 95% confidence level for each Experimental Group: Virtual Interaction (VI) and Tangible Interaction (TI).
Considering the variable Number, the number of blocks used were significantly fewer for the numbers ranging from 1 to 5 compared to the numbers ranging from 6 to 10 (p = 0.0002) and also compared to the numbers ranging from 11 to 13 (p = 0.0003).
3.2.2. Minimum Blocks Coefficient Over Time
Participants reduced the number of blocks used during the 13 sessions that our intervention lasted (see Figure 5). We found a significant positive correlation (ps < 0.0001) between the MBC and sessions for VI (0.84) and for TI (0.87) groups. We also explored whether the number of blocks employed was significantly different at different moments of our intervention by analysing the MBC Mean for the first and last three sessions for both groups. Interestingly, in the first three sessions, the MBC was greater for the VI group, i.e., children used fewer blocks (p < 0.0001). In contrast, when analysing the last three sessions, the MBC did not differ between either group.
Figure 5
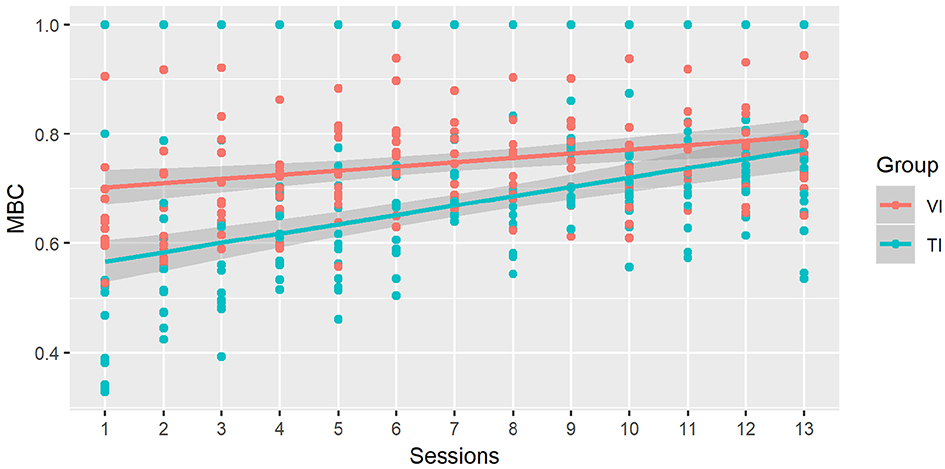
Minimum Blocks Coefficient (MBC) for each session and experimental group. We applied a linear model to data points with a 95% confidence level.
3.2.3. Minimum Blocks Coefficient and Mathematics Improvement
We explored the relationship between the number of blocks employed during the intervention (measured by MBC) and the amount of mathematical improvement (dScores: Post-Test scores − Pre-Test Scores) and found no correlation (p > 0.05). Neither TI nor VI groups showed a significant correlation between MBC and dScore when analyzed separately (p > 0.05).
Further, we decided to analyze the differences in the number of blocks employed comparing the performance of the Better and Worse Improvers. Thus, we divided all participants by the median of the dScore comprising two groups. The Better Improvers were the children with a dScore above the median, while the Worse Improvers were the ones whose dScore was below the median (see Figure 6). We found a significant negative correlation between MBC and dScores for the Better Improvers (cor = −0.50, p = 0.021), but not for the Worse Improvers. In conclusion, the children that had a greater improvement were the children using more blocks than the minimum blocks necessary to build the numbers required by the game. In contrast, we did not observe any change in the number of blocks used by the children who did not improve in mathematics.
Figure 6
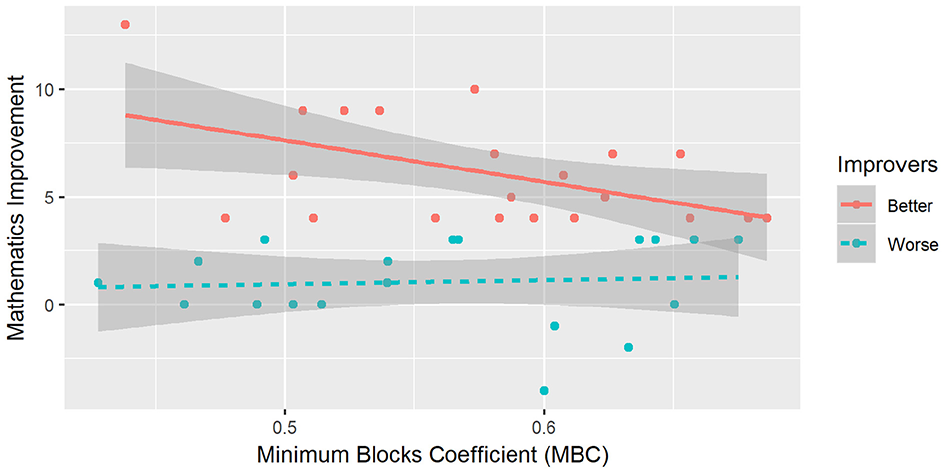
Minimum Blocks Coefficient by mathematics improvement for better and worse improvers. We applied a linear model to data points with a 95% confidence level.
3.2.4. Minimum Blocks Coefficient and Mathematics Performance
We were also interested in the relationship between the Minimum Blocks Coefficient (MBC) and mathematical performance (Pre-Test scores). Analysis indicated that Pre-Test scores were positively correlated with the MBC (cor = 0.41, p = 0.009; see Figure 7). Children who had greater Pre-Test scores at the beginning of this study had the tendency to use less number of blocks during the game.
Figure 7
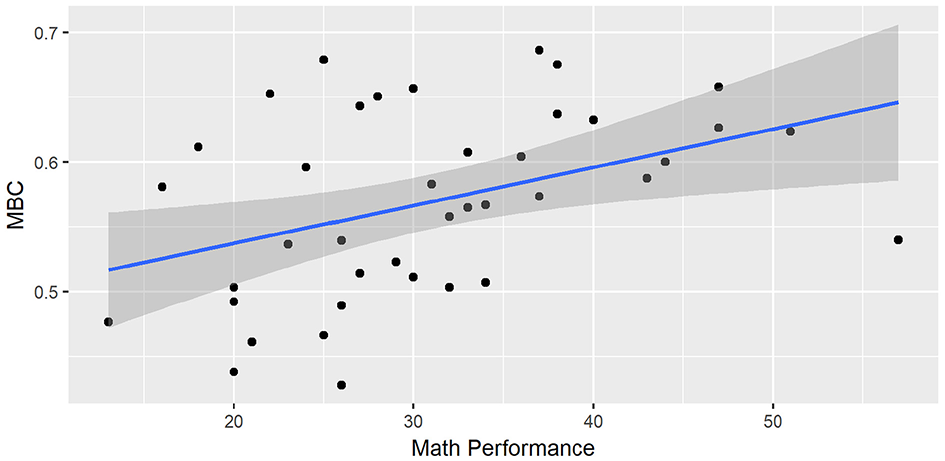
Minimum Blocks Coefficient (MBC) by math performance (pre-test scores). We applied a linear model to data points with a 95% confidence level.
4. Discussion
4.1. Impact of Manipulatives on Mathematical Learning
Our results indicate that the tangible manipulative group showed an advantage in mathematics scores after training compared to the control group. Our findings highlight the possibility of improving mathematical ability by practicing implicit number composition tasks assisted by tangible manipulatives.
We did not find significant differences either between the two types of manipulatives (virtual and tangible), or between virtual manipulatives and the control group when considering mathematical improvement tested by TEMA-3. It may be the case that virtual tangibles also have an impact in Post-Test scores, which was not observed due to the lack of statistical power of the present study.
4.2. Virtual and Tangible Manipulatives Led to Different Strategies in Number Composition
We analyzed children's behavior during our intervention to look for possible differential profiles in their evolution during training. Our tablet-based intervention allowed us to record the children's responses every time they submitted a block to compose a number. Our results enabled us to reflect on the role of specific actions performed by children affecting the learning process, and how learning could be influenced by the interactive properties of the blocks rendered as a representational assistance (Manches and O'Malley, 2016).
It was observed that the TI and VI groups significantly differed in the numbers of blocks used to compose a number. VI employed significantly fewer blocks compared with TI, showing that the different type of manipulatives could have led to different problem solving strategies. TI children opted to compose numbers using more varied combination of blocks, i.e., they used more number composition strategies. This suggests that the affordances of physical objects do trigger more diverse solutions (Manches and O'Malley, 2016), which have been advocated to prompt better learning experiences in numerosity knowledge (Alibali and Goldinmeadow, 1993; Chi et al., 1994; Siegler and Shipley, 1995) and specifically foster mastery of basic number combinations (Baroody and Tiilikainen, 2003; Sarama and Clements, 2009).
Our results are in accordance with Manches et al. (2010) results that found that children employed a significantly greater number of solutions when they used plastic blocks as manipulatives, comparing with a condition in which children were aided with a visual representation drawn on paper. For instance, it is easier to detect the “reversion” strategy (5-2, 2-5) when you can hold and displace objects representing these quantities (2 and 5). This finding supports the view that objects affordances implicitly carry information that could be relevant to reflect on abstract concepts, through conceptual metaphors. In our study, we compared tangible blocks (TI group) against virtual blocks (VI group). The use of virtual blocks allowed the children to drag, transform, and move blocks which allows a richer interaction compared to blocks drawn on paper. However, when compared to virtual blocks, tangible blocks enabled a more diverse combination of blocks to compose numbers as also observed elsewhere (Manches et al., 2010).
4.2.1. Strategies Evolution in Number Composition
When we analyzed strategies during training sessions we found that at the beginning of the training both groups employed more blocks to compose numbers with a tendency to diminish in the last sessions. This tendency to diminish may represent an approach to optimal performance (when the number is composed by the minimal quantity of possible blocks), probably reflecting learning toward increasing efficient and fastest strategies in number composition (Baroody and Dowker, 2003).
This is in line with the fact that composing and decomposing strategies becomes semiautomatic or automatic with effective and faster answers to basic number combinations. Children may automatize some combinations of a number through practice, resulting in an association with their counting knowledge. This association encourages efficiency, preventing children from repeatedly practicing all the possible combinations (Baroody, 2006). In our study, children at the beginning started by practicing various combinations of numbers. For instance, in the first sessions to form the number 5 children might use several combinations as 1+1+1+1+1, 2+2+1, 2+1+1+1, reflected by low MBC scores. Nevertheless, at the end of the training sessions children were able to answer more effectively, reflected by high MBC scores. For instance, to form the number 5 they answered with the block 5 or by adding just two blocks as 2+3 or 4+1, which is quicker and more direct.
Analyses showed that the mean of blocks used in the first three sessions was significantly smaller for the VI group, whereas both groups employed the same number of blocks in the last three sessions. This suggests that besides the tendency of both groups to optimize responses, they presented a different profile in their evolution during training. Children who used tangible manipulatives had the tendency to use more blocks and showed a more pronounced decrease in the number of blocks used during the intervention compared to children who used virtual manipulatives. This finding may be connected to the observed improvement in maths scores (measured by TEMA-3) for the TI group. The number of combinations used in the TI may have contributed to achieving mastery in mathematical knowledge, since mastery in basic number composition is enriched by experiencing more varied possibilities (Markman, 1978; Bowerman, 1982; Karmiloff-Smith, 1992). In this study, physical object affordances offered the user a richer set of action possibilities, and most probably also a more comprehensive understanding of the phenomenon explored.
4.2.2. Strategies in Additive Composition Task and Mathematical Improvement
We did not find a correlation between the number of blocks employed by children and mathematical improvement in general (all children analyzed together). Nevertheless, when children were divided according to their improvement in mathematics (Post-Test − Pre-Test) after the intervention, it was observed that the greater improvement group showed a positive correlation between number of blocks employed and gain in mathematical knowledge, which was not found for the Worse Improvers.
Therefore, children who showed a greater improvement tended to use more blocks. This outcome may suggest that an optimal performance in number composition (understood as fewer pieces used to form a number equals better performance) would not necessarily lead to a better learning experience. Another hypothesis would be that children who do not already have this mastery in number combinations, i.e., efficient, fast and accurate responses, would benefit more from employing manipulatives to solve additive composition and this might be the case for the “Better Improvers.” Children who improved at maths during training were the ones using more varied block combinations. This is connected to the fact that the use of a greater variety of strategies can result in a better learning outcome (Markman, 1978; Bowerman, 1982; Karmiloff-Smith, 1992).
4.2.3. Strategies in Additive Composition Task and Mathematics
Interestingly, a negative correlation was found between mathematical scores at the Pre-Test (how good the children were at the beginning of the study) and the number of blocks employed. That is, being better at mathematics at Pre-Test implied the use of fewer manipulative blocks, probably due to a better knowledge of retrieval strategies while composing numbers (Rathmell, 1978; Steinberg, 1985; Kilpatrick et al., 2001). Children who were good at maths at the beginning of the training will not necessarily use more strategies because they already have a deeper knowledge in number concept and composition. That is to say, children who have already learned basic combinations of numbers have the ability to use such knowledge to answer quickly and efficiently in a familiar and unfamiliar learning context (Baroody, 2006).
It may seem contradictory that children who obtained the best scores at TEMA-3 (better at mathematics at baseline) used fewer blocks whereas the Better Improvers tended to employ more. However, according to Sarama and Clements (2009), despite seeming paradoxical, those who are better at solving problems with objects, fingers or counting are less likely to persist in these strategies in the future—as already reported by Siegler (1993)—but this is because they trust their answers and therefore move toward more precise strategies based on the retrieval of number combinations, leaving behind what once served as a scaffolding.
These results also suggest that children who will benefit more from the use of manipulative blocks are the children who do not have already mastery in number combinations. The use of enhanced manipulatives may be more suitable for younger children who need to practice and automatize simple number combinations.
4.3. Limitations
The present study has several limitations that should be considered when interpreting the results. It may lack statistical power since the number of participants in each group is small and for such reason, a larger confirmatory study is needed to strengthen the conclusions of the present study. The quasi-experimental design of the current study has more ecological validity (children were kept in their school groups), but it is susceptible to threats on internal validity compared to controlled experimental designs and for that reason we consider our results as exploratory and conclusions are drawn carefully.
4.4. Conclusions
Current findings indicate that the use of tangible manipulatives had a positive impact on mathematical learning. We were able to observe interesting relationships between the level of mathematics and the kind of manipulative strategies chosen by the children when solving number composition tasks. Our results suggest that tangible manipulatives increase action possibilities and may also contribute to a deeper understanding of core mathematical concepts. Playing the game BrUNO with tangible manipulatives promotes meaningful practice of more varied number combinations by encouraging children to focus on patterns and relationships in basic number combinations. In addition, we were able to observe how their responses pattern changed throughout the training leading to the use of less but efficient strategies in the last sessions which may reflect that they achieved mastery in doing such combinations. Thus, training in this basic combinations led to an improvement in mathematics and hopefully may lead children to effectively apply this knowledge in new and unfamiliar number combinations.
From an interaction design perspective (for more details regarding this research and perspective, see Marichal et al., 2017a), the most relevant observation is how the objects' affordances (i.e., the possibility to grasp physical objects or drag virtual ones) somehow shape and constrain users' strategies. In our study, tangible blocks meant a richer interaction, providing the opportunity to explore more number composition possibilities. This possibly led to an improvement in mathematical performance. Thus, depending on the learning task objective (context), we might take advantage of this phenomena, by choosing either tangible, virtual or mixed learning environments. The current study invites researchers to delve deeper in the exploration of the potential for designing interactive activities aimed at fostering learning of specific target content.
Statements
Ethics statement
All children that participated in this research had the informed consent form signed by their parents or legal guardians. The intervention current protocol was approved by the Local Research Ethical Committee of the Faculty of Psychology, and is in accordance with the 2008 Declaration of Helsinki.
Author contributions
AP: substantial contributions to the conception or design of the work, analysis and interpretation of data for the work, drafting and revising it critically for important intellectual content. FG: drafting the work or revising it critically for important intellectual content, interpretation of data for the work. EB: substantial contributions to the conception and design of the work and data acquisition. BF: drafting the work or revising it critically for important intellectual content, analysis, and interpretation of data for the work. GS: substantial contributions to the design of the work. SM: substantial contributions to the design of the work, drafting and revising it critically for important intellectual content.
Funding
This work was supported by Agencia Nacional de Investigación e Innovación (ANII); Fundación Ceibal, Espacio Interdisciplinario, and by Centro Interdisciplinario en Cognición para la Enseñanza y el Aprendizaje (CICEA), Universidad de la República, Uruguay; and by Fundação para a Ciência e a Tecnologia (FCT), I.P., through funding of project mIDR (AAC 02/SAICT/- 2017, project 30347, cofunded by COMPETE/FEDER/FNR), and of the LASIGE Research Unit (UID/CEC/00408/2013), Portugal.
Acknowledgments
We would like to show our gratitude to the children and educators that participated in this work from Escuela Panamá, Montevideo, Uruguay. We also want to thank our colleagues Rita Soria, María Pascale, Mariana Rodriguez, Leonardo Secco, Matías Correa, Leandro Fernández, Dilva Devita, Mariana Borges, Gonzalo Tejera, Alvaro Cabana, Fulvio Capurso, and Rodrigo López who provided insight and expertise that greatly assisted the research and design of CETA; and Catarina Tome-Pires and reviewers for suggestions and comments that greatly improved the manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1
Alibali M. W. Goldin-meadow S. (1993). Gesture-speech mismatch and mechanisms of learning: what the hands reveal about a child's state of mind. Cogn. Psychol.25, 468–523.
2
Anderson S. E. (2003). The school district role in educational change: a review of the literature. Int. Centre Educ. Change. Available online at: http://fcis.oise.utoronto.ca/~icec/workpaper2.pdf
3
Anstrom T. (2006). Supporting students in mathematics through the use of manipulatives. Am. Inst. Res.1–15. Available online at: https://studylib.net/doc/18105288/supporting-students-in-mathematics-through-the-use-of-man
4
Antell S. E. Keating D. P. (1983). Perception of numerical invariance in neonates. Child Dev.54, 695–701. 10.2307/1130057
5
Antle A. N. Wise A. F. (2013). Getting down to details: using theories of cognition and learning to inform tangible user interface design. Interact. Comput.25, 1–20. 10.1093/iwc/iws007
6
Baroody A. J. (2003). The development of adaptive expertise and flexibility: the integration of conceptual and procedural knowledge, in The Development of Arithmetic Concepts and Skills: Constructing Adaptive Expertise, Studies in Mathematical Thinking and Learning, eds BaroodyA. J.DowkerA. (Mahwah, NJ: Lawrence Erlbaum Associates Publishers), 1–33.
7
Baroody A. J. (2006). Why children have difficulties mastering the basic number combinations and how to help them. Teach. Child. Math.13, 22–31. Available online at: https://www.semanticscholar.org/paper/Why-Children-Have-Difficulties-Mastering-the-Basic-Baroody/753415c8d3fe2d6d3089bb0da0d9637dff02af32
8
Baroody A. J. Dowker A. (eds.). (2003). The Development of Arithmetic Concepts and Skills: Constructing Adaptive Expertise.Mahwah, NJ: Lawrence Erlbaum Associates Publishers.
9
Baroody A. J. Tiilikainen S. H. (2003). Two perspectives on addition development, in The Development of Arithmetic Concepts and Skills: Constructing Adaptive Expertise, Studies in Mathematical Thinking and Learning, eds BaroodyA. J.DowkerA. (Mahwah, NJ: Lawrence Erlbaum Associates Publishers), 75–125.
10
Bennett S. Maton K. Kervin L. (2008). The “digital natives” debate: a critical review of the evidence. Br. J. Educ. Technol.39, 775–786. 10.1111/j.1467-8535.2007.00793.x
11
Bliss S. (2006). Test of early mathematics ability-third edition. J. Psychoeduc. Assess.24, 85–98. 10.1177/0734282905282839
12
Bowerman M. (1982). Evaluating competing linguistic models with language acquisition data: implications of developmental errors with causative verbs. Quaderni Semant.3, 5–66.
13
Canobi K. H. Reeve R. A. Pattison P. E. (2002). Young children's understanding of addition concepts. Educ. Psychol.22, 513–532. 10.1080/0144341022000023608
14
Carpenter T. P. Moser J. M. (1982). The development of addition and subtraction problem-solving skills, in Addition and Subtraction: A Cognitive Perspective, eds MoserJ. M.RombergT. A.CarpenterT. P. (Hillsdale, NJ: Lawrence Erlbaurn Associates), 9–24.
15
Carpenter T. P. Moser J. M. (1984). The acquisition of addition and subtraction concepts in grades one through three. J. Res. Math. Educ.15, 179–202.
16
Chao S.-J. Stigler J. W. Woodward J. A. (2000). The effects of physical materials on kindergartners' learning of number concepts. Cogn. Instruct.18, 285–316. 10.1207/S1532690XCI1803_1
17
Chi M. T. De Leeuw N. Chiu M.-H. LaVancher C. (1994). Eliciting self-explanations improves understanding. Cogn. Sci.18, 439–477. 10.1207/s15516709cog1803_3
18
Clements D. H. (1999). Teaching length measurement: research challenges. School Sci. Math.99, 5–11. 10.1111/j.1949-8594.1999.tb17440.x
19
Cuisenaire G. (1968). Les Nombres en Couleurs.Bruxelles: Calozet.
20
Dehaene S. (2011). The Number Sense: How the Mind Creates Mathematics, Revised and Updated EditionNew York, NY: Oxford University Press.
21
Deng Z. Gopinathan S. Lee C. (2013). Globalization and the Singapore Curriculum. From policy.New York, NY: Springer.
22
Dienes Z. P. (1961). Building Up Mathematics.London: Hutchinson Educational.
23
Feigenson L. Carey S. (2003). Tracking individuals via object-files: evidence from infants' manual search. Dev. Sci.6, 568–584. 10.1111/1467-7687.00313
24
Feigenson L. Dehaene S. Spelke E. (2004). Core systems of number. Trends Cogn. Sci.8, 307–314. 10.1016/j.tics.2004.05.002
25
Fuson K. C. (1992). Research on whole number addition and subtraction, in Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics, ed GrouwsD. A. (New York, NY: Macmillan Publishing Co, Inc.), 243–275.
26
Gallistel C. R. Gelman R. (1992). Preverbal and verbal counting and computation. Cognition44, 43–74. 10.1016/0010-0277(92)90050-R
27
Geary D. C. Bow-Thomas C. C. Yao Y. (1992). Counting knowledge and skill in cognitive addition: a comparison of normal and mathematically disabled children. J. Exp. Child Psychol.54, 372–391. 10.1016/0022-0965(92)90026-3
28
Gelman R. Gallistel C. R. (1978). The Child's Understanding of Number.Cambridge: Harvard University Presss.
29
Groen G. Resnick L. B. (1977). Can preschool children invent addition algorithms?J. Educ. Psychol.69:645. 10.1037//0022-0663.69.6.645
30
Horn M. (2012). Topcode: Tangible Object Placement Codes. Available online at: http://users.eecs.northwestern.edu/~mhorn/topcodes/
31
Izard V. Sann C. Spelke E. S. Streri A. (2009). Newborn infants perceive abstract numbers. Proc. Natl. Acad. Sci. U.S.A.106, 10382–10385. 10.1073/pnas.0812142106
32
Karmiloff-Smith A. (1992). Beyond Modularity: A Developmental Perspective on Cognitive Science.London: MIT Press; Taylor and Francis.
33
KAUFMAN E. L. LORD M. W. (1949). The discrimination of visual number. Am. J. Psychol.62, 498–525. 10.2307/1418556
34
Kilpatrick J. Swafford J. Findell B. (eds.). (2001). Adding It Up: Helping Children Learn Mathematics.Washington, DC: National Academies Press.
35
Klahr D. Triona L. Strand-Cary M. Siler S. (2008). Virtual vs. physical materials in early science instruction: transitioning to an autonomous tutor for experimental design, in Beyond Knowledge: The Legacy of Competence, eds ZumbachJ.SchwartzN.SeufertT.KesterL. (Dordrecht: Springer), 163–172.
36
Levine S. C. Jordan N. C. Huttenlocher J. (1992). Development of calculation abilities in young children. J. Exp. Child Psychol.53, 72–103. 10.1016/S0022-0965(05)80005-0
37
Manches A. (2011). Digital manipulatives: tools to transform early learning experiences. Int. J. Technol. Enhanc. Learn.3, 608–626. 10.1504/IJTEL.2011.045451
38
Manches A. O'Malley C. (2016). The effects of physical manipulatives on children's numerical strategies. Cogn. Instruct.34, 27–50. 10.1080/07370008.2015.1124882
39
Manches A. O'Malley C. Benford S. (2010). The role of physical representations in solving number problems: a comparison of young children's use of physical and virtual materials. Comput. Educ.54, 622–640. 10.1016/j.compedu.2009.09.023
40
Marichal S. Rosales A. Perilli F. G. Pires A. C. Bakala E. Sansone G. et al . (2017a). Ceta: designing mixed-reality tangible interaction to enhance mathematical learning, in Proceedings of the 19th International Conference on Human-Computer Interaction with Mobile Devices and Services, MobileHCI '17 (New York, NY: ACM), 29:1–29:13.
41
Marichal S. Rosales A. Sansone G. Pires A. C. Bakala E. Perilli F. G. et al . (2017b). Ceta: open, affordable and portable mixed-reality environment for low-cost tablets, in Proceedings of the 19th International Conference on Human-Computer Interaction with Mobile Devices and Services, MobileHCI '17 (New York, NY: ACM), 47:1–47:7.
42
Markman E. M. (1978). Empirical versus logical solutions to part-whole comparison problems concerning classes and collections. Child Dev.49, 168–177. 10.2307/1128605
43
Martin T. Schwartz D. L. (2005). Physically distributed learning: adapting and reinterpreting physical environments in the development of fraction concepts. Cogn. Sci.29, 587–625. 10.1207/s15516709cog0000_15
44
McGuire P. Kinzie M. B. Berch D. B. (2012). Developing number sense in pre-k with five-frames. Early Childh. Educ. J.40, 213–222. 10.1007/s10643-011-0479-4
45
Miura I. T. Okamoto Y. (2003). Language supports for mathematics understanding and performance, in The Development of Arithmetic Concepts and Skills: Constructing Adaptive Expertise, Studies in Mathematical Thinking and Learning, eds BaroodyA. J.DowkerA. (Mahwah, NJ: Lawrence Erlbaum Associates Publishers), 229–242.
46
Montessori M. (1917). The Advanced Montessori Method: Scientific Pedagogy as Applied to the Education of Children From Seven to Eleven Years.London: W. Heinemann.
47
Morin J. E. Franks D. J. (2009). Why do some children have difficulty learning mathematics? Looking at language for answers. Prevent. School Fail.54, 111–118. 10.1080/10459880903217861
48
Moyer-Packenham P. S. Westenskow A. (2013). Effects of virtual manipulatives on student achievement and mathematics learning. IJVPLE4, 35–50. 10.4018/jvple.2013070103
49
Oakes J. M. Feldman H. A. (2001). Statistical power for nonequivalent pretest-posttest designs: the impact of change-score versus ancova models. Eval. Rev.25, 3–28. 10.1177/0193841X0102500101
50
Piazza M. (2010). Neurocognitive start-up tools for symbolic number representations. Trends Cogn. Sci.14, 542–551. 10.1016/j.tics.2010.09.008
51
Rathmell E. C. (1978). Using thinking strategies to teach the basic facts, in Developing Computational Skills, ed SuydamM. N. (Reston: NCTM-Yearbook), 13–38.
52
Sarama J. Clements D. H. (2009). Early Childhood Mathematics Education Research: Learning Trajectories for Young Children.New York, NY: Routledge.
53
Sarama J. Clements D. H. (2016). Physical and virtual manipulatives: what is “concrete”?” in International Perspectives on Teaching and Learning Mathematics With Virtual Manipulatives, ed Moyer-PackenhamP.S. (Cham: Springer International), 71–93.
54
Schneider B. A. Avivi-Reich M. Mozuraitis M. (2015). A cautionary note on the use of the Analysis of Covariance (ANCOVA) in classification designs with and without within-subject factors. Front. Psychol.6:474. 10.3389/fpsyg.2015.00474
55
Schwartz D. L. Martin T. Pfaffman J. (2005). How mathematics propels the development of physical knowledge. J. Cogn. Dev.6, 65–88. 10.1207/s15327647jcd0601_5
56
Siegler R. Jenkins E. A. (2014). How Children Discover New Strategies.New York, NY: Psychology Press.
57
Siegler R. S. (1984). Strategy choices in addition and subtraction: how do children know what to do?” in Origins of Cognitive Skills, ed SophianC. (Hillsdale, NJ: Erlbaum), 229–293.
58
Siegler R. S. (1993). Adaptive and nonadaptive characteristics of low-income children's mathematical strategy use, in The Challenge in Mathematics and Science Education: Psychology's Response, eds PennerL. A.BatscheG. M.KnoffH. M.NelsonD. L. (Washington, DC: American Psychological Association), 341–366.
59
Siegler R. S. Booth J. L. (2004). Development of numerical estimation in young children. Child Dev.75, 428–444. 10.1111/j.1467-8624.2004.00684.x
60
Siegler R. S. Shipley C. (1995). Variation, selection, and cognitive change, in Developing Cognitive Competence: New Approaches to Process Modeling, eds SimonT. J.HalfordG. S. (Hillsdale, NJ: Lawrence Erlbaum Associates, Inc.), 31–76.
61
Sophian C. McCorgray P. (1994). Part – whole knowledge and early arithmetic problem solving. Cogn. Instruct.12, 3–33. 10.1207/s1532690xci1201_1
62
Steffe L. P. Cobb P. (1988). Construction of Arithmetical Meanings and Strategies.New York, NY: Springer-Verlag.
63
Steinberg R. M. (1985). Instruction on derived facts strategies in addition and subtraction. J. Res. Math. Educ.16, 337–355. 10.2307/749356
64
Verschaffel L. Greer B. De Corte E. (2007). Whole number concepts and operations, in Second Handbook of Research on Mathematics Teaching and Learning, ed LesterF. (Charlotte, NC: Information Age Publishing Inc.), 557–628.
65
Wang J. Goldschmidt P. (2003). Importance of middle school mathematics on high school students' mathematics achievement. J. Educ. Res.97, 3–17. 10.1080/00220670309596624
66
Wilson M. (2002). Six views of embodied cognition. Psychon. Bull. Rev.9, 625–636. 10.3758/BF03196322
67
Wong K. Y. (2009). Mathematics Education: The Singapore Journey, Vol. 2.Singapore: World Scientific Publishing Co.
68
Wong K. Y. Lee N. (2009). Singapore education and mathematics curriculum, in Mathematics Education: The Singapore Journey, eds WongK. Y.LeeP. Y.KaurB.FoongP. Y.NgS. F. (World Scientific), 13–47.
69
Yerushalmy M. (2005). Functions of interactive visual representations in interactive mathematical textbooks. Int. J. Comput. Math. Learn.10, 217–249. 10.1007/s10758-005-0538-2
Summary
Keywords
digital manipulatives, tangible manipulatives, technology-enhanced learning activities, mathematics, additive composition
Citation
Pires AC, González Perilli F, Bakała E, Fleisher B, Sansone G and Marichal S (2019) Building Blocks of Mathematical Learning: Virtual and Tangible Manipulatives Lead to Different Strategies in Number Composition. Front. Educ. 4:81. doi: 10.3389/feduc.2019.00081
Received
16 August 2018
Accepted
23 July 2019
Published
06 September 2019
Volume
4 - 2019
Edited by
Firat Soylu, University of Alabama, United States
Reviewed by
Kasia Muldner, Carleton University, Canada; Jennifer M. Zosh, Pennsylvania State University, United States
Updates
Copyright
© 2019 Pires, González Perilli, Bakała, Fleisher, Sansone and Marichal.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ana Cristina Pires acdpires@di.fc.ul.pt
This article was submitted to Educational Psychology, a section of the journal Frontiers in Education
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.