Game-Based Training to Promote Arithmetic Fluency

The research team designed and evaluated a mobile game to promote rapid retrieval of arithmetic facts among a group of children aged 7–8 years (n = 97). The design of the game was based on principles drawn from research literature in mathematical cognition, game-based learning, and game design. The game trains basic number knowledge within a motivating context. It tested an implication of theory of automatization of arithmetic facts that training of recognition of multiples of single-digit numbers should lead to greater fluency in solving multiplication and division problems. A quasi-experimental design was employed to test whether the game improves retrieval of arithmetic facts. Children played the game in their classrooms for 20 min a day for 2 weeks. Comparisons between pre- and post-tests showed that the game playing group outperformed controls with a medium to large effect size (>0.6). These results suggest an improvement in arithmetic fluency equivalent to around 7 months' progress and provide rare empirical evidence supporting transfer of game-based training to a pencil-and-paper test. The findings are consistent with a connectionist theory of arithmetic skill, by showing that improved recognition of multiples contributes to multiplication and division skill. The theoretical and practical implications of these findings are discussed.

Introduction

This article describes the principles underlying the design of a mobile game designed to promote arithmetic fact retrieval among primary school children, and an evaluation of the game in a classroom setting. The game was developed as part of the Research Adaptivity to Individual Differences in Number Games (RAIDING) project. This work draws on research in mathematical cognition, in game-based learning, and in game design, to create an engaging game that develops learners' performance in solving simple arithmetic problems. In this section, we review the literature that contributed to the rationale for the game design and its evaluation. We focus on those areas most strongly related to mathematical learning and so discuss two main bodies of work; research relating to arithmetic fluency and fact-retrieval, and research relating to game-based learning. Readers with an interest in the game design aspects of the project should see Mees et al. (2017), where a full account is provided.

Arithmetic Fluency

A fluent number sense involves the rapid retrieval and manipulation of stored information relating to number. For example, when presented with the number “6,” people who have had the opportunity to learn about such relationships will automatically think of 5, 7 (due to proximity on the number line) and 12 (double 6). When presented with “5+2,” most people will automatically think of “7.” Many of these fact-retrieval processes are unconscious, and outside the control of learners, but appear to be important components of children's learning of mathematics (Jordan et al., 2003). Moving beyond these examples, fluency of number sense means that children can, for example, solve 19 + 7 by changing the problem into 20 + 6 (drawing on the learned and retrieved fact that 19 + 1 = 20), or solve another problem 8 + 5 – 5 by drawing on the learned and retrieved fact that adding and then subtracting the same number means we end up where we started. The automatic and unconscious retrieval of mathematical facts allows children greater cognitive capacity for other aspects of mathematical thinking and problem solving. The additional cognitive capacity that is made available by the automatic recall of number knowledge can help explain variance in children's multidigit problem performance (Joy Cumming and Elkins, 1999). Building on this, Pegg et al. (2005) have shown that an intervention to improve the automatic recall of basic number facts can lead to improvements in broader measures of mathematical attainment.

Adults typically solve single-digit multiplication problems by retrieval. The proportion of such problems that children solve by retrieval gradually increases with age. Lemaire and Siegler (1995) showed that retrieval becomes the most common solution strategy for single-digit multiplications by the time children reach 8 years of age. Similarly, Cooney et al. (1988) showed that the proportion of problems solved by retrieval increases with age, and that retrieval is the most used strategy from 10 years old. The differences in age between these two studies could potentially be explained by location (one was carried out in France, and the other in the US) and associated cultural/educational differences, or by the relatively small sample sizes.

The research reported in this article is partly motivated by concerns that significant numbers of children are being “left-behind” at the point where their number knowledge can no longer keep up with the demands of the National Curriculum in England. The UK government has recently introduced a pilot of times-tables screening in Year 4 of primary school (8 to 9-year olds). They say that, “As well as being critical for everyday life, knowledge of multiplication tables helps children to solve problems quickly and flexibly, and allows them to tackle more complex mathematics later on in school” (DfE, 2018). However, despite awareness that arithmetic fluency, including knowledge and retrieval of multiplication facts, may be useful for children's mathematics thinking and learning, it is not clear that schools have good knowledge of methods for supporting children to learn such facts. Previous work has shown that such learning is often “out-sourced” to parents, who themselves feel unable to effectively support their children's mathematics learning (Jay et al., 2018).

Foundations for Multiplication

Verguts and Fias (2005) propose a connectionist model of automaticity of multiplication fact retrieval. This model builds on evidence suggesting that facts about numbers are stored in an associative network. It also provides explanation for three effects consistently observed in children's patterns of multiplication solutions:

• Problem Size effect: Problems are more difficult to solve when they involve larger numbers.

• “5” effect: Problems are easier to solve when one of the multiplicands is the number 5.

• Tie effect: Problems are easier to solve when they involve a number being multiplied by itself, e.g., 3 × 3, or 8 × 8.

Verguts and Fias use the example of someone perceiving the problem “7 × 4.” As well as triggering representation of “28,” studies show that this problem will also activate representations of the problem's “neighbor” including “7 × 3,” “7 × 5,” “6 × 4,” and “8 × 4.” Galfano et al. (2003) provide direct evidence for an associative network of number relationships, by showing that perception of two numbers (e.g., 4 and 7 as in the above example) activates not only the correct answer to the multiplication of those two numbers (28), but also the correct answer to near neighbors (21, 35, 24, 32). One implication of this connectionist theory of multiplication for training interventions is that training recall of multiples of single-digit numbers may be an effective way to support children's ability to solve multiplication problems quickly and accurately. In other words, whereas classroom practice tends to train multiplication triples—e.g., 7 × 4 = 28—we propose an approach where we train associations between 4, 8, 12, 16, 20, …, and between 7, 14, 21, 28, 35, …, to achieve the same result. The intervention study reported here aimed to exploit this implication, by designing and evaluating a video game to train associations between single-digit numbers and their multiples. We suggest that training multiples of single-digit numbers is also likely to be effective in contributing to division performance. Less research has been carried out into division problems than multiplication problems, but De Brauwer and Fias (2009) showed, in a longitudinal study, that similar effects could be observed for division problems as for multiplication problems, including those relating to problem size, ties, and the number 5.

Addition Fluency

Alongside rehearsal of multiplication tables, teachers in primary schools also rehearse number bonds; children are encouraged to learn the pairs of numbers that add to give 10, or 20 (Department of Education, 2014). As with evidence regarding multiplication tables, there is evidence to suggest that fluency in the recall of number bonds is associated with mathematics attainment more generally (Cowan et al., 2011). Fluent knowledge of number bonds can support a wider range of problem-solving tasks. For example, the knowledge that 5 + 5 = 10 can be used to derive a solution to 5 + 4 or 5 + 6, and the knowledge that 8 + 2 = 10 can be used in finding a solution to 8 + 5 (Askew, 2013).

Despite its prevalence in classrooms in England, the learning of number bonds has been the subject of far less research than the learning of multiplication tables.

Game-Based Learning to Support Arithmetic Fact Retrieval

Video games offer an extremely promising environment for promoting number sense, as they can provide a high volume of number combinations and manipulations to the learner in a short time. Furthermore, they can adapt in their complexity to the current level of understanding and performance of the learner, while providing continuous and patient feedback (Butterworth et al., 2011; Devlin, 2011). However, while it is easy to find mathematics training solutions, games, and apps online, only a small fraction of existing mathematics learning games are founded on theoretically sound principles. Few integrate mathematics directly into the gameplay, rely on valid theories of learning, and really utilize the possibilities that game technologies provide for learning (Kiili et al., 2015).

Video games also have great promise as a tool for researching children's developing numerical cognition, due to their ability to record high volumes of data relating to children's responses to numerical tasks. An appropriately designed game can be used as an ideal context for the development and extension of methods capturing very small changes in children's learning—so-called microgenetic methods (Siegler and Crowley, 1991). This approach—implementing microgenetic method via a video game platform—can provide an opportunity to address some important current questions about mathematics learning. For example, current education policy in England requires that all children learn their times-tables (up to 12 × 12) by the time they leave primary school. Although some research evidence suggests reasons why some children struggle to encode and recall times-tables and similar number facts [including limitations in working memory, speed of processing, verbal processing, and so on (e.g., Royer et al., 1999)], there remains a clear need for novel methodologies to help researchers understand both typical learning trajectories, and individual differences in learning and development. Such work could have important implications for policy and practice, either in terms of establishing realistic expectations for individual rates of learning, or in terms of supporting children who do not respond positively to existing teaching approaches.

The RAIDING Game

The game was designed around touch-screen controls on (7-inch) tablet devices. It is set in outer space, and the aim is to collect and preserve alien life within the biodomes of a central mothership. The player controls a small flying robot, which can explore an area of space around its base in search of seeds and eggs to nurture in the biodomes. To support the mission, the player must earn credits to buy new components for their mothership, including biodomes, power sources and engines. These “building and collecting” mechanics fuel the economies of the game and motivate the player to continue playing. Fundamental to all of these activities is the “mining” mechanic which provides the player with credits, seeds and eggs. The player's robot must mine asteroids for resources that are converted into credits, but mining also provides the chance to find alien seeds and eggs within the asteroids. There are 100 different aliens to find in total, and each alien prefers a biodome with a particular combination of climate and plants. The inclusion of a variety of collectable elements within the game allowed for multiple reward schedules, including both linear and non-linear performance/reward contingencies; there is a linear relationship between mining activity and credits (for spending) but non-linear relationships between mining activity and receipt of both seeds and eggs, with eggs being received less often than seeds. Previous research has provided strong psychological evidence that non-linear, or uncertain, rewards are a particularly motivating aspect of games for learning (Howard-Jones and Jay, 2016).

Each time an asteroid is approached within the game, the player has the option to begin one of the minigames which requires them to “mine” numbered rocks according to a particular mathematical rule. The minigame will focus either on multiples of a target number or number bonds to a target number, and the player has the option to accept or reject the game. In Figure 1, for example, the player has accepted a game in which they need to select rocks with numbers that are multiples of 2. A correct selection is accompanied by a positive sound effect as the rock flies over to join a stack ready to be converted into credits by a transporter ship—each rock is worth one credit. Once 30 rocks have been collected, the minigame ends with the rocks being crushed and the player is randomly rewarded with any seeds (common) or eggs (rare) found within the asteroid. When a player selects an incorrect rock, an “unhappy” noise sounds but there is no other negative consequence.

FIGURE 1

Figure 1. Screenshot from RAIDING game, 2-times-table mini-game.

The mathematical content of each minigame is determined by a dynamic learner model within the game. A key part of the game design is the adaptivity provided by this learner model (Butterworth et al., 2011; Mees et al., 2018). A new player will begin with access to minigames which require them to identify multiples of 2, 5, or 10, or pairs of rocks that add to 10 (number bonds). When the player reaches a threshold of performance on these tasks, then a new tier is unlocked. For minigames involving multiples, the second tier includes multiples of 3 and 4, while the third tier includes multiple of 6, 7, 8, and 9. For minigames involving number bonds, the second tier involves adding to 20 and the third tier adding to 15. Within each tier, the game provides learners with tasks determined by previous levels of performance. If a player has been good at recognizing multiples of 2 while in tier 1, for example, then the game will be less likely to give “multiples of 2” tasks, and more likely to ask for multiples of 5 or 10.

A key goal of the game design was to ensure that mathematical tasks were an intrinsic component of the “game mechanics” (the repeated activities of a game from which motivating gameplay is derived), rather than using the gameplay as a sugar-coating for mathematical content delivered outside of the gameplay (Habgood and Ainsworth, 2011). This study provides empirical evidence to support the intrinsic role of game mechanics in motivation and learning, and the same authors argue that the “fantasy context” (in this case, the space setting) is irrelevant to this intrinsic relationship (Habgood et al., 2005). The number tasks in the mining mini-games represent the main repeatable gameplay activity of the core loop and typically occupy around half of a player's time in the game. Within the mining game, the number tasks are intrinsic to the game-play rather than a separate bolt-on activity. However, the mining task would have limited longevity on its own, so the rewards earned from the repeated mining activity can be spent on customizing and upgrading the player's spaceship as well as collecting alien lifeforms. Thus, the economies of the game provide a motivating “metagame” to build longer term engagement with the mathematical mining tasks. This pattern also links with the concept of spaced learning (Kelley, 2009), as the game encourages intense periods of focus on number relationships, interspersed with time to build the mothership, plant seeds and so on.

The metagame does contain some opportunities for mathematical thinking and learning—in making decisions about how to spend credits earned, for example—but its main purpose is to promote and support players' investment in, and engagement with, the game. We argue that this is not the same as a “sugar-coating” for the mathematical content of the mining minigames because even though mathematical thinking does not pervade every aspect of the game, where mathematical thinking does occur it is intrinsically part of the game mechanics rather than a “bolt-on” component with no relation to the rest of the game.

Summary of Design Principles

• Mathematical content is an intrinsic component of gameplay.

• The game is adaptive to the player's level of progress.

• Sessioning, return triggers, and multiple linear and non-linear reward schedules are employed to increase engagement.

• The learning content is designed according to theory in mathematical cognition, training associations between single digits rather than training responses to arithmetic problems.

The Study

We carried out a first trial of the RAIDING game, to assess its effectiveness in improving arithmetic performance among a group of 7 to 8-year-old children. We worked with two schools, and all children within the target age-range in both schools took part in the intervention (two classes in each school). Children played the game for 20 min per day for 2 weeks.

Methods

Design

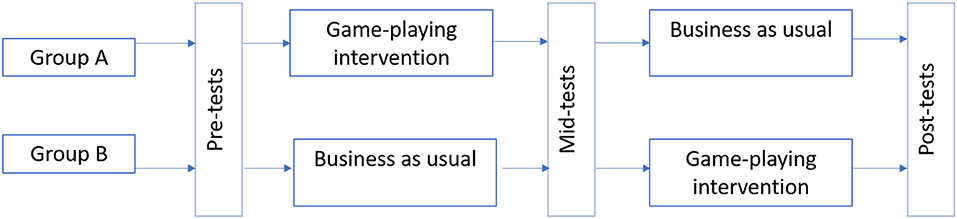
The study employed a between-groups crossover quasi-experimental design. In each school, the two classes were randomly chosen to be group A or group B (see Figure 2). Group A received the game-playing intervention for 2 weeks, followed by a period of business as usual. Group B has a period of business as usual for the first 2 weeks, followed by the 2-week game-playing intervention. Measures of arithmetic fluency were taken before the first 2-week period (pre-test), at crossover (mid-test), and after the second 2-week period (post-test). The primary hypothesis for the study was that game-playing groups would improve more on a test of arithmetic fluency between pre- and mid-test. Comparisons of improvements between mid- and post-test, and additional exploratory analyses of in-game, plus pre-, mid-, and post-test scores were carried out to inform further study.

FIGURE 2

Figure 2. Experimental design.

The crossover design employed in this study allows all participants in the study to experience the game-playing intervention. This was important to the research team for ethical reasons. The comparison between groups at mid-test stage was the primary analysis as this was a fair test between the game-players and controls. In the second stage of the study, after crossover, group A became the controls. However, having played the game for 2 weeks, group A were not a perfect control group. Analyses comparing the groups at post-test were still carried out, in order to see whether group B improved by the same degree and to see whether group A retained any improvement for the first stage—but these should be interpreted with some caution.

Participants

Participants were 97 children aged 7 to 8 years-old in two primary schools. In each school, children were in two mixed-ability classrooms of 30. Participants were those children from these classrooms that met the criteria for eligibility—that they attended for pre- and mid-tests, that they did not have a learning difficulty that prevented them from accessing the game or the pre-/mid-/post-tests, and that they could use a touchscreen device and access the game. Both schools were in broadly average localities with regard to socio-economic status, and children in both schools had broadly average levels of mathematics attainment in national tests.

All 97 participants (49 in the game-playing group, and 48 controls) were included in analyses of comparisons for the first stage (comparisons between pre- and mid-tests). Seven participants were excluded from comparisons between mid- and post-tests due to absence, leaving a total 90 participants for the second stage (45 in each group).

Instruments and Measures

The Westwood 1-min basic facts tests (Westwood, 2000) were used as pre-, mid- and post-tests in order to evaluate progress in arithmetic fluency. This test requires children to complete as many single-digit addition problems as possible in 1 min, followed by subtraction problems, multiplications, and finally divisions. The score resulting from the test is the number of correct solutions given within the time limit; as such the test provides a measure that combines speed and accuracy. A limitation of this test is that it does not differentiate between speed and accuracy, but on the other hand the ease of administration and time required in a classroom setting are major advantages. These tests were administered to children in their usual classroom groups. A standard set of instructions was used for all tests; children were asked to complete the tests individually and in silence. Children were also advised that if they did not know an answer, that they should either make their best guess or move on to the next question.

Additional data were collected during game-play. Actions carried out by players within the game were automatically recorded by the software, including: total duration of play; number of games played; number of rocks selected; and response time and accuracy for each rock selection. These data were used in order to assess the relationships between in-game actions and progress and improvement in arithmetic fluency assessed through pre-/mid-/post-test comparisons.

Procedure

Stage 1: Pre-test

The pre-tests were administered during the week before the start of the intervention. The explanation of the trial, and pre-testing took ~20 min with each group.

Stage 1a: Preparation

In the week before the study began, the tablets used for the project were numbered. A register sheet for the class was generated, based upon the class data gathered at pre-test, assigning each child a tablet. The game was installed, and the tablets were then placed on charge in preparation.

Stage 2: Gameplay

The children began playing the game a week after the pre-test. Each session of gameplay lasted 20 min and there was one session each day over a period of 2 weeks. This resulted in 10 sessions and a total of 200 min of gameplay.

In one school, the gameplay session occurred before the lunch break. The second school had their gameplay sessions at 9 a.m., just after the morning register had been taken and before the mathematics lessons for that day. If a child missed a session, for whatever reason, then they could complete a catch-up session the next day. If a child missed too many consecutive sessions, they would be noted down to allow for the removal of their incomplete data, and then allowed to just play the game at their own pace.

In the initial session, all members of the research team were present. We again briefly explained the project. We then handed out the tablets to the group, with each child receiving their designated tablet. In the event of children being missing from the pre-test, we had allowed for extra room on each register sheet to allow these children to be added. We ensured that additional tablets were available, in the event that we did need more for the group or in case of equipment failure. After the end of the first 20-min session, there was a short debrief to make sure they understood the overall goals of the game.

During the course of the 2 weeks, a researcher from the team attended in order to provide technical support and assistance including maintaining and charging the tablets. The researcher attended on the first, second, third and fifth days of the first week, and on the first, third and fifth day of the second week.

Stage 3: Mid-test

At the end of the final session of gameplay, in which all members of the team attended, we repeated the testing procedure as in stage 1 with both groups. Testing of the gameplaying group took place after they had finished playing the game that day.

Stage 4: Gameplay

The research team returned to the schools on the immediate Monday after the mid-test. At this point, group roles were switched and group B were introduced to the game. For the next 2 weeks the same procedure as in stage 2 was followed.

Stage 5: Post-test

After the final session of gameplay, the same testing procedure as in stages 1 and 3 was followed.

Ethical Considerations

In this project, we referred to the ethical guidelines of the British Educational Research Association (BERA) (2018). Our approach to consent was to gain full informed written consent from school staff first. Then school staff managed a process of informed opt-out consent for parents. Children in the study were verbally informed about the nature of the study and of their right to withdraw. No parents or children opted to withdraw from the study. All data were fully anonymized at all times, and participants were not asked to do anything that they would not normally expect to do in a lesson. The study was approved by the Social Science and Humanities faculty ethics committee, Sheffield Hallam University.

Results

Data analyses were carried out in three stages. Firstly, the improvement in arithmetic performance between pre- and mid-test was compared between pupils in the game-playing group and pupils in the control group. This analysis tested the primary hypothesis, which predicted that playing the game was associated with improvements in arithmetic performance. In the second stage, the two groups' improvements were compared following crossover—between mid- and post-test. Finally, in-game data were analyzed in order to explore possible reasons for individual differences in improvement between pre- and post-test.

Between-Group Comparison of Arithmetic Performance

To assess changes in arithmetic performance over the first 2 weeks of the trial, scores from the Westwood 1-min tests from pre- and mid-test were summed. Figure 3 shows average improvement between pre- and mid-test for pupils in the game-playing group compared with pupils in the control group.

FIGURE 3

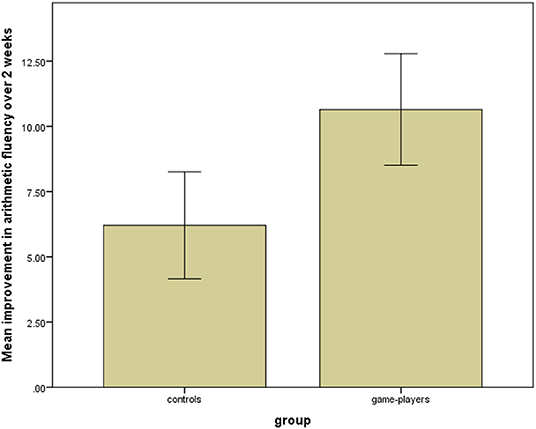
Figure 3. Mean improvement in arithmetic fluency by group for 2-week intervention (error bars represent ±2 SE).

The control group improved by an average 6.20 points (SD = 7.17), while the game-playing group improved by 10.65 (SD = 7.40). An ANCOVA was carried out, with group as the independent variable, mid-test arithmetic fluency as the dependent variable, and pre-test arithmetic fluency as a covariate in order to account for any between-group differences at pre-test. This analysis showed a significant main effect of group [F_(1,94) = 8.73, p = 0.004, partial eta squared = 0.085].

Lord's (1967) paradox casts doubt on the value of the use of covariates when non-randomized studies use groups differing at baseline, and so it was considered prudent to act upon the recommendations of Van Breukelen (2006) and also conduct an independent t-test comparing the improvement in arithmetic fluency observed in the two groups. This also showed a significant difference t = 2.95, df = 95, p = 0.003, Cohen's d = 0.6. An effect size of 0.6 is interpreted as approximately equivalent to 7 months' progress, or as evidence of high impact (Higgins et al., 2011).

Changes After Crossover

After the first 2 weeks of the trial, and the mid-test, the groups swapped roles so that the original control groups became the game-playing groups and the original game-playing groups became controls. Figure 4 shows that during this period, between mid- and post-test, the new game-playing groups improved by an average of 3.6 points (SD = 9.10) and the new controls' average score reduced by 0.9 points (SD = 8.14). The difference between groups was again significant; t = 2.49, df = 88. P = 0.015. Between pre- and post-test, participants in both groups improved by 10.1 points on average. While this analysis post-crossover does not serve so well as a test of the effectiveness of the game in improving arithmetic performance, due to the imperfect control group for this part of the study, it was reassuring to see that the gains observed for the original game-playing group in the first part of the study were not lost over the second part. It was also reassuring to see that the size of difference between groups in the second stage was the same as the size of difference (in the opposite direction) in the first stage.

FIGURE 4

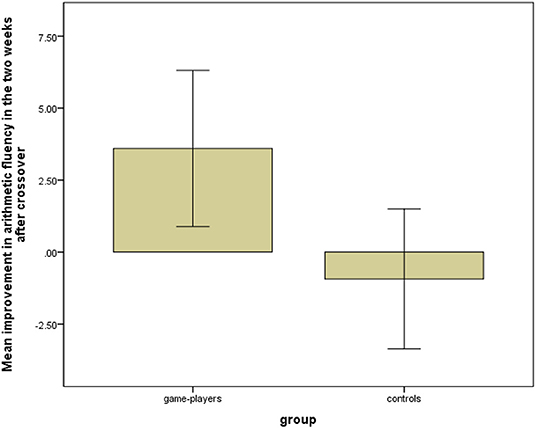
Figure 4. Mean improvement in arithmetic performance following crossover (error bars represent ±2 SE).

Connections Between Gameplay and Outcomes

One of the core design principles for the game was that it should involve players making as many decisions about number as possible in the time that they were playing. Analysis of in-game data showed that participants made an average 2,954 judgements about numbers during the 2-week trial (SD = 891), which is equivalent to ~300 per 20-min session.

Testing the Relationship Between Ability and Engagement

The game was designed to be as engaging for children with an already high level of knowledge of number facts as it was for children with a low level of knowledge. To test whether this aim had been achieved, an analysis of correlation between pre-test arithmetic performance and engagement with the game was undertaken. Engagement with the game was measured as the total number of rocks (numbers) seen by the player over the 2-week intervention. This is because players only see rocks to mine once they have chosen to enter into the mining minigame. Results showed a very small correlation coefficient of −0.07, indicating that children engaged with the game to approximately the same extent, regardless of initial levels of ability.

A further two correlational analyses were undertaken in order to determine whether there was a relationship between pre-test score and the number of rocks (numbers) selected, and between pre-test score and the number of rocks selected correctly. Both correlations were positive, showing that higher pre-test scores were associated with higher levels of rock selection, and higher numbers of correct answers within the game; the correlation coefficient for the relationship between pre-test score and number of rocks selected was 0.18 (p = 0.06) and for the relationship between pre-test score and number of rocks selected correctly was 0.41 (p < 0.005). This means that while pre-test performance did not predict level of engagement with the game, it was clearly associated with performance on mathematical tasks within the game, as expected.

Exploring Connections Between Game Decisions and Outcomes

The final analyses presented here explore relationships between players' gameplay and the improvements they experience in arithmetic. Within the game, players had some choice about what type of minigame to play, focusing on either multiples or number bonds. The analysis of differences in improvement across the four arithmetic operations led to the question of whether such differences were correlated with participants decisions to play a greater proportion of “multiples” vs. “number bonds” minigames.

Table 1 shows correlation coefficients for relationships between participants' experience of the two types of minigames, with improvements in performance in the four operations. The two largest coefficients in the table are for the relationship between experience of the “multiples” minigame and improvements in multiplication and division, respectively. The more “multiples” gameplay that participants experienced, the more they improved in both multiplication and division between pre- and post-test. This result is as expected, although the effect of training recognition of multiples on division performance is higher than might have been predicted.

TABLE 1

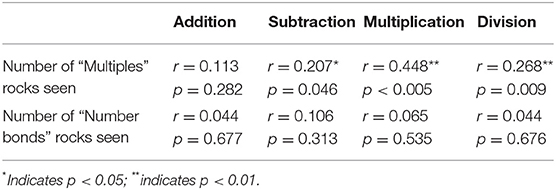
Table 1. Pearson correlation coefficients and significance for relationships between games played and improvement in performance for the four operations (n in all cells = 93).

The more surprising results in Table 1 are that volume of “number bonds” gameplay does not predict improvement in performance in any of the four operations, and that volume of “multiples” gameplay predicts improvement in subtraction. These results will be discussed further below.

Discussion

The findings show that playing the game for 2 weeks led to significant improvements in arithmetic performance, equivalent to ~7 months' progress. The other analyses described in the results section support the claim that improvements were due to the design of the game, as opposed to Hawthorne effect or similar. Improvement in arithmetic fluency was positively correlated with the amount of effort that children put in to progressing within the game. Further to this, children who played more times-tables tasks, as opposed to number-bonds tasks, improved more on multiplication- and division-fluency.

Implications for Theory

As a successful application of theory to game design, this study provides indirect support for the connectionist theory of multiplication described by Verguts and Fias (2005), which in turn builds on Ashcraft (1987). The game trains recognition of membership of times-tables rather than training production or recognition of correct answers to multiplication problems. Similarly, the game trains recognition of pairs of numbers adding to ten, rather than training production or recognition of correct answers to addition problems. We propose that children have improved in their multiplication fluency as a result of developing stronger associations between single-digit numbers and their respective set of multiples. These stronger associations make it more likely than on seeing “7 × 4,” as in a previous example, that participants will have automatically activated “28” as a multiple of both multiplicands. To our knowledge, this is the first training study to have successfully tested the effect of training of multiples knowledge on arithmetic performance. It also provides a rare example of successful transfer of game-based training to a pencil-and-paper test.

It is important to note that this study has not shown the training multiples is a more effective way to support arithmetic development than the normal classroom approach of training responses to multiplication problems. Further studies will be required in order to directly compare the training of multiples with the training of multiplication triples using a game-based learning platform. Ensuring a fair comparison, including balancing engagement and volume of practice across conditions, will be challenging, but the large effect size observed in this study suggests that such further investigation would be worthwhile.

Multiplication and Division

We argued in the introduction to this article that training of associations between single-digit numbers and their multiples may also lend itself to production of answers to division questions. The results show that increased gameplay in the multiples mini-game was associated with increased improvement in both multiplication and division fluency. Thus, this study has provided evidence that the mechanism by which children rapidly or automatically solve simple division problems may be closely aligned with that for solving multiplication problems. We propose that when 28 ÷ 4 is presented, for example, that a set of numbers is activated for both “28” and “4.” Following the training experienced with the game, participants will associate “28” with both 7 and 4, as it appears in both sets of multiples. The effect of the game on division fluency is more novel and surprising than the effect on multiplication fluency, and so will benefit from further research and study.

The observed effect on division performance may be an affordance of the decision to train associations between single-digit numbers and their multiples as non-directed associations. The game trains a connection from 16 to 4, for example, equally as it trains a connection from 4 to 16. This decision removes “x,” “÷,” “multiply,” and “divide,” from training stimuli, and so may allow players of the game to more easily learn associations in a way that allows retrieval in both multiplication and division contexts.

Effects of Number Bonds Training

It is surprising that the “number bonds” minigame appears to have had much less of an effect on participants' learning. The correlation between the number of number bonds trials and improvement in addition fluency was close to zero. In fact, experience of the “multiples” minigame appeared to be more effective in improving addition and subtraction fluency than the “number bonds” minigame. We suggest that this finding may be due to the fact that automaticity in simple additions is due to retrieval of an association between a whole problem (e.g., “2 + 3”) and its solution (e.g., “5”), rather than associations with the two addends (Ashcraft and Fierman, 1982). This study then could be seen as adding to the evidence for dissociation of mechanisms of multiplication and of addition. However, it should be noted that the number bonds mini-game was somewhat more complex than the multiples mini-game—requiring players to select pairs of numbers to fit a rule, rather than single numbers. This complexity, including the additional cognitive load involved in tracking and selecting two moving objects rather than one, may mean that participants learned less in this condition. This is something that could be explored further in future studies.

Implications for Practice

Evidence from this study supports the adage, “practice makes perfect,” but emphasizes the value of using video games to make practice engaging. Indeed, informal conversations with participants toward the end of the intervention suggest that they did not see the game as being about mathematics practice at all—their main focus was on the way that they had built their space station, and the number of aliens that they had successfully hatched. Although in some mathematical games we may want children to be actively aware of the mathematics that they are engaging with, where the aim is to train associative links between numbers this may not be necessary. Analysis of gameplay data showed that children were making ~300 decisions about numbers in each 20-min period of play. It would not be easy to achieve this volume of practice using traditional classroom methods.

Findings concerning the relationship between gameplay and outcomes suggest that it may be possible to use the game both for training and for assessment of arithmetic performance. There was a moderate to large correlation between pre-test scores and the number of correct answers given within the game. With further refinement, it should be possible to derive measures within the game that are strongly predictive of performance outside the game.

The findings of the game raise a question of the value of number bonds training. The mathematics curriculum in England requires that children learn the pairs of numbers that add to 10, or 20, for example (Department of Education, 2014). There is limited evidence in the literature for the value of this, aside from some correlational evidence (Cowan et al., 2011) and theoretical discussion of potential uses (Askew, 2013). This study does not provide any empirical evidence of benefits of number bonds training for arithmetic performance. Although, as noted above, it does not provide strong evidence that number bonds training does not have value—just that number bonds training in this study was not effective.

While we did not collect systematic qualitative data on participants' and teachers' responses to the game, members of the research team were able to make some informal observations and to speak to children and teachers during the intervention. Teachers confirmed our observation that children engaged with the game well for the 2 weeks of the intervention; teachers were happy to see that the game was engaging for children with very different levels of mathematics achievement. Despite some evidence in the literature regarding differences in game-playing behaviors outside of school (Lowrie and Jorgensen, 2011), we observed no difference in engagement with the game due to gender—although data were not systematically collected on gender in the study that could have enabled analysis of any performance differences. Teachers did comment that for some children, the 2-week duration of the intervention was probably a maximum, as those children were unlikely to experience any further benefit after this point. However, teachers also felt that some children would benefit from a longer period of time playing with the game, as these children would be likely to continue to make useful progress beyond 2 weeks. If the game were to be used in schools outside of an evaluation trial, we would recommend that its use be targeted for those most likely to benefit rather than be used as a blanket intervention for all children in a class.

Limitations and Future Research

A key limitation of this research is that the game included multiple innovations and so it is not possible to know which aspects of the game's design were more or less effective in improving arithmetic performance. It is also not possible to know from this study whether 20 min per day for 2 weeks is the optimum duration for this intervention. These limitations lead to the obvious suggestion that further work could now be carried out to isolate particular features of the game's design and determine the contribution of each feature to its apparent success. However, it is also possible that there may be complex interactions among different design components that mean it is not easy to examine them independently of one another. Further study could also vary the length of the intervention to determine how this corresponds to any improvement in arithmetic.

This intervention took place in the classroom. This allowed us to ensure that all participants in the study played the game for 20 min each day, for the 2 weeks of the trial. However, this also meant that children were potentially missing out on other learning that they could have been doing during this time. If children were to play the game at home, they could potentially experience the benefits observed in the trial reported here, without taking time out of the school day. Therefore, it would be useful to test the effectiveness of the game when played at home, outside of school time. A home trial would represent a more sensitive test of children's engagement with the game, as children who did not enjoy the game would not play for the same amount of time as they did in the classroom in the current study.

The iterative approach employed during the design of the game was very helpful in ensuring that it was both engaging for children and contributed to learning. However, it was very time consuming and labor intensive. The positive results from this trial open up the possibility of “live” testing of different versions of the game at scale, to further refine and test various aspects of the design. Different versions of the game could be released via app stores, and data collected via the cloud, in order to measure players' responses in terms of engagement and learning. This data-driven model of development and testing could provide some exciting insights into game-based learning for numeracy and mathematics.

Finally, we hope that the design and evaluation of this game represents evidence for the value of interdisciplinary collaboration in this field. Without expertise from each of the three contributing fields, mathematical cognition, game-based learning, and game design, this project would not have been possible. This kind of interdisciplinary collaboration brings risks—not least that no single member of the team can fully understand all of the detail of the project—but we argue these approaches are vital for future understanding and application of findings relating to children's learning (Jay, 2013).

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Ethics Statement

The study was carried out in accordance with the recommendations of the British Educational Research Association and was approved by the Development & Society faculty ethics committee at Sheffield Hallam University. Written informed consent was gained from the head of school of each participating school.

Author Contributions

TJ led the overall design of the research and wrote the initial draft of this article. JH made substantial contributions to the design of the game and to the research design and contributed to edits and rewrites of the article before submission. MM coded the game and carried out much of the data collection for the study. PH-J contributed to the research design and made edits to the article prior to submission.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The work reported here was funded by a Research Project Grant from the Leverhulme Trust. We are very grateful for this support, and for the participation of schools, teachers, and children in the project.

References

Ashcraft, M. H. (1987). “Children's knowledge of simple arithmetic: a developmental model and simulation,” in Formal Methods in Developmental Psychology (New York, NY: Springer), 302–338. doi: 10.1007/978-1-4612-4694-7_9

CrossRef Full Text | Google Scholar

Ashcraft, M. H., and Fierman, B. A. (1982). Mental addition in third, fourth, and sixth graders. J. Exp. Child Psychol. 33, 216–234. doi: 10.1016/0022-0965(82)90017-0

CrossRef Full Text | Google Scholar

Askew, M. (2013). Mediating learning number bonds through a Vygotskian lens of scientific concepts. South Afr. J. Childh. Educ. 3, 1–20. doi: 10.4102/sajce.v3i2.37

CrossRef Full Text | Google Scholar

British Educational Research Association (BERA) (2018). Ethical Guidelines for Educational Research, 4th Edn. London: BERA.

Butterworth, B., Varma, S., and Laurillard, D. (2011). Dyscalculia: from brain to education. Science 332, 1049–1053. doi: 10.1126/science.1201536

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooney, J. B., Swanson, H. L., and Ladd, S. F. (1988). Acquisition of mental multiplication skill: evidence for the transition between counting and retrieval strategies. Cogn. Instruct. 5, 323–345. doi: 10.1207/s1532690xci0504_5

CrossRef Full Text | Google Scholar

Cowan, R., Donlan, C., Shepherd, D.-L., Cole-Fletcher, R., Saxton, M., and Hurry, J. (2011). Basic calculation proficiency and mathematics achievement in elementary school children. J. Educ. Psychol. 103, 786–803. doi: 10.1037/a0024556

CrossRef Full Text | Google Scholar

De Brauwer, J., and Fias, W. (2009). A longitudinal study of children's performance on simple multiplication and division problems. Dev. Psychol. 45, 1480. doi: 10.1037/a0015465

PubMed Abstract | CrossRef Full Text | Google Scholar

Department of Education (2014). National Curriculum in England: Mathematics Programmes of Study. London: Department of Education.

Devlin, K. (2011). Mathematics Education for a New Era: Video Games as a Medium for Learning. New York, NY: AK Peters/CRC Press. doi: 10.1201/b10816

CrossRef Full Text | Google Scholar

DfE (2018). Multiplication Tables Check Trials to Begin in Schools. Retrieved from: https://www.gov.uk/government/news/multiplication-tables-check-trials-to-begin-in-schools

Galfano, G., Rusconi, E., and Umiltà, C. (2003). Automatic activation of multiplication facts: evidence from the nodes adjacent to the product. Q. J. Exp. Psychol. A, 56, 31–61. doi: 10.1080/02724980244000332

PubMed Abstract | CrossRef Full Text | Google Scholar

Habgood, M. P., Ainsworth, S., and Benford, S. (2005). Endogenous fantasy and learning in digital games. Simul. Gaming 36, 483–498. doi: 10.1177/1046878105282276

CrossRef Full Text | Google Scholar

Habgood, M. P., and Ainsworth, S. E. (2011). Motivating children to learn effectively: exploring the value of intrinsic integration in educational games. J. Learn. Sci. 20, 169–206. doi: 10.1080/10508406.2010.508029

CrossRef Full Text | Google Scholar

Higgins, S., Kokotsaki, D., and Coe, R. (2011). Toolkit of Strategies to Improve Learning: Summary for Schools Spending the Pupil Premium. London: Sutton Trust.

Howard-Jones, P. A., and Jay, T. (2016). Reward, learning and games. Curr. Opin. Behav. Sci. 10, 65–72. doi: 10.1016/j.cobeha.2016.04.015

CrossRef Full Text | Google Scholar

Jay, T. (2013). The possibility and importance of postperspectival working. Educ. Res. Rev. 9, 34–46. doi: 10.1016/j.edurev.2012.11.002

CrossRef Full Text | Google Scholar

Jay, T., Rose, J., and Simmons, B. (2018). Why is parental involvement in children's mathematics learning hard? Parental perspectives on their role supporting children's learning. Sage Open 8, 1–13. doi: 10.1177/2158244018775466

CrossRef Full Text | Google Scholar

Jordan, N., Hanich, L., and Kaplan, D. (2003). A longitudinal study of mathematical competencies in children with specific mathematics difficulties versus children with comorbid mathematics and reading difficulties. Child Dev. 74, 834–850. doi: 10.1111/1467-8624.00571

PubMed Abstract | CrossRef Full Text | Google Scholar

Joy Cumming, J., and Elkins, J. (1999). Lack of automaticity in the basic addition facts as a characteristic of arithmetic learning problems and instructional needs. Math. Cogn. 5, 149–180. doi: 10.1080/135467999387289

CrossRef Full Text | Google Scholar

Kelley, P. (2009). Making Minds: What's Wrong With Education - and What Should We Do About It? London: Routledge.

Google Scholar

Kiili, K., Devlin, K., Perttula, A., Tuomi, P., and Lindstedt, A. (2015). Using video games to combine learning and assessment in mathematics education. Int. J. Serious Games 2, 37–55. doi: 10.17083/ijsg.v2i4.98

CrossRef Full Text | Google Scholar

Lemaire, P., and Siegler, R. S. (1995). Four aspects of strategic change: contributions to children's learning of multiplication. J. Exp. Psychol. Gen. 124:83. doi: 10.1037/0096-3445.124.1.83

PubMed Abstract | CrossRef Full Text | Google Scholar

Lord, E. M. (1967). A paradox in the interpretation of group comparisons. Psychol. Bull. 68, 304–305. doi: 10.1037/h0025105

PubMed Abstract | CrossRef Full Text | Google Scholar

Lowrie, T., and Jorgensen, R. (2011). Gender differences in students' mathematics game playing. Comput. Educ. 57, 2244–2248. doi: 10.1016/j.compedu.2011.06.010

CrossRef Full Text | Google Scholar

Mees, M., Jay, T., and Habgood, J. (2018). “Designing an adaptive learner model for a mathematics game,” in European Conference on Games Based Learning (Sophia Antipolis: Academic Conferences International Limited).

Google Scholar

Mees, M., Jay, T., Habgood, J., and Howard-Jones, P. (2017). “Researching adaptivity for individual differences in numeracy games,” in Extended Abstracts Publication of the Annual Symposium on Computer-Human Interaction in Play (Amsterdam: ACM), 247–253. doi: 10.1145/3130859.3131315

CrossRef Full Text | Google Scholar

Pegg, J., Graham, L., and Bellert, A. (2005). “The effect of improved automaticity of basic number skills on persistently low-achieving pupils,” in Proceedings of the 29 th Conference of the International Group for the Psychology of Mathematics Education, Vol. 4, eds H. L. Chick and J. L. Vincent (Melbourne: PME), 49–56.

Google Scholar

Royer, J. M., Tronsky, L. N., Chan, Y., Jackson, S. J., and Marchant, H. III. (1999). Math-fact retrieval as the cognitive mechanism underlying gender differences in math test performance. Contemp. Educ. Psychol. 24, 181–266. doi: 10.1006/ceps.1999.1004

PubMed Abstract | CrossRef Full Text | Google Scholar

Siegler, R. S., and Crowley, K. (1991). The microgenetic method: a direct means for studying cognitive development. Am. Psychol. 46:606.

PubMed Abstract | Google Scholar

Van Breukelen, G. J. (2006). ANCOVA versus change from baseline had more power in randomized studies and more bias in nonrandomized studies. J. Clin. Epidemiol. 59, 920–925. doi: 10.1016/j.jclinepi.2006.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Verguts, T., and Fias, W. (2005). Interacting neighbors: a connectionist model of retrieval in single-digit multiplication. Memory Cogn. 33, 1–16. doi: 10.3758/BF03195293

PubMed Abstract | CrossRef Full Text | Google Scholar

Westwood, P. (2000). Numeracy and Learning Difficulties: Approaches to Teaching and Assessment. Melbourne, VIC: Australian Council for Educational Research (ACER).

Google Scholar