- 1Department of Psychology, University of Milano-Bicocca, Milan, Italy
- 2Donders Centre for Cognitive Neuroimaging, Donders Institute for Brain, Cognition and Behaviour, Radboud University, Nijmegen, Netherlands
Deductive and logical reasoning is a crucial topic for cognitive psychology and has largely been investigated in adults, concluding that humans are apparently irrational. Yet, from a pragmatic approach, the logical level of meaning is only one of possible communicative interpretations, and the least likely to be assigned if the intent of the task is not adequately transmitted. Indeed, new formulations of the mathematical tasks (syllogisms, selection task, class inclusion task, problem solving) of greater relevance to the problem and to its aim, greatly improved adults’ logical performance. The current study tested whether pragmatic manipulations of task instructions influenced in a similar way children’s performance in deductive and logical tasks (Experiment 1) and in insight problems (Experiment 2). We found that, when task instructions were in accordance with the conversational rules of communication, 10-year-old children substantially improved their performance. We suggest that language use imposes constraints in terms of informativeness and relevance which are crucial in teaching logic and mathematics.
Introduction
Natural language and logic are both intended to transmit meaning effectively or, in other words, to express thoughts. However, they are fundamentally different. In logic, the speaker wants to convey a univocal meaning, and any possible acceptation interfering with it is eliminated. Conversely, in natural language, the speaker constantly exploits the expressive richness of words, and the intended meaning of an utterance can be understood only by considering the relevant context.
Thus, the context, the identity of the speaker and the listener, the shared knowledge, and the aims of the communicative act all contribute to determine the interpretation of an utterance through sophisticated intention-attribution and inferential processes. The study of these processes pertains to the field of pragmatics (Grice, 1989; Mosconi, 1990, 2016; Levinson, 1995; Sperber and Wilson, 1995). Everything that the text communicates concurs in the representation of its meaning: not only what literally is said (the sentence), but also what is implied (the utterance). The distinction between sentence and utterance is the core of Grice’s communication theory, according to which phrases mean more than they literally say. What is implied is inferred from the intentions attributed to the speaker and the context through conversational implicatures. The central idea is that communication is achieved when a recipient recognizes the special kind of intention with which a communicative act is produced. More generally, the Gricean theory of implicature postulates that meaning should be reduced to intention and, therefore, that semantics has to be reduced to psychology (Grice, 1975).
In most occasions, human reasoning has a verbal input in natural language and, contrary to the case of formal languages, there is no univocal interpretation of a sentence. Hence, the view that the verbal input to human mental activity is well defined like in formal logic is an idealization. The consequences for the study and the assessment of human reasoning, judgment, and problem solving are straightforward: a pragmatic approach to the study of thinking and reasoning must consider the relationships between language, communication, and thought (Mosconi and D’Urso, 1974; Mosconi, 1990; Hilton, 1995; Politzer and Macchi, 2000; Bagassi and Macchi, 2016). Communication and thinking could be considered as two sides of the same cognitive process, which realizes in the discourse.
Accordingly, analysis of the discourse is the proper methodology for studying reasoning and teaching how to improve reasoning. Numerous studies (Dulany and Hilton, 1991; Sperber et al., 1995; Macchi, 2000; Politzer and Macchi, 2000; Mosconi and Macchi, 2001; Van der Henst et al., 2002; Macchi and Bagassi, 2006; Baratgin and Politzer, 2010) have shown the importance of the pragmatic approach to the study of adults thinking and reasoning, from problem solving, conditional reasoning, and deductive reasoning to probabilistic reasoning, in which Mosconi (1990), with his analysis of discourse, has been a pioneer.
For instance, in recent studies on deductive reasoning with syllogisms and material implication (Macchi et al., 2019, 2020), we showed that, in adults, poor performance in logic tasks is not necessarily caused by poor logical abilities. Rather, it is caused by the lack of clear communication between the experimenter and participants. The experimenter expects participants to solve a task following the rules of logic, but participants are unaware of it and thus respond adhering to the rules of natural language. Indeed, we found that when the experimenter expresses the task instructions and aim clearly, participants’ performance greatly improves.
Furthermore, many developmental studies on reasoning provide evidence of children’s sensitivity in recognizing the intentions of the speaker, even in the absence of facilitating communicative contexts (Rose and Blank, 1974; McGarrigle and Donaldson, 1975; Kagan, 1981; Markman and Wachtel, 1988; Politzer, 1993, 2016; Gelman and Bloom, 2000; Diesendruck and Markson, 2001; Mosconi and Macchi, 2001). Likewise, many studies (Papafragou and Musolino, 2003; Feeney et al., 2004; Noveck and Sperber, 2004; Sala et al., 2006; Pouscoulous et al., 2007) found that children are able to derive the scalar implicature for “some” if the task is framed in ecological contexts (i.e., movies, storyboards, etc.), which clarify its aim.
Therefore, children’s reasoning performance may depend on their expectations concerning other people’s communicative behavior, as they learn language in a natural context in which conversational implications are an integral part of the meaning conveyed by the statements. This pragmatic hypothesis is supported by the results of a number of experiments concerning class inclusion, conditional reasoning, conservation of numbers, reasoning with quantifiers and connectives (McGarrigle and Donaldson, 1975; Hughes and Donaldson, 1979; Girotto et al., 1989; Politzer, 1993; Politzer and Macchi, 2000; Mosconi and Macchi, 2001; Bagassi et al., 2009).
Another factor that influences adult–child communicative interaction is children’s “attitude of trust” in adults (Harris, 2002; Koenig et al., 2004). In this regard, it has been found that when children have doubts about a given topic, due to their limited epistemic state and the ambiguity of the instructions “they recourse to an important precautionary strategy: attend to the accuracy of what you hear and trust in (previously) reliable informants” and therefore agree with the adult-experimenter (Koenig et al., 2004, p. 698). So, children’s attitude of trust could be a factor masking their reasoning abilities when the task is ambiguous.
In the current study, we argue that for a better understanding of children’s difficulties in solving logical tasks and insight problems, it is crucial to consider that children as well as (or even more than) adults can encounter interpretative difficulties linked to the adoption of natural language and conversational rules. Pragmatic factors can lead them to a misinterpretation of the task instructions. Since pragmatic factors can lead to misinterpretation of task demands, we postulate that by manipulating the instructions, making them clearer, an improvement in children’s performance in logical tasks and understanding problems can be achieved. Pragmatic manipulations not only consist of verbal aspects of the text but also in everything that constitutes the problem: i.e., all those aspects that can create misunderstanding. In the following experiment, the pragmatic manipulation will take place on the figure of the problem in task 1, and on the text of the problem in task 2.
Experiment 1. The Attribution of Intentions in the Assessment Tests of Mathematical Learning
In the light of what has been discussed above, we assume that the problem formulations proposed to school-age children must take into consideration their pragmatic skills, the role exercised by the experimenter–child interaction, and, consequently, the actual message transmitted by the task. If the correspondence between what is said and what is communicated is not fully guaranteed, the wrong answers of the children can be attributed to factors that go beyond the logical–mathematical ability that the task intends to measure. However, the impact that instructions understanding has on task performance is often disregarded. Here, we show that.
For this purpose, two logical tasks were selected from the MAT-2 (a mathematics test for elementary school, see Amoretti et al., 2007), in order to verify the presence of a possible mismatch between the emitted message and the received message. One task involved the understanding of probabilities, while the other concerned geometry.
Notably, this test fits well with recent advances in cognitive psychology supporting the idea that the human mind is inherently probabilistic and works under uncertainty (Baratgin and Politzer, 2006, 2007, 2016). Indeed, children’s inferential abilities are not assessed only with regard to logical axioms, but also in reference to probability theory.
Task 1—Probability
Methods
Participants
In the first task, 60 children attending the fifth grade of a primary school (mean age: 10.4 years; SD: 0.35; F = 27) were randomly assigned to one of two groups. The task was performed as a single activity, without a practice task before. Participants received the instruction by written. One group was administered with the original version of the task, while the other was tested on the experimental version1.
Materials and procedure
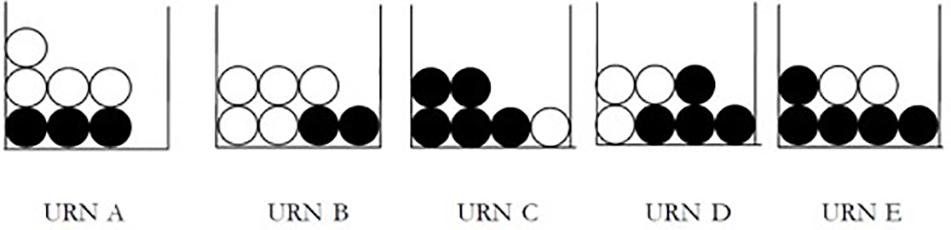
The original version, included in the Logic and Probability section of the MAT-2, presents a series of five urns. Each urn contains white and black balls in different proportions. Participants are asked to identify the urn from which it is more convenient to extract, blindfolded, a white ball. The urns are rectangular and contain seven balls, disposed in two rows, except for an urn in which the balls are arranged in three rows (Figure 1). This arrangement seems to be potentially misleading, shifting the attention of the children from probability calculation to perceptive and contextual reasoning.
Even if the task aims to assess skills related to probabilistic reasoning, it does not request from which urn it is more probable to extract a white ball; rather, it asks to identify from which urn it is more convenient to catch a white ball. In the urn A, a white ball is shown on the top left corner, in a position that seems more easily reachable than any other ball. Hence, it might mislead children into thinking that urn A offers an easier opportunity to catch a white ball. Even if the experimenter expects children to make decisions based on probabilities, the arrangement of the balls (i.e., the perceptual characteristics of the stimuli) offers a different way of deciding, which is entirely justifiable from the children’s point of view.
The perceptual stimulus, therefore, enters into competition with the probabilistic task and the participant should be able to exclude the answer that derives from the perceptual analysis of the stimulus. However, given the request of the task (“from which urn is it more convenient to extract a white ball?”), the perceptual analysis can become crucial and consequently lead to a mismatch between the request of the experimenter and the request as perceived by the participant. In other words, the task seems to draw the attention of the participants on the accessibility of the white ball to be caught, thus making crucial the position of the balls in the urns, rather than their number.
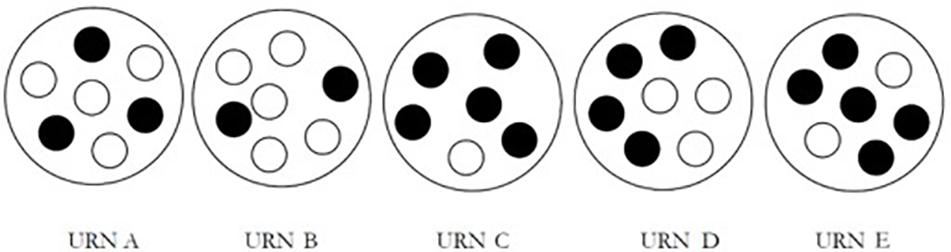
In the experimental version (Figure 2), we propose to overcome these limitations by making urns round and by arranging the seven balls with no specific order.
With this new disposition, the perceptual stimulus does not conflict with the probabilistic task and thus it allows the emergence of the actual logical and mathematical competences of the child.
Each participant was tested individually in order to record, in addition to the answers, the verbal protocols spontaneously expressed, accompanying the solution process2.
Results
The results indicate that, with the original version, only 50% of the participants responded correctly to the question; this percentage increased to 76.7% with the modified version, registering a statistically significant difference between the two versions [χ2(1) = 4.59, p < 0.032, φ = 0.28]. However, what is most interesting concerns the distribution of the answers among the various alternatives (see Table 1).
The experimental version led to an increase in the proportion of correct answers because the number of children selecting the perceptually misleading urn decreased significantly [χ2(1) = 7.92, p < 0.004, φ = 0.36]. Hence, as hypothesized, the disposition of the balls in the urn A in the original version transmitted a misleading message: it was more “convenient” for participants to extract from the urn A not because it was more likely to draw a white ball, but rather just because extracting the white ball was easier. This was confirmed by the analysis of the verbal protocols, which showed that participants are led into thinking that there is a reason why the balls are arranged differently only in urn A (so as to make the white balls more accessible only in this urn) and, consequently, believe they must take this information into account. With the modified version of the task, it emerges that children of 10 years of age can correctly solve this type of probabilistic task to a greater extent than would have been detectable with the original version.
Task 2—Geometry and Fractions
Methods
Participants
The second task was administrated to another group of 60 students from the fifth grade of primary school (mean age: 10.6 years; SD: 0.37; F = 32), who were randomly assigned to one of two versions of the task: an original version and an experimental version3. The task was performed as a single activity, without a practice task before. Participants received the instruction by written.
Materials and procedure
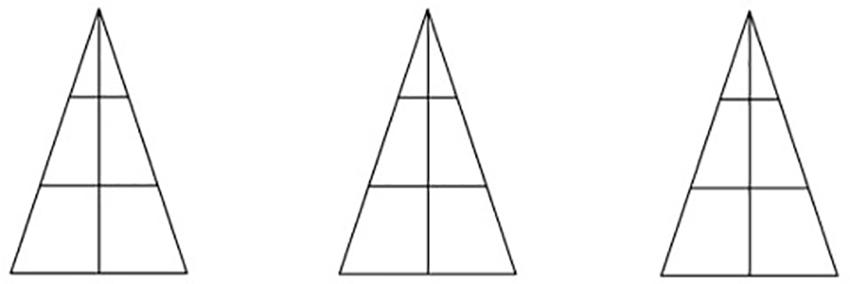
The task consists of a geometry problem, which also introduces the concept of fraction and percentage (Figure 3):
Sketch in three different ways a part of the figure corresponding to the 1/2 fraction.
The correct answer consists in filling in half of each figure, each time using different parts from those already indicated in the previous figures. However, the instruction presents a series of ambiguities from a communicative point of view, which makes it unsuitable to clearly and unequivocally convey its aim. First, it is unclear what “in three different ways” is referring to. It could refer to the ways in which the triangle can be split into halves, as intended by the experimenter, but it could also refer to different ways of shading the triangle (e.g., different types of lines or colors). Furthermore, the triangles are already subdivided in different parts, but it is not made clear to participants whether they should use such subdivisions. Finally, it is asked to outline “a part of the figure”: this aspect is potentially ambiguous too, since the term figure can be referred to each triangle, but also to the set of three triangles which, being presented all together, and being all identical, can be considered as a whole.
Therefore, an alternative version of the question has been formulated to resolve the ambiguities in the transmission of the task goal:
Color 1/2 of the area of each triangle. To color half of the area, use the parts drawn in the triangle, in order to always have different combinations for each of the three triangles.
This version explicitly introduces the concept of “area” of the triangle, a concept necessary to understand that the parts of the figure are symmetrical and can be inverted to build the half of the triangle. In addition, it makes direct reference to the use of the parts in which each triangle has already been divided and to their combined use in different ways.
Each version has been individually submitted to 30 participants. In order to detect the reason for the errors, we also collected verbal protocols spontaneously expressed.
Results
Results indicate a very high percentage of errors in the original version of the task (93.33%). From the analysis of the responses, it was possible to identify some types of recurring errors (see Table 2).
As reported in Table 2, in the original version, the task errors are strictly related to the use of the term “sketch.” Moreover, the wording outlines in three different ways is interpreted by participants in numerous different ways. In the case of errors of type a) and b), participants understand the hatching as drawing a line that divides the triangle or its parts in half. In the case of the error of type d), participants adopt different hatch styles to highlight half of the triangle, without changing the choice of the parts selected, since the type of line varies. Overall, the errors attributable to the participants’ incompetence in identifying three different ways to divide a triangle in half represent only 23.33% of the total errors (answers type f and g).
On the contrary, the results indicate that 70% of correct answers have been obtained with the experimental version of the task. The difference between the correct responses in the original version compared with those obtained in the experimental version is statistically significant [χ2(1) = 20.84, p < 0.001, φ = 0.59].
Experiment 2. Insight Problem Solving in Children
In the second experiment, we investigated the source of problem forming, for the impact that this issue has in problem solving. Sometimes the difficulty in problem solving lies in the calculations to be made, the number of operations to be performed, and the quantity of data to be processed and remembered (procedural problems, for instance, the well-known problem of the Tower of Hanoi). There are, however, other problems in which the difficulty does not lie in the complexity of the calculations, but rather in one or more critical points of the text-problem that are susceptible to misunderstanding (insight problem solving, for instance, the nine-dots problem, see Macchi and Bagassi, 2015).
We will focus on this second type of problems since they allow us to explore our hypothesis regarding the close interconnection between text and solution understanding. In our view, the way of thinking involved in insight problem solving is very close to the process involved in the understanding of an utterance when a misunderstanding occurs. In both cases, a more appropriate meaning has to be selected to resolve the misunderstanding that produced an “impasse.” The default interpretation (i.e., the “fixation”) has to be dropped in order to “restructure,” to grasp another meaning which appears more relevant to the context and the speaker’s intention.
Many studies have already demonstrated the influence of pragmatic factors on insight problem solving in adults (Mosconi, 1990, 2016; Macchi and Bagassi, 2012, 2015, 2018; Bagassi and Macchi, 2016). According to our hypothesis, the difficulty of these problems is never objective and computational, but instead subjective and interpretative. The difficulty of the problem is given by how it is formulated since this brings to the activation of the default interpretation which obscures the solution. A re-formulation of the text, more relevant to the aim of the task, should reduce the problem knot. This time, language and thought would work together in an interrelated interpretative “game.” The importance of how the problem is phrased should not be underestimated, both from the point of view of how the problem is formed in the solver’s mind and how it is solved.
We have examined insight problems with children, exploring as well the hypothesis that a relevant understanding of the text would promote the resolution of this particular type of problems. Three well-known insight problems have been investigated (Dow and Mayer, 2004; Frederick, 2005; Gilhooly and Murphy, 2005) by submitting a new experimental version for each problem where we removed pragmatically unfelicitous factors that could hinder the interpretation relevant to the aim of the task, but leaving the rest unchanged.
Methods
Participants and Procedure
The participants were 82 children (mean age: 10.45 years, SD: 0.49; F = 46) attending the fifth class of primary school4.
Children were randomly assigned to the control group and to the experimental group. They were submitted only one version of each problem to be solved individually, in a randomized order. The task was performed as a single activity, without a practice task before. Participants received the instruction by written. All the children had access to paper and pencil to perform the calculations and to answer the questions. There was no time limit.
Materials
The three problems used in our study are listed below.
(1) The Zoo problem:
Yesterday I went to the zoo and I saw giraffes and ostriches. Altogether they had 30 eyes and 44 legs. How many animals were there?
(2) The Two Coins problem:
In my pocket, I have two Italian coins that together are 70 cents, but one is not 20 cents. How could it be?
(3) The Bat and Ball problem:
A bat and a ball cost $1.10 in total. The bat costs $ 1.00 more than the ball.
How much does the ball cost?___cents.
For what concerns the first problem, we hypothesized that the critical issue was the irrelevant information (in this case, the “44 legs”), that was necessary to inhibit to reach the proper solution. We have thus reformulated the problem (the Zoo Experimental version) in order to point out that not all the given data are relevant to respond correctly:
Yesterday I went to the zoo and saw giraffes and ostriches. Altogether they had 30 eyes and 44 legs. How many animals were there? Try to use the data of the problem that more than others are important to decide how many animals there were.
In the Two Coins problem, the use of “but” seems to rule out the possibility that any 20-cent coins are present. So, in the experimental version, we have removed “but” in order to eliminate the conversational implicature underlying this function word:
In my pocket I have two Italian coins that together are 70 cents; one is not 20 cents. How could it be?
For what concerns the Bat and Ball problem, the answer which immediately comes to mind is 10 cents, which is incorrect as, in this case, the difference between $ 1.00 and 10 cents is only 90 cents, not $1.00 as the problem stipulates. The correct response is 5 cents. Number physiognomics and the plausibility of the cost are traditionally considered responsible for this kind of error (Kahneman, 2003; Frederick, 2005).
These factors aside, we argue that if the rhetoric structure of the text is analyzed, the question concerns only the ball, implying that the cost of the bat is already known. The question gives the key to the interpretation of what has been said in the problem and the given data is thus interpreted in the light of the question. Hence, “The bat costs $ 1.00 more than” becomes “The bat costs $ 1.00,” by leaving out “more than” (as already shown with adults, see Macchi and Bagassi, 2012).
Consequently, we reformulated the text to eliminate this misleading inference:
A bat and a ball cost $1.10 in total. The bat costs $ 1.00 more than the ball.
How much does the ball cost? How much does the bat cost?
Results
Table 3 shows the percentages of children who have provided the correct answer to the problems presented in their original and modified versions. For all the problems, in the experimental conditions, there is statistically significant increase in the number of participants who correctly solved the problems, respectively, for the Zoo problem [χ2(1) 29.99, p < 0.001, φ = 0.60], for the Two Coins problem [χ2(1) 37.29, p < 0.001, φ = 0.67], and for the Bat and Ball problem [χ2(1) 47.74, p < 0.001, φ = 0.76].
Conclusion
In the current paper, we have addressed the role that pragmatic and communicative factors play when solving logical and insight problems. Previous research on adults showed that manipulating the task instructions of logical problems systematically lead to a substantial improvement in their performance (Macchi et al., 2020). However, whether these facilitatory effects extended to children was still unknown. Here, we showed that 10-year-old children’s problem-solving skills are usually underrated, and that when task instructions adhere to conversational rules, children’s logical abilities can emerge.
Experiment 1 focused on two tasks concerning the concepts of probability and geometry. The original versions of the task instructions presented potentially misleading formulations. In the first task, the concept of probability was not mentioned in the instructions, leading participants into thinking that the task could be solved by taking into account the perceptual accessibility of the elements rather than the statistical properties of the environment. Simply by changing the perceptual appearance of the task, we successfully communicated the intention to reason about probability and we obtained a significantly greater number of correct answers. In the second task, the question was ambiguously formulated and thus it did not adequately convey the experimenter’s intention. Our pragmatically valid variation of the task instruction eliminated the types of errors that were typically found in the original version. Overall, considering the communicative aspects of the tasks, we were able to obtain a more effective measure of the mathematical competence of the participants.
In experiment 2, we investigated the influence of pragmatic factors on children’s ability to solve insight problems. Insight problems are fundamentally different from mathematical problems. The latter are usually solved following a step-by-step procedure that gradually leads to the solution (Mosconi, 1990). Conversely, insight problems are often solved with a sudden a-ha! experience. Yet, also insight problems heavily depend on communicative factors, as the cognitive process that leads to the solution shares the interpretative nature that belongs to intention-attribution, which is pivotal in communication (Macchi and Bagassi, 2015). We tested 10-year-old children on classic insight tasks (the Zoo problem, the Two Coins problem, and the Bat and Ball problem) with the original version of the instructions or with a novel version that was devised keeping into account the pragmatic factors at play. The results reported a heavy improvement in children’s performance with the modified version of the task instructions, across all problems. The improved performance that occurred after the reformulations showed that the difficulty in problem solving arose from difficulties in understanding the text.
The studies that have examined problem solving in children have rarely included insight problems (Davidson and Sternberg, 1984, 1998; Sternberg and Davidson, 1995; Bermejo et al., 1996), presumably considering them too complex. However, children often find themselves in new situations in which they must restructure the surrounding context to be able to negotiate it adaptively. Often, too, these situations require children to use their creativity and apply alternative or unconventional thinking. Insight problem solving, given its nature, encourages divergent thinking to a greater extent than procedural tasks (Wertheimer, 1945; Guilford, 1959; Gilhooly, 2016) and is thus crucial to reach a wider understanding of the development of problem-solving skills.
On the educational side, the teaching practices implemented in classes play an essential role in the nature and quality of students’ learning (Good and Brophy, 1972; Dupriez and Dumay, 2009; Slavin, 2009). Future research should thus investigate if a pragmatic approach in teaching practices could alleviate many of the difficulties that students face, especially in mathematics. The need to encourage pragmatic-interpretative skills might also benefit students with learning disabilities, that have been shown to have important developmental gaps in metacognition (Palincsar and Brown, 1987; Wang et al., 1993; Cornoldi and Oakhill, 2013). Precisely for this reason, future studies should explore the relationships among metacognition, pragmatic abilities, and problem solving.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Ethics Statement
The studies involving human participants were reviewed and approved by Comitato Etico di Ateneo, Università degli Studi di Milano-Bicocca. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author Contributions
MB, NS, VC, VS, LC, FP, and LM conceived, planned, and carried out the experiments. All authors discussed the results and contributed to the manuscript.
Funding
Funds recieved for open access publication fees from the Department of Psychology, University of Milano-Bicocca: 2020-CONT-0171, 2017-ATE-0517, and 2018-ATE-0512.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
- ^ Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
- ^ For both tasks, 1 and 2, participants were informed that they were recorded and that verbal protocols would be transcribed. We consider verbal protocols as spontaneous justifications given from the children to their answers. To not render them artificial, children did not receive specific instructions or training, and therefore we do not have a systematic collection of protocols.
- ^ Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
- ^ Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
References
Amoretti, G., Bazzini, L., Pesci, A., and Reggiani, M. (2007). Prove di Matematica – MAT-2. Firenze: Giunti Editore.
Bagassi, M., D’Addario, M., Macchi, L., and Sala, V. (2009). Children’s acceptance of underinformative sentences: the case of some as a determiner. Think. Reason. 15, 211–235.
Bagassi, M., and Macchi, L. (2016). “The interpretative function and the emergence of unconscious analytic thought,” in Cognitive Unconscious and Human Rationality, eds L. Macchi, M. Bagassi, and R. Viale (Cambridge, MA: MIT Press), 43–76.
Baratgin, J., and Politzer, G. (2006). Is the mind Bayesian? The case for agnosticism. Mind Soc. 5, 1–38.
Baratgin, J., and Politzer, G. (2007). The psychology of dynamic probability judgment: order effect, normative theories, and experimental methodology. Mind Soc. 6, 53–66.
Baratgin, J., and Politzer, G. (2010). Updating: a psychologically basic situation of probability revision. Think. Reason. 16, 253–287.
Baratgin, J., and Politzer, G. (2016). “Logic, probability and inference: a methodology for a new paradigm,” in Cognitive Unconscious and Human Rationality, eds In L. Macchi, M. Bagassi, and R. Viale (Cambridge, MA: MIT Press), 119–142.
Bermejo, M. R., Sternberg, R. J., and Sánchez, M. D. P. (1996). How solve verbal and mathematical insight problems children with high general intelligence level. Faisca 4, 76–84.
Cornoldi, C., and Oakhill, J. V. (eds) (2013). Reading Comprehension Difficulties: Processes and Intervention. New York: Routledge.
Davidson, J. E., and Sternberg, R. J. (1984). The role of insight in intellectual giftedness. Gifted Child Q. 28, 58–64.
Davidson, J. E., and Sternberg, R. J. (1998). “Smart problem solving: how metacognition helps,” in Metacognition in Educational Theory and Practice, eds D. J. Hacker, J. Dunlosky, and A. C. Graesser, (New York: Routledge), 61–82.
Diesendruck, G., and Markson, L. (2001). Children’s avoidance of lexical overlap: a pragmatic account. Dev. Psychol. 37, 630–641.
Dow, G. T., and Mayer, R. E. (2004). Teaching students to solve insight problems: evidence for domain specificity in creativity training. Creat. Res. J. 16, 389–398.
Dulany, D. E., and Hilton, D. J. (1991). Conversational implicature, conscious representation, and the conjunction fallacy. Soc. Cogn. 9, 85–110.
Dupriez, V., and Dumay, X. (2009). “Les conceptions de la justice des enseignants du primaire,” in Les Sentiments de Justice d et Sur L’école, eds M. Duru-Bellat et and D. Meuret (Bruxelles: De Boeck), 141–157.
Feeney, A., Scrafton, S., Duckworth, A., and Handley, S. J. (2004). The story of some: everyday pragmatic inference by children and adults. Can. J. Exp. Psychol. 58, 121–132. doi: 10.1037/h0085792
Gelman, S. A., and Bloom, P. (2000). Young children are sensitive to how an object was created when deciding what to name it. Cognition 76, 91–103. doi: 10.1016/s0010-0277(00)00071-8
Gilhooly, K. J. (2016). Incubation and intuition in creative problem solving. Front. Psychol. 7:1076. doi: 10.3389/fpsyg.2016.01076
Gilhooly, K. J., and Murphy, P. (2005). Differentiating insight from non-insight problems. Think. Reason. 11, 279–302.
Girotto, V., Blaye, A., and Farioli, F. (1989). A reason to reason: pragmatic basis of children’s search for counter examples. Eur. Bull. Cogn. Psychol. 9, 297–321.
Good, T. L., and Brophy, J. E. (1972). Behavioral expression of teacher attitudes. J. Educ. Psychol. 63, 617–624.
Grice, H. P. (1975). “Logic and conversation,” in Syntax and Semantics, Vol. 3. Speech acts eds P. Cole and J. Morgan (New York, NY: Academic Press), 41–58.
Harris, P. (2002). “What do children learn from testimony?,” in The Cognitive Basis of Science, eds P. Carruthers, S. Stich, and M. Siegal (Cambridge: Cambridge University Press), 316–334.
Hilton, D. J. (1995). The social context of reasoning: conversational inference and rational judgment. Psychol. Bull. 118, 248–271.
Hughes, M., and Donaldson, M. (1979). The use of hiding games for studying the coordination of viewpoints. Educ. Rev. 31, 133–140.
Kagan, J. (1981). The Second Year: The Emergence of Self Awareness. Cambridge, MA: Harvard University Press.
Kahneman, D. (2003). Maps of bounded rationality: psychology for behavioral economics. Am. Econ. Rev. 93, 1449–1475. doi: 10.3758/s13423-016-1198-z
Koenig, M. A., Clément, F., and Harris, P. L. (2004). Trust in testimony: children’s use of true and false statements. Psychol. Sci. 15, 694–698.
Levinson, S. C. (1995). “Interactional biases in human thinking,” in Social Intelligence and Interaction, ed. E. N. Goody (Cambridge: Cambridge University Press), 221–261.
Macchi, L. (2000). Partitive formulation of information in probabilistic problems: beyond heuristics and frequency format explanations. Organ. Behav. Hum. Decis. Process. 82, 217–236.
Macchi, L., and Bagassi, M. (2006). “Biased communication and misleading intuition of probability,” in Proceedings of the International Workshop on Intuition and Affect in Risk Perception and Decision Making, Bergen.
Macchi, L., and Bagassi, M. (2012). Intuitive and analytical processes in insight problem solving: a psycho-rhetorical approach to the study of reasoning. Mind Soc. 11, 53–67.
Macchi, L., and Bagassi, M. (2015). When analytic thought is challenged by a misunderstanding. Think. Reason. 21, 147–164.
Macchi, L., and Bagassi, M. (2018). A new test for rationality: contributions and outstanding issues. Am. J. Psychol. 131, 237–240.
Macchi, L., Caravona, L., Poli, F., Bagassi, M., and Franchella, M. A. (2020). Speak your mind and I will make it right: the case of “selection task”. J. Cogn. Psychol. 32, 93–107.
Macchi, L., Poli, F., Caravona, L., Vezzoli, M., Franchella, M. A. G., and Bagassi, M. (2019). How to get rid of the belief bias: boosting analytical thinking via pragmatics. Eur. J. Psychol. 15, 595–613.
Markman, E. M., and Wachtel, G. F. (1988). Children’s use of mutual exclusivity to constrain the meanings of words. Cogn. Psychol. 20, 121–157.
Mosconi, G. (2016). “A psycho-rhetorical perspective on thought and human rationality,” in Cognitive Unconscious and Human Rationality, eds L. Macchi, M. Bagassi, and R. Viale (Cambridge, MA: MIT Press), 347–363.
Mosconi, G., and Macchi, L. (2001). The role of pragmatic rules in the conjunction fallacy. Mind Soc. 2, 31–57.
Palincsar, A. S., and Brown, D. A. (1987). Enhancing instructional time through attention to metacognition. J. Learn. Disabil. 20, 66–75.
Papafragou, A., and Musolino, J. (2003). Scalar implicatures: experiments at the semantics–pragmatics interface. Cognition 86, 253–282.
Politzer, G. (1993). La Psychologie du Raisonnement: Lois de la Pragmatique et Logique Formelle. Ph.D. Dissertation, University of Paris VIII, Saint-Denis.
Politzer, G. (2016). The class inclusion question: a case study in applying pragmatics to the experimental study of cognition. SpringerPlus 5:1133. doi: 10.1186/s40064-016-2467-z
Pouscoulous, N., Noveck, I. A., Politzer, G., and Bastide, A. (2007). A developmental investigation of processing costs in implicature production. Lang. Acquis. 14, 347–375.
Rose, S. A., and Blank, M. (1974). The potency of context in children’s cognition: an illustration through conservation. Child Dev. 45, 499–502.
Sala, V., Macchi, L., Bagassi, M., and D’Addario, M. (2006). I bambini sono davvero “più logici” degli adulti? Il caso del quantificatore “Alcuni”. G. Ital. Psicol. 33, 559–582.
Slavin, R. E. (2009). Cooperative Learning: Theory, Research, and Practice. Boston, MA: Allymand Bacon.
Sperber, D., Cara, F., and Girotto, V. (1995). Relevance theory explains the selection task. Cognition 57, 31–95.
Sperber, D., and Wilson, D. (1995). Postface to the Second Edition of Relevance: Communication and Cognition. Oxford: Blackwell.
Van der Henst, J.-B., Sperber, D., and Politzer, G. (2002). When is a conclusion worth deriving? A relevance-based analysis of indeterminate relational problems. Think. Reason. 8, 1–20.
Wang, M. C., Haertel, G. D., and Walberg, H. J. (1993). Toward a knowledge base for school learning. Rev. Educ. Res. 63, 249–294.
Keywords: deductive reasoning, logical reasoning, insight problems, pragmatic approach, primary school children, task instructions
Citation: Bagassi M, Salerni N, Castoldi V, Sala V, Caravona L, Poli F and Macchi L (2020) Improving Children’s Logical and Mathematical Performance via a Pragmatic Approach. Front. Educ. 5:54. doi: 10.3389/feduc.2020.00054
Received: 10 February 2020; Accepted: 20 April 2020;
Published: 14 May 2020.
Edited by:
Alessandro Antonietti, Catholic University of the Sacred Heart, ItalyReviewed by:
Gaston Saux, Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), ArgentinaJean Baratgin, Université Paris 8, France
Copyright © 2020 Bagassi, Salerni, Castoldi, Sala, Caravona, Poli and Macchi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Laura Macchi, bGF1cmEubWFjY2hpQHVuaW1pYi5pdA==
 Maria Bagassi
Maria Bagassi Nicoletta Salerni1
Nicoletta Salerni1 Francesco Poli
Francesco Poli Laura Macchi
Laura Macchi