Characteristics of Effective Self-Regulated Learning Interventions in Mathematics Classrooms: A Systematic Review

Wang, Ying; Sperling, Rayne A.

doi:10.3389/feduc.2020.00058

SYSTEMATIC REVIEW article

Front. Educ., 29 May 2020

Sec. Educational Psychology

Volume 5 - 2020 | https://doi.org/10.3389/feduc.2020.00058

This article is part of the Research Topic Psychology and Mathematics Education View all 40 articles

Characteristics of Effective Self-Regulated Learning Interventions in Mathematics Classrooms: A Systematic Review

$\nYing Wang$ Ying Wang^*

Rayne A. Sperling

Department of Educational Psychology, Counseling, and Special Education, The Pennsylvania State University, University Park, PA, United States

Several meta-analyses suggest that identifiable characteristics of self-regulated learning interventions result in improvement in students' academic performance and self-regulatory competence across content areas. Nevertheless, little is known about recent interventions and about specific characteristics of interventions that may be domain specific. In this systematic review, we targeted mathematics and reviewed 36 self-regulated learning intervention studies conducted with school-aged learners. We examined patterns of effective interventions with identified characteristics, such as theoretical guidance, type of strategies instructed, type of outcome assessments, and targeted outcomes. Findings revealed that those interventions grounded in metacognition-oriented theories and those interventions that targeted multiple strategies including cognitive, metacognitive, and motivational, tended to yield effective increases in both mathematics achievement and self-regulated learning. The review also examined patterns within interventions conducted from 1992 to 2020. Findings indicate recent interventions tend to adopt a social-cognitive SRL model and employ standardized knowledge assessments. Implications for practice and future self-regulated learning interventions in mathematics are discussed.

Introduction

One focus of education is to develop self-regulated learners. Self-regulated learners are active agents who use a repertoire of knowledge and strategies to regulate their learning adaptively and efficiently (Zimmerman, 1990, 2002; Schraw and Moshman, 1995). Self-regulated learners also examine their strengths and weakness against academic task standards in order to set appropriate goals, deploy strategies, adapt to varying environments, and to overcome obstacles (Winne and Hadwin, 1998; Zimmerman, 2002). In addition to vast theoretical support that self-regulated learning strategies should result in increased learning (e.g., Zimmerman, 1990), findings from intervention studies establish that effective self-regulated learning (SRL) is associated with improved academic achievement (e.g., Schmitz and Wiese, 2006). Recent systematic reviews and meta-analytic studies (online learning: Broadbent and Poon, 2015; long-term effects of metacognitive strategy training: de Boer et al., 2018; learning strategies: Donker et al., 2014) examined different aspects of SRL interventions. Particularly, in the last decade, Dignath and colleagues conducted two comprehensive meta-analyses and examined the effectiveness of SRL interventions for primary and secondary school students (Dignath and Büttner, 2008; Dignath et al., 2008). Their findings demonstrated that students improved their academic performance as well as their self-regulatory strategy use through SRL interventions. In terms of academic domain, findings supported that SRL interventions were more effective for mathematics than language arts.

Given these previous findings, we were interested in a focused examination of possible unique elements that contribute to effective SRL interventions in mathematics in school-aged learners. School mathematics is a known gatekeeper to future careers in STEM fields (e.g., Douglas and Attewell, 2017; Scott et al., 2017; Woods et al., 2018; Torbey et al., 2020). Achievement and engagement in school mathematics are also critical factors for post-secondary mathematics enrollment (e.g., Byun et al., 2015; McDonald, 2016). Therefore, a specific focus on mathematics SRL interventions is warranted.

While students may benefit from general self-regulated learning interventions, effective SRL is domain- and task-specific. The strategies students employ, their motivational beliefs and efficacy, and the nature of their metacognitive knowledge and regulation would vary given a specific learning task and by academic domain (Rickey and Stacy, 2000). Further, self-regulated learning in mathematics may also present unique challenges. For example, Pape and colleagues recognized the critical and unique role that SRL can play in supporting mathematical thinking in middle school learners (e.g., Pape et al., 2003; Bell and Pape, 2014). Among other scholars, Aminah et al. (2018) also recognized the need for instruction to target SRL elements for effective mathematical thinking. Their work particularly targeted metacognitive teaching and learning in high school students.

However, there are differences in intervention elements for older learners (e.g., middle school and high school students) when compared to younger learners (e.g., kindergarten and young elementary students). Specifically, older learners may need more intense intervention activities and an incorporation of cognitive, motivational, and metacognitive elements to improve their mathematics learning effectively. There are several reasons. First, students in higher grade levels are at a critical time to develop learning in mathematics and to build trajectories toward STEM fields and other career paths (Anderton et al., 2017; Berger et al., 2020; Torbey et al., 2020). Second, students often do not successfully master mathematics content, especially as the demands of higher-level mathematics increase (Cleary and Chen, 2009; Grønmo et al., 2015). Particularly, mathematics may be more challenging for students who are experiencing the difficult transition from elementary to advanced mathematics. Challenges in advanced mathematics curriculum may lead to students' failure, a lack of interest in gaining mathematics achievement, and a detrimental decrease in engagement and subsequent learning in mathematics (Anderton et al., 2017; Berger et al., 2020). Effective self-regulatory strategies may serve to support older learners and mitigate the challenges they face. Young children, in comparison, face different challenges, such as recognizing and writing down mathematical symbols (Hughes, 1986), which requires different teaching and learning strategies.

To our knowledge, there is no previous systematic review of SRL interventions for mathematics targeting both young children and their older peers. With the emergence of new theoretical models of SRL and additional intervention studies, a more refined analyses of SRL interventions in mathematics is warranted. Therefore, in this systematic review, we identified the effective characteristics of existing SRL interventions focused on students' mathematics learning. Our intent is both to inform additional research and to advise effective classroom practice.

Theoretical Models of SRL

SRL interventions are guided by theoretical models. SRL theoretical models include those proposed by Boekaerts (1996); Winne and Hadwin (1998); Pintrich (2000); Zimmerman (2000); Efklides (2011). Two theoretical reviews (Puustinen and Pulkkinen, 2001; Panadero, 2017) identified and compared models of SRL. Through their analysis, Puustinen and Pulkkinen (2001) determined SRL models can be categorized as motivation-oriented models, strategy-oriented models, and those with both orientations. Specifically, both Boekaerts' and Pintrich's models of SRL emphasize motivation and examine motivational factors in relation to students' learning. Pintrich, for example, incorporated motivational and affective aspects reflecting learners' self-efficacy and goal orientation during self-regulatory processes. Interventions grounded in these models target varied elements of SRL. For instance, corresponding to the affective component of Pintrich's model, Tzohar-Rozen and Kramarski (2014) examined fifth graders' mathematics achievement and affective self-regulation through a 5 week intervention designed to promote positive emotions with affective self-regulatory strategy use. Students were asked to reflect and self-question their emotions before, during, and after task completion, and to regulate possible negative emotions. Findings demonstrated that students who received the intervention significantly decreased negative emotions.

In comparison, Winne and Hadwin's SRL model is strategy-oriented and emphasizes metacognition. Specifically, this model defines SRL as a metacognition-driven process where learners regulate their learning and use of strategies based upon task context Winne and Hadwin (1998, 2008). Duffy and Azevedo (2015) adopted this model and examined undergraduates' growth in academic achievement and SRL through MetaTutor, a hypermedia tutoring system. MetaTutor aimed to scaffold students' SRL strategy use during their learning of the human circulatory system by providing prompts and feedback from a virtual tutor agent. Students in the experimental condition received prompts and feedback from the virtual tutor and were compared to students who received no prompts nor feedback. The prompts served as a reminder of strategy use and encouraged students to deploy specific SRL strategies for particular learning situations, such as rereading and assessing their own understanding of the human circulatory system, during the learning process. Findings indicated that students in the prompt and feedback condition demonstrated more frequent use of SRL strategies and improved achievement performance. Consistent with Winne and Hadwin's model, they emphasized teaching students' task-specific SRL strategies in context-specific situations.

In contrast, Zimmerman's three-phased cyclical SRL model (i.e., forethought phase, performance phase, and self-reflection phase) is considered both motivation- and strategy-oriented. The forethought phase reflects students' motivational factors (e.g., self-efficacy) in setting goals for a task, and strategic factors in planning use of strategies. The performance phase reflects motivational factors in completing the task and strategic factors in using strategies during task completion. For instance, students may use self-instructions as a strategy, as well as maintain motivation during the performance phase. Finally, the third, self-reflection phase, determines students' satisfaction with their task product, which, in turn, influences their next phases in setting goals, planning, and strategy use. With the interaction between motivation and strategy orientations, Zimmerman's phased cyclical model grounded in social-cognitive theory, provides a framework often adopted by researchers and practitioners. As the model describes self-regulatory processes in detail, it can provide insight into the effective design and testing of interventions for students' SRL and academic achievement (Panadero and Alonso-Tapia, 2014).

A more recent theoretical review by Panadero (2017) further examined SRL models and included newly emerged models and more recent empirical evidence. For instance, Efklides's (2011) model, which considers both metacognitive and affective perspectives [metacognitive and affective model of self-regulated learning (MASRL)] leverages previous theoretical SRL models. Specifically, Efklides' model includes a person level, which refers to a learner's characteristics, and a person-and-task level, referring to the interaction between a learner's characteristics and the nature of the task. The person level reflects Zimmerman's SRL model with a focus on affect; and the person-and-task level reflects Winne and Hadwin's SRL model that focuses on the task context. Dina and Efklides (2009) adopted the preliminary MASRL model and examined relationships among person characteristics, mathematics performance, and emotions by creating individual student profiles. As a result, they identified eight student profiles that reflected various person characteristics, such as self-anxiety, performance ability, and self-concept. The findings of the profiles further indicated that students with varied person characteristics had different task perceptions and varied levels of performance, as expected and supported by the MASRL model.

As such, the theoretical orientation adopted to support an intervention may directly influence elements of the intervention, the instructional strategies employed by the intervention, the degree and nature of scaffolding in an intervention, as well as the role and nature of feedback and assessments employed. Corresponding to Panadero (2017), the impact of interventions varied based upon their theoretical framework and therefore it is critical to consider which theoretical framework was adopted when examining the effectiveness of SRL interventions. In short, all aspects of an intervention may be influenced by the choice of theoretical framework. This review sought to explore these impacts.

Effectiveness of SRL Interventions

As noted, Dignath et al. (2008) conducted two meta-analyses focused on the effective characteristics of SRL interventions in classrooms. Their work demonstrated general improvement in students' academic performance and SRL through intervention, with an average effect size of 0.69 (Cohen's d). Dignath et al. (2008) first examined the effects of existing interventions on primary school students' SRL and academic performance based upon 48 comparisons resulting from 30 articles across academic content domains. They reported that, based on the included studies, interventions that targeted mathematics performance demonstrated the highest effect (d = 1.00). In comparison, SRL interventions that targeted reading and writing performance demonstrated less effect (d = 0.44). In further analysis, Dignath et al. (2008) categorized the intervention strategies into cognitive strategy, metacognitive strategy, and motivational strategy interventions. Findings showed that students benefited most from the combination of metacognitive and cognitive strategies or metacognitive and motivational strategies, when compared to interventions of cognitive strategies alone. Instruction of motivational strategies alone was also quite effective for both academic performance and SRL outcomes. Dignath and her colleagues further concluded that the most effective SRL interventions were grounded in social cognitive theory, and included instruction or training of combined cognitive, metacognitive, and motivational strategies (2008).

Building upon their previous review, Dignath and Büttner (2008) expanded their meta-analysis to include interventions conducted with secondary school students and drew comparisons to those with primary school students. They included 35 studies and reported that, overall, secondary school students' academic performance (d = 0.71) improved slightly better than primary school students (d = 0.68) through SRL interventions. Specifically, reading and writing performance demonstrated higher effect sizes for secondary school students (d = 0.92) than primary school students (d = 0.44) with the implementation of SRL interventions. In mathematics, however, SRL interventions were more effective for primary school students' mathematics performance (d = 0.96) than secondary school students (d = 0.23). These findings may correspond to the high difficulty and intensity in mathematics that secondary students confront. It also indicated the need to develop effective SRL interventions in mathematics for older students. Importantly, although the effect for secondary students in mathematics was lower than primary students, secondary students were reported to use strategies more effectively (d = 0.88) than primary students (d = 0.72). This finding corresponds to the developmental nature of SRL as secondary students tend to have a larger repertoire of strategies available to support their learning processes (Flavell, 1979; Flavell et al., 1995; Kuhn, 2000; Brown et al., 1996). Consistent with findings from Dignath and her colleagues' previous review, they reported that instruction for secondary school students with combined metacognitive and motivational strategies led to higher effectiveness when compared to cognitive strategies alone. However, little is known about how cognitive, metacognitive, and motivational strategies may affect students' SRL and learning in mathematics specifically. The present review examined how these types of strategies were varied in students' SRL and academic performance in mathematics.

Taking a closer look of strategies included in SRL interventions, a later meta-analysis by Donker et al. (2014) focused on specific types of strategies and substrategies that were implemented in SRL interventions with primary and secondary school students for writing, science, mathematics, and comprehensive reading. With a focus on strategy characteristics that may improve students' academic performance, they reported that, overall, strategy training in mathematics was more effective than comprehensive reading. Interestingly, cognitive strategies were found more effective in mathematics than motivational strategies, in contrast with Dignath et al. (2008). Donker et al. (2014) further examined student characteristics that may affect the effectiveness of interventions. Findings demonstrated that both primary and secondary school students benefited from interventions, however, there was not a significant difference between primary and secondary students. This differs from Dignath and Büttner (2008) where SRL interventions were overall more effective for primary school students when compared to secondary students in mathematics. In the present review, we sought to understand these inconsistent findings and to identify elements that may contribute to effective SRL interventions in mathematics.

SRL in Mathematics

SRL interventions are beneficial for learners' improved performance in a variety of academic domains. Empirical evidence indicated that SRL was associated with academic performance in general. For instance, Zimmerman and Martinez-Pons (1986) examined high school students' use of 14 SRL strategies by conducting a structured interview procedure across six different learning contexts including learning situations across domains (i.e., writing assignments and mathematics assignments) in classrooms and at home. Through the interviews, Zimmerman and Martinez-Pons (1986) found that, when compared to low-performing students, high-performing students utilized multiple strategies instead of a single strategy. High-performing students also reported more frequent use of SRL strategies than low-performing students who reported rarely using strategies. This evidence supported that SRL strategies were associated with academic achievement across academic domains and task contexts. However, SRL is also considered domain specific as it is related to students' cognitive skills in specific academic domains. For example, Moos and Azevedo (2008) reported that college students with high prior knowledge in biology tended to use monitoring and planning strategies frequently during a learning task with hypermedia when compared to students with low prior knowledge. Schunk (1987) also suggested that the domain specificity of SRL can be explained by the characteristics of self-efficacy. Specifically, self-efficacy refers to students' perceived capabilities to perform a future specific task (Bandura, 1986). Students tend to perceive their capabilities more accurately when more specific information is provided for the task. In SRL, the extent to which students feel self-efficacious about performing a task determines the plans and goals they set before the task, the strategies they use during the task, and the self-evaluation standards they compare against the final task product.

Within the domain of mathematics, Cleary et al. (2017) tested a SRL intervention (SREP) and found increases in middle school students' SRL and mathematics performance. Grounded in Zimmerman's SRL model, the SREP intervention guided students to understand SRL concepts, practice self-regulated strategies, and reflect on their performance. Similarly, Desoete et al. (2003) previously reported students' improvement in mathematics and SRL. In their study, students who were assigned to the metacognition condition received training sessions of metacognitive strategies. Findings demonstrated that students in the metacognition condition improved cognitive and metacognitive skills in mathematics than students in the control condition.

The above evidence is extracted from short-term SRL interventions, while longitudinal studies also showed significant improvement in students' mathematics achievement and SRL. For instance, Núñez et al. (2013) implemented a school-year long mentoring program with teacher mentors that taught 7th graders SRL strategy use to enhance their language and mathematics achievement and their SRL and motivation. Students were asked to read stories about how a story character overcame obstacles and deployed SRL strategies in different learning situations. Mentors then directed students to learn from those stories and self-evaluate their declarative knowledge, procedural knowledge, and conditional knowledge of different SRL strategy use (e.g., taking notes) during learning. Mentors also led discussions about how students could best deploy identified SRL strategies as well as build a larger repertoire of strategies. As a result, Núñez et al. (2013) reported that both students' SRL strategy use and their mathematics achievement were improved. Although these interventions demonstrated effective results in students' SRL and mathematics achievement, an examination of how these intervention activities were designed and delivered to students is in need.

Specifically, a variety of treatment traits of existing interventions can be further examined (e.g., types of strategies implemented). These treatment traits may reveal why existing SRL interventions for older mathematics students were less effective when compared to their younger peers. Further, identification of such treatment traits may also inform future directions in developing effective SRL interventions.

One overall purpose of this systematic review was to identify the effective characteristics of existing SRL interventions in mathematics, with a particular focus on older students relative to young elementary school students. Our second goal was to identify patterns of effective mathematics SRL interventions over time. Since the most recent systematic reviews of SRL interventions were conducted more than 10 years ago (i.e., Dignath and Büttner, 2008; Dignath et al., 2008), a timely update is warranted. Instruction of SRL strategies in classrooms may have changed. Therefore, examination of patterns and changes may reveal strengths and weaknesses of SRL interventions and how these interventions have evolved over time. We sought an in-depth understanding of existing SRL interventions with these goals. Overall, we have two research questions as following:

1. What are the effective characteristics of existing SRL interventions in mathematics for school-aged students?

2. What are the patterns of SRL interventions in mathematics over time?

Methods

Inclusion Criteria and Search Procedures

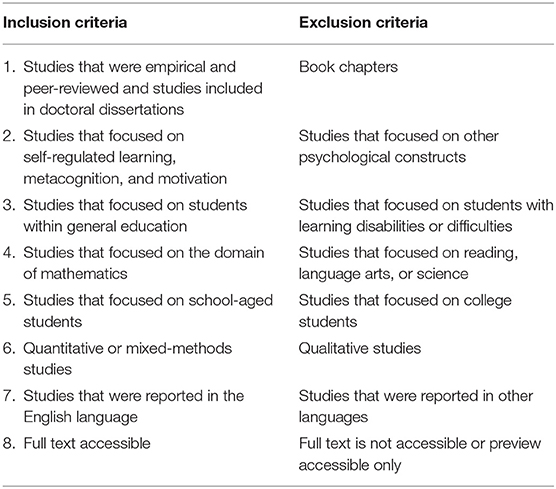
This systematic review examined the characteristics of existing and publicly available intervention studies of SRL in mathematics classrooms. We developed a three-tier search strategy through electronic databases including PsycINFO, Educational Resources Information Center (ERIC), ProQuest Education, and Google Scholar. Our search of literature was limited to articles with publication years between 1990 and 2020. We further established specific inclusion criteria in line with the purpose of this review. The inclusion and exclusion criteria for the sampled studies are presented in Table 1. Book chapters were excluded from our search.

TABLE 1

Table 1. Inclusion and exclusion criteria.

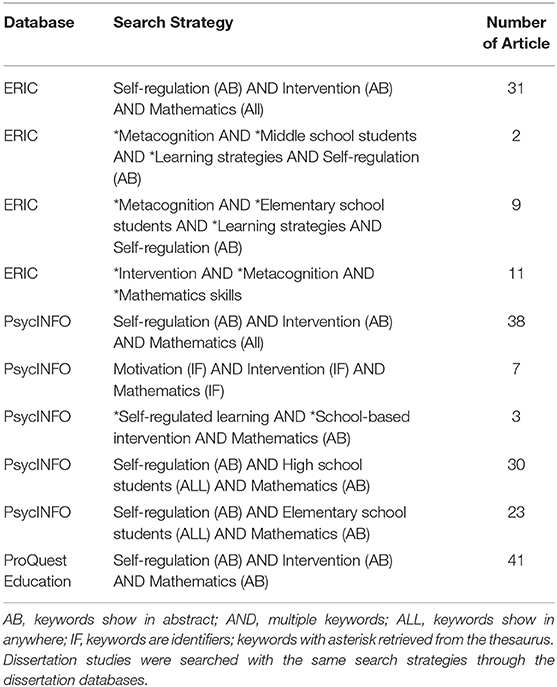
We reviewed over 291 articles with our literature search and 36 articles met the inclusion criteria for the present systematic review. Specifically, we carried out the literature search in three tiers: online library database search, referrals search from the identified studies, and individual studies found through search existing review studies. We completed the first tier of search through PsycInfo, ERIC, and ProQuest for peer-reviewed articles using the following search terms: self-regulation, intervention, mathematics, metacognition, middle school students, high school students, learning strategies, motivation, self-regulated learning, school-based intervention. We conducted 10 searches with different combinations of these terms. We also searched the doctoral dissertation studies with the same search terms as we used for journal articles. Detailed search strategies are presented in Table 2.

TABLE 2

Table 2. Search strategies.

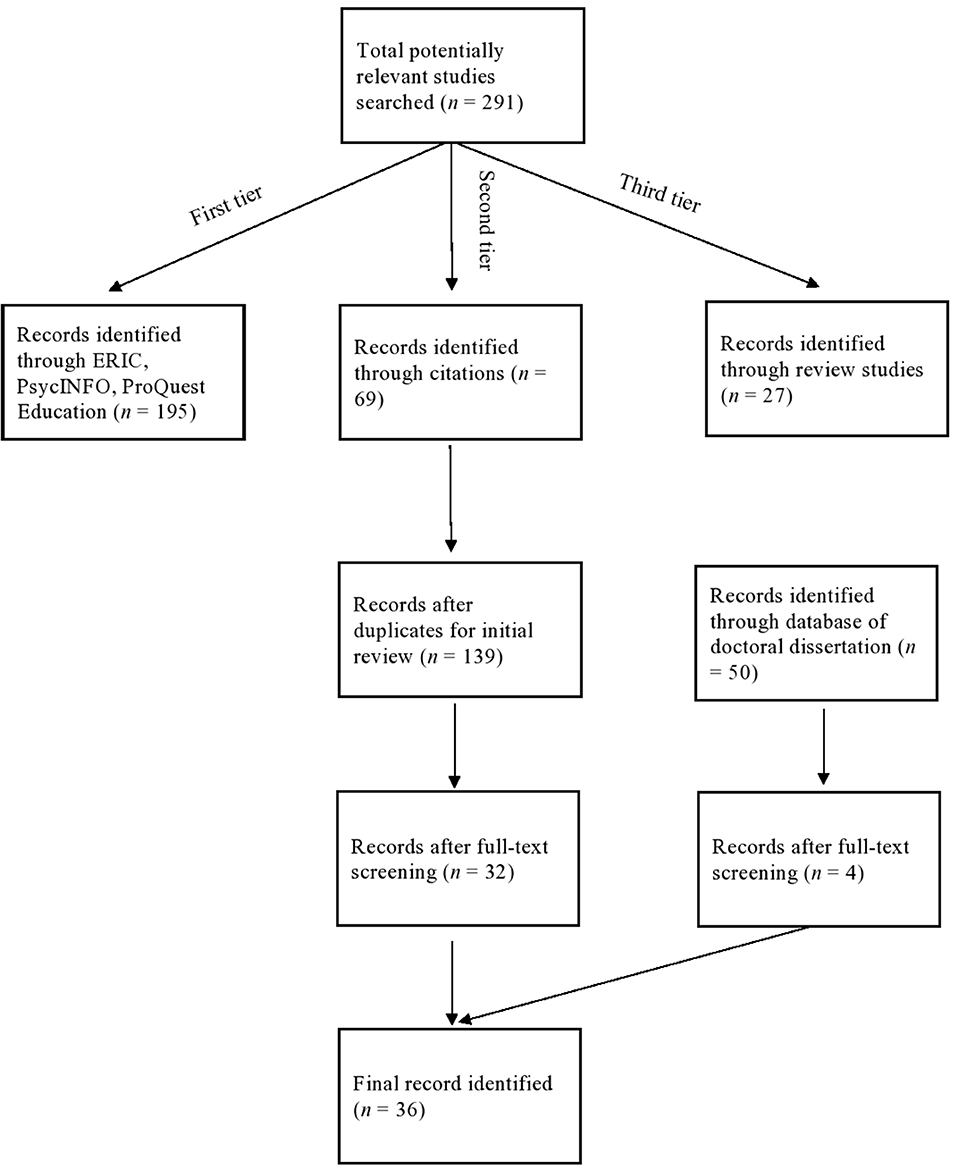
The identification of studies included two iterations. Our first identification of studies was conducted in 2017. We reviewed each of the studies from the first-tier search based on the established inclusion criteria. Duplicated studies and studies that did not meet the inclusion criteria were removed. After the first tier of search, we identified 13 studies to include. Through the second tier, we examined the citations of all the identified studies from the first-tier search and recognized studies that might potentially meet our inclusion criteria. We then accessed these studies from citations through Google Scholar. As a result, eight additional studies were identified. In the third tier, we extracted individual studies that met the inclusion criteria from existing meta-analysis and other review studies in the area of self-regulated learning. We identified four additional studies. Thus, the final number of identified studies was 28. We further conducted an updated identification of studies in 2020 including studies published between 2017 and 2020 and eligible doctoral dissertation studies. As a result, we identified 36 studies for the present review. Two independent raters' agreement of excluded articles reached 100%. Figure 1 shows the search and screening procedures and the article delimitation process.

FIGURE 1

Figure 1. Flowchart of article delimitation.

Coding Scheme

To promote comparisons with existing research and for consistency within existing reviews of SRL interventions, a coding scheme was adapted and expanded based on Dignath and Büttner (2008) to categorize the characteristics of the identified studies. Overall, our coding categories for the identified articles reflected categories and subcategories within six overarching themes: theoretical orientation, characteristics of the sample, characteristics of the treatment, type of the assessment instrument, type of outcome variables, and information for estimated effect sizes. Detailed coding categories including sub-categories are shown in Table 3.

TABLE 3

Table 3. Coding scheme for identified studies.

Theoretical Orientation

As established, the theoretical framework or model is foundational when designing and developing an intervention. Interventions based on different theoretical models may result in varied effects on students' achievement and SRL (Puustinen and Pulkkinen, 2001; Panadero, 2017). Therefore, we coded theoretical models of SRL for each identified study to examine potential differences in intervention effectiveness. Across interventions, the theoretical models of SRL were categorized into three larger theoretical orientations: social-cognitive theory-oriented (e.g., Zimmerman's model), metacognition theory-oriented (e.g., Winne's model), and motivation theory-oriented (e.g., Pintrich's model). Most of the studies were designed based on one theoretical orientation. When a study was grounded in more than one theoretical orientation, it was coded as combination of theoretical orientations. A few studies did not state clearly which theoretical model was adopted. We coded these studies without a clear statement of theory as “unknown.”

Sample Characteristics

Sample characteristics included the total size of a sample, the size of a treatment group, and the size of a control group. This category also included the geographical location where the intervention was implemented and participants' age and grade level information.

Treatment Characteristics

Treatment characteristics specified elements of the design of an intervention or of the training. Coded subcategories included: type of study design, nature of control group, condition assignment, delivery mode, teacher training, type of strategy, and duration of intervention. Specifically, the implementation of a pre- or post-test, and the assignment of a control group as a comparison group were coded as types of study design (e.g., pre-post-control design). When a control group was assigned, the nature of the control group was also categorized. Particularly, a control group was coded as “received nothing,” “received alternative treatment,” or received “other.” Experimental designs and quasi-experimental designs were categorized separately based upon the involvement of random assignment. Furthermore, delivery mode indicated the agent, such as the teacher or a researcher, who delivered the intervention. Moreover, when teachers were the agents, whether they received a training session from authors was coded as Yes or No.

According to Boekaerts (1999), there are three types of self-regulated learning strategy interventions (i.e., cognitive strategies, metacognitive strategies, and motivational strategies). Specifically, cognitive strategies are content-specific or domain-specific in mathematics. Strategies that focus on enhancing students' problem-solving skills or any other content-specific skills were coded as cognitive strategies. Metacognitive strategies were coded when an intervention involved the improvement of certain self-regulatory constructs. For example, strategies that help students to monitor, plan, and regulate their learning processes were coded as metacognitive strategies. Finally, motivational strategies refer to strategies that target students' motivation and affect for learning mathematics. For example, interventions designed to enhance students' self-efficacy or affective self-regulation, were coded as motivational strategies. The duration of interventions was also coded, specifying the number of treatment sessions and the number of total hours from available information provided in the articles.

Types of Achievement Assessment

When a pretest was administered, differences in the pretest were coded as either some group differences or no group differences. The types of assessment that measured mathematics achievement outcomes were coded into three categories based on our review of the identified studies: standardized knowledge test, researcher-developed test, and teacher-developed test. With respect to students' changes in SRL, we specified the type of SRL measure that was used including self-report questionnaires, calibration techniques, students' diaries, think-aloud approach, and mathematics discourse analysis.

Types of Outcome Variables

In line with our purposes for the present systematic review, we focused on two types of outcome variables, mathematics achievement and SRL-related outcomes. Specifically, we examined whether students' mathematics performance and SRL improved through intervention, and therefore statistical significance of results was also coded.

Effect Size Estimates

To compare the effectiveness of the interventions on students' mathematics performance and SRL, effect size estimates of students' math performance scores and scores on SRL measures were calculated with the statistical information provided by the authors of the articles. Information needed for effect size calculations was guided by Lipsey and Wilson (2001)'s coding scheme for effect sizes. Eight studies did not provide adequate information for effect size calculations for mathematics outcomes. Moreover, ten studies did not include adequate information for calculating effect sizes of SRL outcomes. The authors of these studies were contacted; however, the required information was not available and therefore, these studies were excluded for the calculations of effect size estimates.

Effect size estimates were calculated by an effect size calculator developed by David Wilson [read Lipsey and Wilson (2001) for more information]. In particular, Cohen's d was calculated by obtaining the mean difference between the conditions on the posttest (i.e., mean score of experimental condition minus mean scores of the control condition) and then divided by the pooled standard deviation obtained from the study. Thus, a positive Cohen's d indicates an increase on the outcome variable and a negative Cohen's d indicates a decrease on the outcome variable. The extent of effectiveness was determined by the magnitude of the effect size (small effect: d = 0.2; medium effect: d = 0.5; large effect: d = 0.8, Cohen, 1988).

Most of the studies were designed as pre- and post-test control with two groups. Some studies, however, included more than two groups. In these cases, we identified the treatment group with a SRL component and then calculated the effect size based on the difference in outcome between the SRL treatment group and the control group. For instance, Tzohar-Rozen and Kramarski (2017) examined the extent to which fifth graders' mathematics achievement benefited from a self-regulation intervention. Their intervention included three conditions including a metacognitive regulation condition, an affective regulation condition, and a control condition. In the metacognitive regulation condition, students were explicitly trained to ask themselves questions during the mathematics problem-solving process. In comparison, the affective regulation condition had an emphasis on students' emotion, which is not the focus of the present review. Therefore, in this case, we only calculated the effect size for the difference between the metacognitive regulation condition and the control condition. Furthermore, some studies included multiple achievement outcomes to compare with the control condition. For instance, Kramarski and Zoldan (2008) administered two mathematics achievement tests because their intervention addressed two specific content areas: linear functions (e.g., definition of linear functions) and graph interpretation (e.g., interpretation of linear graphs). Therefore, there were two effect sizes calculated for the achievement measures. For such studies, the average of two effect sizes was recorded.

Two independent raters coded the theoretical orientation and type of strategy for each identified article as these two coding categories were considered more likely to contain variation in coding when compared with other categories, such as sample size and location. For instance, some researchers did not explicitly state their strategy was cognitive, metacognitive, or motivational, which required the two raters to identify the type of strategy based on their research experience and other information provided in the study. The exact agreement for the category of theoretical orientation was 0.82 and was 0.71 for the type of strategy between two raters. Discrepancies in coding were resolved by discussion.

Results

Research Question 1: Characteristics of the Existing SRL Interventions in Mathematics

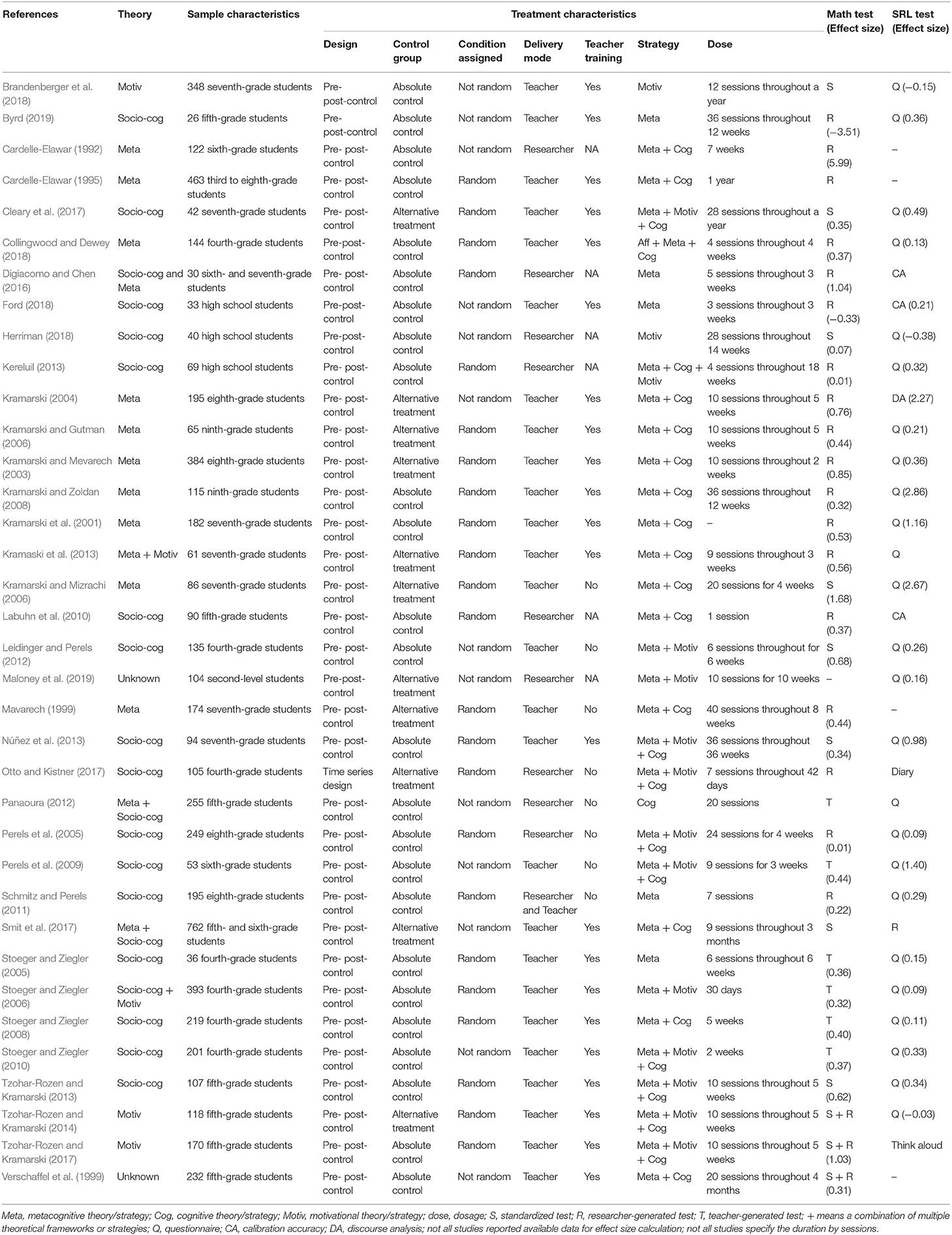
Our overarching purpose was to examine the characteristics of the existing SRL mathematics interventions for school-aged students. The identified studies were published between 1992 and 2020. We particularly focused on five elements: the theoretical orientation that these studies adopted, the characteristics of the sample, the characteristics of the treatment, the assessment of mathematics achievement and SRL, and the estimated effect sizes associated with these four characteristics on outcome variables (i.e., mathematics achievement outcome and SRL outcome) across 28 years. Detailed information about the categories is presented in Table 4. We considered these characteristics as necessary elements to identify and describe SRL interventions in mathematics.

TABLE 4

Table 4. Coding information of the identified studies.

To further address our purpose, we also compared trends with previous meta-analyses (Dignath and Büttner, 2008; Dignath et al., 2008). Dignath and Büttner (2008)'s meta-analysis provided a snapshot of SRL intervention characteristics in promoting self-regulated learning across academic domains at primary and secondary schools. They suggested potential effective training characteristics for SRL and critical implications for classroom practice. The present systematic review focused on the domain of mathematics and drew comparisons to characteristics identified by Dignath and Büttner (2008). We also examined and compared some other characteristics and their effects on mathematics with those previously reported, such as students' participation in cooperative learning and the delivery approach of strategic instructions.

Theoretical Orientation

Overall, the theoretical orientations adopted by the identified studies corresponded to our coding categories and the extant SRL models. Specifically, of the 36 identified studies, design of 15 intervention studies was solely grounded in social-cognitive perspectives, 10 studies solely adopted metacognitive theories, four studies solely adopted motivational theories, five studies were grounded in a combination of theoretical frameworks [i.e., combination of metacognitive and social-cognitive theoretical orientation (n = 3), combination of motivational and social-cognitive theoretical orientations (n = 1), and combination of metacognitive and motivational theoretical orientations (n = 1)]. However, two studies lacked explicit description of the theoretical perspective adopted and were coded as unknown.

Including the studies with combined theoretical orientations, a number of 19 studies were grounded in social-cognitive theories. For instance, Zimmerman's cyclical model was consistently adopted across these studies. Studies grounded in Zimmerman's model, in general, were designed with different stage goals aligned to the three cyclical phases that he proposed. For instance, Otto and Kistner (2017) implemented a training program to enhance fourth-grade students' SRL in mathematics learning. Five training sessions were distributed in three phases: pre-action phase, action phase, and post-action phase. The pre-action phase consisted of two sessions focused on guiding students, for example, to set goals and make plans toward the upcoming tasks. The action phase consisted of two sessions focused on the active process of mathematics problem-solving during task completion. Finally, the post-action phase consisted one session focused on evaluating and reflecting on learning results after task completion. As such, this type of intervention design corresponds to Zimmerman's SRL cyclical model as well as its sub-processes.

In comparison, studies grounded in Pintrich's model an emphasized learners' motivation and affective self-regulation. Specifically, we identified three studies solely grounded in Pintrich's model, which is motivation-oriented, and an additional two grounded in a combination of motivational and metacognitive or social-cognitive theoretical orientation. For instance, Tzohar-Rozen and Kramarski (2014) adopted Pintrich's model (2000) in their study focused on students' emotion regulation, metacognitive regulation, and mathematics achievement. Specifically, in the training sessions, teachers were asked to promote students' positive emotions and to deliver affective self-regulation strategies toward mathematics problem-solving through teacher-student dialogues. Collectively, although Zimmerman's and Pintrich's models both have some social-cognitive and motivational perspectives, they target different foci when guiding the design of interventions.

Notably and interestingly, within the 14 studies (i.e., 10 single metacognitive-oriented theories and four combined metacognitive-oriented theories) grounded in metacognitive theoretical orientation, seven of these studies were conducted by the same research team, Kramarski and her colleagues. These seven studies adopted an established mathematics and metacognition training model called “IMPROVE” developed by Mevarech and Kramarski (1997). The IMPROVE model represented teaching and learning strategies for students' metacognitive development and mathematics learning and specifically included Introduction of new mathematics topics (I), Practicing (P), Reviewing (R), Obtaining mastery skills (O), Verifying learning results (V), and Enriching learning content (E). According to Mevarech and Kramarski (1997), IMPROVE was grounded in a metacognitive perspective and encouraged students to use metacognitive questioning strategies during mathematics task completion to improve their problem-solving and monitoring process. These seven studies were application of the IMPROVE model and produced positive effects for students' metacognition and mathematics learning. These positive effects suggest that interventions grounded in metacognitive theories can be valuable in practice for students' mathematics learning, although more research is needed to examine the degree of generalizability from such interventions.

Effect size estimates indicated that metacognition-oriented interventions resulted in better effects for improving students' mathematics performance and SRL, when compared to social-cognitive theory. This finding supported that the design of an intervention grounded in different theoretical perspectives may produce differential effects on students' mathematics achievement and changes in SRL.

Newer SRL models developed in the recent decade, such as Efklides (2011)'s model (Metacognitive and Affective Model of Self-Regulated Learning-MASRL), were not directly adopted in our identified studies. Notably, however, several authors cited MASRL in their introduction. For instance, when Cleary et al. (2017) described the multidimensional and dynamic nature of SRL in their literature review section and cited Efklide's model to illustrate the refinement of SRL theoretical models in the recent years. Future researchers may investigate person and task level characteristics in promoting students' SRL through intervention grounded in this model.

Sample Characteristics

Across the 36 studies, the sample sizes ranged broadly from 26 to 762 (M = 161.36, SD = 145.29). For instance, Digiacomo and Chen (2016) conducted a metacognitive intervention with 30 middle school students randomly assigned to two conditions and measured students' predictive accuracy and post-dictive accuracy of their performance judgments. They reported insignificant statistical results on mathematics performance and the accuracy of performance judgments. However, the effect size represented a large effect on students' mathematics performance (d = 1.036). This indicated that the statistical significance of this study may be limited by the small sample size when compared to the practical significance. However, some studies that included large samples, such as Cardelle-Elawar (1995) (n = 489), and Stoeger and Ziegler's intervention (2006) (n = 393), demonstrated statistically significant and practically effective results in general. Specifically, Cardelle-Elawar (1995) reported that students in the experimental condition significantly outperformed students in the control condition. Similarly, Stoeger and Ziegler (2006) reported statistically significant improvement on both mathematics and SRL outcomes. A medium effect size was found on students' mathematics achievement between treatment and control conditions (d = 0.32). Nonetheless, these large sample sizes did not always indicate practically effective and statistically significant outcomes on either mathematics achievement or SRL. For instance, with a sample size of 249 students, Perels et al. (2005) (n = 249) reported minimal effects on both students' mathematics performance (d = 0.01) and SRL (d = 0.09), when compared to the control group. This may be explained by the increasing difficulty of implementation as sample size increases. In particular, the treatment fidelity of the studies may be hard to control and maintain, especially when it involves cooperation among multiple teachers and/or schools, as well as consistent training and communication. Thus, it is understandable that there was not a single pattern to describe the effectiveness of an intervention and its sample size.

Although we searched literature across primary and secondary grade levels, the grade levels across samples did not vary widely in our review, ranging from Grade 4 to Grade 9. Specifically, after we read through these excluded studies with very young children, we found that these studies usually tend to have a focus on behavioral self-regulatory strategies and outcomes for students with learning disabilities or difficulties. For instance, Fuchs et al. (2003) delivered a SRL intervention for 3rd graders' mathematics learning focused on children with disabilities. Another longitudinal study conducted by Vauras et al. (1999) focused on Grade 3 students with learning problems. They asked students to complete the word problem solving task by following and repeating a set of steps in order to help them learn the strategies. Studies that focused on younger children also tended to target the behavioral aspect of self-regulation. For example, DeFlorio et al. (2019) assessed kindergarten children' self-regulation by asking them to perform gift wrap tasks. Thus, studies like these with a special group of students and a different focus of SRL from our goals of the systematic review, were excluded from our selection.

We further coded the location where the intervention was implemented. We recognized that more studies were conducted outside of the United States, with many studies conducted in Israel and Germany. For instance, the interventions conducted by Kramaski and her research team, which represent almost one third of our selection, all took place in Israel.

Treatment Characteristics

Among the 36 intervention studies, we identified several distinct characteristics regarding the SRL treatment: the types of strategy implemented, the duration of the intervention, the delivery of training, and students' participation in cooperative learning.

We identified three types of strategies including cognitive strategies, metacognitive strategies, and motivational strategies throughout the selected studies. Some interventions only implemented one type of strategy, while others incorporated multiple strategies. The majority of studies implemented combined strategies (n = 27) and 24 studies included metacognitive strategies. Specifically, 10 studies implemented a combination of all three types of strategies, 14 studies implemented the combination of metacognitive and cognitive strategies, three studies implemented the combination of metacognitive and motivational strategies, six studies implemented metacognitive strategies only, two studies implemented motivational strategies only, and one study implemented cognitive strategies only.

Strategies that were categorized as metacognitive had a focus on training students' metacognitive awareness to be self-regulated learners in mathematics. For instance, Kramarski and Zoldan (2008) implemented both metacognitive and cognitive strategies for ninth graders. In particular, they compared the effects of three metacognitive strategies on students' mathematical reasoning, including error diagnosis, self-questioning, and the combination of the two. Students in the error diagnosis condition were asked to evaluate their answers to math problems and diagnose their incorrect answers with potential justifications. Students assigned in the self-questioning condition were required to ask themselves questions while they were solving math problems. For example, students would ask themselves whether they understood the question before they started to solve the problem. These two strategies both aimed at training students' metacognitive thinking during a mathematical reasoning task. Kramarski and Zoldan (2008) reported that students who received the combination of the two metacognitive strategies demonstrated the most effective improvement on the problem-solving task (d = 0.38) when compared to students who received no strategy training. Furthermore, students who received the combination of the two outperformed students who received either the error diagnosis strategy only or self-questioning strategy only. These strategies demonstrated increased performance in the problem-solving task and but also increased metacognitive monitoring. Specifically, students in the combination condition outperformed students in the control condition on self-monitoring errors in the posttest (d = 2.69).

In comparison, interventions coded as cognitive strategies focused on teaching students for particular mathematical problem-solving tasks. Panaoura (2012) implemented a mathematical model that included six stages to solve a mathematical problem: understanding the phenomenon under investigation, constructing a mathematical model, working through the mathematical model using disciplinary methods, interpreting the outcome of the computational work, evaluating the model by checking the interpreted outcome, and communicating the solution of the problem. Thus, this strategy model focuses on guiding students to perform better on the mathematical problem-solving task. Specifically, students were asked to complete the mathematical problem-solving task on a computer following the six stages corresponding to the model. Panaoura (2012) reported that students demonstrated improved performance and self-regulated strategy use. Information was unavailable to calculate the effect size of the intervention.

Moreover, a few studies implemented motivational strategies combined with other strategies. In particular, these studies focused on enhancing students' self-efficacy and goal setting in mathematics learning. For instance, Perels et al. (2009) implemented an intervention focused on improving students' self-motivation and goal pursuit in mathematics learning. Results showed that students in the experimental group demonstrated improved mathematics achievement performance (d = 0.44) and improved self-regulation overall (d = 1.40).

Throughout the 36 studies, we identified emerging patterns regarding the association between types of strategies and effectiveness. That is, studies that included multiple types of strategies tended to be more effective than studies that included a single strategy. This pattern is consistent with results reported by Dignath and Büttner (2008). Specifically, they reported that interventions for secondary school students that solely include cognitive strategies were less effective than those that combined metacognitive and motivation strategies. Training students with multiple strategies may assist them to better deploy strategies as one strategy may complement students' understanding of others. For instance, learning metacognitive strategies helps students to be better aware of which cognitive or motivational strategy is appropriate for a particular task or situation. However, findings from the present review indicated some exceptions. For example, Perels et al. (2005) implemented a combination of all three types of strategies with limited benefit for mathematics performance or SRL outcomes (i.e., d for math = 0.01, d for SRL = 0.09).

The duration of the intervention also varied among the 36 studies. Specifically, based on the available information provided in the studies, intervention duration ranged from one session to 49 sessions. Overall, there was no consistent pattern in the relationship between the duration of intervention and effect size. For instance, Schmitz and Perels (2011) obtained an effect size of d = 0.22 on students' mathematics performance with their 49 day intervention; while Digiacomo and Chen (2016) obtained an effect size of d = 1.04 with their one session and 3.75 h intervention. Perhaps some interventions tend to produce immediate large effects that may fade as the intervention persists. This idea is not consistent with results reported by Dignath and Büttner (2008). Specifically, Dignath and Büttner (2008) reported that interventions with a longer duration tended to be more effective. Their finding aligns with former research on the development of metacognition and self-regulation as well as the development of strategies (Alexander et al., 1998; Kuhn, 2000). In general, it requires time for students to generalize and master new strategies and providing students with adequate time during intervention allows them to practice newly learned strategies.

Nevertheless, no consistent pattern was identified in the present review. There may be several explanations. First, perhaps, the sample size of studies was small due to our specific inclusion criteria. Second, not all the studies reported specific hours or sessions that interventions were delivered to students. Last, other training characteristics may play a stronger role in intervention effects such that duration of interventions did not form a trend. While counter intuitive, these findings correspond to previous research. de Boer et al. (2018) also reported no effects for intervention duration on students' academic performance when metacognitive strategies were implemented in interventions.

Further, how interventions were delivered was coded as either training delivered by researchers or training delivered by teachers. Dignath and Büttner (2008) reported that interventions had more effective outcomes if the training instructions were delivered by researchers when compared to teacher delivered training. The present review, however, does not support this finding. First, in the studies reviewed here, the majority of interventions were delivered by teachers, with 10 studies delivered by researchers. Therefore, there were not enough cases to determine which delivery approach is more effective. Notably, the intervention (i.e., Cardelle-Elawar, 1992) that had the highest effect size on achievement performance was researcher-delivered. It may be that the majority of interventions were delivered by teachers because SRL interventions in mathematics are highly related to mathematical curricula, thereby making teachers best suited to deliver intervention. Further, most interventions were conducted in classrooms during class sessions and having teachers deliver them may result in both less disruption and greater external validity.

In addition, students' cooperative learning was defined by whether the experimenters or instructors created an environment that encouraged students to discuss or work together. For instance, Perels et al. (2009) designed their intervention with an element of group work. Specifically, in their first two sessions of self-regulation strategy training, they asked students to learn strategies in a group format involving communication with each other. Students were also asked to work together to make posters representing their strategy learning. Results indicated positive effects on both mathematics achievement performance (d = 0.44) and SRL as measured by a questionnaire that the research team constructed (d = 1.40). Findings from Dignath and Büttner (2008) supported benefit for cooperative learning and reported that group work had a positive impact on intervention effect sizes. Similarly, in the present review, interventions that included group work all demonstrated positive effects on mathematics and SRL, with small to large effect sizes (i.e., d = 0.31 to 0.44 for mathematics; d = 0.21 to 1.40 for SRL). Most studies (n = 24) that we identified, however, encouraged students' independent work instead of group work with only 12 studies emphasizing on group work. Nonetheless, given the benefit of group work on the effects of SRL interventions, group work may be a viable way to enhance the outcomes of an intervention.

The type of the mathematics assessment administered was another important characteristic examined in the identified intervention studies. Three types of mathematics assessments were identified and included. Standardized math tests (n = 8), teacher-generated math tests (n = 6), and researcher-generated math tests (n = 21). Three studies administered more than one of these assessments: Tzohar-Rozen and Kramarski (2014), Tzohar-Rozen and Kramarski (2017), and Verschaffel et al. (1999).

Overall, 28 studies had available information for the calculation of effect sizes, as well as explicit information with regard to the type of assessment. Most researcher-generated assessments demonstrated higher effect sizes when compared to teacher-generated and standardized mathematics assessments. Moreover, teacher-generated achievement assessments tended to be associated with lower effect sizes than researcher-generated and standardized assessments. The strength of intervention effects on researcher-generated achievement assessments may be the result of their close association with the elements of the intervention.

Research Question 2: Patterns of SRL Mathematics Interventions Over Time

We were also interested in identifying any patterns of elements of SRL interventions in mathematics over time and examined patterns for theoretical frameworks, treatment characteristics, and types of achievement assessments.

Theoretical Framework

The timeline of theoretical frameworks indicates some interesting trends. First, metacognition was the primary focus of SRL mathematics interventions in the 1990s and early twenty first century. Social cognitive theory, particularly Zimmerman's model, was not a focus of intervention until 2005. Since then, however, the model has been highly influential. Similarly, since 2006, Pintrich's SRL model with a focus on motivation, also became more frequently adopted by SRL researchers. These trends indicate the changing influence of SRL theories, with most of the recent intervention studies in mathematics grounded in Zimmerman's cyclical model rather than previous emphasis on metacognition frameworks.

Treatment Characteristics

We first examined the implementation of strategies developed between 1992 and 2020. Findings show that metacognitive strategies aimed at promoting students' self-regulated learning appeared throughout the entire timeline. Notably, however, motivational strategies were not of focus until 2006, and have since became much more popular, after 2012, especially in combination with cognitive and metacognitive strategies. This increase is likely associated with the development and refinement of SRL theories that more recently include affective factors in more recent SRL models. The inclusion of multiple strategies in SRL interventions for mathematics was quite consistent across time and represented one of the most common features of all interventions.

The types of assessments used in interventions demonstrated some trends across time. Specifically, researcher-generated achievement tests are the most common throughout the timeline. All the identified studies that were published from 1992 to 2004 administered researcher-generated achievement tests only. Notably, teacher-generated achievement tests first appeared in 2005. Then, the administration of standardized achievement tests appeared in 2006. Standardized achievement assessments were more often administered from 2012 to 2018. Moreover, the combination of both researcher-generated achievement tests and standardized achievement tests appeared in more recent years. Interestingly, teacher-generated achievement tests tended to produce a roughly consistent magnitude of effect (Mean of effect sizes d = 0.24) while researcher-generated achievement tests tended vary from the lowest effect at −3.51 to the highest at 5.99.

Discussion

Overall, the characteristics that we identified in this systematic review support the effectiveness of SRL interventions in mathematics for school-aged students. This systematic review contributes to the literature in several ways. First and broadly, to our knowledge, this is the first systematic review focused on SRL interventions in mathematics. The picture generated from this systematic review may directly inform research and practice in mathematics to improve SRL interventions and to support student learning as self-regulation may be best targeted to specific academic domains (Wolters and Pintrich, 1998). Indeed, although mathematics as an academic domain requires domain-general strategies that support students' learning, mathematics also requires specific and unique strategies less employed in other domains or within specific mathematics content or curricula. Further, an updated systematic review of SRL interventions allows researchers to draw comparisons with previous review studies and discern developmental patterns of SRL interventions across the last decades. The present review demonstrates patterns among SRL interventions over time and can inform future research directions in SRL interventions with regard to refinement of theoretical support, implementation of a combination of strategies within intervention, and approaches of delivering the intervention.

While this systematic review provided a critical update to previous reviews and contributed to understanding of effective SRL intervention in mathematics, there are recognized limitations. First, we identified the effective characteristics in mathematics. However, characteristics of SRL interventions may work differently in other academic domains. Updating and investigating intervention characteristics for other domains is a future direction. Second, some intervention studies included in this review did not report adequate information for the calculation of effect size. This may result in an incomplete understanding of the effectiveness of SRL interventions. Future research may address this issue with comprehensive meta-analyses. Third, we acknowledge that there may be characteristics of the interventions that we did not identify or overlooked that may prove important. For instance, the inclusion of psychometric properties of the measures used may be a characteristic to further examine. Thus, future research may expand upon our coding scheme to capture additional intervention characteristics, such as delivery method (e.g., online format of instructions in mathematics courses: Broadbent and Poon, 2015). Finally, a large portion of the studies included in this review were conducted by the same research team (i.e., Kramarski and colleagues). Drawing conclusions from one research model may result in limited understanding of the benefits of interventions more broadly. As more SRL interventions in mathematics are developed from additional perspectives, future research will allow comparison across interventions.

Author Contributions

YW conceived the presented idea of conducting a systematic review in self-regulated learning interventions in mathematics. RS supervised the project. YW and RS both contributed to the project, the main conceptual ideas, the outline, and the analyses. YW wrote the manuscript with support from RS.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alexander, P. A., Graham, S., and Harris, K. R. (1998). A perspective on strategy research: progress and prospects. Educ. Psychol. Rev. 10, 129–154. doi: 10.1023/A:1022185502996