Individualized Assignments, Group Work and Discussions: How They Interact With Class Size, Low Socioeconomic Status, and Second Language Learners

Introduction

Increasingly heterogeneous classrooms are common throughout developed countries. These classrooms include second language learners and learners from low socioeconomic status (SES), both of which may negatively affect the development of competencies in early secondary school (Björklund and Salvanes, 2011; Solari et al., 2014). An important job of educators is to provide instruction for a diverse group of learners. Inclusive teaching techniques such as individualized assignments, group work, and discussions are often considered effective teaching techniques in heterogeneous classrooms (Tomlinson and Imbeau, 2011; Tomlinson and Moon, 2013; Cohen et al., 2014; Miller et al., 2017). However, large-scale assessments of teaching techniques which asses the efficacy of these techniques for diverse learners are uncommon. Additionally, class size can affect the utilization of each of these teaching techniques (Blatchford and Russell, 2018). This paper utilizes data from a large-scale assessment to examine the roles of individualized assignments, group work, and discussions on math and language competency, and it examines the relationships between these teaching techniques, student background, and class size.

Migrant background and low SES have been repeatedly linked to worse educational outcomes in both language and math skills. The link between a lower SES and poorer education outcomes has been demonstrated in many countries around the world (White, 1982; Lekholm and Cliffordson, 2008; Currie, 2009; Björklund and Salvanes, 2011; Rambo-Hernandez and McCoach, 2014; Sirin, 2016; DeVries et al., 2018). Furthermore, recent studies have indicated that income levels and job categorization are weaker correlates of cognitive function than parental education levels (Eilertsen et al., 2016) while parental educational behavior is a better indicator (Rindermann and Baumeister, 2015). Additionally, being a non-native speaker is also a risk factor for low achievement in reading (Solari et al., 2014) and other skills (Crosnoe and Fuligni, 2012).

Effective teaching strategies can significantly reduce the negative effects of disadvantaged backgrounds (Torres, 2018), and individualized instruction is a hallmark feature of universal design for learning (Tomlinson and Imbeau, 2011; Bešić et al., 2016; Ok et al., 2016). Through such individualized instruction, children are provided specialized tasks (e.g., classwork and homework) based upon their current ability level. Similarly, group work promotes student learning and development (Tomlinson and Imbeau, 2011; Miller et al., 2017). Group work can improve the engagement of children to foster their learning (Roseth et al., 2008; Cohen et al., 2014). Furthermore, groups of heterogeneous ability levels can provide a greater boost for at-risk and lower achieving children (Marzano et al., 2003; Igel and Urquhart, 2015). Meanwhile, effective classroom discussions can also foster learning (Tomlinson and Imbeau, 2011; Jocz et al., 2014). However, not all students gain equally from discussions (e.g., Kang and Keinonen, 2018). Group work and discussions can provide learners individualized, student centered instruction, but the outcomes of these approaches may be inconsistent across student and teacher ability levels (Kang and Keinonen, 2018).

There is mounting evidence of that greater benefits of group work and individualized instruction for learners with certain backgrounds. For instance, King-Sears et al. (2015) found that implementing universal design principles (UDL) in the classroom produced greater benefits at posttest for learners with disabilities. Meanwhile, learners with an immigrant background may be more engaged in mathematics learning in group work settings (Takeuchi et al., 2019), which may result in a greater benefit for learners with a migration background. Meanwhile in a qualitative study in Iceland, Benediktsson and Ragnarsdottir (2019) found that some immigrant children had very positive experiences and others negative experiences with group work. Relatedly, another exploratory study recently indicated that high achieving children may experience group work quite differently than other children (Cera Guy et al., 2019) and that they may not be more motivated or engaged by it. In the same token, learners with a migration background may be more worried and anxious about participating in classroom discussions, leading to a lower level of participation and fewer benefits (Maeda, 2017). On the other hand, discussions highlighting multiple methods and equal participation may be more beneficial for second language learners (Banes et al., 2018).

Teaching strategies are also affected by class size. Class size alone is generally found to have a small, but significant effect on learning outcomes with larger classes leading to slightly worse outcomes on average (Brühwiler and Blatchford, 2011; Krassel and Heinesen, 2014; Watson et al., 2016). Early evidence of this was well-summarized by Glass and Smith's (1979) meta-analysis, which indicated a continuous improvement for shrinking class sizes below around 30 students. However, in a re-examination of their data, Phelps (2011) argued for a more nuanced and careful conclusion. He argued that the relationship between class-size and achievement was a complex one. This is in line with Hattie (2005) conclusion that class size reductions do not necessarily result in improved performance. Class size may affect related student variables such as a sense of belonging, cohesion, and motivation (e.g., Harfitt and Tsui, 2015), and it may affect teacher variables such as classroom management, teaching techniques, the use of group work (Blatchford and Russell, 2018), and amount of individual attention for each student (Blatchford et al., 2011). Indeed, the use and effectiveness of teaching techniques may vary based on class size (Wright et al., 2017). Blatchford and Russell's (2018) conclusion is that class size may not have a direct effect on student learning, but instead, it affects classroom groups, management, and teaching. As a result, group work and individualized instruction may be more suited to smaller classes where classroom management is easier. Whereas, in larger classrooms, teacher techniques such as discussions may suffer less from a larger class size.

One recent large-scale study examined effective use of teaching techniques. Hofmann and Mercer (2016) focused on group work and discussion specific techniques in math classes, but they do not extend their results to other subjects, teaching techniques, or diverse learners. Instead, they focus on specific strategies for teachers to improve teaching techniques rather than how those techniques interact with student and classroom variables. The National Education Panel Study [NEPS; (Blossfeld et al., 2011)] provides a useful database to examine specific teaching techniques in relationship to learner ability level, background, and classroom situation. NEPS is a large-scale, multi-cohort study, which tracks many psychological, sociological, economic, educational, and other variables for a large, representative sample of German children, adolescents, and adults. Within such a dataset, longitudinal connections can be found between teaching techniques and a diverse set of learner risk factors.

The present study examines the role of low SES, as indicated by parental education levels, and second language learning on the development of math and reading skills in secondary students between grades seven and nine. We also examine the role of teachers' self-reported use of individualized assignments, group work, and discussions. Lastly, we examine the effects of class size and possible interactions between class size and the use of group work, discussions, and individualized assignments. Our data comes from teacher questionnaires and student competency test results in NEPS (Blossfeld et al., 2011). NEPS tracks the longitudinal development of multiple cohorts drawn from representative samples across Germany. We use data from the third cohort (SC3), which started data collection in the fifth grade. NEPS's unique combination of surveys and competency tests allowed us to investigate three research questions examining the interaction of these critical factors in the development of reading and math competency.

1) How do lower parental education levels and second language learning effect the development of reading and math competency in secondary school? We expect that both of these factors will negatively impact competency gain in both reading and math in seventh to ninth grade (Solari et al., 2014; Gebhardt et al., 2015; DeVries et al., 2018).

2) How does the use of individualized assignments, group work, and discussions effect the development of reading and math competency in secondary schools? We expect that the use of these three teaching techniques will overall benefit the instruction of children (Roseth et al., 2008; Tomlinson and Imbeau, 2011; Tomlinson and Moon, 2013; Miller et al., 2017). We further expect such techniques will produce a greater benefit for second language learners and for learners whose parents lack a university degree (e.g., Banes et al., 2018; Kang and Keinonen, 2018; Takeuchi et al., 2019).

3) How does class size affect the development of reading and math competency in secondary school and does it interact with the use of group work, classroom discussions, and individualized assignments? We expect to find that a larger classroom has a small, negative effect on competency (Glass and Smith, 1979; Phelps, 2011), and that it interacts negatively with teaching techniques suited to smaller classes [i.e., group work and individualized assignments; (Harfitt and Tsui, 2015; Wright et al., 2017; Blatchford and Russell, 2018)].

Methods

Participants and Sample

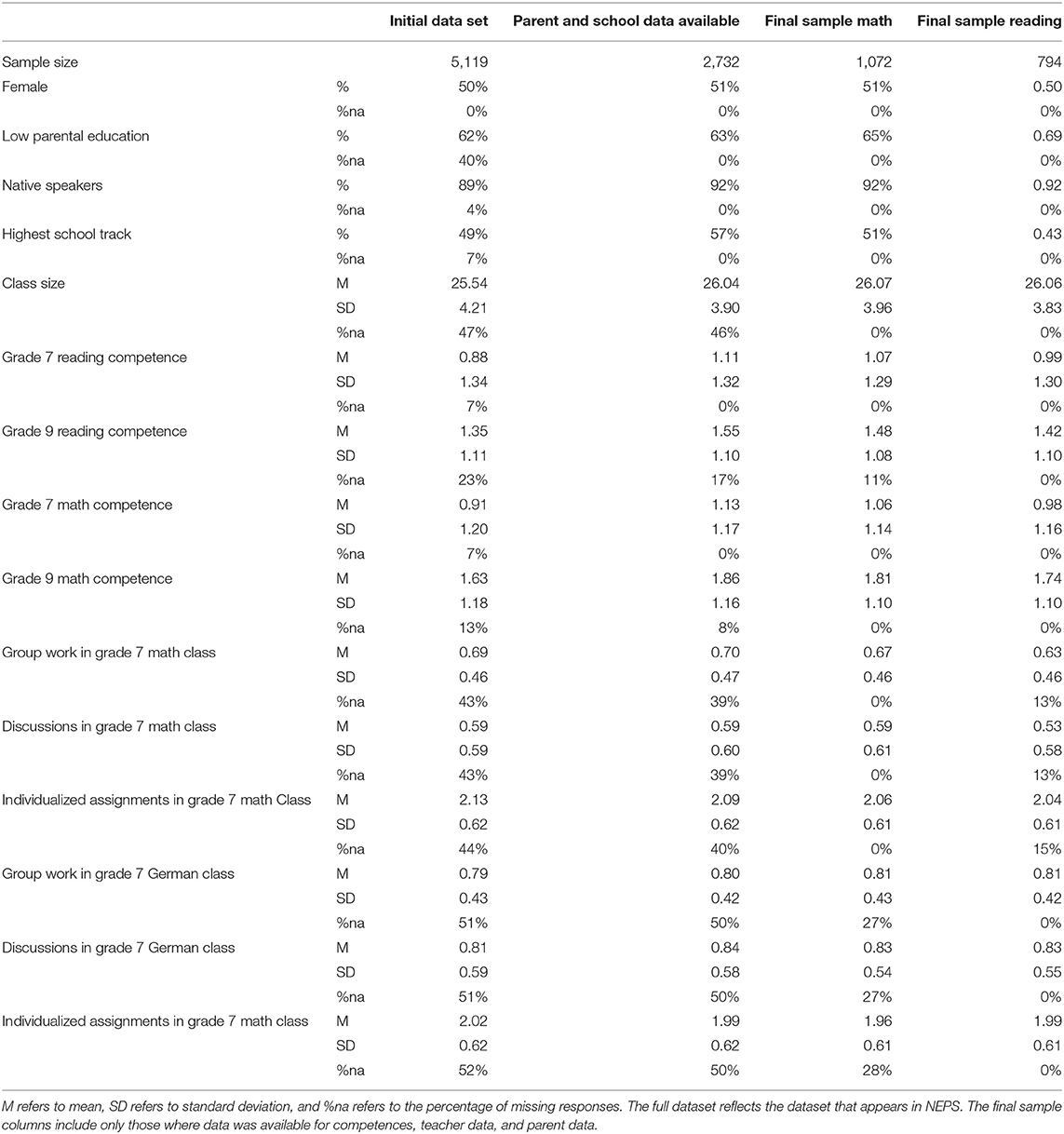
NEPS is a longitudinal study whose questionnaires are administered in waves that are roughly a year apart from each other. In our study, we considered only students that participated in waves three through five (seventh through ninth grade, N = 5,119). In order to account for drop-outs and to obtain an appropriate sample in terms of school type, federal state, regional classification, and funding institution, we weighted these students according to the provided sampling weights, which were specific to students who participated in these three waves (Steinhauer and Zinn, 2016). However, our analysis combines responses from three resources, students, their respective parents, and the respective subject specific teachers. Not all respective parents and teachers participated in the study. Self-reported, parent-reported, and school track data were available for 2,732 students. From this sample we obtained separate samples for math and German classes because the availability of teacher responses and competence data was subject specific. Complete reading competence data and German teacher questionnaire data were available for 794 students, and complete math competence data and math teacher questionnaire data were available for 1,072 students. A descriptive overview over the samples is given in Table 1, which includes the weighted means and proportions of missing data for all variables in the aforementioned samples. For all non-dichotomous variables, standard deviations are also provided. All values in Table 1 include sample weights. The initial dataset column includes the summary for all students who participated in waves 3 (7th grade) and 5 (9th grade) of the longitudinal study. The parent and school data column includes a summary for the subsample of all students whose student (first language), parent (obtained university degrees), and school track data was available. The last two columns summarize the subsample for which all data (competence, teaching techniques, and class size) of the German or the math courses are available.

TABLE 1

Table 1. Descriptive statistics and missing data.

Variables

Competence

We used Warm's likelihood estimates (based on item response theory) for reading and math competence provided in the NEPS data set. For a full description of the test characteristics see Carstensen and Pohl (2012). Reading and math competence tests were administered at the beginning of grades seven and nine.

Student Background

Native language was determined by student questionnaire. Students whose native language was not German were considered second language learners. Parental education was determined by parent questionnaire based on Comparative Analysis of Social Mobility in Industrial Nation (CASMIN) data from NEPS. Parental education was rated as high if the one or both parents had a university degree. Otherwise, it was rated as low. The education level of the partner of a single parent was treated as missing, and thus overall parental education level was considered as missing if one parent indicated they lacked a university degree and the other parent's data was missing.

Teaching Techniques

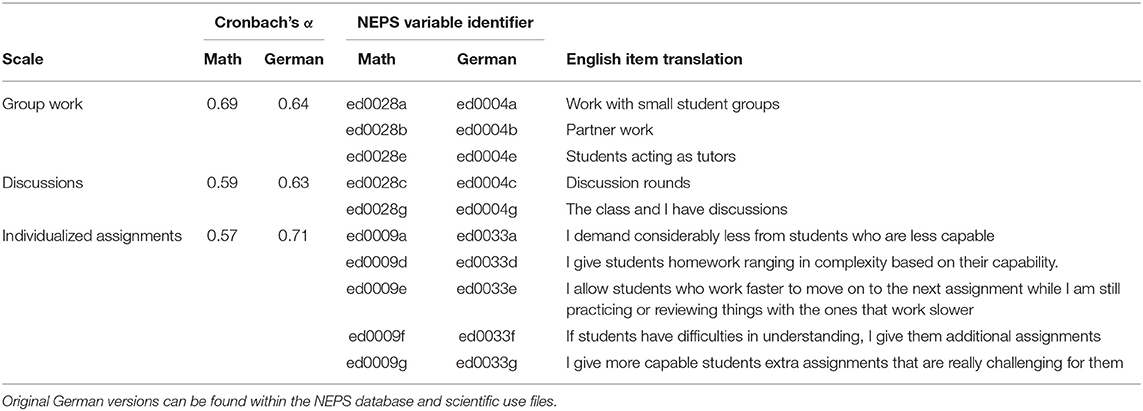
A summary of the instruments used and their reliability measures can be found in Table 2. The selection of teaching techniques came from two separate teacher instruments included within the NEPS database. Group work and discussions came from an exploratory factor analysis (EFA) of items the nine items included in ed0004 (German classrooms) and ed00028 (math classrooms) with varimax rotation. The best fit was the 3-factor solution, which had a significantly better fit than the 2-factor solution, χ² (8) for 3-factors vs. 2-factors = 241.143, p < 0.001. A 4-factor solution was not considered due to issues with identification. Loadings above 0.3 were used to sort the items into group work, discussions, and presentations. However, only one item loaded onto presentations, so this factor was discarded. One item representing project work (item f) loaded approximately equally (0.38 and 0.36) onto the remaining two factors. This item was dropped from our analyses because both factors were of interest.

TABLE 2

Table 2. Questionnaire scales and items.

We also examined the seven items included in ed0009 and ed0033 about teachers' individualized instructions in math and German classes. The same EFA procedure was followed, with a 2-factor solution providing the best fit, χ² (6) for 2-factors vs. 1-factor = 346.701, p < 0.001. A 3-factor solution was not considered due to identification problems. This resulted in a factor focusing entirely on group composition (homogenous or heterogeneous grouping), and a factor examining individualized instruction techniques regarding assignments and demands within the classroom. We choose the second factor to focus on, and did not further analyze the factor of group composition because of the theoretical goals of this article did not include the issue of homogenous or heterogeneous groups. The resulting scales are further detailed below.

The use of group work and discussions was determined by teacher questionnaires from the 7th grade math and German teachers. We provide NEPS translations of the original German language questionnaires. The original versions may be found within the NEPS database. Questions were answered along a 6-point discretized frequency response from “Never” to “almost every lesson.” Group work came from the average response from three items, including “Work with small student groups,” “Partner work,” and “Students acting as tutors (peer tutoring).” The frequency of discussions came from the average response to “Discussion rounds” and “The class and I have discussions.” Before averaging, the responses were converted into an approximate weekly rate based on the following conversions: never (~0 times per week), once or twice per school year (~0.04 times per week), Every few months (~0.1 times per week), every 2–4 weeks (~0.33 times per week), Once per week (~1 time per week), (almost) every lesson (~2 times per week).

Individualized assignments were determined by a separate five point Likert scale (“does not apply at all” to “applies completely”). This questionnaire was also collected from the 7th grade German and Math teachers. The five items included were: “I demand considerably less from students who are less capable,” “I give students homework ranging in complexity based on their capability,” “I allow students who work faster to move on to the next assignment while I am still practicing or reviewing things with the ones that work slower,” “If students have difficulties in understanding, I give them additional assignments,” and “I give more capable students extra assignments that are really challenging for them.” The raw average of the Likert responses was taken for individualized assignments.

In the event of team-taught classes, the average response for each responding teacher was taken for each class unit on each of the three scales. A full description of the final scales along with Cronbach's alpha can be seen in Table 2. Of note is the relatively low Cronbach's alpha for individualized instruction. With the removal of item a, this would rise to 0.68, but this was not done in order to keep the scale consistent across both classes. Similarly, a low Cronbach's alpha was present for discussions in the German class, but as this scale only included two items, such this value is not greatly informative.

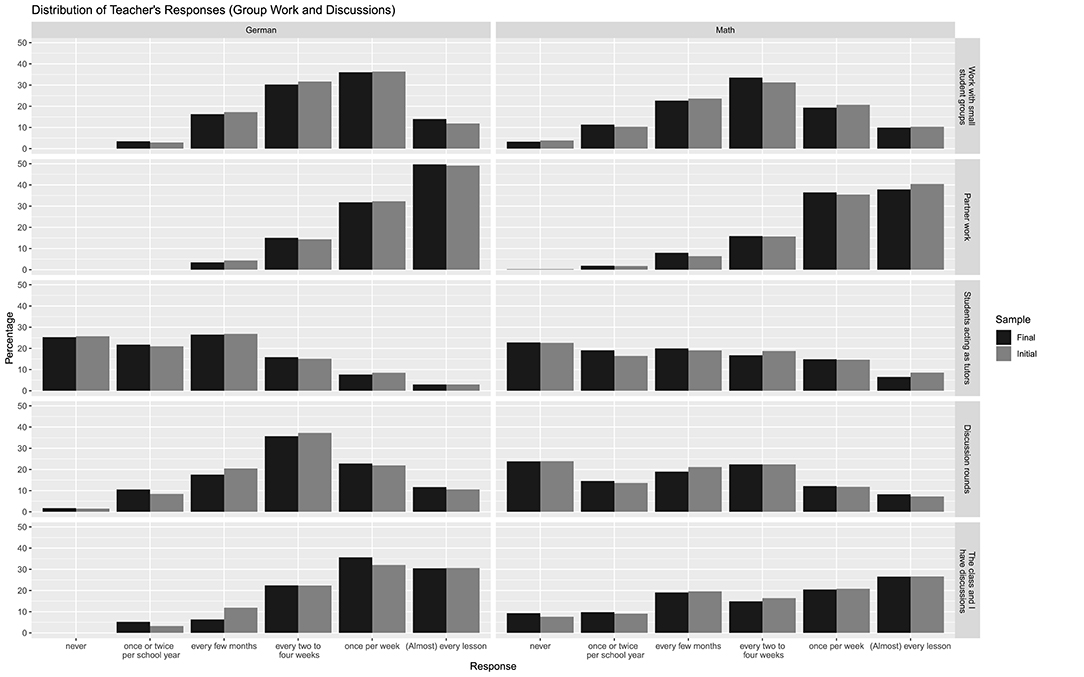
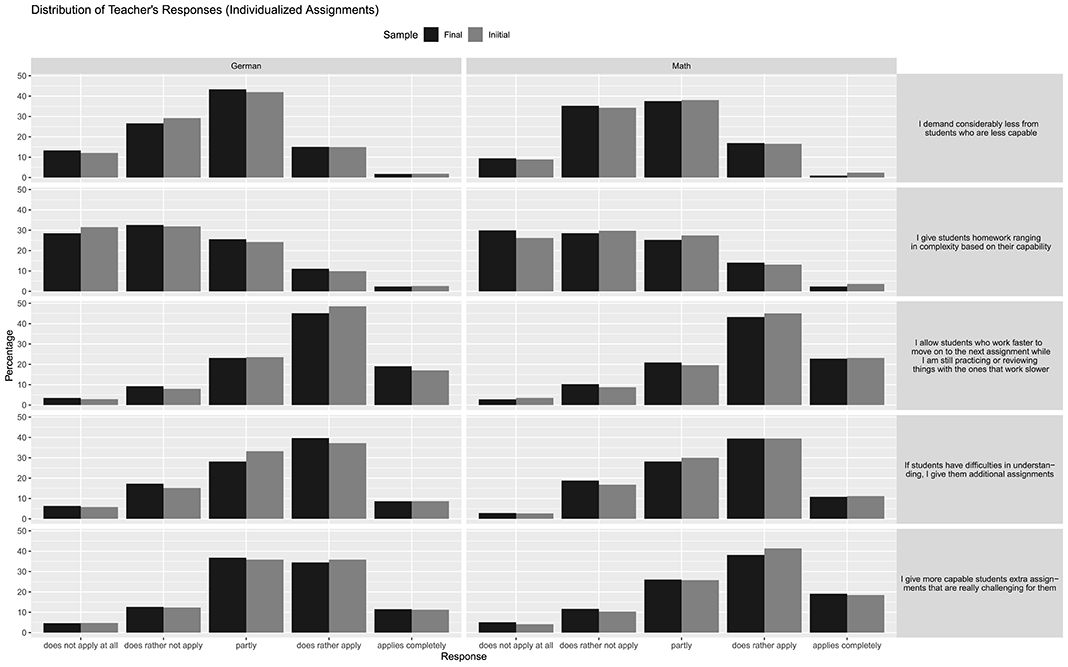
Figures 1 and 2 display the responses of teachers to questions about their teaching methods. The given percentages are purely based on the teacher data, meaning that they do not account for number of students (in the sample) in their classroom, that they do not account for the number of teachers that taught a specific student (in seventh grade), and that they do not incorporate the sampling weights of each student. In the figures, each row corresponds to a specific question. There are separate columns for both subjects. On the x-axis, each possible response category is notated, while on the y-axis, the percentage of responses in each category (ignoring all missing data) is notated. Figures 1 and 2 include the sample of all teachers in our data (in dark gray), and the final sample used in our models (in black). Responses are roughly normal, although skewed in some cases. All response categories include some responders, except for German, where certain responses to group work or discussions were never used. Lastly, there are no strong differences in the response patterns between teachers who responded and those teachers included in our final analysis.

FIGURE 1

Figure 1. Distribution of teacher's responses (Group work and Discussions).

FIGURE 2

Figure 2. Distribution of teacher's responses (Individualized assignments).

Class Size

The size of the German and math courses were not recorded by NEPS. We used class sizes reported by the class teacher instead, which will coincide with the size of the respective course in the vast majority of cases. If a class had multiple teachers, their responses were averaged.

Missing Data in the Sample

As seen in Table 1, the marginal distributions of all variables stay very close to the initial NEPS sample (i.e., mean and standard deviation). With the most apparent discrepancies in the dataset underlying our reading model where the proportion of parents without a university degree increases from 62 to 69 percent and mean reading competency grade seven increases from 0.88 to 0.99. A similar shift in math competencies in the data set exists with a shift in seventh grade math competence of 0.91 to 1.06 and in ninth grade of 1.63 to 1.81 with a slightly lower standard deviation for both grades.

Analyses

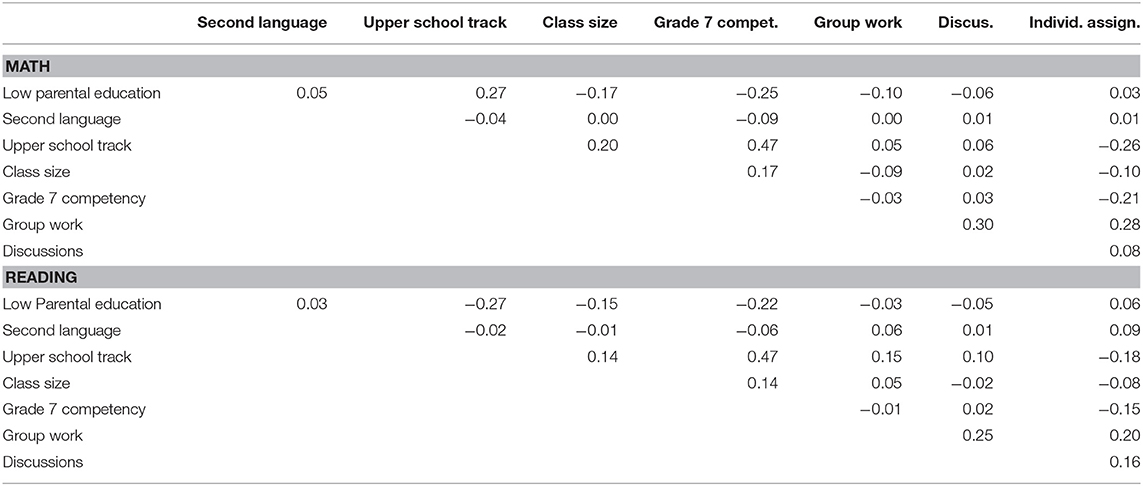
In order to answer our research questions, we estimated the parameters of a linear mixed effects model for both reading and math competence. In both models, we wished to incorporate all effects of interest as well as all major contributing factors whose omission might bias estimates. Competence at grade 9 was the outcome variable. Predictors included the three teaching techniques, parental education level (low or high), second language learner (native speaker vs. non-native speaker), class size, and the competency at grade 7. We centered class size at 26 students, which corresponds to the mean class size rounded to nearest integer in both subsamples. The centering allows for an easier interpretation of the other effects, as these are than computed for a (typical) class of 26 students. Also included were the two-way interactions between background variables and teaching technique as well as teaching technique and grade 7 competence. Lastly, because German schools are separated into tracks, we also included a binary predictor for attending an upper track school (Gymnasium) or any other school type. Interactions between school track and teaching technique were also included. A description of the correlations between all predictor variables can be found in Table 3. Although some correlations were relatively high (r = 0.47 for upper school track by grade 7 competence), the overall matrix indicates multicollinearity issues are unlikely. All modeled factors and their interactions are explicitly listed in Table 4.

TABLE 3

Table 3. Correlations of predictor variables.

TABLE 4

Table 4. Summary of the Math and Reading model results.

In an intermediate step, we fitted two models, one for reading and one for math competence, using the same predictors but no interaction effects. Adding the interaction terms improved model fit, ${\chi }_{\text{math}}^2$ (15) = 33.112, p < 0.01 and ${\chi }_{\text{reading}}^2$ (15) = 25.458, p < 0.05.

Estimation was done in R (R Core Team, 2018) using the package lme4 (Bates et al., 2015). Survey weights for students participating through waves 3 (Grade 7) and 5 (Grade 9) were used to account for the sampling process used in NEPS and drop-out following the recommendations of Rohwer (2011). The R package lmerTest (Kuznetsova et al., 2017) provided p-values.

Accounting for Class Structure

In order to account for bias caused by school selection and shared nuisance effects of the classroom (or course) environment, a random intercept on course level was incorporated into the models. It should be noted that were 210 different classes identified in the math subsample and 172 in the reading subsample. For the majority of classes in both subsamples only 5 or fewer students were sampled (i.e., in the initial data set in Table 1). The class size mean and standard deviation are seen in Table 1.

Treatment of Missing Data

Only complete cases entered the analysis (the resulting subsamples marginal distributions are listed in Table 1). It should be noted, in general multiple imputations (MI, see Schafer and Grahm, 2002 for an introduction) allows for a better treatment of missing data. However, MI relies on the missing at random (MAR) assumption, which requires knowledge of variables associated to missing data and the actual value that is missing. In our data, MAR was not justifiable because the virtually all of dropped cases are due to missing teacher or parent responses. In most of these cases, the respective entity did not participate in NEPS at all. This means we had no data from the particular respondent to use as a basis for imputation.

Results

Student Background Variables

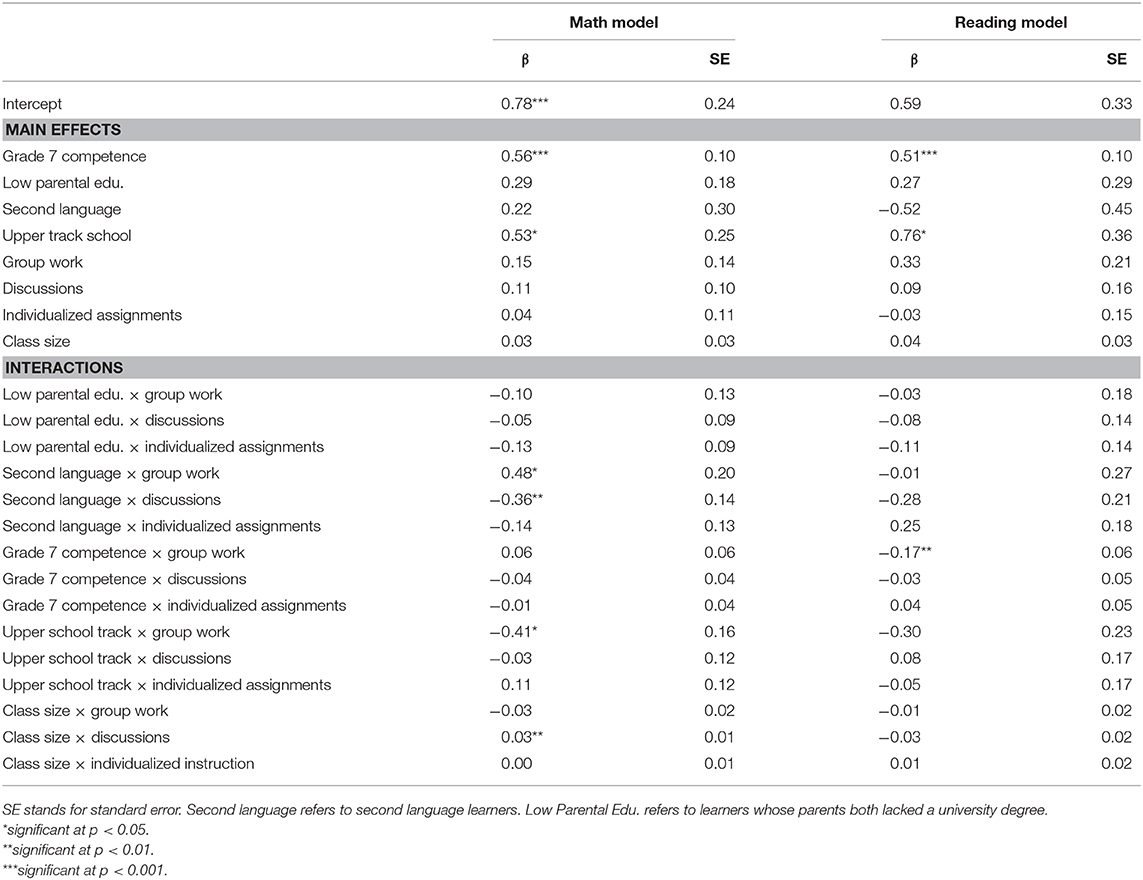
Table 4 summarizes both the reading and math models. In both the math and reading models, competency at grade 7 significantly predicts competency at grade 9, β_math = 0.56, SE = 0.10, p < 0.001, and β_reading = 0.51, SE = 0.10, p < 0.001. In both models, students attending the upper secondary track improved more than those attending other tracks, β_math = 0.53, SE = 0.25, p < 0.05, and β_reading = 0.76, SE = 0.36, p = 0.04. There were no significant main effects of parental education level or second language learning in either model, all ps > 0.10. Because the prior competency was incorporated into both models, this indicates that the rate of change between grades 7 and 9 were not affected by these variables.

Teaching Techniques

Also seen in Table 4, are the main effects of teaching techniques on 9th grade competency. In the math model, there were no significant effects of frequency of group work, discussion, or individualized assignments, p > 0.05.

There were a number of significant interactions between teaching techniques and student background variables in the math model. Second language learners had higher German competency after receiving group work, β = 0.48, SE = 0.20, p = 0.02, and lower when discussions were more common, β = −0.36, SE = 0.14, p = 0.01. Meanwhile, group work resulted in less of an improvement for children attending the upper school track, β = −0.41, SE = 0.16, p = 0.01. There were no other significant interactions between student background and teaching technique in the math model, all ps > 0.05.

There was only one significant interaction between teaching technique and student background variables in the reading model. Namely, children with a higher reading competency at grade 7, improved less when receiving group work, β = −0.17, SE = 0.06, p = 0.01. No other interactions between student background and teaching variables were significant in the reading model, all ps > 0.05.

The significant interactions in the math model are described in Figures 3 and 4, which plot the predicted competence based on an average class size with a random intercept of zero and the mean value for either discussions or group work as appropriate (see Table 1 for the actual values). Note that since there is no meaningful way to aggregate across school track, we include splits across school track in the upper and lower plots in the figures. These figures show a crossover effect of group work and discussions where more group work is better for non-native speakers and more discussions are less effective for non-native speakers.

FIGURE 3

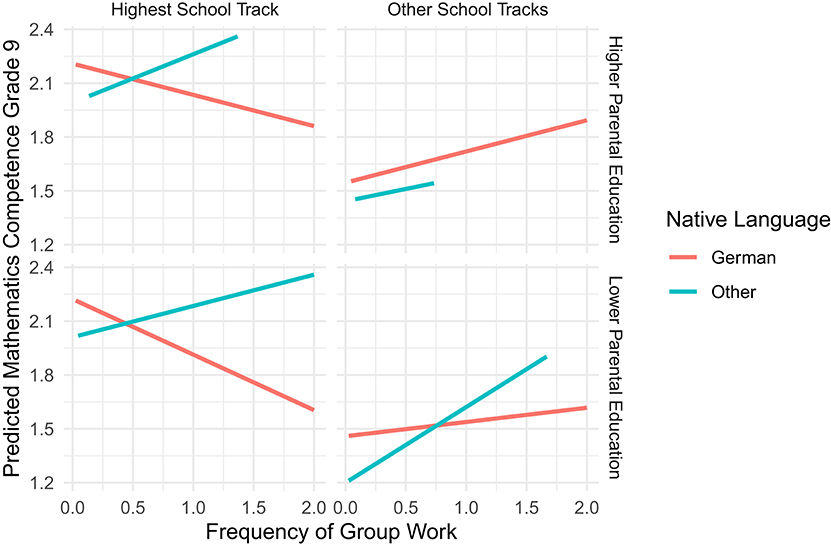
Figure 3. Predicted effects of group work for a typical class. Plotted are the predicted values based upon our regression models for a classroom of typical size and ability level. Lines are not interpolated past the values extant in the data, which results in a shorter line in some cases.

FIGURE 4

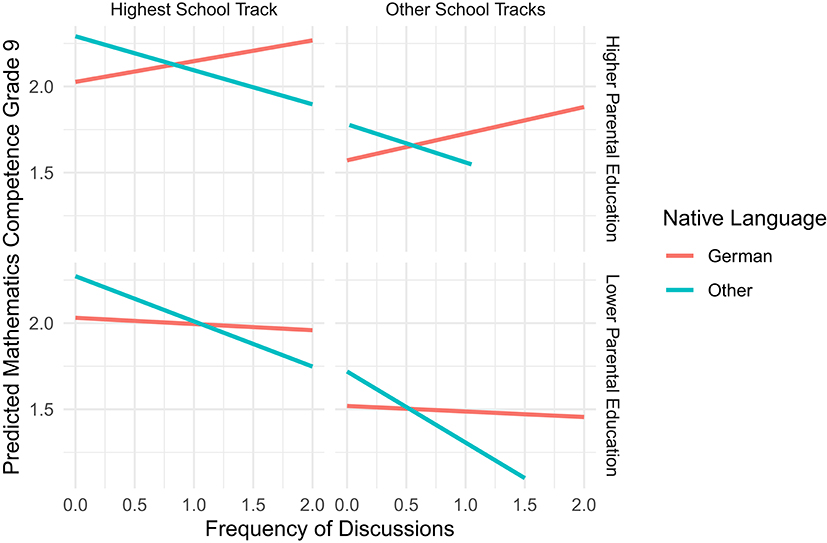
Figure 4. Predicted effects of discussions for a typical class. Plotted are the predicted values based upon our regression models for a classroom of typical size and ability level. Lines are not interpolated past the values extant in the data, which results in a shorter line in some cases.

Class Size

There was no significant main effect of class size in either the reading or the math model, both ps > 0.10. However, in the math model, students in larger classes receiving discussions improved slightly more, β = 0.03, SE = 0.01, p < 0.01. There were no other significant interactions in the math or reading models of class size and teaching techniques, all ps > 0.05.

Discussion

This article provides evidence for a differential impact of different teaching techniques based upon classroom size and the background of the learner. We found that specific teaching techniques in 7th grade have an effect on competency in 9th grade. In particular, we found that students in classes with more group work in 7th grade have a greater increase in mathematical competency after 2 years, while the opposite is true for discussions. Meanwhile, discussions were demonstrated to be slightly more effective in larger math classrooms than in smaller math classrooms. However, in the reading model, the only significant interaction was for the prior ability level with the use of group work, where children of a lower ability level who received more group work in grade 7, had a higher competence in grade 9. It is of particular interest that these interactions were found, but no main effects of the teaching technique, classroom size, or student background were found. Indeed the only significant main effect in either the reading or math models was school track, where learners in the highest school track outgained those in other tracks.

These interactions correspond to research suggesting that learners receive differential benefits from specific teaching techniques based upon classroom situation and background data. This is in line with some previous findings that group work can better facilitate classroom learning for second language learners (e.g., Benediktsson and Ragnarsdottir, 2019; Takeuchi et al., 2019); however the findings of worse gains for second language learners from discussions contrasts with some previous work which predicted a similar boost (Banes et al., 2018). Banes et al. argued that discussions were only beneficial within a given context that encouraged equal participation. We have no data on the quality of the implementation of teaching techniques, so the use of classroom discussions in our sample may not be particularly indicative of whether each learner is encouraged to participate. Indeed, second language learners may feel barriers to participation (e.g., Maeda, 2017).

Another unexpected finding is that group work is less effective for math learners in the highest school track. A similar interaction for the reading model was found, where learners with a higher ability level did worse with more group work. This supports the findings of Cera Guy et al. (2019), who found that higher ability learners may not be more engaged by group work settings and that they produce a similar amount of effort as if they were working individually. However, this would likely result in no difference, whereas we found a negative coefficient in this case. Further, we did not investigate a possible triple interaction between school track, second language, and group work. It may be that group work is only negatively associated with later competence for native speakers in the highest school tracks.

Also noteworthy are several predicted effects that were not found. We predicted slower attainments for non-native speakers and children whose parents lacked a university degree, but this was not found. The only significant effect of a background variable can be seen in a greater rate of improvement in math and reading competency for children attending the upper secondary education track. It may be that 2 years' time is not a long enough period to observe a difference in rate of change, or it may simply mean that there is only a mean-level difference and no difference in rate of change. The latter interpretation is supported by the findings of Rambo-Hernandez and McCoach (2014) growth analysis of reading competency and SES. They found mean-level differences in competency based on SES, but no strong difference in rates of growth.

We also did not detect a main effect for class size, although there was an interaction between class size and discussions in the math class. This contrasts with prior findings that smaller class sizes related to better learning [i.e., (Krassel and Heinesen, 2014)], although in some studies the effects of class size was very small (e.g., Watson et al., 2016), or affected by additional factors (Hattie, 2005).

Additionally, most of the predicted interactions in the reading model were not detected. The only interaction detected was the above-mentioned grade 7 competency by group work. Since some effects were descriptively of similar size as the corresponding Math model, this indicates, that we lack power to detect any possible effects due to the slightly smaller sample and the more restricted range of frequency of used teaching techniques. More work is needed in this area. Similarly, we found none of the predicted effects for individualized instruction. This may because the individualized instructions reflect attitudes rather than frequency of use (as used by the other teacher questions). More work is needed regarding the role of individualization.

Please note, that our math and reading models should not be compared directly using coefficients or effect sizes for two reasons. First, the samples from the two models are not identical or independent from each other. Second, we did not test comparability of the teacher scales between both types of teachers. In order to compare the effectiveness of teaching techniques across subjects, a multivariate outcome model is recommended for future research. Further, it may be possible to accomplish this with data from NEPS, provided there is a justifiable imputation model that allows the retention of a sufficiently large and representative sample of students and teachers.

There are a number of notable strengths of this study. We predicted competency based on the instruction techniques from 2 years prior. We accounted for the effects of school track. We used a random-intercept model to account for course-specific competence levels. In addition, we used a large dataset. Nonetheless, limitations remain. We only possessed data about teaching styles at a single measurement point, and it is possible that teachers are already adapting their teaching styles based on classroom size or composition. However, Hattie (2002) argues that this is unlikely, as teachers rarely change their styles based on classroom composition. Parent and teacher non-participation was substantial and may be related to all variables considered. As a result, the removal of students with non-participating parents/teachers could have biased our results. Furthermore, panel attrition was accounted by reweighting, which keeps the sample representative but only with respect to factors on which the weights are based. Because we looked at the long-term effects (2-years later), smaller more immediate effects may be missed. Longitudinal tracking studies over a shorter timeframe (a semester or a single school-year) should also be done. Furthermore, we could only use teacher responses about their own teaching techniques. Other studies should examine teaching techniques using more objective measures. This is especially important because of the relatively low reliability in some of our measures of teaching techniques, which may have biased some of our measures of variance (Woodhouse et al., 1996; Dedrick et al., 2009). In this regard, we also did not examine the suitability of teaching techniques with characteristics of the teachers, which may explain a great deal of the variance in the effectiveness of these techniques. Similarly, we did not distinguish between the effectiveness of a teaching style in a particular class setting and the effectiveness on the individual level (e.g., Enders and Tofighi, 2007). We are also limited by the items included in the NEPS database when constructing our scales. Further research is needed to verify the quality of these items and scales in other contexts. Lastly, our results need to be compared with different school levels, such as primary school and later secondary school. Similarly, analyses of changes of teaching styles over times may also be informative.

Conclusion

While not related to main effects, group work, and discussions had situational effects based on student background and class size in math and reading which were detectable 2 years later. Students' math competency in grade nine was higher for second language learners who received more group work-based instruction in grade seven. Conversely, math competency in grade nine was lower for second language learners who received more discussion-based instruction in grade seven. At the same time, discussions in larger math classes were associated with a more competency gain than discussions in smaller math classes. Furthermore, group work instruction related to lower math competency for learners in the upper secondary school track. Also, learners with a lower grade seven reading competency did have a higher reading competency in grade nine when receiving more group work-based instruction.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: http://dx.doi.org/10.5157/NEPS:SC3:8.0.1.

Ethics Statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent to participate in this study was provided by the participants' legal guardian/next of kin.

Author Contributions

JD served as primary author of the manuscript, writing most of the manuscript and proofing and adapting contributions from other authors. MG and JD developed theoretical bases for chosen analyses. Analyses were performed by CS. CS wrote many sections of the methods and results and the interpretation of the results. PD provided feedback and refinement for analyses and methodology. PD and MG provided additional manuscript supervision.

Funding

Funding for this research was provided by the DFG Priority Programme 1646, Education as a Lifelong Process, project number 390666287. We acknowledge financial support by Deutsche Forschungsgemeinschaft and Technische Universität Dortmund/TU Dortmund Technical University within the funding programme Open Access Publishing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This paper uses data from the National Educational Panel Study (NEPS): Starting Cohort Grade 5, 10.5157/NEPS:SC3:8.0.0. From 2008 to 2013, NEPS data was collected as part of the Framework Program for the Promotion of Empirical Educational Research funded by the German Federal Ministry of Education and Research (BMBF). As of 2014, NEPS is carried out by the Leibniz Institute for Educational Trajectories (LIfBi) at the University of Bamberg in cooperation with a nationwide network.

References

Banes, L. C., Ambrose, R. C., Bayley, R., Restani, R. M., and Martin, H. A. (2018). Mathematical classroom discussion as an equitable practice: effects on elementary english learners' performance. J. Lang. Ident. Educ. 17, 416–433. doi: 10.1080/15348458.2018.1500464

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67, 1–48. doi: 10.18637/jss.v067.i01

CrossRef Full Text | Google Scholar

Benediktsson, A. I., and Ragnarsdottir, H. (2019). Communication and group work in the multicultural classroom: immigrant students' experiences. Eur. J. Educ. Res. 8, 453–465. doi: 10.12973/eu-jer.8.2.453

CrossRef Full Text | Google Scholar

Bešić, E., Paleczek, L., Krammer, M., and Gasteiger-Klicpera, B. (2016). Inclusive practices at the teacher and class level: the experts' view. Eur. J. Spec. Needs Educ. 32, 329–345. doi: 10.1080/08856257.2016.1240339

CrossRef Full Text | Google Scholar

Björklund, A., and Salvanes, K. (2011). “Education and family background,” in Handbooks in economics. Handbook of the economics of education: Vol. 3, eds E. A. Hanushek, L. Woessmann, and S. Machin (Amsterdam: North Holland), 201–247. doi: 10.1016/B978-0-444-53429-3.00003-X

CrossRef Full Text | Google Scholar

Blatchford, P., Bassett, P., and Brown, P. (2011). Examining the effect of class size on classroom engagement and teacher-pupil interaction: differences in relation to pupil prior attainment and primary vs. secondary schools. Learn. Instruct. 21, 715–730. doi: 10.1016/j.learninstruc.2011.04.001

CrossRef Full Text | Google Scholar

Blatchford, P., and Russell, A. (2018). Class size, grouping practices and classroom management. Int. J. Educ. Res. 96, 154–163. doi: 10.1016/j.ijer.2018.09.004

CrossRef Full Text | Google Scholar

Blossfeld, H-P., Roßbach, H-G., and von Maurice, J., (eds.). (2011). “Education as a lifelong process. The German National Educational Panel Study (NEPS). Zeitschrift für Erziehungswissenschaft:.

Google Scholar

Brühwiler, C., and Blatchford, P. (2011). Effects of class size and adaptive teaching competency on classroom processes and academic outcome. Learn. Instruct. 21, 95–108. doi: 10.1016/j.learninstruc.2009.11.004

CrossRef Full Text | Google Scholar

Carstensen, C. H., and Pohl, S. (2012). NEPS Technical Report - Scaling the Data of the Competence Tests (NEPS Working Paper No. 14). Bamberg: Otto-Friedrich-Universität. Retrieved from Nationales Bildungspanel website: https://www.neps-data.de/Portals/0/Working%20Papers/WP_XIV.pdf

Google Scholar

Cera Guy, J. N. M. T., Williams, J. M., and Shore, B. M. (2019). High- and otherwise-achieving students' expectations of classroom group work: an exploratory empirical study. Roeper Rev. 41, 166–184. doi: 10.1080/02783193.2019.1622166

CrossRef Full Text | Google Scholar

Cohen, E. G., Lotan, R. A., Darling-Hammond, L., and Goodlad, J. I. (2014). Designing Groupwork: Strategies for the Heterogeneous Classroom, 3rd Edn. New York, NY: Teachers College Press.

Google Scholar

Crosnoe, R., and Fuligni, A. J. (2012). Children from immigrant families: introduction to the special section. Child Dev. 83, 1471–1476. doi: 10.1111/j.1467-8624.2012.01785.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Currie, J. (2009). Healthy, wealthy, and wise: socioeconomic status, poor health in childhood, and human capital development. J. Econ. Literat. 47, 87–122. doi: 10.1257/jel.47.1.87

CrossRef Full Text | Google Scholar

Dedrick, R. F., Ferron, J. M., Hess, M. R., Hogarty, K. Y., Kromrey, J. D., Lang, T. R., et al. (2009). Multilevel modeling: a review of methodological issues and applications. Rev. Educ. Res. 79, 69–102. doi: 10.3102/0034654308325581

CrossRef Full Text | Google Scholar

DeVries, J. M., Rathmann, K., and Gebhardt, M. (2018). How does social behavior relate to both grades and achievement scores? Front. Psychol. 9:857. doi: 10.3389/fpsyg.2018.00857

PubMed Abstract | CrossRef Full Text | Google Scholar

Eilertsen, T., Thorsen, A. L., Holm, S. E. H., Bøe, T., Sørensen, L., and Lundervold, A. J. (2016). Parental socioeconomic status and child intellectual functioning in a Norwegian sample. Scand. J. Psychol. 57, 399–405. doi: 10.1111/sjop.12324

PubMed Abstract | CrossRef Full Text | Google Scholar

Enders, C. K., and Tofighi, D. (2007). Centering predictor variables in cross-sectional multilevel models: a new look at an old issue. Psychol. Methods 12, 121–138. doi: 10.1037/1082-989X.12.2.121

PubMed Abstract | CrossRef Full Text | Google Scholar

Gebhardt, M., Sälzer, C., Mang, J., Müller, K., and Prenzel, M. (2015). Performance of students with special educational needs in Germany: findings from programme for International student assessment 2012. J. Cogn. Educ. Psychol. 14, 343–356. doi: 10.1891/1945-8959.14.3.343

CrossRef Full Text | Google Scholar

Glass, G. V., and Smith, M. L. (1979). Meta-analysis of research on class size and achievement. Educ. Eval. Policy Anal. 1:2. doi: 10.3102/01623737001001002

CrossRef Full Text | Google Scholar

Harfitt, G. J., and Tsui, A. B. M. (2015). An examination of class size reduction on teaching and learning processes: a theoretical perspective. Br. Educ. Res. J. 41, 845–865. doi: 10.1002/berj.3165

CrossRef Full Text | Google Scholar

Hattie, J. (2005). The paradox of reducing class size and improving learning outcomes. Int. J. Educ. Res. 43, 387–425. doi: 10.1016/j.ijer.2006.07.002

CrossRef Full Text | Google Scholar

Hattie, J. A. C. (2002). Classroom composition and peer effects. Int. J. Educ. Res. 37, 449–481. doi: 10.1016/S0883-0355(03)00015-6

CrossRef Full Text | Google Scholar

Hofmann, R., and Mercer, N. (2016). Teacher interventions in small group work in secondary mathematics and science lessons. Lang. Educ. 30, 400–416. doi: 10.1080/09500782.2015.1125363

CrossRef Full Text | Google Scholar

Igel, C., and Urquhart, V. (2015). Generation Z, meet cooperative learning. Middle Sch. J. 43, 16–21. doi: 10.1080/00940771.2012.11461816

CrossRef Full Text | Google Scholar

Jocz, J. A., Zhai, J., and Tan, A. L. (2014). Inquiry learning in the Singaporean context: factors affecting student interest in school science. Int. J. Sci. Educ. 36, 2596–2618. doi: 10.1080/09500693.2014.908327

CrossRef Full Text | Google Scholar

Kang, J., and Keinonen, T. (2018). The effect of student-centered approaches on students' interest and achievement in science: relevant topic-based, open and guided inquiry-based, and discussion-based approaches. Res. Sci. Educ. 48, 865–885. doi: 10.1007/s11165-016-9590-2

CrossRef Full Text | Google Scholar

King-Sears, M. E., Johnson, T. M., Berkeley, S., Weiss, M. P., Peters-Burton, E. E., Evmenova, A. S., et al. (2015). An exploratory study of universal design for teaching chemistry to students with and without disabilities. Learn. Disabil. Q. 38, 84–96. doi: 10.1177/0731948714564575

CrossRef Full Text | Google Scholar

Krassel, K. F., and Heinesen, E. (2014). Class-size effects in secondary school. Educ. Econ. 22, 412–426. doi: 10.1080/09645292.2014.902428

CrossRef Full Text | Google Scholar

Kuznetsova, A., Brockhoff, P. B., and Christensen, R. H. B. (2017). LmerTest package: tests in linear mixed effects models. J. Stat. Softw. 82, 1–26. doi: 10.18637/jss.v082.i13

CrossRef Full Text | Google Scholar

Lekholm, A. K., and Cliffordson, C. (2008). Discrepancies between school grades and test scores at individual and school level: effects of gender and family background. Educ. Res. Eval. 14, 181–199. doi: 10.1080/13803610801956663

CrossRef Full Text | Google Scholar

Maeda, J. (2017). Self-efficacy reduces impediments to classroom discussion for International students: fear, embarrassment, social isolation, judgment, and discrimination. IAFOR J. Educ. 5, 141–159. doi: 10.22492/ije.5.2.07

CrossRef Full Text | Google Scholar

Marzano, R. J., Pickering, D. J., and Pollock, J. E. (2003). Classroom Instruction that Works: Research-based Strategies for Increasing Student Achievement ([Nachdr.]). Alexandria: Association for Supervision and Curriculum Development.

Google Scholar

Miller, N. C., McKissick, B. R., Ivy, J. T., and Moser, K. (2017). Supporting diverse young adolescents: cooperative grouping in inclusive middle-level settings. Clear. House J. Educ. Strateg. Issues Ideas 90, 86–92. doi: 10.1080/00098655.2017.1285661

CrossRef Full Text | Google Scholar

Ok, M. W., Rao, K., Bryant, B. R., and McDougall, D. (2016). Universal design for learning in Pre-K to grade 12 classrooms: a systematic review of research. Exceptionality 25, 116–138. doi: 10.1080/09362835.2016.1196450

CrossRef Full Text | Google Scholar

Phelps, J. L. (2011). Another look at the glass and smith study on class size. Educ. Considerat. 39, 3–14. doi: 10.4148/0146-9282.1100

CrossRef Full Text | Google Scholar

R Core Team. (2018). R: A Language and Envirnment for Statistical Computing. Retrieved from R Foundation for Statistical Computing website: https://www.R-project.org/

Google Scholar

Rambo-Hernandez, K. E., and McCoach, D. B. (2014). High-achieving and average students' reading growth: contrasting school and summer trajectories. J. Educ. Res. 108, 112–129. doi: 10.1080/00220671.2013.850398

CrossRef Full Text | Google Scholar

Rindermann, H., and Baumeister, A. E. E. (2015). Parents' SES vs. parental educational behavior and children's development: a reanalysis of the Hart and Risley study. Learn. Individ. Diff. 37, 133–138. doi: 10.1016/j.lindif.2014.12.005

CrossRef Full Text | Google Scholar

Rohwer, G. (2011). Using Sampling Weights for Model Estimation? (NEPS Working Paper No. 4). Bamberg: Otto-Friedrich-Universität. Retrieved from Nationales Bildungspanel. website: https://www.neps-data.de/Portals/0/Working%20Papers/WP_IV.pdf

Google Scholar

Roseth, C. J., Johnson, D. W., and Johnson, R. T. (2008). Promoting early adolescents' achievement and peer relationships: the effects of cooperative, competitive, and individualistic goal structures. Psychol. Bull. 134, 223–246. doi: 10.1037/0033-2909.134.2.223

PubMed Abstract | CrossRef Full Text | Google Scholar

Schafer, J. L., and Grahm, J. W. (2002). Missing data: Our view of the state of the art. Psychol. Methods. 7, 147–177. doi: 10.1037/1082-989X.7.2.147

PubMed Abstract | CrossRef Full Text | Google Scholar

Sirin, S. R. (2016). Socioeconomic status and academic achievement: a meta-analytic review of research. Rev. Educ. Res. 75, 417–453. doi: 10.3102/00346543075003417

CrossRef Full Text | Google Scholar

Solari, E. J., Petscher, Y., and Folsom, J. S. (2014). Differentiating literacy growth of ELL students with LD from other high-risk subgroups and general education peers: evidence from grades 3-10. J. Learn. Disabil. 47, 329–348. doi: 10.1177/0022219412463435

PubMed Abstract | CrossRef Full Text | Google Scholar

Steinhauer, H. W., and Zinn, S. (2016). NEPS Technical Report for Weighting: Weighting the Sample Of Starting Cohort 3 of the National Educational Panel Study (Waves 1 to 3) (NEPS Working Papers No. 63). Bamberg: Otto-Friedrich-Universität. Retrieved from NEPS website: https://www.neps-data.de/Portals/0/Working%20Papers/WP_LXVI.pdf

Google Scholar

Takeuchi, M. A., Bryan, V., Valera, S., and Dadkhahfard, S. (2019). Immigrant students' stories about learning mathematics in groups. Can. J. Sci. Math. Technol. Educ. 19, 237–253. doi: 10.1007/s42330-019-00056-8

CrossRef Full Text | Google Scholar

Tomlinson, C. A., and Imbeau, M. B. (2011). Managing a Differentiated Classroom: Grades K-8; a Practical Guide. New York, NY: Scholastic.

Google Scholar

Tomlinson, C. A., and Moon, T. R. (2013). Assessment and Student Success in a Differentiated Classroom. Alexandria: ASCD. Retrieved from http://site.ebrary.com/lib/alltitles/docDetail.action?docID=10774725

Google Scholar

Torres, R. (2018). Tackling inequality? Teacher effects and the socioeconomic gap in educational achievement. evidence from Chile. Sch. Eff. Sch. Improve. 29, 383–417. doi: 10.1080/09243453.2018.1443143

CrossRef Full Text | Google Scholar

Watson, K., Handal, B., and Maher, M. (2016). The influence of class size upon numeracy and literacy performance. Qual. Assur. Educ. 24, 507–527. doi: 10.1108/QAE-07-2014-0039

CrossRef Full Text | Google Scholar

White, K. R. (1982). The relation between socioeconomic status and academic achievement. Psychol. Bull. 91, 461–481. doi: 10.1037/0033-2909.91.3.461

CrossRef Full Text | Google Scholar

Woodhouse, G., Yang, M., Goldstein, H., and Rasbash, J. (1996). Adjusting for measurement error in multilevel analysis. J. R. Stat. Soc. Ser. A 159, 201–212. doi: 10.2307/2983168

CrossRef Full Text | Google Scholar

Wright, M. C., Bergom, I., and Bartholomew, T. (2017). Decreased class size, increased active learning? Intended and enacted teaching strategies in smaller classes. Active Learn. High. Educ. 20, 51–62. doi: 10.1177/1469787417735607

CrossRef Full Text | Google Scholar