- 1Department Humanities, Institute Special Education, Leibniz University Hanover, Hanover, Germany
- 2Department Educational Studies, Institute Psychology, University Duisburg-Essen, Essen, Germany
- 3Centre for Education Practice Research, University of Johannesburg, Johannesburg, South Africa
- 4Department Human Sciences, Institute Inclusive Education, University of Potsdam, Potsdam, Germany
Early numeracy has been found to be one of the strongest predictors for later success in learning. Equipping children with a sound conceptual numerical understanding should therefore be a focus of early primary school mathematics. Assessments that are aligned to empirically validated learning progressions can support teachers to understand their students learning better and target instruction accordingly. This study examines numeracy learning of 101 first grade students over the course of one school year using progression-based assessments. Findings show that the students' performance increased significantly over time and that the initial conceptual numerical understanding had a positive effect on the students' learning progress as well as their end of school year performance. Analyzing the performance data based on the levels of the underlying developmental model uncovered an increasing elaboration of conceptual numerical understanding over time, but also individual differences within this process that need to be addressed through targeted intervention.
Introduction
Research suggests that children's mathematical knowledge varies quite substantially when commencing formal schooling in Grade 1 (Bodovski and Farkas, 2007; Dowker, 2008), and that without appropriate teaching, differences in mathematical performance tend to be consistent over time (Aunola et al., 2004; Morgan et al., 2011; Missall et al., 2012; Navarro et al., 2012). Furthermore, early numeracy concepts were found to be the strongest predictor for later learning (Duncan et al., 2007; Krajewski and Schneider, 2009; Romano et al., 2010; Claessens and Engel, 2013). Early knowledge in numeracy predicted not only success in mathematics, but also success in reading (Lerkkanen et al., 2005; Duncan et al., 2007; Romano et al., 2010; Purpura et al., 2017) and was a stronger predictor for later academic achievement than other developmental skills, such as literacy, attention, and social skills (Duncan et al., 2007). In a similar vein, the initial numeracy skills of children at the transition to school do not only predict later achievement but also the learning growth children are likely to show.
A number of recent studies examining the development of math performance in primary school suggest a cumulative growth pattern (Aunola et al., 2004; Bodovski and Farkas, 2007; Morgan et al., 2011; Geary et al., 2012; Missall et al., 2012; Salaschek et al., 2014; Hojnoski et al., 2018). For a detailed synthesis of early numeracy growth studies, see Salaschek et al. (2014). Cumulative development, also known as Matthew effect (Stanovich, 1986), is characterized by a gradual accumulation of knowledge and skills over time. Children who start with good skills and sophisticated knowledge increase their performance more than those who start with lower levels of proficiency. This growth pattern was found among unselected populations of primary school students (Aunola et al., 2004; Salaschek et al., 2014) as well as for specific groups of students, such as children with learning difficulties (Geary et al., 2012), speech language impairments (Morgan et al., 2011) and disability (Hojnoski et al., 2018). Further, studies examining the effects of learning progress-related predictors found a significant effect of the initial learning status (intercept) as well as the learning growth (slope) on later math performance (Keller-Margulis et al., 2008; Kuhn et al., 2019).
In accordance with these research findings, we propose that the acquisition of early numeracy in first grade is exceedingly crucial for children's later performance at school. To support teachers in providing early numeracy instruction that is tailored to the student's individual levels of understanding, we designed a formative assessment tool—hereafter called Learning Progress Assessment (LPA)—based on a learning progression approach. In this study, we used the LPA to shed more light onto first grade students' development of conceptual numerical understanding and simultaneously further investigate the quality of the instrument.
Defining Early Numeracy and Conceptual Knowledge
Mathematics represents a complex construct that is composed of various skills which are usually organized within five domains: numbers and operations, geometry, measurement, algebra, and data analysis (Clements and Sarama, 2009). These domains are also described in the German National Educational Standards (KMK, 2004) which are applied in the mathematics curricula of the different federal states of Germany. A significant amount of research has been conducted in the domain of numbers and operations covering the field of arithmetic. In early primary school (first and second grade), numbers and operations, also referred to as early numeracy (Aunio and Niemivirta, 2010) or symbolic number sense (Jordan et al., 2010), encompasses the skills of number knowledge, verbal counting, basic calculations, and quantity comparison. Early numeracy has been found to be the area of early mathematics most predictive for later success in mathematics (Mazzocco and Thompson, 2005). In this paper the terms numeracy and arithmetic are used interchangeably.
Early numeracy skills, such as basic operations, are underpinned by conceptual knowledge that assigns meaning to the procedures and arithmetic facts. In contrast to procedural knowledge that involves knowing how to perform a calculation, conceptual knowledge involves understanding why arithmetical problems can be solved in a certain way (Hiebert and Lefevre, 1986). Conceptual understanding of early numeracy skills is considered the foundation for developing sound mathematical skills later on (Gelman and Gallistel, 1978). Hence, one objective of the German National Educational Standards is to initiate a change in German mathematics education away from focusing on the pure knowledge of arithmetic facts and the performance of routine procedures toward conceptual understanding (KMK, 2004). However, conceptual knowledge and procedural skills should be considered as iterative, each prompting the learning of the other (Rittle-Johnson et al., 2001).
Learning Progressions in Early Numeracy
Learning progressions, also known as learning trajectories, conceptualize learning as “a development of progressive sophistication in understanding and skills within a domain” (Heritage, 2008, p. 4). In other words, learning progressions describe how knowledge, concepts and skills within a certain domain typically develop and what it means to improve in that area of learning. Black et al. (2011) describe learning progression as a pathway, or “road map” (p. 4) that presents knowledge and skill development as sequential in its increase in complexity.
According to Clements and Sarama (2009) learning trajectories consist of three parts: a mathematical goal, often given by the curriculum, a developmental path “along which children develop to reach that goal” (p. 3), and a set of instructional activities matched to each level of the developmental path that help children to develop higher levels of understanding. By applying this 3-fold approach, Clements and Sarama (2009) created and empirically investigated learning progressions for a variety of mathematical areas, including early numeracy skills, such as counting, comparing numbers, composing numbers, and addition and subtraction. Empson (2011) pointed out that the idea of learning progressions as a “series of predictable levels” (Sarnecka and Carey, 2008, p. 664) is not new within mathematics research. For example, Gelman and Gallistel's (1978) description of children's acquisition of counting skills and Fuson's (1988) model of children's development of number concepts are well-established and broadly recognized. Such historical approaches built the theoretical foundation for more recent empirically-supported models that aim to describe development through the concept of learning progressions.
For example, in their model of number-knower levels Sarnecka and Carey (2008) describe the developmental process that occurs between being able to recite the counting list while pointing at objects to being able to understand the “cardinal principle” (Gelman and Gallistel, 1978). The number-knower levels framework is supported by studies using the “Give-N” or “Give-A-Number” task (Le Corre and Carey, 2007; Lee and Sarnecka, 2011). In this task, children were requested to generate subsets of a particular number from a larger set of objects that is placed in front of them (e.g., “Give me three marbles”).
Fritz et al. (2013) published a model that aims to map the development of early numeracy, with a particular focus on conceptual understanding. This model of conceptual numerical development has been empirically validated in cross-sectional as well as longitudinal studies (Fritz et al., 2018) and builds the theoretical foundation of the LPA introduced in this study. The model describes six successive, hierarchical levels of increasing numerical sophistication, with each level characterized by a central numerical concept. The model emphasizes a conceptual progression, in which less sophisticated concepts build the foundation for more sophisticated concepts and understands development in the sense of “overlapping waves” (Siegler and Alibali, 2005). This means, the levels describe an increasing elaboration of conceptual understanding, rather than distinct, exclusive stages of ability. Table 1 shows the central numerical concept for each level and a short description of the associated skills. For a detailed description of the model, see Fritz et al. (2013).

Table 1. Development model of conceptual numerical understanding by Fritz et al. (2013).
Learning Progression-Based Assessments
Internationally, the learning progression approach has been applied to inform educational standards, national curricula, and large scale assessments, as well as formative assessment practices (e.g., Daro et al., 2011; ACARA, 2017). To serve these different purposes, learning progressions differ in their scope (i.e., the amount of instructional time and content) and their grain size (i.e., the level of detail provided about changes in student thinking) (Gotwals, 2018). For example, a learning progression with a larger scope and grain size may be more appropriate to inform educational standards than formative assessment practices because standards need to describe students' understanding over a longer period of time. To be useful for formative assessment purposes, learning progressions with a smaller scope and grain size would be more suitable to support teachers in their instructional decision making, as these types of progressions describe “nuances in the shifts in student thinking” (Gotwals, 2018, p. 158). Research on the quality of instruction has suggested that formative assessment is important practice for teachers to support their students' learning best (Black and Wiliam, 1998; Wiliam et al., 2004; Kingston and Nash, 2011). However, in a meta-analysis Stahnke et al. (2016) findings suggest that mathematics teachers tend to struggle with choosing adequate tasks to support their students learning and have difficulties interpreting tasks and identifying their potential for instruction. As learning progressions describe how the development in a certain domain typically looks like, we support the premise of Clements et al. (2008), which stated that assessments that are aligned to learning progressions are important tools to support formative assessment practices. Such assessments can inform instruction that is targeted to the students' individual levels of understanding.
To our knowledge, however, there are only few progression-based numeracy assessments available in Germany. Even fewer have been empirically validated. Most of the German formative mathematics assessments, which are also psychometrically tested, aim to monitor how well students progress in learning the content specified in a certain year level curriculum, but do not take the developmental perspective into account (Strathmann and Klauer, 2012; Salaschek et al., 2014; Gebhardt et al., 2016; Kuhn et al., 2018).
Rationale of the Study and Research Questions
The present study sought to add to previous research by examining the LPA for use within the German school context which was designed in alignment to the model of conceptual numerical development by Fritz et al. (2013). The goal of this study was to provide insights into the first grade students' conceptual numerical development as well as to further investigate the quality of the LPA, but not to evaluate the effectiveness of the interventions. Therefor four research questions were addressed.
Research question 1: To what extent does numerical performance (assessed through the LPA) change over time? In line with other mathematical growth studies in early primary school (e.g., Bodovski and Farkas, 2007), a significant increase in performance over time was expected.
Research question 2: To what extent does the numerical knowledge prior to school predict change in numerical performance over time? Based on previous studies examining the effects of domain specific predictors on math learning, such as those by Krajewski and Schneider (2009) a positive effect of the numerical pre-knowledge on the children's numerical development was expected. A cumulative growth pattern predicted by the numerical knowledge prior to school was also anticipated, in line with findings by Salaschek et al. (2014).
Research question 3: To what extent do numerical knowledge prior to school and change in numerical performance over time predict numerical performance at the end of Grade 1? It was hypothesized that the numerical knowledge prior to school would explain a relatively high share of the variance of the numerical performance at the end of the school year. With regard to findings from Kuhn et al. (2019) it was further expected that the LPA would also be a significant predictor for numeracy performance at the end of the school year.
Research question 4: How does the conceptual numerical understanding change over the course of Grade 1? As suggested by findings of Fritz et al. (2018) it was expected that most children would start school at Level III (concept of cardinality). Over the course of Grade 1 the students are expected to gain about one conceptual level, reaching Level IV or V (concept of part-part-whole relations or concept of equidistant number line intervals) by the end of the school year. Given the considerable heterogeneity of mathematical knowledge in German first graders (e.g., Peter-Koop and Kollhoff, 2015), it was also postulated that a wide range of levels would be found.
Method
Participants and Procedure
As part of a longitudinal Response-to-Intervention study, a total of 101 (55% female) first grade students (MAge = 78.24 months, SD = 3.89) from six classes of two German primary schools were examined over the course of one school year. The schools were located in an urban area with a higher socioeconomic status. The data was collected by trained Master students of the Inclusive Education program of the local university.
The first grade students' conceptual numerical knowledge was assessed at the beginning of school using the “Mathematics and arithmetical concepts in preschool age” (MARKO-D; Ricken et al., 2013) as a pre-test, and re-assessed at the end of the school year using the “Mathematics and arithmetical concepts of first grade students” (MARKO-D1; Fritz et al., 2017) as a post-test. Between the two MARKO-D tests, the Learning progress assessment (LPA) was applied over nine measurement points (LPAt1 to LPAt9) starting at about 12 weeks after the beginning of school with ~4 weeks in between each measurement. All students received general teaching according to the requirements of the German curriculum (Landesinstitut für Schule und Medien Berlin-Brandenburg (LISUM), 2015). Some students participated in additional mathematical interventions as part of the Response-to-Intervention study (e.g., Gerlach et al., 2013).
Instruments
MARKO-D Test Series
The MARKO-D (Ricken et al., 2013) and MARKO-D1 (Fritz et al., 2017) tests are standardized, Rasch scaled diagnostic instruments that have been designed based on the development model of arithmetical concepts by Fritz et al. (2013) described previously (see Table 1). Based on the levels of the model, the tests aim to capture children's understanding of arithmetical concepts for different levels and age groups (MARKO-D: Levels I to V, Age: 48–87 months; MARKO-D1: Levels II to VI, Age: 71–119 months). The test items are presented in a randomized order. The MARKO-D tests are linked by 22 anchor items spread over different developmental levels. Both tests are conducted as individual tests in a one-on-one situation and take ~30 min each. The children's performance data can be analyzed quantitatively (based on raw scores, transferred into T-scores and percentile ranks), as well as qualitatively (based on response patterns, transferred into individual conceptual levels).
Learning Progress Assessment (LPA)
The LPA aims to assess the children's performance within the different levels of the same developmental model (see Table 1). In contrast to the MARKO-D tests (Ricken et al., 2013; Fritz et al., 2017), the LPA, however, does not assess all levels in one test. Instead, it uses shorter tests that are targeted to the student's current numerical understanding and applied formatively within group settings.
In this study the short tests were targeted to the students' current level of proficiency based on their performance on the previous test. For the first measurement point of the LPA, the performance on the MARKO-D test served as decision criterion for assigning the appropriate test version. The short tests of the LPA were conducted in small groups of students at the same developmental level and took ~15 min. The instructions were read aloud by trained Master students whilst the first grade students solved the given assessment tasks in individual test booklets.
Each short test consisted of 15 items covering three levels (five items per level): the student's current level of proficiency, the previous level and the subsequent level. As a result, at each measurement point up to five different test versions were used (Levels I to III, Levels II to IV, Levels III to V, Levels IV to VI, Levels V to VI+). The test items were drawn from a pool of items operationalizing the levels of the model. The item pool consisted of 90 dichotomous items (I:12, II:17, III:10, IV:12, V:14, VI:13, VI+:12). The hypothesized developmental levels of the items had been empirically evaluated in previous cross-sectional and longitudinal studies (Balt et al., 2017). Subsets of five items per level, including one linking item per level, were drawn from the item pool and randomly assigned to each measurement time. In a multi-matrix test booklet design (Johnson, 1992), linking items are items all tests have in common. As such, they provide a reference point for evaluating the difficulty of the remaining items and enable a concurrent scaling of all items within the Rasch model (von Davier, 2011). With the exception of the linking items, there was no repetition of the same items in consecutive measurements to avoid memory effects.
Please note that the twelve VI+ items did not relate to the developmental model. These items were introduced at measurement point seven to cater for students who performed above Level VI at the time. The items were expected to be more difficult as they assessed the concepts of Levels V and VI but within a higher number range.
Data Analysis
The Rasch model was used as the underlying mathematical model to build the progression-based assessments used in this study (MARKO-D tests and LPA). Within the Rasch model item and person parameters are mapped on a joint scale. The numerical performance data of the students obtained through the MARKO-D tests and the LPA were scaled applying simple dichotomous Rasch models (Rasch, 1960). MARKO-D and MARKO-D1 were combined onto one scale and calibrated simultaneously based on linking items, and the short tests of the LPA were mapped on another scale based on their linking items. Thus, numeracy performance was measured on two separate scales (MARKO-D/D1 and LPAt1 to LPAt9). The item parameters of the measurement models were fitted using Conditional-Maximum-Likelihood (CML) estimation and person parameters were determined based on the Maximum-Likelihood estimation (ML). The specification of the measurement models as well as its goodness of fit were evaluated using the eRM package (Mair and Hatzinger, 2007) within R software (R Core Team, 2017, Version 1.2.1335). The goodness of fit to the Rasch model was assessed through item-fit analyses. The assumption of sample invariance of the LPA scale was tested through Andersen Likelihood Ratio Tests (LRT) (Andersen, 1973). For the LRT tests, the median was used as an internal split criterion to compare the item parameter estimations for students with higher and lower test scores. Gender was used as an external split criterion to determine whether the item parameter estimation differed significantly between male and female students. No systematic difference between different subgroups of the sample should be found if the Rasch model is valid (van den Wollenberg, 1988).
After fitting and testing the Rasch model, the person parameters of both numeracy scales (MARKO-D tests and LPA) were used to investigate the student's numerical development over the course of Grade 1. To account for the characteristics of the longitudinal design of the study (e.g., time as an independent variable), linear Mixed Models were used to address research question 1 (the effect of time on numeracy performance) and research question 2 (the effect of numerical knowledge prior to school on numeracy development in first grade). Competing models were compared using log likelihood tests, with the more complex model retained if that fitted the data significantly better (Bliese and Ployhart, 2002). To address research question 3 (the effect of numerical knowledge prior to school and change in numerical performance over time on numerical performance at the end of the school year), the “Random-Intercept-Random-Slope” model from the previous linear Mixed Models analysis was used to estimate intercept and slope parameters for each student based on the LPA (compare Kuhn et al., 2019). The individual intercepts and slopes served as learning progression related predictors for end of school year numeracy performance (MARKO-D1Post) analyzed through hierarchical multiple regression. To address research question 4 (change in conceptual numerical understanding), the students' performance on the MARKO-D tests as well as on the LPA tests was allocated to the levels of the developmental model following the reporting standards of the MARKO-D test series. The standards propose that full understanding of the numerical concept of a level can be assumed when at least 75% of the items within this level were solved correctly, given that (a) each test item could be reliably assigned to the theoretically founded developmental levels and their associated underlying numerical concepts, and (b) the hierarchy of the levels was valid (Ricken et al., 2013). For this study we assumed that the items of the LPA met both conditions and therefore the application of the 75% criterion was valid (see also Balt et al., 2017).
Results
Item Fit Analysis
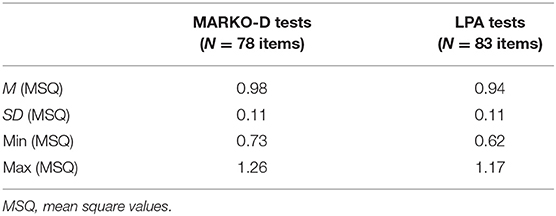
Mean square values (MSQ) were used to assess the Rasch model fit on the item level. MSQ values represent the residuals between the Rasch model expectations and the observed responses (Wu and Adams, 2013). Ideally, MSQ scores have a value of 1, however a range between 0.75 ≤ MSQ ≤ 1.30 is considered acceptable (Bond and Fox, 2007). Table 2 shows that the MSQ values of both scales (MARKO-D tests and LPA) were close to 1 on average with a small standard deviation of 0.11 which indicates a reasonable item fit. For single items, the MSQ values were also reasonable as none exceeded the range of an acceptable fit. Please note that the number of items within each scale is reduced due to the common linking items.
Person Parameter Analysis
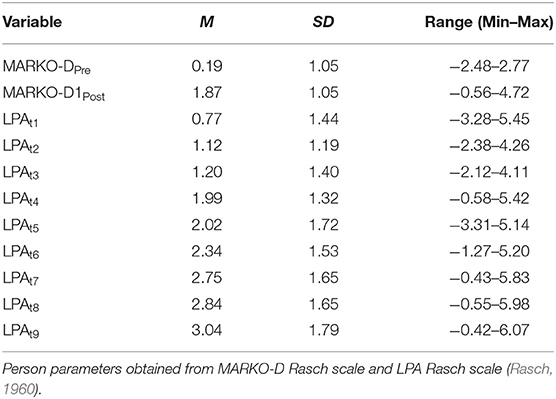
Table 3 shows the descriptive statistics of the person parameters of the two scales (MARKO-D tests and LPA) based on the Rasch model (Rasch, 1960).
The person parameters significantly increased from the beginning (MARKO-DPre) to the end of the school year (MARKO-D1Post), t(96) = −19.03, p < 0.001, r = 0.89. The significant increase in performance over time was also captured in between the pre-and the post-test through the LPA tests (LPAt1-LPAt9), t(747) = 23.47, p < 0.001, r = 0.65 (compare Model 2 in Table 5).
Item Parameter Analysis
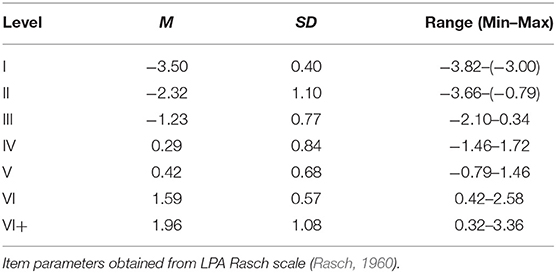
Table 4 shows the descriptive statistics of the item parameters of the LPA item pool for each level of the developmental model (see Table 1). The mean difficulty of the items significantly increased from Level I to VI+, F(6, 82) = 52.63, p < 0.001, r = 0.89.
Sample Invariance Analysis
Median Split
The Andersen LRT (Andersen, 1973) with median as the internal split criterion showed a non-significant result (χ2 = 59.86; df = 57; p = 0.37), indicating that the estimations of the item parameters did not differ significantly between students with low and high scores in the LPA.
Gender Split
The Andersen LRT (Andersen, 1973) with gender as the external split criterion showed a significant result (χ2 = 112.76; df = 69; p = 0.001), indicating that some item parameter estimations differed significantly between male and female students. As recommended by Koller et al. (2012) a Wald test was applied to identify the items that show a bias toward a certain gender. The Wald test found that the statistic item parameter estimations of three items showed significant differences between genders (p < 0.05). Rerunning the Andersen LRT after excluding these three items from the analysis led to a non-significant result (χ2 = 79.67; df = 66; p = 0.12).
Growth Analysis
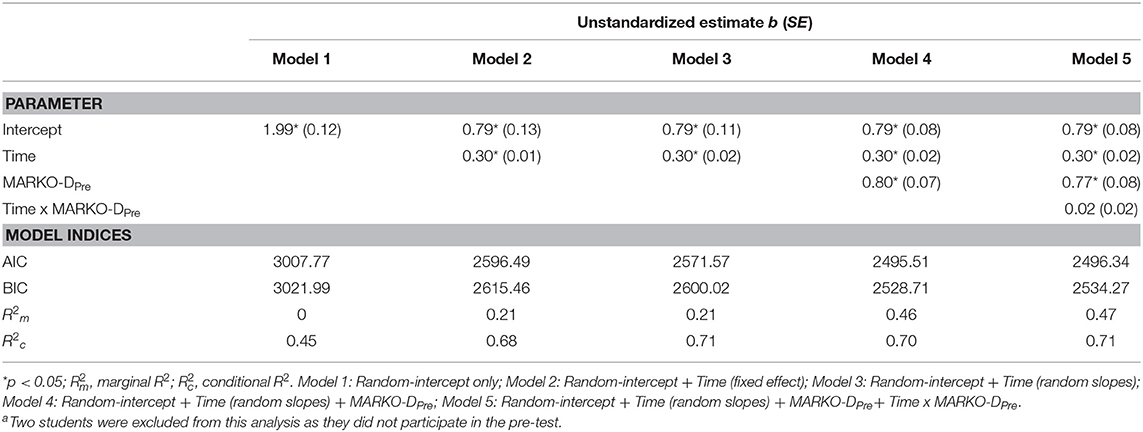
We started the growth model building process with the “Random intercept only” model (Model 1) as the baseline model and subsequently added more complexity. In Model 2, “Time” was added as a fixed effect (independent variable) to model its relationship with the students' performance in the LPA (dependent variable). The first measurement of the LPA was conducted about 12 weeks after the beginning of school. Each step in “Time” represents 4 weeks of schooling. In Model 3, “Random slopes” were introduced to account for possible differences in growth patterns over time. In Model 4, the grand mean centered person parameters (Enders and Tofighi, 2007) of the variable MARKO-DPre were added to the previous model as a predictor for possible intercept variation. In Model 5 the interaction term “Time x MARKO-DPre” was added to test for potential effects of numerical knowledge prior to school on numeracy development.
Table 5 displays the model parameters of the linear Mixed Models. The model comparison suggests that adding the fixed effect of “Time” significantly improved the fit of Model 2 compared to the Baseline model. Introducing “Random slopes” further improved the fit of Model 3. The average growth predicted through the “Random-Intercept-Random-Slope” model (Model 3) was 0.30 (SE = 0.02, p < 0.01) with a SD of 0.10. The average intercept was 0.79 (SE = 0.11, p < 0.01) with a SD of 0.98. Adding “MARKO-DPre” as a second predictor to the model improved the fit of Model 4 compared to Model 3. However, adding the interaction term “Time × MARKO-DPre” in Model 5 did not significantly improve the model fit. The model indices in Table 5 also indicate that model fit and explained variance increase with increasing complexity up to Model 4.
Prediction Analysis
The small intraclass correlation (ICC) of 0.01, estimated as part of the growth model building process, indicates that the hierarchical structure of the data is not likely to affect the subsequent regression analysis. Multicollinearity between the predictors, tested through variance inflation factors, also appeared to be unproblematic as all factors were smaller than 3.5 (Meyers, 1990).
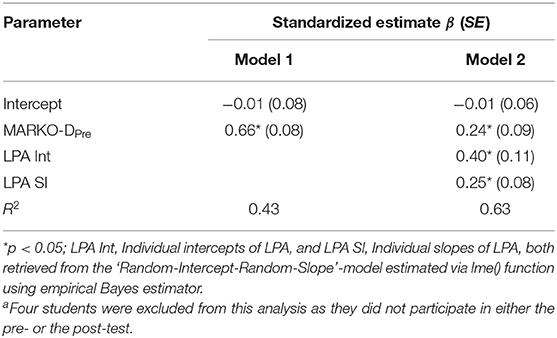
Model 1 in Table 6 shows that the performance in the pre-test (MARKO-DPre) explains 43% of the variation in the post-test performance (MARKO-D1Post). Introducing the individual intercept and slope parameters from the LPA to the model (Model 2) adds 20% of explained variance. The model parameters indicate that the LPA related predictors make a significant contribution to the model.
Level-Based Analysis
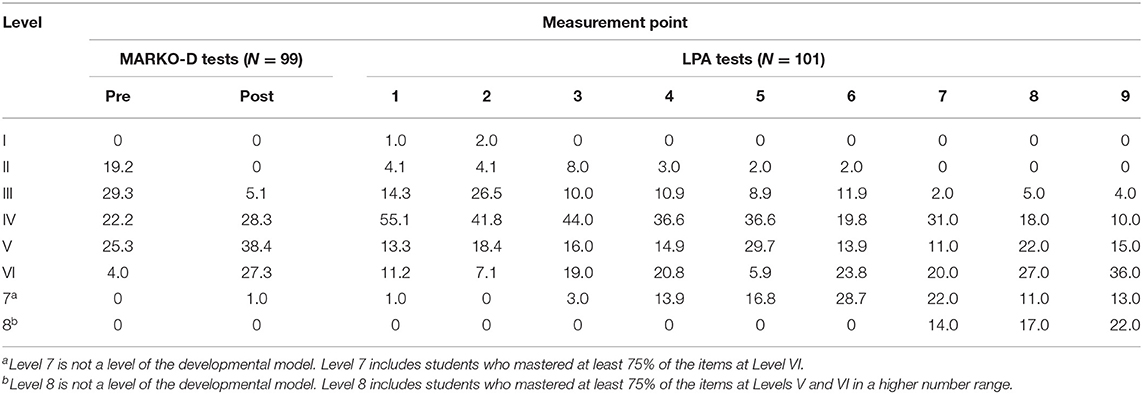
Drawing on the 75% criterion (see section Data Analysis of this paper) the students were allocated to the different levels of the developmental model (see Table 1). Table 7 displays the relative frequencies of the level allocations based on the students' pre- and post-test performance (MARKO-D tests) and their LPA results over the nine measurement points. Inferential statistics indicate significant differences in level distributions between the pre- and the post-test, χ2(6) = 57.41, p < 0.001, rSp = 0.48, as well as between the LPA tests, χ2(56) = 351.37, p < 0.001, rSp = 0.46.
The results of both measures (MARKO-D tests and LPA) show that the number of students at Levels I to IV decreased, whereas the number of students at Levels V, VI, and above increased as the school year progressed. From pre- to post-test the students gained one conceptual level on average (Mdn = 1) with 40% of the students gaining even more than one level. The students' conceptual change in numerical understanding over the course of Grade 1 assessed through the LPA is visualized in Figure 1.
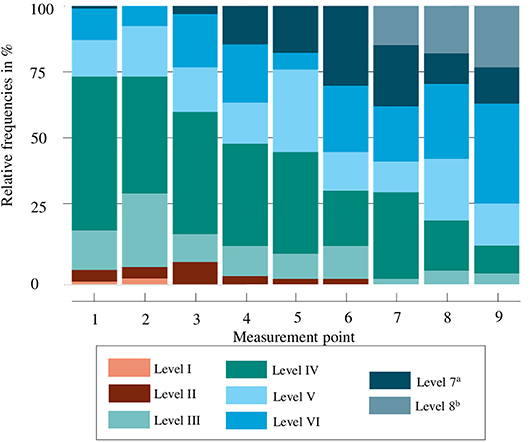
Figure 1. Level-based analysis of the LPA (N = 101). aLevel 7 is not a level of the developmental model. In this figure, Level 7 includes students who mastered at least 75% of the items at Level VI. bLevel 8 is not a level of the developmental model. In this figure, Level 8 includes students who mastered at least 75% of the items at Levels V and VI in a higher number range.
Discussion
The purpose of the study was to investigate the extent to which progression-based assessments can be used to describe the development of conceptual numerical understanding of children at the transition to school. The overarching goal was to build a progression-based formative assessment tool that is empirically tested and supports teachers in their everyday practice of teaching students at different levels of numerical understanding.
Prior to addressing the research questions, we would like to briefly discuss the results of the Rasch scaling. The item fit analysis, as well as the sample invariance tests, indicate that the Rasch model was valid for the purpose of this study. All items showed an acceptable fit and no systematic difference could be found between high and low performing students within the sample. Three items were identified to have a gender bias, which was resolved by removing these items from the analysis. This procedure may constitute a methodological limitation of this study as the χ2 statistic is known to be highly sensitive to large df (Wheaton et al., 1977).
This study was guided by four research questions. The first research question considered the effect of time on the students' performance in the LPA to examine the extent to which the assessment is able to detect changes in performance over time. The results of the linear Mixed Models analysis show that the students' performance increased significantly over the course of Grade 1. In accordance with studies using curriculum-based formative assessments (Salaschek et al., 2014; Kuhn et al., 2019) these findings suggest that the progression-based LPA, used in this study, was also able to detect changes in performance over time.
The second research question concerned the effect of numerical knowledge prior to formal schooling (assessed through MARKO-D in the pre-test) on numeracy learning over the course of Grade 1 (as assessed through the LPA). In line with recent studies examining early numeracy as predictor for successful numeracy learning (e.g., Krajewski and Schneider, 2009; Claessens and Engel, 2013; Nguyen et al., 2016), this study further supports the positive effect of numerical pre-knowledge on the subsequent acquisition of more sophisticated numeracy skills. However, a cumulative growth pattern, as described in several studies (see Salaschek et al., 2014), is not reflected in this study, as shown by the lack of significant interaction of “Time x MARKO-DPre.” Considering the profound conceptual understanding many of the students in this study's sample showed in the pre-test at the beginning of school (almost 30% on Levels V and VI), this finding is not surprising. The LPA is aligned to a developmental model that covers a clearly defined number of developmental levels. Children who already start at the higher levels of the model, consequently, cannot be reliably assessed beyond the scope of the model as their learning progresses. To reduce this effect, more difficult items were introduced at measurement point seven, but it is still likely that the actual growth of students beyond Level VI was larger than reflected by the LPA. This may have skewed the results as over the course of Grade 1, a larger number of students exceeded the levels described by the model and assessed through the LPA. In future studies it would be interesting to examine whether a cumulative growth pattern could be found in a sample of low and average performing students. Another reason for the lack of interaction may be the context of the data collection, as the LPA data was gained as part of a longitudinal Response-to-Intervention study. Though the assessment has not been linked to a specific type of intervention yet, the intervention the students received within this study may have affected their individual growth. Nonetheless, we assume that this was not problematic for the purpose of this study, as the goal was to investigate the extent to which the LPA can be used to describe numerical development independent of the type of intervention the students received.
The third research question examined the predictive effect of the LPA on numerical performance at the end of the school year (assessed through MARKO-D1 in the post-test). As expected, the student's pre-test MARKO-D performance explained a fair share of the MARKO-D1 post-test performance (43%). However, introducing the LPA parameters into the model significantly increased the explained variation of the student's post-test performance by 20%. This finding may be interpreted as an indicator for the prognostic validity of the LPA. It should, however, be considered that all measures used in this study (MARKO-D tests and LPA) built on the same developmental model. Hence, further evidence should be collected by using different types of assessment to support the assumption of the (prognostic) validity of the LPA.
The fourth research question sought to provide a more detailed picture of how the conceptual change of numerical understanding appears over the course of Grade 1. The use of progression-based assessments in this study, suggested a heterogeneity of children's numerical understanding at the beginning of school. The students did not only differ significantly in their overall test scores, but also in their individual levels of conceptual numerical knowledge. The MARKO-D test (pre-test) indicated that 19% of the students demonstrated a conceptual understanding of the ordinal number line (Level II). Approximately 50% showed an understanding of the concepts of cardinality (Level III) or part-part-whole relations (Level IV), which can be considered average according to the norming sample of the MARKO-D test (Ricken et al., 2013). The pre-test results further revealed that almost 30% of the students demonstrated an extensive informal numerical knowledge at the beginning of school in the form of a conceptual understanding of equidistant number line intervals (Level V) or units in numbers (Level VI). The MARKO-D1 (post-test) indicated that the number of students at the lower levels decreased whereas the number of students at the higher levels increased with an average gain of one conceptual level over the course of the school year. Similar results had been reported by Fritz et al. (2018).
The analysis of the LPA based on the 75% criterion also showed an increase of the share of students with more sophisticated concepts over time, while the number of students with lower conceptual knowledge decreased. At the first two measurement points, there were 1 to 2% of the children at Level I, who at the time were developing their number word sequence and counting skills. The LPA data suggested that all children of the sample had fully acquired the concept of counting by the third measurement point. 2% of the children, however, spent an extended period of time, up to the sixth measurement point, developing the ordinal number line concept characteristic for Level II. Compared to their classmates the students at Levels I or II were lacking important conceptual prerequisites that build the foundation for the acquisition of more sophisticated numeracy skills. More importantly, these prerequisites are demanded by the curriculum that usually introduces addition and subtraction during the first half of Grade 1. This means, these students may be at risk for developing mathematical learning difficulties, as their conceptual understanding and procedural skills (e.g., error-prone counting strategies) are not likely to be viable for more complex arithmetic problems and the larger number range they will encounter later on in Grade 1 and in Grade 2. To prevent that the gap between their current numerical knowledge and the curriculum expectations gets bigger, these students should immediately receive intervention that is targeted to their individual level of conceptual understanding.
The level-based analysis of the LPA tests further showed that after 12 weeks of schooling (first measurement point of the LPA) 55% of the children were working toward understanding the concept of part-part-whole relations (Level IV) and 25% had an even more sophisticated conceptual understanding associated with Levels V (concept of equidistant number line estimations) or VI (concept of units in numbers). These children demonstrated a sound understanding of the concept of part-part-whole relations (within the number range up to 20) and were able to master arithmetical problems flexibly without necessarily depending on counting strategies. By the end of the school year, 14% of the students were allocated at Levels III or IV, while 86% of the students were working at Level V or above. The latter number was larger based on the LPA test (86%) than based on the MARKO-D1 test (67%). This discrepancy may be explained by differences in the time of the assessment (~6 weeks in between the two measurements), the type of assessment (MARKO-D1 as an individual test vs. the LPA as a group test), and the number of items (MARKO-D1 with 48 items vs. LPA test with 15 items).
These insights into the developmental process of conceptual numerical understanding of first grade students highlight the importance of progression-based assessments to support mathematics teachers. The current version of the LPA was particularly suitable to describe the development of low and average performing students. The development of students beyond Level VI could, however, not be reliably assessed with the LPA due to the limitations of the underlying developmental model. By using this type of assessment, teachers stand to not only gain a deeper insight into their students' learning, but also a better understanding of how numeracy learning typically progresses and a student's location within this learning pathway (Black et al., 2011), enabling teachers to derive and target intervention accordingly. The progression-based assessments used in this study (MARKO-D tests and LPA) come along with an empirically validated pathway description of numeracy learning (Fritz et al., 2018) as well as instructional activities for targeted interventions (e.g., Gerlach et al., 2013).
Given the importance of early numeracy for future learning, progression-based assessments seem especially important for early primary school mathematics. For this reason, further empirical research is needed to provide teachers with this approach to assessment, thereby adding to the curriculum-based instruments that are currently available in Germany. This study is one step toward the goal of designing such an instrument.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Ethics Statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent to participate in this study was provided by the participants' legal guardian/next of kin.
Author Contributions
MB, AF, and AE designed the tasks and instruments used in this study. MB and AE planned the study design and carried out the data collection. MB performed the computations and drafted the manuscript advised by AF and AE. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
ACARA (2017). National Numeracy Learning Progression. Retrieved from Australian Curriculum, Assessment and Reporting Authority website: https://www.australiancurriculum.edu.au/media/3635/national-numeracy-learning-progression.pdf
Andersen, E. B. (1973). A goodness of fit test for the Rasch model. Psychometrika 38, 123–140. doi: 10.1007/BF02291180
Aunio, P., and Niemivirta, M. (2010). Predicting children's mathematical performance in grade one by early numeracy. Learn. Individ. Differ. 20, 427–435. doi: 10.1016/j.lindif.2010.06.003
Aunola, K., Leskinen, E., Lerkkanen, M.-K., and Nurmi, J.-E. (2004). Developmental dynamics of math performance from preschool to grade two. J. Educ. Psychol. 96, 699–713. doi: 10.1037/0022-0663.96.4.699
Balt, M., Ehlert, A., and Fritz, A. (2017). Theoriegeleitete Testkonstruktion dargestellt am Beispiel einer Lernverlaufsdiagnostik für den mathematischen Anfangsunterricht [A theory-based assessment of the learning process in primary school mathematics]. Empirische Sonderpädagogik 2, 165–183.
Black, P., and Wiliam, D. (1998). Assessment and classroom learning. Assess. Educ. 5, 7–74. doi: 10.1080/0969595980050102
Black, P., Wilson, M., and Yao, S.-Y. (2011). Road maps for learning: a guide to the navigation of learning progressions. Meas. Interdiscip. Res. Perspect. 9, 71–123. doi: 10.1080/15366367.2011.591654
Bliese, P. D., and Ployhart, R. E. (2002). Growth modeling using random coefficient models: model building, testing, and illustrations. Organ. Res. Methods 5, 362–387. doi: 10.1177/109442802237116
Bodovski, K., and Farkas, G. (2007). Mathematics growth in early elementary school: The Roles of beginning knowledge, student engagement, and instruction. Elem. Sch. J. 108, 115–130. doi: 10.1086/525550
Bond, T. G., and Fox, C. M. (2007). Applying the Rasch Model: Fundamental Measurement in the Human Sciences, 2nd Edn. Mahwah, NJ: Lawrence Erlbaum Associates.
Claessens, A., and Engel, M. (2013). How important is where you start? Early mathematics knowledge and later school success. Teach. Coll. Rec. 119, 1–29.
Clements, D. H., and Sarama, J. (2009). Learning and Teaching Early Math: The Learning Trajectories Approach. Florence: KY: Routledge.
Clements, D. H., Sarama, J., and Liu, X. H. (2008). Development of a measure of early mathematics achievement using the Rasch model: the research-based early maths assessment. Educ. Psychol. 28, 457–482. doi: 10.1080/01443410701777272
Daro, P., Mosher, F. A., and Corcoran, T. B. (2011). Learning Trajectories in Mathematics: A Foundation for Standards, Curriculum, Assessment, and Instruction. Retrieved from Consortium for Policy Research in Education (CPRE): http://repository.upenn.edu/cpre_researchreports/60
Dowker, A. (2008). Individual differences in numerical abilities in preschoolers. Dev. Sci. 11, 650–654. doi: 10.1111/j.1467-7687.2008.00713.x
Duncan, G. J., Dowsett, C. J., Claessens, A., Magnuson, K., Huston, A. C., Klebanov, P., et al. (2007). School readiness and later achievement. Dev. Psychol. 43, 1428–1446. doi: 10.1037/0012-1649.43.6.1428
Empson, S. B. (2011). On the idea of learning trajectories: promises and pitfalls. Math. Enthus. 8, 571–596.
Enders, C. K., and Tofighi, D. (2007). Centering predictor variables in cross-sectional multilevel models: a new look at an old issue. Psychol. Methods 12, 121–138. doi: 10.1037/1082-989X.12.2.121
Fritz, A., Ehlert, A., and Balzer, L. (2013). Development of mathematical concepts as basis for an elaborated mathematical understanding. South Afr. J. Childh. Educ. 3, 38–67. doi: 10.4102/sajce.v3i1.31
Fritz, A., Ehlert, A., and Leutner, D. (2018). Arithmetische konzepte aus kognitiv-entwicklungspsychologischer Sicht [Artihmetic concepts from a cognitive developmental-psychology perspective]. J. Math. Didakt. 39, 7–41. doi: 10.1007/s13138-018-0131-6
Fritz, A., Ehlert, A., Ricken, G., and Balzer, L. (2017). MARKO-D1+: Mathematik- und Rechenkonzepte bei Kindern der ersten Klassenstufe—Diagnose MARKO-D1+: Mathematics and Arithmetical Concepts of First-Grade Students, 1st Edn. Göttingen: Hogrefe.
Geary, D. C., Hoard, M. K., Nugent, L., and Bailey, D. H. (2012). Mathematical cognition deficits in children with learning disabilities and persistent low achievement: a five-year prospective study. J. Educ. Psychol. 104, 206–223. doi: 10.1037/a0025398
Gebhardt, M., Diehl, K., and Mühling, A. (2016). Online-Lernverlaufsmessung für alle Schülerinnen und Schüler in inklusiven Klassen. Www.LEVUMI.de [Online learning progress monitoring for all students in inclusive classes. Www.LEVUMI.de]. Z. Heilpädagogik 67, 444–453. doi: 10.17877/DE290R-20375
Gelman, R., and Gallistel, C. R. (1978). The Child's Understanding of Number. Cambridge, MA: Harvard University Press.
Gerlach, M., Fritz, A., and Leutner, D. (2013). MARKO-T: Mathematik- und Rechenkonzepte im Vor-und Grundschulalter—Training [MARKO-T: Mathematics and Arithmetical Concepts in Preschool and Primary School—Intervention]. Göttingen: Hogrefe.
Gotwals, A. W. (2018). Where are we now? Learning progressions and formative assessment. Appl. Measure. Educ. 31, 157–164. doi: 10.1080/08957347.2017.1408626
Heritage, M. (2008). Learning Progressions: Supporting Instruction and Formative Assessment. Retrieved from Council of Chief State School Officers website: http://www.ccsso.org/documents/2008/learning_progressions_supporting_2008.pdf
Hiebert, J., and Lefevre, P. (1986). “Conceptual and procedural knowledge in mathematics: an introductory analysis,” in Conceptual and Procedural Knowledge: The Case of Mathematics, ed J. Hiebert (Hillsdale, NJ: Lawrence Erlbaum Associates, Inc, 1–27.
Hojnoski, R. L., Caskie, G. I. L., and Miller Young, R. (2018). Early numeracy trajectories: baseline performance levels and growth rates in young children by disability status. ?Top. Early Child. Spec. Educ. 37, 206–218. doi: 10.1177/0271121417735901
Johnson, E. G. (1992). The design of the national assessment of educational progress. J. Educ. Meas. 29, 95–110. doi: 10.1111/j.1745-3984.1992.tb00369.x
Jordan, N. C., Glutting, J., and Ramineni, C. (2010). The importance of number sense to mathematics achievement in first and third grades. Learn. Individ. Differ. 20, 82–88. doi: 10.1016/j.lindif.2009.07.004
Keller-Margulis, M. A., Shapiro, E. S., and Hintze, J. M. (2008). Long-term diagnostic accuracy of curriculum-based measures in reading and mathematics. School Psychol. Rev. 37, 374–390.
Kingston, N., and Nash, B. (2011). Formative assessment: a meta-analysis and a call for research. Educ. Meas. Issues Pract. 30, 28–37. doi: 10.1111/j.1745-3992.2011.00220.x
KMK (2004). Beschlüsse der kultusministerkonferenz: Bildungsstandards im Fach Mathematik für den Primarbereich. Beschluss vom 15.10.2004 [Resolutions of the Standing Conference of the Ministers of Education and Cultural Affairs: Educational Standards for Primary School Mathematics. Resolution of 15.10.2004]. Avaliable online at: https://www.kmk.org/fileadmin/veroeffentlichungen_beschluesse/2004/2004_10_15-Bildungsstandards-Mathe-Primar.pdf
Koller, I., Alexandrowicz, R., and Hatzinger, R. (2012). Das Rasch Modell in der Praxis: Eine Einführung in eRM [The Rasch Model in Practice: An Introduction into eRM]. Vienna: facultas.wuv UTB.
Krajewski, K., and Schneider, W. (2009). Early development of quantity to number-word linkage as a precursor of mathematical school achievement and mathematical difficulties: findings from a four-year longitudinal study. Learn. Inst. 19, 513–526. doi: 10.1016/j.learninstruc.2008.10.002
Kuhn, J.-T., Schwenk, C., Souvignier, E., and Holling, H. (2019). Arithmetische Kompetenz und Rechenschwäche am Ende der Grundschulzeit. Die Rolle statusdiagnostischer und lernverlaufsbezogener Prädiktoren [Arithmetic skills and mathematical learning difficulties at the end of elementary school: the role of summative and formative predictors]. Empirische Sonderpädagogik 2, 95–117.
Kuhn, J.-T., Schwenk, C., Raddatz, J., Dobel, C., and Holling, H. (2018). CODY-M 2-4: CODY-Mathetest für die 2.-4. Klasse [CODY-M 2-4: CODY Math Test for 2nd to 4th Grade]. Düsseldorf: Kaasa Health.
Landesinstitut für Schule und Medien Berlin-Brandenburg (LISUM) (2015). Bildungsserver Berlin Brandenburg. Rahmenlehrplan-Online [Curriculum-Online]. Avaliable online at: https://bildungsserver.berlin-brandenburg.de/rlp-online/
Le Corre, M., and Carey, S. (2007). One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition 105, 395–438. doi: 10.1016/j.cognition.2006.10.005
Lee, M. D., and Sarnecka, B. W. (2011). Number-knower levels in young children: insights from Bayesian modeling. Cognition 120, 391–402. doi: 10.1016/j.cognition.2010.10.003
Lerkkanen, M.-K., Rasku-Puttonen, H., Aunola, K., and Nurmi, J.-E. (2005). Mathematical performance predicts progress in reading comprehension among seven-year olds. Eur. J. Psychol. Educ. 20, 121–137. doi: 10.1007/BF03173503
Mair, P., and Hatzinger, R. (2007). Extended Rasch modeling: the eRM package for the application of IRT models in R. J. Stat. Softw. 20. doi: 10.18637/jss.v020.i09
Mazzocco, M. M. M., and Thompson, R. E. (2005). Kindergarten predictors of math learning disability. Learn. Disabil. Res. Pract. 20, 142–155. doi: 10.1111/j.1540-5826.2005.00129.x
Missall, K. N., Mercer, S. H., Martínez, R. S., and Casebeer, D. (2012). Concurrent and longitudinal patterns and trends in performance on early numeracy curriculum-based measures in kindergarten through third grade. Assess. Eff. Interv. 37, 95–106. doi: 10.1177/1534508411430322
Morgan, P. L., Farkas, G., and Wu, Q. (2011). Kindergarten children's growth trajectories in reading and mathematics: who falls increasingly behind? J. Learn. Disabil. 44, 472–488. doi: 10.1177/0022219411414010
Navarro, J. I., Aguilar, M., Marchena, E., Ruiz, G., Menacho, I., and Van Luit, J. E. H. (2012). Longitudinal study of low and high achievers in early mathematics: longitudinal early mathematics. Br. J. Educ. Psychol. 82, 28–41. doi: 10.1111/j.2044-8279.2011.02043.x
Nguyen, T., Watts, T. W., Duncan, G. J., Clements, D. H., Sarama, J. S., Wolfe, C., et al. (2016). Which preschool mathematics competencies are most predictive of fifth grade achievement? Early Child Res Q. 36, 550–560. doi: 10.1016/j.ecresq.2016.02.003
Peter-Koop, A., and Kollhoff, S. (2015). “Transition to school: prior to school mathematical skills and knowledge of low-achieving children at the end of grade one,” in Mathematics and Transition to School: International Perspectives, eds B. Perry, A. MacDonald, and A. Gervasoni (Singapore: Springer Singapore), 65–83.
Purpura, D. J., Logan, J. A. R., Hassinger-Das, B., and Napoli, A. R. (2017). Why do early mathematics skills predict later reading? The role of mathematical language. Dev. Psychol. 53, 1633–1642. doi: 10.1037/dev0000375
R Core Team (2017). R: A Language and Environment for Statistical Computing (Version 1.2.1335). Avaliable online at: http://www.R-project.org/
Rasch, G. (1960). Studies in Mathematical Psychology: I. Probabilistic Models For Some Intelligence and Attainment Tests. Oxford: Nielsen & Lydiche.
Ricken, G., Fritz, A., and Balzer, L. (2013). MARKO-D: Mathematik- und Rechenkonzepte im Vorschulalter—Diagnose [MARKO-D: Mathematics and Arithmetical Concepts in Preschool Age—Diagnosis], 1st Edn. Göttingen: Hogrefe.
Rittle-Johnson, B., Siegler, R. S., and Alibali, M. W. (2001). Developing conceptual understanding and procedural skill in mathematics: an iterative process. J. Educ. Psychol. 93, 346–362. doi: 10.1037//0022-0663.93.2.346
Romano, E., Babchishin, L., Pagani, L. S., and Kohen, D. (2010). School readiness and later achievement: replication and extension using a nationwide Canadian survey. Dev. Psychol. 46, 995–1007. doi: 10.1037/a0018880
Salaschek, M., Zeuch, N., and Souvignier, E. (2014). Mathematics growth trajectories in first grade: cumulative vs. compensatory patterns and the role of number sense. Learn. Individ. Diff. 35, 103–112. doi: 10.1016/j.lindif.2014.06.009
Sarnecka, B. W., and Carey, S. (2008). How counting represents number: what children must learn and when they learn it. Cognition 108, 662–674. doi: 10.1016/j.cognition.2008.05.007
Siegler, R. S., and Alibali, M. W. (2005). Children's Thinking. Englewood Cliffs, NJ: Prentice Hall.
Stahnke, R., Schueler, S., and Roesken-Winter, B. (2016). Teachers' perception, interpretation, and decision-making: a systematic review of empirical mathematics education research. ZDM Math. Educ. 48, 1–27. doi: 10.1007/s11858-016-0775-y
Stanovich, K. E. (1986). Matthew effects in reading: Some consequences of individual differences in the acquisition of literacy. Read. Res. Q. 21, 360–407. doi: 10.1598/RRQ.21.4.1
Strathmann, A. M., and Klauer, K. J. (2012). LVD-M 2-4. Lernverlaufsdiagnostik Mathematik für die Zweiten bis Vierten Klassen [LVD-M 2-4. Learning Progress Assessment Mathematics for Second to Fourth Grade]. Göttingen: Hogrefe.
van den Wollenberg, A. (1988). “Testing a latent trait model,” in Latent Trait and Latent Class Models, eds R. Langeheine and J. Rost (Boston, MA: Springer), 31–50.
von Davier, A. A. (2011). Statistical Models For Test Equating, Scaling, and Linking. New York, NY: Springer.
Wheaton, B., Muthén, B., Alwin, D. F., and Summers, G. F. (1977). Assessing reliability and stability in panel models. Sociol. Methodol. 8, 84–136. doi: 10.2307/270754
Wiliam, D., Lee, C., Harrison, C., and Black, P. (2004). Teachers developing assessment for learning: Impact on student achievement. Assess. Educ. 11, 49–65. doi: 10.1080/0969594042000208994
Keywords: early numeracy, development, assessment, learning progression, primary school
Citation: Balt M, Fritz A and Ehlert A (2020) Insights Into First Grade Students' Development of Conceptual Numerical Understanding as Drawn From Progression-Based Assessments. Front. Educ. 5:80. doi: 10.3389/feduc.2020.00080
Received: 13 October 2019; Accepted: 18 May 2020;
Published: 17 June 2020.
Edited by:
Robbert Smit, University of Teacher Education St. Gallen, SwitzerlandReviewed by:
Ann Dowker, University of Oxford, United KingdomGavin T. L. Brown, The University of Auckland, New Zealand
Jack Pun, City University of Hong Kong, Hong Kong
Anthony M. Li, University of Oxford, United Kingdom, in Collaboration with Reviewer JP
Copyright © 2020 Balt, Fritz and Ehlert. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Miriam Balt, bWlyaWFtLmJhbHRAaWZzLnVuaS1oYW5ub3Zlci5kZQ==
 Miriam Balt
Miriam Balt Annemarie Fritz
Annemarie Fritz Antje Ehlert
Antje Ehlert