- 1Faculty of Human Sciences, University of Regensburg, Regensburg, Germany
- 2Faculty of Mathematics, University of Regensburg, Regensburg, Germany
- 3Faculty of Languages, Literature, and Culture, University of Regensburg, Regensburg, Germany
A central task of educational research is to examine common issues of teaching and learning in all subjects taught at school. At the same time, the focus is on identifying and investigating unique subject-specific aspects on the one hand and transdisciplinary, generalizable effects on the other. This poses various methodological challenges for educational researchers, including in particular the aggregation and evaluation of already published study effects, hierarchical data structures, measurement errors, and comprehensive data sets with a large number of potentially relevant variables. In order to adequately deal with these challenges, this paper presents the core concepts of four methodological approaches that are suitable for the analysis of transdisciplinary research questions: meta-analysis, multilevel models, latent multilevel structural equation models, and machine learning methods. Each of these approaches is briefly illustrated with an example inspired by the interdisciplinary research project FALKE (subject-specific teacher competencies in explaining). The data and analysis code used are available online at https://osf.io/5sn9j. Finally, the described methods are compared, and some application hints are given.
Introduction
Interdisciplinarity is a key feature of empirical educational research. However, while this defining characteristic was for a long time primarily related to the participation and cooperation of various academic disciplines (e.g., pedagogy, psychology, sociology, or educational studies; see Deutscher Bildungsrat [German Education Council], 1974; Gräsel, 2015), in recent years, it has gained a within-field content-related dimension with regard to the diverse school subjects under investigation. The validity of findings from mathematical and scientific contexts, on which instructional research has mainly focused so far, is being questioned with regard to disparate teaching and learning conditions and subject-specific cultures in the human and social sciences–and their generalizability, in principle, is doubted (e.g., Praetorius et al., 2018; Schlesinger et al., 2018; Wisniewski et al., 2020). So, the school subject becomes an information-bearing grouping variable at a higher level, which must be adequately considered in the data analysis. The term transdisciplinary educational research is accordingly understood here as research in different school subjects in order to analyze subject-specific peculiarities and interdisciplinary differences on the one hand, and transdisciplinary similarities and generalizable effects on the other. Four different methodological approaches are suitable for this purpose, namely meta-analysis, multilevel models, (latent) multilevel structural equation models, and machine learning, which will be briefly presented individually below. In each case, the underlying theoretical model will be explained and possible applications in transdisciplinary research will be concisely illustrated using a reduced data set from the multidisciplinary research project FALKE (Fachspezifische Lehrerkompetenzen im Erklären; English: Subject-specific teacher competencies in explaining) as an example.
FALKE involved educational scientists of eleven different school subjects (Art, Biology, Chemistry, English, German, History, Mathematics, Music, Physics, Primary School Education, and Protestant Religious Education) and scientists of German linguistics as well as of speech science and training (see also Schilcher et al., 2020b). Using a joint study design, they investigated the quality of teaching explanations in the participating school subjects. For this purpose, five transdisciplinary criteria (structuredness, addressee orientation, linguistic comprehensibility, speech and body expression, personality effect) and one domain-specific criterion per subject (e.g., the importance of causality structures in History) were conceptualized and operationalized with corresponding items in an online questionnaire. In addition, six explanatory videos (seven in the case of the school subject Music), with varying didactical approaches (e.g., inductive vs. deductive) were created for each subject and shown to school students as typical addressees of explanations and (student) teachers as (prospective) experts in explaining. These two groups (N = 3.116 participants) first rated the videos globally and then according to the six criteria mentioned, each of which was represented by an individual scale. One of the main transdisciplinary research questions was, e.g., which of the criteria are relevant for the global rating of teaching explanations as being of high quality and whether the relationships are similar across all school subjects or whether there are differences between subjects.
Since a complete presentation of the FALKE project is beyond the scope of this paper (for details see Schilcher et al., 2020a), the investigation of this research question will be limited in the following to the correlation between structuredness and global rating for didactic and illustrative purposes. However, it will be examined under four different methodological approaches (meta-analysis, multilevel models, multilevel structural equation models, and machine learning). The data and script of these exemplary analyses, which were carried out using the statistical software R (R Core Team, 2019), are available online at https://osf.io/5sn9j.
Meta-Analytical Approaches in Interdisciplinary Studies
With the aim of recording previous research in a certain area as comprehensively and systematically as possible and reporting its state of the art and core results concisely (e.g., Seidel and Shavelson, 2007; Hattie, 2009), meta-analytical procedures have long been part of the methodical inventory in educational research. Primary effects are summarized and weighted according to mathematically defined, objectifiable criteria and publication bias, content, as well as methodological quality and, in particular, sample size of primary studies can be taken into account as influencing variables. Thus, meta-analyses can reduce the distracting effects of sampling errors, measurement errors, and other artifacts that create the impression of extreme, sometimes even contradictory results of primary studies, and at the same time provide a measure of their consistency (Borenstein et al., 2009; Schmidt and Hunter, 2015). Which kind of effect size is applied in a meta-analysis is of secondary importance, as long as they are independent of study design aspects (such as sample size, covariates used, etc.), easy to calculate from the typically reported statistical information, and have good technical properties for further processing (e.g., known distribution; Borenstein et al., 2009). Accordingly, meta-analyses commonly use standardized distance measures (e.g., Cohen's d or Hedges' g) or standardized correlation measures (e.g., Pearson's product-moment correlation r).
The estimated meta-effect is nothing other than a weighted average, whereby its meaning and the weighting of the individual studies depend on two different theoretical assumptions about their distribution: a fixed effect model or a random effects model. In the fixed effect model, it is assumed that the same true population effect Φ underlies each individual study (i = 1,…, k; k number of primary studies), which means that all analyzed effects are the same, and that the observed effect Zi deviates only by sampling error εi with Zi = Φ + εi. Since these sampling errors depend largely on the sample size of the primary studies, the weight wi of the respective effects is calculated as a function of the sample size Ni, so that more precisely estimated effects receive larger weights, while more roughly estimated ones receive smaller weights when determining the estimated population effect:
The only source of variance is thus the sampling error of the studies εi with assumed εi ~ N(0; σ2).
However, since research designs of primary studies, even if they are identical, are sometimes carried out with varying details and because target populations differ (e.g., in terms of age, education, socioeconomic status, or subject-specific culture), the assumption of the fixed effect model is rarely correct. The true effect sizes Zi in all studies (i = 1,…, k; k number of primary studies) may be similar but are not likely to be identical. Accordingly, a random effects model assumes that the true effect sizes are a random sample from the population of all possible study effects and (normally) distributed around the true overall effect Φ. The true effects of the individual studies deviate from this by a study-specific value ζi and by a sampling error εi with Zi = Φ + ζi + εi. Thus, the variance comprises two components: an inter-study variance τ2 and an intra-study variance σ2, both of which are included in the weighting () for the estimation of the meta-effect–on the one hand, in accordance with the random distribution assumption, and on the other hand, to take into account the precision (sample size) of each individual study i:
(for details Borenstein et al., 2009; Schmidt and Hunter, 2015).
This not only shows that the fixed effect model is a special case of the random effects model when the inter-study variance τ2 is zero, and the use of a random effects model is generally recommended. Rather, attention shifts from the overall effect to the distribution of study effects when these vary substantially, and the meta-analytical procedures are functional continuations of analyses used in primary studies (e.g., analysis of variance, multiple regression; Borenstein et al., 2009). Thus, in analogy to one-way analysis of variance, the measure Q for the weighted square sums, which follows a central χ2 distribution with df = k–1 degrees of freedom, and a corresponding null hypothesis significance test are used to check whether the heterogeneity of the individual study effects differs from zero. The variance of the effect size parameters of the primary studies is denoted as τ2 with the corresponding standard deviation . In addition, the parameter I2 expresses the proportion of the total variance (= inter- and intra-study variance) that is actually due to the heterogeneity of the study effects. Thus, I2 is a measure of the inconsistency within the study effects and is comparable with the coefficient of determination of classical variance-analytical procedures R2. According to Higgins et al. (2003), tentative benchmarks or conventions for the proportion of true inter-study variance in the total variance are 25% low, 50% medium, and 75% high. Even small values for I2, however, may present good reasons for the inter-study variance to be elucidated, for example by subgroup analyses or meta-regressions (see Borenstein et al., 2009; Schmidt and Hunter, 2015).
In the transdisciplinary educational context, meta-analytical procedures can be applied as usual to combine the results of several studies on one or more subjects (e.g., Seidel and Shavelson, 2007; Praetorius et al., 2018). On the other hand, however, their application is particularly suitable when, within an interdisciplinary research approach, several subject-specific studies with the same study design are to be compared and generalized. This specific usage is finally illustrated by an example from the FALKE project, in which among many other things the relationship between structuredness and global rating of explanations in eleven different school subjects was investigated. The corresponding correlation results, including the precision of the respective estimates, which are represented in the forest plot with 95% confidence intervals, and the distribution of the subject-specific effects are shown in Figure 1.
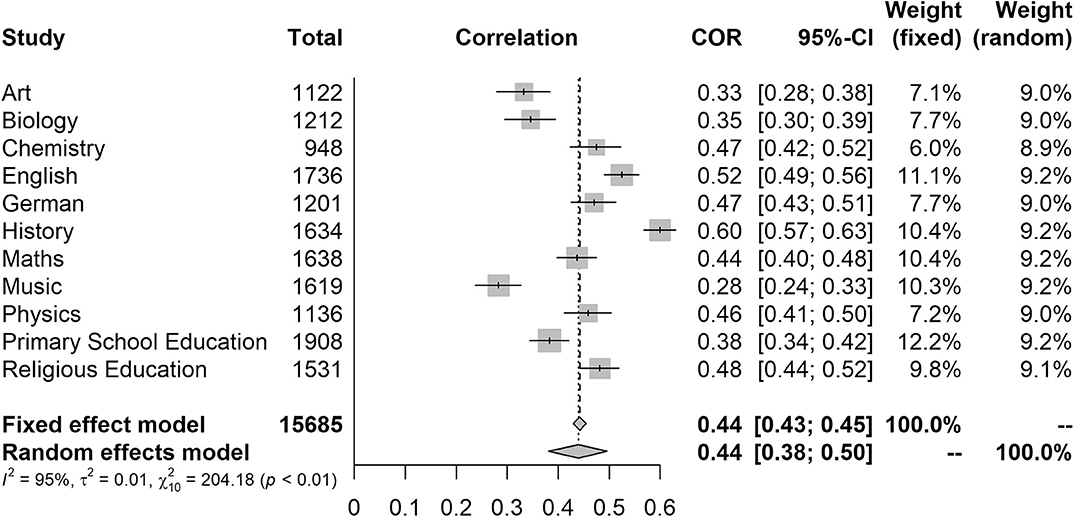
Figure 1. Forestplot for the subject-specific relationships between structuredness and global rating and results of the fixed effect and random effects model.
In order to investigate the size of the correlation between structuredness and global rating across all school subjects, the meta-effect was determined using both the fixed and the random effects model, with both approaches leading to the same result (r = 0.44). Figure 1 clearly shows the different weightings that correspond to the sample sizes of the primary studies in the fixed effect model. Also, based on the hypothetical assumption that the true effect is identical in each subject, the estimation of the meta-effect turns out to be rather precise (CI0.95 = [0.43; 0.46]).
However, it seems theoretically more sound to assume that the effects observed in the individual studies are only a random sample due to, among other factors, subject-specific practices, different explanatory themes and addressees, and heterogeneous sample compositions–clearly, a random effects model seems more suitable. In this model, the studies are weighted almost equally (see also Figure 1) and the confidence interval of the meta-effect is larger (CI0.95 = [0.38; 0.50]), since the distribution of the subject-specific effects is also taken into account. As expected, this heterogeneity is significant ( p < 0.01), and the inter-study variance is τ2 = 0.01 (standard deviation: τ = 0.10). This variance can almost completely (I2 = 95%) be attributed to a true heterogeneity between the subject-related correlations and must be clarified in further analyses (Schilcher et al., 2020a).
Hierarchical Data Structures and Manifest Multilevel Models
While meta-analytical approaches for investigating transdisciplinary issues are based on published results data, for raw data structured according to studies (here: school subjects), multilevel models are used to simultaneously determine the (residual) variance of the study-related effect size parameters and the overall effect size (Raudenbush and Bryk, 2002). The hierarchical data structures to be considered here, in which analysis objects at the individual level can be assigned to one or more superordinate units, are well-known in educational research from a large number of applications and are accordingly widely discussed in the methodological literature (Ditton, 1998; Raudenbush and Bryk, 2002; Marsh et al., 2012; Beretvas et al., 2015; Nagengast and Rose, 2018). For example, students (level 1) are nested in classes (level 2), classes in schools (level 3), schools in administrative units (level 4), administrative units in countries (level 5), and so forth. The resulting potential similarity or dependence of measured values within the same category, the size of which can be determined by means of the intraclass correlation coefficient (ICC), violates the independence assumption of errors required by close to all classical models. This violation endangers the validity of statistical conclusions, since spurious correlations between variables, biased estimates of model parameters, underestimation of standard errors and, with regard to null hypothesis significance testing, inflated Type-1-error probabilities are some of the possible consequences (Ditton, 1998; Raudenbush and Bryk, 2002; Snijders and Bosker, 2012; Beretvas et al., 2015; Nagengast and Rose, 2018).
By specifying residual matrices at both the individual and the grouping levels (the mixing of the error terms is the reason for the often-used term “mixed models” instead of multilevel models), multilevel models explicitly consider hierarchical structures in the data. Also, these models allow for the straightforward inclusion of features and their relationships at different aggregation levels, since these are (mathematically) independent of each other (e.g., level 1: mathematics achievement, socio-economic status; level 2: classroom climate, class size; level 3: school track, school facilities; level 4: infrastructure, curriculum; level 5: gross domestic product, development level; cf. Snijders and Bosker, 2012; Beretvas et al., 2015; Nagengast and Rose, 2018). Compared to a conventional ordinary least squares regression model, the equation of a simple hierarchical model with two levels, for example, contains two additional random components (also with mean zero), which model the deviations u0j from the group-specific regression intercepts from the overall intercept γ00 on the one hand, and the deviations u1j of the group-specific regression slopes from the overall slope γ10 on the other hand:
with Yij representing the dependent variable, Xij the value of the independent variable, and rij represents the error term of the entity i, with i = 1,…, nj, in group j, with j = 1,…, k. The application of this so-called ‘random coefficient model’, in which regression constants as well as the predictors' regression weights vary freely over superordinate levels, is illustrated below in simplified examples with only transdisciplinary (2 levels) or with longitudinal and transdisciplinary data structure (3 levels).1
Multilevel Models (Considering Context-Related Data Structures)
With reference to the example in section Meta-Analytical Approaches in Interdisciplinary Studies, the correlation between structuredness and global rating of explanations for the eleven school subjects involved in the FALKE project will be investigated, taking into account the overall (transdisciplinary) correlation as well as the variance of the subject-specific relationships shown in Figure 2. To this end, a simple random coefficient regression with the dependent variable global rating and the independent variable structuredness is used to model the nested data structure arranged by school subject, in which the regression intercepts and slopes are variably modeled at subject level. The unstandardized results of this estimation, with both variables were measured on the same six-category response scale, are shown in Table 1.
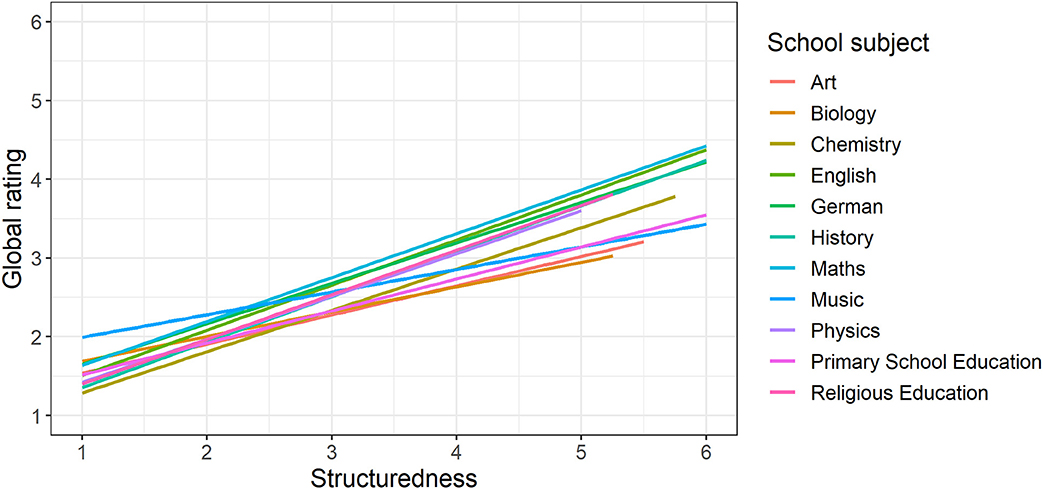
Figure 2. Line graph of the subject-specific relationships between structuredness and global rating. Scaling of structuredness and global rating 1 = very good, …, 6 = insufficient.
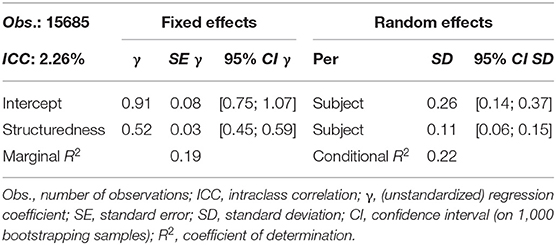
Table 1. Random coefficient model with the dependent variable global rating for eleven school subjects.
As can be seen from Table 1, the global (transdisciplinary) regression coefficient for structuredness is γ10 = 0.52 and is significant. This means that, starting from the global intercept of γ00 = 0.91 (intersection of the overall regression line with the ordinate axis; cannot be interpreted in a meaningful way here), the global rating, on average, increases by about half a unit for each rating unit by which the structuredness increases. In terms of content, this shows that there is a positive correlation between the structuredness and the global rating of an explanation, that is, on average, the better structured an explanation is perceived the better it is rated overall. But this correlation is not the same in all subjects. In the present case of only one predictor variable, the intercepts (SD = 0.26) as well as slopes (SD = 0.11) not only vary significantly between the school subjects, so that in individual subjects there may be lower or higher starting levels and smaller or larger correlations between global rating and structuredness, which are visualized in Figure 2 (for numerical details see Table 2). Rather, there is a significant correlation of r = −0.86 (CI0.95[−0.97; −0.50]) between intercepts and slopes: the smaller the intercept, the greater the slope between global rating and structuredness or, in other words, the better very well-structured explanations are globally rated in an interdisciplinary comparison, the worse are very poorly structured explanations. On the one hand, this can be seen numerically from Table 2, which is additionally presented here for illustration purposes and contains the subject-specific model coefficients. On the other hand, the effect is shown graphically in Figure 2.

Table 2. Subject-specific coefficients for the random coefficient model in Table 1.
The variance explained by the present hierarchical model is acceptable for both the fixed effects (marginal R2 = 0.19) as well as the fixed and random effects together (conditional R2 = 0.22). In conclusion, it should be noted that with previous z-standardization of the variables global rating and structuredness per school subject, the reported random coefficient model (apart from small deviations and discrepancies due to different estimation procedures and rounding) leads to the same results as the random effects model of the meta-analysis (section Meta-Analytical Approaches in Interdisciplinary Studies), thus highlighting the obvious parallels between these two approaches.
Mixed Linear Models (Considering Longitudinal Data Structures)
Longitudinal data structures are a fairly regular case in educational research, for example when investigating the effectiveness of teaching methods with a pre- and a post-test, offer a specific application situation for multilevel models. Each person is assigned at least two measurement values (e.g., the pre- and the post-test results). The data can therefore be thought of as ‘nested within persons’. At the same time, the persons are often divided into different groups (e.g., control and experimental group) at random or systematically according to different test conditions. According to Hilbert et al. (2019), mixed linear models with dummy-coded predictor variables are particularly suitable for analyzing studies with this type of design, since they are superior to traditional methods such as repeated measurement ANOVAs or OLS regressions with regard to less stringent model assumptions and higher statistical power (see also Raudenbush and Bryk, 2002). The approach proposed by Hilbert et al. is easily applicable to a transdisciplinary context by extending the nesting of the model to take different school subjects into account. For an exemplary case, data from the FALKE project will again be used to illustrate the model.
In (almost) all school subjects, two explanatory videos present the same teaching content using two didactically different approaches (A vs. B). These video pairs were shown to students on the one hand, and to teachers on the other, and both groups were asked to give their global rating (Schilcher et al., 2020b). An illustration of the results is provided in Figure 3, which shows differences in the rating depending on the group, didactical method, and subject.
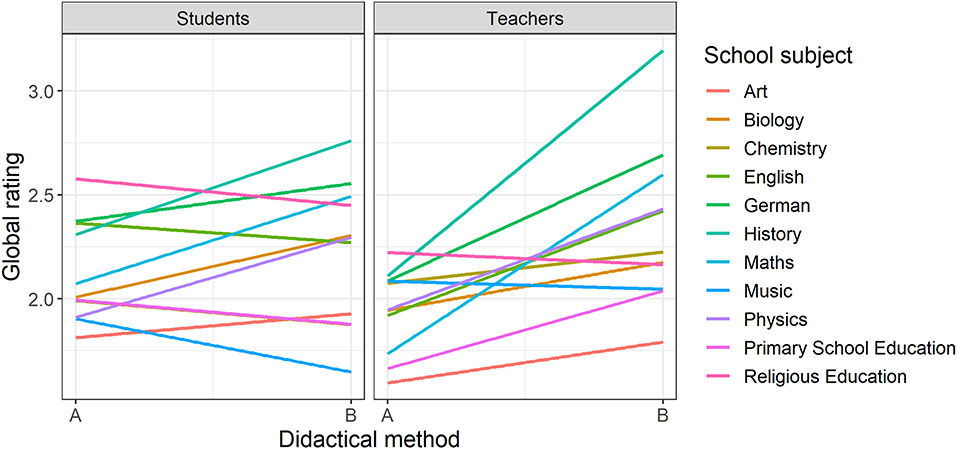
Figure 3. Line graph of the subject-specific relationships between method and global rating, separated by students, and teachers.
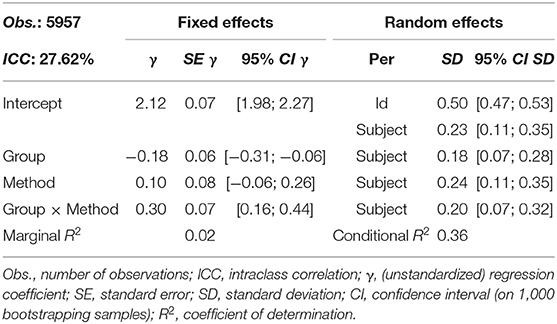
In order to analyze the differences shown in Figure 3 with a linear mixed model, the variable for the didactical method of a video pair (A: 0 vs. B: 1) as well as the variable for group membership (students: 0 vs. teachers: 1) are dummy-coded. The model includes both main effects as well as the interaction effect of the variables. Importantly, the interaction effect represents the additional rating difference between didactical method A and B for teachers compared to the students. Since the data are nested within persons, a person-specific residual term is included on the second level. In addition, school subject grouping is modeled as a third level, by which the regression intercept and slope parameters of all predictors may vary to obtain estimates for both the generalized effects and the transdisciplinary distribution of effects. The (non-standardized) coefficients of the corresponding linear mixed model are shown in Table 3.
Across all school subjects, students rate didactical method A on average with γ00 = 2.12, although this value varies significantly between disciplines (SD = 0.23; Table 3). The corresponding rating of the teachers is on average significantly lower by γ10 = −0.18 than compared to the students' and shows a significant variation from discipline to discipline (SD = 0.18). While there is no significant overall tendency among students across school subjects in favor of the didactical variant B (γ01 = 0.10, but the 95% CI includes the value 0), the significant transdisciplinary interaction effect between group and method (γ11 = 0.30) is: Compared to method A, the teachers assigned didactical method B a significantly higher average rating than the students (for an exhaustive description of the different model parameters and their interpretation, see Hilbert et al., 2019). In the present model, the variance that is explained by the fixed effects is small (marginal R2 = 0.02), that explained by fixed and random effects is appropriate (conditional R2 = 0.36). Thus, an interdisciplinary generalization of the results only appears to make sense regarding the transdisciplinary variance of the effects.
Latent Multilevel Structural Equation Models
The multilevel models described above are based on manifest scale values for each construct such as sum or mean values or the proportion of correctly solved tasks. However, any multiple indicators of the constructs, their factor structure and particularly measurement errors are not considered in manifest models (Marsh et al., 2012; Beretvas et al., 2015). This implies the assumption that all relevant variables are directly observable (and measured without errors), which hardly seems possible–in particular regarding typical target variables in the social sciences and educational research, such as (cognitive) abilities, knowledge, competence, skills, attitudes, or motivation. In contrast, structural equation models take up the basic idea of latent modeling, that is to capture a feature which is not directly observable only by means of various indicators, in whose manifestations this feature is reflected. Latent models split the variance of the manifest indicators into the measurement error component and the component of the latent variable on which the scale values are based. At the same time, the use of latent structural equation models allows the analysis of complex variable systems with several exogenous and endogenous elements (Kline, 2011; Beretvas et al., 2015; Nagengast and Rose, 2018).
By extending the multilevel approach, these advantages can also be used in latent multilevel structural equation models in which features can be measured and analyzed simultaneously at different levels of analysis (e.g., students, classes, school, subject; Raudenbush and Bryk, 2002). Possible applications of such models, for example in the context of instructional quality research, are shown by Baumert et al. (2010), Kunter et al. (2013) as well as Wisniewski et al. (2020) and their particular merit is underlined by Marsh et al. (2012). Because of the specific methodological requirements of educational research, in which manifest variables mostly reflect influences from several levels, these authors suggest the use of double latent models, which will be illustrated below using a simplified example.
Analogous to sections Meta-Analytical Approaches in Interdisciplinary Studies and Multilevel Models (Considering Context-Related Data Structures), the transdisciplinary relationship between structuredness and global rating of explanations is examined, taking into account individual differences (level 1) and heterogeneous subject cultures (level 2). For this purpose, a (latent) multilevel structural equation model, in which the structuredness is simultaneously indicated at levels 1 and 2 by the four items belonging to this latent construct, is estimated (Figure 4). The manifest value of the global rating indicator is decomposed into latent variance components at levels 1 and 2 as endogenous variables in each case. Figure 4 shows the corresponding measurement and structure models including the standardized factor loadings, variances, and regression coefficients (without residuals). The proportion of variance that can be explained by the school subject structure (ICC 1) is 2.27% [see section Multilevel Models (Considering Context-Related Data Structures), Table 1], the reliability of the subject-specific group means is 0.97 (ICC 2; Bliese, 2000) and the local and global fit values of the model are acceptable (Figure 4; Hu and Bentler, 1999). The standardized correlation between structuredness and global rating is β1 = 0.49 (p < 0.01) at individual level and β2 = 0.66 (p < 0.01) at subject level. Thus, due to the high factor reliability, the latent transdisciplinary effect of R2 = 0.44 (= ) corresponds to the (measurement error-afflicted) estimates of the meta-analysis (section Meta-Analytical Approaches in Interdisciplinary Studies) and the multilevel model with standardized coefficients [section Multilevel Models (Considering Context-Related Data Structures)].
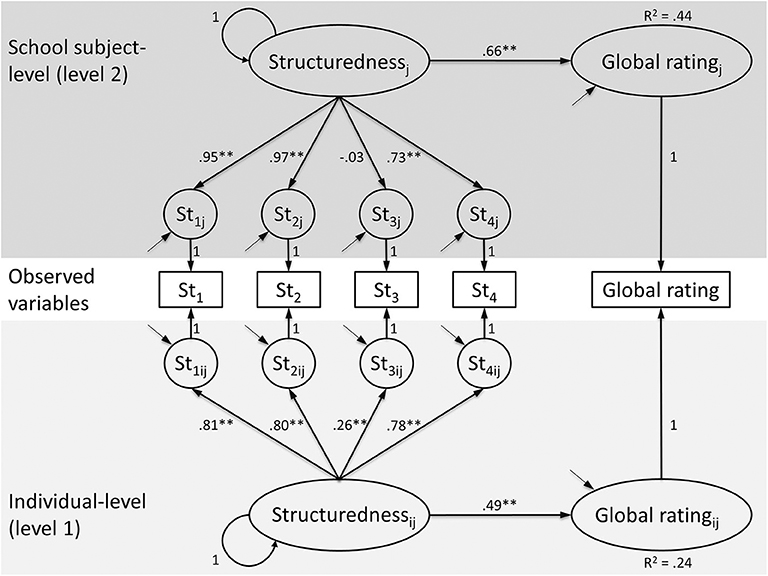
Figure 4. (Doubly) Latent structure equation model for the correlation between structuredness and global rating at individual and school subject level. Latent constructs are represented as circles and indicators of these variables as squares. The boxes representing the observed variables are associated with both individual and subject-specific constructs (see Marsh et al., 2012); residual variances are not reported. The subscripts ij indicate that these variables take on different values for each student i in each classroom j. Number of observations: 15,639, number of clusters: 11; χ2(10) = 173.13**, CFI = 0.99, RMSEA = 0.03, SRMR (within) = 0.02, SRMR (between) = 0.09; *p < 0.05, **p < 0.01.
Machine Learning Methods
Although the methods presented so far are suitable and proven for a large number of applications in the field of educational science, they require stringent distributional and model assumptions and can only handle a relatively restricted number of variables and constructs. This makes it difficult to adequately analyze large, weakly structured or short-lived datasets, which are summarized under the collective term “big data,” increasingly available due to digitalization and also necessary to investigate the multifaceted complexity of many educational phenomena. In order to meet these methodological challenges, various data mining methods have been applied for many years and are constantly being further developed, which has been particularly favored by the rapid increase in computing power over the last two decades (Romero and Ventura, 2020; for an overview, see Fischer et al., 2020). These include machine learning methods, which enable an effective analysis of enormous amounts of data and complex data structures almost without distributional assumptions. So far, machine learning approaches have only rarely been used in empirical educational research (e.g., Kotsiantis, 2012), but they represent a promising alternative for the analysis of national and international large scale studies, such as PISA (Programme for International Student Assessment) or TIMSS (e.g., Depren et al., 2017; Yoo, 2018; Trends in International Mathematics and Science Study), for secondary analyses (e.g., Pargent and Albert-von der Gönna, 2018) or, as will be outlined in the following, for the investigation of transdisciplinary analyses.
From a theoretically unlimited number of variables, those relevant for predictions are automatically selected by machine learning algorithms and overfitting is prevented by a strict distinction between training and test data with resampling methods using multiple loops. This method is called (nested) resampling, because the entire sample of cases is recursively split into a training set, typically comprising two thirds of the data, and a test set, comprising the remaining third. The model is then trained with the training data only until the most predictive variables are selected (or equipped with large weights) and their interaction is modeled. The accuracy of the resulting model, however, is estimated through the performance of the test data, which has not been used to train the model. Overfitting the model to the training data therefore results in worse fit on the test data (because even random aspects of the training data enter the model, which have no bearing in the test data; Efron and Hastie, 2016). This procedure requires the data to be labeled before training, so that the prediction accuracy can be determined by the percentage of correctly predicted labels in the test data. These labels may be categorical or numerical. For categorical data, the percentage of the correct category is usually used as a measure of prediction accuracy, while for numerical data, the mean squared error is often employed. Machine learning with labeled data is termed “supervised learning,” because the correctness of the result can be supervised through comparison of the labels with the predictions of the model.
This means that the models can be more easily generalized than conventional analysis methods, even though they are typically more exploratory and less theory-driven than classical statistical models (Efron and Hastie, 2016). A widespread criticism regarding machine learning techniques lies within the data-driven inherently exploratory approach of these models, which is partly simply the downside of their greatest strength, namely the lack of model assumptions. However, several techniques have been developed to look into the former blackbox that machine learning used to represented. Feature engineering has become a more and more prominent part of machine learning. It refers to the preparation of predictor variables (typically called “features” in the context of machine learning) to pre-process variables in a usually meaningful way to make them more valuable for the model. Goerigk et al. (2020), for example, extracted factor scores from structural equation models to use them as features in their models. The rapidly growing field of interpretable machine learning uses various techniques to infer the effect of single variables on the prediction accuracy, usually graphically illustrated through variable importance plots, partial dependence plots, or accumulated local dependence (Molnar, 2019). As will be illustrated below in an exemplary analysis of the FALKE data, using sum scores of scales and variable importance plots can lead to interpretable, theory-based results, even though this is not the core-strength of the machine learning techniques.
To provide a simple example, a random forest (Breiman, 2001) was used to analyze the FALKE data. One of the advantages of this (and most other common) machine learning model(s) is that it is not based on distributional and linearity assumptions. Random forest models simply randomize and average a large number of mathematical trees that split the sample according to the most suitable splitting points in the most suitable variable. In this example, the random forest model was used to predict the school subject of a video through the ratings on the six constructs operationalized in FALKE (including the global rating). In addition, feature importance (see Molnar et al., 2018) was estimated by sampling to determine which construct is most valuable for the prediction of the school subject. Despite the low number of predictors and high number of categories, this model already assigns 58.1% of all test set cases to the correct school subject. Notably, in contrast to the performance estimates presented in the previous sections (such as R2), this is the accuracy for the testing sample, meaning cases the model has not been trained with. As shown in the representation of the variable importance (Figure 5), as expected, the subject-specific construct that operationalizes aspects typical for explanations in this subject (e.g., substance-particle level in Chemistry or acoustic vs. visual approaches in Music; Schilcher et al., 2020a) clearly has the greatest predictive power.
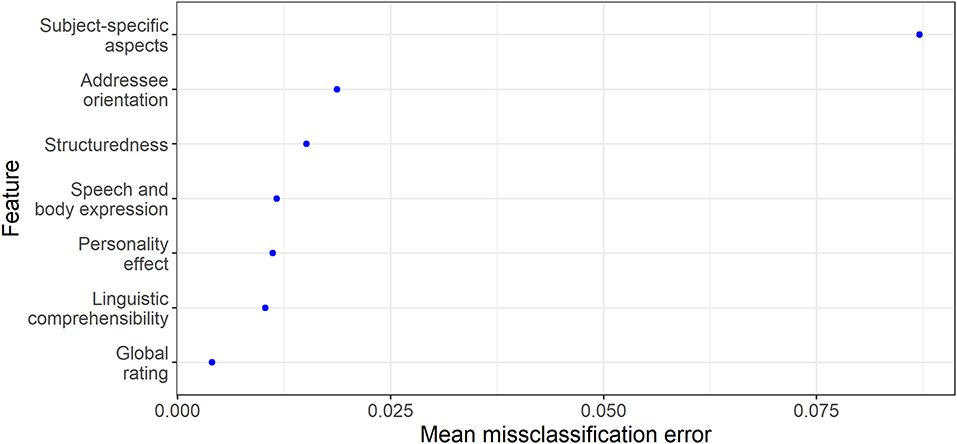
Figure 5. Feature importance plot regarding the prediction of school subject membership by the six constructs and the global rating operationalized in FALKE.
Comparative Conclusion and Further Recommendations
In the preceding sections, four different methods were presented for adequately dealing with methodological challenges such as meta-analytical approaches, hierarchical data structures, large measurement errors, or big and complex amounts of data, which are often present in transdisciplinary empirical educational research. The first three of these approaches–meta-analyses, multilevel models and latent multilevel structural equation models–are based, as cross-references between the respective sections illustrate, on the same classical framework of the Generalized Linear Model, which has several limitations. For instance, the choice of model is not only limited by the level of measurement and distributional assumptions. Rather, the requirement of a particular (mostly linear) relationship between variables itself is by no means self-evident, especially in teaching and learning contexts, and complex relational structures can easily be missed or even interpreted in erroneous ways with linear models. Moreover, the number of variables that can be considered simultaneously in is typically rather small due to multicollinearity problems and this also restrict the mapping of more complex relationships. Since the models are typically fitted exclusively to the respective underlying sample and rarely cross-validated or re-evaluated on the basis of additional samples, the classically reported coefficient of determination R2 usually substantially overestimates their predictivity and their generalizability must therefore be critically questioned. Machine learning methods, on the other hand, do not have these limitations of the classical General Linear Model and can take them into account in modeling (see section Machine Learning Methods). Due to their versatile application potential, they thus enrich the current inventory of methods in transdisciplinary educational research (but also in empirical educational research in general) and appear to be an integral part of the future state of the art methods, especially for the analysis of “big data” (Efron and Hastie, 2016; Stachl et al., 2020). Their primarily explorative approach can be monitored and verified by contemporary interpretable machine learning methods (Molnar, 2019). On the other hand, machine learning models have not been developed for theory-testing purposes, but to maximize model predictivity, often at the expense of interpretability. The strength of the three approaches based on (generalized) linear models is the focus on testable hypotheses and the direct and interpretable quantification of deviations from proposed model fit.
In conclusion, it should be noted that all of the presented methods require rather large samples (Marsh et al., 2012), although the recommendations for minimum sample sizes (per analysis level) vary depending on the type of analysis as well as the model type and complexity and are controversially discussed in the methodological literature (e.g., Borenstein et al., 2009; Hox, 2010; Marsh et al., 2012). For the aggregation and evaluation of already published study effects, the application of a meta-analysis with a random effects model is appropriate. Here, the number of underlying effects should be enough to obtain a meaningful estimate of the between-studies variance. Using the statistical software R (R Core Team, 2019), central packages for meta-analyses are “meta” (Balduzzi et al., 2019) and “metafor” (Viechtbauer, 2010), and further information about meta-analysis that could not be presented in this brief introduction is provided by Borenstein et al. (2009) and Schmidt and Hunter (2015). Multilevel analyses with manifest variables are suitable, however, if hierarchical data structures exist due to context variables, but also due to measurements at several time points. A ratio of 30 : 30 is often given as the minimum for simple two-level models, but this is only a vague benchmark that depends mainly on the concrete data situation. Also, even though theoretically possible, rarely can more than three levels be modeled meaningfully and estimated in hierarchical models. Useful R packages for multilevel models are “multilevel” (Bliese, 2016), “lme4” (Bates et al., 2015), “lmerTest” (Kuznetsova et al., 2017) as well as “MuMIn” (Barton, 2020). Further application notes are provided by Ditton (1998), Raudenbush and Bryk (2002), Hox (2010), and Snijders and Bosker (2012). If measurement errors or more complex relationships between variables are to be modeled additionally, the use of latent multilevel structural equation models is recommended. Besides an appropriate ratio of persons and parameters to be estimated (at least 10 : 1), from a multilevel perspective the effective sample size is the number of higher level units (at least 50), not just the number of individual level subjects. For the analysis of these models using R, the packages “lavaan” (Rosseel, 2012) and “sem” (Fox et al., 2017) are necessary and additional references to latent (multilevel) structure equation modeling can be found in Kline (2011) and Marsh et al. (2012). Finally, the benefits and efficiency of machine learning methods become more apparent the more extensive and confusing the data set to be analyzed is (≫1,000 persons and/or variables). A basic R package for the application of machine learning methods is “mlr” (Bischl et al., 2016) and an in-depth introduction is provided by Efron and Hastie (2016).
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: Open Science Framework https://osf.io/5sn9j.
Ethics Statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent to participate in this study was provided by the participants' legal guardian/next of kin.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This publication is a result of the KOLEG project (Kooperative Lehrerbildung Gestalten) at the University of Regensburg, which was funded by the German Federal Ministry of Education and Research as part of the joint quality offensive for teacher training by the federal and state governments (grant number: 01JA1512).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank the numerous students, student teachers, teachers, and teacher trainers of the different school subjects very much for their voluntary participation in the study. We also thank the editors and reviewers of Frontiers for their critical and very helpful comments on earlier versions of this paper.
Footnotes
1. ^In order to make the examples clear and comprehensible, the modelling of further levels that may be contained in the data (e.g., class, school) is avoided for didactical reasons.
References
Balduzzi, S., Rücker, G., and Schwarzer, G. (2019). How to perform a meta-analysis with R: a practical tutorial. Evid. Based Ment. Health 22, 153–160. doi: 10.1136/ebmental-2019-300117
Barton, K. (2020). MuMIn: Multi-Model Inference. R Package Version 1.43.17. Available online at: https://CRAN.R-project.org/package=MuMIn
Bates, D., Maechler, M., Bolker, B., and Walker, S. (2015). Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67, 1–48. doi: 10.18637/jss.v067.i01
Baumert, J., Kunter, M., Blum, W., Brunner, M., Voss, T., Jordan, A., et al. (2010). Teachers' mathematical knowledge, cognitive activation in the classroom, and student progress. Am. Educ. Res. J. 47, 133–180. doi: 10.3102/0002831209345157
Beretvas, S. N., Whittaker, T. A., and Stafford, R. E. (2015). “Statistical modeling methods for classroom management research,” in Handbook of Classroom Management, 2nd Edn, eds E. T. Emmer and E. J. Sabornie (New York, NY: Routledge), 519–537.
Bischl, B., Lang, M., Kotthoff, L., Schiffner, J., Richter, J., Studerus, E., et al. (2016). mlr: machine learning in R. J. Mach. Learn. Res. 17, 1–5.
Bliese, P. (2000). “Within-group agreement, non-independence, and reliability,” in: Multilevel Theory, Research, and Methods in Organisations, eds K. Klein and S. Kozlowski (San Francisco: Jossey-Bass), 349–381.
Bliese, P. (2016). multilevel: Multilevel Functions. R package version 2.6. Available online at: https://CRAN.R-project.org/package=multilevel
Borenstein, M., Hedges, L. V., Higgins, J. P. T., and Rothstein, H. R. (2009). Introduction to Meta-Analysis. Chichester: John Wiley & Sons. doi: 10.1002/9780470743386
Depren, S. K., Aşkin, Ö. E., and Öz, E. (2017). Identifying the classification performances of educational data mining methods: a case study for TIMSS. Educ. Sci. Theory Pract. 17, 1605–1623. doi: 10.12738/estp.2017.5.0634
Deutscher Bildungsrat [German Education Council] (1974). Empfehlungen der Bildungskommission – Aspekte für die Planung der Bildungsforschung. Bonn: Bundesdruckerei.
Ditton, H. (1998). Mehrebenenanalyse. Grundlagen und Anwendungen des Hierarchisch Linearen Modells. Weinheim/München: Beltz Juventa.
Efron, B., and Hastie, T. (2016). Computer Age Statistical Inference. Algorithms, Evidence, and Data Science. New York, NY: Cambridge University Press. doi: 10.1017/CBO9781316576533
Fischer, C., Pardos, Z. A., Baker, R. S., Williams, J. J., Smyth, P., Yu, R., et al. (2020). Mining big data in education: affordances and challenges. Rev. Res. Educ. 44, 130–160. doi: 10.3102/0091732X20903304
Fox, J., Nie, Z., and Byrnes, J. (2017). sem: Structural Equation Models. R package version 3.1-9. Available online at: https://CRAN.R-project.org/package=sem
Goerigk, S., Hilbert, S., Jobst, A., Falkai, P., Bühner, M., Stachl, C., et al. (2020). Predicting instructed simulation and dissimulation when screening for depressive symptoms. Eur. Arch. Psychiatry Clin. Neurosci. 270, 153–168. doi: 10.1007/s00406-018-0967-2
Gräsel, C. (2015). “Was ist Empirische Bildungsforschung?,” in: Empirische Bildungsforschung. Strukturen und Methoden, 2nd Edn, eds H. Reinders, H. Ditton, C. Gräsel, and B. Gniewosz (Wiesbaden: Springer), 15–30. doi: 10.1007/978-3-531-19992-4_1
Hattie, J. A. C. (2009). Visible Learning: A Synthesis of over 800 Meta-Analyses Relating to Achievement. London: Routledge. doi: 10.4324/9780203887332
Higgins, J., Thompson, S. G., Deeks, J. J., and Altman, D. G. (2003). Measuring inconsistency in meta-analyses. BMJ 327, 557–560. doi: 10.1136/bmj.327.7414.557
Hilbert, S., Stadler, M., Lindl, A., Naumann, F., and Bühner, M. (2019). Analyzing longitudinal intervention studies with linear mixed models. Test. Psychometrics Methodol. Appl. Psychol. 26, 101–119. doi: 10.4473/TPM26.1.6
Hox, J. (2010). Multilevel analysis. Techniques and Applications, 2nd Edn, New York, NY: Routledge. doi: 10.4324/9780203852279
Hu, L., and Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: conventional criteria versus new alternatives. Struct. Equ. Model A Multidisc. J. 6, 1–55. doi: 10.1080/10705519909540118
Kline, P. (2011). Principles and Practice of Structural Equation Modeling. New York, NY: Guilford Press.
Kotsiantis, S. B. (2012). Use of machine learning techniques for educational proposes: a decision support system for forecasting students' grades. Artif. Intell. Rev. 37, 331–344. doi: 10.1007/s10462-011-9234-x
Kunter, M., Klusmann, U., Baumert, J., Richter, D., Voss, T., and Hachfeld, A. (2013). Professional competence of teachers: effects on instructional quality and student development. J. Educ. Psychol. 105, 805–820. doi: 10.1037/a0032583
Kuznetsova, A., Brockhoff, P. B., and Christensen, R. H. B. (2017). lmertest package: tests in linear mixed effects models. J. Stat. Softw. 82, 1–26. doi: 10.18637/jss.v082.i13
Marsh, H. W., Lüdtke, O., Nagengast, B., Trautwein, U., Abduljabbar, A. S., and Köller, O. (2012). Classroom climate and contextual effects: conceptual and methodological issues in the evaluation of group-level effects. Educ. Psychol. 47, 106–124. doi: 10.1080/00461520.2012.670488
Molnar, C. (2019). Interpretable Machine Learning. A Guide for Making Black Box Models Explainable. Morrisville: Lulu Press.
Molnar, C., Casalicchio, G., and Bischl, B. (2018). iml: An R package for interpretable machine learning. J. Open Source Softw. 3:786. doi: 10.21105/joss.00786
Nagengast, B., and Rose, N. (2018). “Quantitative Bildungsforschung und Assessments,” in Handbuch Bildungsforschung, eds R. Tippelt and B. Schmidt-Hertha Vol. 2, 4th Edn, (Wiesbaden: Springer), 669–688. doi: 10.1007/978-3-531-19981-8_28
Pargent, F., and Albert-von der Gönna, J. (2018). Predictive modeling with psychological panel data. Zeitschrift für Psychologie 226, 246–258. doi: 10.1027/2151-2604/a000343
Praetorius, A.-K., Klieme, E., Herbert, B., and Pinger, P. (2018). Generic dimensions of teaching quality. The German framework of three basic dimensions. ZDM Mathe. Educ. 50, 407–426. doi: 10.1007/s11858-018-0918-4
R Core Team (2019). R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna, Austria.
Raudenbush, S. W., and Bryk, A. S. (2002). Hierarchical Linear Models. Applications and Data Analysis Methods. Thousand Oaks, CA: Sage.
Romero, C., and Ventura, S. (2020). Educational data mining and learning analytics: an updated survey. WIREs Data Mining Knowledge Discovery 10 (3). doi: 10.1002/widm.1355
Rosseel, Y. (2012). lavaan: an R package for structural equation modeling. J. Stat. Softw. 48, 1–36. doi: 10.18637/jss.v048.i02
Schilcher, A., Krauss, S., Lindl, A., and Hilbert, S. (2020a). FALKE – Fachspezifische Lehrerkompetenzen im Erklären: Untersuchungen zur Beurteilung und zu Kriterien unterrichtlicher Erklärqualität aus der Perspektive von 13 Fachbereichen. Weinheim/Basel: Beltz Juventa.
Schilcher, A., Lindl, A., Hilbert, S., Krauss, S., Asen-Molz, K., Ehras, C., et al. (2020b). Experiences from transdisciplinary research. Front. Educ. 5, in preparation.
Schlesinger, L., Jentsch, A., Kaiser, G., König, J., and Blömeke, S. (2018). Subject-specific characteristics of instructional quality in mathematics education. ZDM Math. Educ. 50, 475–490. doi: 10.1007/s11858-018-0917-5
Schmidt, F. L., and Hunter, J. E. (2015). Methods of Meta-Analysis. Correcting Error and Bias in Research Findings, 3rd Edn, Thousand Oaks, CA: Sage. doi: 10.4135/9781483398105
Seidel, T., and Shavelson, R. J. (2007). Teaching effectiveness research in the past decade: the role of theory and research design in disentangling meta-analysis results. Rev. Educ. Res. 77, 454–499. doi: 10.3102/0034654307310317
Snijders, T. A. B., and Bosker, R. J. (2012). Multilevel analysis. An Introduction to Basic and Advanced Multilevel Modelling, 2nd Edn. London: Sage.
Stachl, C., Pargent, F., Hilbert, S., Harari, G., Schoedel, R., Vaid, S., et al. (2020). Personality research and assessment in the era of machine learning. Eur. J. Personal. doi: 10.1002/per.2257. [Epub ahead of print].
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. J. Stat. Softw. 36, 1–48. doi: 10.18637/jss.v036.i03
Wisniewski, B., Zierer, K., Dresel, M., and Daumiller, M. (2020). Obtaining secondary students' perceptions of instructional quality: two-level structure and measurement invariance. Learn. Instruct. 66:101303. doi: 10.1016/j.learninstruc.2020.101303
Keywords: transdisciplinarity, meta-analysis, multilevel model, linear mixed model, structural equation model, machine learning, explaining, instructional quality
Citation: Lindl A, Krauss S, Schilcher A and Hilbert S (2020) Statistical Methods in Transdisciplinary Educational Research. Front. Educ. 5:97. doi: 10.3389/feduc.2020.00097
Received: 22 April 2020; Accepted: 28 May 2020;
Published: 17 July 2020.
Edited by:
Matthias Stadler, Ludwig Maximilian University of Munich, GermanyReviewed by:
Antoine Fischbach, University of Luxembourg, LuxembourgJan Dörendahl, University of Luxembourg, Luxembourg
Copyright © 2020 Lindl, Krauss, Schilcher and Hilbert. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alfred Lindl, YWxmcmVkLmxpbmRsQHVyLmRl
 Alfred Lindl1*
Alfred Lindl1* Stefan Krauss
Stefan Krauss Sven Hilbert
Sven Hilbert