Motivational and Emotional Orientation, Engagement, and Achievement in Mathematics. A Case Study With One Sixth-Grade Classroom Working With an Electronic Textbook on Fractions

Introduction

Implementation of digital media in classrooms is one central goal of recent educational policies and of global interest in research on teaching and learning—particularly in times of increased use of digital learning due to the COVID-19 pandemic. One reason for that is the commonly agreed upon idea that technology-enriched classroom instruction (compared to traditional “non-technological” learning settings) offers a variety of advantages for learning—which is largely supported by empirical results (e.g., Reinhold et al., 2020a; Roschelle et al., 2010; Özyurt et al., 2014; and see Hillmayr et al., 2020 for an overview of the current literature). In particular, recent research supports the hypothesis that the use of technology in secondary school mathematics and science supports students’ cognitive learning outcomes (i.e., better acquisition of conceptual and procedural knowledge of the content), yet the effectiveness of interventions varies largely and is dependent on how digital media is implemented in classrooms (Hillmayr et al., 2020).

When considering not only cognitive learning outcomes, but also motivational and emotional learning outcomes, empirical results also support the hypothesis that technology-enriched classroom instruction is beneficial for students’ motivation and attitudes toward the subjects learned (e.g., Özmen, 2008; Aliasgari et al., 2010; Rahman et al., 2014; and see Higgins et al., 2019 for an overview). Recent meta-analyses revealed that the effectiveness of interventions on motivation and attitudes depends considerably on the specific conditions of the implementation of digital media into mathematics classrooms (Higgins et al., 2019).

These results are in agreement with the main argument of the media debate (Clark, 1994; Kozma, 1994)—that is, not the mere medium has an effect, but its design features and its implementation. In fact, bringing together these two recent metanalytical studies (Higgins et al., 2019; Hillmayr et al., 2020), it becomes apparent that effects of implementing digital media into classrooms moderate both, cognitive and non-cognitive learning outcomes.

However, up to now, only little is known about how to explain these effects. To bring the two—i.e., effects on cognitive and non-cognitive learning outcomes—together, a framework that describes how motivation and action interact seems necessary (Kanfer and Ackerman, 1989). As previous studies rarely used a holistic approach to combine motivational and emotional prerequisites, as well as egagement and performance outcomes in one model, we do not know yet how this overall association works when students learn with digital media. Hence, the goal of the present study is to better understand the role of motivation and emotion in learning with digital media, and to address the gap of research on how motivational, emotional, and behavioral aspects interact in these learning settings. This has been identified as a sine qua non for research on digital learning (Hillmayr et al., 2020).

We suggest that the general model for determinants and course of motivated action as product of person and situation (Figure 1, Heckhausen and Heckhausen, 2018; see also Blum et al., 2018; Sternberg, 2019) can be utilized successfully to explain the broad variety of positive effects of digital media when learning mathematics. This approach argues that students’ action arises as product of situational (i.e., instructional design features of an interactive electronic textbook to learn basic fraction concepts) and individual factors (i.e., domain-specific motivational and emotional orientations). Our hypothesis is that person × situation results in individual forms of emotional and behavioral engagement (that describes students’ action while learning), which in turn predict achievement after tuition (Figure 1). In particular, this approach considers individual prerequisites as one relevant predictor of learning success (see also the “Aptitude-Treatment Interaction approach to skill acquisition” by Kanfer and Ackerman, 1989; and examples of its implementation in mathematics classrooms in Bakri et al., 2020; Maskur et al., 2020).

FIGURE 1

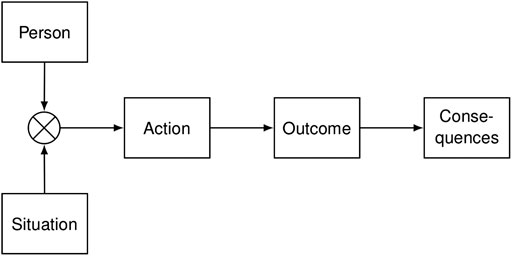
FIGURE 1. General model for determinants and course of motivated action as product of person and situation (Heckhausen and Heckhausen, 2018). In the present study regarding learning mathematics, we operationalize person as motivational and emotional orientations (i.e., mathematics anxiety, self-concept, and enjoyment) in the situation of working with an interactive and electronic textbook on fractions. Action encompasses measures that aim to describe if and how students make use of the learning opportunities offered in the electronic textbook—conceptualized as both, motivational-emotional engagement described by students’ states (i.e., intrinsic motivation, situational interest, perceived competence and autonomy support, and perceived demand), and behavioral engagement derived from process data capturing student’s interactions with the e-textbook (i.e., count and time measures). The result is measured as the cognitive learning outcome in a written posttest (i.e., conceptual and procedural knowledge of fractions). Extrinsic consequences do not lie within the scope of the present study.

In the following paragraphs, we describe in detail our operationalization of situational and personal factors—such as motivation, emotion, and behavior—relevant for learning mathematics in general and with digital media in particular. By integrating these factors into the above-mentioned model (Figure 1) we suggest a holistic model to describe the process and the outcome of learning with digital media. Drawing on that, we investigated the relationship between students‘ domain-specific motivational and emotional orientations, and their emotional and behavioral engagement while learning mathematics with digital media in classrooms. For that, we utilized an electronic textbook on fractions, which has already proven successful in authentic learning scenarios (Reinhold et al., 2020a). In this article, we report a case study with 27 students from one sixth-grade classroom, learning basic fraction concepts with this electronic textbook (e-textbook). The goal of this explorative study is to evaluate whether the holistic model for determinants and course of motivated action as product of person and situation is suitable to describe students’ individual learning in technology-supported classroom scenarios.

Situational Factors: Interactive Electronic Textbooks

One of the most used learning materials in schools are textbooks (Fan et al., 2018), which are starting to be developed digitally—offering specific ways to tailor mathematics instruction to individual students’ needs, to embed assessment and reporting, and to manage classroom activities (Pepin et al., 2017). Interactive e-textbooks can be classified as Digital Curriculum Resources (DCR). These are “specifically organized systems of digital resources in electronic formats that articulate a scope and sequence of curricular content” (Pepin et al., 2017, 647). From a mathematics education point of view, the question of how instructional material can be designed and technologically implemented is important for fostering students‘ learning (Reinhold et al., 2020a).

From the perspective of instructional design research, the cognitive theory of multimedia learning (Mayer, 2014) provides a broad framework describing the potential of interactive electronic textbooks. They can consist of multimedia content combining texts and pictures (Wilson et al., 2002; Lew, 2016, p. 106; Yerushalmy, 2016; Sheen and Luximon, 2017; Usiskin, 2018), and they can embed interactive learning contents like, for instance, dynamic representations (Choppin et al., 2014; Yerushalmy, 2014; Lew, 2016; Yerushalmy, 2016).

Moreover, interactive e-textbooks can support teachers with implementing individualized learning during classroom instruction. Even in large and heterogeneous learning groups, e-textbooks offer the opportunity to adapt to the learner’s prior knowledge by adjusting task difficulty (Leutner, 2002; Leutner, 2004; Yerushalmy, 2014; Usiskin, 2018). In addition, they can offer scaffolds for aiding problem solving processes that can be accessed autonomously (Hoch et al., 2018b; Reinhold et al., 2020a), and they can embed immediate individualized feedback on students' solution attempts (Embong et al., 2012; Choppin et al., 2014; Lew, 2016).

Through these aspects of instructional design and individualization, we consider e-textbooks (and digital learning tools, in general) to also induce a positive motivational-emotional mindset—and thereby lead to higher classroom engagement that may influence learning positively. However, these factors have received substantially less attention in previous research on technology-enhanced learning than cognitive aspects (e.g., Hillmayr et al., 2020).

Individual Factors: Motivational and Emotional Orientations

Motivational and emotional orientations form a common operationalization of rather stable mathematics-related affects (McLeod, 1989; McLeod, 1992; Schukajlow et al., 2012; Schiepe-Tiska and Schmidtner, 2013; Hannula et al., 2016). Important aspects are mathematics-related anxiety, self-concept, and enjoyment—as distinguishable manifestations of an inseparable interplay (Zan et al., 2006; Dowker et al., 2016). These facets can explain individual performance differences in mathematics (Hembree, 1990; Ma and Kishor, 1997; Núñez-Peña et al., 2013; Stankov and Lee, 2014; Lai et al., 2015; Hannula et al., 2016; Schukajlow et al., 2017). Moreover, they influence decisions for or against mathematical and scientific education (Ma, 1999; Köller et al., 2000; Pekrun et al., 2007; Dowker et al., 2016) and effect decisions to choose a profession that may require a high proportion of mathematical knowledge (Ashcraft and Moore, 2009).

Mathematics-related anxiety is a feeling of concern that occurs when working on mathematical problems (Richardson and Suinn, 1972). In general, mathematics related anxiety has negative effects on learning mathematics as well as applying mathematics (Hembree, 1990; Ma, 1999; Ashcraft and Moore, 2009; Dowker et al., 2016). For instance, Ashcraft and Kirk (2001) showed that anxious students had access to fewer cognitive resources in a mental arithmetic task than less anxious students with comparable mathematical abilities. In addition to an influence on working memory capacity (Ashcraft and Ridley, 2005), Maloney et al. (2011) could show that intuitive notions of numerical magnitude are also worsened by mathematics anxiety. In addition, mathematics-related anxiety can negatively influence mathematical thought processes and performance in test situations through physiological reactions—such as stress, restlessness or distracting thoughts (Strohmaier et al., 2020). In a meta-analysis, Ma (1999) found that mathematics anxiety and mathematics performance are negatively correlated, i.e., lower mathematics anxiety is associated with better mathematics performance, and vice versa—with the latter effect being stable across gender groups, class levels, and all ethnic groups studied (see also Namkung et al., 2019).

Mathematics-related self-concept describes a student’s self-perception regarding his or her mathematical competence. In general, it develops through both experience with and interpretations of the individual’s environment (Shavelson et al., 1976; Marsh et al., 2012). In school contexts, the mathematics-related self-concept arises mainly through social comparisons with other students and through comparisons of one’s own performance in other subjects. Self-concept is related to performance, the development of interests, course choices, and well-being at school (Köller et al., 2006; Marsh and Martin, 2011; Möller et al., 2011), which makes the development of a realistic self-concept an educational goal itself (Schiepe-Tiska and Schmidtner, 2013).

Enjoyment in mathematics is a positive emotional orientation to deal with certain mathematical contents. According to control-value theory, it can be conceptualized as an achievement-related emotion that is important for learning (Pekrun, 2006; Schukajlow and Rakoczy, 2016) and—as such—it is considered a desirable goal of education (Kunter, 2005).

There is an overall and broad consensus that motivational and emotional oriantations strongly influence learning in general and mathematics in particular. Yet, up to our knowledge there are no specific studies of how they influence learning mathematics with digital media. Following the holistic model described above (Figure 1) we argue that they should be taken into account when designing and evaluating any learning environment and especially when focusing on digital learning environments, which bear the potential to offer particularly motivating learning scenarios.

Motivation and Behavior: Students’ Classroom Engagement

Students’ classroom engagement is a multifaceted process variable, important for academic outcomes in general (Appleton et al., 2006; Skinner et al., 2008), and achievement in mathematics in particular (Singh et al., 2002; Barkatsas et al., 2009; Fung et al., 2018). Engagement consists of a behavioral, emotional, and cognitive dimension (Fredricks et al., 2004; Fredricks and McColskey, 2012). The present study focuses on emotional and behavioral engagement, which are explained in the following.

Emotional Engagement

Commonly agreed-upon conceptualizations of emotional engagement are closely related to “students’ affective reactions in the classroom” (Fredricks et al., 2004, 63), aiming at a description of the “emotional quality of children’s involvement in initiating and carrying our learning activities” (Skinner and Belmont, 1993, 572). We conceptualize such motivational-emotional engagement as a combination of different states, following the ideas of expectancy-value theory of achievement motivation (Eccles et al., 1983; Wigfield and Eccles, 2000) and self-determination theory (Ryan and Deci, 2000; Deci and Ryan, 2012).

Within the field of educational psychology, intrinsic motivation is understood as a students’ desire to engage in learning (mathematics) with no present external rewards but the rewards being “inherent in the activity. Even though there may be secondary gains, the primary motivators are the spontaneous, internal experiences that accompany the behavior” (Deci and Ryan, 1985, p. 11; see also; Renninger, 2000; Krapp, 2005). Such activity-inherent rewards can be enjoyment, or the feeling of the task being important for oneself, which offers a commonly agreed-upon conceptualization of intrinsic motivation in mathematics education (Middleton and Spanias, 1999; Hannula et al., 2016; Schukajlow et al., 2017). Intrinsic motivation is related to an individuals’ perceived competence and autonomy (Ryan and Deci, 2000; Deci and Ryan, 2012).

Perceived competence support is a students’ awareness of if and how they are informed about their own competence in mathematics during classroom teaching (Ryan and Deci, 2000; Deci and Ryan, 2012). Consequently, perceived autonomy support can be conceptualized as students’ awareness of if and how their need for autonomy (Ryan and Deci, 2000; Deci and Ryan, 2012) is addressed during the learning of mathematics in school. We consider both facets elements of students’ situation-specific motivational-emotional engagement: They describe two basic needs, which are important for classroom practice, differ between individual students, and can be altered through specific situations during tuition (Deci, 1971; Deci and Ryan, 1985; Skinner and Belmont, 1993).

Situational mathematical interest can support learning processes (Hidi and Renninger, 2006) and has long-term positive effects on the willingness to engage in mathematics (Pekrun et al., 2006). It may serve as the foundation for the development of a more general domain specific interest (Krapp, 2002; Hidi and Renninger, 2006). In addition, research has shown a positive correlation between mathematics achievement and mathematics-related interest (Köller et al., 2001) on the one hand and task-related interest on the other hand (Schukajlow and Krug, 2014). Yet, it is noteworthy that results in the field of mathematics education vary between studies—with different operationalizations of mathematics-related interest being one possible explanation (Ufer et al., 2017). Situational interest is caused by external factors (Eccles et al., 1983; Hidi, 1990; Krapp and Prenzel, 2011), for example a mathematical task, or specific interactive elements or scaffolds of an e-textbook, as described above.

We utilize students’ perceived demand as an operationalization of the negative value cost (Eccles et al., 1983), that is negative aspects of engaging in particular classroom activities or tasks while learning mathematics in school. Such perceived demand can be influenced by motivational and emotional orientations, for example “performance anxiety and fear of both failure and success” (Wigfield and Eccles, 2000, p. 280) and students’ realization of how much effort is needed to complete the task successfully. The latter aspect is closely related to cognitive overload, which is well-discussed in the field of mathematics education (Tarmizi and Sweller, 1988; Ayres, 2001, 2006) and, for instance, is one main reason for systematic errors in solving algebraic equations (Ayres, 2001).

As mentioned above, there is empirical evidence that digital media bear potential to support students’ emotional engagement (Özmen, 2008; Aliasgari et al., 2010; Rahman et al., 2014; Higgins et al., 2019). Yet, up to our knowledge it is not clear how motivational orientations relate to emotional engagement in technology-supported learning scenarios and whether emotional engagement can explain positive effects of learning with digital media.

Behavioral Engagement

Behavioral engagement refers to the extent to which students are involved in the learning process actively, as indicated by observable behaviors (e.g., time on task, concentration, effort, participation; see Fredricks et al., 2004). Behavioral engagement is considered an important aspect for learning in school contexts: It can explain individual differences in achievement after classroom instruction and varies considerably between students (Kelly, 2007; Jurik et al., 2013, 2014; Clarke et al., 2016; Böheim et al., 2020). Results of empirical studies suggest that positive behavioral engagement is linked to positive academic outcomes (Christenson et al., 2012; Sedova et al., 2019), while negative behavioral engagement—for example inattentive, withdrawn, or disruptive behaviors—is associated with low academic outcomes (Finn et al., 1995).

In technology-enriched learning scenarios, novel forms of assessing behavioral engagement, which are not viable in scenarios without digital media, emerge. Here, process data (or logfile data) referring to students’ interactions with e-textbooks, educational technology, or software in general (Goldhammer et al., 2017; Hoch et al., 2018b) offer a unique opportunity to assess behavioral engagement anonymously, objectively, unobtrusively, and during the actual learning process (Henrie et al., 2015). In such scenarios, quantitative observational measures are commonly used as operationalizations for behavioral engagement, which tend to be positively correlated to learning outcomes (Junco and Clem, 2015; Hew et al., 2016; Huang et al., 2019). They encompass time and count measures (Henrie et al., 2015; Hoch et al., 2018b).

We argue that the conceptual idea of time measures for assessing behavioral engagement can be rooted down to models for the utilization-of-learning-opportunities (Helmke, 2010; Seidel, 2014) in educational psychology (Hoch et al., 2018b). Within these frameworks, classroom instruction is thought of as an offered learning opportunity, provided by the teacher (Helmke, 2010; Seidel, 2014). Active learning time is one agreed-upon operationalization for how students make use of such learning opportunities (Winfield, 1987; Helmke, 2010). Yet, recent studies suggest that the anticipated relation of higher active learning time and better learning outcomes may not be that simple or direct (Hoch, 2021; Hattie, 2009; Goldhammer et al., 2014; Goldhammer et al., 2017; Kovanović et al., 2015; Hoch et al., 2018b). This opens up questions for potential interactions or moderations, such as prior knowledge as well as the need for additional measures of behavioral engagement.

A second category of process data derived from technology-enriched learning environments are count measures. They can rather easily be administered by “counting how many actions students take within the system” (Hoch et al., 2018b, 843). They can encompass, for instance, the number of postings in an online forum (Henrie et al., 2015), the number of completed tasks in a learning environment (Hew et al., 2016; Huang et al., 2019), or how often students ask for assistance autonomously (Hoch, 2021; Feng et al., 2006; Zheng et al., 2019). Although research suggests a tendency of more frequent task behavior (i.e., higher scores in such count measures) being positively related to higher learning outcomes (Henrie et al., 2015; Junco and Clem, 2015; Hew et al., 2016; Huang et al., 2019), such relation—again—may not be that simple or direct as anticipated, as individual characteristics, such as prior knowledge, may moderate this effect (Hoch, 2021).

The Present Study

We investigated the relationship between students’ domain-specific motivational and emotional orientations and their emotional and behavioral classroom engagement while working with an e-textbook on fractions. We argue that emotional and behavioral engagement may predict cognitive learning outcomes when learning with e-textbooks: The design of this study followed the general model for determinants and course of motivated action as product of person and situation (Figure 1, see also Heckhausen and Heckhausen, 2018). In this context, we considered individualized learning with the e-textbook in mathematics classrooms the situation and mathematics-related motivational and emotional orientations as characteristics of the person. We assume students’ action (i.e., if and how students make use of the learning opportunities offered in the e-textbook, operationalized as behavioral and emotional engagement) to be influenced by person × situation which in turn leads to different cognitive learning outcome after tuition as a result.

To investigate this relationship, we utilized an electronic textbook on fractions, which has already proven successful in authentic learning scenarios in a large cluster-randomized controlled trial with 1,005 students in grade 6 (Reinhold et al., 2020a). For the purpose of this case study, we assumed that this electronic textbook offers a suitable way of introducing fractions in mathematics classrooms.

In this study, emotional engagement was assessed after students engaged in learning fractions. For that, we utilized self-reports as one commonly used and rather easy to administer measurement for assessing engagement (Fredricks and McColskey, 2012; Wiebe et al., 2014; Henrie et al., 2015). In addition, we utilized unobtrusively collected, machine-coded, and objective process data measures, indicating students’ behavioral engagement while working with an e-textbook on basic fraction concepts during mathematics classroom instruction.

As we conducted a case-study with one classroom, we aim at deriving hypotheses for future research—focusing on the following research questions:

RQ1: What is the relationship between students’ motivational and emotional orientation and their classroom engagement in mathematics while working with an electronic textbook?

For RQ1, we investigated correlations between motivational and emotional orientations (i.e., mathematics-related anxiety, self-concept, and enjoyment) and emotional engagement (i.e., intrinsic motivation, competence and autonomy support, situational interest, and perceived demand), as well as behavioral engagement (i.e., count and time measures reflecting e-textbook-use derived from process data). We assumed enjoyment and self-concept to be positively correlated, as well as anxiety to be negatively correlated with preferable emotional and behavioral engagement.

RQ2: Are emotional and behavioral engagement while working with an electronic textbook unique predictors of students’ cognitive learning outcomes?

For RQ2, we predicted that gains in mathematics knowledge about fractions was related to students' emotional and behavioral engagement. We expected to derive hypotheses about which student characteristics should be considered beneficial for learning in e-textbook-scenarios, assuming emotional and behavioral engagement two distinct and desirable predictors for achievement—with the latter one bearing the potential to interact with prior knowledge.

Methods

Sample

Participants were 27 sixth-grade students (14 girls and 13 boys) from one German Gymnasium classroom. The Gymnasium is the highest public secondary school within the three-track secondary school system in Bavaria, Germany, with students demonstrating above-average grades at the end of primary school. In the present curriculum, fractions are taught in grade six for the first time in Bavaria.

Material

We used the e-textbook from the ALICE:fractions project (Reinhold et al., 2020a), which offers a beneficial way of introducing fractions (i.e., curriculum) based on theoretically established instructional design principles for suitable digital learning offers (i.e., implementation).

The curriculum to teach basic fraction concepts covers i. the part-whole concept with one and many wholes (Behr et al., 1983); ii. fraction magnitude (Reinhold et al., 2020b); iii. expanding and simplifying fractions, i.e., divisions becoming more refined or coarser (Prediger, 2006; Lamon, 2012); iv. fractions on the number line (Bright et al., 1988); v. fractions representing more than one whole and mixed numbers (Padberg and Wartha, 2017); and vi. the comparison of the size of two fractions (Reinhold et al., 2020b). This curriculum focuses on conceptual rather than procedural knowledge of fractions—allowing for transitions between a variety of non-symbolic and symbolic representations of fractions, providing intuitive pathways to core fraction concepts, and making sure students explore non-symbolic fractions before more formal representations (see Reinhold, 2019; Reinhold et al., 2020a for a more detailed analysis of the content with regards to evidence-based mathematics instruction).

The implementation of the material as an e-textbook on iPads focused on technology-enhanced learning. Several aspects guided us in developing the e-textbook: i. making use of touchscreen technology to achieve congruent user interactions with the e-textbook (Black et al., 2012); ii. lowering students (actual and perceived) demand and supporting their perceived competence while learning fractions through adaptive task difficulty (Kickmeier-Rust and Albert, 2010) and individual exploratory feedback (Hattie and Timperley, 2007); and iii. yielding opportunities for autonomous learning within the given structured classroom scenarios by implementing self-regulated graded assistance providing hints for solution steps during mathematical problem solving (Paas, 1992). The e-textbook was designed within the iBooks Author framework, utilizing CindyJS (von Gagern et al., 2016) as the programming environment for all interactive content, i.e., a total of 92 HTML5 widgets (see Hoch, 2021; Hoch et al., 2018b; Reinhold et al., 2020a for a more detailed overview of the technological implementation). The e-textbook is available online under a CC-BY 4.0 license (Hoch et al., 2018a)—with sample widgets demonstrating key features implemented in the e-textbook shown in Figure 2.

FIGURE 2

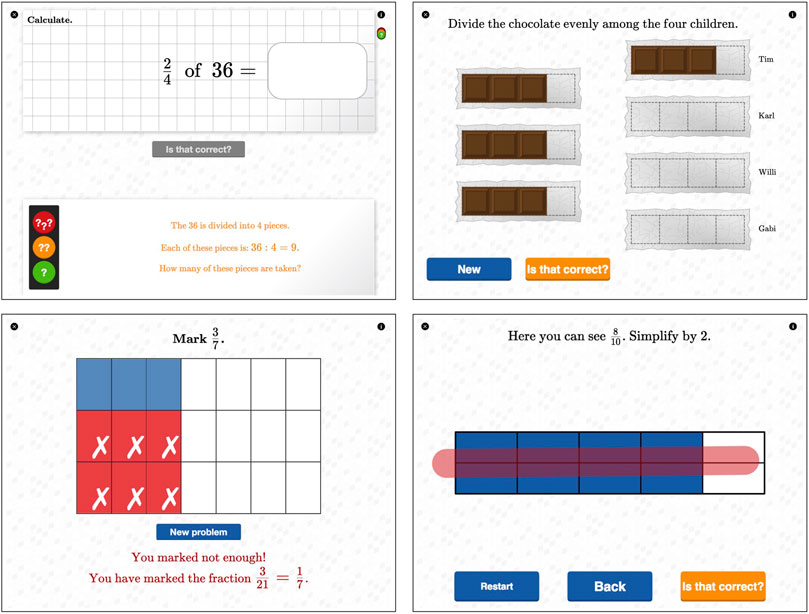
FIGURE 2. Sample widgets from the e-textbook “Fractions. Getting in touch with rational numbers” by Hoch et al. (2018a), demonstrating four key features implemented. Note. The screenshots show: self-regulated graded assistance providing hints for solution steps for solving the problem “2/4 of 36” (above, left); interactive diagrams offering opportunities for individual explorations of new content, here equal sharing of three chocolate bars with four kids (above, right); individual exploratory feedback with regards to the students wrong solution and the correct solution in marking 3/7 in a rectangular diagram (below, left); and utilizing congruent gestures as user interaction on the touchscreen by vanishing the middle line to coarsen the given partition in 8/10 (below, right).

Instruments

We utilized paper-pencil tests, paper-based self-reports, and measures derived from process data of the e-textbook. We describe the scales in detail within the next paragraphs and present an overview of the scales in Table 1.

TABLE 1

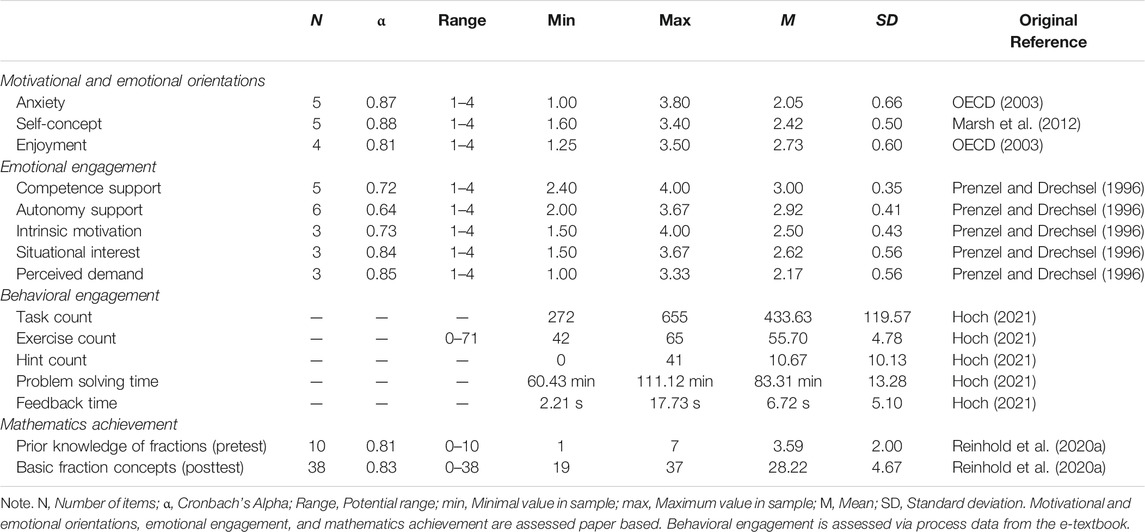
TABLE 1. Instruments used to operationalize motivational and emotional orientations, emotional engagement, and behavioral engagement.

Motivational and Emotional Orientations

We operationalized students’ motivational and emotional orientations in mathematics with self-reports asking students about their mathematics-related anxiety, self-concept, and enjoyment. We used 4-point Likert scales, with 1 = the least acceptance and 4 = the highest acceptance of a given statement.

Mathematics-related anxiety was assessed using the PISA ANXMAT scale (5 items, Cronbach’s α = 0.87). The scale consisted of statements like “I worry about getting bad grades in math” (OECD, 2003).

Mathematics-related self-concept was assessed using the PISA SCMAT scale (5 items, Cronbach’s α = 0.88). One sample item is “I have always been convinced that mathematics is one of my best subjects” (Marsh et al., 2012).

Enjoyment of mathematics was assessed using the PISA INTMAT scale (4 items, Cronbach’s α = 0.81). The scale consisted of items like “I am looking forward to my mathematics lessons” (OECD, 2003).

Emotional Engagement

We operationalized students’ emotional engagement with self-reports on their perceived intrinsic motivation, competence and autonomy support, situational interest, and perceived demand. All scales were adopted from Prenzel and Drechsel (1996). We used 4-point Likert scales, with 1 = the least acceptance and 4 = the highest acceptance of a given statement.

Students intrinsic motivation was assessed as students’ desire to engage in learning mathematics using the e-textbook with no present external rewards (3 items, Cronbach’s α = 0.85). A sample item is “I really get into it in mathematics lessons”.

Students’ perceived competence support encompassed the awareness for if and how they are informed about their own competence in mathematics during their work with the e-textbook (5 items, Cronbach’s α = 0.72). One sample item is “During mathematics lessons I am informed about my individual progress”.

Perceived autonomy support was assessed as the awareness for if and how students’ need for autonomy is addressed during learning with the e-textbook (6 items, Cronbach’s α = 0.64). The scale consisted of items like “During my mathematics lessons I have the opportunity to try out new things myself”.

Their situational interest encompassed interest in the present mathematics lessons (3 items, Cronbach’s α = 0.73). The scale consisted of items like “In my mathematics class I am curious”.

Perceived demand was operationalized as negative aspects of engaging in particular mathematics lessons, closely related to a perceived cognitive overload while learning mathematics (3 items, Cronbach’s α = 0.84). One sample item is “In mathematics class everything just happens too fast for me”.

Behavioral Engagement

We operationalized behavioral engagement with five different scales derived from process data of the e-textbook. We draw on a variety of count and time measures, as proposed by Hoch (2021). The scales were selected from the literature with the goal of covering the material key features. In particular, engagement with interactive exercises is indicated by two count measures, task count (the total amount of tasks solved by each student as in Feng et al., 2006; Huang et al., 2019) and exercise count (the number of different exercises each student accessed as in Zheng et al., 2019), as well as a time measure, the total problem solving time (for all tasks, e.g., Feng et al., 2006; Zheng et al., 2019). Usage of the material’s hint system is measured by hint count (the total number of requested hints, e.g., Anozie and Junker, 2006; Feng et al., 2006; Zheng et al., 2019). How students made use of the offered adaptive feedback is represented by their feedback time (mean time in feedback phases, e.g., Anozie and Junker, 2006; Ayers and Junker, 2008).

Mathematics Achievement

In order to control for effects of prior knowledge of fractions not acquired at school, a pretest (10 items, Cronbach’s α = 0.81) was conducted before the intervention. The aim of this instrument was to assess preconceptions of fractions, which was not acquired as formal knowledge in schools, since students were not taught fractions at school before the intervention. That is why the pretest focused on every-day fractions (e.g., 1/2, or 3/4) and contained items adapted from an existing German test for preconceptions of fractions (Padberg, 2002). A detailed description of the pretest items can be found in Reinhold et al. (2020a). The complete German test booklet is shown in Reinhold (2019).

To measure knowledge of basic fraction concepts after the intervention, a posttest (38 items, Cronbach’s α = 0.83) was conducted using a second test instrument. Here, items focused on the part-whole concept, expanding and simplifying fractions, and comparing fractions. In this test, both procedural knowledge (i.e., handling fractions in symbolical representation, no transition between representations necessary) and conceptual knowledge (i.e., operating with iconic representations of fractions, or transitions between non-symbolic and symbolic representations) were assessed. For the purpose of this study, the instrument is utilized as a unidimensional measure for the cognitive learning outcome of the intervention. A detailed description of the posttest items can be found in Reinhold et al. (2020a). Again, the complete German test booklet is shown in Reinhold (2019).

Procedure

Intervention and data collection were conducted at the beginning of the school year 2019/2020 with the approval of the Bavarian Ministry of Education, the school’s principal, and the class’s mathematics teacher. Students and their parents gave informed consent to take part in the study on a voluntary basis and without any remuneration.

During the intervention, students worked with the described e-textbook on iPads. As behavioral engagement was derived from the process data logged by the iPad, we made sure that each student worked on the same iPad in each lesson. For that, the iPads were numbered, and the iPad numbers were allocated to the students by their teacher. The mathematics teacher was advised to use the e-textbook for at least half of their instruction time, to make use of the given introductions for each topic and to let his students study with the interactive exercises. For that, the teacher was handed a detailed booklet with information about the educational objectives, and how to implement the e-textbook into his classroom. This procedure is identical to the Scaffolded Curriculum group, reported in Reinhold et al. (2020a)—yet the sample reported here was not part of the cited study.

The intervention was conducted during regular classroom instruction time and covered a total of sixteen consecutive 45-minute-lessons in four weeks. Right before the first lesson of the intervention, the pretest on prior knowledge of fractions (15 min) was conducted as a paper-pencil test and domain-specific motivational and emotional orientations (10 min) were assessed with paper-based self-reports. During the 16 lessons of the intervention, the e-textbook anonymously recorded process data of all relevant student-technology-interactions that are necessary to derive the five measures that were used to operationalize behavioral engagement. The teacher did not have access to this data at any time during or after the intervention, and students and their parents were informed about this kind of data collection. Immediately after the last lesson of the intervention, a posttest on basic fraction concepts (55 min) was conducted as a paper-pencil test, and emotional engagement (10 min) was assessed with paper-based self-reports.

Data and Statistical Analysis

Regarding process data, we logged a total of 11,451 unique observations. Each process data point contained information about the logging interactive exercise, the specific task, and start and end times for the activity (task solution or hint request). Logs were saved on the iPads for the duration of the intervention. This approach enabled a totally offline working environment that was necessary since no internet access could be guaranteed in classroom and due to the prevailing data policies. All data were transmitted to a university server after data collection and parsed into a relational database (see also Hoch, 2021; Hoch et al., 2018b for a more detailed description of the data collection and storage).

Raw logs were preprocessed in order to calculate the five process measures as described in Hoch (Hoch, 2021; see also Hoch et al., 2018b). In particular, problem solving time was preprocessed by capping the logarithm of each time at the mean plus two standard deviations of the time for all solutions on the particular exercise (Goldhammer et al., 2014). Students’ time in feedback phases was derived by calculating the time between two consecutive tasks of the same interactive exercises and afterward preprocessed just as problem solving time.

For answering RQ1, we utilized Pearson correlations between measures of motivational and emotional orientations, and emotional engagement, or respectively behavioral engagement.

For answering RQ2, we conducted a two-step analytical approach. First, we reduced the dimensions of emotional and behavioral engagement to one dimension in each case, using Principal Component Analysis (PCA). For the prediction of cognitive learning outcomes, we only used the first principal components (PC1) of emotional and behavioral engagement as predictor variables. Second, we utilized Generalized Linear Mixed Models (GLMM), predicting the likelihood for students giving a correct answer in a posttest item on fraction concepts (for a detailed overview of the benefits of using LMMs instead of regression analysis or ANOVA, see Brauer and Curtin, 2018). All models allowed for items and students random intercepts. The prior knowledge model does only contain a predicting fixed effect for prior knowledge (Pretest outcome). The full model contains additional fixed effects for emotional engagement (PC1 of intrinsic motivation, competence and autonomy support, situational interest, and perceived demand), behavioral engagement (PC1 of task count, exercise count, hint count, problem solving time, and feedback time), as well as the interaction of behavioral engagement and prior knowledge. All metric predictors (i.e., prior knowledge, emotional engagement, and behavioral engagement) were standardized at the sample. Therefore, the reported log odds represent the unique change in the likelihood for a correct answer when the specific predictor is one SD above the sample mean. Of specific interest for the interpretation of the results is the Proportion Change in Variance (PCV) on the student random intercept that illustrates how including specific predictors into the model reduce variance components on the student level that are assumed random in the prior knowledge model (Nakagawa and Schielzeth, 2013). This can be used to estimate explained variance in GLMMs.

Due to an error in the data collection on the iPad of one student, randomly missing process data for this student had to be partly imputed. For that, we proceeded by the following rationale. First, we reduced process data in the full sample to those interactive exercises that were logged for all students. Second, we calculated the five process measures for all 27 students on this reduced dataset. Third, we identified the student that showed a pattern on all five process measures most similar to the one student with missing process data. We chose the student showing the lowest sum of absolute deviations in the five process measures when compared to the student with missing data. Forth, on all interactive exercises with missing data, we imputed the data from this best match. Following this procedure, we imputed 257 log entries, which is 2.2% of the total process data used in this study, and 49.3% of the process data for the student with data missing.

All analyses were conducted in R (R Core Team, 2008). Graphs were constructed using the ggplot2 package (Wickham and Chang, 2016) and the GLMMs were calculated using the lme4 package (Bates et al., 2015).

Results

Descriptive Analyses

We assessed mathematics-related motivational and emotional orientations with self-reports on 4-point Likert-scales before the intervention. Students reported an anxiety of M = 2.05 (SD = 0.66). Their self-concept was M = 2.42 (SD = 0.50), and their enjoyment was M = 2.73 (SD = 0.60), indicating substantial variance in motivational and emotional orientations in the sample (see Table 1).

Similarly, emotional engagement was again assessed with self-reports on 4-point Likert-scales after the intervention. Students reported an intrinsic motivation while learning fractions with the e-textbook of M = 2.50 (SD = 0.43). There perceived competence support was M = 3.00 (SD = 0.35), and their perceived autonomy support was M = 2.92 (SD = 0.41) during the intervention. Their situational interest was M = 2.62 (SD = 0.56). They reported a perceived demand of M = 2.17 (SD = 0.56) while learning fractions with the e-textbook. Considering these values and the true range of the scales (see Table 1), we concluded that students showed substantially different emotional engagement regarding learning fractions with the e-textbook.

We assessed behavioral engagement via unobtrusively collected, machine-coded, and objective time and count measures while working with the e-textbook during mathematics classroom instruction. Students engaged in an average of 433.63 (SD = 119.57) interactive tasks during the four-week intervention. Their classroom work covered M = 55.70 (SD = 4.78) exercises from the e-textbook, which is about 78% of all exercises provided. They requested graded assistance M = 10.67 (SD = 10.13) times, which was possible in 15 interactive exercises in the e-textbook. Their total time spent on tasks was on average 83.31 min (SD = 13.28), and they viewed the adaptive feedback for about 6.72 s (SD = 5.10) after each task. With a focus on task count, exercise count and problem solving time—bearing in mind both the mean values, the standard deviations, and the true range of these scales (see Table 1)—we conclude that the use of the e-textbook during mathematics instruction differed largely between students. This is noteworthy, as all students in this sample came from the same classroom, were instructed by the same teacher, and therefore shared the same general classroom practice during the intervention.

Regarding their mathematics achievement, students solved on average 35.9% (SD = 20.0) of items in the pretest (i.e., prior knowledge of fractions) correct. During the four-week fractions intervention, they solved on average 73.8% (SD = 8.0) of all tasks they engaged in during their work with the e-textbook correct. On the posttest, they solved on average 74.3% (SD = 12.3) of all items in the posttest correct.

Students’ Motivational and Emotional Orientations and Their Classroom Engagement

The first question we asked was, how the relationship could be described between students’ motivational and emotional orientations regarding mathematics and their classroom engagement while working with an e-textbook on fractions. We assumed enjoyment and self-concept to be positively correlated, and anxiety to be negatively correlated with preferable emotional and behavioral engagement. For that, we utilized Pearson correlations between motivational and emotional orientations and emotional as well as behavioral engagement.

Emotional Engagement

Scatterplots showing Pearson correlations between motivational and emotional orientations and emotional engagement are shown in Figure 3. Given the directions of the correlations, we consider the results to be in line with our hypothesis.

FIGURE 3

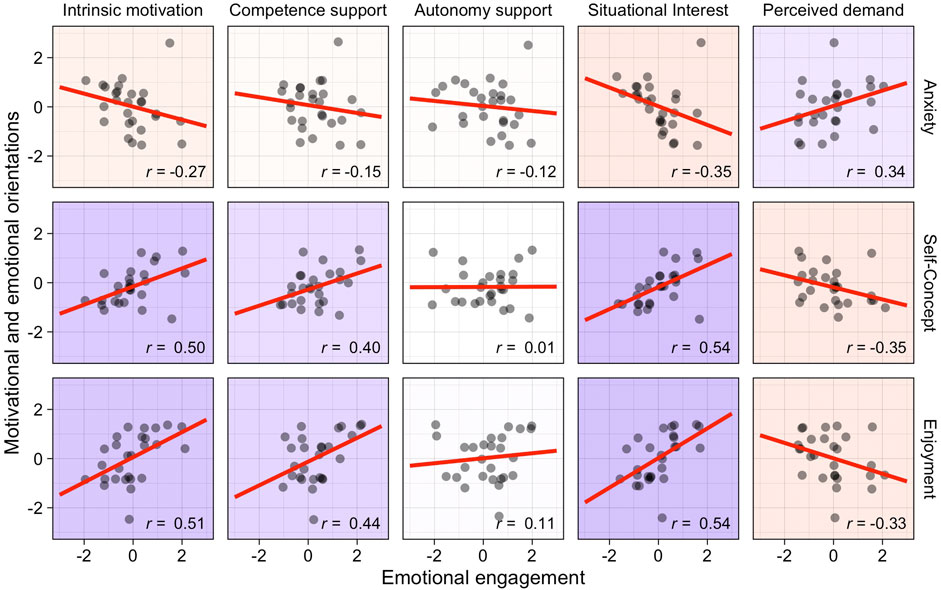
FIGURE 3. Correlations between motivational and emotional orientations (vertical) and emotional engagement (horizontal). Scales are given in standard deviations from the sample mean. Background colors indicate the direction of the correlation (red = negative, blue = positive). Correlation coefficients represent Pearson correlations. Points are jittered by up to 0.1 standard deviations to minimize overplotting.

Anxiety was negatively correlated with all four scales that operationalized preferable emotional engagement, i.e., intrinsic motivation, competence and autonomy support, and situational interest. Notably, students with higher anxiety were less intrinsically motivated, r = −0.27, and less situationally interested, r = −0.35, but perceived a higher demand, r = 0.34.

Self-concept was positively correlated with preferable emotional engagement. Students reporting a higher self-concept did perceive higher intrinsic motivation, r = 0.50, higher competence support, r = 0.40, and higher situational interest, r = 0.54, but lower perceived demand, r = −35.

For the relation between enjoyment and emotional engagement, a similar pattern as reported for self-concept was found. Students enjoying mathematics were more intrinsically motivated, r = 0.51, reported higher competence support, r = 0.44, and higher situational interest, r = 0.54—and perceived learning fractions with the e-textbook less demanding, r = −0.33.

These results show that—in line with our assumption and previous research on motivation and emotion in mathematics education—students’ domain-specific motivational and emotional orientations were closely related to their situation-specific emotional engagement during the learning of fractions with the e-textbook. Yet, it is noteworthy that neither anxiety, nor self-concept, nor enjoyment showed a substantial correlation with students’ perceived autonomy support—although students did differ in their perceived autonomy support during the intervention (Table 1 and Figure 3).

Behavioral Engagement

Scatterplots showing Pearson correlations between motivational and emotional orientations and behavioral engagement are shown in Figure 4. Given the directions of the correlations, we consider the results to be in line with our hypothesis.

FIGURE 4

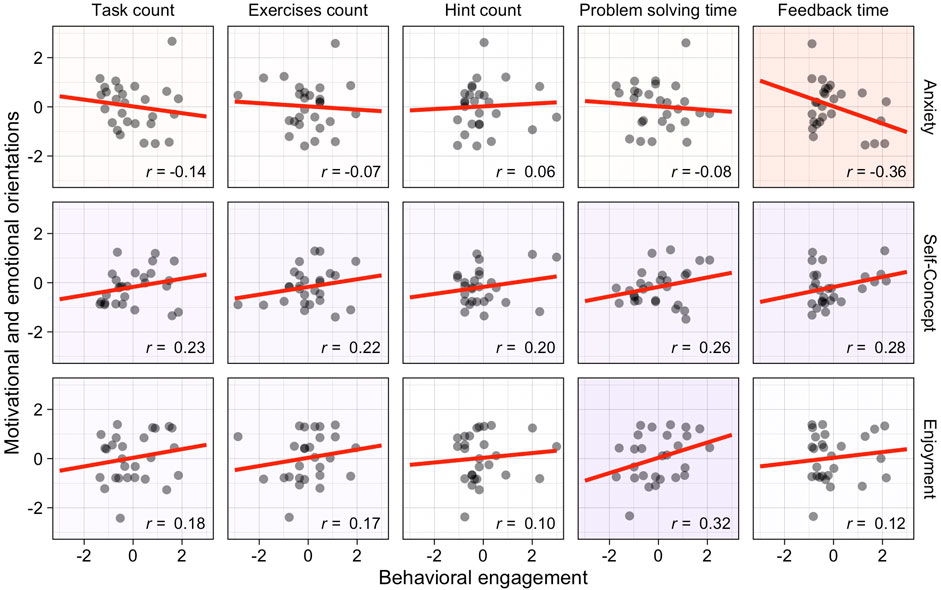
FIGURE 4. Correlations between motivational and emotional orientations (vertical) and behavioral engagement (horizontal). Scales are given in standard deviations from the sample mean. Background colors indicate the direction of the correlation (red = negative, blue = positive). Correlation coefficients represent Pearson correlations. Points are jittered by up to 0.1 standard deviations to minimize overplotting.

The one notable correlation of anxiety was the negative correlation with feedback time, r = −0.36. Students reporting higher anxiety invested less time in viewing feedback after completing tasks. All in all, anxiety was associated with non-preferable behavioral engagement (Figure 4).

Self-concept was positively correlated to all five measures of behavioral engagement, yielding the highest positive correlation with feedback time, r = 0.28, and problem solving time, r = 0.26. More confident students spent more time working on the tasks and on processing feedback, they engaged in more tasks in a larger variety of different widgets, and requested hints more often (Figure 4). Thus, we consider self-concept to be related to preferable behavioral engagement while learning fractions with the e-textbook.

Likewise, enjoyment was positively correlated with all measures of behavioral engagement, yielding the highest positive correlation with problem solving time, r = 0.32. Students reporting higher enjoyment in mathematics worked longer on the interactive tasks in the e-textbook, and tended to solve more and a larger variety of tasks (Figure 4).

The Relation Between Emotional and Behavioral Engagement and Cognitive Learning Outcomes

The second question we asked was whether emotional and behavioral engagement while working with an e-textbook can be considered unique predictors of students’ cognitive learning outcomes. We expected to derive hypotheses about which of students’ states should be considered beneficial for learning in e-textbook-scenarios—assuming emotional and behavioral engagement two distinct predictors for achievement besides prior knowledge. For that, we first reduced the dimensions of emotional and behavioral engagement (to reduce the shared variance by the specific measures of these constructs before the predictive analysis) by conducting two PCAs. Secondly, we performed GLMMs to predict achievement in the posttest by prior knowledge, emotional and behavioral engagement, and the interaction of behavioral engagement with prior knowledge.

Results of the PCAs of emotional engagement and behavioral engagement are illustrated with biplots in Figure 5. For emotional engagement, the first principal component (PC1) explained 66.3% of the total variance on all five scales. PC1 describes preferable emotional engagement—with intrinsic motivation, competence and autonomy support, as well as situational interest corresponding positively to the scale, but perceived demand corresponding negatively to the scale (Figure 5, left). Information lost when describing emotional engagement only with PC1 is largest in perceived autonomy support (Figure 5, left). Regarding the second PCA, the first principal component explained 45.5% of the total variance in students’ behavioral engagement, which was assessed with the five count and time measures derived from process data from the use of the e-textbook. Here, PC1 describes preferable behavioral engagement, with all measures contributing positively to the scale (Figure 5, right). When referring only to PC1 to describe students’ behavioral engagement, most information is lost on how long they viewed feedback after completing a task (Figure 5, right). In the following analysis, emotional and behavioral engagement are both represented by the first principal components in the corresponding PCAs (i.e., the x-axes in Figure 5).

FIGURE 5

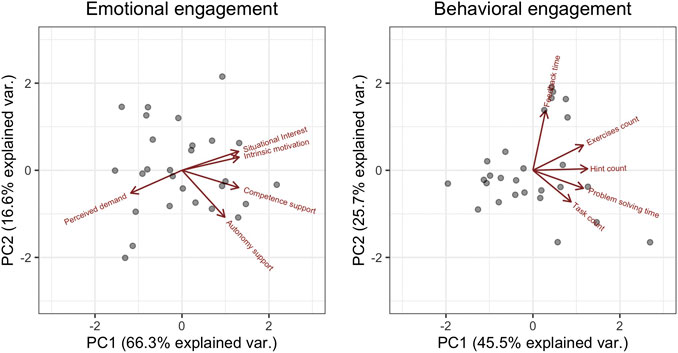
FIGURE 5. Biplots of the principal component analyses of emotional engagement (left) and behavioral engagement (right), showing the two principal components with the largest explained variance on the x- and y-axis, and the contribution of the original scales to those principal components as arrows. Scales are given in standard deviations from the sample mean. Both first principal components are used in the GLMM.

Estimates of the GLMMs, predicting the likelihood for students giving a correct answer in a posttest item on basic fraction concepts after the intervention are given in Table 2. The estimated marginal mean for a student with average prior knowledge and emotional and behavioral engagement to give a correct answer to an item of average difficulty was 79.4, 95% CI [71.7, 85.4].

TABLE 2

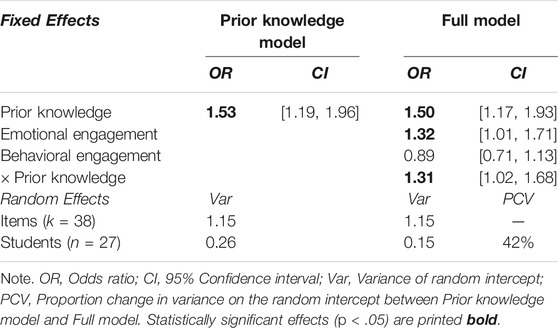
TABLE 2. Parameter estimates for the GLMMs predicting the likelihood to obtain a correct answer in posttest items on fraction concepts after the intervention.

Information about the unique effects of specific predictors can be derived from the odds ratios in the full model—with an odds ratio below one indicating a negative effect of the predictor and an odds ratio above one indicating a positive effect. Prior knowledge of fractions was the strongest significant unique predictor of achievement in the posttest. An increase in pretest achievement of one SD led to a 50% higher probability to give a correct answer in the posttest, p = 0.002 (Table 2). As expected, knowledge of everyday fractions should be considered relevant for learning fractions in school. Besides prior knowledge, emotional engagement predicted cognitive learning outcomes significantly. An increase in emotional engagement of one SD led to a 32% higher probability to give a correct answer in the posttest, p = 0.039 (Table 2). Thus, intrinsic motivation, the perception of competence and autonomy support, and situational interest while learning fractions with the e-textbook proved to be relevant for achieving learning goals—even after controlling for content-specific prior knowledge. While behavioral engagement did not predict cognitive learning outcomes significantly, p = 0.356 (Table 2), the interaction between prior knowledge and behavioral engagement was significant, OR = 1.31, p = 0.036 (Table 2). Students with higher prior knowledge did benefit more from an increased behavioral engagement in the learning tasks provided by the e-textbook (i.e., more tasks solved, engaged in a larger variety of different exercises, more hints requested autonomously, higher total problem solving time, longer time spent on individual feedback) than students with lower prior knowledge.

Given these results, we considered prior knowledge, emotional, and behavioral engagement unique and relevant individual characteristics that account for differences in cognitive learning outcomes after learning with an e-textbook. For the estimation of the size of this effect, the PCV is of specific interest. In our analysis, the PCV represents the random variance between students explained due to adding specific predictors to the model when compared to the prior knowledge model. Here, including emotional and behavioral engagement besides prior knowledge resulted in a substantial PCV of 44%.

Discussion

Motivation and Engagement While Working With e-Textbooks

In the present study, we aimed to describe the relationship between students’ motivational and emotional orientations in mathematics, their emotional and behavioral classroom engagement while working with an e-textbook on fractions, and their cognitive learning outcomes.

Regarding our first research question, this study sheds light on the relationship between students’ motivational and emotional orientations and their engagement while working on an interactive e-textbook. We could show that rather stable orientations had a substantial impact on how emotionally engaged students were with the e-textbook. We consider this not self-evident, as one could assume that e-textbooks (and educational technology, in general) may lead to high emotional engagement in all students, regardless of their domain-specific orientations, as working with digital media could be considered engaging per se (Higgins et al., 2019; Hillmayr et al., 2020; see also Jeno et al., 2019 for a discussion of the novelty effect). Furthermore, the directions of the correlations between students’ orientations and their emotional engagement are noteworthy: Anxiety, as a negative orientation, was negatively correlated with preferable emotional engagement, while self-concept and enjoyment, as positive orientations, were positively correlated with preferable emotional engagement. Again, this is not self-evident from our point of view, as one could expect that also students showing less-preferable motivational and emotional orientations in mathematics might want to engage in individualized learning formats that take into account their individual mathematics competence and yield adaptive scaffolds.

Here, one noteworthy result is the rather unspecific correlation between students’ orientations and their perceived autonomy support. This result can be interpreted as a desirable goal when designing interactive and adaptive DCR—as it shows that also students with less-preferable orientations regarding mathematics perceived their learning with the e-textbook as autonomous. Yet, as perceived autonomy support varied substantially between students, this also opens the question about which personal characteristics besides the examined motivational and emotional orientations may have an effect on the perceived autonomy support when learning with educational technology.

Summarizing these findings, we conclude that even though the design of interactive DCR aims at addressing all students regardless of their orientations by yielding adaptive scaffolds—such as positive feedback on students’ task work (Deci, 1971; Deci and Ryan, 1985), immediate individual and exploratory feedback (Hattie and Timperley, 2007; Steenbergen-Hu and Cooper, 2013), as well as adaptive task difficulty (Hoch et al., 2018b; Reinhold et al., 2020a), and leeway for different actions, freedom of choosing tasks and advice, and possibilities for exploration (Prenzel and Drechsel, 1996)—less-preferable domain-specific motivational and emotional orientations still hinder students to engage in these well-developed electronic learning environments.

In line with this argumentation are the results regarding the relationship between orientations and behavioral engagement. Although the effects were substantially smaller than for emotional engagement, the direction of the correlations were very similar: Self-concept and enjoyment were positively correlated with all indicators of behavioral engagement, while for anxiety correlations pointed in the other direction. One noteworthy finding is the rather clear negative correlation between mathematics anxiety and the time students spent on feedback. This finding can be considered counterintuitive at first sightas one might suppose especially anxious students to make use of adaptive and exploratory feedback to their individual perceived struggle when learning mathematics. Yet, our results rather suggest avoidance behavior (Finn et al., 1995) in students showing high anxiety: Time on feedback, as well as the total number of tasks and the total problem solving time was negatively correlated with anxiety indicating that anxious students avoided working with the learning environment. This interpretation is also in line with the results regarding self-concept and behavioral engagement, showing that less confident students also tended to take fewer hints, and tended to spend less time on feedback than more confident students.

Regarding our second research question, we argue that emotional and behavioral engagement can be considered two distinct predictors for achievement besides prior knowledge. We found that students’ engagement could explain a substantial part of the variance in their cognitive learning outcome—after controlling for prior knowledge. It is noteworthy that while emotional engagement has shown to be a unique predictor, the interaction of behavioral engagement and prior knowledge was predictive for achievement, i.e., higher behavioral engagement was more beneficial for students who had higher prior knowledge of fractions before the intervention. We consider this an important finding for the development of e-textbooks in particular and technology-enriched learning environments in general: Although the development of our e-textbook focused on evidence-based principles for designing multimedia learning environments with interactive and adaptive scaffolds to support individualized learning, the latter result shows that students with better cognitive prerequisites benefited more from engaging in the implemented features.

Our study was following the general model for determinants and course of motivated action (Heckhausen and Heckhausen, 2018). Following this rationale, we hypothesized that characteristics of a person first lead to emotional and behavioral engagement (RQ1), which in turn determine learning success (RQ2). Although we could not investigate the underlying model to full extent—given the exploratory nature of our study with the focus on one classroom—our results support the theoretical model (see Figure 1). Thus, we consider the model applicable to describe and explain individual differences in learning outcomes in technology-enriched learning scenarios underlining the idea that (emotional and behavioral) classroom engagement is a reasonable mediator for the effect of domain-specific motivational and emotional orientations on achievement in learning settings that utilize educational technology.

Concluding on our findings, we argue that one key element for effective implementation of digital media into mathematics classrooms is engagement. The results of this exploratory study point to a substantial role of engagement with regard to achievement in technology-enriched learning scenarios. This is in line with the goal of promoting higher engagement through the individualization of learning experiences in most evidence-based design principles and features implemented in educational technology. To promote engagement in students, both content and technological implementation should be considered conclusively when designing digital learning environments (Reinhold et al., 2020a)—This is particularly true for students with less promising motivational and emotional orientations in mathematics and less promising prior knowledge.

Limitations and Future Directions

The aim of the present study was to derive hypotheses for further research regarding the role of motivational and emotional orientations and engagement for learning in technology-enriched scenarios. We reported a case study with one sixth-grade classroom that comes with specific limitations by design which should be kept in mind when interpreting the results. As all 27 students were taught by the same teacher, we cannot answer questions regarding the specific role of the teacher on students emotional and behavioral engagement during the intervention. Regarding that, one noteworthy result is the small to negligible correlations between motivational and emotional orientations and count measures of behavioral engagement—opening up questions about whether these count measures are altered by the teacher rather than individual characteristics. Yet, there was a substantial variation in those count measures, raising the question of other characteristics on the student level to account for behavioral engagement, which is a question that we cannot answer with the present data.

The focus on high-achieving students may be considered another limitation of the present study, as this could lead to a bias in emotional engagement as well as motivational and emotional orientations regarding mathematics. However, Table 1 reveals a large variation in mathematics anxiety, self-concept, and enjoyment, as well as the other self-reported measures for emotional engagement. Therefore, we do not think that there is a relevant bias in the current data regarding high achieving students that would affect the results reported in this study.

In addition, the sample size of this study did not allow for a full mediation analysis following the theoretical model for motivation considered (Figure 1), but only for distinct analyses of constrained parts of the model. Here, a substantially larger sample size could allow for testing a path model, which would validate the findings of our case study and yield further insights into the development of emotional and behavioral engagement during the learning of mathematics with e-textbooks.

Our study did not contain a print-control group, learning the content of basic fraction concepts in a “traditional, non-technology-enriched” scenario. Future research should address the question whether the effect of motivational and emotional orientations, emotional engagement, and behavioral engagement on achievement differs between digital and non-digital classroom settings. This is arguably an important question, that could inform practice about the underlying mechanisms in mathematics classroom instruction and potential similarities or differences when teaching in digital and non-digital settings.

Moreover, a print-control group would allow for the investigation of effects of technology-enriched mathematics instruction on students motivational and emotional orientations considered as outcomes—i.e., whether technology-enriched mathematics instruction has the potential to yield a higher positive impact on students’ mathematics-related motivation and emotions than paper-based instruction. Throughout this article, we argued that interactive and adaptive scaffolds in e-textbooks (or DCR in general) bear such potential on a theoretical level. Yet, empirical evidence is needed to foster the assumption that they help teachers to address multidimensional educational goals –cognitive learning gains and motivational and emotional orientations, see Schiepe-Tiska et al., 2016a; Schiepe-Tiska et al., 2016b). These are of specific interest, as for instance, in Germany, nearly half of the fifteen-year-olds in the 2012 PISA survey reported they were afraid of poor grades in mathematics, and only about 39% stated that they enjoy mathematics (Schiepe-Tiska and Schmidtner, 2013).

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Ethics Statement

FR: drafting the article. FR, SH, AS: data collection. FR, SH, AS-T, AS, KR: conception or design of the work, data analysis and interpretation, critical revision of the article, and final approval of the version to be published.

Author Contributions

FR, drafting the article; FR, SH, AS, data collection; FR, SH, AST, AS, KR, conception or design of the work, data analysis and interpretation, critical revision of the article, and final approval of the version to be published.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Software used in this study was developed in the “ALICE:fractions” project. We want to thank Bernhard Werner and Jürgen Richter-Gebert for their great contribution to the project. We want to thank all students and their teacher for taking part in the study.

References

Aliasgari, M., Riahinia, N., and Mojdehavar, F. (2010). Computer‐assisted instruction and student attitudes towards learning mathematics. Educ. Bus. Soc. 3, 6–14. doi:10.1108/17537981011022779

CrossRef Full Text | Google Scholar

Anozie, N. O., and Junker, B. W. (2006). “Predicting end-of-year accountability assessment scores from monthly student records in an online tutoring system,” in AAAI’06 workshop on educational data mining, Boston, MA, July 16–17, 2006.

CrossRef Full Text | Google Scholar

Appleton, J. J., Christenson, S. L., Kim, D., and Reschly, A. L. (2006). Measuring cognitive and psychological engagement: validation of the student engagement instrument. J. Sch. Psychol. 44, 427–445. doi:10.1016/j.jsp.2006.04.002

CrossRef Full Text | Google Scholar

Ashcraft, M. H., and Kirk, E. P. (2001). The relationships among working memory, math anxiety, and performance. J. Exp. Psychol. Gen. 130, 224–237. doi:10.1037//0096-3445.130.2.224

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashcraft, M. H., and Moore, A. M. (2009). Mathematics anxiety and the affective drop in performance. J. Psychoeduc. Assess. 27, 197–205. doi:10.1177/0734282908330580

CrossRef Full Text | Google Scholar

Ashcraft, M. H., and Ridley, K. S. (2005). “Math anxiety and its cognitive consequences: a tutorial review,” in Handbook of mathematical cognition. Editor J. I. D. Campbell (New York: Psychology Press), 315–327.

CrossRef Full Text | Google Scholar

Ayers, E., and Junker, B. (2008). IRT modeling of tutor performance to predict end-of-year exam scores. Educ. Psychol. Meas. 68, 972–987. doi:10.1177/0013164408318758

CrossRef Full Text | Google Scholar

Ayres, P. (2006). Impact of reducing intrinsic cognitive load on learning in a mathematical domain. Appl. Cognit. Psychol. 20, 287–298. doi:10.1002/acp.1245

CrossRef Full Text | Google Scholar

Ayres, P. L. (2001). Systematic mathematical errors and cognitive load. Contemp. Educ. Psychol. 26, 227–248. doi:10.1006/ceps.2000.1051

PubMed Abstract | CrossRef Full Text | Google Scholar

Böheim, R., Knogler, M., Kosel, C., and Seidel, T. (2020). Exploring student hand-raising across two school subjects using mixed methods: an investigation of an everyday classroom behavior from a motivational perspective. Learn. InStruct. 65, 101250. doi:10.1016/j.learninstruc.2019.101250

CrossRef Full Text | Google Scholar

Bakri, H., Syamsuddin, A., and Babo, R. (2020). Applying the aptitude treatment interaction (ATI) learning model in mathematics learning to improve mathematical concept understanding of 5th grade of elementary school students. J. Crit. Rev. 7, 55–58. doi:10.31838/jcr.07.07.10

CrossRef Full Text | Google Scholar

Barkatsas, A., Kasimatis, K., and Gialamas, V. (2009). Learning secondary mathematics with technology: exploring the complex interrelationship between students’ attitudes, engagement, gender and achievement. Comput. Educ. 52, 562–570. doi:10.1016/j.compedu.2008.11.001

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting linear mixed-effects models using lme4. J. Stat. Software 67. doi:10.18637/jss.v067.i01

CrossRef Full Text | Google Scholar

Behr, M., Lesh, R. A., Post, T. R., and Silver, E. (1983). “Rational number concepts,” in Acquisition of mathematics Concepts and processes. Editors R. Lesh, and M. Landau (New York: Academic Press), 91–125.

CrossRef Full Text | Google Scholar

Black, J. B., Segal, A., Vitale, J., and Fadjo, C. L. (2012). “Embodied cognition and learning environment design,” in Theoretical foundations of learning environments. Editors D. Jonassen, and S. Land (Oxford: Routledge), 198–223.

CrossRef Full Text | Google Scholar

Blum, G. S., Rauthmann, J. F., Göllner, R., Lischetzke, T., and Schmitt, M. (2018). The nonlinear interaction of person and situation (nips) model: theory and empirical evidence. Eur. J. Pers. 32, 286–305. doi:10.1002/per.2138

CrossRef Full Text | Google Scholar

Brauer, M., and Curtin, J. J. (2018). Linear mixed-effects models and the analysis of nonindependent data: a unified framework to analyze categorical and continuous independent variables that vary within-subjects and/or within-items. Psychol. Methods 23, 389–411. doi:10.1037/met0000159

PubMed Abstract | CrossRef Full Text | Google Scholar

Bright, G., Behr, M., Post, T. R., and Wachsmuth, I. (1988). Identifying fractions on number lines. J. Res. Math. Educ. 19, 215–232. doi:10.2307/749066

CrossRef Full Text | Google Scholar

Choppin, J., Carsons, C., Bory, Z., Cerosaletti, C., and Gillis, R. (2014). A typology for analyzing digital curricula in mathematics education. Int. J. Educ. Math. Sci. Technol. 2, 11–25. 10.18404/ijemst.95334

CrossRef Full Text | Google Scholar

S. L. Christenson, A. L. Reschly, and C. Wylie (Editors) (2012). Handbook of research on student engagement. Boston, MA: Springer US.

CrossRef Full Text | Google Scholar

Clark, R. E. (1994). Media will never influence learning. ETR&D 42, 21–29. doi:10.1007/BF02299088

CrossRef Full Text | Google Scholar

Clarke, S. N., Howley, I., Resnick, L., and Penstein Rosé, C. (2016). Student agency to participate in dialogic science discussions. Learn. Cult. Soc. Interact. 10, 27–39. doi:10.1016/j.lcsi.2016.01.002

CrossRef Full Text | Google Scholar

Deci, E. L. (1971). Effects of externally mediated rewards on intrinsic motivation. J. Pers. Soc. Psychol. 18, 105–115. doi:10.1037/h0030644

CrossRef Full Text | Google Scholar

Deci, E. L., and Ryan, R. M. (1985). Intrinsic motivation and self-determination in human behavior. Boston, MA: Springer US.

CrossRef Full Text | Google Scholar

Deci, E. L., and Ryan, R. M. (2012). “Motivation, personality, and development within embedded social contexts: an overview of self-determination theory,” in The oxford handbook of human motivation. Editor R. M. Ryan (Oxford University Press), 84–108.

CrossRef Full Text | Google Scholar

Dowker, A., Sarkar, A., and Looi, C. Y. (2016). Mathematics anxiety: what have we learned in 60 years? Front. Psychol. 7, 508. doi:10.3389/fpsyg.2016.00508

PubMed Abstract | CrossRef Full Text | Google Scholar

Eccles, J. S., Adler, T. F., Futterman, R., Goff, S. B., Kaczala, C. M., Meece, J. L., et al. (1983). “Expectations, values and academic behaviors,” in Achievement and achievement motivation. Editor J. T. Spence (San Francisco: W. H. Freeman), 75–146.

CrossRef Full Text | Google Scholar

Embong, A. M., Noor, A. M., Hashim, H. M., Ali, R. M., and Shaari, Z. H. (2012). E-books as textbooks in the classroom. Procedia Soc. Behav. Sci. 47, 1802–1809. doi:10.1016/j.sbspro.2012.06.903

CrossRef Full Text | Google Scholar

L. Fan, L. Trouche, C. Qi, S. Rezat, and J. Visnovska (Editors) (2018). Research on mathematics textbooks and teachers’ resources. Cham: Springer International Publishing.

CrossRef Full Text | Google Scholar

Feng, M., Heffernan, N. T., and Koedinger, K. R. (2006). “Predicting state test scores better with intelligent tutoring systems: developing metrics to measure assistance required,” in Intelligent tutoring systems lecture notes in computer science. Editors M. Ikeda, K. D. Ashley, and T.-W. Chan (Berlin, Heidelberg: Springer Berlin Heidelberg), 31–40.

CrossRef Full Text | Google Scholar

Finn, J. D., Pannozzo, G. M., and Voelkl, K. E. (1995). Disruptive and inattentive-withdrawn behavior and achievement among fourth graders. Elem. Sch. J. 95, 421–434. doi:10.1086/461853

CrossRef Full Text | Google Scholar

Fredricks, J. A., Blumenfeld, P. C., and Paris, A. H. (2004). School engagement: potential of the concept, state of the evidence. Rev. Educ. Res. 74, 59–109. doi:10.3102/00346543074001059

CrossRef Full Text | Google Scholar

Fredricks, J. A., and McColskey, W. (2012). “The measurement of student engagement: a comparative analysis of various methods and student self-report instruments,” In Handbook of Research on student engagement. Editors S. L. Christenson, A. L. Reschly, and Cathy (Boston: Springer), 763–782.

CrossRef Full Text | Google Scholar

Fung, F., Tan, C. Y., and Chen, G. (2018). Student engagement and mathematics achievement: unraveling main and interactive effects. Psychol. Sch. 55, 815–831. doi:10.1002/pits.22139

CrossRef Full Text | Google Scholar

Goldhammer, F., Naumann, J., Rölke, H., Stelter, A., and Tóth, K. (2017). “Relating product data to process data from computer-based competency assessment,” In Competence assessment in education. Editors D. Leutner, J. Fleischer, J. Grünkorn, and E. Klieme (Cham: Springer), 407–425.

CrossRef Full Text | Google Scholar

Goldhammer, F., Naumann, J., Stelter, A., Tóth, K., Rölke, H., and Klieme, E. (2014). The time on task effect in reading and problem solving is moderated by task difficulty and skill: insights from a computer-based large-scale assessment. J. Educ. Psychol. 106, 608–626. doi:10.1037/a0034716

CrossRef Full Text | Google Scholar

Hannula, M. S., Di Martino, P., Pantziara, M., Zhang, Q., Morselli, F., Heyd-Metzuyanim, E., et al. (2016). “Attitudes, beliefs, motivation and identity in Mathematics Education,” in An overview of the field and future directions. Hamburg: Springer Open.

CrossRef Full Text | Google Scholar

Hattie, J., and Timperley, H. (2007). The power of feedback. Rev. Educ. Res. 77, 81–112. doi:10.3102/003465430298487

CrossRef Full Text | Google Scholar

Hattie, J. (2009). Visible learning. A synthesis of over 800 meta-analyses relating to achievement. London: Routledge.

CrossRef Full Text | Google Scholar

J. Heckhausen, and H. Heckhausen (Editors) (2018). Motivation and action. Cham: Springer International Publishing.

CrossRef Full Text | Google Scholar

Helmke, A.. (2010). Unterrichtsqualität und Lehrerprofessionalität. Diagnose, Evaluation und Verbesserung des Unterrichts [Quality of teaching and teacher proficiency. Diagnosis, evaluation and improvement of teaching]. 3rd Edn. Seelze: Klett Kallmeyer.

CrossRef Full Text | Google Scholar

Hembree, R. (1990). The nature, effects and relief of mathematics anxiety. J. Res. Math. Educ. 21, 33–46. doi:10.2307/749455

CrossRef Full Text | Google Scholar

Henrie, C. R., Halverson, L. R., and Graham, C. R. (2015). Measuring student engagement in technology-mediated learning: a review. Comput. Educ. 90, 36–53. doi:10.1016/j.compedu.2015.09.005

CrossRef Full Text | Google Scholar

Hew, K. F., Huang, B., Chu, K. W. S., and Chiu, D. K. W. (2016). Engaging Asian students through game mechanics: findings from two experiment studies. Comput. Educ. 92–93, 221–236. doi:10.1016/j.compedu.2015.10.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Hidi, S. (1990). Interest and its contribution as a mental resource for learning. Rev. Educ. Res. 60, 549–571. doi:10.3102/00346543060004549

CrossRef Full Text | Google Scholar

Hidi, S., and Renninger, K. A. (2006). The four-phase model of interest development. Educ. Psychol. 41, 111–127. doi:10.1207/s15326985ep4102_4

CrossRef Full Text | Google Scholar

Higgins, K., Huscroft-D’Angelo, J., and Crawford, L. (2019). Effects of technology in mathematics on achievement, motivation, and attitude: a meta-analysis. J. Educ. Comput. Res. 57, 283–319. doi:10.1177/0735633117748416

CrossRef Full Text | Google Scholar

Hillmayr, D., Ziernwald, L., Reinhold, F., Hofer, S. I., and Reiss, K. M. (2020). The potential of digital tools to enhance mathematics and science learning in secondary schools: a context-specific meta-analysis. Comput. Educ. 153, 103897. doi:10.1016/j.compedu.2020.103897

CrossRef Full Text | Google Scholar

Hoch, S. (2021). Process data from digital textbooks as an instrument for mathematics education research. Doctoral dissertation. Munich, Germany: Technical University of Munich mediaTUM.

CrossRef Full Text | Google Scholar

Hoch, S., Reinhold, F., Werner, B., Reiss, K., and Richter-Gebert, J. (2018a). Fractions. Getting in touch with rational numbers [Web version]. Munich, Germany: Technical University of Munich. Available at: https://alice.edu.tum.de/ (Accessed July 29, 2020).

CrossRef Full Text | Google Scholar

Hoch, S., Reinhold, F., Werner, B., Richter-Gebert, J., and Reiss, K. (2018b). Design and research potential of interactive textbooks: the case of fractions. ZDM Math. Edu. 50, 839–848. doi:10.1007/s11858-018-0971-z

CrossRef Full Text | Google Scholar

Huang, B., Hew, K. F., and Lo, C. K. (2019). Investigating the effects of gamification-enhanced flipped learning on undergraduate students’ behavioral and cognitive engagement. Interact. Learn. Environ. 27, 1106–1126. doi:10.1080/10494820.2018.1495653

CrossRef Full Text | Google Scholar

Jeno, L. M., Vandvik, V., Eliassen, S., and Grytnes, J.-A. (2019). Testing the novelty effect of an m-learning tool on internalization and achievement: a Self-Determination Theory approach. Comput. Educ. 128, 398–413. doi:10.1016/j.compedu.2018.10.008

CrossRef Full Text | Google Scholar

Junco, R., and Clem, C. (2015). Predicting course outcomes with digital textbook usage data. Internet High Educ. 27, 54–63. doi:10.1016/j.iheduc.2015.06.001

CrossRef Full Text | Google Scholar

Jurik, V., Gröschner, A., and Seidel, T. (2013). How student characteristics affect girls’ and boys’ verbal engagement in physics instruction. Learn. InStruct. 23, 33–42. doi:10.1016/j.learninstruc.2012.09.002

CrossRef Full Text | Google Scholar

Jurik, V., Gröschner, A., and Seidel, T. (2014). Predicting students’ cognitive learning activity and intrinsic learning motivation: how powerful are teacher statements, student profiles, and gender? Learn. Indiv Differ 32, 132–139. doi:10.1016/j.lindif.2014.01.005

CrossRef Full Text | Google Scholar

Köller, O., Baumert, J., and Schnabel, K. (2001). Does interest matter? The relationship between academic interest and achievement in mathematics. J. Res. Math. Educ. 32, 448–470. doi:10.2307/749801

CrossRef Full Text | Google Scholar

Köller, O., Daniels, Z., Schnabel, K. U., and Baumert, J. (2000). Kurswahlen von Mädchen und Jungen im Fach Mathematik: zur Rolle von fachspezifischem Selbstkonzept und Interesse [Course Selections of Girls and Boys in Mathematics: the Role of Academic Self-Concept and Interest]. Z. für Padagogische Psychol. 14, 26–37. doi:10.1024//1010-0652.14.1.26

CrossRef Full Text | Google Scholar

Köller, O., Trautwein, U., Lüdtke, O., and Baumert, J. (2006). Zum Zusammenspiel von schulischer Leistung, Selbstkonzept und Interesse in der gymnasialen Oberstufe [On the Interplay of Academic Achievement, Self-Concept, and Interest in Upper Secondary Schools]. Z. für Padagogische Psychol. 20, 27–39. doi:10.1024/1010-0652.20.12.27

CrossRef Full Text | Google Scholar

Kanfer, R., and Ackerman, P. L. (1989). Motivation and cognitive abilities: an integrative/aptitude-treatment interaction approach to skill acquisition. J. Appl. Psychol. 74, 657–690. doi:10.1037/0021-9010.74.4.657

CrossRef Full Text | Google Scholar

Kelly, S. (2007). Classroom discourse and the distribution of student engagement. Soc. Psychol. Educ. 10, 331–352. doi:10.1007/s11218-007-9024-0

CrossRef Full Text | Google Scholar

Kickmeier-Rust, M. D., and Albert, D. (2010). Micro-adaptivity: protecting immersion in didactically adaptive digital educational games. J. Comput. Assist. Learn. 26, 95–105. doi:10.1111/j.1365-2729.2009.00332.x

CrossRef Full Text | Google Scholar

Kovanović, V., Gašević, D., Dawson, S., Joksimović, S., Baker, R. S., and Hatala, M. (2015). Does time-on-task estimation matter? Implications for the validity of learning analytics findings. J. Learn Anal. 2, 81–110. doi:10.18608/jla.2015.23.6

CrossRef Full Text | Google Scholar

Kozma, R. B. (1994). Will media influence learning? Reframing the debate. Edu. Technol. Res. Develop. 42, 7–19. doi:10.1007/BF02299087

CrossRef Full Text | Google Scholar

Krapp, A. (2005). Basic needs and the development of interest and intrinsic motivational orientations. Learn. InStruct. 15, 381–395. doi:10.1016/j.learninstruc.2005.07.007

CrossRef Full Text | Google Scholar

Krapp, A., and Prenzel, M. (2011). Research on interest in science: theories, methods, and findings. Int. J. Sci. Educ. 33, 27–50. doi:10.1080/09500693.2010.518645

CrossRef Full Text | Google Scholar

Krapp, A. (2002). Structural and dynamic aspects of interest development: theoretical considerations from an ontogenetic perspective. Learn. InStruct. 12, 383–409. doi:10.1016/S0959-4752(01)00011-1

CrossRef Full Text | Google Scholar

Kunter, M. (2005). Multiple Ziele im Mathematikunterricht [Multiple goals in mathematics teaching]. Munster: Waxmann.

CrossRef Full Text | Google Scholar

Lai, Y., Zhu, X., Chen, Y., and Li, Y. (2015). Effects of mathematics anxiety and mathematical metacognition on word problem solving in children with and without mathematical learning difficulties. PloS One 10, e0130570. doi:10.1371/journal.pone.0130570

PubMed Abstract | CrossRef Full Text | Google Scholar

Lamon, S. J. (2012). Teaching fractions and ratios for understanding: essential content knowledge and instructional strategies for teachers. Abingdon: Routledge.

CrossRef Full Text | Google Scholar

Leutner, D. (2002). “Adaptivität und Adaptierbarkeit multimedialer Lehr- und Informationssysteme [Adaptivity and adaptability of multimedia teaching and information systems],” in Information und Lernen mit Multimedia und internet: Lehrbuch für Studium und praxis. Editors L. J. Issing, and P. Klimsa (Weinheim: Beltz), 115–126.

CrossRef Full Text | Google Scholar

Leutner, D. (2004). “Instructional design principles for adaptivity in open learning environments,” in Curriculum, plans, and processes in instructional design. International perspectives. Editors N. M. Seel, and S. Dijkstra (Mahwah, NJ: Erlbaum), 289–308.

CrossRef Full Text | Google Scholar

Lew, H. (2016). “Developing and implementing ‘smart’ mathematics textbooks in Korea: issues and challenges,” in Digital curricula in school mathematics research issues in mathematics education. Editors M. Bates, and Z. Usiskin (Charlotte, NC: Information Age Publishing, Inc.), 35–52.

CrossRef Full Text | Google Scholar

Möller, J., Retelsdorf, J., Köller, O., and Marsh, H. W. (2011). The reciprocal internal/external frame of reference model: an integration of models of relations between academic achievement and self-concept. Am. Educ. Res. J. 48, 1315–1346. doi:10.3102/0002831211419649

CrossRef Full Text | Google Scholar

Ma, X. (1999). A meta-analysis of the relationship between anxiety toward mathematics and achievement in mathematics. J. Res. Math. Educ. 30, 520. doi:10.2307/749772

CrossRef Full Text | Google Scholar

Ma, X., and Kishor, N. (1997). Assessing the relationship between attitude toward mathematics and achievement in mathematics: a meta-analysis. J. Res. Math. Educ. 28, 26. doi:10.2307/749662

CrossRef Full Text | Google Scholar

Maloney, E. A., Ansari, D., and Fugelsang, J. A. (2011). The effect of mathematics anxiety on the processing of numerical magnitude. Q. J. Exp. Psychol. 64, 10–16. doi:10.1080/17470218.2010.533278

CrossRef Full Text | Google Scholar

Marsh, H. W., and Martin, A. J. (2011). Academic self-concept and academic achievement: relations and causal ordering. Br. J. Educ. Psychol. 81, 59–77. doi:10.1348/000709910X503501

PubMed Abstract | CrossRef Full Text | Google Scholar

Marsh, H. W., Xu, M. K., and Martin, A. J. (2012). “Self-concept: a synergy of theory, method, and application,” in APA educational psychology handbook. Editors K. R. Harris, S. Graham, and T. C. Urdan (Washington, DC: American Psychological Association), 427–458.

CrossRef Full Text | Google Scholar

Maskur, R., Sumarno, , Rahmawati, Y., Pradana, K., Syazali, M., Septian, A., et al. (2020). The effectiveness of problem based learning and aptitude treatment interaction in improving mathematical creative thinking skills on curriculum 2013. Eur. J. Ed Res. 9, 375–383. doi:10.12973/eu-jer.9.1.375

CrossRef Full Text | Google Scholar

Mayer, R. E. (2014). “Cognitive theory of multimedia learning,” in The cambridge handbook of multimedia learning. Editor R. E. Mayer (New York: Cambridge University Press), 31–48.

CrossRef Full Text | Google Scholar

McLeod, D. B. (1992). “Research on affect in mathematics education: a reconceptualization,” in Handbook of research on mathematics, teaching and learning. Editor D. A. Grouws (New York: Macmillan), 575–596.

CrossRef Full Text | Google Scholar

McLeod, D. B. (1989). “Beliefs, attitudes, and emotions: new views of affect in mathematics education,” in Affect and mathematical problem solving. Editors D. B. McLeod, and V. M. Adams (New York, NY: Springer New York), 245–258.

CrossRef Full Text | Google Scholar

Middleton, J. A., and Spanias, P. A. (1999). Motivation for achievement in mathematics: findings, generalizations, and criticisms of the research. J. Res. Math. Educ. 30, 65. doi:10.2307/749630

CrossRef Full Text | Google Scholar

Núñez-Peña, M. I., Suárez-Pellicioni, M., and Bono, R. (2013). Effects of math anxiety on student success in higher education. Int. J. Educ. Res. 58, 36–43. doi:10.1016/j.ijer.2012.12.004

CrossRef Full Text | Google Scholar

Nakagawa, S., and Schielzeth, H. (2013). A general and simple method for obtaining R² from generalized linear mixed-effects models. Methods Ecol. Evol. 4, 133–142. doi:10.1111/j.2041-210x.2012.00261.x

CrossRef Full Text | Google Scholar

Namkung, J. M., Peng, P., and Lin, X. (2019). The relation between mathematics anxiety and mathematics performance among school-aged students: a meta-analysis. Rev. Educ. Res. 89, 459–496. doi:10.3102/0034654319843494

CrossRef Full Text | Google Scholar

Özmen, H. (2008). The influence of computer-assisted instruction on students’ conceptual understanding of chemical bonding and attitude toward chemistry: a case for Turkey. Comput. Educ. 51, 423–438. doi:10.1016/j.compedu.2007.06.002

CrossRef Full Text | Google Scholar

Özyurt, Ö., Özyurt, H., Güven, B., and Baki, A. (2014). The effects of UZWEBMAT on the probability unit achievement of Turkish eleventh grade students and the reasons for such effects. Comput. Educ. 75, 1–18. doi:10.1016/j.compedu.2014.02.005

CrossRef Full Text | Google Scholar

OECD (2003). The PISA 2003 Assessment framework—mathematics, reading, science and problem solving knowledge and skills. Paris: OECD Publishing.

CrossRef Full Text | Google Scholar

Paas, F. (1992). Training strategies for attaining transfer of problem-solving skill in statistics: a cognitive-load approach. J. Educ. Psychol. 84, 429–434. doi:10.1037/0022-0663.84.4.429

CrossRef Full Text | Google Scholar

Padberg, F. (2002). “Anschauliche Vorerfahrungen zum Bruchzahlbegriff und zu einfachen Rechenoperationen mit Brüchen in Modellierungskontexten [Descriptive prior knowledge on fractions in modelling contexts],” in Didaktik der Bruchrechnung. Gemeine Brüche – Dezimalbrüche (Heidelberg: Springer Spektrum), 289–299.

CrossRef Full Text | Google Scholar

Padberg, F., and Wartha, S. (2017). Didaktik der Bruchrechnung [Didactics of fractions]. 5th Edn. Berlin, Heidelberg: Springer Spektrum.

CrossRef Full Text | Google Scholar

Pekrun, R. (2006). The control-value theory of achievement emotions: assumptions, corollaries, and implications for educational research and practice. Educ. Psychol. Rev. 18, 315–341. doi:10.1007/s10648-006-9029-9

CrossRef Full Text | Google Scholar

Pekrun, R., vom Hofe, R., Blum, W., Frenzel, A. C., Goetz, T., and Wartha, S. (2007). “Development of mathematical competencies in adolescence: the PALMA longitudinal study,” in Studies on the educational quality of schools. The final report on the DFG Priority Programme. Editor M. Prenzel (Münster, Germany: Waxmann), 17–37.

CrossRef Full Text | Google Scholar

Pekrun, R., vom Hofe, R., Blum, W., Götz, T., Wartha, S., and Jullien, S. (2006). “Projekt zur Analyse der Leistungsentwicklung in Mathematik (PALMA). Entwicklungsverläufe, Schülervoraussetzungen und Kontextbedingungen von Mathematikleistung bei Schülerinnen und Schülern der Sekundarstufe I [Project for the Analysis of Performance Development in Mathematics (PALMA). Developmental trajectories, pupil prerequisites and contextual conditions of mathematics achievement in secondary school students],” in Untersuchungen zur bildungsqualität von Schule. Abschlussbericht des DFG-schwerpunktprogramms. Editors M. Prenzel, and L. Allolio-Näcke (Münster, Germany: Waxmann), 21–53.

CrossRef Full Text | Google Scholar

Pepin, B., Choppin, J., Ruthven, K., and Sinclair, N. (2017). Digital curriculum resources in mathematics education: foundations for change. ZDM 49, 645–661. doi:10.1007/s11858-017-0879-z

CrossRef Full Text | Google Scholar

Prediger, S. (2006). Vorstellungen zum Operieren mit Brüchen entwickeln und erheben: vorschläge für vorstellungsorientierte Zugänge und diagnostische Aufgaben [Develop and elevate ideas for operating with fractures: proposals for imaginative approaches and diagnostic tasks]. Praxis der Mathematik in der Schule 48, 8–12.

CrossRef Full Text | Google Scholar

Prenzel, M., and Drechsel, B. (1996). Ein Jahr kaufmännische Erstausbildung: veränderungen in Lernmotivation und Interesse [One year of initial business management training: changes in learning motivation and interest]. Unterrichtswissenschaft 24, 217–234.

CrossRef Full Text | Google Scholar

R Core Team (2008). R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing.

CrossRef Full Text | Google Scholar

Rahman, M. J. A., Ismail, M. A. H., and Nasir, M. (2014). Development and evaluation of the effectiveness of computer-assisted physics instruction. Int. Educ. Stud. 7, 14–22.

CrossRef Full Text | Google Scholar

Reinhold, F., Hoch, S., Werner, B., Richter-Gebert, J., and Reiss, K. (2020a). Learning fractions with and without educational technology: what matters for high-achieving and low-achieving students? Learn. InStruct. 65, 101264. doi:10.1016/j.learninstruc.2019.101264

CrossRef Full Text | Google Scholar

Reinhold, F., Obersteiner, A., Hoch, S., Hofer, S. I., and Reiss, K. (2020b). The interplay between the natural number bias and fraction magnitude processing in low-achieving students. Front. Educ. 5, 29. doi:10.3389/feduc.2020.00029

CrossRef Full Text | Google Scholar

Reinhold, F. (2019). Wirksamkeit von Tablet-PCs bei der Entwicklung des Bruchzahlbegriffs aus mathematikdidaktischer und psychologischer Perspektive [Effectiveness of Tablet PCs in Developing Initial Fraction Concepts from a Mathematics Education and Psychology Perspective]. Wiesbaden: Springer.

CrossRef Full Text | Google Scholar

Renninger, A. (2000). “Individual interest and its implications for understanding intrinsic motivation,” in Intrinsic and extrinsic motivation: the search for optimal motivation and performance Educational psychology series. Editors C. Sansone, and J. M. Harackiewicz (San Diego: Academic Press), 375–407.

CrossRef Full Text | Google Scholar

Richardson, F. C., and Suinn, R. M. (1972). The mathematics anxiety rating scale: psychometric data. J. Counsel. Psychol. 19, 551–554. doi:10.1037/h0033456

CrossRef Full Text | Google Scholar

Roschelle, J., Shechtman, N., Tatar, D., Hegedus, S., Hopkins, B., Empson, S., et al. (2010). Integration of technology, curriculum, and professional development for advancing middle school mathematics: three large-scale studies. Am. Educ. Res. J. 47, 833–878.

CrossRef Full Text | Google Scholar

Ryan, R. M., and Deci, E. L. (2000). Self-determination theory and the facilitation of intrinsic motivation, social development, and well-being. Am. Psychol. 55, 68–78. doi:10.1037/0003-066X.55.1.68

PubMed Abstract | CrossRef Full Text | Google Scholar

Schiepe-Tiska, A., Heine, J.-H., Lüdtke, O., Seidel, T., and Prenzel, M. (2016a). Mehrdimensionale Bildungsziele im Mathematikunterricht und ihr Zusammenhang mit den Basisdimensionen der Unterrichtsqualität [Multidimensional educational goals in mathematics teaching and their relation to the basic dimensions of teaching quality]. Unterrichtswissenschaft 44, 211–225.

CrossRef Full Text | Google Scholar

Schiepe-Tiska, A., Roczen, N., Müller, K., Prenzel, M., and Osborne, J. (2016b). “Science-related outcomes: attitudes, motivation, value beliefs, strategies,” in Assessing contexts of learning methodology of educational measurement and assessment. Editors. S. Kuger, E. Klieme, N. Jude, and D. Kaplan (Cham: Springer International Publishing), 301–329.

CrossRef Full Text | Google Scholar

Schiepe-Tiska, A., and Schmidtner, S. (2013). “Mathematikbezogene emotionale und motivationale Orientierungen, Einstellungen und Verhaltensweisen von Jugendlichen in PISA 2012 [Mathematics related emotional and motivational orientations, attitudes and behaviour of adolescents in PISA 2012],” in PISA 2012. Fortschritte und Herausforderungen in deutschland. Editors M. Prenzel, C. Sälzer, E. Klieme, and O. Köller (Münster, Germany: Waxmann), 99–122.

CrossRef Full Text | Google Scholar

Schukajlow, S., and Krug, A. (2014). “Are interest and enjoyment important for students’ performance?” In Proceedings of the 38th Conference of the international Group for the Psychology of mathematics Education and the 36th Conference of the north American Chapter of the Psychology of mathematics education. Editors P. Liljedahl, C. Nicol, S. Oesterle, and D. Allan (Vancouver: PME), 129–136.

CrossRef Full Text | Google Scholar

Schukajlow, S., Leiss, D., Pekrun, R., Blum, W., Müller, M., and Messner, R. (2012). Teaching methods for modelling problems and students’ task-specific enjoyment, value, interest and self-efficacy expectations. Educ. Stud. Math. 79, 215–237. doi:10.1007/s10649-011-9341-2

CrossRef Full Text | Google Scholar

Schukajlow, S., Rakoczy, K., and Pekrun, R. (2017). Emotions and motivation in mathematics education: theoretical considerations and empirical contributions. ZDM Math Educ. 49, 307–322. doi:10.1007/s11858-017-0864-6

CrossRef Full Text | Google Scholar

Schukajlow, S., and Rakoczy, K. (2016). The power of emotions: can enjoyment and boredom explain the impact of individual preconditions and teaching methods on interest and performance in mathematics? Learn. InStruct. 44, 117–127. doi:10.1016/j.learninstruc.2016.05.001

CrossRef Full Text | Google Scholar

Sedova, K., Sedlacek, M., Svaricek, R., Majcik, M., Navratilova, J., Drexlerova, A., et al. (2019). Do those who talk more learn more? The relationship between student classroom talk and student achievement. Learn. InStruct. 63, 101217. doi:10.1016/j.learninstruc.2019.101217

CrossRef Full Text | Google Scholar

Seidel, T. (2014). Angebots-Nutzungs-Modelle in der Unterrichtspsychologie. Integration von Struktur- und Prozessparadigma [Utilization-of-learning-opportunities models in the psychology of Instruction: integration of the paradigms of structure and of process]. Z. für Padagogik 60, 850–866.

CrossRef Full Text | Google Scholar

Shavelson, R. J., Hubner, J. J., and Stanton, G. C. (1976). Self-concept: validation of construct interpretations. Rev. Educ. Res. 46, 407–441. doi:10.3102/00346543046003407

CrossRef Full Text | Google Scholar

Sheen, K. A., and Luximon, Y. (2017). Student perceptions on future components of electronic textbook design. J. Comp. Educ. 4, 371–393. doi:10.1007/s40692-017-0092-7

CrossRef Full Text | Google Scholar

Singh, K., Granville, M., and Dika, S. (2002). Mathematics and science achievement: effects of motivation, interest, and academic engagement. J. Educ. Res. 95, 323–332. doi:10.1080/00220670209596607

CrossRef Full Text | Google Scholar

Skinner, E. A., and Belmont, M. J. (1993). Motivation in the classroom: reciprocal effects of teacher behavior and student engagement across the school year. J. Educ. Psychol. 85, 571–581. doi:10.1037/0022-0663.85.4.571

CrossRef Full Text | Google Scholar

Skinner, E. A., Furrer, C., Marchand, G., and Kindermann, T. (2008). Engagement and disaffection in the classroom: Part of a larger motivational dynamic? J. Educ. Psychol. 100, 765–781. doi:10.1037/a0012840

CrossRef Full Text | Google Scholar

Stankov, L., and Lee, J. (2014). Quest for the best non-cognitive predicator of academic achievement. Educ. Psychol. 34, 1–8. doi:10.1080/01443410.2013.858908

CrossRef Full Text | Google Scholar

Steenbergen-Hu, S., and Cooper, H. (2013). A meta-analysis of the effectiveness of intelligent tutoring systems on K–12 students’ mathematical learning. J. Educ. Psychol. 105, 970–987. doi:10.1037/a0032447

CrossRef Full Text | Google Scholar

Sternberg, R. J. (2019). Four ways to conceive of wisdom: wisdom as a function of person, situation, person/situation interaction, or action. J. Value Inq. 53, 479–485. doi:10.1007/s10790-019-09708-2

CrossRef Full Text | Google Scholar

Strohmaier, A. R., Schiepe-Tiska, A., and Reiss, K. M. (2020). A comparison of self-reports and electrodermal activity as indicators of mathematics state anxiety. Frontline Learn. Res. 8, 16–32. doi:10.14786/flr.v8i1.427

CrossRef Full Text | Google Scholar

Tarmizi, R., and Sweller, J. (1988). Guidance during mathematical problem solving. J. Educ. Psychol. 80, 424–436. 10.1037/0022-0663.80.4.424

CrossRef Full Text | Google Scholar

Ufer, S., Rach, S., and Kosiol, T. (2017). Interest in mathematics = interest in mathematics? What general measures of interest reflect when the object of interest changes. ZDM Math. Edu. 49, 397–409. doi:10.1007/s11858-016-0828-2

CrossRef Full Text | Google Scholar

Usiskin, Z. (2018). Electronic vs. paper textbook presentations of the various aspects of mathematics. ZDM Math. Edu. 50, 849–861. doi:10.1007/s11858-018-0936-2

CrossRef Full Text | Google Scholar

von Gagern, M., Kortenkamp, U., Richter-Gebert, J., and Strobel, M. (2016). “CindyJS: mathematical visualization on modern devices,” in Proceedings of mathematical software—ICMS 2016: 5th international conference, Berlin, Germany, July 11–14, 2016 Editors G.-M. Greuel, T. Koch, P. Paule, and A. Sommese (Cham: Springer), 319–326.

CrossRef Full Text | Google Scholar

Wickham, H., and Chang, W. (2016). ggplot2: create elegant data visualisations using the grammar of graphics. Available at: http://CRAN.R-project.org/package=PMCMR (Accessed 2016).

CrossRef Full Text | Google Scholar

Wiebe, E. N., Lamb, A., Hardy, M., and Sharek, D. (2014). Measuring engagement in video game-based environments: investigation of the user engagement scale. Comput. Hum. Behav. 32, 123–132. doi:10.1016/j.chb.2013.12.001

CrossRef Full Text | Google Scholar

Wigfield, A., and Eccles, J. S. (2000). Expectancy-value theory of achievement motivation. Contemp. Educ. Psychol. 25, 68–81. doi:10.1006/ceps.1999.1015

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, R., Landoni, M., and Gibb, F. (2002). “Guidelines for designing electronic books,” in Research and advanced technology for digital libraries. Editors M. Agosti, and C. Thanos (Berlin, Heidelberg: Springer), 47–60.

CrossRef Full Text | Google Scholar

Winfield, L. F. (1987). Teachers’ estimates of test content covered in class and first-grade students’ reading achievement. Elem. Sch. J. 87, 437–454. doi:10.1086/461507

CrossRef Full Text | Google Scholar

Yerushalmy, M. (2014). “Challenges to the authoritarian roles of textbooks,” in Proceedings of the international conference on mathematics textbook research and development (ICMT-2014), Southampton, England, July 24, 2014. Editors K. Jones, C. Bokhove, G. Howson, and L. Fan (Southampton: University of Southampton), 13–20.

CrossRef Full Text | Google Scholar

Yerushalmy, M. (2016). “Inquiry curriculum and E-textbooks: technology changes that challenge the representation of mathematics pedagogy,” in Digital curricula in school mathematics Research issues in mathematics education. Editors M. Bates, and Z. Usiskin (Charlotte, NC: Information Age Publishing, Inc.), 87–108.

CrossRef Full Text | Google Scholar

Zan, R., Brown, L., Evans, J., and Hannula, M. S. (2006). Affect in mathematics education: an introduction. Educ. Stud. Math. 63, 113–122. doi:10.1007/s10649-006-9028-2

CrossRef Full Text | Google Scholar

Zheng, G., Fancsali, S. E., Ritter, S., and Berman, S. R. (2019). Using instruction-embedded formative assessment to predict state summative test scores and achievement levels in mathematics. J. Learn. Analyt. 6, 153–174. doi:10.18608/jla.2019.62.11

CrossRef Full Text | Google Scholar