- 1TUM School of Education, Technical University of Munich (TUM), Munich, Germany
- 2Leibniz Institute for Science and Mathematics Education (IPN), Kiel, Germany
- 3Chair of Mathematics Education, Ludwig-Maximilians-University (LMU) Munich, Munich, Germany
Formative assessment of student learning is a challenging task in the teaching profession. Both teachers’ professional vision and their pedagogical content knowledge of specific subjects such as mathematics play an important role in assessment processes. This study investigated mathematics preservice teachers’ diagnostic activities during a formative assessment task in a video-based simulation. It examined which mathematical content was important for the successful assessment of the simulated students’ mathematical argumentation skills. Beyond that, the preservice teachers’ use of different diagnostic activities was assessed and used as an indicator of their knowledge-based reasoning during the assessment situation. The results showed that during the assessment, the mathematical content focused on varied according to the level of the simulated students’ mathematical argumentation skills. In addition, explaining what had been noticed was found to be the most difficult activity for the participants. The results suggest that the examined diagnostic activities are helpful in detecting potential challenges in the assessment process of preservice teachers that need to be further addressed in teacher education. In addition, the findings illustrate that a video-based simulation may have the potential to train specific diagnostic activities by means of additional instructional support.
Introduction
Every day, teachers find themselves in classroom teaching situations in which they are gathering information about the learning prerequisites and processes of their students (Praetorius et al., 2013; Thiede et al., 2015; Herppich et al., 2018). This information serves as the basis for pedagogical decisions, such as adaptive teaching (Vogt and Rogalla, 2009; Südkamp et al., 2012). To guide such decisions, a major source of information is on-the-fly formative assessment in classroom situations. Often, these are short one-on-one teacher–student interactions in which a teacher has the opportunity to monitor a student during instructional tasks (Birenbaum et al., 2006; Klug et al., 2013; Furtak et al., 2016). However, prior research has shown that many novice teachers struggle with the high density of information in such situations (Levin et al., 2009). As these situations are highly relevant for teachers, preservice teachers should already be prepared to handle such situations during their initial university-based teacher education.
Research on teachers’ assessment skills in diagnostic situations has prompted many studies on the accuracy of teacher judgments (Helmke and Schrader, 1987; Hosenfeld et al., 2002; McElvany et al., 2009). Mostly, prior research identified what is difficult to assess and what are typical errors teachers make in their judgments. However, to go a step further and find ways to foster teachers’ assessment skills, the identification of teachers’ pivotal dispositions is essential (see e.g., Blömeke et al., 2015); a professional knowledge base and motivational characteristics, such as individual interest, are often stated as important teacher dispositions that affect assessment skills during the diagnostic process (e.g., Kramer et al., 2020). Beyond that, recent research has been increasingly interested in situation-specific activities in the assessment process, the missing link between a teacher’s disposition and actual performance in a specific situation (Heitzmann et al., 2019; Bauer et al., 2020; Leuders and Loibl, 2020; Loibl et al., 2020).
The current study investigated preservice teachers’ diagnostic activities in the process of assessing students’ mathematical argumentation skills. In terms of professional vision, the components of noticing and knowledge-based reasoning about relevant information can be linked to these diagnostic activities (Goodwin, 1994; van Es and Sherin, 2008; Seidel and Stürmer, 2014).
First, the study explored the situation-specific noticing in the assessment process from a pedagogical content knowledge perspective, in this case, from the perspective of mathematics education (Reiss and Ufer, 2009). Students’ mathematical argumentation skills are composed of a broad set of knowledge facets, for example, content knowledge or knowledge about valuable problem-solving strategies (Schoenfeld, 1992) and various sub-skills (e.g., Sommerhoff et al., 2015). Based on prior mathematics education research (Chinnappan and Lawson, 1996; Ufer et al., 2008; Sommerhoff et al., 2015), it was assumed that these knowledge facets and sub-skills were meaningful indications that provided a means to accurately assess a student’s individual ability to handle mathematical proofs. In the student assessment process, it is, therefore, highly relevant to be able to notice these knowledge facets and sub-skills. Thus, the question arises as to what extent preservice teachers can draw their attention to these aspects in a diagnostic situation.
Second, knowledge-based reasoning about the diagnostic situation was examined. As a teacher, describing without judgment or interpreting based on professional knowledge are important diagnostic activities on the way to make informed decisions (Seidel and Stürmer, 2014). Thus, the question arises as to what extent preservice teachers show diagnostic activities that belong to deep knowledge-based reasoning processes. The insights of the current study serve as a basis for further understanding preservice teachers’ assessment skills and their challenges in the assessment process. In the long term, these insights can help to further improve innovative educational technologies, such as video-based simulations, by means of providing additional adaptive instructional support.
Teacher Assessment Skills in the Classroom
Continuously assessing students’ current individual learning processes is one of the essential tasks to be mastered in the teaching profession. Adapting teaching to the learning process and addressing students’ individual learning needs are basic requirements (DeLuca et al., 2016; Herppich et al., 2018). Formative assessment skills can, therefore, be found in most teacher competence frameworks and are seen as a key component to be addressed as early as possible in teacher training (Baumert and Kunter, 2006; Darling-Hammond and Bransford, 2007; European Commission, 2013). Also, teachers themselves state that formative assessment skills are one of the most crucial skills for mastering teaching (Fives and Gill, 2015). Currently, there are multiple perspectives on assessment skills as part of teachers’ professional competences. One of the possibly most far-reaching and simultaneously general conceptions is the framework suggested by Blömeke et al. (2015), which incorporates different research perspectives on professional competences and skills. In the context of formative teacher assessment, the framework differentiates between teacher dispositions relevant for a specific professional competence, diagnostic activities that are carried out in a specific situation, and the performance resulting from these dispositions and activities in a specific situation.
Regarding teacher assessment and diagnostic competences, prior research has focused largely on teacher performance in the form of accurate student judgment (Schrader and Helmke, 1987; Hosenfeld et al., 2002; McElvany et al., 2009). It could be shown, for example, that teachers can assess student achievement relatively accurately, whereby students are perceived holistically so that other individual characteristics, such as self-concept or ability, are easily intermingled (Südkamp et al., 2012; Kaiser et al., 2013). There are also several approaches that have examined teachers’ professional dispositions and their influence on performance regarding judgment accuracy (e.g., Kunter and Trautwein, 2013). Generally, research suggests that one of the most important dispositions for teachers’ assessment skills is their professional knowledge base (see e.g., Glogger-Frey et al., 2018). In particular, teachers’ pedagogical content knowledge is strongly linked to higher assessment performance (Karing, 2009).
Currently, research is engaged in further understanding the assessment process and uncovering professionally relevant diagnostic activities. In doing so, researchers draw on conceptual models from other fields, such as general psychology or medical decision-making. Some approaches use the lens model of perception by Brunswick (1955) to understand how teachers come to their judgments to derive starting points in fostering the assessment process (Nestler and Back, 2016). Other approaches use the model of diagnostic reasoning by Croskerry (2009), which originated in medicine and distinguishes diagnostic activities in the assessment process in two ways: (i) heuristically, intuitive activities (Leuders and Loibl, 2020) and (ii) more systematic, analytical activities (Fischer et al., 2014). It is also becoming more common to use the professional vision framework to describe diagnostic activities in assessment situations when looking at them from an analytical perspective (Goodwin, 1994; Seidel and Stürmer, 2014). Here, a distinction is made between the noticing of information and the subsequent knowledge-based reasoning and interpretation of the information.
On-the-fly assessment situations, in particular, are meaningful professional contexts in which diagnostic activities have to be carried out that can serve as authentic situations to observe these activities (Shavelson et al., 2008). However, these situations are rather challenging methodologically when attempting to measure cognitive processes and activities in a short period of time within a real classroom. In order to capture and study these diagnostic activities, the use of video has been found useful in research over the last years (Gaudin and Chaliès, 2015; van Es et al., 2020). By embedding video clips in assessment or learning environments, such as simulations, authentic yet also more controllable assessment situations can be created in which the diagnostic activities in the assessment process can be systematically studied (Heitzmann et al., 2019). In some cases, recent research approaches even go a step further and use techniques such as eye tracking to further study attentional processes in assessment situations (Seidel et al., 2020).
Teacher Professional Vision
A great deal of information teachers gain about their students for adaptive teaching comes from observation in the classroom while teaching (Karst et al., 2017; Südkamp and Praetorius, 2017). Teachers have to draw their attention to particular aspects in a classroom and the information it contains, as not all ongoing classroom information can be processed at the same time (Gegenfurtner et al., 2020). In order to better understand the link between teachers’ attentional foci, the processing of this information, and the final performance in assessing students, it is important to study what student-related information teachers notice and how teachers apply their professional knowledge to reason about this noticed information, which are taken as cues for their evaluations and explanations. For this purpose, noticing and knowledge-based reasoning (Goodwin, 1994; van Es and Sherin, 2002; Seidel and Stürmer, 2014) are seen as important diagnostic activities that can help to explain the link to the final diagnosis (see Figure 1).
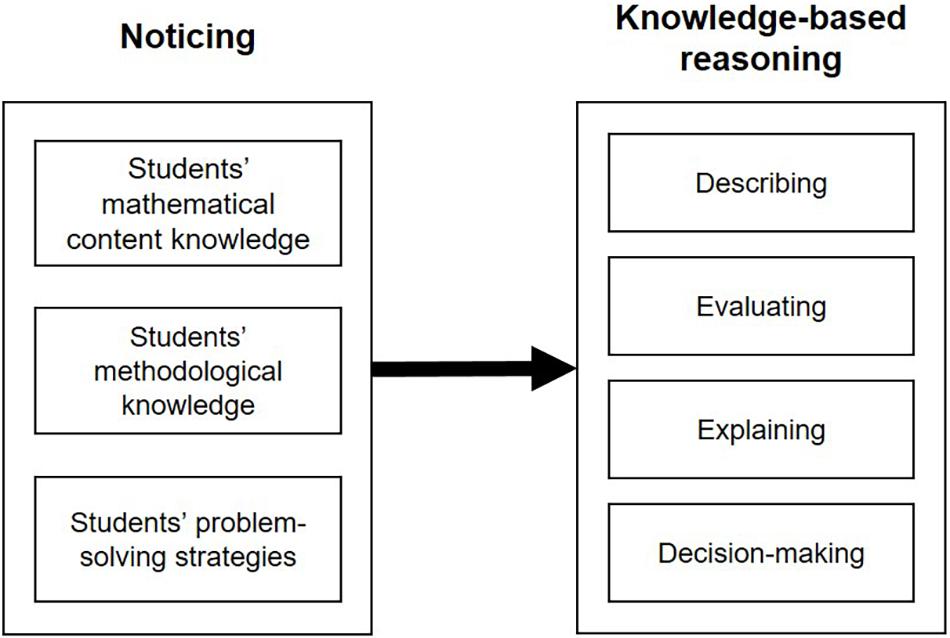
Figure 1. Teachers’ diagnostic activities when assessing students’ mathematical argumentation skills.
The teacher professional vision framework, therefore, is seen as an important conceptual model to further study teachers’ situation-specific professional skills (Seidel and Stürmer, 2014). In this context, the diagnostic activity noticing refers to the perception of relevant events in the classroom (van Es and Sherin, 2008; Schack et al., 2017), while knowledge-based reasoning is the act of interpreting the noticed information based on one’s professional knowledge (Gegenfurtner et al., 2020). Seidel and Stürmer (2014) distinguish three different knowledge-based reasoning activities: describing, explaining, and predicting. Describing refers to the verbalization of noticed information without making any further judgments. Explaining refers to the linking of described information to professional concepts and knowledge. Finally, predicting refers to the ability to draw conclusions about the students’ learning. These activities can also be found under the concept of situation-specific skills in the description of teachers’ competences by Blömeke et al. (2015); explaining can be seen as part of the activity of interpreting, whereas predicting can be seen as part of teachers’ decision-making (Kramer et al., 2020). Similarities can also be found in the work of Fischer et al. (2014) on scientific reasoning in general, independent of assessment situations and teacher professional competencies. For example, what Fischer et al. (2014) call “evidence evaluation” can be understood in the sense of an interpretation of information (or evidence) that requires further explanation (Bauer et al., 2020). The activity of drawing conclusions can be related to aspects of decision-making, as used in Blömeke et al. (2015). Although these three frameworks (Fischer et al., 2014; Seidel and Stürmer, 2014; Blömeke et al., 2015) differ in their labels for the activities and their granularity, they have a great deal in common and could each be used to describe teachers’ diagnostic activities during assessment situations. To investigate knowledge-based reasoning in the assessment process focused on in this study, we followed the structure of Blömeke et al. (2015) and particularly, examined the diagnostic activities of interpreting and decision-making. For a deeper analysis of the activity of interpreting, we differentiated the activities describing and explaining, as emphasized by Seidel and Stürmer (2014), as well as evaluating, as emphasized by Fischer et al. (2014) (see Figure 1).
In research on teacher professional vision, videos are often used as stimuli to study noticing and knowledge-based reasoning activities (Sherin et al., 2011; van Es et al., 2020). Video clips have an advantage in that the course of action can be slowed down or even scripted. As a consequence, the complexity of classroom situations can be reduced, and particular activities regarding a teacher’s professional vision can be uncovered to a stronger extent (Sherin et al., 2009; van Es et al., 2020). The related research has shown differences between experienced teachers and preservice teachers in their noticing and knowledge-based reasoning (Schäfer, 2014; Seidel et al., 2020). The results indicate that expert and novice teachers differ relatively little with regard to general noticing skills (Begrich et al., 2020). However, experts outperform novices with regard to their knowledge-based reasoning skills. Whereas novice teachers tend to be better able to precisely describe classroom situations, experts show more elaborated reasoning skills with regard to explaining situations based on their professional knowledge (Stürmer et al., 2013). Still, little is known about professional vision in on-the-fly assessment situations, in particular regarding domain-specific knowledge-based reasoning activities and how these can be captured in digital environments, such as video-based simulations.
Students’ Mathematical Argumentation Skills
As mathematics is a proving science, handling mathematical argumentations and proofs is a crucial mathematical activity (Boero, 2007). That makes mathematical argumentation and proof an important educational goal in secondary education worldwide (e.g., Kultusministerkonferenz, 2012; CCSSI, 2020), as well as an important student competence that has to be assessed during classroom situations. Mathematical argumentation is generally understood as a broad term that includes all activities that focus on the generation and evaluation of mathematical hypotheses and open questions (Reiss and Ufer, 2009). In contrast, mathematical proving is seen more narrowly as a more formal form of mathematical argumentation that follows specific norms of the mathematical community (Stylianides, 2007) to show the validity of an assumption. For example, only deductive conclusions are accepted in a mathematical proof (Heinze and Reiss, 2003; Pedemonte, 2007). Although proving is a central mathematical activity, empirical studies have repeatedly shown that students have substantial problems with handling mathematical proofs (Harel and Sowder, 1998; Healy and Hoyles, 2000; Heinze, 2004). For example, it has been shown that insufficient understanding of mathematical relationships, such as if-then statements, can lead to typical errors (Duval, 2007).
The successful construction of proofs by a student depends on several prerequisites (Heinze and Kwak, 2002; Lin, 2005; Ufer et al., 2009). Knowing which prerequisites students need in order to handle mathematical proof and being able to assess students’ individual availability of these prerequisites in diagnostic classroom situations enables teachers to adapt their teaching to ensure deep understanding as a learning outcome (Beck et al., 2008; Herbst and Kosko, 2014). Research on proving in mathematics education provides indications as to which student sub-skills and knowledge facets influence the ability to prove (van Dormolen, 1977). Based on the research (e.g., Ufer et al., 2008; Chinnappan et al., 2011; Sommerhoff et al., 2015), the following prerequisites can be considered among the most important: the students’ mathematical content knowledge, their methodological knowledge, and their problem-solving strategies. A students’ mathematical content knowledge refers to knowledge of definitions, propositions, and terms from the field of mathematics in which the proof has to be constructed (Weigand et al., 2014). In the field of geometry, for example, the knowledge of the correct sum of internal angles in triangles is part of that knowledge (see also Heinze, 2002). In diagnostic situations, cues indicating the availability of a student’s sufficient mathematical content knowledge can be noticed quite directly by its application in the written proof or by its verbalization in a teacher-student interaction (Codreanu et al., in press). For the activity of proving as a formal form of mathematical argumentation, which follows certain norms of the (local) mathematical community, it is also important to know those norms that define an acceptable mathematical proof (Heinze and Reiss, 2003). Part of this so-called methodological knowledge is, for example, to know which kind of arguments are allowed in a mathematical proof (deductive reasoning patterns). Cues for the availability of methodological knowledge in diagnostic situations can be seen during the formulation of single steps in the process of constructing a proof, as well as in the entire process of proving, that is, when using inferential reasoning to connect individual information during the proving process. Finally, research in secondary school contexts has shown that knowledge about and the use of problem-solving strategies is also crucial for the successful handling of mathematical proofs (Schoenfeld, 1992). This includes strategies such as decomposing a task down into small steps (Pólya, 1973; Chinnappan and Lawson, 1996). In contrast to both of the prior prerequisite types, the application of such strategies can only be noticed in consideration of the whole process of proving or if the student explicates such a strategy, which, however, is rare if not explicitly prompted. Thus, finding according cues may be less direct than, for example, those for sufficient mathematical content knowledge.
In on-the-fly situations in class, teachers need to pay attention to those events that are important for assessment (Seidel and Stürmer, 2014). To accurately assess students’ skills in handling mathematical proofs, teachers need to identify and filter information about the students’ sub-skills and knowledge facets that are predictive for those skills (see Figure 1). Research on teacher judgment has shown that more salient characteristics, such as achievement or declarative knowledge, can be assessed more accurately than characteristics that have fewer observable cues (Kaiser et al., 2013), for example, motivational-affective characteristics, students’ epistemologies (like those related to proof), or mostly implicit knowledge. Therefore, it is likely that preservice teachers may be able to observe cues for students’ mathematical content knowledge more precisely and accurately, compared to more complex prerequisites, such as students’ problem-solving strategies, which are rarely explicitly mentioned but can be implicitly observed in students’ behavior. In addition, in situations in which teachers have to consider combinations of different student characteristics, they tend to struggle most with inconsistent, as compared to consistent, combinations (Südkamp et al., 2018). Therefore, students that show a consistent availability of all relevant facets (mathematical knowledge, methodological knowledge, and use of problem-solving strategies) should be assessed more accurately than students with partially inconsistent combinations of the three facets.
The Present Study
The main aim of the present study was to provide further insight into teachers’ handling of situation-specific professional tasks such as on-the-fly student assessment and the involved diagnostic processes when assessing students’ argumentation skills. For this, a video-based simulation was used in order to create controllable as well as comparable classroom situations for the participants. First, the assessment process was described by examining the preservice teachers’ noticing based on whether they could focus on professionally relevant information (RQ 1). Second, the diagnostic activities of knowledge-based reasoning were explored (RQ 2).
RQ1a: To what extent do preservice teachers notice different facets of students’ mathematical argumentation skills in an on-the-fly assessment situation?
The individual level of three considered prerequisites of mathematical argumentation skills (mathematical content knowledge, methodological knowledge, and problem-solving strategies) shown by a simulated student should be perceived by preservice teacher participants. We expected that simulated students’ mathematical content knowledge would be perceived most frequently, as it is salient in what simulated students say and write in their task solutions. Furthermore, especially without basic mathematical content knowledge, it is hard to solve a proof task, as the simulated students are solving during the simulation. A focus on the mathematical content is, therefore, helpful to get a first impression of the simulated students’ level of argumentation skills. In contrast, both students’ problem-solving strategies and their methodological knowledge will likely not be explicitly expressed. They will rather be visible in (the combination of multiple) student actions and the student’s general behavior and approach when working on the proof task. However, when comparing problem-solving strategies and methodological knowledge, the latter might be slightly easier to assess, as it not only relates to the general approach to the task (or a subtask) but may also be visible in particular individual actions of the simulated students (e.g., the use of specific examples as a general argument). Therefore, we assumed that participants would notice these two prerequisites less frequently, whereas methodological knowledge would tend to be somewhat easier on which to focus.
RQ1b: Are there differences in the preservice teachers’ noticing for students with different levels of mathematical argumentation skills?
The more a student struggles with a mathematical proof task, the less a teacher will focus on the prerequisite methodological knowledge and problem-solving strategies, as the students’ problems are already salient in his or her mathematical content knowledge. However, intermediate and, in particular, strong students will show only few difficulties with the mathematical content so that the teachers’ focus should shift increasingly to the less salient prerequisites, such as methodological knowledge and problem-solving strategies. Thus, we expected preservice teachers to focus most strongly on mathematical content knowledge with struggling students; methodological knowledge and problem-solving strategies would be increasingly addressed in the assessment process of stronger students.
RQ2a: To what extent do preservice teachers show knowledge-based reasoning as diagnostic activities in the process of assessing students?
We assumed that preservice teachers would be able to show knowledge-based reasoning activities in an assessment process. Therefore, we expected to observe aspects of knowledge-based reasoning, such as describing, evaluating, explaining, and decision-making in the teacher’s assessment of the students’ mathematical argumentation skills. Since these diagnostic activities have a natural step-by-step structure, we assumed that preservice teachers would tend to describe and evaluate more than explain or suggest in making decisions. Giving explanations using conceptual professional knowledge and making a decision by integrating different pieces of evidence that were noticed and interpreted should be difficult for preservice teachers to apply in an assessment situation. Therefore, we expected a rather small percentage of these diagnostic activities in the process of knowledge-based reasoning.
RQ2b: Are there differences in the preservice teachers’ knowledge-based reasoning for students with different levels of mathematical argumentation skills?
We assumed that the diagnostic activities of knowledge-based reasoning would be strongly dependent on the individual student the preservice teachers were assessing. When assessing students in similar on-the-fly assessment situations (e.g., students who are working on the same geometrical proof task), teachers need similar professional conceptual knowledge to explain the course of actions or the students’ level of knowledge. Thus, deep knowledge-based reasoning activities like explaining or decision-making about further learning support that requires a similar professional knowledge base should occur as often in the assessment, independent of the students’ level of mathematical argumentation skills.
Materials and Methods
Participants
A total of N = 51 preservice high-school teachers with a mathematics major, 37 (73%) females and 14 (27%) males, from a German university participated in the study in the summer semester of 2019. The preservice teachers participated in the study voluntarily, and their participation was remunerated. On average, they were 22.1 (SD = 2.6) years old. Most participants were in the fourth semester of their bachelor’s degree in teaching secondary school mathematics. They had already completed several mathematics courses (three or more courses for over 85% of participants) and courses in mathematics education (three or more courses for over 90% of participants) in previous semesters.
Content of the Simulation
The video-based simulation used for the study represented a typical on-the-fly assessment situation with one-on-one teacher-student interactions with four simulated students. In the portrayed situation, four simulated seventh graders were all working on the same mathematical proof task; they had to prove that opposite sides of a parallelogram were of equal length based on the information that a parallelogram’s pairs of sides were parallel. The students simulated in the video were played by actors; their actions and dialogue were scripted to represent different levels of mathematical argumentation skills. Simulated Student A (i.e., the struggling student) had the weakest mathematical argumentation skills, which ranged up to those of Student D (i.e., the strong student), who had adequate skills to handle the proof1.
Each video clip contained cues about the students’ argumentation skills. Cues for all three prerequisites (mathematical content knowledge, methodological knowledge, and problem-solving strategies) could be found both in the spoken and written word. The videos were scripted to ensure that the cues appeared evenly distributed across the individual videos, students, and prerequisites. After the production of the staged videos, two members of the research team checked the simulated students’ level of mathematical argumentation skills. In doing so, they rated the skills regarding the three prerequisites on a 4-point Likert scale (1 = “mostly not available” to 4 = “available”). Figure 2 shows the mean values for the prerequisites, which were calculated from the expert ratings of the individual sub-facets of the three prerequisites.
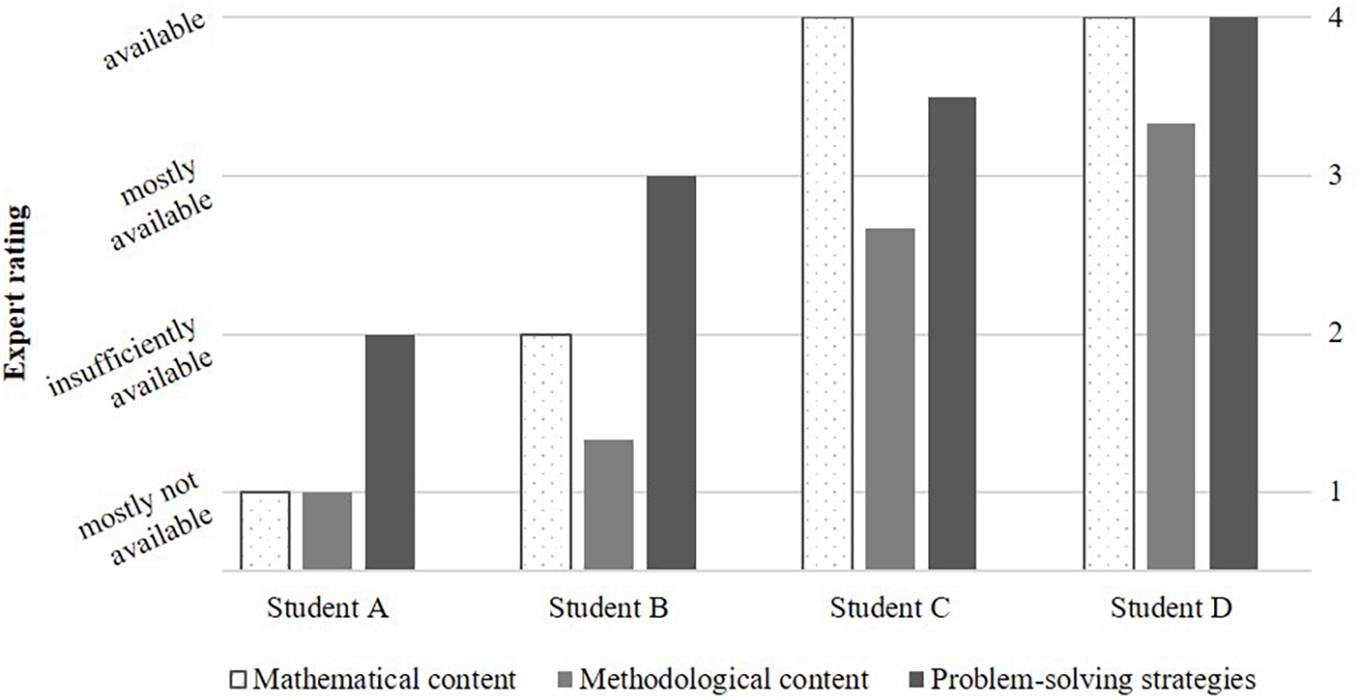
Figure 2. Availability of central prerequisites for the simulated students’ mathematical argumentation skills.
Procedure of the Study
The participants of the study worked for 1 h on the video-based simulation (for a detailed description of the video-based simulation, see Codreanu et al., 2020, in press). At the beginning of the simulation, the participants are introduced to the assessment situation; the participants take the role of a preservice intern accompanying a simulated teacher in his class. The participants are then introduced to their assessment task; the simulated teacher asked them to assess the mathematical argumentation skills of four simulated students (while he is mostly absorbed by the remaining students in the class) so that he could choose tasks for their individual learning support in subsequent classes. Moreover, the participants received information on the three students’ prerequisites of mathematical argumentation skills on which they were asked to focus, as well as on the components an assessment text should ideally contain (see Figure 3, area A).
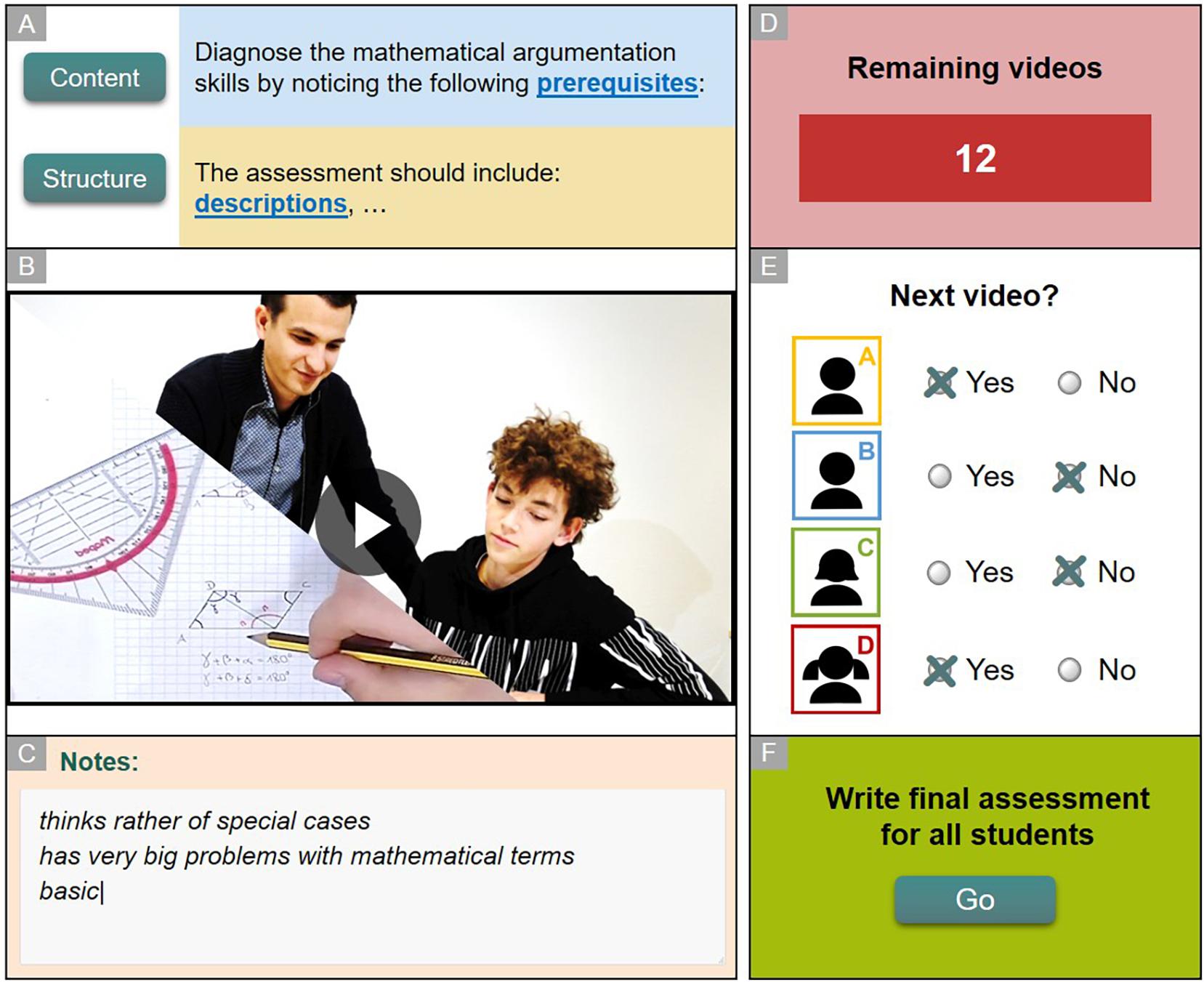
Figure 3. Outline of the assessment process in the video-based simulation with the areas (A) Introduction to assessment task. (B) Video clips showing the teacher-student interactions. (C) Participants’ notes. (D) Number of remaining video clips. (E) Participants’ influence on the course of actions in the simulation. (F) Final assessment.
In the actual assessment process, participants could then work independently in the simulated classroom situation to gather information about the simulated students by watching short video clips and taking notes (see Figure 3, areas B and C). In a video clip, the simulated teacher and one simulated student are discussing the students’ progress and argumentation in the context of the given geometry proof task (Figure 3, area B). After observing each simulated student in a video clip, participants were able to choose to either further observe the simulated student or to decide that they had gathered sufficient information for the assessment of this particular simulated student (Figure 3, area E). In total, a maximum of 20 video clips could be observed, and participants were free to decide how to distribute these observations among the simulated students (Figure 3, area D). Participants were also asked to write a free text assessment of each simulated student, which was introduced in the simulation as being passed on to the simulated teacher (Figure 3, area F). Besides, participants would rate the students’ prerequisites on 4-point Likert scales (see Codreanu et al., 2020).
Measures
Coding of Free Text Assessments
In advance of the actual coding by the researchers, the participants’ free text assessments were segmented into separate coding units representing distinct statements. The formation of the coding units was done semi-automatically. However, care was taken to ensure that meaningful units intended by the participants were recognized and grouped in one coding unit via a subsequent manual check. Afterward, all the units were independently coded by two researchers. To determine the inter-rater reliability, Cohen’s κ was calculated. Subsequently, the coding units for which both coders did not agree were jointly examined and classified based on a consensus method.
Coding Scheme
The codes were identified using both deductive and inductive methods. First, particular codes were defined deductively based on the literature. Second, the operationalization of the codes was tested and inductively refined by both coders based on a dataset from a prior validation study of the video-based simulation (N = 28; cf. Codreanu et al., 2020).
Noticing
The final coding scheme consisted of three different codes for the content of the assessment mentioned within the free text assessments: students’ mathematical content knowledge, methodological knowledge, and problem-solving strategies (see Table 1). The code mathematical knowledge included all statements that referred to the simulated students’ knowledge about definitions, propositions, rules, and terms in the geometry of figures. Methodological knowledge included statements that referred to the simulated students’ knowledge about the nature of proofs and specifically about necessary criteria for the acceptance of a mathematical proof (Sommerhoff and Ufer, 2019). The problem-solving strategies code was used to classify all units that referred to the simulated students’ use of heuristic or metacognitive strategies to solve the problem or to monitor and control their learning process. Importantly, the coder could classify a unit with one or more of the content codes in order to accommodate statements that included both content aspects (e.g., “She has good basic knowledge, but is not good at translating this into valid arguments,” which contains the student’s mathematical content knowledge and methodological knowledge). If the unit could not be assigned to one of the three codes, it was classified as others. Independently coding the content in all of the assessment texts, the two researchers achieved a Cohen’s κ of 0.94.
Knowledge-Based Reasoning
For coding knowledge-based reasoning, four different codes were applied, following the professional vision literature (cf. Seidel and Stürmer, 2014), as well as the literature for scientific reasoning and argumentation (cf. Fischer et al., 2014): description, evaluation, explanation, and decision-making (see Table 2). Describing refers to the ability to limit oneself to the description of a concrete course of action, as seen in the video clips of the simulation without any further judgments. The code evaluation was used whenever a writer inferred a general pattern of behavior of the student or the students’ level of knowledge. Explanation included statements that named reasons for a course of action or the students’ level of knowledge. Decision-making refers to recommendations for the individual learning support of the student in subsequent classes. In parallel, each unit that was coded to include (at least) one of the three prerequisite noticing codes was classified with one or more of the knowledge-based reasoning codes. If a unit could not be assigned to one of these knowledge-based reasoning codes, it was classified as others. Independently coding the knowledge-based reasoning in all of the assessment texts, the two researchers achieved a Cohen’s κ of 0.82.
Data Analysis
Descriptive statistics were computed to describe and explore the participants’ diagnostic activities in the assessment of the simulated students. Additionally, one-way repeated-measures analyses of variances (rmANOVAs) were computed with Bonferroni-adjusted post-hoc comparisons to reveal differences in the assessment texts regarding the noticing and knowledge-based reasoning activities. All participants were included in these analyses.
Results
All of the 51 participants wrote a free text assessment for each of the four simulated students, so 204 assessments were analyzed. The segmenting of the texts resulted in 787 individual coding units (simulated Student A: 173, B: 227, C: 203, and D: 184). A χ2-test showed that the number of coding units was not significantly different from what would be expected among the simulated students (χ2 = 4.21, df = 3, p = 0.240). On average, a single assessment text consisted of 3.86 coding units with a standard deviation of SD = 2.17 and a wide range from one up to 13 coding units. The number of coding units in an assessment text varied more between participants (SDbetween = 1.90) than within the four text assessments of a participant (SDwithin = 1.01). Similar to the study of Codreanu et al. (2020), participants showed only moderate results regarding their assessment accuracy (M = 0.46, SD = 0.12). The assessment accuracy was expressed as the normalized agreement with the expert solution and ranged from 0.00 (no agreement with the solution) to 1.00 (perfect agreement with the solution).
Noticing: Analysis of Noticed Mathematical Content
In the participants’ assessment texts, 847 codes represented noticed students’ prerequisites. The majority of the 787 coding units (86.30%) received only a single code. Participants mainly noticed prerequisites that were predictive for students’ performance in handling mathematical argumentations in proofs (only 13.46% of the 847 codes belonged to the code others). Figure 4 shows the percentages of the noticed students’ prerequisites in the assessment texts.
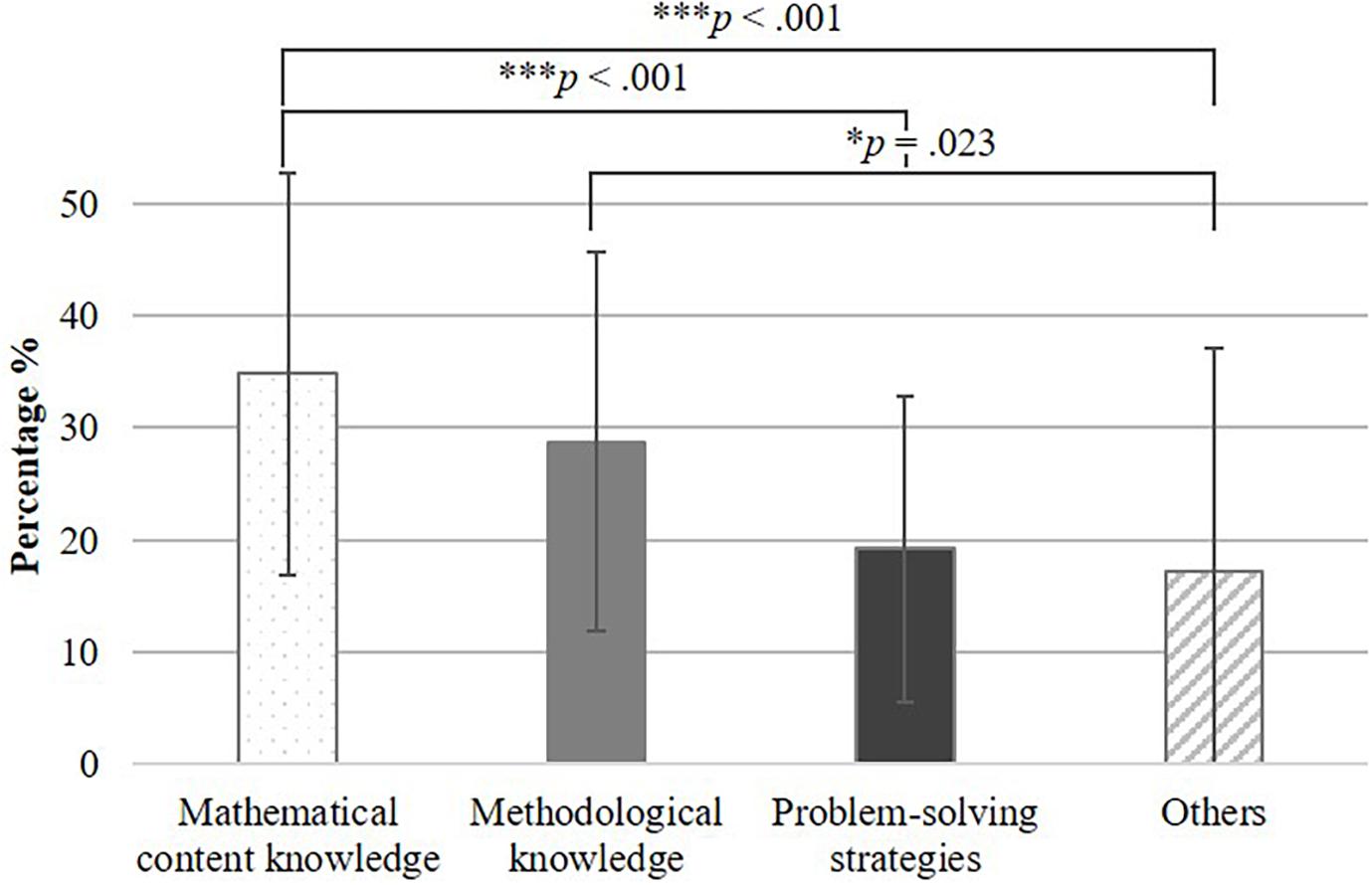
Figure 4. The noticed content of the assessment texts with the following significance levels: *p < 0.05; **p < 0.01; ***p < 0.001.
As conjectured, preservice teachers noticed mathematical content knowledge most frequently when assessing simulated students (34.81% of all codes in the assessment texts were mathematical content knowledge codes, SD = 17.94%). The simulated students’ methodological knowledge was noticed in 28.78% of the texts (SD = 16.96%), and assumed problem-solving strategies were noticed the least frequently (M = 19.23%, SD = 13.66%). The rmANOVA showed significant differences between the noticed prerequisites, [F(3, 150) = 8.73, p < 0.001], with a partial eta squared of η = 0.15. The post-hoc pairwise comparisons revealed a significant difference (Bonferroni-adjusted p < 0.001) between mathematical content knowledge and problem-solving strategies (15.58%, SE = 3.96%).
Comparing the participants’ assessment texts of the four simulated students, further differences in the preservice teachers’ noticing can be observed (Figure 5). In assessing the struggling simulated student (Student A), the participants mainly noticed aspects of mathematical content knowledge. A rmANOVA for the struggling simulated student showed that the proportion of mathematical content knowledge codes was significantly higher than the proportion of other codes (see Figure 5). Thus, the participants tended to focus on the prerequisite in which the struggling student had the most obvious problems. In contrast, the mathematical content knowledge with its salient cues played a much smaller role in the assessments of the other simulated students. The assessments of the two medium-level students (B and C) showed a lesser focus on the students’ methodological knowledge. For these two simulated students, the mathematical content knowledge was not sufficient to assess their mathematical argumentation skills accurately. In conjunction with this, a shift in the focus toward the methodological knowledge and problem-solving strategies prerequisites can be described. In order to assess the strong simulated student (student D), a further shift of focus toward problem-solving strategies was observed. The assessment texts of the strong simulated student displayed that there were no significant differences in the noticing of all three prerequisites, [F(3, 150) = 2.56, p = 0.057]. In general, the better a simulated student was able to handle the given mathematical proof task, the more balanced the preservice teachers were in noticing the different prerequisites of mathematical argumentation skills in this video-based simulation.
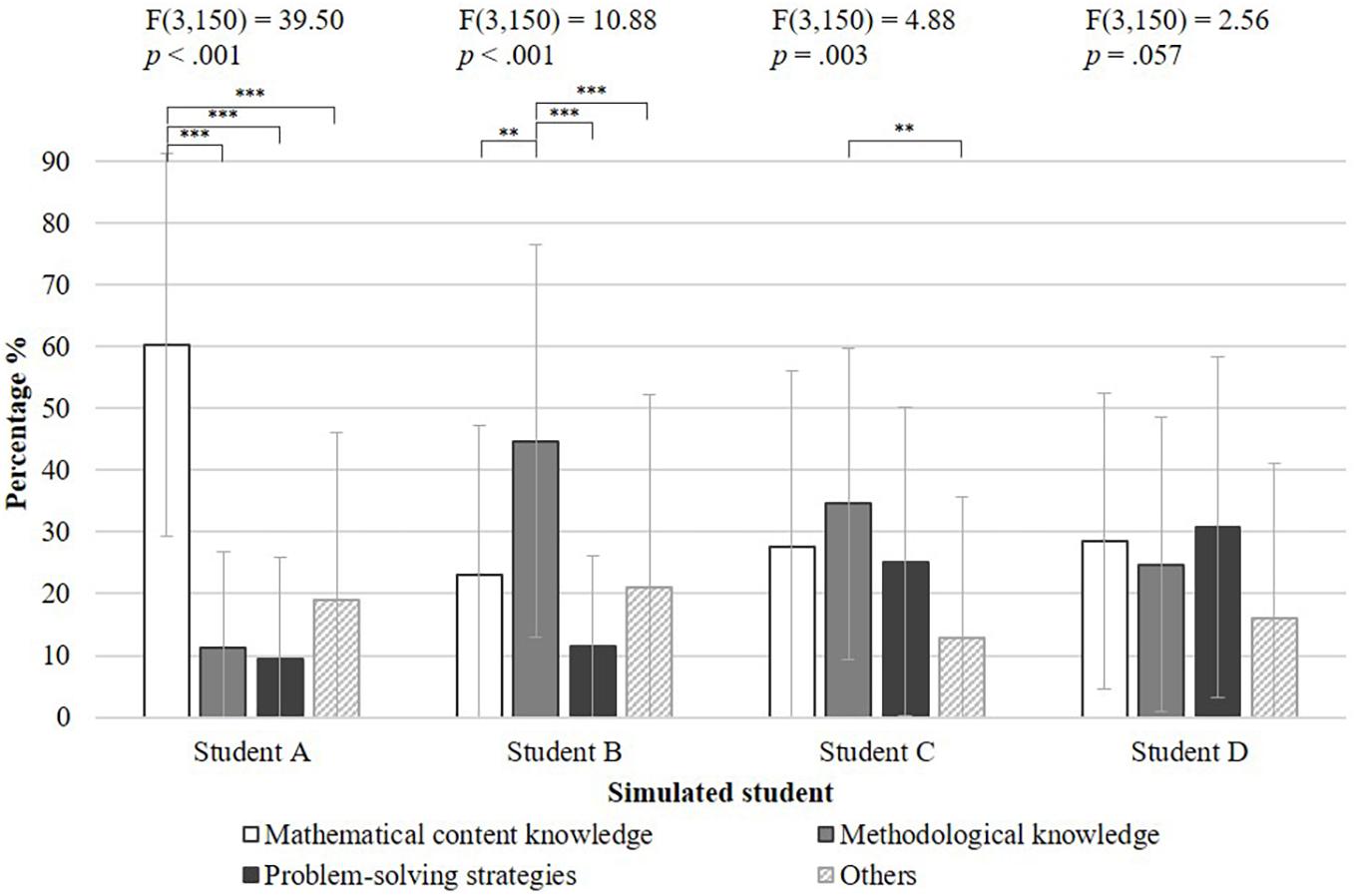
Figure 5. Differences in the noticed prerequisites of the four simulated students with the following significance levels: **p < 0.01 and ***p < 0.001.
Knowledge-Based Reasoning: Analysis of Diagnostic Activities
In the participants’ assessment texts, 806 knowledge-based reasoning codes were assigned to 673 coding units that were coded with the students’ three prerequisites. Figure 6 shows the distribution of knowledge-based reasoning activities across the four applied codes for the activities: description, evaluation, explanation, and decision-making.
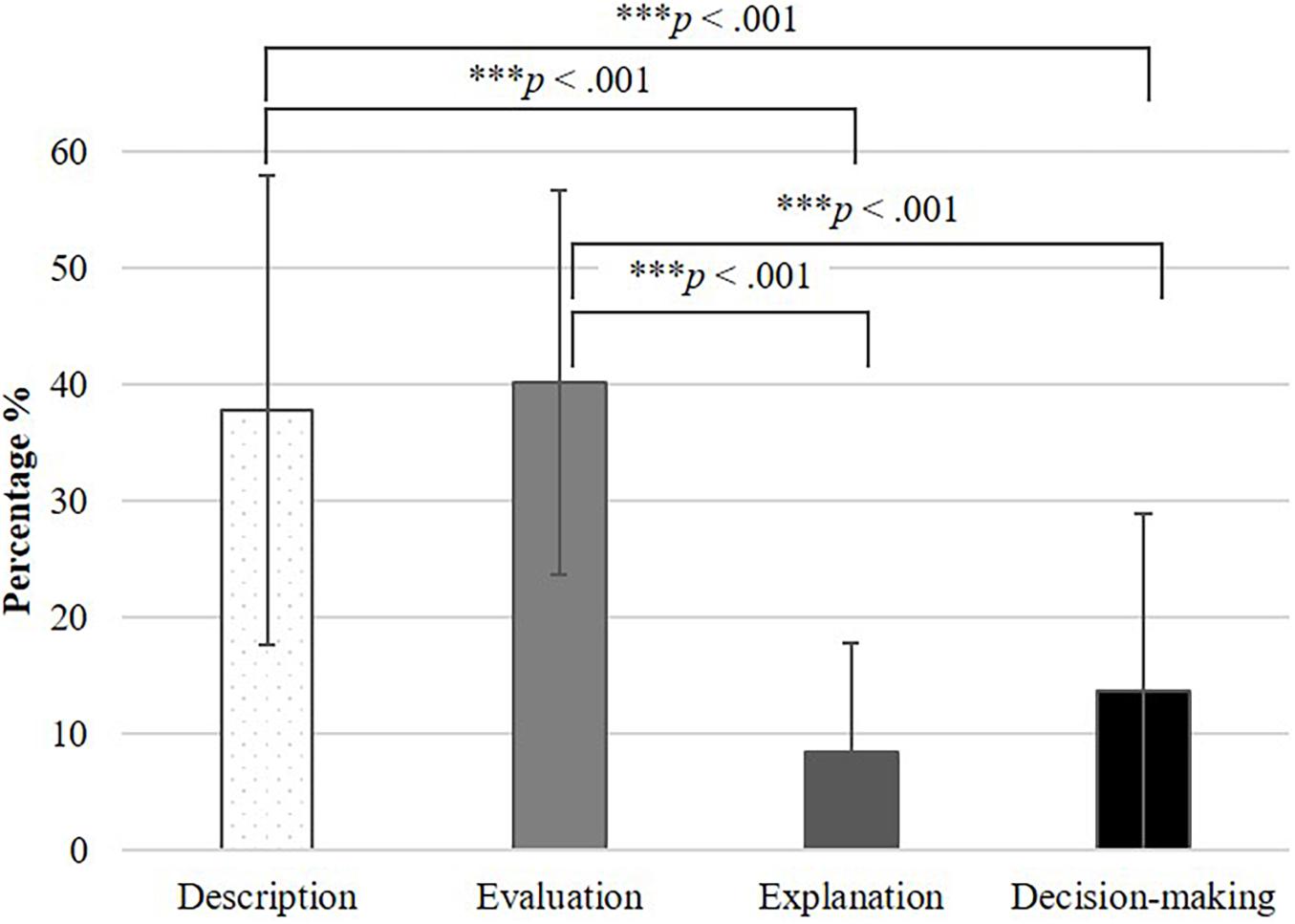
Figure 6. Distribution of knowledge-based reasoning activities with the following significance level: ***p < 0.001.
As conjectured, participants were mostly describing (M = 37.72%, SD = 20.16%) concrete situations and events, but also generalizing them to overall patterns of behavior (evaluation: M = 40.20%, SD = 16.54%). Overall, only a few explanations for simulated students’ actions or their level of knowledge were given (explanation: M = 8.38%, SD = 9.39%). Furthermore, decision-making (e.g., individual learning support) was only coded in a very small part of the assessment texts (decision-making: M = 13.70%, SD = 15.16%). A rmANOVA showed significant differences between knowledge-based reasoning activities, [F(3, 150) = 38.93, p < 0.001], with a partial eta squared of η = 0.44. Post-hoc pairwise comparisons revealed significant differences between each pairing of one of the two highest (description/evaluation) with one of the two lowest (explanation/decision-making) activities (see Figure 6). Diagnostic activities, such as describing and evaluating, were found more often in the assessments than activities, such as explaining and decision-making, which required a deeper application of professional knowledge to the situation-specific assessment task.
Comparing the participants’ assessment texts of the four simulated students, further insights into the participants’ knowledge-based reasoning activities can be given (Figure 7). Overall, nearly the same distributions of knowledge-based reasoning activities can be shown for each simulated student (Students A–D). This is in line with our conjectures that knowledge-based reasoning activities would be equally required for each simulated student. In assessing each simulated student, the reasoning activities of describing and evaluating were more prominent than the activities of explaining and decision-making. In order to compare proportions of knowledge-based reasoning activities, rmANOVAs were calculated with post-hoc comparisons. The omnibus tests comparing the relative frequencies of the activities among the four simulated students were not significant for the activities explaining [F(3, 150) = 0.50, p = 0.684] and decision-making [F(3, 150) = 0.26, p = 0.854], thus indicating that the percentages of codes regarding these activities were similar across the students. Although the omnibus test for the activity evaluation was significant [F(3, 150) = 2.92, p = 0.044], no pairwise comparison among the simulated students reached significance. Finally, the rmANOVA for describing showed significant differences in the percentage of descriptions in the assessment texts [F(3, 150) = 3.27, p = 0.030] among the four simulated students. The post-hoc pairwise comparisons revealed a significant difference between the descriptions for the struggling Student A and the medium-low-level Student B of 15.88% (SE = 4.79%, Bonferroni-adjusted p = 0.007).
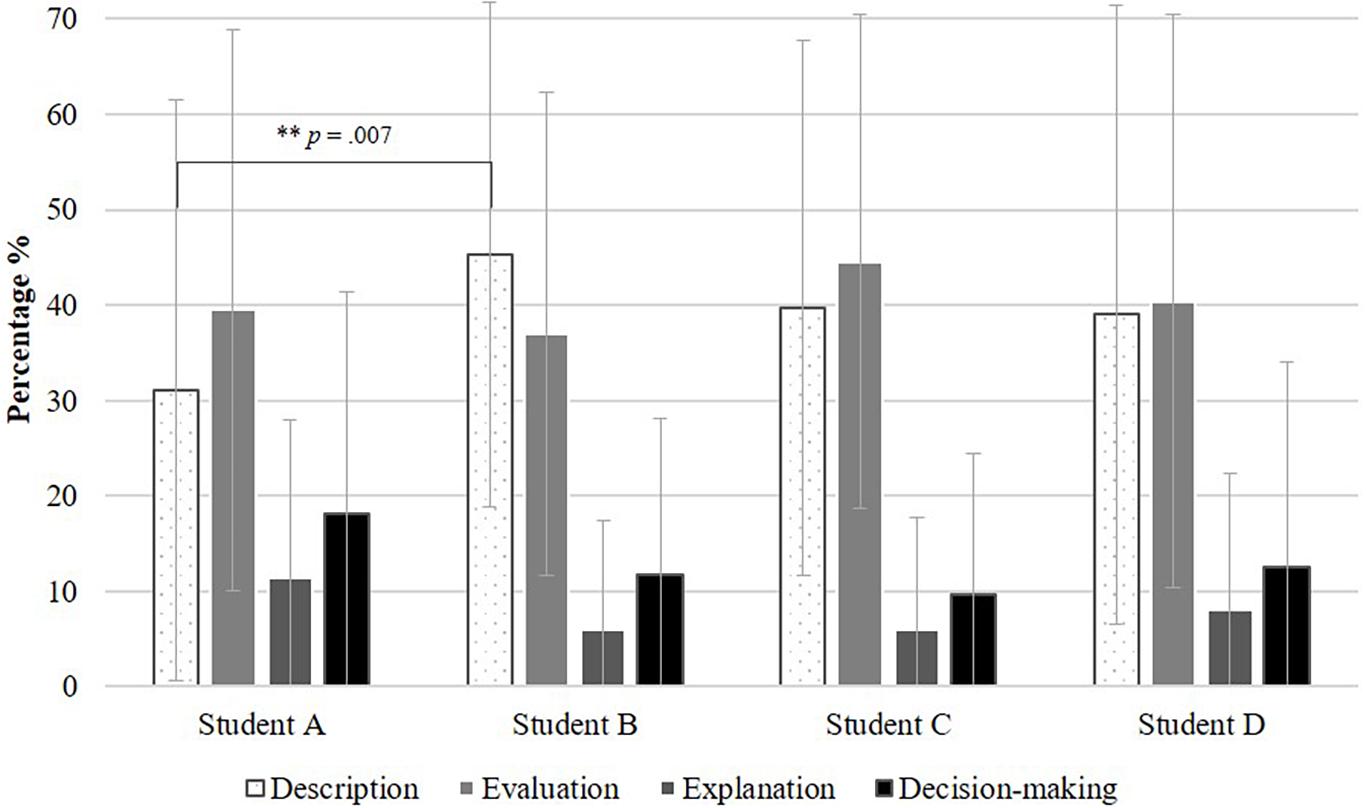
Figure 7. Differences in knowledge-based reasoning activities for the four simulated students with the following significance level: **p < 0.01.
Discussion
This study examined preservice teachers’ assessment skills in a formative assessment situation (Heitzmann et al., 2019). Such on-the-fly assessment situations present challenges for many novice teachers in their first years of teaching (Levin et al., 2009). This paper addressed the assessment process of preservice teachers and showed the potential challenges with the diagnostic activities performed in the process. Since assessment skills are context-specific (Blömeke et al., 2015), they were examined in the context of a video-based simulation. This environment offered an authentic classroom situation and, at the same time, the possibility to closely observe the assessment process in a standardized way, which is rather complicated in real-life situations (Grossman and McDonald, 2008; Codreanu et al., 2020). Of particular interest were diagnostic activities, such as noticing and knowledge-based reasoning. Noticing was examined in terms of focusing on relevant information for a subsequent pedagogical decision, as suggested by a subject-specific perspective (Ufer et al., 2008; Sommerhoff et al., 2015). Knowledge-based reasoning considers diagnostic activities that are emphasized in the research on teachers’ professional vision (Goodwin, 1994; van Es, 2011; Seidel and Stürmer, 2014) and in research on scientific reasoning and argumentation (Fischer et al., 2014), which incorporates findings from other disciplines, such as medicine, as well (Radkowitsch et al., 2020).
Noticing Different Students’ Prerequisites Adaptively
In describing the diagnostic activity of noticing from a mathematical education perspective (Schoenfeld, 2011), preservice teachers’ noticing was examined concerning whether they focused on relevant prerequisites for the students’ mathematical argumentation skills (Heinze and Kwak, 2002; Lin, 2005). The findings showed that in the video-based simulation, preservice teachers were able to notice the relevant prerequisites for an assessment that served as the basis for a pedagogical decision. Thus, the findings are in line with the validation study of the video-based simulation, which showed that the embedded assessment task had an adequate level of difficulty and was not too cognitively demanding for preservice teachers (Codreanu et al., 2020). However, the noticing in the video-based simulation took place in a situation with a reduced level of complexity in which the density of irrelevant cues was minimized as much as possible while still considering the authenticity of the situation (Grossman and McDonald, 2008). For comprehensive teacher training on assessment skills at a university, it would be helpful to increase the complexity of the situations regarding the required noticing activities step by step, in order to familiarize the preservice teachers with the professional teaching practice through several approximations (Grossman et al., 2009).
Preservice teachers noticed all the predictive prerequisites in the assessment situation, but the intensity of the preservice teachers’ foci varied across them. Mathematical content knowledge, as a prerequisite with predominantly salient cues (Weigand et al., 2014), was noticed more frequently than prerequisites with less salient cues, such as the use of problem-solving strategies (Chinnappan and Lawson, 1996). This can be seen as analogous to other research in which constructs, such as a prior knowledge base, that have clearly observable cues for an assessment are better noticed than constructs such as self-concept (Kaiser et al., 2013). In the specific situation of this video-based simulation, it has to be considered that without the necessary mathematical content knowledge, it would be difficult for the students to handle the proof task at all. A focus on this particular prerequisite was, therefore, a good point at which to make a first partial assessment. From the results, it can be concluded that preservice teachers were able to notice the relevant information, after a precise introduction on what to focus, and proceeded efficiently to get an impression of the unknown students and their skills. For environments that examine preservice teachers’ assessment skills, attention should be paid that participants are intensively instructed as to which prerequisites are relevant for the assessment of the specific student skills.
When looking at the diagnostic activities that depended on the students’ level of mathematical argumentation skills, differences in the noticing of students’ prerequisites became apparent. The focus of the preservice teachers adapted to the individual students and their skill levels. If a struggling student has the most difficulty in coping with the task due to deficient mathematical content knowledge, this prerequisite was most strongly emphasized in the assessment. If the lack of knowledge of an intermediate student was lower concerning the mathematical content and became more conspicuous for the methodological knowledge, the preservice teachers’ focus also shifted toward the methodological knowledge. If a strong student had few difficulties in coping with the task at all, the preservice teachers’ assessment was balanced regarding the predictive prerequisites. This confirmed our conjecture that preservice teachers could shift their focus efficiently to the dominant difficulties of a student. This showed that preservice teachers not only saw the student with his or her level of thinking holistically (Südkamp et al., 2012; Kaiser et al., 2013) but also noticed the particular prerequisites individually. For further teacher training on assessment skills, it would be helpful to increase the complexity of the noticing activity (Grossman et al., 2009). Here, it would be interesting to examine how preservice teachers would notice less consistent student profiles, which incorporate argumentation skills that vary regarding their prerequisites. Especially for strong preservice teachers, this would be a way to further challenge and promote their assessment skills.
Uneven Distribution of Knowledge-Based Reasoning Activities
Describing the knowledge-based reasoning in the assessment process, preservice teachers were examined concerning whether they showed diagnostic activities like describing, evaluating, explaining, and decision-making. All four of the coded knowledge-based reasoning activities were found in the preservice teachers’ assessment texts. This was an indication that the coding scheme, which was developed using the frameworks of Blömeke et al. (2015) from research on competences, Seidel and Stürmer (2014) from research on professional vision, and Fischer et al. (2014) from research on scientific reasoning and argumentation was helpful in describing the assessment process. Looking at the preservice teachers’ diagnostic activities regarding knowledge-based reasoning, there were significant differences in the frequency of these diagnostic activities. The course of action of the assessment situation was described quite frequently. This goes hand in hand with prior research on teacher education, in which it was shown that describing was the dominant diagnostic activity in the knowledge-based reasoning of preservice teachers (Stürmer et al., 2013).
The diagnostic activity of evaluating, which was derived from Fischer et al.’s (2014) framework, also accounts for a substantial part of the preservice teachers’ knowledge-based reasoning. This is in line with the findings from Bauer et al. (2020), who showed that evaluating is a predominant diagnostic activity in both teachers’ assessments and medical diagnosing. By adding this activity to the coding scheme, the activity of interpreting relevant information (Blömeke et al., 2015) was analyzed with more differentiation. In this way, it could be evaluated whether diagnostic activities that were relevant in disciplines like medicine were also of relevance in examining the assessment process in the field of teacher education (Bauer et al., 2020; Radkowitsch et al., 2020). Evaluating focuses on a part of preservice teachers’ interpretations in which they inferred general patterns of students’ behavior or students’ knowledge levels. Although a certain wealth of experience is helpful here, this activity does not necessarily require sound professional knowledge. Compared to this, explaining was part of the analysis of the interpreting activity in which reasons for the course of actions in the classroom situation or the students’ knowledge and skills had to be named. Here, preservice teachers had to draw mainly on their pedagogical content knowledge from mathematics education and link it to the specific assessment situation. This linking to their own professional knowledge could be a reason why this diagnostic activity was rarely found in the assessment texts. In comparing novice teachers with expert teachers, prior research found that there was a clear difference in this diagnostic activity (Stürmer et al., 2013). In the current study, since the diagnostic activity of interpreting was differentiated and divided into explaining and evaluating, this could be an additional reason why explaining was less present here. To reveal such fine-grained differences and, thus, to take a closer look into the assessment process in an on-the-fly assessment situation, findings from other disciplines such as research on scientific reasoning and argumentation contributed. Finally, decision-making was also a diagnostic activity that preservice teachers seldom showed in the assessment. This could be due to the fact that teachers’ assessment skills were closely related to the pedagogical actions that followed an assessment (Beck et al., 2008; Südkamp et al., 2017). An assessment that emphasizes the students’ mathematical argumentation skills rather than pedagogical consequences, such as teacher actions in the subsequent class, may be challenging for preservice teachers. Overall, the frequency of the preservice teachers’ diagnostic activities regarding knowledge-based reasoning showed a similar pattern as expected.
In analyzing the frequency of knowledge-based reasoning activities while considering the assessments of different students with different mathematical argumentation skills, a robust pattern of the diagnostic activities across the different cases emerged. This was in contrast to the diagnostic activity of noticing students’ prerequisites in which the preservice teachers’ focus adaptively shifted between the cases. Since the preservice teachers had to assess the same student skills in similar assessment situations, they needed similar professional knowledge for the knowledge-based reasoning about the students. This explains why we found hardly any differences in the knowledge-based reasoning activities across different students with different levels of mathematical thinking.
Altogether, preservice teachers showed relatively good performance in noticing students’ predictive prerequisites for their mathematical argumentation skills. Regarding knowledge-based reasoning, preservice teachers usually showed all the diagnostic activities that were examined in this study. Nevertheless, the final assessments of students’ mathematical argumentation skills were only moderately accurate. This indicated that the preservice teachers did not operate properly in the assessment process between noticing relevant information and providing a final assessment. What caused the mediocre assessment was unclear, but the diagnostic activities that were not frequently shown by the preservice teachers, such as explaining, could be a factor that should be addressed in further teacher training on assessment skills. For the development of the video-based simulation toward a digital learning environment, scaffolds should be developed that address exactly this point. In further research, not only could the quantity of diagnostic activities be taken into account, but also the quality of the individual diagnostic activities may provide further insights into the assessment process. A highly structured assessment process in which the particular diagnostic activities are to be individually carried out is one possible approach (Kramer et al., 2020). In a further step, scaffolding the links between the diagnostic activities and fostering their connection can help preservice teachers in developing their assessment skills.
Limitations
Some methodological issues need to be considered when interpreting the results of this study. First, the sample of the study was quite small and homogeneous. The participants showed few differences in their professional knowledge and experiences. In a preceding knowledge test, their performance showed little variance, and concerning previous experiences from the teachers’ professional practice, the sample gave a relatively homogeneous picture. The recruitment of the participants took place mainly in one lecture. Most participants of the lecture participated in the study. Thus, it would be interesting to collect data at other stages during teacher education or even from students with other majors. Second, the preservice teachers’ assessment process was measured in only one particular video-based simulation with a specific situation concerning mathematical argumentations and proofs. For a broader perspective, future studies may investigate the assessment process of preservice teachers in different contexts. These situations can arise from teaching mathematics, if the noticing is of interest, as well as from other school subjects like, for example, biology (Kramer et al., 2020), when it comes to domain independent aspects of knowledge-based reasoning activities. Third, the assessment process and its diagnostic activities were examined by the analysis of the final assessment texts. A view into the preservice teachers’ notes, written down during the assessment process, showed that several passages of the final assessment texts already occurred during the actual process. However, this study did not include live process data. Measuring process data live in the process can have its disadvantages, as the preservice teachers’ assessment process can be disrupted and influenced by the measurement. For example, the method of recording think-aloud protocols requires previous training for the participants, and even then, the question arises as to how valid activities in an authentic process can be observed using think-aloud methods (Charters, 2003; Cotton and Gresty, 2006). In contrast, an investigation of the diagnostic activities that arise in the assessment process and are reflected in the outcome does not disturb the assessment process itself and can still provide insights into the process and its diagnostic activities. Generally, it would be interesting to have a deeper look into the assessment process to gain further insights into diagnostic activities. In particular, simulations with their log data can provide further information about the assessment process regarding some research questions (Radkowitsch et al., 2020).
Conclusion
The present study investigated preservice teachers’ assessment processes in a typical on-the-fly assessment situation in mathematics, a class conducted as a video-based simulation. It contributes to the field of teacher education in three ways. First, the study provides conceptual value, since it outlines how the use of different perspectives in examining the assessment process highlights supplementary aspects that can be combined in meaningful and powerful ways. A domain-specific view on noticing in connection with multiple perspectives on knowledge-based reasoning provided collective insights into the assessment process and its diagnostic activities. Second, the study provides methodological value, since the use of the video-based simulation showed that such simulations are suitable for approximating on-the-fly assessment situations and decomposing them for preservice teachers at a university. With this approach, preservice teachers’ assessment skills can be examined in a context-specific way in authentic classroom situations. Third, the results of this study have practical relevance for teacher education, since scaffolds can be developed based on them to extend the video-based simulation to a learning environment. With the insights into the assessment process gathered in this study, prompts can be embedded adaptively to the preservice teachers’ needs. This provides support to assess students’ skills accurately in a simulation. By increasing the complexity of assessment situations according to a preservice teacher’s level of assessment skills within a teacher training program, important teacher skills can be effectively promoted in university education.
Data Availability Statement
The datasets presented in this article are not readily available because the dataset will be uploaded to a publicly accessable repository as part of the dataset of the DFG research group COSIMA (FOR2385). Requests to access the datasets should be directed to corresponding author.
Ethics Statement
The studies involving human participants were reviewed and approved by the Deutsche Gesellschaft für Psychologie (DGPs). The patients/participants provided their written informed consent to participate in this study.
Author Contributions
EC, DS, SH, SU, and TS designed the study. EC, DS, and SH mainly developed the coding scheme. EC and SH performed the data collection. EC and DS performed the data analyses. EC wrote the manuscript in collaboration with DS, while TS and SU provided feedback. All authors contributed to the article and approved the submitted version.
Funding
This work was funded by the grant from the Deutsche Forschungsgemeinschaft (DFG) to TS, SU, Birgit Neuhaus, and Ralf Schmidmaier (Grant no. 2385, SE 1397/11-1). The funders had no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the participants in our study. Furthermore, we thank our research team for their engagement in data collection and analysis.
Footnotes
- ^ The names of the simulated students have been changed for this article to increase readability. In the original simulation, the simulated students had arbitrary German first names.
References
Bauer, E., Fischer, F., Kiesewetter, J., Shaffer, D. W., Fischer, M. R., Zottmann, J. M., et al. (2020). Diagnostic activities and diagnostic practices in medical education and teacher education: an interdisciplinary comparison. Front. Psychol. 11:562665. doi: 10.3389/fpsyg.2020.562665
Baumert, J., and Kunter, M. (2006). Stichwort: professionelle kompetenz von lehrkräften. Z. Erziehungswiss. 9, 469–520. doi: 10.1007/s11618-006-0165-2
Beck, E., Baer, M., Guldimann, T., Bischoff, S., Brühwiler, C., Müller, P., et al. (2008). Adaptive lehrkompetenz: analyse und struktur, veränderbarkeit und wirkung handlungssteuernden lehrerwissens. Pädagogische Psychol. Entwicklungspsychol. 63:214.
Begrich, L., Fauth, B., and Kunter, M. (2020). Who sees the most? Differences in students’ and educational research experts’ first impressions of classroom instruction. Soc. Psychol. Educ. 23, 673–699. doi: 10.1007/s11218-020-09554-2
Birenbaum, M., Breuer, K., Cascallar, E., Dochy, F., Dori, Y., Ridgway, J., et al. (2006). A learning integrated assessment system. Educ. Res. Rev. 1, 61–67. doi: 10.1016/j.edurev.2006.01.001
Blömeke, S., Gustafsson, J.-E., and Shavelson, R. J. (2015). Beyond dichotomies. Z. Psychol. 223, 3–13. doi: 10.1027/2151-2604/a000194
Boero, P. (2007). “New directions in mathematics and science education,” in Theorems in School: From History, Epistemology and Cognition to Classroom Practice, Vol. 2, ed. P. Boero (Rotterdam: Sense Publ).
Brunswick, E. (1955). Representative design and probabilistic theory in a functional psychology. Psychol. Rev. 62, 193–217. doi: 10.1037/h0047470
CCSSI (2020). Common Core State Standards for Mathematics. Available online at: www.corestandards.org/Math/ (accessed September 7, 2020).
Charters, E. (2003). The use of think-aloud methods in qualitative research an introduction to think-aloud methods. Brock Educ. J. 12, 68–82.
Chinnappan, M., Ekanayake, M. B., and Brown, C. (2011). Specific and general knowledge in geometric proof development. SAARC J. Educ. Res. 8, 1–28. doi: 10.4324/9780203731826-1
Chinnappan, M., and Lawson, M. J. (1996). The effects of training in the use of executive strategies in geometry problem solving. Learn. Instr. 6, 1–17. doi: 10.1016/S0959-4752(96)80001-6
Codreanu, E., Huber, S., Reinhold, S., Sommerhoff, D., Neuhaus, B. J., Schmidmaier, R., et al. (in press). “Diagnosing mathematical argumentation skills: a video-based simulation for pre-service teachers,” in Learning to Diagnose with Simulations: Examples from Teacher Education and Medical Education, eds F. Fischer and A. Opitz (Berlin: Springer). doi: 10.14689/ejer.2019.84.9
Codreanu, E., Sommerhoff, D., Huber, S., Ufer, S., and Seidel, T. (2020). Between authenticity and cognitive demand: finding a balance in designing a video-based simulation in the context of mathematics teacher education. Teach. Teacher Educ. 95:103146. doi: 10.1016/j.tate.2020.103146
Cotton, D., and Gresty, K. (2006). Reflecting on the think-aloud method for evaluating e-learning. Br. J. Educ. Technol. 37, 45–54. doi: 10.1111/j.1467-8535.2005.00521.x
Croskerry, P. (2009). A universal model of diagnostic reasoning. Acad. Med. J. Assoc. Am. Med. Coll. 84, 1022–1028. doi: 10.1097/ACM.0b013e3181ace703
Darling-Hammond, L., and Bransford, J. (2007). Preparing Teachers for a Changing World: What Teachers Should Learn and be Able to do. San Francisco, CA: Jossey-Bass.
DeLuca, C., LaPointe-McEwan, D., and Luhanga, U. (2016). Teacher assessment literacy: a review of international standards and measures. Educ. Assess. Eval. Account. 28, 251–272. doi: 10.1007/S11092-015-9233-6
Duval, R. (2007). “Cognitive functioning and the understanding of mathematical processes of proof,” in New Directions in Mathematics and Science Education: Vol. 2. Theorems in School: From History, Epistemology and Cognition to Classroom Practice, ed. P. Boero (Rotterdam: Sense Publ), 137–162.
European Commission (2013). Supporting Teacher Competence Development: For Better Learning Outcomes. Available online at: http://ec.europa.eu/assets/eac/education/experts-groups/2011-2013/teacher/teachercomp_en.pdf (accessed September 9, 2020).
Fischer, F., Kollar, I., Ufer, S., Sodian, B., Hussmann, H., Pekrun, R., et al. (2014). Scientific reasoning and argumentation: advancing an iinterdisciplinary research agenda in education. Frontline Learn. Res. 5:28–45.
Fives, H., and Gill, M. G. (eds) (2015). International Handbook of Research on Teachers’ Beliefs. Milton Park: Routledge.
Furtak, E. M., Kiemer, K., Circi, R. K., Swanson, R., León, V., de Morrison, D., et al. (2016). Teachers’ formative assessment abilities and their relationship to student learning: findings from a four-year intervention study. Instr. Sci. 44, 267–291. doi: 10.1007/s11251-016-9371-3
Gaudin, C., and Chaliès, S. (2015). Video viewing in teacher education and professional development: a literature review. Educ. Res. Rev. 16, 41–67. doi: 10.1016/j.edurev.2015.06.001
Gegenfurtner, A., Lewalter, D., Lehtinen, E., Schmidt, M., and Gruber, H. (2020). Teacher expertise and professional vision: examining knowledge-based reasoning of pre-service teachers, in-service teachers, and school principals. Front. Educ. 5:59. doi: 10.3389/feduc.2020.00059
Glogger-Frey, I., Herppich, S., and Seidel, T. (2018). Linking teachers’ professional knowledge and teachers’ actions: judgment processes, judgments and training. Teach. Teacher Educ. 76, 176–180. doi: 10.1016/j.tate.2018.08.005
Grossman, P., Compton, C., Igra, D., Ronfeldt, M., Shahan, E., and Williamson, P. W. (2009). Teaching practice: a cross-professional perspective. Teachers Coll. Rec. 111, 2055–2100.
Grossman, P., and McDonald, M. (2008). Back to the future: directions for research in teaching and teacher education. Am. Educ. Res. J. 45, 184–205. doi: 10.3102/0002831207312906
Harel, G., and Sowder, L. (1998). Students’ proof schemes: results from exploratory studies. CBMS Issues Math. Educ. 7, 234–283. doi: 10.1090/cbmath/007/07
Healy, L., and Hoyles, C. (2000). A study of proof conceptions in algebra. J. Res. Math. Educ. 31, 396–428. doi: 10.2307/749651
Heinze, A. (2002). Aber ein Quadrat ist kein Rechteck - Schülerschwierigkeiten beim Verwenden einfacher geometrischer Begriffe in Jahrgang 8. Zentralbl. R Didaktik Math. 34, 51–55. doi: 10.1007/BF02655704
Heinze, A. (2004). Schülerprobleme beim Lösen von geometrischen Beweisaufgaben —eine Interviewstudie—. Zentralbl. Didaktik Math. 36, 150–161. doi: 10.1007/BF02655667
Heinze, A., and Kwak, J. Y. (2002). Informal prerequisites for informal proofs. Zentralbl. Didaktik Math. 34, 9–16. doi: 10.1007/BF02655688
Heinze, A., and Reiss, K. (2003). Reasoning and Proof: Methodological Knowledge as A Component Of Proof Competence. ed. M. A. Mariotti. Available online at: www.lettredelapreuve.itlCERME3PapersiHeinze-paperl.pdf
Heitzmann, N., Seidel, T., Hetmanek, A., Wecker, C., Fischer, M. R., Ufer, S., et al. (2019). Facilitating diagnostic competences in simulations in higher education a framework and a research agenda. Frontline Learn. Res. 7:1–24. doi: 10.14786/flr.v7i4.384
Helmke, A., and Schrader, F.-W. (1987). Interactional effects of instructional quality and teacher judgement accuracy on achievement. Teach. Teacher Educ. 3, 91–98. doi: 10.1016/0742-051X(87)90010-2
Herbst, P., and Kosko, K. (2014). “Mathematical knowledge for teaching and its specificity to high school geometry instruction,” in Research in Mathematics Education. Research Trends in Mathematics Teacher Education, eds J.-J. Lo, K. R. Leatham, and L. R. van Zoest (New York, NY: Springer International Publishing), 23–45. doi: 10.1007/978-3-319-02562-9_2
Herppich, S., Praetorius, A.-K., Förster, N., Glogger-Frey, I., Karst, K., Leutner, D., et al. (2018). Teachers’ assessment competence: integrating knowledge-, process-, and product-oriented approaches into a competence-oriented conceptual model. Teach. Teacher Educ. 76, 181–193. doi: 10.1016/j.tate.2017.12.001
Hosenfeld, I., Helmke, A., and Schrader, F.-W. (2002). Diagnostische kompetenz. unterrichts- und lernrelevante schülermerkmale und deren einschätzung durch lehrkräfte in der unterrichtsstudie SALVE. Z. Padagogik (Beiheft) 48, 65–82.
Kaiser, J., Retelsdorf, J., Südkamp, A., and Möller, J. (2013). Achievement and engagement: how student characteristics influence teacher judgments. Learn. Instr. 28, 73–84. doi: 10.1016/j.learninstruc.2013.06.001
Karing, C. (2009). Diagnostische kompetenz von grundschul- und gymnasiallehrkräften im leistungsbereich und im bereich interessen. Z. Pädagogische Psychol. 23, 197–209. doi: 10.1024/1010-0652.23.34.197
Karst, K., Klug, J., and Ufer, S. (2017). “Strukturierung diagnostischer Situationen im inner- und außerunterrichtlichen handeln von lehrkräften,” in Pädagogische Psychologie und Entwicklungspsychologie: Vol. 94. Diagnostische Kompetenz von Lehrkräften: Theoretische und methodische Weiterentwicklungen, eds A. Südkamp and A.-K. Praetorius (Münster: Waxmann), 102–114.
Klug, J., Bruder, S., Kelava, A., Spiel, C., and Schmitz, B. (2013). Diagnostic competence of teachers: a process model that accounts for diagnosing learning behavior tested by means of a case scenario. Teach. Teacher Educ. 30, 38–46. doi: 10.1016/j.tate.2012.10.004
Kramer, M., Förtsch, C., Stürmer, J., Förtsch, S., Seidel, T., and Neuhaus, B. J. (2020). Measuring biology teachers’ professional vision: development and validation of a video-based assessment tool. Cogent Edu. 7:1823155. doi: 10.1080/2331186X.2020.1823155
Kultusministerkonferenz (2012). Bildungsstandards im Fach Mathematik für die Allgemeine Hochschulreife. KMK. Berlin: Standing Conference of the Ministers of Education and Cultural Affairs of Germany.
Kunter, M., and Trautwein, U. (2013). Psychologie des Unterrichts. StandardWissen Lehramt, Vol. 3895. Paderborn: Ferdinand Schöningh.
Leuders, T., and Loibl, K. (2020). Processing probability information in nonnumerical settings - teachers’ bayesian and non-bayesian strategies during diagnostic judgment. Front. Psychol. 11:678. doi: 10.3389/fpsyg.2020.00678
Levin, D. M., Hammer, D., and Coffey, J. E. (2009). Novice teachers’ attention to student thinking. J. Teacher Educ. 60, 142–154. doi: 10.1177/0022487108330245
Lin, F.-L. (2005). “Modeling students’ learning on mathematical proof and refutation,” in Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education(1), (Melbourne, Vic), 3–18.
Loibl, K., Leuders, T., and Dörfler, T. (2020). A framework for explaining teachers’ diagnostic judgements by cognitive modeling (DiaCoM). Teach. Teacher Educ. 91:103059. doi: 10.1016/j.tate.2020.103059
McElvany, N., Schroeder, S., Hachfeld, A., Baumert, J., Richter, T., Schnotz, W., et al. (2009). Diagnostische Fähigkeiten von Lehrkräften bei der Einschätzung von Schülerleistungen und Aufgabenschwierigkeiten bei Lernmedien mit instruktionalen Bildern [Teachers’ diagnostic skills to judge student performance and task difficulty when learning materials include instructional pictures]. Z. Pädagogische Psychol. 23, 223–235. doi: 10.1024/1010-0652.23.34.223
Nestler, S., and Back, M. (2016). “Accuracy of judging personality,” in The Social Psychology of Perceiving Others Accurately, eds J. A. Hall, M. S. Mast, and T. V. West (Cambridge: Cambridge University Press).
Pedemonte, B. (2007). How can the relationship between argumentation and proof be analysed? Educ. Stud. Math. 66, 23–41. doi: 10.1007/s10649-006-9057-x
Pólya, G. (1973). How to Solve It: A New Aspect of Mathematical Method. Princeton, NJ: Princeton science library. Princeton Univ. Press.
Praetorius, A.-K., Berner, V.-D., Zeinz, H., Scheunpflug, A., and Dresel, M. (2013). Judgment confidence and judgment accuracy of teachers in judging self-concepts of students. J. Educ. Res. 106, 64–76. doi: 10.1080/00220671.2012.667010
Radkowitsch, A., Fischer, M. R., Schmidmaier, R., and Fischer, F. (2020). Learning to diagnose collaboratively: validating a simulation for medical students. GMS J. Med. Educ. 37:Doc51. doi: 10.3205/zma001344
Reiss, K., and Ufer, S. (2009). Was macht mathematisches Arbeiten aus? Empirische Ergebnisse zum Argumentieren, Begründen und Beweisen. Jahresber. Deutschen Math. Vereinigung 111, 1–23. doi: 10.1007/978-3-642-41864-8_1
Schack, E. O., Fisher, M. H., and Wilhelm, J. A. (2017). Research in Mathematics Education. Teacher Noticing: Bridging and Broadening Perspectives, Context, and Framework. Cham: Springer, doi: 10.1007/978-3-319-46753-5
Schäfer, S. (2014). Pre-Service Teachers’ Cognitive Learning Processes With Regard to Specific Teaching and Learning Components in The Context of Professional Vision. (Doctoral dissertation, Technische Universität München) [Dissertation]. Technische Universität München, München.
Schoenfeld, A. H. (1992). “Learning to think mathematically: problem solving, metacogntion, and sense making in mathematics,” in Handbook of Research on Mathematics Teaching and Learning, ed. D. Grouws (New York, NY: Simon andSchuster), 334–370.
Schoenfeld, A. H. (2011). “Noticing Matters. A lot. Now what?,” in Mathematics Teacher Noticing: Seeing Through Teachers’ Eyes, eds M. G. Sherin, V. R. Jacobs, and R. A. Philipp (Milton Park: Routledge), 223–238.
Schrader, F.-W., and Helmke, A. (1987). Diagnostische kompetenz von lehrern: komponenten und wirkungen [Diagnostic competences of teachers: components and effects]. Empirische Pädagogik 1, 27–52.
Seidel, T., Schnitzler, K., Kosel, C., Stürmer, K., and Holzberger, D. (2020). Student characteristics in the eyes of teachers: differences between novice and expert teachers in judgment accuracy, observed behavioral cues, and gaze. Educ. Psychol. Rev. 33, 69–89. doi: 10.1007/s10648-020-09532-2
Seidel, T., and Stürmer, K. (2014). Modeling and measuring the structure of professional vision in preservice teachers. Am. Educ. Res. J. 51, 739–771. doi: 10.3102/0002831214531321
Shavelson, R. J., Young, D. B., Ayala, C. C., Brandon, P. R., Furtak, E. M., Ruiz-Primo, M. A., et al. (2008). On the impact of curriculum-embedded formative assessment on learning: a collaboration between curriculum and assessment developers. Appl. Measur. Educ. 21, 295–314. doi: 10.1080/08957340802347647
Sherin, M. G., Linsenmeier, K. A., and van Es, E. A. (2009). Selecting video clips to promote mathematics teachers’ discussion of student thinking. J. Teacher Educ. 60, 213–230. doi: 10.1177/0022487109336967
Sherin, M. G., Russ, R. S., and Colestock, A. A. (2011). “Accessing mathematics teachers’ in-the-moment noticing,” in Mathematics Teacher Noticing: Seeing Through Teachers’ Eyes, eds M. G. Sherin, V. R. Jacobs, and R. A. Philipp (Milton Park: Routledge), 79–94.
Sommerhoff, D., and Ufer, S. (2019). Acceptance criteria for validating mathematical proofs used by school students, university students, and mathematicians in the context of teaching. ZDM 51, 717–730. doi: 10.1007/s11858-019-01039-7
Sommerhoff, D., Ufer, S., and Kollar, I. (2015). “Research on mathematical argumentation: a descriptive review of PME proceedings,” in Proceedings of 39th Psychology of Mathematics Education conference, (Hobart, TAS), 193–200.
Stürmer, K., Seidel, T., and Schäfer, S. (2013). Changes in professional vision in the context of practice. Gruppendynamik Organisationsberatung 44, 339–355. doi: 10.1007/s11612-013-0216-0
Stylianides, A. J. (2007). Proof and proving in school mathematics. J. Res. Math. Educ. 38, 289–321.
Südkamp, A., Hetmanek, A., Herppich, S., and Ufer, S. (2017). “Herausforderungen bei der empirischen Erforschung diagnostischer Kompetenz,” in Pädagogische Psychologie und Entwicklungspsychologie: Diagnostische Kompetenz von Lehrkräften: Theoretische und methodische Weiterentwicklungen, Vol. 94, eds A. Südkamp and A.-K. Praetorius (Münster: Waxmann), 95–101.
Südkamp, A., Kaiser, J., and Möller, J. (2012). Accuracy of teachers’ judgments of students’ academic achievement: a meta-analysis. J. Educ. Psychol. 104, 743–762. doi: 10.1037/a0027627
Südkamp, A., and Praetorius, A.-K. (2017). Pädagogische Psychologie und Entwicklungspsychologie: Diagnostische Kompetenz von Lehrkräften: Theoretische und methodische Weiterentwicklungen, Vol. 94. Münster: Waxmann.
Südkamp, A., Praetorius, A.-K., and Spinath, B. (2018). Teachers’ judgment accuracy concerning consistent and inconsistent student profiles. Teach. Teacher Educ. 76, 204–213. doi: 10.1016/j.tate.2017.09.016
Thiede, K. W., Brendefur, J. L., Osguthorpe, R. D., Carney, M. B., Bremner, A., Strother, S., et al. (2015). Can teachers accurately predict student performance? Teach. Teacher Educ. 49, 36–44. doi: 10.1016/j.tate.2015.01.012
Ufer, S., Heinze, A., and Reiss, K. (2008). “Individual predictors of geometrical proof competence,” in Proceedings of the Joint Meeting of the 32nd Conference of the International Group for the Psychology of Mathematics Education, Vol. 1, eds O. Figueras and A. Sepúlveda (Morelia), 361–368.
Ufer, S., Heinze, A., and Reiss, K. (2009). “Mental models and the development of geometrical proof competency,” in Proceedings of the 33rd Conference of the International Group for the Psychology of Mathematics Education, (Thessaloniki), 257–264.
van Dormolen, J. (1977). Learning to understand what giving a proof really means. Educ. Stud. Math. 1977, 27–34. doi: 10.1007/bf00302502
van Es, E. A. (2011). “A framework for learning to notice student thinking,” in Mathematics Teacher Noticing: Seeing Through Teachers’ Eyes, eds M. G. Sherin, V. R. Jacobs, and R. A. Philipp (Milton Park: Routledge), 134–151.
van Es, E. A., and Sherin, M. G. (2002). Learning to Notice: scaffolding new Teachers‘ interpretations of classroom interactions. J. Technol. Teacher Educ. 10, 571–596.
van Es, E. A., and Sherin, M. G. (2008). Mathematics teachers’ “learning to notice” in the context of a video club. Teach. Teacher Educ. 24, 244–276. doi: 10.1016/j.tate.2006.11.005
van Es, E. A., Tekkumru-Kisa, M., and Seago, N. (2020). “Leveraging the power of video for teacher learning,” in The International Handbook of Mathematics Teacher Education, ed. O. Chapman (Leiden: Brill Sense), 23–54. doi: 10.1163/9789004418967_002
Vogt, F., and Rogalla, M. (2009). Developing adaptive teaching competency through coaching. Teach. Teacher Educ. 25, 1051–1060. doi: 10.1016/j.tate.2009.04.002
Keywords: assessment skills, educational technology, mathematical argumentation, professional vision, teacher assessment, video-based simulation
Citation: Codreanu E, Sommerhoff D, Huber S, Ufer S and Seidel T (2021) Exploring the Process of Preservice Teachers’ Diagnostic Activities in a Video-Based Simulation. Front. Educ. 6:626666. doi: 10.3389/feduc.2021.626666
Received: 06 November 2020; Accepted: 06 April 2021;
Published: 30 April 2021.
Edited by:
Monica Thomas Billen, California State University, Fresno, United StatesReviewed by:
Manpreet Kaur Bagga, Partap College of Education, IndiaYu Hua Bu, East China Normal University, China
Copyright © 2021 Codreanu, Sommerhoff, Huber, Ufer and Seidel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Elias Codreanu, ZWxpYXMuY29kcmVhbnVAdHVtLmRl
 Elias Codreanu
Elias Codreanu Daniel Sommerhoff
Daniel Sommerhoff Sina Huber1
Sina Huber1 Stefan Ufer
Stefan Ufer Tina Seidel
Tina Seidel
