- 1Department of Educational and Learning Sciences, Utrecht University, Utrecht, Netherlands
- 2Nieuwenhuis Institute, Faculty of Behavioural and Social Sciences, University of Groningen, Groningen, Netherlands
- 3Behavioural Science Institute, Radboud University, Nijmegen, Netherlands
The approximate number system (ANS) theory and the ANS mapping account have been the most prominent theories on non-symbolic numerosity processing and symbolic number processing respectively, over the last 20 years. Recently, there is a growing debate about these theories, mainly based on research in adults. However, whether the ANS theory and ANS mapping account explain the processing of non-symbolic numerosity and symbolic number in childhood has received little attention. In the current ERP study, we first examined whether non-symbolic numerosity processing in 9-to-12-year-old children (N = 34) is intuitive, as proposed by the ANS theory. Second, we examined whether symbolic number processing is rooted in non-symbolic numerosity processing, as proposed the ANS mapping account. ERPs were measured during four same-different match-to-sample tasks with non-symbolic numerosities, symbolic numbers, and combinations of both. We found no evidence for intuitive processing of non-symbolic numerosity. Instead, children processed the visual features of non-symbolic stimuli more automatically than the numerosity itself. Moreover, children do not seem to automatically activate non-symbolic numerosity when processing symbolic numbers. These results challenge the ANS theory and ANS mapping account in 9-to-12-year-old children.
Highlights
• Children’s non-symbolic (NS) numerosity and symbolic number processing was assessed
• ERPs show that NS numerosity and symbolic number processing is not intuitive
• Instead, children process visual features of NS stimuli automatically
• The data do not support automatic activation of numerosity during number processing
• Thus, the results challenge the ANS theory and ANS mapping account in children
Introduction
Numerical processing is an important early marker of mathematical performance (e.g., Schneider et al., 2017). Numerical processing can be subdivided into non-symbolic numerosity processing (e.g., comparison between two sets of dots) and symbolic number processing (e.g., comparison between two Arabic numerals or number words). A prominent theory on non-symbolic numerosity processing is the ANS (approximate number system) theory. This theory states that approximate numerosity, i.e., the number of objects in a set, is intuitively extracted when one is confronted with a set of objects, such as a dot pattern (Dehaene, 1997). This means that the visual properties of a set of objects are removed or normalized, such that the numerosity of the set can easily be established, and that this process goes without much effort. The ANS mapping account concerns symbolic number processing, and theorizes that symbolic number processing in adults is rooted in non-symbolic numerosity processing. Approximate non-symbolic numerosity is thought to be activated automatically when processing symbolic numbers (Dehaene, 1997). There is currently a hot debate about whether the ANS theory and ANS mapping account hold or whether alternative theories are more likely to explain non-symbolic numerosity processing and symbolic number processing (see for example Leibovich et al., 2017, including commentaries on this paper). The aim of the present study was to examine whether the ANS theory and ANS mapping account do underlie non-symbolic numerosity processing and symbolic number processing in children. An event-related potential (ERP)-paradigm was employed to gain insight into the processing of non-symbolic numerosity and symbolic number.
ERP-research on the validity of the ANS theory and ANS mapping account in children is limited. ERP-research in adults shows both evidence confirming the ANS theory (Temple and Posner, 1998; Paulsen and Neville, 2008; Hyde and Spelke, 2009; Hyde and Spelke, 2012; Park et al., 2017; Van Rinsveld et al., 2020) and ANS mapping account (Dehaene, 1996; Temple and Posner, 1998; Pinel et al., 2001; Libertus et al., 2007), as well as more recent evidence against the ANS theory (Gebuis and Reynvoet, 2012; Soltész and Szűcs, 2014; Van Hoogmoed and Kroesbergen, 2018) and ANS mapping account (Van Hoogmoed and Kroesbergen, 2018). Children’s numerical processing mechanisms may either be the same or different from those in adults. Research has shown that even infants seem to have a rudimentary understanding of non-symbolic numerosity (e.g., Xu and Spelke, 2000; Xu et al., 2005; Xu and Arriaga, 2007). However, it is not yet completely clear whether this is purely based on numerosity, or whether it is based on the visual features of a set of objects (Gebuis et al., 2016). Moreover, the development of symbolic number processing only starts at a later age.
From a developmental perspective, the early acquisition of symbolic number in young children may be intertwined with non-symbolic numerosity processing, as children usually start grasping numerical information by counting small amounts of non-symbolic objects (e.g., toys, pieces of fruit, or various body parts; Gelman, and Gallistel, 1978). Based on the ANS mapping account, this symbolic information will remain to activate their non-symbolic counterparts, even into adulthood. However, Carey (2004), Carey (2009), Carey (2011) claims that only small numbers are acquired based on non-symbolic numerosities, not based on the ANS, but on parallel individuation. The acquisition of numbers larger than four would be dependent on verbal counting routines and the notion that the next number in the routine represents N + 1 instead of direct mapping onto non-symbolic numerosities. However, other possible mechanisms that help children acquire number symbols have been proposed in several commentaries on Carey’s paper (2011). For example, children’s understanding of number is argued to occur prior to learning verbal principles such as counting, and this knowledge of number might foster development of numerical representations (Gelman, 2011; Gentner and Simms, 2011; Landy et al., 2011; Spelke, 2011).
In older children in kindergarten, symbolic number processing has been shown to be related to children’s mapping skills (i.e., linking symbolic numbers and non-symbolic numerosities; Kolkman et al., 2013). It might thus be the case that symbolic number and non-symbolic numerosity processing in (young) children—in contrast to adults—(partly) rely on a common mechanism. However, this does not necessarily mean that children automatically activate numerosity when confronted with numbers as proposed by the ANS mapping account, especially not when they are older and more proficient in dealing with symbolic numbers. There is indeed evidence that processing of symbolic (large) numbers predicts processing of non-symbolic numerosity in kindergartners instead of vice versa, which suggests that symbolic processing does not necessarily build on the ANS (Lyons et al., 2018). Instead, there may be a bidirectional relationship between the development of symbolic and non-symbolic processing (Goffin and Ansari, 2019). Together, this implies that the processing of non-symbolic numerosity might not be as intuitive in children as assumed by the ANS theory and that the ANS may not be automatically activated when processing symbolic number, as proposed by the ANS mapping account.
The present study had two aims. The first aim was to investigate whether non-symbolic numerosity processing in children between 9 and 12 years of age is intuitive, in line with the ANS theory, or whether numerosities are processed based on the processing of visual features instead, as is proposed by alternative theories such as the sensory-integration theory (Gebuis et al., 2016) and sense of magnitude theory (Leibovich et al., 2017). Second, we examined whether children’s processing of symbolic number can be explained by the ANS mapping account, or whether this processing is independent of numerosity, based on symbol-symbol associations (e.g., Reynvoet and Sasanguie, 2016).
Non-Symbolic Numerosity Processing
The ANS theory states that non-symbolic numerosity processing relies on an innate approximate number system (Dehaene, 1997). Non-symbolic stimuli are thought to be processed by an intuitive estimation of numerosity (i.e., the number of objects in a set), independently of physical features of the stimuli, such as the size of the objects. Proof of concept for this theory is mainly based on behavioral ratio effects within comparison tasks: Comparing two non-symbolic numerosities is more difficult (i.e., lower accuracy and slower reaction times) when these numerosities are closer in magnitude, and thus have a ratio closer to 1 (see Guillaume and Van Rinsveld, 2018 for a meta-analysis). This ratio effect is assumed to result from a mental number line wherein numerosities that are spatially located together are automatically co-activated, suggesting that non-symbolic numerosities are processed intuitively. Results from ERP research mirror the behavioral results by showing early ratio-dependent ERP amplitudes around 200 ms after stimulus presentation, suggesting that numerosity processing is fast (Temple and Posner, 1998; Libertus et al., 2007; Paulsen and Neville, 2008; Hyde and Spelke, 2009; Hyde and Spelke, 2011; Hyde and Spelke, 2012).
Although the ANS theory suggests that stimuli are processed independent of physical properties, physical features are inherently related to numerosity in real life. For instance, if one child has two pieces of candy and another child has four pieces of candy, then the second child’s candy will occupy more of the visual space (i.e., total area and surface of the candy). According to the ANS theory, these visual features would be removed in a very early stage of numerical processing (e.g., Dehaene, 1997), after which numerosities are estimated or compared. However, instead of estimating numerosity after removal of visual features, one might better use visual properties of the objects to determine which child has the most candy.
To prevent the use of visual properties to estimate or compare numerosities, most research on non-symbolic numerosity processing therefore aims to control for visual properties of the stimuli. Even when using this kind of control, some studies still find early effects of numerosity, independent of visual features (Park et al., 2016; Fornaciai et al., 2017), which could be interpreted as evidence for the ANS theory. However, there are also studies that show that with proper control over visual features, effects of numerosity are absent or only starting around 650 ms (Gebuis and Reynvoet, 2012; Soltész and Szűcs, 2014; Van Hoogmoed and Kroesbergen, 2018). These results do not align with the ANS theory, since intuitive processing is unlikely to take such a long time, because it should take little effort. Hence, these results are better explained by alternative theories, such as the sensory-integration theory which posits that the integration of visual features is at the basis of an approximation of numerosity (Gebuis et al., 2016).
In children, it has become evident that the processing of non-symbolic stimuli relies more and more on actual non-symbolic numerosity with age and education, whereas physical properties of the stimuli become less relevant (Park, 2018; Piazza et al., 2018). This may reflect the increasing precision of the ANS (Halberda and Feigenson, 2008). Alternatively, it may reflect a growth in inhibition, withdrawing the child from intuitively responding to visual features and basing their decisions on the number of elements instead (Fuhs and McNeil, 2013; Gilmore et al., 2013). The argument of increasing precision of the ANS would result in early effects of numerosity (more specifically ratio) in the ERP with smaller and relatively short-lasting effects for visual properties. However, growth in inhibition would result in late effects of numerosity in the ERP in combination with early and possibly longer-lasting effects of visual properties. Our first aim was thus to examine whether non-symbolic numerosity processing is indeed intuitive, as proposed by the ANS theory (Dehaene, 1997), resulting in early effects of numerosity. Alternatively, children could process visual features more automatically than numerosity, which would be more in line with the sensory-integration theory (Gebuis et al., 2016), resulting in early effects of visual features in combination with later or no effects of numerosity.
Event-Related Potential Correlates of Non-symbolic Numerosity Processing in Children
Previous ERP research shows similarities in ERPs of non-symbolic numerosity processing between 5- and 8-year-old children and young adults (Temple and Posner, 1998; Heine et al., 2013; Soltész and Szűcs, 2014). Children and adults show similar neural activation over the parietal cortices when processing non-symbolic numerosity. For instance, similar ratio effects were displayed in the early ERP components N1 and P2p for children and adults (Temple and Posner, 1998). However, visual properties of the stimuli were not controlled in this study and only small numerosities were included (1–9). Other research controlling visual properties showed systematic numerosity distance effects in typically developing children in second and third grade in the parietal regions between 280 and 600 ms (Heine et al., 2013). Effects were found for subitizing, counting and estimation. The fact that effects for non-symbolic numerosity processing in children are more compelling for later ERPs (when controlling for visual properties of the stimuli), seems to indicate that this is not an automatic, but a more conscious process. In the current study, early effects of ratio would support the ANS theory, whereas either late ERP components related to numerosity, or no components related to numerosity at all, in combination with early and longer-lasting effects of visual features, may align better with the sensory-integration theory (also depending on the processing of the visual features of the stimuli).
Symbolic Number Processing
The ANS mapping account theorizes that symbolic number processing is rooted in the processing of the corresponding non-symbolic numerosity (Dehaene, 1997). As such, when encountering a number, the corresponding numerosity is assumed to be automatically activated in adults. Evidence for this account is mainly based on similar ratio effects for symbolic numbers and non-symbolic numerosities, which was assumed to be due to similar overlapping representations of numerosities and numbers (Dehaene et al., 1990; Verguts and Van Opstal, 2005; Holloway and Ansari, 2008; Sasanguie et al., 2012; Sasanguie et al., 2013). The timing of these non-symbolic ratio effects and symbolic distance effects is also similar, as has been shown by ERP research (Dehaene, 1996; Temple and Posner, 1998; Libertus et al., 2007). Arguments for the ANS mapping account thus seem convincing.
However, recent research has challenged the ANS mapping account, by raising several theoretical concerns about important assumptions (e.g., is it an evolutionary system; Reynvoet and Sasanguie, 2016) and caveats (e.g., inconsistent findings; Gevers et al., 2016) in those theories. For example, ratio and distance effects have also been found in non-numerical comparison tasks such as ordering letters of the alphabet, which do not have overlapping representations (Van Opstal et al., 2008). This implies that the effects are likely task-related instead of numerosity-related. Based on these results one cannot conclude that numerosity and number share the same numerical representation. Recently, symbolic numbers have been suggested to be processed independently of numerosity (Lyons et al., 2012; Sasanguie et al., 2017). Moreover, we showed that adults do not automatically activate numerosities when processing symbolic numbers (Van Hoogmoed and Kroesbergen, 2018). Measuring EEG (ERPs) during four different match-to-sample tasks (i.e., including non-symbolic numerosities, symbolic numbers, and combinations of both), we demonstrated that processing a non-symbolic target is different when the target is preceded by a non-symbolic prime compared to being preceded by a symbolic prime. If one would assume that a symbolic prime automatically activates the corresponding non-symbolic numerosity, one would expect that the processing of the non-symbolic target would not differ based on whether it is preceded by a symbolic or non-symbolic prime. As such, these results suggest that even when a task requires mapping (e.g., comparison between a symbolic number and a non-symbolic numerosity), symbolic stimuli are not automatically mapped onto their corresponding non-symbolic numerosities in adults.
From a developmental perspective, it seems that symbolic number processing is intertwined with non-symbolic numerosity processing in (young) children. When children learn numbers, they learn them by mapping these onto numerosities. For example, many children start learning numbers by counting their (and others) body parts (e.g., how many eyes, how many arms, how many fingers do you have?). However, symbolic skills appear to take a more prominent place than non-symbolic skills in the development of mapping skills in four-to six-year-old children (Kolkman et al., 2013). Whereas non-symbolic skills are related to symbolic skills and mapping skills in the first year of kindergarten, the relation between non-symbolic and symbolic skills becomes insignificant in the second year. Moreover, research shows that symbolic processing predicts non-symbolic skills as soon as children have initial number understanding, instead of the other way around (Lyons et al., 2018). This suggests that if these skills are still related in older children, non-symbolic (i.e., numerosity) processing may not be the primary format as proposed by the ANS mapping account. Instead, (larger) symbolic numbers may be acquired by the successor function (i.e., the next number in the counting row is exactly one more than the previous number), and may be embedded in a semantic network of numbers instead of grounded in the ANS (Krajcsi et al., 2016; Krajcsi et al., 2018; Reynvoet and Sasanguie, 2016). This may explain why the relation between non-symbolic and symbolic number weakens with age (e.g., Kolkman et al., 2013).
In purely symbolic tasks, children from kindergarten to third grade, as well as children in sixth grade have been found to use digits’ physical properties to determine their magnitude, rather than their numerical value in a same-different task. No distance effect was found for numerical value (Defever et al., 2012). In a mixed notation task–in which digits needed to be compared to non-symbolic numerosities–a distance effect was found, showing no development with age until the end of primary school (Defever et al., 2012). In contrast, other research on symbolic digit comparison and comparison of non-symbolic numerosities (controlled for physical properties) found that the sizes of the symbolic and non-symbolic distance effects both decreased between six and eight years of age. The researchers concluded that children’s magnitude representations become more precise as they grow older (Holloway and Ansari, 2009). Whether the distance effect becomes more fine-tuned with age or not, it seems evident that an effect is present in children, even when controlling for visual properties of the non-symbolic stimuli. Therefore, it could be that in children symbolic number processing is rooted in non-symbolic numerosity processing, in line with the ANS mapping account and findings in younger children. This may especially be the case when numbers need to be related to numerosities, which may involve either activation of the non-symbolic numerosity based on the processing of the symbolic number, or the activation of notation-independent code that is also activated by non-symbolic numerosities (Piazza et al., 2007). However, based on adult literature, it may also be that older children do not activate the corresponding numerosity in a purely symbolic task (e.g., Marinova et al., 2018; Marinova et al., 2021). In mapping tasks, they may map numerosities onto numbers, thus in the opposite direction as predicted based on the ANS mapping account (e.g., Van Hoogmoed and Kroesbergen, 2018).
Event-Related Potential Correlates of Symbolic Number Processing
Previous research shows several differences in ERP correlates of symbolic number processing between adults and children or adolescents (Temple and Posner, 1998; Soltész, Szűcs et al., 2007). While amplitude and direction of the P2p effect for ratio in a number comparison task in five-year-old children was similar to the effect of adults, the effect was delayed in children (Temple and Posner, 1998). Regarding the ratio effect, differences between adolescents (with math problems, and matched controls) and adults (without math problems) were found as well (Soltész et al., 2007). Slope and topography of the (late) ratio effects were different, being more mature in adults. These findings seem to indicate that symbolic processing changes over development, as differences in ERP components or scalp locations were found respectively. Soltész et al. (2007) proposed that differences in the late ERP components reflect differences in complex symbolic number processing between adolescents and adults. Note that similar differences in symbolic number processing between children and adults have been found in fMRI research (Ansari et al., 2005). These studies seem to suggest that numerical processing mechanisms in children and adolescents differ from adult mechanisms. This may indicate that symbolic number processing relates to non-symbolic numerosity processing in a different way in adults and children.
The Current Study
In the current study, we examined the electrophysiological correlates of the processing of non-symbolic numerosity and symbolic number in children between 9 and 12 years of age. Electro-encephalograms (EEGs) were administered during four match-to-sample tasks with two ratios, measuring the ratio effect in processing of non-symbolic stimuli, symbolic stimuli, or a combination between non-symbolic primes and symbolic targets and vice versa. The non-symbolic stimuli were controlled for visual features using the script of Gebuis and Reynvoet (2011). In this setup, ratio effects for non-symbolic processing, symbolic processing, and mapping of non-symbolic numerosities and symbolic numbers could be measured. Moreover, effects of task format and of visual properties (i.e., surface, area, and diameter) of the stimuli could be examined.
Based on the intuitive processing of non-symbolic numerosity as proposed by the ANS theory, one would expect early effects of ratio in the non-symbolic task. Moreover, one would expect no later or long-lasting effects of visual properties, since these would be removed/normalized in an initial step based on the ANS theory. However, based on the alternative sensory-integration theory, one would expect more long-lasting effects of visual properties, and only later or no ratio effects for numerosity. With regards to symbolic processing, based on the ANS mapping account, one would expect to find similar (possibly slightly delayed) ratio effects as compared to the non-symbolic condition, since numerosity would be automatically extracted from the symbolic stimuli, and then processed similarly to the non-symbolic stimuli (i.e., either in a non-symbolic or notation-independent format). An additional way to examine whether non-symbolic numerosity and symbolic number are mapped onto each other (based on the ANS theory), is a comparison between tasks with the same primes or targets. If symbolic numbers and non-symbolic numerosities are mapped onto each other, one would expect that the processing of non-symbolic primes is the same, regardless of whether these are followed by non-symbolic or symbolic targets. Similarly, the processing of non-symbolic targets would be the same regardless of whether these are proceeded by non-symbolic or symbolic primes. Thus, differences in processing of non-symbolic stimuli depending on task, would provide evidence against the ANS mapping account.
Method
Participants
Participants were 50 children from grade 3 to 6 in primary school. Seven children were excluded due to recording problems (partly due to a broken Ground-electrode), and nine children were excluded due to noisy data (see below). The final sample consisted of 34 children (16 boys and 18 girls) in grade 3 to 6, with a mean age of 10.71 years (SD = 0.78). All participants had normal or corrected-to-normal vision.
Procedure
Participants were recruited via a letter they received from their schools. The major part of the participants (24 participants) were tested individually in a separate room within their schools. The procedure was explained to them verbally with supporting pictures. The other part of the participants (10 participants) was tested in the lab. The children were informed that they could choose to stop participating at every moment. Informed consent was signed by their parents.
After applying the EEG, the participants were seated behind the computer. The task instruction was read from the screen together with the child. Participants were told that there would be a break after each task. The administrator of the task stayed with the child during the experiment to answer any questions, and if necessary, to encourage the child to pursue. The ERP tasks were presented in a random order. After the four tasks, the EEG cap was removed from the participant. All tasks including application and removal of the EEG-cap lasted about 45–60 min. The parents of all the participants gave written informed consent in accordance with the Declaration of Helsinki. The research was approved by the ethics review board of the faculty of Social and Behavioral Sciences of Utrecht University.
Tasks
Non-Symbolic (Ns-Ns)
In the non-symbolic task, trials consisted of a prime picture with dot patterns and a target picture with dot patterns, see Figure 1. The dot patterns were generated in Matlab with the script described in Gebuis and Reynvoet, 2011. This script allows for controlling the relation between the number distance and visual properties, as well as the congruency in area subtended, density, total surface of the dots, average diameter, and total circumference. The visual properties of the stimuli were documented, enabling division of the data based on visual properties as well (Gebuis and Reynvoet, 2011). The number of dots for the primes ranged between 20 and 40, with both smaller and larger targets at ratio 0.5, and 0.7. As such, all numbers ranged between 10 and 80. A trials started with the presentation of a prime for 750 ms, then a blank screen jittered between 400 and 600 ms, and a target presented for 750 ms. The inter trial interval was jittered between 1,000 and 1,500 ms. In total, 88 trials were presented to the children. Twenty trials were presented for each distance x size (target larger vs. target smaller than prime). In addition to that, we included eight trials in which the numerosity of the prime and the target were the same. Participants were instructed to passively watch the stimuli and only respond by pressing the space bar if they thought the prime and target stimuli displayed the same quantity as soon as possible during stimulus presentation or during the following blank screen (ITI).
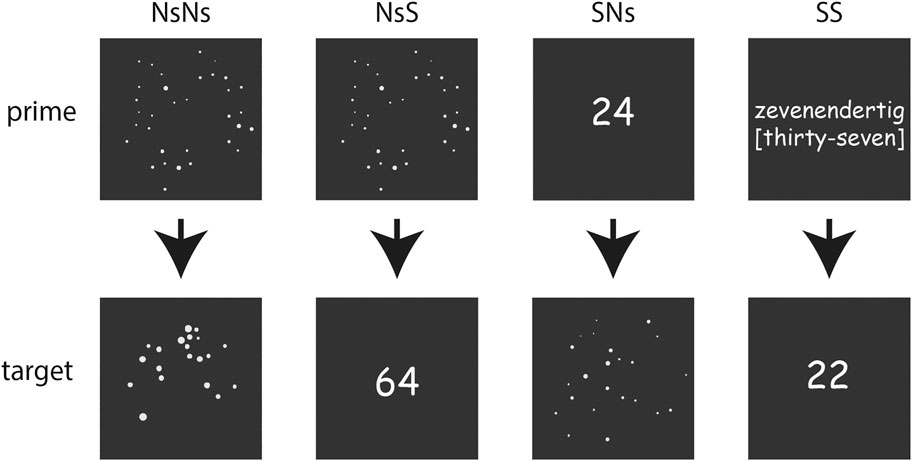
FIGURE 1. Overview of the stimuli-formats in the different tasks with the upper line presenting the primes for each task, and the lower line presenting the targets.
Non-Symbolic–Symbolic (Ns-S)
The Ns-S task was identical to the Ns-Ns task with the exception that the targets were presented as digits instead of dot patterns. Moreover, both the prime and target were presented for 1,000 ms.
Symbolic–Non-symbolic (S-Ns)
The S-Ns task was identical to the Ns-S task with the exception that the primes were presented as digits instead of dot patterns and targets were presented as dot patterns instead of digits.
Symbolic (S-S)
The S-S task was identical to the Ns-S task with the exception that the primes were presented as number words, instead of dot patterns.
Analyses
Behavioral
Participants were instructed to only respond to trials in which the prime and target depicted the same numerosity. As such, a non-response to the trials in which the prime and target did not match was taken as correct response. Mean accuracy per ratio, per task was calculated in SPSS, version 23. To examine whether performance was above chance in each task, one-sample t-tests were carried out against a test-value of 0.5. Bivariate correlations between performance and age were carried out separately for each task.
Event-Related Potential
Recording and Preprocessing
For the 24 participants tested at schools, data were recorded with a 32 electrode active cap (Biosemi, Amsterdam, Netherlands) with a sampling rate of 2048 Hz. Additional electrodes were placed on both mastoids, and below and next to the eyes. The system records data without reference. The electrode offset was kept below 50 µV. For the ten participants that were tested in the lab, data were recorded with a 32-electrode ActiCAP (Brain Products GmbH) and were recorded online with a sampling rate of 500 Hz. Measured activity was filtered online using a 125 Hz lowpass filter, and a time constant of 10 s. Impedance was kept below 50 µV.
After recording, all data were imported into Matlab 2017a (The MathWorks Inc., 2017) and analyzed using the Fieldtrip toolbox (Oostenveld et al., 2011). Data of all participants were downsampled to 500 Hz, rereferenced to the linked mastoids, and low-pass filtered at 40 Hz. ICA was used to identify and delete eye blinks and horizontal eye movements. After that, data were manually inspected for bad channels. Bad channels were removed and replaced with a weighted sum of the surrounding channels. Deleted channels were never adjacent to each other. Data (primes and targets) were segmented from 200 ms before to 1,000 ms after stimulus onset and baseline corrected. After artifact rejection, the data were averaged per ratio per task for the targets (MNtrials = 34.2, range 24–40). Data from target larger than prime and target smaller than prime were collapsed because of the limited number of trials included (Van Hoogmoed and Kroesbergen, 2018). To examine the effects of visual properties, averages were generated for small and large diameter, small and large area, and small and large surface based on all non-symbolic primes and targets (mean Ntrials = 31.7, range Ntrials 19–40). The 40 trials with the largest and 40 trials with the smallest surface/area/diameter were selected to generate averages with similar amounts of trials as compared to the number of trials per ratio. Averages for primes and targets within each task were also computed (MNtrials = 71.9, range 53–88).
Analyses
Grand averages were computed over the 28 common electrodes in both recording systems. Since the time course of the differences between conditions was unknown because of the mixed findings in previous research, cluster based permutation tests were carried out (Oostenveld et al., 2011). For the Ratio effects in the tasks, four separate permutation tests were carried out, one for each task. Similar permutation tests were performed for the physical parameters on small vs. large (mean) diameter, area (within the convex hull), and surface (of the dots). To test for differences in the processing of non-symbolic and symbolic stimuli depending on task, three cluster based permutation tests were carried out: one to compare the processing of non-symbolic primes in the NsNs-task vs. the NsS-task, one to compare the processing of the non-symbolic targets in the NsNs-task vs. the SNs-task, and one to compare the processing of the symbolic targets in the NsS-task and the SS-task.
A dependent-samples t-test on amplitude for each channel x sample between 0 and 1,000 ms served as input for the cluster based permutation test. Spatio-temporal clusters were defined based on these t-statistics (α = 0.05). These clusters were entered into the cluster-based permutation test (500 permutations or 1,000 permutations if the obtained |p-α| < 0.002). Since cluster-based statistics (clusterstats) are calculated for positive and negative slopes separately, the p-values were compared to α = 0.025 (0.05/2) for all analyses (Fieldtrip, n. d.; for an example see Van Hoogmoed and Kroesbergen, 2018). Note that by using cluster-based permutation tests, the whole cluster is tested as one test-statistic. As such, the latency and exact location of a cluster are only descriptive (Sassenhagen and Draschkow, 2019).
Results
Behavioral
Accuracy for each task is reported in Table 1 for matching pairs and non-matching pairs separately. For matching pairs, a correct response was a button press, whereas for non-matching pairs, a correct response consisted of refraining from a button press. Performance was above chance on task level in all tasks; for the NsNs task (M = 0.69, SD = 0.12), t (33) = 9.74, p < 0.001, d = 1.67, for the NsS task (M = 0.67, SD = 0.12), t (33) = 8.67, p < 0.001, and d = 1.49, for the SNs task (M = 0.63, SD = 0.11), t (33) = 6.74, p < 0.001, d = 1.16, and for the SS task (M = 0.97, SD = 0.03), t = 86.13, p < 0.001, and d = 14.77. However, participants had difficulty identifying matching trials, with the proportion of correctly answered trials ranging from 0.34 to 0.80. Age of the participants did not significantly relate to performance in any of the tasks (0.038 ≤ r ≤ 0.255). Exploratory analyses revealed a small difference between the performance on the NsS-task and the SNs-task, t (33) = 2,12, p = 0.041, d = 0.36.

TABLE 1. Mean proportion correct and standard deviations for matching and non-matching trials per task.
Event-Related Potential
Distance Effects for Ratio per Task
ERPs for the different Ratios are depicted in Figure 2 for each task separately. A permutation test on the difference between ratio 0.5 and ratio 0.7 in the NsNs-task resulted in a significant negative cluster for Ratio, largest negative clusterstat = −1836.8, p = 0.022, reflecting a parietal distance effect between 650 and 950 ms (see Figure 3). No significant positive cluster was found, largest positive clusterstat = 148.3, p = 0.329. For the NsS-task, no positive clusters were found. Moreover, no significant negative cluster was found, largest negative clusterstat = −352.2, p = 0.216, which reflects no significant ratio effect for the NsS-task. For the SNs-task, no significant positive or negative clusters were found, largest positive clusterstat = 161.1, p = 0.371, largest negative clusterstat = −100.8, p = 0.485, which reflects no significant ratio effect for the SNs-task. For the SS-task, two significant effects of distance were found. The first cluster, positive clusterstat = 2121.9, p = 0.012, reflects a very early effect, around 50–300 ms over the centro-parietal scalp regions. The second cluster, positive clusterstat = 2089.2, p = 0.012, reflects a broadly distributed effect between 700 and 800 ms (See Figure 4). No negative clusters were found.
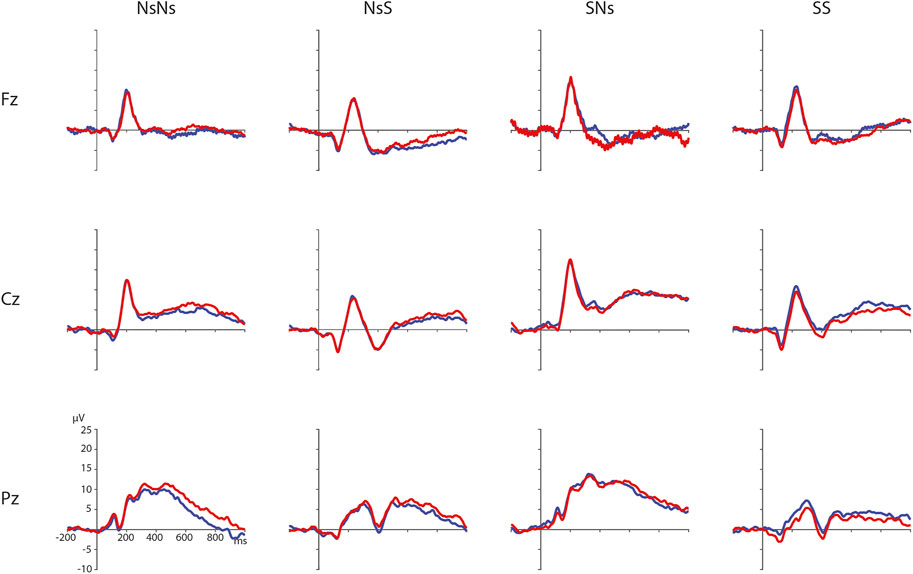
FIGURE 2. Distance effects per task on electrodes Fz, Cz, and Pz (electrodes chosen for illustration purposes only) with ratio 0.5 in blue and ratio 0.7 in red.

FIGURE 3. Topoplots of the differences between the ratio’s in the NsNs-task per time window with asterisks representing the significant differences between the ratios based on α = 0.05.
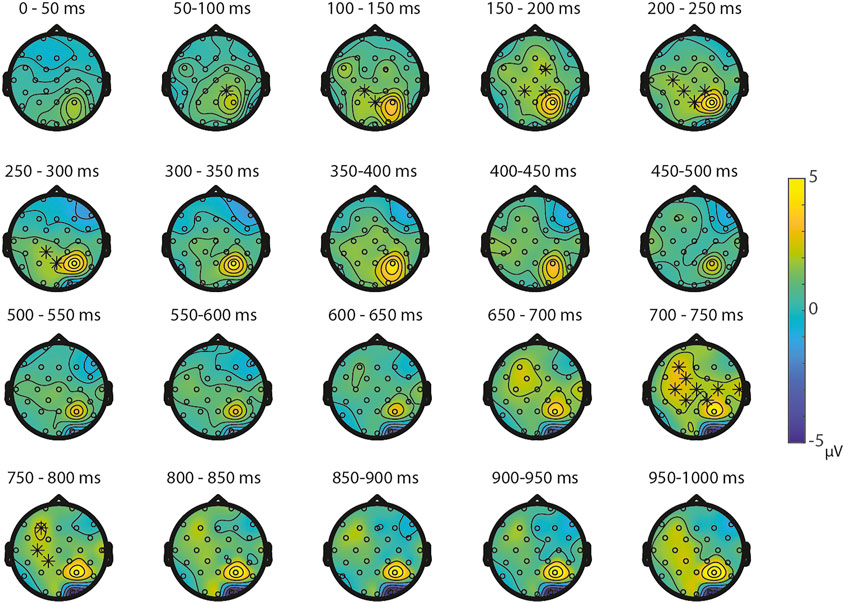
FIGURE 4. Topoplots of the differences between the ratio’s in the SS-task per time window with asterisks representing the significant differences between the ratios based on α = 0.05.
Distance Effects for Visuals
ERPs for the different visual features are depicted in Figure 5. For the visual feature area, the permutation test (1,000 permutations) resulted in no significant positive or negative clusters, largest positive clusterstat = 223.7, p = 0.241, largest negative clusterstat = −1217.3, p = 0.035. For the visual feature surface (1,000 permutations), the results showed no significant positive cluster, largest clusterstat = 333.7, p = 0.208, but a significant negative cluster, clusterstat = -2499.0, p = 0.013. This cluster reflects a relatively early difference from around 200 ms to around 300 ms over the parieto-occipital scalp regions (see Figure 6). For the visual feature diameter, the results showed no significant positive cluster, largest clusterstat = 275.8, p = 0.275, but a significant negative cluster, clusterstat = −2005.3, p = 0.009, reflecting a occipital difference between small and large diameter from around 200–300 ms (see Figure 7).
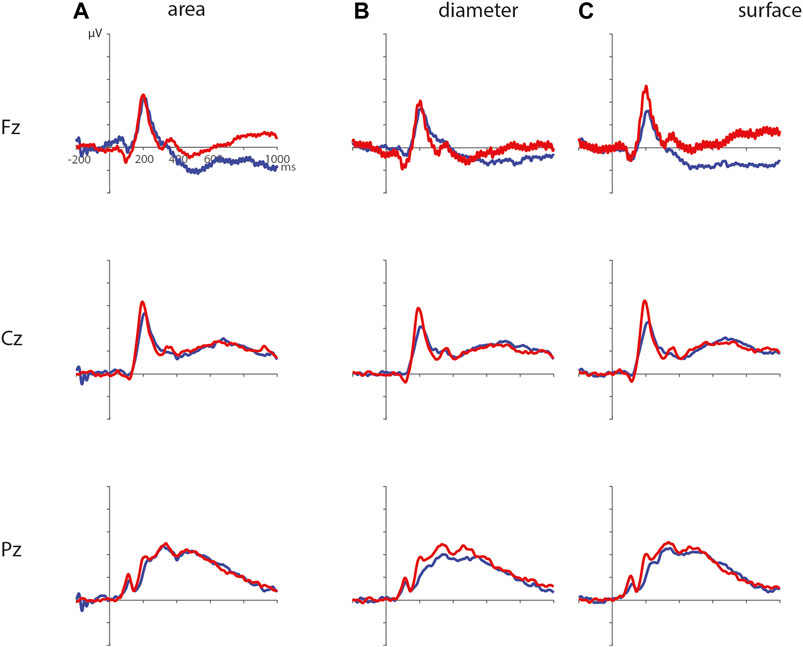
FIGURE 5. ERPs for the different visual features with small area (A), diameter (B), and surface (C) in blue, and large area, diameter, and surface in red.
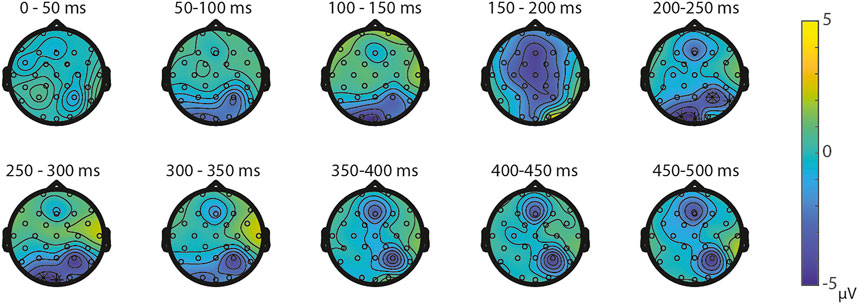
FIGURE 6. Topoplots of the differences between small and large surface per time window with asterisks representing the significant differences between the small and large surface based on α = 0.05.
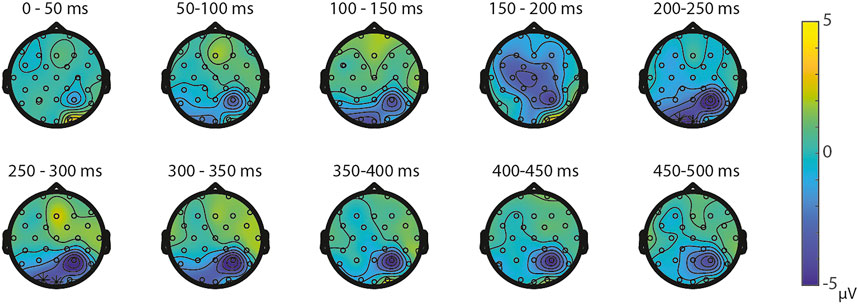
FIGURE 7. Topoplots of the differences between small and large diameter per time window with asterisks representing the significant differences between the small and large diameter based on α = 0.05.
Differences Between Tasks
To assess whether processing of stimuli is related to task format, we investigated differences in processing non-symbolic primes in the NsNs-task and NsS-task, non-symbolic targets in the NsNs-task and SNs-task, and symbolic targets in the NsS-task and SS-task (see Figure 8).
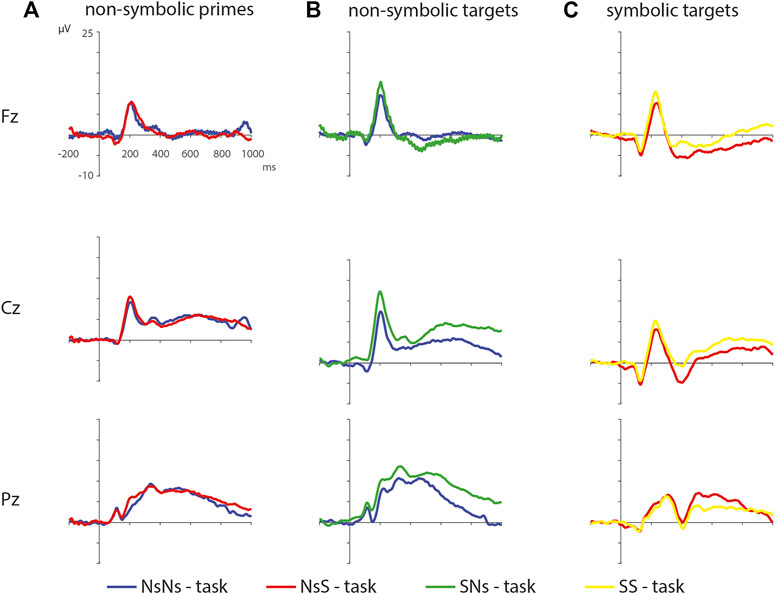
FIGURE 8. ERPs of the non-symbolic primes in the NsNs-task and the NsS-task (A), the non-symbolic targets in the NsNs-task and the SNs-task (B), and the symbolic targets in the NsS-task and the SS-task (C).
Symbolic primes were not compared between tasks, since the primes in the SNs-task consisted of digits, whereas the primes in the SS-task consisted of written number words. For the non-symbolic primes, no significant differences were found between the NsNs-task and the NsS-task, largest positive clusterstat = 218.1, p = 0.307, largest negative clusterstat = −1148.2, p = 0.054, showing no evidence for differences in the processing of non-symbolic primes based on whether it is followed by a symbolic target or by a non-symbolic target. For the non-symbolic targets, no significant positive clusters were found, largest positive clusterstat = 392.2, p = 0.152, but a significant negative cluster was found, clusterstat = −6507.1, p = 0.012. This cluster reflects a widespread (fronto)central difference moving toward the parietal scalp regions between 100 ms 350 ms (see Figure 9) reflecting a difference between the processing of non-symbolic targets in the NsNs-task and the NsS-task. For the symbolic targets, a significant positive cluster was found, clusterstat = 3724.4, p = 0.012, reflecting a long lasting occipital difference (200–700 ms) between the processing of symbolic targets in the NsS-task and the SS-task (see Figure 10). No significant negative clusters were found, largest clusterstat = −2141.2, p = 0.040.
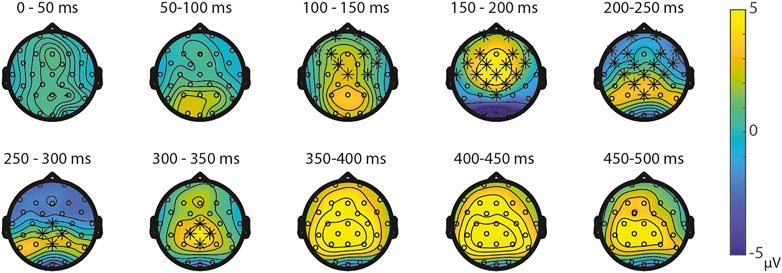
FIGURE 9. Topoplots of the differences between the non-symbolic targets in the NsNs-task and the SNs-task with asterisks representing significant differences based on α = 0.05.
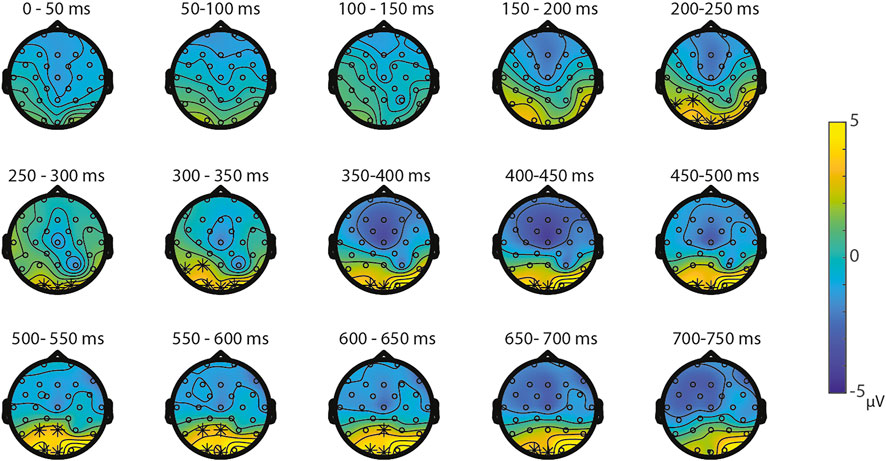
FIGURE 10. Topoplots of the differences between the symbolic targets in the NsS-task and the SS-task with asterisks representing significant differences based on α = 0.05.
Discussion
The first aim of the present study was to examine whether non-symbolic numerosity processing in 9-to-12-year-old children is intuitive and thus relatively fast, in line with the ANS theory (Dehaene, 1997), or whether visual properties of stimuli play a role in processing the numerosity, in line with the sensory-integration theory (Gebuis et al., 2016; Gevers et al., 2016). The second aim was to examine whether children process symbolic numbers by automatically mapping them onto non-symbolic numerosities, in line with the ANS mapping account (Dehaene, 1997). Alternatively, children may process numbers without automatically activating the corresponding numerosity, for example based on symbol-symbol associations (Krajcsi et al., 2016; Reynvoet and Sasanguie, 2016).
Non-Symbolic Numerosity Processing
The behavioral data in the non-symbolic task show performance above chance level. However, accuracy on the matching trials was relatively low, which indicates that the children had difficulty determining whether two numerosities were the same. The accuracy on ratio 0.5 was higher than on ratio 0.7, which is in line with the expectations based on previous research (e.g., Guillaume and Van Rinsveld, 2018). The ERP data showed only a late parietal effect for ratio in the completely non-symbolic task, starting at 650 ms after the presentation of the target, in line with previous research (Soltész and Szűcs, 2014). However, earlier effects for the visual feature surface and diameter were found over the occipital scalp regions, starting around 200 ms, suggesting that these are processed automatically, even though the task focused on numerosity. Children thus seem to process visual features more automatically than numerosity of non-symbolic stimuli. Based on the ANS theory, one would have expected an earlier distance effect for ratio of numerosity. As such, our findings do not convincingly support the ANS theory (Dehaene, 1997).
In earlier research in adults, we argued that the presence of a long-lasting effect of visual properties starting early was not in line with the ANS theory (Van Hoogmoed and Kroesbergen, 2018). Instead, we argued that these findings were in line with two recent theories that have been proposed as alternatives for the ANS theory: The sensory-integration theory and sense of magnitude theory (Gebuis et al., 2016; Leibovich et al., 2017), both suggesting that visual features are not removed before processing numerosity, but are at the basis of this process. However, the results in adults differed from those in children. The duration of the effect of the visual features was shorter and a late ratio effect was present in children, but not in adults. As such, the results found in this study do not support the sensory-integration theory either. Another possible hypothesis may be that children do not use visual features as the basis for the processing of numerosity, but first process the visual features, and inhibit their response based on these visual features (Fuhs and McNeil, 2013; Gilmore et al., 2013). After that, they may still consciously process the numerosity, causing the late effects of ratio. However, this possibility requires additional research.
Another difference between the effects of visual properties in previous research with adults (Van Hoogmoed and Kroesbergen, 2018) and the current study in children was that the visual features showing a distance effect in the non-symbolic task in children were surface and diameter as opposed to area in adults. This difference, however, complements a developmental study on the effects of visual features in children and adults (Gilmore et al., 2016). That study revealed that adults indeed rely more on the convex hull (or area) of non-symbolic stimuli, whereas in primary school children the dot size (or surface) was most important. This is in line with the current results. Additionally, it has been suggested that the contribution of any visual feature to non-symbolic numerosity processing is dependent on the type of stimuli, the setting, and the context of a task (Leibovich and Henik, 2014). As such, the specific visual feature that shows the result is deemed less important than the finding of effects for visual features itself.
Our results differ from the recent results on automatic processing of numerosity, even as early as the visual cortex (Park et al., 2016; Fornaciai et al., 2017; Starr et al., 2017; Park, 2018; DeWind et al., 2019). In these studies, a fixed number of five numerosities was used instead of the ratios of numerosities that were used in the present study. Moreover, control over visual properties was carried out in a different manner in which visual properties seem to correlate more with the presented numerosity compared to the current study. In such passive paradigms without focus on numerosity, it is likely that participants automatically process the most salient features of the stimuli (either numerosity or a visual property; see Leibovich et al., 2017). In our paradigm, the focus of the participants was specifically on numerosity, since we instructed them to press a button in case of matching numerosities. Even then, there was more evidence for early processing of visual features as compared to processing of the numerosity, which suggests that this was more intuitive.
To conclude, we argued that our results do not align with the ANS theory, but neither with the sensory integration theory. This argument was based mainly on the late effects of ratio, which are in contrast with earlier ERP-studies showing P2p-effects in comparison tasks (e.g., Temple and Posner; Heine et al., 2013). The current task differs from the comparison task in that it may first be necessary to estimate the numerosity (after removal/normalization of visual features), and then compare it to the numerosity that is kept in memory. The normalization of visual features may be reflected in the effects of visual features around 200–300 ms. The late parietal effect for ratio starting around 650 ms may reflect the next step, i.e., the comparison itself. As such, the process could be similar to what would be expected based on the ANS theory. However, the timing of the effects suggest that the processing of the numerosity is not intuitive, but requires effort.
Symbolic Number Processing
For the completely symbolic task, we found a very early effect of ratio between 50 and 300 ms over the central scalp, and a late effect for ratio over the central scalp between around 700 and 800 ms. A ratio effect in a symbolic task may reflect overlapping representations of non-symbolic numerosity and symbolic number (Van Opstal and Verguts, 2011), which would support the ANS mapping account. However, this would mean that the symbolic numbers activate the non-symbolic representation and show a distance effect based on these non-symbolic representations. In that case, one would expect a similar ratio effect in the non-symbolic task as well, something that was not supported by our results. The early effect was not present in the non-symbolic task. Moreover, the late effect was spread over the (left)-fronto-central scalp in the symbolic task and more parietal in the non-symbolic task. The results thus suggest that non-symbolic numerosity processing and symbolic number processing rely on different mechanisms. This idea is supported by recent work showing only weak relations between the processing of non-symbolic numerosity and symbolic number in adults and children (see Leibovich and Ansari, 2016 and Reynvoet and Sasanguie, 2016 for reviews).
The ratio effect found in the symbolic task may be better explained by alternative accounts, such as the discrete semantic system (DSS; Krajcsi et al., 2016) or a symbol-symbol association account (Reynvoet and Sasanguie, 2016). Both accounts suggest that relations between symbolic numbers are at the basis of symbolic number processing instead of relations between a symbolic number and the corresponding numerosity. According the DSS theory, numbers are stored in nodes in a network, similar to the mental lexicon or other conceptual networks. The strength of the connections between the nodes is proportional to the strength of the semantic relations (Krajcsi et al., 2016). Related to this theory, Reynvoet and Sasanguie argue initially small numbers gain meaning through coupling to the OTS, but larger numbers gain meaning through the ordinal relation between numbers. The strength of connections between the nodes (stronger connection for numbers closer to each other) or the ordinal relation between numbers may explain the ratio effects found in symbolic tasks, including the symbolic task in the current study. With regards to the mapping tasks, based on the ANS mapping account, one would expect that humans automatically activate numerosity when they are processing symbolic numbers, especially when these need to be mapped onto non-symbolic numerosities. In this study, this would have resulted in similar ratio effects in all tasks, including the mapping tasks (although maybe different in exact timing). However, no significant effects of numerosity were found in the mapping tasks. Moreover, if numerosity would be activated automatically, this activation should be independent of task format. Thus, based on the ANS mapping account, non-symbolic numerosity processing should not differ between completely non-symbolic tasks and mapping tasks. The ERP data showed no evidence for differences in processing non-symbolic primes within different task formats, but do show significant differences in the processing of non-symbolic targets between task formats. This implies that the activation of non-symbolic numerosity is not automatic, and thus not in line with the ANS mapping account.
The differences in non-symbolic processing based on task format contradict fMRI studies showing that, under passive viewing conditions, non-symbolic and symbolic stimuli both activate the hIPS (Dehaene et al., 2003; Piazza et al., 2007). The authors interpreted these results as evidence for the integration between symbolic numbers and non-symbolic numerosities. Their findings thus seem to be in line with the ANS mapping account. However, the fact that the hIPS is involved in symbolic and non-symbolic processing does not necessarily mean that both formats are processed in the same manner. Moreover, more recent, fine-grained fMRI research shows different regions involved in symbolic vs. non-symbolic processing (e.g., Bulthé et al., 2014; Bulthé et al., 2015; Holloway, Price, and Ansari, 2010; see Sokolowski et al., 2017 for a meta-analysis), indicating that both formats may be processed in different ways. The effect in our study indeed reflected larger ERP amplitudes for non-symbolic targets following symbolic primes compared to non-symbolic primes. This may indicate that more resources are allocated to non-symbolic numerosity processing during mapping than during the comparison of similar formats (Kadosh, Lammertyn, and Izard, 2008; Landgraf et al., 2010). Thus, our results substantiate other research showing differences in non-symbolic processing based on task format.
These results raise the question based on which format mapping tasks are solved. In our previous study in adults (Van Hoogmoed and Kroesbergen, 2018), we argued that tasks with mixed stimuli might be solved by attaching a symbolic number to the numerosity of a dot pattern and comparing this symbolic number to the presented digit. As such, it was suggested that symbolic number processing was the primary format in mapping tasks. The exploratory analysis on the differences in behavior between the SNs-task and the NsS-task in the current study could be seen as support for this argument. These results show that it was easier for the children to compare a symbolic target to a non-symbolic prime than to compare a non-symbolic target to a symbolic prime. However, whereas these results are provide some evidence against the notation-independent code, they do not necessarily inform us about the primary format of processing. The results could imply that the non-symbolic prime already activated the symbolic number, after which the symbolic target was matched to this symbolic number, meaning that symbolic processing was the primary format. However, it could also mean that the format of processing is dependent on the format of the prime, and that activation of the non-symbolic format based on a symbolic target (in the NsS-task) was easier than activation of the symbolic format based on a non-symbolic target (in the SNs-task). Moreover, the ERP results showed differences in the processing of the symbolic targets based on task format as well. If number would be the primary format of processing, one would not expect a dependency on task. This may suggest that non-symbolic numerosity processing is not rooted in symbolic number processing either, but processing format may be based on specific task demands.
Additional insights would have been possible based on a comparison between symbolic primes in the different task formats. However, we could not compare the symbolic primes to subsequent non-symbolic targets and symbolic targets, because the symbolic primes we used had a different format in both tasks. The symbolic primes consisted of digits (e.g., “10”) in the mapping task, whereas the symbolic primes consisted of number words (e.g., “ten”) in the symbolic task. The reason for this is that we prioritized the analyses of the (symbolic) targets: In the completely symbolic task, the prime and target had to be physically different in order to prevent children to compare visual properties of the number instead of its magnitude. Still, the notion that children do not anticipate the format of the target seems to hold, as there was no difference between the non-symbolic primes. This appears to suggest that children remember the (non-symbolic) prime in the original format, and only start processing the prime when the target is presented. This may explain the difference between the ERPs to symbolic targets in the mapping task vs. the symbolic task, but does not inform us about the format of processing. The behavioral data suggest that the mapping task was more difficult for children, which probably resulted in the differences in ERPs. This delayed processing of the prime in children may well be different from the way adults approach the task, irrespective of differences in the processing of numerosities and numbers itself.
Limitations
Several limitations of the present study should be acknowledged. First, the absence of responses to the non-matching trials in the experiment might have confounded the results, because non-response trials (in this case 91% of the trials) might be due to irrelevant functions (e.g., distraction, boredom, uncertainty in decision-making) instead of correct task performance and may have made the task more difficult compared to an active comparison task. This difficulty can be inferred from the low accuracy on the matching trials. However, we explicitly aimed for a match-to-sample task with mainly non-response, because previous research on non-symbolic numerosity and symbolic number has suggested that active same-different tasks and active comparison tasks may tap into different cognitive processes (Van Opstal et al., 2008; Van Opstal and Verguts, 2011). Whereas the ratio effect in comparison tasks may be caused by a general decision process, in the same-different task, it is thought to be due to co-activation based on neural overlap between numbers. While acknowledging the limitations of the more passive task, the behavioral results show that there is a ratio effect in all tasks included non-symbolic stimuli. This suggests that children were actively engaged in the task, although their engagement may have been lower than in a traditional comparison task which requires a response to each trial.
A second limitation is the quite large age range of the participants. Previous research showed that susceptibility to perceptual cues is affected by the age of the participating children (Defever et al., 2013). However, the age range of participating children was much larger in that study. Moreover, our behavioral results did not show significant relations between performance and age. Therefore, we did not include age as a factor in our analyses. Future research with a larger sample and a larger age range could shed light on possible differences between different age groups.
A third limitation is that we did not directly examine the effect of visual properties on the processing of numerosity. Instead, we examined the effects of numerosity and visual features separately, and qualitatively compared them. Moreover, we chose to create stimuli such that the overlap between numerosity and visual features was as limited as possible (based on Gebuis and Reynvoet, 2011). This has led to a larger differences in visual features as compared to ratio differences. Previous research has shown that the variation in visual features impacts the judgment of numerosity (e.g., Nys and Content, 2012; Clayton et al., 2015; Gilmore et al., 2016). Future research should include a full comparison of the different methods of constructing visual stimuli (including more difficult ratios), and directly compare the impact of these different ways of constructing stimuli on numerosity processing. Such an endeavor would help to gain a comprehensive understanding of numerosity processing under different circumstances.
Conclusion
To conclude, our results show very late numerosity-related ratio effects, in combination with early effects related to the visual features of non-symbolic stimuli. As such, these results seem to contradict the ANS theory, and suggest that processing of non-symbolic numerosity is unlikely to be automatic. Moreover, we found that non-symbolic numerosity is not automatically activated when processing symbolic numbers, which contrasts the ANS mapping account (Dehaene, 1997). Although children can relate numbers and numerosities, given their behavioral ratio effect in the mapping tasks, this process does not seem to be automatic. In adults, it has been suggested that symbolic number could be the primary format of processing, and non-symbolic numerosity processing would possibly occur by estimating the number of dots, and then compare the numbers in a symbolic format (Van Hoogmoed and Kroesbergen, 2018). However, this hypothesis does not seem to hold either, since we found that the processing of symbolic targets is also dependent on task format in children. This may however be due to the fact that children, contrary to adults, do not anticipate on the upcoming target. The difference between the symbolic targets in the mapping task and the purely symbolic task might be explained by the notion that children still need to process the prime once the target it presented. Future research including both a blocked design and a mixed design (i.e., manipulating expectancy of a certain format) would be suitable to examine this idea. Moreover, future research including younger children could shed light on differences in the dependence or independence of symbolic number processing on non-symbolic numerosity processing over development. This may substantiate the current evidence against the ANS theory and ANS mapping account.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://osf.io/a85rs/.
Ethics Statement
The studies involving human participants were reviewed and approved by the Ethics Review Board of the Faculty of Social and Behavioral Sciences of Utrecht University. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author Contributions
AvH and EK set up the experiment, AvH set up data collection and data analysis. AvH and MH analyzed the data. AvH, MH, and EK contributed to writing the manuscript.
Funding
This research was funded by the Dutch Scientific Organization (NWO), Aspasia grant number 015.008.028, awarded to EK.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Dennis Hofman and Jos Jaspers for the technical support during data collection. We would like to thank Sanne van der Ven, Isabelle van Hasselt, Daniela van Wijngaarden, Anniek van Dijk, Jasmijn van Engeland, Hilde Vuijk-Biewenga, and Vivian Campschoer for their help in collecting the data.
References
Ansari, D., Garcia, N., Lucas, E., Hamon, K., and Dhital, B. (2005). Neural Correlates of Symbolic Number Processing in Children and Adults. Neuroreport 16 (16), 1769–1773. doi:10.1097/01.wnr.0000183905.23396.f1
Bulthé, J., De Smedt, B., and Op de Beeck, H. P. (2014). Format-dependent Representations of Symbolic and Non-symbolic Numbers in the Human Cortex as Revealed by Multi-Voxel Pattern Analyses. NeuroImage 87, 311–322. doi:10.1016/j.neuroimage.2013.10.049
Bulthé, J., De Smedt, B., and Op de Beeck, H. P. (2015). Visual Number Beats Abstract Numerical Magnitude: Format-dependent Representation of Arabic Digits and Dot Patterns in Human Parietal Cortex. J. Cogn. Neurosci. 27 (7), 1376–1387. doi:10.1162/jocn_a_00787
Carey, S. (2004). Bootstrapping & the Origin of Concepts. Daedalus 133 (1), 59–68. doi:10.1162/001152604772746701
Carey, S. (2009). Where Our Number Concepts Come from. J. Philos. 106 (4), 220–254. doi:10.5840/JPHIL2009106418
Carey, S. (2011). Précis of the Origin of Concepts. Behav. Brain Sci. 34 (3), 113–124. doi:10.1017/S0140525X10000919
Clayton, S., Gilmore, C., and Inglis, M. (2015). Dot Comparison Stimuli Are Not All Alike: The Effect of Different Visual Controls on ANS Measurement. Acta Psychol. 161, 177–184. doi:10.1016/j.actpsy.2015.09.007
Defever, E., Sasanguie, D., Vandewaetere, M., and Reynvoet, B. (2012). What Can the Same-Different Task Tell Us about the Development of Magnitude Representations? Acta Psychol. 140 (1), 35–42. doi:10.1016/j.actpsy.2012.02.005
Defever, E., Reynvoet, B., and Gebuis, T. (2013). Task- and Age-dependent Effects of Visual Stimulus Properties on Children's Explicit Numerosity Judgments. J. Exp. Child Psychol. 116 (2), 216–233. doi:10.1016/j.jecp.2013.04.006
Dehaene, S., Dupoux, E., and Mehler, J. (1990). Is Numerical Comparison Digital? Analogical and Symbolic Effects in Two-Digit Number Comparison. J. Exp. Psychol. Hum. Percept. Perform. 16 (3), 626–641. doi:10.1037/0096-1523.16.3.626
Dehaene, S., Piazza, M., Pinel, P., and Cohen, L. (2003). Three Parietal Circuits for Number Processing. Cogn. Neuropsychol. 20 (3-6), 487–506. doi:10.1080/02643290244000239
Dehaene, S. (1996). The Organization of Brain Activations in Number Comparison: Event-Related Potentials and the Additive-Factors Method. J. Cogn. Neurosci. 8 (1), 47–68. doi:10.1162/jocn.1996.8.1.47
Dehaene, S. (1997). The Number Sense: How the Mind Creates Mathematics. New York: Oxford University Press.
DeWind, N. K., Park, J., Woldorff, M. G., and Brannon, E. M. (2019). Numerical Encoding in Early Visual Cortex. Cortex 114, 76–89. doi:10.1016/j.cortex.2018.03.027
Fornaciai, M., Brannon, E. M., Woldorff, M. G., and Park, J. (2017). Numerosity Processing in Early Visual Cortex. NeuroImage 157, 429–438. doi:10.1016/j.neuroimage.2017.05.069
Fuhs, M. W., and McNeil, N. M. (2013). ANS Acuity and Mathematics Ability in Preschoolers from Low-Income Homes: Contributions of Inhibitory Control. Dev. Sci. 16 (1), 136–148. doi:10.1111/desc.12013
Gebuis, T., and Reynvoet, B. (2011). Generating Nonsymbolic Number Stimuli. Behav. Res. 43 (4), 981–986. doi:10.3758/s13428-011-0097-5
Gebuis, T., and Reynvoet, B. (2012). Continuous Visual Properties Explain Neural Responses to Nonsymbolic Number. Psychophysiol 49 (11), 1649–1659. doi:10.1111/j.1469-8986.2012.01461.x
Gebuis, T., Cohen Kadosh, R., and Gevers, W. (2016). Sensory-integration System rather Than Approximate Number System Underlies Numerosity Processing: A Critical Review. Acta Psychol. 171, 17–35. doi:10.1016/j.actpsy.2016.09.003
Gelman, R., and Gallistel, C. (1978). The Child's Understanding of Number. Cambridge, MA: Harvard University Press.
Gelman, R. (2011). The Case for Continuity. Behav. Brain Sci. 34 (3), 127–128. doi:10.1017/S0140525X10002712
Gentner, D., and Simms, N. (2011). Language and Analogy in Conceptual Change. Behav. Brain Sci. 34 (3), 128–129. doi:10.1017/S0140525X10002736
Gevers, W., Kadosh, R. C., and Gebuis, T. (2016). “Sensory Integration Theory: An Alternative to the Approximate Number System,” in Continuous Issues in Numerical Cognition. Editor A. Henik (New York, NY: Elsevier), 405–418. doi:10.1016/B978-0-12-801637-4.00018-4
Gilmore, C., Attridge, N., Clayton, S., Cragg, L., Johnson, S., Marlow, N., et al. (2013). Individual Differences in Inhibitory Control, Not Non-verbal Number Acuity, Correlate with Mathematics Achievement. PLoS One 8 (6), e67374. doi:10.1371/journal.pone.0067374
Gilmore, C., Cragg, L., Hogan, G., and Inglis, M. (2016). Congruency Effects in Dot Comparison Tasks: Convex hull Is More Important Than Dot Area. J. Cogn. Psychol. 28 (8), 923–931. doi:10.1080/20445911.2016.1221828
Goffin, C., and Ansari, D. (2019). How Are Symbols and Nonsymbolic Numerical Magnitudes Related? Exploring Bidirectional Relationships in Early Numeracy. Mind, Brain Educ. 13 (3), 143–156. doi:10.1111/mbe.12206
Guillaume, M., and Van Rinsveld, A. (2018). Comparing Numerical Comparison Tasks: A Meta-Analysis of the Variability of the Weber Fraction Relative to the Generation Algorithm. Front. Psychol. 9, 1–9. doi:10.3389/fpsyg.2018.01694
Halberda, J., and Feigenson, L. (2008). Developmental Change in the Acuity of the "number Sense": The Approximate Number System in 3-, 4-, 5-, and 6-Year-Olds and Adults. Dev. Psychol. 44 (5), 1457–1465. doi:10.1037/a0012682
Heine, A., Wißmann, J., Tamm, S., De Smedt, B., Schneider, M., Stern, E., et al. (2013). An Electrophysiological Investigation of Non-symbolic Magnitude Processing: Numerical Distance Effects in Children with and without Mathematical Learning Disabilities. Cortex 49 (8), 2162–2177. doi:10.1016/j.cortex.2012.11.009
Holloway, I. D., and Ansari, D. (2008). Domain-specific and Domain-General Changes in Children's Development of Number Comparison. Dev. Sci. 11 (5), 644–649. doi:10.1111/j.1467-7687.2008.00712.x
Holloway, I. D., and Ansari, D. (2009). Mapping Numerical Magnitudes onto Symbols: The Numerical Distance Effect and Individual Differences in Children's Mathematics Achievement. J. Exp. Child Psychol. 103 (1), 17–29. doi:10.1016/j.jecp.2008.04.001
Holloway, I. D., Price, G. R., and Ansari, D. (2010). Common and Segregated Neural Pathways for the Processing of Symbolic and Nonsymbolic Numerical Magnitude: An fMRI Study. Neuroimage 49 (1), 1006–1017. doi:10.1016/j.neuroimage.2009.07.071
Hyde, D. C., and Spelke, E. S. (2009). All Numbers Are Not Equal: An Electrophysiological Investigation of Small and Large Number Representations. J. Cogn. Neurosci. 21 (6), 1039–1053. doi:10.1162/jocn.2009.21090
Hyde, D. C., and Spelke, E. S. (2011). Neural Signatures of Number Processing in Human Infants: Evidence for Two Core Systems Underlying Numerical Cognition. Dev. Sci. 14 (2), 360–371. doi:10.1111/j.1467-7687.2010.00987.x
Hyde, D. C., and Spelke, E. S. (2012). Spatiotemporal Dynamics of Processing Nonsymbolic Number: An Event‐related Potential Source Localization Study. Hum. Brain Mapp. 33 (9), 2189–2203. doi:10.1002/hbm.21352
Kadosh, R. C., Lammertyn, J., and Izard, V. (2008). Are Numbers Special? an Overview of Chronometric, Neuroimaging, Developmental and Comparative Studies of Magnitude Representation. Prog. Neurobiol. 84 (2), 132–147. doi:10.1016/j.pneurobio.2007.11.001
Kolkman, M. E., Kroesbergen, E. H., and Leseman, P. P. M. (2013). Early Numerical Development and the Role of Non-symbolic and Symbolic Skills. Learn. Instruction 25, 95–103. doi:10.1016/j.learninstruc.2012.12.001
Krajcsi, A., Lengyel, G., and Kojouharova, P. (2016). The Source of the Symbolic Numerical Distance and Size Effects. Front. Psychol. 7, 1–16. doi:10.3389/fpsyg.2016.01795
Krajcsi, A., Lengyel, G., and Kojouharova, P. (2018). Symbolic Number Comparison is Not Processed by The Analog Number System: Different Symbolic and Non-Symbolic Numerical Distance and Size Effects. Front. Psychol. 9, 124. doi:10.3389/fpsyg.2018.00124
Landgraf, S., Meer, E., and Krueger, F. (2010). Cognitive Resource Allocation for Neural Activity Underlying Mathematical Cognition: A Multi-Method Study. ZDM Math. Educ. 42, 579–590. doi:10.1007/s11858-010-0264-7
Landy, D., Allen, C., and Anderson, M. L. (2011). Conceptual Discontinuity Involves Recycling Old Processes in New Domains. Behav. Brain Sci. 34 (3), 136–137. doi:10.1017/S0140525X10002153
Leibovich, T., and Ansari, D. (2016). The Symbol-Grounding Problem in Numerical Cognition: A Review of Theory, Evidence, and Outstanding Questions. Can J. Exp. Psychol. 70 (1), 12. doi:10.1037/cep0000070
Leibovich, T., and Henik, A. (2014). Comparing Performance in Discrete and Continuous Comparison Tasks. Q. J. Exp. Psychol. 67 (5), 899–917. doi:10.1080/17470218.2013.837940
Leibovich, T., Katzin, N., Harel, M., and Henik, A. (2017). From “Sense of Number” to “Sense of Magnitude”: The Role of Continuous Magnitudes in Numerical Cognition. Behav. Brain Sci. 40, 1–62. doi:10.1017/s0140525x16000960
Libertus, M. E., Woldorff, M. G., and Brannon, E. M. (2007). Electrophysiological Evidence for Notation independence in Numerical Processing. Behav. Brain Funct. 3 (1), 1–15. doi:10.1186/1744-9081-3-1
Lyons, I. M., Ansari, D., and Beilock, S. L. (2012). Symbolic Estrangement: Evidence against a strong Association between Numerical Symbols and the Quantities They Represent. J. Exp. Psychol. Gen. 141 (4), 635–641. doi:10.1037/a0027248
Lyons, I. M., Bugden, S., Zheng, S., De Jesus, S., and Ansari, D. (2018). Symbolic Number Skills Predict Growth in Nonsymbolic Number Skills in Kindergarteners. Dev. Psychol. 54 (3), 440–457. doi:10.1037/dev0000445
Marinova, M., Sasanguie, D., and Reynvoet, B. (2018). Symbolic Estrangement or Symbolic Integration of Numerals with Quantities: Methodological Pitfalls and a Possible Solution. PLoS One 13 (7), e0200808. doi:10.1371/journal.pone.0200808
Marinova, M., Sasanguie, D., and Reynvoet, B. (2021). Numerals Do Not Need Numerosities: Robust Evidence for Distinct Numerical Representations for Symbolic and Non-symbolic Numbers. Psychol. Res. 85, 764–776. doi:10.1007/s00426-019-01286-z
Nys, J., and Content, A. (2012). Judgement of Discrete and Continuous Quantity in Adults: Number Counts!. Q. J. Exp. Psychol. 65 (4), 675–690. doi:10.1080/17470218.2011.619661
Oostenveld, R., Fries, P., Maris, E., and Schoffelen, J.-M. (2011). FieldTrip: Open Source Software for Advanced Analysis of MEG, EEG, and Invasive Electrophysiological Data. Comput. Intelligence Neurosci. 2011, 1–9. doi:10.1155/2011/156869
Park, J., DeWind, N. K., Woldorff, M. G., and Brannon, E. M. (2016). Rapid and Direct Encoding of Numerosity in the Visual Stream. Cereb. Cortex 26 (2), bhv017–763. doi:10.1093/cercor/bhv017
Park, J., DeWind, N. K., and Brannon, E. M. (2017). Direct and Rapid Encoding of Numerosity in the Visual Stream. Behav. Brain Sci. 40, 2532–2544. doi:10.1017/S0140525X16002235
Park, J. (2018). A Neural Basis for the Visual Sense of Number and its Development: A Steady-State Visual Evoked Potential Study in Children and Adults. Dev. Cogn. Neurosci. 30, 333–343. doi:10.1016/j.dcn.2017.02.011
Paulsen, D. J., and Neville, H. J. (2008). The Processing of Non-symbolic Numerical Magnitudes as Indexed by ERPs. Neuropsychologia 46 (10), 2532–2544. doi:10.1016/j.neuropsychologia.2008.04.003
Piazza, M., Pinel, P., Le Bihan, D., and Dehaene, S. (2007). A Magnitude Code Common to Numerosities and Number Symbols in Human Intraparietal Cortex. Neuron 53 (2), 293–305. doi:10.1016/j.neuron.2006.11.022
Piazza, M., De Feo, V., Panzeri, S., and Dehaene, S. (2018). Learning to Focus on Number. Cognition 181, 35–45. doi:10.1016/j.cognition.2018.07.011
Pinel, P., Dehaene, S., Rivière, D., and LeBihan, D. (2001). Modulation of Parietal Activation by Semantic Distance in a Number Comparison Task. NeuroImage 14 (5), 1013–1026. doi:10.1006/nimg.2001.0913
Reynvoet, B., and Sasanguie, D. (2016). The Symbol Grounding Problem Revisited: A Thorough Evaluation of the ANS Mapping Account and the Proposal of an Alternative Account Based on Symbol-Symbol Associations. Front. Psychol. 07, 1–11. doi:10.3389/fpsyg.2016.01581
Sasanguie, D., De Smedt, B., Defever, E., and Reynvoet, B. (2012). Association between Basic Numerical Abilities and Mathematics Achievement. Br. J. Dev. Psychol. 30 (2), 344–357. doi:10.1111/j.2044-835X.2011.02048.x
Sasanguie, D., Göbel, S. M., Moll, K., Smets, K., and Reynvoet, B. (2013). Approximate Number Sense, Symbolic Number Processing, or Number-Space Mappings: What Underlies Mathematics Achievement? J. Exp. Child Psychol. 114 (3), 418–431. doi:10.1016/j.jecp.2012.10.012
Sasanguie, D., De Smedt, B., and Reynvoet, B. (2017). Evidence for Distinct Magnitude Systems for Symbolic and Non-symbolic Number. Psychol. Res. 81 (1), 231–242. doi:10.1007/s00426-015-0734-1
Sassenhagen, J., and Draschkow, D. (2019). Cluster‐based Permutation Tests of MEG/EEG Data Do Not Establish Significance of Effect Latency or Location. Psychophysiology 56 (6), e13335. doi:10.1111/psyp.13335
Schneider, M., Beeres, K., Coban, L., Merz, S., Susan Schmidt, S., Stricker, J., et al. (2017). Associations of Non-symbolic and Symbolic Numerical Magnitude Processing with Mathematical Competence: a Meta-Analysis. Dev. Sci. 20 (3), e12372–16. doi:10.1111/desc.12372
Sokolowski, H. M., Fias, W., Mousa, A., and Ansari, D. (2017). Common and Distinct Brain Regions in Both Parietal and Frontal Cortex Support Symbolic and Nonsymbolic Number Processing in Humans: A Functional Neuroimaging Meta-Analysis. Neuroimage 146, 376–394. doi:10.1016/j.neuroimage.2016.10.028
Soltész, F., and Szűcs, D. (2014). Neural Adaptation to Non-symbolic Number and Visual Shape: an Electrophysiological Study. Biol. Psychol. 103, 203–211. doi:10.1016/j.biopsycho.2014.09.006
Soltész, F., Szűcs, D., Dékány, J., Márkus, A., and Csépe, V. (2007). A Combined Event-Related Potential and Neuropsychological Investigation of Developmental Dyscalculia. Neurosci. Lett. 417, 181–186. doi:10.1016/j.neulet.2007.02.067
Spelke, E. S. (2011). Quinian Bootstrapping or Fodorian Combination? Core and Constructed Knowledge of Number. Behav. Brain Sci. 34 (3), 149–150. doi:10.1017/S0140525X10002220
Starr, A., DeWind, N. K., and Brannon, E. M. (2017). The Contributions of Numerical Acuity and Non-numerical Stimulus Features to the Development of the Number Sense and Symbolic Math Achievement. Cognition 168, 222–233. doi:10.1016/j.cognition.2017.07.004
Temple, E., and Posner, M. I. (1998). Brain Mechanisms of Quantity Are Similar in 5-Year-Old Children and Adults. Proc. Natl. Acad. Sci. 95 (13), 7836–7841. doi:10.1073/pnas.95.13.7836
Van Hoogmoed, A. H., and Kroesbergen, E. H. (2018). On the Difference between Numerosity Processing and Number Processing. Front. Psychol. 9, 1–13. doi:10.3389/fpsyg.2018.01650
Van Opstal, F., and Verguts, T. (2011). The Origins of the Numerical Distance Effect: The Same-Different Task. J. Cogn. Psychol. 23 (1), 112–120. doi:10.1080/20445911.2011.466796
Van Opstal, F., Gevers, W., De Moor, W., and Verguts, T. (2008). Dissecting the Symbolic Distance Effect: Comparison and Priming Effects in Numerical and Nonnumerical Orders. Psychon. Bull. Rev. 15 (2), 419–425. doi:10.3758/PBR.15.2.419
Van Rinsveld, A., Guillaume, M., Kohler, P. J., Schiltz, C., Gevers, W., and Content, A. (2020). The Neural Signature of Numerosity by Separating Numerical and Continuous Magnitude Extraction in Visual Cortex with Frequency-Tagged EEG. Proc. Natl. Acad. Sci. USA 117 (11), 5726–5732. doi:10.1073/pnas.1917849117
Verguts, T., and Van Opstal, F. (2005). Dissociation of the Distance Effect and Size Effect in One-Digit Numbers. Psychon. Bull. Rev. 12 (5), 925–930. doi:10.3758/BF03196787
Xu, F., and Arriaga, R. I. (2007). Number Discrimination in 10-Month-Old Infants. Br. J. Dev. Psychol. 25, 103–108. doi:10.1348/026151005X90704
Xu, F., and Spelke, E. S. (2000). Large Number Discrimination in 6-Month-Old Infants. Cognition 74 (1), 1–11. doi:10.1016/S0010-0277(99)00066-9
Keywords: ANS mapping account, ANS theory, children, non-symbolic numerosity processing, symbolic number processing, ERP
Citation: van Hoogmoed AH, Huijsmans MDE and Kroesbergen EH (2021) Non-Symbolic Numerosity and Symbolic Numbers are not Processed Intuitively in Children: Evidence From an Event-Related Potential Study. Front. Educ. 6:629053. doi: 10.3389/feduc.2021.629053
Received: 13 November 2020; Accepted: 16 June 2021;
Published: 30 June 2021.
Edited by:
Korbinian Moeller, Loughborough University, United KingdomReviewed by:
Mathieu Guillaume, Stanford University, United StatesMarie Coppola, University of Connecticut, United States
Reviewed by:
Madeline Quam, University of Connecticut, in collaboration with reviewer MCCopyright © 2021 van Hoogmoed, Huijsmans and Kroesbergen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anne H. van Hoogmoed, QW5uZS52YW5ob29nbW9lZEBydS5ubA==
 Anne H. van Hoogmoed
Anne H. van Hoogmoed Marije D. E. Huijsmans3
Marije D. E. Huijsmans3 Evelyn H. Kroesbergen
Evelyn H. Kroesbergen