Supporting Student Success and Persistence in STEM With Active Learning Approaches in Emerging Scholars Classrooms

Over the last several decades, Emerging Scholars Programs (ESPs) have incorporated active learning strategies and challenging problems into collegiate mathematics, resulting in students, underrepresented minority (URM) students in particular, earning at least half of a letter grade higher than other students in Calculus. In 2009, West Virginia University (WVU) adapted ESP models for use in Calculus I in an effort to support the success and retention of URM STEM students by embedding group and inquiry-based learning into a designated section of Calculus I. Seats in the class were reserved for URM and first-generation students. We anticipated that supporting students in courses in the calculus sequence, including Calculus I, would support URM Calculus I students in building learning communities and serve as a mechanism to provide a strong foundation for long-term retention. In this study we analyze the success of students that have progressed through our ESP Calculus courses and compare them to their non-ESP counterparts. Results show that ESP URM students succeed in the Calculus sequence at substantially higher rates than URM students in non-ESP sections of Calculus courses in the sequence (81% of URM students pass ESP Calculus I while only 50% of URM students pass non-ESP Calculus I). In addition, ESP URM and ESP non-URM (first-generation but not URM) students succeed at similar levels in the ESP Calculus sequence of courses (81% of URM students and 82% of non-URM students pass ESP Calculus I). Finally, ESP URM students’ one-year retention rates are similar to those of ESP non-URM students and significantly higher than those of URM students in non-ESP sections of Calculus (92% of ESP URM Calculus I students were retained after one year, while only 83% of URM non-ESP Calculus I students were retained). These results suggest that ESP is ideally suited for retaining and graduating URM STEM majors, helping them overcome obstacles and barriers in STEM, and increasing diversity, equity, and inclusion in Calculus.

1 Introduction

West Virginia University (WVU) received a National Science Foundation Louis Stokes Alliance for Minority Participation grant as part of a ten-institution alliance in Kentucky and West Virginia (KY-WV LSAMP) beginning in 2006. This grant provided a mechanism for programming to support the success of underrepresented minority (URM) students, to increase retention of these students in mathematics classes and, in turn, to support them through their STEM majors. A variety of activities related to the goals of the LSAMP program have been implemented at WVU over the years. In 2009, two WVU mathematics faculty members participated in a Professional Enhancement Program (PREP) workshop hosted by the Mathematical Association of America (MAA) on developing and implementing Emerging Scholars Programs (ESPs) and decided to embed the program in calculus as a focal point for the WVU LSAMP efforts to facilitate student success and persistence in STEM.

The concept for ESP was developed at the University of California at Berkeley in 1977 out of a desire to increase diversity in their student population. Uri Treisman observed that students in some (primarily Asian) minority groups had created their own small learning communities (Asera, 2001; Hsu et al., 2008). Students in these communities supported each other’s mathematical understanding by working together to prepare for classes, complete assignments, and study the material while students from other minority backgrounds traditionally underrepresented in STEM fields often struggled to flourish in the mathematics courses they encountered (Asera, 2001). Treisman acted on a conjecture that one of the core problems facing many URM students in their academic work is the lack of a community with shared experiences. Students who lack community support as they move through their academic programs may experience isolation and disconnects that pose significant barriers to success. In a community of peers, the development of mathematical ideas can happen in ways that stem from cultural similarities. ESP implementations build communities of students around shared experiences and identities to mitigate a sense of isolation and have been shown to increase success among URM students (Fullilove and Treisman, 1990; Bonsangue and Drew, 1995; Moreno et al., 1999).

Pedagogical Frameworks and Principles

The traditional ESP model developed by Treisman recruited URM students for out-of-class problem sessions in which groups composed primarily of URM students worked on challenging mathematics problems on blackboards in an engaged classroom (Asera, 1988). Groups worked simultaneously on the same problems and were able to watch the progress of the other groups. During these sessions, which were scheduled multiple times per week for a total of four to six hours of out-of-class work, each group presented their work on specific problems and interacted with other groups. These sessions were very successful in elevating URM students to a similar performance in Calculus as non-URM students (Hsu et al., 2008). Prior to attending the PREP workshop, out-of-class Calculus Seminars had been developed at WVU to increase engagement and provide extra support for students in calculus, but the sessions were not targeted specifically to any particular demographic. The sessions were not compulsory for any students and were not regularly attended. The faculty investigators at WVU then decided that a specially designated section of ESP calculus could be implemented and utilize inquiry-based learning methodologies to immerse students in a community of learners.

After attending the MAA PREP workshop on ESP and based upon experiences facilitating supplementary problem sessions in Calculus, we integrated problem sessions into the class structure to build small learning communities for URM students in STEM disciplines. At the time, no reports of integrating an ESP-style structure into the daily class sessions had been reported at any other institution. The innovative structure would create engaged learning communities in every aspect of the course, not separate from the lectures. The students would spend the majority of their time developing the concepts of Calculus and interacting with their communities to master the material.

The success of traditional ESP was based on a structure of small communities of students working on sets of problems out-of-class as a supplement to the discussions of solutions to problems as an entire class. We designed this to be a central aspect of the WVU ESP Calculus class while keeping the small communities intact. By doing this, we were building learning communities of URM Calculus students of three or four students with periodic whole-class discussions. In those whole class discussions, the small communities worked together to present their solutions.

Standards and Competencies for ESP Students

Our implementation of ESP in Calculus established a number of classroom and community norms in order to create a safe, professional atmosphere that cultivates learning. Students work as a group, deriving conceptual ideas of the topic, building procedural knowledge, giving presentations in the class and taking assessments that test both procedural and conceptual learning. Course faculty clearly articulate expectations for group learning, and the classroom facilities are configured to optimize the group learning dynamic (i.e., setting up tables and chairs for group work, creating space for presentations like whiteboards, markers for each group, etc.). In addition, groups are expected to present their work, while other students supportively engage in small group and whole class discussions. This is done by establishing an environment of constructive feedback and encouragement. Finally, students are asked to present clear solutions in all forums. Within this format of formal presentation and real-time, respectful feedback, it is observed that students can make adjustments to their work towards mathematical accuracy (i.e., using equal signs, using correct notation, showing sufficient amount of work to support conclusions), and in turn towards mathematical understanding. As the semester unfolds and students become acquainted with the professionalism of the ESP Calculus experience, they come to know that any group member may be called upon to present the group’s solution to a problem. These expectations work to build a learning community with the goal of maximizing every student’s success.

Competencies for the ESP Calculus class are three-fold. First, students should gain a solid understanding of typical Calculus problems. Second, students should not memorize formulas, but they should know the answer to why the mathematics works. Last, students should know how to apply the knowledge and understanding they have built in Calculus to solve non-routine and more challenging problems, which can accelerate students to the next level of both conceptual and procedural understanding.

Learning Environment

Working with Department, College, and University administration, space within the department was identified and renovated to support the active learning environment for the course, and recruitment efforts were launched to identify students for the course. Given the university demographics, we extended recruitment efforts beyond URM students to include first-generation students (the institution defines a first-generation college student as a student for whom neither parent had completed a four-year college degree) to include other students who could potentially benefit from community building. All students eligible for Calculus who met the URM and/or first-generation requirement were invited to enroll in the course through a personalized letter from the director of the program that was sent by e-mail and postal mail to their home address. All interested students were accepted into the course, though not all eligible students elected to enroll. Half of the students enrolled in the section were URM or first-generation college students. Recruitment efforts effectively interacted with WVU’s population of URM and first-generation students though only a small number of those students enrolled in the course and so other students were invited. The first ESP calculus course was then taught to 24 students in the Fall 2009 term. The two MAA PREP participants were designated as the course’s primary and secondary instructors, and a graduate assistant was assigned to provide further direct student support and attend each class session. The ESP section was scheduled to meet for two-hour sessions three times per week, rather than one-hour sessions four times per week. The team set a schedule of weekly out-of-class meetings and teams of students, referred to as learning communities, were formed for each class session. To support ongoing community ties, instructors were assigned to Calculus I and stayed with the same cohort of students from Calculus I through Differential Equations. Since the inaugural ESP Calculus class, URM students have been the primary focus of recruitment using personalized letters, while filling up any remaining seats with first generation students. Due to space limitations of the renovated ESP Calculus classroom, at most twenty URM and first-generation were recruited for the ESP Calculus classes (compared to 30–40 for the traditional Calculus classes).

Because the instruction was inquiry-based, there was no textbook for ESP Calculus and most class sessions followed a format of engaged learning. That format began with a short interactive review followed by an intensive sequence of pointed questions to construct new concepts. This instructor-focused portion of the class was intentionally short-often no more than ten minutes. Then, a problem set was distributed, and student work began. In their small learning communities, students would be given a basic concept-building block and then asked to complete exercises and solve problems to develop the idea. The work was overseen by a graduate student and two instructors who circulated the room, and most often responded to questions with questions in an engaged dialogue. Exams for Calculus, including the ESP section, were written and administered uniformly by the Department. This provision allowed for easy ongoing comparisons of student progress by the course instructional team as well as more thoughtful deliberation on the course’s structure going forward.

To build a learning community in Calculus I for a given set of students, we started by dividing students into groups of three or four students. Each group member brought their own perspective and their own unique strengths in mathematics to complement those of the others. Working on a set of problems within a given topic in Calculus, the small groups encountered a range of problems designed to build conceptual understanding, problems similar to those common in textbooks, and problems that combined multiple principles and challenged students to a build a broader understanding of the material (Figure 1 for a sample of problems from part of one of the worksheets on derivatives of inverse trigonometric functions). At different points in each class, groups were asked to present solutions to the entire class, answering questions from other students and addressing comments. These class discussions were structured similarly to colloquium talks in that students were given constructive criticism from the instructional team. To formalize the process, a theme of mutual respect was introduced and reinforced early in the term; presenters were thanked with applause and students were encouraged to give presenters constructive criticism and comments. These supportive components of the learning environment were essential to building notions of mutual respect leading to productive discussion that included all students. Near the end of most class sessions, especially when a few problems remained unsolved from the worksheet, groups were assigned out-of-class work and asked to be prepared to present solutions at the beginning of the next class. In addition, individual student work was assigned as a set of homework problems.

FIGURE 1

FIGURE 1. Sample ESP worksheet.

Worksheets were designed to cover problems that provoked students to build material from the basic conceptual elements. In addition, to achieve the desired level of understanding, after working through those basic conceptual elements, groups worked on a variety of problems to further reinforce the connections with more traditional Calculus problems as part of an engaged learning community in which they felt safe. This reinforcement comes about from working with each other to develop detailed and clear solutions to problems and explaining strategies and concepts to other groups.

Learning Objectives

As noted above, the learning objectives for the ESP Calculus sequence includes both content and skill-oriented outcomes as well as meta-cognitive development. Students should gain a solid understanding of typical Calculus problems that involve concepts and skills identified in traditionally accepted calculus courses. As noted in Hughes-Hallett (2006), a primary goal for students is to develop conceptual understanding. Within that, the learning objectives for ESP align with those identified by experts surveyed in Sofronas et al. (2011) and cover conceptual and skill mastery core concepts for introductory calculus students within the topic areas of limits, derivatives, applications of the derivative, and integration. Our approach was built around the notion that students should not memorize formulas, but they should be able to communicate the ways in which the mathematics works. That is, they should be able to derive (or prove) the concepts in Calculus. Once a student has developed a conceptual understanding of Calculus, they will then be able to recall formulas and derivations—or build them from that understanding—when needed. In addition, they can concentrate on applying concepts to a variety of different problems. Finally, Sofronas et al. (2011) also observe that calculus students should develop connections and relationships between concepts and skills, and apply the knowledge and understanding they have built in Calculus to solve non-routine and more challenging problems. This last step can accelerate students to the next level of both conceptual and procedural understanding as it leads to higher levels of meta-cognition and the ability to transfer knowledge to new situations.

Data and Results

West Virginia University is a Research I institution in the Eastern United States with a primarily white student body population. Calculus I covers differential Calculus (limits, derivatives, and applications of derivatives) and introduces Integral Calculus. A full treatment of Integral Calculus is covered in Calculus II.

Participants

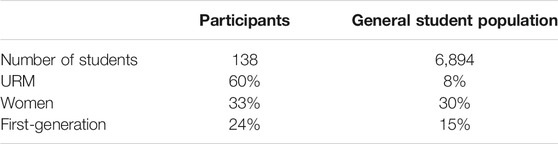
The participants in this study were students in ESP Calculus between 2009–2019. During this time, 138 students enrolled in ESP Calculus I, 60% of them URM, 33% of them women, and 24% of them were first-generation students (Table 1). During the same period, 6,894 students enrolled in the traditional Calculus I course, 8% of them URM, 30% of them women, and 15% of them first-generation students. Most participants in the study were STEM majors (96%) with the majority being Engineering majors (67%), consistent with the university’s overall major trends. Most participants were freshman (80%).

TABLE 1

TABLE 1. Demographics of participants.

Methods

This work explores the success of students both in passing a college mathematics class and in continuing in college one year after completing the mathematics class. Both outcomes are dichotomous and are explored within the framework of logistic regression.

The logistic regression models developed here allow the comparison of the effect of a treatment on some outcome controlling for a set of background variables. We model the impact of the change to the ESP classroom approach on a number of student outcomes including pass rates and persistence and use these models to estimate the likelihood or odds of improved outcomes if a student is present in an ESP class. We can then compute the odds ratio for these outcomes, namely the ratio of the odds of a successful outcome in ESP to the odds in other classes. If the odds ratio (OR) is greater than 1, then a one unit increase in the variable represents a $100\text{\%*}(\text{OR}-1)$ increase in the odds of the positive outcome. If the odds ratio is less than one, then a one unit increase in the variable increases the odds of the negative outcome by $100\text{\%*}((1/\text{OR})-1)$; the odds of the negative outcome is the inverse of the odds of the positive outcome.

Analysis and Outcomes

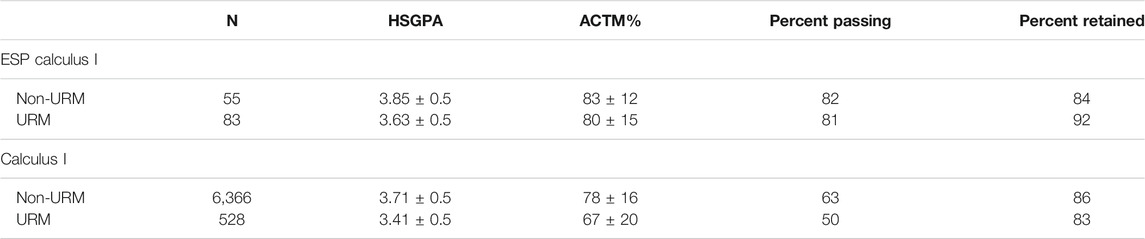
This quantitative analysis will focus on Calculus I, which serves the largest cohort of students requiring any version of calculus at our institution (versions of business calculus and slower-paced calculus are available for students at our university depending on their major but serve fewer students). We explore the rate at which students pass Calculus I (defined as earning a C or higher), and the rate at which students in the class are still enrolled in college one year after completing the class (the 1-year retention rate) for ESP Calculus I and regular Calculus I. For most students taking Calculus I, a grade of C is required to progress in their majors. Students’ general academic preparation was characterized by their high school GPA (HSGPA) and their ACT or SAT mathematics percentile score (ACTM%). Table 2 presents descriptive statistics and values presented are the mean $\left(\text{M}\right)$ ± standard deviation (SD).

TABLE 2

TABLE 2. Descriptive statistics.

Table 2 shows that students in the ESP course have generally superior high school preparation as measured by ACTM% or HSGPA than students in the traditional calculus course. For the remaining analysis in this work, we focus on the results for URM students; future work will explore the effect on first-generation students. The difference in HSGPA and ACTM% between URM and non-URM students in the ESP course was also lower than students in the traditional calculus course. In traditional calculus, URM students pass the class at a significantly lower rate (χ² (1) = 32.74, p < 0.001) and are retained a significantly lower rate (χ² (1) = 5.63, p = 0.018) than non-URM students. In ESP calculus, URM students pass the class at the same rate (χ² (1) = 0.00, p = 1) and are retained at the same rate (χ² (1) = 1.33, p = 0.249) as non-URM students. The differences in passing rate between the two classes is also significant (χ² (1) = 26.36, p < 0.001) as is the difference in one-year retention rate (at the p < 0.1 level) (χ² (1) = 2.89, p = 0.089). For URM students, the difference in passing rate between the two classes is also significant (χ² (1) = 26.36, p < 0.001) as is the difference in retention rate (χ² (1) = 3.63, p = 0.057).

The overall course grade average was similar for URM and non-URM students in the ESP Calculus I course (URM 2.86 ± 1.2, non-URM 2.83 ± 1.2); however, in the traditional Calculus I course, URM students scored substantially lower grades than non-URM students (URM 1.72 ± 1.4, non-URM 2.20 ± 1.4). All grades are on a 4-point scale with A = 4 and F = 0; only students who completed the course for a grade are included in the average.

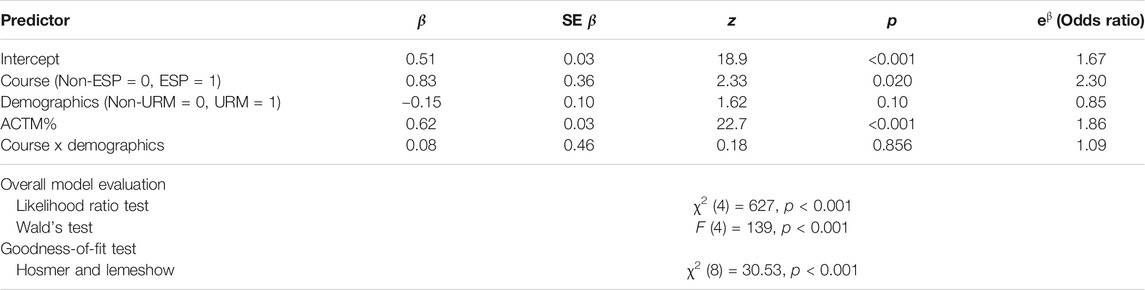
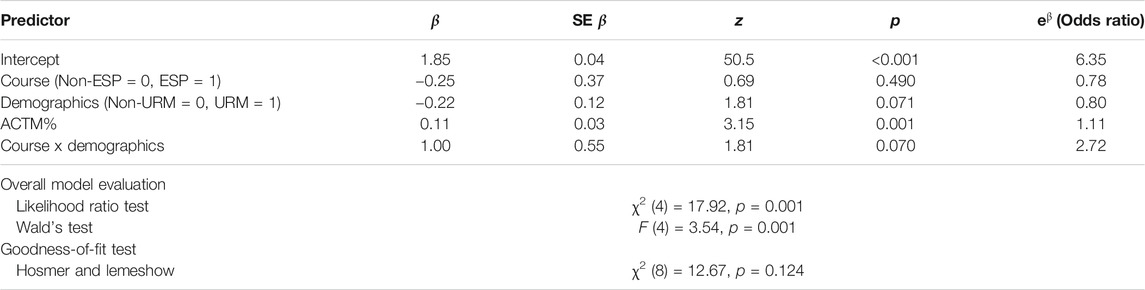
The two classes have different student populations with the ESP class having a somewhat more academically prepared population and, therefore, the differences identified could have resulted from these population differences. To determine whether this was the case, we controlled for academic preparation; the effect of the classes on passing and retention was investigated with logistic regression using ACTM% as a control variable. ACTM% was normalized by subtracting the mean and dividing by the standard deviation. These regressions also used the dichotomous variables Course (Non-ESP = 0, ESP = 1) and Demographics (Non-URM = 0, URM = 1). To investigate whether the ESP course had an additional effect for URM students, interaction terms were added to the regression in the form of the product Course x Demographics. If the ESP course had an additional supportive effect for URM students, then the odds ratio of the interaction would be greater than 1.

First, the dichotomous outcome of passing the class was investigated as shown in Table 3. For this model, the interaction term was not significant; ESP and Non-ESP URM students pass each class at the same rate when correcting for ACTM% scores. All students pass the ESP course with twice the odds (odds ratio = 2.3) as the traditional calculus course. Students with higher ACT mathematics scores have an advantage in both courses; a one-standard-deviation increase in ACT scores nearly doubles the odds of passing (odds ratio = 1.86). A likelihood ratio test and Wald test indicate the model presented in Table 3 is a significant improvement over the null model including only the intercept. However, the Hosmer and Lemeshow (1980) suggests the model is not particularly well fitting. A well-fitting model does not have a significant p-value in this test.

TABLE 3

TABLE 3. Logistic regression predicting passing calculus I.

A similar model was used to investigate one-year retention; the results are shown in Table 4. This model was also a significant improvement over the null model using the Wald test and the likelihood ratio test; however, this model was also well-fitting using the Hosmer and Lemeshow goodness-of-fit test. The ESP course had a dramatic positive effect on the retention of URM students improving the odds of retention by almost a factor of 3 (odds ratio = 2.72). While this result is only significant at the p < 0.10 level, the small sample size suggests it may be more appropriate to examine the size of the effect measured by the odds ratio. Prior preparation was much less important to one-year retention (odds ratio = 1.11), than it was to passing the course (odds ratio = 1.86).

TABLE 4

TABLE 4. Logistic regression predicting retention to college one year after calculus I.

Discussion and Implications

The current study examined differences in pass rates and in continuation in college one year post - course for URM and first generation non-URM students in ESP Calculus courses compared to their non-ESP counterparts. Results of analyses showed that ESP URM students succeeded in the Calculus sequence at substantially higher rates than URM students in non-ESP sections in the sequence. In addition, ESP URM and ESP non-URM students succeeded at similar levels in the ESP Calculus sequence of courses. Finally, ESP URM students’ one-year retention rates were similar to those of ESP non-URM students, and significantly higher than those of URM students in non-ESP sections of Calculus. These results suggest that ESP is ideally suited for retaining and graduating URM STEM majors, helping to overcome obstacles and barriers in STEM, and increasing diversity, equity, and inclusion in Calculus.

The ESP URM students in this study sample are also LSAMP scholars and are therefore high achievers: to be admitted and remain in the program, scholars should have and maintain a 3.0 GPA. Results from a recent study of 20 LSAMP scholars by Burt et al. (2020) revealed that LSAMP scholars in that alliance also entered their LSAMP program with academic strengths, and that, as in the current study, LSAMP provided necessary formal academic support. The KY-WV LSAMP in this study provides scholars with a sense of belonging and support, while ESP Calculus provides a math learning community in which students experience positive learning and mentoring experiences, encouragement and recognition from peers and teachers that is lacking in non-ESP courses, mitigating the isolation and disconnects that pose significant barriers to success (Fullilove and Treisman, 1990; Bonsangue and Drew, 1995; Moreno et al., 1999). Positive results for first-generation students from this study indicate that the ESP course was also beneficial in retaining and graduating STEM majors from this population. It is unlikely that self-selection into ESP alone could explain these results for both groups of students in ESP, particularly since ESP and non-ESP URM students passed each class at the same rate when correcting for prior preparation.

The data collected for this study formed part of a larger research project guided in part by Tinto’s theory of retention (Tinto, 1975; Tinto, 2007), which incorporates both academic and non-academic factors. The project is further informed by Social Cognitive Career theory (SCCT) (Lent et al., 2000). Given the social aspect of the learning community model fostered by ESP combined with the strong positive attitudes and beliefs about the course expressed by the students and the intent of the program to build identification as STEM learners, the SCCT model provides a coherent framework for analyzing the different interacting components observed here. SCCT incorporates Tinto’s non-cognitive factors known to be important in retaining students and expands them for use in groups underrepresented in STEM. Tinto’s sense of self-efficacy, STEM identity, and belonging have important implications for such groups. The ESP model addressess self-efficacy, STEM identity, and belonging in the social structures that it develops within its cohorts. The communication ideas to peers gives them a chance to develop mathematics in ways that make sense to the students themselves, and the sustained mathematical practices in that environment reinforce factors within the SCCT framework that support STEM learner success and persistence. Interviews conducted during the 2020 pandemic with six current and former recent ESP students indicated that they highly valued the community aspect of ESP and every current scholar reported missing the ESP community during online instruction required as a result of the pandemic.

Results from a recent meta-analysis on the impact of active learning methods on failure rates of over 9,000 URM undergraduate students in STEM courses demonstrated that active learning reduced achievement gaps in examination scores by 33% and gaps in passing rates by 45% (Theobald et al., 2020), but only in STEM classes that implemented high-intensity active learning methods like those employed in this study. Furthermore, while many studies have examined the importance of active learning methods for URM success and retention in STEM, few of them addressed the success of both URM and first-generation students in the context we explored in this study. We believed this was very important, as investigators in the department posited, based on previous research, that first-generation students, along with their URM peers, shared a common background and lack of support structures that may have resulted in a lack of understanding of academic expectations and rigor that support other students (Wingate, 2006). This premise was initially tested and confirmed in related work (Deshler et al., 2016) and continues to be an important aspect of the Emerging Scholars Program at WVU.

As noted above, the active learning methods employed in this and similar studies also provides students with a learning community, so we conclude that active learning alone is not responsible for narrowing gaps. The Treisman paradigm requires a sizeable time commitment from students and educators alike; while this is a potential roadblock, as many URM and first-generation students have jobs and other time commitments that can prevent them from participating in ESP, this time commitment is also partly responsible for creating the cohesive learning community (Lee et al., 2018). Theobald et al. (2020) results highlight the interaction of active learning and community in positive results. They proposed that the heads-and-hearts hypothesis explained the extensive variation in efficacy observed among studies; this hypothesis posits that meaningful reductions in achievement gaps only occur when course designs combine deliberate practice with inclusive teaching, as was the case in this study. Note that the heads-and-heart hypothesis fits well within both Tinto’s framework and SCCT and that other recent evidence also demonstrates that learning communities increase the success and retention for first generation and URM STEM students (Solanki et al., 2019; Van Sickle et al., 2020).

Based on ESP student demand, we decided that we would expand ESP to Calculus II during the first semester offering ESP Calculus I in 2009, and for several years we offered ESP Calculus I and II each academic year. With the support of the Mathematics Department prior to the Fall 2013 and continued ESP student demand, we decided to expand ESP to Calculus III and Differential Equations. We have continued to offer ESP for Calculus I and Calculus III in the Fall semesters and Calculus II and Differential Equations in the Spring semesters since 2013. Despite the initial work involved in beginning such a program, the outcomes for the students are compelling while the initial start-up is manageable. To implement a similar program, it may be necessary to lobby administrators and other leadership to allocate instructional time of faculty teams to build a program and to reconfigure physical classroom space. Committing to the process for multiple terms and to giving an ambitious classroom environment the attention it will need can yield outstanding results.

Although it is true that ESP calculus is more time intensive and therefore more costly to implement initially than standard lecture courses, if more students remain enrolled to graduation, the cost could be offset by an increase in tuition dollars resulting from increased retention. More important are the positive impacts including increasing equity in higher education and broadening participation in STEM. The sense of community built within ESP and other learning community focused active learning classroom environments afford students the opportunity to develop mathematics in a culturally responsive (Gay, 2018), meaningful way that resonates with their own experiences. The sustained access to these environments builds agency and identity for students within mathematics and other disciplines, supporting the persistence needed for long-term success in these disciplines. Forty years ago, Treisman’s ESP methods (Asera, 2001) showed that URM students could achieve grade distributions equal to or greater than the class as a whole (15 ± 20), while more recent studies show that if his methods are not diluted, the results are equally positive (Lee et al., 2018; Theobald et al., 2020). Therefore, results from this study and others support calls to replace traditional lecture with evidence-based, active-learning course designs across STEM disciplines and that these innovative in instructional strategies can increase equity in higher education.

Acknowledgement of Constraints

Because these students self-selected into ESP and were better prepared academically, there are limitations to the conclusions that can be drawn from the positive results found in this study; however, similar results have been found by other researchers, suggesting that results from similar ESP-like programs would also be positive (Solanki et al., 2019; Van Sickle et al., 2020). In addition, it is important to study ESP students because they are highly motivated, high achieving students, to gain insight into methods for increasing success for other underrepresented students. This study was also conducted at a single institution in a primarily rural state with many first-generation students, thus, whether or not ESP would prove effective for suburban or urban students is not known. As noted, a hurdle in recruiting for this work was the lack of a diverse student body at this institution, and additional qualitative and quantitative research at different institutions with differing demographic compositions is needed to determine if results are similar in other contexts. This work targeted mathematics courses but it should be extended to determine if the results are similar for other STEM courses.

Permission to Reuse and Copyright

Figures, tables, and images will be published under a Creative Commons CC-BY licence.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the West Virginia University Institutional Review Board. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

All authors contributed to drafting and revising the article. All authors also read and approved the final manuscript. DM and MP implemented the instructional setting, and JS analyzed the data.

Funding

The ESP program was funded by the National Science Foundation (HRD-LSAMP: KY-WV Mid-Level Alliance #1305039, 2013–2019) and the research is supported by the National Science Foundation (HRD Louis Stokes STEM Pathways and Research Alliance: KY-WV LSAMP, 1826763, 2018–2023).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to acknowledge that the Emerging Scholars Program in Calculus is an activity at West Virginia University under the National Science Foundation Louis Stokes Alliance for Minority Participation grant (HRD-LSAMP: KY-WV Mid-Level Alliance #1305039, 2013–2019). We would be remiss if we did not acknowledge the most important piece of the ESP Calculus classes, the students, class assistants, and instructors. Finally, we would also like to thank NSF LSAMP community and the reviewers for their suggestions to improve earlier versions of this article.

References

Asera, R. (2001). Calculus and Community: A History of the Emerging Scholars Program. A Report of the National Task Force on Minority High Achievement. New York, NY: College Entrance Examination Board.

Asera, R. (1988). The Math Workshop: A Description. CBMS Issues Mathematics Educ. 1, 47–62.

Google Scholar

Bonsangue, M. V., and Drew, D. E. (1995). Increasing Minority Students' Success in Calculus. New Dir. Teach. Learn. 1995 (61), 23–33. doi:10.1002/tl.37219956106

CrossRef Full Text | Google Scholar

Burt, B. A., Stone, B. D., Motshubi, R., and Baber, L. D. (2020). STEM Validation Among Underrepresented Students: Leveraging Insights from a STEM Diversity Program to Broaden Participation. J. Divers. Higher Educ. doi:10.1037/dhe0000300

CrossRef Full Text | Google Scholar

Deshler, J. M., Miller, D., and Pascal, M. (2016). An Active Classroom: The Emerging Scholars Program at West Virginia University. Probl. Resour. Issues Mathematics Undergraduate Stud. 26 (9). doi:10.1080/10511970.2016.1191570

CrossRef Full Text | Google Scholar

Fullilove, R. E., and Treisman, P. U. (1990). Mathematics Achievement Among African American Undergraduates at the University of California, Berkeley: An Evaluation of the Mathematics Workshop Program. J. Negro Educ. 59 (3), 463–478. doi:10.2307/2295577

CrossRef Full Text | Google Scholar

Gay, G. (2018). Culturally Responsive Teaching: Theory, Research, and Practice. New York, NY: Teachers College Press.

Hosmer, D. W., and Lemesbow, S. (1980). Goodness of Fit Tests for the Multiple Logistic Regression Model. Comm. Stats. - Theor. Methods 9, 1043–1069. doi:10.1080/03610928008827941

CrossRef Full Text | Google Scholar

Hsu, E., Murphy, T. J., and Treisman, P. U. (2008). Supporting High Minority Achievement in Introductory Collegiate Mathematics Courses: What We Have Learned from 30 Years of the Emerging Scholars Program. Making Connect. Res. Pract. Undergraduate Mathematics Educ. 18 (73), 205–220.

Google Scholar

Hughes-Hallett, D. (2006). What Have We Learned from Calculus Reform? the Road to Conceptual Understanding. MAA Notes 69, 43–47.

Google Scholar

Lee, S., Crane, B. R., Ruttledge, T., Guelce, D., Yee, E. F., Lenetsky, M., et al. (2018). Patching a Leak in an R1 University Gateway STEM Course. PLoS One 13 (9), e0202041. doi:10.1371/journal.pone.0202041

PubMed Abstract | CrossRef Full Text | Google Scholar

Lent, R. W., Brown, S. D., and Hackett, G. (2000). Contextual Supports and Barriers to Career Choice: A Social Cognitive Analysis. J. Couns. Psychol. 47 (1), 36–49. doi:10.1037/0022-0167.47.1.36

CrossRef Full Text | Google Scholar

Moreno, S. E., Muller, C., Asera, R., Wyatt, L., and Epperson, J. (1999). Supporting Minority Mathematics Achievement: the Emerging Scholars Program at the University of Texas at Austin. J. Women Minorities Sci. Eng. 5 (1). doi:10.1615/jwomenminorscieneng.v5.i1.40

CrossRef Full Text | Google Scholar

Sofronas, K. S., DeFranco, T. C., Vinsonhaler, C., Gorgievski, N., Schroeder, L., and Hamelin, C. (2011). What Does it Mean for a Student to Understand the First-Year Calculus? Perspectives of 24 Experts. J. Math. Behav. 30, 131–148. doi:10.1016/j.jmathb.2011.02.001

CrossRef Full Text | Google Scholar

Solanki, S., McPartlan, P., Xu, D., and Sato, B. K. (2019). Success with EASE: Who Benefits from a STEM Learning Community? PLoS One 14 (3), e0213827. doi:10.1371/journal.pone.0213827

PubMed Abstract | CrossRef Full Text | Google Scholar

Theobald, E. J., Hill, M. J., Tran, E., Agrawal, S., Arroyo, E. N., Behling, S., et al. (2020). Active Learning Narrows Achievement Gaps for Underrepresented Students in Undergraduate Science, Technology, Engineering, and Math. Proc. Natl. Acad. Sci. USA 117, 6476–6483. doi:10.1073/pnas.1916903117

PubMed Abstract | CrossRef Full Text | Google Scholar

Tinto, V. (1975). Dropout from Higher Education: A Theoretical Synthesis of Recent Research. Rev. Educ. Res. 45, 89–125. doi:10.3102/00346543045001089

CrossRef Full Text | Google Scholar

Tinto, V. (2007). Research and Practice of Student Retention: What Next? J. Coll. Student Retention: Res. Theor. Pract. 8 (1), 1–19.

Google Scholar

Van Sickle, J., Schuler, K. R., Holcomb, J. P., Carver, S. D., Resnick, A., Quinn, C., et al. (2020). Closing the Achievement Gap for Underrepresented Minority Students in STEM: A Deep Look at a Comprehensive Intervention. J. STEM Educ. Innov. Res. 21 (2), 5–18.

Google Scholar

Wingate, U. (2006). Doing Away with ‘study Skills'. Teach. Higher Educ. 11 (4), 457–469. doi:10.1080/13562510600874268

CrossRef Full Text | Google Scholar