Comparing Two Subjective Rating Scales Assessing Cognitive Load During Technology-Enhanced STEM Laboratory Courses

Introduction

Experimentation in laboratory-like environments is an integral aspect of higher science education (Trumper, 2003; Hofstein and Lunetta, 2004; Lunetta et al., 2005). Guided by a predefined task, learners manipulate experimental setups and observe scientific phenomena in order to explore or verify functional relationships between specific quantities in interaction with their theoretical background (American Association of Physics Teachers, 2014; Lazonder and Harmsen, 2016). Although this inquiry-based format allows for unique hands-on learning experiences, various empirical studies revealed contrary results concerning the learning gain of laboratory courses (Volkwyn et al., 2008; Zacharia and Olympiou, 2011; de Jong et al., 2013; Wilcox and Lewandowski, 2017; Husnaini and Chen, 2019; Kapici et al., 2019). In response, technology-based approaches are applied to support students during experimentation and thereby ensure essential learning and raise the effectiveness of experimentation as a learning scenario (de Jong et al., 2013; Zacharia and de Jong, 2014; de Jong, 2019; Becker et al., 2020).

The most common way to evaluate the effectiveness of new approaches is to apply conceptual knowledge tests to measure learning gains based on content-related knowledge (Etkina et al., 2006; Vosniadou, 2008; de Jong, 2019). However, this procedure does not account for learning as a complex cognitive process. Since the focus of conceptual knowledge tests is merely on learning outcomes, it remains unclear whether and how the learning effects could be further increased and learning processes made more efficient. This gap is closed by considering cognitive load theory (CLT; Sweller et al., 1998, 2019; Sweller, 2020), which provides a useful framework to describe learning in terms of information processing and which respects human cognitive architecture as well as learners’ prior knowledge and the demands of the instruction. Hence, to evaluate the effects of a learning scenario, investigations should not only solely consider the effectiveness in terms of higher scores in knowledge tests but also the efficiency in terms of an optimal level of cognitive demands. This integration of cognitive processes as a key element of learning scenarios requires sensitive and valid measurement instruments to determine the cognitive load.

CLT outlines the working memory and the long-term memory as those entities that are central for processing information and building up knowledge structures (Sweller et al., 1998, Sweller et al., 2019) called schemata (Sweller et al., 1998). Already stored knowledge can be retrieved from long-term memory to support information processing in working memory. While the long-term memory is considered permanent and unlimited in terms of capacity, working memory is limited by the number of information elements that can be processed simultaneously (Baddeley, 1992; Sweller et al., 1998, Sweller et al., 2019; Cowan, 2001). Consequently, learners cannot process information with any desired complexity, which means that to ensure successful learning, this limited capacity should be respected. Any processing of information requires mental processes that consume working memory capacity, which is called cognitive load. CLT distinguishes three types of cognitive load (Sweller, 2010; Sweller et al., 1998, Sweller et al., 2019): intrinsic cognitive load (ICL), extraneous cognitive load (ECL), and germane cognitive load (GCL). ICL is related to the complexity of the learning content and depends on the learner’s prior knowledge as already built-up schemata reduce the number of elements that must be processed simultaneously in working memory. ECL refers to processes that are not essential and therefore hamper learning such as searching for relevant information within the environment or maintaining pieces of information in mind over a longer time (Mayer and Moreno, 2003). GCL represents the amount of cognitive resources devoted to processing information into knowledge structures. The amount of ECL imposed by a task affects the remaining resources that can be devoted to germane processing. Current theoretical considerations suggest that GCL cannot be essentially distinguished from ICL as both are closely related to processes of schema acquisition (Kalyuga, 2011; Jiang and Kalyuga, 2020). As a consequence, a reinterpretation of CLT as a two-factor model (ICL/ECL) is discussed. GCL is integrated into this model as a function of working memory resources needed to deal with the ICL of a task instead of representing an independent source of working memory load (Sweller, 2010; Sweller et al., 2019).

One of the main goals of CLT is to derive design guidelines for learning materials and environments that ensure that learning processes can proceed efficiently and undisturbed by irrelevant processing steps (Sweller et al., 2019). This can be achieved by removing unnecessary and distracting information as well as by a reasonable presentation format to avoid split-attention that consumes cognitive capacities and impairs essential learning (Mayer and Moreno, 1998; Ayres and Sweller, 2014). Therefore, elements of information that need to be associated with each other in learning should be presented without delay and in spatial proximity as described by the multimedia design principles of temporal and spatial contiguity (Mayer and Fiorella, 2014). These principles are empirically proven to reduce ECL and support learning in multimedia learning scenarios (Schroeder and Cenkci, 2018).

Scientific experimentation in STEM laboratory courses is assumed to be a highly complex learning scenario since learners are confronted with numerous sources of information such as experimental setups and measurement data which are presented in various representational forms. Although most of the given elements are typical features of the laboratory situation, not all of them are essential for the learning process. As CLT is considered universal and applicable to various learning scenarios, its framework can also be applied to laboratory courses (Thees et al., 2020).

Since cognitive load has rarely been seen as a main variable to investigate the impact of hands-on laboratory courses, there existed no valid measurement instruments that 1) addressed the aforementioned characteristics of scientific hands-on experimentation including context-specific load-inducing sources and 2) provided results that allowed for a differentiated interpretation of the three load types. Former investigations by Kester et al. (Kester et al., 2005; Kester et al., 2010) used the one-item scale by Paas (1992) in the context of virtual science experiments, i.e., screen-based electricity simulations, to rate mental effort as a measure of cognitive load. There, the authors revealed higher transfer performance for learning with integrated rather than split-source formats. However, no differences concerning mental effort were found, which could be due to the limitations of the one-item cognitive load measurement (Kester et al., 2010). We intended to address this gap for real hands-on experiments by considering existing instruments that are known to differentiate load types and adapting them to fit the context of lab courses.

Even though current theoretical approaches integrate GCL in a dual intrinsic-extraneous load typology of cognitive load, Klepsch et al. (2017) argued that creating supportive learning scenarios requires a comprehensive understanding of task-related aspects of cognitive load (ICL/ECL) as well as of a learner’s deliberately devoted germane resources (GCL) and their interactions. On these grounds, a differentiated measurement of cognitive load capturing its three-partite nature is still considered expedient.

The search for adequate instruments to measure the three types of cognitive load has a long history in cognitive load research. The most common approaches use subjective rating scales where participants rate their perceived cognitive load by evaluating their agreement with predefined statements (Brünken et al., 2003; Krell, 2017; Jiang and Kalyuga, 2020). There exist essentially two different rating scales that are proven to differentially measure the three types of load. These are the cognitive load scale (CLS; 10-item questionnaire) developed by Leppink et al. (2013) and the (second version of the) naïve rating scale (NRS; 8-item questionnaire) by Klepsch et al. (2017). Both scales were applied in various learning contexts (Leppink et al., 2014; Altmeyer et al., 2020; Andersen and Makransky, 2021a; Andersen and Makransky, 2021b; Becker et al., 2020; Kapp et al., 2020; Klepsch and Seufert, 2020, Klepsch and Seufert, 2021; Skulmowski and Rey, 2020; Thees et al., 2020), while the reliability of the subscales and the valid measurement of the three load types were confirmed multiple times (Klepsch et al., 2017; Becker et al., 2020; Klepsch and Seufert, 2020; Thees et al., 2020; Andersen and Makransky, 2021a; Andersen and Makransky, 2021b). However, their application in different contexts usually requires moderate adaptations.

With the objective of identifying an appropriate scale to measure the three types of cognitive load in the complex context of STEM laboratory courses, we adapted two existing cognitive load scales. We based our work on the original scales as presented in Leppink et al. (2013) and Klepsch et al. (2017) as well as former adaptations of the CLS in the target context by Thees et al. (2020). In this process, both scales were adapted regarding terminology and partly extended to take various characteristics of the laboratory environment into account. Although these adaptations are highly plausible, they require empirical, evidence-based validation of the resulting scales in the intended learning context. Accordingly, the main research question of the present study was whether the adapted scales can be considered as valid measurement instruments of cognitive load for the context of STEM laboratory courses.

Validity is defined as the appropriateness of interpreting test scores in an intended manner (Kline, 2000; AERA et al., 2011; Kane, 2013). The presented analyses followed the concepts given by the Standards for Educational and Psychological Testing (AERA et al., 2011) where the overall evidence for validity is based on considering multiple sources of evidence such as content, internal structure, relation to other variables, and response processes. As mentioned before, the main emphases of the application and interpretation of the scales are the suitability for the special context and the differentiated measurement of the three types of cognitive load. Based on this, the following sources of evidence were considered and evaluated during the presented analyses.

A prerequisite for interpreting test scores in the target context of STEM laboratory courses is that the items adequately represent the addressed constructs (ICL, ECL, and GCL) in terms of their formulation. In this sense, adequate items must match the sources of cognitive load that are part of STEM experiments as a learning environment. This evidence based on content (AERA et al., 2011) was considered during the item development, i.e., the adaptation of the original items toward the target context. In order to successfully distinguish between the three types of cognitive load, each adapted scale is expected to show a three-partite internal structure that matches the structure inherited by the original scales. This evidence based on internal structure (AERA et al., 2011) was considered during the analysis of the presented dataset. The simultaneous application of two adapted scales that are intended to measure the same constructs allowed for evaluating convergent and discriminant evidence to determine whether the same constructs were addressed by the respective subscale and whether different types of load could be clearly distinguished. The evaluation of properly addressing the intended constructs was further addressed by inducing group-specific differences by an external factor. By varying the presentation format of crucial information that was relevant to the learning process, ECL was varied, and the analyses evaluated whether the adapted scales could detect these induced differences. In addition, the scales should not indicate any differences in ICL since the complexity of the content and the experimental tasks as well as the representational forms were equal for both groups. Furthermore, a negative correlation between prior knowledge and ICL was expected, which is intended to verify the reduction of perceived content-related complexity due to the already built-up knowledge structures. These aspects related to an outer criterion and were considered evidence based on relations to other variables (AERA et al., 2011). As both scales are applied as rating scales and the individual process of rating each item is not considered part of the analyses, evidence based on response processes (AERA et al., 2011) was not considered in the present analyses.

In the present study, both adapted scales were applied after learners had participated in a technology-enhanced laboratory course unit examining hands-on experiments in the context of electricity. The experimental tasks and the overall procedure followed the study design of Altmeyer et al. (2020). Participants had to explore basic physical quantities by setting up several electric circuits and observing automatically provided measurement data while manipulating fundamental parameters. To induce differences in ECL by an external factor, two experimental learning conditions were included to contrast the spatial arrangement of the learning-relevant measurement data as a between-subject factor. One group received a split-source format where the data were anchored as virtual displays to their corresponding component using augmented reality and therefore spread across the learning environment. The other group received an integrated format where the data were grouped together on a single display. Former studies in the context of hands-on electricity laboratory courses have emphasized that measurement values, which have to be compared and related to each other in order to learn successfully, should be presented in spatial proximity (Altmeyer et al., 2020; Kapp et al., 2020; Thees et al., 2020) to avoid the well-known split-attention effect (Schroeder and Cenkci, 2018). Hence, the split-source format was expected to trigger unnecessary search processes, and the corresponding group was expected to rate higher ECL than the group with the integrated format. Both groups received the same experimental tasks and equal representational forms of the data to avoid differences in the complexity of the learning material. In terms of the evaluation of validity sources, this leads to the following hypotheses.

Hypothesis based on the internal structure is as follows:

(H1) Since both adapted scales are intended to differentiate the three types of cognitive load, confirmatory factor analyses are expected to prove their three-partite internal structure.

Hypotheses based on relation to other variables are as follows:

(H2) Since both adapted scales include subscales that are intended to measure the same latent variable, high correlations between corresponding subscales (convergent evidence) and low correlations between different subscales (discriminant evidence) are expected.

(H3) The integrated presentation of measurement data reduces perceived ECL compared to the split-source format.

(H4) Since the complexity of the learning material was not varied and participants were randomly assigned to the conditions, equal ratings for ICL are expected.

(H5) Since ICL depends on learners’ prior knowledge, negative correlations between prior knowledge scores and ICL ratings are expected.

Furthermore, insufficient evidence for the internal structure might cast doubt on the appropriateness of the respective adaptations and challenge validity evidence based on content or other variables. In reaction, the construction of a new scale based on the overall item pool is considered a useful procedure to contribute to scale development for the target context, leading to the following research question:

(RQ) Is it possible to merge both scales into a new scale that fulfills the intended three-partite structure as well as detects the induced differences in ECL?

Materials and Methods

Item Development

While the NRS was already available in German (Klepsch et al., 2017), the CLS had to be translated to implement it in German university courses. We translated the scale with an emphasis on maintaining the meaning of the original items while applying comprehensible and grammatically correct formulations. We have already implemented the translated scale in previous studies (Altmeyer et al., 2020; Thees et al., 2020), where it has proven useful in principle, and we have further refined it for the present study. As both scales were not originally intended to be used in the context of STEM laboratory courses, all the items had to be adapted. The most important aspect was to emphasize the experiment itself consisting of the experimental tasks and procedures as well as all the components of the experimental setup and the learning environment, such as data displays and instruments. The adaptation intended to point out that the scales are referring to the cognitive load induced by the experimental tasks and not any accompanying activities such as pre- or posttests or preparation phases which are mandatory for graded laboratory courses. Hence, any formulations referring to general terms such as “lecture,” “lesson,” or “activity” were replaced by “experiment” or “experimental task.” The results can be found in Tables 1, 2.

TABLE 1

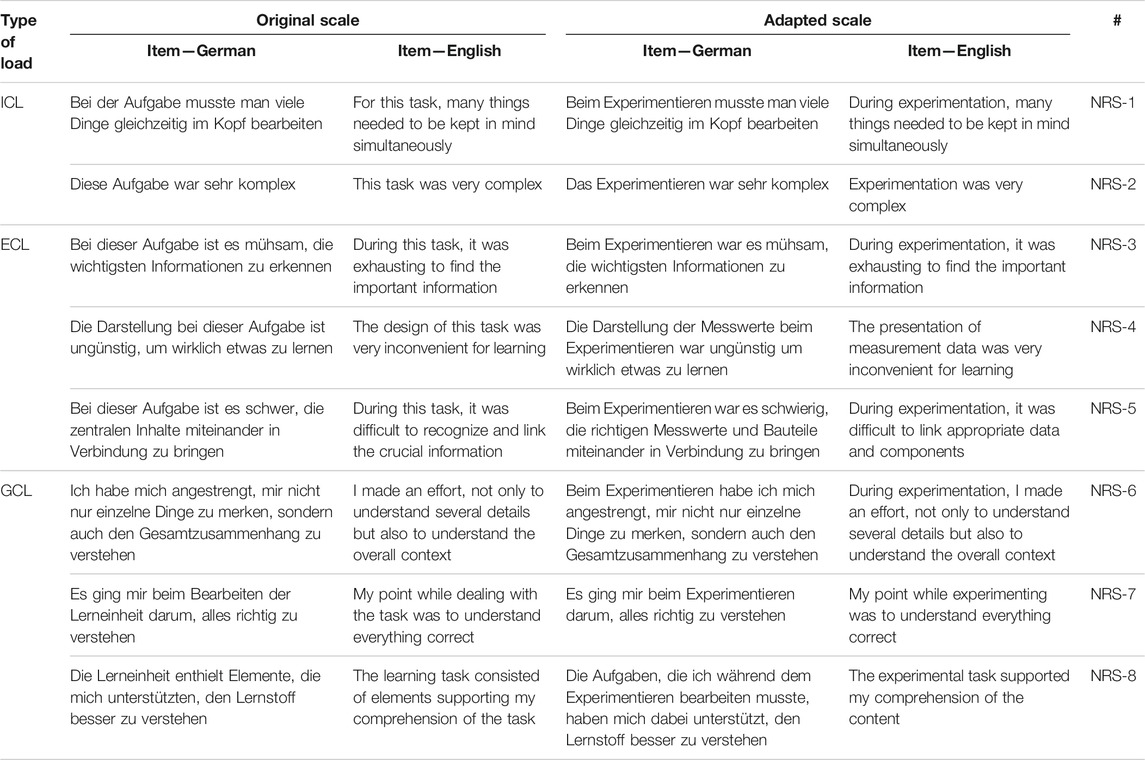
TABLE 1. Original and adapted NRS, based on the work of Klepsch et al. (2017).

TABLE 2

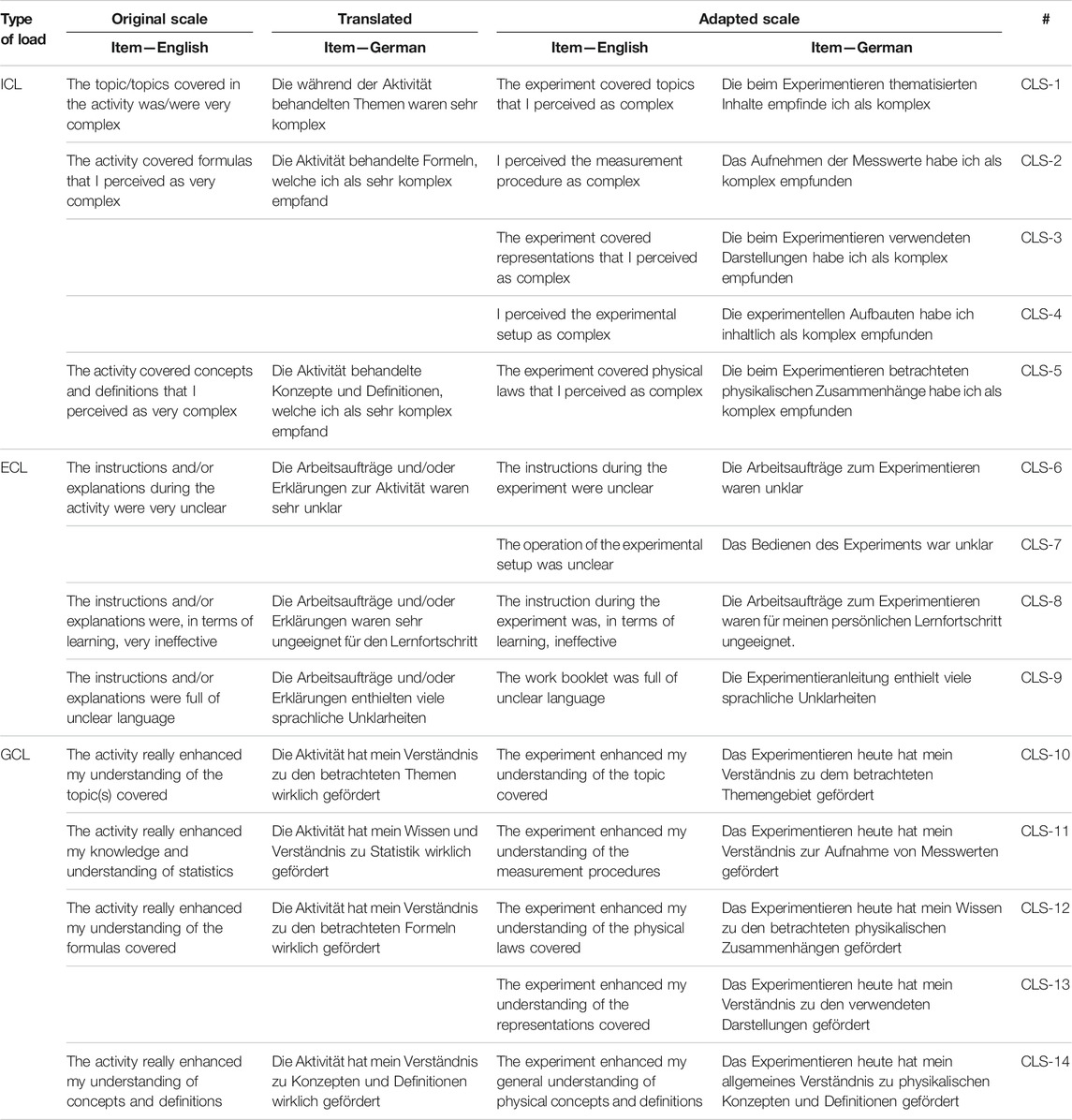
TABLE 2. Original and adapted CLS, based on the work of Leppink et al. (2013).

Concerning the NRS (Table 1), the items of the ICL and GCL subscales were adapted by replacing the term “activity” as mentioned before. For the ECL subscale, the term “information” was specified as “measurement data.” These data are seen as the crucial information of the scientific context and the basis for any learning process as the information about the mutual dependencies between the physical quantities of the behavior of experimental components is solely represented by the data. The 7-point Likert scale level was adopted from the original work by Klepsch et al. (2017), including the labeling of the scale range as “absolutely wrong” (left endpoint; German: “Stimme überhaupt nicht zu”) and “absolutely right” (right endpoint; German: “Stimme voll zu”).

Concerning the CLS (Table 2), the references within the items were also adjusted to the “experiment.” Furthermore, for the ICL and GCL subscales, the contents of the learning scenario (formerly statistics and corresponding formulas) were replaced by “measurement procedure,” “representations,” and “physical laws.” This resulted in one additional item for each subscale (CLS-3 and CLS-12). Another item was added to the ICL subscale referring to the complexity of the experimental setup (CLS-4). For ECL, the term “instructions” was directed to the “experimental task” and the “work booklet.” There, another item was added concerning the operation of the experimental setup (CLS-7). Hence, the original 10-item scale was expanded to a 14-item scale in order to capture various facets of the context. Furthermore, the scale range was adjusted to a six-point Likert scale. Within this step, the term “very” was excluded from each item. The labeling of the scale range was adopted from the original work by Leppink et al. (2013), ranging from “not at all” (left endpoint; German: “Trifft gar nicht zu”) to “completely the case” (right endpoint; German: “Trifft voll und ganz zu”).

Participants

The sample originally consisted of N = 117 engineering students from a medium-sized German university (approximately 14,000 students in total) who attended the same introductory physics lecture. Six of them had to be excluded due to language problems, and another 16 students had to be excluded due to missing values in the overall dataset. The remaining N = 95 students constitute the sample for all further analyses. Participants were randomly assigned to group 1, receiving an integrated presentation format (N = 48; 15% female, 81% male; age: M = 19.8, SD = 1.3; semester: M = 1.9, SD = 1.3), and group 2 (N = 47; 15% female, 74% male; age: M = 20.1, SD = 1.5; semester: M = 2.3, SD = 1.7), receiving a split-source presentation format. The investigation was conducted during the winter semester 2019. Participation was reimbursed with a bonus percentage of 5% for the final examination score.

Materials

During the intervention, participants performed structured physics experiments for which they had to construct several electrical circuits and analyze measurement data to derive fundamental laws for voltage and current (well known as Kirchhoff’s laws), which are based on a former study by Altmeyer et al. (2020). This inquiry process was guided by structured task descriptions in which six different circuits were examined. Learners had to build up these circuits with typical educational equipment (i.e., cables, a voltage source, and resistors) based on a given circuit diagram and answered a set of single-choice items concerning the relation of voltage or amperage at all components based on the observed data. To observe a variety of data in order to derive physical laws, learners were encouraged to manipulate fundamental parameters of the experiment, i.e., the source voltage (Figure 1). The data were provided automatically via a technology-enhanced measuring system and were visualized in real time. Hence, every interaction with the experiment that led to a change in its physical properties could be immediately observed as a change in the displayed data. The experimental tasks were, in terms of the complexity of the examined circuits and the required prior knowledge, comparable to such experiments that are part of the corresponding introductory physics laboratory courses which are mandatory for university STEM programs. Hence, the learning content and the complexity of the laboratory work instructions matched the curriculum of university engineering students.

FIGURE 1

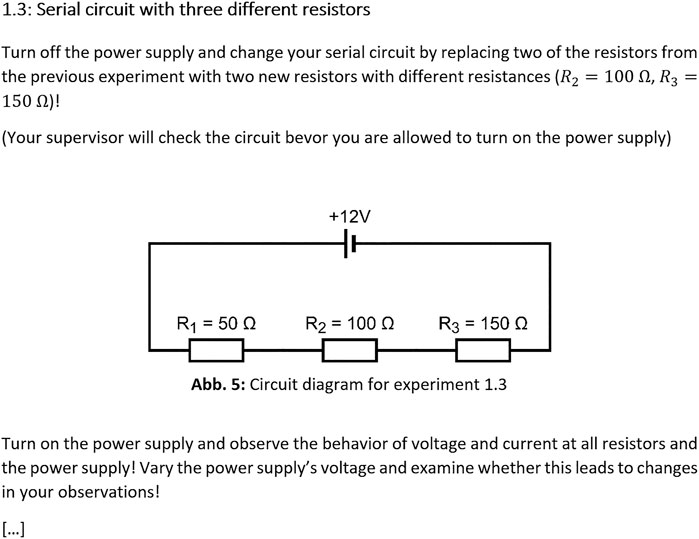
FIGURE 1. Example of the experimental task description (translated for this publication, corresponds to the circuits given in Figures 2, 3).

The learning environment consisted of the following: a work booklet that detailed the experimental tasks and circuit diagrams and the experimental components such as wires, a range of resistors, a voltage source, and a device that virtually displayed the automatically gathered measurement data (Figures 2, 3). For group 1, the measurement data were presented in a clearly arranged matrix on a tablet display (Figure 2). For group 2, smartglasses (Microsoft HoloLens, first-generation developer edition) were used as a see-through head-mounted augmented reality device, and the measurement values were presented as virtual 3D components next to the corresponding real parts of the electric circuits within the visual field of the smartglasses using visual marker recognition (Figure 3). Both groups received equal representational forms, i.e., numerical values and a virtual needle deflection. Accordingly, the only difference between the two groups was the spatial arrangement of the virtual real-time measurement displays. Further information on the technical implementation of the learning environment was described by Altmeyer et al. (2020) and Kapp et al. (2020).

FIGURE 2

FIGURE 2. The learning environment as experienced by group 1 (presentation of the measurement data via separate display on a tablet).

FIGURE 3

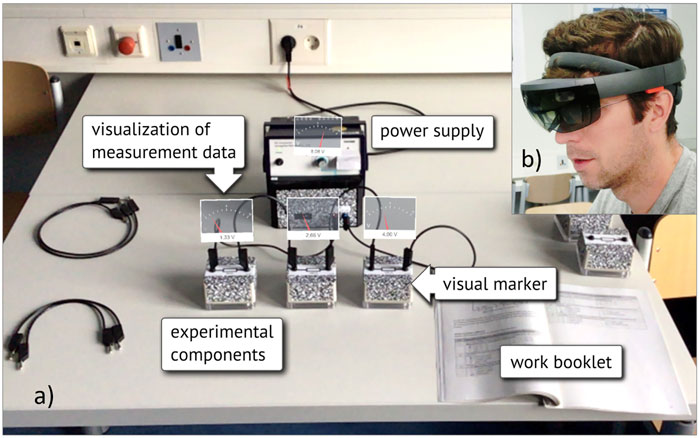
FIGURE 3. (a) Representation of the AR view as seen through the smartglasses by participants. (b) Researcher wearing smartglasses.

Both adapted subjective rating scales were applied as shown in Tables 1, 2 in order to measure cognitive load in a differentiated way.

Prior knowledge was determined via conceptual knowledge consisting of 10 single-choice items, which were also used in a similar form by Altmeyer et al. (2020). These items were selected from a conceptual knowledge test originally developed by Urban-Woldron and Hopf (2012) and Burde (2018) based on their compatibility with the physical concepts (i.e., voltage and current in simple circuits, Kirchhoff’s laws) and the complexity of the circuits (i.e., parallel and serial circuits with few components) addressed during the experimentation phase. Five of the items were directly related to circuits that were part of the experimental tasks and were therefore considered “instruction-related” in subsuming analyses. The items were already available in German, but to match the formal representation of the instructions from the experiment, we adapted the symbols of the circuit diagrams (symbols for resistors, voltage source, etc.). An example item can be found in Figure 4.

FIGURE 4

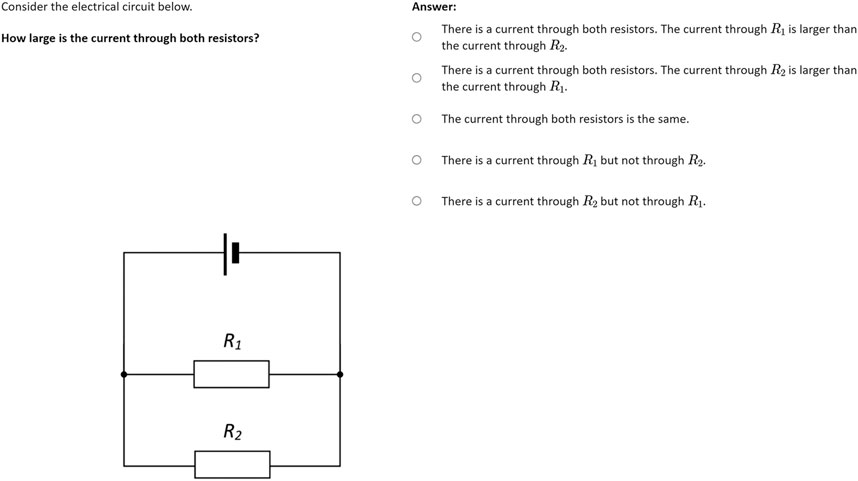
FIGURE 4. Example of the conceptual knowledge items as presented to the participants (Urban-Woldron and Hopf, 2012, translated for this publication).

Furthermore, knowledge tests concerning concrete measurement data and a usability questionnaire were applied, but these were excluded from the presented analyses (Thees et al., in preparation). Eventually, students were asked for demographic data on a voluntary basis.

Procedure

After receiving general information about the study and data protection as well as providing written consent for participation, the students completed the prior knowledge test (pretest). All the items were presented consecutively on a computer screen, and completion took approximately 10 min.

Afterward, participants were introduced to the actual learning environment, i.e., the work booklet, the experimental components, and the operation of the displaying device (tablet or smartglasses). They were randomly assigned to one of the two intervention groups. Students using the smartglasses were able to wear their own glasses or contact lenses at the same time without any limitation.

The introduction was followed by the experimentation phase, in which students conducted the six experimental tasks as presented in the work booklet. After setting up each circuit, a supervisor checked and corrected the wiring in order to ensure safe experimentation. Students did not prepare for this experiment, and no further guidance or support was provided. The experimentation phase lasted approximately 30 min.

Subsequently, participants consecutively completed the subjective cognitive load rating scales as paper–pencil tests, starting with the adapted CLS. Each student received the same order of items, but the items were presented in a randomized order so that they were not grouped by their intended three-partite structure. Answering both questionnaires took less than 10 min.

Eventually, students answered questions concerning demographic data on a voluntary basis in a paper–pencil format.

Data Analysis

For each subscale, the mean values were calculated as scores, which were scaled to [0; 1] afterward.

To provide evidence based on the internal structure, the reliability of each subscale for both scales was calculated as internal consistency (Cronbach’s alpha; α_c) with the conventional threshold of α_c = 0.70 for acceptable reliability (Kline, 2000). In addition, confirmatory factor analyses (CFA) were conducted for both scales, evaluating their intended three-factorial structure representing the three types of cognitive load (addressing H1). There, correlations between the factors (i.e., the subscales) were allowed.

To provide evidence based on relations to other variables, both scales were compared following the procedure of a traditional multitrait–multimethod analysis (Campbell and Fiske, 1959) in order to search for convergent and discriminant evidence as each method (scale) addresses each trait (type of load). There, the correlations between the subscale scores for the two applied methods as well as the reliability scores in terms of internal consistency were considered and compared via a correlation table called MTMM matrix (addressing H2). Although there are no clear guidelines concerning thresholds, strong evidence is indicated if the correlations between the same traits measured by different methods are higher than the correlations between different traits measured by different methods. The traditional evaluation of the correlation table was complemented with a subsuming confirmatory MTMM, which was calculated as a correlated trait–correlated method model via a CFA, which allowed for correlations between all components (Eid, 2000). Furthermore, it was checked whether the scales could detect differences in the subscales between the two intervention types (grouping variable) during the study. Therefore, group-specific ECL scores were compared using a two-sided independent sample t-test (addressing H3). An equivalent t-test was conducted to compare group-specific ICL scores (addressing H4). In addition, the correlations between the ICL subscales and the score in the pretest were included. There, a negative correlation was expected as higher prior knowledge is assumed to reduce the complexity of the content due to already existing knowledge schemata (addressing H5).

Going one step further, we intended to combine both scales in order to merge them into a new scale with better model fit concerning the tripartite structure (addressing RQ). This was based on an exploratory factor analysis (EFA), which was conducted using all items of both scales together. In this instance, the Kaiser–Meyer–Olkin measure revealed a good sampling adequacy with an overall KMO = 0.79. The individual KMO_j values were in the range of [0.65; 0.89]. Furthermore, Bartlett’s test of sphericity, χ²(231) = 1,006.4, p < 0.001, revealed adequate item correlations. The scree plot and a parallel analysis were taken into account to determine the optimal number of factors, which was found to be three. Since the factors to be extracted were allowed to correlate with each other, an oblique factor rotation (“oblimin”) was applied. As the intention was to find a short and concise scale, we limited the number of items included for each subscale to three. Two new models were developed based on the factor loadings and the relation to the group variable in the presented study. Both scales were evaluated by conducting a confirmatory factor analysis with their intended three-factorial structure.

In general, the significance level for type I errors was considered as α = 0.05. For each confirmatory analysis, the following indices were applied with their corresponding cutoff values indicating acceptable model fit: the comparative fit index (CFI) and the Tucker–Lewis index (TLI), each ≥0.95, as well as the root mean square error of approximation (RMSEA) and the standardized root mean square residual (SRMR), each ≤ 0.08.

All the confirmatory analyses were conducted using the lavaan package (version 0.6-6) in the R programming language (version 3.6.0). For the EFA, the psych package (version 1.8.12) was used.

Results

Validity Evidence Based on Internal Structure

The reliability analyses revealed insufficient values for the NRS, α_c(ICL) = 0.52, α_c(ECL) = 0.53, and α_c(GCL) = 0.62, and mixed results for the CLS, α_c(ICL) = 0.86, α_c(ECL) = 0.43, and α_c(GCL) = 0.90. Concerning the NRS, all the subscales did not reach the common threshold of α_c = 0.70. In contrast, the subscales of the CLS for ICL and GCL showed satisfying results, but not for ECL.

The subsuming CFA also revealed no clear results. Concerning the NRS, the model fit indices did not reach the conventional thresholds, CFI = 0.83, TLI = 0.72, RMSEA = 0.11, and SRMR = 0.09. Concerning the CLS, RMSEA = 0.07 indicated an acceptable model fit, while the other indices narrowly missed the range for acceptable values, CFI = 0.94, TLI = 0.93, and SRMR = 0.09. In sum, there was no consistent indication of an acceptable model fit for both scales concerning the assumed structure with three inherent factors, which contradicts Hypothesis 1.

Validity Evidence Based on Relations to Other Variables

In order to compare the behavior of both adapted scales in terms of an MTMM approach, a correlation table based on Pearson’s correlation was calculated (MTMM matrix; Table 3). Here, the correlations between the two methods concerning each trait (monotrait–heteromethod coefficients) became significant (p < 0.05) with a range of r = 0.48 to r = 0.55 (Cohen, 1988), indicating convergent evidence between the two scales. These correlations were higher than those significant correlations between different traits measured by different methods (heterotrait–heteromethod coefficients), emphasizing discriminant evidence. The same results were found concerning the correlations between different traits measured by the same method (heterotrait–monomethod coefficients), which were also lower than the monotrait–heteromethod coefficients. Furthermore, the patterns (ranks and sign of correlations) of the monomethod–heterotrait blocks were comparable for both methods. In contrast, the reliability values (Cronbach’s α_c) showed high variance. In sum, based on the correlation table (Table 3), these findings emphasized convergent and discriminant evidence.

TABLE 3

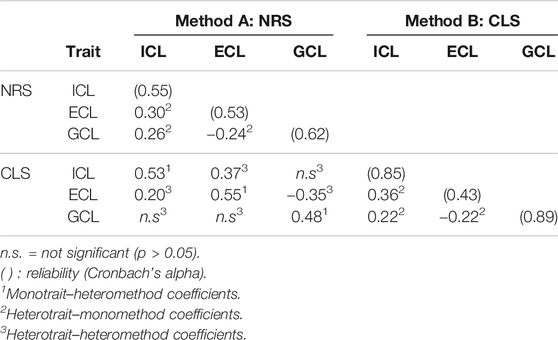
TABLE 3. Correlation table for MTMM analysis (MTMM matrix; only correlations with p < 0.05 are displayed).

The subsuming confirmatory MTMM analysis revealed acceptable values for RMSEA = 0.06 and SRMR = 0.08. In contrast, CFI = 0.93 and TLI = 0.91 were slightly below the range for acceptable model fit.

Table 4 shows the group-dependent scores for each subscale. The results from the independent-sample t-test revealed for the adapted NRS a significant difference in favor of group 1 (lower ECL) in accordance with Hypothesis 3, while the CLS showed no group-specific differences. However, both NRS and CLS indicate no differences between groups concerning ICL in accordance with Hypothesis 4. Details of the test statistics can be found in Table 4.

TABLE 4

TABLE 4. Group-specific results for both adapted scales.

Furthermore, there were no significant correlations between the pretest results and the ICL-related subscales, both for the full pretest scores, r = −0.12 and p = 0.25 for the NRS, r = −0.02 and p = 0.82 for the CLS, and the intervention-related items, r = −0.07 and p = 0.51 for the NRS, r = 0.01 and p = 0.89 for the CLS. These results contradict Hypothesis 5.

Evaluation of Combined Scales

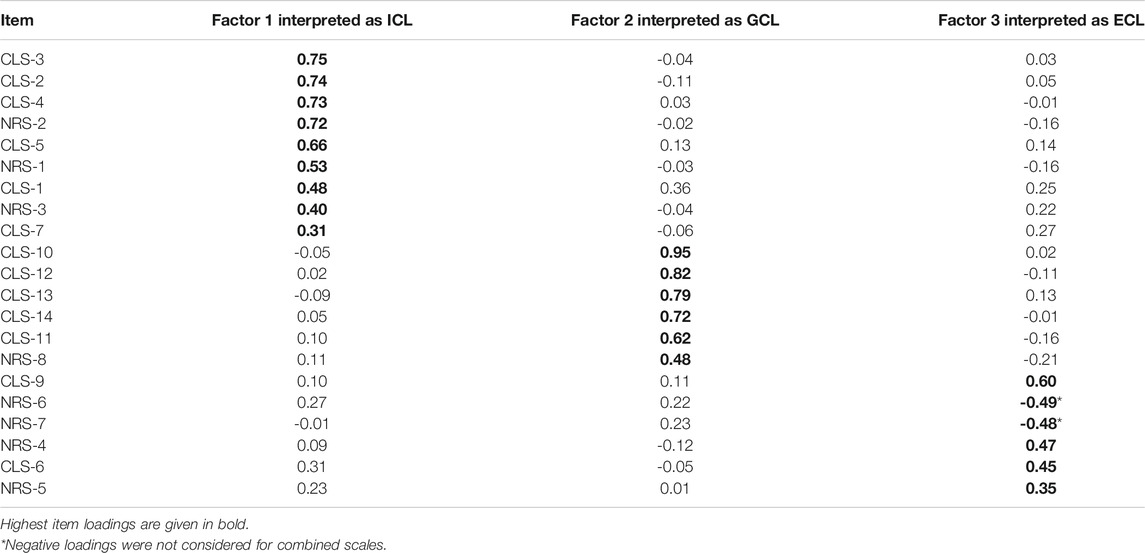
All the items of both scales were taken into account to merge them into a new scale. First, an exploratory factor analysis was conducted to evaluate which items group together. Both the scree plot and a parallel analysis indicate a three-factorial structure. The items with the highest loading indicate conformity with the types of load known from theory, although some items with lower loadings are not grouped in accordance with their intended position. Table 5 displays the extracted factor loadings.

TABLE 5

TABLE 5. Results of the EFA for all items of both NRS and CLS.

For the first new model (referred to as model 1), the three items with the highest (positive) loadings were included because they represent their respective factor in a reliable manner. Hence, the ICL consisted of the items CLS-2, CLS-3, and CLS-4, the ECL subscale consisted of CLS-9, NRS-4, and CLS-6, and the GCL subscale consisted of CLS-10, CLS-12, and CLS-13. The subsuming CFA revealed adequate to good model fit, CFI = 0.98, TLI = 0.98, RMSEA = 0.05, and SRMR = 0.06.

In this way, model 1 corresponds directly to the structure revealed by the EFA for the given dataset. In terms of validity, it therefore meets the evidence source of the internal structure. The second model (referred to as model 2) aimed to integrate another source of evidence (evidence based on relation to other variables) by including those items in the ECL subscale that had proven to be sensitive toward the induced differences between the groups. Hence, for model 2, the same items as in model 1 were used to merge the ICL and GCL subscales because of their high loadings. For the ECL subscale, we used the full subscale of the NRS (NRS-3, NRS-4, and NRS-5) in order to incorporate the ability to detect a significant difference in terms of ECL. A subsuming confirmatory factor analysis also revealed adequate to good model fit, CFI = 1.0, TLI = 1.0, RMSEA = 0.00, and SRMR = 0.06.

Since both new models shared the same items for ICL and GCL, they reached the same (sufficient) level of reliability for these subscales, α_c(ICL) = 0.79 and α_c(GCL) = 0.90. They slightly differed concerning the reliability of their ECL subscales, α_c(ECL, model 1) = 0.54 and α_c(ECL, model 2) = 0.57 which are still below the desired cutoff value α_c = 0.70. Furthermore, the sensitivity toward group-specific differences in ECL seemed to be inherited as model 1 showed no significant difference, t(90.3) = −0.64 and p = 0.52, while model 2 adopted the significant differences from the full adapted NRS, t(89.3) = 2.17 and p = 0.033.

Discussion

Validity Based on Content

Both scales had to be adapted, and the CLS had to be expanded to fit the desired context. Since experimenting in STEM laboratory courses has been commonly based on generating and interpreting the measurement data, the measurement procedure and the corresponding quantities as well as their functional relationships and scientific laws are the main source of the information that has to be processed in order to generate new knowledge structures. Especially concerning the adapted and expanded CLS, the item development included all those relevant sources of content-related complexity in the subscales dedicated to measure ICL as well as GCL, whereas the items of the NRS merely consisted of general expressions. Hence, the adapted CLS appears to be slightly advantageous as a higher number of typical aspects from the learning scenario were directly addressed within the items.

Following the concept of ECL as presented by CLT, processes that do not contribute to essential learning originate from irrelevant and distracting elements. These include language issues and presentation formats that demand unnecessary search processes and representational holding. While the CLS originally included text comprehension as a source of ECL, the adapted version was not expanded toward the presentation formats (e.g., by addressing distracting search processes in the items), though this was a specific part of the presented study. In this case, the adapted CLS could be limited in its ability to cover all relevant load-inducing aspects that learners face throughout the experimental procedure. In contrast, the NRS already addressed presentational aspects, which were retained for the adapted version.

In sum, all subscales covered relevant aspects of the learning environment, but each with a specific main emphasis toward instructional design aspects. Based on the item formulation, the adapted CLS seems to address more precisely ICL and GCL, while the adapted NRS seems to address ECL in a more sensitive way for the context of laboratory learning scenarios. Furthermore, this emphasizes a general need for developing and validating specific instruments that directly address the characteristics of learning scenarios and include all crucial load-inducing elements. A more general item formulation might be too abstract, which could result in participants not being able to relate the items to the given situation without being further introduced to the intention and the meaning of the respective scale (e.g., Klepsch et al., 2017).

Validity Evidence Based on Internal Structure

Concerning their internal consistency for the given dataset, the subscales of the adapted NRS and adapted CLS cannot be seen as sufficiently reliable. Moreover, these low indices are far below those of the original work by Klepsch et al. (2017) and therefore challenge the benefits and appropriateness derived from the content analysis (Validity Based on Content). It is probable that the a priori specification of load-inducing content will not fit the subjective impressions of the learners during the experimentation phase. In contrast, the subscales for ICL and GCL of the adapted CLS show a good internal consistency. Except for ECL, the values are in the range of the original work by Leppink et al. (2013) or former adaptions of the scale (Thees et al., 2020; Andersen and Makransky, 2021a, Andersen and Makransky, 2021b). Here again, the insufficient reliability for ECL casts doubt on whether the items of this specific subscale are appropriate to measure the intended type of cognitive load. Especially in comparison with the findings of Thees et al. (2020), who used a very similar formulation of the ECL items in another scientific context (thermodynamics instead of electricity), these results challenge a broad applicability of a simple adaption of the original CLS and raise the question of how to integrate context-specific sources of load while the overall pedagogical approach remains comparable (e.g., inquiry-based learning).

The results of the CFA also undermine the intended internal structure of each scale as the model fit indices do not provide sufficient formal evidence for the three assumed factors. Hence, the confirmatory analysis strengthens criticisms of the appropriateness of the three-factorial structure as intended during the item development. This might be a consequence of a rather small sample size because the conventional rule of thumb that the number of participants should be more than 10 times the number of items is only reached for the adapted NRS, but not for the CLS. Another limiting factor might be the reduction of the scale range from a 10-point to a six-point scale for the adapted CLS.

In sum, these findings reveal that the intended internal structure of the instruments is not fully represented in the data, which constrains the interpretation of the single subscales. We must therefore reject the first hypothesis and question the appropriateness of the adapted scales to differentiate between three different types of load in the context of technology-enhanced laboratory courses. Although the CFAs mostly narrowly missed the acceptable range for the fit indices, which can be interpreted as a case of a too small sample size, the low indices for internal consistency as the reliability measure for four out of six subscales remain the main issue for the internal structure.

Validity Based on Relations to Other Variables

Assuming the three-factorial structure of the scales as validated in various former studies, a traditional MTMM matrix based on a correlation table was analyzed. Although the reliability of all the subscales adapted from the NRS and for EL adapted from the CLS was not sufficient, significant correlations and repeating patterns indicate convergent and discriminant validity between the two scales. This means that the corresponding subscales in both approaches have meaningful coincidence and that each subscale can be distinguished from the others according to their interpretation as different types of cognitive load. These findings preliminarily emphasize the scales’ appropriateness as load-measuring instruments. However, the strength of evidence is limited due to missing cutoff values for the traditional interpretation of correlation patterns. Furthermore, the results could not be sufficiently reproduced by a confirmatory MTMM approach as not all indices indicate an acceptable model fit. Hence, although there are promising findings based on the traditional comparison of correlation patterns, we cannot provide sufficient formal evidence for convergent and discriminant validity, which means that the second hypothesis is not clearly supported by the data of the present study. Thus, the MTMM analysis does not support the internal structure of both scales as being directed to the same three different latent variables.

Concerning the contrasted presentation formats, a sensitive scale was expected to reflect group-specific differences in ECL in favor of group 1. For the given dataset, only the adapted NRS revealed a significant difference between the two intervention groups. As expected, group 1 reported lower scores for ECL. Hence, the findings support the third hypothesis for the adapted NRS and emphasize it as the more sensitive scale toward the contrasted presentation formats and the accompanying load sources, i.e., the spatial split of related information elements. The missing sensitivity of the adapted CLS toward differences in ECL might be the consequence of a biased focus on language issues and an insufficient adaptation toward other load-inducing sources for this specific subscale. However, these findings are in accordance with a study conducted by Skulmowski and Rey (2020), who also revealed that the NRS is more likely to detect differences in ECL than the CLS. In their research, the authors also argued that the original items of the CLS might focus too much on the verbal aspects of the learning scenario, while the NRS addresses information processing in a more generalized way.

Both adapted scales did not show significant differences concerning ICL scores, which is in accordance with the intention to provide both groups with equal content, experimental setups, and representational forms of the measurement data. Hence, the fourth hypothesis is supported for both scales. However, there is no significant correlation between the scores of both ICL subscales and the specific or full prior knowledge scores, which contradicts the theory-based expectation that learners with lower prior knowledge will perceive a higher ICL. Eventually, a missing correlation might indicate that learners’ prior knowledge was sufficient as a conceptual prerequisite to successfully conduct the experimental tasks. However, this leads to a rejection of the fifth hypothesis because this result does not support the compliance of the ICL subscale with the theoretical concept of ICL in terms of the CLT.

In sum, the direct comparison between the two adapted scales via the MTMM matrix emphasizes but does not prove convergent and discriminant evidence due to insufficient support by the confirmatory model fit. The relation to the grouping variable for the given study emphasizes the adapted NRS as more sensitive toward differences in ECL, which is in accordance with previous findings. As expected, both scales reveal equal ICL ratings for both groups. However, the relation between ICL and prior knowledge could not be verified. Eventually, the relation to other variables revealed mixed to rather unfavorable results as most of the underlying hypotheses had to be rejected.

Combined Scales

As the internal structure of each adapted scale remains challenged after considering evidence based on the reliability scores as well as after the CFAs and the MTMM approaches, we decided to construct a combined instrument based on the given item pool of both scales. As the first step, the EFA revealed a three-factorial structure for the combined dataset. In addition, the items with the highest factor loadings indicate accordance with the expected underlying latent variable so that the three factors can be interpreted as related to the three types of cognitive load (Table 5). Given the self-imposed restriction of using only three items per factor to obtain a concise scale, two models were derived that considered those items with the highest positive factor loadings and findings from validity evidence based on the relation to the grouping variable.

Both models showed acceptable to good model fit in subsuming CFAs concerning their three-factorial internal structure, emphasizing their capability to differentiate between the three types of load. While the subscales for ICL and GCL are equal in both models and consist of items from the adapted CLS, the models differ concerning the ECL subscale. While model 1 follows the ranking of factor loadings from the EFA, resulting in a mix of items from both adapted NRS and CLS, model 2 inherits the full ECL subscale from the adapted NRS. This step is not based on the findings from the EFA, but respects the fact that this particular subscale was able to detect group-specific differences in ECL which are likely to exist in studies that contrast presentation formats to address well-known multimedia effects such as split-attention (Schroeder and Cenkci, 2018). Hence, model 2 constitutes a further development as it integrates validity evidence based on the relation to other variables.

However, both models still suffer from low internal consistency concerning ECL, which reduces the reliability of the acceptable model fits. This issue might result from the fact that the items dedicated to measuring ECL cover different load-inducing elements such as data presentation or verbal components. Hence, they cannot be expected to equally contribute to the score, and so, reaching a high internal consistency remains difficult. Andersen and Makransky (2021b) even considered ECL as a multidimensional variable, which presents a plausible reason for our low internal consistency findings. Eventually, we follow the results of the presuming EFA by considering ECL as an unidimensional factor which addresses multiple learning-irrelevant elements.

In sum, model 2 is considered the best scale based on the given item pool and the given dataset. Concerning the content of the new subscales for ICL and ECL, the items refer to concrete aspects of the experimental tasks, i.e., those components that are a priori determined the basis of the learning process. Hence, the combination of both NRS and CLS showed that the most valuable items for the given dataset were taken from the CLS, but the NRS provided a meaningful supplement. Furthermore, the restriction to three items per subscale emphasizes the need to focus on those elements of the learning environment that are mandatory to deal with during the learning process.

Future Work

To address a wider range of technology-based learning scenarios, our adapted versions could be enhanced by integrating items from other adaptations. For example, Andersen and Makransky (2021a) included the term “information display format” as a source of load in their ECL subscale, which was based on the original CLS. This term would directly address the contrasted presentation formats in our study without any bias toward a certain technology. On the contrary, such general formulations require a clarification as to what they are referring to, such as by a short introduction prior to the subjective rating, where the term is specified for each intervention group.

As most of the samples used in comparable studies consist of university students, studies validating the application of the considered scales in school contexts are missing. At the school level, learners are expected to have a different amount of prior knowledge and metacognitive skills. Hence, the measurement of cognitive load based on subjective experiences could be much more challenging (Brünken et al., 2003; Klepsch et al., 2017). Therefore, the scales have to be adapted concerning the item formulation as well as the scale levels and the endpoint labeling. In addition, items on passive load (mental load) and active load (mental effort), developed by Klepsch and Seufert (2021), could be added. The authors could show that the item on passive load related to the ICL factor of their scale and the item on active load related to the GCL factor. Klepsch and Seufert recommended the use of these additional items with children and tasks that require learners’ self-regulation (e.g., laboratory work). Such adaptation might demand further investigations toward validity evidence. Future work might consider expert ratings for the item content to strengthen the explanatory power of the content-related evidence (Brünken et al., 2003; Klepsch et al., 2017). Furthermore, it will be essential to validate the new and further developed scales on a large sample as well as to consider that further (back-) translations of the presented (German) scales might affect validity aspects.

In the present study, only some of all possible sources providing evidence for the validation of the cognitive load scales were examined. Future studies should not only experimentally manipulate the ECL but also systematically manipulate all three types of cognitive load and verify whether the developed scales can also reflect variations in the ICL and GCL. Manipulation of ICL could be achieved by contrasting laboratory tasks with different levels of complexity or by contrasting groups with different levels of prior knowledge (evidence based on the relation to other variables). However, previous research suggesting that a subject’s ability to reliably differentiate between ICL and ECL depends on a sufficient level of prior knowledge (Zu et al., 2021) should also be considered. GCL could be manipulated by providing or not providing self-regulation prompts during student experimentation.

Another option for analyzing validity evidence based on the relation to other variables could be a direct comparison between subjective ratings and objectives measures such as eye-tracking data. Recent developments of mobile eye-tracking devices allow for collecting data in dynamic situations such as laboratory courses and might even be applied to augmented reality-based learning scenarios (Kapp et al., 2021) so that various approaches of technology-enhanced learning scenarios can be accompanied by both the subjective rating scales and the objective gaze-based measures. Nevertheless, the interpretation should consider prior research indicating that there might be no linear relationship between objective and subjective measures but that they rather cover different facets of cognitive load (Minkley et al., 2021).

Conclusion

In this article, we present supporting and critical points regarding the validity of two popular subjective cognitive load-rating scales in the context of technology-enhanced science experiments. Although the content of the adapted items seemed to be promising in terms of addressing various facets of the learning environment, the low internal consistency and the insufficient evidence for the intended three-factorial structure negate the appropriateness of the adapted scales. However, based on the correlations between the subscales, there are various indications that the addressed latent variables (i.e., ICL, ECL, and GCL) are comparable in both scales and can be distinguished from each other. Again, these assumptions cannot be formally confirmed based on the given dataset. In sum, three of five deduced hypotheses toward different sources of evidence in terms of validity had to be rejected due to insufficient formal evidence. Hence, there are no sufficient results that favor either the adapted NRS or the adapted CLS, although they seem to be convincing regarding their content.

The interpretation of this conflict is twofold. First, for the learning context under investigation, we question the current state of the adapted scales as they are not appropriate to measure different types of cognitive load. This would explain the insufficient reliability and the insufficient model fits concerning the assumed internal structure. In contrast, one could assume that the items of both scales are capable of representing the real load-inducing elements, but each scale addresses some but not all facets of the learning environment. Hence, solely by combining both item pools, it was possible to reach an adequate scale (model 2). At this point, the advantages of both adapted scales were combined to form a promising new scale for the context of complex science learning scenarios (although this scale is not without its flaws). The internal consistency of the ECL subscales is not acceptable but can be made plausible via the inherent multiple aspects covered by the items.

The presented study is an example of applying known and empirically validated scales to an essential and realistic learning scenario from STEM education. Since inquiry-based learning scenarios contain multiple information sources, researchers must develop new instruments to be able to correctly measure cognitive load. Moreover, the issues raised in the analyses show that it is necessary to seek for validity based on different sources such as content, internal structure, and relation to other variables. In this sense, we want to encourage the community to contribute to the question of how to create valid and suitable questionnaires to determine cognitive load in specific complex learning scenarios.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics Statement

Ethical review and approval were not required for the study on human participants in accordance with the local legislation and institutional requirements. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

MT: conceptualization, methodology, formal analysis, investigation, writing, and supervision; SK: software, methodology, formal analysis, and investigation; KA: methodology and investigation; SM: conceptualization, methodology, and writing; RB: conceptualization, resources, and funding acquisition; JK: conceptualization, resources, writing, project administration, and funding acquisition.

Funding

The dataset this paper draws upon was collected as part of the research projects GeAR (grant no. 01JD1811B) and gLabAssist (grant no. 16DHL1022), both funded by the German Federal Ministry of Education and Research (BMBF). The funding source had no involvement in preparing and conducting the study or in preparing the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

AERAAPANCME (2011). Report and Recommendations for the Reauthorization of the institute of Education Sciences. Washington D.C: American Educational Research Association.

Altmeyer, K., Kapp, S., Thees, M., Malone, S., Kuhn, J., and Brünken, R. (2020). The Use of Augmented Reality to foster Conceptual Knowledge Acquisition in STEM Laboratory Courses-Theoretical Background and Empirical Results. Br. J. Educ. Technol. 51, 611–628. doi:10.1111/bjet.12900

CrossRef Full Text | Google Scholar

American Association of Physics Teachers (2014). AAPT Recommendations for the Undergraduate Physics Laboratory Curriculum, https://www.aapt.org/Resources/upload/LabGuidlinesDocument_EBendorsed_nov10.pdf.

Andersen, M. S., and Makransky, G. (2021a). The Validation and Further Development of a Multidimensional Cognitive Load Scale for Virtual Environments. J. Comput. Assist. Learn. 37, 183–196. doi:10.1111/jcal.12478

CrossRef Full Text | Google Scholar

Andersen, M. S., and Makransky, G. (2021b). The Validation and Further Development of the Multidimensional Cognitive Load Scale for Physical and Online Lectures (MCLS-POL). Front. Psychol. 12, 642084. doi:10.3389/fpsyg.2021.642084

PubMed Abstract | CrossRef Full Text | Google Scholar

Ayres, P., and Sweller, J. (2014). “The Split-Attention Principle in Multimedia Learning,” in The Cambridge Handbook of Multimedia Learning. Editor R. E. Mayer. Second edition (New York: Cambridge University Press), 206–226.

Google Scholar

Baddeley, A. (1992). Working Memory. Science 255, 556–559. doi:10.1126/science.1736359

PubMed Abstract | CrossRef Full Text | Google Scholar

Becker, S., Klein, P., Gößling, A., and Kuhn, J. (2020). Using mobile Devices to Enhance Inquiry-Based Learning Processes. Learn. Instruction 69, 101350. doi:10.1016/j.learninstruc.2020.101350

CrossRef Full Text | Google Scholar

Brünken, R., Plass, J. L., and Leutner, D. (2003). Direct Measurement of Cognitive Load in Multimedia Learning. Educ. Psychol. 38, 53–61. doi:10.1207/S15326985EP3801_7

CrossRef Full Text | Google Scholar

Burde, J.-P. (2018). Konzeption und Evaluation eines Unterrichtskonzepts zu einfachen Stromkreisen auf Basis des Elektronengasmodells. Berlin: Logos. doi:10.30819/4726

CrossRef Full Text

Campbell, D. T., and Fiske, D. W. (1959). Convergent and Discriminant Validation by the Multitrait-Multimethod Matrix. Psychol. Bull. 56, 81–105. doi:10.1037/h0046016

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences 2. ed. Hillsdale, NJ: Erlbaum.

Cowan, N. (2001). The Magical Number 4 in Short-Term Memory: A Reconsideration of Mental Storage Capacity. Behav. Brain Sci. 24, 87–114. doi:10.1017/s0140525x01003922

PubMed Abstract | CrossRef Full Text | Google Scholar

de Jong, T., Linn, M. C., and Zacharia, Z. C. (2013). Physical and Virtual Laboratories in Science and Engineering Education. Science 340, 305–308. doi:10.1126/science.1230579

PubMed Abstract | CrossRef Full Text | Google Scholar

de Jong, T. (2019). Moving towards Engaged Learning in STEM Domains; There Is No Simple Answer, but Clearly a Road Ahead. J. Comput. Assist. Learn. 35, 153–167. doi:10.1111/jcal.12337

CrossRef Full Text | Google Scholar

Eid, M. (2000). A Multitrait-Multimethod Model with Minimal Assumptions. Psychometrika 65, 241–261. doi:10.1007/bf02294377

CrossRef Full Text | Google Scholar

Etkina, E., van Heuvelen, A., White-Brahmia, S., Brookes, D. T., Gentile, M., Murthy, S., et al. (2006). Scientific Abilities and Their Assessment. Phys. Rev. ST Phys. Educ. Res. 2, 113. doi:10.1103/PhysRevSTPER.2.020103

CrossRef Full Text | Google Scholar

Hofstein, A., and Lunetta, V. N. (2004). The Laboratory in Science Education: Foundations for the Twenty-First century. Sci. Ed. 88, 28–54. doi:10.1002/sce.10106

CrossRef Full Text | Google Scholar

Husnaini, S. J., and Chen, S. (2019). Effects of Guided Inquiry Virtual and Physical Laboratories on Conceptual Understanding, Inquiry Performance, Scientific Inquiry Self-Efficacy, and Enjoyment. Phys. Rev. Phys. Educ. Res. 15, 31. doi:10.1103/PhysRevPhysEducRes.15.010119

CrossRef Full Text | Google Scholar

Jiang, D., and Kalyuga, S. (2020). Confirmatory Factor Analysis of Cognitive Load Ratings Supports a Two-Factor Model. TQMP 16, 216–225. doi:10.20982/tqmp.16.3.p216

CrossRef Full Text | Google Scholar

Kalyuga, S. (2011). Cognitive Load Theory: How Many Types of Load Does it Really Need? Educ. Psychol. Rev. 23, 1–19. doi:10.1007/s10648-010-9150-7

CrossRef Full Text | Google Scholar

Kane, M. T. (2013). Validating the Interpretations and Uses of Test Scores. J. Educ. Meas. 50, 1–73. doi:10.1111/jedm.12000

CrossRef Full Text | Google Scholar

Kapici, H. O., Akcay, H., and de Jong, T. (2019). Using Hands-On and Virtual Laboratories Alone or Together―Which Works Better for Acquiring Knowledge and Skills? J. Sci. Educ. Technol. 28, 231–250. doi:10.1007/s10956-018-9762-0

CrossRef Full Text | Google Scholar

Kapp, S., Barz, M., Mukhametov, S., Sonntag, D., and Kuhn, J. (2021). ARETT: Augmented Reality Eye Tracking Toolkit for Head Mounted Displays. Sensors 21, 2234. doi:10.3390/s21062234

PubMed Abstract | CrossRef Full Text | Google Scholar

Kapp, S., Thees, M., Beil, F., Weatherby, T., Burde, J.-P., Wilhelm, T., et al. (2020). “The Effects of Augmented Reality: A Comparative Study in an Undergraduate Physics Laboratory Course,” in Proceedings of the 12th International Conference 1on Computer Supported Education, May 2–4, 2020 (SciTePress - Science and Technology Publications), Vol. 2, 197–206. doi:10.5220/0009793001970206

CrossRef Full Text | Google Scholar

Kester, L., Kirschner, P. A., and van Merriënboer, J. J. G. (2005). The Management of Cognitive Load during Complex Cognitive Skill Acquisition by Means of Computer-Simulated Problem Solving. Br. J. Educ. Psychol. 75, 71–85. doi:10.1348/000709904X19254

CrossRef Full Text | Google Scholar

Kester, L., Paas, F., and van Merriënboer, J. J. G. (2010). “Instructional Control of Cognitive Load in the Design of Complex Learning Environments,” in Cognitive Load Theory. Editors J. L. Plass, R. Moreno, and R. Brunken (Cambridge: Cambridge University Press), 109–130.

Google Scholar

Klepsch, M., Schmitz, F., and Seufert, T. (2017). Development and Validation of Two Instruments Measuring Intrinsic, Extraneous, and Germane Cognitive Load. Front. Psychol. 8, 1997. doi:10.3389/fpsyg.2017.01997

PubMed Abstract | CrossRef Full Text | Google Scholar

Klepsch, M., and Seufert, T. (2021). Making an Effort versus Experiencing Load. Front. Educ. 6 (56). doi:10.3389/feduc.2021.645284

CrossRef Full Text | Google Scholar

Klepsch, M., and Seufert, T. (2020). Understanding Instructional Design Effects by Differentiated Measurement of Intrinsic, Extraneous, and Germane Cognitive Load. Instr. Sci. 48, 45–77. doi:10.1007/s11251-020-09502-9

CrossRef Full Text | Google Scholar

Kline, P. (2000). The Handbook of Psychological Testing. 2. ed. London: Routledge.

Krell, M. (2017). Evaluating an Instrument to Measure Mental Load and Mental Effort Considering Different Sources of Validity Evidence. Cogent Edu. 4, 1280256. doi:10.1080/2331186X.2017.1280256

CrossRef Full Text | Google Scholar

Lazonder, A. W., and Harmsen, R. (2016). Meta-Analysis of Inquiry-Based Learning. Rev. Educ. Res. 86, 681–718. doi:10.3102/0034654315627366

CrossRef Full Text | Google Scholar

Leppink, J., Paas, F., van der Vleuten, C. P. M., van Gog, T., and Van Merriënboer, J. J. G. (2013). Development of an Instrument for Measuring Different Types of Cognitive Load. Behav. Res. 45, 1058–1072. doi:10.3758/s13428-013-0334-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Leppink, J., Paas, F., van Gog, T., van der Vleuten, C. P. M., and van Merriënboer, J. J. G. (2014). Effects of Pairs of Problems and Examples on Task Performance and Different Types of Cognitive Load. Learn. Instruction 30, 32–42. doi:10.1016/j.learninstruc.2013.12.001

CrossRef Full Text | Google Scholar

Lunetta, V. N., Hofstein, A., and Clough, M. P. (2005). “Learning and Teaching in the School Science Laboratory: An Analysis of Research, Theory, and Practice,” in Handbook of Research on Science Education. Editors S. K. Abell, and N. G. Lederman (New York, NY: Lawrence Erlbaum; Routledge), 393–441.

Google Scholar

Mayer, R. E., and Moreno, R. (1998). A Split-Attention Effect in Multimedia Learning: Evidence for Dual Processing Systems in Working Memory. J. Educ. Psychol. 90, 312–320. doi:10.1037/0022-0663.90.2.312

CrossRef Full Text | Google Scholar

Mayer, R. E., and Moreno, R. (2003). Nine Ways to Reduce Cognitive Load in Multimedia Learning. Educ. Psychol. 38, 43–52. doi:10.1207/s15326985ep3801_6

CrossRef Full Text | Google Scholar

Mayer, R., and Fiorella, L. (2014). “Principles for Reducing Extraneous Processing in Multimedia Learning: Coherence, Signaling, Redundancy, Spatial Contiguity, and Temporal Contiguity Principles,” in The Cambridge Handbook of Multimedia Learning. Editor R. E. Mayer. Second edition (New York: Cambridge University Press), 279–315.

Google Scholar

Minkley, N., Xu, K. M., and Krell, M. (2021). Analyzing Relationships between Causal and Assessment Factors of Cognitive Load: Associations between Objective and Subjective Measures of Cognitive Load, Stress, Interest, and Self-Concept. Front. Educ. 6 (56). doi:10.3389/feduc.2021.632907

CrossRef Full Text | Google Scholar

Paas, F. G. W. C. (1992). Training Strategies for Attaining Transfer of Problem-Solving Skill in Statistics: A Cognitive-Load Approach. J. Educ. Psychol. 84, 429–434. doi:10.1037/0022-0663.84.4.429

CrossRef Full Text | Google Scholar

Schroeder, N. L., and Cenkci, A. T. (2018). Spatial Contiguity and Spatial Split-Attention Effects in Multimedia Learning Environments: a Meta-Analysis. Educ. Psychol. Rev. 30, 679–701. doi:10.1007/s10648-018-9435-9

CrossRef Full Text | Google Scholar

Skulmowski, A., and Rey, G. D. (2020). Subjective Cognitive Load Surveys lead to Divergent Results for Interactive Learning media. Hum. Behav. Emerg. Tech. 2, 149–157. doi:10.1002/hbe2.184

CrossRef Full Text | Google Scholar

Sweller, J. (2020). Cognitive Load Theory and Educational Technology. Education Tech. Res. Dev. 68, 1–16. doi:10.1007/s11423-019-09701-3

CrossRef Full Text | Google Scholar

Sweller, J. (2010). Element Interactivity and Intrinsic, Extraneous, and Germane Cognitive Load. Educ. Psychol. Rev. 22, 123–138. doi:10.1007/s10648-010-9128-5

CrossRef Full Text | Google Scholar

Sweller, J., van Merriënboer, J. J. G., and Paas, F. (2019). Cognitive Architecture and Instructional Design: 20 Years Later. Educ. Psychol. Rev. 31, 261–292. doi:10.1007/s10648-019-09465-5

CrossRef Full Text | Google Scholar

Sweller, J., van Merriënboer, J. J. G., and Paas, F. G. W. C. (1998). Cognitive Architecture and Instructional Design. Educ. Psychol. Rev. 10, 251–296. doi:10.1023/a:1022193728205

CrossRef Full Text | Google Scholar

Thees, M., Kapp, S., Strzys, M. P., Beil, F., Lukowicz, P., and Kuhn, J. (2020). Effects of Augmented Reality on Learning and Cognitive Load in university Physics Laboratory Courses. Comput. Hum. Behav. 108, 106316. doi:10.1016/j.chb.2020.106316

CrossRef Full Text | Google Scholar

Trumper, R. (2003). The Physics Laboratory - A Historical Overview and Future Perspectives. Sci. Edu. 12, 645–670. doi:10.1023/a:1025692409001

CrossRef Full Text | Google Scholar

Urban-Woldron, H., and Hopf, M. (2012). Entwicklung eines Testinstruments zum Verständnis in der Elektrizitätslehre [Development of a diagnostic instrument for testing studen understanding of basic electricity concepts]. Z. für Didaktik der Naturwissenschaften 18, 201–227.

Google Scholar

Volkwyn, T. S., Allie, S., Buffler, A., and Lubben, F. (2008). Impact of a Conventional Introductory Laboratory Course on the Understanding of Measurement. Phys. Rev. ST Phys. Educ. Res. 4, 4. doi:10.1103/PhysRevSTPER.4.010108

CrossRef Full Text | Google Scholar

Vosniadou, S. (2008). International Handbook of Research on Conceptual Change. New York: Routledge.

Wilcox, B. R., and Lewandowski, H. J. (2017). Developing Skills versus Reinforcing Concepts in Physics Labs: Insight from a Survey of Students' Beliefs about Experimental Physics. Phys. Rev. Phys. Educ. Res. 13, 65. doi:10.1103/PhysRevPhysEducRes.13.010108

CrossRef Full Text | Google Scholar

Zacharia, Z. C., and de Jong, T. (2014). The Effects on Students' Conceptual Understanding of Electric Circuits of Introducing Virtual Manipulatives within a Physical Manipulatives-Oriented Curriculum. Cogn. Instruction 32, 101–158. doi:10.1080/07370008.2014.887083

CrossRef Full Text | Google Scholar

Zacharia, Z. C., and Olympiou, G. (2011). Physical versus Virtual Manipulative Experimentation in Physics Learning. Learn. Instruction 21, 317–331. doi:10.1016/j.learninstruc.2010.03.001

CrossRef Full Text | Google Scholar

Zu, T., Munsell, J., and Rebello, N. S. (2021). Subjective Measure of Cognitive Load Depends on Participants' Content Knowledge Level. Front. Educ. 6 (56). doi:10.3389/feduc.2021.647097

CrossRef Full Text | Google Scholar