- 1Department of Mathematics and Computer Science, University of Bremen, Bremen, Germany
- 2Department of Rehabilitation and Special Education, University of Cologne, Cologne, Germany
Introduction: The use of eye tracking (ET) in mathematics education research has increased in recent years. Eye tracking is a promising research tool in the domain of functions, especially in graph interpretation. It promises to gain insights into learners’ approaches and ways of thinking. However, for the domain of functions and graph interpretation, it has not yet been investigated how eye-tracking data can be interpreted. In particular, it is not clear how eye movements may reflect students’ cognitive processes. Thus, in this study, we investigate in how far the eye-mind hypothesis (EMH), which states broadly that what the eye fixates is currently being processed, can be applied to this subdomain. This is particularly true for contextual graphs, whose data originate from real-world situations, and which are of central importance for the development of mathematical literacy. The aim of our research is to investigate how eye movements can be interpreted in the domain of functions, particularly in students’ interpretations of contextual graphs.
Methods: We conducted an exploratory case study with two university students: The students’ eye movements were recorded while they worked on graph interpretation tasks in three situational contexts at different question levels. Additionally, we conducted subsequent stimulated recall interviews (SRIs), in which the students recalled and reported their original thoughts while interpreting the graphs.
Results: We found that the students’ eye movements were often related to students’ cognitive processes, even if indirectly at times, and there was only limited ambiguity in the interpretation of eye movements. However, we also found domain-specific as well as domain-general challenges in interpreting eye movements.
Discussion: Our results suggest that ET has a high potential to gain insights into students’ graph interpretation processes. Furthermore, they point out what aspects, such as ambiguity and peripheral vision, need to be taken into consideration when investigating eye movements in the domain of functions.
Introduction
The use and relevance of eye tracking (ET), the capturing of a person’s eye movements using ET devices, in research significantly increased in recent years (König et al., 2016). In mathematics education, too, ET is gaining interest and is used in numerous areas and contexts (Strohmaier et al., 2020). Whereas some ET studies take an embodied perspective on eye movements, in that mind and eye movements are considered as parts of the body as an entity (e.g., Abrahamson and Bakker, 2016), other ET studies take a more psychological perspective by understanding eye movements “as a window to cognition” (König et al., 2016, p. 2). However, in both frameworks, ET is used in particular to investigate students’ thinking and learning processes. Therefore, many studies rely on the eye-mind hypothesis (EMH) (Just and Carpenter, 1976b), which presumes a close relationship between what persons fixate on and what they process. However, studies from various fields revealed several limitations of this assumption (Underwood and Everatt, 1992; Anderson et al., 2004; Kliegl et al., 2006; Schindler and Lilienthal, 2019; Wu and Liu, 2022). Therefore, the relationship between eye movements and cognitive processes should be examined carefully for every subdomain to reduce the inherent ambiguity and uncertainty in interpreting gaze data.
Our study follows up on this uncertainty regarding the application of the EMH and the need to investigate domain-relatedly how eye movements can be interpreted. We focus on the relationship between eye movements and cognition in the domain of functions. In general, the domain of functions is an interesting field to study for the following reason: It is characterized by having very high relevance for both everyday life and school lessons (Friel et al., 2001). Especially in the first case, functions are often related to a situational context, for example, when they are used to model empirical phenomena. In our study, we are interested in the interpretation of graphs. Specifically, we study what we call contextual graphs. These are graphs whose data originate from measured values of real-world situations. In the digital age, graphs are pervasive in society and in everyday lives and, thus, also an important topic in mathematics education (Friel et al., 2001). When data are visualized in graphs, their meaning is not directly accessible, but must be inferred from the graph (Freedman and Shah, 2002). This involves relating the graphical information to a situational context (Leinhardt et al., 1990; van den Heuvel-Panhuizen, 2005). Previous research has revealed numerous types of errors and difficulties students encounter when interpreting graphs (e.g., Clement, 2001; Gagatsis and Shiakalli, 2004; Elia et al., 2007). Since both, mathematical aspects and the situational context, are relevant for the interpretation of graphs, this dialectic nature of functions may play a special role for the interpretation of eye movements.
To investigate students’ work with functions, especially graphs, ET appears to be a promising research tool. Recent studies in the domain of functions have used ET to investigate the role of graphic properties and verbal information for graph interpretation (Kim et al., 2014) and have observed how students make transitions between mathematical representations (Andrá et al., 2015). These results indicate that ET has potential for investigating students’ work with functions. This would link to the results from various other mathematical domains where the analysis of eye movements appears to be promising (Strohmaier et al., 2020; Schindler, 2021).
Since the interpretation of gaze data is not trivial and the EMH, on which many studies rely, has limitations, researchers need to know how ET can be applied in a certain domain. Thus, before one can pursue the long-term goal to validly apply ET in empirical studies focusing on the domain of functions, methodological studies are essential. Yet, to the best of our knowledge, researchers have not yet investigated how eye movements can be interpreted and to what extent the EMH can be applied in the domain of graph interpretation. Therefore, the aim of this paper is to investigate how eye movements can be interpreted in the domain of functions with respect to the EMH, in particular in students’ interpretations of contextual graphs. Its aim is methodological in that it investigates the opportunities and challenges of ET. In particular, we ask the following research questions:
(1) Do students’ eye movements correspond to their cognitive processes in the interpretation of graphs, and how?
(2) In how far are students’ eye-movement patterns ambiguous or unambiguous?
Both research questions focus additionally on the role of the situational context, as it is our overarching goal to also get a better understanding of its impact for the relationship between eye movements and cognitive processes.
Our study builds on the work by Schindler and Lilienthal (2019) as they have investigated in the field of mathematics education research to what extent the EMH applies in the subdomain of geometry and how eye movements can be interpreted. On the one hand, our study connects to their study, as both deal with graphical forms of representation (hexagon and graph of a function, respectively). On the other hand, our study advances it with respect to the dimension of application. In contrast to purely inner-mathematical geometrical problems, we use graphs of contextual functions that relate to a real-world context. We examine these application-related contexts and their effects on the interpretation of eye movements in the subdomain of graph interpretation.
Schindler and Lilienthal (2019) conducted a case study using ET and stimulated recall interviews (SRIs), which illustrated that the interpretation of eye movements in this domain turns out to be challenging. Eye movements in geometry often cannot be interpreted unambiguously since mapping gaze patterns with cognitive or affective processes is not bijective. The design of our study was similar. In an exploratory case study, two university students worked on contextual graphs in three different situational contexts, wearing ET glasses. Directly after, SRIs were conducted with the students, in which they watched a gaze-overlaid video of their work on the tasks and recalled their thoughts while interpreting graphs. The analyzed data consist of the transcripts of all utterances from the SRI alongside with the eye movements from the work on the tasks.
Eye tracking and the eye-mind hypothesis in mathematics education research and beyond
Research on eye movements has considerably increased in recent years (König et al., 2016), also in mathematics education research. ET is used in many fields in mathematics education (e.g., numbers and arithmetic, reasoning and proof, and the use of representations), applying numerous methods to gather and analyze data (Strohmaier et al., 2020). In mathematics education research, a distinction can be made between studies that take an embodied perspective on eye movements (e.g., Abrahamson et al., 2015; Abrahamson and Bakker, 2016) and those that take a psychological perspective (e.g., Andrá et al., 2015; Bruckmaier et al., 2019; Wu and Liu, 2022). Embodiment theories do not consider the mind and the body as separate entities since cognition is grounded in sensorimotor activity and, thus, eye movements are an integral part of cognition (Abrahamson and Bakker, 2016). The aim of using ET from a psychological perspective, in contrast, is to draw conclusions about cognitive processes by capturing eye movements. Here, eye movements are understood as a window to cognitive processes (König et al., 2016). Cognitive processes are defined as “any of the mental functions assumed to be involved in the acquisition, storage, interpretation, manipulation, transformation, and use of knowledge. These processes encompass such activities as attention, perception, learning, and problem solving” (American Psychological Association [APA], 2022). However, ET “is not mind reading” (Hannula, 2022, p. 30), but can provide insights into information processing, e.g., to “understand how internal processes of the mind and external stimuli play together” (Kliegl et al., 2006, p. 12). The gained insights can enrich the understanding of how learners acquire knowledge (Schunk, 1991). Indeed, Strohmaier et al. (2020) summarize studies that focus on “aspects of visualization” as well as those referring to “cognitive processes that cannot be consciously reported” (p. 167) as two of the three areas in mathematics education research where ET is particularly beneficial. Still, the relationship between eye movements and cognition is not immediately clear. Therefore, Schindler and Lilienthal (2019) emphasize that a discussion is needed about how ET data can be interpreted, i.e., to what extent the EMH applies, irrespective of what perspective (embodied or psychological) on eye movements one takes, in different mathematical domains.
Just and Carpenter (1976b) hypothesize that “the eye fixates the referent of the symbol currently being processed” (p. 139; EMH). According to this hypothesis, the eyes fixate the object that is currently on the top of attention. The EMH was derived from cognitive research dealing with reading (Just and Carpenter, 1976a). In addition to reading research, many researchers use them in other fields as the basis for their data analysis and interpretation. However, meanwhile it is known that these assumptions must be considered with caution, as there are some limitations. Even studies from the original field, i.e., reading research, have shown that information from previous fixated words and upcoming, not yet fixated, words also influence fixation durations of the current word (Underwood and Everatt, 1992; Kliegl et al., 2006). This “weakens the assumptions, because what is being fixated is not necessarily what is being processed” (Underwood and Everatt, 1992, p. 112). Moreover, there are situations in which words are processed by the participant although they are skipped, i.e., not fixated (Underwood and Everatt, 1992). Kliegl et al. (2006) summarize that the “complexity of the reading process quickly revealed serious limits of the eye-mind assumption” (p. 13). In a related area, the eye-mind hypothesis was challenged by observing eye movements during retrieval processes of read sentences. Again, the limitations of the assumptions became apparent: “Eye movements say nothing about the underlying retrieval process because the process controlling the switch in gazes is independent of the process controlling retrieval” (Anderson et al., 2004, p. 229). The fact that the EMH is also applied and investigated in completely different fields, namely in science, is shown in a study by Wu and Liu (2022) in scientific argumentation using multiple representations. They “examined the degree of consistency between eye-fixation data and verbalization to ascertain how and when the EMH applies in this subdomain of scientific argumentation” (Wu and Liu, 2022, p. 551) in order to contribute to reduce the ambiguity and clarify the validity of ET data in this subdomain. They conclude that “verbalizations and eye fixations did not necessarily reflect the same or similar cognitive processes” (Wu and Liu, 2022, pp. 562–563). They call for researchers to examine what factors have an influence on the relationship between eye-fixations and mental processes, i.e., on the EMH such as task/domain properties or prior knowledge. In mathematics education, Schindler and Lilienthal (2019) have illustrated in the subdomain of geometry that the EMH only partially holds true, which suggests that also in other mathematical subdomains the interpretation of ET data is not trivial either. One more reason for this is that eye movements do not only indicate cognitive processes, but also affective processes, i.e., processes characterized by emotional arousal, such as excitement about a discovery or panicking because of noticing a mistake (Schindler and Lilienthal, 2019). Hunt et al. (2014) found that mathematics anxiety affects (arithmetic) performance, as evidenced in significant positive correlations between math anxiety and gaze data, such as fixations, dwell-time, and saccades. Stress can also affect gaze behavior, as suggested by a study by Becker et al. (2022). Here, stress of mathematics teachers was indicated in the diagnosis of difficulty-generating task features and found to affect higher processing and related gaze behavior.
Therefore, the relationship between eye movements and cognitive (and affective) processes, i.e., how eye movements can be interpreted, needs to be investigated first. In the field of functions, this investigation is still missing. Thus, we take a first step in this direction and analyse eye movements and their interpretations for the subdomain of graph interpretation.
Eye tracking in the field of functions
Little ET research has been pursued in the domain of functions so far, so its potential for this domain is still unknown. Strohmaier et al. (2020) do not include the domain of functions as an own category in their survey; they classify some studies under the term “use of representations.” Anderson et al. (2004), Andrá et al. (2015) compared experts and novices when focusing on different representations of functions. They showed that there are quantitative and qualitative differences between experts and novices that indicate that experts proceed more systematically than novices in terms of the order of looking at and considering the representations that may correspond to each other. Kim et al. (2014) investigated graph interpretation with line graphs and vertical/horizontal bar graphs of students with dyslexia. They measured reaction times and showed that the gap in reaction times between college students with and without dyslexia increases with the increasing difficulty of the graph and the question. Shvarts et al. (2014) investigated the localization of a target point in a Cartesian coordinate system and showed that experts have the ability to use additional essential information and to distinguish essential parts of visual representations, whereas novices often focused on irrelevant parts. In addition, there are studies referring to less typical representations of functions. Boels et al. (2019) studied strategies interpreting histograms and case-value plots. The most common strategies they found for students’ interpretations of these graphs are a case-value plot interpretation strategy and a computational strategy. Reading values from linear versus radial graphs is the focus of Goldberg and Helfman’s (2011) investigation that outlines three processing stages in reading values on graphs [(1) find dimension, (2) find associated datapoint, (3) get datapoint value].
In contrast to all these empirical studies, the focus of our ET study follows a novice approach in the domain of functions as it has a methodological focus. It investigates in what ways eye movements correspond to cognitive processes in students’ interpretations of contextual graphs. In this subdomain, it is not yet clear how the situational context influences the relationship between eye movements and cognitive processing. We assume that diverse and complex cognitive processes accompany the occurrence of situational context as additional dimension. With our methodologically focused study, we hope to contribute to a better interpretation of the results in the domain of functions. As context is also relevant in other mathematical and scientific domains, our results might also be important for other mathematical domains in which context plays a role.
Graph interpretation in mathematics education
The concept of function is central in mathematics, regardless of the level at which mathematics is studied (e.g., Sajka, 2003; Doorman et al., 2012). While there is disagreement among mathematicians around which aspects of a function are crucial (Thompson and Carlson, 2017), what is understood as a function is less controversial. Dirichlet–Bourbaki authored a widely acknowledged definition, which Vinner and Dreyfus (1989) summarize as:
A correspondence between two non-empty sets that assigns to every element in the first set (the domain) exactly one element in the second set (the codomain). To avoid the term correspondence, one may talk about a set of ordered pairs that satisfies a certain condition (p. 357).
With regard to functions, three typical kinds of external representations can be distinguished: tabular, graphical, and algebraic (Sierpinska, 1992). Our work focuses on graphical representations, specifically on graphs, whose data originate from measured values of real-world situations. We call these graphs contextual graphs. These graphs are very common in daily life, but mostly underrepresented in school lessons. In school, the focus is rather on function types such as linear or exponential graphs. Nevertheless, contextual graphs are of central importance for the development of an ample mathematical literacy, especially with respect to the translation between real-world data and mathematical representations. In particular, recognizing and being able to interpret different representations of data belongs to statistical literacy and is central for the development of critical thinking (Garfield et al., 2010). Thus, learning how to deal with contextual graphs contributes to enable students to understand (media) reports using graphical representations and distinguish between credible and incredible information, interpret and critically evaluate them in order to use them as a basis for decision-making (Sharma, 2017).
Real-world contexts play a major role in interpreting contextual graphs. Graphs visualize data, which correspond to a functional context, such as the development of stock market prices, temperatures, or training processes. When data are visualized in graphs, their meaning is not directly accessible, but must be inferred from the graph (Freedman and Shah, 2002). Individuals have to make sense of the given information by processing it cognitively. To derive meaning from the information given in contextual graphs, it is necessary that the data must not only be extracted and understood, but also must be related to the situational context (Leinhardt et al., 1990; see e.g., van den Heuvel-Panhuizen, 2005 for contexts). Sierpinska (1992) points out that recontextualization (the reconstruction of the context from the given data, see van Oers, 1998, 2001) and the ability to relate given graphical information to a situational context together are the main difficulties that students face when interpreting graphs. This ability also depends on how much the setting of the graph is contextualized or abstract (Leinhardt et al., 1990).
When students interpret graphs, different levels of questions can be involved:
An elementary level focused on extracting data from a graph (i.e., locating, translating); an intermediate level characterized by interpolating and finding relationships in the data as shown on a graph (i.e., integrating, interpreting), and an advanced/overall level that requires extrapolating from the data and analyzing the relationships implicit in a graph (i.e., generating, predicting). At the third level, questions provoke students’ understanding of the deep structure of the data presented (Friel et al., 2001, p. 130).
These levels of graph interpretation involve different cognitive processes, related to the perception and interpretation of graphs. It can be assumed that the analysis of students’ eye movements can provide valuable insights into students’ graph interpretation processes. This would suggest that ET is a valuable method to investigate how students interpret this kind of visual representations.
Materials and methods
Participants, task design, and setting
We studied eye movements to investigate cognitive processes while working with functions represented as graphs. We conducted a case study with two university students. It can be assumed that they are more experienced in interpreting graphs than school students. In addition, they are more adept at reporting on their cognitive processes in SRIs, which was crucial for this exploratory study. We further chose two students with different backgrounds and affinity with respect to mathematics, in order to obtain a wider range of gaze patterns and approaches when working on the tasks. We chose two 21- and 28-years-old German university students. Gerrit (21) studied Engineering and Management with a focus on Production Engineering. He had a high affinity for and was interested in mathematics. Mathematics was a relevant domain in his professional field, so he was regularly occupied with mathematics at the time of study. In contrast, Elias (28) was an education student with a focus on German and history and did not have a specific interest in mathematics. At the time of study, he, therefore, was not used to work on mathematical problems. Both participants were communicative and volunteered to be participants in our study.
We presented graphs in three different situational contexts (Figures 1–3). They are inspired by the material published by the Shell Centre (1985): Two units deal with the change of velocity in a car race and a roller coaster ride, respectively and the third shows the change of the filling height of a vessel that is constantly being filled with water. Each unit consists of five tasks in which the participants were asked to interpret data from the graphs at different question levels, as specified by Friel et al. (2001; see Figures 2, 3). Each unit starts with an information slide about the situational context and the graph. This way, the participants have a chance to familiarize themselves with them. The first question asks them to describe the change of the velocity/filling height (intermediate level). The following two tasks ask them to extract information from the graph in the form of a single point (elementary level). Either a point on the abscissa is given to which the corresponding point on the ordinate must be found by reading information from the graph (task two), or vice versa (task three). In task four, the participants have to describe the change of the velocity/filling level in a specified interval (intermediate level) and interpret their result with regard to the situational context (overall level). Task five focuses on the interpretation of the whole graph, as the participants need to pick and justify the one out of four or five realistic images which they think represents the situation best (overall level).
The students worked on the tasks individually. The tasks were presented on a 24″ screen (60 Hz, viewing distance: ∼60 cm), each task on a single slide. There was no time restriction for working on the tasks. The students gave their answers orally, while the sound was recorded by the built-in microphone of the ET glasses (see section “(Un)Ambiguity of eye movements patterns”). The students were able to get to the next task by autonomously clicking the computer mouse. The first author of this paper was the instructor of this work and was present during the students’ individual work on the tasks. The instructor did not intervene while the students were working on the tasks unless the students directly addressed her and asked something. The instructor responded to the participants’ questions in terms of task formulation, but did not provide any help with regard to the mathematical content.
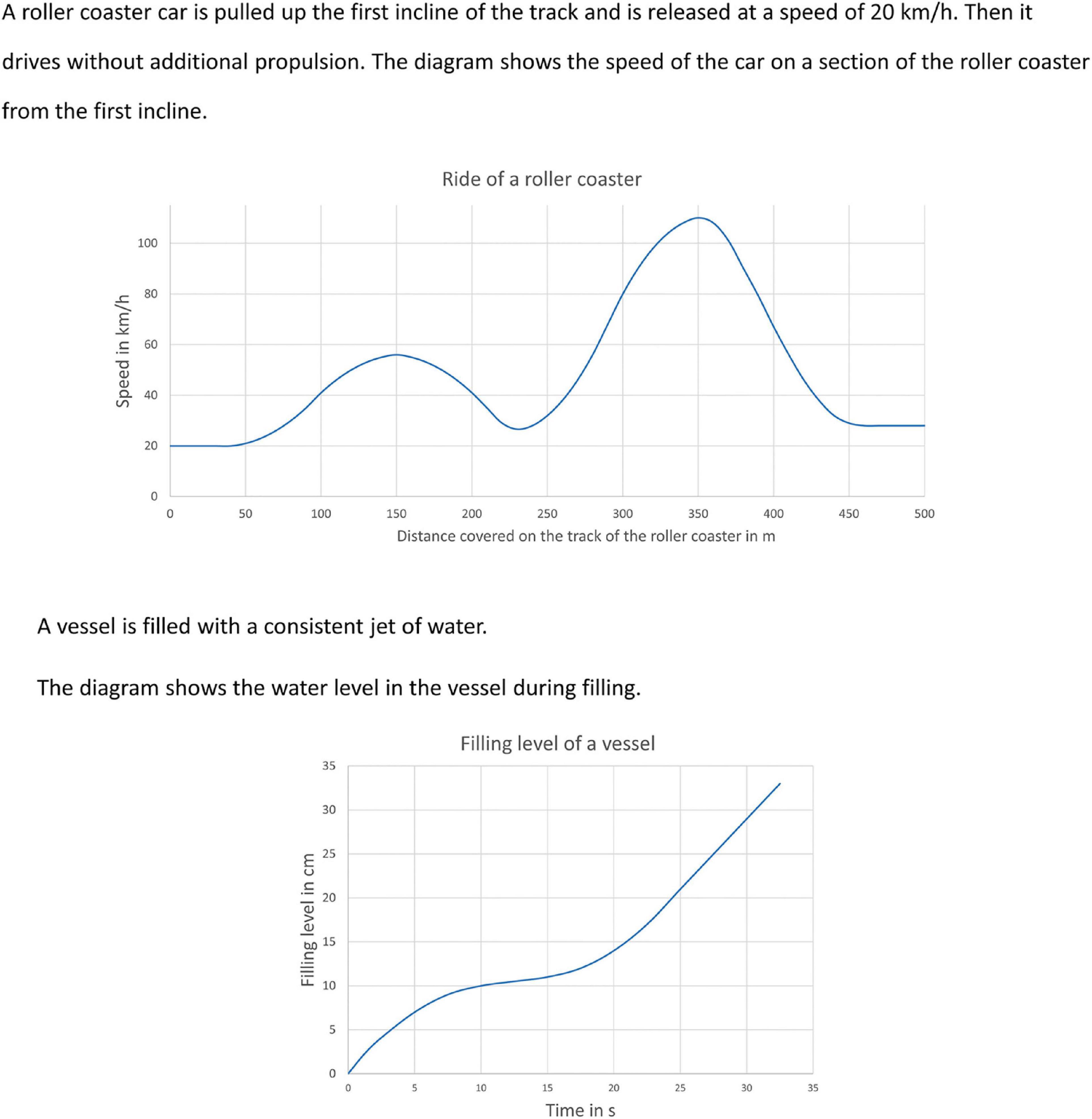
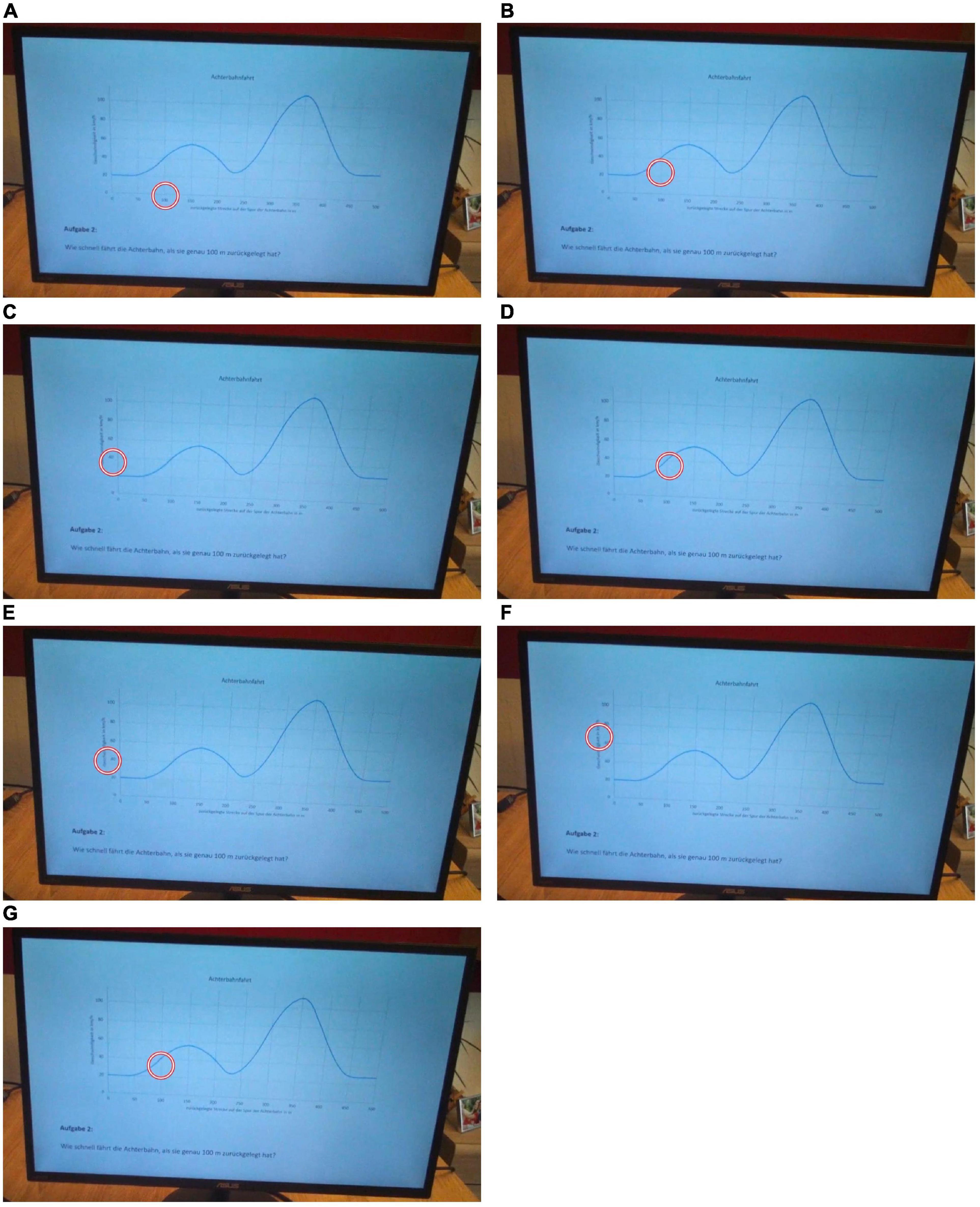
Figure 1. Situational contexts: change of velocity in a roller coaster ride, change of filling height in a vessel; translated to English.
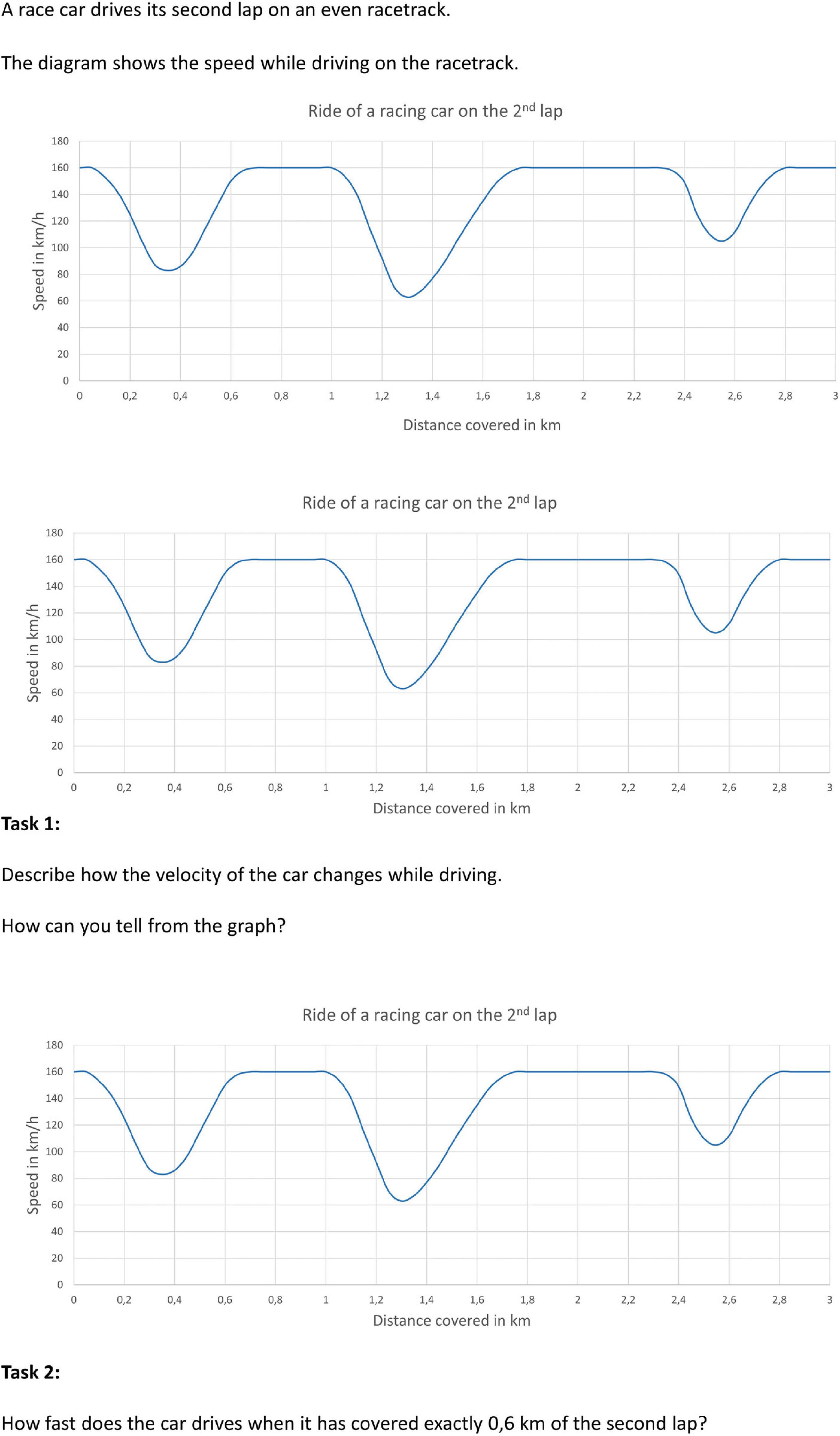
Figure 2. Introduction and tasks 1, 2 given to the students on the situational context: change of velocity in a car race; translated to English.
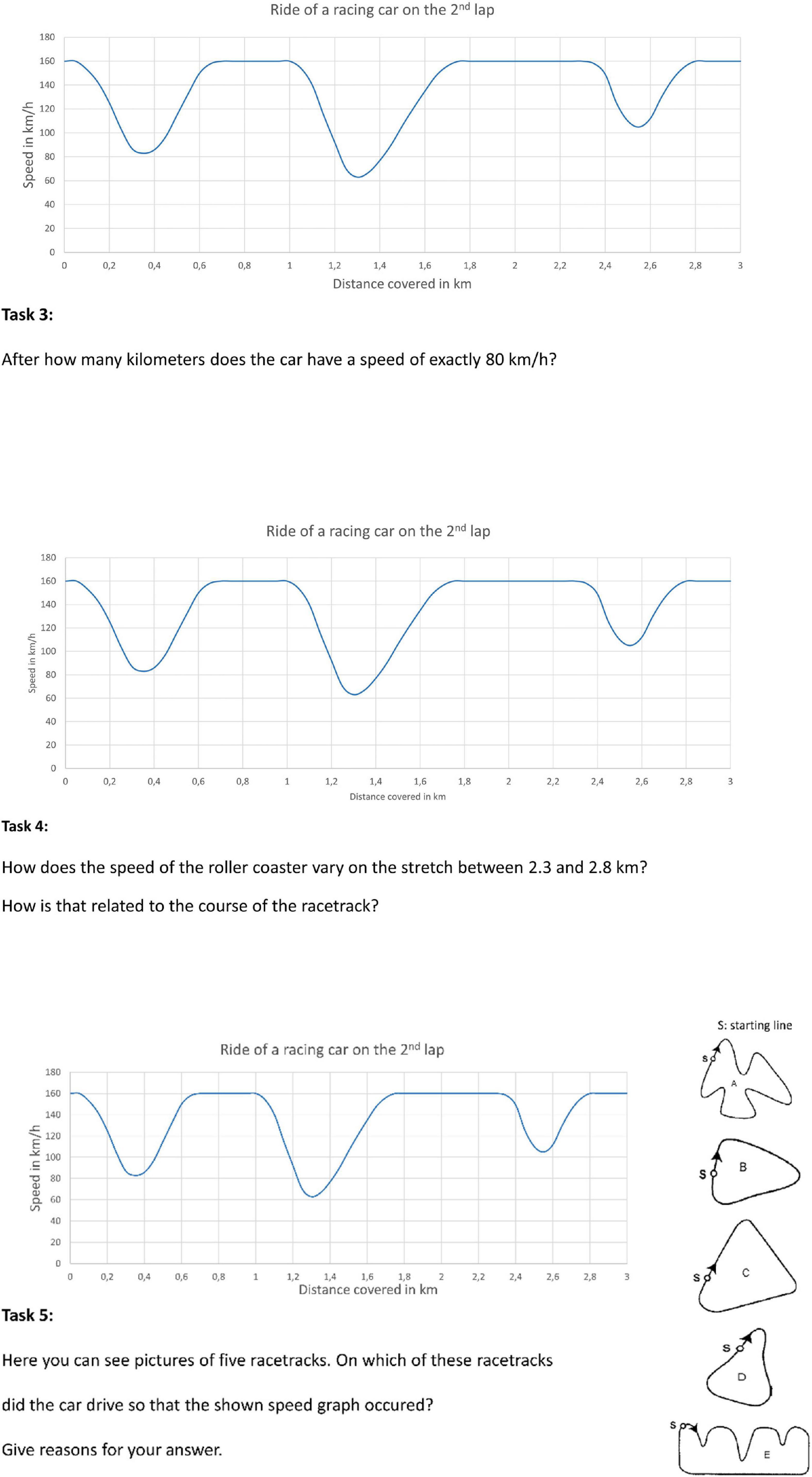
Figure 3. Tasks 3–5 given to the students on the situational context: change of velocity in a car race; translated to English.
Eye tracker and eye tracking data
To record eye movements, we decided to use a head-mounted system, as the integrated scene camera also records gestures and student utterances in a time-synchronized manner. Moreover, this system has the advantage that all data are synchronized and this does not have to be done subsequently, what is also important for the timely conduction of the SRIs. We used Tobii Pro Glasses 2 with 50 Hz. The binocular eye tracker allows tracking gazes through ET sensors and infrared illuminators. At the beginning of data collection, first, a single-point calibration was performed with the eye tracker to enable the transfer function that maps the gaze point onto the scene image. Then, an additional nine points calibration verification was performed, so that we could later check the measurement’s accuracy. We repeated this verification procedure toward the end of the students’ work to find possible deviations from the beginning. Gaze estimation under ideal conditions with Tobii Pro Glasses 2 is 0.62° (Tobii Pro AB, 2017). In our study, the average accuracy from the calibration at the beginning and the end of data collection was 1.1°, which corresponded to 1.15 cm on the screen we used. This inaccuracy was taken into account in the task design by placing all relevant task elements appropriately far enough apart. In addition, we also considered the inaccuracy in the course of data interpretation by not making any statements about situations in which it could not be clearly determined what the person was looking at, despite the spacious task design.
According to Holmqvist and Andersson (2017), in only 2° of the humans’ visual field, high-acuity vision is possible. This small area is called fovea. The ET method makes use of the small size of the fovea, since the eye must be directed to the area in which information is aimed to be extracted. Nevertheless, the surrounding part of the visual field, the large area of peripheral vision, is used for orientation. In it, the information processed is blurred and in black and white, but serves as an indication of the next target of the gaze, or to perceive movement in the periphery (Holmqvist and Andersson, 2017). Most eye movement studies predominantly analyse fixations (moments when the eye remains relatively still; approx. 200 ms up to some seconds) and saccades (quick eye movements between fixations; approx. 30–80 ms) (Holmqvist and Andersson, 2017). Hannula (2022) emphasizes that “different methods have been developed to analyse eye movement behavior. As in all areas of research, a phase of qualitative research has been necessary to get a basic understanding of the eye movements in a specific task” (p. 20). Therefore, our study focuses on a methodological research question, building on a qualitative approach. We investigate how eye movements can be interpreted in the domain of functions with respect to the EMH, particularly in students’ interpretation of contextual graphs. Hence, we decided not to limit ourselves to certain measures (e.g., fixation durations, dwell time, or areas of interest), but to analyze raw data (Holmqvist and Andersson, 2017). Our purpose is not only to know where the student’s attention is when interpreting contextual graphs, but also to interpret the eye movements themselves and relate them to cognitive processes. We, therefore, use eye movements as displayed in gaze-overlaid videos. The gaze-overlaid videos were produced by the software. See here Thomaneck et al. (2022) for an example. Figure 4 shows an example of a successive gaze sequence as displayed in a gaze-overlaid video and Figure 5 a merged visualization of this gaze sequence as a gaze plot, in which the order of fixations and the respective duration are displayed through the size of the corresponding circle.
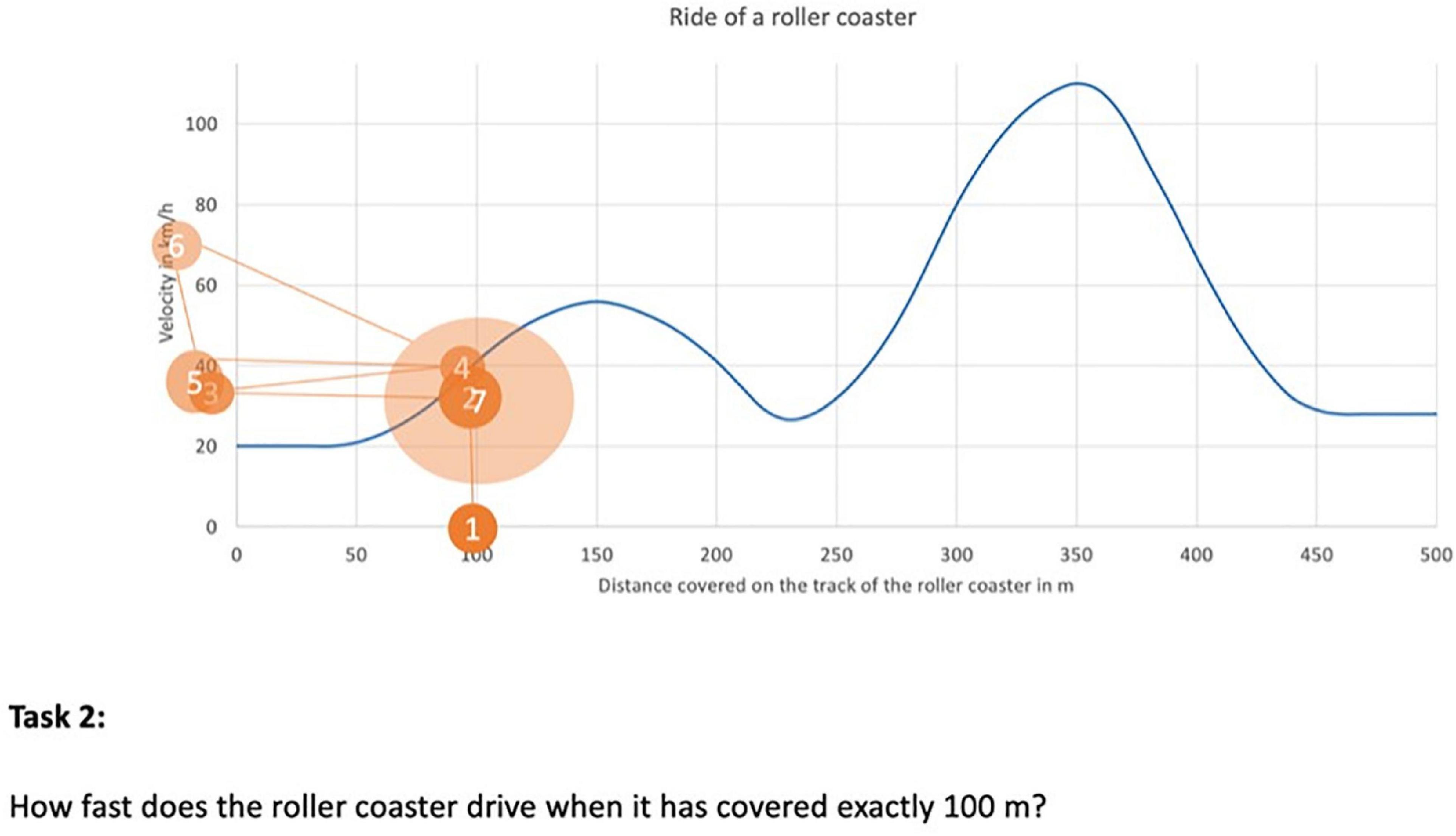
Figure 5. Gaze plot for the gaze sequence presented in Figure 4.
Stimulated recall interview based on gaze-overlaid video
Lapses in memory often are a problem in traditional interviews. Dempsey (2010) expounds that “motivations and rationales that informants describe retrospectively may not conform to those they actually held in the moment of experience” (p. 349). SRI is a special form of interview in that participants are invited to recall their thinking during an event that is prompted by a stimulus. SRI is well suited to investigate cognitive processes (Lyle, 2003), since it “gives participants a chance to view themselves in action as a means to help them recall their thoughts of events as they occurred” (Nguyen et al., 2013, p. 2).
One kind of stimulus for this form of interview are gaze-overlaid-videos. These are videos that show the original scene, overlaid with gazes from the ET. Stickler and Shi (2017) point out that gaze-overlaid videos provide a strong stimulus for SRI, because this stimulus makes eye movements visible, which, for the participants, are usually not conscious. In our study, the gaze videos show the participants’ processes of solving contextual graph interpretation tasks as a stimulus for recalling their cognitive processes while solving the tasks.
It is important to keep the time span short between ET and SRI and to ensure that the questions asked in the interview situation do not alter the cognitive processes that have taken place at the time of the event (Dempsey, 2010; Schindler and Lilienthal, 2019). In our study, the SRI was carried out by the first author about 30 min after the participants had completed the ET tasks. The SRIs lasted between 8 and 15 min per situational context. We used the video captured by the ET glasses, overlaid with the recorded gaze data and supplemented with the voice recording by the Tobii Controller Software (Tobii Pro AB, 2014) as stimulus. Prior to the SRI, the participants were told that they would see their eye movements in the form of a red circle. Then they were familiarized with the aim of the interview: that they should explain these gazes and explain their original thoughts to make their approaches understandable for the interviewer. The interviewees also wore the ET glasses during the SRI, so that verbal utterances and potential gestures could be recorded. The questions invited them to express their thoughts, or explain the rationales after having watched the stimulus. For example, we asked, What did you do there?, or Why did you look so closely at this section of the graph at this moment? Either the participants paused the video autonomously to explain their eye movements, or the interviewer herself stopped the recording and invited them to clarify the situation by asking a related question. The kind of questions was planned in advance to ensure that similar questions and wordings were chosen in both interviews. While the students were working on the tasks, the interviewer had the opportunity to observe the eye movements on a second screen and, thus, had time to consider at what moments she would pause the video if the students did not stop it themselves. Additional follow-up questions also arose spontaneously during the interview situations. Whether or not the interviewer posed follow-up questions, also depended on how detailed the students explained their eye movements.
In the SRIs, we found that both participants, Elias and Gerrit, were able to answer most of the questions and to comprehensibly explain their eye movements. Moreover, we strongly assume that their utterances actually correspond to their original cognitive processes, for the following reasons: It is known from psychological literature that the more deeply a stimulus has been analyzed, the better it can be recalled. Craik and Lockhart (1972) distinguish for instance between preliminary stages of processing that are concerned with the analysis of physical or sensory features and later stages of processing that combine new input with previous knowledge and are concerned with pattern recognition and the extraction of meaning. In our study, a deep analysis of the stimulus by the participants can be assumed, since the tasks dealt with can be characterized by pattern recognition and the extraction of meaning and, thus, belong to later stages of processing. In addition, the students are reminded of their processing of the tasks by showing them their gaze-overlaid videos, which provide reflection-aiding. Nevertheless, in the few situations when they could not recall their original thoughts, they openly admitted it. This indicated that the gaze-overlaid video was a strong stimulus for the SRI in our study and the resulting utterances were a good data basis for our analyses. However, it should be noted here that the data is based primarily on what students say. Even though there are strong indications and arguments that these are credible and actually reflect their original thoughts, it cannot be entirely ruled out that these are complete and always true. Nevertheless, we consider the combination of ET and SRIs to be extremely helpful, as it allows us to get close to the thoughts and learning processes of the participants.
Data analysis
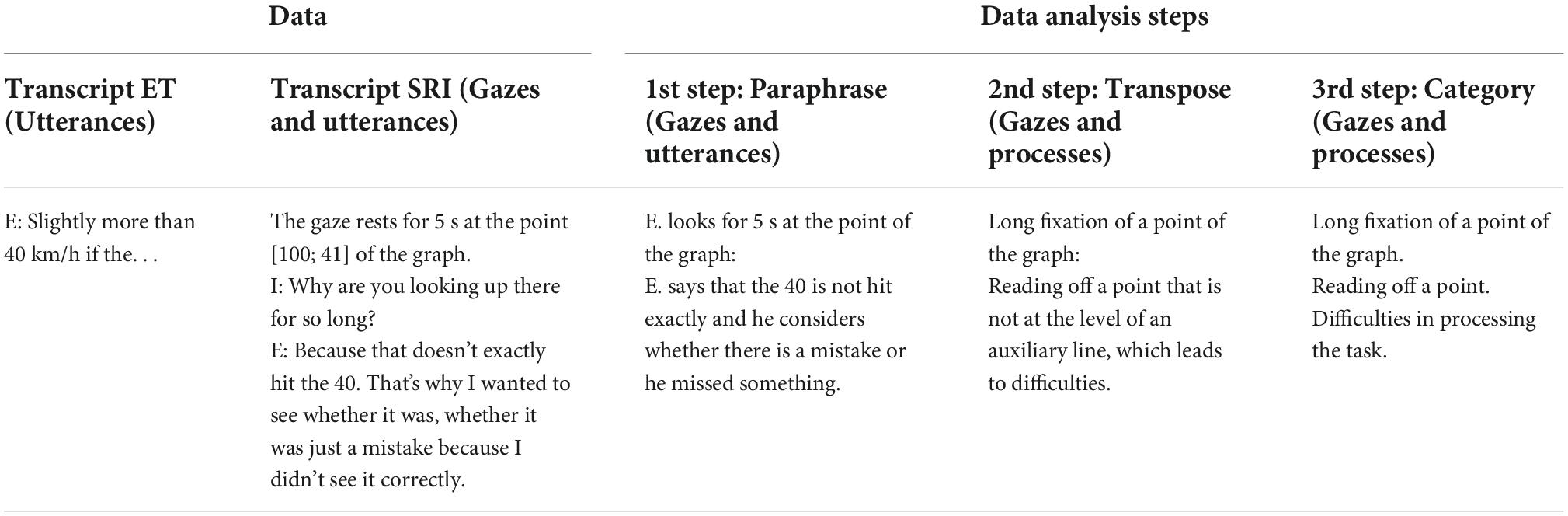
To analyze the data, we first transcribed the utterances from the ET videos, including the given answers to the tasks. The transcripts were organized in the first column of a table (see Table 1). The second column contained the transcription of gazes and utterances from the SRI video. When the video was paused in the SRI, the utterances and potential gestures of both the interviewer and participant were inserted in the corresponding line in the table. Thus, by presenting the eye movements and simultaneously spoken words on the same line (Table 1), we display which events happened concurrently. Afterward, we analyzed the SRI transcripts following Schindler and Lilienthal’s (2019) adaption of Mayring’s (2014) four steps of qualitative content analysis for ET-data (see data analysis steps in Table 1 and the corresponding gaze sequence as displayed in a gaze-overlaid video in Figure 4 and the corresponding gaze plot in Figure 5). We chose to use inductive category development, due to the explorative and descriptive nature of the research aim in this study.
The first step in Mayring’s approach is the transcription, which, in our case, embraces both, the transcriptions of the utterances from the task processing, as well as the transcription of gazes and utterances from the SRI. In a first analytical step (Mayring: paraphrase), we paraphrased the elements from the transcripts with attention to relevance for our research interest, which include the eye movements and the interpretations given by the participants in the SRI. In the next transposing step (Mayring: generalization), the paraphrases were uniformed stylistically. Only after this, in the third step, did the actual development of categories take place (Mayring: reduction). Throughout the whole analytical process, we distinguished between gaze categories (shown in the upper part of the cells) and interpretation categories that describe the cognitive processes associated with the respective gazes (lower part of the cells following the colon). We carried out these steps with one third of the data to develop the category system. Then, the remaining data was organized using the preliminarily developed categories. Subsequently, we revised the category system by partially re-naming categories to unify the nomenclature. Furthermore, we arranged the categories in thematic main categories (e.g., gazes on the text, gazes on the graph, or recurring gaze sequences for the gaze categories).
When the interpretation was unclear and the assignment of the categories appeared to be uncertain, for example, because the interpretations given in the SRI were too imprecise or too general, we tried to verify our interpretation with the help of the utterances from the ET video in the left column. Finally, all interpretations that belonged to a certain gaze category were grouped to show all cognitive interpretations that matched a certain gaze pattern in our data. Examples of gaze patterns are gaze jumps between a point of the graph and the corresponding point of the axis or several gazes in succession at points of a graph section.
Results
In the following, we present the results with respect to the two research questions: (1) Do students’ eye movements correspond to their cognitive processes in the interpretation of graphs, and how? (2) In how far are students’ eye-movement patterns ambiguous or unambiguous? Table 2 (correspondences of eye movements and cognitive processes) and Table 3 (unambiguous eye movement patterns and associated cognitive processes) provide a summary of the main results presented in the following sections.
Correspondence of eye movements and cognitive processes
In ET research, a close relationship between eye movements and cognitive processes is often assumed. The underlying basic assumption is that what the eyes fixate on is cognitively processed at that very moment. We will present our results with respect to research question 1 below.
Correspondences of eye movements and cognitive processes
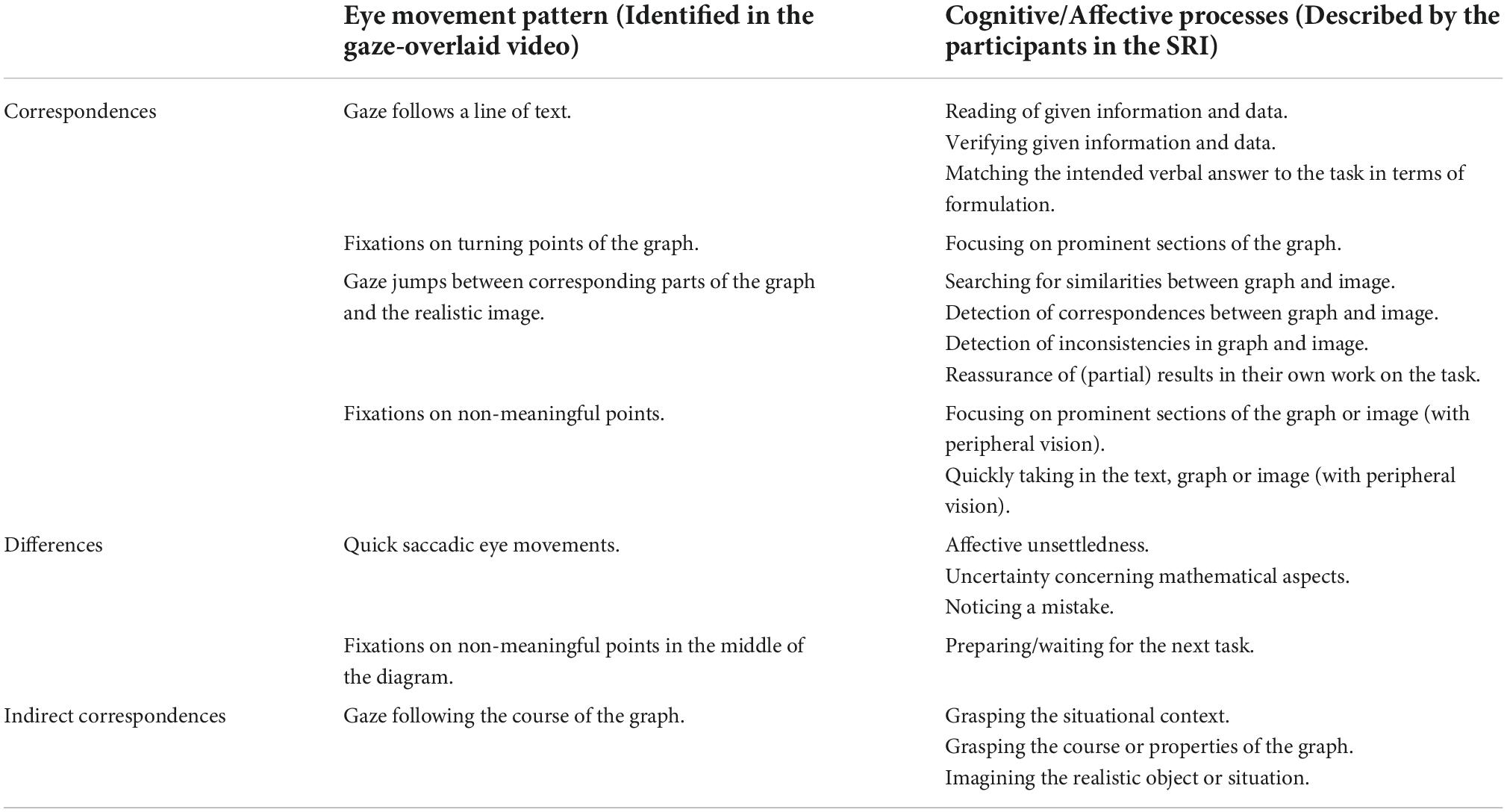
Our analyses suggest that students’ eye movements were related to their cognitive processes in most instances. This applies to all elements of the stimuli (text, diagram, and graph). For instance, gazes that followed a line of text were explained in such a way that the text was read and understood. According to the participants, a fixation on the axis label served to grasp the meaning of an axis, whereas gazes on the marked points on the axes were used to orientate and find certain points (e.g., for reading a value or naming an interval). A gaze following the course of a graph section can indicate that the participant grasps the meaning and memorizes the course and certain properties of the graph. These are just a few of many examples, where the EMH held true, that is, where the cognitive processes were closely related to the students’ eye movements.
Differences between eye movements and cognitive processes
Although the EMH held true in many instances, we also observed several situations in which the eye movements were not aligned with the students’ cognitive processes. The gaze pattern where it was most obvious that the EMH did not hold true, was that of quick gaze jumps on different points of the (digital) task sheet – even semantically non-meaningful ones, i.e., areas from which no relevant information can be extracted to solve the task. The participants explained this eye movement pattern in different ways. What all of these instances had in common was that the places, where the students looked at, were not semantically related to the students’ cognitive processing. Instead, emotional arousal dominated when this eye movement pattern occurred. For example, Elias described that he was in a state of affective unsettledness. He mistrusted the task and could not cope with the realistic image given as part of the fifth task. When the interviewer asked him about his quick eye movements in this situation in the SRI, he explained, “I felt tricked because I thought this is really one-to-one (chuckling) the same. […] Because I’m just completely insecure at that moment and thinking I missed something.” (All quotations from the data are translated from German by the authors.) We made similar observations in situations when the students noticed a mistake in their own answer, or felt insecure about mathematical aspects of the tasks. In all these instances, the eye movements appeared to be related to affective arousal. Thus, in addition to cognitive processes, affective processes are also reflected in the eye movements. Although the affective processes are related to the cognitive processes taking place, the EMH does not hold here, because the eye movements reflect the affective processes prevailing at that moment.
Another interesting eye movement pattern, in which the EMH did not hold true, occurred several times with both participants at the end of a subtask. After finishing and responding to a task, their eyes fixated on non-meaningful points in the middle of the diagram on the digital task sheet. However, no relevant information to solve the task can be extracted here, so these points were semantically not meaningful. Elias explained that he looked at this point, because he “immediately knew that directly after this, the next will appear right away, the next page.” This eye movement, thus, had no reference point in terms of the functional context or the requirements of the task.
Additionally, there were situations in which participants seemed to focus on a single point on the task. The SRI, however, revealed that they did not actually semantically process the information displayed at the fixated point, but, rather, perceived the surrounding area with peripheral vision. The peripheral area is the region of vision outside the point of fixation, in which we cannot see sharply (see section “Eye tracker and eye tracking data”). In our data, it sometimes seemed as if the participants fixated on a non-meaningful point on the slide, but actually covered a larger area of the stimulus using their field of vision. For instance, referring to the ET video, Gerrit focused several times on a point slightly above a minimal turning point or a little below a maximum turning point. However, the respective turning point is included in the area of peripheral vision. By calculating the ET accuracy (see section “Eye tracker and eye tracking data”), we could ensure that there was no technical error in the measurement. When the interviewer asked him in the SRI what he was doing there, he replied: “Eh, there I looked at the peaks of the graph again.” Thus, he confirmed that he was cognitively processing a larger area, the peaks of the graph, and that the point he was fixating on was not identical to the focus of his thoughts. A similar situation appeared, for example, when the participants fixated on a single point of the graph or the realistic image, but actually covered a larger section of it or perceived the object as a whole, for example, to determine whether it changed in contrast to the previous task. Thus, the students did not cognitively process exactly what they fixated on, but, with the help of peripheral vision, a larger area of their field of vision. Considering this, the EMH does hold true again, though it does in a broader sense. As peripheral vision can capture information in every ET study, independent from the mathematical content, this is a domain-general challenge for the interpretation of eye movements.
Indirect correspondences of eye movements and cognitive processes: Graph vs. context
We observed instances where it was ambiguous whether the EMH held true or not. The ambiguous cases referred to situations in which the participants fixated on a certain object of the stimulus, but the cognitive processes that they described in the SRI did not directly relate to this object, but to the situational context of the task. In the SRIs, it became clear that when the students looked at the graph, their thoughts were often related to the situation and the real objects. For instance, in the task presenting the car race, Gerrit fixated on several points of the graph, partially jumping between the axis and the graph. He explained, “Eh, I looked for when the speed decreases. And that should actually stand for that you brake, like driving into a curve. And then the speed, of course, increases again. This means that you are through the curve and can accelerate again.” Here, Gerrit described cognitive processes aligning with the situational context. In another case, Elias described in the SRI for the same task, “I try […] to complete this image by simply figuring out, how much distance does it drive? And when could the curve appear? How long is the curve? […]. That’s why the curve must have a certain shape.” Elias, when gazing at the graph, was imagining the race course and trying to capture the situation as precisely as possible with the aid of the graph. We found similar instances with eye movements that followed the course of the graph, while the participants were thinking about the situational context. These cases can be described as an implicit support of the EMH conditioned by the additional dimension of the situational context: Although the gazes related exclusively to the graph, the cognitive processes also partly related to the situational context. Thus, this challenge is specific for the domain of functions, in particular for the interpretation of contextual graphs, that is, graphs of functions that are linked to data from real-world situations.
(Un)Ambiguity of eye movements patterns
As indicated in the previous section, certain eye movement patterns can relate to different cognitive processes (ambiguous eye movement patterns), whereas others appear to always relate to the same cognitive process (unambiguous eye movement patterns). We will present the detailed results with respect to research question 2 below.
Unambiguous eye movements patterns
We found four eye movement patterns that were related to a singular cognitive process, reported by the students in the SRIs (Table 3). The first two relate to elements of the graph (labeling of axes and title of the diagram), which the students interpreted (grasp and understand the elements’ meaning). The third eye movement pattern was related to processing the general task in our study: When the students’ gazes rested on non-meaningful points in the center of the task sheet, after the participants had finished a subtask, they were preparing/waiting for the next subtask to come on the next slide.
In addition, we found an unambiguous eye movement pattern, where the eye movements were related to affective processes (see section “Differences between eye movements and cognitive processes”). Quick saccadic eye movements on different points of the stimulus, or on non-meaningful points of the task sheet, where the gaze wandered “hectically” over the task sheet, were related to emotional arousal. For instance, the pattern appeared over a period of 14 s when Elias was in a state of affective unsettledness. He described, “I’m just completely insecure at that moment and think I missed something.” Other examples for quick saccadic eye movements occurred in situations in which emotional arousal related to processing the task, such as if the participant felt insecure about the task concerning mathematical aspects, noticed a mistake in his earlier work, or had difficulties completing the task. All these instances have in common that the eye movement pattern indicates emotional arousal.
Ambiguous eye movement patterns
To illustrate, in which situations the interpretation of the gaze movements were ambiguous, we first give some examples before moving on to a more general observation regarding this aspect.
A frequent eye movement pattern that was associated with different cognitive processes was presented in Table 2: The gaze fixated a point on one axis, moved to the corresponding point on the graph, and then moved on to the particular point on the other axis. One interpretation of this gaze pattern given by the participants was reading off the point of the graph. More specifically, they describe how they searched for the given point on the ordinate, then moved to the corresponding point in the graph, and, finally, read the value on the abscissa. Gerrit, for example, describes his approach to this in the context of the process of filling a vessel: “I looked and searched for the point of 20 s on the x-axis and then read the corresponding y-value.” The second interpretation given in the SRI was that the students wanted to reassure themselves regarding their (partial) results.
A second example of an ambiguous eye movement pattern was following the course of a graph section with the gaze. On the one hand, the students reported that they wanted to grasp or memorize the course of the graph. On the other hand, the students tried to grasp and understand the situational context of the graph (see section “Indirect correspondences of eye movements and cognitive processes: graph vs. context”). For instance, Gerrit described, “Because I’ve tried to imagine how the filling level changes when the graph increases or when it no longer increases that much.” Thus, on the one hand, there are interpretations of eye movements on the graph referring to the graph itself and, on the other hand, interpretations referring to the situational context.
The third example is a gaze pattern that occurs exclusively in the last task of each situational context, in which the students have to decide which realistic image is appropriate for the graph. The gazes jump between (corresponding) parts of the graph and the realistic image. This gaze pattern indicates a wide range of cognitive processes, such as comparing graph and image, building figurative imagination, recognizing correspondences between graph and image, recognizing discrepancies between graph and image, excluding an image.
Overall, it can be seen that the degree of ambiguity varies for the different gaze patterns. There are gaze patterns that are almost unambiguous, such as the example given here first. The participants exclusively interpret this gaze pattern in the two ways mentioned above [reading off a point vs. reassuring of (partial) results]. Next, there are gaze patterns where there are somewhat more possibilities for interpretation, such as following the graph with the gaze (second example) to grasp or memorize the graph vs. grasp and understand the situational context related to the graph. There are remarkably many relating cognitive processes (e.g., comparing graph and image, building figurative imagination, recognizing correspondences between graph and image, recognizing discrepancies between graph and image, excluding an image) to the gaze pattern of gaze jumps between (corresponding) parts of the graph and the realistic image, what was our third example in this section.
Discussion
The aim of this article was to investigate how eye movements can be interpreted in the domain of functions with respect to the EMH, particularly in students’ interpretations of contextual graphs. We conducted an exploratory case study with two students, in which we investigated (1) if students’ eye movements correspond to their cognitive processes in the interpretation of graphs, and how and (2) in how far students’ eye-movement patterns are ambiguous or unambiguous. We used ET together with SRIs and the cases of two university students with different proficiency to investigate these methodological lines of inquiry.
We found that the students’ eye movements often corresponded to their cognitive processes. This suggests that studying the eye movements of students interpreting contextual graphs can provide researchers with insights into the students’ cognitive processes, which confirms the potential that ET has in this domain. However, in some instances, the eye movements tracked to elements on the digital task sheet that had little to do with the associated cognitive processes. Besides cognitive processes, thanks to our bottom-up coding procedure, we were also able to find affective processes that participants gave as explanations for their eye movements. For example, we found that quick gaze jumps indicate affective arousal and that the fixation of a non-meaningful point of the slide at the end of a subtask can be interpreted as students preparing or waiting for the subsequent task. Furthermore, we have encountered a domain-general phenomenon, namely that the appearance of a fixation of a single point can also indicate peripheral vision, by means of which a surrounding area is perceived. Particularly interesting is the case, where cognitive processes correspond indirectly with eye movements. The students look at the graph, but perceive or imagine the situational context of the task that is caused by the additional dimension of this domain. When investigating whether the eye movement patterns were ambiguous or unambiguous, we identified that some eye movement patterns were related to a singular cognitive process, while we found that others had different associated cognitive processes.
Taken together, these results indicate that it is valuable to analyse eye movements in students’ interpretations of graphs, since they relate closely to students’ cognitive processes, and ambiguities are limited. However, to know exactly what the eye movements indicate, one needs additional information from the SRI in some situations, since, even with using ET, it is not possible to read the student’s minds (Hannula, 2022). It seemed to be relatively apparent when the students were thinking about something other than the task, or were emotionally unsettled, so that their eye movements were no longer related to the semantics of the displayed stimuli on the task sheet. The fact that eye movements relate to both cognitive and affective processes confirms the findings from studies in other subdomains, in which both kinds of processes were found (Hunt et al., 2014; Schindler and Lilienthal, 2019; Becker et al., 2022).
Generally, our findings about the relationship of eye movements and cognitive processes are partially domain-general and partially domain-specific for functions and the interpretation of contextual graphs. One domain-general finding provided insight into students’ readings of text. According to the participants, following a line of text with the gaze could be assigned to the cognitive process of reading and understanding the text. However, it is important to distinguish whether the text was read for the first time for information retrieval, or whether it was re-read in the further course of task processing to verify the information and data provided, or to match the intended verbal answer with the task in terms of formulation. Reading the text is only one example of the occurrence of the phenomenon that the same kind of eye movements can relate to different cognitive processes depending on the phase of task processing the student is in. There are similar findings with other eye movements. Based on our results, we hypothesize that there are at least three distinct phases in processing graph interpretation tasks: (1) initial orientation, in which an overview of the task and representations is obtained; (2) carrying out an approach to solve the task; (3) checking with respect to one’s own results or/and in relation to the formulation of the task. This can be seen, for example, in the second task, in which a value has to be read off the y-axis. For example, the three phases have the following form when Elias works on the roller coaster context: First, in the initial orientation, the gaze follows the line of text twice. Here, he reads and understands the task. Then, his gaze jumps to several points on the two axes, to the heading of the diagram, as well as to the labels of both axes, to a point on the graph and again to the label of the x-axis. According to the information from the SRI, he gets an overview of the diagram, checks whether it is the same as in the previous task and makes sure which quantities are applied to the axes. Then the second phase begins, in which he carries out his solution process. His gaze fixates the point on the x-axis that is indicated in the text, jumps to the corresponding point on the graph and to the corresponding value on the y-axis. This is where he actually reads off the value. In the third phase, the checking of one’s results with relation to the task, his gaze jumps several times between the relevant point on the graph and its value on the y-axis and then rests a little longer on the point of the graph. According to the SRI, this serves to assure himself of his own result. Then, in order to be able to give a suitable answer to the task that is also adapted to its formulation, his gaze jumps back again to the labels of the y-axis and the line of text. Elias’ eye movements are an exemplary sequence of gazes in the respective phases. Our empirical data show that these gazes are often additionally enriched with supplementary gaze repetitions, e.g., reading off a certain point again and again. Even in this study with a very small sample, however, it became clear that these three phases do not occur with every person and every task. In routine tasks, for instance, some phases seem to be very short or even omitted. Yet, in more complex tasks, in which the approach is not clear from the outset, it is indicated that there may be a further phase, in which one considers how one could solve the task. This additional phase, however, could also be understood as an extended initial orientation phase. Moreover, there may be further additional phases that could not be observed in this study. However, the phases that could be observed in our study are very similar to the famous four-phase model of problem solving (Pólya, 1945) – (i) understanding the problem, (ii) devising a plan, (iii) carrying out the plan, and (iv) looking back – or more recent versions of this first version of this model. Still, they also differ in some nuances from the phases we observed, since our tasks (apart from one) were no typical problem-solving tasks. For instance, the second task, which served as illustrating example above, does not pose a problem for the students, but is a routine task. In this task, there was no need to search for a solution approach, so that only three phases could be observed here. However, the fact that the respective phase of task processing has an influence on the interpretation of eye movements should be taken into account in further studies. Therefore, further studies are needed to determine in which subdomains and for which task types such phases occur, and which eye movements and aligning cognitive processes emerge. In this regard, Schindler and Lilienthal (2020) studied a student’s creative process when solving a multiple solution task. They identified similar phases: (1) looking for a start; (2) idea/intuition; (3) working further step-by-step (including verification, finding another approach, finding mistakes in previous approach, correcting the old approach); (4) finding a solution (including verification) or discarding the approach (Schindler and Lilienthal, 2020). Even if the task type used in their study is very different from those of this study and there are steps that do not appear in this study (e.g., intuition; finding another approach), some elements are comparable (e.g., an initial phase: orientation vs. looking for a start; verification processes). In particular, the findings of Schindler and Lilienthal (2020) for creative processes in multiple solution tasks illustrate that ET is beneficial for observing phases in task processing in detail. Therefore, it can be assumed that ET could also be an appropriate tool to identify phases in other fields or further specify existing phase models, e.g., of problem solving.
As another domain-general result, we found that quick saccadic eye movements, where the gaze was “hectically” wandering around on the task sheet, indicated affective unsettledness or other kinds of emotional arousal. For the domain of geometry, Schindler and Lilienthal (2019) found very similar results. In further studies in other (mathematical) domains, this observation should be further examined and verified, and when indicated, a domain-general theory of these kinds of eye movements and aligning affective processes in task processing could be developed. Wu and Liu (2022) call for the higher goal of scientific research “to formulate general rules that describe the applicability of the EMH under various subdomains” (p. 567). We consider our findings regarding the consideration of the phase of task processing and the appearance of affective processes as an initial step toward these general rules.
In addition to these domain-general findings in task processing, there are also numerous eye movements and aligning processes that relate directly to the interpretation of graphs. According to Friel et al. (2001), graph interpretation tasks can be assigned to elementary, intermediate, or overall level (see section “Introduction”). Elementary tasks require the extraction of information from the data. We implemented this in our task design as the reading of certain points from the graph. We found that one gaze pattern occurred repeatedly in these tasks and, thus, seems to be typical for this question level: The gaze fixated on a point on one axis, then moved to the corresponding point on the graph, and then moved on to the particular point on the other axis (see Table 2; this pattern was also found by Goldberg and Helfman, 2011). Similar to reading the text, these eye movements also occurred again in a later phase of processing the task, when the students wanted to validate the points or results. Here, again, ambiguity of the interpretation can be minimized by including the phase of task processing into the evaluation. However, one must keep in mind that the university students in our study knew how to read points of a graph; they were already proficient at elementary-level tasks. Whether eye movements can be (almost) unambiguously interpreted if the participants do not yet master this process remains an open question. We assume that different eye movement patterns might be possible.
The interpretation of eye movements, in our study, is less clear for intermediate and overall level tasks. We found that in tasks of these levels, there are other typical eye movements (e.g., intermediate level: following the line of the graphs; overall level: gaze jumps between parts of the graph and the realistic image). These gaze patterns have a higher, respectively a very high degree of ambiguity (see section “Ambiguous eye movement patterns”), since complex cognitive processes are included and there are interpretations referring to the graph, but also those referring to the situational context. This is because when the level of questioning increases, a reference to the situational context, in which the graph is embedded, must be established (Leinhardt et al., 1990; Sierpinska, 1992), which is much more demanding. The graphs in our tasks are contextualized (van Oers, 1998, 2001) since the data originate from a real-world situation and are represented in abstract contextual graphs. The students, when interpreting the graph in higher-level tasks, need to recontextualize the graph. Our findings indicate that the higher the task level is the more ambiguity is involved in the interpretation of eye movement patterns. Wu and Liu (2022) identified that the EMH holds as long as the information in the stimuli can be easily identified and does not necessarily hold when the information is less precise. Our findings specify this as they show that the degree of ambiguity of the interpretation of eye movements increases when the information of the representations are more difficult to extract, e.g., because of the task requirement to link the information from the graph to the situational context. In further studies, these processes and relationships should be investigated in more detail – also to examine to what extent this relationship between ambiguity and task level is a general rule that can be extended to other subdomains. This would be conceivable, for example, in the field of geometry. The study by Schindler and Lilienthal (2019) uses an inner-mathematical problem with a regular hexagon as a task. However, one could also set application-related tasks here, for example, on tiling a surface with hexagonal tiles, which would add an additional dimension – similar to the situational context in the graphs we used – which could cause ambiguity with respect to the interpretation of eye movements.
In addition to this domain-specific challenge in interpreting eye movements, we also found a domain-general challenge related to the specifics of ET methodology: The eye tracker suggests foveal vision since it is not able to display peripheral vision (Holmqvist and Andersson, 2017). Yet, in line with Kliegl et al. (2006), who observed parafoveal processing of previous and upcoming words in reading research, and Schindler and Lilienthal (2019) in mathematics education, we found that students use peripheral vision to perceive information when processing tasks by capturing larger areas than just a single focal point. Without additional SRI and only relying on ET, we would have made partially incorrect assumptions regarding the interpretation of eye movements in some instances. This further illustrates how carefully the interpretation of ET data must be handled.
Before we summarize this study and its contributions, we want to mention some limitations. The study was conducted with only two university students. However, since this is an exploratory study, the results are still meaningful and provide a good starting point for further studies that should, for example, clarify the transferability of the results to (secondary) students. Due to the methodological focus of the study, it was nevertheless possible to gain relevant insights into the interpretation of eye movements in students’ interpretations of graphs. Furthermore, it is important to note that for investigating the correspondences between eye movements and according cognitive processes, we could not directly access students’ cognitive processes, but used SRIs to gain insights into them. Based on the gaze-overlaid videos, the students recalled their original thoughts during their work on the tasks and reported their cognitive processes. This means that our interpretations were influenced by what the students reported. However, the two university students were well able to report and recall their thoughts in the SRIs directly after the original work on the tasks, which provided us with valuable and interesting insights.
In summary, we see high potential and benefits in using ET for the detailed study of students’ processes in the interpretation of graphs. Our findings show that this requires a very careful approach to the interpretation of eye movements, i.e., to the application of the EMH. Our study contributes to increase the validity of using ET in the domain of graph interpretation, but also in other domains. We found that domain-general aspects, such as peripheral vision, influence the interpretation of eye movements. Therefore, when conducting ET studies, one must always keep in mind that this type of visual information acquisition cannot be captured by technology. Study directors must consider that it is not always (only) the area specified by the visualized viewpoint that is acquired, but possibly the surrounding area as well. In addition, different phases of task processing might play a role for the interpretation of eye movements with relation to cognitive processes, as they can cause ambiguity. Often, however, there are related cognitive processes to the eye movements that merely serve a different intention due to different phases of task processing (see section “Ambiguous eye movement patterns”), so that the ambiguity can be minimized by including the phase of task processing in the interpretation of eye movements. This can occur in many types of tasks and, thus, domains where multi-step processes are used to arrive at a solution. Our findings, moreover, suggest that the task level influences the degree of ambiguity. In the interpretation of contextual graphs, the additional dimension of situational context causes this partially. However, we cannot rule out the possibility that in other domains there may be other influencing factors that have a similar effect. Therefore, when interpreting ET data, it is necessary to check in each case, whether such an additional dimension, in the form of a situational context or of some other kind, exists. To conclude, with our methodological study, we hope to increase the validity of ET studies in the domain of functions and in particular, the interpretation of (contextual) graphs, but also to be able to give clues for other domains on how eye movements can be interpreted and what influencing factors they may have.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors.
Ethics statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. The patients/participants provided their written informed consent to participate in this study.
Author contributions
AT, MV, and MS contributed to conception and design of the study and wrote the manuscript. AT conducted the study, collected the data, and performed the data analysis. All authors read and approved the submitted version.
Funding
This publication fee was covered by the State and University Library Bremen.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abrahamson, D., and Bakker, A. (2016). Making sense of movement in embodied design for mathematics learning. Cogn. Res. Princ. Implic. 1:33. doi: 10.1186/s41235-016-0034-3
Abrahamson, D., Shayan, S., Bakker, A., and van der Schaaf, M. (2015). Eye-tracking piaget: Capturing the emergence of attentional anchors in the coordination of proportional motor action. Hum. Dev. 58, 218–244. doi: 10.1159/000443153
American Psychological Association [APA] (2022). Cognitive processes. APA dictionary of psychology. Available online at: https://dictionary.apa.org/cognitive-process (accessed on Oct 25, 2022).
Anderson, J. R., Bothell, D., and Douglass, S. (2004). Eye movements do not reflect retrieval processes: Limits of the eye-mind hypothesis. Psychol. Sci. 15, 225–231. doi: 10.1111/j.0956-7976.2004.00656.x
Andrá, C., Lindström, P., Arzarello, F., Holmqvist, K., Robutti, O., and Sabena, C. (2015). Reading mathematics representations: An eye-tracking study. Int. J. Sci. Math. Educ. 13, 237–259. doi: 10.1007/s10763-013-9484-y
Becker, S., Spinath, B., Ditzen, B., and Dörfler, T. (2022). Den stress im Blick – lokale Blickbewegungsmaße bei der Einschätzung schwierigkeitsgenerierender merkmale von mathematischen textaufgaben unter stress. J. Math. Didakt. doi: 10.1007/s13138-022-00209-7
Boels, L., Bakker, A., Van Dooren, W., and Drijvers, P. (2019). Conceptual difficulties when interpreting histograms: A review. Educ. Res. Rev. 28, 1–23. doi: 10.1016/j.edurev.2019.100291
Bruckmaier, G., Binder, K., Krauss, S., and Kufner, H.-M. (2019). An eye-tracking study of statistical reasoning with tree diagrams and 2 × 2 tables. Front. Psychol. 10:632. doi: 10.3389/fpsyg.2019.00632
Clement, L. L. (2001). What do students really know about functions? NCTM 94, 745–748. doi: 10.5951/MT.94.9.0745
Craik, F. I. M., and Lockhart, R. S. (1972). Levels of processing: A framework for memory research. J. Verbal Learn Verbal Behav. 11, 671–684. doi: 10.1016/S0022-5371(72)80001-X
Dempsey, N. P. (2010). Stimulated recall interviews in ethnography. Qual. Sociol. 33, 349–367. doi: 10.1007/s11133-010-9157-x
Doorman, M., Drijvers, P., Gravemeijer, K., Boon, P., and Reed, H. (2012). Tool use and the development of the function condept: From repeated calculations to functional thinking. Int. J. Sci. Math. Educ. 10, 1243–1267. doi: 10.1007/s10763-012-9329-0
Elia, I., Panaoura, A., Eracleous, A., and Gagatsis, A. (2007). Relations between secondary pupils’ conceptions about functions and problem solving in different representations. Int. J. Sci. Math. Educ. 5, 533–556. doi: 10.1007/s10763-006-9054-7
Freedman, E. G., and Shah, P. (2002). “Toward a model of knowledge-based graph comprehension,” in diagrammatic representation and inference, eds M. Hegarty, B. Meyer, and N. H. Narayanan (Berlin, HD: Springer), 18–30. doi: 10.1007/3-540-46037-3_3
Friel, S. N., Curcio, F. R., and Bright, G. W. (2001). Making sense of graphs: Critical factors influencing comprehension and instructional implications. J. Res. Math. Educ. 32, 124–158. doi: 10.2307/749671
Gagatsis, A., and Shiakalli, M. (2004). Ability to translate from one representation of the concept of function to another and mathematical problem solving. Educ. Psychol. 24, 645–657. doi: 10.1080/0144341042000262953
Garfield, J., del Mas, R., and Zieffler, A. (2010). “Assessing important learning outcomes in introductory tertiary statistics courses,” In Assessment methods in statistical education: An international Perspective, eds P. Bidgood, N. Hunt, and F. Jolliffe (New York, NY: Wiley), 75–86. doi: 10.1002/9780470710470
Goldberg, J., and Helfman, J. (2011). Eye tracking for visualization evaluation: Reading values on linear versus radial graphs. Inf. Vis. 10, 182–195. doi: 10.1177/1473871611406623
Hannula, M. S. (2022). “Explorations on visual attention during collaborative problem solving,” in proceedings of the 45th conference of the international group for the psychology of mathematics education, Vol. 1, (dialnet), 19–34.
Holmqvist, P. K., and Andersson, D. R. (2017). Eye tracking: A comprehensive guide to methods, paradigms, and measures, 2. Edn. Lund Eye-Tracking Research Institute.
Hunt, T. E., Clark-Carter, D., and Sheffield, D. (2014). Exploring the relationship between mathematics anxiety and performance: An eye-tracking approach. Appl. Cogn. Psychol. 29, 226–231. doi: 10.1002/acp.3099
Just, M. A., and Carpenter, P. A. (1976b). Eye fixations and cognitive processes. Psychol. Rev. 87, 329–354. doi: 10.1016/0010-0285(76)90015-3
Just, M. A., and Carpenter, P. A. (1976a). The role of eye-fixation research in cognitive psychology. Behav. Res. Methods 8, 139–143. doi: 10.3758/BF03201761
Kim, S., Lombardino, L. J., Cowles, W., and Altmann, L. J. (2014). Investigating graph comprehension in students with dyslexia: An eye tracking study. Res. Dev. Disabil. 35, 1609–1622. doi: 10.1016/j.ridd.2014.03.043
Kliegl, R., Nuthmann, A., and Engbert, R. (2006). Tracking the mind during reading: The influence of past, present, and future words on fixation durations. J. Exp. Psychol. Gen. 135, 12–35. doi: 10.1037/0096-3445.135.1.12
König, P., Wilming, N., Kietzmann, T. C., Ossandón, J. P., Onat, S., Ehinger, B. V., et al. (2016). Eye movements as a window to cognitive processes. J. Eye Mov. Res. 9, 1–16.
Leinhardt, G., Zaslavsky, O., and Stein, M. K. (1990). Functions, graphs, and graphing: Tasks, learning, and teaching. Rev. Educ. Res. 60, 1–64. doi: 10.3102/00346543060001001
Lyle, J. (2003). Stimulated recall: A report on its use in naturalistic research. Br. Educ. Res. J. 29, 861–878. doi: 10.1080/0141192032000137349
Nguyen, N. T., McFadden, A., Tangen, D. D., and Beutel, D. D. (2013). “Video-stimulated recall intervies in qualitative research,” in joint australian association for research in education conference of the australian association for research in education (AARE), (Australian Association for Research in Education), 1–10.
Sajka, M. (2003). A secondary school student’s understanding of the concept of function—A case study. Educ. Stud. Math. 15, 229–254. doi: 10.1023/A:1026033415747
Schindler, M. (2021). “Eye-Tracking in der mathematikdidaktischen Forschung: Chancen und Herausforderungen,” in vorträge auf der 55. tagung für didaktik der mathematik - jahrestagung der gesellschaft für didaktik der mathematik vom 01. märz 2021 bis 25. märz 2021, (Oldenburg: Gesellschaft für Didaktik der Mathematik), doi: 10.17877/DE290R-22326
Schindler, M., and Lilienthal, A. J. (2019). Domain-specific interpretation of eye tracking data: Towards a refined use of the eye-mind hypothesis for the field of geometry. Educ. Stud. Math. 101, 123–139. doi: 10.1007/s10649-019-9878-z
Schindler, M., and Lilienthal, A. J. (2020). Students’ creative process in mathematics: Insights from eye-tracking-stimulated-recall interviews on students’ work on multiple solution tasks. Int. J. Sci. Math. Educ. 18, 1565–1586. doi: 10.1007/s10763-019-10033-0
Schunk, D. H. (1991). Learning theories: An educational perspective. New York, NY: Macmillan Publishing Co, Inc.
Sharma, S. (2017). Definitions and models of statistical literacy: A literature review. Open Rev. Educ. Res. 4, 118–133. doi: 10.1080/23265507.2017.1354313
Shell Centre (1985). The language of functions and graphs. An examination module for secondary schools. Manchester: Joint Matriculation Board by Longman.
Shvarts, A., Chumachemko, D., and Budanov, A. (2014). “The development of the visual perception of the Cartesian coordinate system: An eye tracking study,” in Proceedings of the 38th conference of the international group for the psychology of mathematics education and the 36th conference of the north american chapter of the psychology of mathematics education, (Canada), 313–320.
Sierpinska, A. (1992). “On understanding the notion of function,” in The concept of function. aspects of epistomology and pedagogy, [maa notes, volume25], eds E. Dubinsky and G. Harel (Washington, DC: Mathematical Association of America), 25–58.
Stickler, U., and Shi, L. (2017). Eyetracking methodology in SCMC: A tool for empowering learning and teaching. ReCALL 29, 160–177. doi: 10.1017/S0958344017000040
Strohmaier, A. R., MacKay, K. J., Obersteiner, A., and Reiss, K. M. (2020). Eye-tracking methodology in mathematics education research: A systematic literature review. Educ. Stud. Math. 104, 147–200. doi: 10.1007/s10649-020-09948-1
Thomaneck, A., Vollstedt, M., and Schindler, M. (2022). Example of a gaze-overlaid video. Available online at: https://www.youtube.com/watch?v=RUiMmKU8hWY (accessed November 29, 2022).
Thompson, P. W., and Carlson, M. P. (2017). “Variation, covariation, and functions: Foundational ways of thinking mathematically,” in Compendium for research in mathematics education, ed. J. Cai (Reston, VA: National Council of Teachers of Mathematics), 421–456.
Tobii Pro AB (2014). Tobii pro glasses 2 controller software (Version 1.114.20033) [Computer software]. Danderyd: Tobii Pro AB.
Tobii Pro AB, (2017). Eye tracker data quality report: Accuracy, precision and detected gaze under optimal conditions—controlled environment. Danderyd, Sweden: Tobii Pro AB.
Underwood, G., and Everatt, J. (1992). The role of eye movements in reading: Some limitations of the eye-mind assumption. Adv. Psych. Res. 88, 111–169. doi: 10.1016/S0166-4115(08)61744-6
van den Heuvel-Panhuizen, M. (2005). The role of contexts in assessment problems in mathematics. Learn. Math. 25, 2–9.
van Oers, B. (1998). The fallacy of decontextualization. Mind. Cult. Act. 5, 135–142. doi: 10.1207/s15327884mca0502_7
Vinner, S., and Dreyfus, T. (1989). Images and definitions for the concept of function. J. Res. Math. Educ. 20, 356–366.
Keywords: eye tracking (ET), eye-mind hypothesis, eye movements, functions, graph interpretation, contextual graphs, stimulated recall
Citation: Thomaneck A, Vollstedt M and Schindler M (2022) What can eye movements tell about students’ interpretations of contextual graphs? A methodological study on the use of the eye-mind hypothesis in the domain of functions. Front. Educ. 7:1003740. doi: 10.3389/feduc.2022.1003740
Received: 26 July 2022; Accepted: 21 November 2022;
Published: 12 December 2022.
Edited by:
Dor Abrahamson, University of California, Berkeley, United StatesReviewed by:
Alik Palatnik, Hebrew University of Jerusalem, IsraelRotem Abdu, David Yellin College of Education, Israel
Copyright © 2022 Thomaneck, Vollstedt and Schindler. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Aylin Thomaneck, YXlfdGhAdW5pLWJyZW1lbi5kZQ==
 Aylin Thomaneck
Aylin Thomaneck Maike Vollstedt
Maike Vollstedt Maike Schindler
Maike Schindler