- Institute of Education, University of Reading, Reading, United Kingdom
This large survey study set out to ascertain whether gender differences in teachers’ mathematical epistemic beliefs exist, and the extent to which teachers’ gender as well as their teaching experience level, education level, and socio-economic setting of the schools can predict these beliefs. Specifically, the study examined teachers’ beliefs concerning the structure, stability, and source of mathematical knowledge. This is crucial given that previous research have demonstrated the potential role of teachers’ mathematical epistemic beliefs in shaping their mathematics teaching, and hence their students’ mathematics learning outcomes and perceptions of the subject. The current study drew on survey data collected from 745 primary teachers using items from the Thai Teachers’ Mathematics Education-related Beliefs (TTMEB) questionnaire. The data were analysed using Independent-samples t-test and multiple regression. The findings reveal a very limited to no effect of gender on teachers’ mathematical epistemic beliefs, and also alert us to the fact that when it comes to exploring factors that shape one’s beliefs, their exogenous characteristics, such as the socio-economic setting of where they live and work, should too be taken into account. Overall, the study helps to dispel any myths about gender differences in the way male and female teachers perceive mathematics, specifically the nature of mathematical knowledge.
Introduction
Epistemic beliefs (EBs henceforth) are one’s beliefs about the nature of knowledge and knowing (Greene et al., 2016). The concept of EBs can be traced back to the pioneering work of scholars on this topic in the 1990s (e.g., Schommer, 1990) who at the time referred to this concept as epistemological beliefs. It was not until early 2000s when scholars, such as Kitchener (2002) argued that as epistemological beliefs directly translates to “beliefs about the theory of knowledge,” it would thus be more accurate to adopt the adjective epistemic when referring to beliefs about the nature of knowledge and knowing (as opposed to beliefs about the theory of knowledge and knowing), especially when referring to beliefs espoused by students and teachers as opposed to philosophers. That said, it is not uncommon to still see recent literatures on the topic still referring to the concept as epistemological beliefs (e.g., Depaepe et al., 2016; Rott, 2021), highlighting the on-going lack of clarity and agreement in the adoption of the term within the field of educational research. Further complication arose when some scholars (e.g., Chinn et al., 2011) prefer to use the term epistemic cognition as opposed to epistemic beliefs, arguing that specific cognitive processes are involved in the formulation of one’s epistemic perspectives. The current study, however, subscribes to the view of Schommer-Aikins (2004) who argues that the aforementioned formulation process is arguably more subconscious in nature, and thus the term epistemic beliefs will be adopted in this manuscript.
Moreover, while the debate on the domain-generality versus domain-specificity of EBs is still on-going, an increasing number of recent empirical evidence (e.g., Schommer-Aikins and Duell, 2013; Löfström and Pursiainen, 2015) seems to suggest that EBs are more likely domain-specific, that is they are specific to the discipline in which they are situated in. In the context of mathematics education, mathematical epistemic beliefs (MEBs henceforth) are thus framed as beliefs about the nature of mathematical knowledge and how mathematical knowledge is acquired.
Exploring teachers’ MEBs is crucial, particularly when a growing number of empirical studies over the past two decades have shown the potential role of teachers’ MEBs in shaping their mathematics teaching (e.g., Stipek et al., 2001; Rott, 2020), and hence their students’ mathematics learning outcomes and perceptions of the subject (Schommer-Aikins et al., 2005). However, one of the specific areas that is still significantly under-researched is the extent to which teachers’ MEBs are affected by their personal characteristics, specifically their gender. According to Clark et al. (2014, p. 253), citing Rothenberg (2007), “elements of […] gendered experiences pervade our perspectives and associated behaviors.” Thus, gender becomes an important teacher characteristic to take into account when examining teachers’ beliefs. It can be argued that if there was a significant gender difference in MEBs, then it would be important for both in- and pre-service teachers to reflect on as part of their instructional practice and training.
The current study thus set out to ascertain whether gender differences in teachers’ MEBs exist, and the extent to which gender can predict these beliefs. Such focus will provide an important and original contribution to this international research field. In the following sections, the nature of EBs, specifically MEBs, and existing research on gender-related differences therein will be discussed in more detail.
Theoretical Perspectives
Nature of (Mathematical) Epistemic Beliefs
As previously stated, EBs can generally be described as beliefs concerning the nature of knowledge and knowledge acquisition. In their seminal and widely-cited review of six pioneering epistemic studies (i.e., Perry, 1970; Belenky et al., 1986; Schommer, 1990; Kuhn, 1991; Baxter Magolda, 1992; King and Kitchener, 1994), Hofer and Pintrich (1997) highlight four recurring themes, namely two EBs relating to the nature of knowledge (structure of knowledge and stability of knowledge) and two EBs concerning knowledge acquisition (source of knowledge and knowledge justification). There is a high degree of overlap, however, between source of knowledge and knowledge justification; hence in the rest of this article, they are discussed together as source of knowledge. Each of these EBs is traditionally described as either sophisticated (e.g., knowledge as unrelated, fixed and authority as source of knowledge) or naïve (e.g., knowledge as interconnected, ever changing, and reasoning as source of knowledge) following the tradition set by Schommer (1990). In the context of this study, the author joins calls to move away from using these labels which carry with them value-laden judgements (Fives and Buehl, 2017), and instead the study will use labels as drawn from philosophical perspectives to describe the different EBs concerning the structure, stability and source of (mathematical) knowledge as detailed below.
Structure of (Mathematical) Knowledge
The structure of knowledge belief is concerned with the organisation of knowledge. In the context of mathematics, this belief can be framed as whether mathematical knowledge is a collection of unrelated (or related) mathematical concepts and skills. At one end of the spectrum, there is the instrumentalist view which perceives mathematics as a collection of unrelated facts, rules and skills (Ernest, 1989). Such instrumentalist view – or as the current study prefers to call isolationist view for clarity – is in stark contrast to the connectionist perspective which views mathematics as a network of connections of different mathematical concepts and skills (Askew, 2002). In the context of mathematics teaching and learning, it is plausible to conjecture that isolationist teachers would be more likely to teach mathematical concepts and skills in discrete units while their connectionist counterparts would be more likely to try to make meaningful connections between mathematical concepts and skills in their teaching.
Stability of (Mathematical) Knowledge
The stability of knowledge belief is concerned with the extent to which knowledge is fixed and permanent or evolving. Leading philosophers of mathematics, such as Lerman (1990) and Ernest (1995, 2014) generally describe the former view as absolutist, where mathematical knowledge is viewed as “timeless truths” (Lerman, 1990, p. 54) and hence highly stable, permanent and fixed. At the other end of the spectrum, fallibilism describes the belief that mathematical knowledge is indeed “fallible and eternally open to revision, both in terms of its proofs and its concepts” (Ernest, 1995, p. 452). In the context of mathematics teaching and learning, it is thus conceivable that mathematics teachers who subscribe to the absolutist perspective might be more likely to teach in a way that encourage their students to memorise facts and formula, treating them as immutable. On the other hand, fallibilist teachers would be more likely to encourage their students to be critical of any given facts and encourage them to prove their answers by using different methods to arrive at an answer.
Source of (Mathematical) Knowledge
The source of knowledge belief is concerned with one’s belief about where knowledge comes from or how it is acquired. The Platonist and constructivist perspectives represent two key stances within this belief. Platonists would argue that mathematical knowledge exists “outside space and time [and] independent of any consciousness, individual or social” (Hersh, 1997, p. 9). To put it differently, mathematical knowledge has always been out there waiting to be discovered. According to this perspective, the notion of, for example, one plus one equal two has existed even before the existence of humans. Humans merely discover mathematical knowledge that has already existed. On the other hand, constructivist would argue that mathematics is in fact a social construction, invented by humans, and this invention is an on-going process (Lerman, 1990; Ernest, 2014). While the thought of waking up one morning to learn that mathematicians have decided that one plus one will no longer equal two is hard to imagine, constructivists would stand firm in their belief, at least, philosophically, that mathematical knowledge is constructed socially and that any change in mathematical knowledge and facts would thus theoretically be possible. In the context of mathematics teaching and learning, it is thus conceivable that mathematics teachers who subscribe to the Platonist perspective might be more likely to believe that the authority (e.g., teachers and textbooks) are the source of knowledge. The role of the students is limited to learning one particular method(s) approved by that authority. On the other hand, constructivist teachers would be more likely to encourage their students to construct their own knowledge and find different ways to solve mathematical problems where mathematical discussions, collaborations and debates are encouraged, and where different methods, solutions and answers are invited.
It is worth noting that within each of these three MEBs, the contrasting positions (e.g., isolationist vs connectionist) are not binary positions, and should be seen more as a spectrum where an individual’s MEB could exist at any point along the continuum of that specific MEB.
Gender Differences in Teachers’ Mathematical Epistemic Beliefs
Not only did the current study seek to examine teachers’ MEBs, it also wanted to do so through the lens of gender. Given the increasing number of empirical studies pointing to gender differences among students (favouring boys) across a wide range of variables, ranging from mathematics self-efficacy (Ganley and Lubienski, 2016; Markovits and Forgasz, 2017) to mathematics anxiety (Griggs et al., 2013; Hill et al., 2016), it can then be argued that males and females appear to develop different relationships with, and thus different perceptions of, mathematics. These differences in beliefs are arguably not caused cognitively; rather, following Hofer and Pintrich’s (1997) view, it can be claimed that any differences between males’ and female’s beliefs are a consequence of different genders “providing differing opportunities, affordances, and constraints on development” of personal epistemology (p. 129).
Potential gender-related patterns in EBs have been widely researched, but mainly in relation to students’ EBs (e.g., Marzooghi et al., 2008; Phan, 2008; Tang, 2010). Of the very few empirical studies that explored teachers’ EBs in relation to gender, the majority of the studies (e.g., Chan, 2004; Lee et al., 2013; Baydar, 2020) are not specific to mathematics. While several empirical studies that explored mathematics teachers’ beliefs through the gender lens were found (e.g., Li, 2004; Clark et al., 2014; de Kraker-Pauw et al., 2016), these beliefs are concerned with, for example, mathematics teaching and learning in general or beliefs about students’ mathematical abilities, and not related to MEBs. Given an increasing amount of empirical evidence that supports the view that EBs are domain-specific (e.g., Choi and Kwon, 2012; Schommer-Aikins and Duell, 2013), the lack of attention to potential gender-related patterns in mathematics-specific teacher EBs is a concern.
Of the three MEB empirical studies identified, findings are inconclusive. For example, using a five-point Likert Epistemological Beliefs scale, Ertekin et al.’s (2009) survey study of 247 male and 273 female secondary mathematics pre-service teachers in Turkey found that, in relation to the eight-item “Belief that a Single Truth Exists” sub-scale, female secondary mathematics pre-service teachers were significantly more likely than their male counterparts to believe that knowledge is fixed and absolute. While Ertekin et al. (2009) did not offer an explanation for this gender difference, they conclude broadly that “certain cognitive, sociological or psychological effects based on gender could generate different epistemological understandings” (p. 192).
However, no gender differences were found in the other studies. Specifically, Nisbet and Warren’s (2000) survey study of 398 in-service primary teachers in Australia found no significant gender differences in teachers’ responses to the five-item “A static view of mathematics” belief sub-scale (including items, such as “Today’s mathematics is no different from mathematics of long ago”). Similarly, Handel’s (2002) study of 122 secondary mathematics teachers in Australia also found no significant difference in the way male and female teachers responded to the “Maths consists of unrelated topics” survey item. Regardless of gender, the teachers viewed mathematics as a collection of related topics.
It is worth highlighting that these studies varied in key aspects, for example, teacher status (in-service vs pre-service), school level (primary teachers vs secondary teachers), and more importantly the instruments adopted to capture teachers’ beliefs. Thus, the differences in findings across the studies are arguably to be expected.
Other Characteristics Potentially Influencing Teachers’ Mathematical Epistemic Beliefs
In addition to focusing on teachers’ gender as a potential variable that could shape teachers’ MEBs, the current study is also interested in exploring the potential influence of other variables, namely the socio-economic setting of the schools; teachers’ teaching experience level, and their education level. Once again, of the very few empirical studies that have explored the potential roles of these variables in shaping teachers’ MEBs, all of them are very dated. That the current study sets out to offer latest findings on the potential of these factors provides further justification for the study.
The socio-economic setting of the schools. Drawing from Pintrich (2002), Conley et al. (2004, p. 201) attribute any significant differences in EBs to the possible mechanisms for class effects where “there might be class differences in the […] knowledge structures […] that might emerge from the nature of interactions with people and institutions in different contexts” which could lead to people in different socio-economic classes having “different ways of representing knowledge and ways of thinking that could create group differences in epistemological thinking.” That said, the empirical findings have so far not supported this perspective. For example, Handel’s (2002) study of 122 secondary school mathematics teachers in Australia found no significant differences in the Structure of Mathematical Knowledge belief of teachers teaching in Disadvantaged Schools Program (DSP) schools versus non-DSP schools. Regardless of the socio-economic setting of the schools, the teachers appeared to endorse making connections between different units of mathematics. Similarly, Arredondo and Rucinski’s (1996) study of 126 teachers and principals from primary and secondary schools in Chile found no significant difference in the way private and state school teachers responded to the Knowledge is certain scale. Regardless of the socio-economic setting of the schools, the teachers appeared to subscribe to the view that knowledge is fixed. The current study will thus re-examine the role of socio-economic setting of the schools in shaping teachers’ MEBs by using latest research data to contribute to this on-going debate.
Teaching Experience Level
Chai et al.’s (2009) study of 413 pre-service teachers in Singapore found a significant difference in the teachers’ Source of Mathematical Knowledge belief whereby teachers at the start of their 9-month teacher preparation programme (i.e., when they were less experienced) appeared to have a significantly stronger belief that knowledge lies in external authorities than when they became more experienced at the end of the course. Such difference in teachers’ beliefs among teachers of different teaching experience levels is also found in Arredondo and Rucinski’s (1996) study (as previously discussed) though in their study it is the principals (i.e., more experienced teachers) who appeared to have a significantly stronger belief than ordinary teachers (i.e., less experienced teachers) that external authorities are the main source of knowledge. Perry et al. (1999) argued that differences in teachers’ beliefs could be explained by the fact that more experienced teachers might “have sufficient experience and position power to enable them to look beyond basic survival in the classroom and at least contemplate that there might be other ways of learning and teaching mathematics” (p. 49). Elsewhere, differences in beliefs about mathematics among teachers of different teaching experience levels, however, were not found. Nisbet and Warren’s (2000) study of 398 primary school teachers in Australia, for example, found no significant difference in the way teachers with 0–5; 6–10; 11–15; and over 15 years of teaching experience responded to the A static view of teaching mathematics scale, comprising items, such as “The good thing about mathematics is that it is an unchanging subject” and “Today’s mathematics is no different from mathematics of long ago.” Again, the current study sets out to examine the role of teaching experience in shaping teachers’ MEBs using latest research data to contribute to this on-going debate.
Teachers’ Education Level
Another variable that could provide insights into the development of teachers’ MEBs is the level of their education. In Schommer’s (1998) study of 418 adults from 170 occupations in the United States, a significant difference in the way those with only a high school education, an undergraduate education, and a graduate education responded to the Stability of Knowledge scale was found whereby the more educated the participants, the less likely they were to believe that knowledge is fixed, for example. Yet, Nisbet and Warren’s (2000) study (as previously discussed) which collected data from teachers of different (mathematics) educational qualification levels (e.g., those with Year 10, Year 12, teacher education course in mathematics, University mathematics qualifications) reported no significant difference in their response to the A Static View of Mathematics scale, comprising items, such as “The good thing about mathematics is that it is an unchanging subject” and “Today’s mathematics is no different from mathematics of long ago.” Regardless of the teachers’ (mathematics) education qualification levels, they did not have a specific view on this belief.
The Current Study
Drawing from the research gaps as previously outlined, the current study thus set out to address the following research questions:
1. Are there significant gender differences in teachers’ mathematical epistemic beliefs?
2. How much of teachers’ mathematical epistemic beliefs are explained by gender, socio-economic setting, years of teaching experience and highest attained educational qualification?
Methods
Design of the Study and Instrument
The study drew on survey data collected from primary teachers in Thailand as part of a larger study (Trakulphadetkrai, 2012) using the 22-item 5-point Likert scale Thai Teachers’ Mathematics Education-related Beliefs (TTMEB) questionnaire developed by Trakulphadetkrai (2012). That the study collected data from teachers in Thailand is justified by the fact that teachers’ MEBs have been shown to be socio-culturally influenced (Felbrich et al., 2012; Xenofontos, 2018). Thus, one cannot assume that the findings of the few existing studies on gender differences in teachers’ MEBs (which were conducted in Australia and Turkey, for example) could be applied unproblematically to Thai teachers.
The questionnaire was constructed using a combination of relevant items from existing survey instruments (e.g., Nisbet and Warren, 2000; Barkatsas and Malone, 2005; Ernest, 2008) and items developed from observations of primary Mathematics lessons and interviews with eight primary teachers in four Thai state primary schools. By combining existing survey items and those newly constructed items using fieldwork data, this gave a 99-item pilot survey instrument, covering 16 aspects of teachers’ mathematics education-related beliefs, grouped under four broad categories i.e., (1) beliefs concerning the nature of mathematical knowledge (“Source of Mathematical Knowledge”; “Stability of Mathematical Knowledge”; “Structure of Mathematical Knowledge”); (2) beliefs concerning mathematics learning (“Roles of Learners”; “Pupils’ Autonomy”; “Prior Knowledge”; “Personal Relevance”); (3) beliefs concerning mathematics teaching (“Roles of Teachers”; “Classroom Organisation”; “Classroom Activities”; “Assessment”; “Intended Instructional Outcome”; “Use of Mathematics Textbooks”); and (4) beliefs concerning constraints to mathematics teaching (“Classroom Mobility”; “Time”; “Exams and Math Core Curriculum”).
The survey instrument was piloted with 98 primary teachers in Thailand. The exploratory factor analysis (EFA) was then performed on the pilot survey data to reduce the number of survey items from the original 99 items (covering 16 aspects of teachers’ mathematics education-related beliefs) to just 26 items which provides a meaningful, robust and interpretable set of factors. One final round of EFA was performed on the main dataset as drawn from 745 survey respondents, and this helped to further reduce the number of survey items from 26 to 22 [See Trakulphadetkrai (2012) for full discussions on the EFA processes adopted in the study]. While the majority of these items were related to eight beliefs concerning mathematics teaching and learning (i.e., “Source of Mathematical Skills,” “Constraints to Mathematics Teaching,” “Classroom Authority,” “Mathematical Proficiency Preference” and “School Mathematics as Relevant Experience”), six survey items were related specifically to the three epistemic belief scales, and teachers’ response to these items will form the focus of this manuscript. Specifically, the Structure of Mathematical Knowledge scale consists of the following two items: “New mathematical knowledge is built independently of all previous ones” and “When I teach new topics in mathematics, I always make a fresh start.” The Stability of Mathematical Knowledge scale consists of “Today’s mathematical concepts are no different from those of long ago” and “Basic mathematical facts will always remain exactly the same,” while the Source of Mathematical Knowledge scale consists of “Mathematical concepts existed even before the existence of human beings” and “Mathematical concepts are not created, but discovered.” For each of these items, “1” indicates “Strongly Agree” while “5” indicates “Strongly Disagree.”
The wording of these survey items was phrased so that a very low score on the Structure of Mathematical Knowledge scale (i.e., an average score that is closer to 1) indicates isolationist teachers who firmly believe that different aspects or topics of mathematics are unrelated. A very high score on this scale (i.e., an average score that is closer to 5) indicates connectionist teachers who strongly believe in the interconnectedness of mathematical topics. In relation to the Stability of Mathematical Knowledge scale, a very low score on this scale indicates absolutist teachers who firmly believe that mathematical knowledge is permanent and fixed. On the other hand, teachers who score very highly on this scale would be perceived as fallibilist, subscribing to the view that mathematical knowledge is evolving. Finally, a very low score on the Source of Mathematical Knowledge scale implies Platonist teachers who strongly believe that mathematical knowledge has always been out there waiting to be discovered. The opposite is true for constructivist teachers who score very highly on this scale as they subscribe to the view that mathematical knowledge is created.
Participants
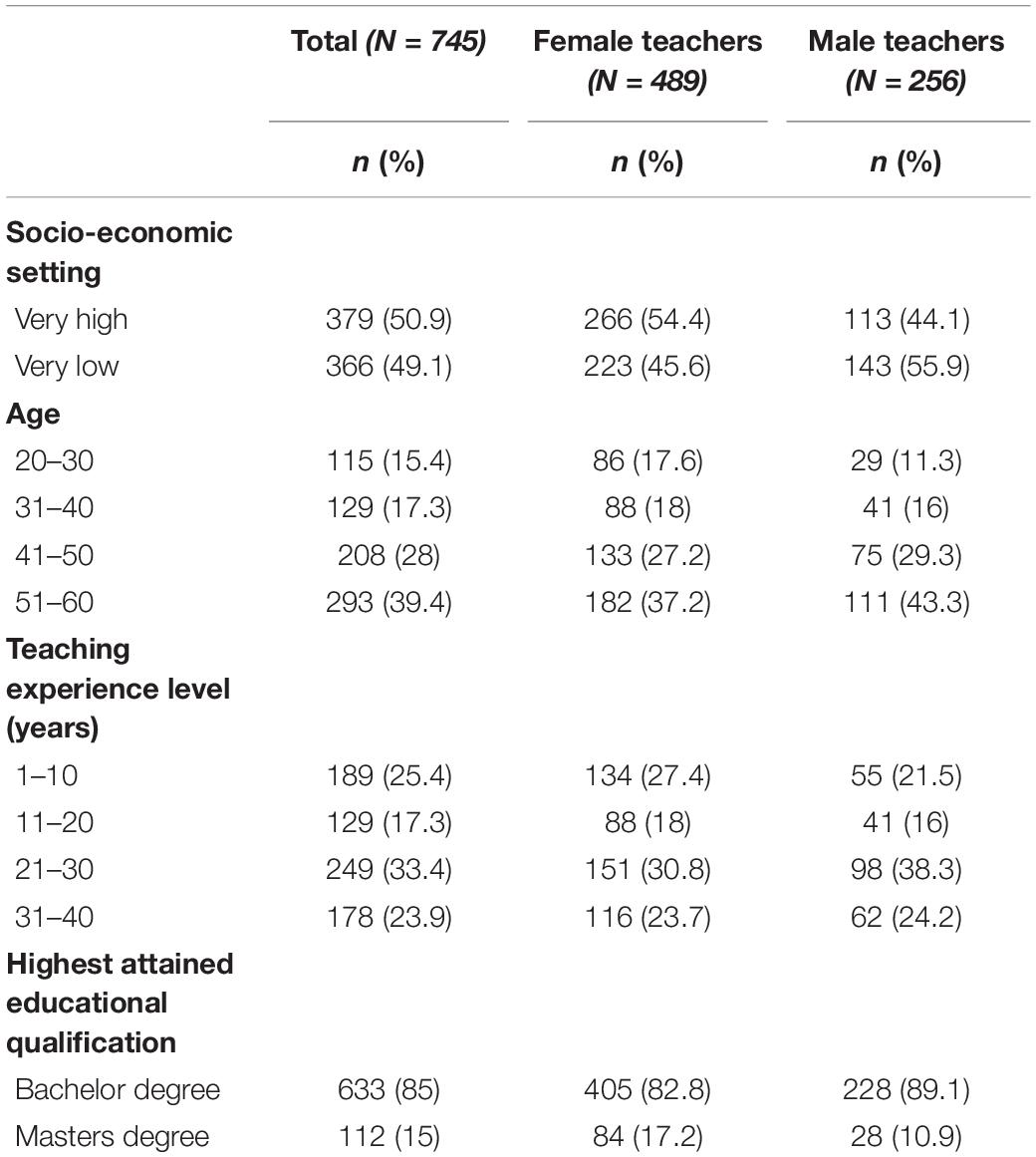
To ensure the representativeness of the sample, purposive sampling strategy was employed whereby 500 primary teachers teaching in provinces in each of the two socio-economic settings in Thailand were asked to complete the final TTMEB survey, totalling 1,000 teachers. The two socio-economic regions were classified as very high and very low, using the United Nations Development Programme’s (UNDP) Human Development Index (HDI), a well-established socio-economic status indicator (UNDP, 2007). The survey was completed by 745 teachers, resulting in a 74.5% response rate. Around 63.64% of these participants were female (N = 489) and 36.36% male (N = 256). The proportion of male and female teachers across the different age bands, teaching experience levels and academic qualifications were similar. A summary of these personal characteristics can be found in Table 1. The survey was e-mailed to teachers as a Word attachment, accompanied by an information sheet explaining the aim of the study and explaining that by completing and returning the survey, participants gave their consent for their anonymised data to be used in the study.
Data Analysis
To address the first research question, an Independent-samples t-test was performed to ascertain the extent to which male and female primary teachers in Thailand differ in their beliefs on the structure, stability and source of mathematical knowledge. The analysis was two-tailed as no specific predictions were made about which gender was more likely to believe in each of the three beliefs (Field, 2017). Drawing from the central limit theorem, Swift and Piff (2014) argue that for larger sample size (> 30), the distribution of the sample mean approximates a normal distribution. Given the study’s sample size (N = 745), a decision was thus made to use parametric tests.
To address the second research question, multiple linear regression was separately performed on each of the three mathematical epistemic beliefs (i.e., the dependent variables). This analysis was employed to measure the extent to which these three beliefs could be explained by gender, socio-economic region, years of teaching experience and highest attained educational qualification. For all of these analyses, all four predictors were entered at the same time in one block as there is no theoretical justification to suggest that one particular predictor can explain more variance in the beliefs than other factors. The four predictors met the no multicollinearity assumption as their Variance Inflation Factor (VIF) are below 10 (Hair <suffix>Jr.</suffix> et al., 1995): gender (1.02), socio-economic setting (1.01), years of teaching experience (1.01), and highest attained educational qualification (1.01). Scatter plots indicated a linear relationship between each of the three dependent variables and the four predictors. P-P plots indicated that the standardised residuals of the three dependent variables were relatively normally distributed. The sample size of 745 teachers met the sample size assumption for regression (i.e., 8 x number of independent variables + 50; Green, 1991). Finally, the predictors were either continuous (actual number of years of teaching experience) or binary (gender, socio-economic setting, and highest qualification). The three dependent variables are continuous as individual ordinal item scores were combined and standardised to calculate the respective total score of the three belief scales.
Results
Research Question 1 (“Are There Significant Gender Differences in Teachers’ Mathematical Epistemic Beliefs?”)
The only significant gender difference [t(452) = −4.76, p < 0.001] was found in the Structure of Mathematical Knowledge belief (see Table 2). While both male and female teachers appeared to be connectionist, subscribing to the view that different areas of mathematical knowledge are related, female teachers held this belief slightly more firmly than their male counterparts. Such statistically significant gender difference was, to an extent, to be expected given the study’s large sample size. However, in real terms, the difference was very small (0.29) and is arguably negligible. This is confirmed by the small effect size (Hedges’ g = 0.38).

Table 2. Results of the independent-samples t-test comparing female and male teachers on the three mathematical epistemic beliefs.
There did not appear to be any significant difference (t(743) = −1.08, p > 0.05) in the way male and female teachers viewed the Stability of Mathematical Knowledge belief. Regardless of their gender, Thai primary teachers appeared to be on the borderline in relation to this belief given their mean scores which were very close to the middle Likert scale score of 3. Similarly, there also did not appear to be any significant difference (t(743) = −0.44, p > 0.05) in the way male and female teachers viewed the Source of Mathematical Knowledge belief. Regardless of their gender, Thai teachers appeared to be Platonist-oriented, believing that knowledge has always existed and waiting to be discovered, instead of being created.
Across all three beliefs, the standard deviations were relatively low in each of the two cohorts, indicating that variation in the beliefs within both groups was low.
Research Question 2 (“How Much of Teachers’ Mathematical Epistemic Beliefs Are Explained by Gender, Socio-Economic Setting, Years of Teaching Experience and Highest Attained Educational Qualification?”)
Structure of Mathematical Knowledge
In relation to teachers’ Structure of Mathematical Knowledge belief, the multiple regression analysis indicated that the four predictors together explained around 5.8% of the variance of the belief (see Table 3). Despite it being statistically significant, the variance is very small in real terms.
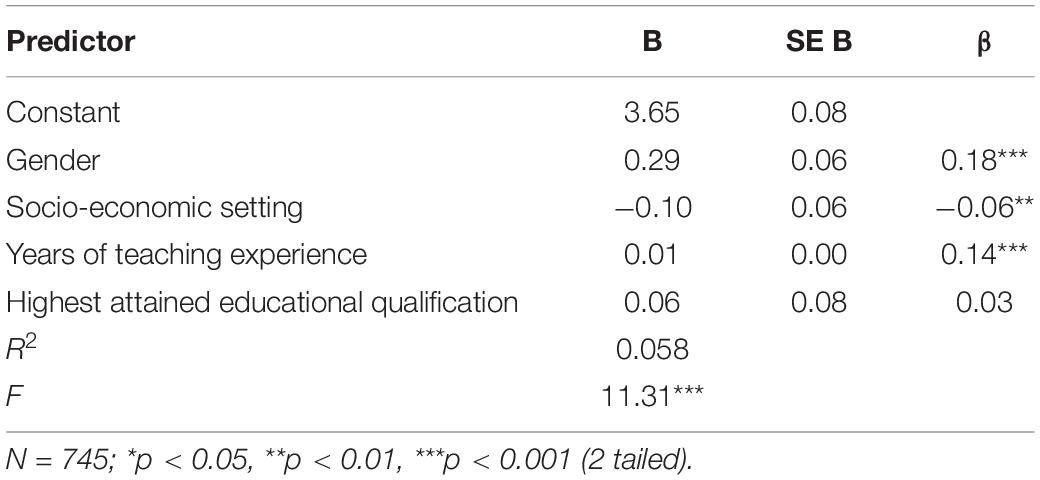
Table 3. Multiple regression analysis predicting the Structure of Mathematical Knowledge belief from gender, socio-economic setting, years of teaching experience, and highest attained education qualification.
When the predictors were examined individually, it was found that while the education level failed to predict the Structure of Mathematical Knowledge belief, gender, socio-economic setting and years of teaching experience were significant predictors. Specifically, a unit change in gender (i.e., the change from male to female) resulted in an increase of 0.29 in the obtained average 5-point Likert score on this belief scale, suggesting that female teachers held a marginally stronger connectionist perspective than their male counterparts, viewing different aspects of mathematical knowledge as being related. Regarding socio-economic setting, a unit change in this independent variable (i.e., the change from the very high to the very low socio-economic setting) resulted in a decrease of 0.10 in the obtained average score on this belief scale, suggesting that teachers teaching in the very low socio-economic setting, on average, are only marginally less likely to subscribe to the connectionist perspective. In terms of years of teaching experience, for every extra year of teaching experience, additional 0.01 would be added to the Structure of Mathematical Knowledge score, implying that the more experienced a teacher is, the more connectionist they become. However, an increase of 0.01 in the 5-point Likert scale score, while statistically significant, is arguably negligible in real terms.
Stability of Mathematical Knowledge
The results of the regression (see Table 4) indicated that while the four predictors explain around 1.3% of the variance of the Stability of Mathematical Knowledge belief, this was not statistically significant. When the predictors were examined individually, it was found that none of the predictors significantly predicted the Stability of Mathematical Knowledge belief, except for socio-economic setting. Specifically, a unit change in this independent variable (i.e., the change from the very high to the very low socio-economic setting) resulted in a decrease of 0.13 in the obtained average score on this belief scale, suggesting that teachers teaching in the very low socio-economic setting, on average, held a marginally stronger belief that mathematical knowledge is permanent and fixed than their counterparts teaching in the very high socio-economic setting.
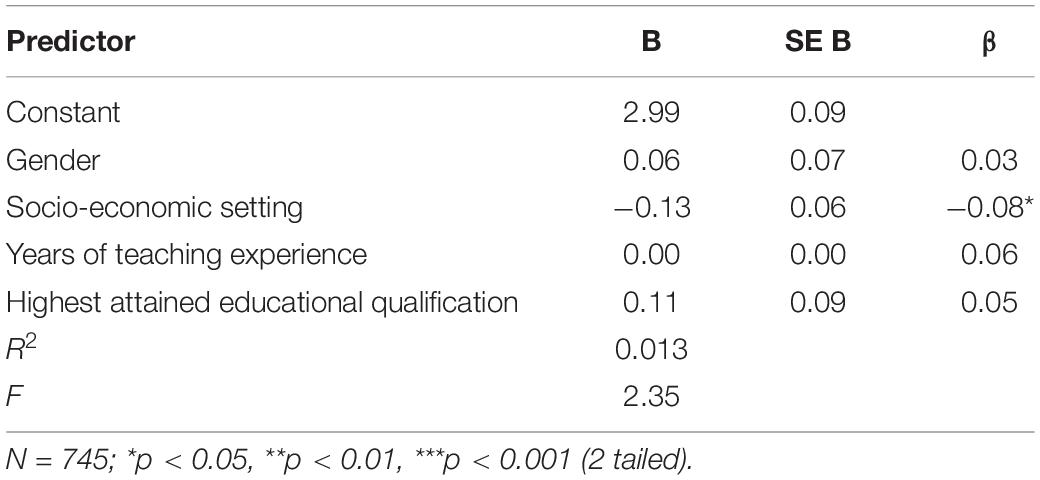
Table 4. Multiple regression analysis predicting the Stability of Mathematical Knowledge belief from gender, socio-economic setting, years of teaching experience and highest attained education qualification.
Source of Mathematical Knowledge
The results of the regression (see Table 5) indicated that the four predictors together explained around 2.1% of the variance of the belief. Despite it being statistically significant, the variance is very small in real terms. When the predictors were examined individually, it was found that only socio-economic setting, and years of teaching experience were able to significantly predict the Source of Mathematical Knowledge belief. Specifically, a unit change in the socio-economic setting variable (i.e., the change from the very high to the very low socio-economic setting) resulted in a decrease of 0.15 in the obtained average score on this belief scale. This suggests that teachers teaching in the very low socio-economic setting, on average, held a marginally weaker belief that mathematical knowledge has always been out there waiting to be discovered than their counterparts teaching in the very high socio-economic setting. Finally, for every extra year of teaching experience, additional 0.01 would be added to the Source of Mathematical Knowledge score, implying that the more experienced a teacher is, the weaker their belief that mathematical knowledge has always been out there and waiting to be discovered. However, an increase of 0.01 in the 5-point Likert scale score, while statistically significant, is arguably negligible in real terms.
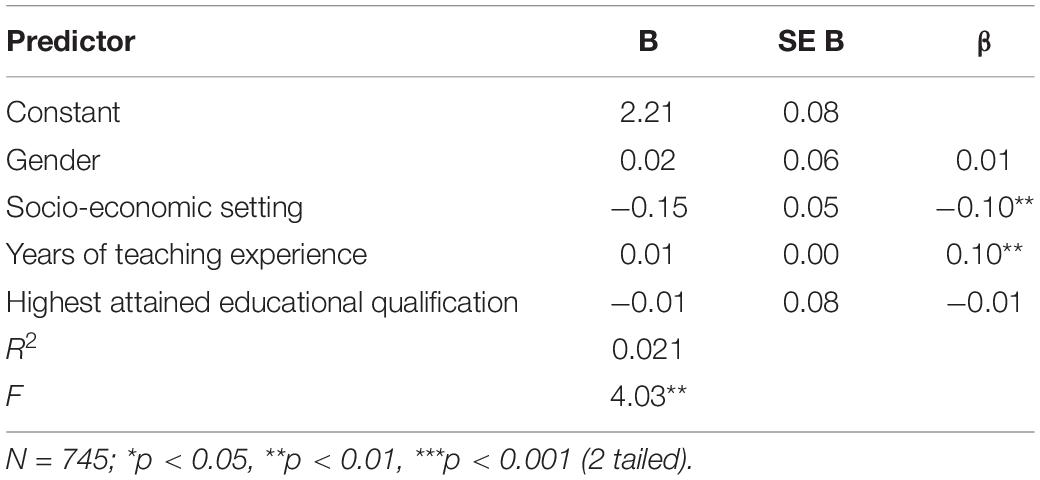
Table 5. Multiple regression analysis predicting the source of mathematical knowledge belief from gender, socio-economic setting, years of teaching experience, and highest attained education qualification.
Discussion
The findings reveal a very limited to no effect of gender on teachers’ mathematical epistemic beliefs. Specifically, while gender was a significant predictor of teachers’ Structure of Mathematical Knowledge belief, its effect size is very small to the point of being negligible in real terms. Such statistically significant gender difference was, to an extent, to be expected given the study’s large sample size. In the context of the Thai primary teachers in the current study, both male and female teachers appeared to be connectionist, subscribing to the view that aspects of mathematical knowledge are related. This finding is in line with that of Handel’s (2002) study which found no significant gender differences in the way the teachers responded to the “Maths consists of unrelated topics” survey item.
As briefly noted, gender failed to explain variation in Stability and Source of Mathematical Knowledge beliefs (and hence there being no significant gender differences in these two beliefs). In the context of this study, the teachers – regardless of their gender – appeared to remain neutral in relation to the Stability of Mathematical Knowledge belief. In relation to the Source of Mathematical Knowledge belief, they very much believed that mathematical knowledge has always existed, waiting to be discovered. Such lack of significant gender differences was largely in line with previous studies’ findings (e.g., Nisbet and Warren, 2000; Chan, 2004; Lee et al., 2013) though it was inconsistent with the finding of Ertekin et al.’s (2009) study which concluded that male teachers were more likely to believe that mathematical knowledge is fixed and absolute.
The present study also examined three other predictors, namely socio-economic setting of the schools, teachers’ years of teaching experience and their education level. While education level did not seem to predict any of the beliefs, socio-economic setting of the schools and the number of years of teaching experience did. Socio-economic setting of the schools, in particular, was found to significantly predict all three beliefs though with very small effects. Specifically, teachers teaching in the very high socio-economic setting appeared to hold a marginally stronger belief that mathematical knowledge is a collection of related topics and skills; is more likely to change; and is more likely to have been created than waiting to be discovered. This finding is thus consistent with the perspectives of Conley et al. (2004) who attributed any significant differences in EBs to the possible mechanisms for class effects. In relation to the Structure of Mathematical Knowledge belief specifically, this finding is, however, inconsistent with the finding of Handel’s (2002) study of 122 secondary school mathematics teachers in Australia. Regardless of the setting (Disadvantaged Schools Program (DSP) schools versus non-DSP schools), the teachers appeared to endorse making connections within different units of mathematics. Regarding the Stability of Mathematical Knowledge belief, the finding is also inconsistent with that of Arredondo and Rucinski’s (1996) study of 126 teachers and principals from primary and secondary schools in Chile, which found no significant difference in the way private and state school teachers responded to the Knowledge is certain scale. Regardless of the socio-economic setting of the school, the teachers in their study appeared to subscribe to the view that knowledge is fixed. Finally, in relation to the Source of Mathematical Knowledge belief, the current study has not been able to find any similar study to compare the findings with. That teachers in the very low socio-economic (and often rural) setting appeared to hold a significantly stronger belief than their counterparts teaching in the very high socio-economic (and often urban) setting in viewing mathematical knowledge as something that has always existed and waiting to be discovered or passed down to them could be explained by how Thai people living in the rural part of the country traditionally hold stronger cultural values (Komin, 1991). According to Hofstede et al. (2010), these cultural values include being respectful to authority figures, such as teachers, and expecting them to hand down knowledge. To question their authority or to challenge their knowledge would be considered rude. Arguably then, this means teachers teaching in the very low socio-economic and rural setting are more likely to view any form of knowledge as being passed down from them to their students as opposed to viewing knowledge as something for the students to attempt to construct themselves.
Regarding years of teaching experience, it appeared to have a small, but significant, effect on the Structure and Source of Mathematical Knowledge beliefs whereby the more experienced a teacher is, the less they viewed aspects of mathematics as being disconnected and the less they believed that mathematical knowledge has always been out there, waiting to be discovered. Specifically in relation to the former belief, this study’s finding is consistent with that of Handel’s (2002) study. It could be argued that when teachers become more experienced, they have a more holistic view of mathematics through having had more opportunities to make connections between aspects of mathematics, both between topics and skills and between school mathematics and the mathematics children experience in their everyday life. Regarding the Source of Mathematical Knowledge belief, this study’s finding resonates that of Chai et al.’s (2009) study which found a significant difference, whereby teachers at the start of their 9-month teacher preparation programme (i.e., when they were less experienced) appeared to have a significantly stronger belief that knowledge lies in external authorities than when they became more experienced at the end of the course. The current study’s finding also corroborates the findings of Arredondo and Rucinski’s (1996) study (as previously discussed) which reported a significant difference in the way principals and ordinary teachers responded to the Depend on authority item. The study found that principals (i.e., more experienced teachers) appeared to have a significantly stronger belief than ordinary teachers (i.e., less experienced teachers) that external authorities are the main source of knowledge. Overall, it could be conjectured that when teachers become more experienced, they are more likely to become critical of educational issues, such as government’s educational policies and curriculum, and are less likely to take things as given. When this mentality is translated to their mathematics teaching, it could encourage these teachers to teach mathematics without relying solely on external authorities like textbooks, and instead teaching children to learn mathematics through validating mathematical facts themselves.
Conclusion
As previously noted, the relationship between teachers’ MEBs and their gender is an under-researched area. The current study filled this gap in research and was able to use a large dataset to empirically demonstrate that gender has very little to no effect in shaping teachers’ MEBs. To an extent, this is promising as the study helps to dispel any myths about gender differences in the way males and females perceive mathematics, specifically the nature of mathematical knowledge. Given the potential role of teachers’ MEBs in shaping their mathematics teaching (e.g., Stipek et al., 2001; Rott, 2020), and hence their students’ mathematics learning outcomes and perceptions of the subject (Schommer-Aikins et al., 2005), it is somewhat reassuring to see that regardless of the gender of one’s (mathematics) teacher, their mathematical epistemic beliefs on the whole are similar. The findings of the current study also alerts us to the fact that when it comes to exploring factors that shape one’s beliefs, their exogenous characteristics, such as the socio-economic setting of where they live and work, should too be taken into account.
Given that the study’s survey data were collected from teachers in Thailand only, any generalisation of its findings in other socio-cultural contexts is limited. It would certainly be useful for more research to be done in other socio-cultural contexts and for cross-cultural comparisons to be made.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Ethics Statement
The studies involving human participants were reviewed and approved by University of Cambridge’s Faculty of Education. The patients/participants provided their written informed consent to participate in this study.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The author would like to thank the University of Reading for funding the Open Access fee for this article.
References
Arredondo, D. E., and Rucinski, T. T. (1996). “Epistemological beliefs of Chilean educators and school reform efforts,” in Paper Presented at the Tercer Encuentro National de Enfoques Cognitivos Actuales en Educacion, November 7-8, 1996, Santiago.
Barkatsas, A., and Malone, J. (2005). A typology of mathematics teachers’ beliefs about teaching and learning mathematics and instructional practices. Math. Educ. Res. J. 17, 69–90. doi: 10.1007/BF03217416
Baydar, A. (2020). Epistemological beliefs of preservice teachers. High. Educ. Stud. 10, 44–52. doi: 10.5539/hes.v10n3p44
Belenky, M. F., Clinchy, B. M., Goldberger, N. R., and Tarule, J. M. (1986). Women’s Ways of Knowing: The Development of Self, Voice and Mind. New York, NY: Basic Books.
Chai, C. S., Teo, T., and Lee, B. C. (2009). The change in epistemological beliefs and beliefs about teaching and learning: a study among pre-service teachers. Asia Pac. J. Teach. Educ. 37, 351–362. doi: 10.1080/13598660903250381
Chan, K. W. (2004). Preservice teachers’ epistemological beliefs and conceptions about teaching and learning: cultural implications for research in teacher education. Aust. J. Teach. Educ. 29, 1–13. doi: 10.14221/ajte.2004v29n1.1
Chinn, C. A., Buckland, R. W., and Samarapungavan, A. (2011). Expanding the dimensions of epistemic cognition: arguments from philosophy and psychology. Educ. Psychol. 46, 141–167. doi: 10.1080/00461520.2011.587722
Choi, J., and Kwon, N. Y. (2012). The general and domain-specific epistemological beliefs of Korean preservice mathematics teachers. Asia Pac. Educ. Res. 21, 353–364.
Clark, L. M., DePiper, J. N., Frank, T. J., Nishio, M., Campbell, P. F., Smith, T. M., et al. (2014). Teacher characteristics associated with mathematics teachers’ beliefs and awareness of their students’ mathematical dispositions. J. Res. Math. Educ. 45, 246–284. doi: 10.5951/jresematheduc.45.2.0246
Conley, A. M. M., Pintrich, P. R., Vekiri, I., and Harrison, D. (2004). Changes in epistemological beliefs in elementary science students. Contemp. Educ. Psychol. 29, 186–204. doi: 10.1016/j.cedpsych.2004.01.004
de Kraker-Pauw, E., van Wesel, F., Verwijmeren, T., Denessen, E., and Krabbendam, L. (2016). Are teacher beliefs gender-related? Learn. Individ. Dif. 51, 333–340. doi: 10.1016/j.lindif.2016.08.040
Depaepe, F., De Corte, E., and Verschaffel, L. (2016). “Mathematical epistemological beliefs,” in Handbook of Epistemic Cognition, eds J. A. Greene, W. A. Sandoval, and I. Braten (New York, NY: Routledge), 147–164.
Ernest, P. (1989). “The impact of beliefs on the teaching of mathematics,” in Mathematics Teaching: The State of the Art, ed. P. Ernest (New York, NY: Falmer Press), 249–253.
Ernest, P. (1995). Values, gender and images of mathematics: a philosophical perspective. Int. J. Math. Educ. Sci. Technol. 26, 449–462. doi: 10.1080/0020739950260313
Ernest, P. (2014). “What is mathematics, and why learn it?,” in Masterclass in Mathematics Education, eds P. Andrews and T. Rowland (London: Bloomsbury), 3–14. doi: 10.5040/9781350284807.ch-001
Ertekin, E., Dilmaç, B., Delice, A., and Aydin, E. (2009). Teacher trainees’ epistemological beliefs: effects of gender, institution, and discipline. New Educ. Rev. 18, 184–196.
Felbrich, A., Kaiser, G., and Schmotz, C. (2012). The cultural dimension of beliefs: an investigation of future primary teachers’ epistemological beliefs concerning the nature of mathematics in 15 countries. ZDM 44, 355–366. doi: 10.1007/s11858-012-0418-x
Fives, H., and Buehl, M. M. (2017). “The function of beliefs: teachers’ personal epistemology on the pinning block,” in Teachers’ Personal Epistemologies: Evolving Models for Informing Practice, eds G. Schraw, J. L. Brownlee, L. Olafson, and M. V. V. Brye (Charlotte, NC: Information Age Publishing Inc), 25–54.
Ganley, C. M., and Lubienski, S. T. (2016). Mathematics confidence, interest, and performance: examining gender patterns and reciprocal relations. Learn. Individ. Dif. 47, 182–193. doi: 10.1016/j.lindif.2016.01.002
Green, S. B. (1991). How many subjects does it take to do a regression analysis? Multiv. Behav. Res. 26, 499–510. doi: 10.1207/s15327906mbr2603_7
Greene, J. A., Sandoval, W. A., and Braten, I. (2016). “An introduction to epistemic cognition,” in Handbook of Epistemic Cognition, eds J. A. Greene, W. A. Sandoval, and I. Braten (New York, NY: Routledge), 1–16. doi: 10.4324/9781315795225
Griggs, M. S., Rimm-Kaufman, S. E., Merritt, E. G., and Patton, C. L. (2013). The Responsive Classroom approach and fifth grade students’ math and science anxiety and self-efficacy. Sch. Psychol. Q. 28, 360–373. doi: 10.1037/spq0000026
Hair, J. F. Jr., Anderson, R. E., Tatham, R. L., and Black, W. C. (1995). Multivariate Data Analysis. New York, NY: Macmillan Publishing Company.
Handel, B. P. (2002). “Teachers’ mathematical beliefs and gender, faculty position, teaching socio-economic area, teaching experience and academic qualifications,” in Paper Presented at the Second Biennial Self-Concept Enhancement and Learning Facilitation (SELF) Research Centre International Conference, August 6-8, 2002, Sydney, NSW.
Hersh, R. (1997). What is Mathematics, Really?. Oxford: Oxford University Press. doi: 10.1515/dmvm-1998-0205
Hill, F., Mammarella, I. C., Devine, A., Caviola, S., Passolunghi, M. C., and Szűcs, D. (2016). Maths anxiety in primary and secondary school students: gender differences, developmental changes and anxiety specificity. Learn. Individ. Dif. 48, 45–53. doi: 10.1016/j.lindif.2016.02.006
Hofer, B. K., and Pintrich, P. R. (1997). The development of epistemological theories: beliefs about knowledge and knowing and their relation to learning. Rev. Educ. Res. 67, 88–140. doi: 10.3102/00346543067001088
Hofstede, G., Hofstede, G. J., and Minkov, M. (2010). Cultures and Organizations: Software of the Mind. New York, NY: McGraw-Hill.
King, P. M., and Kitchener, K. S. (1994). Developing Reflective Judgment: Understanding and Promoting Intellectual Growth and Critical Thinking in Adolescents and Adults. San Francisco, CA: Jossey-Bass.
Kitchener, R. (2002). Folk epistemology: an introduction. New Ideas Psychol. 20, 89–105. doi: 10.1016/S0732-118X(02)00003-X
Komin, S. (1991). Psychology of the Thai People: Values and Behavioral Patterns. Bangkok: National Institute of Development Administration.
Kuhn, D. (1991). The Skills of Argument. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511571350
Lee, J. C.-K., Zhang, Z., Song, H., and Huang, X. (2013). Effects of epistemological and pedagogical beliefs on the instructional practices of teachers: a Chinese perspective. Aust. J. Teach. Educ. 38, 120–146. doi: 10.14221/ajte.2013v38n12.3
Lerman, S. (1990). Alternative perspectives of the nature of mathematics and their influence on the teaching of mathematics. Br. Educ. Res. J. 16, 53–61. doi: 10.1080/0141192900160105
Li, Q. (2004). Beliefs and gender differences: a new model for research in mathematics education. Interchange 35, 423–445. doi: 10.1007/BF02698892
Löfström, E., and Pursiainen, T. (2015). Knowledge and knowing in mathematics and pedagogy: a case study of mathematics student teachers’ epistemological beliefs. Teach. Teach. Theory Pract. 21, 527–542. doi: 10.1080/13540602.2014.995476
Markovits, Z., and Forgasz, H. (2017). “Mathematics is like a lion”: elementary students’ beliefs about mathematics. Educ. Stud. Math. 96, 49–64. doi: 10.1007/s10649-017-9759-2
Marzooghi, R., Fouladchang, M., and Shemshiri, B. (2008). Gender and grade level differences in epistemological beliefs of Iranian undergraduate students. J. Appl. Sci. 8, 4698–4701. doi: 10.3923/jas.2008.4698.4701
Nisbet, S., and Warren, E. (2000). Primary school teachers’ beliefs relating to mathematics, teaching and assessing mathematics and factors that influences these beliefs. Math. Teach. Educ. Dev. 2, 34–47.
Perry, B., Howard, P., and Tracey, D. (1999). Head mathematics teachers’ beliefs about the learning and teaching of mathematics. Math. Educ. Res. J. 11, 39–53. doi: 10.1007/BF03217349
Perry, W. G. (1970). Forms of Intellectual and Ethical Development in the College Years: A Scheme. New York, NY: Holt, Rinehart and Winston.
Phan, H. P. (2008). Multiple regression analysis of epistemological beliefs, learning approaches and self-regulated learning. Electron. J. Res. Educ. Psychol. 6, 157–184. doi: 10.25115/ejrep.v6i14.1262
Pintrich, P. R. (2002). “Future challenges and directions for theory and research on personal epistemology,” in Personal Epistemology: The Psychology of Beliefs About Knowledge and Knowing, eds B. K. Hofer and P. R. Pintrich (Mahwah, NJ: Lawrence Erlbaum Associates), 389–414.
Rothenberg, P. S. (2007). Race, Class, and Gender in the United States: An Integrated Study. New York, NY: Worth Publishers.
Rott, B. (2020). Teachers’ behaviors, epistemological beliefs, and their interplay in lessons on the topic of problem solving. Int. J. Sci. Math. Educ. 18, 903–924. doi: 10.1007/s10763-019-09993-0
Rott, B. (2021). Inductive and deductive justification of knowledge: epistemological beliefs and critical thinking at the beginning of studying mathematics. Educ. Stud. Math. 106, 117–132. doi: 10.1007/s10649-020-10004-1
Schommer, M. (1990). Effects of beliefs about the nature of knowledge on comprehension. J. Educ. Psychol. 82, 498–504. doi: 10.1037/0022-0663.82.3.498
Schommer, M. (1998). The influence of age and education on epistemological beliefs. Br. J. Educ. Psychol. 68, 551–562. doi: 10.1111/j.2044-8279.1998.tb01311.x
Schommer-Aikins, M. (2004). Explaining the epistemological belief system: introducing the embedded systemic model and coordinated research approach. Educ. Psychol. 39, 19–29. doi: 10.1207/s15326985ep3901_3
Schommer-Aikins, M., and Duell, O. K. (2013). Domain specific and general epistemological beliefs their effects on mathematics. Rev. Investig. Educ. 31, 317–330.
Schommer-Aikins, M., Duell, O. K., and Hutter, R. (2005). Epistemological beliefs, mathematical problem solving beliefs, and academic performance of middle school students. Elem. Sch. J. 105, 290–304. doi: 10.1086/428745
Stipek, D. J., Givvin, K. B., Salmon, J. M., and MacGyvers, V. L. (2001). Teacher’s beliefs and practices related to mathematics instruction. Teach. Teach. Educ. 17, 213–226. doi: 10.1016/S0742-051X(00)00052-4
Swift, L., and Piff, S. (2014). Quantitative Methods. New York, NY: Palgrave Macmillan. doi: 10.1007/978-1-137-33794-8
Tang, J. (2010). Exploratory and confirmatory factor analysis of epistemic beliefs questionnaire about mathematics for Chinese junior middle school students. J. Math. Educ. 3, 89–105.
Trakulphadetkrai, N. V. (2012). An Exploratory Mixed-Method Study of Thai Primary School Teachers’ Beliefs Concerning Mathematical Knowledge, Its Learning and Teaching. Unpublished Doctoral Thesis. University of Cambridge.
UNDP (2007). Thailand Human Development Report 2007. New York, NY: United Nations Development Programme.
Keywords: gender, mathematical beliefs, personal epistemology, mathematics teaching and learning, epistemic beliefs
Citation: Trakulphadetkrai NV (2022) Mathematical Epistemic Beliefs: Through the Gender Lens. Front. Educ. 7:832462. doi: 10.3389/feduc.2022.832462
Received: 09 December 2021; Accepted: 14 March 2022;
Published: 25 April 2022.
Edited by:
Douglas F. Kauffman, Medical University of the Americas – Nevis, United StatesReviewed by:
Taro Fujita, University of Exeter, United KingdomTzung-Jin Lin, National Taiwan Normal University, Taiwan
Copyright © 2022 Trakulphadetkrai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Natthapoj Vincent Trakulphadetkrai, bi50cmFrdWxwaGFkZXRrcmFpQHJlYWRpbmcuYWMudWs=
 Natthapoj Vincent Trakulphadetkrai
Natthapoj Vincent Trakulphadetkrai