- 1IPN – Leibniz Institute for Science and Mathematics Education, Kiel, Germany
- 2Ruhr-Universität Bochum, Bochum, Germany
- 3IWM – Leibniz-Institut für Wissensmedien, Tübingen, Germany
- 4DIPF – Leibniz Institute for Research and Information in Education, Frankfurt, Germany
National educational standards stress the importance of science and mathematics learning for today’s students. However, across disciplines, students frequently struggle to meet learning goals about core concepts like energy. Digital learning environments enhanced with artificial intelligence hold the promise to address this issue by providing individualized instruction and support for students at scale. Scaffolding and feedback, for example, are both most effective when tailored to students’ needs. Providing individualized instruction requires continuous assessment of students’ individual knowledge, abilities, and skills in a way that is meaningful for providing tailored support and planning further instruction. While continuously assessing individual students’ science and mathematics learning is challenging, intelligent tutoring systems show that it is feasible in principle. However, the learning environments in intelligent tutoring systems are typically not compatible with the vision of how effective K-12 science and mathematics learning looks like. This leads to the challenge of designing digital learning environments that allow for both – meaningful science and mathematics learning and the reliable and valid assessment of individual students’ learning. Today, digital devices such as tablets, laptops, or digital measurement systems increasingly enter science and mathematics classrooms. In consequence, students’ learning increasingly produces rich product and process data. Learning Analytics techniques can help to automatically analyze this data in order to obtain insights about individual students’ learning, drawing on general theories of learning and relative to established domain specific models of learning, i.e., learning progressions. We call this approach Learning Progression Analytics (LPA). In this manuscript, building of evidence-centered design (ECD), we develop a framework to guide the development of learning environments that provide meaningful learning activities and data for the automated analysis of individual students’ learning – the basis for LPA and scaling individualized instruction with artificial intelligence.
Introduction
National educational standards (e.g., National Research Council, 2012; Sekretariat der ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2020) and international organizations (e.g., OECD, 2016) stress the importance of science and mathematics learning for today’s students. Knowledge about science and mathematics is key to understand and engage global challenges such as the climate catastrophe or the ongoing COVID-19 pandemic. However, across disciplines, students frequently struggle to meet learning goals about core concepts like energy (Neumann et al., 2013; Herrmann-Abell and DeBoer, 2017), evolution (Todd and Romine, 2016; Todd et al., 2022), reaction kinetics (Bain and Towns, 2016), or the derivation concept (vom Hofe, 1998).
Digital learning environments enhanced with artificial intelligence hold the promise to address this issue by providing individualized instruction and support for students at scale. Scaffolding and feedback, for example, are both most effective when tailored to students’ needs (Narciss et al., 2014). Providing individualized instruction requires continuous assessment of students’ individual knowledge, abilities, and skills in a way that is meaningful for providing tailored support and planning further instruction, i.e., students’ learning needs to be assessed relative to the relevant domain specific models of learning.
While continuously assessing individual students’ science and mathematics learning is challenging, intelligent tutoring systems show that it is feasible in principle (e.g., Nakamura et al., 2016). However, the learning environments in intelligent tutoring systems are typically not compatible with the vision of how effective K-12 science learning (National Research Council, 2012, 2018) looks like, i.e., instruction rooted in inquiry learning approaches such as project-based learning that puts students engagement in scientific practices at the center. This leads to the challenge of designing digital learning environments that allow for both – meaningful science and mathematics learning and the reliable and valid assessment of individual students’ learning.
Today, digital devices such as tablets, laptops, or digital measurement systems increasingly enter science and mathematics classrooms. In consequence, students’ learning increasingly produces rich product (e.g., students’ written answers in a digital workbook) and process (e.g., mouse movement in a digital modeling tools) data. This data is large, heterogeneous, and dynamic and thus challenging to analyze. Yet in principle, this data should allow continuous assessment of individual students’ learning and thus provide the basis for individualized instruction. Learning Analytics techniques can help to automatically analyze this data in order to obtain insights about individual students’ learning, drawing on general theories of learning and relative to established domain specific models of learning, i.e., learning progressions. We call this approach Learning Progression Analytics (LPA).
In this manuscript, building of evidence-centered design (ECD) (Mislevy et al., 2003), we develop a framework to guide the development of learning environments that provide meaningful learning activities and data for the automated analysis of individual students’ learning – the basis for LPA and scaling individualized instruction with artificial intelligence.
Learning progression analytics
Learning in science and mathematics
Following research that indicates that the learning of science and mathematics content cannot be separated from the doing of science or mathematics, modern standards such as the Next Generation Science Standards (National Research Council, 2007) or the German Bildungstandards (Sekretariat der ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2020) emphasize that students should not only develop knowledge about science or mathematics ideas but be enabled to use that knowledge to make sense of phenomena. To demonstrate such knowledge-in-use (Harris et al., 2016) requires that students have well-organized knowledge networks as those are a prerequisite for fluent application and retrieval (Bransford, 2000; National Academies of Sciences, Engineering, and Medicine, 2018). The knowledge-integration perspective (Linn, 2006) emphasizes the importance of well-organized knowledge networks and views learning as a process of developing increasingly connected and coherent sets of ideas. Building coherent connections between ideas, however, is a process that takes time and instruction that provides opportunities for students to establish these connections (Sikorski and Hammer, 2017; National Academies of Sciences, Engineering, and Medicine, 2018) and see their explanatory value (Smith et al., 1994).
Project-based learning (PBL) is a pedagogy grounded in learning sciences research that is well aligned with the modern vision of science and mathematics instruction just outlined, i.e., it emphasizes that learning about science and mathematics requires the active construction of knowledge by using ideas in meaningful contexts (Krajcik and Shin, 2014; Jacques, 2017). A core feature of PBL in order to reach this goal is that instruction is centered around phenomena which are tied together by a driving question. A typical PBL unit consists of a driving question with several sub-driving questions which are guiding instruction. These questions act as an advance organizer and help students develop a need-to-know, i.e., they elicit a desire to learn and make students realize that there is an important problem that genuinely needs to be solved. This need-to-know then drives and sustains students’ motivation to engage in scientific and mathematical practices such as asking questions, conducting experiments, constructing explanations, developing models, or engaging in argumentation (proving) to make sense of phenomena. Throughout a unit, students then repeatedly engage in these practices and develop and refine a set of ideas they use to make sense of the driving question. In this way, PBL supports students in developing well-organized knowledge networks and the ability to apply this knowledge, i.e., knowledge-in-use (Schneider et al., 2020).
While PBL provides a framework for structuring science and mathematics instruction, it does not provide guidance on how to structure the content of a given domain. This has been the focus of research on learning progressions (Duncan and Rivet, 2013). Learning progressions are descriptions of “successively more sophisticated ways of reasoning within a content domain that follow one another as students learn” (Smith et al., 2006). Learning progressions, building on general theories of learning, focus on core aspects of a domain and delineate a series of intermediate stages from a lower anchor – representing students’ tentative understandings upon entry into the learning progression – to an upper anchor representing mastery of the domain, or aspect thereof (Duschl et al., 2011). The intermediate stages represent ideal trajectories of learning as a means of aligning instruction and assessment (Duncan and Hmelo-Silver, 2009; Duschl et al., 2011; Lehrer and Schauble, 2015). These trajectories are hypothetical in nature and need empirical validation (Duschl et al., 2011; Hammer and Sikorski, 2015; Jin et al., 2019). In science, learning progressions have been developed and investigated for core concepts, such as energy (Neumann et al., 2013; Yao et al., 2017), matter (Hadenfeldt et al., 2016) and its transformation (Emden et al., 2018), genetics (Castro-Faix et al., 2020), or the concept of number (Sfard, 1991). However, this research has triggered much debate (Steedle and Shavelson, 2009; Duschl et al., 2011; Shavelson and Kurpius, 2012) mostly revolving around how individual learners’ trajectories align with the hypothesized one (underlying the sequence of classroom activities; e.g., Duschl et al., 2011; Hammer and Sikorski, 2015; Lehrer and Schauble, 2015; Bakker, 2018). As typically used designs with few points of data collection distributed across months or even years do not allow for evaluating individual students’ learning, let alone reconstructing their learning trajectories (see also Duschl et al., 2011), to date, this issue has not been resolved. What makes matters worse is that students do not typically progress in a linear fashion, e.g., they may move back and forth between levels of a learning progressions or jump across entire levels. This phenomenon has coined the term “messy middle” to characterize the phase of students’ learning between novice and mastery (Gotwals and Songer, 2009) where it is often difficult to place a student in a model with current research designs and methodologies (e.g., Duncan and Rivet, 2018; Todd et al., 2022).
In summary, PBL is a model for science and mathematics instruction rooted in learning sciences research that supports students in developing knowledge-in-use about science and mathematics (Holmes and Hwang, 2016; Chen and Yang, 2019; Schneider et al., 2020) and learning progressions provide domain specific models of learning to guide instruction (Sfard, 1991; Duncan and Rivet, 2018). However, in order to guide instruction at the individual level on a day-to-day basis, the resolution of current learning progression research designs (cross-sectional or using few measurement time points often spread far apart) is insufficient.
Assessing student learning using data from digital technologies
As digital technologies increasingly permeate science and mathematics classrooms, a new opportunity arises to assess students’ learning on the grain size needed for individualized instruction: data from students’ interactions with digital technologies. Much research on assessing student learning using data from their interactions with digital technologies has been done in the context of intelligent tutoring systems (e.g., Ma et al., 2014). Intelligent tutoring systems present students with tasks and based on the assessments of students’ learning on one task, ITSs choose next steps or tasks to match learners’ individual needs. ITSs monitor student learning through a process called student modeling (Pelánek, 2017). In the context of science and mathematics instruction where tasks are often ill-defined, e.g., when students engage in authentic scientific or mathematical inquiry tasks, learning analytics techniques such as machine learning (ML) are used for student modeling. An example for this approach is InqITS (Gobert et al., 2015). InqITS was originally developed as a series of microworlds to support students in developing scientific (and/or mathematical) inquiry skills, such as formulating hypotheses, designing and carrying out experiments as well as interpreting data and drawing conclusions. InqITS provides a series of activities supporting students in developing scientific and mathematical inquiry skills, tracks students’ learning across these performances and provides students and teachers with in-time feedback – based on ML algorithms (Gobert et al., 2018). InqITS can, for example, automatically score students’ explanations provided in an open response format (Li et al., 2017) using the commonly used claim, evidence, reasoning (CER) framework (McNeill et al., 2006). In summary, research on ITSs has demonstrated that it is in principle possible to use the data that is generated when students engage in scientific and mathematical inquiry activities in digital learning environments to assess individual students’ learning in science and mathematics on a grain size sufficient for individualized instruction. At the same time, a series of activities in an intelligent tutoring system does still not reflect a science or mathematics curriculum.
Toward learning progression analytics
In the preceding sections, we have discussed that past work in the learning sciences, science and mathematics education, and educational technologies, especially the sub-field of learning analytics, has produced (a) models of how effective science and mathematics learning can generally be facilitated, e.g., the pedagogy of project-based learning (Krajcik and Shin, 2014; Schneider et al., 2020), (b) domain specific models of learning about specific scientific or mathematics concepts and practices, that is, learning progressions (see, e.g., Sfard, 1991; Hadenfeldt et al., 2016; Osborne et al., 2016), and (c) methods and techniques for automatically assessing students’ learning trajectories from the data that is generated when students engage in digital learning environments (Gobert et al., 2015). Thus, at the intersection of the learning sciences, learning progression research, and learning analytics, the building blocks are available for realizing a vision where individualized science and mathematics learning can be delivered at scale using digital learning environments enhanced with artificial intelligence. We call the area of work that aims at realizing this vision Learning Progression Analytics (LPA).
A key challenge for learning progression analytics is how to design the learning environments that allow to automatically assess students’ learning trajectories (as a prerequisite for later individualized learning supports such as adaptive scaffolds). While frameworks for the design of effective science and mathematics instruction and curriculum materials such as Storyline Units (Reiser et al., 2021), Storylines (Nordine et al., 2019), or the principles of project-based learning more generally (e.g., Petrosino, 2004; Miller and Krajcik, 2019) exist, these frameworks do not address the specific considerations and affordances that allow for a valid and reliable assessment of students’ learning trajectories. Frameworks for designing valid and reliable science or mathematics assessments (that can be evaluated automatically), however, e.g., on a conceptual level the assessment triangle (Pellegrino et al., 2001), on a general level evidence-centered design (e.g., Mislevy et al., 2003), and on a procedure level the procedure by Harris et al. (2016, 2019), have a complementary blind-spot: they do not consider the affordances of crafting engaging science and mathematics instruction and curriculum. In other words, we can design good curriculum but the tasks therein are not necessarily good assessments and we can design good assessment tasks but a series of assessment tasks is not necessarily a good curriculum.
To address this issue, we present a framework and procedure for developing learning environments that address the needs of learning progression analytics, i.e., learning environments that provide engaging science and mathematics instruction and valid and reliable assessment of students’ learning trajectories. We base our framework and procedure on ideas rooted in the assessment triangle, evidence-centered design, and the design cycle for education.
Developing learning environments for learning progression analytics
A distinctive feature of the learning environments needed for learning progression analytics is that the tasks that students engage in during the curriculum allow to draw inferences about students’ learning. These inferences should be supported by evidence. As students’ learning cannot be directly measured, we need to engage in a process of evidentiary reasoning. The 2001 NRC report Knowing What Students Know: The Science and Design of Educational Assessment (Pellegrino et al., 2001) introduces the assessment triangle (Figure 1) to describe the core elements – cognition, interpretation, and observation –and relations between these elements in the process of evidentiary reasoning.
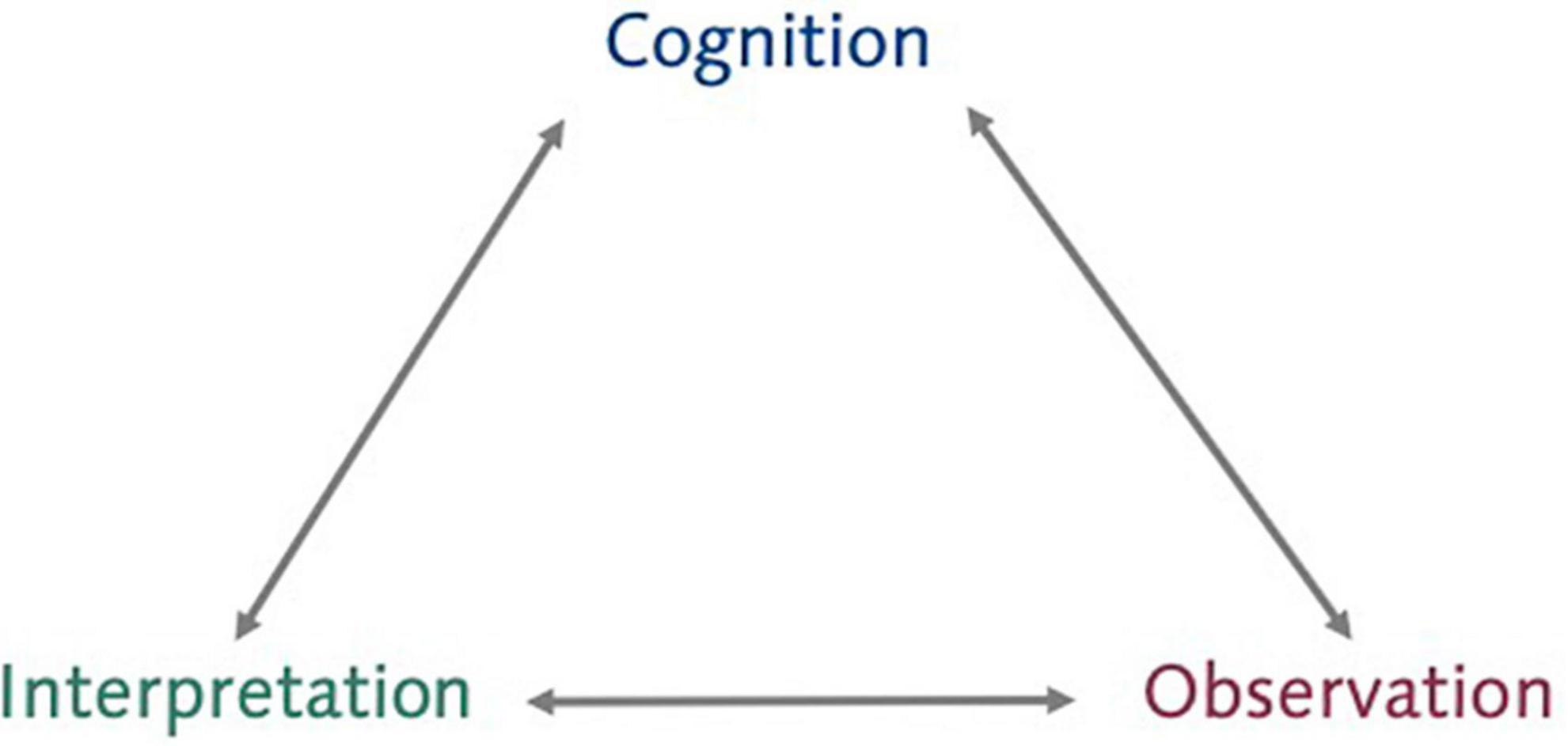
Figure 1. Assessment triangle, adapted from Pellegrino et al. (2001).
The cognition corner represents the model of learning in a given domain. In the context of science or mathematics, this means domain specific models of learning, i.e., learning progressions (Sfard, 1991; Duncan and Rivet, 2018), and underlying general models reflected for example in the knowledge integration theory (Linn, 2006), knowledge-in-pieces (diSessa, 1988) or coordination class theory (Mestre, 2005). In order to be an effective basis for a process of evidentiary reasoning, these models should represent the best supported understanding of how students typically learn and express their learning in the domain of interest. Further, the grain size in which these models are expressed must meet the affordances of the instructional context, e.g., if students learn about different manifestations of energy, a model that describes all learning about manifestations as just one large aspect is limited in its usefulness. In this way, the description of students’ learning in the cognition corner forms the basis for all further evidentiary reasoning and the evaluation of the validity of the assessment.
The observation corner represents a description of the features and affordances of tasks that are suitable to provide evidence about students’ learning as specified in the cognition corner. Correctly specifying these features and affordances is critical to generating high-quality data that provides a maximum of information regarding the aims of assessment.
Lastly, the interpretation corner represents how the data generated when students engage in tasks is to be processed and analyzed to provide that information about students’ learning. Thus, this corner represents the methods used to make inferences from data, typically in the form of statistical models.
Overall, it is crucial that the components in the assessment triangle align. Otherwise, the chain of evidentiary reasoning will break and no valid inferences can be made about students’ learning.
The assessment triangle as a model for evidentiary reasoning in assessment serves as a conceptual basis for frameworks for actually developing assessments. One such framework that has been successfully used to develop high quality science and mathematics assessments that align with the goals of modern science or/and mathematics instruction expressed in standard documents (e.g., National Research Council, 2012; Sekretariat der ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2020) such as three-dimensional learning (Harris et al., 2016) and knowledge-in-use (Harris et al., 2019) is evidence-centered design (Mislevy et al., 2003).
Evidence-centered design
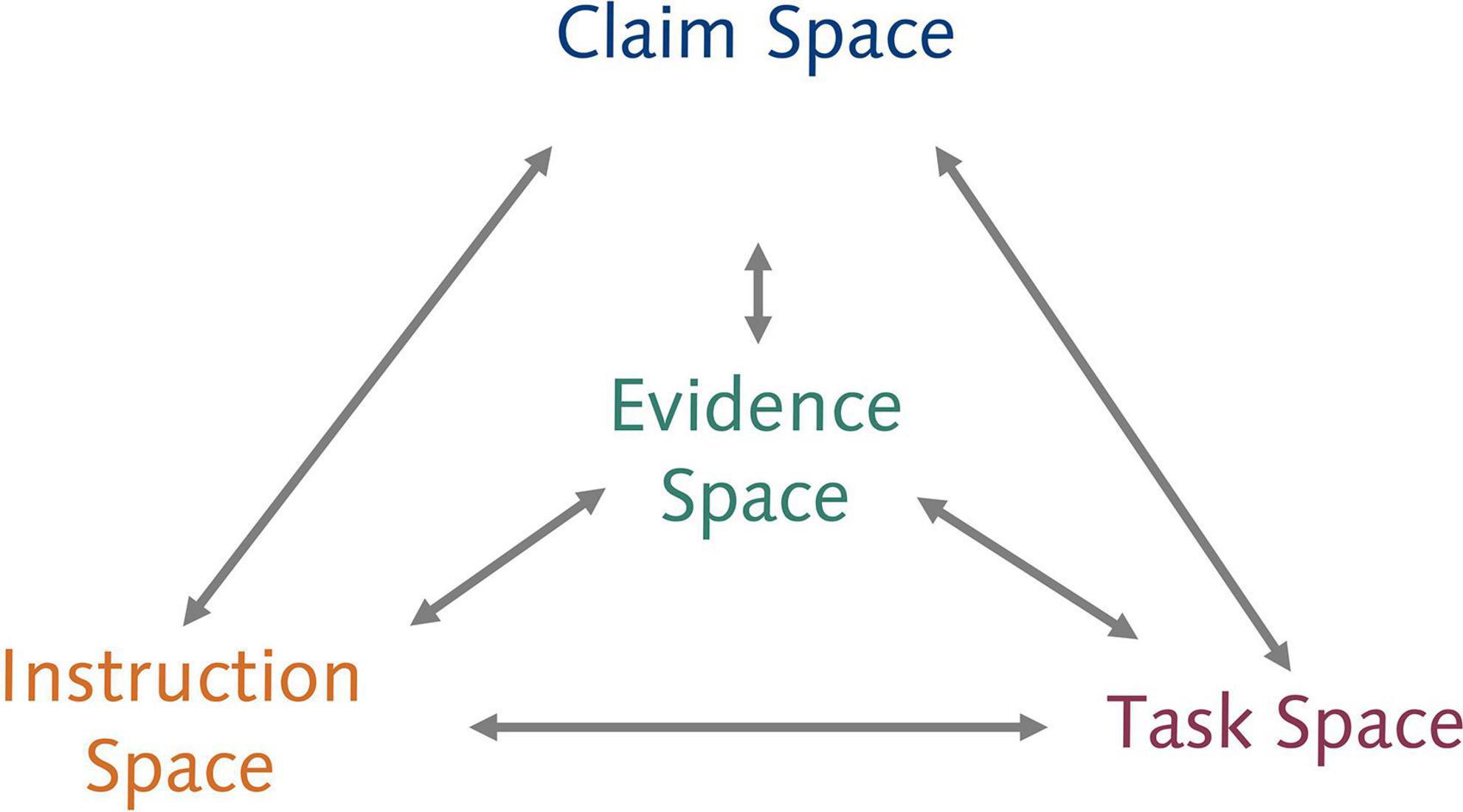
Robert Mislevy and his colleagues (see, e.g., Mislevy et al., 2003; Mislevy and Haertel, 2007; Rupp et al., 2012; Arieli-Attali et al., 2019) were instrumental in the development of the evidence-centered design framework for the development of assessments. It guides the process of evidentiary reasoning through the delineation of three spaces: the claim, evidence, and task space (Mislevy et al., 2003) that map onto the elements in the assessment triangle. Figure 2 lays out the logic of evidentiary reasoning as an assessment argument is developed by moving through the design spaces. The journey of evidentiary reasoning begins with the delineation of the claim space which requires the specification of the claims that one wants to make about the construct of interest, e.g., students’ learning. This involves unpacking the complexes of knowledge, abilities, and skills and any combination thereof that constitute competence in a domain. Thorough unpacking and precise formulation of the knowledge students are expected to have and how they are expected to use it – based on a thorough analysis of the domain and respective models of students’ learning – is most critical in this step. Next, evidence statements are formulated. These statements should describe as clearly and precisely as possible the features of student performances that will be accepted as evidence that a student has demonstrated the requirements to meet a claim. Now, the form of tasks that are expected to elicit the desired performances are specified in the task model. This involves defining fixed features that tasks must or must not have and variable features, i.e., features that may differ across tasks addressing the same claim. This part of the procedure leads to the design part of the assessment argument: precisely formulated claims and evidence statements describing concrete performances support the development of tasks that are strongly aligned with the construct as specified in the claim space.
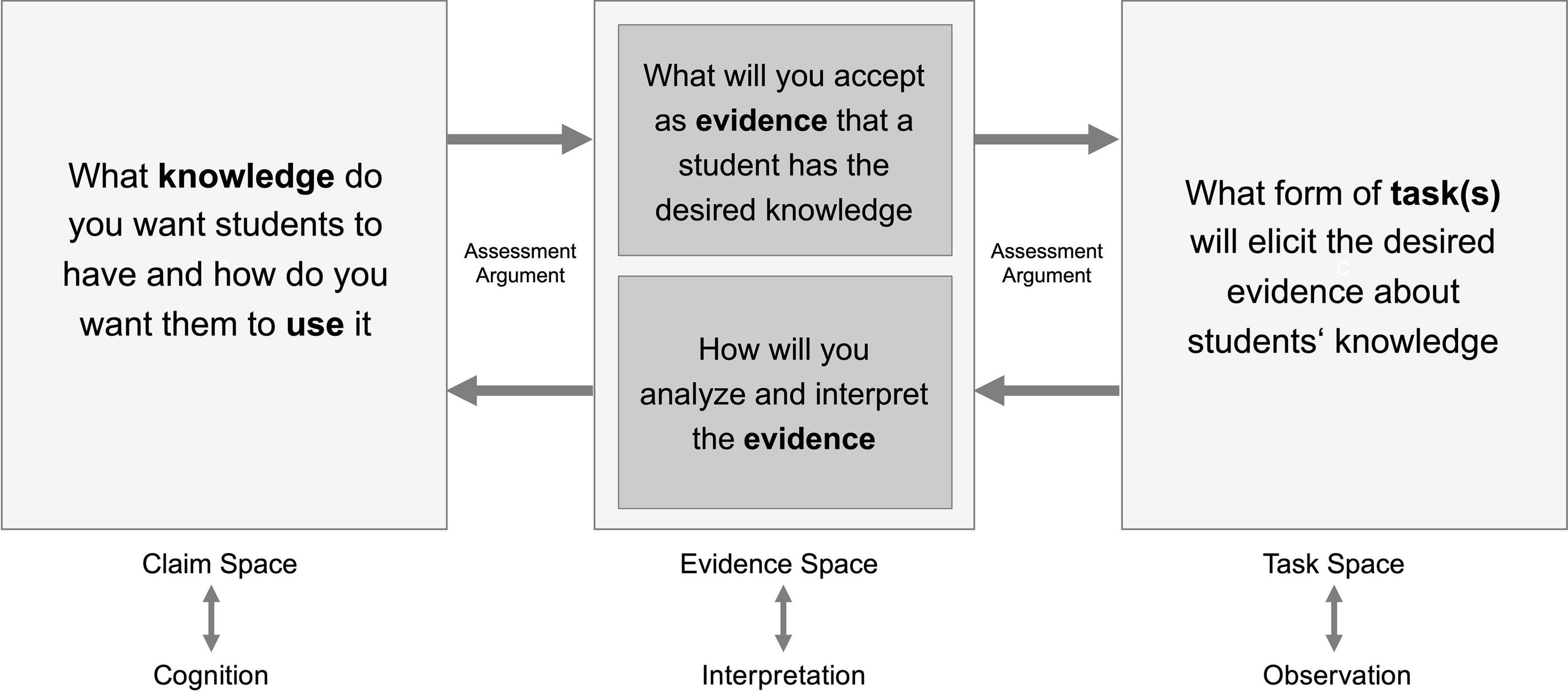
Figure 2. Simplified representation of evidence-centered design, adopted from Pellegrino et al. (2015).
With developed tasks at hand, the next step is to define an evidentiary scheme for the tasks, i.e., based on what performances we expect to observe, how we will evaluate these performances in the light of the evidence statements and how these evaluations will be combined into evidence supporting (or not supporting) the claims about the construct, e.g., students’ knowledge. This information then needs to be condensed into a scoring guide and a (statistical) model that describes how scores are eventually summarized into numbers that reflect to what extent students are meeting a claim. This part can be considered the use part of the assessment argument. Together, the use and design part of the assessment argument aim to ensure an optimal alignment of claims, evidence and tasks.
While evidence-centered design has been successfully used to develop science assessment tasks (e.g., Harris et al., 2019) and extensions of evidence-centered design that strengthen the connection between learning and assessment have been made (e.g., Kim et al., 2016; Arieli-Attali et al., 2019), these extensions do not provide guidance on how to develop series of tasks that function as a curriculum and also as assessment tasks. Arieli-Attali et al. (2019), for example, when describing the extended task model in their extension of evidence-centered design, focus on integrating adaptive supports such as feedback or scaffolds but do not discuss how to provide other functions of curriculum, e.g., engaging students over time (Schneider et al., 2020). Thus, current extensions of evidence-centered design remain relatively assessment-centered and provide little guidance in how to negotiate between the needs of assessment and crafting engaging science and mathematics instruction.
Extending evidence-centered design for learning progression analytics
In the past, evidence-centered design has been used to develop assessment tasks. However, when we want to detect learning, the tasks that students engage in will need to be embedded in a learning environment, i.e., they need to fulfil a range of criteria from both, an assessment and curriculum or learning environment design perspective. This is reflected in extension of the evidence-centered design in the ECD4LPA model in Figure 3. It shows the central components in the design and development of learning environments for learning progression analytics and how they influence each other. The relations between the claim space, the task space, and the evidence space follow from the assessment perspective and have been covered in the preceding sections. The instruction space nexus represents principles for the design of effective learning environments as well as affordances and constraints of the (technical and social) context in which the actual learning environment is implemented. The connections between the three traditional evidence-centered design spaces and the instruction space represent the constraints and affordances that the learning environment imposes on the claim, evidence, and task space and vice versa. Considering those contingencies is what allows the development of not only assessment tasks but rather learning tasks that still allow for a valid and reliable assessment.
Claim space — Instruction space
The claim space determines which knowledge, skills, and abilities should be targeted in what order and in what level of detail in the learning environment. However, the requirements of developing engaging instruction (Fortus, 2014; Schneider et al., 2020), e.g., by following the principles of project-based learning such as having a meaningful driving question or establishing a need-to-know also need to be considered. For example, this may result in adding skills or knowledge elements that are not strictly necessary based on the domain specific model articulated in the claim space but which are necessary in order to develop a need-to-know for students or for covering an engaging context. The benefit of explicitly articulating such addition elements is that instead of ending up as construct irrelevant sources of variance, these elements can be incorporated into the claim space, effectively extending the scope of the assessment.
Instruction space — Task space
The task space determines what features a task needs to have from an assessment perspective. These requirements need to be balanced with the features of effective learning tasks in an engaging curriculum as specified in the instruction space. For example, from a learning environment perspective, a large variety of tasks that include diverse contexts may be favorable whereas this variation provides a challenge from an assessment perspective.
Instruction space — Evidence space
The learning environment defined in the instruction space determines what types of evidence, i.e., data sources, will be available and thus imposes constraints on the evidentiary statements. For example, the modeling software used in a learning environment may not allow the qualification of the relation between objects in a model. Thus, there will be no evidence available about this aspect of modeling or other ways of finding evidence for this component will be required. On the other side, the evidence model can guide and inform the design of the learning environment, e.g., by mandating a modeling software that allows to qualify the relation between objects in a model.
A procedure for developing learning environments for learning progression analytics
In this section, we will describe how we applied the extended evidence-centered design framework for Learning Progression Analytics presented in the last section in a project that aims at developing digital learning environments for physics-, chemistry-, biology-, and mathematics instruction in German secondary schools that allow automatic assessment of students’ learning. We will first introduce a procedure we developed to support this process and then provide examples for each step. Examples will focus on the physics and biology unit.
Figure 4 shows the central steps of the procedure. The first step, unpacking the competence model, is in the upper left corner. Here, the claim space is delineated by unpacking the knowledge, skills, and abilities in the targeted domain. This involves careful domain analysis and consideration of respective domain specific models of learning (learning progressions). Based on this process, learning performances are derived. Learning performances describe the activities which students are supposed to engage in to facilitate and demonstrate learning.
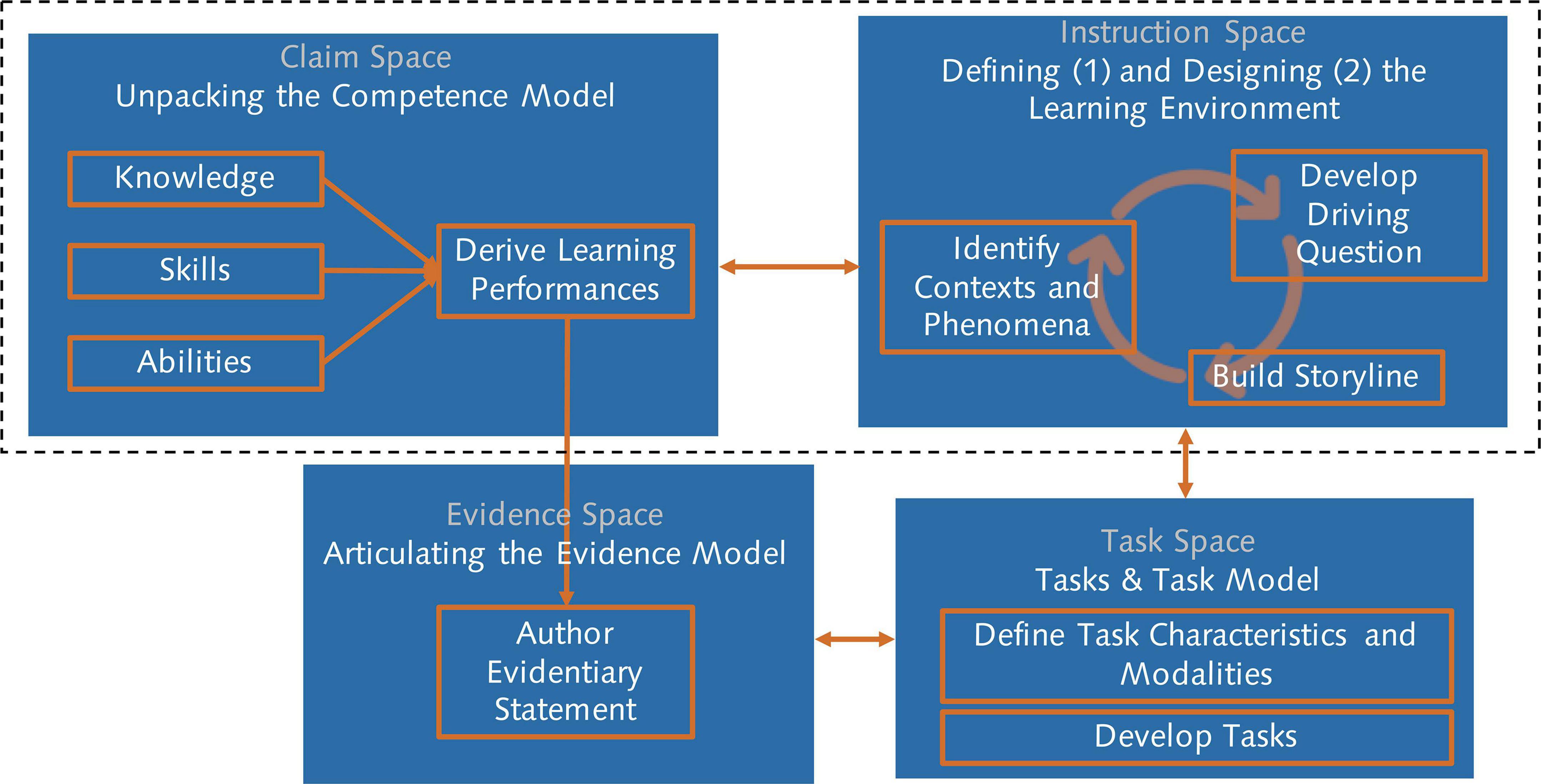
Figure 4. A procedure for developing digital learning environments that allow for the automated assessment of learning.
The physics learning environment, for example, focuses on energy and core practices include constructing explanations, developing models, and analyzing data. Based on an existing learning progression (Neumann et al., 2013) and standard documents (Ministerium für Bildung, Wissenschaft und Kultur des Landes Schleswig-Holstein, 2019), learning performances were defined or selected (e.g., Students analyze and interpret data to compare different types of engines based on their efficiency).
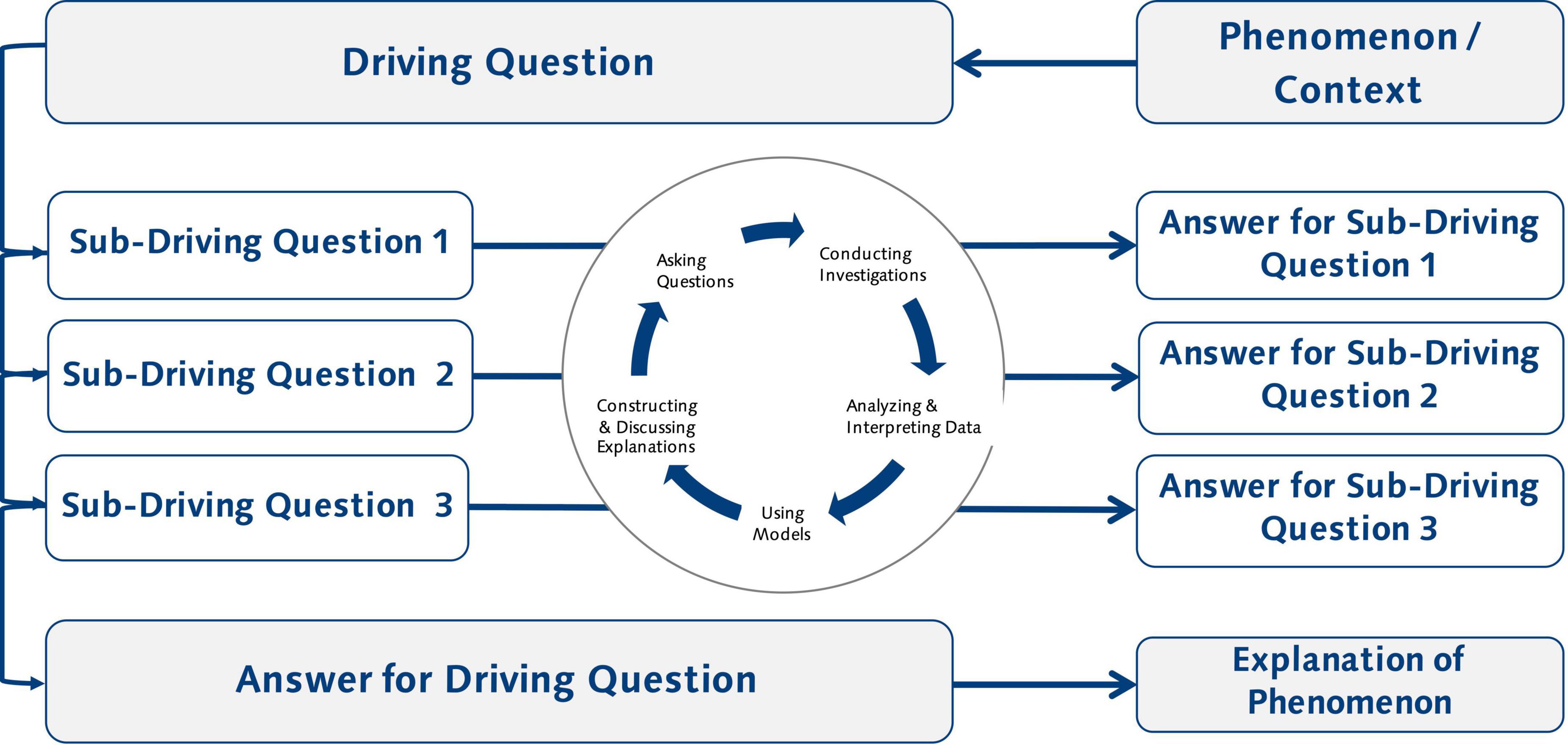
The next step is to define the learning environment, i.e., delineating the instructional space. This starts by articulating core features of the learning environment. In the context of our project, this included two important decisions: (1) moodle (Dougiamas and Taylor, 2003) would serve as the technical platform for the digital learning environment, and (2) the choice of project-based learning (Krajcik and Shin, 2014) as the central pedagogy guiding the design process. Project-based learning was chosen because it has proven to be highly effective in promoting science learning (Schneider et al., 2020). Further, procedures for the design of respective instruction exist (e.g., Nordine et al., 2019; Reiser et al., 2021). Project-based learning can be considered a form of guided inquiry learning, aligning with the call for doing science or knowledge-in-use reflected in modern science education (e.g., National Research Council, 2012). In project-based learning (Figure 5), students engage in inquiry processes to answer a driving question. During the inquiry processes, students engage in multiple epistemic activities that reflect scientific practices to generate the required knowledge to answer the sub-driving questions.
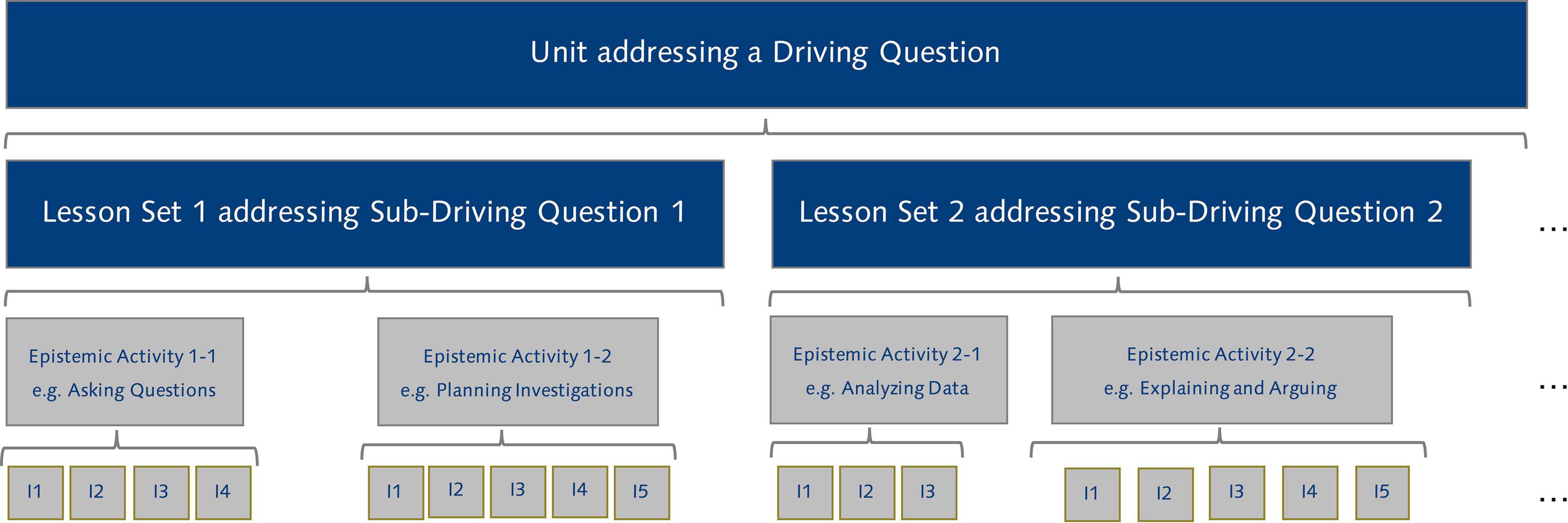
Thus, the basic building blocks for the design of instruction are epistemic activities that are modeled on scientific practices and respective learning progressions (e.g., Osborne et al., 2016) as well as structural models (e.g., McNeill et al., 2006). Scientific practices can be considered as sequences of certain smaller steps, e.g., constructing a scientific explanation involves formulating a claim, identifying evidence supporting the claim, and providing the reasoning for why the evidence supports the claim (CER scheme, McNeill et al., 2006; see also Toulmin, 2008). This leads to the following principle building blocks of instruction (Figure 6): a series of interactions that reflect the steps of the scientific practices which function as epistemic activities that are combined to answer a sub-driving question in a lesson set and finally a series of lessons sets that answer a unit level driving question.
As a result of the choice of project-based learning as a model for instruction, the next step is identifying contexts and phenomena that motivate and allow for learning about the derived learning performances. Next, a driving question and storyline need to be developed. This is an iterative process where we used the storyline planning tool (Nordine et al., 2019) although other models for planning respective instruction can also be used in principle.
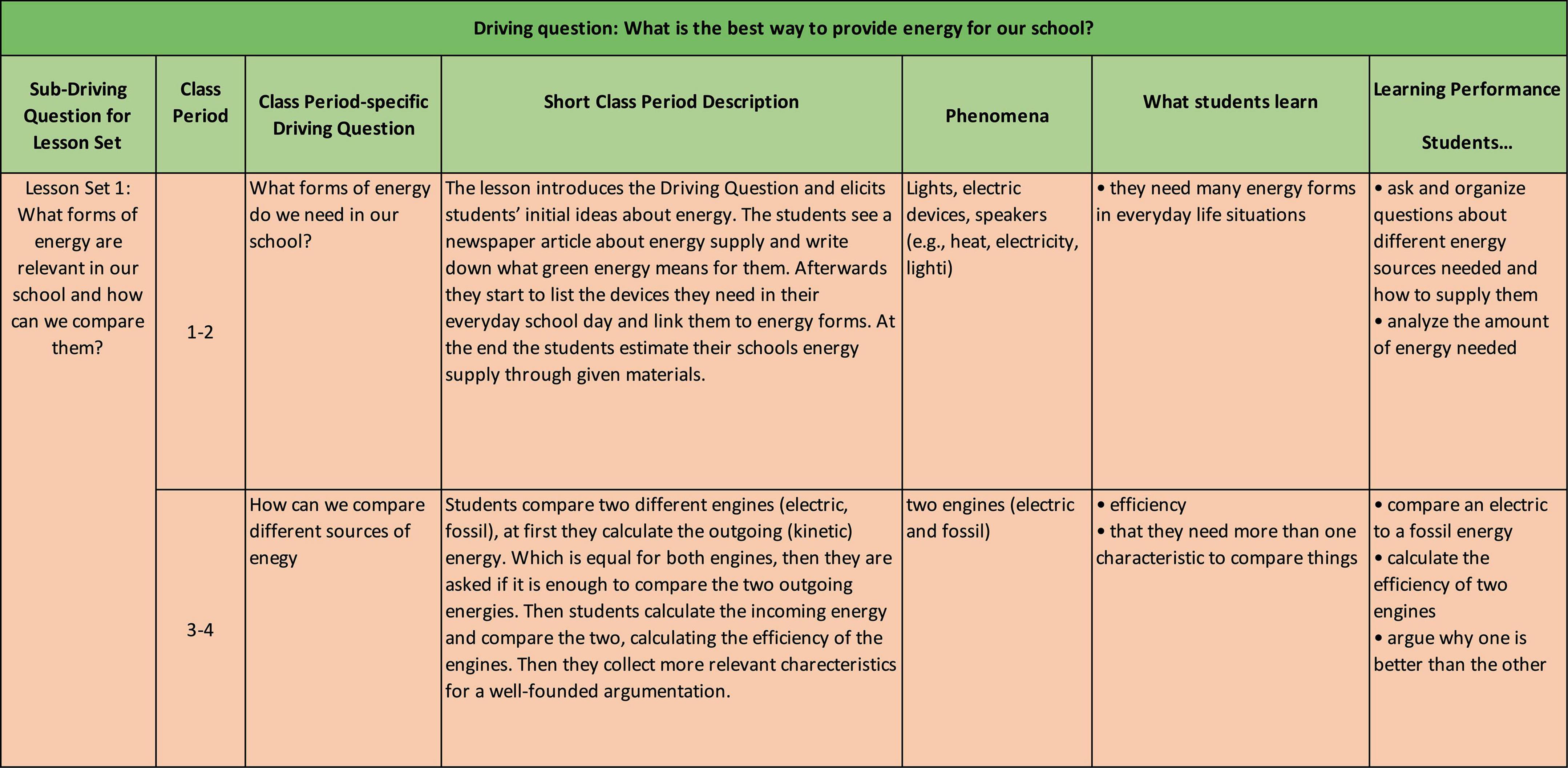
Figure 7 shows an excerpt of the resulting storyline including the driving question for the physic learning environment. Based on the complete storyline, we carefully checked to what extent all learning performances specified in the competence model were covered in the unit and whether the phenomena, contexts or instructional requirements such as developing a need-to-know introduced new knowledge, skills, abilities, or learning performances and accordingly revised the competence model and storyline until alignment was reached.
At this point, the major components in the claim space and instruction space are settled, i.e., the elements in the dashed box in Figure 4 have been defined and brought into alignment. Thus, the next step is to delineate the evidence space and task space and bring them into alignment. In addition, the task model needs to reflect the affordances of the learning environment, that is, alignment between the instruction space and task space is also needed. The goal of this alignment process is to specify a model for the development of tasks for the learning environment that are both engaging opportunities for learning and reliable opportunities for valid assessments. For this purpose, we used a method called Fellowship of the Learning Activity and Analytics (FoLA2, see Schmitz et al., 2022). The method is based on the Design Cycle for Education (DC4E) model (Scheffel et al., 2019) and emphasizes collaboration between different stakeholders such as educators, instructional designers, researchers, and technology specialists. Figure 8 shows an example from our design process. The general idea is to break-up an instructional sequence into so-called interactions (middle row of the board in Figure 8) and to define for each interaction how technology can be used in a learning enhancing way (top row of the board in Figure 8) and what it is that one wants to learn about students’ learning from that interaction (bottom row of the board in Figure 8; note that we focused on students’ learning but the focus of what one wants to learn about could also be different, e.g., teachers use of the technology or how the technology was used). This structure maps very well onto the smallest building block of instruction in Figure 6, i.e., the individual steps of the scientific practices also called interactions.
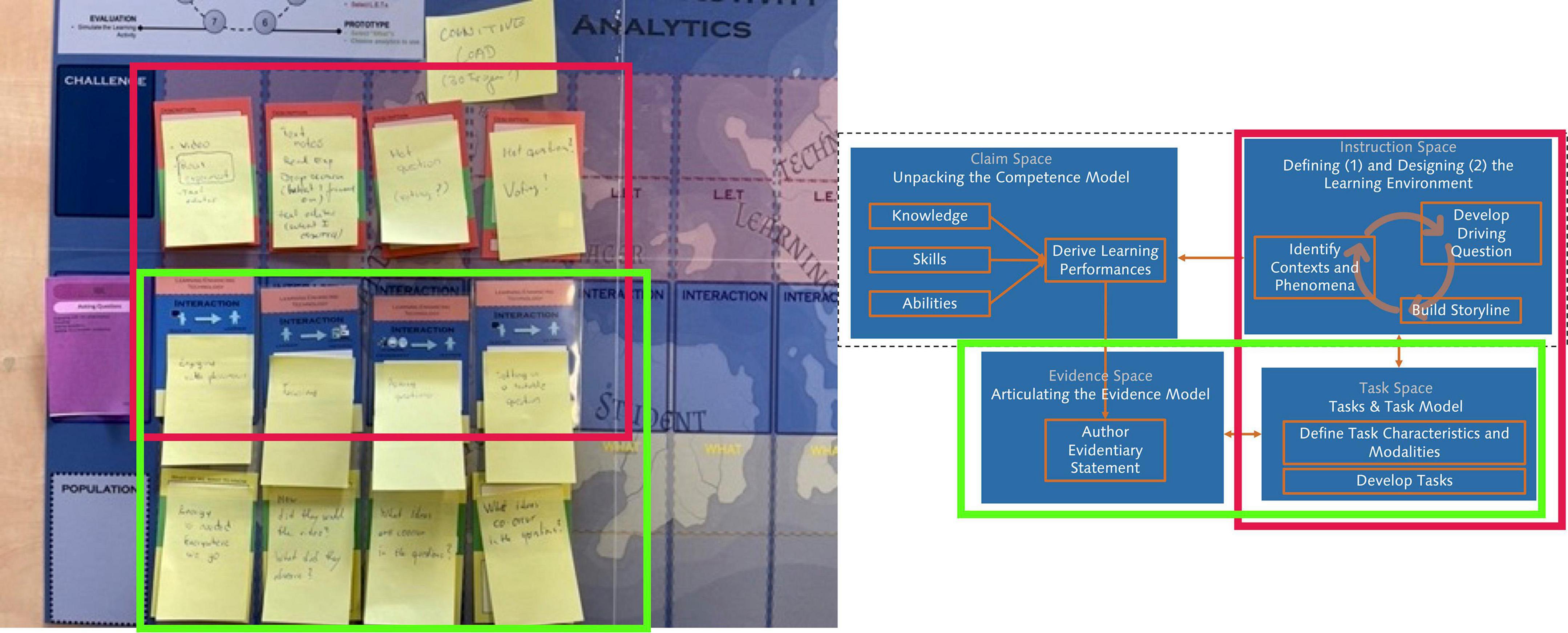
Figure 8. FoLA2 use example for the scientific practice of asking questions, red and green boxes indicate how FoLA2 supports alignment between different spaces in evidence-centered design.
In the context of our project, the curriculum designers first defined the sequence of interactions of each scientific practice needed for the inquiry process in project-based learning (Figure 5). Next, they worked with partners with strong backgrounds in the learning sciences and educational technologies to find learning enhancing technologies and consider what one could learn about students’ learning – as delineated in the claim space in form of a competence model – from these interactions. By delineating how learning enhancing technologies can be used in the different interactions, the alignment between the task space and instructional space is brought about, emphasizing the perspective of instructional and learning support in task design (red boxes in Figure 8). Respectively, by delineating what we can learn about students’ learning from these interactions, alignment between the task space and evidence space is facilitated, emphasizing the assessment perspective in task design (green boxes in Figure 8). As a result, we were able to develop templates for task design for each scientific practice that provide engaging opportunities for learning and reliable opportunities for valid assessments. With these templates and the previously developed storyline, we could now develop the actual tasks for the learning environment. This represents the culmination of the design part in the assessment argument in the standard evidence-centered design model (see also Figure 2).
What follows after the design part in the assessment argument is the use part of the assessment argument. Here, the central element is to author evidentiary statements as the basis for rubric design and scoring. Regardless of what exactly one wants to assess, i.e., what knowledge, skills, abilities, and learning performances, what can in principle be assess has already been delineated using the Fellowship of the Learning Activity and Analytics method which greatly reduces the work in authoring evidentiary statements. In the context of our project, we authored evidentiary statements for each interaction in an epistemic activity. Based on the interaction, it can in principle provide evidence about students’ knowledge, skills, abilities, and the extent to which they have met a learning performance. Figure 9 shows an excerpt from an evidentiary statement from an asking questions epistemic activity. The excerpt shows the first three interactions of the epistemic activity in the sources of evidence column: (1) asking potential research questions, (2) formulating hypotheses, (3) selecting hypotheses to investigate. Crosses indicate which of the constructs in the evidentiary statement column can be assessed in a respective interaction. Evidentiary statements are listed for different kinds of constructs (learning performances, knowledge elements, and skills) to be assessed. The bottom row provides information about the modality of each data source. Finally, the color-coding (yellow and green) of the cells with row counts of the crosses in the sources of evidence column can be interpreted as a baseline indicator of reliability. For example, in case of the first learning performance (Students ask research questions about differences of Guppys), there is only one cross in the sources of evidence column resulting in a row count of one, i.e., this learning performance is only assessed in one interaction. In contrast, for the second learning performance (Students develop hypotheses for their research questions.) the row count is two, i.e., this learning performance is assessed in two interactions. Thus, with more opportunities for measurement, an assessment of the second learning performance can be considered more reliable than an assessment of the first learning performance. In this way, the evidentiary statements provide the foundation and guidance for preparing scoring rubrics and developing (statistical) models for the evaluation of students’ learning based on the artifacts they produce when they engage with the digital learning environment.
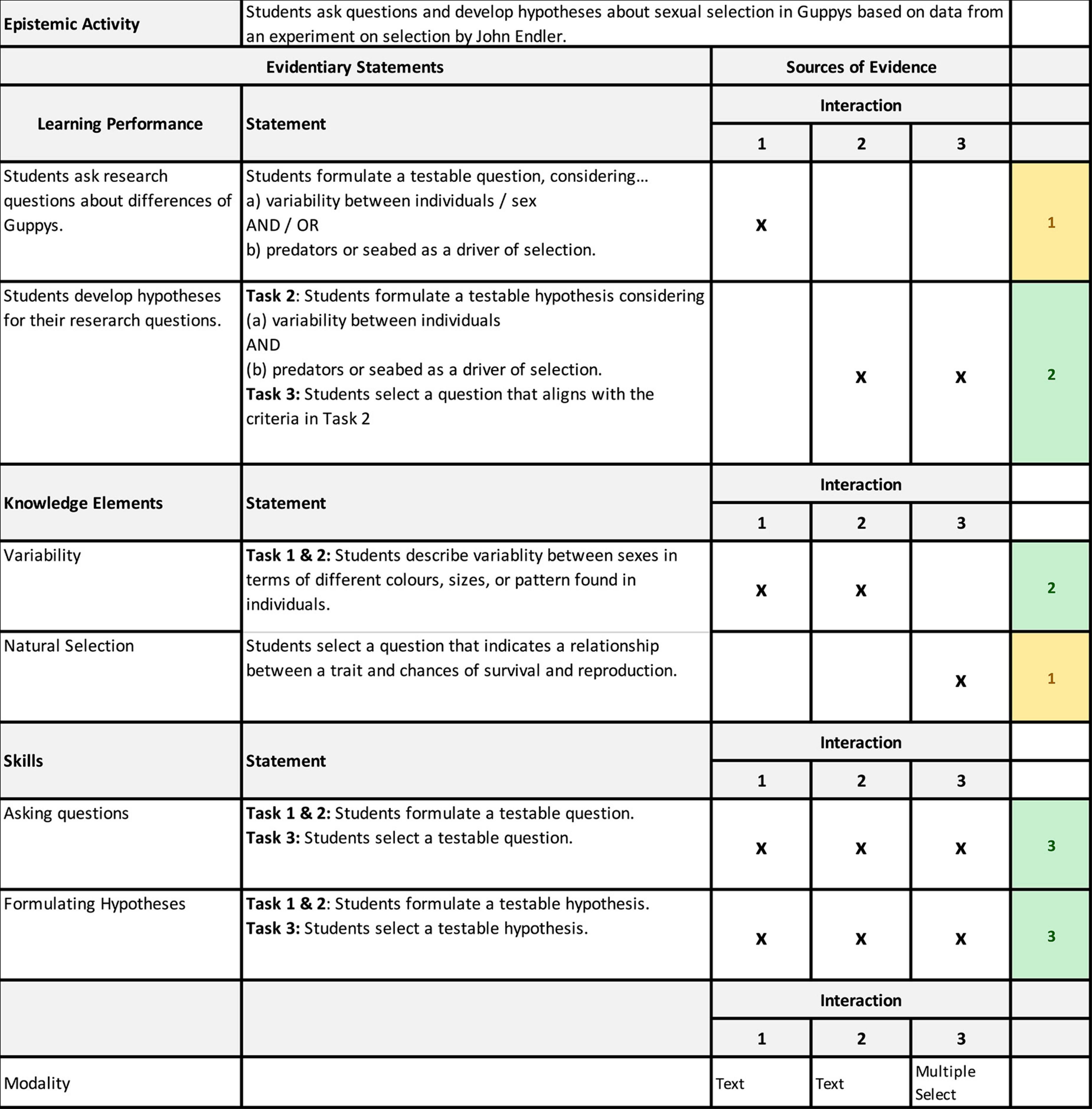
Figure 9. Evidentiary statement excerpt from an asking question epistemic activity [Tasks adapted from: Staatsinstitut für Schulqualität und Bildungsforschung München (2016, 08. Mai). Aufgabe: Guppys sind unterschiedlich. https://www.lehrplanplus.bayern.de/sixcms/media.php/72/B8_LB_5_Evolution_Guppy.pdf].
As our extension of evidence-centered design does not add innovations to the remaining steps toward a working digital learning environment for the automated analysis of students’ learning, i.e., developing rubrics, scoring student answers, and developing automated scoring procedures, we end the description of the procedure at this point. However, we note that while the description of the procedure here has been fairly linear, the overall process is iterative in principle and can involve multiple cycles to refine the digital learning environment and, if necessary, adapt it to changes in the context of the larger educational system (e.g., changes in educational standards, student population, available technologies, etc.) it is used in.
Discussion
In the preceding sections, we have presented an extension of evidence-centered design – ECD4LPA –that adds a new perspective in form of the instruction space. Considering the instruction space is needed to design tasks that go beyond the requirements of assessment and reflect the needs of engaging (science and mathematics) instruction. Further, we have presented a concrete procedure including examples that show how a digital science and mathematics learning environment can be developed that allows for the (automated) analysis of students’ learning.
The presented framework goes beyond existing extensions of evidence-centered design (e.g., Arieli-Attali et al., 2019) in that it incorporates a prominent role for the affordances of designing coherent curriculum and engaging instruction – the instruction space. At the same time, the presented framework also goes beyond existing frameworks for the development of (science and mathematics) curriculum and instruction such as storyline units (Reiser et al., 2021) which lack an explicit assessment perspective.
From an assessment perspective, the challenges of validity, reliability, and equity always warrant discussion. The question of the validity of the assessments that result from the proposed framework is addressed through the very process of evidentiary reasoning that is foundational to evidence-centered design. In other words, if the proposed framework is thoroughly implemented and the alignment between all components critically investigated and rectified if necessary, a strong validity argument in the sense of Kane (1992) can be made. To address the question of reliability, we have incorporated a notion of reliability in how we author evidentiary statements, i.e., the color-coding in Figure 9 designed to highlight constructs that are only measured once and thus have potentially low reliability. This provides a chance for revising the instruction so that more opportunities for measuring the respective construct arise. If this is impossible, it may also be warranted to exclude the construct from the assessment. However, before, excluding the construct alternative measures of reliability for single item measures could also be explored (e.g., Ginns and Barrie, 2004). The remaining issue of equity remains a challenge. While inquiry-based instruction (as emphasized in our examples) can contribute to equitable science and mathematics teaching (Brown, 2017) and frameworks such as Universal Design for Learning (Rose et al., 2018) can support the development process of equitable assessments, anchoring such practices and frameworks in the instruction, task, and evidence space can only represent a first effort toward equity. It will require continued effort in the form critiquing and revising the developed learning environments to realize an equitable science learning (Quinn, 2021).
Equity is also an issue in the context of the learning analytics which are envisioned in the framework and procedure here. Recent research has demonstrated and documented the widespread range of equity issues in the context of machine learning or artificial intelligence methods, i.e., learning analytics techniques, more broadly (O’Neil, 2016; Benjamin, 2019; Cheuk, 2021; Crawford, 2021). While frameworks for addressing equity issues in learning analytics exist (e.g., Floridi et al., 2018), they rarely provide guidance for the concrete issues and highly disciplinary affordances that designers face (see also Kitto and Knight, 2019). As the extension of evidence-centered design (ECD4LPA) and the procedure presented in this manuscript are about designing learning environments and assessments, future work will need to sharpen out how to provide guidance that is helpful for designers in addressing equity challenges in the context of the learning analytics component.
Another area for future work regards the range of learning analytics techniques that are relevant in this framework. In this manuscript, the examples provided focused mostly on student generated text were the techniques to apply are straight forward in principle [e.g., using standard student modeling techniques (Pelánek, 2017) and supervised machine learning for text answers (see, e.g., Maestrales et al., 2021)]. However, as digital tools used in classrooms such as tablet computers offer increasingly more data sources such as video, audio, acceleration, etc. multi-modal learning analytics (Lang et al., 2017) are increasingly feasible. For example, Spikol et al. (2018) recently used multi-modal learning analytics to predict engagement in a project-based learning environment. Thus, an avenue for future work in learning progression analytics is to explore the potential of these techniques and further extend the presented procedure to provide respective support during the design process.
Another avenue for future work regarding both the procedure and the learning analytics components is to move beyond the focus on cognitive constructs reflected in the examples in this manuscript. While evidence-centered design is not principally limited to cognitive constructs in the sense of knowledge, abilities, and skills, it has rarely been applied to assess affective constructs such as engagement. However, affect and motivation are important in science learning (Fortus, 2014). Here, learning analytics techniques such as sentiment analysis or automated emotion detection could be helpful to detect students’ affective and motivational states and thus provide an even more detailed picture of students’ learning (see also Grawemeyer et al., 2017).
Finally, the framework and procedure presented here have originated in work with a focus on science education. However, in principle there are no reasons why the framework and procedure might not be applied in the humanities and social sciences as evidence-centered design which is foundational to the framework and procedure is domain general. Adopting the framework and procedure to learning in other domains would require to reconsider the science education specific choices, e.g., the domain specific models of learning or the overall pedagogy. In fact, Hui et al. (2022) provide a compelling example of how a digital work book is used in English language learning to monitor and model students’ learning.
Conclusion
We have motived the need for an extension of evidence-centered design by introducing the vision of learning progression analytics, i.e., delivering individualized (science and mathematics) learning at scale using digital learning environments enhanced with artificial intelligence. The first step in realizing this vision is to develop digital learning environments that allow to automatically assess individual students’ learning. We hope that the framework and procedure presented in this manuscript can provide guidance and orientation in the respective development process. Future work will need to consider the next step – after students’ learning has been assessed – more closely where another layer of complexity is added to the design process of learning environments: designing adaptive support systems such as feedbacks or scaffolds and presenting assessment information to teachers in a way that allows them to act in learning supporting ways based on that information.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
MK contributed to conception and design of the manuscript. All authors contributed to the presented framework and materials, manuscript revision, read, and approved the submitted version.
Funding
This work was supported by the Leibniz Foundation.
Acknowledgments
MK thanks Elisabeth Schüler for her support in preparing this manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Arieli-Attali, M., Ward, S., Thomas, J., Deonovic, B., and von Davier, A. A. (2019). The expanded evidence-centered design (e-ECD) for learning and assessment systems: A framework for incorporating learning goals and processes within assessment design. Front. Psychol. 10:853. doi: 10.3389/fpsyg.2019.00853
Bain, K., and Towns, M. H. (2016). A review of research on the teaching and learning of chemical kinetics. Chem. Educ. Res. Pract. 17, 246–262. doi: 10.1039/C5RP00176E
Bakker, A. (2018). Design research in education. A practical guide for early career researchers. Milton Park: Routledge.
Benjamin, R. (2019). Race after technology: Abolitionist tools for the new jim code. polity. Medford, MA: Polity.
Bransford, J. (2000). How people learn: Brain, mind, experience, and school (Expanded ed). Washington, DC: National Academy Press.
Brown, J. C. (2017). A metasynthesis of the complementarity of culturally responsive and inquiry-based science education in K-12 settings: Implications for advancing equitable science teaching and learning. J. Res. Sci. Teach. 54, 1143–1173. doi: 10.1002/tea.21401
Castro-Faix, M., Duncan, R. G., and Choi, J. (2020). Data-driven refinements of a genetics learning progression. Journal of Res. Sci. Teach. 58, 3–39. doi: 10.1002/tea.21631
Chen, C.-H., and Yang, Y.-C. (2019). Revisiting the effects of project-based learning on students’ academic achievement: A meta-analysis investigating moderators. Educ. Res. Rev. 26, 71–81. doi: 10.1016/j.edurev.2018.11.001
Cheuk, T. (2021). Can AI be racist? Color-evasiveness in the application of machine learning to science assessments. Sci. Educ. 105, 825–836. doi: 10.1002/sce.21671
Crawford, K. (2021). Atlas of AI: Power, politics, and the planetary costs of artificial intelligence. New Haven, CT: Yale University Press.
diSessa, A. (1988). “Knowledge in pieces,” in Constructivism in the computer Age, eds G. E. Forman and P. B. Pufall (Hilsdale, NJ: Erlbaum).
Dougiamas, M., and Taylor, P. (2003). “Moodle: Using learning communities to create an open source course management system,” in Proceedings of edmedia + innovate learning 2003, eds D. Lassner and C. McNaught (Honolulu, HI: AACE).
Duncan, R. G., and Hmelo-Silver, C. E. (2009). Learning progressions: Aligning curriculum, instruction, and assessment. J. Res. Sci. Teach. 46, 606–609. doi: 10.1002/tea.20316
Duncan, R. G., and Rivet, A. E. (2013). Science learning progressions. Science 339, 396–397. doi: 10.1126/science.1228692
Duncan, R. G., and Rivet, A. E. (2018). “Learning progressions,” in International handbook of the learning sciences, eds F. Fischer, C. Hmelo-Silver, S. Goldman, and P. Reimann (New York, NY: Routledge), 422–432.
Duschl, R., Maeng, S., and Sezen, A. (2011). Learning progressions and teaching sequences: A review and analysis. Stud. in Sci. Educ. 47, 123–182. doi: 10.1080/03057267.2011.604476
Emden, M., Weber, K., and Sumfleth, E. (2018). Evaluating a learning progression on ‘Transformation of Matter’ on the lower secondary level. Chem. Educ. Res. Pract. 19, 1096–1116. doi: 10.1039/C8RP00137E
Floridi, L., Cowls, J., Beltrametti, M., Chatila, R., Chazerand, P., Dignum, V., et al. (2018). AI4People—An Ethical framework for a good AI society: Opportunities, risks, principles, and recommendations. Minds Mach. 28, 689–707. doi: 10.1007/s11023-018-9482-5
Ginns, P., and Barrie, S. (2004). Reliability of single-item ratings of quality in higher education: A replication. Psychol. Rep. 95, 1023–1030. doi: 10.2466/pr0.95.3.1023-1030
Gobert, J. D., Kim, Y. J., Sao Pedro, M. A., Kennedy, M., and Betts, C. G. (2015). Using educational data mining to assess students’ skills at designing and conducting experiments within a complex systems microworld. Think. Skills Creat. 18, 81–90. doi: 10.1016/j.tsc.2015.04.008
Gobert, J. D., Moussavi, R., Li, H., Sao Pedro, M., and Dickler, R. (2018). “Real-time scaffolding of students’ online data interpretation during inquiry with Inq-ITS using educational data mining,” in Cyber-physical laboratories in engineering and science education, (Berlin: Springer), 191–217.
Gotwals, A. W., and Songer, N. B. (2009). Reasoning up and down a food chain: Using an assessment framework to investigate students’ middle knowledge. Sci. Educ. 94, 259–281. doi: 10.1002/sce.20368
Grawemeyer, B., Mavrikis, M., Holmes, W., Gutiérrez-Santos, S., Wiedmann, M., and Rummel, N. (2017). Affective learning: Improving engagement and enhancing learning with affect-aware feedback. User Model. User-Adapt. Interact. 27, 119–158. doi: 10.1007/s11257-017-9188-z
Hadenfeldt, J. C., Neumann, K., Bernholt, S., Liu, X., and Parchmann, I. (2016). Students’ progression in understanding the matter concept. J. Res. Sci. Teach. 53, 683–708. doi: 10.1002/tea.21312
Hammer, D., and Sikorski, T.-R. (2015). Implications of complexity for research on learning progressions. Sci. Educ. 99, 424–431. doi: 10.1002/sce.21165
Harris, C. J., Krajcik, J. S., Pellegrino, J. W., and DeBarger, A. H. (2019). Designing knowledge-in-use assessments to promote deeper learning. Educ. Meas. Issues Pract. 38, 53–67. doi: 10.1111/emip.12253
Harris, C. J., Krajcik, J. S., Pellegrino, J. W., and McElhaney, K. W. (2016). Constructing assessment tasks that blend disciplinary core Ideas, crosscutting concepts, and science practices for classroom formative applications. Menlo Park, CA: SRI International.
Herrmann-Abell, C. F., and DeBoer, G. E. (2017). Investigating a learning progression for energy ideas from upper elementary through high school. J. Res. Sci. Teach. 55, 68–93. doi: 10.1002/tea.21411
Hui, B., Rudzewitz, B., and Meurers, D. (2022). Learning processes in interactive CALL systems: Linking automatic feedback, system logs, and learning outcomes. Open Sci. Framework [Preprint]. doi: 10.31219/osf.io/gzs9r
Jacques, L. A. (2017). What does project-based learning (PBL) look like in the mathematics classroom. Am. J. Educ. Res. 5, 428–433. doi: 10.12691/education-5-4-11
Jin, H., van Rijn, P., Moore, J. C., Bauer, M. I., Pressler, Y., and Yestness, N. (2019). A validation framework for science learning progression research. Int. J. Sci. Educ. 41, 1324–1346. doi: 10.1080/09500693.2019.1606471
Kim, Y. J., Almond, R. G., and Shute, V. J. (2016). Applying evidence-centered design for the development of game-based assessments in physics playground. Int. J. Test. 16, 142–163. doi: 10.1080/15305058.2015.1108322
Kitto, K., and Knight, S. (2019). Practical ethics for building learning analytics. Br. J. Educ. Technol. 50, 2855–2870. doi: 10.1111/bjet.12868
Krajcik, J. S., and Shin, N. (2014). “Project-Based Learning,” in The Cambridge handbook of the learning sciences Second edition, ed. R. K. Sawyer (Cambridge, MA: Cambridge University Press), doi: 10.1017/CBO9781139519526.018
Lang, C., Siemens, G., Wise, A., and Gasevic, D. (eds) (2017). Handbook of learning analytics (First). Beaumont, AB: Society for Learning Analytics Research (SoLAR), doi: 10.18608/hla17
Lehrer, R., and Schauble, L. (2015). Learning progressions: The whole world is NOT a stage. Sci. Educ. 99, 432–437. doi: 10.1002/sce.21168
Li, H., Gobert, J., and Dickler, R. (2017). Automated assessment for scientific explanations in on-line science inquiry. Int. Educ. Data Min. Soc. 1, 214–219.
Linn, M. C. (2006). The knowledge integration perspective on learning and instruction. In The Cambridge handbook of: The learning sciences. Cambridge, MA: Cambridge University Press.
Ma, W., Adesope, O. O., Nesbit, J. C., and Liu, Q. (2014). Intelligent tutoring systems and learning outcomes: A meta-analysis. J. Educ. Psychol. 106, 901–918. doi: 10.1037/a0037123
Maestrales, S., Zhai, X., Touitou, I., Baker, Q., Schneider, B., and Krajcik, J. (2021). Using machine learning to score multi-dimensional assessments of chemistry and physics. J. Sci. Educ. Technol. 30, 239–254. doi: 10.1007/s10956-020-09895-9
McNeill, K. L., Lizotte, D. J., Krajcik, J., and Marx, R. W. (2006). Supporting students’ construction of scientific explanations by fading scaffolds in instructional materials. J. Learn. Sci. 15, 153–191.
Mestre, J. P. (2005). Transfer of learning from a modern multidisciplinary perspective. Charlotte, NC: Information Age Publication.
Miller, E. C., and Krajcik, J. S. (2019). Promoting deep learning through project-based learning: A design problem. Disciplinary Interdiscip. Sci. Educ. Res. 1:7. doi: 10.1186/s43031-019-0009-6
Ministerium für Bildung, Wissenschaft und Kultur des Landes Schleswig-Holstein (Ed.) (2019). Fachanforderungen Physik.
Mislevy, R. J., Almond, R. G., and Lukas, J. F. (2003). A brief introduction to evidence-centered design. ETS Res. Rep. Ser. 1, 1–29.
Mislevy, R. J., and Haertel, G. D. (2007). Implications of evidence-centered design for educational testing. Educ. Meas. Issues Pract. 25, 6–20. doi: 10.1111/j.1745-3992.2006.00075.x
Nakamura, C. M., Murphy, S. K., Christel, M. G., Stevens, S. M., and Zollman, D. A. (2016). Automated analysis of short responses in an interactive synthetic tutoring system for introductory physics. Phys. Rev. Phys. Educ. Res. 12:010122. doi: 10.1103/PhysRevPhysEducRes.12.010122
Narciss, S., Sosnovsky, S., Schnaubert, L., Andrès, E., Eichelmann, A., Goguadze, G., et al. (2014). Exploring feedback and student characteristics relevant for personalizing feedback strategies. Comput. Educ. 71, 56–76. doi: 10.1016/j.compedu.2013.09.011
National Academies of Sciences, Engineering, and Medicine. (2018). How people learn II: Learners, contexts, and cultures. Washington, DC: National Academies Press, doi: 10.17226/24783
National Research Council (2018). Science and engineering for grades 6-12: Investigation and design at the center B. Moulding, N. Songer, & K. Brenner eds Washington, DC: National Academies Press. doi: 10.17226/25216
National Research Council. (2007). Taking science to school: Learning and teaching science in grades K-8. Washington, DC: National Academies Press.
National Research Council. (2012). A framework for K-12 science education. Washington, DC: The National Academies Press.
Neumann, K., Viering, T., Boone, W. J., and Fischer, H. E. (2013). Towards a learning progression of energy. J. Res. Sci. Teach. 50, 162–188. doi: 10.1002/tea.21061
Nordine, J. C., Krajcik, J., Fortus, D., and Neumann, K. (2019). Using storylines to support three-dimensional learning in project-based science. Sci. Scope 42, 86–92.
O’Neil, C. (2016). Weapons of math destruction: How big data increases inequality and threatens democracy, 1st Edn. New York, NY: Crown.
OECD. (2016). PISA 2015 assessment and analytical framework: Science, reading, mathematic and financial literacy. Paris: OECD, doi: 10.1787/9789264255425-en
Osborne, J. F., Henderson, J. B., MacPherson, A., Szu, E., Wild, A., and Yao, S.-Y. (2016). The development and validation of a learning progression for argumentation in science. J. Res. Sci. Teach. 53, 821–846. doi: 10.1002/tea.21316
Pelánek, R. (2017). Bayesian knowledge tracing, logistic models, and beyond: An overview of learner modeling techniques. User Model. User-Adapt. Interact. 27, 313–350. doi: 10.1007/s11257-017-9193-2
Pellegrino, J. W., Chudowsky, N., and Glaser, R. (2001). Knowing what students know (3. print). Availble online at: http://gso.gbv.de/DB=2.1/PPNSET?PPN=487618513 (accessed January 31, 2022).
Pellegrino, J. W., DiBello, L. V., and Goldman, S. R. (2015). A framework for conceptualizing and evaluating the validity of instructionally relevant assessments. Educ. Psychol. 51, 59–81. doi: 10.1080/00461520.2016.1145550
Petrosino, A. (2004). Integrating curriculum instruction and assessment in project based instruction: A case study of an experienced teacher. J. Sci. Educ. Technol. 13, 447–460. doi: 10.1186/s12913-016-1423-5
Quinn, H. (2021). Commentary: The role of curriculum resources in promoting effective and equitable science learning. J. Sci. Teach. Educ. 32, 847–851. doi: 10.1080/1046560X.2021.1897293
Reiser, B. J., Novak, M., McGill, T. A. W., and Penuel, W. R. (2021). Storyline units: An instructional model to support coherence from the students’. Perspect. J. Sci. Teach. Educ. 32, 805–829. doi: 10.1080/1046560X.2021.1884784
Rose, D. H., Robinson, K. H., Hall, T. E., Coyne, P., Jackson, R. M., Stahl, W. M., et al. (2018). “Accurate and informative for all: Universal design for learning (UDL) and the future of assessment,” in Handbook of accessible instruction and testing practices, eds S. N. Elliott, R. J. Kettler, P. A. Beddow, and A. Kurz (Salmon Tower Building, NY: Springer International Publishing), 167–180. doi: 10.1007/978-3-319-71126-3_11
Rupp, A. A., Levy, R., Dicerbo, K. E., Sweet, S. J., Crawford, A. V., Calico, T., et al. (2012). Putting ECD into practice: The interplay of theory and data in evidence models within a digital learning environment. J. Educ. Data Min. 4, 49–110. doi: 10.5281/ZENODO.3554643
Scheffel, M., van Limbeek, E., Joppe, D., van Hooijdonk, J., Kockelkoren, C., Schmitz, M., et al. (2019). “The means to a blend: A practical model for the redesign of face-to-face education to blended learning,” in Transforming learning with meaningful technologies, Vol. 11722, eds M. Scheffel, J. Broisin, V. Pammer-Schindler, A. Ioannou, and J. Schneider (Salmon Tower Building, NY: Springer International Publishing), 701–704. doi: 10.1007/978-3-030-29736-7_70
Schmitz, M., Scheffel, M., Bemelmans, R., and Drachsler, H. (2022). FoLA2–A method for co-creating learning analytics-supported learning design. J. Learn. Anal.
Schneider, B. L., Krajcik, J. S., Lavonen, J., and Salmela-Aro, K. (2020). Learning science: The value of crafting engagement in science environments. New Haven, CT: Yale University Press.
Sekretariat der ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland (2020). Bildungsstandards im Fach Physik für die Allgemeine Hochschulreife.
Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on process and objects as different sides of the same coin. Educ. Stud. Math. 22, 1–36.
Shavelson, R. J., and Kurpius, A. (2012). “Reflections on learning progressions,” in Learning progressions in science, (Paderborn: Brill Sense), 13–26.
Sikorski, T.-R., and Hammer, D. (2017). Looking for coherence in science curriculum. Sci. Educ. 101, 929–943. doi: 10.1002/sce.21299
Smith, C. L., Wiser, M., Anderson, C. W., and Krajcik, J. (2006). FOCUS ARTICLE: Implications of research on children’s learning for standards and assessment: A proposed learning progression for matter and the atomic-molecular theory. Meas. Interdiscip. Res. Perspect. 4, 1–98. doi: 10.1080/15366367.2006.9678570
Smith, J. P., diSessa, A., and Roschelle, J. (1994). Misconceptions reconceived: A constructivist analysis of knowledge in transition. J. Learn. Sci. 3, 115–163. doi: 10.1207/s15327809jls0302_1
Spikol, D., Ruffaldi, E., Dabisias, G., and Cukurova, M. (2018). Supervised machine learning in multimodal learning analytics for estimating success in project-based learning. J. Comput. Assist. Learn. 34, 366–377. doi: 10.1111/jcal.12263
Steedle, J. T., and Shavelson, R. J. (2009). Supporting valid interpretations of learning progression level diagnoses. J. Res. Sci. Teach. 46, 699–715. doi: 10.1002/tea.20308
Todd, A., and Romine, W. L. (2016). Validation of the learning progression-based assessment of modern genetics in a college context. Int. J. Sci. Educ. 38, 1673–1698. doi: 10.1080/09500693.2016.1212425
Todd, A., Romine, W., Sadeghi, R., Cook Whitt, K., and Banerjee, T. (2022). How do high school students’ genetics progression networks change due to genetics instruction and how do they stabilize years after instruction? J. Res. Sci. Teach. 59, 779–807. doi: 10.1002/tea.21744
Toulmin, S. E. (2008). The uses of argument (8th. Printing). Cambridge, MA: Cambridge University Press.
Holmes, V.-L., and Hwang, Y. (2016). Exploring the effects of projectbased learning in secondary mathematics education. J. Educ. Res. 109, 449–463. doi: 10.1080/00220671.2014.979911
vom Hofe, R. (1998). Probleme mit dem Grenzwert–Genetische Begriffsbildung und geistige Hindernisse: Eine Fallstudie aus dem computergestützten Analysisunterricht [Problems with the limit–Genetic concept formation and mental obstacles: A case study from computational calculus instruction]. J. für Mathematik-Didaktik 19, 257–291.
Keywords: learning progression, evidence-centered design (ECD), machine learning (ML), automated assessment, learning sciences, learning analytics (LA), science education, mathematics education
Citation: Kubsch M, Czinczel B, Lossjew J, Wyrwich T, Bednorz D, Bernholt S, Fiedler D, Strauß S, Cress U, Drachsler H, Neumann K and Rummel N (2022) Toward learning progression analytics — Developing learning environments for the automated analysis of learning using evidence centered design. Front. Educ. 7:981910. doi: 10.3389/feduc.2022.981910
Received: 29 June 2022; Accepted: 04 August 2022;
Published: 22 August 2022.
Edited by:
Muhammet Usak, Kazan Federal University, RussiaReviewed by:
Hassan Abuhassna, University of Technology Malaysia, MalaysiaRodina Ahmad, University of Malaya, Malaysia
Copyright © 2022 Kubsch, Czinczel, Lossjew, Wyrwich, Bednorz, Bernholt, Fiedler, Strauß, Cress, Drachsler, Neumann and Rummel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marcus Kubsch, a3Vic2NoQGxlaWJuaXotaXBuLmRl
 Marcus Kubsch
Marcus Kubsch Berrit Czinczel1
Berrit Czinczel1 Jannik Lossjew
Jannik Lossjew Sascha Bernholt
Sascha Bernholt Ulrike Cress
Ulrike Cress Hendrik Drachsler
Hendrik Drachsler Knut Neumann
Knut Neumann Nikol Rummel
Nikol Rummel