- Faculty of Education in Science and Technology, Technion, Haifa, Israel
This study explores secondary school students’ competencies and motivation to engage in mathematical modelling (MM) tasks in a Virtual Learning Environment (VLE). The study is based theoretically on the didactical modelling cycle and the sub-competencies required for its application, the situated expectancy-value theory, and the VLEs’ design literature. Participants were 770 ninth graders who took part in a 5-day online summer camp, designed as a VLE, aiming at introducing them to mathematics within the tech industry. Research tools include Padlet MM tasks and observations for assessing students’ MM sub-competencies, as well as a pre-post motivation questionnaire for assessing students’ motivation to engage in MM tasks within the VLE. Observations and motivation questionnaires were also used to identify design features of the VLE that support students’ competencies and motivation. Findings show students’ demonstration of diverse levels of MM sub-competencies in forming a mathematical model, and mainly moderate-high levels in solving mathematical questions within the model and in interpreting the results. Students improved their self-concept of ability and task difficulty expectancies, as well as their attainment and interest values of MM tasks. Finally, the VLE’s structured activities and learning materials, along with instructional support and collaborative learning, supported students’ demonstration of MM sub-competencies and motivation to engage in MM. The study contributes to the literature regarding students’ demonstration of MM sub-competencies and their motivation to engage in MM in a VLE setting.
1. Introduction
Students’ experiences in mathematical modelling (MM) tasks can prepare them for their future citizenship, careers, and scientific issues of life by developing their competencies and motivation to understand, solve, and reason about problems in an interdisciplinary and real-world context (Blum and Niss, 1991; OECD, 2001; Niss, 2015; Niss and Højgaard, 2019). In particular, applying mathematics in a scientific-engineering context mediates the relevance of mathematics in STEM fields, by presenting a vision of the skills required by engineers and scientists (Sharkia and Kohen, 2021; Barak et al., 2022).
MM involves solving a real-world problem in a cyclic and iterative way that starts with understanding and simplifying a real-world problem to the extent that it can be solved mathematically, detecting a mathematical model and applying the solution, and interpreting and validating the results in accordance with reality (Blum and Niss, 1991; Kaiser, 2005, 2007; Jankvist and Niss, 2020).
There has been a growing interest in integrating MM into school curricula due to its potential benefits for fostering students’ competencies and interest in mathematics (Niss, 2003; Kaiser, 2005; Blum, 2011; Niss and Blum, 2020). However, substantial research evidence indicates that MM is challenging to school students even when they possess a strong mathematical background, since the MM process is demanding and requires competencies not typically acquired through school mathematics. This barrier prevents students from progressing in the MM solution process (Jankvist and Niss, 2020; Niss and Blum, 2020).
In recognition of the challenges students face due to lack of necessary competencies, there is clearly a growing need to support students’ engagement in the MM solution process. This led to the use of technological tools as didactical aids, such as graphing calculators and spreadsheets (Galbraith and Stillman, 2006), or dynamic geometry software (Greefrath et al., 2018). Yet, research in this field revealed that the use of technology did not significantly diminish students’ difficulties to apply MM competencies and added a further cognitive challenge to use these technological tools within the modelling process. Virtual learning environments (VLEs) have been documented in literature as technological environments that in addition to offering technological and pedagogical aids, are designated to support students’ collaborative learning by providing structured learning materials, facilitating educational interactions through represented information and social interactions, and encouraging students’ active learning (Dillenbourg et al., 2002). The interactive and cooperative learning opportunities in this environment indicate a potential for students’ engagement in MM, since students’ solution of MM tasks in collaboration and through exchange of ideas was found to support the development of MM competencies (Galbraith and Clatworthy, 1990; Maaß, 2006). Yet, scant research had applied VLE to support MM learning, such as the study conducted by Rosa and Orey (2019) who demonstrated that a VLE, which allowed students to communicate with professionals and academic personnel from various regions of the country supported a collaborative and reflective exchange of ideas, which in turn contributed to their progress in the MM solution (Rosa and Orey, 2019).
Along with considering how to provide didactical support for students during MM, it is essential to acknowledge that their barriers to progress in MM may reduce their motivation to engage in MM tasks (Jankvist and Niss, 2020; Niss and Blum, 2020). However, few studies have explored students’ motivation to engage in MM tasks, particularly their expectancies of coping with them and their values related to MM tasks (Krawitz and Schukajlow, 2018).
In this study students’ engagement in MM tasks within a VLE is examined by evaluating their demonstration of MM sub-competencies (Maaß, 2006; Blum and Leiß, 2007; Kaiser, 2007), along with their motivational expectancies and values (Eccles-Parson et al., 1983; Eccles and Wigfield, 2020), and by identifying the design features of the VLE that support both.
2. Theoretical background
2.1. The mathematical modelling framework and sub-competencies
This study is based on the mathematical modelling cycle, suggested by Kaiser (2005) and Blum and Leiß (2007). This framework was chosen, among other modelling cycles, since it emphasizes a student solving MM tasks applying coginitive abilities; thus, it offers a didactical view to direct teachers and students during their engagement in the solution of MM tasks representing real-world problems (Niss and Blum, 2020).
Researchers claim that in order to progress in the MM process, students should possess mathematical and extra-mathematical knowledge, which is related to the cognitive competencies needed to engage in the various MM phases (Maaß, 2006; Hankeln et al., 2019; Niss and Højgaard, 2019; Niss and Blum, 2020). However, there is an additional emphasis in literature on the willingness to apply MM competencies, which is necessary to respond to mathematical challenges in both mathematical and extra-mathematical contexts (Maaß, 2006; Niss and Højgaard, 2011, 2019; Kaiser et al., 2015; Niss and Blum, 2020). Out of several perspectives of MM competencies, we rely on the Germen modelling group concept of evaluation of sub-competencies that students should utilize while engaging in each of the MM phases of the modelling cycle (Maaß, 2006; Kaiser, 2007; Niss and Blum, 2020; Cevikbas et al., 2021). Maaß (2006), identified five sub-competencies, each of which enables to carry out one single modelling cycle phase, while a sub-competency consist of the abilities and skills necessary to conduct each phase correctly and purposefully, as well as the willingness to apply these skills and abilities (Maaß, 2006; Kaiser, 2007). The modelling cycle begins as a modeler problem solver is introduced to a real situation representing a real-world problem, which should be simplified to form a real-world model. Simplifying refers to the sub-competency to understand the real problem and set up a real-world model by making assumptions, recognizing quantities and variables, constructing relations between variables, and prioritizing substantial information over irrelevant information. The second phase involves mathematising the real model and forming a mathematical model. This referes to the sub-competency to set up a mathematical model from the real-world model, which includes formulating mathematically the quantities and relations, simplifying them, reducing them if possible, and using mathematical notations or graphical representations. The third phase consists of working mathematically until mathematical results are obtained. It relies on the sub-competency to solve mathematical questions within the mathematical model (henceforth referred as solving mathematically), including the use of strategies and mathematical knowledge such as procedures to solve the problem, until reaching the mathematical results. The fourth phase is interpreting the mathematical results back to the reality context. This consists of the sub-competency to interpret mathematical results in a real situation that includes interpreting the mathematical results in extra-mathematical context, generalizing the solutions of a special situation, and communicating the results using mathematical language. The fifth phase is validating the interpreted results back to the to the context of the real-world problem. This requires the sub-competency to validate the solution that includes critical examination and reflection on the solution, repeating the whole modelling process or parts of it when the solution does not suit the situation, considering other ways to solve the problem and questioning the model in general. In case that one cycle of five phases is not sufficient to resolve the real-world problem, this process should be repeated several times, either as a whole or partially. In this study, the students are not involved in the validation phase of the modelling cycle, thus we do not consider the validating sub-competency in our data analysis.
2.2. Students’ motivation to engage in MM tasks
This study relies on the situated expectancy-value theory (SEVT), which is at the core of achievement motivation theories; thus, it is suitable to be explored during engagement in academic tasks (Wigfield and Eccles, 2020; Schukajlow et al., 2022). This theory was formed based on the expectancy-value theory (Eccles-Parson et al., 1983), which describes how students’ choice of engagement, persistence, and performance in an academic activity are related to their expectancies to succeed in it, and their value of the activity. The SEVT theory further emphasizes that students’ expectancies and task value are influenced by personal factors including the social, cultural, and situational aspects (Atkinson and Reitman, 1956; Eccles-Parson et al., 1983; Eccles and Wigfield, 2020; Wigfield and Eccles, 2020). The definition of individuals’ expectancies to succeed in a given academic task stem from earlier theories and is defined by their self-concept of ability to perform appropriate skills required in it and their evaluation of the difficulty of the task (Eccles-Parson et al., 1983). Individuals’ value of their success in an academic task comprises four main aspects. First is the attainment value, which is the importance of succeeding in the task, in a sense that it strengthens personal characteristics, challenges, fulfills, empowers, or meets social needs. Attainment value derives from the extent of the fit of the individuals’ perceptions of the characteristics of the task and their perceptions of themselves (self-schema), their social and personal identities, and the extent that the task enables the performance of behaviors that are central to them or that express the individuals’ characteristics. The second aspect is the intrinsic value, which is the immediate enjoyment derived from engaging in the task; thus, a high value is expressed through a deep engagement and persistence in it. The third aspect is the utility value, which is the extent of the usefulness of the task for an individual’s present or future goals, in terms of extrinsic motivation, career goals, and desired end-state. The fourth aspect is the cost value, which is the interference of the activity in performing other activities; it is linked to negative aspects such as anxiety, fear of failure, and the amount of effort required (Eccles-Parson et al., 1983; Wigfield and Eccles, 1992, 2020; Eccles and Wigfield, 2020).
2.3. A VLE for supporting students’ engagement in MM tasks
A virtual learning environment (VLE) is a technology enhanced learning environment, designed to support teaching and learning through the direct interaction of tutors and students (Dillenbourg et al., 2002). As with other online learning platforms, VLEs enable learning objectives to be focused on, they scaffold students’ understanding of the relevant content, and support learners in their effort to master it (Mayer, 2019). In fact, VLEs are adaptable to a variety of educational and professional training platforms, such as schools, organizations, and universities (Mueller and Strohmeier, 2011), and they can be used to promote a wide range of skills (Dillenbourg et al., 2002; Limniou and Smith, 2010; Estriegana et al., 2021). The design of a VLE needs to be aligned with the cognitive abilities of the learners as well as acknowledgement of the aspects that motivate them (Ainley and Armatas, 2006).
In this study, we follow the VLE’s design features that were described by Dillenbourg et al. (2002). First, as a designed information space, VLEs enable online sharing of organized and accessible learning materials, such as audios, videos, and simulations. The effectiveness of these activities on student learning relies on the quality of learning materials and the support of teachers, as well as the relevency of the learning materials to students’ abilities, prior knowledge and interest. Second, as a social space, VLEs allow collaboration of tutors and students, either via synchronous or asynchronous modes, which can further contribute to providing valuable feedback from tutors and peers during collaborative learning. It relays on norms of collaboration and different patterns of it such as speaking in videoconferencing, exchanging materials online and building online learning communities. Collaboration in a VLE can be enhanced through interactivity in students’ learning and instructional support that scaffolds and provides examples; further, such online community of inquiry allows students to construct knowledge and understanding by asking questions, answering colleagues, and reflecting of other ideas in the group. Third, as a represented virtual space, though it is virtual, it enables to create awareness of studetns being in a particular online space; such as the virtual experience of parallel group work in solving problems in separate virtual breakout rooms, or attendance in a virtual tour; this experience can influence participants’ motivation and cognitive behavior. Fourth, VLEs support active engagement of students during learning, since when provided with a set of activities, they may produce content and share it, such as notes, getting references from tutors, or creating text, webpages, and graphical objects. Fifth, VLEs integrate various technologies and pedagogical approaches, such as to provide and manage information and students’ communication.
Our study builds upon earlier research into the impact of VLE features on students’ learning as well as motivation to participate in learning within the VLE (Ainley and Armatas, 2006; Orey and Rosa, 2018). We address the following research questions:
1. What MM sub-competencies do students demonstrate while engaging in MM tasks in a VLE?
2. How do students express their motivation to engage in MM in a VLE, in terms of their expectancies and values?
3. How do VLE design features support (if at all) students’ MM sub-competencies and motivation to engage in MM?
3. Methodology
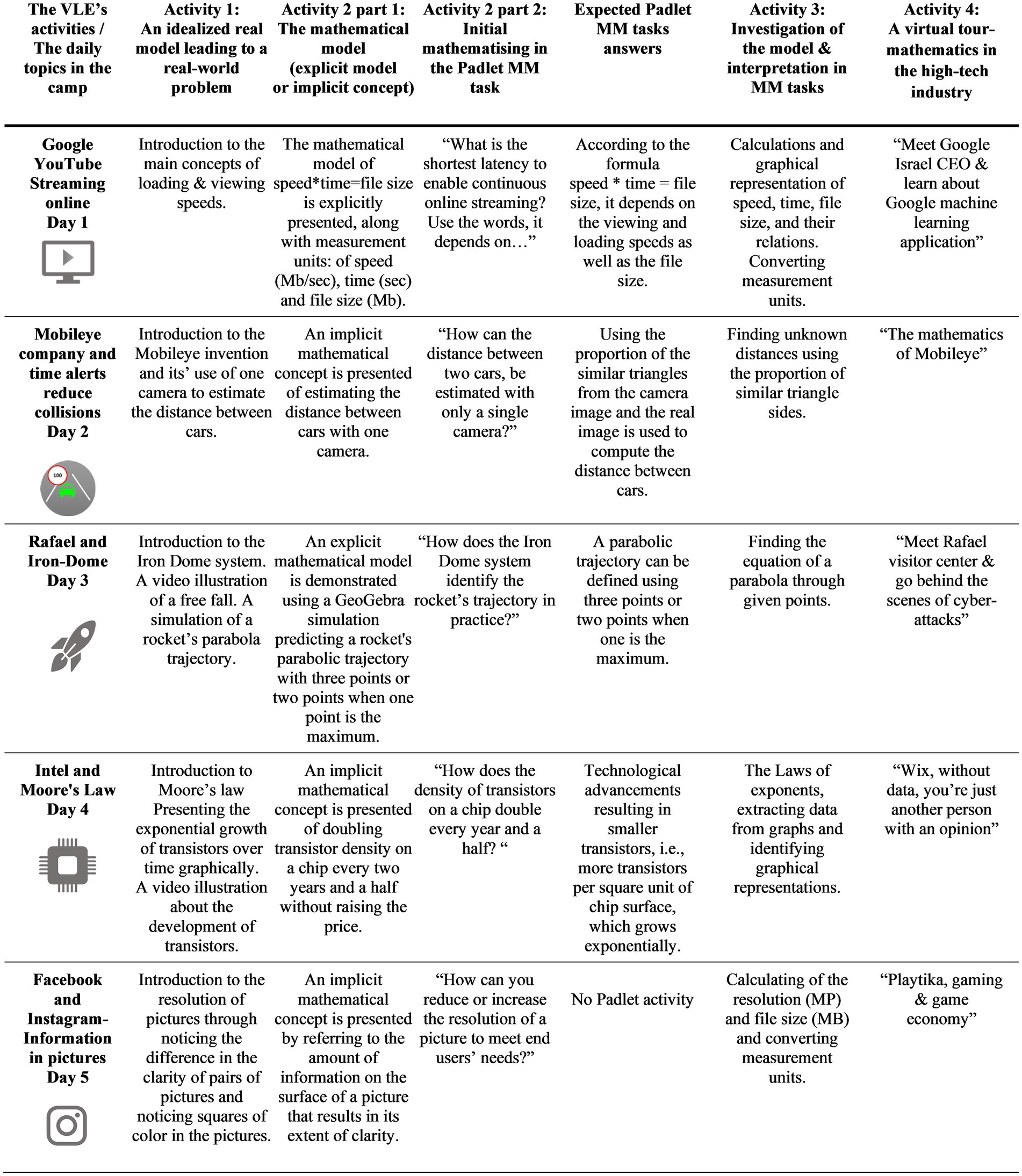
The study explored an online summer camp, held in August 2020, during the COVID-19 outbreak, in two subsequent time cycles. The camp was structured as a VLE and aimed to introduce students who graduated from ninth grade to mathematics within the tech industry. Each cycle consisted of 5 days with 2 h of MM activities based on MM tasks that were designed in scientific-engineering contexts for the Integrated Math & Technology (i-MAT) research and development project (Kohen and Orenstein, 2021; Kohen and Gharra-Badran, 2022). This project involves the design of MM tasks as well as PD programs for math leaders and teachers to practice the tasks in a school context (Kohen and Nitzan-Tamar, 2022). Coaches in the camp were STEM undergraduate students with no preliminary professional experience in teaching, but with extensive background in STEM. Most of them worked in both camp’s cycles. They participated in a one-day training that was instructed by two members of the i-MAT research and development team. The training included a thorough engagement with the didactical aspects of the i-MAT MM tasks, such as how to encourage discussion with students and more. In particular, the schedule and activities of each day were reviewed. Further, the first author of this paper explained about the objectives of the research in aspects of students’ competencies and motivation as well as the timing of applying the research tools.
3.1. The VLE’s activities and MM tasks
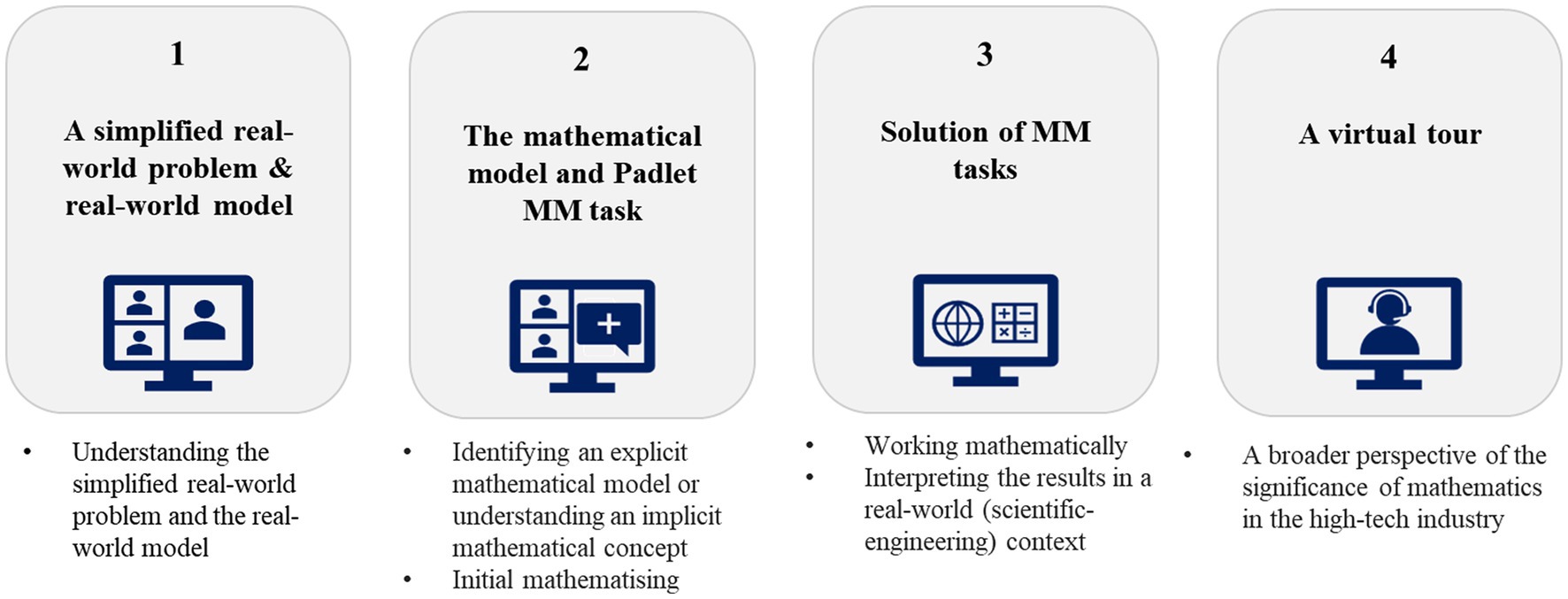
The summer camp was structured as a VLE, aimed to function as a represented virtual space in which students met through video conferencing each day for 2 h of MM activities, conducted in groups of 20–25 students in separate breakout rooms, supervised by coaches. These MM activities were designed with a scientific-engineering context, to demonstrate how mathematics can be applied to high-tech applications. Coaching instruction and online learning materials, which represent the VLE as a designed information space, aimed to mediate the mathematical and scientific-engineering contexts in the tasks. Various media and pedagogical approaches were used to meet this objective, including textual conceptualization, online Padlet bulletin board, video, and picture illustrations, and GeoGebra simulations. The VLE aimed to function as a social space, with the coaches conducting the MM activities, leading the discussion, managing students’ participation, providing feedback, and addressing students’ sharing of ideas in the online chat. The VLE’s daily MM activities (see Figure 1) aimed to provide students with a comprehensive understanding of the didactical modelling cycle solution process. It targeted students’ active engagement while experiencing each phase separately, moving from one phase to another, and applying MM sub-competencies within phases.
The first- and second-MM activities emphasize the VLE as a designed information space, by mediating the scientific-engineering background and the mathematical model through online learning materials and the coaching instruction support. The first activity is based on one of the i-MAT MM tasks introduced each day of the camp, presenting a simplified real-world model related to an application of a well-known high-tech company. The scientific-engineering background of the task is presented in a simplified way and leads to a real-world problem that can be solved with secondary school mathematics. In this activity students are expected to understand the simplified real-world model and problem. For instance, on the first day of the camp, which focused on exposure to the Google company, students were introduced to the YouTube streaming online MM task (for the full task, see http://www.imat.org.il). The task presents a simplified scientific-engineering background, with clear explanations of online streaming, viewing, and loading concepts. There is then a problem: “How can direct and continuous streaming be guaranteed?” This is followed by introducing and explaining the latency time concept, as a preventative measure (Figure 2 illustrates sample slides of this task).
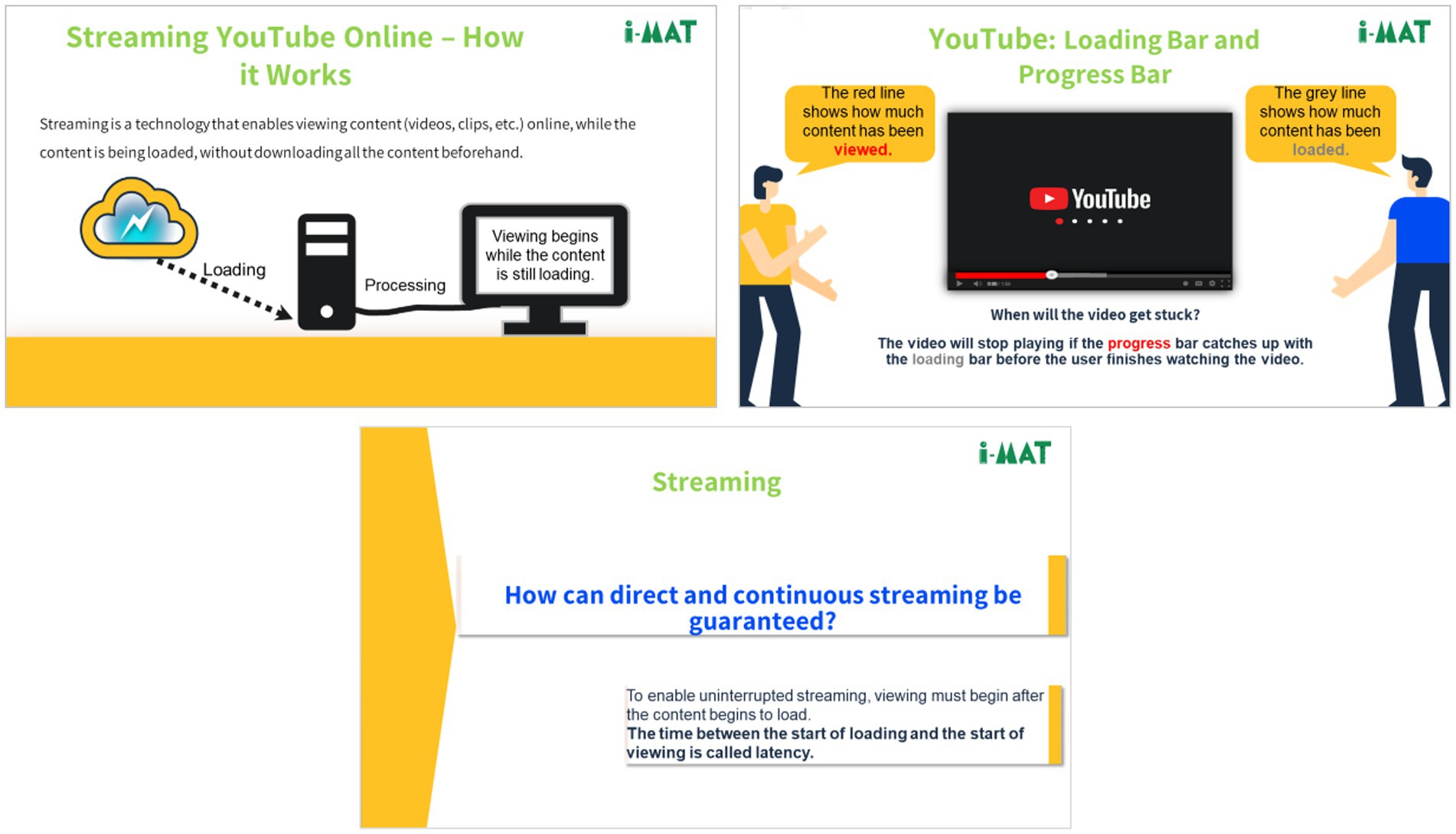
Figure 2. Sample slides from the YouTube MM task, presenting the simplified scientific-engineering real-world model and the real-world problem, as part of the VLE’s first activity.
The second activity involves introduction to the mathematical model and initial mathematising of the real-world problem. In the first part of this activity, students are introduced to an explicit mathematical model or implicit mathematical concept, which can be used to solve the problem. For instance, regarding the YouTube MM task, students are introduced to the explicit mathematical model with the given formula of speed*time = file size, which corresponds to their prior knowledge of mathematical topic of motion problems. It is given explicitly due to the added difficulty of relating the scientific-engineering concepts to the motion problems topic. Further, since streaming involves both loading and viewing, it requires extra mathematical knowledge which is provided to students. For instance, it is explained that the loading and viewing file size are equal when the viewing is complete. Moreover, measurement units of speed (Mb/s), time (s), and file size (Mb) are explained (see Figure 3).

Figure 3. Sample slides from the YouTube MM task, presenting the explicit mathematical model, in the first part of the VLE’s second activity.
Having grasped the explicit mathematical model, or implicit mathematical concept related to the mathematical model, students are then asked to apply initial mathematising by answering a question in the Padlet bulletin board application (henceforth referred as the Padlet MM task). When exposed to an explicit mathematical model, students are expected to identify the use of it for the solution of the problem. Whereas, if exposed to an implicit mathematical concept, they should express an understanding of how it relates to the solution of the problem. As an example, in the YouTube MM task, students were asked: “What is the shortest latency to enable continuous online streaming? start your answer with the words: it depends on….” The pre-provided explicit model is speed*time = file size, and students are expected to identify that it depends on the viewing and loading speeds as well as the file size. Another example is the Moore’s law Padlet MM task, in which students are asked: “How does the density of transistors on a chip double every year and a half?” The pre-provided implicit mathematical concept is based on that the technological advancement of transistors leads to the rapid growth of density per square unit of a chip. Students are expected to express their understanding and explain the rapid growth which relates to their prior knowledge of the law of exponents.
The Padlet MM tasks are part of the various technological tools embedded in the VLE, and were applied only during the first 4 days, while in the fifth day the initial mathematising was conducted in collaboration in the plenary. After the Padlet MM task, students return to the plenary, where the coach displays the responses in the Padlet and assures understanding of the mathematical model.
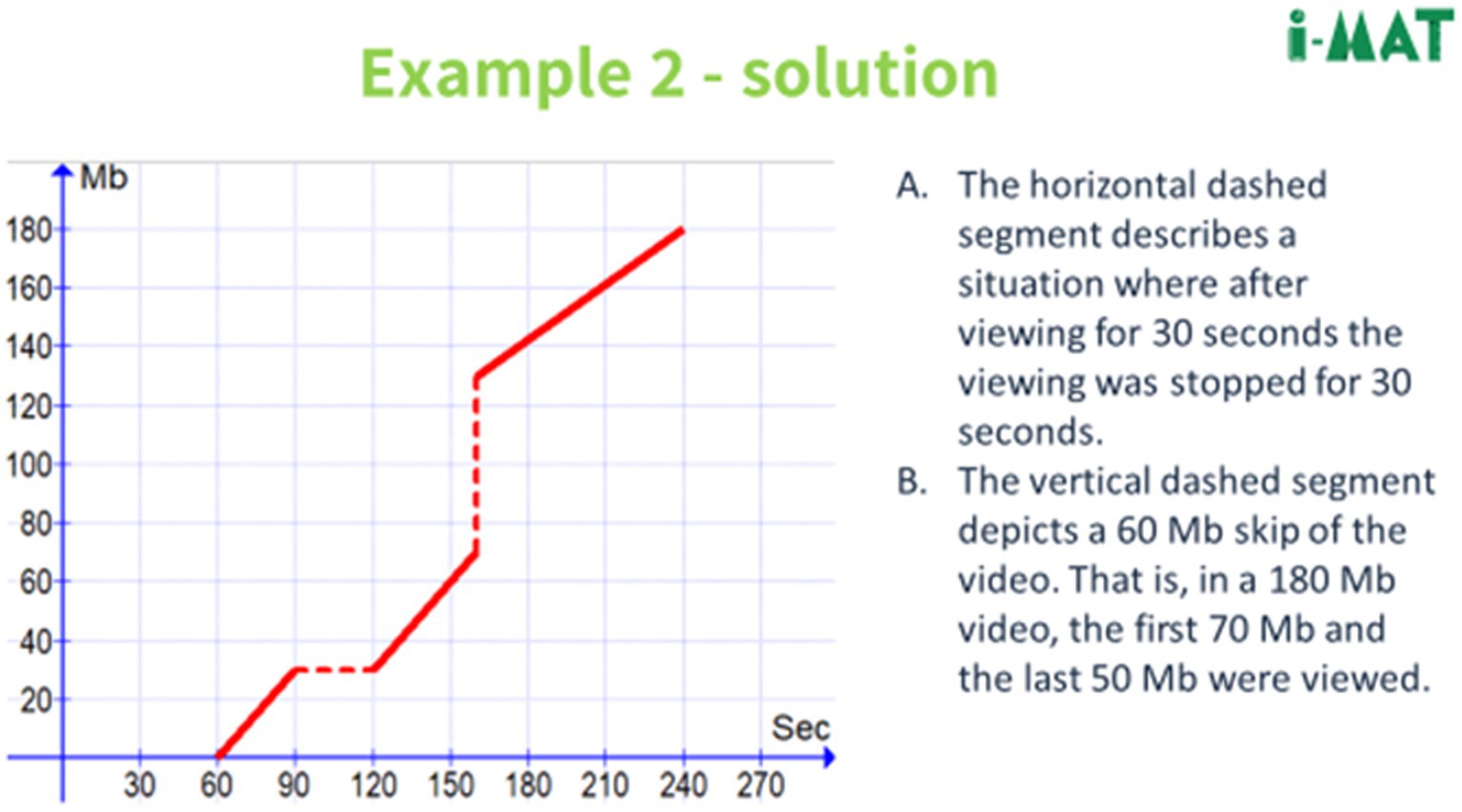
The third activity is designed for the coach and students’ collaborative learning to foster a social space in the VLE as well as active engagement in solving MM tasks (referred to as examples in the summer camp slides), where they are expected to work mathematically to obtain mathematical results. For instance, one task that relates to the YouTube context requires calculating the possible range of latency time, while the loading and viewing speeds, as well as the viewing time were given (see Figure 4, example 1). Further, these tasks also include sections where students are required to interpret the results in a scientific-engineering real-world context, such as to interpret a graphical representation of the online streaming in terms of its meaning in a scientific-engineering context (see Figure 4, example 2).
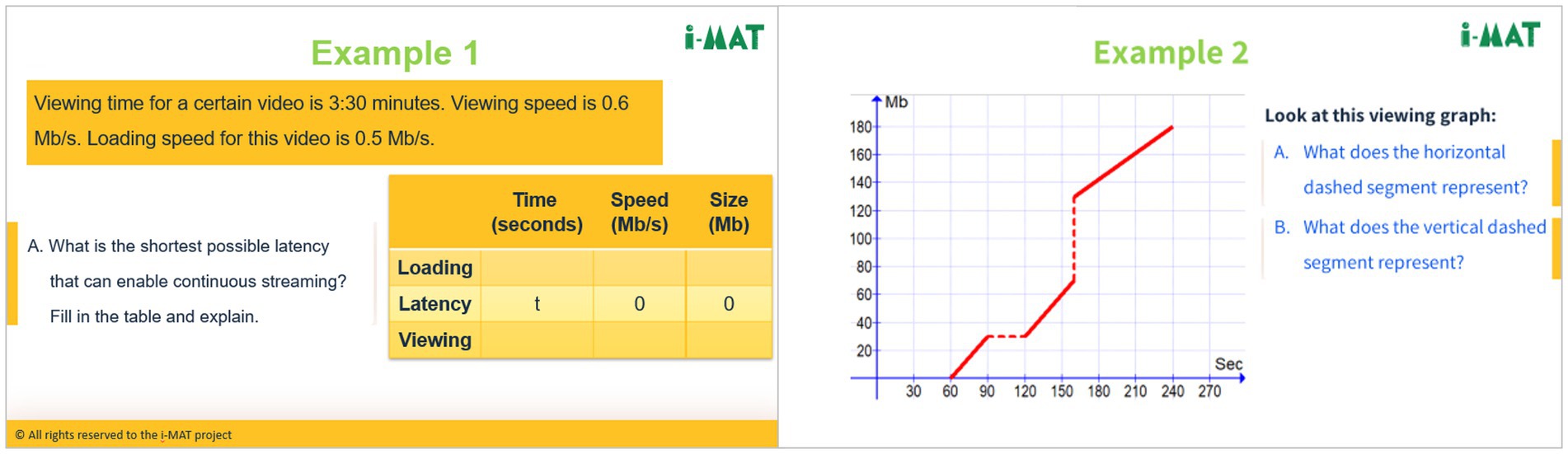
Figure 4. Sample slides from the YouTube MM task, presenting two MM tasks in the VLE’s third activity.
The fourth activity emphasize the VLE as a represented virtual space, including a virtual tour in the high-tech company related to the application that was introduced in the MM task, in each of the camp days. Students watched pre-recorded videos conducted with a leading scientist or engineer at that company, which aimed to broaden their perspective regarding the use of mathematics in the high-tech industry. Some of the presenters motivated the students by explaining the significance of math in solving real-world technological challenges, such as a pre-recorded interview that was held with Google Israel CEO, conducted by a girl in the ninth grade (see Figure 5). Others introduced additional aspects of the applications that relate to the MM task during that camp day, or to additional applications developed at the company. An example for that is a pre-recorded lecture by a Google engineer (see Figure 5), who explained the purpose of applying machine learning in Google, and more specifically, how objects are recognized by computer software and the significance of mathematics in this process.
Figure 6 summarizes the VLE’s 5 days of activity, elaborating on the four activities applied in the context of each day.
3.2. Participants
The participants consisted of 770 students who graduated the ninth grade (44% females) from all over Israel and that had participated in one of two cycles of the online summer camp. All the participants were devided into 34 groups (17 in each camp cycle); each group included between 20 and 25 students and a coach. Most students (about 90%) were in a track of studying mathematics at an advanced level in 10th grade. The summer camp included various sectors of the Israeli society and students that are resident of central and peripheral areas in Israel, yet we did not oblige identification of these aspects in the questionnaires. The summer camp was advertised online intensely in various media channels such as social media Facebook, websites, and more, trying to reach ninth grade students, parents, and teachers. The registration was free of charge and no selection of the registered students was made.
This study was approved by the university’s Institutional Review Board (#IRB-2020-069). A consent form, which stated the study’s objectives, was signed by the parents when they registered their children to the summer camp, in which they agreed to the research’s collection and analysis of data from the summer camp.
3.3. Research tools
Three research tools are used in this study: (a) Four Padlet MM tasks that were collected as part of the second activity in the first 4 days of the summer camp, and aimed to assess students’ MM sub-competencies while applying the initial mathematising phase; (b) Four different observations that were held during the first day of the summer camp in four different groups, aiming to assess students’ MM sub-competencies while working mathematically and interpreting. Observations were further explored for the VLE’s features aimed at supporting students’ MM sub-competencies; and (c) a pre-post MM SEVT motivation questionnaire close and open-ended questions were used to examine students’ motivation to engage in MM tasks in the VLE, and the VLE’s support in students’ motivation respectively.
3.3.1. The Padlet MM task
The Padlet is a collaborative web platform in which users can upload, organize, and share content using virtual bulletin boards. It enables to post anonymous online comments that are automatically saved in a designated online file. In each Padlet MM task, students were expected to apply initial mathematising of the real-world problem, based on the previously provided information regarding the mathematical concepts and relations. By initial mathematising we mean that they either had to identify an explicit mathematical model, or understand an implicit mathematical concept, each provided before the task.
3.3.2. Observations
Each cycle of the summer camp included 17 groups that worked online with one coach each. Each group was recorded all day throughout the 5-day camp, so in total there were 170 (17*2 cycles*5 days) recorded observations. Out of the 34 recorded observations of the first day of camp, we randomly selected four observations of different groups led by different coaches. The context of these observations was the “Google—streaming YouTube.” Three observations were retrieved from the first cycle of summer camp, and one from the second cycle. All four observations were transcribed verbatim. We chose to focus on merely four observations, as we aimed to detect students’ MM sub-competencies, rather than a change in them which we did not anticipate would occur in a 5-day camp. Second, the analysis of the four observations had shown to provide sufficient data to display students’ demonstration of MM sub-competencies. Third, we chose to avoid the complexity of analysis within different MM tasks context, which would have required comparing normalized data.
3.3.3. MM SEVT motivation questionnaire
3.3.3.1. The close ended part: Motivation to engage in MM tasks
The questionnaire was designed for the current study, based on the Situated Expectancy-Value Theory (SEVT) of Eccles and colleagues, regarding engagement in a mathematics academic task (Eccles-Parson et al., 1983; Eccles and Wigfield, 2020). The close-ended pre-post questionnaire part measures students’ motivation to engage in MM tasks and was distributed at the end of the first day of the camp and at the end of the fifth day. Students were instructed to respond to the questionnaire after experiencing the solution of MM tasks in a scientific-engineering context as initial experience and continuous experience. They were required to rank items in the questionnaire using a six-level Likert scale, ranging from 1—“strongly disagree” to 6—“strongly agree.” Students’ expectancy of self-concept of ability was measured by items regarding their demonstration of MM sub-competencies required to carry out the modelling cycle phases (N = 8). An example of an item evaluating students’ expectancy of self-concept of ability regarding the sub-competency of understanding the real problem and set up a real-world model is: “When I tackle a complex situation in mathematics, I try to simplify it by identifying conditions and making appropriate assumptions.” Their expectancy regarding the task’s difficulty was evaluated by one item regarding the adaptability of the task’s difficulty to students’ current knowledge and understanding. Students’ value of MM tasks was evaluated by items regarding their attainment value (N = 2) in relation to their importance for personal growth, for example: “After I solve a task, I think back on my way of thinking during the solution, which helps me understand and learn more in the future.” Furthermore, items regarding their intrinsic value (N = 4) included for example: “I am interested in solving real-world mathematical problems that are relevant to everyday life.” Lastly, utility value of engaging MM tasks was evaluated by one item regarding the benefit of effort for achieving future goals. We decided not to include items of cost value in the questionnaire, due to their negative context, which was not relevant in this study since students were not obligated to register or remain at summer camp.
Construct validity was assessed through a Principal Axis Factor (PAF) with a Varimax (orthogonal) rotation that confirmed the two main factors of the questionnaire, i.e., the expectancy and value, with a simple structure (factor loadings ≥ 0.30). Further content validity, which was carried out by two experts as judges, confirmed the sub-division to factors within each of the two main factors.
3.3.3.2. SEVT questionnaire open-ended part: Motivation to engage in MM in a VLE
The open-ended question in the pre-post questionnaire part aimed to investigate what motivated students to engage in MM in a VLE setting. The pre-questionnaire was applied after their initial experience in MM activities in the first day of camp, and focused on what motivated them to join the camp. They were asked to continue with the following: “I enrolled in this summer camp because…,” The post-questionnaire, applied in the end of the last day of camp, focused on what motivated them to remain in the summer camp. Students were asked to continue with the following: “During the summer camp, I enjoyed…” While tackling mathematical and extra-mathematical contexts, students managed demanding MM academic tasks without being obligated to enroll or remain in the summer camp. Since asked about their choice to enroll and about their experiences of enjoyment, we expected their answers to include their expectancies and values of the design features of the VLE while connecting it to their engagement, persistence, and performance in the summer camp. We relied on the expectancy-value theory of students choosing to engage, persist, and perform in an academic activity based on their expectancies and values (Eccles-Parson et al., 1983).
3.4. Data analysis
As a response to the first research question, we analyzed students’ MM sub-competencies, as captured on the Padlet MM task and the observations, using a directed content analysis (Hsieh and Shannon, 2005). The unit of analysis for the Padlet MM task was students’ full response to this task as evidence for their MM sub-competencies during the mathematising phase. With respect to observations, the unit of analysis was determined by students’ replies during the collaborative solution of MM tasks, where students could demonstrate their sub-competencies. Since the first two activities (see Figure 1) did not include collaborative solution of MM tasks, it could not add data regarding students’ demonstration of MM sub-competencies during the simplifying nor the mathematising phases. Therefore, we applied directed content analysis focusing on analysis units that were taken from the third activity that was focused on the working mathematically and interpreting phases.
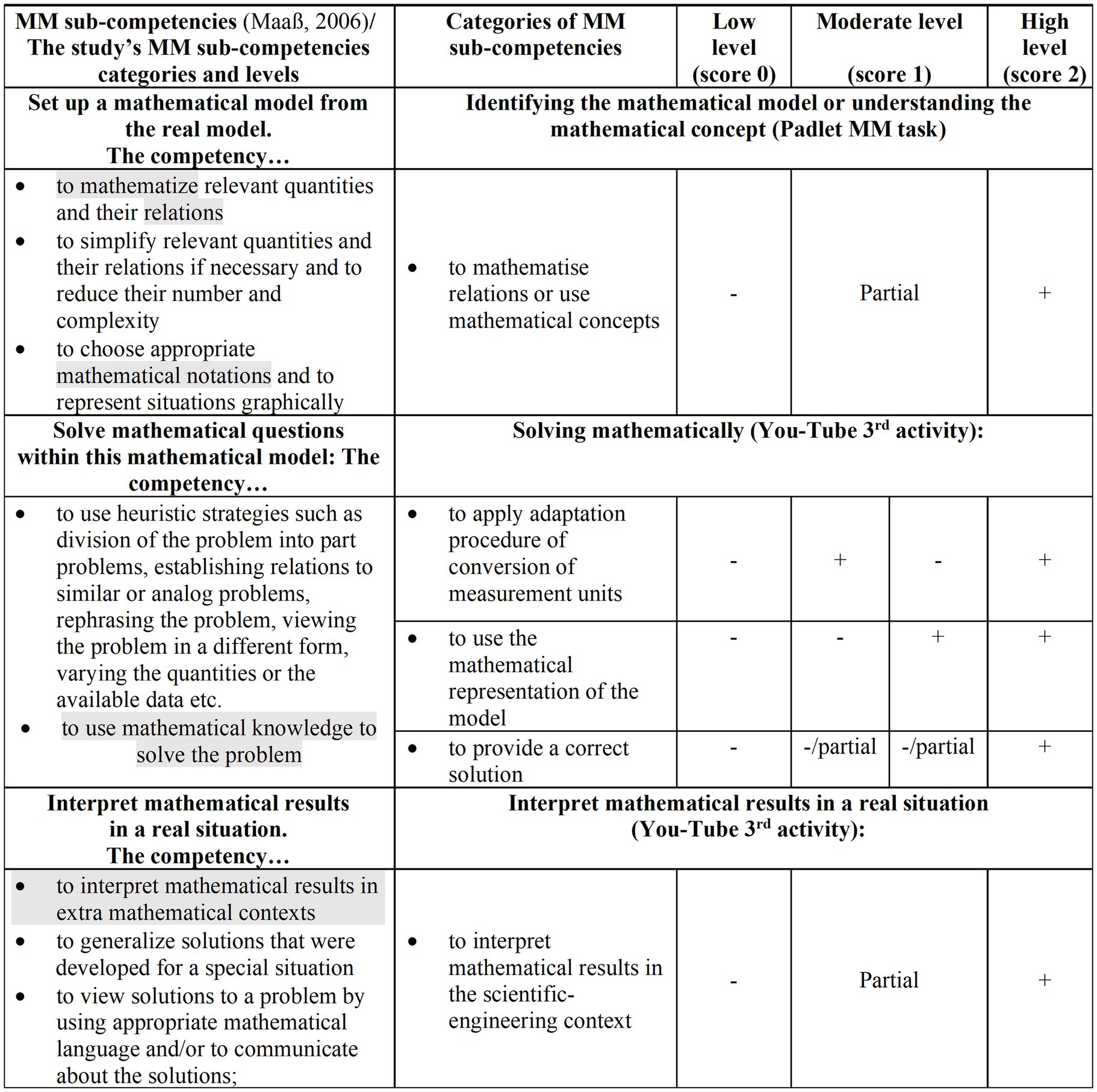
Coding was held based on a rubric designed for this study, which includes two dimensions: the type of sub-competency and its level. For the first dimension, we based our coding on the definitions made by Maaß (2006), identify students’ MM sub-competencies. For exploring these sub-competencies in the context of the current study we further refined or added categories related to each of the sub-competencies, as follows: regarding the Padlet analysis units, considering the initial mathematising as parallel to the mathematising phase, we aimed to detect students’ sub-competency to set up a mathematical model from the real model (Maaß, 2006). Yet, initial mathematising for the MM tasks explored in this study depends on the explicit mathematical model or implicit mathematical concept provided before the task at hand. Therefore, we rephrased the sub-competency to identify the mathematical model or understand a mathematical concept. Since Maaß (2006) definition includes mathematising quantities and relations, simplifying and reducing them, and the use of mathematical notations, we formed a specific category of mathematising relations or using mathematical concepts.
Regarding the third activity of MM tasks’ solution in the YouTube scientific-engineering context, we first aimed to detect students’ sub-competency of solving mathematically (Maaß, 2006), while applying the working mathematically phase. Within the definition by Maaß (2006) of using strategies and using mathematical knowledge to solve the problem, we suggest the categories of applying adaptation procedure of conversion of measurement units, using the mathematical representation of the model and providing a correct solution. Second, we aimed to detect students’ sub-competency of interpreting mathematical results in a real situation (Maaß, 2006) during the interpreting of the results phase. Within the definition made by Maaß (2006) of interpreting mathematical results in extra mathematical contexts, generalizing solutions, and using mathematical language, we suggest the specific category of interpreting the results in a scientific-engineering context.
Once the first dimension of the rubric was applied, analysis units were then ranked to one of three levels based on the second dimension of the rubric. When a category is correctly applied, an analysis unit is assessed at a high level of the sub-competency, when partially applied it is coded at a moderate level, and when it is incorrectly applied it is coded at a low level.
The rubric is presented in Figure 7, where the first column shows the original definitions of sub-competencies by Maaß (2006). The first dimension of the rubric appears on the second column, by adapted categories describing the sub-competencies. A second dimension is represented by the last three columns, namely the level of sub-competencies. Based on the shaded sentences, we adapted the categories of sub-competencies to the context of the i-MAT MM tasks. There is a + or − sign to indicate whether the category has been applied correctly or incorrectly.
The rubric was designed by the first author and validated and refined over a large extent of students’ answers data in this research, reaching 90% of agreement between two mathematical education experts.
As a response to the second RQ, we analyzed students’ motivation to engage in MM tasks as captured in the closed-ended part of the MM SEVT motivation questionnaire. MANOVA statistical tests were applied to investigate the difference between the two-time measures regarding both aspects of students’ motivation toward MM tasks engagement, i.e., expectancies and value. Note that due to the large number of study participants and the sampling method, we assumed that the conditions for this multivariate test are met.
For the third research question, we kept the focus of our analysis on the third activity. We aimed to investigate how the VLE’s design features support students’ demonstration of MM sub-competencies. As a first step, a thematic analysis of all the replies by coaches and students during the collaborative solution of MM tasks was conducted. In the course of data analysis, seven emerging themes of the VLE design features were revealed (Dillenbourg et al., 2002). The second step was to extract paragraphs with double coding for both MM sub-competencies (as detailed above) and VLE design features, for illustrating how the VLE design supported students’ MM sub-competencies.
Finally, to examine students’ motivation to engage in a VLE of MM, we focus on the open-ended MM SEVT motivation questionnaire. We applied directed content analysis (Hsieh and Shannon, 2005), aiming to find categories of expectancy (self-concept of ability and task difficulty) and value (attainment, interest, and utility) which are related to the VLE’s features. The units of analysis were students’ responses, yet it was possible that one response could have been divided into smaller units that were coded according to several categories. On average, 1.3 coding units were attributed to each student’s response for the pre-questionnaire and 1.16 coding units were attributed per student in the post-questionnaire. During the analysis, we identified categories relating only to the value aspects of attainment (N = 3 categories), intrinsic (N = 7 categories), and utility (N = 1 category). Attainment and intrinsic value were addressed by sub-categories within the VLE’s design context, while the utility was addressed generally. Based on this, we were able to relate only the attainment and intrinsic sub-categories to the VLE’s design features (Dillenbourg et al., 2002).
For all the qualitatively analyzed data, i.e., the Padlet MM task, observations data, and the open-ended question data, we calculated frequencies to display a quantitative picture of the data.
4. Findings
4.1. Students demonstrated MM sub-competencies while engaging in MM tasks in a VLE
4.1.1. Initial mathematising in the Padlet MM tasks
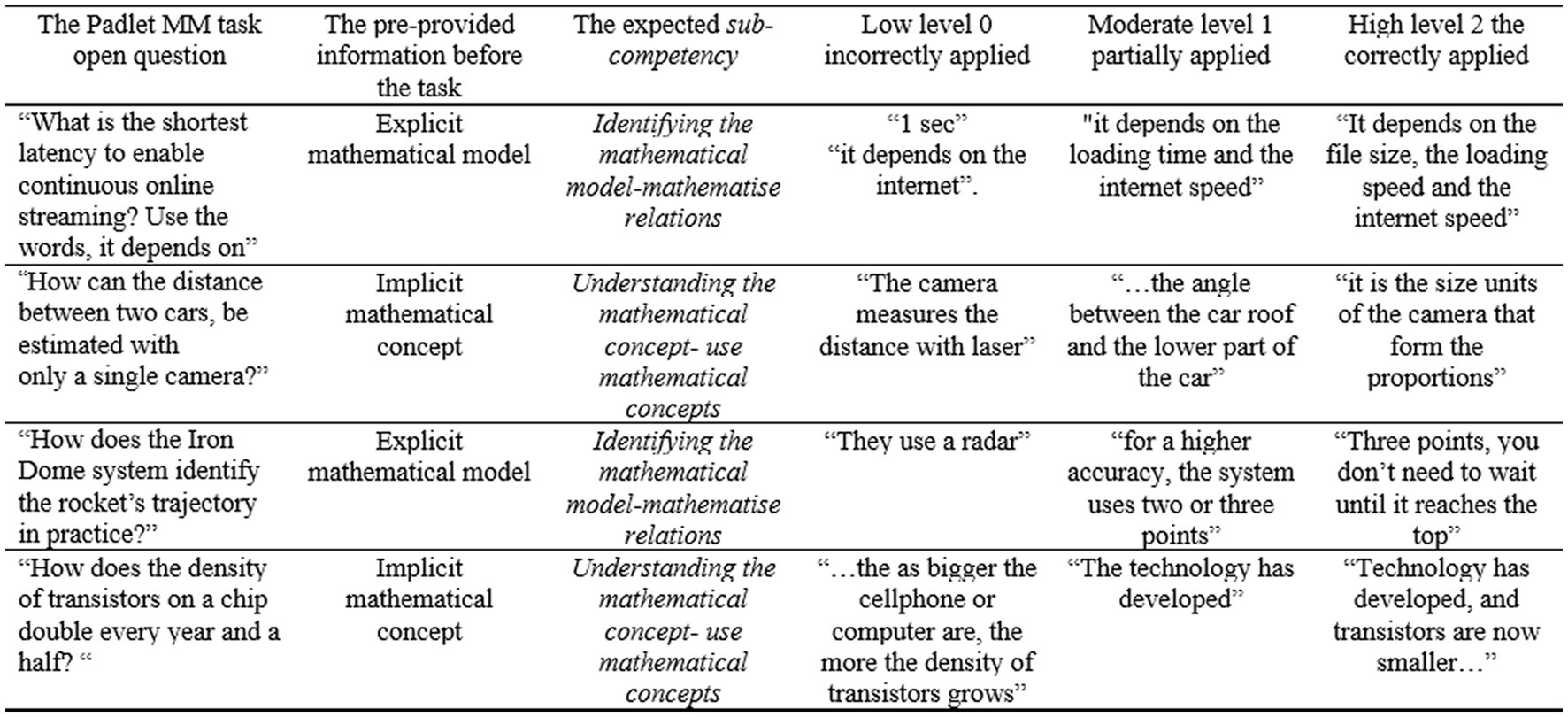
Students’ responses to the various Padlet MM tasks were assessed for revealing their MM sub-competency of setting up a mathematical model from the real-world model during the mathematising phase. With our acknowledgement of the diversity of MM tasks in their scientific-engineering and mathematical contexts, we focus on each task separately, aiming to explore which tasks enabled students’ demonstration of this sub-competency as expected in the task. Figure 8 presents examples of students’ answers to exemplify the content analysis procedure and ranking of students’ identification of the mathematical model or understanding the mathematical concept.
Figure 9 displays the frequencies of levels in this sub-competency, while ranked answers per task accumulate to 100%.
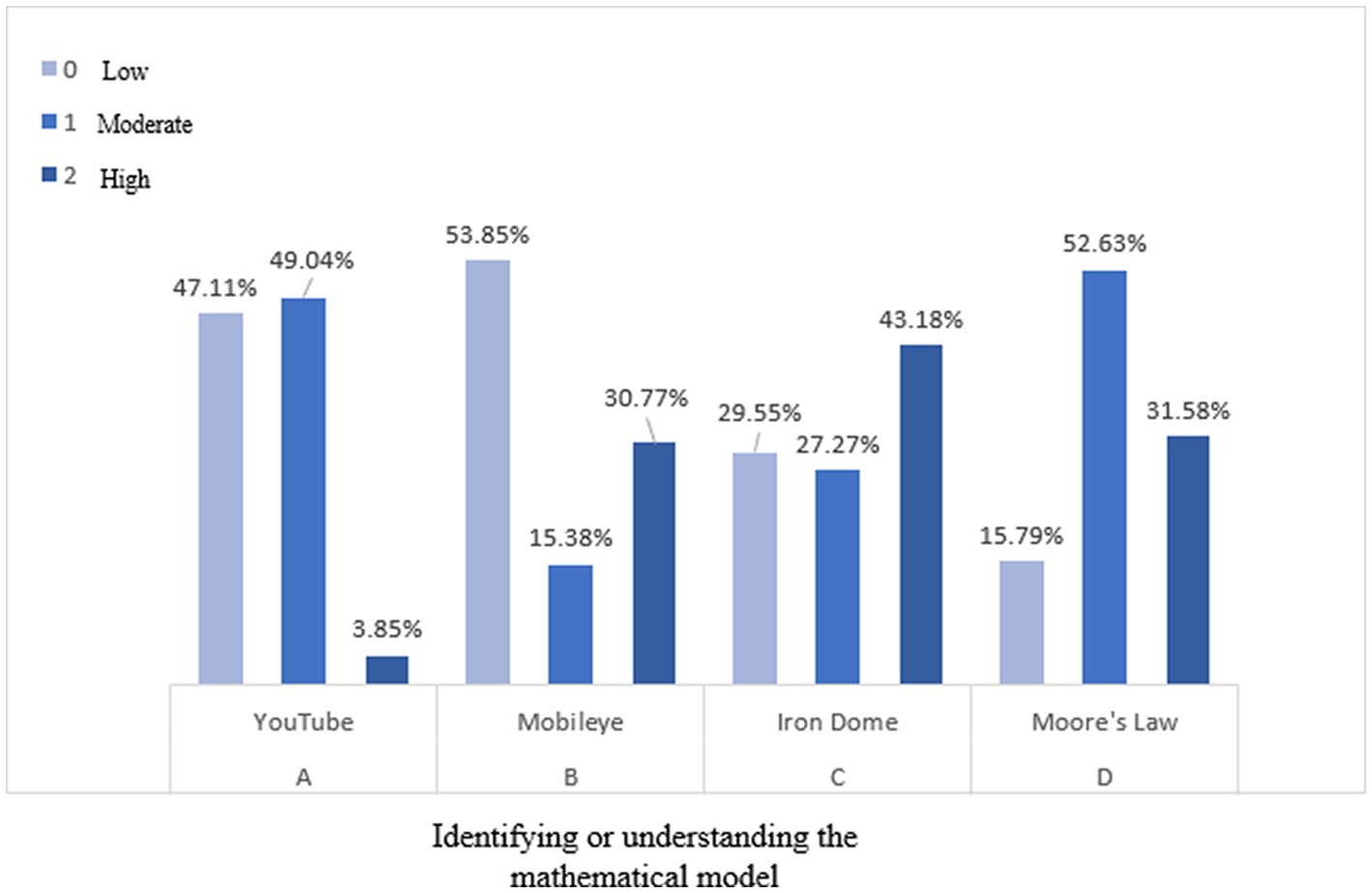
Figure 9. The levels of sub-competencies to identify the mathematical model or understand the mathematical concept in the various Padlet MM tasks.
The YouTube MM task was the first experience of students in initial mathematising. Before the Padlet the scientific-engineering context was mediated through conceptualization in text and pictures leading to an explicit mathematical model representation of speed*time = file size. Though it related to students’ prior knowledge of motion problems, it seems that they were challenged in identifying it as an answer to the problem presented in the MM task. Most of the answers were ranked to low or moderate levels of identifying the mathematical model sub-competency (47.11, 49.04%), including no or partial reference to the loading and viewing speeds or to the file size.
Moving on to the Mobileye MM task, students were challenged with a totally open question that uses implicit mathematical concept of estimation of the distance between cars using one camera. Though it related to students’ prior knowledge of the proportion of similar triangles, it obliged possessing extra-mathematical knowledge regarding the camera-image and real image that was not provided before the task. Furthermore, the presented text and pictures did not include a reference to this concept. It resulted mainly in answers ranked to low or moderate levels of understanding the mathematical concept (53.85, 15.38%), including no use or partial use of the proportion concept. It is noteworthy that 30.77% of answers were ranked to high level. In the Iron Dome MM task, an explicit mathematical model was presented before the task related to students’ prior knowledge of the parabola. It was mediated through various media such as text, pictures, videos, and GeoGebra simulations presenting and experiencing the parabola trajectory of the rocket. The mathematical model of using three or two points when one of them is the maximum point was explained. It resulted in most of answers ranked as moderate or high levels of identifying the mathematical model sub-competency (27.27, 43.18%), including partial or correct reference to the points. Finally, in the Moore’s law Padlet MM task, the implicit mathematical concept of the rapid growth of the density of transistors was related to students’ prior knowledge of exponents. The development of technology resulting in smaller transistors was mediated through various media such as text, pictures, and videos. This resulted in most of the answers ranked to moderate or high levels of understanding the mathematical concept (52.63, 31.58%), including partial or correct reference to the rapid growth of density per chip.
4.1.2. Working mathematically and interpreting in the third MM activity
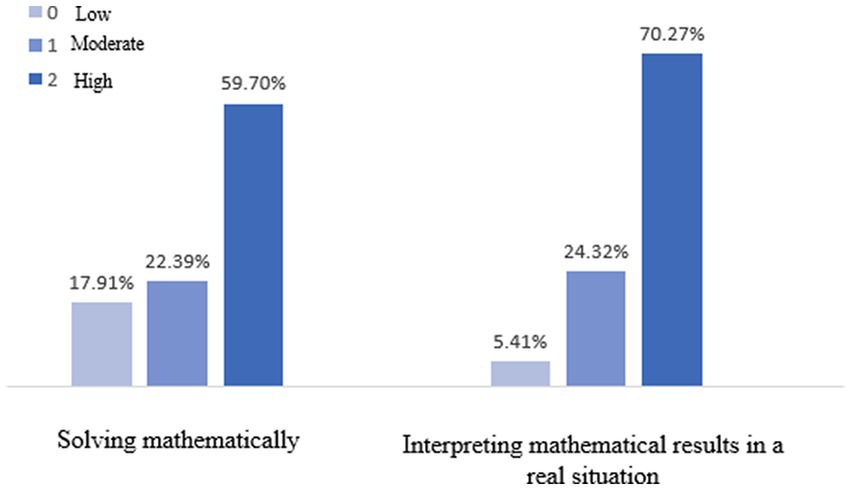
Students’ responses in the third activity of the YouTube MM task, show mainly high levels of the sub-competency of solving mathematically (59.70%) that consists of three categories, i.e., applying adaptation procedure of conversion of measurement units, using the mathematical representation of the model and providing a correct solution. Further, students’ answers show mainly high levels of interpreting the results in a real situation (70.27%). Figure 10 presents the frequencies of levels of these two sub-competencies, where the related bars for each sub-competency accumulate to 100%.
The solution of example 1 of the YouTube MM task (see Figure 4), represents the phase of working mathematically. Students were required to calculate the latency range to enable continuous streaming. A correct solution path involves the following steps: first, applying adaptation procedure by converting the measurement units by first converting 3:30–3.5 min, then converting it to 210 s. Next, based on the mathematical representation of the model of speed*time = file size, multiplying the viewing time of 210 s by the viewing speed of 0.6 Mb/s to obtain the file size of 126 Mb. At this point, there is a need to understand that the file size for complete loading and viewing is the same. Further step included dividing the file size of 126 Mb by the loading speed of 0.5 Mb/s to obtain a loading time of 252 s. Finally, calculating the latency time by subtracting the loading time and the viewing time and providing the correct solution. See Example 1 section A in Figure 11 for the solution of this MM task.
Each category in students’ solution path was ranked to the relevant level according to the rubric, showing that 70% of students’ answers were ranked at a high level, 18% at a moderate level, and 12% at a low level. An example of a moderately ranked answer is: “So, we have 210 min…amm…s… then I divided the 210 first in 0.5 and then I divide 210 in 0.6, the difference between them is the latency time.” The student converted the measurement units correctly, reaching 210 s, and was trying to calculate latency by subtracting two quantities. Yet, the mathematical model of speed*time = file size, was incorrectly used by him, as he was suggesting that speed and time should be divided rather than multiplied.
The solution of example 2 of the YouTube MM task (see Figure 4), represents the interpreting of the results phase. Students were required to interpret a graphical representation in the YouTube streaming real-world context. Specifically, they had to interpret the meaning of a horizontal vs. a vertical dashed lines within a viewing graph that represents the video file size by time.
Figure 12 presents the solutions for the two sections of this example.
Students demonstrated mainly high and moderate levels of interpreting (73, 23%). An example of a student’s answer ranked at a high level in both sections a and b is: “Wait, the red line is the viewing line, right, so it means that there is a segment that is perpendicular to the Y axis, so maybe the person stopped the video, and it is parallel to the X axis, so he moved it forward.” The student showed an understanding of the mathematical representation in the extra mathematical context in both sections. In section a, he interpreted the horizontal dashed line as time progressed, and further correctly interpreted the file size as unchanged, thus concluded that the video has stopped. Regarding section b, he interpreted correctly the vertical dashed line as forward movement when the file size grows at once. Another answer that was ranked at a moderate level for the first section of example 2, included a partial explanation of a student who said: “…It is possible that the slopes are changing after the stops.” The student reflected on the scientific-engineering context of a hold in viewing by using the word “stops.” However, he did not relate it to the horizontal dashed segment in the graph, thus it is unclear whether the student is referring to the correct mathematical representation of a stop.
4.2. Students’ motivation to engage in MM tasks
The pre-post MM SEVT motivation questionnaire’s closed and open-ended part findings present students’ motivation to engage in MM tasks, as they were captured at the end of the first day and the last day of the summer camp. One-way multivariate ANOVA (MANOVA), followed by ANOVAs, was conducted to determine whether there is a difference between the two-time measures regarding both aspects of students’ motivation toward MM learning, i.e., expectancies and value. There was a statistically significant difference in students’ motivation at the beginning and at the end of the summer camp, for both expectancies—F (5, 1,192) = 5.39, p < 0.001; partial η2 = 0.02, and value—F (3, 1,194) = 8.76, p < 0.001; partial η2 = 0.02. As shown in Table 1, the ANOVAs revealed that students’ expectancies toward MM learning were more positive at the end of the summer camp, regarding their self-concept of ability to apply particular categories of the MM sub-competencies in each of the modelling cycle phases, and toward the task difficulty. Furthermore, the findings indicate that student’s value of MM tasks engagement enhanced at the end of the summer camp regarding their attainment and intrinsic values; however, similar levels of motivation were found over time with regard to students’ values of utility.
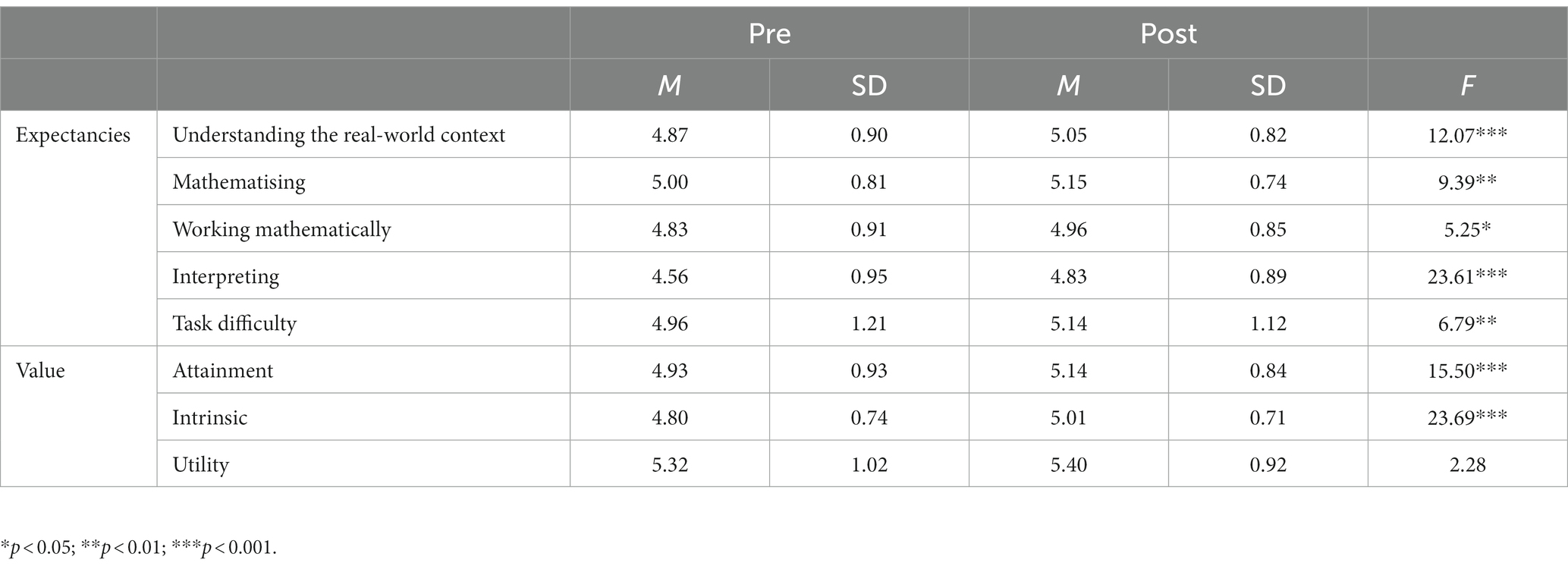
Table 1. Descriptive statistics and F values for the comparison of expectancies and value aspects over time.
4.3. The support of the VLE’s design features in students’ MM sub-competencies and motivation
After identifying the end-product, namely, students’ sub-competencies and motivation to engage in MM, it is quite natural to pursue the design features of the VLE leading to these desirable objectives.
In what follows, we first present an overview of the seven themes identified in the first step of the thematic analysis of coaches’ and students’ responses during the third activity. We then connect these themes to the various VLE design features in accordance with literature definitions. Following that, we present selected paragraphs retrieved from the third activity that illustrate how the VLE design supported students’ MM sub-competencies.
4.3.1. The VLE’s design features support during the third MM activity
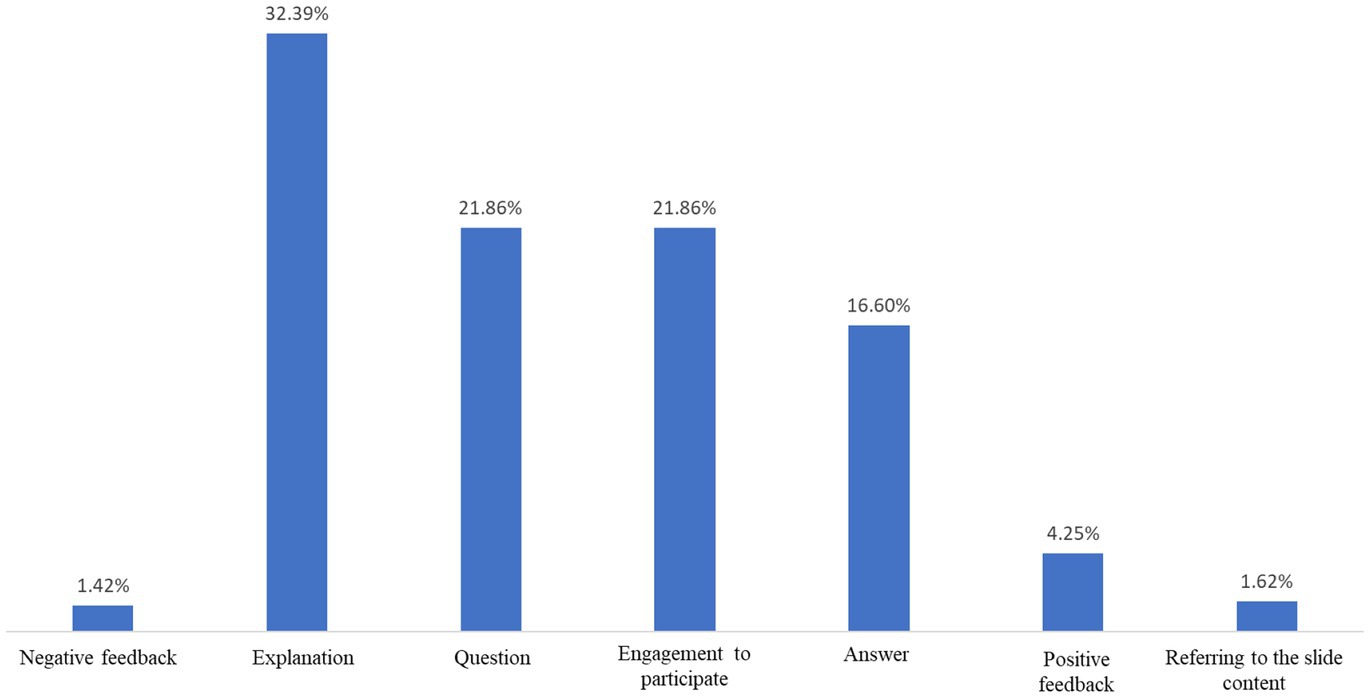
Figure 13 presents the distribution of themes, representing the VLE design features during the third MM activity. A total of 100% is obtained by adding up all the themes revealed in the four explored observations.
As a designed information space, the slide references refer to the shared organized information within the VLE. As a social space, the VLE design was characterized by explanations, question, engagement to participate, answers, and positive feedback. Explanation was mainly used for mathematical procedures and relations as well as for interpreting the results in the scientific-engineering context. The questions reflected the effort of students and coaches to focus on the course of the MM tasks solution. Engagement to participate included both coaches encouraging students to participate and students asking to participate. A coach’s answer included repeating a part of the solution the students did not understand, while students’ answers consisted of suggesting quantities, mathematical relations, or referring to the scientific-engineering context. In order to encourage students to share their ideas, the coaches provided positive feedback and rarely used negative feedback. In cases where students provided incorrect answers, coaches explained and encouraged them until they understood. Positive feedback was also provided by the students when they confirmed their understanding. After reviewing all the features observed, it was evident that the coaches fostered a supportive atmosphere to provide students with the comfort and safety to make mistakes and learn from one another during the collaborative solution of MM tasks.
4.3.2. The VLE support during the phases of working mathematically and interpreting
4.3.2.1. The support of the VLE in students’ sub-competency of solving mathematically
The first example is of a student (student A) that rushes to provide the latency time range expected in the YouTube MM task, example 1, section A (see Figure 11). The student fails to convert the measurement units as he addresses 3:30–3.3. Then he uses the mathematical model correctly by multiplying 3.3 as the time by the viewing speed of 0.6 Mb/s, receiving a wrong result of the file size of 1.98 Mb. Through instructional support and collaborative learning, the VLE serves as a social space. The coach used questions to direct students toward converting units of measurement, engaged their participation, and provided positive feedback. As a result, students answered and engaged to participate. Overall, the short discussion started with a wrong answer and ended with students correctly converting measurement units and applying a high level of solving mathematically.
Student A: “The answer is 1.98 Mb.”
Coach: “But the time is in seconds and not in Mb, the file size is in Mb, the latency is in sec…let us start together. What is problematic about the question?”
Student B: “The time is presented in minutes and you have to convert it to seconds.”
Student C: “I have an answer.”
Coach: “I’m happy, please save it. So, at 3.5 min, who can convert to seconds?”
Several students answered together: “210.”
The second example background is that a group of students failed to find the latency time range as requested in the YouTube MM task, example 1, section A (see Figure 11). The coach addressed this challenge by using a didactic tool, a table, and exemplified the VLE as a designed information space. Still, student M expressed his difficulties to understand. He kept on asking questions, receiving support and direction from the coach, until he was satisfied. Suddenly, student I also started expressing her misunderstanding and then student M suggested to explain it to her. Through instructional support and collaborative learning, the VLE shows its great potential as a social space. The coach continuous support resulted in student M understanding, who was then encouraged to explain to student I. In this brief discussion, a student helps a colleague to apply the solving mathematically sub-competency, after experiencing the same challenges and being instructed by their coach.
Student I: “If it is 210 s, then how did you get 252?
Student M: “Can I please explain?”
Coach: “Yes of course.”
Student M: “OK. So, the file size is equal in both, now time*speed is the file size…so you change the subject in the formula… because you do not have the time and you divide 126 by 0.5, and you get the time.”
Student I:” You divide 126 in what?”
Student M: “divide by 0.5.”
Student I: “So that is the file size divided by speed?”
Student M: “Exactly, so you find the time.”
Student I: “But I did not understand why if you get 252 s you have to wait 42 s?”
Coach: “The difference.”
Student M: “The difference between the loading and viewing time.”
Student K: “I really have to explain it to you; so, if you turn 0.5 into ½, then 126 divided by ½, you turn the denominator into the numerator and that helps.” (Students suggested the use of a calculator)
Student J: “So it is 4.2 min.”
Coach: “If you multiply it by 60, you’ll get 252 s.”
Student J: “That’s right.”
Student M: “Because it is the same video.”
4.3.2.2. The support of the VLE in students’ sub-competency of interpreting the mathematical results in a scientific-engineering context
The third example takes place during the solution of the YouTube MM task, example 2 sections A and B (see Figure 12). Instructional support and collaboration exemplify the role of the VLE as a social space. The coach facilitated the interpretation of the graphical representation by asking questions, providing positive feedback, and engaging students. As a result, students’ answers became sharpened, demonstrating high levels of their interpreting sub-competency.
Coach: “The following graph depicts something strange. Can anyone say what is it?
Student S: “There were advertisements.”
Coach: “Nice, someone else?”
Student T: “There are places where the graph is straight in one direction, time passes, but there is no loading, which means there is an advertisement or something and there is another one that loads but when there is no time.”
Coach: “Very nice, so actually the red line represents viewing, I started watching from 60 s on what does that mean?”
Student U: “Wait, the red line is the viewing line, right, so it means that there is a segment that is perpendicular to the Y axis, so maybe the person stopped the video, and when it is parallel to the Y axis, so he moved it forward.”
Student U: “It means you skipped the whole beginning of the video.”
Coach: “Right, I did not skip, actually I had a latency time of 60 s. I…viewed approximately 30 Mb of the video, and what happened in between 90 and 120?”
Student W: “It was stuck.”
Coach: “Correct.”
4.3.3. The VLE support in students’ motivation to engage in MM
In the open-ended question about what motivated students to join/remain in the summer camp as an indication of their value of learning MM within the VLE context, we found the following categories.
Firstly, students expressed their attainment and intrinsic values toward learning in the VLE. These were classified as categories which relate to the VLE as a designed information space in general, or toward mathematics or toward the scientific-engineering (STEM) context (for the intrinsic value, it was also expressed by their value toward MM learning). Furthermore, students expressed their intrinsic value of particular design features in the VLE: (a) the pedagogy of the VLE as a social space as well as in the use of a variety of technologies and pedagogical approaches, (b) the content of the VLE as a designed information space and a represented virtual space, and (c) the context of the VLE in general. Finally, students’ utility value was mostly captured by their value of the VLE as a designed information space. We conducted chi-squared tests to explore the association between the time of measure (at the beginning and at the end of the summer camp) and the various value aspects, i.e., attainment, intrinsic, and utility. Adjusted residuals were obtained for each cell to determine significant relations for the time of measurement (Sharpe, 2015). There was a statistically significant association between the time of measurement and attainment, χ2(2) = 20.23, p < 0.001, as well as intrinsic, χ2(6) = 487.79, p < 0.001.
As utility was mentioned as one category, it was not included in the below-mentioned findings. Nonetheless, utility was mentioned significantly more after the first day of the summer camp than after the last day (140 vs. 3). Table 2 presents proportions (count and %) and adjusted residuals (AR) for the value aspects of attainment and intrinsic values, distributed by the time of measurement. Each value aspect accumulates to 100%, separately. Each main column of attainment and intrinsic is divided into sub-columns representing the categories, i.e., types of attainment and types of intrinsic. These categories are assigned to the VLE’s design features, as mentioned above them in the main row.
The main findings reveal that students’ attainment value of the VLE as a designed information space after the first day, was expressed mainly toward math attainment value, such as a student who wrote: “My goal is to deepen my knowledge of mathematics.” However, at the end of the camp students expressed more intensely their general attainment value, such as: “I learned a lot of new things that I could not learn at school… that are beneficial for youth to know.” Students’ scientific-engineering (STEM) attainment value was the least intense in responses, with no significant difference between time periods. One example from the first day: “I want to learn and expand my knowledge in high-tech and technological topics,” and from the last day:” I enjoyed learning about the high tech and advanced technology.”
Students’ intrinsic value of the VLE as a designed information space was expressed after the first day as more related to general and math values than other intrinsic values, such as by writing: “I find this camp interesting,” “I’m interested in math.” In the last day of the summer camp, compared to the first day, students barely expressed the intrinsic values of general, math, STEM, and MM; instead, they focused more and more intensely on the design features of the VLE of content, pedagogy, and context. Students’ intrinsic value of the VLE’s content as a designed information space and a represented virtual space, is exemplified in the following examples: “I enjoyed learning and understanding how mathematics connects to many things that we use,” or “It was a great opportunity for me to get a deeper insight into the high-tech industry through interesting lectures and presentations.” Students’ intrinsic value of the VLE’s pedagogy as a social space and a technology-based pedagogical environment is exemplified in the following responses: “It was interesting to work within the group with people at my level”; “…the interesting topics and the instructor who made me want to learn more,” “the thorough explanations”; “… the atmosphere in the classroom - you can feel most comfortable asking anything that is not clear,” “I can make mistakes and it is OK”; “The way it is presented, the challenges it poses, the knowledge that enriches me and the different ways of thinking.” Students’ intrinsic value of the VLE’s context as a general view of the VLE’s experience, is presented in the following example: “I enjoyed everything because I got new information, and it was a fun experience.
5. Discussion
The study investigated a short-term VLE, conducted during a 5-day summer camp, designed to engage ninth grade students in MM tasks in a tech-related, scientific-engineering context. Next, we discuss the students’ demonstration of MM sub-competencies and motivation to engage in MM tasks in the VLE context. We also discuss the VLE features and their focus on supporting students’ MM sub-competencies and motivation to engage in MM.
5.1. Students’ demonstration of MM sub-competencies in the context of VLE
The findings indicate that the students displayed various levels of sub-competencies during initial mathematising, which was measured through their use of a VLE technological tool, namely the Padlet bulletin. During the process of initial mathematising, students were required to identify the previously provided mathematical model or understand a mathematical concept that should be used to solve i-MAT MM tasks. Such scaffolding is particularly important in cases where students should be provided with a necessary scientific-engineering background that is not part of their education (Kohen and Orenstein, 2021; Kohen and Nitzan-Tamar, 2022). Students are not used to mathematising in their mathematics school lessons (Niss and Blum, 2020), and in the context of this study, for most of students, this was their first experience with MM tasks, particularly with a tech-related scientific-engineering context. Mathematising in itself is a challenging phase; it requires mastering the mathematical knowledge, coping with a heuristic strategy and applying implemented anticipation, i.e., visioning the next modelling phase of working mathematically aligned with the real-world model (Maaß, 2006; Kaiser, 2007; Niss and Blum, 2020). Indeed, students struggled with the first two MM tasks, and fared better with the next two on behalf of their accumulated experience and the fact that the later were scaffolded with technological aids. Despite the partial coping with initial mathematising, it did not impair students’ demonstration of solving mathematically and interpretation (which we discuss below). This underscores the importance of mathematising even when it is not performed fully.
Proceeding to the third activity, that represent the VLE as a social space, students demonstrated mainly moderate-high levels of the sub-competencies of solving mathematically and interpreting the results. They managed to convert the measurement units and use the mathematical representation of the model, until they achieved a correct solution. Students are familiar with converting units, but using mathematical representations of models is not common in school mathematics (Niss and Blum, 2020; Kohen and Nitzan-Tamar, 2022). Adding to that is the students’ ability to correctly interpret the achieved mathematical results, which reflects the extent of their mental engagement in understanding the extra-mathematical situation (Maaß, 2006; Kaiser, 2007; Niss and Blum, 2020). Taken together, during the third VLE activity, and through collaborative learning focused on solving the MM tasks, the students displayed a high level of intriguing competencies, which constitute the core of the modelling cycle (Kaiser, 2005; Borromeo Ferri, 2018; Niss and Blum, 2020).
This evidence of progress in solving the MM tasks, within a VLE context aligns with earlier research regarding a MM focused VLE (Orey and Rosa, 2018; Rosa and Orey, 2019). However, our study provides evidence for identifying and evaluating MM competency in a VLE context that relates to school students; it supplements these earlier studies that focus on students’ progress in their MM tasks in other learning settings.
5.2. Students’ motivation to engage in MM in the VLE’s context
Students’ expectancies indicating their self-concept of ability regarding categories of MM sub-competencies reveal a greater significance regarding the understanding of the real-problem and forming a real-world model as well as interpreting the mathematical results. These two MM sub-competencies play an extremely important role, which is what mainly distinguishes MM tasks from other school mathematics tasks (Niss and Blum, 2020). Accordingly, this is a worthy finding that sheds light on students’ self-concept of ability to engage in MM tasks within a VLE context, even in the short term. Students expressed their self-concept of ability to understand the simplified real situation and problem in a scientific-engineering context within the context of the VLE’s activities. They also expressed confidence in forming a mathematical model as they actually performed it partially in the Padlet MM task. The findings regarding both sub-competencies are important, as they are a gate for the simplifying and mathematising phases in the MM process, which very often create a blockage to enter it and persist in it (Niss and Blum, 2020). Considering the MM tasks in a scientific-engineering context, which were the focus of this study, this is a particularly significant finding, since students’ experiences during secondary school have a lasting effect on their persistence in STEM fields (Nitzan-Tamar and Kohen, 2022).
Students also increased their positive expectancies regarding the MM task’s difficulty, which can be explained by the fact that the high expectancies to succeed in an academic task rely on a high self-concept of ability to apply it which builds a positive perception regarding the ability to cope with the task difficulty (Eccles-Parson et al., 1983; Eccles and Wigfield, 2020).
Overall, in the context of the solution of MM tasks in the VLE, students had shown more positive expectancies toward their self-concept of ability and their coping with the difficulty of the task. Students increased their attainment value of MM tasks over time, in relation to the importance they attach to their personal growth.
Joining these insights of more positive expectancies and values of students regarding their engagement in MM tasks, with the prior section of their demonstration of MM sub-competencies as observed in the first day, strengthen earlier research findings. First, since students that value the importance of an academic task and have an intrinsic motive to make an effort to succeed in it are more likely to engage, perform, and persist in the task (Eccles-Parson et al., 1983; Eccles and Wigfield, 2020). Second, it implies on the context of the VLE, the collaborative learning and instructional support and the way they influenced the enhancement in students’ self-concepts of their mathematical competencies and intrinsic motivation. This corresponds with earlier research of the expectancy-value theorists, which correlate such positive effects with students’ engagement in collaborative learning (Wigfield et al., 1998).
5.3. The support of the VLE’s design features in students’ demonstration of sub-competencies and motivation to engage in MM
Each day, the MM activities provided students with a holistic experience that relied on the VLE theoretical aspects in all parameters (Dillenbourg et al., 2002; Limniou and Smith, 2010; Mueller and Strohmeier, 2011; Mayer, 2019). First, the VLE MM activities, as elaborated in the methodology section constituted a designed information space, relying on designated MM learning materials, provided by the i-MAT project. These activities offered a structured process whereby the students were taught to apply MM sub-competencies gradually, while distinguishing and emphasizing each MM phase in the process. In this aspect, the VLE focused on strengthening students’ MM sub-competencies and suggested MM tasks based on mathematical content that is compatible to secondary school students. The structured MM activities preserved the learning objectives of the didactical modelling cycle, in line with the online learning features required in a VLE. Students were led in a scaffold path, using designated materials, which supported their understanding of the simplified real-world problem, moving on to scaffolding their understanding of the mathematical model before, within, and after the Padlet MM tasks. Furthermore, there was evidence for the support of students’ demonstration of the sub-competencies of solving mathematically and interpreting of the results. This supports earlier research advocating a scaffolded solution plan for students, resulting in their development of MM sub-competencies (Blum, 2011; Schukajlow et al., 2015). In addition, these findings are consistent with previous studies examining the use of VLEs in other contexts, which were found to be effective in this study when applied to MM learning (Dillenbourg et al., 2002; Mayer, 2019). As a designed information space, the VLE enabled online sharing of the learning materials providing instructional support through the VLE activities. First, by introducing the simplified situation and problem using pictures, videos, and simulations; second by engaging students in the technological feature of a bulletin board for the initial mathematising; and third by using simplified MM tasks where students actively engaged in working mathematically and interpreting. The VLE functioned as a social space, consisting of on online collaborative learning with the support and feedback of coaches. They led the MM activities, explaining, answering, asking questions, providing positive feedback, and engaging students to participate, while scaffolding their understanding of the scientific-engineering context and supporting them through their efforts. These aspects correspond with the online learning features required in a VLE (Mayer, 2019). The instructional support and collaborative learning of the VLE as a social space were emphasized in the third activity and supported students’ demonstration of moderate-high sub-competencies of solving mathematically and interpreting the results. The VLE, functioned as a represented virtual space, where students engaged in MM tasks within separated video conference groups and participated in the virtual tours to broaden their perspectives regarding the use of mathematics to solve real-world problems.
With respect to students’ motivation, the VLE design features support in students’ motivation was expressed by their elaboration of their values of the VLE design features more intensely at the end of the summer camp. Students seemed to develop a more general view of attainment value of learning in the MM VLE. After the VLE, they intensely referred to their values of the VLE as a designed information space and a represented virtual space, as well as a social space and a technological and pedagogical based environment and finally valuing the whole VLE experience.
6. Conclusion
Taken together, the VLE supported students’ MM sub-competencies through a designed information space including structured activities and designated learning materials as well as a technologically based environment. Although incorporating high-quality learning materials and technological tools into the VLE is essential, it is not sufficient by itself to facilitate students’ demonstration of cognitive abilities (Dillenbourg et al., 2002; Limniou and Smith, 2010; Estriegana et al., 2021). The VLE’s social space was found to be the beating heart in this study, manifested through instructional support and collaboration, along with students’ active engagement. These VLE design features supported students’ progress in the modelling cycle through an awareness of the process and its components. First, it acknowledges that there is a real world that uses mathematics to solve problems. Second, it acknowledges that, as young students, they can apply known mathematical procedures to solve such problems. And third, that they can explain the mathematical results in a real-world context. The instructional support utilized the structured MM activities and technology-based environment to guide the students safely throughout the MM process, supporting their positive expectancies to succeed in the solution of MM tasks. The VLE further provided students with an attainment value, through the tech-related context mediated by the VLE activities. It facilitated intrinsic values, when students persisted and outperformed in working mathematically and in interpreting the results. These aspects are reflected by students’ expressing more positive expectancies and values of the MM tasks as well as a growing value of the VLE’s design features. The VLE was an online island of mathematics and real-world contexts, applied through structured and technology-based activities, and mediated by a supportive and empowering instructional support through the facilitation of collaborative learning. Students were introduced to a real-world context, experienced initial mathematising, and successfully demonstrated MM sub-competencies while applying the working mathematically and interpreting phases. They fostered this unique and new learning perspective, which embeds the added value of a scientific-engineering context, and requires a new type of effort based on the students’ performance of a new set of skills, all of which are significant to prepare them for their future lives and careers (Kohen and Nitzan-Tamar, 2022; Nitzan-Tamar and Kohen, 2022). Finally, the VLE connected students from all over the country, in both peripheral and central areas, girls and boys, Jews and various minorities, all focused on one objective: their cognitive and motivational growth toward achieving their current and future goals.
6.1. Limitations
The study included substantial evidence of the recorded activities of the VLE throughout the summer camp in both cycles. Our choice of four observations, although randomly selected, still focused on the first summer camp day for the YouTube MM task context. This should be considered as a limitation because there may be observations that did not lead to the positive findings regarding students’ MM sub-competencies. However, revealing students demonstration of MM sub-competencies and the VLE design features support in them, obtained a saturation of data (Creswell, 2013) due to these aspects provided the required data for this analysis.
The coaches practiced the VLE for their first time, and they were not experienced teachers, which can change the effect of the VLE design features on students’ MM sub-competencies and motivation. In addition, it can illustrate and imply that when a teacher will be trained to lead collaborative learning through MM activities, whether online or in class, it might lead to a more positive effect on students’ MM sub-competencies and motivation. In the opposite, it can be claimed that the coaches did gain professional teaching experience through the first camp cycle. Referring all aspects, a professional teaching proficiency is not acquired in 5 days of initial experience, and it is recommended to apply more studies of MM learning within VLEs, in both formal and informal platforms to make MM more accessible and learnable.
The rubric for evaluating students’ MM competencies was designed according to the engagement with i-MAT tasks in a scientific-engineering context. Thus, it can be claimed that it limits its use in other MM tasks. Yet we kept the rephrasing of the MM sub-competencies to be remained within the scope of the literature-based definitions. Therefore, we believe that it can be used in other MM tasks contexts.
The short-term period of the summer camp can be questioned regarding the fostering of MM sub-competencies and the motivational aspects of expectancies and values. We do not state that development or fostering took place; we only detected the demonstration of sub-competencies. This can be explained by the fact that the students who participated in the VLE could transform their prior competencies to cope with the structured activities as well as the simplified scientific-engineering context. It also represents a major challenge for performing such a transformation (Niss and Blum, 2020); therefore, if it occurred within the VLE’s structured activities, it is quite an accomplishment in itself.
We did not inquire students’ demonstration of sub-competencies or the VLE features’ support during the simplifying phase and only partially during the mathematising phase. Due to the time limit, the VLE’s objective to expose students to diverse tasks and the scientific-engineering context, which adds complexity and should be simplified in advance, students were unable to apply complete sub-competencies within these phases. Future studies should explore both aspects in the context of the VLE since these first two phases in the modelling cycle often prevent students from progressing in the MM process (Niss and Blum, 2020).
6.2. Study contribution
The first theoretical contribution relates to the categorization made for mathematical modelling sub-competencies based on current theoretical definitions (Maaß, 2006). Secondly, our use of the SEVT framework (Eccles-Parson et al., 1983; Eccles and Wigfield, 2020) for exploring students’ motivation to engage in MM is not prevalent, especially when it is combined with the investigation of MM sub-competencies. The MM solution process requires students to engage, persist and perform in academic tasks which integrate mathematical and extra-mathematical contexts via demonstration of designated sub-competencies, therefore challenge students worldwide (Niss and Blum, 2020). The use of this theory in this study provided a path to examine what students expect and value when engaging in such tasks. Thirdly, the study relates the research-based definitions of the VLE design features with the two theoretical models of MM sub-competencies and SEVT when revealing the support of the VLE design features in students’ sub-competencies and motivation for MM.
The methodological contribution of this study lies first in the observation analysis, applying different theoretical lenses, especially in the third activities analysis, which had two layers of coding. First, the MM sub-competencies were ranked using the content analysis of students’ replies during the collaborative solution of MM tasks. Second, a thematic analysis of students’ and coaches’ replies was then used to code them to different VLE design features. Furthermore, our offered methodology contribution is in the rubric designed, through the use of literature-based definitions and their extension with new categories, which were used to identify and assess students’ MM sub-competencies. Finally, is the dual analysis in the pre-post MM motivation questionnaire regarding students’ motivation to engage in MM tasks as well as the VLE’s design features reflected by students as motivating.
From a practical viewpoint, this study offers a short-term VLE that applies collaborative learning of MM tasks in a scientific-engineering context, which led to secondary school students’ application of MM competencies and their enhanced expectancies and values while engaging in MM tasks.
Data availability statement
The datasets presented in this article are not readily available. Requests to access the datasets should be directed to emVoYXZpdGtAdGVjaG5pb24uYWMuaWw=.
Ethics statement
This research was reviewed and approved by the Behavioral Sciences Ethics Committee of the Technion, Israel. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author contributions
ZK: conceptualization, supervision, formal analysis, software, writing—review and editing, and validation. OC-N: conceptualization, formal analysis, investigation, resources, data curation, writing—original draft, software, and methodology. All authors contributed to the article and approved the submitted version.
Acknowledgments
It is with great respect that the authors acknowledge the partial funding provided by the Trump Foundation for this research. We also greatly appreciate the R&D group from the i-MAT project for their support and contribution to this research, particularly Dr. Ortal Nitzan-Tamar, Hadas Handelman, and Niza Sion.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ainley, M., and Armatas, C. (2006). “Motivational perspectives on students’ responses to learning in virtual learning environments” in The International Handbook of Virtual Learning Environments. eds. J. Weiss, J. Nolan, J. Hunsinger, and P. Trifonas (Netherlands: Springer), 365–394.
Atkinson, J. W., and Reitman, W. R. (1956). Performance as a function of motive strength and expectancy of goal-attainment. J. Abnorm. Soc. Psychol. 53, 361–366. doi: 10.1037/h0043477
Barak, M., Ginzburg, T., and Erduran, S. (2022). Nature of Engineering: A Cognitive and Epistemic Account with Implications for Engineering Education. Sci. Educ. 1–19. doi: 10.1007/s11191-022-00402-7
Blum, W., and Leiß, D. (2007). “How do students and teachers deal with modelling problems?,’’ in Mathematical modelling (ICTMA 12): Education, engineering and economics. eds. C. Haines, P. Galbraith, W. Blum, and K. Sanowar (Chichester, UK: Horwood), 222–231.
Blum, W., and Niss, M. (1991). Applied mathematical problem solving, modelling, applications, and links to other subjects - state, trends and issues in mathematics instruction. Educ. Stud. Math. 22, 37–68. doi: 10.1007/BF00302716
Borromeo Ferri, R. (2018). Learning How to Teach Mathematical Modelling in School and Teacher Education. Cham, Switzerland: Springer International Publishing.
Cevikbas, M., Kaiser, G., and Schukajlow, S. (2021). A systematic literature review of the current discussion on mathematical modelling competencies: state-of-the-art developments in conceptualizing, measuring, and fostering. Educ. Stud. Math. 109, 205–236. doi: 10.1007/s10649-021-10104-6
Creswell, J. W. (2013). Qualitative Inquiry and Research Design: Choosing Among Five Approaches. 3rd Edn. Thousand Oaks: Sage.
Dillenbourg, P., Schneider, D., and Synteta, P. (2002). “Virtual learning environments” in 3rd Hellenic Conference “Information & Communication Technologies in Education”, 3–18.
Eccles, J. S., and Wigfield, A. (2020). From expectancy-value theory to situated expectancy-value theory: a developmental, social cognitive, and sociocultural perspective on motivation. Contemp. Educ. Psychol. 61:101859. doi: 10.1016/j.cedpsych.2020.101859
Eccles-Parson, J. F., Adler, T., Futterman, R., Goff, S. B., Kaczala, C. M., Meece, J., et al. (1983). “Expectancies, values, and academic behaviors” in Achievement and Achievement Motivation. ed. J. T. Spence (San Francisco, CA: Freeman), 79–146.
Estriegana, R., Medina, J., Robina, R., and Barchino, R. (2021). Virtual Learning Environment to Encourage Students’ Relationships and Cooperative Competence Acquisition. Ann. Conf. Innov. Technol. Comp. Sci. Educ. ITiCSE 52–59. doi: 10.1145/3430665.3456363
Galbraith, P., and Clatworthy, N. (1990). Beyond standard models - meeting the challenge of Modelling. Educ. Stud. Math. 21, 137–163. doi: 10.1007/BF00304899
Galbraith, P., and Stillman, G. (2006). A framework for identifying student blockages during transitions in the modelling process. ZDM 38, 143–162. doi: 10.1007/BF02655886
Greefrath, G., Hertleif, C., and Siller, H. (2018). Mathematical modelling with digital tools-a quantitative study on mathematising with dynamic geometry software. ZDM 50, 233–244. doi: 10.1007/s11858-018-0924-6
Hankeln, C., Adamek, C., and Greefrat, G. (2019). “Assessing sub-competencies of mathematical Modelling—development of a new test instrument” in Lines of Inquiry in Mathematical Modelling Research in Education. eds. G. Kaiser, G. A. Stillman and J. P. Brown (Switzerland AG: Springer Nature), 143–160.
Hsieh, H. F., and Shannon, S. E. (2005). Three approaches to qualitative content analysis. Qual. Health Res. 15, 1277–1288. doi: 10.1177/1049732305276687
Jankvist, U. T., and Niss, M. (2020). Upper secondary school students’ difficulties with mathematical modelling. Int. J. Math. Educ. Sci. Technol. 51, 467–496. doi: 10.1080/0020739X.2019.1587530
Kaiser, G. (2005). “Mathematical modelling in school-examples and experiences,’’ in Mathematikunterricht Im Spannungsfeld von Evolution Und Evaluation. Festband Für Werner Blum, vol. 99 (Hildesheim: Franzbecker), 99–108.
Kaiser, G. (2007). “Modelling and modelling competencies in school” in Mathematical Modelling (ICTMA 12):Education, engineering and economics, 110–119.
Kaiser, G., Brand, S., Kaiser, G., Stillman, G. A., Blum, W., and Salett Biembengut, M. (2015). “Modelling competencies: past development and further perspectives” in Mathematical Modelling in Education Research and Practice: Cultural, Social, and Cognitive Influences. eds. G. A. Stillman, W. Blum and M. S. Biembengut (Cham: Springer), 129–149.
Kohen, Z., and Gharra-Badran, Y. (2022). A rubric for assessing mathematical modelling problems in a scientific-engineering context. Teach. Math. Appl. Int. J. IMA. doi: 10.1093/teamat/hrac018
Kohen, Z., and Nitzan-Tamar, O. (2022). Contextual mathematical Modelling: problem-solving characterization and feasibility. Educ. Sci. 12:454. doi: 10.3390/educsci12070454
Kohen, Z., and Orenstein, D. (2021). Tech-related real-world problems and how they can be modeled for the secondary mathematics curriculum. doi: 10.1007/s10649-020-10020-1
Krawitz, J., and Schukajlow, S. (2018). Do students value Modelling problems, and are they confident they can solve such problems? Value and self-efficacy for Modelling, word, and intra-mathematical problems. ZDM Int. J. Math. Educ. 50, 143–157. doi: 10.1007/s11858-017-0893-1
Limniou, M., and Smith, M. (2010). Teachers’ and students’ perspectives on teaching and learning through virtual learning environments. Eur. J. Eng. Educ. 35, 645–653. doi: 10.1080/03043797.2010.505279
Maaß, K. (2006). What are modelling competencies? Katja Zentralb. Für Didak. Math. 38, 113–142. doi: 10.1007/BF02655885
Mayer, R. E. (2019). Thirty years of research on online learning. Appl. Cogn. Psychol. 33, 152–159. doi: 10.1002/acp.3482
Mueller, D., and Strohmeier, S. (2011). Design characteristics of virtual learning environments: state of research. Comput. Educ. 57, 2505–2516. doi: 10.1016/j.compedu.2011.06.017
Niss, M. (2015). “Mathematical competencies and PISA” in Assessing Mathematical Literacy. eds. S. Kaye and T. Ross (Switzerland: Springer International Publishing), 35–56.
Niss, M., and Blum, W. (2020). The Learning and Teaching of Mathematical Modelling. London & New York: Routledge
Niss, M., and Højgaard, T. (2011). Competencies and mathematical learning: Ideas and inspiration for the development of mathematics teaching and learning in Denmark (English translation of original 2002) (p. IMFUFA-tekst:i, om og med matematik og fysik No.). Roskilde University: IMFUFA.
Niss, M., and Højgaard, T. (2019). Mathematical competencies revisited. Educ. Stud. Math. 102, 9–28. doi: 10.1007/s10649-019-09903-9
Nitzan-Tamar, O., and Kohen, Z. (2022). Secondary school mathematics and entrance into the STEM professions: a longitudinal study. Int. J. STEM Educ. 9, 1–26. doi: 10.1186/s40594-022-00381-9
Orey, D. C., and Rosa, M. (2018). Developing a mathematical modelling course in a virtual learning environment. ZDM 50, 173–185. doi: 10.1007/s11858-018-0930-8
Rosa, M., and Orey, D. C. (2019). Mathematical modelling as a virtual learning environment for teacher education programs. Uni-Pluriversidad 19, 80–102. doi: 10.17533/UDEA.UNIPLURI.19.2.04
Schukajlow, S., Blomberg, J., Rellensmann, J., and Leopold, C. (2022). The role of strategy-based motivation in mathematical problem solving: the case of learner-generated drawings. Learn. Instr. 80:101561. doi: 10.1016/j.learninstruc.2021.101561
Schukajlow, S., Kolter, J., and Blum, W. (2015). Scaffolding mathematical modelling with a solution plan. ZDM 47, 1241–1254. doi: 10.1007/s11858-015-0707-2
Sharkia, H., and Kohen, Z. (2021). Flipped classroom among minorities in the context of mathematics learning: the israeli case. Mathematics 9:1500. doi: 10.3390/math9131500
Sharpe, D. (2015). Chi-square test is statistically significant: Now what?. Pract. Assess. Res. Eval. 20:8.
Wigfield, A., and Eccles, J. S. (1992). The development of achievement task values: a theoretical analysis. Dev. Rev. 12, 265–310. doi: 10.1016/0273-2297(92)90011-P
Wigfield, A., and Eccles, J. S. (2020). “35 years of research on students’ subjective task values and motivation: A look back and a look forward,” in Advances in motivation science Vol. 7. ed. A. Elliot, (New York: Elsevier), 161–198.
Keywords: mathematical modelling, modelling competencies, virtual learning environment, expectancy-value (EV) theory, secondary school
Citation: Cohen-Nissan O and Kohen Z (2023) Secondary school students’ competencies and motivation to engage in mathematical modelling tasks in a virtual learning environment. Front. Educ. 8:1140364. doi: 10.3389/feduc.2023.1140364
Edited by:
Gilbert Greefrath, University of Münster, GermanyReviewed by:
Irene Ferrando, University of Valencia, SpainPiera Biccard, University of South Africa, South Africa
Copyright © 2023 Cohen-Nissan and Kohen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zehavit Kohen, emVoYXZpdGtAdGVjaG5pb24uYWMuaWw=
 Orit Cohen-Nissan
Orit Cohen-Nissan Zehavit Kohen
Zehavit Kohen