Making mathematics together by modeling shared experiences

Introduction: This article illustrates a pedagogical approach to integrating models and modeling in Geometry with mathematics teacher-learners (MTLs). It analyzes the work of MTLs in a course titled “Computers, Teaching, and Mathematical Visualization” (or “MathViz”), which is designed to engage MTLs in making mathematics together. They use a range of both physical and virtual models of 2-manifolds to formulate and investigate geometric conjectures of their own.

Objectives: The article articulates the theoretical basis and design rationale of MathViz; it analyzes illustrative examples of the discourse produced in collaborative investigations; and it describes the impact of this approach in the students’ own voices.

Methods: MathViz has been iteratively refined and researched over the past 6 years. This study focuses on one iteration, aiming to capture the phenomenological experience of the MTLs as they structured and pursued their own mathematical investigations. Video data from two class sessions of the Fall 2021 iteration of the course are analyzed to illustrate the discourse of collaborating students and the nature of their shared inquiry. Excerpts from this class’s Learning Journals are then analyzed to capture themes across students’ experience of the course and their perspectives on its impact.

Results: Analysis of students’ discourse (while investigating cones) shows how they used models and gesture to make sense of geometric phenomena; forged connections with investigations they had conducted throughout the course on different surfaces; and articulated and proved mathematical conjectures of their own. Analysis of students’ Learning Journals illustrates how experiences in MathViz contributed to their conceptualization of making mathematics together, using a variety of models and technologies, and developing a set of practices that that they could introduce with their future students.

Discussion: An argument is made that this approach to collective mathematical investigation is not only viable and valuable for MTLs, but is also relevant to philosophical reflections about the nature of mathematical knowledge-creation.

1. Introduction

A key conjecture of this article—as well as of the course from which its data are drawn—is that teacher-learners can benefit from opportunities to connect rich disciplinary learning experiences with their emergent conceptions of their future classrooms and of themselves as teachers. This article examines how mathematics teacher-learners (MTLs) used physical and virtual models to formulate and conduct their own investigations into the intrinsic geometry of 2-manifolds, and how this semester-long experience impacted their views of mathematics teaching and learning. In particular, it explores how experiences of making mathematics together supported MTLs’ view that mathematical creativity and discovery could be accessible to all students, and not just an exceptional few.

This is also a project of didactical phenomenology (Freudenthal, 1983), where MTLs are invited to “step into the learning process of mankind” (p. ix), around conceptualizing Euclidean and non-Euclidean approaches to mathematizing two-dimensional space (cf. Moreno-Armella et al., 2018). Because the MTLs have the freedom (and the need) to construct and select models to support their own investigations, it illuminates how they experience mathematical practices associated with discovery. And because it asks them to use their own inquiry experiences as a lens on teaching possibilities in their future classrooms, it includes them in a type of autodidactical phenomenology.

The teachers’ investigations in this “MathViz” course have a radical openness. Students generate definitions of their own, and they formulate and investigate conjectures that express emergent curiosities. Although I have taught the course six times engaging roughly the same mathematical terrain, the texture of the theorems and findings created by each group have been unique.

Students in the course have generally had some prior experience with Euclidean Geometry, and this provides a basis for them to explore comparative geometries. However, students often see their prior geometry experience as closed off and terminated, and some of them have strong negative memories of it. MathViz thus follows Nemirovsky’s (2018) idea of “pedagogies of emergent leaning,” first to revitalize students’ conceptions of planar geometry through shared and embodied intrinsic experiences in the plane, and then to mobilize that intrinsic perspective to imagine and mathematize embodied experiences of the local and global geometry of other 2-manifolds.

In their journey from the plane to spheres, cylinders, cones, and hyperbolic planes, students notice unfamiliar phenomena; wonder about their meaning; ask questions that articulate their conceptions of these phenomena in terms understood by the community; and formulate and investigate conjectures about them. In the course of this work, the classroom group develops multifaceted relations among (a) mathematical contexts, objects, and actions; (b) models of various kinds (physical and virtual, specific and general); and (c) shared mathematical experiences (see Figure 1).

FIGURE 1

Figure 1. Interactions among mathematics, models, and experience.

2. Models and modeling in MathViz

Models in MathViz include models of mathematical structures and systems (e.g., a Lénárt model of the geometry of the sphere). They also include models of forms of experience (e.g., turtle geometry as a model of experiences of wayfinding and navigation). Further, forms of mathematical experience (e.g., taking an intrinsic perspective) can be seen as influencing the use of models (e.g., using a dynamic geometry construction to analyze possible paths in turtle geometry). And mathematical practices (e.g., proving a conjecture) can guide the social use of models to create and stabilize shared experiences among the community (e.g., when collaboratively constructing a proof). Given this cluster of relations, MathViz amplifies both the types and modalities of model (virtual/computational, and physical models in various materials) and the forms of experience that students can use models to invoke (e.g., embodied experiences, narratives, and artistic expression).

2.1. Manipulatives and models for MTLs

MathViz bridges a traditional distinction between models of mathematics on one hand and modeling with mathematics on the other (cf. Hirsch and McDuffie, 2016). A classic example of a “model of mathematics” is a manipulative. At one level, then, MathViz could be interpreted as providing MTLs authentic experiences with manipulatives in service of their own learning. Thoughtful, generative use of manipulatives is important for learners of all ages (Bartolini and Martignone, 2020), and in the digital era, it is increasingly important for teachers and students to develop fluency and expressivity with mathematical representations across media (Nemirovsky and Sinclair, 2020). A rich area of research is investigating the balance between virtual and physical manipulatives—selecting between modalities (Moyer-Packenham and Westenskow, 2013), sequencing them (Hunt et al., 2011), or, more generally, understanding the interactions between learning experiences with each type (Maschietto and Soury-Lavergne, 2013; Brady and Lehrer, 2021; Soury-Lavergne, 2021).

Researchers also raise questions about teachers’ and students’ stances toward manipulatives, and about when and how they should be employed. For instance, Kamii et al. (2001) argue that a given manipulative may be helpful at one stage of development and not at others. For the MTLs in MathViz, as for all learners, “ascribing mathematical meanings to empirical phenomena” (Voigt, 1994, p. 172) involves active interpretive work, as “physical embodiments of mathematical ideas” are not “transparent” (Brown, 1996, p. 120) but involve ambiguity and polysemy.

In some teaching settings, this can be seen as an unfortunate liability—in particular, when a physical apparatus is designed to convey the designer’s targeted mathematical notions. In particular, it should not be assumed that any such manipulative will itself “automatically determine the way it is used and conceived of by the students” (Bartolini and Martignone, 2020). The intended mental constructions and associations may not be evident or constructed by the learners (Ball, 1992; Uttal et al., 1997; McNeil and Jarvin, 2007), and the very “semiotic potential” (Bartolini Bussi and Mariotti, 2008) of manipulatives can result in students’ emphasizing personal and idiosyncratic interpretations of their work with them, at the expense of the intended mathematical meanings.

In an important sense, these findings simply reflect that a manipulative can become problematic when its expressive semiotic power as a model is neglected. This recalls the famous model-of/model-for contrast (e.g., Fox Keller, 2000), in which viewing a model as a simple, objective, stable, or transparent embodiment of an idea robs it of power. In contrast, the instrumental use of a model, by an actor or community for a purpose (Morgan and Morrison, 1999) reveals how it can be a generative tool to mediate thought. Nührenbörger and Steinbring (2008) agree that the “theoretical ambiguity” of models and manipulatives—which “makes manipulatives suitable to all school levels, up to university, as a context where fundamental processes, as defining, conjecturing, arguing, and proving, are fostered” (Bartolini and Martignone, 2020).

2.2. A dual relation between mathematics and its experiential embodiments

In this context, MathViz offers a setting where, in service of processes of mathematical investigation and discovery, the construction of physical and virtual embodiments of emergent mathematical ideas can be generative. When a group of learners create or choose physical materials and models that then play an “anchoring, although not determining” (Brown, 1996, p. 121) role in their investigations, they can reveal how material models guide their own thinking and collaboration by infrastructurally or “architecturally” (Kaput, 1991) formatting their shared environment (cf. Greeno, 1994). In this way, the inquiry group can use embodiments of mathematical ideas to shape their communication and collective thinking. Here, the dual relation between mathematical ideas and their worldly embodiments becomes apparent, creating a bridge between modeling mathematics (where aspects of mathematics are expressed in tangible materials and experience), and modeling with mathematics (where essential aspects of the phenomenal world are expressed in mathematical constructs).

Freudenthal (2002) discusses both sides of this dual relation between the “noumenal” world of mathematics and the “phainomenal” world of experience. For him, models play an essential, “intermediary” role in the “process of mathematizing” (Freudenthal, 2002, p. 34). In turn, “mathematizing” is a conceptual process that applies broadly, to “the entire organizing activity of the mathematician, whether it affects mathematical content and expression, or more naive, intuitive, say lived experience, expressed in everyday language” (Freudenthal, 2002, p. 31). Mathematizing thus transforms the learner’s “reality” (p. 30), and in Freudenthal’s view, learners can only mathematize that which is experientially real to them. Gravemeijer and Terwel (2000) clarify that Freudenthal here views “reality” as including the whole of a person’s lived, embodied experiences and interpretive perspectives. Dienes (1960), designer of Dienes blocks, similarly describes the construction of mathematics as a “crystallizing” or “distilling” of experience and emphasizes the dynamic relation between an idea and its embodiments.

Within the mathematics-models-experience framework depicted in Figure 1, then, mathematizing in MathViz builds on forms of sensemaking in which MTLs create and use models and material embodiments to make the geometry of 2-manifolds experientially real. They work together to make geometric phenomena into a shared reality, which can then be mathematized and investigated; and their use of a variety of models deeply mediates this process.

3. Pedagogical framework

MathViz is designed for undergraduate and master’s level students in a teacher education program. The course has grown up in friendly soil, and I owe the privilege of developing and offering it to the program’s commitment to blending specific disciplinary forms of inquiry with reflections on teaching and learning (cf. Hundley et al., 2018). The course design itself has built upon prior work by eminent researchers in mathematics education such as Pat Thompson, Rogers Hall, and especially Rich Lehrer. And the approaches to geometry that MathViz embodies are inspired by the visionary perspectives of Papert (1980), Henderson (1996), Henderson and Taimina (2005, 2006), Lénárt (2010), and Taimina (2018).

I have taught MathViz for the past six years, refining and adapting it with each iteration, in order to amplify opportunities for students to draw upon their own perspectives and experiences as they make mathematics together. This expression (to make mathematics) comes from an opening discussion in the course, about the ambiguity of the Spanish verb “hacer,” in hacer matemáticas. A very different impression is created by “doing” versus “making” mathematics. In MathViz, we aim to amplify the “making mathematics” alternative, whenever possible. Making and modeling are intertwined as MTLs engage in embodied planar experiences at “walking scale” using surveyor’s ribbon and other props; “agent-based” computational environments from Snap! to NetLogo to physical robots; “dynamic geometry” environments such as GeoGebra; and physical models such as Lénárt Spheres and polydrons, along with constructions in paper, crocheted yarn, and other flexible media.

3.1. Conceptual map of the course

Early activities in the course explore the range of what Henderson and Taimina (2005) call the historical “strands” of geometry. Problems and inspirations arise from navigation, visual art, dance, architecture, and mechanical engineering. They revive students’ interest in fundamental questions (such as the problem of verifying “straight-ness” of paths or parts of shapes) and they underscore the fundamental roles of perspective (e.g., the intrinsic perspective of turtle geometry) and context (e.g., cultural context, as highlighted by ethnomathematics (D’Ambrosio, 1985), or more local activity contexts such as choreography in multi-body dance). The fundamental mathematizing work required to articulate geometric structure across these diverse settings creates the need for students to construct or adapt models for particular purposes. Moreover, these early efforts raise important generative tensions that extend through the course: intrinsic-extrinsic; local–global; geometric-topological; and procedural-descriptive.

These initial activities engage with elementary phenomena, and the class soon generates findings and questions that reveal the potential richness of inquiring seriously into such fundamentals. For example, on the first day of the course, the class uses surveyor’s ribbon and flags to mark off polygonal paths on the college lawn. As questions emerge, these walking-scale paths are re-represented and re-constructed using both Turtle Geometry and dynamic geometry environments. One of the findings that reliably emerges is a conjecture that Papert (1980) calls the “total turn angle theorem” and that Abelson and DiSessa (1986) refine as the “closed path theorem.” Indeed, many of the students discover that the turn angles of the closed paths they are creating all sum to 360 degrees. Arguments for why this should be true begin to emerge in debate, as also do some counter-examples. Different classes respond to these counter-examples in different ways. For example, they may establish more explicit rules about how to measure turn angles, or they may restrict the set of paths covered by the emerging theorem (e.g., to “convex” paths). Later, when reading Lakatos’s Proofs and Refutations, students recognize analogs of the arguments they made in these early debates, now attributed to some of the most famous European mathematicians in history.

Moreover, as in Lakatos (1976), while attempting to formulate a proof that explains why (cf. De Villiers, 1998) the total turn angle is 360 degrees, students generate innovative perspectives on the matter. For example, even after restricting to five-legged paths, the “monster” (Lakatos, 1976) pentagon shown in Figure 2B was produced, which had a total turn angle of 720 = 2 × 360. Constructing shapes in GeoGebra and then walking them as paths marked with tape, one student said she could “see” Figure 2B as a double loop, whereas the path of Figure 2A was a single loop. Elaborating her idea involved imagining “inflating” the shape of the path in a way that made the pointed vertices into smooth curves and revealed that the path in Figure 2B made two loops.

FIGURE 2

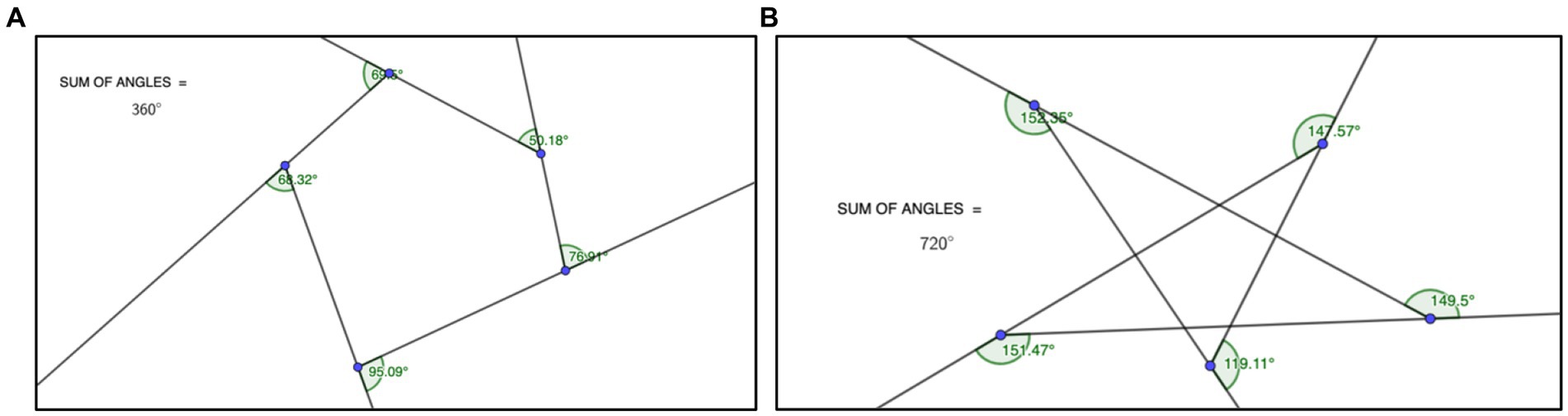
Figure 2. (A): a pentagonal path with a total turn angle of 360 degrees. (B): a “monster” pentagon—a five-sided path with a total turn angle of 720 degrees.

The unexpected depth of some of these initial explorations sets the stage for the class to appreciate the constructive role of definitions (cf. Kobiela and Lehrer, 2015) and the value of asking good questions (cf. Lehrer et al., 2013). In the course of these sessions, we introduce the convention of organizing ideas into “Notice,” “Wonder,” “Question,” and “Conjecture” statements. Meanwhile, analyzing finite and infinite structures on the plane (e.g., Euclidean constructions, isometry transformations and symmetries, tessellations, frieze patterns and wallpaper groups) helps to enrich the sense of the plane as a realm where rich mathematics can be made.

In the second phase of the course, we move from the plane to other surfaces (2-manifolds), beginning with the sphere, and moving to the cylinder, to cones of various cone-angles, and to the hyperbolic plane, with briefer explorations of the flat torus and mobius strip. Our comparative approach highlights the interdependence between geometric phenomena and the ambient space. Moreover, the exigencies of different questions and arguments highlight the complementary virtues and limitations of different types of models. Most notably, students develop dialogic relations between physical and virtual models to support their investigations.

Students also find creative ways to adapt structures and operations identified on the plane, to make sense on and of the new surfaces. For instance, starting from tessellations in the plane, and removing the “no gaps” rule opens a connection to nets of polyhedra: the gaps between edges cause the shape to come out of the plane when the edges are brought together. Constructing these shapes and adapting the “inflating” idea above for closed paths suggests conjectures about relations between polyhedra and tessellations of the sphere. Then, thinking about this action as having a “reverse” direction, students considered removing the “no overlaps” rule of tessellations: now, bringing overlapping edges together produces ripply surfaces that can act as tessellations (and models) of the hyperbolic plane.

On each of the new surfaces, “familiar” results and objects from the plane are disrupted (e.g., “What is a square on the sphere?”). Sometimes generalizations are proposed in response (“We think a square is actually a regular quadrilateral – equal sides and angles. But on the sphere, the angles will not be 90 degrees!”), along with methods of creating them (“In our idea, square-ness is based on reflection and rotation symmetries. Create one by drawing the diagonals first, which capture these symmetries. They are perpendicular bisectors of each other, with the same length.”) These can in turn lead to puzzling new results (“We followed your rule and we made a bunch of concentric squares on the sphere. The angles can be as almost small as 90 degrees, but then when they get to be almost 180 degrees each, the square turns into a single straight line – the great circle at the ‘equator’”).

During this phase of the course, the class increasingly relies on their own “notice, wonder, question, conjecture” statements to fuel discussions. They develop experience with pursuing investigations inspired by their own, and their classmates’, idiosyncratic perspectives and noticing, and they become familiar with how to articulate their questions and conjectures in ways definite enough to be pursued. Moreover, they find that these community-generated investigations can produce novel and exciting results. Class sessions become increasingly focused on this style of exploration, with the course structure merely introducing new surfaces, suggesting broad directions, and ensuring that inquiry groups have visibility into each other’s emerging findings.

Because the studies of 2-manifolds are comparative, ideas and achievements from earlier in the course continually return, to be revised or to provide inspiration for new conjectures and investigations. In addition, several other basic structures provide continuity over the semester. Every week, students create entries in a Learning Journal, which I read and respond to within two days. This supports students in developing a reflective writing space and gives me the feedback I need to tune aspects of the course. Second, each student devises and pursues a personal Mathematical Investigation in the second part of the course, following on a “mini-investigation” in the first part. These projects give students confidence that they can formulate and pursue rich mathematical investigations. Finally, collaborative inquiry groups are shuffled randomly for each session of the class; randomized grouping is both an instructional principle and an essential component in ensuring that emergent lines of investigation enrich each other rather than diverging over time.

4. Research questions

The MathViz course has been refined iteratively to support and study the collective learning of MTLs. It has offered an “existence proof” that MTLs can engage in making mathematics together as a community, and one of the salient features of the course has been how participants use models of various types to structure and communicate about collaborative investigations. Because MTLs in the course are encouraged to use their experiences as learners as a lens on their emerging conceptions of classroom teaching, the course provides a rich reflection space about how classroom groups might construct geometric ideas with models. The first research question for this study motivates interactional analyses of MTLs as they engage in notice/wonder/question/conjecture processes, constructing and articulating proofs of their findings:

How can we conceptualize the processes of making mathematics together in MathViz, with a focus on the MTLs’ collaborative creation and use of physical and computational models to structure their shared investigations?

While this study does not fully adopt a phenomenological approach to the MTLs experiences, it does recognize the importance of an “insider” perspective on the processes through which MTLs interactively construct both mathematics and their community of mathematical inquiry. A first step in understanding the dynamics of this setting is to capture “thick descriptions” (Geertz, 1973) of participants’ experiences. Thus, the second research question focuses on these experiences and how MathViz students see them as relevant:

How do students experience making mathematics together in MathViz, and how do they contextualize these experiences as an influential factor in their emerging identities both as mathematicians and mathematics educators?

5. Methods

5.1. Participants

One subset of MathViz students are pre-service undergraduate secondary mathematics teachers, who are also required to have a major in Mathematics. The double major creates a cultural divide between mathematics courses and education courses, which students frequently remark on. In the iteration of the course described here, undergraduates made up an unusually large proportion of the class: 7 of the 9 students. The other subset are students in one of two Master’s programs: one in Secondary Mathematics Education, and another in Learning and Design. Master’s students often have prior classroom teaching experience. (This was the case for both of the Master’s students in the class described here).

5.2. Data sources

Each iteration of MathViz has been conducted as a research study as well as a course. In the iteration analyzed here, all nine enrolled students in the course gave their consent for class sessions to be videorecorded and their work for the course to be used as research data. Data sources for this study included student-created artifacts and videos of class sessions.

5.2.1. Student-created artifacts

These consisted of digital captures of students’ productions during the course. Many of the course activities were technology-mediated, producing artifacts that supported and captured collaborations. In addition to environments designed by the author, these included Google Docs, Sheets, and Slides documents. Students’ Learning Journals also provided an account of their thinking over the course, which supported the second research question in particular.

5.2.2. Videos of class sessions

In each session after the first, a single stationary classroom camera was positioned at the back of the room, to capture the workspaces of student groups. This camera arrangement was chosen to minimize the intrusiveness of the recording to the students’ interactive investigations.

6. Findings

6.1. Investigations on cones

In responding to Research Question #1, I focus on the class’s two days’ engagement with cones, for several reasons. First, cones are sometimes omitted from investigations of 2-manifolds, because they are neither smooth nor homogeneous. The cone point is a singular point, which introduces much of the ‘exotic’ geometric phenomena of the surface. In fact, the local geometry of a cone away from its cone point is indistinguishable from that of the plane. Yet, the intrinsic perspective is valuable in surfacing and in investigating many of these exotic features.

Second, cones form a family of surfaces. By varying the cone angle, students identify categories of cones and make statements about what is possible across their different categories. Moreover, this family of cones includes the plane (which can be seen as a cone with 360-degree cone-angle), and it includes cones with greater than 360-degree cone angles. To create cones with cone angle less than 360 degrees, a sector is cut from the plane, causing the familiar conical shape to form. In contrast, for cones with cone angles greater than 360 degrees, a sector is spliced into the plane, causing the shape to “ripple” (see Figure 3).

FIGURE 3

Figure 3. (A) A 450-degree cone is formed by “splicing” a 90-degree sector into a circular disk (a 360-degree cone). (B): when the sector is spliced in, the cone ripples. (C): the cone can be manipulated to flatten part of it. (In this configuration, one can see how interior corners of rooms are 450-degree cones).

Third, provocative analogies exist between cones with cone angle less than 360 and spheres on one hand; and between cones with cone angle greater than 360 and hyperbolic planes on the other. The cone point creates (in global properties of cones) analogs of some of the local geometric features of these homogeneous surfaces. In a sense, the cone point “concentrates” non-planar effects that are “distributed” over the whole surface of the sphere and hyperbolic plane. These analogies and the connections between local and global effects emerge in students’ insights, and they help to unite themes that have come up on each of the surfaces they have investigated earlier in the course.

Finally, the existence of a family of cones parameterized by cone angle creates a modeling challenge for students as they attempt to formulate and prove conjectures across the family. A variety of types of models and strategies for modeling cones exist, and putting these in conversation with one another activates some of the modeling practices that students have appropriated over the semester.

6.1.1. Models used in the cones investigation

6.1.1.1. Rigid plastic physical cones

These models are useful for getting a feel for the distinctive properties of cones with cone-angles less than 360 degrees. The firmness of the material permits students to use tests of straightness including stretching elastic between two points and laying a ribbon along paths between two points. Similarly, they can use patty paper to test the symmetries of paths conjectured to be straight. Finally, by fitting paper or parchment around a plastic cone and then unwrapping, students can ‘undo’ the construction operation to return to a flat sector, or an n-fold branched covering, of the conical shape.

6.1.1.2. Paper and parchment cones

These models are formed by cutting sectors out of large disks (for cone angles less than 360 degrees) or by adding in sectors (for cone angles greater than 360 degrees). They are extremely useful for exploring geometric behavior empirically across different cone angles, and for connecting findings on computational and physical models that operate in flat form (on a screen or on flat paper) with the look and feel of the surface in its conical shape. Often, converting to the folded conical shape is a necessary step for students to believe a result arrived at through manipulation of one of the computational models described below. When made of parchment, paper models can also convert an n-fold covering into a multi-layered conical shape, allowing markings on each ‘sheet’ of the cover to be visible through layers of parchment. Finally, paper models are also the only option that students in MathViz have for creating models of cones of cone angle greater than 360 degrees.

6.1.1.3. Computational turtle geometry models

Using the NetLogo environment (Wilensky, 1999), I created a set of microworlds (Papert, 1980) that enable students to place intrinsic computational agents (‘turtles’) in a flattened, single-sheet representation of a cone with any cone angle less than 360 degrees. Using turtle geometry commands (forward, back, right, left) and drawing commands (pen down, pen up), students can create paths on virtual cones. The results can then be printed, allowing students to assemble the cone and see how the turtles’ path is in fact consistent with the cone’s geometry, as it exits one edge of the single-sheet and returns on the other. This computational environment permits rapid experimentation with many possible paths, enabling students to create illuminating examples. And printing also allows a student to share multiple copies of her constructions with a group, bridging to other paper models of cones.

6.1.1.4. Computational models of the n-fold covering

These GeoGebra documents allow students to experiment with dynamically configurable versions of the n-fold covering, to get familiar with its properties. For example, in an 85-degree cone, a 4-fold covering is possible in the plane. Each point of the cone’s surface is represented four times, once in each ‘sheet’ of the covering space. The n-fold covering is typically used in flattened form, where students can use a straightedge to join copies of a point A with copies of a point B, to determine ways of connecting these two points in the cone with straight paths. Copying these to parchment paper, however, students can verify that when rolled into conical form, these paths are indeed straight, and thanks to the semi-transparency of the parchment, they can tell which of the paths between point copies are distinct and which are duplicates.

6.1.2. Student discourse in investigating properties of cones

During two 3-h class sessions, MathViz students grappled in groups with properties of geodesics (straight paths) and triangles or n-gons on cones of different cone angles. Analyses of their discourse will highlight three features:

1. Students leveraged embodied and intrinsic experiences to stabilize and make sense of the geometric phenomena they observed across models.

2. Students reasoned in a comparative way across the set of 2-manifolds they had encountered in the course.

3. Students made their own mathematics together, which they built systematically and grounded in emergent, shared understandings.

6.1.2.1. Leveraging embodied experiences to coordinate intrinsic and extrinsic perspectives

Students began their cones investigations by “messing about” (cf. Hawkins, 2002) with both physical and computational models, to get a sense of what could happen there. During this time, the class operated in what Goffman (1981) describes as an “open state of talk” (p. 143). Students were intensely engaged in manipulating models, but were nevertheless peripherally aware of each other’s activity. Occasionally, they communicated in bursts of dialog, but they did not seem to expect coherent arguments from each other at this stage. Themes were being developed, and it seemed there was a tacit agreement that the group was building a foundation that would only later be strong enough to support a demanding audience. In such settings, it was not always clear that interlocutors fully understood each other – rather, they were testing ideas that would recur later with greater confidence and attention to rigor.

For example, Jena, Clara, Teva, and Mike were at the same table, busily manipulating and reasoning about the relation between paper and plastic physical models and the one-sheet computational models. Mike asked Clara and Jena, also at the same table, how they knew the cone angle of the plastic models they were working with.¹

Mike: How do you know the cone angle of these guys? Like, how do you know the degree…of [tapping the plastic model] this

Jena: Oh, of the…[gesturing with two forearms in a triangle]

Mike: Yeah. Guess? Guesswork?

Teva: No [inaudible] a way [holding up a paper model]. If you look at the… If you measure the circumference of a circle [tapping the cone point; twirling her index finger around the cone near the cone point], and then divide by the radius. Then it gives you a ratio that tells you the cone angle, in radians.

Mike: [1 second pause; blank expression] Wow!

Teva: Right, because when it’s flat [i.e., a plane] you do the circumference divided by the radius, and you get, um, 2π

Mike: Oh, but that would depend on where you put the [pointing with a pencil tip at Teva’s cone]

Teva: No, because you’re taking the circumference and dividing by the radius, so the ratio, [sliding thumb and forefinger in a ring around the cone model] all the way down the cone…should be the same, cause…like anywhere on the plane, no matter how big the circle is, the ratio between the radius and the circumference is 2π?

Mike: Mm-hm

Teva: So it’s the same on the cone, the ratio of the radius and the circumference is always the cone angle.

Mike: Oh. I see your argument. But wouldn’t it be easier just to measure the base?

Teva: Um, well, a cone doesn’t have a base, but yes …

Mike: Well, like [pointing at the plastic cone model]

Jena: Wait, so the formula is … [picking up and touching the base]

Teva: But you don’t … [pointing at Jena’s model and the idea she infers from Jena’s gesture] you can’t measure the radius along the base. You have to [gesturing vertical-diagonally up and down repeatedly, indicating the ‘slant height’ up to the cone point] measure the radius as a geodesic; like a point on the base to the cone point.

This exchange highlighted the early state of students’ fluency and shared understanding of cones and of the features of the different models. Mike’s question arose as he looked up from some intensive work in cutting, constructing, and drawing on a paper printout from a computational model. A salient feature of his model (the proportion of the disk remaining after cutting, i.e., the cone angle) was invisible and unknown in the plastic model, raising a question about how he could connect across models. Meanwhile, Teva was exploring how an agent on a cone could intrinsically determine the cone-angle of its world, following a suggestion from the reading that the students had done before class. Understanding this method depended on interpreting key terms (circle, radius) in ways that relied on adopting an intrinsic perspective on the cone. Teva appeared to have stabilized this perspective, so that for her, the “circle” in question was a set of points on the cone at a given distance from the cone point (measured along a geodesic ‘generator’ on the cone). Teva additionally saw this as an extension of the situation on the plane.

However, these analogies were not yet helpful to Mike and Jena. The connection between the plane and the cone was not yet apparent to them, and the construct of a circle on the cone as a path that maintained a fixed distance from the cone point, was not yet stable. When Teva accepted Mike’s supposition that a circle of this kind could be “the [circumference of the] base,” she was correct, but for Mike and Jena, who appeared still to be thinking extrinsically, the (entire) base was salient as a part of the model. Teva’s explanation was sound, but the other students were not yet ready to enter into her way of thinking. During these struggles to communicate, the heavy use of gesture in this sequence was remarkable, including Teva’s final gesture, which both engaged with and countermanded the gestures of Mike and Jena. This gestural richness indicates the ways that physical models were supporting emergent sensemaking about fundamental aspects of the cones’ geometry.

6.1.2.2. Reasoning in a comparative way across 2-manifolds

At the other table, Dillon made an observation that would later have a shaping influence on other classmates’ investigations:

Dillon: The other thing I am pretty sure about is that all lines on the cone are exactly the same.

Olivia: … are the same… ?

Mike: [from the other table] … are insane!

Mike’s attunement here to a discussion that emerged elsewhere in the classroom is characteristic of the “open state of talk.” After laughing, Dillon continued, having secured Olivia’s attention.

Dillon: So on the cylinder, we had like turning lines [gesturing a helix winding upward]; vertical lines [gesturing by holding his forearm rigid vertically]; and circle lines [initially gesturing with rigid horizontal forearm, then changing to trace a horizontal circle with his index finger around the girth of the imaginary cylinder].

Olivia: Yeah.

Dillon: But on the sphere, and the plane, there’s just one type of line.

Olivia: Ok

Dillon: So, I think the cone is the same situation

Olivia: … as the sphere?

Dillon: … as the sphere, or the cylinder—sorry, the sphere or the plane. Because it’s like, on the branched covering of it, like you can only draw the line [gesturing a line, with a cutting motion] at some distance to the center

Olivia: Ok

Dillon: [repeating the cutting gesture] and no matter how you’re drawing it, like it’s the same thing. Because [making a rotating, steering wheel gesture] you can …

[1 second pause]

Dillon: [picking up a paper model of a cone] The cone has like a stretching map [pulling fingers down the cone from the cone point]? Where you can take a little cone, and stretch it [fumbling with the model] stretch it down.

[0.5 second pause]

Dillon: And that’ll like bring a line, OUT from the center.

CB: It’s zooming in, right?

Dillon: Yeah. It’s, it’s a similarity. So, vaguely. Yah.

Olivia: [.5 second pause] Hm … ok

Dillon: So, what that means is that if we understand how ONE geodesic works, we understand how ALL of them work … On a certain cone angle.

Olivia: Ok! [1 second pause] Because…

Dillon: because

Olivia: because you can just stretch it

Dillon: yeah, you can stretch it

Olivia: So, if it doesn’t cross, on one model … if you could like make it longer, it will cross.

As with the prior conversation, Dillon’s explanation was heavily augmented with elaborate gestures, as he enacted different manifestations of straight paths across different surfaces (spheres and cylinders) and across different models of the cone. His argument from the n-fold cover focused on the limited degrees of freedom (i.e., apparently one, actually zero) that we have in drawing a straight path; and his “similarity” mapping of small cone models to larger cone models emphasized the infinite extent of the mathematical cone. Though Olivia may not yet have initially grasped the nuance of this explanation, in her final response, she connected Dillon’s proposition to the problem she had been discussing with the group – namely, that geodesic paths on small cone models might not reveal all of their self-intersection behavior before they exited the physical model.

6.1.2.3. Making their own mathematics, grounded in shared understandings and definitions

After an initial share-out, where groups surfaced what they “noticed” and “wondered” about, the class established a shared Google Sheet for empirical findings relating cone angle, “number of self-intersections” a geodesic could have on that cone; “number of leaves in a planar n-fold covering,” and “minimum number of lines required to form an n-gon,” allowing the class to benefit from separate investigations and constructions with models. Then students reconfigured themselves into groups, to dive deeper into particular questions. At the end of the session, they came together to share their results.

6.1.2.3.1. Self-intersections

Dillon and Teva pursued the question of the number of self-intersections of a geodesic, depending on the cone angle. This investigation depended on Dillon’s insight about all geodesics being the same, which Teva appeared to have fully absorbed. The two presented their findings as a statement in radians. Dillon said, “If the cone angle equals π/N, then a geodesic has (N-1) [self] intersections.” Moreover, he explained that they thought this value was a “threshold,” saying “if you have got anything smaller; if you cut off some small amount of it [writing “π/N – epsilon”], it has N [self] intersections.”

The class requested examples, which they then saw agreed with the empirical data in the Google sheet. For instance, for N = 1, the 180-degree cone had the noticeable feature that geodesics created parallel rays [zero self-intersections] as they passed around the cone point. For any cone with angle less than 180 degrees (“180-epsilon”), these rays were not be parallel and would ultimately intersect (one self-intersection).

After this empirical grounding, Teva explained how she had thought about the conjecture, based on a physical manipulation she did with the paper model:

Teva: The other thing to … in terms of a way to think about this is … um, we know that right at 90 degrees, there’s one intersection, right? So if you take [picking up paper model] a cone that’s 90 degrees… This is not an exact representation, but it’s like sort of a way that I was thinking about it, which I think sort of helps in some ways conceptually justify this? But if you take an 90-degree cone and then you bend it over to make a 45-degree cone [crushing the 90-degree cone as in Figure 4B, then forming the half-angle cone]…. If we know a geodesic intersects itself once on a 90-degree cone, if you then [gesturing with her arms imitating the sides of the cone model] fold it around, there’s one intersection with 2 lines. Each of these two are sort of their own geodesic, that are going to intersect again, so that is where the three comes from. Cause there is one intersection already on the 90-degree cone, and then when you sort of wrap it around again, each of the lines …that make this intersection—intersect themselves—which gives us two more intersections.

FIGURE 4

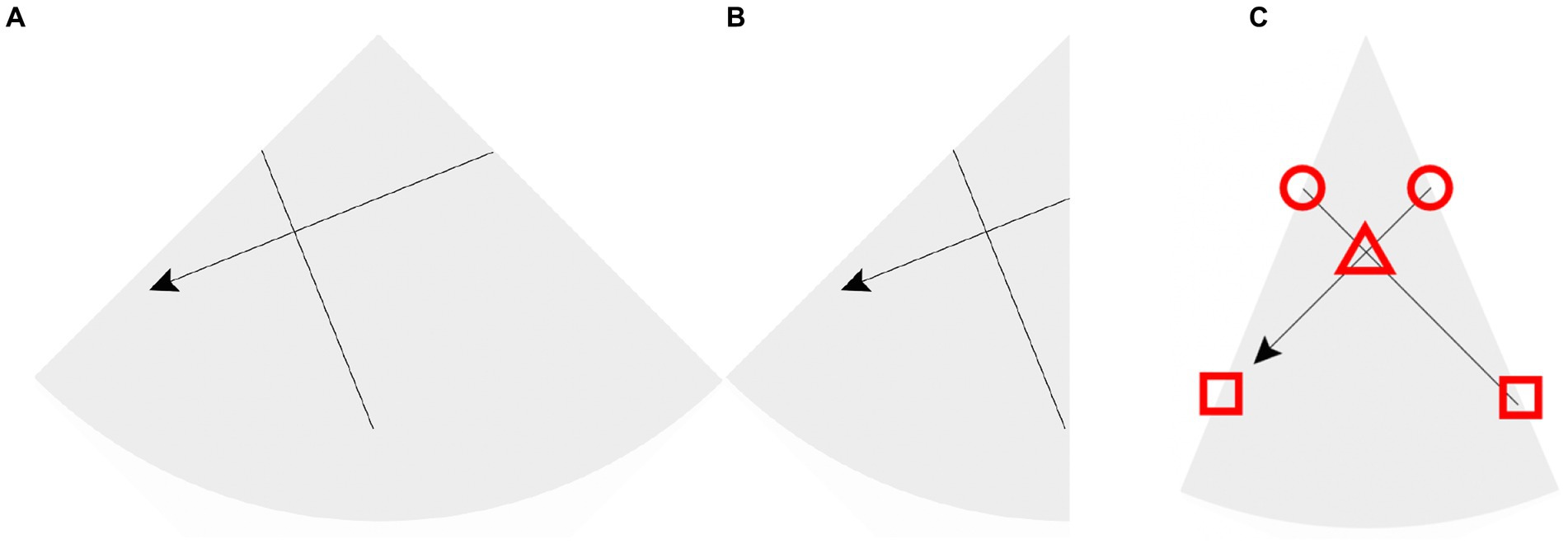
Figure 4. Teva’s manipulation of a self-intersection on a 90-degree cone (A). Crushing the cone and forming a 45-degree cone from the visible half (B), Teva claims that the one self-intersection on the 90-degree cone produces three on the 45-degree cone. The circle, triangle, and square annotations on (C) show the locations of the self-intersections that Teva claims will occur.

In terms of Teva’s and Dillon’s formula, if we grant that there are N-1 self-intersections in a cone of angle 180/N, Teva’s folding suggests 2(N-1) + 1 self-intersections in a cone of angle 180/2 N. That is, 2 N-2 + 1 = 2 N-1 self-intersections, as desired. The class discussed how this approach gave support for the conjecture (in powers of 2 for N, given the result for N = 1 (180) and N = 2 (90)). Mike noted this was “like induction” but concrete because it was grounded in Teva’s folding demonstration.

6.1.2.3.2. Strange triangles

Mike then shared results from his solo inquiry investigating turtle-geometry paths on a 75-degree cone. He had found that a single straight path could create a “triangle,” whose interior angles were 75, 75, and 30 degrees (see Figure 5A). After making one such figure in a computational model, he was surprised to find that when he launched turtles in random directions, a triangle was always created with interior angles 75, 75, 30.

FIGURE 5

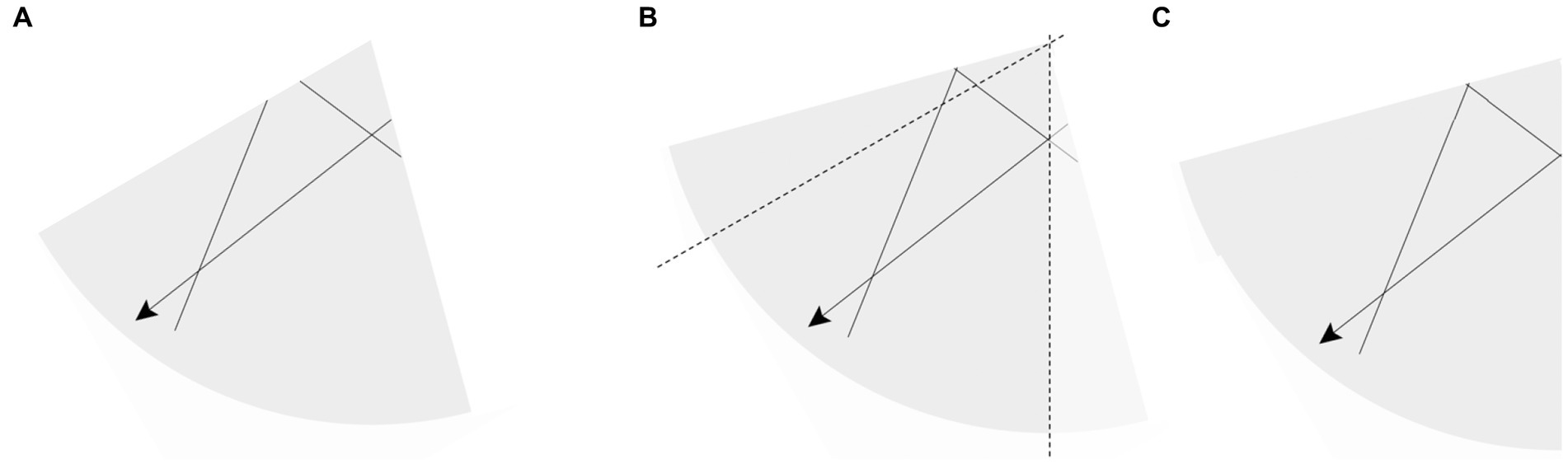
Figure 5. (A) One of the figures Mike was studying. (B,C): Mike’s transformation of the paper model of a 75-degree cone, cutting off a sector from the right and transferring it to the left, to shift the seam.

Mike then realized that his figure was a paradox: it was formed by one straight path, it had two distinct vertices, but it had three distinct ‘interior’ angles. Was it a triangle? From the perspective of a turtle geometry path, it was a triangular figure created by a movement that had no turns. As Mike had said earlier to me, to make the figure “you are…you just keep walking, there is no turning, you just keep walking!” In presenting to the class, Mike also shared a manipulation of the single sheet model he devised, shown in Figures 5B,C. Cutting off a sector from the right edge of the model, he transferred this to the left side, thereby shifting the location of the “seam.” This action corresponded to rotating one’s perspective on the rolled-up model. He shared how to do this and showed how it changed the way several geodesics on small cones looked.

6.1.2.3.3. Another definition of triangle

Olivia, Jena, and Tracy shared that they had also explored triangles. However, they defined a triangle (and an n-gon in general) differently from Mike. Whereas Mike focused on (interior) angles, Olivia, Jena, and Tracy said that for them, a triangle was based on a configuration of three distinct points. So, they required that a triangle have three vertices (and thus, for them, Mike’s Figure 5 was not a triangle but a 2-gon, formed by a single geodesic). In their investigation, they generated a large number of empirical examples for cones of different cone angles.

Olivia: We struggled really a lot ah with ah figuring out how to like visualize the line intersecting itself multiple times, but we basically determined at that—if you look at the cone data….—we filled out the sections named, column E and column G. Um, and have determined that, at 45 degrees there’s three – we have not done 22.5 yet, but um. 90, less than 90 but greater than 45 seems to be 2, there’s 2 intersections, self-intersections, but you still need to have 2 lines [to create a triangle] because even though it may seem like a triangle is created, that is not the case, it is actually a 2-gon. And it looks like a triangle, but one of the two corners of the triangle have the same vertex, so it is a 2-gon, instead of a 3-gon, which was kind of confusing at first.

After the class processed the different implicit or explicit definitions of “triangle” that different groups had adopted, I reminded the group of Mike’s shape (Figure 5):

CB: Mike had a one-sided, two verticed—two-vertexed—three-angled, “triangle,” whose interior angles added up to 180…

Mike: … with a turn angle of zero …

CB: With a turn angle of zero, because it was one line…

Olivia: That’s fantastic.

Class: [laughter]

Mike: Now

CB: … which was a definition-killer.

The group’s investigations on Day 1 thus covered important ground and incorporated a variety of styles of engaging with physical and computational models. (The groups of students not mentioned above were exploring tessellations of the cone and how to inscribe a cone in a sphere.) These investigations had also de-settled definitions and increased the students’ sense that strange but quantifiable phenomena could occur on cones.

6.1.2.4. Mathematics-making discourse on Day 2

In the next class session, students chose between investigating cones of cone-angle greater than 360 degrees, or beginning to work with hyperbolic planes. This analysis will follow the four students— Teva, Olivia, Mike, and Tracy—who elected to explore cones. They were seated further from the camera, unfortunately, and so the conversation of the five hyperbolic modelers sometimes made their discourse inaudible. In particular, Tracy’s voice could rarely be heard. While the prior section focused on moments of insight, connection, and interaction, this section traces the unfolding arc of these four students’ inquiry as they discerned patterns in their findings and then formed and iteratively refined their quantitative conjectures about n-gons on cones.

The first strange phenomenon that the group noticed on cones with large cone angles was that there were pairs of points that could not be connected with a straight path. As the group explored what to make of this strange property, Teva made some tentative statements about how a turn on a path can only ‘account for’ 180 degrees. Soon thereafter, she made a connection to polygons, saying:

Teva: I don’t think it’s possible to make a triangle on a cone whose cone angle is greater than 540

Olivia: Wait, can you explain that again?

Teva: Well it’s the idea is that you can’t connect two points where you have to turn more than 180 degrees.

Olivia: Right

Teva: I just feel that there is some connection, with like three sides and just three times 180 if you can make a triangle on it?

Olivia: Mmm!

Mike suggested that they investigate this impossibility by approaching it from below:

Mike: I wonder if we get a 450 cone, and then like draw a boundary condition triangle, and then argue that if it goes over 540, then one of the sides – you can’t draw it?

After some time working on this proposition, Teva wondered, “So maybe a quadrilateral is always possible around the cone point?” This triggered some resistance in her classmates. She then mused:

Teva: Well, no! I wonder if, I wonder if like, ok you can’t make a triangle around the cone point if the angle is 3x360, er, 3x180. [.5 second pause] So maybe you can’t make a squ- quadrilateral around it if it’s 4x180.

Olivia endorsed this conjecture by sharing her experience of drawing sides across sections of a large cone that she and Tracy had constructed. In that case it was easy to draw the fourth side, but she reasoned that if more and more material were in the cone, it would get harder and harder to do so. Olivia and Tracy then set out to make a 720 cone and test the emergent conjecture.

I asked them to state this conjecture; they improved it to say that a quadrilateral is impossible if the cone angle is greater than or equal to 720. Mike then attempted to generalize:

Mike: Maybe, Teva’s argument is that, like, you can’t draw an N-gon if the cone angle is more than 180 times N

Teva: Yeah-exactly. Or equal to.

I then asked if there was any connection to the smaller cone-angle cones they investigated the prior week. Reviewing their data, they recalled that on a 180-degree cone, the geodesic was parallel to itself, but if the cone angle were just a little smaller, like 179, it would self-intersect. Coordinating with their generalized conjecture, they interpreted this as saying:

If the cone angle is 180 or more, you can’t draw a 1-gon

If the cone angle is 360 or more, you can’t draw a 2-gon.

An implicit, related conjecture was also that if a cone was under the threshold cone angle, the n-gon in question was possible. Absorbing their working (but still implicit) definition from this week and its tension with her explicit definition from the prior week, Olivia asked:

Olivia: So, how do you draw a 2-gon on a 180?

Mike: It’s two lines, on the thing

Olivia: Oh- that’s how we’re defining it?

Teva: And you can create an enclosed space, with a finite area, using two lines.

Olivia: Are we calling it a 2-gon based on the number of [inaudible – vertices?]

Teva: …on the number of lines. To make a figure with finite area.

The group spent the next 30 min deep in model-based inquiry, investigating the conjecture they had articulated. This appeared to be an important period for assimilating and becoming comfortable with what they had discovered. Throughout this time, Olivia and Tracy invested a large amount of effort in constructing paper cones of various cone angles, and then drawing and measuring angles of polygonal paths on them. This empirical grounding gave the four-student group the advantage of being able to discern patterns in data and check emerging conjectures against concrete cases. The value of this work appeared as the group generated its second and stronger conjecture.

Teva: My other argument – I would say that as we approach 180xN for the cone angle – for example, as we approach 540 – a triangle’s angles are going to get closer and closer to 0.

Olivia: Yeah

Teva: So for any … the sum of the angles, get closer and closer to 0 … as we approach 180 x N. So, a quadrilateral, as we get closer and closer to 540, where it’s non-existent.

Teva’s idea here leveraged representational imagination (Brady, 2018) to envision possible constructions across cones. Beginning from a particular path on a specific cone, she imagined retracing it while the underlying space varied. She held an N-sided figure in her mind, and imagined this figure on a series of cones with increasing cone-angle. Mike clarified his understanding:

Mike: So, is there a relationship between interior angle sums and the cone angle?

Teva: YES, there has to be [pause]. So now I’m thinking – the smaller the cone angle, the larger the sums of the interior angles of an n-gon.

Here, Teva saw an implication of her idea, which is that when the cone angle decreased, it caused a closed path’s angles to increase. Yet, was this only a qualitative relation?

Teva: I don’t know whether there’s a mathematical relation …

Mike: Let’s do some guesswork – just throwing stuff out. If it’s a 270, then a… Then every triangle has interior 180? Right? It adds to the 360. – as the angle increases… Dump all of ‘em on the cone angle, and then we’re left with zero.

Mike proposed that they conjecture a quantitative relation by guessing, generalizing from cases they knew. His initial thinking was confused, but it intrigued Teva:

Teva: That’s interesting. Right, so I wonder. [pause] Right now what we just said is that as we approach 180xN the sum of the interior angles of an n-gon must approach 0. [pause]. But now – you’re saying the sum of the angles of the n-gon is equal to 180N minus the cone-angle. [pause] That would be an interesting.

Mike grasped that this would extend the finding they had developed in the first half of the class:

Mike: If that’s true, then this [pointing to board] is a corollary.

Olivia then reiterated, and brought in evidence from the concrete cases she and Tracy had been constructing.

Olivia: So, your cone angle, plus the sum of the interior angles of an n-gon IS 180xN? ‘Cause you just said … So, let’s try it on this one. So, we know that the [sum of the] interior angles is 92 …

Teva: [inaudible] … and your thing [cone angle] is 360 + 270 = 630.

Mike: It’s a quadrilateral

Teva: And 180 x 4 = 720…. So it DOES work in that case!

Mike: Rounding to 90 degrees. Uh-huh! It’s not a proof, but it’s an example.

Teva decided to capture the conjecture in the class Google Doc:

Teva: I’m going to type it in here. As we approach a cone angle of 180 times N from below …

Mike: The [Teva’s Surname] Theorem

Teva: …the sum of the interior angles of an n-gon will approach zero. And the idea is that the sum of the interior angles of an n-gon that includes the cone point is equal to 180*N minus the cone angle.

The group then turned to further testing:

Teva: It works with that one [pointing to Olivia’s paper model]. Did you measure on this one yet [pointing to one of Tracy’s constructions]?

Tracy: sum is… 20 + 30 + 40… Ok yah. This [the cone angle] was 450.

Teva: The total angle sum of the triangle was 90.180*n = 540 – so ….

Mike: WOW!

They continued to try examples to verify the conjecture in particular cases, and they also explored different ways of looking at the insight. Apparently inspired by generalizing a known fact about the triangle on the plane, Teva thought aloud:

Teva: A corollary—anything that’s a multiple of 360, the interior angles around the cone point would sum to 180… so, for 360x1, a triangle has interior 180. For 720, a 5-gon has interior 180.

Olivia: So, this was a … 5-gon on a 720 cone.

Teva: A 5-gon on a 720, the angles will add up to 180. If the cone angle is 180N, then for a N+1 gon, the interior angles will add up to 180.

Mike: I think there’s something — I think there’s some even-odd going on.

Teva: Any cone angle 180N, the sum of the interior angles … of an N+1 gon will be 180.

Mike: Yes yees—sorry. 720 … times 4, so a pentagon …

Mike: The plane is 2 * 180. Therefore, a 2+1 gon … triangle… has interior angles 180!

Mike recognized that this conversation was another way of drawing out implications of the main conjecture, and he saw how it could be expanded beyond the domain they had explored to this point – back to cones of cone-angle less than 360 degrees.

Mike: So if our theory is correct, this would all be true. [pause] And that would also mean that a 2-gon in a 180 cone would have interior angle 180…

Olivia: … which makes sense! Because remember they [the two ends of a geodesic] are parallel.

Mike: Right? Like this guy? [picks up the unfolded paper model from the prior class].

Teva: And you would just connect it [i.e., the drawing a line between the two parallel rays would make a 2-gon, with 2 supplementary angles].

Mike: OOH!!!

Upon making this extension and connection to the prior week’s work, Mike was unable to contain his enthusiasm and jumped up from his seat.

Teva: But we have to check it. I think we’re right about

Mike: … except for when N is zero. Like you can’t …

Mike recognized that the formula makes sense for only positive integers N. But now that the 2-gon had been incorporated, there were also opportunities to explore 1-gons (geodesics and their self-intersections), where the formula also held. For instance, on a 90-degree cone, a geodesic self-intersects at 90 degrees. For this 1-gon, 180*1–90 = 90. They continued to connect existing data to their conjecture – for example, a triangle on a 495-degree cone, that they created by splicing a 135-degree sector into a disk, had interior angles summing to 45 degrees.

Although the group had already touched on cones of cone-angle less than 360 degrees above, with the 180-degree cone, this was still a novel area.

Olivia: That’s really cool!

Teva: The only thing, it is not so helpful with is when we get less than 180 as the cone angle. Then you can make any n-gon, and we do not know about the… WELL, I wonder …

Mike: Like we should …

Teva: Like if I made a 3-gon on a 180, then it should sum up to 360. I assume, but maybe it doesn’t hold, but that it would also work for like… ‘cause we were just looking at triangles whose angles sum up to less than 180 because we were looking at [cones > 360]. But I assume it would also hold if it’s more than 180.

After a while longer working with the models, Olivia raised a related question about the turn angles (or “exterior angles”) of the shapes they have been constructing:

Olivia: I wonder what the exterior angles would do ….

Olivia tested with the 495-degree cone that they had analyzed earlier.

Olivia: The turn angles on the 495 [360+135] cone, add up to 492.

Teva: It WOULD makes sense that the turn angles would add up to the cone angle!

This finding, too, was closely connected with the main conjecture, and it also made a link with the first theorem that the students ever formulated in the course – namely, for the plane [360-degree cone] the total turn angle of a [non-self-intersecting] polygonal path is 360 degrees.

The final leap that the group made in this session occurred as Olivia, Teva, Tracy, and Mike presented their findings to the class. This exchange was lost to the video record, as the camera’s battery died, but the other group asked whether their conjecture could be extended to the cylinder. One of the students proposed that the cylinder might be thought of as a kind of “degenerate” cone with cone angle 0. A “monster” (Lakatos, 1976) that the class had discovered earlier, on the cylinder, was a “triangle” that circumnavigated the cylinder (see Figure 6).

FIGURE 6

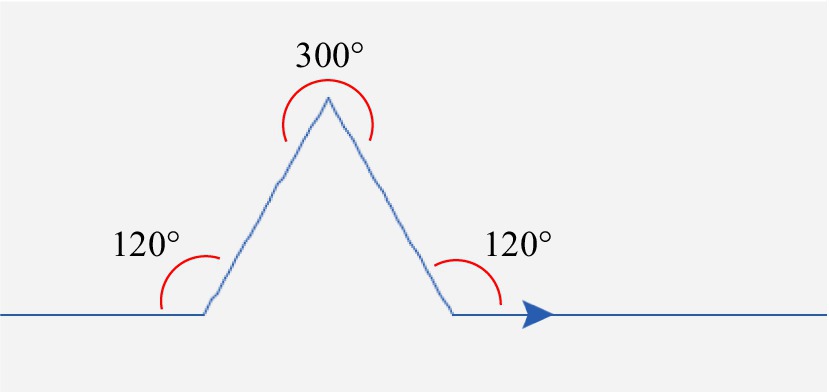
Figure 6. A “triangular” turtle path on an “unrolled” version of the cylinder. (To create the cylinder, “glue” the left and right edges.) This path produces “interior” angles (measured above the path) of 120, 300, 120.

In light of the present discussion, this could be a candidate for applying the Theorem. The interior angles of this “monster” triangle” were: 120, 300, 120, which produced an angle sum of 540. The class was delighted to find that this did in fact equal 180*3 minus the ‘cone angle’ (if taken to be 0)!

6.1.3. Summary of the cones investigations

Across these two sessions, MTLs built upon features of cones and their models that were salient to them—whether because they were puzzling and distinctive or because they suggested connections with phenomena characteristic of other surfaces (e.g., spheres or cylinders). In the first session, they began with open explorations, in which they struggled to balance intrinsic and extrinsic perspectives and to understand the affordances and limitations of different model types. In the course of that session, they recognized that the distinctive forms of symmetry of the cone (rotation and dilation about the cone point) allowed for manipulations of physical models (e.g., Mike’s technique for shifting the seam), and enabled drawings that initially appeared as particular cases to be understood as general (e.g., Dillon’s “there is just one type of line”). Gestural expression and analogies with prior investigations supported the practical dissemination of these insights among the group. In the second session, the group explored polygons enclosing the cone point—leveraging Dillon’s insight about geodesics to make general existence and non-existence statements, as well as quantitative claims about angle sums of such polygons. Having simplified the problem on a cone with given cone angle, they were free to consider how their claims varied as the cone angle varied. They used definitions flexibly and powerfully (e.g., their shifting definition of n-gon), and they generated parameterized systems of claims, which ended in unifying not only cones of all angles, but also the cylinder as a “degenerate” case. In pursuing this investigation, they leveraged each other’s distinctive perspectives (e.g., Teva’s intrinsic sense; Mike’s willingness to brainstorm; Olivia’s and Tracy’s persistent construction and measurement of cases), to refine, expand, and prove their claims.

6.2. Impact of a semester of MathViz investigations

Students’ learning journals provided insight into how they experienced the course and how it impacted their emerging identities as mathematics teachers, addressing Research Question 2. To give voice to all of the students in this iteration of MathViz, I draw upon the class’s final journal entries, in which they reflected on the course as a whole. I identified three themes across their entries, each described in a section below.

6.2.1. The empowering experience of extended, collective, and student-driven investigations

Nina described how the investigations of the course helped her to appreciate her own ability to think creatively in mathematics, and to recognize the role of such thinking in learning:

Continuously asking ‘why’ questions, I learned how to form wonders, brainstorm ways to investigate, and answer my own questions with my own findings. Through this, I found out that math can be very creative and self-driven. … The best part of being creative with math was that the results were always unexpected. It was more than just not knowing the answer to my own question. Sometimes, I was confused by my own questions. Sometimes, I was wondering if my questions had any substance or novelty. Sometimes, the answer was given to me and I did not understand how it was derived. All of these experiences were frustrating and challenging, but at the same time, they were captivating and encouraging.

As Nina’s comments suggest, it took some time for students to become comfortable with the MathViz approach. Jena mentioned how the enthusiastic response of a visitor to the class helped her to appreciate the class’s achievements:

It was really reinforcing to realize from an outside perspective having Bharath [Sriraman] come and participate in our class what interesting and out of the box thinking we are doing in this class….It made me realize how conceptual the learning we were doing really was.

Similarly, Olivia, who had expressed skepticism about the course’s approach early on, came to a strong sense that not only had she achieved valuable endpoints of inquiry, but also that the questions and conjectures she generated on the way themselves had value. She said of her math investigation, “I am really proud of my findings and conjectures.”

The positive affect in these reflections suggests that while making mathematics together, they also shifted their images of themselves as agentic participants in mathematical practices who were capable of making genuine mathematical discoveries. Consistent with the work of developing mathematical identities, students noted how much they appreciated the supportiveness of their classmates. For example, Nell wrote, “Something else that I love is how well-accepted all responses are. There is never any negativity in the room and everyone is always very supportive of one another.” Clara also wrote:

Our classroom environment specifically gave all of us space to grow individually & productively. Yes, we were all on the same path, but more open-ended assignments (like this learning journal) gave us room to go take detours and side routes. Following our own interests not only kept us continually connected to the material, but definitely increased our capacity to learn. All of this is really because you gave us space to ask questions. Adapting the class to our interests & notions was complicated, but showed us that our inquiries & curiosities matter & math is so big that we have room to spread out within it. I hope to be able to do this someday as a teacher.

Reflecting on her experience over the semester, Jena recalled working with Dillon, using polydrons to build polyhedra and envision tessellations of spheres (“we struggled to build a perfect sphere and felt quite thrilled when we succeeded at the end of class.”) And she remembered when she and Nell “thought of using sunlight for the purpose of reflection” in a physical model, saying “we found such a cool approach” to study that isometry transformation. Finally, she recalled “mathematical debates between Olivia, Clara, and I about what makes a triangle a true triangle” (across different surfaces). About these images of making mathematics, Jena said: “These sounded like they were heading nowhere at the moment, but looking back, they were all precious explorations. As a class, I truly think that we broadened our perspective on math. I very much enjoyed our growth and struggles!” Finally, Teva wrote:

This course has given me the opportunity to engage with math in a new way and has prompted me to think more broadly about what math is. Being a student in this class also reminded me of my love for math.... The second part of the course really gave me the opportunity to think about and experience what it means to create math. It was new for me to have the opportunity to come up with math conjectures and then share them with my peers as a mathematical discovery.

Concrete experiences of making mathematics together gave students new perspectives on the nature of mathematics and on what a math classroom could be like. These new images featured a sense that all students were capable of creativity and mathematical innovation: for instance, Dillon said, “I’ve never been sure that a math classroom can facilitate genuine exploration for everyone in the class, but I think you are pulling this off.”

6.2.2. Contrasting images of mathematics compared to those garnered in a Math Major

As suggested above, MathViz contrasted with students’ prior experiences of mathematics as students. Registering this contrast is important, as it underscores the challenges involved for MTLs in fashioning images of mathematics as open and inviting and of themselves as capable makers of mathematics. Along these lines, Teva wrote, “Despite having majored in math in college, I never had the opportunity to participate in ‘making’ math. Math was always presented to me as something that was already established, and I viewed it as a set of rules to be followed to come to a correct answer.” She now questioned this as a model for her teaching:

Because I enjoyed math, I did not have any issues with the way math was presented to me and my resulting relationship with it as someone “doing” something that was already established. However, it was clear to me that my peers (when I was a student) and many of my students (when I was a teacher) were not okay with this relationship with math and found learning math unengaging and irrelevant to their lives. I think reframing math as something that students can create has the potential to make it much more meaningful to the students. ….[I] hope that I’ll be able to give my students the empowering experience of being able to ‘make’ math by investigating, discovering, and conjecturing about math topics that we cover in class.

Similarly, Tracy drew a contrast with her other math classes, on the topics of authentic teamwork, the diversity of mathematical inquiry, and making connections between math and other topics:

All my other math classes are standard lecture style, with professors telling me information that I have to memorize. In this course we had to figure most information out ourselves, which I really enjoyed. I really got to understand and experience the teamwork required in math that I do not really experience in my other classes....This class really made me view geometry and math in a whole different view, especially seeing how ideas from this class [were] made into very different math investigations for each person. It was interesting to see different views of mathematics and how it is everywhere, even in topics and subjects that do not seem related to math at all.

6.2.3. Nina’s contrast focused on her sense of agency

Instead of being told exactly what to learn and memorize, I felt like a pioneer in control of the journey. Continuously asking ‘why’ questions, I learned how to form wonders, brainstorm ways to investigate, and answer my own questions with my own findings. Through this, I found out that math can be very creative and self-driven.

Finally, Dillon said he felt that “all…math majors should have a course like this in their major.” And he remarked that “It is funny that I’m getting this in a Math Ed class though.” This suggested that the value he found in MathViz was intrinsic to the making of mathematics, and not exclusively centered in pedagogical matters. Indeed, across the group, these comments suggest that students did not simply enjoy MathViz as a course, but that they appreciated it as an opportunity to construct “a whole different view” of mathematics—one where the theorems were not “already established” facts that students simply need to “memorize” and where a learner is “a pioneer in control of the journey.”

6.2.4. Students’ sense of the value of technology-enabled models for their own future teaching

Teachers in the US face significant logistical barriers in integrating technology in their classrooms. When MathViz students reflected on the role of computational models in their future classrooms, they were thus in part signaling the value they attributed to using models in making mathematics. Teva made connections between her experiences using technologies as a student in MathViz and her plans for future teaching:

The beginning of the course introduced me to technology that could be used in a math classroom, and … examples of what its implementation could look like. I’m excited about the possibility of using some of the technology as an exploratory environment in math classrooms, especially since most technology I used when teaching was just to get students to practice & more like animated worksheets. The first part of the course opened up for me the large sea of possibilities for which technology can be used when teaching math.

For Nina, too, technology-supported models and environments helped to substantiate a coherent alternative approach to mathematics:

Moving on from Scratch to Turtle Geometry, the hands-on coding allowed me to be more interactive and creative. Then, as we transitioned to transformations, I began to drift away from hanging onto things I knew to questioning the most fundamental elements, such as ‘What is a line?’ ‘What is a straight line?’ ‘What is a curve?’ It was such a notable transition. In the meantime we also had fun while doing this.

Jena reflected that “It was certainly useful to use both physical models that we could cut, manipulate and visualize in our hands as well as the virtual model on both GeoGebra and turtle programming.” She also felt that this diversity of media could be responsive to student diversity: “I think that as technology becomes more advanced and more integrated into classrooms it is important as their teacher to be accustomed to different forms of learning. Some students will love the new technology and others will only be able to visualize it with physical models.”

Finally, Clara wrote about the value she saw in “placing the responsibility of technology on students” She remarked that,

We were able to learn such valuable lessons with our computers to a depth we could not have reached on paper. Thinking about teaching high school math, 3D visualization software can help my students continue their learning. Especially for more visual learners, technology might make more sense. Moreover, if I want students to take more ownership over their math, the inclusion of computers might open up a space for their exploration. Overall, seeing computers as a tool—with a specific use for a specific time and place is beneficial to a productive classroom with engaged learners.

These views of computational modeling tools as supporting students in exploring questions, inquiring into fundamentals, and taking ownership of their learning are coherent with MTLs’ experiences of mathematical investigations in which they saw models across modalities as supports for all students in making mathematics together.

7. Discussion and conclusions

The MathViz course offers a proof of concept for a proposition central to a broader debate about the nature of STEM: namely, that mathematical creativity and the experience of making mathematics are essential features of mathematical practice, to be experienced by all participants, rather than only a select few. The course offered Math majors in the university’s Secondary Education program a new view of mathematics learning and teaching that they found useful in conceptualizing their future teaching practice. While it is problematic that not all MTLs have such experiences within their mathematics major, it is encouraging that an education course could support a change in students’ conceptions (cf. Liljedahl, 2005, on the impact of experiences of discovery in math).

It is worth recognizing that not all philosophers of science and mathematics have held the view that epistemic creativity is accessible to everyone, even within the professional sphere. Indeed, Kuhn’s (1970) famous distinction between “revolutionary” science (which occurs infrequently) and the “puzzle solving” of “normal science” (which occurs regularly), can implicitly limit the experience of disciplinary creativity to the infrequent eruptions of exceptional contributors. At the level of epistemology, this view focuses the study of scientific discovery on the psychology of genius rather than on the logic of discovery (Lakatos, 1976) or of the collective practices that characterize “epistemic cultures” (Knorr Cetina, 1999).

Within mathematics, too, the view that creativity might be a property of the few has been widely held. Henderson (1996) describes a dispute between two famous mathematicians on this subject. René Thom, the renowned topologist, argued in a 1971 paper about the importance of cultivating “intuition” in all mathematics students, and in particular in the curricula of public schools (Thom, 1971). In a rebuttal, Jean Dieudonné wrote:

I am convinced that, since 1700, 90 per cent of the new methods and concepts introduced in mathematics were imagined by four or five men in the eighteenth century, about thirty in the nineteenth, and certainly not more than a hundred since the beginning of our century. These creative scientists are distinguished by a vivid imagination coupled with a deep understanding of the material they study. This combination deserves to be called “intuition.” (Dieudonné, 1973, p. 16, qtd in Henderson, 1996; emphasis added).

Given this, Dieudonné argued that mathematics teaching will be entrusted to merely “adequately educated” teachers, who “will not be gifted with the exceptional ‘intuition’ of the creators” (16).

In contrast to Dieudonné’s elitist view, Lakatos’s (1976) perspective on the “logic of discovery” places emphasis on collective and discursive interactions as the source of innovation and creative power. Refining the views of his mentor, Karl Popper (1963), Lakatos paints a picture of mathematical work that features bold conjectures made by ordinary participants, along with a communal, discursive process of “proving,” which foregrounds collective efforts at “improving” these fallible conjectures. There are also signals that a turn to collective, collaborative inquiry is actually occurring within professional mathematics. Fields Medal winner Timothy Gowers envisioned and supported the successful pursuit of “massively collaborative mathematics” (Gowers and Nielsen, 2009) in the Polymath projects, which resulted in the proofs of six theorems over five years. More broadly, Grossman (2002) documented a substantial and accelerating trend toward co-authorship in the MathSciNet Mathematical Reviews database.

Mathematics education can contribute to the epistemological debate on collaboration and mathematical creativity by developing effective instructional designs that honor the creative power of all individuals and groups and, most importantly, give them concrete experiences of the thrill of “making” mathematics together. And we can contribute to the design of environments that foster inclusive mathematical collaboration by supporting and studying such activity in classrooms that involve MTLs, whose role as both learners and emerging teachers positions them as valued informants on the processes involved in creating and participating in communities of inquiry.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the author.

Ethics statement

The studies involving human participants were reviewed and approved by Vanderbilt University IRB (under the IRB-approved “Trajectories in Learning to Teach” project). The patients/participants provided their written informed consent to participate in this study.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

Collaborative computational modeling in MathViz was enabled in part by the Group-based Cloud Computing (GbCC) system, which was created with support of the US National Science Foundation under Grant No. 1614745.

Acknowledgments

The author wishes to acknowledge the students of MathViz, both during the iteration studied here and over the entire history of the course, for their enthusiastic participation in the course and their willingness to engage in making mathematics together through open-ended, collaborative inquiry.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^In the transcripts, gestures and other non-verbal communications are described in square brackets. Pseudonyms are used for MTLs throughout, while “CB” designates the author.

References

Abelson, H., and DiSessa, A. (1986). Turtle geometry: the computer as a medium for exploring mathematics. Cambridge, MA: MIT press.

Google Scholar

Ball, D. L. (1992). Magical hopes: Manipulatives and the reform of math education. American Educator: the professional journal of the American Federation of Teachers 16.

Google Scholar

Bartolini Bussi, M. G., and Mariotti, M. A. (2008). “Semiotic mediation in the mathematics classroom: artefacts and signs after a vygotskian perspective” in Handbook of international research in mathematics education. eds. L. English, M. Bartolini, G. Jones, R. Lesh, B. Sriraman, and D. Tirosh (New York: Routledge).

Google Scholar

Bartolini, M. G., and Martignone, F. (2020). Manipulatives in mathematics education. Encyclopedia of mathematics education, 487–494.

Google Scholar

Brady, C. (2018). Modeling and the representational imagination. ZDM 50, 45–59.

Google Scholar

Brady, C., and Lehrer, R. (2021). Sweeping area across physical and virtual environments. Dig.l Exp. Math. Educ. 7, 66–98. doi: 10.1007/s40751-020-00076-2

CrossRef Full Text | Google Scholar

Brown, T. (1996). The phenomenology of the mathematics classroom. Educ. Stud. Math. 31, 115–150. doi: 10.1007/BF00143929

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Ambrosio, U. (1985). Ethnomathematics and its place in the history and pedagogy of mathematics. For Learn. Math. 5, 44–48.

Google Scholar

De Villiers, M. (1998). “An alternative approach to proof in dynamic geometry” in Designing learning environments for developing understanding of geometry and space. eds. R. Leher and D. Chasan (Mahwah: Lawrence Erlbaum).

Google Scholar

Dienes, Z. P. (1960). Building up mathematics. London: Hutchinson Educational.

Google Scholar

Dieudonné, J. A. (1973). Views: Should we teach “modern” mathematics? An affirmation from a founder of Bourbaki of the principles of the new curricula in mathematics. Am. Sci. 61, 16–19.

PubMed Abstract | Google Scholar

Fox Keller, E. (2000). Models of and models for: Theory and practice in contemporary biology. Philos. Sci. 67, S72–S86. doi: 10.1086/392810

PubMed Abstract | CrossRef Full Text | Google Scholar

Freudenthal, H. (1983). Didactical Phenomenology of Mathematical Structures. Netherlands: Springer Netherlands.

Google Scholar

Freudenthal, H. (2002). Revisiting mathematics education: China lectures. New York: Kluwer Academic Publishers.

Google Scholar

Geertz, C. (1973). The interpretation of cultures. New York: Basic Books.

Google Scholar

Goffman, E. (1981). Forms of Talk. Philadelphia: University of Pennsylvania Press.

Google Scholar

Gowers, T., and Nielsen, M. (2009). Massively collaborative mathematics. Nature 461, 879–881. doi: 10.1038/461879a

PubMed Abstract | CrossRef Full Text | Google Scholar

Gravemeijer, K., and Terwel, J. (2000). Hans Freudenthal: a mathematician on didactics and curriculum theory. J. Curric. Stud. 32, 777–796. doi: 10.1080/00220270050167170

CrossRef Full Text | Google Scholar

Greeno, J. G. (1994). Gibson’s affordances. Psychol. Rev. 101, 336–342. doi: 10.1037/0033-295X.101.2.336

PubMed Abstract | CrossRef Full Text | Google Scholar

Grossman, J. W. (2002). The evolution of the mathematical research collaboration graph. Congressus Numerantium, 201–212.

Google Scholar

Hawkins, D. (2002). The informed vision: essays on learning and human nature. New York: Algora Publishing.

Google Scholar

Henderson, D. (1996). Alive mathematical reasoning. In Proceedings of the 1996 Annual Meeting of the Canadian Mathematics Education Study Group.

Google Scholar

Henderson, D. W., and Taimina, D. (2005). Experiencing geometry: Euclidean and non-Euclidean with history. Hoboken: Prentice Hall.

Google Scholar

Henderson, D. W., and Taimina, D. (2006). “Experiencing meanings in geometry” in Mathematics and the aesthetic, New approaches to an ancient affinity. eds N. Sinclair, D. Pimm, and W. Higginson (New York, NY: Springer) 58–83.

Google Scholar

Hirsch, C. R., and McDuffie, A. R. (2016). Annual Perspectives in Mathematics Education 2016: Mathematical Modeling and Modeling Mathematics. Reston, VA: National Council of Teachers of Mathematics.

Google Scholar

Hundley, M., Palmeri, A., Hostetler, A., Johnson, H., Dunleavy, T. K., and Self, E. A. (2018). “Developmental trajectories, disciplinary practices, and sites of practice in novice teacher learning: a thing to be learned” in Innovative practices in teacher preparation and graduate-level teacher education programs. eds D. Polly, M. Putman, T. Petty, and A. Good (Hershey, Pennsylvania: IGI Global) 153–180.

Google Scholar

Hunt, A. W., Nipper, K. L., and Nash, L. E. (2011). Virtual vs. concrete manipulatives in mathematics teacher education: is one type more effective than the other? Curr. Middle Level Educ. 16, 1–6.

Google Scholar

Kamii, C., Lewis, B. A., and Kirkland, L. (2001). Manipulatives: When are they useful? J. Math. Behav. 20, 21–31. doi: 10.1016/S0732-3123(01)00059-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaput, J. J. (1991). Notations and representations as mediators of constructive processes. In: E. GlasersfeldVon (ed). Radical Constructivism in Mathematics Education. Dordrecht: Springer.

Google Scholar

Knorr Cetina, K. (1999). Epistemic cultures: How the sciences make knowledge. Cambridge, MA: Harvard University Press.

Google Scholar

Kobiela, M., and Lehrer, R. (2015). The codevelopment of mathematical concepts and the practice of defining. J. Res. Math. Educ. 46, 423–454. doi: 10.5951/jresematheduc.46.4.0423

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuhn, T. S. (1970). The structure of scientific revolutions. Chicago, IL: University of Chicago Press.

Google Scholar

Lakatos, I. (1976). Proofs and refutations: The logic of mathematical discovery. Cambridge, UK: Cambridge University Press.

Google Scholar

Lehrer, R., Kobiela, M., and Weinberg, P. J. (2013). Cultivating inquiry about space in a middle school mathematics classroom. ZDM 45, 365–376. doi: 10.1007/s11858-012-0479-x

CrossRef Full Text | Google Scholar

Lénárt, I. (2010). Gauss, Bolyai, Lobachevsky—in General Education? (Hyperbolic Geometry as Part of the Mathematics Curriculum). In Proceedings of Bridges 2010: Mathematics, Music, Art, Architecture, Culture.

Google Scholar

Liljedahl, P. G. (2005). Mathematical discovery and affect: The effect of AHA! Experiences on undergraduate mathematics students. Int. J. Math. Educ. Sci. Technol. 36, 219–234.

Google Scholar

Maschietto, M., and Soury-Lavergne, S. (2013). Designing a duo of material and digital artifacts: The Pascaline and Cabri Elem e-books in primary school mathematics. ZDM 45, 959–971. doi: 10.1007/s11858-013-0533-3

CrossRef Full Text | Google Scholar

McNeil, N., and Jarvin, L. (2007). When theories don’t add up: Disentangling the manipulatives debate. Theory Pract. 46, 309–316. doi: 10.1080/00405840701593899

CrossRef Full Text | Google Scholar

Moreno-Armella, L., Brady, C., and Elizondo-Ramirez, R. (2018). Dynamic hyperbolic geometry: building intuition and understanding mediated by a Euclidean model. Int. J. Math. Educ. Sci. Technol. 49, 594–612. doi: 10.1080/0020739X.2017.1418915

CrossRef Full Text | Google Scholar

Morgan, M. S., and Morrison, M. (1999). Models as mediators: Perspectives on natural and social science Cambridge: (Cambridge University Press).

Google Scholar

Moyer-Packenham, P., and Westenskow, A. (2013). Effects of virtual manipulatives on student achievement and mathematics learning. Int. J. Virtual Pers. Learn. Environ. 4, 35–50. doi: 10.4018/jvple.2013070103

CrossRef Full Text | Google Scholar

Nemirovsky, R. (2018). “Pedagogies of emergent learning” in Invited Lectures from the 13th International Congress on Mathematical Education. eds H. Kaiser, M. Forgasz, A. Graven, E. Kuzniak, E Simmt, and B. Xu (Cham: Springer International Publishing) 401–421.

Google Scholar

Nemirovsky, R., and Sinclair, N. (2020). On the Intertwined Contributions of Physical and Digital Tools for the Teaching and Learning of Mathematics. Dig. Exp. Math. Educ. 6, 107–108. doi: 10.1007/s40751-020-00075-3

CrossRef Full Text | Google Scholar

Nührenbörger, M., and Steinbring, H. (2008). “Manipulatives as tools in teacher education” in International handbook of mathematics teacher education. eds. D. Tirosh and T. Wood (Rotterdam: Sense).

Google Scholar

Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. New York: Basic Books.

Google Scholar

Popper, K. (1963). Conjectures and refutations: The growth of scientific knowledge. New York, NY: Routledge & Kegan Paul.

Google Scholar

Soury-Lavergne, S. (2021). Duos of digital and tangible artefacts in didactical situations. Dig. Exp. Math. Educ. 7, 1–21. doi: 10.1007/s40751-021-00086-8

CrossRef Full Text | Google Scholar

Taimina, D. (2018). Crocheting adventures with hyperbolic planes: tactile mathematics, art and craft for all to explore. Boca Raton: CRC Press.

Google Scholar

Thom, R. (1971). "Modern" Mathematics: An Educational and Philosophic Error? A distinguished French mathematician takes issue with recent curricular innovations in his field. Am. Sci. 59, 695–699.

Google Scholar

Uttal, D. H., Scudder, K. V., and DeLoache, J. S. (1997). Manipulatives as symbols: A new perspective on the use of concrete objects to teach mathematics. J. Appl. Dev. Psychol. 18, 37–54. doi: 10.1016/S0193-3973(97)90013-7

CrossRef Full Text | Google Scholar

Voigt, J. (1994). Negotiation of mathematical meaning and learning mathematics. Educ. Stud. Math. 26, 275–298. doi: 10.1007/BF01273665

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilensky, U. (1999). NetLogo. [Computer software]. Northwestern University: Evanston, IL: Center for Connected Learning and Computer-Based Modeling. https://netlogoweb.org/.

Google Scholar