Quantum science in a nutshell: fostering students' functional understanding of models

1. Introduction

In the coming years, as the significance of modern quantum technologies continues to escalate (Greinert et al., 2022), there will be a growing need to raise awareness among the future generation for these technologies. Therefore, developing and testing educational materials for learners is of high priority. To contribute to this objective, this article introduces a synchronous online course titled “Quantum Science in A Nutshell” tailored for high school students. The primary aim of the course is to familiarize secondary school students with the quantum physical concepts of photons, which play a crucial role in comprehending the fundamental principles of quantum physics (Krijtenburg-Lewerissa et al., 2017; Bitzenbauer and Meyn, 2020). The course focuses on general ideas about models in physics in the beginning to pave students a way to develop a functional understanding of quantum models, and to foster students' conceptual understanding of quantum topics [for an overview, see Krijtenburg-Lewerissa et al. (2017) and further details on this idea are also presented in the research background section of this article].

Although there exists a substantial body of research literature on the development of quantum physical ideas in learners, most of it is focused on describing and evaluating conceptions the learners have about quantum physics itself. For example, there were detailed studies on students' ideas of photons (Mashhadi and Woolnough, 1999), electrons in the atomic shell (McKagan et al., 2010), spin (Taber, 2005), or tunneling (Özcan et al., 2009). Additionally, several educational pathways dedicated to the teaching of quantum physics and their effects on learning (e.g., see Michelini et al., 2000; Weissman et al., 2022; Aehle et al., 2022; Pospiech, 2021; Seskir et al., 2022) have been in the focus of quantum physics education research. Recently, research has indicated that students' understanding of models can facilitate the development of a deeper students' conceptual understanding of quantum physics aspects (Ubben, 2020; Ubben and Bitzenbauer, 2022, 2023). Considering that developing an understanding of models holds significance not only in the realm of quantum physics education but also for acquiring knowledge of science in general, adopting a learning approach that considers this perspective has the potential to not only enhance our understanding of teaching and learning quantum physics but also contribute to the broader field of science education research. Therefore, we present an approach to integrate teaching about models into a course about quantum optics and analyse its effects on the development of a functional understanding of models among learners.

In Section 2, theoretical background information is presented regarding the design principles for online courses, learning in quantum physics, and developing a functional understanding of models to describe the underlying theoretical principles used in this article. In Section 3, the course itself is described in detail, including its goals and how it incorporates the principles laid out in Section 2. In Section 4, the research questions are stated, and in Section 5, the methodology used to answer the research questions is described in detail. The results of this study are reported in Section 6. Finally, Section 7 discusses the study's results, and Section 9 provides a conclusion and an outlook into the future regarding the implementation of the course and what was learned from it.

2. Theoretical background

2.1. Design principles for online courses

In the process of creating an online course, it is crucial to establish a learning environment which supports students' learning processes. To attain this objective, a plethora of research has been conducted, offering perspectives and criteria that should be considered when developing an online course (for example, see Debattista, 2018; Daniels et al., 2019; Freericks et al., 2019; Gegenfurtner and Ebner, 2019; Gegenfurtner et al., 2020; Mukhtar et al., 2020; Shi, 2020; Martin et al., 2021). Debattista (2018) conducted research on online education and examined four different rubrics, which were then combined into a comprehensive framework. The rubric developed by Debattista (2018) has already served as a methodological framework to design online courses in the past (for example, see Bitzenbauer and Zenger, 2022).

The first item of Debattista's rubric for online learning is the instructional design of the course (Debattista, 2018). Meaning, the creator of the online course has to be clear about what it should teach the students, which methods are used to achieve this, and what structure is given to the course (Czerkawski and Lyman, 2016). Freericks et al. (2019) also suggest testing the course material thoroughly before presenting it in order to prevent errors and mistakes.

The course should start with a course opening (see also Shackelford and Maxwell, 2012). Besides a good course structure that conveys and teaches the desired topics to the students, an adequate course opening is necessary to introduce the students to the course and the platform where it is held according to Debattista (2018). Here, the instructor should introduce him- or herself and give a summary of the course, with its topic and goals made clear to the students as an advance organizer. Lastly, a thorough explanation of the learning environment (e.g., the learning management system used) should be given. In the case of synchronous online learning courses, this also includes announcing the communication tool.

Interaction and community should play a central role in the online course (see also Swan, 2001; Jaggars and Xu, 2016). It should incorporate student-teacher and student-student interactions. The instructor should give students opportunities to actively participate. Of course, the instructor has to manage and support these interactions adequately. This aspect is also mentioned in other studies, which show that students and teachers wish for more interactivity in online courses (Gegenfurtner et al., 2020; Mukhtar et al., 2020).

The next aspect in Debattista's rubric is instructional resources for teaching and learning (Debattista, 2018). Learning materials have to be accessible to the students, with clear instructions on how to use them. It is suggested to incorporate a variety of different multimedia and learning materials (for example, see Stavredes and Herder, 2013) with proper citation of external sources ensured by the instructor.

In developing and implementing online courses—similar to in-class teaching—learner support plays a vital role as discussed by various scholars (cf. Graf and Liu, 2010; Ssekakubo et al., 2013; Han and Shin, 2016). According to Debattista (2018), students should always have access to help and support, whether that be on technical, educational, or administrative problems which may arise within the course, in order to ensure a smooth running of the course. To guarantee this, the technology design is of great importance as well: The technologies employed should be used in a student-centered way, be neatly implemented into the course, and provide a secure environment for the students. It should also be taken into account that the course should be accessible on multiple devices and without the need for exceptional hardware (cf. Graf and Liu, 2010). Finally, a simple interface for use and navigation is recommended. In this context, learning management systems have proven profitable (Vai and Sosulski, 2011).

A further item in the rubric of Debattista (2018) is the thorough course evaluation—both in a formative and a summative sense—aimed at enabling students and instructors to give feedback about the course (see also Stevens and Levi, 2013; Baldwin et al., 2018; Kumar et al., 2019). This helps with the instructional design cycle where the creator reviews the different parts (academic, technical, and administrative) of the course based on the provided feedback (Debattista, 2018). Lastly, a proper course closing is necessary.

In Section 3.2, we describe as to how Debattista's criteria were taken into account in the development of the online course Quantum Science in A Nutshell presented in this article. In the next Section, however, we first provide deeper insights into the theoretical background of teaching and learning quantum science.

2.2. Learning quantum science: developing a functional understanding of models

Learning quantum physics content and understanding quantum physics concepts is a major hurdle for many learners at both the high school and university levels. Many problems in learning quantum physics have already been empirically documented [for an overview, see Krijtenburg-Lewerissa et al. (2017)]: Classical notions still persist even after exposure to quantum physics topics. For example, quantum objects like photons and electrons are still assigned a definite trajectory, or learners state that quantum physics measurement results are only unknown before measurement and not indeterminate.

An empirically based explanation for these learning difficulties is that learners' conceptions, i.e., learners' mental models, are assigned too much reality: learners evaluate models not only on how well they can describe and explain phenomena, but also often consider them to be true to reality in terms of appearance. This high perception of Fidelity of Gestalt regarding quantum physical ideas prevents learners from abstracting and interpreting models as purely abstract descriptions and explanations. An empirical study by Ubben and Heusler (2021) showed that experts and novices differ on precisely this point: novices often assign a very gestalt character to their conceptions, whereas experts do not and see the visualizations and appearance of models and conceptions only as information carriers without real-world meaning and have thus achieved a purely functional understanding of models.

As found in Ubben and Heusler (2021) and Ubben and Bitzenbauer (2022), there are several types of understanding models in (quantum) physics that classify different stages of learning:

1. Non-developed type. Models of physics are not understood. Persons having this type of understanding do not know what models in physics are and what they are used for, save for perhaps declarative knowledge that is not deeper understood.

2. Architectural type. In this type of understanding, the appearance—or gestalt—of the model is the central focus. Models in physics are in this type only seen as visual illustrations, like the architectural model of a house or a model ship in a bottle on a shelf. A person with this type of understanding might imagine an electron as a little blue ball or a photon as a ball of light, but will not think about what these entities do, or how they work.

3. Dual type. In this type of understanding, models are understood as up- or down-scaled, sometimes simplified, versions of reality. In this type of understanding, both the appearance and the functions underlying the model are the focus. A person with this type of understanding might e.g., think that an atom is really a small solar system or that a photon really is a ball of light moving on a wavy line.

4. Functional type. A functional understanding (or abstract understanding) of models in physics means that models are only seen as tools that encapsulate descriptions of functionalities, relations and processes. Illustrations and visualizations are understood as carriers and not as up- or down-scaled versions of reality. A person with this type of understanding might e.g., think of an atom as a balloon, but only takes that appearance as signifying functional probability densities. Mathematical understanding aligns with this form of understanding, since mathematical symbols solely depict underlying relationships and functionalities, rather than being associated with up- or down-scaled representations of objects or phenomena of reality.

In general, older high school students or university students are found to be of the latter two types (Ubben and Heusler, 2021). The difference between them is the amount of Fidelity of Gestalt ascribed to the model, with Functional Fidelity being relatively high in the respective age group (Ubben, 2020; Ubben and Bitzenbauer, 2022). Therefore, this aspect was decided to be the focus of talking about models in the course as well: One approach to enable learners to abstract quantum physical concepts from given models is therefore to make them explicitly aware of the low Fidelity of Gestalt of models. This cannot be done only in the context of quantum physics, since a too high perception of Fidelity of Gestalt can generally hinder abstraction (Ubben, 2020), but especially in quantum physics there are many visualizations in circulation that may cause misinterpretations of the models shown.

3. Online course: quantum science in a nutshell

3.1. Core idea and learning goals

The name of our course says it all: The core idea behind the course is to provide a compact, yet elaborate introduction to quantum science at the secondary school level. A particular focus of the course is to promote the rigorous application of scientific thought processes in order to help students develop a functional model understanding in the quantum context (see Section 2.2). For example, the students learn that the quantum formalism does not allow for a space-time interpretation of what happens between preparation and measurement or that quanta should not be confused with classical particles—therefore, the students are introduced to quantum physics via quantum optics experiments with heralded photons because

• Students have comprehensive experiences with the physics of light from their regular classes in school which we can draw upon, and

• Prior research has shown that quantum optics approaches may be efficient in fostering students' functional model understanding in the quantum realm (cf. Bitzenbauer, 2021).

A detailed description of the design, organizational aspects as well as content structure of our course is given in Section 3.3.

Besides the above mentioned aspects, the implementation of our course in a synchronous online format ensures “that the benefits of education and learning are widely shared” as demanded in the guidelines for responsible research and innovation (Wilford et al., 2016, p. 10). Lastly, the course is aimed at paving the way for students to get a grasp of the technological and societal relevance of the so-called quantum technologies 2.0. The presented course requires no prerequisite understanding of quantum physics from students, as the pertinent principles are qualitatively introduced within the course.

Taken together, the primary objectives of the online course featured in this article are as follows: The students ….

1. Develop a functional model understanding with low Fidelity of Gestalt regarding quantum phenomena,

2. Become informed of the significance of quantum physics in contemporary technology, and

3. Get a grasp of genuine quantum principles such as quantum superposition, non-locality, quantum random, and quantum entanglement which are considered the nucleus of quantum theory according to Weissman et al. (2022).

3.2. Course development

The online course Quantum Science in the Nutshell is implemented via the open source learning management system ILIAS (https://www.ilias.de/en/) and was developed for use in the synchronous format. Interested instructors can request access to the online course for themselves and their students free of charge from the authors of this article and can then integrate the course into their quantum physics teaching, either in regular classes or as an optional program—the latter option seems particularly suitable in regions where quantum physics is not a facultative part of the secondary school physics curriculum. A guideline for the course implementation with both subject-specific and didactic comments is made available to teachers after access to the course has been approved.

The course consists of two consecutive parts (for a detailed description of the course contents see Section 3.3). Both parts of the course can be covered within a time frame of 3 h, normally implemented by two 1.5 h sessions with a break of 30 min between the sessions. Hence, a total of 6 h (4 × 1.5 h) excluding break times is required for the implementation of the whole course.

Table 1 provides an overview of how we incorporated the design principles proposed by Debattista (2018) during the course development process.

TABLE 1

Table 1. Overview of the integration of Debattista's e-learning rubric (Debattista, 2018) in the development of the online course “Quantum Science in a Nutshell.”

In terms of content, our online course was developed in close accordance with the teaching concept of quantum physics for the secondary school level presented by Bitzenbauer and Meyn (2020). A description of the course content is given in the next section.

3.3. Description of the course

3.3.1. Course part I: from models to quantum models

The first part of the course was focusing on teaching about the meaning and nature of models in quantum physics. As an introduction, students were confronted with a newspaper article about quantum computing where several electrons were depicted as balls. The participants of the course were then asked for their view on physics models in general and to give their own definitions for what a model in physics is and post it on a padlet. They were also asked to find or create pictures of models they knew or deemed as good examples for a physics model. The statements were then sorted into the categories appearance/illustration and functionality with statements referring to both aspects being put into a middle column, see for an example Figure 1. This sorting was used to illustrate that physics models can be understood in terms of both appearance and in terms of functionality/processes. Though this was not a measurement of the types of understanding, only some of the students focused solely on the functional part of a physics model and did not see the appearance/gestalt as only a carrier medium. The task was in general used to show that the appearances of physics models are only for getting a grip on concepts and that the underlying processes of physics models are what is important.

FIGURE 1

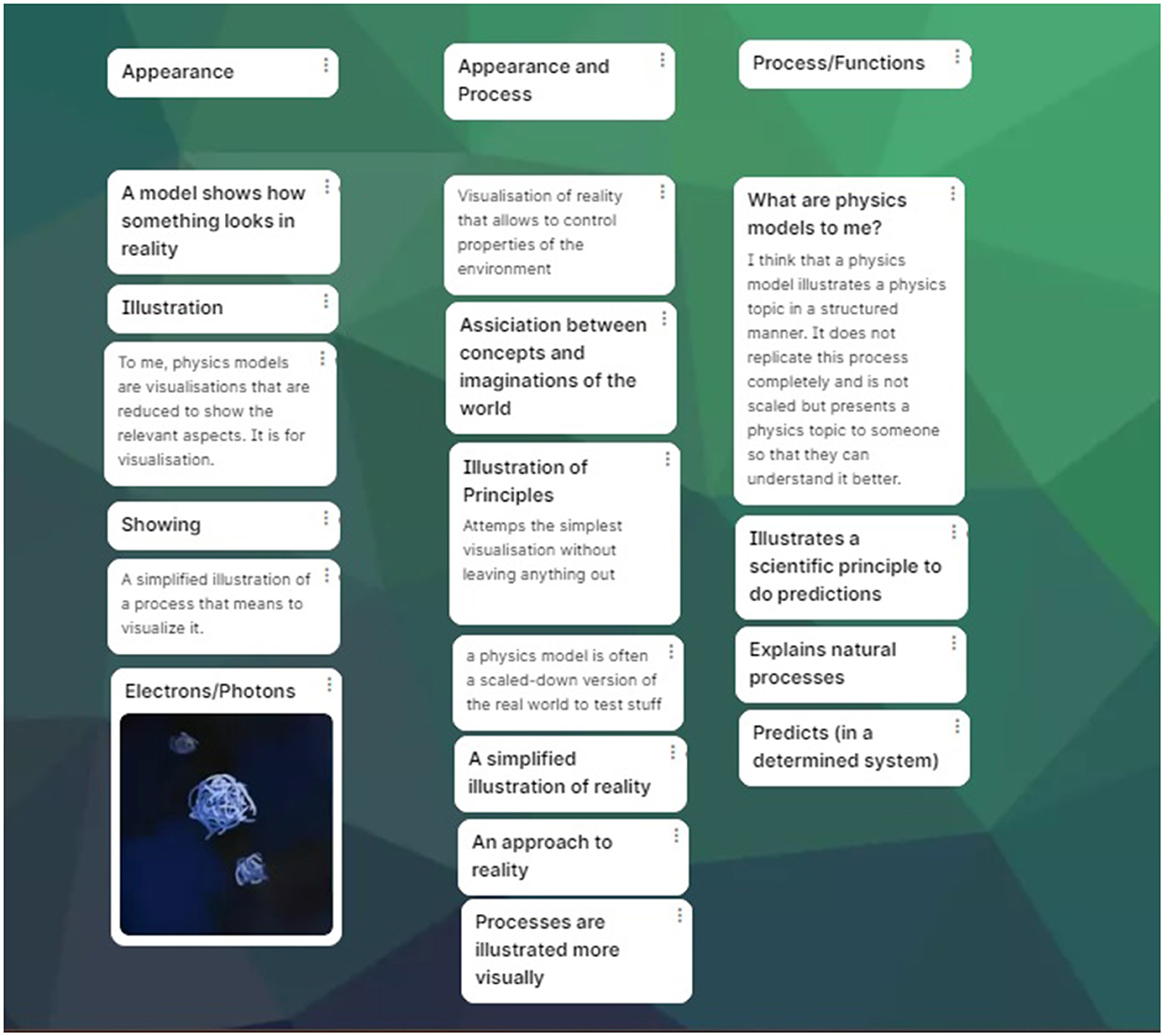
Figure 1. Students' statements regarding the nature of models in physics, roughly sorted into the categories appearance (left), functionality (right) and both (middle) after collection. The items have been freely translated from German. Of course, this is not part of the evaluation of the course itself but still gives an insights into students' views that we collected during the course.

After the task, statements about prominent models in physics were used to broaden the discussion and look at models from different areas of physics as well. The statements were namely:

1. The earth is flat.

2. Electrons are small balls.

3. Light consists of rays.

4. Magnets are made of tiny elementary magnets.

5. Electricity is many spherical electrons moving in a conductor.

6. The sun revolves around the earth.

7. Stars in the sky do not move.

8. Photons are light particles flying around in space.

Students then were asked to discuss each of the statements regarding the question whether the statement is correct. From the discussions, students were made aware of the fact that all the statements were models with varying degrees of functionality. With this task, our aim was therefore to discuss that models are never correct but that they explain processes and ideas in reality to varying degrees of success. It was also discussed with the students how models can evolve when new knowledge is found. From the last statement, the course was taken back into the domain of quantum physics and the visualizations of electrons and photons were discussed. After concluding that images about quantum objects are just visualizations of ideas and might be inappropriate or become obsolete with new knowledge, the course shifted into its second part on single photons.

3.3.2. Course part II: from quantum optics to quantum technologies

Following the discussion of various aspects about models in physics with the course participants, the focus transitioned to the domain of quantum physics. Thereby, the students were initially equipped with technical and experimental concepts necessary for analyzing the results obtained from experiments involving heralded photons in subsequent stages. In the following, we only sketch the key ideas of this course part since it has already been described in detail elsewhere (for example, see Bitzenbauer and Meyn, 2020; Bitzenbauer, 2021; Bitzenbauer et al., 2022).

Firstly, the students were introduced to fundamental optical components commonly employed in quantum optics laboratories. This encompassed elucidating the purpose of mirrors in adjusting quantum optics experiments and the effects of a beam splitter on incident light (see, for example Prasad et al., 1987; Loudon, 2000). Secondly, the participants received instruction on the characteristics of single-photon avalanche diodes (SPADs), also known as avalanche photodiodes (see, for example Cova et al., 1981). SPADs function as binary detectors, showing either “no click” or a “click” (Zambra et al., 2005). The focus on detectors was chosen since they are a fundamental part of any experiment with heralded photons and no complex quantum physical model is required to understand the basic functioning. During the course, the participants were asked (a) what they already knew about detectors in general, (b) what properties detectors for quantum objects might require and (c) why detectors are even needed in quantum physics in more general. In terms of content, the discussion included aspects such as quantum efficiency, dark count rate, and dead time. The model of a snow avalanche was used to more thoroughly explain the meaning of SPADs' main properties (e.g., see Donhauser et al., 2020). Thirdly, the students were familiarized with spontaneous parametric downconversion (PDC), a quantum electrodynamic process in which the interaction of laser light with a nonlinear crystal (such as β-barium borate) results in the emission of photon pairs while maintaining energy and momentum conservation. The spectral properties of the downconverted photons are influenced by the phasematching properties of the nonlinear material. For an overview of PDC, see Couteau (2018). In the online course, an interactive screen experiment developed by Bronner et al. (2009b) was used to present the setup of a coincidence experiment comprising a PDC source and two SPADs, allowing the preparation of single-photon Fock states.

In a further step, the coincidence experiment was extended with a beam splitter cube and an additional detector to demonstrate the anticorrelation of single-photon states at the beam splitter. Again, an interactive screen experiment developed by Bronner et al. (2009b) was used to allow the participants to observe the lack of coincident clicks between two detectors at the two output ports of a beam splitter (apart from random coincidences): “A single photon can only be detected once” (Grangier et al., 1986, p. 173). The experimental observations were supported by discussing the ideas of quantum superposition and quantum random as presented by Bronner et al. (2009a).

Then, the course explored the behavior of single-photon states in an interferometer experiment. In this context, the students realized that the “quantum interference phenomenon shown experimentally is a consequence of the interplay of superposition and nonlocality” (Scholz et al., 2020, p. 17), while the classical notion of assigning a space-time trajectory to a single-photon state does not apply. Finally, the quantum principles investigated in the quantum optics experiments were leveraged to make the students get a grasp of introductory quantum technology aspects: In a first activity, the students were provided with an interpretation of the beam splitter cube as a physical realization of a Hadamard gate. Based on that, the students implemented the Quantum Penny Flip Game originally proposed by Meyer (1999) using the IBM Quantum Composer (https://quantum-computing.ibm.com/composer/files/new) as suggested by Müller and Greinert (2021). In this activity, the students experienced that quantum superposition is crucial for quantum computing applications. In a second activity, the BB84 protocol with single-photons was introduced as an example for quantum communication (Bloom et al., 2022). The course concluded with a summary of the key aspects covered throughout.

4. Research questions

With the evaluation of our synchronous online course presented in this article, we aim at a clarification of the following research questions:

1. To what extent was the online course effective in improving the students' understanding of models in general?

2. To what extent was the online course effective in fostering functional conceptions of photons among students?

3. How is the students' understanding of models correlated with the Functional Fidelity in students' views of photons?

5. Methods

5.1. Study design

The study was conducted as a one group pretest-posttest design. The online course that this study was based on (cf. Section 3.3) took place over two weekends (3 h each) in 2022. Due to the absence of comparable traditional instructions against which our intervention (cf. Section 3.3) can be compared, we opted not to employ a control group design, as explained in previous work by Veith et al. (2022).

5.2. Participants

The sample presented in our study consisted of N = 59 high school students (aged 16–18) who voluntarily participated in the course described in Section 3.1. Before taking part in our study, all students participated in introductory lessons on quantum physics of photons as part of their regular physics lessons as mandated in the German high-school curriculum. These lessons specifically followed the curricula outlined by the federal states of Bavaria and North Rhine-Westphalia as the participants' schools were situated in these regions of Germany. In the following, we only present results for participants who completed both the pretest as well as the posttest.

5.3. Instruments

For both the pretest and the posttest, we utilized two instruments adopted from the literature, that were administered online using the LimeSurvey tool (https://www.limesurvey.org/de/): On the one hand, we assessed students' understanding of the roles of scientific models in physics (cf. Table 2). To this end, we adopted items from the item group “models as exact replicas” (ER) from Treagust et al. (2002). With these items we approach students' Fidelity of Gestalt as part of their general model understanding. Here, each item presents a statement where students have to rate their agreement on a scale from 1 to 5 (1 = disagree, 2 = rather disagree, 3 = undecided, 4 = rather agree, 5 = agree). The items were slightly adjusted to fit into the context of models in physics. In the following, we will address this second instrument using the abbreviation Role of Scientific Models (RSM).

TABLE 2

Table 2. All items of the RSM instrument.

The second part of the test was aimed at measuring students' mental models of photons' properties and behavior by using the questionnaire presented by Bitzenbauer (2021). This questionnaire comprises 10 items in total of which the first six address quantum objects' properties and behavior and the following four address probability interpretation within quantum physics. In coherence with the RSM instrument, each item presents a statement where students have to rate their agreement on a scale from 1 to 5 (1 = disagree, 2 = rather disagree, 3 = undecided, 4 = rather agree, 5 = agree). All items are presented in Table 3 and were used in previous research (Ireson, 1999; Müller and Wiesner, 2002; Ubben and Bitzenbauer, 2022). It is noteworthy that these items (a) are based on quantum mechanics' ensemble interpretation and (b) “are specifically intended to challenge mechanistic or deterministic ways of thinking” (Ubben and Bitzenbauer, 2022, p. 7) making them suitable for investigating students' mental models. As such, in the following we will refer to this instrument using the abbreviation Mental Model of Photons (MMP).

TABLE 3

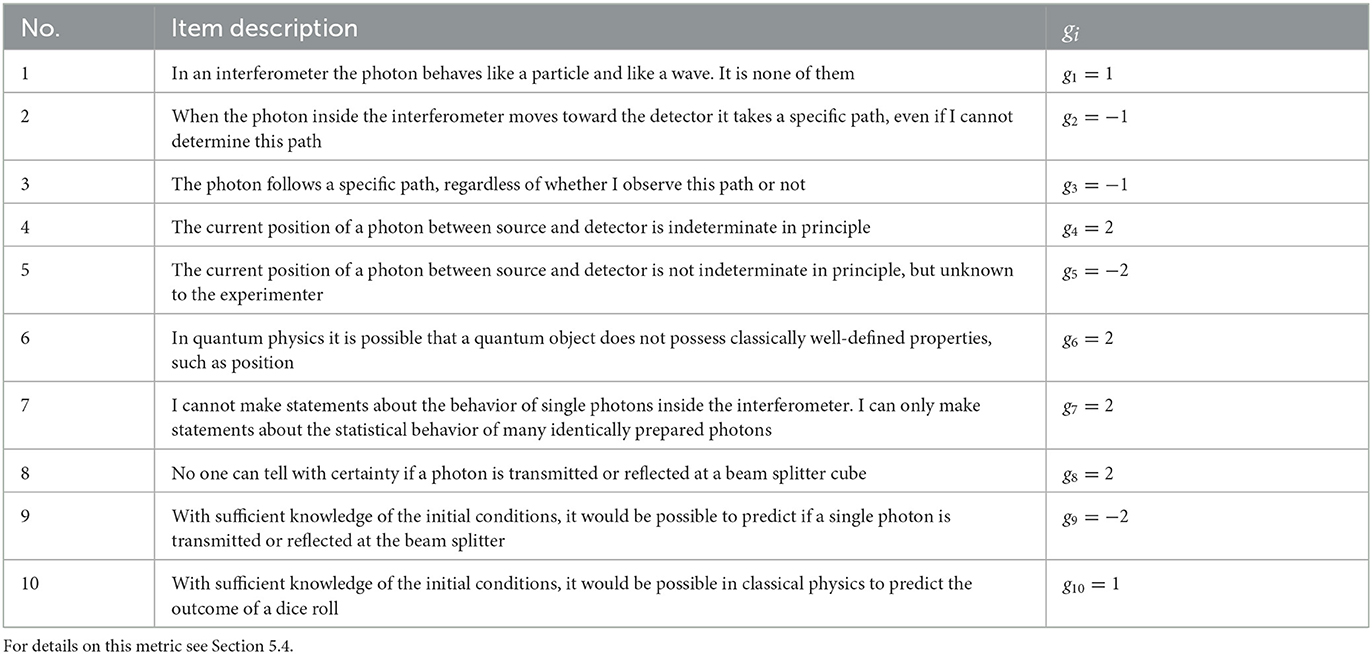
Table 3. MMP instrument items adopted from Bitzenbauer (2021) and their corresponding weighting factors g_i.

5.4. Data analysis

Regarding the first two research questions we analyzed the effectiveness of the course by comparing the students' ratings in the pretest with the ones in the posttest. For the third research question, we computed conception indices Müller (2003) for each participant in a first step. A conception index is a metric used to operationalize learners' conceptions of quantum physics. For a given person it ranges from –100 to +100 where –100 indicates mechanistic or deterministic ways of thinking and +100 indicates quantum physics-adequate conceptions. We calculated it in accordance to Müller (2003) via

$C=\frac{{\displaystyle {\sum }_{i=1}^n{g}_i·50·(v_i-3)}}{{\displaystyle {\sum }_{i=1}^n\left|g_i\right|}}$

where v_i is the respondent's rating of item i (in our context v_i∈{1, …, 5}) and g_i is the weighting factor of item i. The weighting factor for each item is provided in Table 3—for further details we refer the reader to Bitzenbauer (2021). As Ubben and Bitzenbauer (2022) indicate, a high Functional Fidelity is comparable to a high value in conception index and a high Fidelity of Gestalt to a low value in conception index. Lastly, in order to analyse the correlation of the students' understanding of models with the Functional Fidelity in their views of photons we correlated the conception indices with the responses on the RSM instrument for each item (cf. Table 2). Since the items on this instrument yield ordinally scaled data, we used Spearman's ρ where according to Hemphill (2003) coefficients with |ρ| <0.20 are referred to as weak, 0.20 ≤ |ρ| ≤ 0.30 as medium and 0.30 <|ρ| as strong.

6. Results

6.1. Development of students' model understanding

Regarding the students' development of model understanding we assessed their answer patterns on the RSM instrument. The proportion of their (dis-)agreements is provided in Table 4.

TABLE 4

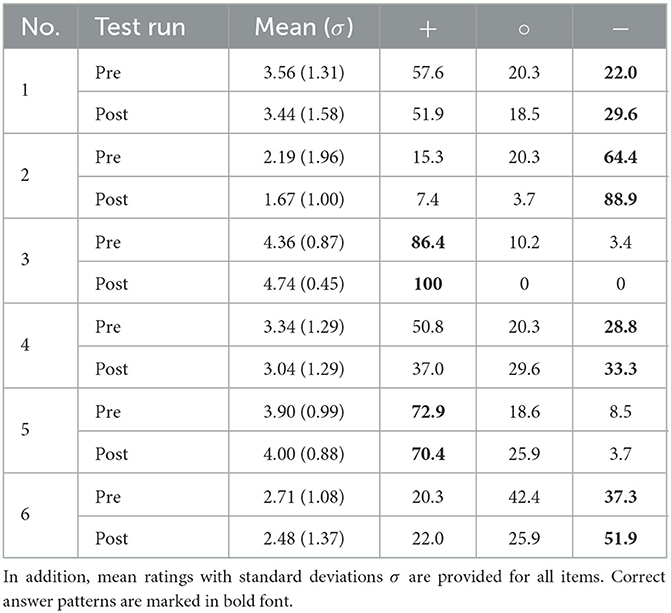
Table 4. Proportion of students' agreements (+, rating: 4 = rather agree, 5 = agree), disagreements (−, rating: 2 = rather disagree, 1 = disagree) and undecided votes (°, rating: 3 = undecided) on the RSM instrument.

We observe an increase in the share of students marking a correct answer for almost every item of the instrument with item 5 being the only exception. The most notable increases are recorded for items 2 and 3 (cf. Figure 2).

FIGURE 2

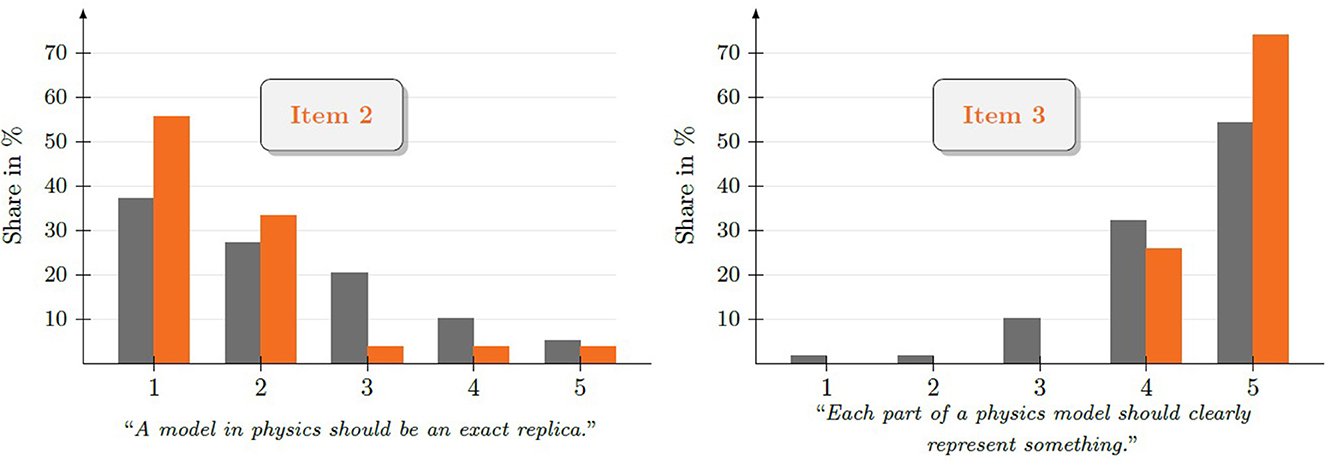
Figure 2. Relative number of responses in the pretest (gray) and posttest (orange) for each answer option on items 2 and 3 of the RSM instrument.

While for item 2 with 24.5% we record the largest increase in correct answer patterns from pretest to posttest, for item 3 we observe an almost perfect answer pattern in the posttest. The greatest dissent among learners can be located in item 4, where even in the posttest no answer option was chosen by more than 50%.

6.2. Development of students' understanding of photons

The students' responses on the MMP instrument are summarized in Table 5. Here, we strikingly observe an increase of correct answers for every item of the instrument. The difference in pre- and posttest regarding the share of correct answers ranges from 6.2% (item 2) to 56.1% (item 9) with the average difference being 35.4%. The most notable changes, which will be discussed in Section 7, are visualized in Figure 3.

TABLE 5

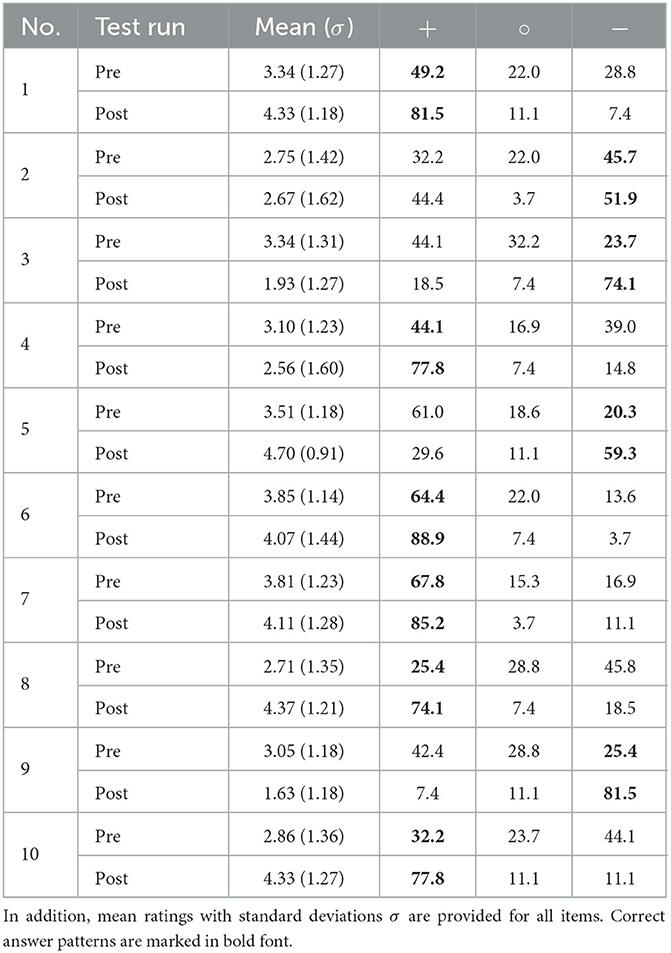
Table 5. Proportion of students' agreements (+, rating: 4 = rather agree, 5 = agree), disagreements (−, rating: 2 = rather disagree, 1 = disagree) and undecided votes (°, rating: 3 = undecided) on the MMP instrument.

FIGURE 3

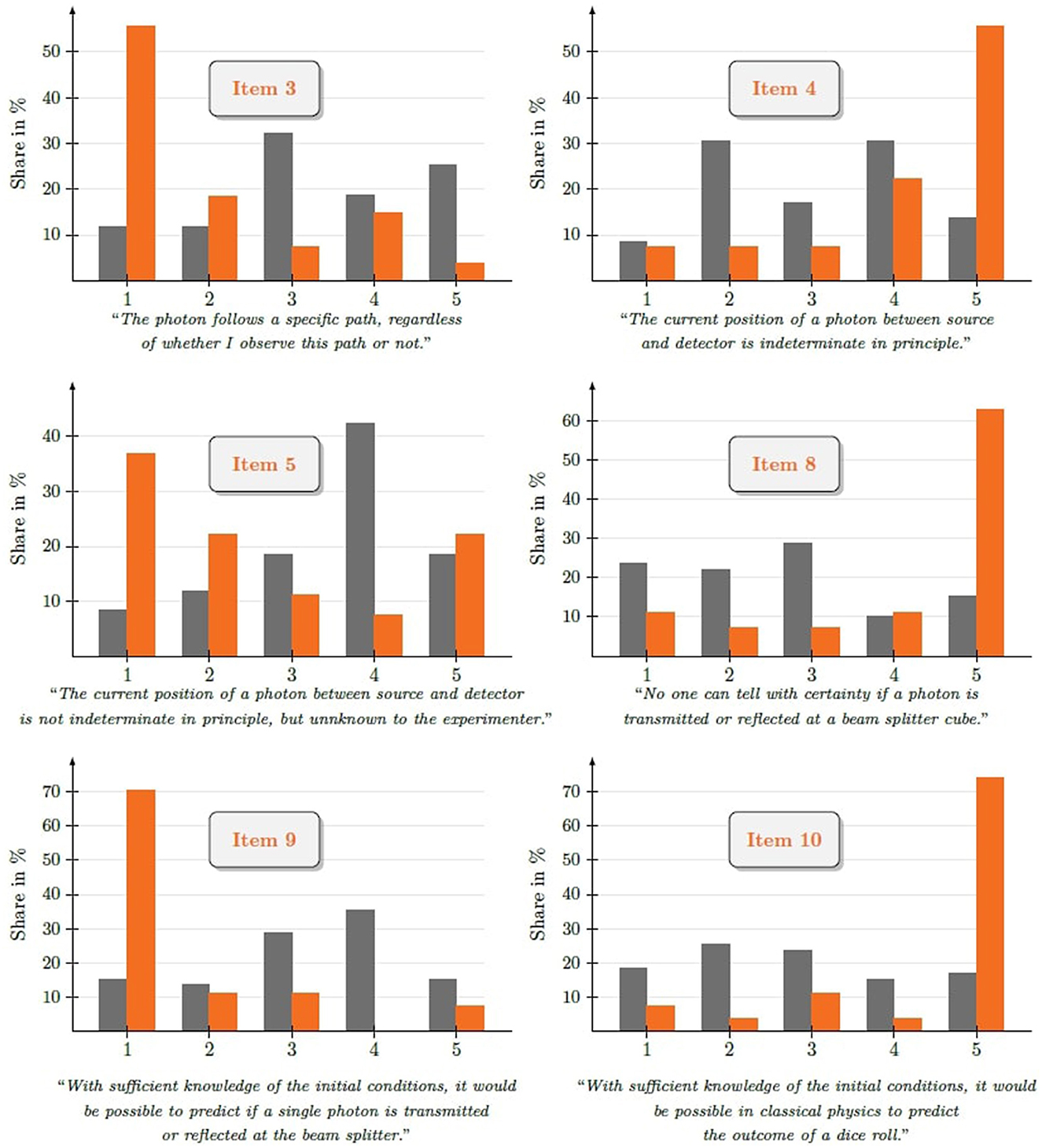
Figure 3. Relative number of responses in the pretest (gray) and posttest (orange) for each answer option on items of the MMP instrument for which the most notable changes from pre- to posttest points in time were observed.

The students' responses on items 4 and 5 (cf. Figure 3) show a vast improvement from pretest to posttest. While in the pretest the students overall took an indecisive stance with regards to the position of a photon between source and detector (item 4), a tendency toward mechanistic thinking occurred—over 40% held the opinion that the position is just unknown to the experimenter (item 5). In contrast, in the posttest more than half of all participants completely agreed with the statement that the position is indeterminate in principle (item 4) and consequently disagreed with the statement in item 5. This advancement in quantum physics-adequate conceptions is substantiated by the response patterns in items 8 and 9. While in the pretest the patterns yield inconclusive results, the posttest responses draw a clear picture: Over 60% of the learners strongly agreed with the statement in item 8 and over 70% strongly disagreed with item 9, indicating a decreased degree of mechanistic ways of thinking. The contrast in classical and quantum physics ways of thinking is further underpinned by the chirality of the response patterns on item 9 and item 10. In the pretest we observe a huge variance in students' responses on both items, especially we can even detect a transfer of classical ideas into the quantum realm from the pretest responses on item 9. In contrast, we find consensus in the posttest: The participants agreed with the behavior of a single photon at a beam splitter cube not being predictable, while in classical physics, indeed, the outcome of a dice roll could—in principle—be determined. Hence, the distinction between classical and quantum random seems to have become obvious to our course participants at the posttest point in time.

Lastly, it is noteworthy that the pre- and posttest results for items 2, 6, and 7 yielded the least discernible difference. This observation is most likely linked to the fact that the share of correct responses on those items, dealing with the position of a photon, were the highest in the pretest. With almost two thirds of all participants already responding correctly in the pretest there is much less room for improvement in comparison to the other test items.

6.3. Relationship between students' understanding of models and photons

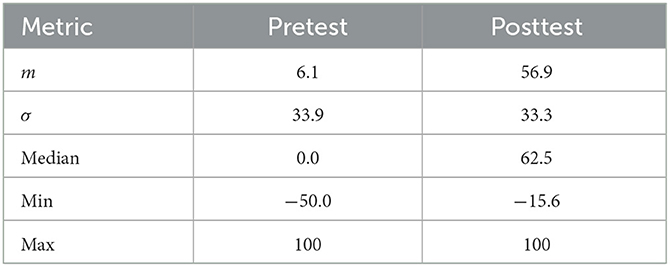
To investigate the relationship between students' understanding of models in general on the one hand, and their (functional) understanding of the photon model on the other hand, we first calculated the conception index (cf. Section 5.4) for each participant. The conception indices range from −46.9 to 100 in the pretest with an average of 6.1. In the posttest, they range from −15.6 to 100 with an average of 56.9. All descriptive statistics for this metric are provided in Table 6.

TABLE 6

Table 6. Descriptive statistics on the conception indices for the participants.

In a next step, we correlated the conception indices with the students' responses on the items in the RSM instrument. The results are provided in Table 7. While the absolute values of the correlations differ vastly among all items, it is noteworthy that none of them but one are statistically significant, indicating only insignificant deviation from ρ = 0. This observation holds for both the pretest and the posttest as supported through the average correlations for both points in time, calculated after a Fisher z-transformation (ρ_pre = −0.06, ρ_post = 0.01). In summary, our results indicate no significant correlations between the variables.

TABLE 7

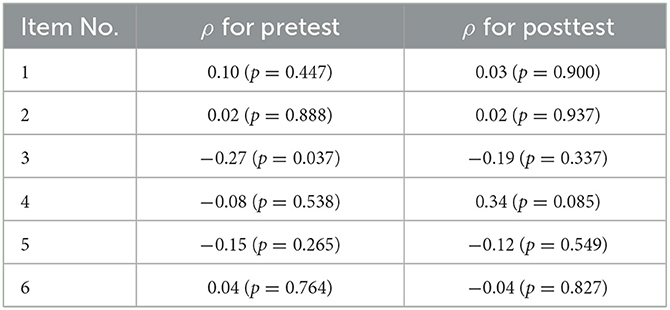
Table 7. Spearman's correlation coefficient ρ between the students' functional understanding of models in the photon context expressed via the conceptions index (see Table 6) and each items of the RSM instrument for both the pretest and posttest.

7. Discussion

In the following subsections, the results of the empirical evaluation of the course regarding the research questions will be discussed.

7.1. Discussion of research question 1

Through participation in the online course Quantum Science in a Nutshell presented in this article, the participants' model understanding has slightly improved in terms of pre-posttest comparison. More students agreed that a model is not a direct replica (item 2) and everyone agreed that each part of a physics model should clearly represent something (item 3). Hence, the data shows that minor positive effects on model understanding were facilitated by the course with Fidelity of Gestalt decreasing and Functional Fidelity increasing. This is an important observation since a large number of scholars stressed that a general problem regarding students' understanding of scientific models is that the models are often seen as exact replicas of reality (Grosslight et al., 1991; Treagust et al., 2002; Pluta et al., 2011).

Although the improvements in terms of general model understanding observed throughout the course are to be considered rather small, their potential relevance for student learning is not to be underestimated: Prior research, e.g., by Gobert and Pallant (2004) as well as Schwarz and White (2005), has emphasized the positive impact that a sophisticated understanding of models can have on learning and comprehending scientific content knowledge. This suggests that possessing an (advanced) knowledge of models might be highly beneficial for acquiring a deeper understanding of scientific concepts. That this holds particularly true for learning about quantum concepts is underpinned by Kalkanis et al. (2003): The authors identify students' inadequate comprehension of models in science as a primary source of students' difficulties in quantum physics, especially in terms of their classical-mechanistic views, in relation to quantum concepts (Kalkanis et al., 2003).

Consequently, it seems worth to continue pursuing the chosen path with our online course, namely fostering students' understanding on models in general first, and to head to (different) specific contexts afterwards, e.g., in quantum physics, as has already been suggested by Leach et al. (2000). Vice versa, Galili and Goren (2022) suggest that also a delayed organizer, i.e., introducing models in a specific context first before heading for the overarching perspective regarding models in general, might be a sensible approach to support student learning about models on the one hand, and in specific contexts on the other hand. We propose that future research should investigate the specific interrelations between students' general model understanding and their functional understanding in the quantum realm with suitable study designs and instruments.

7.2. Discussion of research question 2

Compared to the understanding of models in general, the students' functional understanding of photons (measured in terms of the conception index calculated from the students' ratings of the MMP scale items) improved more evidently throughout the course: The conception index on average improved by 50 points (see Table 6). In terms of students' conceptions of quantum physics (regarding the photon context), two major observations where crucial:

1. The distinction between quantum and classical randomness appears to have become clearer to course participants, as evidenced by a comparison of their ratings for items 9 and 10 in the pre- and post-test (Figure 3).

2. Furthermore, a considerable number of students seemed to have relinquished the idea that quantum objects possess well-defined trajectories in space (items 3 and 4).

Both of these exemplary findings advocate that our online course supported a classical-to-quantum transition in the thinking of (at least an essential part of) the study participants. This is a promising result, as multiple empirical studies have demonstrated that students often adhere to their naive realist perspectives (e.g., see Henriksen et al., 2018) or classical-mechanistic mental models (e.g., see Taber, 2005), despite the fact that the formalism of quantum physics does not allow for a space-time description of quantum phenomena.

The above findings should be evaluated with the following background: The study participants did not join this study as complete novices in terms of quantum physics. They had previously been introduced to quantum physics and specifically learned about the photon as a quantum object in the context of a conventional quantum physics course as part of their regular physics education at school. Against this background, the increase in functional model understanding of the photon within the sample is particularly noteworthy. Prior to the intervention reported here, the learners seemed to possess predominantly visual conceptions of the photon (conception index in the pretest: m = 6.1, σ = 33.9). The extent to which the course can promote sustainable conceptual development could be clarified through a delayed follow-up assessment in future studies.

Further research should also explore to what extent the observed progress in students' functional understanding of the photon can be attributed to the explicit instruction on models in general provided during the initial section of the course. Previous research suggests that the contribution of this course section may not have been insignificant, as supported by the literature in the previous Subsection 7.1: for example, Bitzenbauer (2021) conducted a quasi-experimental field study to investigate the impact of a course on secondary school students' that followed the approach presented in this paper in a face-to-face setting, with similar didactics and content, except for the exclusion of the first section of our online course on general models. The MMP scale was used to track students' progress toward a functional understanding of photons in this study as well. The results hinted that the course improved the students' functional understanding (i.e., the conception index) by around 30 points in pre-posttest comparison, while we observed an increase of 50 points on average in our study. However, this comparison must be regarded with caution due to the different educational settings (face-to-face vs. online): In particular, the higher increase in students' functional understanding of photons in our case cannot be traced back to the additional course part on models in general without further ado.

7.3. Discussion of research question 3

No significant correlations were observed between the level of students' functional understanding of photons, and their model understanding in general, as shown in Table 7. This is consistent with the literature in so far that Fidelity of Gestalt, which was the main focus of the items on model understanding (RSM scale) and Functional Fidelity, which was the main focus of the instrument testing understanding of photons (MMP scale), are not or only weakly correlated (Ubben and Heusler, 2021; Ubben and Bitzenbauer, 2022): for example, Ubben and Heusler (2021) observed a weak correlation between the general understanding of models in physics in terms of a replicate conception and the appearance of classically formed mental models of the atomic shell in students' ideas.

It is widely accepted that students' conceptions are highly context-dependent (cf. Bahtaji, 2023), which further underpins the observed relationships: The weak correlations align with the literature as the MMP scale only measures students' model understanding of photons, while the RSM scale assesses their general model understanding.

8. Limitations

Our study has some limitations that need to be considered in order to frame our findings: First, our sample comprises N = 59 secondary school students who voluntarily participated in our study. While this sample size is sufficient to resolve general tendencies regarding the learning effectiveness of the course, we refrain from applying inferential statistics to our data. Further research with larger samples is needed for a more comprehensive evaluation of the course. Specifically, when asking for its impact on students' conceptual development in quantum physics the use of concept inventories allowing for a valid assessment of students' understanding of basic quantum (optics) principles seems sensible. In the sense of Design-Based research (cf. Anderson and Shattuck, 2012), we will use the results of this study to refine our course in a further design step prior to conducting additional cycles of evaluation with larger samples in the future.

Second, in addition to the sample size, it is noteworthy that the participating students represent a rather positive sample and are by no means representative of all secondary school students, since they voluntarily chose to participate in an extracurricular course on quantum physics. Therefore, it is likely that the results reported in this article represent a description of what model understanding development is possible in learners in the best case scenario when it comes to learning quantum physics in secondary school, particularly when offering instruction inspired by or following the course presented in this article. This limitation primarily pertains to the effectiveness of the course presented here (research questions 1 and 2), while most probably leaving the more fundamental finding regarding the non-significantly different from zero correlations between general model understanding and a functional understanding of the photon model unaffected (research question 3).

Third, in this study we utilized the MMP instrument (cf. Table 3) to examine students' mental models regarding the properties and behavior of photons. This questionnaire is widely accepted in the field of quantum physics education research and has been implemented in various previous studies on quantum physics learning as shown before. However, the RSM instrument used to assess students' perception of models in physics (cf. Table 2) only evaluated one aspect of students' understanding of models, which is the Fidelity of Gestalt. Therefore, we propose developing a survey instrument that includes specifically designed test items to assess students' general understanding of models in physics, which addresses both the Fidelity of Gestalt and Functional Fidelity dimensions in future research. Such an instrument will provide more comprehensive insights into the development of students' model understanding and its relationship with their understanding of models in the quantum realm.

9. Conclusion and outlook

This study suggests that explicit teaching of the role that models have in physics assisted students with understanding the model of photons in a functional way. However, it seems to have only a modest effect on fostering students' understanding of modeling in physics in general. It is worth testing the path of teaching quantum physics from concrete and tangible, which in this case, is the phenomena that photons present, toward more abstract conceptualization (Pospiech et al., 2021). This path advocates for introducing more theoretical aspects of modeling in general after the concrete foundations were established. Similar moves in classical mechanics showed that a delayed organizer is beneficial in that sense (Galili and Goren, 2022). This might support students in (a) generalizing the functional role of models in physics, and in (b) better understanding aspects of the nature of science which is so often connected to teaching quantum physics (Stadermann and Goedhart, 2020).

In addition, the investigation presented here should also be applied in further contexts of quantum physics, e.g., regarding electrons. Follow-up research could inspect if functional-type understanding of models in one context (e.g., photon) induces functional-type understanding of other topics in quantum physics. Fostering an understanding of models in physics might, hence, assist in dealing with or diminishing misconceptions, like the one of the electron as a smeared entity around the atom's nucleus. Therefore, future research should adopt a bi-directional approach to study the possible dependencies between functional-type model understandings and misconceptions in a given field.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent to participate in this study was provided by the participants' legal guardian/next of kin.

Author contributions

MU: conceptualization, methodology, investigation, data curation, writing—original draft, and writing—review and editing. JV: formal analysis, writing—original draft, writing—review and editing, and visualization. AM: validation, writing—original draft, and writing—review and editing. PB: conceptualization, methodology, investigation, writing—original draft, and writing—review and supervision. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aehle, S., Scheiger, P., and Cartarius, H. (2022). An approach to quantum physics teaching through analog experiments. Physics 4, 1241–1252. doi: 10.3390/physics4040080

CrossRef Full Text | Google Scholar

Anderson, T., and Shattuck, J. (2012). Design-based research: a decade of progress in education research? Educ. Res. 41, 16–25. doi: 10.3102/0013189X11428813

PubMed Abstract | CrossRef Full Text | Google Scholar

Bahtaji, M. (2023). Examining the physics conceptions, science engagement and misconceptions of undergraduate students in stem. J. Balt. Sci. Educ. 22, 10–19. doi: 10.33225/jbse/23.22.10

CrossRef Full Text | Google Scholar

Baldwin, S., Ching, Y.-H., and Hsu, Y.-C. (2018). Online course design in higher education: a review of national and statewide evaluation instruments. TechTrends 62, 46–57. doi: 10.1007/s11528-017-0215-z

CrossRef Full Text | Google Scholar

Bitzenbauer, P. (2021). Effect of an introductory quantum physics course using experiments with heralded photons on preuniversity students' conceptions about quantum physics. Phy. Rev. Phys. Educ. Res. 17, 020103. doi: 10.1103/PhysRevPhysEducRes.17.020103

CrossRef Full Text | Google Scholar

Bitzenbauer, P., and Meyn, J.-P. (2020). A new teaching concept on quantum physics in secondary schools. Phys. Educ. 55, 055031. doi: 10.1088/1361-6552/aba208

CrossRef Full Text | Google Scholar

Bitzenbauer, P., Veith, J. M., Girnat, B., and Meyn, J.-P. (2022). Assessing engineering students' conceptual understanding of introductory quantum optics. Physics 4, 1180–1201. doi: 10.3390/physics4040077

CrossRef Full Text | Google Scholar

Bitzenbauer, P., and Zenger, T. (2022). Online course on quantum physics: reading primary sources with secondary school students. Phys. Teach. 60, 572–577. doi: 10.1119/5.0054100

CrossRef Full Text | Google Scholar

Bloom, Y., Fields, I., Maslennikov, A., and Rozenman, G. G. (2022). Quantum cryptography—a simplified undergraduate experiment and simulation. Physics 4, 104–123. doi: 10.3390/physics4010009

CrossRef Full Text | Google Scholar

Bronner, P., Strunz, A., Silberhorn, C., and Meyn, J.-P. (2009a). Demonstrating quantum random with single photons. Eur. J. Phys. 30, 1189. doi: 10.1088/0143-0807/30/5/026

CrossRef Full Text | Google Scholar

Bronner, P., Strunz, A., Silberhorn, C., and Meyn, J.-P. (2009b). Interactive screen experiments with single photons. Eur. J. Phys. 30, 345. doi: 10.1088/0143-0807/30/2/014

CrossRef Full Text | Google Scholar

Couteau, C. (2018). Spontaneous parametric down-conversion. Contemp. Phys. 59, 291–304. doi: 10.1080/00107514.2018.1488463

CrossRef Full Text | Google Scholar

Cova, S., Longoni, A., and Andreoni, A. (1981). Towards picosecond resolution with single-photon avalanche diodes. Rev. Sci. Instrum. 52, 408–412. doi: 10.1063/1.1136594

CrossRef Full Text | Google Scholar

Czerkawski, B. C., and Lyman, E. W. (2016). An instructional design framework for fostering student engagement in online learning environments. TechTrends 60, 532–539. doi: 10.1007/s11528-016-0110-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Daniels, M., Sarte, E., and Cruz, J. D. (2019). Students'perception on e-learning: a basis for the development of e-learning framework in higher education institutions. IOP Conf. Ser. Mater. Sci. Eng. 482, 012008. doi: 10.1088/1757-899X/482/1/012008

CrossRef Full Text | Google Scholar

Debattista, M. (2018). A comprehensive rubric for instructional design in e-learning. Int. J. Inf. Learn. Technol. 35, 93–104. doi: 10.1108/IJILT-09-2017-0092

CrossRef Full Text | Google Scholar

Donhauser, A., Bitzenbauer, P., and Meyn, J.-P. (2020). “Von Schnee- und Elektronenlawinen: Entwicklung eines Erklärvideos zu Einzelphotonendetektoren,” in PhyDid B - Didaktik Der Physik - Beiträge Zur DPG-Frühjahrstagung, 1. Available online at: https://ojs.dpg-physik.de/index.php/phydid-b/article/view/1021

Google Scholar

Freericks, J., Cutler, D., Kruse, A., and Vieira, L. (2019). Teaching quantum mechanics to over 28, 000. nonscientists. Phys. Teach. 57, 326–329. doi: 10.1119/1.5098924

CrossRef Full Text | Google Scholar

Galili, I., and Goren, E. (2022). Summary lecture as a delay organizer of cultural content knowledge. Sci. Educ. 32, 737. doi: 10.1007/s11191-022-00348-w

CrossRef Full Text | Google Scholar

Gegenfurtner, A., and Ebner, C. (2019). Webinars in higher education and professional training: a meta-analysis and systematic review of randomized controlled trials. Educ. Res. Rev. 28, 100293. doi: 10.1016/j.edurev.2019.100293

CrossRef Full Text | Google Scholar

Gegenfurtner, A., Zitt, A., and Ebner, C. (2020). Evaluating webinar-based training: a mixed methods study of trainee reactions toward digital web conferencing. Int. J. Train. Dev. 24, 5–21. doi: 10.1111/ijtd.12167

CrossRef Full Text | Google Scholar

Gobert, J., and Pallant, A. (2004). Fostering students' epistemologies of models via authentic model-based tasks. J. Res. Sci. Teach. 13, 7–22. doi: 10.1023/B:JOST.0000019635.70068.6f

CrossRef Full Text | Google Scholar

Graf, S., and Liu, T.-C. (2010). Analysis of learners' navigational behaviour and their learning styles in an online course. J. Comput. Assist. Learn. 26, 116–131. doi: 10.1111/j.1365-2729.2009.00336.x

CrossRef Full Text | Google Scholar

Grangier, P., Roger, G., and Aspect, A. (1986). Experimental evidence for a photon anticorrelation effect on a beam splitter: a new light on single-photon interferences. Europhys. Lett. 1, 173. doi: 10.1209/0295-5075/1/4/004

CrossRef Full Text | Google Scholar

Greinert, F., Müller, R., Bitzenbauer, P., Ubben, M., and Weber, K.-A. (2022). Requirements for future quantum workforce — a delphi study. J. Phys. Conf. Ser. 2297, 012017. doi: 10.1088/1742-6596/2297/1/012017

CrossRef Full Text | Google Scholar

Grosslight, L., Unger, C., Jay, E., and Smith, C. (1991). Understanding models and their use in science: conceptions of middle and high school students and experts. J. Res. Sci. Teach. 28, 799–822. doi: 10.1002/tea.3660280907

CrossRef Full Text | Google Scholar

Han, I., and Shin, W. S. (2016). The use of a mobile learning management system and academic achievement of online students. Comput. Educ. 102, 79–89. doi: 10.1016/j.compedu.2016.07.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Hemphill, J. F. (2003). Interpreting the magnitudes of correlation coefficients. Am. Psychol. 58, 78–79. doi: 10.1037/0003-066X.58.1.78

PubMed Abstract | CrossRef Full Text | Google Scholar

Henriksen, E., Angell, C., Vistnes, A., and Bungum, B. (2018). What ist light? students' reflections on the wave-particle duality of light and the nature of physics. Sci. Educ. 27, 81–111. doi: 10.1007/s11191-018-9963-1

CrossRef Full Text | Google Scholar

Ireson, G. A. (1999). Multivariate analysis of undergraduate physics students' conceptions of quantum phenomena. Eur. J. Phys. 20, 193. doi: 10.1088/0143-0807/20/3/309

CrossRef Full Text | Google Scholar

Jaggars, S. S., and Xu, D. (2016). How do online course design features influence student performance? Comput. Educ. 95, 270–284. doi: 10.1016/j.compedu.2016.01.014

CrossRef Full Text | Google Scholar

Kalkanis, G., Hadzidaki, P., and Stavrou, D. (2003). An instructional model for a radical conceptual change towards quantum mechanics concepts. Sci. Educ. 87, 257. doi: 10.1002/sce.10033

CrossRef Full Text | Google Scholar

Krijtenburg-Lewerissa, K., Pol, H., Brinkmann, A., and van Joolingen, W. (2017). Insights into teaching quantum mechanics in secondary and lower undergraduate education. Phys. Rev. Phys. Educ. Res. 13, 010109. doi: 10.1103/PhysRevPhysEducRes.13.010109

CrossRef Full Text | Google Scholar

Kumar, S., Martin, F., Budhrani, K., and Ritzhaupt, A. (2019). Award-winning faculty online teaching practices: elements of award-winning courses. Online Learn. 23, 160–180. doi: 10.24059/olj.v23i4.2077

CrossRef Full Text | Google Scholar

Leach, J., Millar, R., Ryder, J., and Séré, M.-G. (2000). Epistemological understanding in science learning: the consistency of representations across contexts. Learn. Instr. 10, 497–527. doi: 10.1016/S0959-4752(00)00013-X

CrossRef Full Text | Google Scholar

Loudon, R. (2000). The Quantum Theory of Light. Oxford: Oxford University Press.

Google Scholar

Martin, F., Bolliger, D. U., and Flowers, C. (2021). Design matters: development and validation of the online course design elements (OCDE) instrument. Int. Rev. Res. Open Distrib. Learn. 22, 46–71. doi: 10.19173/irrodl.v22i2.5187

CrossRef Full Text | Google Scholar

Mashhadi, A., and Woolnough, B. (1999). Insights into students' understanding of quantum physics: visualizing quantum entities. Eur. J. Phys. 20, 511. doi: 10.1088/0143-0807/20/6/317

CrossRef Full Text | Google Scholar

McKagan, S., Perkins, K., and Wieman, C. (2010). Design and validation of the quantum mechanics conceptual survey. Phys. Rev. Spec. Top.-Phys. Educ. Res. 6, 020121. doi: 10.1103/PhysRevSTPER.6.020121

CrossRef Full Text | Google Scholar

Meyer, D. A. (1999). Quantum strategies. Phys. Rev. Lett. 82, 1052. doi: 10.1103/PhysRevLett.82.1052

CrossRef Full Text | Google Scholar

Michelini, M., Ragazzon, R., Santi, L., and Stefanel, A. (2000). Proposal for quantum physics in secondary school. Phys. Educ. 35, 406. doi: 10.1088/0031-9120/35/6/305

CrossRef Full Text | Google Scholar

Mukhtar, K., Javed, K., Arooj, M., and Sethi, A. (2020). Advantages, limitations and recommendations for online learning during covid-19 pandemic era. Pak. J. Med. Sci. 36, 27–31. doi: 10.12669/pjms.36.COVID19-S4.2785

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller, R. (2003). Quantenphysik in der Schule. Berlin: Logos Verlag.

Google Scholar

Müller, R., and Greinert, F. (2021). Playing with a quantum computer. arXiv. [preprint]. doi: 10.48550/arXiv.2108.06271

CrossRef Full Text | Google Scholar

Müller, R., and Wiesner, H. (2002). Teaching quantum mechanics on an introductory level. Am. J. Phys. 70, 200. doi: 10.1119/1.1435346

CrossRef Full Text | Google Scholar

Özcan, Ö., Didiş, N., and Taşar, M. F. (2009). Students' conceptual difficulties in quantum mechanics: potential well problems. Hacettepe Univ. Eğitim Fak. Derg¨. 36, 169–180.

Google Scholar

Pluta, W., Chinn, C., and Duncan, G. (2011). Learners‘ epistemic criteria for good scientific models. J. Res. Sci. Teach. 48, 486–511. doi: 10.1002/tea.20415

CrossRef Full Text | Google Scholar

Pospiech, G. (2021). “Quantum cryptography as an approach for teaching quantum physics,” Teaching-Learning Contemporary Physics: From Research to Practice, eds B. Jarosievitz, and Sükösd (New York, NY: Springer), 19–31. doi: 10.1007/978-3-030-78720-2_2

CrossRef Full Text | Google Scholar

Pospiech, G., Merzel, A., Zuccarini, G., Weissman, E., Katz, N., Galili, I., et al. (2021). The role of mathematics in teaching quantum physics at high school. Teaching-Learning Contemporary Physics: From Research to Practice, eds B. Jarosievitz, and Sükösd (New York, NY: Springer), 47–70. doi: 10.1007/978-3-030-78720-2_4

CrossRef Full Text | Google Scholar

Prasad, S., Scully, M. O., and Martienssen, W. (1987). A quantum description of the beam splitter. Opt. Commun. 62, 139–145. doi: 10.1016/0030-4018(87)90015-0

CrossRef Full Text | Google Scholar

Scholz, R., Wessnigk, S., and Weber, K.-A. (2020). A classical to quantum transition via key experiments. Eur. J. Phys. 41, 055304. doi: 10.1088/1361-6404/ab8e52

CrossRef Full Text | Google Scholar

Schwarz, C., and White, B. (2005). Metamodeling knowledge: developing students' understanding of scientific modeling. Cogn. Instr. 23, 165–205. doi: 10.1207/s1532690xci2302_1

CrossRef Full Text | Google Scholar

Seskir, Z. C., Migdał, P., Weidner, C., Anupam, A., Case, N., Davis, N., et al. (2022). Quantum games and interactive tools for quantum technologies outreach and education. Opt. Eng. 61, 081809–081809. doi: 10.1117/1.OE.61.8.081809

CrossRef Full Text | Google Scholar

Shackelford, J. L., and Maxwell, M. (2012). Sense of community in graduate online education: contribution of learner to learner interaction. Int. Rev. Res. Open Distrib. Learn. 13, 228–249. doi: 10.19173/irrodl.v13i4.1339

CrossRef Full Text | Google Scholar

Shi, G. (2020). Research on the influence of online learning on students' desire to learn. J. Phys. Conf. Ser. 1693, 012055. doi: 10.1088/1742-6596/1693/1/012055

CrossRef Full Text | Google Scholar

Ssekakubo, G., Suleman, H., and Marsden, G. (2013). Designing mobile lms interfaces: learners' expectations and experiences. Interact. Technol. Smart Educ. 10, 147–167. doi: 10.1108/ITSE-12-2012-0031

CrossRef Full Text | Google Scholar

Stadermann, H., and Goedhart, M. (2020). Secondary school students' views of nature of science in quantum physics. Int. J. Sci. Educ. 42, 997–1016. doi: 10.1080/09500693.2020.1745926

PubMed Abstract | CrossRef Full Text | Google Scholar

Stavredes, T., and Herder, T. (2013). A Guide to Online Course Design: Strategies for Student Success. Hoboken, NJ: John Wiley and Sons.

Google Scholar

Stevens, D. D., and Levi, A. J. (2013). Introduction to Rubrics: An Assessment Tool to Save Grading Time, Convey Effective Feedback, and Promote Student Learning. Sterling, VA: Stylus Publishing, LLC.

Google Scholar

Swan, K. (2001). Virtual interaction: design factors affecting student satisfaction and perceived learning in asynchronous online courses. Dist. Educ. 22, 306–331. doi: 10.1080/0158791010220208

CrossRef Full Text | Google Scholar

Taber, K. (2005). Learning quanta: barriers to stimulating transitions in student understanding of orbital ideas. Sci. Educ. 89, 94–116. doi: 10.1002/sce.20038

CrossRef Full Text | Google Scholar

Treagust, D. F., Chittleborough, G., and Mamiala, T. L. (2002). Students' understanding of the role of scientific models in learning science. Int. J. Sci. Educ. 24, 357–368. doi: 10.1080/09500690110066485

CrossRef Full Text | Google Scholar

Ubben, M., and Bitzenbauer, P. (2023). Exploring the relationship between students' conceptual understanding and model thinking in quantum optics. Front. Quantum Sci. Technol. 2, 1207619. doi: 10.3389/frqst.2023.1207619

CrossRef Full Text | Google Scholar

Ubben, M., and Heusler, S. (2021). Gestalt and functionality as independent dimensions of mental models in science. Res. Sci. Educ. 51, 1349–1363. doi: 10.1007/s11165-019-09892-y

CrossRef Full Text | Google Scholar

Ubben, M. S. (2020). Typisierung des Verständnisses mentaler Modelle mittels empirischer Datenerhebung am Beispiel der Quantenphysik. Berlin: Logos Verlag. doi: 10.30819/5181

CrossRef Full Text | Google Scholar

Ubben, M. S., and Bitzenbauer, P. (2022). Two cognitive dimensions of students' mental models in science: fidelity of gestalt and functional fidelity. Educ. Sci. 12, 163. doi: 10.3390/educsci12030163

CrossRef Full Text | Google Scholar

Vai, M., and Sosulski, K. (2011). Essentials of Online Course Design: A Standards-based Guide. London: Routledge. doi: 10.4324/9780203838310

CrossRef Full Text | Google Scholar

Veith, J. M., Bitzenbauer, P., and Girnat, B. (2022). Exploring learning difficulties in abstract algebra: the case of group theory. Educ. Sci. 12, 516. doi: 10.3390/educsci12080516

CrossRef Full Text | Google Scholar

Weissman, E. Y., Merzel, A., Katz, N., and Galili, I. (2022). Phenomena and principles: presenting quantum physics in a high school curriculum. Physics 4, 1299–1317. doi: 10.3390/physics4040083

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilford, S., Fisk, M., and Stahl, B. (2016). Guidelines for Responsible Research and Innovation. Leicester: Centre for Computing and Social Responsibility, De Montfort University.

Google Scholar

Zambra, G., Andreoni, A., Bondani, M., Gramegna, M., Genovese, M., Brida, G., et al. (2005). Experimental reconstruction of photon statistics without photon counting. Phys. Rev. Lett. 95, 063602. doi: 10.1103/PhysRevLett.95.063602

PubMed Abstract | CrossRef Full Text | Google Scholar