- 1African Center of Excellence for Innovative Teaching and Learning Mathematics and Science, University of Rwanda, College of Education, Kayonza, Rwanda
- 2Department of Mathematics, Science and Physical Education, University of Rwanda, College of Education, Kayonza, Rwanda
Introduction: Teachers’ knowledge and positive attitudes significantly impact educational settings. This study aimed to assess teachers’ mathematical knowledge for teaching (MKT) and their pedagogical content knowledge (PCK) attitudes.
Methodology: It was conducted on all 23 mathematics teachers from Rwandan teacher training colleges (TTCs). Employing a survey design, standardized performance and attitude tests were utilized, employing instruments known for their standardization, validity, and reliability.
Results: The findings informed that teachers possess a low MKT but a high PCK attitude. Thus, they performed the MKT test poorly as the average score was below 50%. However, teachers were found to have better content knowledge than other MKT constructs and performed better in pattern function and algebra than in other areas of mathematics. Teachers demonstrated a highly positive attitude toward integrating PCK in teaching mathematics.
Discussion: Such a positive attitude was inferred from the pedagogical training offered by implementing a competency-based curriculum. Therefore, teachers need to improve their MKT performance, and more research is needed on other teachers apart from those in TTCs.
Introduction
Rwanda initiated the implementation of a competency-based curriculum (CBC) 8 years ago, marking a significant shift from the traditional knowledge-based curriculum (REB, 2015). This transition was driven by recognizing that education should impart knowledge, foster practical skills, and promote positive attitudes among graduates. The move to a CBC has been well documented in numerous reports and research papers, demonstrating its importance and impact (Ndihokubwayo et al., 2019a,b; JICA, 2020; Nsengimana et al., 2020).
While studies have explored teachers’ perceptions of CBCs and highlighted some challenges, such as resistance to change (Ndihokubwayo and Habiyaremye, 2018), a notable lack of research has focused on implementing a CBC in mathematics education. Given the significance of mathematics education in the curriculum and the potential influence of the new teaching approach, assessing teachers’ readiness and competence in teaching mathematics within this context becomes crucial. To address this gap, this study aims to evaluate Rwandan teacher training colleges (TTC) teachers’ mathematical knowledge for teaching (MKT) and their attitudes toward pedagogical content knowledge (PCK). MKT measures serve as a valuable tool for assessing teachers’ mathematical knowledge, shedding light on their ability to explain mathematical concepts effectively (Ball et al., 2008). Furthermore, the study of MKT has highlighted challenges that teachers may face, including a potential imbalance between subject matter knowledge and pedagogical knowledge (Chen and Huang, 2013).
In addition to MKT, this study explores teachers’ attitudes toward pedagogical content knowledge (PCK). PCK encompasses subject matter expertise and the ability to convey this knowledge effectively to students (Shulman, 1987). It involves understanding students’ difficulties with specific topics, choosing appropriate teaching strategies, and recognizing common misconceptions (Shulman, 1987). Assessing PCK attitudes can provide insights into teachers’ readiness to implement a CBC, which emphasizes cross-cutting issues and generic competencies (Rwanda Education Board, 2015; Ndihokubwayo et al., 2020).
The study focuses on algebra and function content, recognizing their significance in the mathematics curriculum. Previous research has indicated that teachers in various countries, including the United States and China, encounter difficulties teaching these topics (Zhou et al., 2013). By investigating teachers’ MKT and PCK attitudes in the context of a CBC, this study aims to inform policymakers and educational stakeholders about the current state of teacher training and support. Ultimately, the quality of primary education hinges on well-prepared teachers, who, in turn, lay the foundation for higher levels of education. This study contributes to the broader goal of achieving Rwanda’s national aspiration of becoming a middle-income country by 2030, emphasizing the pivotal role of primary education.
To guide our investigation, the following research questions have been formulated:
i. What are the strengths and areas for growth in MKT for TTC teachers?
ii. How do TTC teachers perceive their current PCK for teaching mathematics?
Theoretical literature review
In this literature review, we delve into existing perspectives on mathematics teachers’ knowledge for teaching. The review is structured into two major sections: “Knowing Mathematics as a Well-Educated Individual and Knowing it as a Mathematics Teacher” and “Mathematical Knowledge Needed for Teaching.”
Mathematical knowledge needed for teaching
Over the years, researchers in mathematics education (Shulman, 1986; Hill et al., 2008; Skott et al., 2013; Kind, 2015) have conducted empirical observations, interviews, tests, and other methods to explore teachers’ practices and thought processes when teaching mathematics. These researchers have sought to identify patterns in observed phenomena and generate models and theories that describe the components and structures of teachers’ knowledge.
One critical question in mathematics education is, “What sets apart the teaching of mathematics from knowing mathematics for other professions?” Is it solely the ability to care for students, knowledge of the subject matter, or the management of large groups of students? The answer is more nuanced as it involves not only the ability to care for students and knowledge of the subject matter but also the effective management of large groups of students. Educational psychologists, such as Shulman (1987), have framed this question differently, emphasizing the need for teachers to understand the subject matter systematically. He categorized this knowledge into subject matter knowledge (SMK) and pedagogical content knowledge (PCK).
Subject matter knowledge emphasizes the teacher’s depth of knowledge about the subject matter. Effective teachers can answer complex questions and devise solutions to intricate problems. They must recognize mistakes in student thinking and subject resources. In essence, they must be subject experts. PCK entails knowing how to teach effectively. It encompasses theories and principles of teaching and learning, understanding the needs of learners, and classroom behavior management. PCK transcends specific subject disciplines and focuses on facilitating learning in various situations.
Teachers must master both subject matter knowledge and pedagogical content knowledge to excel in their profession. A skilled teacher possesses expertise in the subject matter and the art of effectively teaching it, including selecting appropriate resources, metaphors, activities, and sequences tailored to specific students’ needs. Teachers must also understand their students’ prior knowledge, skills, and requirements to plan their teaching effectively. This understanding is called syntactic knowledge and involves fitting new learning into a topic’s broader scheme of knowledge. Moreover, teachers must anticipate and understand common misconceptions students might develop in their subject area. Shulman’s framework underlines the need for teachers to possess both content and pedagogical content knowledge. Effective teaching goes beyond merely conveying what one knows; it requires specialized expert knowledge. In 1986, Lee Shulman identified a gap in educational policies, research, and practices—a tendency to focus on pedagogical aspects while overlooking subject matter knowledge. He proposed a theoretical framework, “Knowledge Growth in Teaching,” with three components contributing to teachers’ mathematical knowledge for teaching (MKT). This framework was later adopted by Deborah Ball and her team from the University of Michigan (Ball et al., 2008).
Content knowledge encompasses the knowledge organization in the teacher’s mind, including substantive and syntactic structures. Substantive structure relates to how fundamental concepts and principles of a discipline are organized, incorporating facts, learning processes, and connections between them. Syntactic structure pertains to how mathematical truth and validity are established and involves understanding how to prove ideas. Pedagogical knowledge focuses on how teachers transform knowledge to facilitate successful learning. It includes using resources, motivating learners, and employing strategies such as problem-based learning to convey subject matter effectively. Curricular knowledge involves understanding the instructional materials available for teaching a subject and topics at a given level and selecting appropriate materials for specific circumstances.
This framework formed the basis for the model of MKT, which was designed to demonstrate the relationship between subject matter knowledge (SMK) and pedagogical content knowledge (PCK), as portrayed in Figure 1.
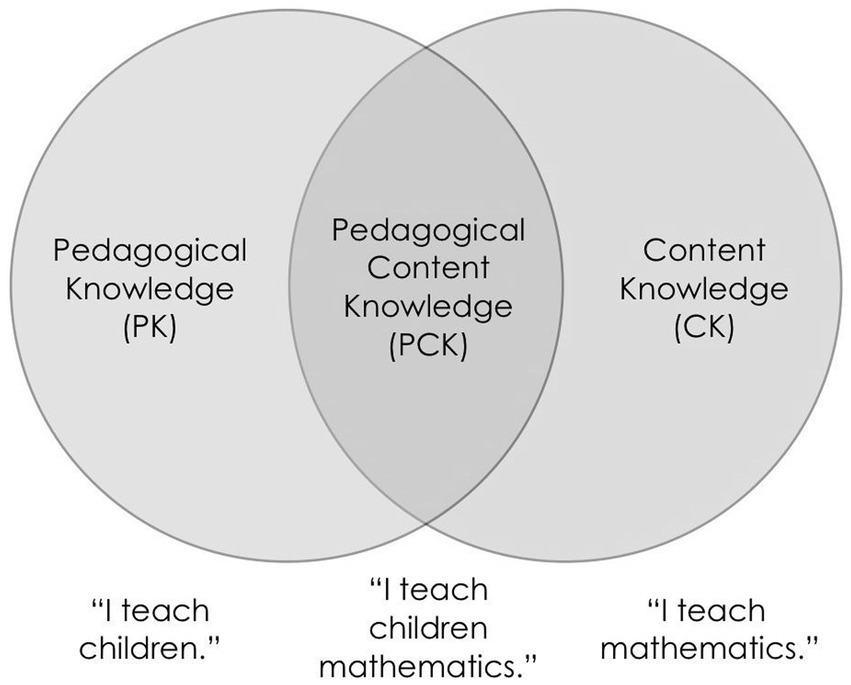
Figure 1. Pedagogical content knowledge framework (Shulman, 1987, p.8). Alt text: https://amiealbrecht.com/2023/01/02/what-knowledge-is-required-for-teaching/.
Knowing mathematics as a well-educated individual and knowing it as a mathematics teacher
Teaching and supporting students’ learning needs specialization of knowledge for teaching mathematics. Knowing, learning, and using mathematics as a teacher requires specialized knowledge (Ball and Feiman-Nemser, 1988). Mathematical knowledge needed for teaching mathematics suggests a type of professional mathematical knowledge unique to teaching. Ball and her colleagues say that teaching special mathematics is not something that any well-educated grown-up can do as well. To find out if students are learning mathematics well, a teacher might know why the answers are wrong, which is probably what the average well-educated can do when they see teachers doing mathematics.
Teaching and supporting students in learning mathematics demand specialized knowledge. Teaching mathematics requires more than knowing and using mathematics as a well-educated individual (Ball and Feiman-Nemser, 1988). It necessitates a unique form of professional mathematical knowledge tailored to teaching. Effective teaching involves understanding why students’ answers are incorrect and knowing how to address their misconceptions. Recent research, such as that by Ball et al. (2008), has explored teachers’ content knowledge for teaching mathematics, revealing that successful math instruction relies on a combination of subject matter knowledge (SMK) and pedagogical content knowledge (PCK). These domains encompass common content knowledge (CCK), mathematical horizon knowledge, specialized content knowledge (SCK), knowledge of content and students (KCS), knowledge of content and teaching (KCT), and knowledge of the curriculum, as demonstrated in Figure 2.
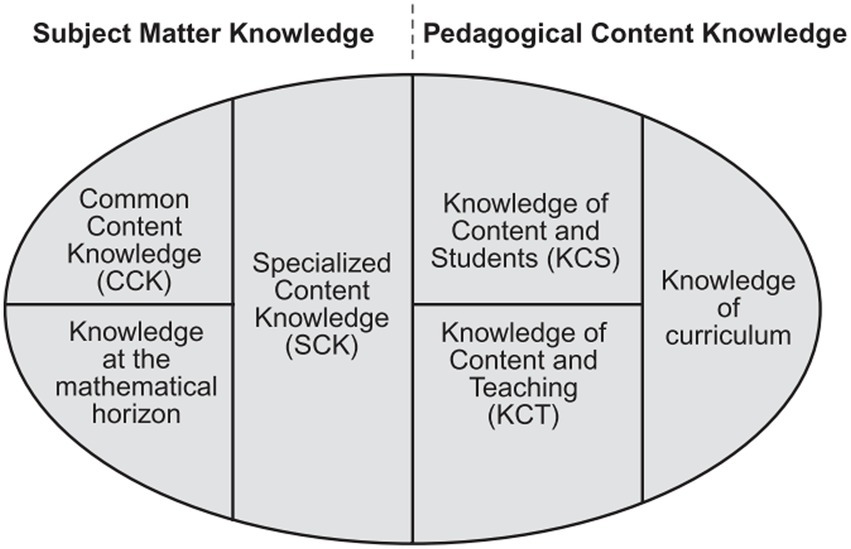
Figure 2. Domains of mathematical knowledge for teaching (Ball et al., 2008). Alt text: This figure has two parts; the right side is pedagogical content knowledge, while the left side is subject matter knowledge.
Methodology
Research design
This study intended to assess the pedagogical content knowledge for teaching possessed by mathematics teachers in Rwandan teacher training colleges. It used a survey design (Fraenkel et al., 2012) with standardized performance (Hill et al., 2004) and attitude (Aksu et al., 2014) tests. Rwanda implemented a new curriculum in 2016, which seeks that learners absorb knowledge, skills, and values. The MKT instrument provides a wide range of mathematical areas and its teaching procedures. Thus, a competent teacher can be measured by this instrument. For instance, a teacher with content knowledge will provide effective knowledge to students, and a teacher with good pedagogical knowledge will easily teach the students in appropriate ways, and thus, these students will be able to gain knowledge and practice learned knowledge (i.e., skills). A teacher who possesses technological knowledge will allow students to gain skills and appreciate such skills in their use in real-life situations (i.e., attitude and values). A teacher who knows their students and a teacher who knows the curriculum (intended, implemented, and attained) will be able to handle students according to their ability and elevate them at the national level.
Population and sample
Research has shown that primary education is crucial to smoothly attaining and upgrading high education (Kanamugire et al., 2019; Ndihokubwayo and Murasira, 2019). Various studies documented practices in Rwandan primary education settings and found that educational colleges need more support than any other school (Ndihokubwayo et al., 2018, 2019c; Uworwabayeho et al., 2020). Rwanda has 16 teacher training colleges (TTCs). These TTCs accommodate four career options: science and mathematics education, social studies education, languages education, and early childhood and lower primary education (REB, 2020). The purposive sampling method was used, employing all TTCs’ mathematics teachers in March 2021. Thus, 23 TTC teachers from 16 colleges participated in this study.
Ethical consent and data collection procedures
Before data collection, the researchers obtained an ethical clearance from the unit of research and innovation at the University of Rwanda College of Education. After that, we invited teachers and asked them to participate in the study. We set the schedule, and they were asked to sit for the test. The time given was 90 min. After finishing the tests, they were given a token of appreciation, such as ball pens or a dinner. After finishing the MKT test, the follow-up PCK attitude scale followed.
Instruments
Performance test
For performance, we adapted the mathematical knowledge for teaching (MKT) measures by Hill et al. (2004). Rwanda is among the countries that test teachers’ knowledge of teaching mathematics by adapting the United States items for one major reason: the knowledge and skill underlined in the CBC are the theory of mathematical knowledge for teaching.
However, though the MKT measures, such as those counted in trends of mathematical knowledge for teaching, are carefully considered for international use, in many countries, including Rwanda, these measures have to be argued for the language, culture, and initial examples used in these items. Subsequently, this article argues the use of these items in Rwanda because the test developers accounted for the use of these items by considering the culture of teaching mathematics in the United States only. From one country to another, teachers have different beliefs about the structure of lesson planning and the engagement of students when responding to teachers, etc. For instance, teachers in Rwanda prepare the lesson by addressing the cross-cutting issue and indicating the generic competencies to be developed in the lesson. Though these items would be adapted in Rwanda, the researchers considered how multiple items are selected and adapted. It was anticipated that based on the answers to each item, teachers’ knowledge would subsequently be measured in both subject content and pedagogical content knowledge. These items were used for the pilot in normal schools and later in TTCs. Since the items were developed based on the concept that emerges from practical teaching in the United States, we looked at methodological challenges that would be encountered and suggested the suitability of these measures to study teachers’ knowledge in the Rwandan context of teaching mathematics.
The items for use were selected based on the related subtopic areas generally found in the Rwandan textbooks and CBC content. These subtopic areas include numbers and operations, linear equations and inequalities, functions, plane geometry, and number patterns. Content knowledge was measured under the common and specialized domains of subject knowledge. The knowledge of pedagogy was measured under the knowledge of teaching and knowledge of helping students understand the concept as domains of pedagogical content knowledge.
The MKT measures contain 35 questions. Since some questions have subquestions, the total number of items is 64. The measures comprise different MKT constructs and mathematical constructs. For instance, Number Concepts and Operations (NCOP) has four items (1a–2) that cover CCK, 11 items (3a–9) that cover SCK, 17 items (10a–17d) that cover KCS, four items (20–230) that cover KCT, and four items (29a–d) that cover C.K. Thus, NCOP covers 40 out of 64 items (or 22 out of 35 questions). Pattern function and algebra (PFA) has 12 items (31a–34) that cover SCK. Thus, PFA covers 12 out of 64 items or four out of 35 questions. Geometry (GEO) has one item (18) that covers KCS and four items (24–27) that cover KCT. Thus, GEO covers five out of 64 items (corresponding to five questions). Proportional reasoning (PR) has one item (19) that covers KCS and four items (30a–d) that cover CK. Thus, PR covers five out of 64 (two out of 35 questions). Finally, Rational numbers (RAT) has one item (28) that covers KCT and one item (35) that covers SCK. Thus, RAT covers two out of 64 items (corresponding to two questions). Figure 3 shows all these.
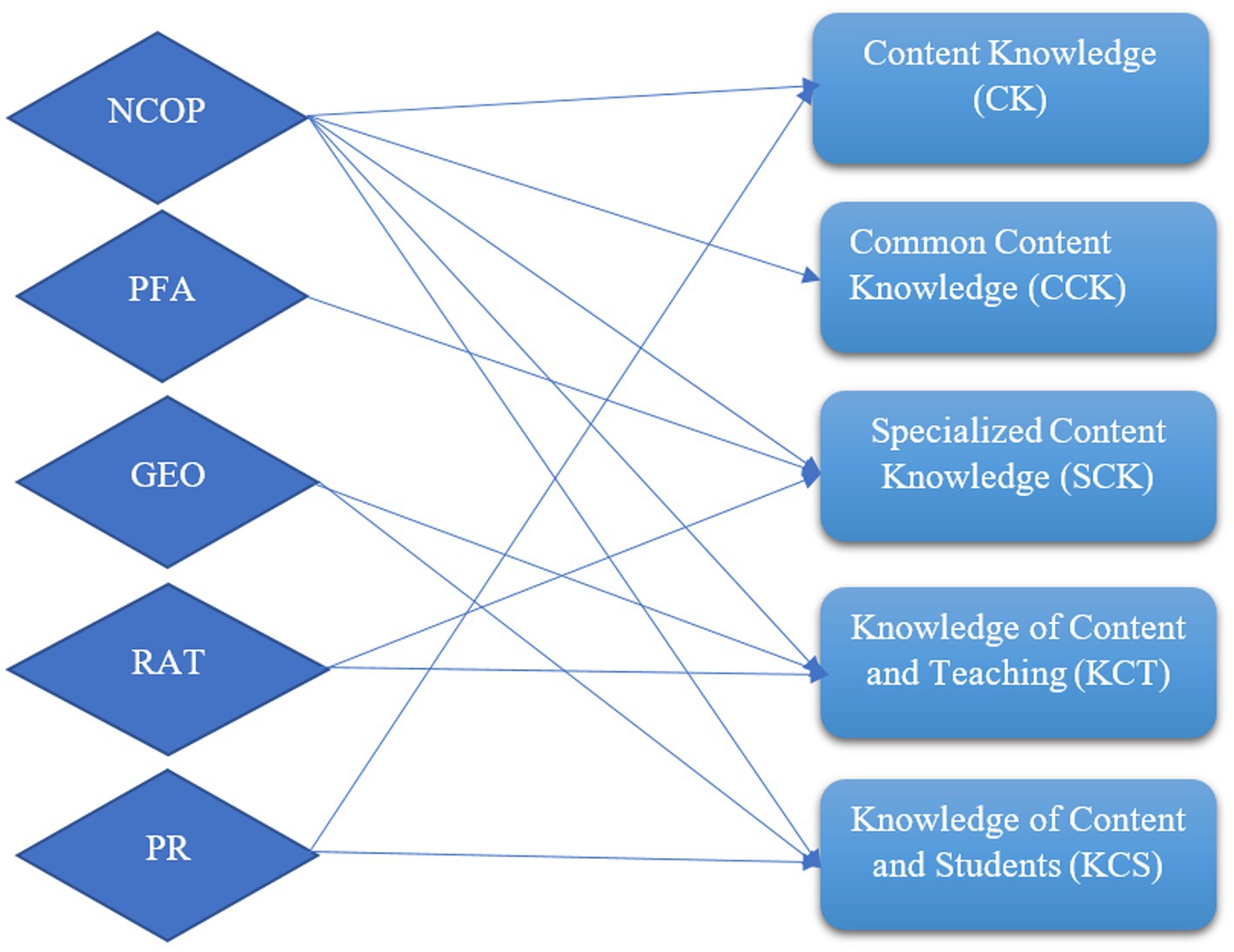
Figure 3. The connection between Mathematics content and PCK constructs. Alt text: The mathematics content is elaborated on the left side, and PCK constructs are arranged on the right side.
Items were reviewed by mathematics educators and mathematicians in Rwanda to determine whether these items reflect situations that arise in Rwandan colleges. These reviewers discussed whether the items sound more familiar to Rwandan teachers or whether the mathematical language used is familiar to the respondents in terms of understanding well. We then compiled tables listing all the changes made. Note that though we modified some items, we did not change the sense and meaning of the original versions from the owner developers.
Attitude test
In our study, we adopted the Pedagogical Content Knowledge Scale for Pre-Service Teachers, which was originally developed by Aksu et al. (2014). Aksu et al.’s study aimed to develop a scale to determine pre-service teachers’ pedagogical content knowledge. Their research involved 768 pre-service teachers from different universities in Türkiye and included a comprehensive process encompassing a literature review, creating an item pool, expert opinions, scale administration, and reliability and validity assessments. In the original study by Aksu et al. (2014), the item pool was constructed through interviews with pre-service teachers and teacher essay writing assignments on pedagogical content knowledge. After administration to a large sample of pre-service teachers, factor analysis was employed to refine the scale, resulting in a final set of 38 items. The internal reliability of the final scale, as indicated by Cronbach’s Alpha, was found to be 0.967, demonstrating strong internal consistency. Given the rigorous development process and established reliability and validity of the PCK Scale for Pre-Service Teachers by Aksu et al. (2014), we adopted the 38-item version of this scale in our study to measure Rwandan TTC teachers’ attitudes toward pedagogical content knowledge. This ensured our instrument was based on a validated and reliable measure of pedagogical content knowledge attitudes.
Data analysis
Validation and reliability
After compiling the teachers’ responses to multiple-choice items, a psychometric analysis method was used to measure how the respondents’ abilities match with the required knowledge of teaching mathematics, and independently, the item difficulties were calculated based on the respondents’ responses. We were interested in knowing how Rwandan TTC teachers perform these items because this would determine whether we are measuring similar constructs. All teachers’ responses were entered into SPSS, and we closely estimated the point biserial correlation to rate the number of right and wrong scores that teachers received on the given items and the total scores that the teachers received when summing up the scores across the items. We also calculated Cronbach’s alpha and saw how the related items are performed. The relative item difficulties were estimated to determine whether the respondents mastered the tested concept. With the use of SPSS, addressing item difficulties in standard deviation, zero scales represent the teacher’s ability on average, and lower zero describes the easier items. Cronbach’s alpha is measured between a 0 and 1 scale. A higher Cronbach’s alpha indicates that the content is reliable to the respondents. If the item responses are highly correlated, the test takers’ ability is the same (Landau and Everitt Chapman, 2004). A high Pearson correlation (r = 0.76) using the Split-half method was obtained in the MKT performance test, while a very high Cronbach alpha (α = 0.93) using the internal consistency method was obtained in the PCK attitude scale.
Data outcome
We calculated the mean scores and standard deviations of all the constructs. We plotted the graph showing the percentage of teachers who performed each MKT item and the percentages of those who agreed or disagreed with the PCK scales. For the PCK scales, we combined strongly agree and agree to agree, strongly disagree, and disagree to disagree, while neutral remained neutral. We did this to narrow down the raw data and ease the visualization. Since the number of respondents was small (<30), we used non-parametric tests. Non-parametric tests of two or more related samples were computed to find differences between MKT constructs and mathematical areas.
Results of the study
To what extent do TTC teachers perform the MKT test?
The first research question is intended to measure Rwandan TTC teachers’ mathematics knowledge for teaching. The teachers possessed good knowledge in content knowledge (C.K.); in only one MKT construct did they obtain a higher-than-average score (54.89%). They possessed low knowledge of knowledge in content and teaching (KCT; M = 11.11%, SD = 10.50%). Likewise, the teachers’ well-performed questions related to pattern function and algebra (PFA) as in only one area of mathematics did they obtain a higher-than-average score (57.24%). They performed lowly (M = 6.52%, SD = 17.21%) in rational numbers (RAT). The overall score shows that teachers did not reach the average score (50%). They obtained 41.77% as the mean score and 8.97% as the standard deviation (see Table 1).
Computing non-parametric tests (two or more related samples), Friedman’s ANOVA by ranks revealed that the distributions of MKT constructs (CCK, SCK, KCS, KCT, and CK) were not the same (p = 0.000). Similarly, Friedman’s ANOVA by ranks revealed that the distributions of mathematics areas (NCOP, GEO, PR, PFA, and RAT) were not the same (p = 0.000). Therefore, inferential statistics showed that Rwanda TTC teachers statistically significantly possessed heterogeneous knowledge of MKT. The same significance was realized in mathematics areas.
Further analysis was performed to investigate alternative conceptions or difficulties the teachers faced in the MKT test; this is documented in Figure 4. About 39 of the 64 items (61%) were performed by below 50% of the teachers. Thus, only 39% of the items were correctly performed by more than 50% of the teachers. For instance, all 23 teachers failed Q18, Q20, and Q28 completely, having scored 0 on these questions. All KCT items were performed by only below 30% of the teachers.
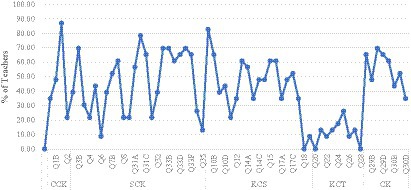
Figure 4. Teachers’ conceptual understanding of MKT content. Alt text: The vertical axis is the percentage of teachers, and the horizontal axis shows test items within the PCK constructs.
To what extent do TTC teachers perceive PCK in teaching mathematics?
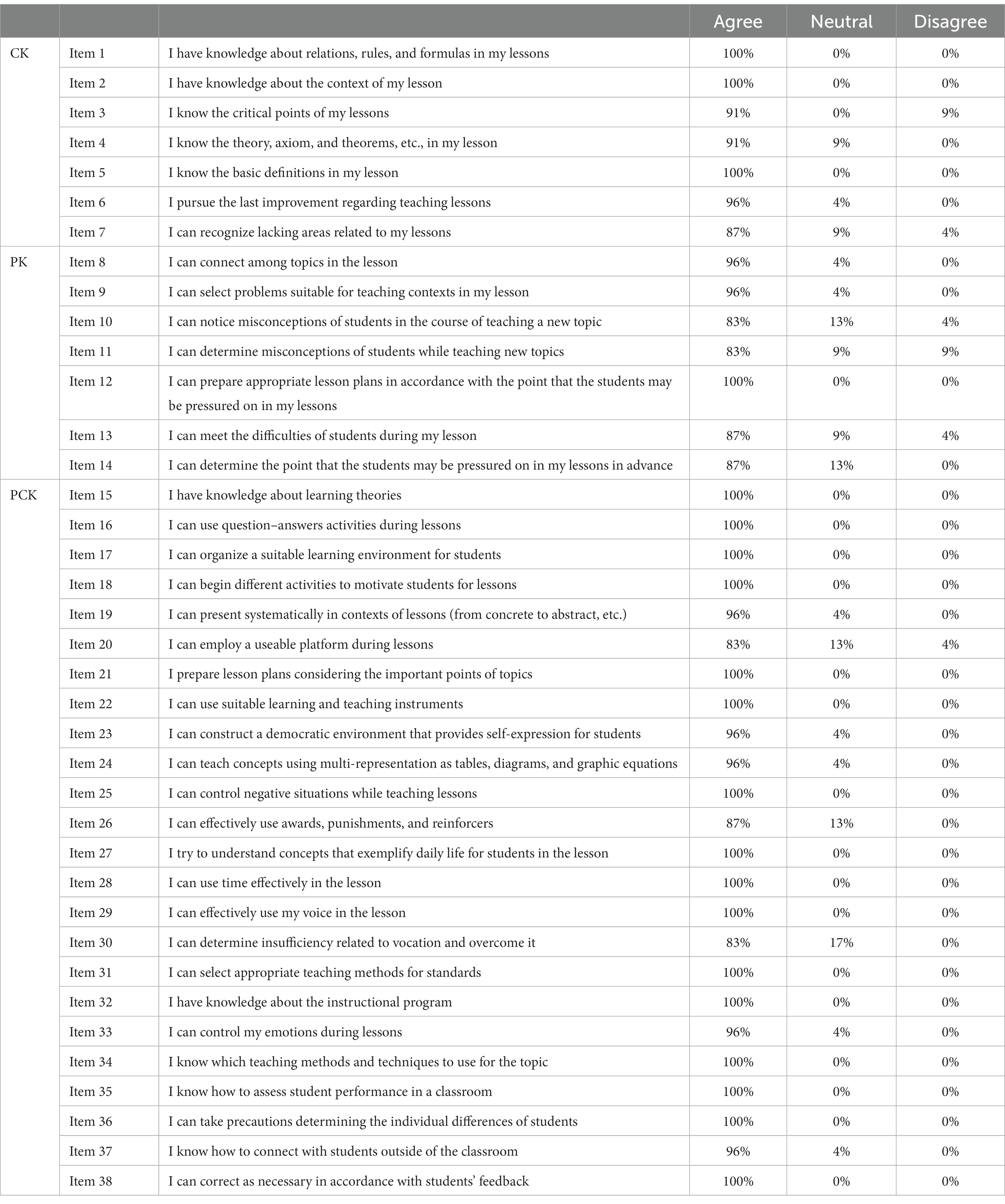
To reveal the teachers’ perceptions or attitudes toward PCK in teaching mathematics, a highly positive outcome was found across all the PCK scales and among all 23 teachers. Table 2 displays the results related to the Rwandan teacher training college (TTC) teachers’ attitudes.
The lowest CK item (from item 1 to 7) rated by teachers was “I can recognize lacking areas related to my lessons (item 7),” which was rated by 87% of the teachers, while other items were rated by more than 90% of the teachers in an agreement position. The most lowly rated PK items were item 10, “I can notice misconceptions of students in the course of teaching a new topic,” and item 11, “I can determine misconceptions of students while teaching new topics,” and these were rated equally by 83% of the teachers. The most lowly rated PCK items were item 20, “I can employ a useable platform during lessons,” and item 30, “I can determine insufficiency related to vocation and overcome it,” and these were rated equally by 83% of the teachers.
Discussion of results
The non-homogeneity in MKT constructs and mathematics areas may be depicted for various reasons. First of all, teachers performed the MKT test below average because this is an international test, and teachers might not be well prepared. However, some items require critical thinking, which the Rwandan CBC emphasizes. Therefore, we thought teachers would do the test carefully and critically. Another reason may be that the curriculum implemented in TTCs (REB, 2020) is lighter compared to the one implemented in general secondary schools (REB, 2015). Thus, some topics might be difficult for these teachers because they do not tackle them in their daily routines. They did not perform well on the items related to rational numbers given that this area got few items in the whole test. Thus, rational numbers (RAT) covered only two out of 64 items or two out of 35 questions (see Appendix A). The reason why teachers poorly performed on items related to KCT while they highly performed on items related to CK needs further investigations.
Among the recent studies that used MKT measures of Hill et al. (2004), Blazar and Kraft (2017) focused on how teachers affect students’ achievement on standardized tests and found that upper-elementary teachers have large effects on self-reported measures of students’ self-efficacy in mathematics classes. Teachers who are effective at improving test scores were often found to be not equally effective at improving students’ attitudes and behaviors (Blazar and Kraft, 2017). Likewise, Maloney et al. (2015) found that the effects of parents’ mathematical anxiety are specific to children’s mathematics achievement. The study conducted by Shulman (1987) on knowledge for teaching showed that some teachers struggle to deliver the packaged knowledge enabled by pedagogical content to students. Teachers are practitioners to support students. The findings of the Zambian study revealed that most mathematics teachers did not possess enough conceptual understanding of soft skills, and most were unaware of the methods and assessment strategies that incorporate soft skills (Busaka et al., 2022). Mukuka et al. (2021) suggested that mathematics self-efficacy and task-specific self-efficacy beliefs collectively and significantly can mediate the effect of the instructional approach on mathematical reasoning. The study conducted in Rwandan schools by JICA (2020) on mathematics and science lesson studies categorized teaching practice into four methods: presentation of the task, asking about knowledge and skills, asking how students think, and asking about attitude. The results indicated that (80%) of the questions were related to task presentation, which gives instructions to students. There were only a few questions essential for developing mathematical thinking or attitudes.
About 12 of the 64 items were performed by only below 20% of teachers. These questions (Q6, Q35 from SCK, Q18 and Q19 from KCS, and Q20, Q21, Q22, Q23, Q24, Q26, Q27, and Q28 from KCT) posed tremendous challenges to teachers (see Figure 4 in the results section). For instance, Q6 was about “Model 1 1/2 × 2/3,” asking teachers to show a representing model of the multiplication of fractions (see Figure 5). The question is related to the number concepts and operations (NCOP) in specialized content knowledge (SCK). Only 9% of the teachers could select option (c) as a correct answer. The teachers do not possess observational methods to frame an abstract mathematical concept into a pictorial instructional strategy.
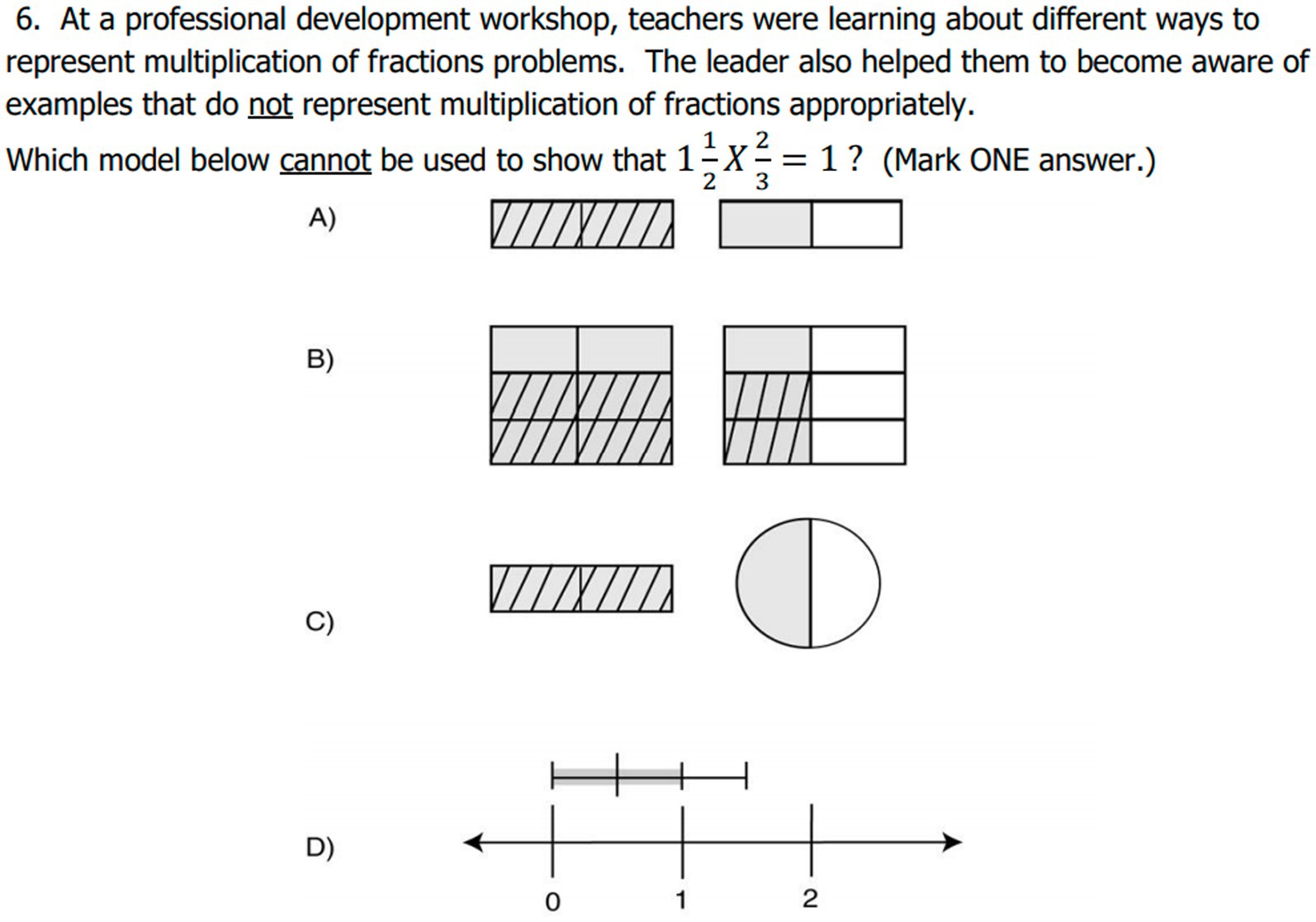
Figure 5. Q6 about the model of multiplication of a fraction. Alt text: This question was picked from the test and provided to facilitate the discussion of the results.
Q18 provided a scenario related to symmetry in polygons (Figure 6). It was classified into geometry topics. No teacher was able to answer it correctly (see Figure 4 in the results section). The teachers were not able to reveal that students confused lines of symmetry with rotating half the figure onto the other half (answer d). Such knowledge of content and students (KCS)-related competence lacking among TTC teachers shows that pedagogical skill is still needed to know the students they teach. Teachers should think on behalf of their students and analyze possible conceptions. This may help them to progress well in the lesson.

Figure 6. Q18 about symmetry in polygons. Alt text: This question was picked from the test and provided to facilitate the discussion of the results.
Similarly, Q20 belongs to KCT, and none answered it correctly (see Figure 4 in the results section). It is related to NCOP, which places value on young learners (Figure 7). Teachers could not reveal that straws and rubber bands would be the most appropriate tools to introduce the idea of grouping by tens and ones to young learners. Such a pedagogical selection shows that Rwandan TTC teachers still need a deep understanding of pedagogical skills related to each level of education. The link between syllabus content and pedagogical approaches is still needed.

Figure 7. Q20 about placing value on young learners. Alt text: This question was picked from the test and provided to facilitate the discussion of the results.
Q28, related to knowledge of content and teaching (KCT), was also failed by every teacher in our study (see Figure 4 in the results section). This question is related to rational numbers (RAT). It was difficult for a teacher to analyze and evaluate a better and easier pattern to convert fractions into decimals (Figure 8).

Figure 8. Q28 about converting fractions. Alt text: This question was picked from the test and provided to facilitate the discussion of the results.
In general, the items in KCT were poorly performed. Such results show that Rwandan TTCs teachers struggle with connecting content knowledge and teaching. In fact, the competency-based curriculum implemented in 2016 (REB, 2015) would have answered such an issue, but this study reveals that the change from knowledge to competency-based pedagogy is still problematic. Such results obtained from TTC teachers would initially suggest that the curriculum framework specific to TTCs came out recently (REB, 2020); however, all teachers in Rwanda have been involved in training offered by REB and several developmental partners (DPs) since 2016. Therefore, further investigations into other teachers in general secondary schools would clarify and support our findings. Would like to investigate this in our future studies.
Teachers were found to have a positive attitude toward PCK in teaching mathematics. They perceived it and agreed with the PCK scale at more than 83%. On the contrary, a study by Moh’d et al. (2021) that used the same scale (Aksu et al., 2014) found a moderate level of PCK among mathematics teachers in selected secondary schools in Zanzibar. The findings from a study conducted to examine mathematical problem-solving beliefs among Rwandan secondary school teachers indicated that most teachers showed a positive attitude toward advancing problem-solving in the mathematics classroom, although they exposed different views on its implementation (Dorimana et al., 2021). The authors highlighted the role of problem-solving as an approach that helps teachers use time adequately and helps students develop critical thinking and reasoning that enable them to face challenges in real life. Such beliefs from general secondary schools need to be compared to beliefs among TTC teachers as teacher trainers. The pre-service teachers also need to be investigated and compared to their trainers to implement effective remedies.
Conclusion and study implications
This study intended to assess the pedagogical content knowledge for teaching that mathematics teachers in Rwandan teacher training colleges possess. We adapted MKT measures and the PCK scale to reach the study aim. Teachers poorly performed the test (M = 41.77%), though they demonstrated a very high and positive attitude (>83%) toward PCK in teaching mathematics. It was found that teachers do not have the same knowledge in MKT constructs and mathematics areas. Thus, they performed better in CK and poorly in KCT. They showed a good knowledge of pattern function and algebra (PFA) and a low knowledge of rational numbers (RAT), though this low performance was attributed to the low number of items in the test. Since our sample was limited due to the number of available schools, further studies are needed to cover many teachers and compare TTC teachers with general secondary school or TVET teachers. It was good that TTC teachers have a positive PCK attitude; however, they need to enhance their level of mathematics content knowledge since their performance was low. Curriculum designers and pre-service teacher universities should look into the problem and gap in delivered mathematics content.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving human participants were reviewed and approved by the Research and Innovation Unit at URCE. Written informed consent to participate in this study was provided by the participants.
Author contributions
HH has conceived the study, designed the study, collected and analyzed the data, and wrote the manuscript. CN has supervised the student, conceived the study, and reviewed the manuscript. PN has supervised the student, designed the study, and edited the manuscript. All authors contributed to the article and approved the submitted version.
Funding
HH received financial support from the African Center of Excellence for Innovative Teaching and Learning Mathematics and Science (ACEITLMS).
Acknowledgments
All the teachers who participated in this study are acknowledged. The administration of teacher training colleges that allowed us to conduct the study is appreciated.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpsyt.2023.1257460/full#supplementary-material
References
Aksu, Z., Metin, M., and Konyalıoğlu, A. C. (2014). Development of the pedagogical content knowledge scale for pre-service teachers: the validity and reliability study. Mediterr. J. Soc. Sci. 5, 1365–1377. doi: 10.5901/mjss.2014.v5n20p1365
Ball, D. L., and Feiman-Nemser, S. (1988). Using textbooks and Teachers' guides: a dilemma for beginning teachers and teacher Educators1' 2′ 3. Curric. Inq. 18, 401–423. doi: 10.1080/03626784.1988.11076050
Ball, D. L., Thames, M. H., and Phelps, G. (2008). Content knowledge for teaching: what makes it special? J. Teach. Educ. 59, 389–407. doi: 10.1177/0022487108324554
Blazar, D., and Kraft, M. A. (2017). Teacher and teaching effects on Students' attitudes and behaviors. Educ. Eval. Policy Anal. 39, 146–170. doi: 10.3102/0162373716670260
Busaka, C., Umugiraneza, O., and Kitta, S. R. (2022). Mathematics teachers' conceptual understanding of soft skills in secondary schools in Zambia. Euras. J. Math. Sci. Technol. Educ. 18, em2128–em2139. doi: 10.29333/ejmste/12160
Chen, S. Y., and Huang, P. R. (2013). The comparisons of the influences of prior knowledge on two game-based learning systems. Comp. Educ. 68, 177–186. doi: 10.1016/j.compedu.2013.05.005
Dorimana, A., Uworwabayeho, A., and Nizeyimana, G. (2021). Examining mathematical problem-solving beliefs among Rwandan secondary school teachers. Int. J. Learn. Teach. Educ. Res. 20, 227–240. doi: 10.26803/ijlter.20.7.13
Fraenkel, J. R., Wallen, N. E., and Hyun, H. H. (2012). How to Design and Evaluate Research in Education. 8th Edn New York: McGraw Hill.
Hill, H. C., Ball, S., Ball, D. L., Schilling, S. G., Hill, H. C., Ball, S., et al. (2008). Unpacking pedagogical content knowledge: conceptualizing and measuring teachers' topic specific knowledge of students. J. Res. Math. Educ. 39, 372–400. doi: 10.5951/jresematheduc.39.4.0372
Hill, H. C., Schilling, S. G., and Ball, D. L. (2004). Developing measures of teachers' mathematics knowledge for teaching. Elem. Sch. J. 105, 11–30. doi: 10.1201/9780203498385.ch6
JICA (2020). The project for supporting institutionalizing and improving quality of SBI activity (SIIQS): Project completion report (Issue January). Available at: https://openjicareport.jica.go.jp/pdf/12327383.pdf
Kanamugire, C., Yadav, L. L., and Mbonyiryivuze, A. (2019). Tutors' perceptions about science curriculum reforms and challenges for their implementation in teacher training colleges in Rwanda. Afric. J. Educ. Stud. Math. Sci. 15, 101–116. doi: 10.4314/ajesms.v15i1.9
Kind, V. (2015). On the beauty of knowing then not knowing: pinning down the elusive qualities of PCK. Re-Exam. Pedagog. Content Knowled. Sci. Educ., 178–195.
Landau, S., and Everitt Chapman, B. S. (2004). A Handbook of Statistical Analyses using SPSS Library of Congress Cataloging-in-Publication Data Available at: https://www.academia.dk/BiologiskAntropologi/Epidemiologi/PDF/SPSS_Statistical_Analyses_using_SPSS.pdf
Maloney, E. A., Ramirez, G., Gunderson, E. A., Levine, S. C., and Beilock, S. L. (2015). Intergenerational effects of parents' math anxiety on children's math achievement and anxiety. Psychol. Sci. 26, 1480–1488. doi: 10.1177/0956797615592630
Moh’d, S. S., Uwamahoro, J., Joachim, N., and Orodho, J. A. (2021). Assessing the level of secondary mathematics Teachers' pedagogical content knowledge. Euras. J. Math. Sci. Technol. Educ. 17, em1970–em1911. doi: 10.29333/ejmste/10883
Mukuka, A., Mutarutinya, V., and Balimuttajjo, S. (2021). Mediating effect of self-efficacy on the relationship between instruction and students' mathematical reasoning. J. Math. Educ. 12, 73–92. doi: 10.22342/JME.12.1.12508.73-92
Ndihokubwayo, K., and Habiyaremye, H. T. (2018). Why did Rwanda shift from knowledge to competence based curriculum? Syllabuses and textbooks point of view. Afric. Res. Rev. Int. 12, 38–48. doi: 10.4314/afrrev.v12i3.4
Ndihokubwayo, K., Habiyaremye, H. T., and Rukundo, J. C. (2019a). Rwandan new Competence Base: curriculum implementation and issues; sector-based trainers. LWATI. J. Contemp. Res. 16, 24–41.
Ndihokubwayo, K., Mugabo, R. L., Byusa, E., and Habiyaremye, H. T. (2019b). Training strategies used in straightening competence-based curriculum in Rwanda. Educ. Policy Manag. Q. 11, 77–87. doi: 10.48127/spvk-epmq/19.11.77
Ndihokubwayo, K., and Murasira, G. (2019). Teacher’s training college learners’ expectations for their future teaching. LWATI. J. Contemp. Res. 16, 1–10.
Ndihokubwayo, K., Nyirigira, V., Murasira, G., and Munyensanga, P. (2020). Is competence-based curriculum well monitored? Learning from Rwandan sector education officers. Rwandan J. Educ. 5, 1–12.
Ndihokubwayo, K., Shimizu, K., Ikeda, H., and Baba, T. (2019c). An evaluation of the effect of the improvised experiments on student-teachers' conception of static electricity. LWATI. J. Contemp. Res. 16, 55–73.
Ndihokubwayo, K., Uwamahoro, J., and Ndayambaje, I. (2018). Use of improvised experiment materials to improve teacher training college students' achievements in physics, Rwanda. Afric. J. Educ. Stud. Math. Sci. 14, 63–77.
Nsengimana, T., Rugema Mugabo, L., Hiroaki, O., and Nkundabakura, P. (2020). Reflection on science competence-based curriculum implementation in sub-Saharan African countries. Int. J. Sci. Educ. Part B 1–14. doi: 10.1080/21548455.2020.1778210 (Epub ahead of print).
REB (2015). Comptence-based curriculum. Curriculum framework pre-primary to upper secondary. Available at: http://reb.rw/fileadmin/competence_based_curriculum/syllabi/curriculum_framework_final_printed.compressed.pdf
REB (2020). Competence-Based Curriculum Summary of Curriculum Framework for Teacher Training Colleges. Rwanda Basic Education Board.
Shulman, L. (1986). Those who understand: knowledge growth in teaching. Am. Educ. Res. Assoc. 15, 4–14.
Shulman, L. (1987). “Knowledge and teaching: foundations of the new reform” in Harvard Educational Review, vol. 57, 1–23. Available at: https://people.ucsc.edu/~ktellez/shulman.pdf
Skott, J., van Zoest, L., and Gellert, U. (2013). Theoretical frameworks in research on and with mathematics teachers. ZDM Int. J Math. Educ. 45, 501–505. doi: 10.1007/s11858-013-0509-3
Uworwabayeho, A., Flink, I., Nyirahabimana, A., Peeraer, J., Muhire, I., and Gasozi, A. N. (2020). Developing the capacity of education local leaders for sustaining professional learning communities in Rwanda. Soc. Sci. Hum. Open 2:100092. doi: 10.1016/j.ssaho.2020.100092
Keywords: competence-based curriculum, knowledge for teaching, MKT measures, PCK scale, Rwandan mathematics teachers, teacher training college
Citation: Habiyaremye HT, Ntivuguruzwa C and Ntawiha P (2023) Rwandan teacher training college’s mathematics teachers’ pedagogical content knowledge for teaching: assessment toward competency-based curriculum. Front. Educ. 8:1214396. doi: 10.3389/feduc.2023.1214396
Edited by:
Maxwell Peprah Opoku, United Arab Emirates University, United Arab EmiratesReviewed by:
Hariharan N. Krishnasamy, Universiti Utara Malaysia, MalaysiaShakila Nur, North South University, Bangladesh
Copyright © 2023 Habiyaremye, Ntivuguruzwa and Ntawiha. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hashituky Telesphore Habiyaremye, aGh0ZWxlc3Bob3JlQGdtYWlsLmNvbQ==
 Hashituky Telesphore Habiyaremye
Hashituky Telesphore Habiyaremye Celestin Ntivuguruzwa2
Celestin Ntivuguruzwa2