How to improve university-enterprise cooperation: application of intuitionistic fuzzy multi-attribute decision-making method based on decision-maker preferences in university-enterprise cooperation satisfaction evaluation

Introduction: University-enterprise cooperation (UEC) is critical for bridging the gap between higher education and industry, enhancing student employability and professional readiness. However, assessing the quality of such cooperation from the student perspective remains a challenge due to subjective uncertainty and varying attribute importance.

Methods: This study, conducted at universities of applied sciences in China, developed an intuitionistic fuzzy multi-attribute decision-making (IFMADM) model to evaluate student satisfaction with UEC. The model integrates intuitionistic fuzzy sets and intuitive fuzzy entropy to handle ambiguity in student responses and to determine the relative importance of cooperation attributes.

Results: Based on survey data from 290 postgraduate students, the analysis revealed that satisfaction with guidance from university and enterprise mentors during enterprise practice significantly impacts overall student satisfaction. Among the evaluated attributes, university tutor guidance received the highest weight.

Discussion: The findings highlight the central role of mentorship in shaping student experiences in UEC. Enhancing guidance mechanisms—particularly from university tutors—can effectively improve the quality and effectiveness of cooperation. The proposed model offers a robust evaluation framework and practical insights for optimizing student-centered UEC practices.

1 Introduction

With the rise of the knowledge-based economy, the critical importance of knowledge and technology has become increasingly evident. In pursuit of individual and collective growth, universities and enterprises have actively pursued collaborations that leverage their complementary strengths (Mahfoudh et al., 2019). This dynamic partnership, commonly referred to as University-Enterprise Cooperation (UEC), extends beyond simple resource sharing and reflects a strategic alliance founded on mutual trust, with the goal of fostering innovation, producing mutual benefits, and promoting a win-win outcome (Ranga et al., 2013; Shapira and Rosenfeld, 2011).

UEC has become a transformative force, driving the co-development of universities and enterprises. For industry, such collaboration enhances innovation capacity and production efficiency, offering a competitive edge in volatile markets (Davey et al., 2014). For universities, UEC improves operational effectiveness and strengthens education quality by aligning academic offerings with real-world demands (Mascarenhas et al., 2018; Smith et al., 2018). As UEC matures, it is increasingly viewed as a defining trend in higher education and a key instrument in promoting sustainable development, innovation, and talent cultivation (Arranz et al., 2022).

This growing importance is reflected in substantial investments by higher education institutions (HEIs) and governments worldwide (Davey et al., 2014; Arranz et al., 2022). As academia-industry partnerships expand, the need for accountability and evidence-based evaluation intensifies. UEC's impact now extends beyond research and education into broader socio-economic domains, necessitating more systematic tools to assess its outcomes, particularly from the perspective of students—its most direct beneficiaries (Clauss and Kesting, 2017; Rybnicek and Königsgruber, 2019).

The objective of this study is to evaluate UEC satisfaction through a novel, student-centered lens. While previous research has addressed institutional performance, innovation output, and employer perspectives (Galan-Muros and Davey, 2019; Quintana et al., 2016; Ripoll Feliu and Diaz Rodriguez, 2017), few studies have focused on how students perceive and evaluate the effectiveness of UEC. This gap is critical, as students' experiential satisfaction directly informs the quality and sustainability of UEC models.

To address this, the study proposes an Intuitionistic Fuzzy Multi-Attribute Decision-Making (IFMADM) model that integrates Intuitionistic Fuzzy Sets (IFS), fuzzy entropy, and decision-maker preferences. This model is particularly suited to handling the uncertainty, subjectivity, and linguistic imprecision inherent in educational evaluations. In addition, we introduce a risk preference factor to account for the evaluator's behavioral tendencies—offering a more adaptive and personalized decision framework rarely considered in conventional models.

UEC is a multifaceted construct encompassing research collaboration, technology transfer, joint teaching, and workforce development. Its evaluation thus requires holistic consideration not only of quantitative indicators but also of qualitative dimensions, such as student satisfaction and perceived learning outcomes. Drawing on Ralph Tyler's foundational evaluation theory (Tyler, 2014) and standards from the Joint Committee on Standards for Educational Evaluation (JCSEE) (2011), this study aims to align the evaluation process with the ultimate educational goal—student-centered transformation.

Prior work by Galan-Muros and Davey (2019) and Smith et al. (2018) provide important institutional and enterprise perspectives on UEC, while Gebbels et al. (2011) and Kliewe et al. (2016) begin to recognize student engagement and outcomes. Yet, these insights lack the quantitative rigor and decision-modeling sophistication needed for actionable guidance.

This paper contributes to bridging that gap by offering an analytical model to measure and prioritize student-perceived attributes of UEC. Using linguistic data from student surveys in Chinese universities of applied sciences, the model transforms qualitative evaluations into structured decision matrices through IFS and fuzzy entropy, producing weighted scores for each indicator. This approach not only enhances interpretability but also offers practical direction for improving UEC implementation.

The rest of the paper is structured as follows: Section 2 reviews the literature on UEC and multi-criteria decision-making (MCDM) methods. Section 3 introduces the proposed IFMADM model. Section 4 applies this model to a real-world case study. Section 5 discusses key findings and implications. Section 6 concludes with reflections and future research directions.

2 Literature review and related works

Recent studies have made significant strides in the evaluation of UEC, utilizing various methodologies to assess and enhance the effectiveness of these collaborations. For instance, Zhou (2024) constructed an evaluation model of UEC innovation ability based on Big Data analysis, employing the CRITIC analysis method to calculate system weights. By integrating the gray correlation analysis method with the ideal sorting TOPSIS method, Zhou established the GRA-TOPSIS evaluation model, offering a comprehensive assessment of talent cultivation within the integration of higher education and industry.

Similarly, Xu (2022) developed an evaluation framework for UEC-based talent development using the CIPP model, which includes background, input, process, and output dimensions. This holistic approach supervises and controls the talent training process, ultimately aiming to improve graduate quality.

In another study, Zhou et al. (2023) proposed a model for selecting suitable enterprise partners for UEC. Using decision trees and the Analytic Hierarchy Process (AHP) to calculate weight values, the final selection was made through a fuzzy comprehensive evaluation method. This approach has proven effective in enhancing the rationality of enterprise partner choices.

The use of fuzzy logic in higher education evaluation has also gained attention. Li et al. (2024) proposed a multi-feature fuzzy evaluation model based on artificial intelligence, incorporating perspectives from instructors, students, and administrators. The model employs an enhanced cuckoo search optimization algorithm to improve instructional effectiveness. Huo et al. (2024) introduced an IVIF-TODIM-MABAC model for assessing university teaching quality using entropy-based interval-valued intuitionistic fuzzy sets (IVIFS), which demonstrates the model's applicability to uncertain data environments.

In light of these advancements, it is evident that UEC plays a pivotal role in advancing the objectives of corporations, universities, and societies. However, despite the growing body of research, there remains a scarcity of studies explicitly focusing on students' satisfaction within the context of UEC, an aspect that is crucial given their integral role as active participants and primary beneficiaries. Recognizing this gap, the current study adopts the framework of Intuitionistic Fuzzy Set (IFS) theory, which was initially proposed by Atanassov and Stoeva (1986). The IFS model allows decision-makers to consider both membership and non-membership perspectives, making it particularly effective in situations characterized by inaccuracy, uncertainty, vagueness, and incompleteness (Zeng et al., 2020; Zhao et al., 2021).

Moreover, recent developments in Multi-Criteria Decision Making (MCDM) methodologies have provided diverse tools to address complex decision-making problems in education and beyond. El-Araby et al. (2022) emphasized the importance of systematic weight allocation using entropy-based approaches. Rasheed et al. (2021) applied intuitionistic fuzzy numbers to investment benefit evaluation, highlighting the need to reduce hesitancy in decision environments.

Several recent studies demonstrate the versatility and cross-domain applicability of MCDM approaches. Obaidat and Mumani (2025) proposed a multiple objective decision analysis model for selecting capacity expansion plans in manufacturing, offering a transparent evaluation process under conflicting objectives. Baydaş et al. (2024) applied a CODAS-based fuzzy MCDM method to evaluate national economic performance, combining normalization and uncertainty handling for robust policy insights. Nguyen and Data-Driven (2025) developed a data-driven MCDM model using spherical fuzzy sets to assess augmented reality providers in education, highlighting the model's adaptability for supplier evaluation under uncertainty. Magableh et al. (2024) introduced a fuzzy-FMEA gray correlation method for prioritizing supply chain nervousness factors, supporting proactive risk management. Wang and Pan (2025) proposed an innovative framework combining Circular Intuitionistic Fuzzy Sets (C-IFS) and Dombi operators to assess teaching quality in cultural heritage education, demonstrating MCDM's capacity for handling vague and subjective educational data.

Further demonstrating the utility of fuzzy logic in complex evaluation settings, Kusterka-Jefmańska et al. (2022) used the Intuitionistic Fuzzy Synthetic Measure (IFSM) to assess quality-of-life indicators in European cities. Faizi et al. (2020) introduced an MCGDM approach combining IFS with the Characteristic Object Method (COMET), improving the robustness of group-based decision-making under uncertainty.

While these studies offer valuable insights into UEC evaluation and the broader use of fuzzy and MCDM techniques, most existing work focuses on institutional, administrative, or organizational dimensions (Mukhametzyanov, 2021). Few studies explicitly incorporate the perspective of students—the direct beneficiaries of UEC—as a core evaluation subject. This gap is particularly significant, as student satisfaction directly influences the perceived success and sustainable development of UEC models.

To address this gap, the present study introduces a novel Intuitionistic Fuzzy Multi-Attribute Decision-Making (IFMADM) model, with three major contributions: (1) It incorporates student satisfaction as the core evaluation target in UEC, offering a learner-centered perspective often overlooked in prior research; (2) It integrates intuitionistic fuzzy sets and entropy weighting to accommodate uncertainty and subjectivity in student responses; (3) It further considers risk preference factors in weight interpretation, advancing the current methodological discourse on MCDM under uncertainty. By incorporating student-driven indicators and addressing ambiguity in multi-attribute evaluation, this study complements and extends the existing body of UEC and MCDM literature with both conceptual and practical contributions.

3 Preliminaries

Some basic concepts of intuitionistic fuzzy are introduced in this section, mainly including intuitionistic fuzzy sets and related theories, operation rules of intuitionistic fuzzy sets and intuitionistic fuzzy numbers and intuitionistic fuzzy entropy.

3.1 Intuitionistic fuzzy sets and related theories

Definition 1 (Atanassov and Stoeva, 1986): Let universal set X be a non-empty set, then IFS A on X can be expressed as

$\begin{array}{l}\text{A}=\left\{<\text{x},{\mu }_A(\text{x}),{\nu }_A(\text{x})>|\text{x}\in \text{X}\right\}\end{array}$

where μ_A(x) defines the degree of the membership and ν_A(x) defines the degree of the non-membership of the element x in universal set X, which is

$\begin{array}{r}{\mu }_A:X\to \left[0,1\right],\text{x}\in \text{X}\to {\mu }_A\in \left[0,1\right]\\ {\nu }_A:X\to \left[0,1\right],\text{x}\in \text{X}\to {\nu }_A\in \left[0,1\right]\end{array}$

At the same time, they should be satisfied

$\begin{array}{l}0\le {\mu }_A+{\nu }_A\le 1\end{array}$

Therefore,

$\begin{array}{l}{\pi }_A=1-{\mu }_A-{\nu }_A\end{array}$

is the degree of hesitation or uncertainty that element x in universal set X belongs to intuitionistic fuzzy set A. Obviously, for any x∈ X, there is 0 ≤ π_A ≤ 1.

3.2 Operation rules of intuitionistic fuzzy sets and intuitionistic fuzzy numbers

The operational principles governing intuitionistic fuzzy sets and intuitionistic fuzzy numbers are delineated as follows.

Definition 2 (Atanassov and Stoeva, 1986): Let universal set X be a non-empty set, A = { < x, μ_A(x), ν_A(x)>|x∈X} and B = { < x, μ_B(x), ν_B(x)>|x∈X} are two intuitionistic fuzzy sets on X, then there are

$\begin{array}{l}\overline{\text{A}}=|<\text{x},{\nu }_A(x),{\mu }_A(x)>|\text{x}\in \text{X}|;\\ A\cap B=\left\{<\text{x},\min ({\mu }_A(x),{\mu }_B(x)),\max ({\nu }_A(x),{\nu }_B(x))>|\text{x}\in \text{X}\right\}\\ A\cap B=\left\{<\text{x},\max ({\mu }_A(x),{\mu }_B(x)),\min ({\nu }_A(x),{\nu }_B(x))>|\text{x}\in \text{X}\right\}\\ A+B=\left\{<\text{x},{\mu }_A\left(\text{x}\right)+{\mu }_B\left(\text{x}\right),{\nu }_A(x)+{\nu }_B(x)>|\text{x}\in \text{X}\right\}\\ A•B=\{<\text{x},{\mu }_A\left(\text{x}\right){\mu }_B\left(\text{x}\right),{\nu }_A(x)+{\nu }_B(x)-{\nu }_A(x){\nu }_B(x)\\ >|\text{x}\in \text{X}\}\\ \lambda A=\left\{<\text{x},1-{(1-{\mu }_A\left(x\right))}^{\lambda },{({\nu }_A(x))}^{\lambda }>|\text{x}\in \text{X}\right\}\\ A^{\lambda }=\left\{<\text{x},{({\mu }_A(x))}^{\lambda },1-{(1-{\nu }_A(x))}^{\lambda }>|\text{x}\in \text{X}\right\}\end{array}$

where λ is a positive integer.

Definition 3 (Atanassov, 1994): If α = < μ_α(x), ν_α(x)> and β = < μ_β(x), ν_β(x)> are two intuitionistic fuzzy numbers, then there are

$\begin{array}{ll}\overline{\alpha }\hfill & =({\nu }_{\alpha },{\mu }_{\alpha })\hfill \\ \alpha \wedge \beta \hfill & =(min({\mu }_{\alpha },{\mu }_{\beta }),\max ({\nu }_{\alpha },{\nu }_{\beta }))\hfill \\ \alpha \vee \beta \hfill & =(max({\mu }_{\alpha },{\mu }_{\beta }),\min ({\nu }_{\alpha },{\nu }_{\beta }))\hfill \\ \alpha \oplus \beta \hfill & =({\mu }_{\alpha }+{\mu }_{\beta }-{\mu }_{\alpha }{\mu }_{\beta },{\nu }_{\alpha }{\nu }_{\beta })\hfill \\ \alpha \otimes \beta \hfill & =({\mu }_{\alpha }{\mu }_{\beta },{\nu }_{\alpha }+{\nu }_{\beta }-{\nu }_{\alpha }{\nu }_{\beta })\hfill \\ \tau \alpha \hfill & =(1-{(1-{\mu }_{\alpha })}^{\tau },{\nu }_{\alpha }^{\tau }),\tau >0\hfill \\ \alpha \tau \hfill & =({\mu }_{\alpha }^{\tau },1-{(1-{\nu }_{\alpha })}^{\tau }),\tau >0\hfill \\ \lambda A\hfill & =\{<x,1-{(1-{\mu }_A(x))}^{\lambda },{({\nu }_A(x))}^{\lambda }>|x\in X\}\hfill \\ A^{\lambda }\hfill & =\{<x,{({\mu }_A(x))}^{\lambda },1-{(1-{\nu }_A(x))}^{\lambda }>|x\in X\}\hfill \end{array}$

The results calculated by applying the operation rules in definition 2 and definition 3 are still intuitionistic fuzzy sets and intuitionistic fuzzy numbers.

Definition 4: With the further study of the theory of intuitionistic fuzzy sets, it is not enough to calculate intuitionistic fuzzy sets and intuitionistic fuzzy numbers by simply relying on the operation rules. Some practical IFS aggregation operators have been developed.

Suppose α_j = (μ_αj, ν_αj)(j = 1, 2, ...n) is a group of intuitionistic fuzzy numbers, and let $\omega \mathrm{\text{=(}}{\omega }_1,{\omega }_2,...,{\omega }_j{\mathrm{\text{)}}}^{\mathrm{\text{T}}}$ be the weight vector of α_j, ω_j∈[0, 1](j = 1, 2, ...n), $\sum _{j=1}^n{\omega }_j=1$, the IFWA operator is as follow (Xu, 2007).

$\begin{array}{ll}IFW{A}_{\omega }({\alpha }_1,{\alpha }_2...{\alpha }_n)=(1-{\displaystyle \prod _{j=1}^n}{(1-{\mu }_{{\sigma }_j})}^{{\omega }_j},{\displaystyle \prod _{j=1}^n}{{\nu }_{{\sigma }_j}}^{{\omega }_j})& (1)\end{array}$

The results obtained by using intuitionistic fuzzy set operators are still intuitionistic fuzzy sets and intuitionistic fuzzy numbers.

3.3 Intuitionistic fuzzy entropy

The exploration of intuitionistic fuzzy entropy has since garnered considerable scholarly attention, with notable contributions emerging in the field. Representative works include the development of a novel intuitionistic fuzzy entropy, crafted through a geometric interpretation of intuitionistic fuzzy sets. This entropy model has found application in the realm of multi-attribute decision-making, showcasing its versatility and relevance in addressing complex decision-making scenarios (Burillo and Bustince, 1996).

Definition 5: Let universal set X = |x₁, x₂, ...x_n|, A = | < x, μ_A(x), ν_A(x)>|x∈X) is a non-empty set, then the expression of intuitionistic fuzzy entropy of A (Kusterka-Jefmańska et al., 2022) is as follows.

$\begin{array}{ll}\text{E(A)}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\frac{\text{1-max(}{\mu }_{\text{A}}\text{(}{\text{x}}_i\text{),(}{\nu }_{\text{A}}\text{(}{\text{x}}_i\text{))}}{\text{1-min(}{\mu }_{\text{A}}\text{(}{\text{x}}_i\text{),(}{\nu }_{\text{A}}\text{(}{\text{x}}_i\text{))}}& (2)\end{array}$

Definition 6 (Burillo and Bustince, 1996): Let universal set X = |x₁, x₂, ...x_n|, A = | < x, μ_A(x), ν_A(x)>|x∈X) and B = | < x, μ_B(x), ν_B(x)>|x∈X) are two intuitionistic fuzzy sets on X, then the intuitionistic fuzzy entropy of A and B, which is expressed by E (A) and E (B), respectively, satisfies the following properties.

$\begin{array}{l}E(A)=0\iff A\text{ is a non}-\text{fuzzy set}\\ E(A)=1\iff {\mu }_A(x)={\nu }_A(x)\\ \text{\hspace{1em}\hspace{1em}\hspace{1em}If A is more fuzzy than B},\text{ then }E(A)\ge E(B);\\ E(A)=E(\overline{A}).\end{array}$

4 The proposed approach

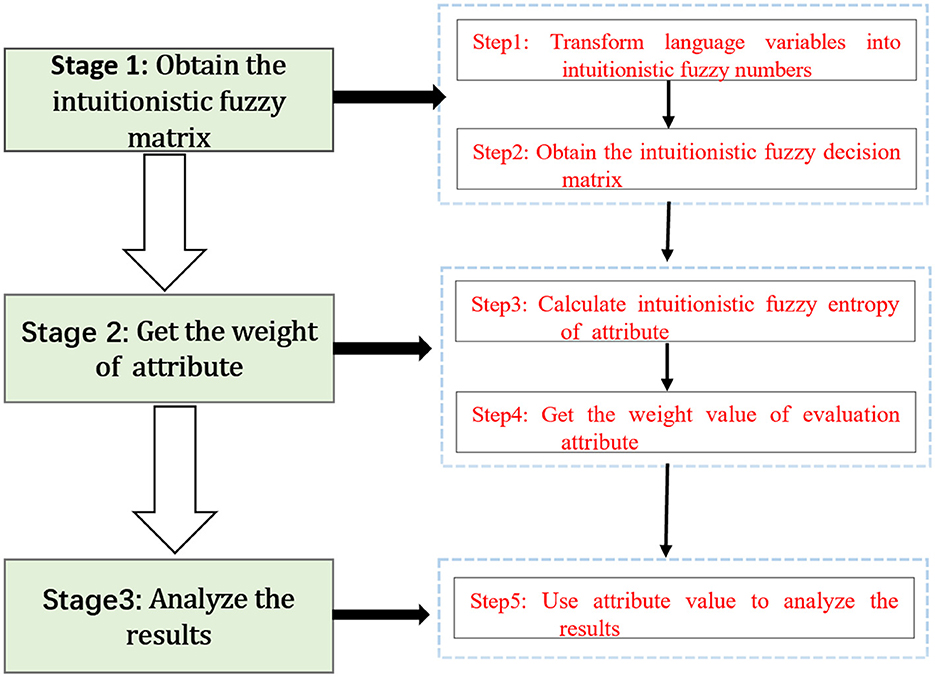
In this part, an intuitionistic fuzzy multi-attribute decision-making method based on decision-maker preferences is used to analyze UEC satisfaction evaluation. The model can be divided into three stages: (1) Language variables are used to access UEC satisfaction evaluation. The linguistic assessment information in fuzzy form underwent a transformation into intuitionistic fuzzy numbers based on language variables. Then we obtained the intuitionistic fuzzy decision matrix; (2) Calculating intuitionistic fuzzy entropy was adopted to get the weights of UEC satisfaction evaluation attribute; (3) Attribute value was used to analyze the results. The flow chart of the model is shown in Figure 1.

Figure 1

Figure 1. The flow chart of the model.

Next, it introduces the process of analyzing UEC satisfaction evaluation in detail.

Stage 1: Obtain the intuitionistic fuzzy matrix

Assume that H = {H₁, H₂, …, H_n} is a group of UEC satisfaction evaluation attribute, surveyed by questionnaire with the language variables. Suppose S = {s₀, s₁, …, s_g} is the linguistic term set, and the questionnaire's linguistic evaluation is given by

$\begin{array}{l}H=\left[\begin{array}{c}\begin{array}{cc}{h}_{11}& h_{12}\\ h_{21}& h_{22}\\ \end{array}\\ \begin{array}{cc}⋮& ⋮\\ h_{k1}& h_{11}\\ \end{array}\\ \end{array}\begin{array}{c}\begin{array}{cc}\cdots & h_{1n}\\ \cdots & h_{2n}\\ \end{array}\\ \begin{array}{cc}\cdots & ⋮\\ \cdots & h_{kn}\\ \end{array}\\ \end{array}\right].\end{array}$

where h_ij is the linguistic expression provided by Kth questionnaire.

Step 1: Transform language variables into intuitionistic fuzzy numbers

In order to standardize the judgment of the questionnaire's linguistic evaluation, all questionnaire's linguistic evaluation is transformed into intuitionistic fuzzy numbers. Then, the intuitionistic fuzzy numbers < μ_α(x), ν_α(x)!π_α(x)> is obtained. Therefore, all the linguistic assessment information given by the questionnaire can be expressed by the intuitionistic fuzzy numbers.

Step 2: Obtain the intuitionistic fuzzy decision matrix

The intuitionistic fuzzy weighted average operator (IFWA) is used to aggregate the intuitionistic fuzzy numbers in the questionnaire, and the comprehensive intuitionistic fuzzy decision matrix of evaluation attributes is obtained.

Stage 2: Get the weight of attribute

Step 3: Calculate intuitionistic fuzzy entropy of attribute

The comprehensive intuitionistic fuzzy decision matrix of evaluation attributes is used combing the intuitionistic fuzzy entropy weight method, using the formula (2). Thus, the intuitionistic fuzzy entropy for the attribute is computed.

Step 4: Get the weight value of evaluation attribute

Due to different domain knowledge and expertise, the weight value of is different. The intuitionistic fuzzy entropy of attribute and the formula is as follows:

$\begin{array}{ll}{\omega }_j=\frac{1-E(C_j)}{{\displaystyle \sum _{q=1}^n}(1-E(C_q))},(j=1,2,3...n)& (3)\end{array}$

It is used to get the weight value of evaluation attribute.

Stage 3: Analyze the results

Step 5: Use attribute value to analyze the results

The weight value of evaluation attribute indicates the intensity of influences received. It represents the influence of the ith attribute on the whole system. Therefore, the larger the weight value, the greater the overall prominence.

5 Illustrative examples

In this section, the viability and efficacy of the proposed model are demonstrated through the conduct of a satisfaction survey within the UEC context.

5.1 Survey and sampling technique

This study enlisted a sample of 290 postgraduate students from diverse universities of applied sciences in China to partake in a survey conducted through a structured questionnaire. The utilization of such research samples aligns with established practices in UEC studies (Davey et al., 2014). Access to the survey was facilitated through a dedicated website made available to postgraduate students affiliated with the universities of applied sciences in China, who willingly consented to participate in the study. The website's primary purpose was to administer a questionnaire, focusing on discerning the factors influencing postgraduate student satisfaction in the context of UEC.

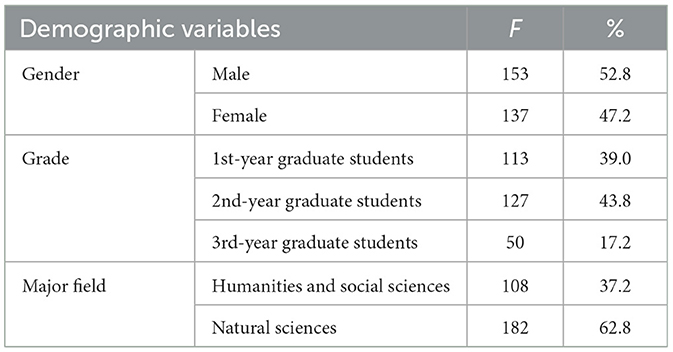
As a crucial component of ethical research practices, all participants received comprehensive information about the study's objectives and the nature of the questionnaire. This pre-emptive disclosure afforded participants the autonomy to either consent or decline to respond to the questionnaire (N = 290), both during and within a 15-min timeframe post-completion. Demographic information of the respondents is detailed in Table 1.

Table 1

Table 1. Demographic information of respondents.

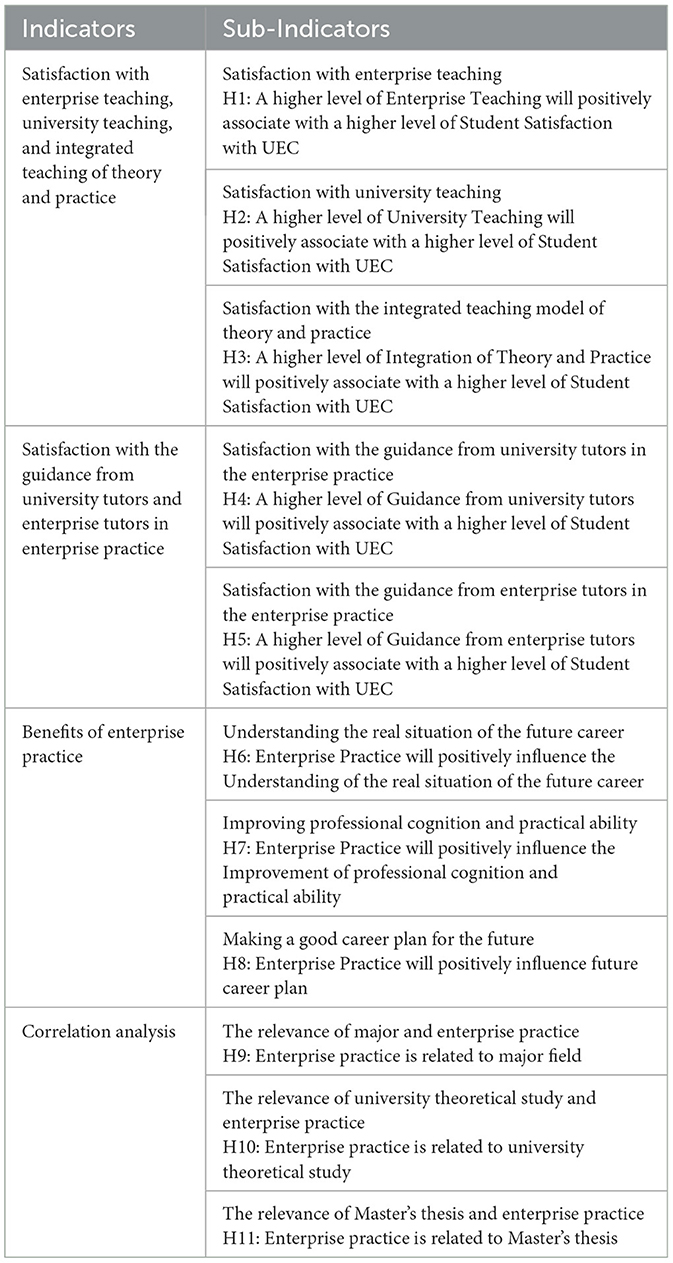
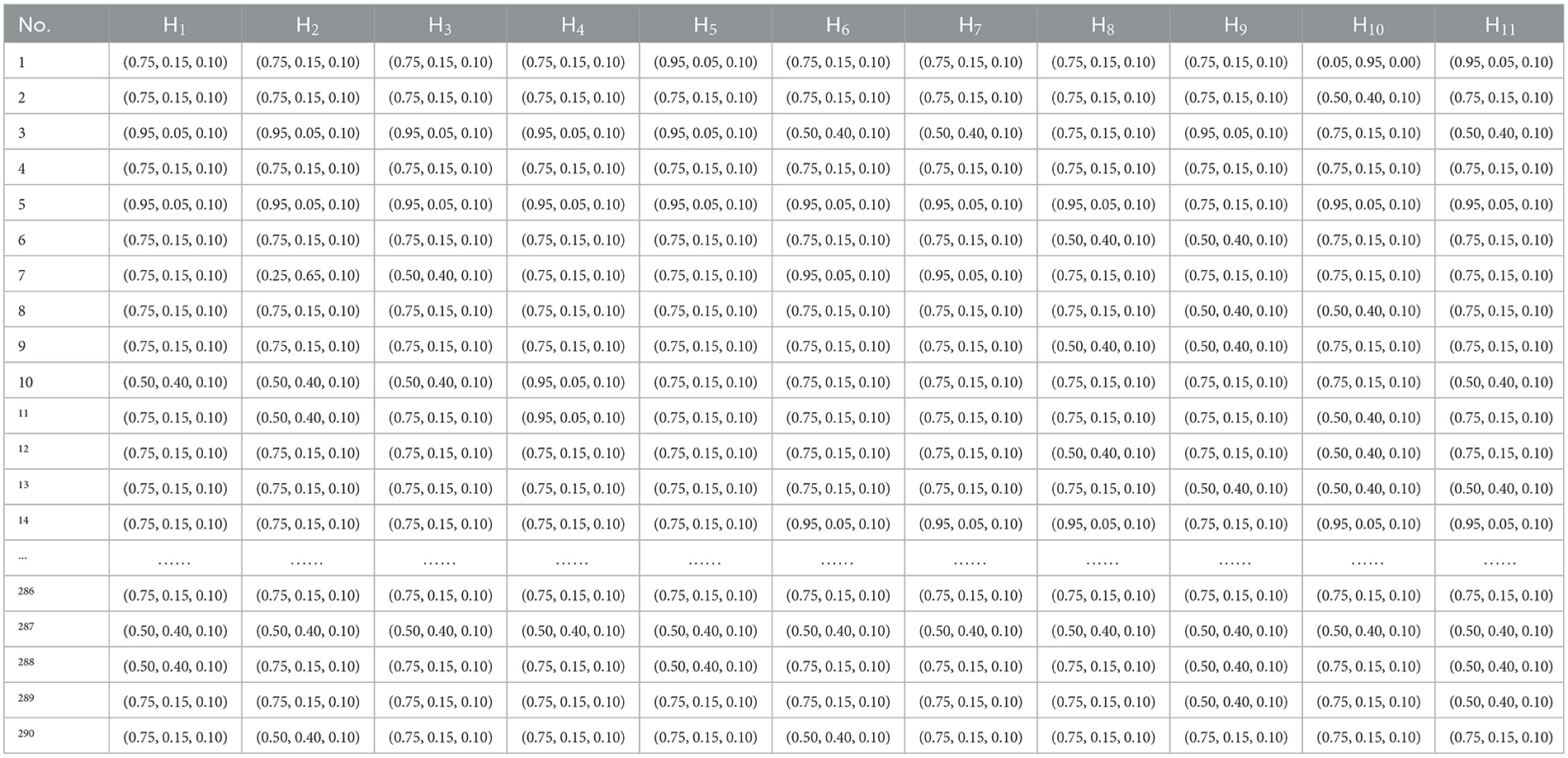
Eleven performance sub-indicators denoted as {H₁, H₂, …, H₁₁} which were used in previous studies were identified to have a significant influence on the satisfaction of UEC. Based on these indicators, we interviewed postgraduates, and made an evaluation of the indicators, which are shown in Table 2.

Table 2

Table 2. Indicators used in the case study.

To ascertain 11 performance sub-indicators, this research engaged a cohort of 290 postgraduates representing diverse academic departments, who participated in surveys administered through a structured questionnaire. The assessment data from these 290 graduate students underwent analysis employing specific methodologies. The evaluation involved the utilization of an established set of language terminology to assess the indicators and determine their reliability across the identified 11 performance indicators.

$S=\left\{\begin{array}{l}{s}_1=\text{very dissatisfied, }{s}_2=\text{dissatisfied, }{s}_3=\text{medium,}\hfill \\ s_4=\text{satisfied, }{s}_5=\text{very satisfied}\hfill \end{array}\right\}$

We got 290 graduate students' linguistic assessments about the direct each performance indicators through the questionnaire survey.

Based on the data of satisfaction survey, the intuitionistic fuzzy multi-attribute decision-making model based on the perspective of decision-making preference proposed in the paper is used for decision-making and evaluation. Since the data obtained is linguistic, it needs to be converted into intuitionistic fuzzy numbers first. In addition, the IFWA operator is used to aggregate the data to obtain a comprehensive intuitionistic fuzzy decision matrix for scheme evaluation and 11 evaluation attributes. The result of aggregation, as the decision maker's deterministic preference value, is suitable for the intuitionistic fuzzy multi-attribute decision-making model based on the decision maker's deterministic preference.

5.2 Intuitionistic fuzzy processing of survey data

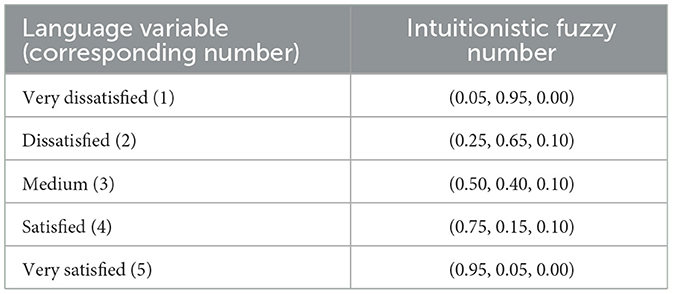
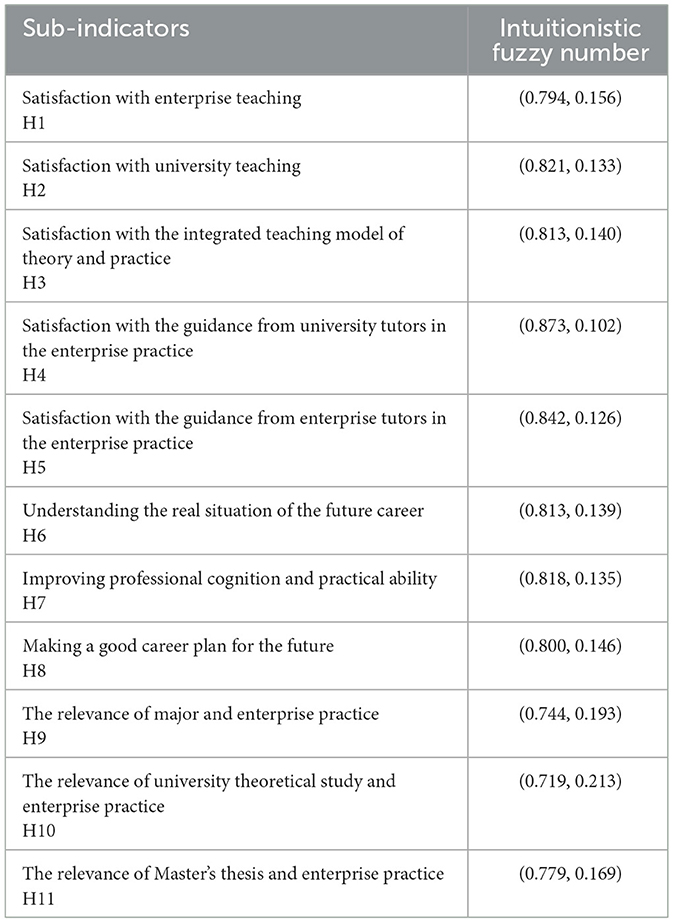
In this paper, the original data obtained through the questionnaire are linguistic variables. In order to better express the uncertainty of the decision results, the linguistic number is converted into an intuitionistic fuzzy number. With reference to the nine-level classification method in the literature, the satisfaction of the results is divided into five levels, which correspond to the intuitionistic fuzzy number in the Table 3.

Table 3

Table 3. Correspondence between language variables and intuitionistic fuzzy numbers.

Then IFWA operator is used to aggregate the intuitionistic fuzzy original data in the questionnaire, as shown in Table 4. The comprehensive intuitionistic fuzzy decision-making matrix of 11 evaluation attributes is obtained, which is shown in Table 5.

Table 4

Table 4. Primitive intuitionistic fuzzy number.

Table 5

Table 5. The comprehensive intuitionistic fuzzy decision-making matrix of 11 evaluation attributes.

The comprehensive decision matrix provided by the Table 5 is used combing the intuitionistic fuzzy entropy weight method, which is the Equation 2.

Then the intuitionistic fuzzy entropy of each attribute is calculated.

$\begin{array}{l}E(H1)=0.2447,E(H2)=0.2059,E(H3)=0.2179,\\ E(H4)=0.1414,E(H5)=0.1810,E(H6)=0.2171,\\ E(H7)=0.2107,E(H8)=0.2340,E(H9)=0.3169,\\ E(H10)=0.3575,E(H11)=0.2664\end{array}$

The intuitionistic fuzzy entropy and the Equation 4 is used.

Therefore, the weight values of each attribute are determined, and the results are as follows.

$\begin{array}{l}\omega (H1)=0.0898,\omega (H2)=0.0945,\omega (H3)=0.0930,\\ \omega (H4)=0.1021,\omega (H5)=0.0974,\omega (H6)=0.0931,\\ \omega (H7)=0.0939,\omega (H8)=0.0911,\omega (H9)=0.0813,\\ \omega (H10)=0.0764,\omega (H11)=0.0873\end{array}$

Then, the intuitionistic fuzzy weighted (IFWA_ω) operator $IFW{A}_{\omega }({\alpha }_1,{\alpha }_2...{\alpha }_n)=(1-\prod _{j=1}^n{(1-{\mu }_{{\sigma }_j})}^{{\omega }_j},\prod _{j=1}^n{{\nu }_{{\sigma }_j}}^{{\omega }_j})$ is used to aggregate the comprehensive evaluation values of the comprehensive intuitionistic fuzzy decision matrix of 11 evaluation attributes, and the aggregated comprehensive value is obtained:

$\begin{array}{l}{\mu }_{\alpha }=1-{(1-0.794)}^{0.0898}{(1-0.821)}^{0.0945}{(1-0.813)}^{0.0930}\\ {(1-0.873)}^{0.1021}{(1-0.842)}^{0.0974}{(1-0.813)}^{0.0931}\\ {(1-0.818)}^{0.0939}{(1-0.800)}^{0.0911}{(1-0.744)}^{0.0813}\\ {(1-0.719)}^{0.0764}{(1-0.779)}^{0.0873}=0.809\\ {\nu }_{\alpha }={(0.156)}^{0.0898}{(0.133)}^{0.0945}{(0.140)}^{0.0930}{(0.102)}^{0.1021}\\ {(0.126)}^{0.0974}{(0.139)}^{0.0931}{(0.135)}^{0.0939}{(0.146)}^{0.0911}\\ {(0.193)}^{0.0813}{(0.213)}^{0.0764}{(0.169)}^{0.0873}=0.145\end{array}$

Next, introduce risk preference factor η, using based on risk preference the intuitionistic fuzzy scoring function

$\begin{array}{ll}{s}^{\eta }(\alpha )=\frac{{\mu }_{\alpha }-{\nu }_{\alpha }}{1-\eta {\pi }_{\alpha }}& (4)\end{array}$

The comprehensive evaluation value is calculated. The result is:

When η = 1, it is assumed that it is a risk chaser, and the calculation result is s^η = 0.696;

When η = 0, it is assumed that it is a risk neutral, and the calculation result is s^η = 0.664;

When η = −1, it is assumed that it is a risk averse person, and the calculation result is s^η = 0.635.

6 Discussion

6.1 Results

UEC is a crucial mechanism for advancing the strategic goals of corporations, universities, and societies. The evaluation and enhancement of UEC are essential for maximizing its impact. This study introduces a novel approach—an Intuitionistic Fuzzy Multi-Attribute Decision-Making (IFMADM) method grounded in decision-maker preferences—to assess UEC. The methodology combines Intuitionistic Fuzzy Sets (IFS) with intuitive fuzzy entropy, establishing an advanced framework for the comprehensive evaluation and enhancement of UEC dynamics.

This research builds on an assessment of students' satisfaction with UEC, proposing an effective intuitionistic fuzzy entropy model to navigate the complexities of UEC evaluation. The model is designed to address uncertainty inherent in the decision-making process through a two-phase approach. In the initial phase, IFS are employed to capture the fuzzy characteristics of decision information, as detailed in the preceding analysis. The subsequent phase incorporates a risk preference factor, categorizing decision evaluation subjects into three distinct types. This innovation addresses a significant gap in traditional evaluations, where the decision-maker's risk attitude is often insufficiently considered.

Within this method, the evaluation values of attributes are analyzed, and the weight values of each attribute are determined. Notably, the sub-indicator “Satisfaction with the guidance from university tutors during enterprise practice (H4)”—where higher levels of guidance are associated with greater student satisfaction with UEC—emerges as the most critical factor (weight value >0.1). This finding underscores H4 as the most influential sub-indicator within the system, with no other sub-indicator surpassing a weight value of 0.1. Additionally, the results indicate that the sub-indicator “Satisfaction with the guidance from enterprise tutors during enterprise practice (H5)” holds the second-highest weight. Both H4 and H5 fall under the broader indicator of “Satisfaction with the guidance from university tutors and enterprise tutors during enterprise practice,” highlighting the significant impact this indicator has on the overall system. Enhancements in these areas are likely to drive improvements across the entire UEC framework.

6.2 Sensitivity analysis

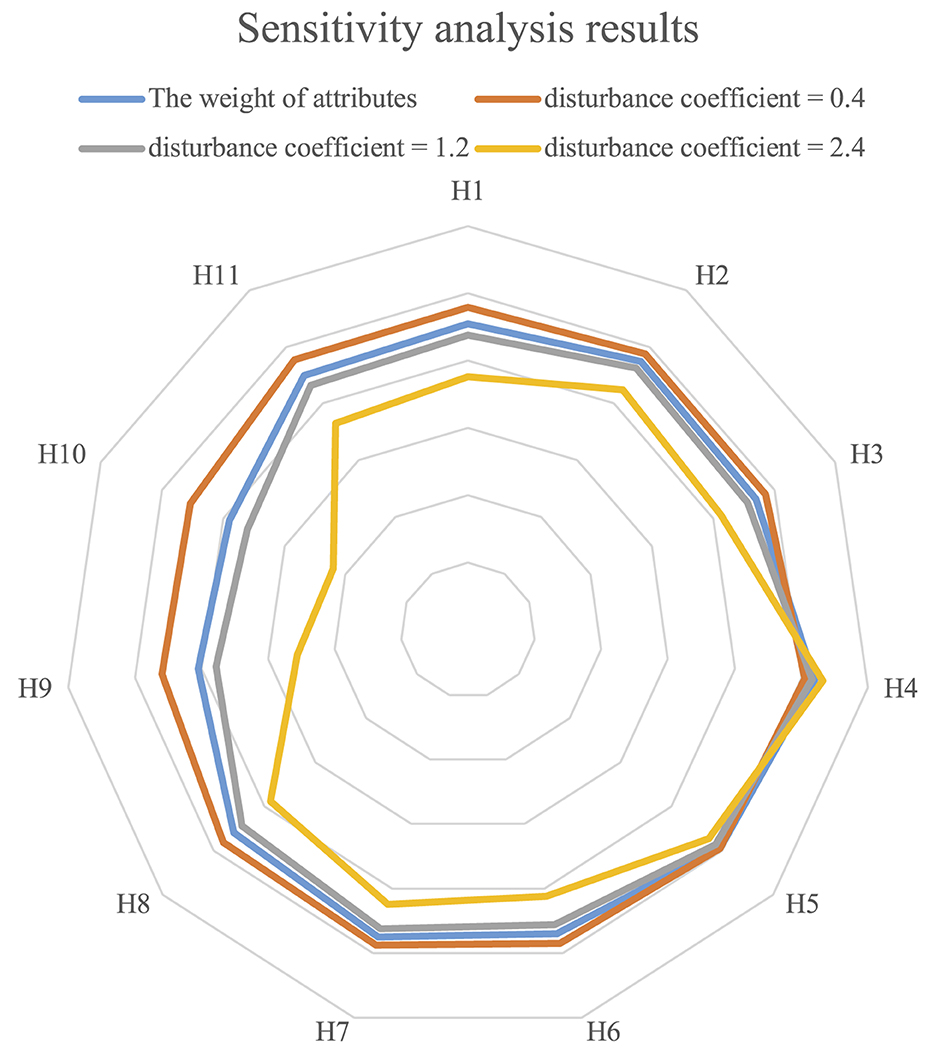
This subsection performs the sensitivity analysis of attribute weight to investigate the impact of various settings of criteria weights over different weight sets. The formula $\xi {\omega }_j+{\sum }_{k=1,k\ne j}^n{\rho }_k{\omega }_k=1$ was used to calculate the value of each attribute weight by disturbance analysis with the assumed disturbance coefficient ξ = 0.4, 1.2, 2.4, respectively. If one value of attribute weight is changed, the values of other attribute weights will change proportionally. That is, the original attribute weight is ω_j(j = 1, 2, ..., n) and the weight value attribute by disturbance analysis is changed to ${\omega }_j^{\text{'}}=\xi {\omega }_j$.

Figure 2 show the results of sensitivity analysis of attribute weights. It can see that blue, orange, gray and yellow lines describe the attribute weights, respectively. When disturbance coefficient ξ = 0.4, all the weight values of attribute except attribute H4 are increased. When disturbance coefficient ξ = 1, 2 and ξ = 2.4, the weight value of attribute changed in the similar way as the condition when disturbance coefficient ξ = 0.4. We can find out that the weight values are stable no matter how the disturbance coefficients change. This consistency demonstrates the robustness of the weighting scheme derived from the intuitionistic fuzzy entropy method. The model exhibits a stable performance across a range of perturbation levels, suggesting that minor fluctuations in decision-maker preferences or data inputs will not significantly alter the evaluation outcome.

Figure 2

Figure 2. Sensitivity analysis results under disturbance conditions.

In practical applications, we recommend setting the disturbance coefficient ξ between 0.8 and 1.2 to reflect reasonable fluctuations in subjective preferences or expert judgment. Extreme values (e.g., ξ < 0.4 or ξ > 2.0) may be used for stress-testing the model but are less likely to reflect real-world scenarios. This sensitivity analysis supports the method's reliability and provides confidence for its deployment in decision-making environments with inherent uncertainty.

6.3 Comparative analysis

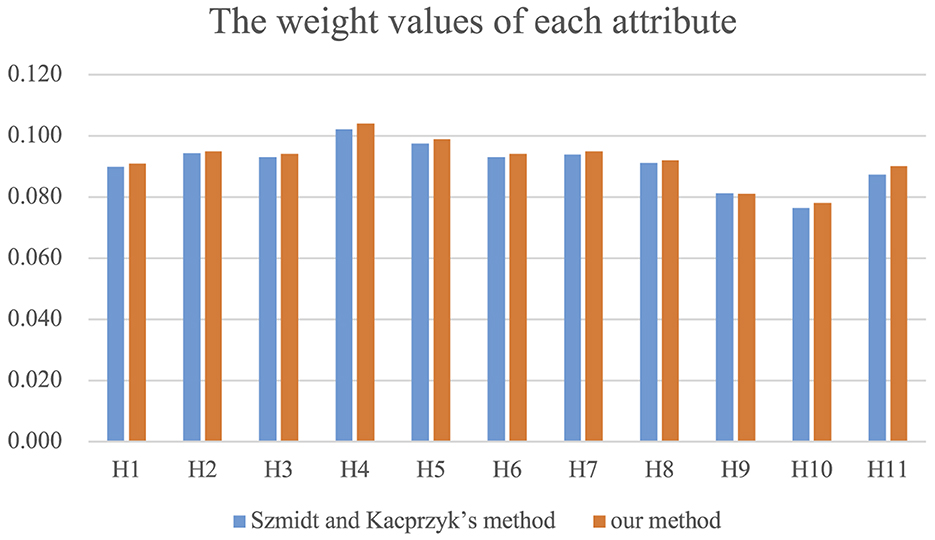
In this subsection, a comparative analysis is conducted between our proposed method and the approach introduced by Szmidt and Kacprzyk (2001). Table 6 presents the intuitionistic fuzzy entropy values for each attribute, highlighting distinctions between the methodologies employed in the two methods.

Table 6

Table 6. The intuitionistic fuzzy entropy of attribute.

A comparative analysis is performed against the method proposed by Szmidt and Kacprzyk (2001). The weight values assigned to each attribute by the respective methods are illustrated in Figure 3. The graphical representation in Figure 3 substantiates the efficacy of the intuitionistic fuzzy multi-attribute decision-making method based on decision-maker preferences. Consequently, the application of this method ensures the reliability of the decision-making outcomes.

Figure 3

Figure 3. The weight values of each attribute by the different methods.

6.4 Potential limitations

However, despite the strengths of the proposed Intuitionistic Fuzzy Multi-Attribute Decision-Making (IFMADM) method, there are potential limitations that should be acknowledged to provide a balanced perspective.

One of the primary limitations lies in the reliance on subjective inputs from decision-makers, which, although mitigated by the use of Intuitionistic Fuzzy Sets (IFS) and entropy measures, still introduces an element of bias into the evaluation process. The effectiveness of the model is closely tied to the accuracy and reliability of these inputs, which can vary depending on the decision-makers' expertise and perspectives.

Another limitation concerns the complexity of the model, which may pose challenges for its practical implementation, particularly in environments where stakeholders may not be familiar with fuzzy logic or advanced decision-making techniques. The model's sophistication, while beneficial for capturing the nuances of UEC, might also limit its accessibility to a broader range of users, necessitating additional training or resources.

Additionally, the model's focus on risk preferences is an innovative feature, but it may not fully capture all dimensions of decision-making in UEC, particularly in dynamic environments where other factors, such as cultural differences or changing economic conditions, may play a significant role. The model could benefit from further refinement to incorporate these external factors more comprehensively.

Finally, while the evaluation identified “Satisfaction with the guidance from university tutors and enterprise tutors in enterprise practice” as critical sub-indicators, the model may not adequately account for the long-term sustainability of UEC outcomes. For instance, while immediate student satisfaction is essential, the model might underemphasize factors such as the long-term impact of UEC on career development or the evolving needs of industries.

In conclusion, while the IFMADM method offers a robust framework for evaluating and enhancing UEC, future research should aim to address these limitations. Enhancing the model's user-friendliness, broadening its scope to include a wider range of decision-making factors, and ensuring that it captures both immediate and long-term outcomes will be crucial for its continued development and practical application.

7 Conclusion

This paper introduces a new evaluation method for UEC satisfaction based on multi-attribute decision-making. To establish a sophisticated framework for the analysis of UEC satisfaction, the proposed method seamlessly integrates Intuitionistic Fuzzy Sets (IFS) with intuitive fuzzy entropy. Through meticulous examination of evaluation values, distinct attribute weights are quantified, delineating the distinct roles each attribute plays in influencing UEC satisfaction levels.

The study reveals that “satisfaction with the guidance from university tutors during enterprise practice” is the most influential factor, followed by “satisfaction with the guidance from enterprise tutors.” These findings underscore the critical importance of strengthening mentorship mechanisms within UEC programs to enhance student satisfaction and educational outcomes. Practically, universities and enterprises should prioritize improving the quality and structure of tutor guidance to ensure more effective cooperation and better student experiences.

By quantifying attribute weights and leveraging the analytical power of intuitive fuzzy entropy, our method contributes to a nuanced evaluation process, providing a robust foundation for decision-making in the realm of UEC. The envisioned integration of game theory promises to elevate this methodology, offering an innovative lens through which to analyze UEC satisfaction, paving the way for further refinement and improvement in collaborative endeavors between academic institutions and enterprises.

In addition to presenting a novel approach to UEC satisfaction evaluation, this study offers new insights into the application of Intuitionistic Fuzzy Sets (IFS) and intuitive fuzzy entropy within the context of multi-attribute decision-making. By systematically quantifying the attribute weights and analyzing their impact on UEC satisfaction, this research not only deepens our understanding of the factors that drive effective university-enterprise collaborations but also introduces a method that can be adapted for broader applications in related fields. The integration of game theory principles in future research will further enhance this methodology, providing a more holistic approach to decision-making processes. The contributions of this paper lie in its innovative combination of fuzzy logic with decision-making frameworks, offering a robust tool for both academic researchers and practitioners aiming to optimize the outcomes of collaborative ventures between universities and enterprises.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

YZ: Methodology, Investigation, Conceptualization, Writing – original draft, Formal analysis, Writing – review & editing. ZZ: Methodology, Formal analysis, Writing – original draft. XC: Writing – original draft, Formal analysis, Methodology, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by Shanghai Pujiang Program (Grant No. 21PJC063) and Chinese Association of Higher Education (Grant No. 24XH0101).

Acknowledgments

The authors wish to thank the reviewers for their invaluable comments and suggestions that enhanced the quality of the paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arranz, N., Arroyabe, M. F., Sena, V., Arranz, C. F., and Fernandez de Arroyabe, J. C. (2022). University-enterprise cooperation for the employability of higher education graduates: a social capital approach. Stud. High. Educ. 47, 990–999. doi: 10.1080/03075079.2022.2055323

Crossref Full Text | Google Scholar

Atanassov, K. T. (1994). New operations defined over the intuitionistic fuzzy sets. Fuzzy Sets Syst. 61, 137–142. doi: 10.1016/0165-0114(94)90229-1

Crossref Full Text | Google Scholar

Atanassov, K. T., and Stoeva, S. (1986). Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20, 87–96. doi: 10.1016/S0165-0114(86)80034-3

Crossref Full Text | Google Scholar

Baydaş, M., Yilmaz, M., Jović, Ž., Stević, Ž., Özuyar, S. E. G., and Özçil, A. (2024). A comprehensive MCDM assessment for economic data: success analysis of maximum normalization, CODAS, and fuzzy approaches. Financ. Innov. 10:105. doi: 10.1186/s40854-023-00588-x

Crossref Full Text | Google Scholar

Burillo, P., and Bustince, H. (1996). Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets. Fuzzy Sets Syst. 78, 305–316. doi: 10.1016/0165-0114(96)84611-2

Crossref Full Text | Google Scholar

Clauss, T., and Kesting, T. (2017). How businesses should govern knowledge-intensive collaborations with universities: an empirical investigation of university professors. Ind. Mark. Manag. 62, 185–198. doi: 10.1016/j.indmarman.2016.09.001

Crossref Full Text | Google Scholar

Davey, T., Plewa, C., and Galán Muros, V. (2014). “University-business cooperation outcomes and impacts–a European perspective,” in Moderne Konzepte des Organisationalen Marketings/Modern Concepts of Organisational Marketing, eds. T. Kliewe and T. Kesting (Wiesbaden: Springer Gabler), 161–176. doi: 10.1007/978-3-658-04680-4_10

Crossref Full Text | Google Scholar

El-Araby, A., Sabry, I., and El-Assal, A. (2022). A comparative study of using MCDM methods integrated with entropy weight method for evaluating facility location problem. Oper. Res. Eng. Sci. Theory Appl. 5, 121–138. doi: 10.31181/oresta250322151a

Crossref Full Text | Google Scholar

Faizi, S., Sałabun, W., Rashid, T., Zafar, S., and Watróbski, J. (2020). Intuitionistic fuzzy sets in multi-criteria group decision making problems using the characteristic objects method. Symmetry 12:1382. doi: 10.3390/sym12091382

Crossref Full Text | Google Scholar

Galan-Muros, V., and Davey, T. (2019). The UBC Ecosystem: putting together a comprehensive framework for university-business cooperation. J. Technol. Transf. 44, 1311–1346. doi: 10.1007/s10961-017-9562-3

Crossref Full Text | Google Scholar

Gebbels, S., Evans, S. M., and Delany, J. E. (2011). Promoting environmental citizenship and corporate social responsibility through a school/industry/university partnership. J. Biol. Educ. 45, 13–19. doi: 10.1080/00219266.2011.537834

Crossref Full Text | Google Scholar

Huo, J., Zhang, W., and Chen, Z. (2024). Enhanced decision-making through an intelligent algorithmic approach for multiple-attribute college English teaching quality evaluation with interval-valued intuitionistic fuzzy sets. Int. J. Knowl. Based Intell. Eng. Syst. 28, 279–294. doi: 10.3233/KES-230299

Crossref Full Text | Google Scholar

Joint Committee on Standards for Educational Evaluation (JCSEE) (2011). The 3rd Edition of the Program Evaluation Standards. Thousand Oaks, CA: Sage Publishers.

Google Scholar

Kliewe, T., Baaken, T., and Kesting, T. (2016). Developing University-business cooperation through evidence-based management: a German case. Int. J. E-Entrepren. Innovat. 6:20. doi: 10.4018/IJEEI.2016070101

Crossref Full Text | Google Scholar

Kusterka-Jefmańska, M., Jefmański, B., and Roszkowska, E. (2022). “Application of the intuitionistic fuzzy synthetic measure in the subjective quality of life measurement based on survey data,” in Modern Classification and Data Analysis. SKAD 2021. Studies in Classification, Data Analysis, and Knowledge Organization, eds. K. Jajuga, G. Dehnel, M. Walesiak (Cham: Springer), 243–261. doi: 10.1007/978-3-031-10190-8_17

Crossref Full Text | Google Scholar

Li, S., Wang, C., and Wang, Y. (2024). Fuzzy evaluation model for physical education teaching methods in colleges and universities using artificial intelligence. Sci. Rep. 14:4788. doi: 10.1038/s41598-024-53177-y

PubMed Abstract | Crossref Full Text | Google Scholar

Magableh, G. M., Mumani, A. A., Obaidat, S. F., and Mistarihi, M. Z. (2024). Fuzzy-FMEA theory approach for prioritizing supply chain nervousness factors. Appl. Sci. 14:4747. doi: 10.3390/app14114747

Crossref Full Text | Google Scholar

Mahfoudh, D., Boujelbene, Y., and Mathieu, J. P. (2019). “University-enterprise cooperation: determinants and impacts,” in Mediterranean Symposium on Enterprise-New Technology Synergy, eds. K. Boussafi, J. P. Mathieu, and M. Hatti (Cham: Springer), 91–121. doi: 10.1007/978-3-030-60933-7_6

PubMed Abstract | Crossref Full Text | Google Scholar

Mascarenhas, C., Ferreira, J. J., and Marques, C. (2018). University–industry cooperation: a systematic literature review and research agenda. Sci. Public Policy 45, 708–718. doi: 10.1093/scipol/scy003

Crossref Full Text | Google Scholar

Mukhametzyanov, I. (2021). Specific character of objective methods for determining weights of criteria in MCDM problems: entropy, CRITIC and SD. Decis. Mak. Appl. Manag. Eng. 4, 76–105. doi: 10.31181/dmame210402076i

Crossref Full Text | Google Scholar

Nguyen, P.-H., and Data-Driven, A. (2025). MCDM approach-based spherical fuzzy sets for evaluating global augmented reality providers in education. IEEE Access 13, 6102–6119. doi: 10.1109/ACCESS.2024.3361320

Crossref Full Text | Google Scholar

Obaidat, S., and Mumani, A. (2025). A multiple objective decision analysis model for capacity expansion plans selection in manufacturing. J. Eng. Res. 13, 480–491. doi: 10.1016/j.jer.2024.02.013

Crossref Full Text | Google Scholar

Quintana, C. D. D., Mora, J. G., Pérez, P. J., and Vila, L. E. (2016). Enhancing the development of competencies: the role of UBC. Eur. J. Educ. 51, 10–24. doi: 10.1111/ejed.12162

Crossref Full Text | Google Scholar

Ranga, M., Hoareau, C., Durazzi, N., Etzkowitz, H., Marcucci, P., Usher, A., et al. (2013). Study on University-Business Cooperation in the US. London: LSE Enterprise.

Google Scholar

Rasheed, F., Kousar, S., Shabbir, J., Kausar, N., Pamucar, D., Gaba, Y. U., et al. (2021). Use of intuitionistic fuzzy numbers in survey sampling analysis with application in electronic data interchange. Complexity 2021, 1–12. doi: 10.1155/2021/9989477

Crossref Full Text | Google Scholar

Ripoll Feliu, V., and Diaz Rodriguez, A. (2017). Knowledge transfer and university-business relations: current trends in research. Intangible Cap. 13, 697–719. doi: 10.3926/ic.990

Crossref Full Text | Google Scholar

Rybnicek, R., and Königsgruber, R. (2019). What makes industry–university collaboration succeed? A systematic review of the literature. J. Bus. Econ. 89, 221–250. doi: 10.1007/s11573-018-0916-6

Crossref Full Text | Google Scholar

Shapira, A., and Rosenfeld, Y. (2011). Achieving construction innovation through academia-industry cooperation—keys to success. J. Prof. Issues Eng. Educ. Pract. 137, 223–231. doi: 10.1061/(ASCE)EI.1943-5541.0000057

PubMed Abstract | Crossref Full Text | Google Scholar

Smith, N. M., Smith, J. M., Battalora, L. A., and Teschner, B. A. (2018). Industry–university partnerships: engineering education and corporate social responsibility. J. Prof. Issues Eng. Educ. Pract. 144:04018002. doi: 10.1061/(ASCE)EI.1943-5541.0000367

PubMed Abstract | Crossref Full Text | Google Scholar

Szmidt, E., and Kacprzyk, J. (2001). Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst. 118, 467–477. doi: 10.1016/S0165-0114(98)00402-3

Crossref Full Text | Google Scholar

Tyler, R. (2014). Basic Principles of Curriculum and Instruction. Beijing: China Light Industry Press. doi: 10.7208/chicago/9780226086644.001.0001

Crossref Full Text | Google Scholar

Wang, Z., and Pan, L. P. (2025). Assessment of teaching quality of traditional decorative patterns in colleges and universities using an MCDM approach and circular intuitionistic information. IEEE Access 13, 22365–22379. doi: 10.1109/ACCESS.2025.3534843

Crossref Full Text | Google Scholar

Xu, Z. (2007). Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 15, 1179–1187. doi: 10.1109/TFUZZ.2006.890678

Crossref Full Text | Google Scholar

Xu, Z. (2022). “Research on application evaluation index system of university enterprise cooperation informatization based on CIPP,” in The 2021 International Conference on Machine Learning and Big Data Analytics for IoT Security and Privacy. SPIoT 2021. Lecture Notes on Data Engineering and Communications Technologies, Vol. 97, eds. J. Macintyre, J. Zhao, and X. Ma (Cham: Springer), 1065–1070. doi: 10.1007/978-3-030-89508-2_138

Crossref Full Text | Google Scholar

Zeng, S., Chen, S. M., and Fan, K. Y. (2020). Interval-valued intuitionistic fuzzy multiple attribute decision making based on nonlinear programming methodology and TOPSIS method. Inf. Sci. 506, 424–442. doi: 10.1016/j.ins.2019.08.027

Crossref Full Text | Google Scholar

Zhao, M., Wei, G., Chen, X., and Wei, Y. (2021). Intuitionistic fuzzy MABAC method based on cumulative prospect theory for multiple attribute group decision making. Int. J. Intell. Syst. 36, 6337–6359. doi: 10.1002/int.22552

Crossref Full Text | Google Scholar

Zhou, M. (2024). Evaluation model construction of school-enterprise cooperation innovation ability based on big data analysis. Appl. Math. Nonlinear Sci. 9:20240163. doi: 10.2478/amns-2024-1701

Crossref Full Text | Google Scholar

Zhou, Y., Huang, L., and Ye, J. (2023). Choice mechanism for construction of university enterprise joint cryptography laboratory and its application in Hainan University. Lect. Notes Electr. Eng. 1045, 618–628. doi: 10.1007/978-981-99-2287-1_89

Crossref Full Text | Google Scholar