- 1Reactor Engineering Division, Reactor Design and Development Group, Bhabha Atomic Research Centre, Mumbai, India
- 2Homi Bhabha National Institute, Mumbai, India
- 3Reactor Safety Division, Reactor Design and Development Group, Bhabha Atomic Research Centre, Mumbai, India
Reliability assessment of passive safety systems is one of the important issues, since safety of advanced nuclear reactors rely on several passive features. In this context, a few methodologies such as reliability evaluation of passive safety system (REPAS), reliability methods for passive safety functions (RMPS), and analysis of passive systems reliability (APSRA) have been developed in the past. These methodologies have been used to assess reliability of various passive safety systems. While these methodologies have certain features in common, but they differ in considering certain issues; for example, treatment of model uncertainties, deviation of geometric, and process parameters from their nominal values. This paper presents the state of the art on passive system reliability assessment methodologies, the accomplishments, and remaining issues. In this review, three critical issues pertaining to passive systems performance and reliability have been identified. The first issue is applicability of best estimate codes and model uncertainty. The best estimate codes based phenomenological simulations of natural convection passive systems could have significant amount of uncertainties, these uncertainties must be incorporated in appropriate manner in the performance and reliability analysis of such systems. The second issue is the treatment of dynamic failure characteristics of components of passive systems. REPAS, RMPS, and APSRA methodologies do not consider dynamic failures of components or process, which may have strong influence on the failure of passive systems. The influence of dynamic failure characteristics of components on system failure probability is presented with the help of a dynamic reliability methodology based on Monte Carlo simulation. The analysis of a benchmark problem of Hold-up tank shows the error in failure probability estimation by not considering the dynamism of components. It is thus suggested that dynamic reliability methodologies must be integrated in passive systems reliability analysis to have a true estimate of system failure probability, and hence the reliability. Third issue is the treatment of independent process parameters variations in passive system reliability analysis. Certain process parameters such as atmospheric temperature can vary with time. Performance of some passive safety systems depends on this parameter. However, the present methodologies do not consider this dynamic variation from the nominal values and hence introduce a subject of discussion.
Introduction
Ever since the inception of nuclear fission, nuclear energy is considered as one of the potential sources of energy for electricity production, which can eliminate or reduce the dependency of human beings on the conventional sources of energy. Until December 2013, 434 nuclear reactors are in operations for electricity production (IAEA, 2014). Nuclear power reactors have two specific characteristics: first, during their operation, they accumulate a large quantity of radioactive fission products from which the public must be protected. Second, significant energy release continues for prolonged period due to the decay heat, even after the reactor is shutdown. Owning to these two specific characteristics of nuclear reactors, they are designed to be equipped with multiple layers of safety systems to minimize or eliminate the associated risk to public or to the environment. In the history of commercial nuclear power plants, there were three major accidents [at Three Mile Island (1979), Chernobyl (1986), and Fukushima (2011)] leading to core melt down. Except Three Mile Island, a large amount of radioactivity was released to the environment. To eliminate the public concerns on nuclear reactor safety, several efforts have been made worldwide to change/modify the designs of nuclear power plants and the regulatory policies. The safety goals for the future nuclear reactors have been accordingly enhanced so that significant release of radioactive material to the environment is practically eliminated and the risk to public due to nuclear plants is negligibly small. The International Nuclear Safety Group (INSAG-12) and INPRO have set the targets of core damage frequency (CDF) of not more than 10−5/reactor year for future nuclear power plants in comparison to the present goal of 10−4 for existing plants. The goal for the large early release frequency (LERF) has been enhanced further to 10−6/reactor year in place of present goal of 10−5/reactor year.
The future reactor concepts are designed on the philosophy of “safety-by-design” for meeting the enhanced goals of nuclear safety. These concepts are designed with inherent safety features so that the reactor has the capability to return to stable safe conditions on its own in the event of any kind of accidents that may arise due to any internal or external events. Such safety characteristics are paramount important for these future reactors, which can minimize or eliminate the necessity of evacuation of public (Nayak and Sinha, 2007). In the current operating reactors, most of the critical safety functions are provided by using active safety systems. However, in order to meet the futuristic goals of safety, relying on these active safety systems alone does not seem to be viable. One of the major problems with active safety systems is that the reliability of these systems cannot be improved beyond a threshold. In addition, these systems are prone to the errors made by operator’s actions and their subjective decisions. Passive systems, on the other hand, are believed to be more reliable than the active safety systems and hence, can provide enhanced protection against any postulated accidents. This is because passive systems do not need human intervention or require external energy sources such as electricity or pneumatic supply for their operation.
IAEA (1991) defines the passive safety system as “A system that is composed entirely of passive components and structures or a system, which uses active components in a very limited way to initiate subsequent passive operation.” As per IAEA-TECDOC-626, passive safety systems can be categorized into four categories, as described below.
Category A
In this category, passive systems do not have moving mechanical components or parts or any moving working fluids. Also, these systems do not depend on any external power sources and any external signal for activation (IAEA, 1991). Some of the examples of this category of passive safety features are physical barriers against the release of fission products, such as fuel cladding and pressure boundary components and systems; core cooling systems relying on heat transfer by radiation, convection, and conduction from nuclear fuel to outer structural parts, etc.
Category B
Unlike category A, these systems have moving working fluids. They do not need external power sources for their actuation and do not have moving mechanical components or parts. Examples of this category of passive safety features are systems operating on natural circulation.
Category C
In this category, passive systems can have moving mechanical parts. The systems may or may not have moving working fluids. These systems do not depend on any external power sources and any external signal for activation. Some of the examples of this category of passive systems are venting by relief valves or rupture discs to prevent overpressure; emergency injection systems consisting of accumulators and check valves.
Category D
This category of passive systems is characterized by passive execution and active initiation for their operation. That means external source of intelligence is required to initiate the process. Operation followed by the initiation of the process is executed by passive means. This category draws a border between active and passive systems. Some of the examples of this category of passive safety features are emergency core cooling systems (ECCS), which get activated by electro-pneumatic valves and are based on gravity driven flow of water, and emergency shutdown systems based on gravity or static pressure driven control rods, which get activated by fail-safe trip logic.
Many of the advanced reactors, e.g., ESBWR (Cheung et al., 1998), AP1000 (Schulz, 2006), CAREM (Delmastro, 2002), AHWR (Sinha and Kakodkar, 2006) incorporate several passive systems in the design of the reactors. Below are some of the examples of advanced water-cooled reactor designs that implement passive safety systems:
AP600 and AP1000
The AP600 and AP1000 are PWRs designed by the Westinghouse Electric Corporation. Both designs employ passive safety systems that rely on gravity, compressed gas, natural circulation, and evaporation to provide for long-term cooling in the event of an accident. Various passive safety systems in AP600/AP1000 are as follows:
• AP1000 passive residual heat removal systems (PRHR),
• AP1000 core make-up tank (CMT),
• AP1000 containment sump recirculation,
• AP1000 passive containment cooling system (PCCS).
Economic Simplified Boiling Water Reactor
ESBWR developed by general electric, is based on the previous simplified boiling water reactor (SBWR) design with some modifications of safety systems and the containment size relative to the reactor power. In ESBWR concepts, the safety is accomplished by eliminating the recirculation pump, thus relying on natural circulation cooling. The coolant is circulated by natural circulation as a result of the density difference between the high void, two-phase fluid in the chimney, and the exterior single-phase liquid in the downcomer. The tall chimney not only enhances the natural circulation flow, but also ensures the ample time for core uncovery before the ECCS comes in play. The emergency core cooling and containment cooling systems do not have an active pump injecting flows and the cooling flows are driven by pressure differences. Large volumes of suppression pool functions not only as a primary heat sink during the initial blow down, but also as coolant inventory to prevent the core uncovery through the gravity equalization lines. Various passive safety features utilized in the ESBWR are as follows:
• Gravity driven cooling system,
• Automatic depressurization system (ADS),
• Isolation condenser system (ICS),
• Standby liquid control system,
• Passive containment cooling system,
• Suppression pool.
Advanced Heavy Water Reactor
Advanced heavy water reactor is a vertical, pressure tube type, heavy water moderated, and boiling light-water-cooled natural circulation reactor. AHWR employs several passive safety features in its design. Various passive safety systems of AHWR are as follows:
• Passive core cooling system,
• Passive core decay heat removal system (PDHRS),
• Emergency core cooling system in passive mode,
• Passive containment isolation system (PCIS),
• Passive containment cooling system,
• Vapor suppression in GDWP,
• Passive poison injection system.
As said before, deployment of passive systems in nuclear reactors provides several benefits, such as avoidance or dependency on active components; such systems are simple and easy to build, operate, and maintain. Elimination of operator intervention or dependency on external sources results in reduction of respective hazards.
Despite the above, there are technological challenges and issues in order to engineer them in the reactor designs. One of the issues with the passive systems is accurate quantification of functional reliability for these systems during normal operation and transients including accidental conditions. These functional failures are the type of failures, which happens because of deviations in boundary conditions of the critical process or geometric parameters on which passive systems performance depends. This is because the driving forces in passive systems are relatively small, and these forces may get affected due to small changes in operating parameters or geometry of the system. The main difficulties in evaluation of functional failure of passive systems arise because of (a) lack of plant operational experience; (b) scarcity of adequate experimental data from integral test facilities or from separate effect tests in order to understand the performance characteristics of these passive systems, not only at normal operation but also during accidents and transients; (c) lack of accepted definitions of failure modes for these systems; and (d) difficulty in modeling certain physical behavior of these systems.
This paper presents the state of the art on passive system reliability assessment, the accomplishments, and remaining issues. Rest of the article is organized as follows: Section “Passive System Reliability Analysis – State of the Art” brings the state of the art on passive system reliability analysis. In Section “Accomplishments in Passive System Reliability Analysis,” accomplishments in the passive system reliability analysis are discussed. Section “Unresolved Issues” discusses the unresolved issues associated with passive systems performance and reliability assessment. Main conclusions of this study are presented in Section “Conclusion.”
Passive System Reliability Analysis – State of the Art
Passive system reliability can be defined as the probability of the system or structure to carry out the defined function for a given mission time [0, t], when operated under specified conditions. The main challenge in defining the reliability of passive system arises from the fact that operating principles of these passive systems are based on the physical phenomena like buoyancy, gravity, or natural convection, rather than being dependent on the active components. Since, these physical phenomena in itself never fails as long as the parameters governing them do not deviate from their nominal values, defining a failure for passive system is indeed very subjective. For example, in advanced nuclear reactors, ICS is used to remove the decay heat under station blackout conditions passively. However, during the operation, the critical process parameters, which govern the performance of ICS may deviate from their nominal values and degrade the heat transfer characteristic such that ICS fails to meet their desired function satisfactorily, which can be, to maintain the system pressure in required range or to keep the clad temperature under certain threshold value.
Reliability analysis of category A passive systems can be carried out using structural reliability methodologies with sufficient accuracy (Burgazzi, 2012). Since passive systems of category C and D involve many static mechanical components, which are among frequently used components in nuclear power plants, the failure data of these components can be used to assess the reliability of these categories of passive systems. However, for category B systems, research is still in progress to bring a unified and internationally acceptable methodology.
A historical perspective to this topic reveals that in mid-1990s, CEA and ENEA agreed to work to evaluate the reliability of passive systems. In University of Pisa (UNIPI), D’Auria and Galassi (2000) studied it further and a few years later, this methodology was proposed as reliability evaluation of passive safety system (REPAS). REPAS (Jafari et al., 2003) methodology was a joint effort of UNIPI, ENEA, University of Rome, and Polytechnic of Milan. In REPAS, failure probability of passive system was evaluated by propagating the epistemic uncertainties of important physical and geometric parameters, which affects the system performance the most. The REPAS methodology recognizes the model uncertainties of the codes. In REPAS, the uncertainties in code predictions are evaluated by performing sensitivity study of input parameters and by code to code comparisons. Jafari et al. (2003) applied this methodology to an experimental natural circulation test loop. Zio et al. (2003) used REPAS for reliability analysis of an ICS. A drawback of REPAS was that, in order to assess the impact of uncertainties on the predicted performance of passive system, a large number of calculations with best estimate codes were needed. Thus, the reliability estimation using REPAS was found to be too expensive in terms of number of code runs, if complete sequences of passive system involvement are to be considered in the accident scenario.
Under the auspices of the European 5th Framework program, a comprehensive methodology reliability method for passive safety functions (RMPS) (Marques et al., 2005) was developed. RMPS inherited the methodological developments of REPAS and improved upon the shortcomings of it. In RMPS, the most important parameters that affect the passive system performance are identified using analytical hierarchy processes (AHP) and sensitivity analysis. These important parameters are chosen for further analysis. A probability distribution function (pdf) of these input parameters is then assigned by using classical data fitting techniques (in case of data available about the parameters) or expert judgment processes (in the absence of sufficient data). Once the distributions for the input parameters are determined, a Monte Carlo sampling technique is used to sample a large number of samples for these parameters. The performance of passive system is then evaluated using best estimate codes such as RELAP or CATHARE. With the outcome of the results of these code runs, the probability of passive system failure is estimated. Various alternative techniques have been proposed in RMPS methodology to limit the large number of time consuming deterministic code runs. Some of such alternative techniques include the use of variance reduction techniques, FORM/SORM (first and second order reliability methods) and use of meta-models like response surface. Two improvement areas have been identified for RMPS methodology after its inception and implementation to various passive systems of water-cooled reactors based on natural circulation – first, for realistic estimation of probability density functions of the input parameters, a engineering judgment process needs to be implemented; second, to assess the impact of uncertainty in these input parameter’s pdfs, appropriate sensitivity analysis must be incorporated (Burgazzi, 2012).
Using a similar approach, Pagani et al. (2005) evaluated the probability of failure of the gas-cooled fast reactor (GFR) natural circulation system. However, they used simpler conservative codes to evaluate the failure of a system.
In RMPS, the treatment of variations of input parameters is done by using probability density function (pdf). The analyst has to have prior information about these pdf. Moreover, functional failure of passive systems is very much dependent on the values of these parameters. It is argued here that, the nominal values of these input parameters cannot have an independent deviation. Since most of the input parameters are linked to states of hardware components, the variations in the nominal values of these parameters can be because of failure/malfunctioning of these components. Hence, assigning arbitrary pdfs for their deviations are debatable.
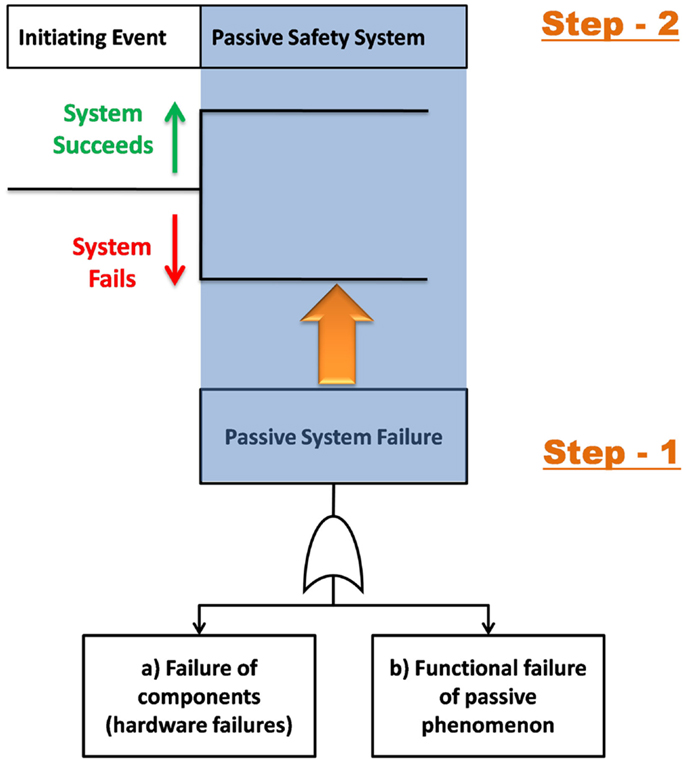
A first effort in integrating the passive systems to the probabilistic safety assessment (PSA) was put forward in the RMPS methodology. According to RMPS methodology, the failure probability of entire passive system can be achieved by combining (a) failure of components (hardware failures, i.e., activating valves and piping failures, etc.) and, (b) functional failure of passive phenomenon, by using an OR gate (Figure 1, step-1). No definitive agreement was reached within the RMPS project on the way how to incorporate passive system reliability into a plant-specific PSA model and only conceptual proposals were provided. However, the integration of passive system into plant-specific PSA is very straightforward, this can be done after the failure probability of passive system is determined. The passive system analyzed can be incorporated into a plant-specific PSA model by introducing an additional heading in the respective Event Tree to incorporate the success or failure of the passive safety system (Figure 1, step-2). However, implementing the above procedure for the reliability assessment of passive system and for its integration with plant-specific PSA has certain shortcomings. The following point summarizes the issues:
• The methodology followed in RMPS, does not account for the interaction between the (a) hardware/component failure and, (b) functional failure of passive system. In actual the hardware/component may fail or degrade during the operation of passive system. It is also possible that functional failure of passive system, which is attributed to a process parameter deviating from its nominal values, must have happened because of some hardware/component’s degradation (e.g., loss in pressure may be caused by malfunction of some I&C systems or valves). The fault tree treatment of considering the hardware failure and functional failure of passive phenomenal separately thus seems to be a subject of improvement.
• The above mentioned event tree treatment of passive system holds good only for one accident scenario. For each of the different initiating events and accident scenarios, passive system needs to be analyzed separately and hence would result in a computationally intensive scheme.
• Instead of following a classical PSA treatment, which is based on the assumptions of same failure rates of the components throughout the mission time, a more advanced form of PSA like living probabilistic safety assessment (LPSA) (Zubair et al., 2010, 2011, 2013) can be utilized for implementing risk informed decision making.
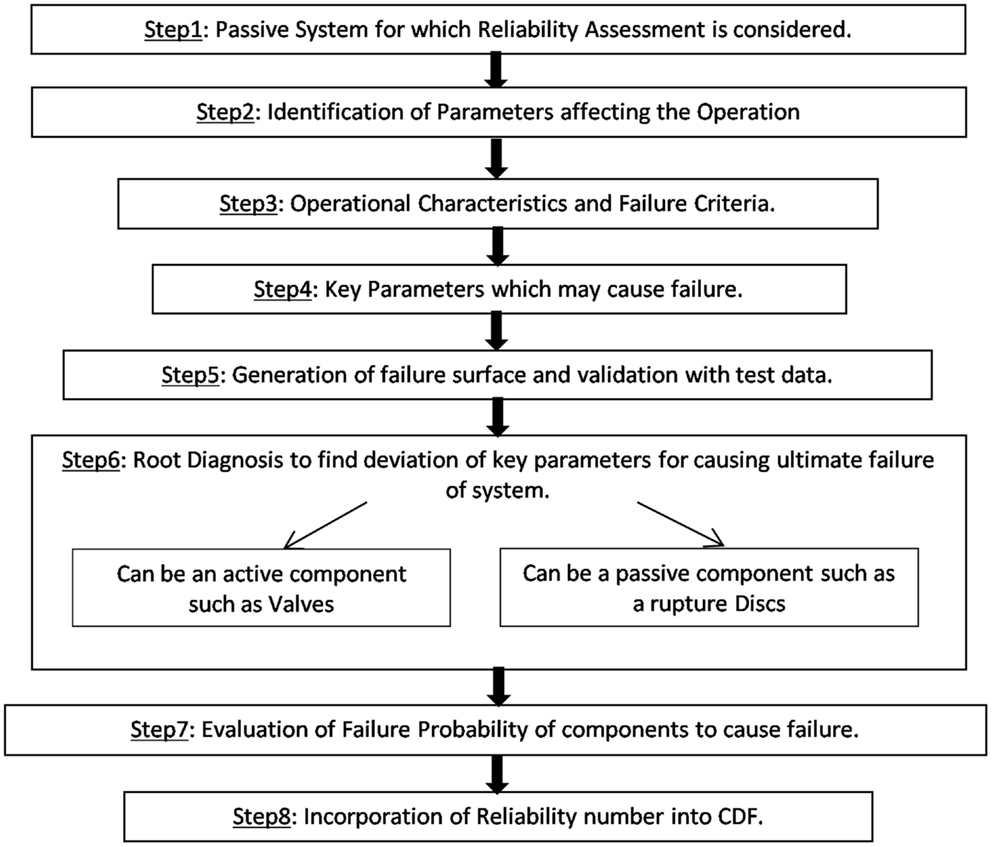
A different methodology called analysis of passive systems reliability (APSRA) (Nayak et al., 2008) was developed in the year 2007. Unlike RMPS, in APSRA methodology, it is attributed that the deviations of input parameters on which passive system performance depends, occur only because of malfunction or failure of mechanical components. In APSRA methodology, first a failure surface is generated by considering the deviations of all those critical parameters, which influence the system performance. These failure surfaces are generated by evaluating the effect of these deviations on passive system performance using qualified T-H codes (e.g., RELAP, CATHARE). Then root-cause analysis is performed to find the cause of these deviations. Once the causes of these deviations are determined, the failure probabilities of these causes are obtained from generic data values as well as from plant operational experience data. Finally, the failure probability of passive system is evaluated using classical PSA techniques like fault tree analysis. The top event for the fault tree is considered as passive system functional failures (for example, passive system unable to maintain the clad temperature below certain threshold) and the basic events are malfunctioning or failed component states. To reduce the uncertainty in code predictions, APSRA methodology suggests relying on experimental data from integral test facilities as well as from separate effect tests (Nayak et al., 2009). Figure 2 illustrates the steps followed in APSRA methodology.
Apart from RMPS and APSRA methodologies, a few alternative approaches have been investigated in the area of reliability assessment of passive systems. In one of the approach developed at ENEA by Burgazzi (2002), the failure probability of passive system is linked only to mechanical component failure or degradation and is estimated from the surrogate models by replacing the T-H codes with fault tree. However, this approach has does not treat deviation of initial and boundary conditions on passive system performance and reliability. Moreover, surrogate models used in this approach fails to capture the interactions among physical phenomena. In another approach, Burgazzi (2007) proposed to predict, the probability of failure of passive system by multiplying the probability of independent failure modes. Only those failure modes were considered, which had the potential to deviate from their nominal conditions or physical mechanisms, which in turn may deviate the passive system performance. This approach may result in providing very conservative estimates of failure probability.
Comparison between RMPS and APSRA Methodologies
While both RMPS and APSRA have certain features in common, for example;
• Both methodologies require best estimate codes to find the T-H performance of the passive systems and the influence of sensitive parameters (including process parameters and model uncertainties) on the system performance.
• Both methodologies define T-H failure criteria of the system.
• Both methodologies use probabilistic and deterministic tools to assess the reliability of the system.
However, they differ in certain aspects, which are as follows:
• One of the biggest differences between RMPS and APSRA is the way both the methods treat the process parameter variation from its nominal value. In RMPS, variation of process parameters is considered through a pdf treatment. For example, the reactor has a nominal operating pressure, which can vary within a range of pressure control system. This variation can be treated by assigning a uniform distribution. APSRA, however, tackles these variations by considering the root diagnosis for example, the variation of pressure from the nominal value could be due to malfunction of the pressure control system, which is basically failure of a hardware system.
• Second difference between RMPS and APSRA is the way both methodologies treat model uncertainties. RMPS treats model uncertainties using pdf similar to process parameter variations and it does not distinguish between the process parameter variations and model uncertainties. On the other hand, APSRA relies on uncertainty estimates of computer codes from experimental validation. In the absence of experimental data, APSRA treats the model uncertainties using a pdf and they are propagated separately after evaluating the failure probability of the system through failure of process parameters.
• Third difference between RMPS and APSRA is the way of evaluating the reliability of passive systems. RMPS uses Monte Carlo evaluation or FORM/SORM (first/second order reliability methods), whereas APSRA predicts failure surface and evaluates reliability using fault tree analysis.
Accomplishments in Passive System Reliability Analysis
The above methodologies REPAS, RMPS, and APSRA have uncovered very important aspects related to passive safety system reliability. Following are noticeable accomplishments of the above methods:
• Definition of reliability of passive system: both the methodologies have a common opinion on the definition of reliability of passive system. Accordingly, passive system reliability can be defined as the probability of system or structure to carry out the defined function (like – decay heat removal, cooling of vessel, keeping clad temperature in a defined range, etc) for a given mission time [0, t], when operated under specified conditions.
• It has been accepted by all the methods that passive system performance and reliability are functions of boundary conditions. Their deviations from the designed nominal conditions could affect the performance and hence reliability. This is true in case of passive systems because of the low driving forces.
• It is also accepted that input parameters and boundary conditions vary between some limits. Some of these parameters and boundary conditions are critical for passive system performance. Key to quantify reliability lies in understanding the deviations and their effects on system performance during the operation and transient conditions. To name a few of initial and boundary conditions are – pressure, water level, reactor power, environment temperature, etc. and some of physical parameters like densities, conductivity, specific heats of fuel, etc.
• In all the methods, defining failure of passive system is given the prime importance and it can be concluded that most of them have defined it as either fail to meet the amount of heat exchanged or to keep maximal clad temperature in a safe range during the operation.
• Since there is limited experience in the operation of passive systems and lack of suitable experimental databases, all the methods rely on simulation by means of best estimate codes like RELAP5 or CATHARE.
Unresolved Issues
The above methodologies lack to explain some of the important issues related to passive systems performance and reliability analysis. These issues are as follows:
Applicability of Best Estimate Codes and Model Uncertainty
It is so far not established whether the so called best estimate codes such as RELAP5 or CATHARE, are applicable for passive systems performance evaluation and their failure. Of course, these codes have been validated over several years using test data from separate effect facilities and integral experiments and it is now well recognized that they are acceptable for conventional water-cooled reactors, which have active safety systems. However, to use such best estimate codes for passive systems is still doubtful.
Why the current codes may not be applicable to passive systems?
Passive system such as natural circulation systems mostly has low driving force. Because of the low driving forces, the flow may not be fully developed. Besides, the natural convection flow velocities can be multidimensional in nature unlike the 1-D flow, which the above codes assume. In addition, in some of the passive decay heat removal systems involving large diameter vessels or pools, which remove the heat by natural convection, there can be existence of thermal stratification in the pools. In such systems, the high density of fluid may settle at the bottom of the vessel and the low-density fluid sits at the top allowing kettle type boiling when heat addition takes place. Besides, heat transfer and pressure loss laws developed for the forced circulation systems may not be applicable to natural circulation based systems. It is thus difficult to accurately model the above phenomena of these passive systems, which strongly affect the system performance and failure. As a result, phenomenological simulations of such natural convection systems could have significant amount of uncertainties, particularly in predictions of (a) natural circulation flow instabilities and heat transfer; (b) condensation in presence of non-condensables; (c) critical heat flux under oscillatory condition; and (d) thermal stratification in large pools.
Natural circulation flow instabilities and heat transfer
While forced and natural circulation flow both are prone to instabilities, natural circulation based systems are more unstable than the forced circulation systems. This oscillatory behavior of natural circulation is due to the non-linear behavior of natural circulation phenomenon. In natural circulation systems, even a small change in driving force affects the flow. The result of this disturbance in turn affects the driving force and thus causes a regenerative feedback mechanism. So far, several attempts have been made to model flow instabilities using different two-phase flow models, which range from the simplest HEM to more rigorous two fluid models. There are concerns for using the models since the void velocity and their distributions and the two-phase frictional pressure drops, are found to affect the stability characteristics significantly (Nayak and Vijayan, 2008). The most difficult part is to ensure the applicability of best estimate codes like RELAP5 for modeling the flow stability in natural circulation systems.
In a study by Taylor and Martin (1992), RELAP5/Mod3 predictions were compared with the experimental data for low flow natural circulation. It was concluded that the trends of natural circulation and forced circulations were predicted with an acceptable degree of accuracy. However, a number of deficiencies were observed in the RELAP5/MOD3 treatment. These deficiencies include geometric, multidimensional, and form loss effects.
In another study conducted by D’Auria et al. (1997), a comparison of RELAP5/Mod3.2 predictions for flow instabilities in a simple natural circulation loop against the experiments conducted for a range of power (100–900 W) was performed. According to this comparative study, the performance of single-phase natural circulation loop was predicted well by RELAP5; but this conclusion was applicable only when a stable flow rate was established. However, it has to be noted that, the stability map predicted by RELAP code had disagreements when compared with the experimental stability map.
Misalea et al. (1999) have shown that both CATHARE and RELAP codes, in absolute terms, showed poor agreement with experimental data for simulation of natural circulation. In this study, the CATHARE code was able to provide satisfactory results for predicting the steady state at low power level, after the initial transient. However, no unstable behavior was predicted. RELAP code predictions were able to show the oscillating quantities; however, the power levels at which RELAP predicted these results, were not same as the experimental observations.
Ambrosini and Ferreri (1998, 2003) assessed the effects of truncation errors on prediction of linear stability boundaries in single-phase natural circulation loop. Among some of the significant findings was, that for a given natural circulation problem, the predicted stability map may considerably differ because of truncation error propagating in the predictions. In this study, the capability of system codes used in safety analysis of light-water reactors was tested for predicting the stability using different first order and second order, implicit and explicit numerical schemes. It was found that second order schemes predicts well in comparison to first order, also first order numerical scheme based system codes are very much prone to the problems brought about by numerical diffusion when applied to flow stability analysis.
RELAP5 predictions also are very sensitive to the nodalization. In a study conducted by Mangal et al. (2012), a numerical simulation was performed by using three different nodalization schemes for an experimental facility (Kumar et al., 2000). The three different nodalization schemes were classified as coarse, base, and fine. In this study, it was observed that choice of these nodalization schemes plays a vital role in revealing the natural circulation behavior. For single-phase flow, it was observed that for all the three different nodalization schemes, RELAP5 simulation results were very close to the experimental observations during the initial heat up condition. However, during boiling two-phase conditions, fine and coarse nodalization schemes resulted in over-predicting the flow at different operating pressures. Whereas only base nodalization scheme predicted results were closer to the experimental results. It could be easily pointed out that RELAP5 prediction for fine nodalizations had very high oscillation amplitude compared to experimental data. With this study, it can be concluded that there can be disparity in the predicted results using RELAP5 and the experiments even if the most appropriate nodalization scheme adopted. The disparity in the predicted results and experimental data can be attributed to the constitutive relations used in RELAP5, which are semi-empirical in nature (Mangal et al., 2012).
Condensation in presence of non-condensables
The effect of non-condensable gases on steam condensation is one of the major safety-related issues, causing heat transfer rates to decrease. Air and accidental presence of hydrogen represent the main non-condensable gases in nuclear power plants. Best estimate codes do have uncertainties in simulating the condensation in presence of non-condensable. In an experimental validation of RELAP5, Hassan and Raja (1993) found that for condensation in presence of non-condensable in U-tube, there were large discrepancy in calculated primary temperatures for several cases and also the nitrogen contents in the tube. Macedo and Torres (2009) have shown that for horizontal condenser tubes of an advanced nuclear reactor, RELAP5 code overestimates heat transfer coefficients for the higher inlet air mass fraction and hence calculated temperatures were smaller than experimental data. Based on the comparison of results from experiments, Fahri (2010) has observed that RELAP5/Mod3.3 cannot evaluate the relationship between mixture Reynolds number and air accumulation at interface leading to under-predicted wall sub-cooling and over-predicted heat transfer coefficient with an unacceptable deviation. While comparing RELAP simulation and experimental results of OSU-MASLWR integral test facility, Nevo et al. (2012) have reported that coupling the primary system containment and the presence of non-condensable in the high pressure containment is challenging for RELAP code. So far, the present system codes have accounted this phenomenon by using empirical relationships. For advanced design of NPP, including in particular passive safety systems where the effect of the non-condensbale gas is predominant, such approach will not be accurate enough (Sarrette, 2003).
Critical heat flux under oscillatory condition
Critical heat flux (CHF) is a parameter of paramount importance, which limits the heat transfer capability of nuclear reactors, heat exchangers and many other heat transfer units. CHF has been extensively investigated during the last few decades, resulting in reasonable understanding of the phenomenon and several reliable prediction models. Boiling systems can show various flow oscillations under natural circulation and/or low-pressure conditions. In water-cooled nuclear reactors, flow oscillations can occur in natural circulation systems. It is well known that flow oscillations can induce a premature CHF at the heat flux level much lower than that for stable conditions. Though the use of natural circulation systems is increased in advanced nuclear reactors and other heat transfer systems, the effect of flow oscillations on CHF has not been sufficiently investigated and is not properly dealt with by existing prediction models. The effects of flow oscillations, which usually occur in actual systems at low pressure and low flow conditions are not reliably handled in existing prediction models (Soon Heung and Won-Pil, 2003).
Thermal stratification in large pools
Thermal mixing and stratification phenomena play major roles for safety of reactor systems with large enclosures, such as post-LOCA gas transport between containment compartments and hydrogen distribution in operating LWRs, long-term passive containment cooling in AP1000, and steam condensation and mixing in the suppression pool and isolation condenser pool of ESBWR. It is important to accurately predict the temperature, density, and/or concentration distributions for both design optimization and safety analysis. However, the individual transport mechanisms governing mixing in containments are characterized by time and length scales that can differ by orders of magnitude. Large volumes and complexity of the interactions of different flow and thermal structures make analysis a daunting task. Current major system analysis codes either have no models or only 0-D models for thermal mixing and stratification in large enclosures. The lack of general thermal mixing and stratification models in those codes severely limits their application and accuracy for safety analysis, especially for passively safe advanced light-water reactors (ALWRs), where the primary system and containments are more strongly coupled (Zhao and Peterson, 2010). The SASSYS code developed by argonne national laboratory (ANL), only provides lumped-volume-based 0-D models that can only give very approximate results and can only handle simple cases with one mixing source (Dunn et al., 2006). COMMIX code developed by ANL uses CFD tools to analyze simple configuration small-scale thermal stratification problems and achieved limited success (Chang and Bottoni, 1994; Kasza et al., 2007). However, the restrictiveness and shortcomings of such applications have been recognized and further research needed to extend the applications to large complex pool mixing systems as highlighted in the review report by ANL (Kasza et al., 2007). Considering the limitations of the inadequate 0-D methods and the inefficient 3-D CFD methods, new accurate and efficient thermal mixing and stratification methods are needed to improve accuracy and reduce modeling uncertainties, especially for system safety analysis.
The uncertainty in these predictions could be only reduced by verifying the codes for different passive systems and relying more on experimental data. Treatment of the residual uncertainties (e.g., scaling uncertainties) when code validation data are available is an important future task as well.
Treatment of Dynamic Failure Characteristics of Components
The methods implemented so far for reliability assessment of passive systems do not consider dynamic failure of components or process. In RMPS, variation of process parameters is considered through a pdf treatment. These pdfs are assumed to be invariant in time. In actual, the parameter variations from their nominal values could be time dependent. APSRA relies in calculating failure probabilities of components for treatment of variation of process parameters through classical fault tree and event tree. These methods only consider binary states of any component failure, i.e., failure or success states; however, the components like mechanical, electrical, instruments, and control systems may fail at intermediate states. Examples of such components are control valves and relief valves. These components may fail at 10% stuck open or 50% stuck open or at any other configurations, rather than just stuck open or closed completely. Some components do not fail directly; they fail after some considerable amount of time, while degradation of function is taking place during accident progression or otherwise. For example, a control valve may get stuck open at 10% and over the time it may transit to 100% open, during which system might be working or may fail. It may so happen that while one component is failing, it accelerates or induces some other component failure, which in turn may lead to system failure much before it is predicted.
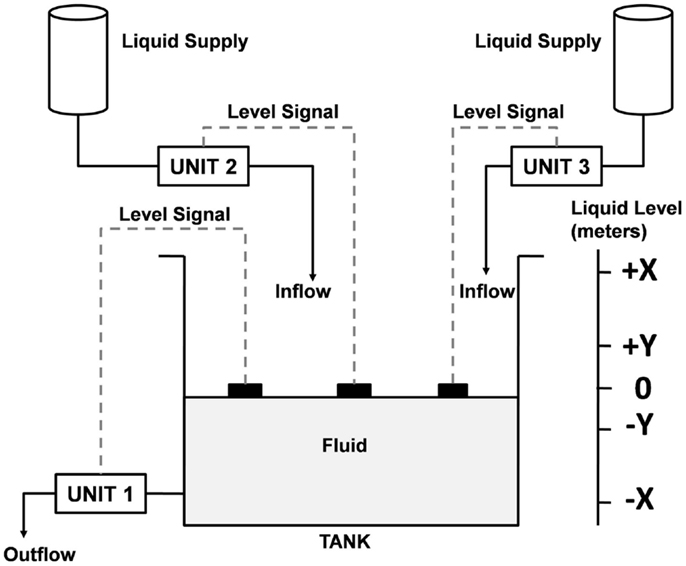
To justify the effect of dynamism of failure of valves, let us take an example of a benchmark problem (Aldemir, 1987; Deoss, 1989; Cojazzi, 1996) details of which can be found in the Supplementary Material. This system consists of a fluid containing tank, which has three separate level control units. Figure 3 shows the diagram of the system. Each control unit (control valve) is independent of the others and has a separate level sensor associated with it. The level sensors measure the fluid level in the tank, which is a continuous process variable. Based on the information from the level sensors, the operational state of the control units is determined. Each flow control unit can be thought of as containing controller, which turns the unit on or off based on the signal from the level sensors, as shown in Figure 3. Failure of the system occurs when the tank either runs dry or overflows. Two cases of particular interest are as follows
• Case A – (Binary failure) Valves fail in either stuck open or stuck closed positions.
• Case B – (degraded failure) Valves may fail at any intermediate positions with some certain probability and then the fault increases at certain rate till the end of mission time or till the valve completely fails open.
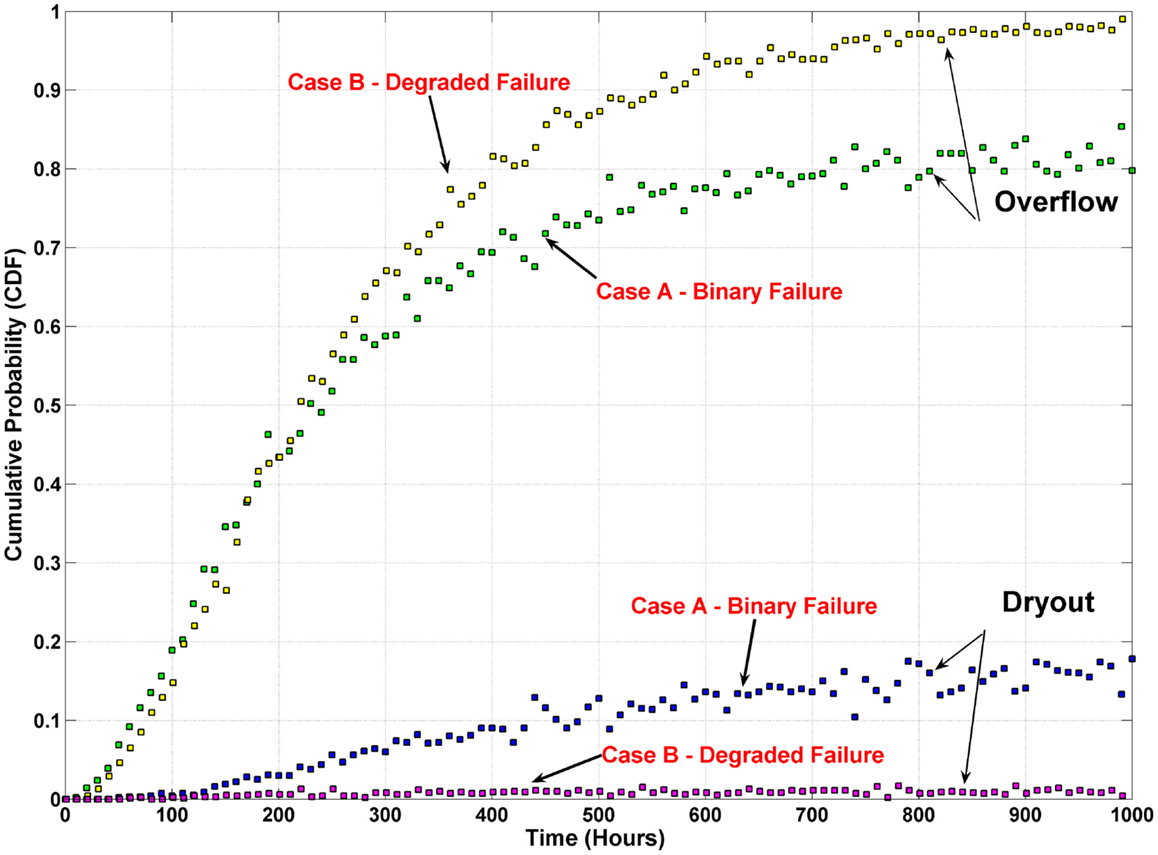
Probability of overflow and dryout in these two cases is evaluated by methodology presented by Chandrakar et al. (2014). The results shown in Figure 4 clearly explains that probabilities of failure are very different when dynamism of valves are considered as compared to classical stuck open and stuck close fault considerations.
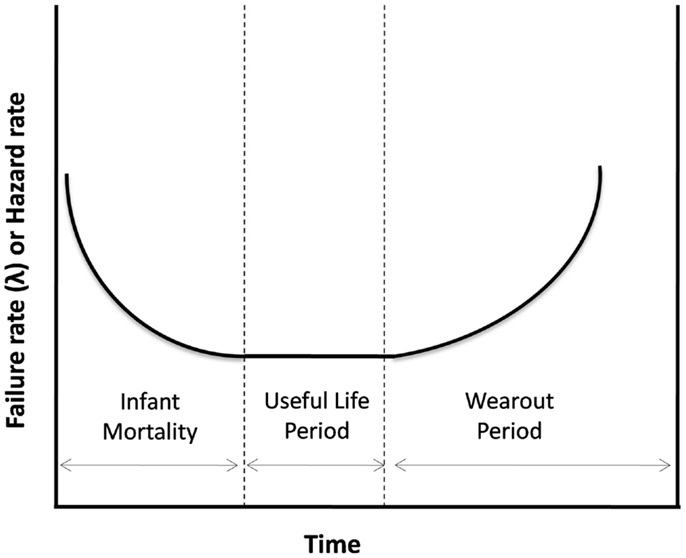
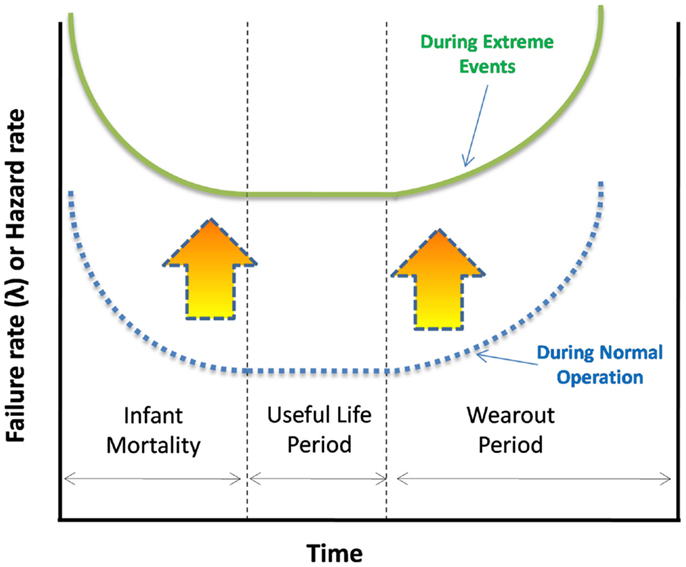
In addition, classical PSA tools consider component failure rates as constant. It is also assumed that these component failure rates represent the “useful life” region of the classical bath-tub curve as shown in Figure 5 for a mechanical component like valve. These failure rates are generally derived from the component failure databases (IAEA, 1988; NSWC, 2006; MIL-HDBK-217E, 1987). Failure rates based on these databases generally represent the failure of components, which are operating within the designed limits and are independent of process parameter effects. During extreme events such as that happened in Fukushima, components of passive systems may be subjected to extreme stress and can have the failure rates, which are much higher than the ones that are adopted from above databases. In such cases, the entire bath-tub curve may be shifted upward as shown in the Figure 6. Also, the process parameter values at the time of operation will have a dominant effect on these failure rates and also on the sequence of the failure of components.
In view of the above, there is a need of dynamic reliability analysis, which considers the evolution of process variable and their effects on component failure rates in reliability analysis. Dynamic reliability methods provide a framework for explicitly capturing the influence of time and process dynamics on scenarios and control actions simultaneously. Dynamic reliability attempts to take into account the ordering and timing of events in the accident propagation, the dependence of transition rates and failure criteria on the process variable values and human operator actions.
State-of-the-art development on dynamic reliability methodologies and application to passive system reliability analysis
In order to have a realistic estimation of passive systems reliability, it is needed to capture the interactions between the hardware states/operator actions with dynamic evolution of process parameters. This can be achieved by integrating the methods for dynamic reliability, also known as dynamic PSA methods with currently developed methodologies for passive system reliability analysis. Dynamic reliability analysis methods can be broadly categorized as (a) state transitions or Markov models; (b) continuous dynamic event trees (DETs); (c) direct simulation.
A review of the dynamic reliability methodology development reveals that the first comprehensive continuous-time method is the continuous-event tree (CET) approach (Devooght and Smidts, 1992a,b; Smidts, 1992). This approach captures the interrelation between the hardware/software with operator actions by using an integral equation, which can be solved by Monte Carlo simulation techniques. To account for the shortcomings of the CET method, continuous cell-to-cell mapping (CCMT) (Tombuyes and Aldemir, 1996) and stimulus-driven theory of probabilistic dynamics (Labeau and Izquierdo, 2005) were developed and implemented. Since continuous time based methods are very computationally intensive, they could not be applied successfully to highly complex problems of real world. To overcome these computational issues, a discrete version of this method was developed (Aldemir, 2013). Currently, the DETs are the most popular approach to discrete-time dynamic PSA. Dynamical logical methodology (DYLAM) (Amendola and Reina, 1984; Cacciabue et al., 1986; Cojazzi, 1996) is the first methodology proposed that uses DETs.
The software that are available for discrete-time dynamic probabilistic safety analysis are ADS-IDAC (Chang and Mosleh, 1998), DENDROS (Munoz et al., 1999), MCDET (Hofer et al., 2002), ADAPT (Catalyurek et al., 2010), ADAPT (Catalyurek et al., 2010), and GA-DPRA (Voroyev and Kudinov, 2011). However, these tools suffer the problem of handling and processing the huge amount of data generated during the analysis and they are computationally intensive.
Integration of dynamic reliability analysis with T-H models is needed for the realistic evaluation of passive systems reliability. In order to enhance capability of the present methodologies to capture the interaction between process parameters and dynamical evolution of system state, it is thus required to use the dynamic reliability methodologies like discrete DETs and advanced Monte Carlo simulations.
Integration of dynamic reliability methodologies in RMPS and APSRA
Reliability methods for passive safety functions follow classical event tree approach for integrating the passive system failure probability into PSA. As said earlier, passive systems performance and reliability heavily depends on the initial conditions, which in RMPS methodology, is considered only for a particular event sequence. However, in real accidental and transient situations, the boundary conditions, and process parameter variations may not necessarily follow the predicted event sequence considered in a classical event tree. The event sequence in actual can be very dynamic. This dynamism of accident and transients can be attributed to several factors like varying operating conditions of reactor, subjective decisions of operator, hardware failure or their degradation with respect to time, and sever conditions generated by some unpredicted natural events like tsunami, earthquake, etc. It is to be noted here, even though passive systems do not need any human intervention for their operation, still the effect of subjective decisions of operator for other active systems working in combination with passive systems can have an adverse effect on passive system performance and reliability. In order to capture this dynamism in RMPS methodology, event trees must be replaced with discrete DETs, which can capture the combinations of interaction between the different scenarios with varying conditions of hardware functionalities and effects of human intervention. In addition, considering a time invariant pdf for all the process parameters (for example, atmospheric temperature) must be corrected accordingly. Since, RMPS methodology, in itself does not consider hardware/component failure or their degradation in passive system reliability evaluation, the dynamism in failure characteristics of hardware/components cannot be accounted in current version of RMPS.
In APSRA methodology, fault tree representation of passive system is used to integrate it with the PSA. In addition, the hardware failure states considered in this methodology does not capture their dynamic failure behavior. In order to capture the overall dynamic behavior of passive system, APSRA methodology, must incorporate the dynamic reliability methodology in propagating the effect of component and hardware failures with respect to time. In addition to the incorporation of dynamic reliability methodology for the hardware failure or degradation, fault tree representation must be modified to discrete dynamic event tree to capture the dynamic accident scenario and human errors.
Treatment of Independent Process Parameters Variations in Passive System Reliability Analysis
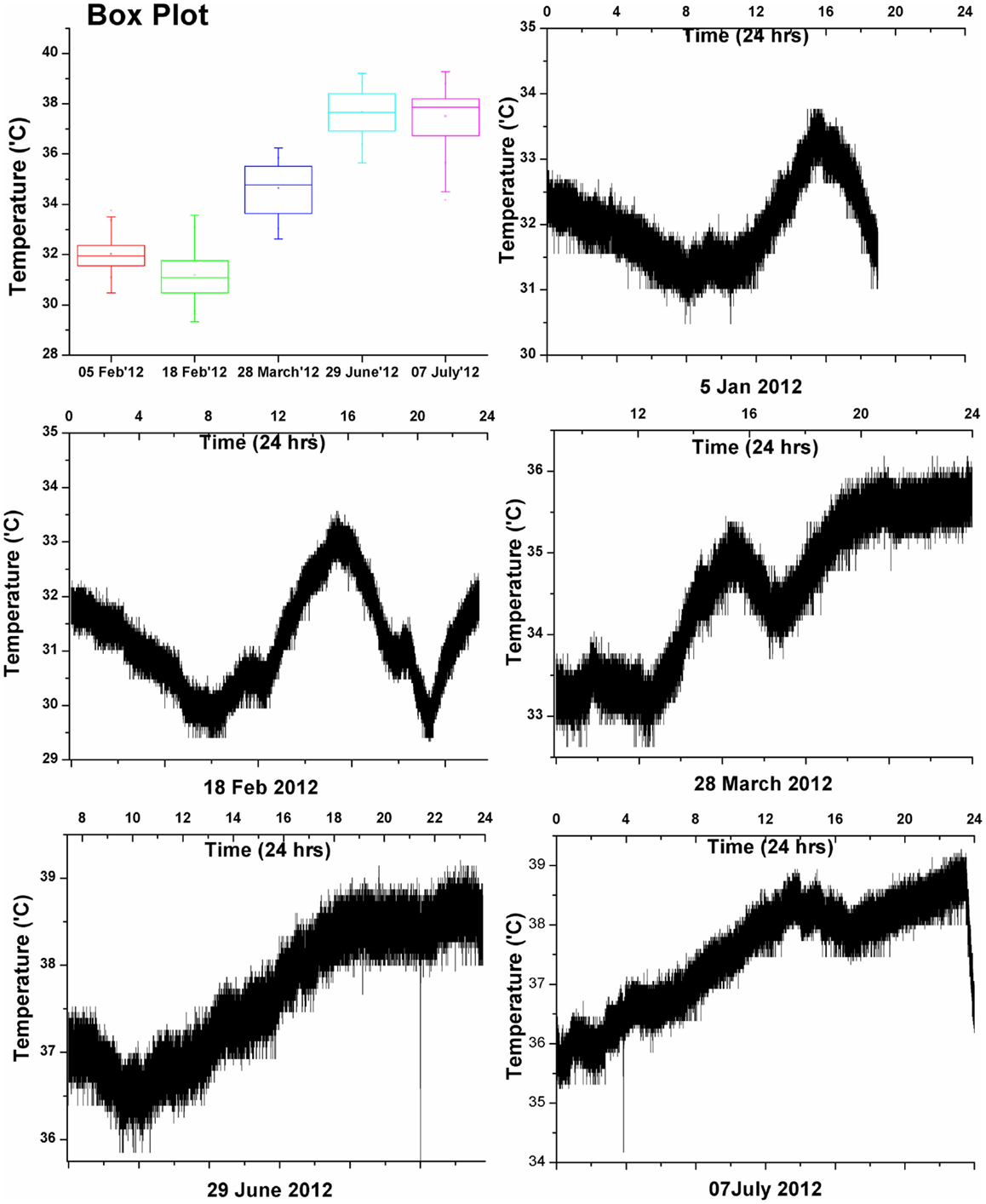
Broadly, the parameters affecting passive system performance can be classified into two types: (a) dependent parameters and (b) independent parameters. Dependent parameters are the ones whose deviations depend upon the output or state of certain hardware or control units, example of such dependent parameters are pressure, sub-cooling, non-condensable gas. Many of dependent parameters are not independent to have their own deviations; rather they are correlated or interdependent (Burgazzi, 2009). Independent parameters are the ones whose deviations do not depend upon certain components rather they have their own patterns and deviations, which cannot be predicted easily; example of such parameter is atmospheric temperature. The dependence of system performance on these types of parameter is quite significant in many passive systems for example passive decay heat removal system. Performance of these systems is very sensitive to the water inlet temperature (sink temperature) or atmospheric temperature or the environment temperature. These parameters vary in time due to their evolution along the mission period of system operation. Environment temperature has certain pattern depending on the season and time of operation (day/night) and some random variations on that; so it cannot be called as an uncertain parameter and treated by a random probability distribution between minimum and maximum for the analysis purpose. Treatment of dynamic variation of such kind of parameters is another unresolved problem in reliability analysis of passive systems. As an example, let us look at the inlet water temperature variation (Figure 7) for one of the natural circulation experimental facility in BARC (Jain et al., 2010), which depends on the ambient condition. One can easily infer from the data that this water temperature has seasonal and temporal variations.
To resolve the uncertainties in the reliability calculations because of assumptions around the parameters like atmospheric temperature, one has to build the models of such parameters from the data that has been continuously monitored around the applications of passive systems. These parameters could be given as real-time data into the simulations once the models are built.
Conclusion
Many of the advanced reactor concepts propose to adopt passive safety systems in order to enhance the defense-in-depth and make nuclear power plants inherently safe even during extreme events like earthquake, tsunami, and floods. Passive safety systems are believed to be more reliable than the active safety systems because of elimination of the need for human intervention, avoidance of external electrical supply, etc. However, incorporation of these systems in the nuclear reactors needs to be tested adequately due to several technical issues; for example:
• lack of plant operational experience;
• scarcity of adequate experimental data from integral test facilities or from separate effect tests in order to understand the performance characteristics of these passive systems, not only at normal operation but also during accidents and transients;
• lack of accepted definitions of failure modes for these systems; and,
• difficulty in modeling certain physical behavior of these systems.
Evaluation of passive system reliability is a challenging task. It involves a clear understanding of the physics of the phenomena and failure mechanism of the system, which the designer must do before prediction of its reliability. Currently, the performance of passive systems and their failure are predicted by so called “best estimate codes.” However, the applicability of the “best estimate codes” to assess the performance and failure of passive systems is not well established due to the lack of sufficient plant/experimental data. That introduces large uncertainties and errors when such codes are applied to evaluate passive system performance.
A historical review shows that a few methodologies such as, REPAS, RMPS, and APSRA have been developed in the past and applied to evaluate reliability of passive systems. It is observed that while these methodologies have certain features in common; but they differ significantly particularly in the treatment of deviations of process parameters from their nominal values and model uncertainty in best estimate codes which are paramount for evaluation of reliability of such systems.
Passive system performance is greatly affected by deviations of process parameters from their nominal values. During extreme events, evolution of these process parameter values may increase/decrease the event occurrence probabilities and failure rate of components. In addition, components of passive systems can fail at any intermediate positions of operations instead of classical assumption of binary state failure. Current methodologies lack treatment of these dynamic failure characteristics of components of passive systems. It is also required to pay attention to the treatment of dynamic variations of independent process parameters such as atmospheric temperature in passive system reliability analysis in future.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at http://www.frontiersin.org/Journal/10.3389/fenrg.2014.00040/abstract
References
Aldemir, T. (1987). Computer-assisted markov failure modeling of process control systems. IEEE Trans. Reliabil. 36, 133–144. doi: 10.1109/TR.1987.5222318
Aldemir, T. (2013). A survey of dynamic methodologies for probabilistic safety assessment of nuclear power plants. Ann. Nucl. Energy 52, 113–124. doi:10.1016/j.anucene.2012.08.001
Ambrosini, W., and Ferreri, J. C. (1998). The effect of truncation error on the numerical prediction of linear stability boundaries in a natural circulation single phase loop. Nucl. Eng Des. 183, 53–76. doi:10.1016/S0029-5493(98)00157-5
Ambrosini, W., and Ferreri, J. C. (2003). Prediction of stability of one dimensional natural circulation with a low diffusion numerical scheme. Ann. Nucl. Energy 30, 1505–1537. doi:10.1016/S0306-4549(03)00119-1
Amendola, A., and Reina, G. (1984). DYLAM-1, A Software Package for Event Sequence and Consequence Spectrum Methodology. EUR-924, CEC-JRC ISPRA. Ispra, Italy: Commission of the European Communities.
Burgazzi, L. (2002). Passive system reliability analysis: a study on the isolation condenser. Nucl. Technol. 139, 3–9.
Burgazzi, L. (2007). Addressing the uncertainties related to passive system reliability. Prog. Nucl. Energy 49, 93–102. doi:10.1016/j.pnucene.2006.10.003
Burgazzi, L. (2009). Evaluation of dependencies related to passive system failure. Nucl. Eng. Des. 239, 3048–3053. doi:10.1016/j.nucengdes.2009.08.019
Burgazzi, L. (2012). Reliability of Passive Systems in Nuclear Power Plants, Nuclear Power-Practical Aspects, ed. W. Ahmed (InTech). Available at: http://www.intechopen.com/books/nuclear-power-practical-aspects/reliability-of-passive-systems-in-nuclear-power-plants
Cacciabue, P. C., Amendola, A., and Cojazzi, G. (1986). Dynamic logical analytical methodology versus fault tree: the case of auxiliary feedwater system of a nuclear power plant. Nucl. Technol. 74, 195–208.
Catalyurek, U., Rutt, B., Metzroth, K., Hakobyan, A., Aldemir, T., Denning, R. S., et al. (2010). Development of a code-agnostic computational infrastructure for the dynamic generation of accident progression event trees. Reliabil. Eng. Syst. Safety 95, 278–304. doi:10.1016/j.ress.2009.10.008
Chandrakar, A., Nayak, A. K., and Gopika, V. (2014). Reliability analysis of process controlled systems considering dynamic failure of components. Int. J. Syst. Assur. Eng. Manag. doi:10.1007/s13198-014-0248-z
Chang, F. C., and Bottoni, M. (1994). Capabilities of Reynolds Stress Turbulence Model in Applications to Thermal Stratification. Minneapolis: American Society of Mechanical Engineers (ASME) pressure vessels and piping conference, 19–23.
Chang, Y. H., and Mosleh, A. (1998). “Dynamic PRA using ADS with RELAP5 code as its thermal hydraulic module,” in PSAM 4, eds A. Mosleh and R. Bari (New York: Springer-Verlag), 2468–2473.
Cheung, Y. K., Shiralkar, B. S., Rao, A. S. (1998). ”Design evolution of natural circulation in ESBWR,” Proceeding of the 6th International Conference on Nuclear Engineering (ICONE-6).
Cojazzi, G. (1996). The DYLAM approach for the dynamic reliability analysis of systems. Reliabil. Eng. Syst. Safety 52, 279–296. doi:10.1016/0951-8320(95)00139-5
D’Auria, F., Frogheri, M., and Misale, M. (1997). “System codes capabilities in predicting instabilities in single phase natural circulation,” in 4th Regional Meeting, Nuclear Energy in Central Europe. eds B. Mavko, and L. Cizelj. Available at: http://inis.iaea.org/search/search.aspx?orig_q=RN:41033743
D’Auria, F., and Galassi, G. M. (2000). Methodology for the Evaluation of the Reliability of Passive Systems. Pisa, Italy: University of Pisa, DIMNP, NT 420 (00).
Delmastro, D. (2002). “Thermal-Hydraulic Aspects of CAREM Reactor,” in Proceeding Technical Committee Meeting on Natural Circulation Data and Methods for Innovative Nuclear Power Plant Design (Vienna).
Deoss, D. L. Jr. (1989). A Simulation Based Model for Dynamic System Availability Analysis. Master’s thesis. Cambridge, MA: MIT.
Devooght, J., and Smidts, C. (1992a). Probabilistic reactor dynamics I: the theory of continuous event trees. Nucl. Sci. Eng. 111, 229–240.
Devooght, J., and Smidts, C. (1992b). Probabilistic reactor dynamics – III: a framework for time dependent interaction between operator and reactor during a transient involving human error. Nucl. Sci. Eng. 112, 101–113.
Dunn, F. E., Fanning, T. H., and Cahalan, J. E. (2006). Preliminary Safety Evaluation of the Advanced Burner Test Reactor. ANL-AFCI-172. Lemont: Argonne National Laboratory.
Fahri, A. (2010). An assessment of RELAP5/Mod3.3 condensation model for high Reynolds number flows. Prog. Nucl. Energy 52, 759–766. doi:10.1016/j.pnucene.2010.06.005
Hassan, Y. A., and Raja, L. L. (1993). Analysis of experiments for steam condensation in the presence of non-condensable gases using the RELAP5/mod 3 code. Nucl. Technol. 104, 76–88.
Hofer, E., Kloos, M., Krzykacz-Hausmann, B., Peschke, J., and Woltereck, M. (2002). An approximate epistemic uncertainty analysis approach in the presence of epistemic and aleatory uncertainties. Reliabil. Eng. Syst. Safety 77, 229–238. doi:10.1016/S0951-8320(02)00056-X
International Atomic Energy Agency. (1988). Component Reliability Data for Use in Probabilistic Safety Assessment. Vienna: IAEA.
International Atomic Energy Agency. (1991). Safety Related Terms for Advanced Nuclear Power Plant. Vienna: IAEA.
Jafari, J., D’Auria, F., Kazeminejad, H., and Davilu, H. (2003). Reliability evaluation of a natural circulation system. Nucl. Eng. Design. 224, 79–104. doi:10.1016/S0029-5493(03)00105-5
Jain, V., Nayak, A. K., Vijayan, P. K., Saha, D., and Sinha, R. K. (2010). Experimental investigation on the flow instability behavior of a multi-channel boiling natural circulation loop at low-pressures. Exp. Therm. Fluid. Sci. 34, 776–787. doi:10.1016/j.expthermflusci.2010.01.007
Kasza, K., Grandy, C., Chang, Y., and Khalil, H. (2007). Argonne Liquid-Metal Advanced Burner Reactor: Components and In-Vessel System Thermal Hydraulic Research and Testing Experience – Pathway Forward. ANL/NE-07/21.
Kumar, N., Rajalakshmi, R., Kulkarni, R. D., Sagar, T. V., Vijayan, P. K., and Saha, D. (2000). Experimental Investigations in High Pressure Natural Circulation Loop. An internal report of Reactor Engineering Division. Mumbai: BARC.
Labeau, P. E., and Izquierdo, J. M. (2005). Modeling PSA problems – I: the stimulus-driven theory of probabilistic dynamics. Nucl. Sci. Eng. 150, 115–139.
Macedo, A. L., and Torres, M. W. (2009). Simulation of Steam Condensation in the Presence of Non-Condensable Gases in Horizontal Condenser Tubes Using RELAP5 for Advanced Nuclear Reactors. Rio de Janeiro: International Nuclear Atlantic Conference (INAC 2009).
Mangal, A., Jain, V., and Nayak, A. K. (2012). Capability of the RELAP5 code to simulate natural circulation behaviour in test facilities. Prog. Nucl. Energy 61, 1–16. doi:10.1016/j.pnucene.2012.06.005
Marques, M., Pignatel, J. F., Saignes, P., D’Auria, P., Burgazzi, L., MÜller, C., et al. (2005). Methodology for the reliability evaluation of a passive system and its integration into a probabilistic safety assessment. Nucl. Eng. Des. 235, 2612–2631. doi:10.1016/j.nucengdes.2005.06.008
MIL-HDBK-217E. (1986). Reliability Prediction of Electronic Equipment. Rome: Air Development Center.
Misalea, M., Frogheria, M., D’Auria, F., Fontani, E., and Garcia, A. (1999). Analysis of single-phase natural circulation experiments by system codes. Int. J. Therm. Sci. 38, 977–983. doi:10.1016/S1290-0729(99)00106-4
Munoz, R., Minguez, E., Melendez, E., Izquierdo, J. M., and Sanchez-Perea, M. (1999). “DENDROS: a second generation scheduler for dynamic event trees,” in M&C’99 – Madrid, eds J. M. Aragones, C. Ahnert, and O. Cabellos (Madrid: Senda Editorial, S.A.), 1358–1367.
Nayak, A. K., Gartia, M. R., Antony, A., Gopika, V., and Sinha, R. K. (2008). Passive system reliability analysis using APSRA methodology. Nucl. Eng. Des. 238, 1430–1440. doi:10.1016/j.nucengdes.2007.11.005
Nayak, A. K., Jain, V., Garita, M. R., Prasad, H., Antony, A., Bhatiya, S. K., et al. (2009). Reliability assessment of passive isolation condenser system of AHWR using APSRA methodology. Reliabil. Eng. Syst. Safety 94, 1064–1075. doi:10.1016/j.ress.2008.12.002
Nayak, A. K., and Sinha, R. K. (2007). Role of passive systems in advanced reactors. Prog. Nucl. Energy 49, 486–498. doi:10.1016/j.pnucene.2007.07.007
Nayak, A. K., and Vijayan, P. K. (2008). Flow instabilities in boiling two-phase natural circulation systems a review. Sci. Technol. Nucl. Install. 2008, 15. doi:10.1155/2008/573192
Nevo, A. D., Rozzia, D., and Agostini, P. (2012). “Investigation of RELAP5 code capability in predicting phenomena in a SMR system,” in 21st International Conference Nuclear Energy for New Europe(LJUBLJANA 2012).
Pagani, L. P., Apostolakis, G. E., and Hejzlar, P. (2005). The impact of uncertainties on the performance of passive systems. Nucl. Technol. 149, 129–140.
Sarrette, C. (2003). Effect of NoncondensableGases on Circulation of Primary Coolant in Nuclear Power Plants in Abnormal Situations. Lappeenranta: Acta Universitatis Lappeenrantaensis, 144.
Schulz, T. L. (2006). Westinghouse AP1000 advanced passive plant. Nucl. Eng. Des. 236, 1547–1557. doi:10.1016/j.nucengdes.2006.03.049
Sinha, R. K., and Kakodkar, A. (2006). Design and development of the AHWR-the Indian thorium fuelled innovative nuclear reactor. Nucl. Eng. Des. 236, 683–700. doi:10.1016/j.nucengdes.2005.09.026
Smidts, C. (1992). Probabilistic reactor dynamics IV: an example of man machine interaction. Nucl. Sci. Eng. 112, 114–126.
Soon Heung, C., and Won-Pil, B. (2003). “Understanding predicting and enhancing critical heat flux,” in The 10th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-10) eds C. Soon Heung, B. Won-Pil, and R. Joy (Seoul).
Taylor, B. K., and Martin, R. P. (1992). “Benchmarking assessment of RELAP5/MOD3 for the low flow and natural circulation experiment,” in The International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-5) (Salt Lake City), 21–24.
Tombuyes, B., and Aldemir, T. (1996). “Dynamic PSA of process control-systems via continuous cell-to-cell-mapping,” in Probabilistic Safety Assessment and Management, eds P. C. Cacciabue and I. A. Papazoglou (New York: Springer-Verlag), 1541–1546.
Voroyev, Y., and Kudinov, P. (2011). “Development and application of a genetic algorithm based dynamic PRA methodology to plant vulnerability search,” in PSA 2011 (LaGrange Park: American Nuclear Society), 559–573. Available at: http://www.scopus.com/inward/record.url?eid=2-s2.0
Zhao, H., and Peterson, P. F. (2010). “An overview of modeling methods for thermal mixing and stratification in large enclosures for reactor safety analysis,” in The International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NUTHOS-8).
Zio, E., Cantarella, M., and Cammi, A. (2003). The analytic hierarchy process as a systematic approach to the identification of important parameters for the reliability assessment of passive systems. Nucl. Eng. Des. 226, 311–336. doi:10.1016/S0029-5493(03)00211-5
Zubair, M., and Gyunyoung, H. (2013). Advancement in living probabilistic safety assessment (lpsa) to increase safety of nuclear power plants. J. Risk Reliabil. 227, 534–539. doi:10.1177/1748006X13485192
Zubair, M., Zhang, Z., and Aamir, M. (2010). A review: advancement in probabilistic safety assessment and living probabilistic safety assessment. Power Energy Eng. Conf. 28–31. doi:10.1109/APPEEC.2010.5449216
Zubair, M., Zhijian, Z., Gyunyoung, H., Ahmed, I., and Muhammad, A. (2013). A computer based living probabilistic safety assessment (LPSA) method for nuclear power plants. Nucl. Eng. Des. 265, 765–771. doi:10.1016/j.nucengdes.2013.09.017
Keywords: passive systems, reliability, REPAS, RMPS, APSRA
Citation: Nayak AK, Chandrakar A and Vinod G (2014) A review: passive system reliability analysis – accomplishments and unresolved issues. Front. Energy Res. 2:40. doi: 10.3389/fenrg.2014.00040
Received: 21 July 2014; Accepted: 18 September 2014;
Published online: 10 October 2014.
Edited by:
Muhammad Zubair, University of Engineering and Technology, PakistanReviewed by:
Muhammad Zubair, University of Engineering and Technology, PakistanKun Chen, Chinese Academy of Sciences, China
Khalil Ur Rahman, Kyung Hee University, South Korea
Copyright: © 2014 Nayak, Chandrakar and Vinod. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arun Kumar Nayak, Reactor Design and Development Group, Bhabha Atomic Research Centre, Trombay, Mumbai 400085, India e-mail:YXJ1bnRoc0BiYXJjLmdvdi5pbg==
 Arun Kumar Nayak
Arun Kumar Nayak Amit Chandrakar
Amit Chandrakar Gopika Vinod3
Gopika Vinod3