Relationships among the energy, emergy, and money flows of the United States from 1900 to 2011

Energy Systems Language models of the resource base for the U.S. economy and of economic exchange were used, respectively, (1) to show how energy consumption and emergy use contribute to real and nominal gross domestic product (GDP) and (2) to propose a model of coupled flows that explains high correlations of these inputs with measures of market-based economic activity. We examined a third power law model of growth supported by excess resources and found evidence that it has governed U.S. economic growth since 1900, i.e., nominal GDP was best explained by a power function of total emergy use with exponent 2.8. We used a weight of evidence approach to identify relationships among emergy, energy, and money flows in the U.S. from 1900 to 2011. All measures of quality adjusted energy consumption had a relationship with nominal GDP that was best described by a hyperbolic function plus a constant and the relationship between all measures of energy consumption and real GDP was best described by a second order polynomial. The fact that energy consumption per unit of real GDP declined after 1996 as real GDP continued to increase indicates that energy conservation or a shift toward less energy intensive industries has resulted in lower fossil fuel use and reduced CO₂ emissions while maintaining growth in real GDP. Since all energy consumption measures versus real GDP deviated from a power law relationship after 1996; whereas, total emergy use did not, we concluded that total emergy use captured more of the factors responsible for the increase in real GDP than did energy measures alone, and as a result, total emergy use may be the best measure to quantify the biophysical basis for social and economic activity in the information age. The emergy to money ratio measured as solar emjoules per nominal $ followed a decreasing trend from a high of 1.01E+14 semj/$ in 1902 to 1.56E+12 semj/$ in 2011 with fluctuations in its value corresponding to major periods of inflation and deflation over this time.

Introduction

In 1994, Ken Watt stated that “For a century two different bodies of theory have been developed to account for the dynamic behavior of society. One assumed that money, interest rates, the policy decisions by governors of central banks, and related variables accounted for historical change. The other assumed the interplay between resource availability, particularly energy, and demographic variables determine societal dynamics. Temporarily the former is in the ascendancy ….” In this context, it is clear to us that a deep understanding of the relationship between economic activity and the energy, material, and information resource base that supports it is essential for guiding economic development, and for minimizing the impacts of wastes, e.g., the effects of excess CO₂ production on the global ecosystem. At present, the dominant economic paradigm used to manage the United States (U.S.) in the twenty-first century is not as fully informed as it could be, i.e., only an understanding of the mutual coupling of money as a counter current to energy, material, and information flows (Odum, 1983) will provide a holistic mechanism for managing society. Watt (1994) goes on to say, “However, the situation will clearly have reversed by shortly after the year 2000. It will have become apparent that the presently dominant theory has no predictive utility. There will be only one completely worked out, synthetic theory to which people will be able to turn for guidance: that developed by Odum, and applied to many situations by his students.” In this paper, we will examine how Energy Systems Theory, EST (Odum, 1983), and the emergy evaluation methods derived from it (Odum, 1996) provide a more robust basis for understanding economic activity than that available from financial methods alone or by using other less comprehensive biophysical approaches, e.g., measures of energy consumption.

One illustration of the way that EST integrates economic activities within the context of their biophysical basis is the emergy to money ratio (EMR). This index relates the economic activities of society in a given year as measured by the nominal Gross Domestic Product (GDP), of a nation, state, or region to the underlying flows of emergy or real wealth¹ that support the economic activities of the system in that year (Odum, 1996). For example, the EMR shows the average power of money to buy real wealth in a system, which then can be compared to the buying power of money in other systems. Thus, if more money circulates for a given flow of real wealth (emergy), or if the flows of real wealth decline for the same money flow, the buying power of money will decline. Either of these events will cause an economic condition called inflation (Odum, 1983, 1996). Therefore, the change in the EMR of a system over time is an indicator of the change in the inflation rate in that system. The inverse of this condition is deflation caused by a declining money flow while the flow of real wealth remains constant, increases, or decreases at a slower rate.

Our general approach is to use theoretical models and hypotheses to guide exploration of ideas about the way that economic activities are integrated within environmental systems and to investigate observed patterns in the relationships among energy, emergy, and money flows of the U.S. from 1900 to 2011. We used EST and the Energy Systems Language (ESL) (Odum, 1983) as the basis for model construction. We created three ESL models, which we used to formulate sets of hypotheses about (1) how national economic systems are organized, (2) how money flows and emergy flows are coupled, and (3) the dynamics that control growth in a national system that has access to excess resources. Note that by drawing an ESL model, interrelated sets of working hypotheses are an outcome of the structure of the model. Together, these models begin to demonstrate that emergy use provides a more robust explanation of economic activity than other biophysical measures and economics alone. In this paper, emergy use and total emergy use both refer to the emergy used annually, solar emjoules/year, to support the U.S. economy and are equivalent to empower. The EST models presented provide a theoretical basis for understanding relationships that may not have been well understood within existing research studies on these topics using other perspectives. In addition, we look for ways to definitively demonstrate that emergy use is superior to measures of energy consumption alone in the ability to explain variations in economic activities, i.e., changes in nominal and real GDP in the U.S. economy over the past 112 years. To accomplish this end, we formulated several null hypotheses (see Theory and Hypothesis), but primarily, we use a weight of evidence approach that combines data analysis with various statistical methods and tests to answer our research questions.

The research questions were designed to gain a better understanding of how measures of energy consumption and emergy use are related to economic activity, i.e., nominal and real GDP. To accomplish this, we focused on the analysis of pairs of variables (Table 1) with the goal of increasing our understanding of the causal relationships among them and the functional forms that best described these relationships. We were also interested in obtaining a better understanding of the causes and magnitude of the great economic events of the twentieth century and, in particular, to investigate the magnitude, causes, and consequences of the Great Recession of 2008–2013 (GR08).

TABLE 1

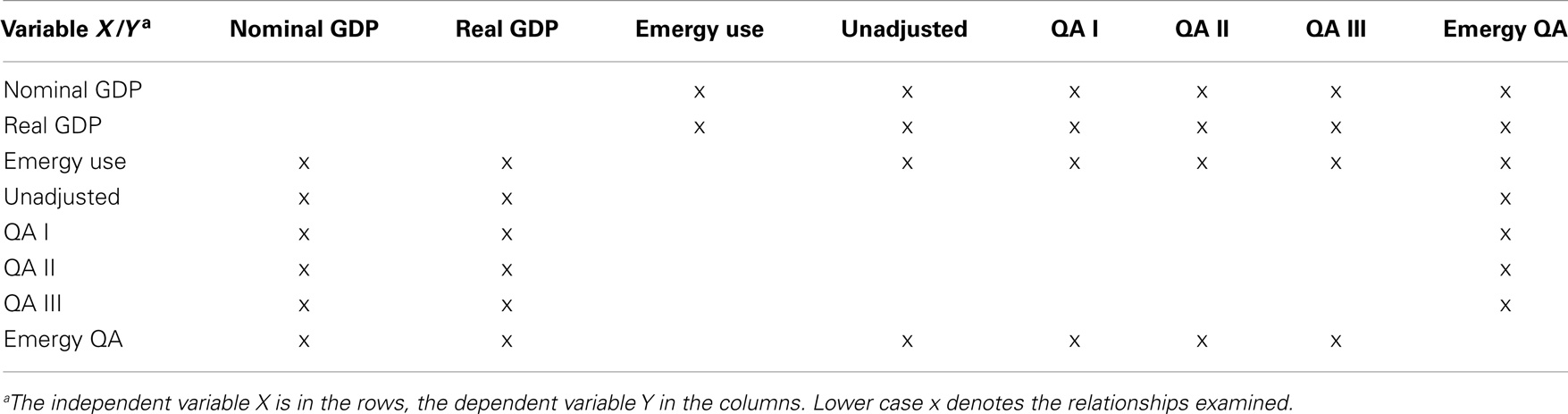
Table 1. Pairs of emergy, energy, and economic variables for which relationships were explored in this paper, where unadjusted, QA I, QA II, QA III, and Emergy QA are the energy consumption variables (see Energy Methods).

Hypotheses cannot be tested without data, and in this case, a new analysis of the emergy basis for the economy of the U.S. from 1900 to 2011 was the vehicle that provided the information needed to formulate questions and evaluate relationships. We used empirical data of known uncertainty gathered by government sources in a uniform manner, along with the latest information on unit emergy values (UEVs) to calculate or update the emergy inputs supporting economic activities of the U.S.

Following the introduction, this paper includes a consideration of previous studies relevant to the analysis (see Past Studies and Events Relevant to the Analysis), a presentation of the theoretical models and hypotheses used in the weight of evidence approach (see Theory and Hypothesis), the emergy, energy, economic, and statistical methods used (see Methods), the results of our analyses (see Results), a discussion of the major findings (see Discussion), and conclusions (see Conclusion). Supplementary Material contains the detailed methods used in evaluating the U.S.; the tables of the UEVs used; and the emergy inputs to the U.S. economy from 1900 to 2011 along with the total emergy use and the EMR.

Past Studies and Events Relevant to the Analysis

Past Studies of the Relationship between Emergy Use and Money Flows (GDP)

The EMR has been calculated in many studies evaluating nations and states for particular years (Odum, 1996; Brown, 2003; Campbell et al., 2005a; Campbell and Ohrt, 2009). However, there are fewer studies that calculate this index over a long period of time. Odum (1996) presents a table that estimates the EMR for the U.S. from 1947 to 1993. Odum made these calculations based on a complete emergy analysis of the U.S. in 1983. The EMRs for years other than 1983 were determined by substituting the available annual data for energy use and Gross National Product (GNP) into the expression for the EMR under the assumption that all other values remained constant over the period. More recently, Tilley (2006) estimated the emergy inputs supporting the U.S. economy from 1790 to 2000 to use in evaluating the emergy basis of technology. Tilley took into account the changing area of the U.S. over this time and he used empirical data and some assumed functional relationships to estimate the emergy inputs supporting the U.S. economy. Tilley’s estimate for the emergy of the minerals required was based on a small subset of the 82 minerals assessed in this study and he notes that this is the most uncertain input in his analysis.

An earlier version of this paper (Campbell and Lu, 2009) contained data on the U.S. system up to 2007. When that study was first performed, the U.S. economy was mired in the depths of the decline that Stiglitz (2010) has called the Great Recession of 2008. We were intrigued by the fact that there was no hint of GR08 in the data on energy consumption and GDP that were available to us at that time, i.e., through 2007. However, the leading edge of the recession was visible in 2007 as evidenced by a decline in the emergy of minerals used to support the U.S. economy in that year. By completing this study in 2013, when an additional 4 years of data were available, we were able to quantify GR08 in terms of the perturbation of emergy, energy, and monetary flows; thereby, increasing our understanding of this event. GR08 will be examined as a subtheme in this paper, because the interrelationships between emergy use, energy consumption, and economic activity can be clearly observed in this perturbation. The financial and economical aspects of GR08 have been examined by Stiglitz (2010) and we will draw on this work along with other general readings on the subject to provide an understanding of the financial and economic conditions that are the context for our examination of the perturbation of emergy, energy, and material flows that characterized this event.

Past Studies of the Relationship between Energy Consumption and GDP and Vice Versa

There have been many studies in energy economics that attempt to establish causality from economic activity to energy consumption or vice versa. Many of these studies focus on verifying that energy use and associated CO₂ production can be reduced without harming economic growth (Huang et al., 2008; Menegaki, 2014). This research has focused primarily on identifying the direction of causality between energy consumption and GDP. In these studies, causality is determined most often using a statistical time series method first proposed by Granger (1969), which has been modified and improved over time (Stern, 1993, 2000; Soytas and Sari, 2003; Oh and Lee, 2004; Amiri and Zibaei, 2012; Menegaki, 2014; Yildirim et al., 2014). Granger proposed that the existence of a causal relationship between two variables could be tested by determining if there was a correlation between past values of a variable, X, and that part of another variable, Y, which cannot be predicted from its own past values. If no correlation is found, the implication is that X has no causal influence on Y (Sims, 1972). Four possible outcomes of the time series analyses of the data are as follows: (1) growth in energy consumption causes or leads to growth in real GDP or in some cases another measure of national income; (2) growth in real per capita GDP leads to growth in energy consumption; (3) mutual causality or a feedback loop with greater GDP leading to greater energy consumption and vice versa; (4) no effect of GDP on energy consumption and vice versa, i.e., neutrality. Many examples of different national studies performed at various times illustrating the different possible results can be found in the references given by Huang et al. (2008). Oh and Lee (2004) point out that over the past 30 years, there have been many studies investigating Granger causality between energy consumption and GDP and vice versa, but that the empirical evidence obtained remains ambiguous and these studies have not resulted in a clear consensus on the nature of this relationship. Our review of more recent literature (Narayan and Popp, 2012; Yildirim et al., 2014) does not demonstrate that the situation has improved very much with the use of different methods. Perhaps the state of these studies is best summed up by Beaudreau (2010), who wrote, “Despite their growing technical sophistication and empirical breadth, Granger energy-GDP causality tests remain inconclusive, leaving unresolved the increasingly relevant debate over the role of energy or energy growth in economic growth.” Even though the results of these studies are variable in space and time and the overall results are inconclusive, understanding the relationship between energy consumption and GDP is not a moot point. In fact, the existence of a relationship in either direction or indeed the non-existence of a relationship may affect the choice of environmental, energy, and economic policies (Lee, 2006).

Another more comprehensive and systems-based approach to gaining an understanding of the basis for economic activity through energy analysis can be found in Hall et al. (1986). Embodied energy and exergy analyses of the relationship between different measures of energy consumption and economic activity in the U.S. economy were considered by Cleveland et al. (1984) and Ayres et al. (2003), respectively. In this study, we will draw on the work of Cleveland et al. (1984) to provide the means for comparing energy consumption measures as predictors of economic activity with emergy measures.

Past Studies of the Relationship between Emergy, Energy, and GDP

Ko and Hall (2003) examined the relationship between nominal GDP and quality-corrected commercial energy use for 17 countries over 35 years and compared the results to the relationship between nominal GDP and total emergy use for the same nations and time period. They found high values for the coefficients of determination for linear regression models of GDP per unit area versus commercial energy use per unit area for those countries over the three times examined (i.e., R² = 0.990, 0.994, and 0.962 for all countries in 1970, 1980, and 1990, respectively). In a similar analysis, they also found high R² values for the linear regression model of area normalized GDP to area normalized total emergy use (i.e., R² = 0.989, 0.994, and 0.949 for all countries in 1970, 1980, and 1990, respectively). Greater differences in the ability of emergy use and quality-corrected energy consumed to explain economic activity of the various nations were observed when the three countries, with the most intense energy, emergy, and economic flows (i.e., Korea, the Netherlands, and the U.S.) were removed from the data set. In this case, the R-squares of the relationships between emergy use and GDP (0.477, 0.692, 0.778 in 1970, 1980, and 1990, respectively) declined more in all three periods examined compared to the decline in the ability of quality adjusted (QA) energy consumption to explain GDP (0.813, 0.784, and 0.801 in 1970, 1980, and 1990, respectively).

Theory and Hypothesis

Overview Model of Society and the Environment

A model that can be used to investigate the relationship between environmental resources and the activity of socioeconomic systems, as described earlier by Watt, is shown in Figure 1. The World System model looks at the relationships between the environment and socioeconomic processes as a whole, but it can also be modified to describe a national system. For the whole Earth, the primary exchanges with the larger extraterrestrial system are solar and gravitational energy entering the Earth (the circles in Figure 1) and long wave radiation reradiated into space as heat (part of the heat sink or arrow to ground symbol in Figure 1). Reflected radiation is indicated by the flow of solar energy leaving the system, J_R. This model shows the hypothesized connections within the system of environment and society in terms of the emergy flows resulting from the work of human beings (J_HW pathways) and the emergy flows from the work of the environment (J_NW pathways), as well as emergy flows of products produced by nature (J_NP) and in the economy (J_EPS). Within the large box indicating the spatial boundaries of the World System, solar and gravitational available energy² entering from outside (two parts of J_NW1) interact with the available energy from the Earth’s heat flow (the third part of J_NW1) to create the secondary available energy flows and processes of the planetary system, e.g., the rain, wind, continental drift, tides, waves, rivers, etc. Over millions of years, the biogeochemical processes of the planet slowly generate storages of fossil fuels and minerals within the Earth’s crust. These processes are designated as J_NW2, which means the flow of nature’s work on the second class of pathways.

FIGURE 1

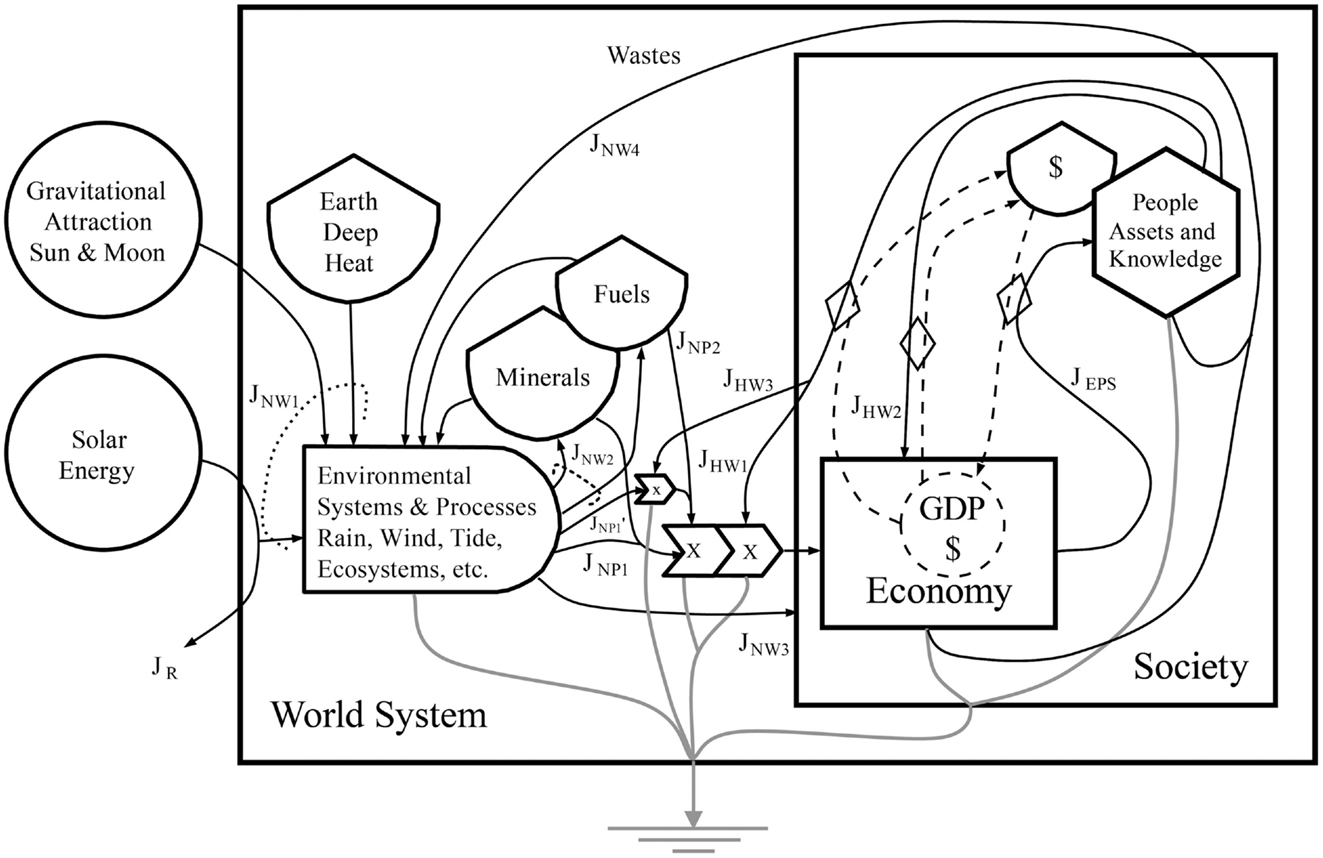
Figure 1. This Energy Systems Language (ESL) diagram of the World System shows the interaction of external energy sources driving slow and fast planetary processes, which support the economies and societies of the world. The diagram represents energy sources (circles), storages (tanks), and flows of materials, energy and information (solid black lines), and money (dashed lines). System boundaries and subsystems are delineated by boxes, the interaction of flows by rectangular arrows containing a mathematical symbol, production systems by the bullet shaped symbol, and consumers by the hexagon. The exchange of money for goods is represented with a diamond symbol (Odum, 1983).

Natural ecosystems also do work that directly and indirectly supports the activities of the world’s ecological and socioeconomic systems. For example, indirect work on pathway J_NW3 includes photosynthesis that fixes carbon and replenishes oxygen in the atmosphere, which is necessary for all life, the movement of clean air that replaces contaminated air over cities and water flows that provide the capacity to dilute municipal wastes. In addition, nature does direct work to transform and process the wastes produced by socioeconomic systems (J_NW4), e.g., the bacterial metabolism that denitrifies sewage wastes and particulate and dissolved organic carbon that chemically bind toxic materials, which then settle at the bottom of water bodies and are ultimately removed from the biosphere by burial in the earth. In this case, material leakage from the socioeconomic systems joins the normal cycles of material processing used to maintain the biosphere that occur within the producer symbol, adding to the load on these processes. Natural products (NP) are used by ecosystems, but some of these products (J_NP1), e.g., soils, timber, groundwater, etc., are appropriated for use by the socioeconomic system. The emergy flow in fuels and electricity (J_NP2) acts to arrange and order material products using the prevailing technology of the time. Humans do work (J_HW1) on the environmental system to extract and process raw materials provided by the work of the environment, i.e., non-renewable products like fossil fuels and minerals, as well as renewable products (J_NP1) like soils or timber. These potentially renewable inflows are considered to be non-renewable when they are being used by the socioeconomic system at a rate that is faster than their natural renewal rate. Also, human work (J_HW2) is used to carry out economic production using raw materials and to perform other processes, e.g., waste treatment and material recycle, as well as other functions of society. People build assets and knowledge through carrying out economic processes and using the economic products and services (J_EPS) produced. In turn, they use these assets along with their knowledge and experience to perform the work processes needed to capture more fossil fuel, mineral, and renewable energies to be used to further build and maintain society.

A special category of human work (J_HW3) is recognized as important in this model, i.e., the work performed to extract available energy from the renewable energy flows (J_NP1′), which can be used directly in running socioeconomic systems. This work creates, maintains, and operates infrastructure capable of transforming renewable energy into electricity or another high quality form of energy that can be used to operate the socioeconomic system. The sustainability of civilization in the long run depends on the success of human endeavors in magnifying work done on pathway J_HW3 to the point where it can carry out most of the work processes needed to support socioeconomic systems. For example, some current research on this problem focuses on strategies and methods to carry out a successful social transition from fossil fuel based economies to renewable economies. Sgouridis (2014) argues that this transition may be characterized by an “energy trap” in which investment in renewable energy technologies before fossil resources peak is insufficient to maintain a post-peak society based largely on renewable energy. He provides a proposal for insuring a successful transition to a sustainable energy future through the implementation of energy-based currencies.

Money flows (dashed lines in Figure 1) track the flows of available energy in human work (J_HW pathways) as a counter current but do not flow counter to nature’s work (J_NW) pathways. This diagram shows how economic processes are dependent on the work processes of nature, but that money does not track or account for these natural work processes; therefore, money flows in a market economy are an incomplete measure of the work required to assure the continued and proper functioning of society and of the value incorporated in economic products and services (J_EPS). A crucial feature of this model is that materials in the form of mineral products, e.g., coal oil, uranium, iron, etc. and NP, e.g., timber, soils, water, etc. are incorporated into economic products and services through the expenditure of fossil fuel and other energies controlled by knowledgeable human actions (e.g., technology). In this model, the flows of minerals, human work, fossil energy, and NP are all part of the same network of coupled interactions; and thus, they are not independent, but rather are functions of one another because of their multiplicative interactions. This model illustrates the conceptual basis that explains why emergy, which can quantify the flows on all pathways, is potentially a better (more complete) measure of economic activities than either money flows or energy consumption alone, each of which quantifies only some of the system’s pathways. To further examine this point, we formulated the following null hypothesis, which we will subsequently test as part of our weight of evidence approach.

H₀: The total emergy use to real GDP ratio will explain less of the variance in economic activity from 1900 to 2011 than will the ratios of unadjusted and QA energy consumption to real GDP.

Energy/Economic Analyses and a Model of Coupled Flows in Economic Exchange

The model in Figure 2A represents the situation investigated by the application of Granger-related methods in the literature on energy economics as described in Section “Past Studies of the Relationship between Energy Consumption and GDP and Vice versa.” Perhaps, one reason that these studies have never produced a comprehensive overall synthesis of the results is that, for the most part, they have been performed in an exploratory manner without a valid underlying model of the process (Beaudreau, 2010). As shown in Figure 2A, the process being examined is one in which the flows of money are coupled through exchange mechanisms (prices) to the purchased flows of energy, materials, and information being supplied to production processes. These exchange mechanisms are governed by the laws of supply and demand and the price mechanism. As a result, plots of money flow versus energy or emergy flow and vice versa are plots of coupled variables, and therefore high positive correlations among these variables are expected. In this model (Figure 2A), Q is a supply of available energy, material, or emergy (in J, g, or semj) and M is an amount of money ($). A flow of some biophysical quantity, J_Q [e.g., in joules per year (J/y)] results from an expenditure of money governed by the supply and demand relationship:

${\mathrm{J}}_{\mathrm{Q}}={\mathrm{J}}_{\mathrm{M}}∕\mathrm{p}=\mathrm{k}\ast \mathrm{M}\ast \mathrm{Q},\mathrm{where\hspace{0.17em}p}\propto \mathrm{1}∕\mathrm{Q}$ (1)

FIGURE 2

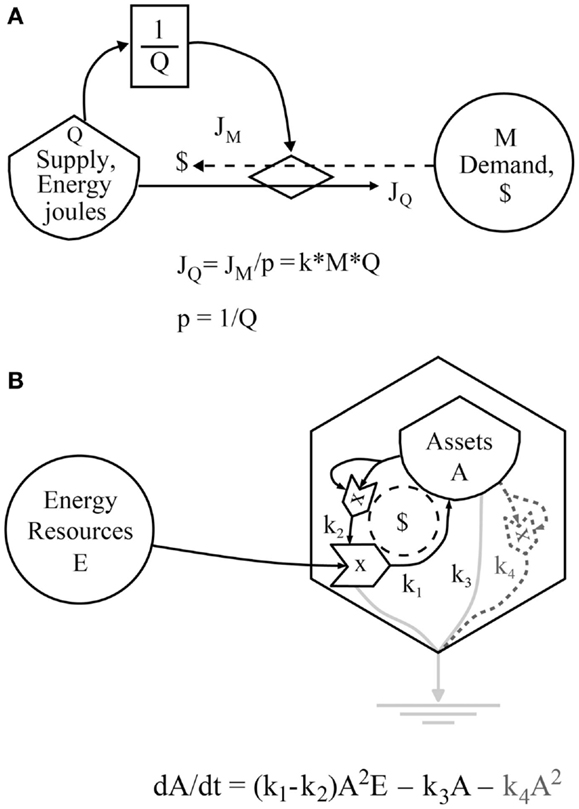
Figure 2. (A) An ESL model of one possible coupling between energy and money flows. A flow of money, J_M, ($/y) directed toward the purchase of available energy Q (Joules) is demand. In this case, the price is inversely proportional to the supply of available energy (1/Q), so as the supply decreases the price is adjusted upward. The flow of energy, J_Q, (J/y) is then proportional to the demand divided by the price. (B) A model of the super-accelerated growth of system assets, A, due to cooperative interactions (A² term on pathway k₂) among people and their institutions. Symbols drawn with dotted dark gray lines and the dark gray term in the equation indicate that a quadratic drain is needed to level growth. The dashed circle indicates the dollar flows coupled to the flow of available energy and light gray lines are used energy leaving the system. The third power law comes into play due to the A²E (E³) interaction.

Here the asterisk sign means multiplication and the price, p (e.g., $/J) is an inverse function of the supply of Q. This formulation mathematically demonstrates the coupling between emergy, energy, or material flows as J_Q and the related money flows (i.e., J_Q = k*M*Q), where k has reciprocal units, so that k (1/$*y)*M ($)*Q (J) gives a flow of available energy (J/y). Alternatively, J_Q (J/y) = J_M ($/y)/p ($/J) where p α 1/Q. In this case, available energy or material flows are necessary for flows of real wealth (emergy) to occur. In addition, to helping us understand the difficulty in definitively establishing causality in a system of coupled flows, the model in Figure 2A informs our analysis of all the relationships between pairs of variables mentioned in the Section “Introduction” (Table 1). Note that the energy consumption variables in unadjusted and QA forms are those used by Cleveland et al. (1984) in their analysis of the U.S. economy from an embodied energy perspective, i.e., based on QA energy consumption (see Energy Methods). Energy analysts have been reluctant to use emergy as a quality adjustment factor (Cleveland et al., 2000), thus we state the following null hypothesis, which we subsequently test:

H₀: The emergy of the energy consumed (Emergy QA) can be shown to be significantly different from other energy consumption variables, i.e., both unadjusted and QA energy consumption.

A Model Describing Growth of the U.S. Economy from 1900 to 2011

Odum (1983) gives a model for super-accelerated growth of the assets of a socioeconomic system, which may result from cooperation among people or social organizations, e.g., companies, religious organizations, institutions, etc. The equation for this model is given in Figure 2B by a modified version of the model in Odum (1983) as follows:

$\mathrm{dA}∕\mathrm{dt}=\left({\mathrm{k}}_{\mathrm{1}}-{\mathrm{k}}_{\mathrm{2}}\right){\mathrm{A}}^{\mathrm{2}}\mathrm{E}-{\mathrm{k}}_{\mathrm{3}}\mathrm{A}-{\mathrm{k}}_{\mathrm{4}}{\mathrm{A}}^{\mathrm{2}}$ (2)

where A is some measure of the total assets of society, e.g., emergy or available energy and E is the available energy or emergy of the resource input (J/y or semj/year). The coefficients, k₁ − k_2, respectively, represent the pathway coefficients (Odum and Odum, 2000) controlling the gross intake of resources and the resources required to capture those resources, so that k₁ − k₂ is analogous to net production of an ecosystem. Pathway coefficients k₃ and k₄ determine the rate of energy or material loss in the linear and quadratic catabolic pathways_. All coefficients have reciprocal units so that the units of the flows on all pathways are correct (Odum and Odum, 2000). Note that drains of higher order (dotted lines and terms, k₄A² in Figure 2B and Eq. 2 shown in dark gray) or drains matched to the growth interactions (Smith, 1976), e.g., the increasing negative effects of pollutants on a growing economy, are needed to stabilize this model.

The capacity of human beings to cooperate in endeavors (Von Foerster et al., 1960) is responsible for the quadratic term in the feedback governing growth (i.e., A²E in Eq. 2, where A² is the quadratic effect of the cooperative use of assets on growth. Since A is a function of E, growth is proportional to E³. Thus, resource inflows should be a function of the third power of the available energy and its associated emergy, which drive asset growth giving rise to a similar growth curve for economic activity (nominal GDP, $ flow in Figure 2B), which is directly coupled to the available energy and emergy flows. Odum notes that although the U.S. appears to have followed this growth curve during the twentieth century, it is not a sustainable pattern as shown above by the need to add higher power drains to level growth.

Since economic activity is coupled as a counter current to energy and emergy flow (Figure 2A), we might expect nominal money flows ($) to follow a super-exponential or a higher power law as a function of the available energy of resources (Canadell and Mooney, 2002) and that in the ideal case of full cooperation, economic activity would be expected to increase in proportion to the third power of the emergy used (Odum, 1983). A similar relationship is expected for energy consumption, since excess resource availability makes super-accelerated growth possible (Odum, 1983, p. 149). In this manner, the emergy of resources is incorporated into the assets of society more rapidly, which can then feedback through interactions to gain more resources in competition with other users. The system with the greatest emergy gains maximizes its empower and will prevail in competition (Odum, 1983, 1996).

In our view, the existence of this relationship has more of the character of an EST legend than it does a well-documented fact. The mathematical evidence is clear that this growth form should be observed for systems with a cooperative feedback to gain available energy, but in practice super-accelerated growth has been rarely demonstrated and then most often in systems unrelated to human cooperation [e.g., the Schlögl chemical reaction in Nicolis and Prigogine (1977)]. Odum noted that the U.S. appears to have followed this growth curve during the twentieth century, but we were not able to find the reference where this was demonstrated. For this reason, we decided to take advantage of the long history of growth in the U.S. economy assembled for this study to look for evidence of this theoretically predicted but empirically elusive relationship. We formulated the following null hypothesis to help us determine if a third power law may have governed growth in the U.S. economy from 1900 to 2011:

H₀: The exponent describing a power function relationship between nominal GDP and total emergy use will fall to a least 2 SD outside of a normal distribution with mean 3 (i.e., a third power law) and SD 0.299 (see Nominal and Real GDP as a Function of Total Emergy Used and Energy Consumed), which is the observed SD of the exponents of the power function relationships between nominal GDP and all measures of energy consumption and total emergy use.

The Link between Emergy Use and Energy Consumed and Economic Activity in Developing and Developed Economies

The correlation observed between total emergy use and measures of economic activity such as GDP will be determined largely by the fraction of the total emergy used that is represented in the GDP calculation. In Figure 1, J_HW1, J_HW2, and J_HW3 represent emergy flows considered within GDP, but the N_W3 pathway is not directly coupled to money flows. In addition, most of the emergy of raw products flowing on J_NP1 and J_NP2 comes from the work of nature, e.g., about 30% of the emergy value of forest products is tracked by money at the point of extraction from nature (Campbell and Cai, 2007). Thus, we might expect the correlation between total emergy use and GDP to be diminished for systems in which the emergy flows on pathways J_NW3, J_NP1, and J_NP2 are large compared to the emergy flows on J_HW1, J_HW2, and J_HW3, as found by Ko and Hall (2003) when the three most energy and economically intensive countries were removed from their analysis. In the case of this analysis of the U.S., the correlation between both energy and emergy use and GDP is expected to be high, because most of the emergy and energy flows supporting a developed economy are directly coupled to economic production functions.

Theoretically, it is plausible that total emergy use to real GDP correlations may exceed the QA energy consumed to real GDP correlations in advanced economies, because minerals and NP, like timber, are required for production processes and also are coupled with GDP, but their contributions to the economy are not completely captured by the QA energy consumption required for their extraction and processing. Therefore, energy consumption measures may not contain all of the relevant information about economic production needed to result in the highest correlations with GDP.

Methods

Emergy Evaluation Methods and Measures

A general introduction to the methods of environmental accounting using emergy can be found in many publications, e.g., Brown and Ulgiati (2004), Campbell et al. (2005a), and Campbell and Ohrt (2009) since they were first put forward by Odum (1996). Emergy is a quantity based on the second law of thermodynamics, because it is a measure that accumulates all the available energy used up in the process of creating any item after converting those energies to a common base, i.e., an emjoule (emj) of solar energy, coal energy, etc. The transformation to emergy units normalizes all inputs to a production process in terms of an equivalent ability to do work, when used within a system that has had time to adapt to its inputs (see The Emergy Basis for Economic Activity: Coupled flows). Emergy is formally defined as the available energy of one kind previously used up directly and indirectly to make a product or service (Odum, 1986, 1988; Scienceman, 1987). Emergy is measured in solar emjoules (semj)³. The emergy of any product or service can be quantified by obtaining data on the available energy or mass of the product or service and then multiplying this value by the appropriate emergy per unit value, UEV, i.e., the transformity (semj/J) for available energy or the specific emergy (semj/g) for mass, etc. Emergy analyses are carried out using transformities, specific emergies, and other UEVs that are determined relative to a particular planetary baseline (Odum, 1996; Campbell, 1998), which in turn, is determined from the equivalences established for the three primary energy inputs to the biogeosphere, i.e., solar radiation, deep heat flow from the Earth, and the gravitational attraction of the sun and moon. In this study, we use the 9.26E+24 semj/y baseline recommended by Campbell (2000) and Campbell et al. (2005b).

First, the method used here to define the EMR for the U.S. is to identify the principal sources of emergy supporting economic processes over the time period of interest. Second, identify sources of data needed to quantify those inputs and develop estimation methods where the specific data needed are not directly available. The third step is to locate or calculate the appropriate UEVs needed to convert the units of the raw data into estimates of annual emergy flow. Next, the raw data values for each year are converted to energy or mass and then multiplied by the appropriate UEV. A new emergy analysis method that was developed after this study avoids double-counting in the evaluation by making the process of specifying inputs mathematically explicit through using the union function from set theory (Morandi et al., 2013, 2014).

A contribution of this study is the use of a more complete evaluation of the emergy supplied to the U.S. economy in the minerals consumed. The quantification of the specific emergies of minerals is a current topic of research; nonetheless, we were able to find specific emergies in Cohen et al. (2007) for many minerals evaluated in this study. However, we found problems with some of Cohen et al.’s (2007) specific emergy values. They estimated the specific emergy of minerals in two ways: (1) the specific emergy of the mineral was determined based on the ore-grade cutoff (OGC) or the concentration of the mineral used in the economy relative to the mineral’s background concentration in the crust and (2) for cases in which the OGC was unknown, they used a relationship between OGC and price to estimate the OGC. We found that Cohen’s numbers obtained from the economic method were often incorrect and as a result, we recalculated several values by finding data on the OGC of the mineral. Crustal concentrations are known with moderate uncertainly. For example, Brobst (1973) gives the crustal concentration of barium as 300–500 ppm. We used 300 ppm as our estimate in calculating the specific emergy of barite, which was corrected from Cohen et al.’s value in this study. Moderate variability also exists in the OGC, e.g., for barite it is 200–300 pounds of recoverable barite per cubic yard with a minimum of 220 lbs per cu. yd to be profitable (Brobst, 1973). The OGC values may change with resource depletion and technological development.

Among emergy researchers, it is well known that the transformities and specific emergy values are, in general, the most uncertain numbers in any calculation. Various methods have been used to reduce uncertainty, e.g., Bastianoni et al. (2005) used a determination of the maximum power transformity of petroleum from its optimum geological formation process to verify the transformity for crude oil that had been determined by back calculation of the relative efficiency of electricity generation and factors relating coal to transportation fuels and transportation fuels to crude oil. In this case, the values agreed within 5%. Most transformities are not known with this accuracy and an incorrect choice in calculation can easily result in an order of magnitude error as was found to be the case for barium in this study. The errors in calculating transformities can be reduced by using a self-consistent method that is scientifically plausible as was done by Cohen et al. (2007) for his method using the OGC.

The ESL model in Figure 3 shows the inputs and internal structures of the U. S. national system following the method of energy analysis for a nation described in detail in Odum (1996) and for a state in Campbell and Ohrt (2009). An emergy evaluation of the EMR for a system does not require a full emergy analysis of the state or nation, i.e., only the evaluated pathways in Figure 3 are needed. For example, exports were not evaluated in this study, because they are not part of the annual emergy required to support the Nation. The evaluation methods used to document emergy inputs to the U.S. economy from 1900 to 2011 are presented in Supplementary Material. The following major classes of emergy inputs were documented: (1) renewable energy sources from the environment, (2) soil erosion, (3) energy consumption, (4) minerals consumed, (5) imported goods other than fuels and minerals, (6) imported services in goods, fuels, and minerals, (7) imported services and (8) immigrants, who bring the emergy of their knowledge and experience into the country. Numbers in italics within standard parentheses reference internet data sources used in the U.S. emergy evaluation and are listed in the Data Sources section found at the end of the supplement to this paper (see Supplementary Material).

FIGURE 3

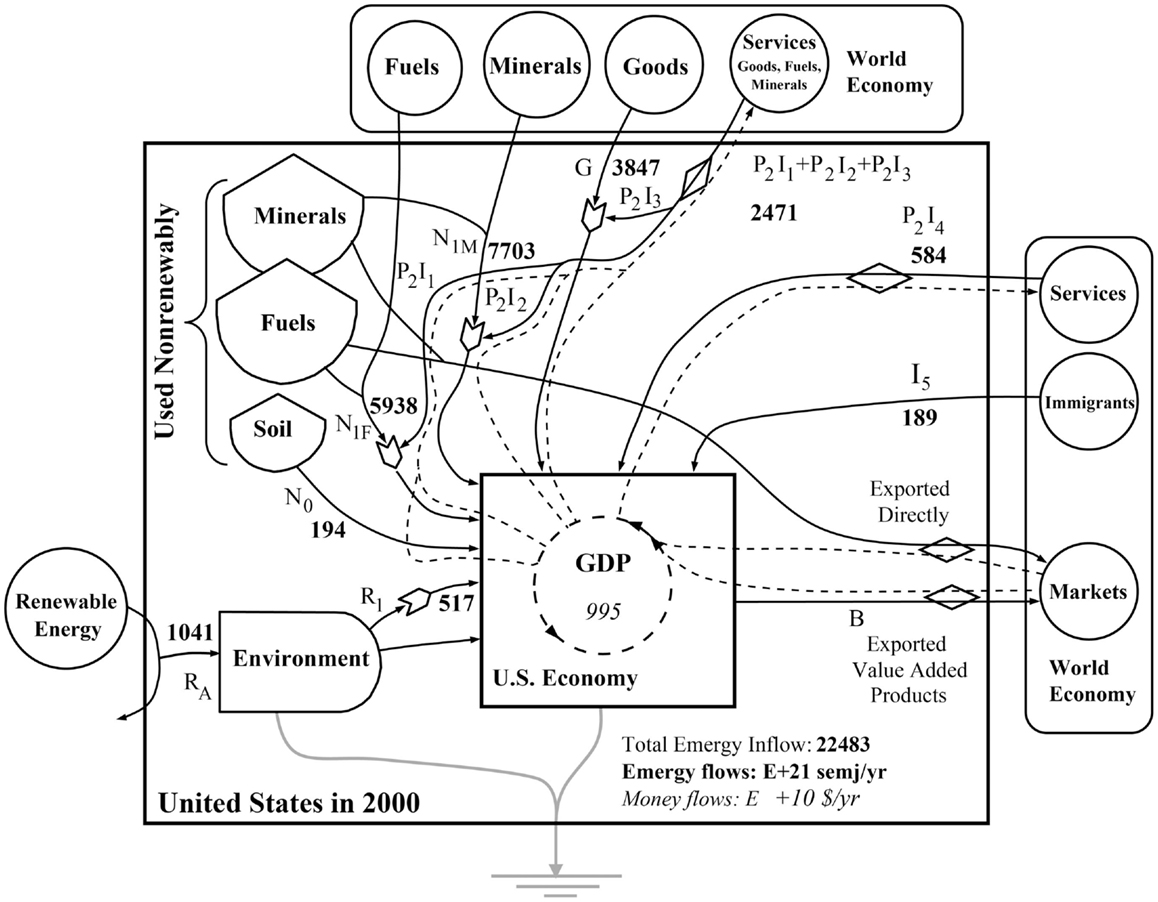
Figure 3. An ESL diagram of the emergy basis for the Untied States evaluated for the year 2000 is shown. ESL symbols are defined in Odum (1983) and briefly in the caption of Figure 1.

Energy Methods

Energy consumption in BTUs was converted to joules and corrected to account for differences in the capacity of different forms of energy to do work by multiplying the various energy sources by quality factors. Three quality adjustments were used following Figure 3 in Cleveland et al. (1984) and Ko and Hall (2003). For Quality Adjustment I (QA I), coal consumption was assigned a factor of 1, natural gas and petroleum consumption were multiplied by a factor of 1.3, and all kinds of electric power by a factor of 4 (Cleveland et al., 1984). For Quality Adjustment II (QA II), we multiplied biomass and coal consumed by 0.92, petroleum and natural gas consumed by 1.74, and all kinds of electric power by a factor of 16.8 (Cleveland et al., 1984). For Quality Adjustment III (QA III), we multiplied primary electricity generated by a factor of 2.6, reflecting the efficiency of turning other forms of energy into electricity (38% thermal efficiency), following Ko and Hall (2003), while including all of the fossil fuel energies with a weighting of 1. The emergy of energy supplied annually by the various energy sources to the U.S. was determined based on the primary source’s contribution of emergy, e.g., the emergy of coal is the primary input and thus the emergy of the secondary use of coal in generating electricity is not considered in comparing the sources’ emergy contributions.

Economic Measures

We obtained data on the economic activity of the U. S. over the periods for which it was available as quantified by the nominal GDP (in current $) and real GDP in chained 2000 dollars⁴. Nominal GDP is adjusted for the change in purchasing power of the dollar over time to determine the real GDP. This was accomplished using the GDP deflator to adjust the dollar values of nominal GDP to reflect prices in a base year.

To further explore the relationship between emergy and money in the U.S. economy, we obtained data on the M1 and M2 money supplies⁵ from 1959 to 2011 and data on the M3 money supply from 1964 to 2011. In addition, we assembled data on the Federal Reserve’s injection of money into financial institutions through a bond buying program called Quantitative Easing (QE), which started in 2008. To obtain the broadest current measure of the money supply in the U.S. economy, we added QE from 2008 to 2011 to estimates of M3 to give M3 plus QE. We determined the velocity of money in each supply, which was needed to understand changes in the U.S. economy observed from 2006 to 2011. In this study, we calculated the ratio of annual emergy use to the dollar storages (money supplies), as well as, the usual ratio using dollar flows (nominal and real GDP) under the assumption that the EMR for a money supply indicates its buying power when placed in circulation, and thus it can serve as a measure of the potential inflationary pressure associated with that money supply.

Money Flows and Storages

Economic data on nominal and real GDP of the U. S. from 1929 to 2011 were obtained from a web posting of the U.S. Department of Commerce, Bureau of Economic Analysis (10). Values for nominal GDP prior to 1929 were obtained from a web posting by Measuring Worth (11). Data for the M1 and M2 money supply from 1959 to 2011 were obtained from a web posting of the Federal Reserve System (12). Data on the M3 money supply and QE were obtained from NowAndFutures.com (13). The velocity of money was calculated by dividing GDP by the various money supplies.

Statistical Methods: Analyses and Tests Performed on the Data

Relationships among the energy, emergy, and monetary measures used in this study with time and with each other were determined using the linear and non-linear regression tools provided in Microsoft Excel 2007 and in Sigma-Plot 11.0. The best fit relationships reported were determined by testing the functional forms (linear, logarithm, exponential, power law, and second order polynomial given in MS Excel and hyperbolic and hyperbolic plus a constant functions provided in Sigma-Plot) using the least squares method. Best fit was determined by choosing the functional form that explained the largest fraction of the variance in the observed data as indicated by the R² of the relationship. We note that regression analyses do not establish cause and effect relationships between the variables tested, but rather are indicative of the similarity or dissimilarity of the relationships between the variables. The Akaike Information Criterion (AIC) was used to confirm the results based on comparison of R-squares, when the number of parameters in the two competing models was different (14).

The data fit to the various models were tested for serial autocorrelation using the Durbin Watson statistic and when appropriate, the regressions were retested with the lag1 differences instead of the raw values, e.g., (Y_t − Y_{t − 1}) versus (X_t − X_{t − 1}). All of the data sets that we tested were positively serially autocorrelated based on the values of the Durbin Watson statistic. In addition, the residuals resulting from the fit of the model to the data were tested for normality and homoscedasticity. The data used was found to be heteroscedastic, but it could be made homoscedastic by log–log transformation. This transformation resulted in a slight decline in the R-squares of the relationships tested. We concluded that we would gain no further understanding by using a log–log transformation on the data.

Because many of the functional relationships tested for different variables had very high R-squares, we used the Kolmogorov–Smirnov test to determine if the distribution of values of the compared variables were statistically different. Distributions of the variables were compared by first sorting the values from lowest to highest and then calculating the frequency distributions of the values using 25 bins. The cumulative distributions of the two variables were then compared by taking the difference, D. If the largest D between bins was greater than the critical D (1.36/√ n, where n = 112) in the Kolmogorov–Smirnov test, the two distributions were considered to be statistically different. We interpreted this as evidence that the observed differences in the characteristics of the two curves being compared were significant, e.g., one relationship with a larger R-square is actually a better descriptor of the data than another with a slightly smaller value of R-square even though both R-squares may be large.

Even though this is a large complex evaluation and there is uncertainty in all of the data that we used, we do not think that this fact has a major affect on our analyses of the relationships among the variables. These relationships depend on the cumulative effects of interactions among the variables over a long time series of data (112 years) during which the magnitude of the variables is growing rapidly. In this regard, the time history of the relationships matters and this affect is expected to overcome the uncertainty in the measurements in any particular year. For example, one could visualize a plot of all of the variables with their uncertainly errors over time represented as an envelope of points; nevertheless, the central tendency of the distributions would be expected to be similar to the curves plotted here.

Results

A summary of the results of the emergy evaluation of the U. S. are given in tabular form in Supplementary Material. This table includes values for each category of annual emergy input to the U.S., the total emergy input, the GDP in nominal $, and the EMR for all years from 1900 to 2011. In this section, first we present the model used to evaluate the emergy basis for the U. S. evaluated for the year 2000. Next, we briefly report the observed temporal patterns of emergy inflows and economic activity including the patterns of energy consumption, mineral use, the economic measures, and the EMRs. The presentation of the temporal patterns in the data concludes our report on the results of the U.S. emergy analysis. Then, we report results from the paired analyses of the functional relationships (Table 1) found between measures of energy consumption, emergy use, and economic activity (i.e., nominal and real GDP). Next, we report the results of comparing economic and emergy-based measures of inflation and finally we consider how the structure of the U.S. economic system has changed from 1900 to 2011 by following the relationships among the scaled values of total emergy use, energy consumption, and real GDP.

Energy Systems Model of the United States

Figure 3 shows the ESL model that we evaluated to determine the emergy base for the U.S. The values shown on the diagram are the annual flows of emergy (in bold) and money (in italics) for the year 2000, which shows the emergy basis for monetary flows in that year. The emergy basis for the U.S. in any year from 1900 to 2011 can be found by substituting the values from Supplementary Material onto the diagram in Figure 3. See Odum (1996) or Campbell and Ohrt (2009) for a detailed explanation of Figure 3. The sum of the human services required to supply the U.S. with goods from outside the nation is P₂I₁ + P₂I₂ + P₂I₃. In our calculation, P₂, the world EMR was assumed to be equal to P₁, the U.S. EMR, and I₁ to I₃ are the monetary values of the products and services imported. If the production systems used to manufacture imports are similar and we assume that the technical knowledge required to produce a particular product is about the same regardless of the location in which the product is produced, it may be reasonable to use the U.S. EMR, P₁, which was known, in place of the world EMR, P₂, which was unknown, i.e., it had not been calculated by methods similar to those used in this study. The U.S. GDP was 9.95 trillion dollars in 2000 and the emergy to dollar ratio was 2.260E+12 semj/$ (2.248E+25 semj/9.95E+12$).

Temporal Patterns of Emergy Inflows, Economic Activity, and the U.S. EMR

The time history of the emergy used in the U.S. from 1900 to 2011 (Figure 4A) shows the emergy inputs to the U.S. economy aggregated by major category. The more comprehensive determination of the mineral emergy inflows to the U.S. showed that minerals were the dominant input from the Great Depression (GD) to the start of GR08. All of the emergy inputs, except renewable energy sources, soil erosion, and immigration, showed a generally rising trend from 1900 to 2006. In 2007, a perturbation of the emergy inflows begins with a 7.1% decline in the emergy of minerals consumed. This event is followed in 2008 by a 2.0% decline in the emergy of the energy consumed and a 3.4% decline in total emergy use. The perturbation is fully developed in 2009, at which time the consumption of both energy and minerals reached their maximum percent declines of 5.3 and 39.9%, respectively. In 2010, all of the affected inputs began to increase.

FIGURE 4

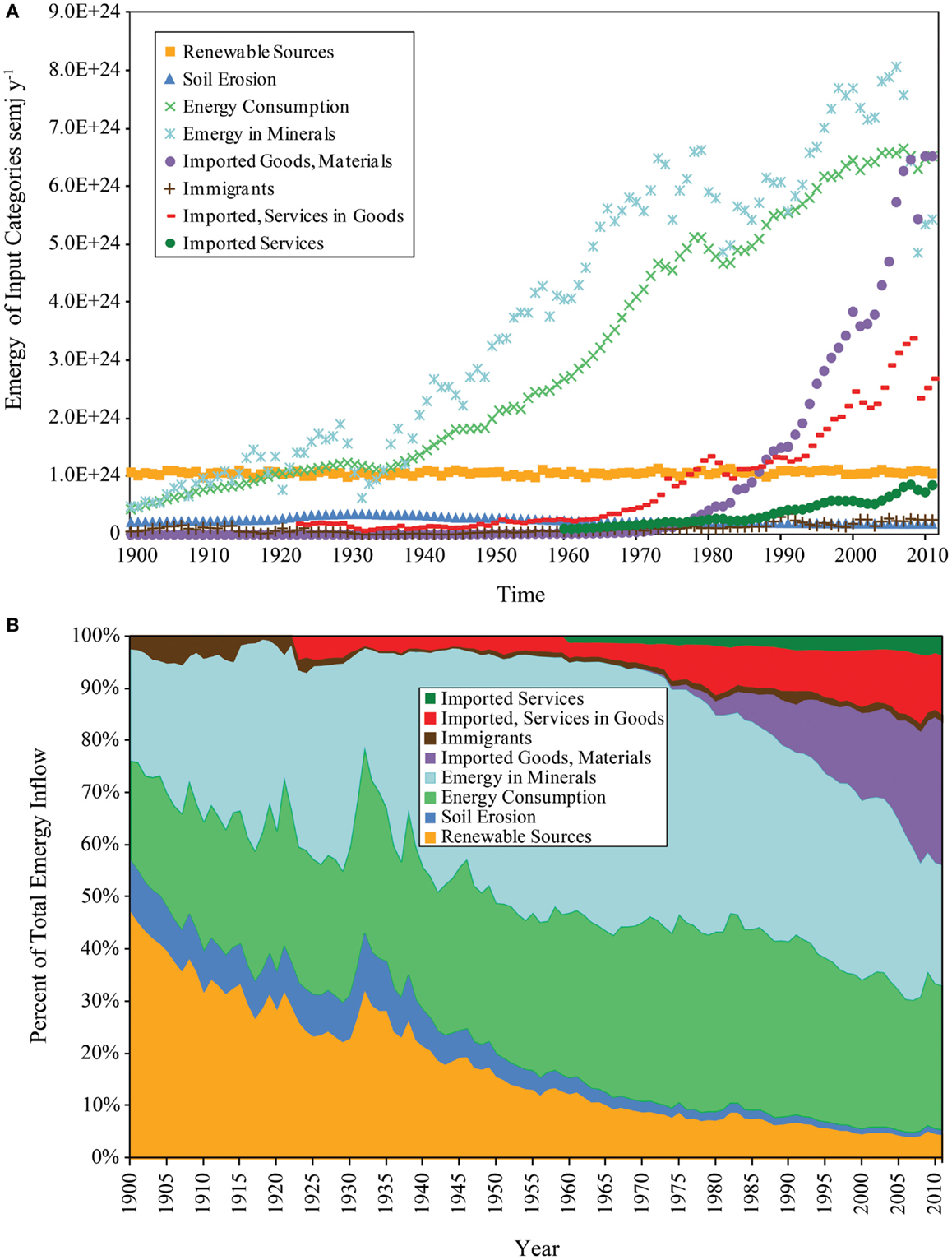
Figure 4. Temporal patterns of emergy inflows to the U.S. economy and of annual emergy use (empower) from 1900 to 2011 are shown. (A) Temporal pattern of the major classes of emergy inflows; (B) structure of the major emergy inflows to the U.S. given as percent composition of the total.

The percent composition of the emergy inputs to the U.S. (Figure 4B) shows a pattern of change from a nation running largely on renewable emergy (47% of total emergy use in 1900) through a period of rapid growth (1900 to the 1970s) in which the energy resources of the nation were used to organize materials (i.e., minerals and renewable products, e.g., timber) into the assets of a powerful industrial society; and finally, from 1980 to 2011, a rapid move to become a consumer nation, which in 2011 obtained 42.9% of the emergy used from imported material goods and services (not counting the emergy of imported fuels and minerals). In 1974, near the end of the industrial growth period, this number was 9.53% of the total emergy used.

Figure 5A shows the progressive expansion of the empower (solar emjoules/year) supporting the U.S. over the study period and the temporal pattern of perturbations, which reflects the major economic disturbances of the past 112 years, e.g., The GD during the 1930s, the global recession of 1957–1958, the Arab oil embargo of 1974–75, the Iranian revolution (1978–1979) and subsequent recession of 1981–1983, the bursting of the speculative, internet, or “dot com bubble” from 2000 to 2003, and the Great Recession from 2008 to 2013. The significance of historical events appearing in the variations of the EMR (Figure 5B) is considered in the Section “Discussion.”

FIGURE 5

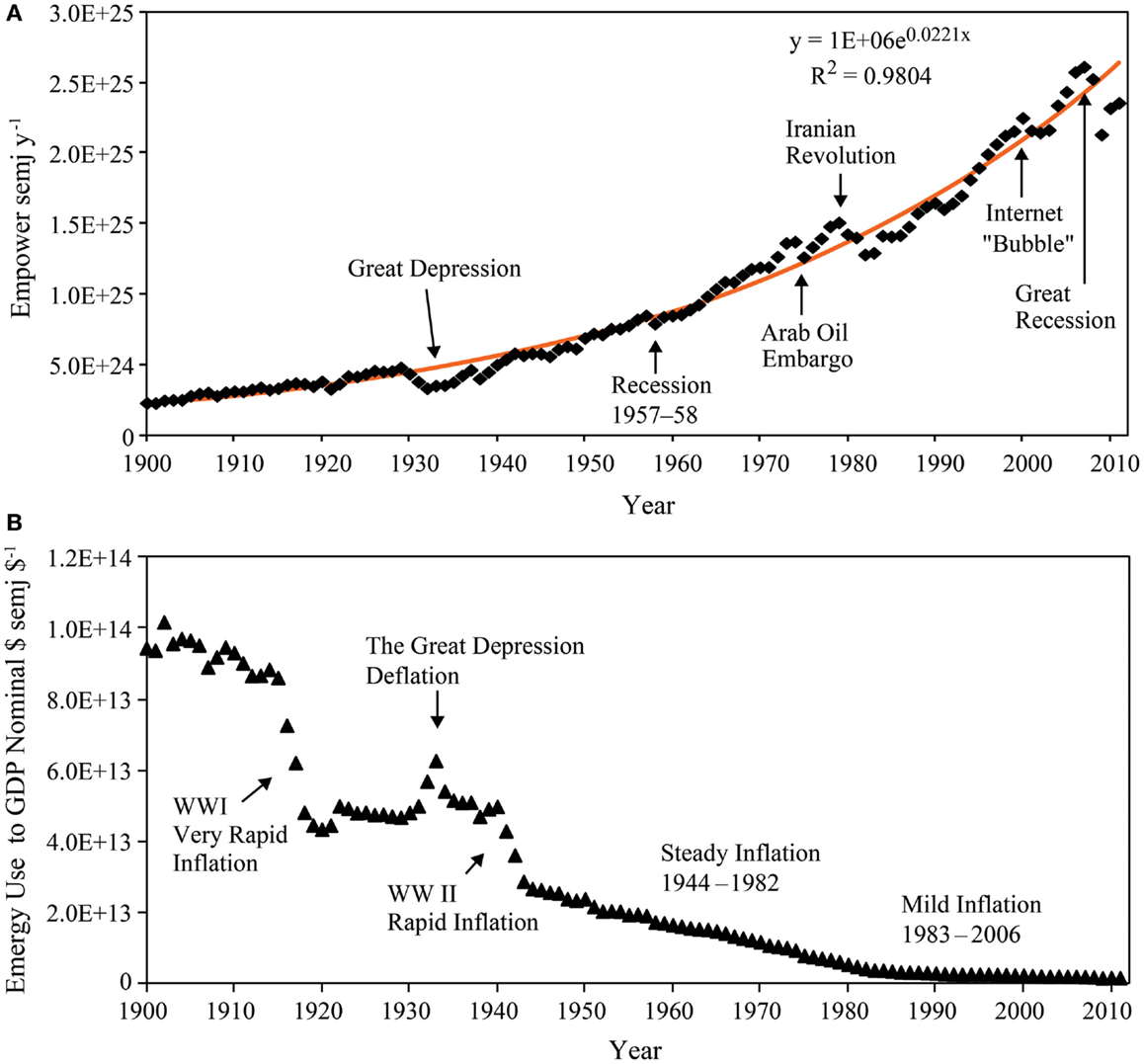
Figure 5. Temporal patterns of empower and the emergy to money ratio of the U.S. (A) The growth of total emergy used in the U.S. economy with some prominent fluctuations identified. (B) The U.S. emergy to money ratio is shown with major periods of inflation and deflation noted.

Temporal patterns of energy consumption

The emergy of the energy consumed in the U.S. from 1900 to 2011 is shown by source in Figure 6A and the temporal changes in the structure of these energy inputs are shown as a percentage of the total energy consumed in Figure 6B. Over this time, the dominant energy source powering the U.S. has changed with the technological development of the nation. This comparison can be done in different ways, which can yield different pictures of energy use in the nation.

FIGURE 6

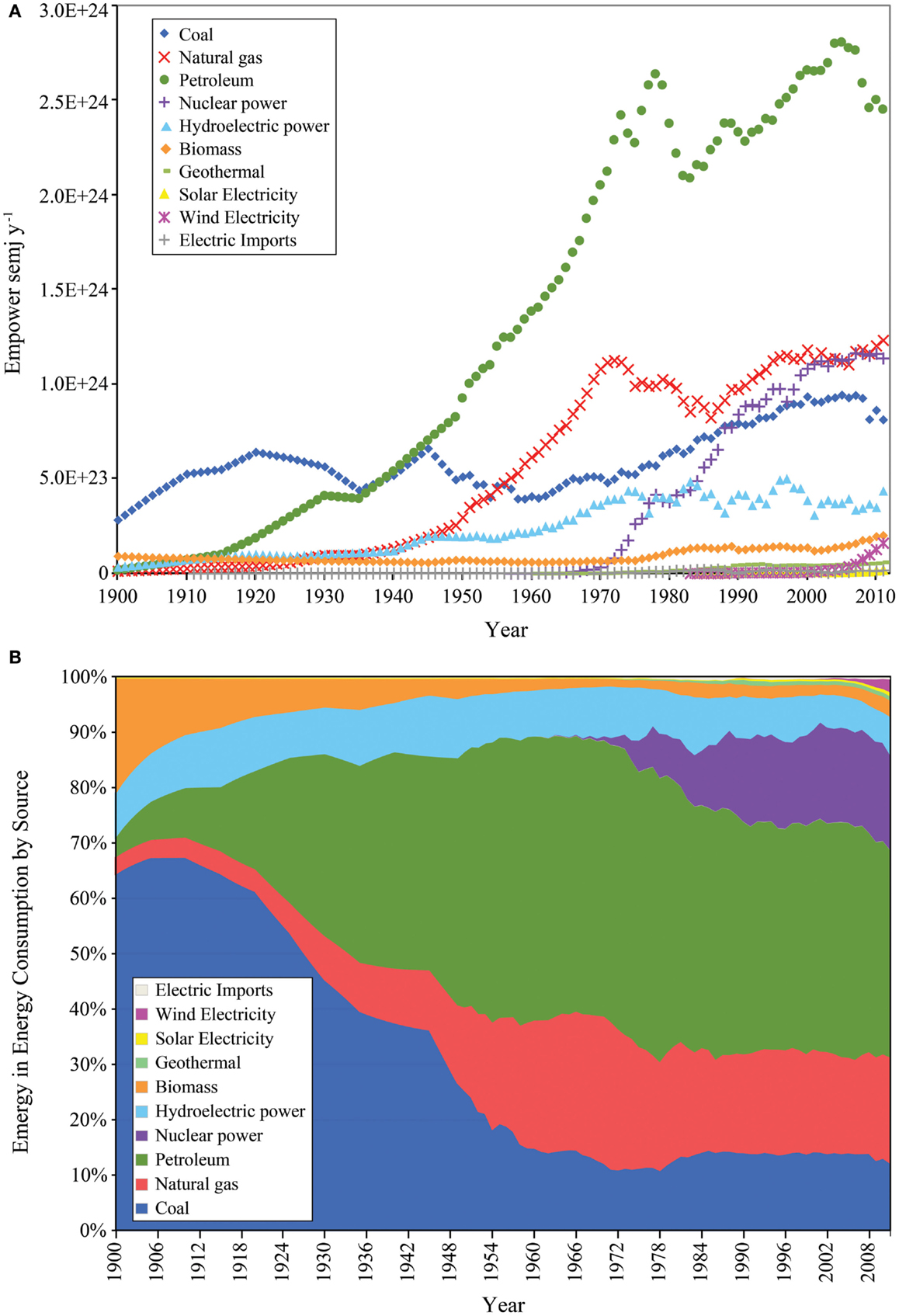
Figure 6. Temporal patterns of the components of the energy consumed in the United States from 1900 to 2011 are shown. (A) Time series of values for the major classes of energy inflows; (B) structure of the major classes of energy input as percent composition.

Non-renewable energy consumption. Before 1935, coal was the most important energy source for the U.S. as measured by both heat content (not shown) and emergy. After that year, the emergy of petroleum consumption exceeded coal and steadily increased along with coal consumption until the end of WWII, when it diverged from coal, growing along with the development of the automobile culture that was a result of the postwar shift in manufacturing capacity from military to consumer goods. The effects of the oil embargo of 1974 are evident in the decline in petroleum use in the U.S. from 1973 to 1975, which was followed by a rapid rebound over the next 3 years and then a 5 year decline in consumption after the Iranian revolution that culminated in the recession of 1982–1983.

After 1956, the emergy of natural gas exceeded that of coal to become the second largest energy source for the U.S. and after 2005, petroleum use in the U.S. declined as the use of natural gas increased. During the 1970s, the consumption of electricity from nuclear power began a rapid increase that continued until 2006. The emergy of electricity supplied to the U.S. from nuclear power exceeded that of hydroelectricity in 1977, coal in 1990, and natural gas in 2005 and 2006, when it briefly became the second largest energy source powering the U.S., as measured by the emergy delivered annually.

Renewable energy consumption. From 1940 to 1976, the consumption of hydroelectric power increased, after which it remained relatively constant with moderate variation among years. The emergy of the biomass consumed declined from 1900 to 1961, after which it increased until 2011, when it was 2.18 times greater than it was in 1900. Wind electricity was first recorded as an energy source for the U.S. in 1983, but it was not until 1998 that it began a super-accelerated increase that carried it past electricity generated from solar and geothermal sources by 2002, so that by 2011 it was contributing 2.7 and 7.4 times the electricity generated by geothermal and solar power, respectively. However, electricity from wind was only 2.5% of the emergy of the energy consumed in the U.S. in that year.

Temporal patterns of mineral use

The time history of the six minerals with the largest emergy inputs to the U.S. economy is shown in Figure 7A. The percent composition of the top 10 mineral inputs shows in a glance how the structure of the mineral emergy inflows has changed (Figure 7B). Some inputs like “iron ore plus imported iron and steel” and “lead” have become progressively less important over time, whereas other inputs like phosphate rock, crushed stone, sand and gravel, and bromine (after 2006, proprietary data, not reported by the USGS) have become progressively more important. Sulfur and cement have maintained their relative importance over time. Barite is a special case that shows a pulsing pattern with a strong peak corresponding to the period from 1977 to 1983. The importance of sand and gravel and crushed stone in the U.S. mineral supply began to increase after WWII. Since 1984, they have made the largest contribution to the mineral emergy of the U.S. economy, despite a very rapid decline after 2006.

FIGURE 7

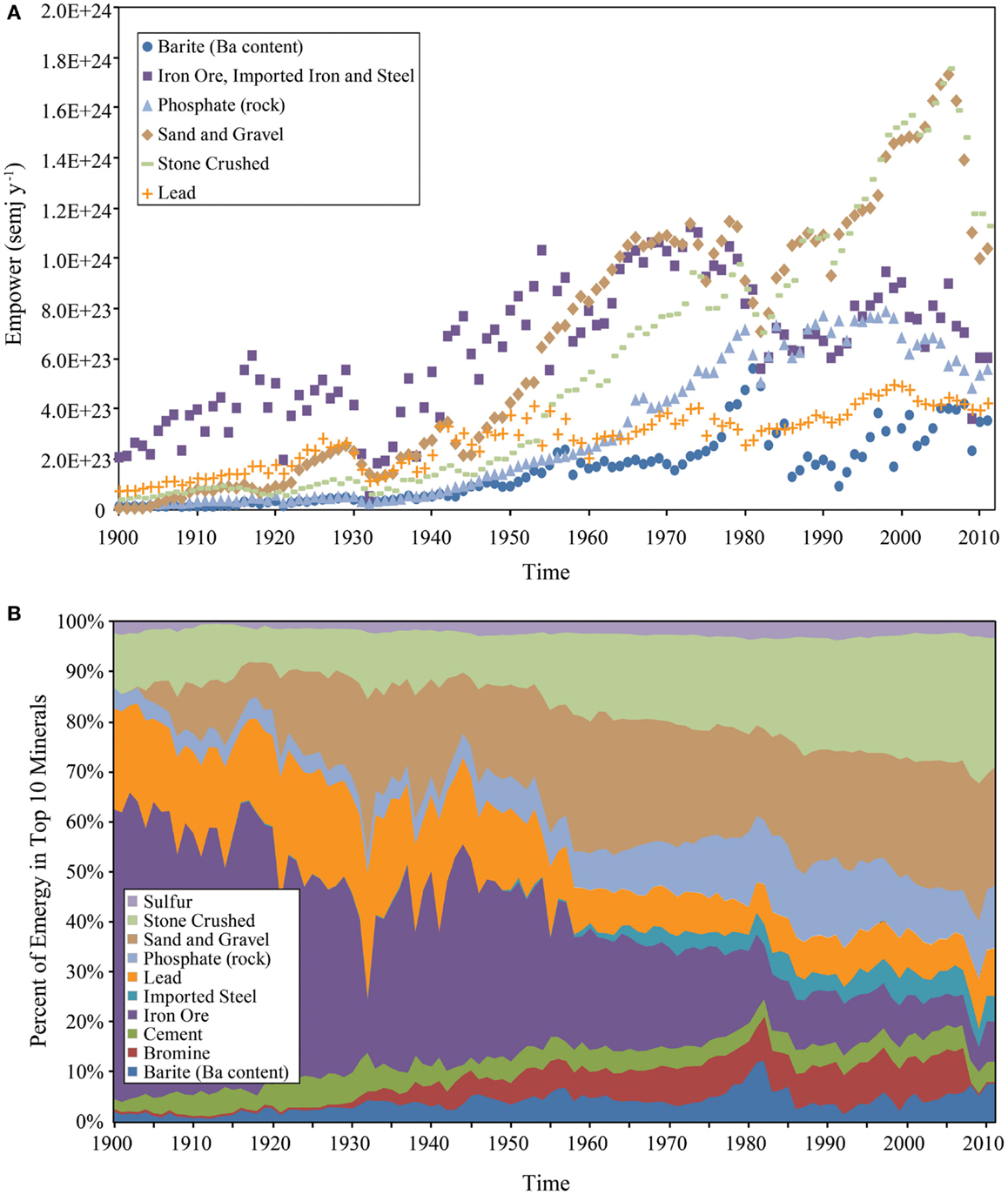
Figure 7. Emergy of some minerals consumed in the U.S. Economy from 1900 to 2011 is shown. (A) Temporal patterns of the six minerals contributing the largest amount of emergy to the U.S. (B) structure of the top 10 minerals shown as percent composition.

Temporal patterns of GDP and of the money supplies

Over the study period, the U.S. Gross Domestic Product in nominal dollars and the Real Gross Domestic Product in chained 2000$ (Figure 8A) are both well-fit by an exponential growth curve (R² = 0.9814 and 0.9881, respectively); a condition that also applies to the growth of the total emergy used (R² = 0.9804) by the U.S. economy (Figure 5A). The pattern of growth for the various measures of the national money supply in nominal dollars from 1959 to 2011 (Figure 8B) follows the same general pattern of increase seen in the emergy base of the nation (Figure 5A) and in the growth of nominal and real GDP. Nominal GDP is a measure of money flow, but it is plotted on Figure 8B as a reference for the size of the money supplies and for the determination of the velocity of money. The M1, M2, and M3 money supplies increased from 1959 to the present with M2 and M3 increasing more rapidly than M1. During the period leading up to GR08 (i.e., 1996–2007), the M1 money supply increased by 20% compared to an increase of 269% in the M3 money supply. The rate of increase of the M3 money supply diverged from that of M2 in 1998 and began a rapid rise that reached a value equal to 99% of the nominal GDP in 2009. After 2008, the M3 money supply was augmented by QE, which resulted in M3 plus QE exceeding GDP by an average of 10% from 2008 to 2011. The velocity of money for the four money supplies is shown from 1959 to 2011 (Figure 8C). In this plot, M1 displays a different pattern from that seen in M2 and M3. The velocities of M2 and M3 generally decline over this period while the velocity of M1 generally increases, but is more variable.

FIGURE 8

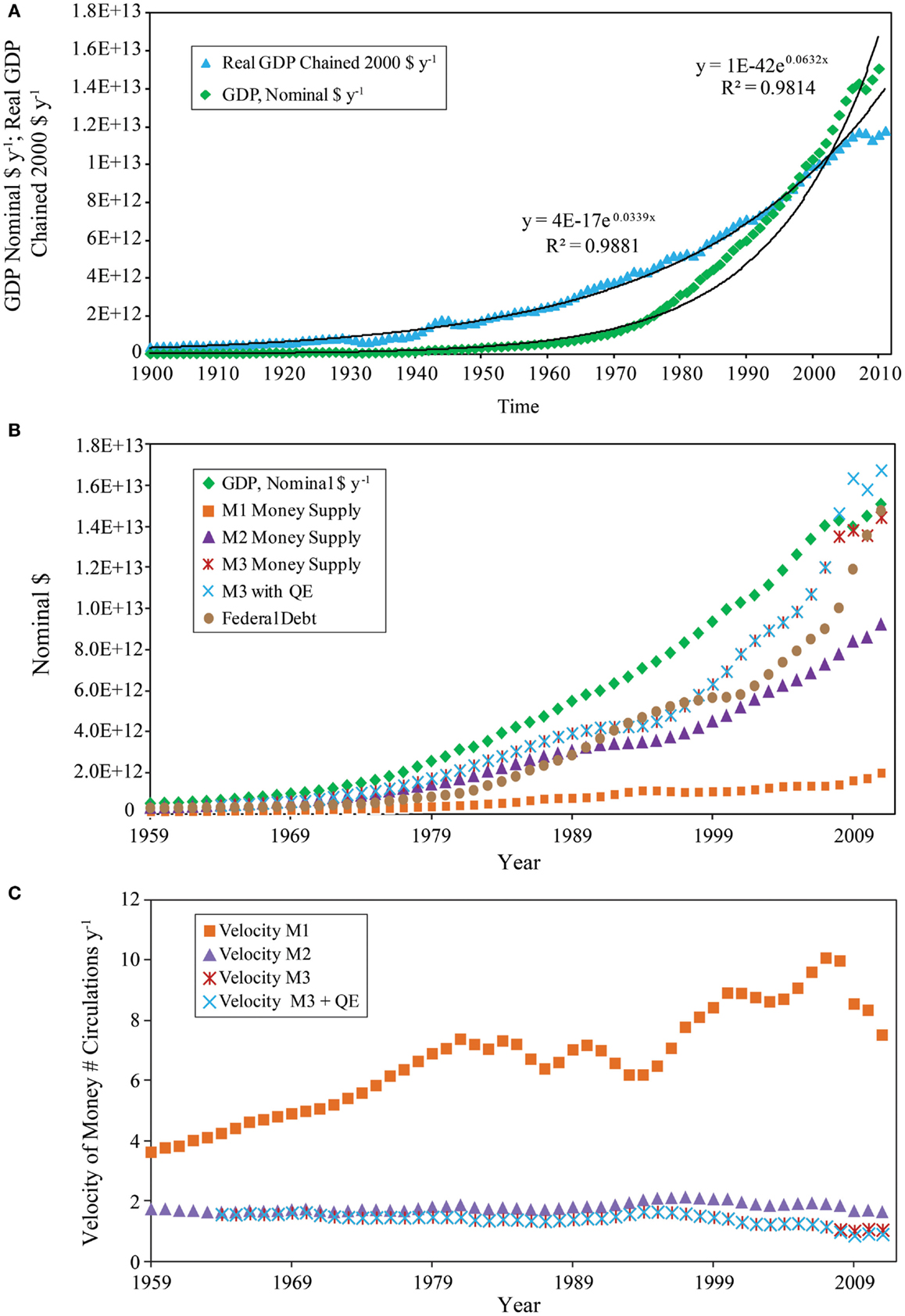
Figure 8. Temporal patterns of money flow and money supply in the U.S. economy, 1900–2011 are shown. (A) Money flow as measured by nominal GDP and real GDP in 2000 chained $; (B) money supplies; M1, M2, M3, M3 plus QE shown with Nominal GDP and the Federal Debt for comparison. (C) Velocity of money in the number of circulations per year.

Temporal patterns of the emergy to money ratios

The EMRs for the money supplies, M1, M2, M3, and money flow, GDP, all in nominal $ were compared over the period from 1959 to 2011 (not shown). For the same annual emergy inflow, higher ratios correspond to smaller monetary storages (Figure 8B). All of these ratios show a general pattern of decline over the period examined. However, the emergy to M1 ratio was more variable than the other measures. It is significant that from 1997 to the present time, the M3 line closely approaches that of the nominal GDP (not shown).

Comparison of emergy use to real GDP with energy consumed to real GDP

The time history of the ratio of emergy use to real GDP (Figure 9A) is well-fit by a power law (R² = 0.9578), but a linear relationship also describes this pattern fairly accurately (R² = 0.9264). Note that the period of inflation from 1940 to 1947 corresponding to WWII is a salient feature of the time series. The ratio of the emergy of the energy consumed to real GDP (Figure 9B) is best fit by a power law (R² = 0.8323), however, a linear relationship also describes this pattern fairly accurately (R² = 0.8082). These two functional relationships imply that the ratio of total emergy use to real GDP explains more of the temporal variance in economic activity than does a ratio of QA energy consumption to real GDP.

FIGURE 9

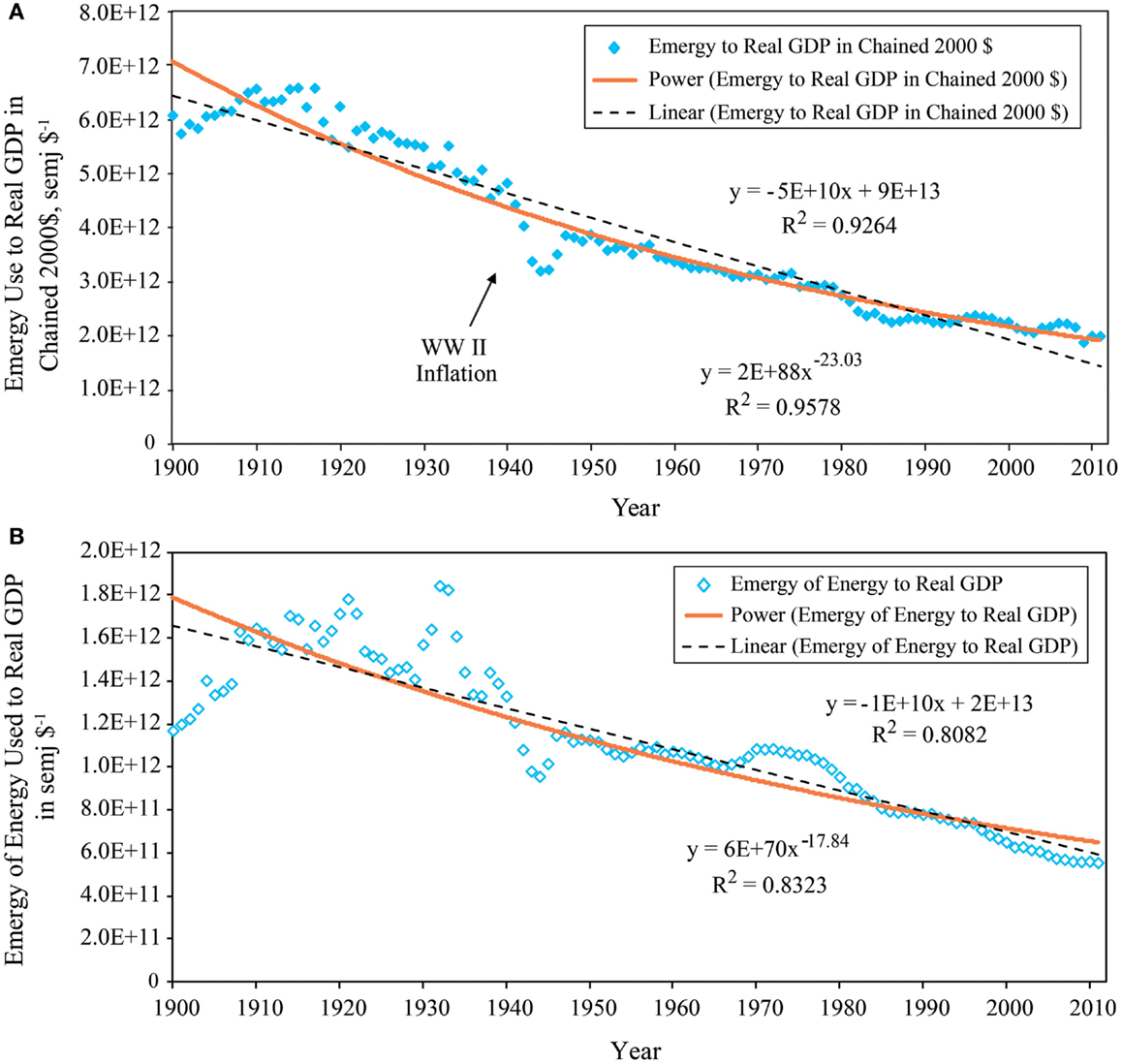
Figure 9. The ratios of emergy use and the emergy of the energy consumed to real GDP of the U.S. economy from 1900 to 2011 are shown. (A) The ratio of emergy use to real GDP in chained 2000 $ showing the fit of linear and power function relationships over time; (B) the ratio of the emergy of the energy consumed to real GDP in chained 2000 $ showing the fit of linear and power function relationships over time.

Functional Relationships among Energy Consumed, Emergy Use, and GDP

Nominal and real GDP as a function of total emergy used and energy consumed

The results of our statistical analyses to determine which mathematical function among the five functional forms evaluated, best described (i.e., explained the most variance in) the relationship between nominal GDP and energy consumption measures is given in Table 2. In this case, the power function explained the most variance between nominal GDP and QA energy consumption for three of the four energy consumption measures tested. The data in Table 2 and in Figure 10A can be used as evidence to evaluate the hypothesis that a third power law has controlled growth of the U.S. economy from 1900 to 2011 (see A Model Describing Growth of the U.S. Economy from 1900 to 2011). Nominal GDP as a power function of total emergy use (exponent 2.826 and R² = 0.9828) explained the most variance in nominal GDP among the five variables tested. The exponents of the five power functions ranged from 2.103 to 2.917 with an average value of 2.605 and SD ± 0.299. The power law relationship for QA II resulted in the highest R² (0.9813) among the energy consumption variables, but it was paired with the lowest value of the exponent (2.103).

TABLE 2

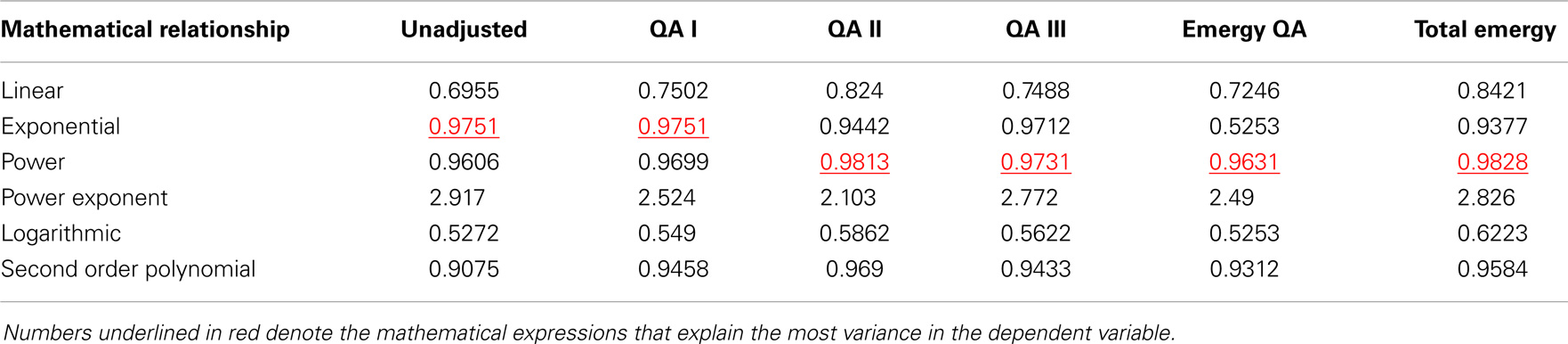
Table 2. The R-squares of mathematical relationships between nominal GDP (Y) and measures of energy and quality adjusted (QA) energy consumed or total emergy used (X).

FIGURE 10

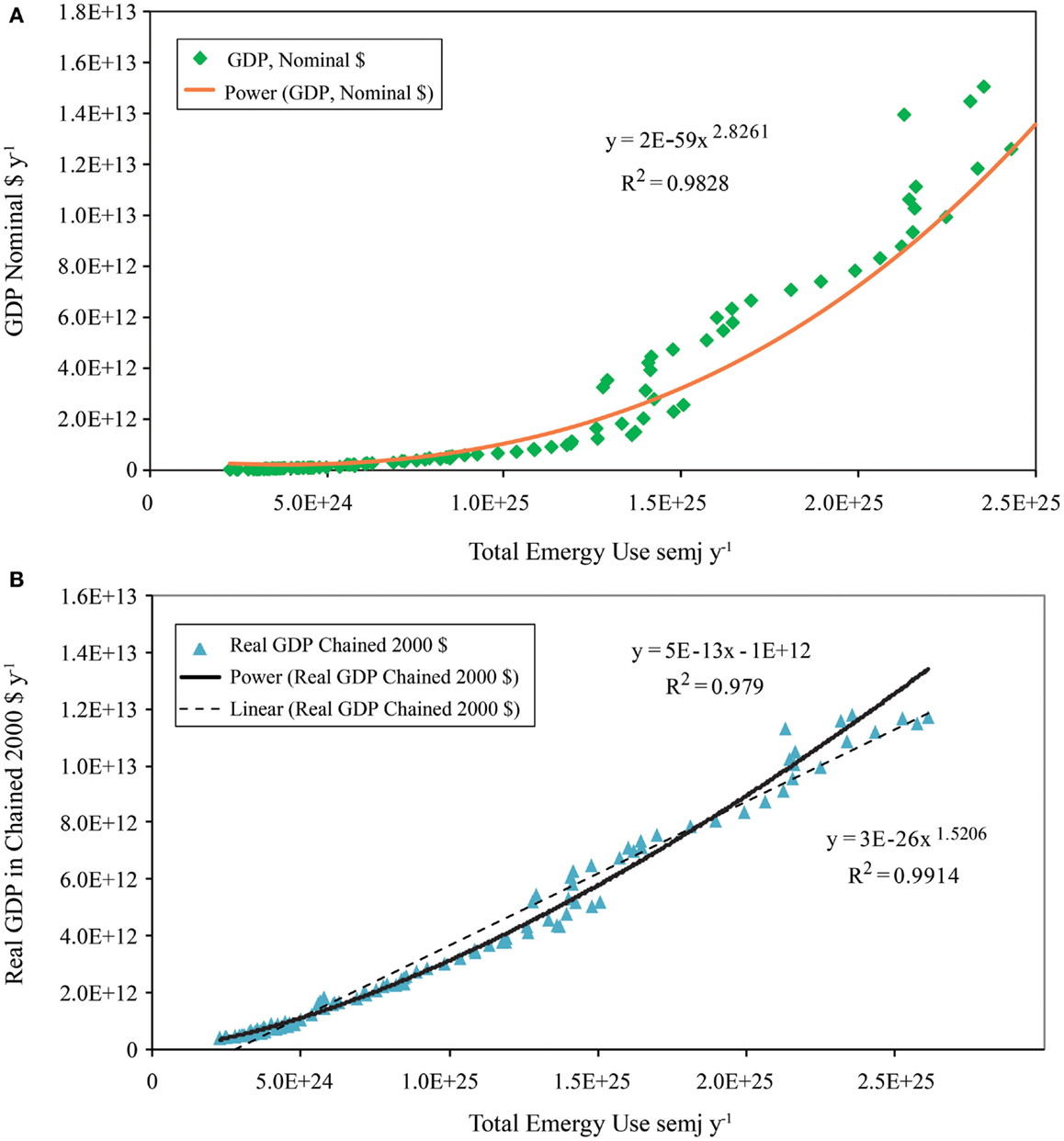
Figure 10. GDP in nominal and in real dollars as a function of total emergy use is shown. (A) Nominal GDP as a function of total emergy use; (B) real GDP as a function of total emergy use.

The best fit for the relationship between real GDP and total emergy use (Figure 10B) was provided by a power function (R² = 0.9914), whereas, a linear model explained 97.9% of the variance. All five measures of energy consumption exhibited relationships with real GDP similar to that of total emergy use (Table 3); however, none had regression relationships that explained more of the variance using either the linear or power law models than that which was explained by the power law and linear relationships of real GDP to total emergy use.

TABLE 3

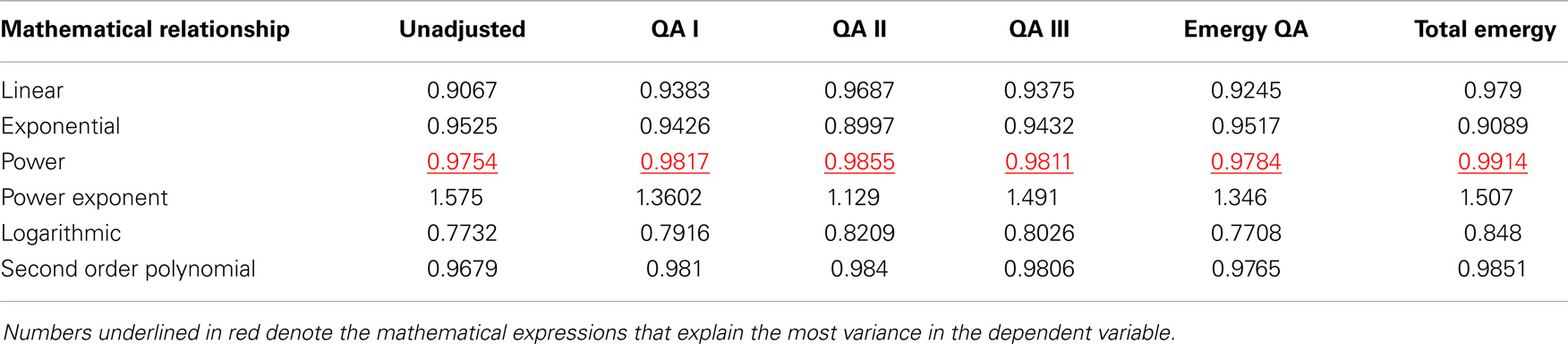
Table 3. The R-squares of mathematical relationships between real GDP (Y) and measures of energy and quality adjusted (QA) energy consumed or total emergy used (X).

Energy consumption measures as a function of emergy measures

A strong linear relationship exists between all measures of energy consumption (BTU/y) in both unadjusted and QA form and the emergy of the energy consumed (semj/year), which is also hypothesized to be a QA measure of energy consumption (i.e., Emergy QA). In this case, the quality adjustment is reflected in the transformities of the various energy inputs (Figure 11A). The relative quality factors are: coal, 1; natural gas, 1.2; petroleum, 1.7; and electricity, 3.3; if determined in a manner similar to that used for the QA adjustments given above (Cleveland et al., 1984; Ko and Hall, 2003). Unadjusted energy and QA I had the highest correlation coefficient (r = 0.9994) with Emergy QA followed by QA III (r = 0.9993), while QA II had the lowest correlation (r = 0.9903).

FIGURE 11

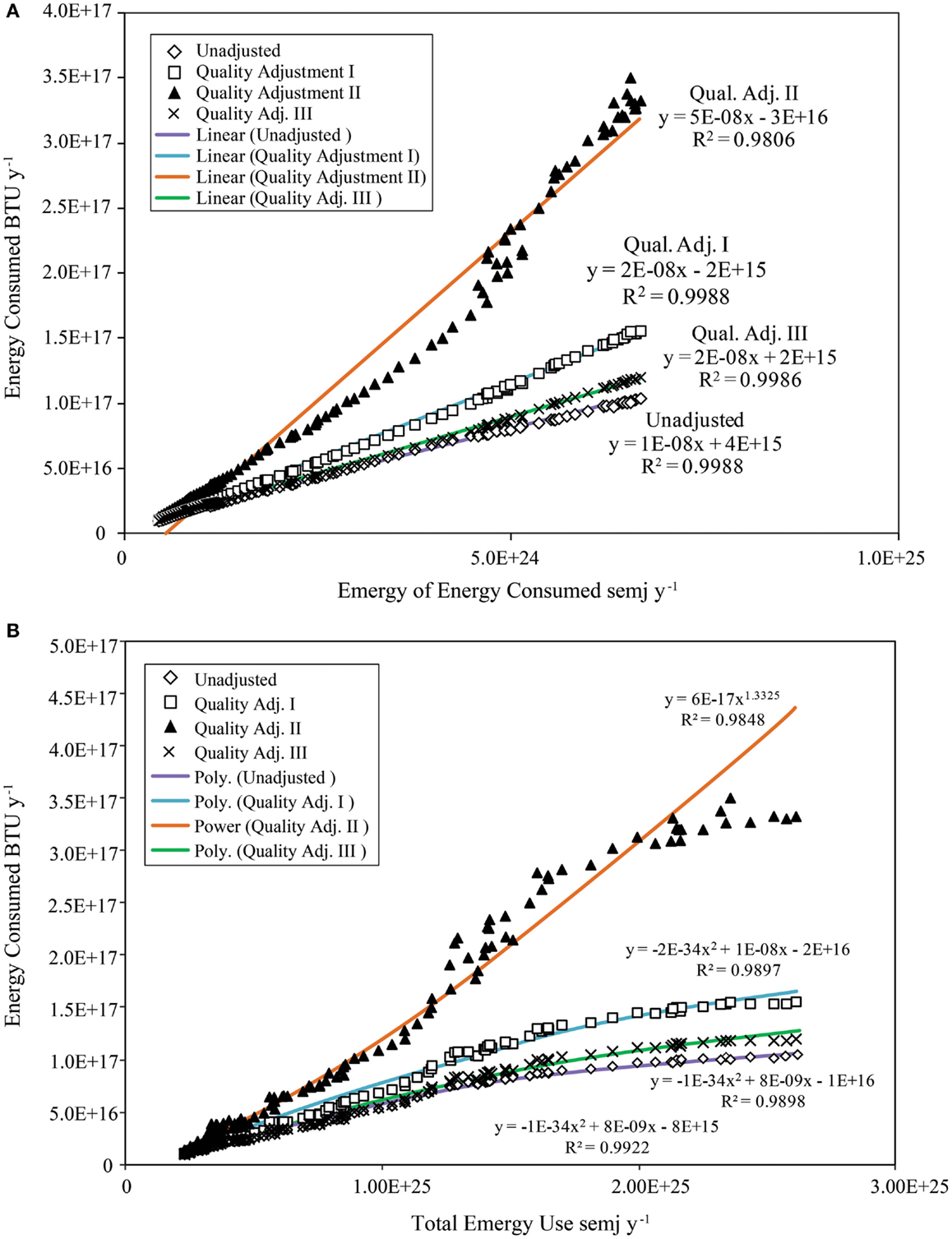
Figure 11. Energy consumption measures as a function of emergy measures. (A) Strong linear relationships were found between the three measures of QA energy consumption and unadjusted energy consumption with the emergy of the energy consumed (Emergy QA). (B) Second order polynomial functions give the best fit to QA I, QA III, and unadjusted energy consumption as a function of total emergy use; however, QA II is best fit by a power law.

The R-squares of the relationships found between measures of energy consumption in BTU/y and Emergy QA in semj/year versus total emergy use (semj/year) showed that three of the four measures of QA energy consumption and unadjusted energy consumption were best fit by a second order polynomial function (Table 4). However, QA II was best fit by a power function (Figure 11B); whereas, a second order polynomial function provided a good, but second best fit (Table 4).

TABLE 4

Table 4. The R-squares of mathematical relationships between measures of the energy and quality adjusted (QA) energy consumed (Y) and total emergy use (X).

Energy consumption and emergy use as functions of nominal and real GDP

Energy consumption and QA energy consumption are plotted against GDP in nominal dollars in Figure 12A and fit with a power function, which is close to the 1/3 power relationship expected from the model (Figure 2B) after inverting the axes from the order in Figure 10A. However, these curves all appear to depart from a power function relationship with nominal GDP after 1996. Table 5 shows that all of the measures of QA energy consumption as a function of nominal GDP were fit best by the hyperbolic function plus a constant, but unadjusted energy consumption was fit best by a log function.

FIGURE 12

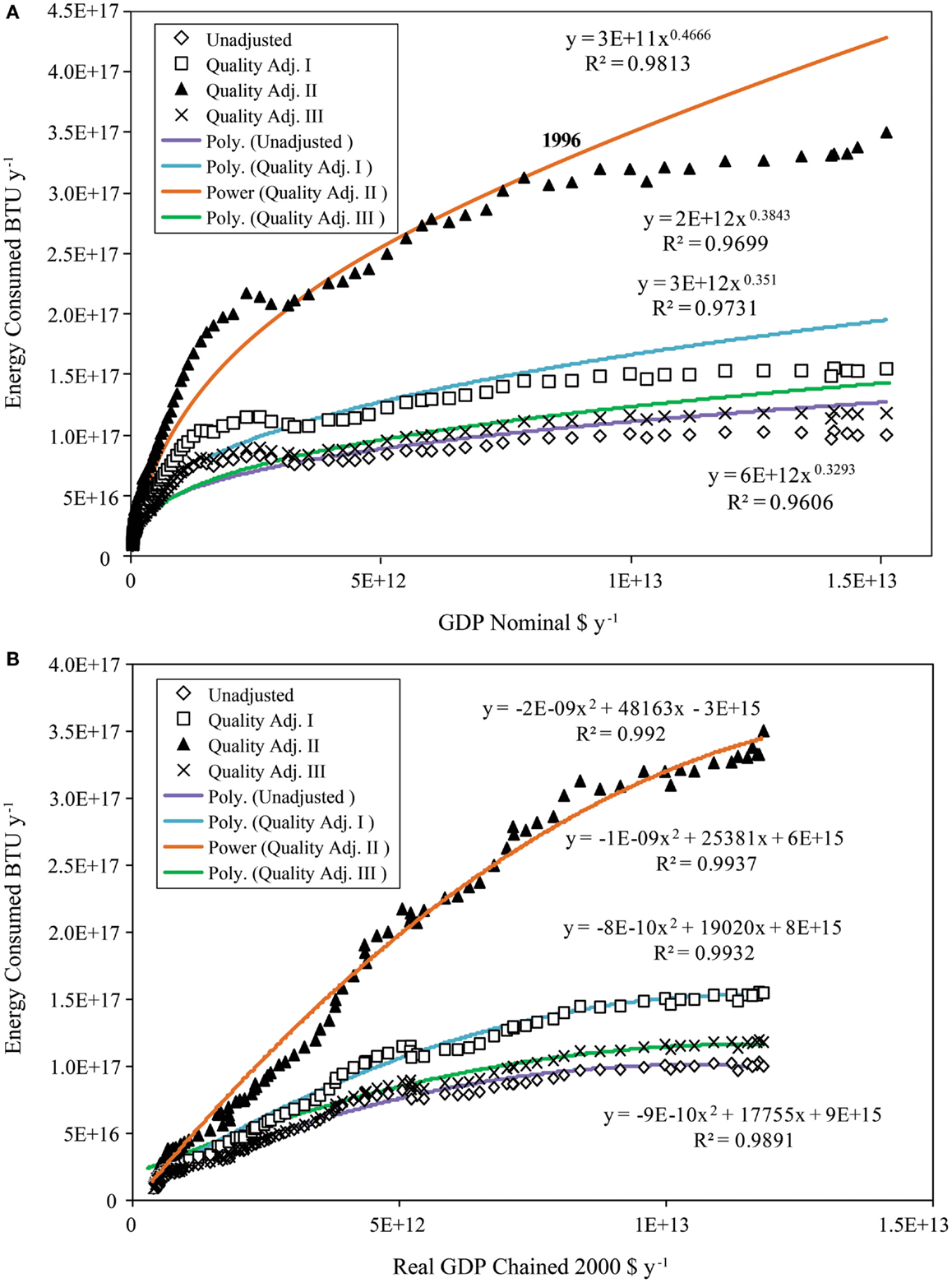
Figure 12. Measures of energy consumption as functions of nominal and real GDP are shown. (A) After 1996, energy consumption and QA energy consumption depart from a power law relationship as a function of nominal GDP; (B) energy and QA energy consumption are best fit by a second order polynomial as a function of real GDP.

TABLE 5

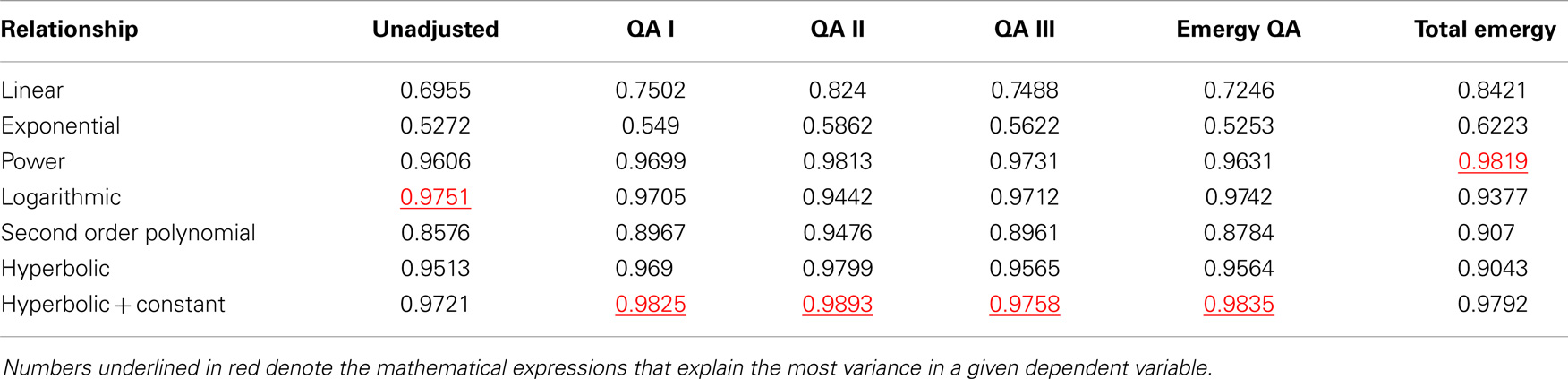
Table 5. The R-squares of mathematical relationships between measures of energy and quality adjusted (QA) energy consumed or total emergy used (Y) and nominal GDP (X).

Unadjusted and QA energy consumption plotted as a function of real GDP (Figure 12B) showed that unadjusted energy consumption and all three quality adjustments exhibit a similar pattern, i.e., they are fit best by a second order polynomial function among the seven functional forms tested in Table 6. If these relationships are represented with a power function as might be expected from the model in Figure 2B, the data deviate from the power relationship markedly after 1996 as shown most clearly for nominal GDP in Figure 12A. Calculations using the data for all measures of energy consumption including Emergy QA show the same pattern as a function of real GDP, i.e., after 1996 energy consumption increased at an average rate that is about 20% of the rate of real GDP growth.

TABLE 6

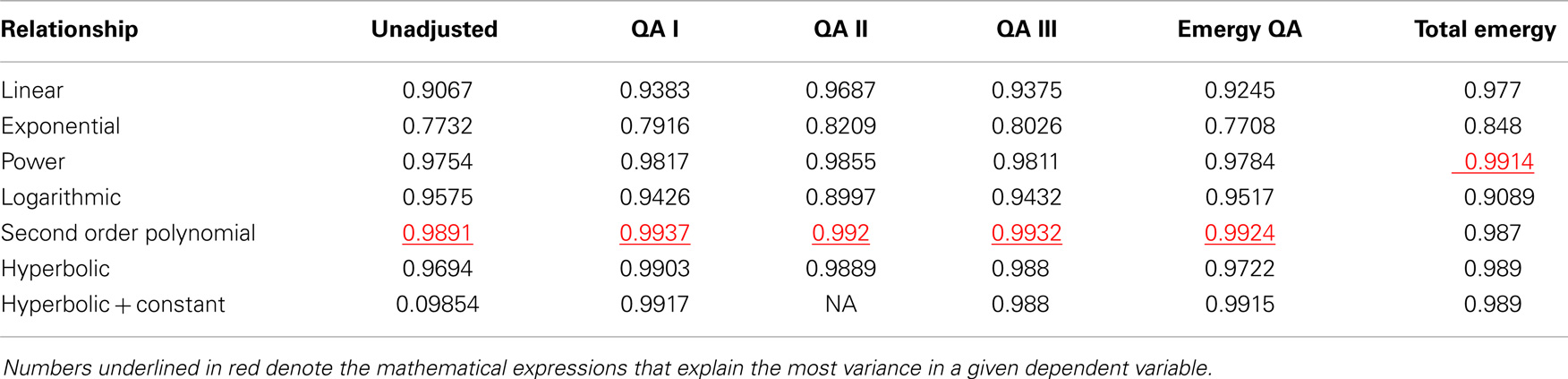
Table 6. The R-squares of mathematical relationships between measures of energy and quality adjusted (QA) energy consumed or total emergy used (Y) and real GDP (X).

The relationship between empower and real GDP (Figure 13) has a pattern that is different from that shown for the variation of the energy consumption variables with real GDP (Figure 12B). In this case, despite the GR08 perturbation, empower continues to follow a power law relationship with real GDP over the entire 112 year period. In contrast, all the energy consumption relationships with real GDP bend after 1996 so that the best fit to their curves is given by a second order polynomial function.

FIGURE 13

Figure 13. Emergy use or empower (semj/year) continues to follow a power law relationship as real GDP increases.

Economic and Emergy Indices of Inflation and Changing System Structure

Real wealth (emergy-based) inflation as measured by the EMR shows a good correspondence with consumer price inflation as measured by the Consumer Price Index (CPI) when the two are plotted together (Figure 14). Allowing for a slight phase shift before 1945, there appears to be a good correspondence between real wealth inflation and consumer price inflation. After 1945, the two curves follow each other until around 1980, but there are differences in the magnitude of events and in their duration and timing. From 1978 to the present, especially from 1996 to 2011, the two measures give a very different picture of inflation in the economy. For example, the percentage change in the CPI shows a relatively constant level of inflation from 1996 until 2007, after which there was a precipitous decline to slight deflation (−0.4%) in 2009 followed by a return to the long term average inflation rate from 2009 to 2011. In contrast, the percent change in the EMR shows an increase from neutrality in 1996 to variable levels of inflation about twice that indicated by the CPI until 2003, followed by deflation (−1.8%) in 2004 and a return to mild inflation from 2005 to 2007. These changes were followed by a rapid rise to an annual inflation rate of 14.4% in 2009 and a subsequent precipitous decline to deflation of −4.7% in 2010 (the CPI shows inflation of 1.6% in this year).

FIGURE 14

Figure 14. Comparison of the percent change in the consumer price index (CPI) and the emergy to money ratio for the United States from 1900 to 2011.

The changing relationships between energy consumption, emergy use, and real GDP over the 112 year period are shown by plotting their values scaled relative to their maxima (Figure 15). In this plot, energy and emergy are closely related in terms of their relative changes from 1900 to 1929. During the GD, emergy use shows a greater relative decline than energy consumption and after WWII the rate of increase of emergy use departs from energy consumption, which increases at a more rapid rate until 1978 at which time both curves experience a major perturbation. Energy consumption recovers from this perturbation by 1983, continuing its increase but at a lower rate. In contrast, by 1983, emergy use has moved sideways to lie on the curve of real GDP increase, which it had been gradually approaching since WWII. Emergy use travels at the same rate of increase as real GDP until 2000, after which it briefly departs from real GDP, but by 2004 its scaled rate of increase has rejoined the real GDP curve, which had been increasing as the rate of energy consumption slowed. The three curves converge in 2007 on the eve of the Great Recession. After 2007, total emergy use plummets, diverging from energy consumption and real GDP, which are now closely related, and show a smaller impact of GR08 than that indicated by the decline in emergy use.

FIGURE 15

Figure 15. Structural change in the U.S. economy from 1900 to 2011 as indicated by changes in the scaled values of energy consumption (Emergy QA), total emergy use, and real GDP.

Discussion

The major topics discussed are as follows: Sections “Interpretations of the Patterns of Events Discernible from Variations in the EMR; Patterns of the Mineral Emergy Inflows; Is “Total Emergy Use” A More Accurate Measure of Economic Activity than Energy Consumption in Developed Economies?; The Emergy Basis for Economic Activity: Coupled Flows; Evidence for the Operation of a Third Power Law Controlling Economic Growth; Energy and QA Energy Consumption Relationships; Real GDP as a Function of Energy Consumption and Total Emergy Use; The Relationship Between Energy Consumption Measures and GDP Measures; The Relationship Between Economic and Emergy Measures of Real Wealth; The Significance of Changes in the Emergy to Money Supply Ratios; Energy Consumption versus Emergy Use as a Means to Explain Economic Activity; Comparison of Emergy and Economic Measures of Inflation; True Magnitude of the Great Recession of 2008; Structural Change in the U.S. Economy and the Future.”

Interpretations of the Patterns of Events Discernible from Variations in the EMR

The salient perturbations along a general pattern of decline (Figure 5B) in the U.S. EMR from 1900 to 2011 can be interpreted as follows: the initial precipitous decline in the ratio corresponds to a period of drastic inflation during WWI (1914–1920), which is followed by a plateau associated with the stable economic conditions of the 1920s. After the stock market crash of 1929, the U.S. EMR rose to a peak (1933) during the deflationary period of the GD, which was followed by a gradual decline in the ratio up to 1940 as the nation recovered from the GD. In 1940, a second precipitous decline began associated with inflationary pressures during WWII (1940–1947). From 1947 to 2011, the EMR of the U.S. exponentially declined as a result of the exponential growth of money in circulation combined with a near linear increase in the annual total emergy use during this time. This period can be divided into two parts: a period from the end of WWII to 1982 characterized by a steady almost linear increase in inflation and a period from 1982 until 2007 during which inflation increased at a slower rate.

Historical events in the U.S. can be better understood by analyzing them from many energy-based perspectives. For example, Hall et al. (2014) use the Energy Return on Investment (EROI) to explain events from 1900 to 2009 in terms of what was possible based on the net energy from the various energy sources available to the U.S. during different time periods.

Patterns of the Mineral Emergy Inflows

In contrast to prior studies of the emergy inflows to national systems (Odum, 1996; Tilley, 2006), minerals were found to be the largest component of emergy use in the U.S. after 1939. The steady growth of construction materials after this time indicates that much of the emergy of minerals was used to build infrastructure. Construction materials are still consistently the largest mineral emergy input to the U.S. being particularly dominant during the rapid growth period from 1960 to the mid 1970s and during the recent home construction boom from 1998 to 2007, but other unexpected materials show their strategic importance when converted to emergy. For example, from 1980 to the 1982 barite contributed 10% of the mineral emergy to the U.S. economy. This, at first, unlikely result made sense when we discovered that 98% of the barite is the most frequently used weighting agent for mud used in drilling for oil, which increased dramatically after the 1974 Arab oil embargo. Other strategic materials are iron ore, which was the most important material input prior to the mid-1950s; phosphate rock, the primary mineral in agricultural fertilizers; bromine, a major fire retardant, manganese used in steel alloys; sulfur, which through sulfuric acid is the basis for many industrial chemicals and a major input to fertilizer manufacture for agriculture.

Is “Total Emergy Use” a More Accurate Measure of Economic Activity than Energy Consumption in Developed Economies?

The World System model (Figure 1) demonstrated that emergy provides a more complete basis for understanding economic activity than energy consumption alone. This theoretical evidence is supported by null hypothesis 1, which we can reject based on the results reported in Figures 9A,B, in which the emergy use to real GDP ratio modeled as both power and linear functions of time accounts for 15% more of the variance than did a typical energy consumption measure, Emergy QA. As further reinforcement of this difference, the Kolmogorov–Smirnov (K–S test) confirmed that the distribution of values within the emergy use to real GDP time series was significantly different from the distribution within the Emergy QA to real GDP time series. In contrast, the Emergy QA distribution of values was indistinguishable from unadjusted energy consumption, QA I, and QA III, but it was significantly different from QA II. As further verification, Emergy QA did not respond to either the GD or GR08 as strongly as the emergy of the minerals consumed. Both energy and minerals responded similarly before the oil embargo of 1974, but the decline in the emergy of mineral consumption in 1975 gave the stronger signal related to this event.

The Emergy Basis for Economic Activity: Coupled Flows

Emergy evaluation can place economic activities on a complete and comprehensive biophysical basis as called for by Cleveland et al. (1984). For example, the conversion of the inputs needed for economic production to solar emjoules quantifies them in terms of their equivalent ability to do work within the context of the system, which has had time to adapt to its inflows (Campbell, 2001). In this case, “Equivalent ability to do work in a system” does not mean that the various energy and material items can perform the same actions, but rather that for items with equal emergy, the system has had to make the same investment of emergy in order to obtain their work. Here, a determination of the work that can be done requires not only the quantification of the available energy (exergy) used in performing an action but also the summation of all of the past use of available energy required to produce the input in units of energy of a single quality, i.e., solar equivalent joules. Thus, what any input can do when used within a system depends not only on the amount of available energy delivered but also on its quality, i.e., the amount of emergy that it carries. An item’s emergy is a measure of the work that it can do, because of our stipulation that the system has had time to adapt to its inputs under evolutionary competition with other systems. Evolutionary pressure on systems to prevail in competition according to the maximum empower principle (Odum, 1996 after Lotka, 1922a,b) leads to the emergy of the available energy inflows matching the quality of the work performed as described in Campbell (2001). We have drawn the model (Figure 1) in a way that implies that fuel, electricity, and human labor act on minerals and the raw materials of the biosphere, transforming them into the structural assets and material flows needed to build and maintain societal infrastructure. The models in Figures 1 and 2 show the foundation for implementing an emergy-based economic method that may give more capacity to predict change and to manage it successfully as called for by Watt (1994).

Coupled flows of real wealth and money form a causal loop

The conceptual model in Figure 2A shows that the theoretical basis for the relationship between energy consumption or emergy use and economic activity is one of two flows coupled by a supply and demand relationship with money moving as a counter current to flows of real wealth. This is the theoretical model underlying the empirical analyses of Granger-related causality and which is needed to understand the studies of causality among energy, emergy, and economic variables. In this model, a change in the money supply can exert pressure to control the rate processes by stimulating greater or lesser applications of human work that in turn is needed to generate the flows of work from the environment. Also, the stores of fossil energy and mineral wealth and available renewable energy in the environment, would be expected to attract investment from social systems under evolutionary pressure to maximize empower of the system (Odum, 1996; Campbell, 2001).

Determining causality with ESL models

Because of the close coupling of the flow of real wealth and the counter flow of money through the laws of supply and demand (Figure 2A) that govern economic production functions, and because feedback loops from the larger system, in part, govern the emergy and money flows in national systems, it may be difficult to decipher the ultimate cause of any given perturbation or pattern through autoregressive methods alone. However, precedence can be established in certain prominent cases, e.g., the OPEC oil embargo shut off oil supply, which disrupted GDP and the 1929 stock market crash disrupted GDP, which then slowed energy consumption. Nevertheless, an alternative way to understand causality is needed. One method is to construct an ESL model (Odum and Odum, 2000) of the system of concern and then evaluate the energy potentials within the system and in its forcing functions that are the basis for action, i.e., the direction and magnitude of a flow. Next calibrate the model, simulate and verify the results, and then perform a sensitivity analysis to determine the relative changes in the output variables that are caused by a perturbation in each of the coupled input factors. The relative capacity of each factor to cause a change in any of the others can be determined in this manner. Causality itself resides in the system network of relationships that are formulated as a set of working hypotheses based on the underlying thermodynamically based causal mechanisms, i.e., the energetic and kinetic aspects of the system of equations in the case of an ESL model. Note that this method is described in this paper, but it is not applied [see Odum and Odum (2000) for applications].

Causal factors presaging the Great Recession of 2008

The order of causality may be traced through a production function to the input that begins to decline before the others, which may be the proximal cause of the decline. In the case of GR08, it was a decline in consumption of building materials (i.e., sand and gravel and crushed stone) in 2007 that lead the way down. Even though the financial crisis of 2008 was only a year away, in 2007 many economists saw no observable signal that something was amiss (Stiglitz, 2010). However, inflation is implied by the rapid rise in the velocity of M1 money from 1995 to 2008, which occurred in spite of the Federal Reserve’s scrupulous attention to containing the growth of the M1 money supply. This increase in the velocity of M1 was apparently fueled by the expansion of the M3 money supply and the consequent inflationary decline in the real wealth to M3 ratio seen from 1997 to 2007. Strangely, the Board of Governors of the Federal Reserve stopped publication of the M3 money aggregate on March 23, 2006, declaring it to be unhelpful in setting monetary policy (16). However, our results combined with the analysis in Stiglitz (2010) imply that these funds contributed to an inflationary expansion of lending and home construction that eventually resulted in the issuing of mortgages to poorly qualified buyers and the packaging of these at-risk loans with sound ones into complex financial products that were triple A rated, but turned out to be worth less than face value once the extent of the bad loans became known.

Evidence for the Operation of a Third Power Law Controlling Economic Growth

The model given in Figure 2B implies that as a result of cooperation between people and social organizations, e.g., religious, industrial, and commercial associations, non-profit institutions etc., we might expect a third power relationship between measures of gross economic activity such as nominal GDP and the energy consumed as well as the emergy used. This hypothesis was supported by the data where we found that total emergy use, unadjusted energy consumption, and QA energy consumption measures could explain the most or second most variance in nominal GDP using a power law relationship, in which the exponent was close to the third power (2.103–2.917, Avg. = 2.61) as indicated by theory. The strongest evidence for the third power law was provided by the relationship of nominal GDP with total emergy use, which paired an exponent of 2.826 with the highest R-square for the relationship. As further confirmation of a third power law governing growth in the U.S. economy over the study period, we can reject null hypothesis 3 (see A Model Describing Growth of the U.S. Economy from 1900 to 2011), because the exponent for the relationship of nominal GDP as a function of total emergy use would have to be <2.402 to accept it. In fact, we can also reject the null hypothesis for the average exponent (2.605) of all energy consumption measures and emergy use, indicating that nominal GDP may also have a third power relationship with energy consumption.

Energy and QA Energy Consumption Relationships

In this section, we consider the significance of the relationships between: (1) QA energy consumption and the emergy of the energy consumed (Emergy QA); (2) unadjusted energy consumption and QA energy consumption and (3) QA II compared to other measures of energy consumption.

Relationship of QA energy consumption to the emergy of the energy consumed

Energy analysts do not often use emergy in their studies, thus it is important to show that the emergy of the energy consumed (Emergy QA) is an appropriate QA energy consumption measure. Emergy QA was shown to have linear relationships with the other QA energy measures with coefficients of determination, R-squares, ranging from 0.9806 to 0.9988. Furthermore, the R-squares of these relationships were only slightly diminished by removing serial autocorrelation from the data set, thus the relationship between the energy consumption variables is not dependent on the past history of the variables. This relationship is further demonstrated by the fact that there was little difference between using the three QA energy measures (QA I, II, III) and Emergy QA when evaluating the relationship between economic activity and energy consumption. For example, the exponent describing the relationship between nominal GDP and Emergy QA was 2.49 and the relationship had an R-square of 0.9613, values that place it within the range of values established by the other measures of QA energy consumption (Table 2). When we evaluated null hypothesis 2 (see Energy/Economic Analyses and a Model of Coupled Flows in Economic Exchange) using the K–S test, we found that the distribution of values in Emergy QA was indistinguishable from unadjusted energy, QA I, and QA III, but it differed from QA II and total emergy use. Thus, we can reject the null hypothesis except for QA II, which implies that Emergy QA is an appropriate QA energy consumption measure and than QA II is not a typical QA energy measure, since its distribution of values is significantly different from unadjusted energy, QA I, QA III, and Emergy QA based on the K–S test.

Unadjusted energy and QA energy consumed

Unadjusted energy consumption behaves somewhat differently from the QA energy consumption measures, as evidenced by the fact that most of the variation in unadjusted energy consumption as a function of nominal GDP was explained by a logarithmic function (Table 5), but a hyperbolic function plus a constant explained the most variance for all measures of QA energy consumption. Furthermore, all of the QA measures explained more of the variance in both nominal and real GDP than did unadjusted energy consumption, indicating that there is an increase in explanatory power gained by quality adjustment as found by Cleveland et al. (1984, 2000).

QA II compared to other measures of energy consumption

A power function of QA II provided a slightly better fit to the data on nominal GDP (i.e., it explained 1–2% more variance) than the other QA measures of energy consumption, but the better fit was obtained at the expense of the greatest deviation of the exponent from the predicted third power law relationship (Table 2). Also, QA II gave the best fit to the economic variables in the models examined by Cleveland et al. (1984); however, the factor (16.8) that was used to adjust the quality of electricity relative to coal is much greater than one would expect based on the relative efficiency of the transformation of coal energy into electric energy (Ko and Hall, 2003). Power functions explaining Emergy QA, QA I, and QA III have R² values lower than QA II, but they are based on quality adjustment factors closer to the relative efficiency of generating electric power from coal. Thus, QA II is apparently a constructed variable not based on a valid underlying theory or process that explains economic activity better than the other energy consumption measures. The K–S test showed it to be an emergy mimic, i.e., the distribution of its values was not distinguishable from the distribution of total emergy use values.

Real GDP as a Function of Energy Consumed and Total Emergy Use

A power law function explained the most variance in real GDP as a function of all energy consumption measures and emergy use. The strongest statistical relationship (R² = 0.9914) for real GDP was found as a function of total emergy use. There was little difference between unadjusted energy consumption and QA energy consumption measures in their ability to explain the variance in real GDP, e.g., there was only a 1% difference in the R² of the fits between the best, QA II, and the worst, unadjusted energy. This observation implies that we might expect similar dynamics to be controlling the relationship between real GDP and all measures of energy consumption.

The Relationship between Energy Consumption Measures and GDP Measures

The relationship of energy consumption measures as a function of nominal GDP

Because the transformation of energy potentials is fundamental to all activity, it is understandable that energy consumption might be taken as the single most important biophysical factor explaining economic activity. Indeed, by its nature energy is not a limiting factor, i.e., it does not reach a saturation level as defined by Liebig’s law, because an additional increment of available energy is required to support the next increment of any ordering process. Thus, available energy is not expected to be present in excess, but if there is an insufficient supply, of course, activities will be constrained. However, the data presented here clearly show that the rate of energy use per unit of nominal and real GDP gained has declined since 1996. The fact that the hyperbolic function plus a constant gives the best fit to the relationship between energy consumption and nominal GDP is significant, because the hyperbolic function describes the limiting factor interaction in enzyme kinetics (Neame and Richards, 1972). Thus, while energy is not normally thought of as a limiting factor under certain conditions, such as its relationship with economic activity in advanced economies, apparently it can take on some of the properties of a limiting factor function.

It is also significant that the hyperbolic function must be paired with a constant term to give the best fit to the relationship between energy consumed and nominal GDP. This implies that there is indeed an incremental increase in energy consumption that is required for an incremental increase in nominal GDP, but in this case a greater increase in nominal GDP was gained for the increment of energy use, e.g., about a fivefold multiplier for nominal GDP for a unit increase in energy use from 1996 to 2011 was calculated from the data. This means that in the near term, there should be some scope for energy conservation while still maintaining moderate economic growth. In our exploratory statistical analysis, which was mentioned in our proceedings paper on this subject (Campbell and Lu, 2009), we found that a double hyperbolic function plus a constant could best explain the departure of energy consumption measures from a power function of nominal GDP with one part of the function applying prior to 1981 and the other for the later years (Figure 12A).

The relationship of energy consumption measures as a function of real GDP

The best fit functional relationships between all measures of energy consumption and real GDP tell an even more surprising story. The best fit curve is a second order polynomial, which implies that energy consumption has begun to bend lower as real GDP increases. This pattern implies that there has been an overall increase in energy efficiency, because as we mentioned earlier some increment of energy increase is always required for any increment of economic production. Such an increase in overall efficiency could result from technological improvements in the efficiency of the energy transformation processes or from the rotation of economic production into less energy intensive industries, e.g., a shift from heavy industry and manufacturing to information-based economic activities.

In this case, the hyperbolic function plus a constant explains almost as much of the variance in real GDP as is explained by the second order polynomial function and the two relationships are close enough that we will not attempt to distinguish definitively between them without further statistical analyses. However, we used the AIC to show that the three parameter second order polynomial model was indeed a better fit to the data than that supplied by the two parameter models, which in most cases was a power function (Tables 4 and 6). Also, AIC was used to confirm that the three parameter hyperbolic plus a constant model was best when compared to competing two parameter models, i.e., those with lower R², in Table 5. Thus, AIC confirmed that the three parameter models provided a better fit of the data on energy consumption measures to real and nominal GDP based on information theoretic criteria.

Empirical confirmation of the functional relationships

Data showing decreased CO₂ emissions from fossil fuels and cement manufacture in the U.S. economy from 2000 to 2012 (Oliver et al., 2013) confirmed the observations from our mathematical and statistical analyses of energy consumption as a function of the measures of economic activity. Thus, we can say that our analysis indicates and the observed data on U.S. CO₂ emissions confirms that there has been and may continue to be scope for implementing policies that reduce the intensity of fossil energy consumption and concomitant CO₂ emissions while still maintaining some scope for growth in real GDP.

The Relationship between Economic and Emergy Measures of Real Wealth

Making allowance for the perturbations listed earlier, the data show that real GDP in chained 2000 $ increased in a near linear manner (R² = 0.979) as a function of total emergy used from 1900 to 2011 (Figure 10B). Thus, real GDP, the economic measure of real wealth, was almost a linear function (a power law fit was somewhat better, explaining an additional 1.24% of the variance) of total emergy use, which purports to be real wealth itself. However, the ratio of total emergy use to real GDP in chained 2000 $ (Figure 9A) declined monotonically from 1902 to 2011 in a near linear manner (the difference in the amount of variance explained between the power law best fit and a linear fit was 3.14%). This occurred because both flows increased over the time period, but real GDP increased at a faster rate (31X versus 11X). Thus, real GDP, the economic measure of “real wealth” appeared to still contain residual inflation compared with the emergy measure of real wealth. Residual inflation in real GDP is particularly apparent during WWII and in the period from 1982 to 2000. This implies that the economic system may have a bias toward structural inflation built into its inflation free measure. Such a bias, if it exists, would discourage unproductive hoarding of money and work toward keeping real wealth (emergy) flowing in the economy. An alternative explanation is that the economic measure (real GDP) maybe capturing a progressively increasing real wealth inflow not well measured by the current emergy methods, e.g., the increasing emergy of information delivered in the work of people (Campbell et al., 2011; Campbell and Lu, 2014).

The Significance of Changes in the Emergy to Money Supply Ratios

The Monetary Control Act of 1980 gave the Federal Reserve the reporting requirements that it needed to more accurately control the growth of the M1 money supply. Returning to Watt’s model above, we note that fiscal policy and adjustment of the money supplies has been a primary tool to control economic activity, at least since 1980. These policies seem to have worked as evidenced by the fact that the M1 money supply and the ratio of total emergy use to M1 remained relatively constant from 1987 to 2007. Over this time, the EMR of the M1 money supply declined 0.2% per annum, whereas, the EMR of nominal GDP declined 2.0% per annum. In comparison, the EMR of real GDP declined only 0.09% per annum over this time, which illustrates the efficacy of the Federal Reserve’s monetary policy. In addition, the closer tracking of real GDP attained through controlling the M1 money supply may explain, in part, the close proportional relationship of total emergy use (growth rate 3.9% per annum) and real GDP (growth rate 4.0% per annum) observed between 1987 and 2007. These observations imply that the Federal Reserve’s policy to control the M1 money supply to counter inflation worked.

In contrast, the ratios of total emergy use to the M2 and M3 money supplies only remained stable from 1986 to 1997 and then began to decline, showing a departure between these two measures and the flows of real wealth in the economy. This decline was particularly apparent for M3, which by 2007 had approached nominal GDP in its magnitude. The expansion of the M3 money supply, the broadest measure of easily available money in the U.S. economy, indicated that inflationary pressures were building from 1997 to 2007 that may have contributed to the speculative “bubble” of lending and construction shown in the material use data, which along with ill-conceived banking practices and other factors (Stiglitz, 2010) resulted in GR08.

In retrospect, we can see that controlling the M1 money supply alone does not tell the whole story of what is needed to control inflation in an economy. In addition, the velocity of money must be considered. Whereas, inflation is clearly seen in the M3 money supply leading up to GR08, the M1 is apparently stable, but when the velocity of money is considered, a strong inflationary pressure in the total flow of M1 is evidenced by the increasing velocity of money. The velocity of M1 increased 4.5% per annum from 1993 to 2007 followed by a precipitous decline in the rate of spending after 2007. Apparently, increased circulation of M1, even while the overall quantity of M1 was being held constant, resulted in a run-up in the EMR for real GDP from 2003 to 2007.

Energy Consumption Versus Emergy Use as a Means to Explain Economic Activity

In theory, total emergy use is a more complete measure of activity in a socioeconomic system than energy consumption alone, simply because it contains information on the inputs driving economic production in addition to energy consumption (Figure 1). In fact, the magnitudes of the emergy inputs demonstrate that mineral and not energy inflows have been the largest emergy input to the U.S. since 1938. Thus, we consider the question, “Is there a fundamental difference between total emergy use and energy consumption measures in terms of their relationships to economic activity?” We have shown (Table 5) that apparently, the relationships of all measures of QA energy consumption as a function of nominal GDP appear to be governed by a hyperbolic function plus a constant. The operation of limiting-factor-related dynamics with regard to energy consumption as a function of nominal GDP, rather that the expected power law relationship is evidenced by the departure of the energy consumption data from a power law relationship for large values of nominal GDP, e.g., after 1996. In addition, the functional relationship that best described all energy consumption measures as a function of real GDP was a second order polynomial, which is a functional form consistent with the higher real or apparent energy transformation efficiencies implied by the hyperbolic plus a constant relationship found for energy consumption as a function of nominal GDP.

In contrast to energy consumption measures, the power law relationship for total emergy use with real GDP continues to hold over the period from 1996 until 2011 (Figure 13). This implies that total emergy use is capturing more of the factors responsible for the increase in real GDP than the energy consumption measures alone. Since the difference between economic and social activities and energy use before and after the introduction of the personal computer (1977–1982) is apparently related to the magnitude and importance of information processing, it is logical that overall energy consumption measures will not reflect this transition completely because of the larger material and information resources now required to support this additional economic activity. However, certain aspects of energy consumption, such as the greater use of electric power to support information processing, may certainly be associated with this change (Cleveland et al., 2000). Nevertheless, the results of our analysis indicate that total emergy use more effectively quantifies the resource base supporting the GDP of the U.S. economy from 1982 to the present time, i.e., during the information age.

Comparison of Emergy and Economic Measures of Inflation

Over most of the time from 1900 to 2007, we found that there appeared to be a good overall correspondence between an economic measure of inflation, the CPI, and the EMR, a measure of inflation given in terms of real wealth, when the percent changes in the two indicators were compared from 1 year to the next. Variations in the EMR are closely tied to fluctuations in resource use, and therefore resource availability. Thus, the global recession of 1957–1958 that was characterized by restriction in resource imports is represented by a larger percent change in the EMR than in the CPI. Also, the characterization of the period from 1996 to 2011 leading up to and including GR08 is very different, when portrayed by the two indices (see Economic and Emergy Indices of Inflation and Changing System Structure). The EMR indicates that the inflationary and deflationary effects of GR08 on the U.S. economy were much greater than portrayed by economic measures of inflation and deflation, such as the CPI with the real wealth measure showing periods of mild to moderate deflation and strong inflation that are not detected by the CPI.

True Magnitude of the Great Recession of 2008

The true magnitude of GR08 can be gaged by comparing changes in the emergy use, energy consumption, and GDP numbers to similar changes during the GD. The percentage decline in the use of emergy to support the U.S. economy during GR08 (measured from the year before the event began to its low point) was 70% of the decline experienced during the GD, whereas, the absolute magnitude of the GR08 decline was 3.35 times greater than that seen in the GD. During GR08, the relative change in energy consumption as measured by Emergy QA was 108% of that experienced during the GD and the absolute value of the change was 11 times greater. In contrast, changes in economic activity characterize GR08 as a much milder event relative to the GD. For example, the percent change in nominal GDP during GR08 was only 0.86% that of the GD and the absolute magnitude of the event was 1.22 times greater. Real GDP gives a similar picture with the relative change in the indicator being 12.8% that of the GD and the absolute magnitude of the event 1.8 times that of the GD. In terms of the decline in real wealth supporting the U.S. economy, GR08 has been a much stronger event than is commonly understood from the changes in real and nominal GDP. Unemployment in the U.S. economy may be a more accurate indicator of the decline in real wealth associated with GR08. For example, in 2008, the U.S. Bureau of Labor Statistics reported an official unemployment rate of 10%, which is 62.3% of the average unemployment (1929–1941) for the time of the GD.

Structural Change in the U.S. Economy and the Future

A transition period (1974 to 1982–3) occurred shortly after the peak in conventional oil production in the U.S. (1970) predicted by Hubbert (1949). Political conditions in the world were rapidly changing at this time. The Iranian Revolution of 1979 following the Arab oil embargo of 1974 further raised the specter of oil limits on U.S. economic productivity. At the same time, the inflationary period of the 1970s was being brought under control by the Federal Reserve’s tight money policy under the direction of Paul Volker. By 1985, investment was flowing again and the nuclear power industry, which had not added much new capacity during the 70s, was adding to electricity production. Coal-fired power plants were also being built and petroleum consumption declined as these two increasing sources of electric power provided more of the energy supporting the U.S. economy. Thus, this transition time corresponds to a de facto shift in the energy policy of the U.S. toward greater reliance on electric power. After 1983, real GDP appears to be a better index of real wealth (i.e., total emergy use), possibly because the emergy inputs to the U.S. economy became more diverse, and therefore, were less dominated by the emergy of the energy sector. Also, changes in the structure of the energy sector reinforced this correspondence, because the changes allowed more of the real wealth in that sector to be tracked by the economy, e.g., electricity contains more human work as a fraction of the total emergy required for its production than petroleum (Bastianoni et al., 2009). In addition, a larger fraction of petroleum use was imported.

This transition period also corresponds to the start of the period of rapid growth in the use of computers and eventually the internet (Day et al., 2005), which in turn is a marker for the socioeconomic transition to the information age. In addition to the dawn of the information age, this transition period in the structure of the energy and emergy basis of the U.S. economy also marks the beginning of the emergence of the U.S. as a nation dependent on imports.

As the Great Recession ends, the question arises, “Will GR08 become another transition point that heralds a structural change in the U.S. economy similar to what happened from 1978 to 1982 and after the GD?” Specifically, will GR08 initiate a transition away from the path of super-accelerated growth that has characterized U.S. economy from 1900 to 2011? Alternatively, will new fossil fuel extraction technologies such as horizontal drilling and fracking make sufficient fossil energy resources available to allow rapid growth to continue for a while longer?

In the long run, such rapid growth cannot continue indefinitely, because finite energy and material supplies will limit increase. The current emphasis on developing a more sustainable world system (United States Environmental Protection Agency (USEPA), 2011), i.e., one where energy and mineral resource use is balanced against the rate of resource depletion and the environmental damage caused by wastes, promises to lead toward a healthier and more prosperous future. The magnitude of the GR08 perturbation may be seen as a warning that the hour for successful implementation of wiser resource management, environmental, and fiscal policies is getting late, yet the results of our study give hope that it may not be too late to move toward a system with a slowing growth curve that focuses on improving system design and quality of life rather than continuing on a trajectory of super-accelerated growth that must ultimately fail. For a longer term perspective on the future, see Odum and Odum’s (2001) discussion of the “prosperous way down” and the description of the cycle of change in Campbell and Garmestani (2012).

In this study, the EMR was shown to be a measure of inflation and deflation in the U.S. economy in terms of the relationship of the flow of real wealth to money. We believe that the rates of decline in the various EMRs discussed in this paper could be used to inform adjustments to monetary policy that, in turn, could lead to a greater flow of real wealth in the U.S. economy; thereby, moving toward the integration of fiscal methods of management with those based on EST principles and biophysical measures such as emergy. Structurally, it can be good policy to build in modest inflation relative to real wealth. This provides an incentive to those that have money, to reinvest it in ways that will produce more emergy flow in the system (i.e., by increasing the productive use of both non-renewable and renewable resources). In our view, policies affecting the money supply, the inflation rate, and the velocity of money relative to the coupled emergy flows are all potentially important in providing information to maximize the flows of real wealth in society. Thus, we recommend that a suite of EMR ratios be designed to set robust monetary policies, i.e., policies that adjust money supplies, the velocity of money, and the inflation rate in a manner that allows the economy to maximize empower (Odum, 1996) through “real wealth building” work⁶.

Conclusion

In this paper, we used a conceptual model (Figure 1) and hypothesis testing (H₀ 1) to demonstrate that from 1900 to 2011, total emergy use has been more closely related to economic activity in the U.S. economy than measures of energy consumption. We used the same model to show that many environmental products and services are not coupled to money flows, and thus, relatively poor correlations between measures of conventional economic activity and emergy use may be expected, for less developed economies as proposed by Ko and Hall (2003).

We used a second conceptual model (Figure 2A) to demonstrate the coupling between emergy use/energy consumption and economic activity, which explains why establishing causality with Granger-related methods has been difficult. As an alternative means of investigating causality within the web of resource and money flows in a developed economy, we suggested performing sensitivity analyses on calibrated ESL simulation models as a way to quantify causality by observing the relative effects of changes in money, energy, and emergy inputs on the storages and flows within the system. We used a third conceptual model of dynamic growth within a system running on excess resources (Figure 2B) and hypothesis testing (H₀ 3) to develop evidence that supports the hypothesis that a third power law based on cooperation to promote growth has governed the increase in U.S. nominal GDP from 1900 to 2011.

We evaluated pairs of variables using linear and non-linear regression methods to better understand the functional relationships between measures of economic activity and measures of energy consumption and total emergy use and vice versa. The major conclusions from the pair-wise analysis are as follows: (1) We used linear regression and hypothesis testing (H₀ 2) to demonstrate that the emergy of energy consumption (Emergy QA) was an appropriate measure of QA energy consumption. (2) Using non-linear regression, we showed that a second order polynomial function provided the best fit for all energy consumption measures as a function of real GDP; indicating that, over the past 18 years, energy conservation measures or changes in the mix of economic activities in the U.S. economy have been effective in decreasing energy consumption per unit of real GDP growth. This result was confirmed by data on the decline in U.S. emissions of CO₂ from 2000 to 2012. (3) Energy consumption measures deviated from a power law relationship for large values of both nominal and real GDP, but emergy use maintained a power law relationship with both measures of economic activity over the entire time examined, indicating that total emergy use may be a better indicator of the requirements for economic growth in the information age. (4) The economic measure, real GDP, was found to have a near linear relationship with total emergy use (real wealth) over the 112 year period examined. However, its EMR (total emergy use/real GDP) showed a trend that contained residual inflation over this time.

The EMR was used to characterize major socioeconomic events occurring in the U.S. from 1900 to 2011 into periods of inflation and deflation in real wealth. In addition, we provided a table of emergy inputs to the U.S. economy from 1900 to 2011 along with the total emergy used, the nominal GDP, and the EMR for each year for use in future emergy analyses including those related to setting economic, fiscal, and environmental policies. To meet the need for integrated fiscal and biophysical methods of evaluating current economic conditions as called for by Watt, we recommend that variations of the EMR be used as a guide to inform adjustments to monetary policy with the goal of building real wealth and maximizing the nation’s empower. This might be accomplished by identifying periods of excessive inflation or deflation in real wealth, when a variety of policy adjustments may be needed.

Author Contributions

All authors made substantial contributions to the design of the work and interpretation of the data. Daniel Elliott Campbell and Hongfang Lu were responsible for the acquisition and analysis of data. All authors contributed to revision and the intellectual content of the paper and all approved the final version. All authors will be accountable for the work and will help ensure that any questions that may arise will be resolved.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This paper is tracking number ORD – 007002 of the U.S. EPA’s Office of Research and Development, National Health and Environmental Effects Research Laboratory, Atlantic Ecology Division. Glen Thursby identified the hyperbolic plus a constant function as the best fit for the relationship between energy consumed and nominal GDP and he provided the analysis of these relationships. Naomi Detenbeck, Cathy Wigand, and Brian Milstead of AED and three reviewers assigned by the journal provided helpful reviews and advice on improving this paper. Although the research in this paper was funded by the USEPA, it has not been subjected to Agency-level review; therefore, it does not necessarily reflect the views of the USEPA.

Supplementary Material

The Supplementary Material for this article can be found online at http://www.frontiersin.org/Journal/10.3389/fenrg.2014.00041/abstract

Footnotes

1. ^Real wealth is what a quantity of available energy, material or information can do when used in a system for its intended purpose as contrasted with its monetary value. For example, a given car will drive only so far on a liter of gas, regardless of the price paid at the pump. Emergy is a normalized measure of work potentials of all kinds when that work is done within its system, i.e., emergy measures real wealth.
2. ^In this paper, available energy refers to energy with the potential to do work or the work that can be done in relation to some ground state, also called exergy.
3. ^We use the abbreviation semj for solar emjoules as proposed by Scienceman (1992). Odum (1988) originally used sej as the abbreviation for solar emjoule; however, he abbreviated the generic unit emjoule as emj (Odum, 1996). An emjoule is a joule of available energy of one kind used in the past. If solar energy is used as the base unit, the unit of emergy is the solar emjoule (semj). Solar emjoules are solar equivalent joules (seJ) that have been used in the past; however, the term solar equivalent joule does not carry the meaning of past use.
4. ^Real GDP reflects the buying power of the dollar referenced to a base year, in this case 2000. “Chaining” uses pairs of years to determine the average quantities of goods and services that could be purchased by a dollar. The second year becomes the first year in the subsequent pair, thus the measure is said to be “chained.”
5. ^M1 funds are currency, traveler’s checks, and demand deposits such as checking account balances. M2 includes all the funds in M1 plus savings accounts and small denomination time deposits. M3 is the broadest measure of the money supply available in the U.S. economy and it includes M1 and M2 plus balances in institutional money market funds, large denomination time deposits of 100,000 or more, repurchase agreement liabilities of depository institutions on U.S. government and federal agency securities, in denominations of 100,000 or greater, and Eurodollars held in foreign banks by U.S. addresses.
6. ^Thinking in this research genre seems to be further advanced in terms of integrating energy measures with monetary policy to chart a sustainable future (Sgouridis, 2014). In our view, the next step after this paper would be to begin similar research using emergy, which provides a more complete biophysical basis for explaining economic activity.

References

Amiri, A., and Zibaei, M. (2012). Granger Causality Between Energy Use and Economic Growth in France with Using Geostatistical Models. Paper No. 36357 2012. Available at: http://mpra.ub.uni-muenchen.de/36357/1/MPRA_paper_36357.pdf MPRA

Google Scholar

Argabright, M. S., Cronshey, R. G., Helms, J. D., Pavelis, G. A., and Sinclair, H. S. Jr. (1996). Historical Changes in Soil Erosion, 1930-1992, the Northern Mississippi Valley Loess Hills. Natural Resources Conservation Service, Resource Economics and Social Sciences Division, Historical Notes Number 5. Washington, DC: U.S. Department of Agriculture.

Google Scholar

Ayres, R. U., Ayres, L. W., and Warr, B. (2003). Exergy, power and work in the US economy, 1900-1998. Energy 28, 219–273. doi: 10.1016/S0360-5442(02)00089-0

CrossRef Full Text | Google Scholar

Bastianoni, S., Campbell, D. E., Ridolfi, R., and Pulselli, F. M. (2009). The transformity of petroleum fuels. Ecol. Model. 220, 40–50. doi:10.1016/j.ecolmodel.2008.09.003

CrossRef Full Text | Google Scholar

Bastianoni, S., Campbell, D. E., Susani, L., and Tiezzi, E. (2005). The solar transformity of oil and petroleum natural gas. Ecol. Model. 186, 212–220. doi:10.1016/j.ecolmodel.2005.01.015

CrossRef Full Text | Google Scholar

Beaudreau, B. C. (2010). On the methodology of energy-GDP Granger causality tests. Energy 35, 3535–3539. doi:10.1016/j.energy.2010.03.062

CrossRef Full Text | Google Scholar

Brandt-Williams, S. L. (2002). Handbook of Emergy Evaluation, Folio #4, Emergy of Florida Agriculture. Gainesville, FL: Center for Environmental Policy, University of Florida, 40.

Google Scholar

Brandt-Williams, S. L., and Pillet, G. (2003). “Fertilizer co-products as agricultural emternalities: quantifying environmental services used in production of food,” in Emergy Synthesis 2, Theory and Application of the Emergy Methodology, eds M. T. Brown, H. T. Odum, D. R. Tilley, and S. Ulgiati (Gainesville, FL: Center for Environmental Policy, University of Florida), 327–338.

Google Scholar

Brobst, D. A. (1973). “Barite,” in United States Mineral Resources, USGS Professional Paper 820, eds D. A. Brobst and W. P. Pratt (Washington, DC: U.S. Government Printing Office), 75–84.

Google Scholar

Brown, M. T. (2003). “Resource imperialism: emergy perspectives on sustainability, international trade, and balancing the welfare of nations,” in Advances in Energy Studies: Reconsidering the Importance of Energy, eds. S. Ulgiati, M. T. Brown, M. Giampietro, R. A. Herendeen, and K. Mayumi (Padova: SGEditoriali), 135–149.

Google Scholar

Brown, M. T., and Ulgiati, S. (2002). Emergy evaluations and environmental loading of electricity production systems. J. Clean. Prod. 10, 321–334. doi:10.1016/S0959-6526(01)00043-9

CrossRef Full Text | Google Scholar

Brown, M. T., and Ulgiati, S. (2004). “Emergy analysis and environmental accounting,” in Encyclopedia of Earth, Vol. 2, ed. C. J. Cleveland (New York: Elsevier Inc.), 229–253.

Google Scholar

Buranakarn, V. (1998). Evaluation of Recycling and Reuse of Building Materials using Emergy Analysis Method. PhD. Dissertation. University of Florida, Gainesville, FL, 257.

Google Scholar

Campbell, D. E. (1998). Emergy analysis of human carrying capacity and regional sustainability: an example using the state of Maine. Environ. Monit. Assess. 51, 531–569. doi:10.1023/A:1006043721115

CrossRef Full Text | Google Scholar

Campbell, D. E. (2000). “A revised solar transformity for tidal energy received by the earth and dissipated globally: implications for emergy analysis,” in Emergy Synthesis Theory and Application of the Emergy Methodology, eds M. T. Brown, S. L. Brandt-Williams, D. Tilley, and S. Ulgiati (Gainesville, FL: Center for Environmental Policy, University of Florida), 255–263.

Google Scholar

Campbell, D. E. (2001). Proposal for including what is valuable to ecosystems in environmental assessments. Environ. Sci. Technol. 35, 2867–2873. doi:10.1021/es001818n

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Campbell, D. E. (2003). “Emergy analysis of the prehistoric global nitrogen cycle,” in Emergy Synthesis 2, Theory and Application of the Emergy Methodology, eds M. T. Brown, H. T. Odum, D. R. Tilley, and S. Ulgiati (Gainesville, FL: Center for Environmental Policy, University of Florida), 221–239.

Google Scholar

Campbell, D. E., Brandt-Williams, S. L., and Meisch, M. E. A. (2005a). Environmental Accounting Using Emergy: Evaluation of the State of West Virginia. Washington, DC: U.S. Environmental Protection Agency, 116.

Google Scholar

Campbell, D. E., Brandt-Williams, S. L., and Cai, T. T. (2005b). “Current technical problems in emergy analysis,” in Emergy Synthesis 3, Proceedings of the 3rd Biennial Emergy Research Conference, eds M. T. Brown, E. Bardi, D. E. Campbell, V. Comar, S.-L. Huang, T. Rydberg, et al. (Gainesville, FL: Center for Environmental Policy, University of Florida), 143–157.

Google Scholar

Campbell, D. E., and Cai, T. T. (2007). “Emergy and economic value,” in Emergy Synthesis 4, Theory and Applications of the Emergy Methodology, Proceedings of the 4th Biennial Emergy Research Conference, eds M. T. Brown, E. Bardi, D. E. Campbell, S.-L. Huang, E. Ortega, T. Rydberg, et al. (Gainesville, FL: Center for Environmental Policy, University of Florida), 483.

Google Scholar

Campbell, D. E., and Garmestani, A. S. (2012). An energy systems view of sustainability: emergy evaluation of the San Luis Basin, Colorado. J. Environ. Manage. 95, 72–97. doi:10.1016/j.jenvman.2011.07.028

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Campbell, D. E., and Lu, H. F. (2009). “The emergy to money ratio of the United States from 1900 to 2007,” in Emergy Synthesis 5, Theory and Applications of the Emergy Methodology, Proceedings of the 5th Biennial Emergy Research Conference, eds M. T. Brown, S. Sweeney, D. E. Campbell, S.-L. Huang, E. Ortega, T. Rydberg, et al. (Gainesville, FL: Center for Environmental Policy, University of Florida), 413–448.

Google Scholar

Campbell, D. E., and Lu, H. F. (2014). Emergy evaluation of formal education in the United States: 1870 to 2011. Systems 2, 328–365. doi:10.3390/systems2030328

CrossRef Full Text | Google Scholar

Campbell, D. E., Lu, H. F., and Kolb, K. (2011). “Emergy evaluation of educational attainment in the United States,” in Emergy Synthesis 6: Theory and Applications of the Emergy Methodology, Proceedings of the 6th Biennial Emergy Research Conference, eds M. T. Brown, S. Sweeney, D. E. Campbell, S.-L. Huang, E. Ortega, T. Rydberg, et al. (Gainesville, FL: Center for Environmental Policy, University of Florida), 483–500.

Google Scholar

Campbell, D. E., Lu, H. F., and Lin, B.-L. (2014). Emergy evaluations of the global biogeochemical cycles of six biologically active elements and two compounds. Ecol. Model. 271, 32–51. doi:10.1016/j.ecolmodel.2013.01.013

CrossRef Full Text | Google Scholar

Campbell, D. E., and Ohrt, A. (2009). Environmental Accounting Using Emergy: Evaluation of Minnesota. Washington, DC: U.S. Environmental Protection Agency, 137.

Google Scholar

Canadell, J. G., and Mooney, H. A. (2002). “Biological and ecological dimensions of global environmental change (in volume: the earth system biological and ecological dimensions of global environmental change),” in Encyclopedia of Global Environmental Change, eds H. A. Mooney, J. G. Canadell, and T. Munn (Chichester: John Wiley & Sons), 1–9. Available at: http://www.globalcarbonproject.org/global/pdf/pep/Canadell&Mooney2001.pdf

Google Scholar

Cleveland, C. J., Costanza, R., Hall, C. A. S., and Kaufmann, R. (1984). Energy and the United States economy: a biophysical perspective. Science 225, 890–897. doi:10.1126/science.225.4665.890

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Cleveland, C. J., Kaufmann, R. K., and Stern, D. I. (2000). Aggregation and the role of energy in the economy. Ecol. Econ. 32, 301–317. doi:10.1016/S0921-8009(99)00113-5

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Cohen, M. J., Sweeney, S., and Brown, M. T. (2007). “Computing the unit emergy value of crustal elements,” in Emergy Synthesis 4: Theory and Applications of the Emergy Methodology. Proceedings of the Fourth Biennial Emergy Conference, eds M. T. Brown and E. Bardi (Gainesville, FL: Center for Environmental Policy, Department of Environmental Engineering Sciences, University of Florida), 16to–11to.

Google Scholar

Day, J. C., Janus, A., and Davis, J. (2005). “Computer and internet use in the United States: 2003,” in Special Studies, U.S. Census Bureau, U.S., Economics and Statistics Administration (Washington, DC: U.S. Census Bureau). Available at: http://benton.org/sites/benton.org/files/internetuse2003.pdf

Google Scholar

Granger, C. W. J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37, 424–438. doi:10.2307/1912791

CrossRef Full Text | Google Scholar

Hall, C. A. S., Cleveland, C. J., and Kauffmann, R. K. (1986). Energy and Resource Quality: The Ecology of the Economic Process. New York: Wiley-InterScience.

Google Scholar

Hall, C. A. S., Lambert, J. G., and Balogh, S. B. (2014). EROI of different fuels and the implications for society. Energy Policy 64, 141–152. doi:10.1016/j.enpol.2013.05.049

CrossRef Full Text | Google Scholar

Huang, B.-N., Hwang, M. J., and Yang, C. W. (2008). Causal relationship between energy consumption and GDP growth revisited: a dynamic panel data approach. Ecol. Econ. 67, 41–54. doi:10.1016/j.ecolecon.2007.11.006

CrossRef Full Text | Google Scholar

Hubbert, M. K. (1949). Energy from fossil fuels. Science 109, 103–109. doi:10.1126/science.109.2823.103

CrossRef Full Text | Google Scholar

Ko, J. Y., and Hall, C. A. S. (2003). “The correlation between GDP and both energy use and emergy use,” in Emergy Synthesis 2: Theory and Applications of the Emergy Methodology, Proceedings of the Second Biennial Emergy Conference, eds M. T. Brown, H. T. Odum, D. Tilley, and S. Ulgiati (Gainesville, FL: Center for Environmental Policy, Department Environmental Engineering Sciences, University of Florida), 51–60.

Google Scholar

Lee, C.-C. (2006). The causality relationship between energy consumption and GDP in G-11 countries revisited. Energy Policy 34, 1086–1093. doi:10.1016/j.enpol.2005.04.023

CrossRef Full Text | Google Scholar

Lotka, A. J. (1922a). Contribution to the energetics of evolution. Proc. Natl. Acad. Sci. U.S.A. 8, 147–151. doi:10.1073/pnas.8.6.147

CrossRef Full Text | Google Scholar

Lotka, A. J. (1922b). Natural selection as a physical principle. Proc. Natl. Acad. Sci. U.S.A. 8, 151–154. doi:10.1073/pnas.8.6.151

CrossRef Full Text | Google Scholar

Lu, H. F., Campbell, D. E., Chen, J., Qin, P., and Ren, H. (2007). Conservation and economic viability of nature reserves: an emergy evaluation of the Yancheng biosphere reserve. Biol. Conserv. 139, 415–438. doi:10.1016/j.biocon.2007.07.014

CrossRef Full Text | Google Scholar

Marceau, M. L., Nisbet, M. A., and VanGeem, M. G. (2006). Life Cycle Inventory of Portland Cement Manufacture. Portland Cement Association R&D Serial No. 2095b. 68. Available at: http://www.nrmca.org/taskforce/item_2_talkingpoints/sustainability/sustainability/sn2095b%20-%20cement%20lci%202006.pdf

Google Scholar

Menegaki, A. N. (2014). On energy consumption and GDP studies; a meta-analysis of the last two decades. Renew. Sustain. Energ. Rev. 29, 31–36. doi:10.1016/j.rser.2013.08.081

CrossRef Full Text | Google Scholar

Morandi, F., Campbell, D. E., and Bastianoni, S. (2014). Set theory applied to uniquely to define the inputs to territorial systems in emergy analyses. Ecol. Model. 271, 149–157. doi:10.1016/j.ecolmodel.2013.01.005

CrossRef Full Text | Google Scholar

Morandi, F., Campbell, D. E., Pulselli, R. M., and Bastianoni, S. (2013). Using the language of sets to describe nested systems in emergy evaluations. Ecol. Model. 265, 85–98. doi:10.1016/j.ecolmodel.2013.06.006

CrossRef Full Text | Google Scholar

Narayan, P. K., and Popp, S. (2012). The energy consumption-real GDP nexus revisited: empirical evidence from 93 countries. Econ. Model. 29, 303–308. doi:10.1016/j.econmod.2011.10.016

CrossRef Full Text | Google Scholar

National Resources Conservation Service (NRCS). (2010). 2007 National Resources Inventory, Soil Erosion on Cropland. Available at: http://www.nrcs.usda.gov/Internet/FSE_DOCUMENTS/nrcs143_012269.pdf

Google Scholar

Neame, K. D., and Richards, T. G. (1972). Elementary Kinetics of Membrane Transport. New York: John Wiley & Sons.

Google Scholar

Nepal, S., and Campbell, E. (2013). “Emergy evaluation of landfills for methane generation, recoverability, and sustainability,” in Emergy Synthesis 7: Theory and Applications of the Emergy Methodology, Proceedings of the 7th Biennial Emergy Research Conference, eds M. T. Brown, S. Sweeney, D. E. Campbell, S.-L. Huang, D. Kang, T. Rydberg, et al. (Gainesville, FL: Center for Environmental Policy, University of Florida), 197–210.

Google Scholar

Nicolis, G., and Prigogine, I. (1977). Self Organization in Non-equilibrium Systems. New York: John Wiley & Sons.

Google Scholar

Odum, H. T. (1986). “Emergy (sic) in ecosystems,” in Ecosystem Theory and Application, ed. N. Polunin (New York: John Wiley & Sons), 337–369.

Google Scholar

Odum, H. T. (1988). Self organization, transformity, and information. Science 242, 1132–1139. doi:10.1126/science.242.4882.1132

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Odum, H. T. (1996). Environmental Accounting, Emergy and Environmental Decision Making. New York: John Wiley & Sons, 370.

Google Scholar

Odum, H. T. (2002). “Material circulation, energy hierarchy, and building construction,” in Construction Ecology, eds C. J. Kibert, J. Sendzimir, and G. B. Guy (London: SPON Press), 37–71.

Google Scholar

Odum, H. T., and Odum, E. C. (2000). Modeling for all Scales: An Introduction to System Simulation. San Diego: Academic Press.

Google Scholar

Odum, H. T., and Odum, E. C. (2001). A Prosperous Way Down, Principles and Policies. Boulder: University of Colorado Press, 326.

Google Scholar

Odum, H.T. (1983). System Ecology: an Introduction. New York: Wiley, 644 [Reprinted (1994) as Ecological and General Systems. Boulder: University Press of Colorado].

Google Scholar

Oh, W., and Lee, K. (2004). Causal relationship between energy consumption and GDP revisited; the case of Korea 1970-1999. Energy Econ. 26, 51–59. doi:10.1016/S0140-9883(03)00030-6

CrossRef Full Text | Google Scholar

Oliver, J. G. J., Janssens-Maenhout, G., Muntean, M., and Peters, J. A. H. W. (2013). Trends in global CO₂ emissions: 2013 Report. The Hague: PBL Netherlands Environmental Assessment Agency, European Commission Joint Research Centre. Available at: http://www.pbl.nl/en/publications/trends-in-global-co2-emissions-2013-report

Google Scholar

Paoli, C., Vassallo, P., and Fabiano, M. (2008). Solar power: an approach to transformity evaluation. Ecol. Eng. 34, 191–206. doi:10.1016/j.ecoleng.2008.08.005

CrossRef Full Text | Google Scholar

Patterson, M. G. (2012). Are all processes equally efficient from an emergy perspective? Analysis of ecological and economic networks using matrix algebra methods. Ecol. Model. 226, 77–91. doi:10.1016/j.ecolmodel.2011.11.016

CrossRef Full Text | Google Scholar

Pritchard, L. (2000). “Appendix A11B: transformities used in calculations,” in Heavy Metals in the Environment, Using Wetlands for their Removal, ed. H. T. Odum (Boca Raton, FL: Lewis Publishers), 261–268.

Google Scholar

Scienceman, D. M. (1987). “Energy and emergy,” in Environmental Economics, eds G. Pillet and T. Murota (Geneva: Roland Leimgruber), 257–276.

Google Scholar

Scienceman, D. M. (1992). “Emvalue and lavalue,” in General Systems Approaches to Alternative Economics and Values, Proceedings of the Twenty-Sixth Annual Meeting, International Society for the Systems Sciences (ISSS), ed. L. Peeno (Denver, CO: ISSS), 848–858.

Google Scholar

Sgouridis, S. (2014). Defusing the energy trap: the potential of energy-denominated currencies to facilitate a sustainable energy transition. Front. Energy Res. 2:1–11. doi:10.3389/fenrg.2014.00008

CrossRef Full Text | Google Scholar

Sims, C. (1972). Money, income, and causality. Am. Econ. Rev. 62, 540–552.

Google Scholar

Smith, C. C. (1976). When and how to reproduce, the tradeoff between power and efficiency. Am. Zool. 16, 763–764.

Google Scholar

Soytas, U., and Sari, R. (2003). Energy consumption and GDP: causality relationship in G-7 countries and emerging markets. Energy Econ. 25, 33–37. doi:10.1016/S0140-9883(02)00009-9

CrossRef Full Text | Google Scholar

Stern, D. I. (1993). Energy use and economic growth in the USA, a multivariate approach. Energy Econ. 15, 137–150. doi:10.1016/0140-9883(93)90033-N

CrossRef Full Text | Google Scholar

Stern, D. I. (2000). A multivariate cointegration analysis of the role of energy in the US macroeconomy. Energy Econ. 22, 267–283. doi:10.1016/S0140-9883(99)00028-6

CrossRef Full Text | Google Scholar

Stiglitz, J. E. (2010). Freefall: America, Free Markets, and the Sinking of the World Economy. New York: W.W. Norton, 441.

Google Scholar

Tilley, D. R. (2006). National metabolism and communications technology development in the United States: 1790 to 2000. Environ. Hist. Camb. 12, 165–190. doi:10.3197/096734006776680227

CrossRef Full Text | Google Scholar

U.S. Department of Agriculture (USDA). (2009). Summary Report: 2007 National Resources Inventory, Natural Resources Conservation Service. Washington, DC: Center for Survey Statistics and Methodology. [Ames, Iowa: Iowa State University, 123. This is an active site with similar information to (S1) and (S2)]. Available at: http://www.nrcs.usda.gov/Internet/FSE_DOCUMENTS/stelprdb1041379.pdf

Google Scholar

United States Environmental Protection Agency (USEPA). (2011). Strategic Sustainability Performance Plan, FY 2010 – FY 2020. Washington, DC: USEPA. Available at: http://www.epa.gov/oaintrnt/documents/sspp2011.pdf

Google Scholar

Von Foerster, H., Mora, P. M., and Amoit, L. W. (1960). Doomsday: Friday, 13 November, A.D. 2026. Science 132, 1291–1295. doi:10.1126/science.132.3436.1291

CrossRef Full Text | Google Scholar

Watt, K. E. F. (1994). Letters to the editor. Ecol. Eng. 3, 83. doi:10.1016/0925-8574(94)90025-6

CrossRef Full Text | Google Scholar

Weast, R. C. (1981). CRC Handbook of Chemistry and Physics. Boca Raton, FL: CRC Press Inc.

Google Scholar

Yildirim, E., Sukruoglu, E., and Aslan, A. (2014). Energy consumption and economic growth in the next 11 countries: the bootstrapped autoregressive metric causality approach. Energy Econ. 44, 14–21. doi:10.1016/j.eneco.2014.03.010

CrossRef Full Text | Google Scholar